Open Access Article
Open Access ArticleDisentangling the structure, optical properties, and photoluminescence emissions of NiW1−xMoxO4 (x = 25, 50, and 75%) solid solutions: experimental and DFT studies†
Amanda Fernandes
Gouveia
 *a,
Marcelo
Assis
*a,
Marcelo
Assis
 ab,
Lara Kelly
Ribeiro
ab,
Lara Kelly
Ribeiro
 ac,
Eduardo de Oliveira
Gomes
a,
Marcio Daldin
Teodoro
d,
Elson
Longo
ac,
Eduardo de Oliveira
Gomes
a,
Marcio Daldin
Teodoro
d,
Elson
Longo
 c and
Juan
Andrés
c and
Juan
Andrés
 *a
*a
aDepartment of Physical and Analytical Chemistry, Universitat Jaume I, Castelló 12071, Spain. E-mail: gouveiad@uji.es; andres@qfa.uji.es
bDepartment of Biosciences, Institute of Health and Society, Universidade Federal de São Paulo, Santos 11015-020, Brazil
cCDMF, Universidade Federal de São Carlos, São Carlos 13565-905, Brazil
dPhysics Department, Universidade Federal de São Carlos, São Carlos 13565-905, Brazil
First published on 24th February 2025
Abstract
Solid solutions, formed by combining two transition metal oxides with distinct properties, offer promising potential for optimizing functional characteristics that may be lacking in the parent materials. In this study, NiWO4 and NiMoO4 semiconductors and homogeneous NiW1−xMoxO4 (x = 25, 50, and 75%) solid solutions were successfully synthesized via a co-precipitation method followed by heat treatment, without any surfactants or toxic solvents. Using a combination of characterization techniques—including X-ray diffraction, Raman and infrared spectroscopy, X-ray fluorescence, diffuse reflectance spectroscopy, and photoluminescence (PL) spectroscopy—alongside density functional theory calculations, we elucidate the relationship between the structure, electronic properties, and PL emissions at the atomic level. Furthermore, we propose a relay mechanism in the conduction band, where an electron transport ladder through the Ni–O–W/Mo framework acts as a driving force to modulate PL emissions.
1 Introduction
Solid solutions composed of complex metal oxides are integral to modern semiconductor technology, with applications ranging from sensor to catalysis.1–4 This extended multifunctionality arises from the synergistic effects induced by the coexistence of multiple metal cations, partially filled d orbitals, and highly electronegative oxygen anions. Tungstates and molybdates (MWO4 and MMoO4, where M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn, Co, Ni, Zn, and Cu) hold immense potential in the field of inorganic semiconductors due to their unique physical–chemical properties.5–12
Mn, Co, Ni, Zn, and Cu) hold immense potential in the field of inorganic semiconductors due to their unique physical–chemical properties.5–12
Among these semiconductors, nickel tungstate (NiWO4, NW) and nickel molybdate (NiMoO4, NM) exhibit structural stability as well as interesting electronic and electrochromic properties,13,14 which form the basis for a wide range of applications, including catalysts, photovoltaic electrochemical cells, electrocatalytic oxygen evolution reactions, and sensors, among others.15–24 Both NW and NM are characterized by a monoclinic phase and consist of mixed-valence transition metal oxides, in which Ni2+ and W6+/Mo6+ occupy octahedral sites. More specifically, NW crystallizes in the P2/c space group and C2h point group symmetry, featuring [NiO6] and [WO6] clusters.7 In turn, NM belongs to the C2/m space group, also with C2h point group symmetry, but with [NiO6] and [MoO6] clusters.25 This structural similarity suggests that the formation of a solid solution should be easily achievable, resulting in distinct properties compared to the pure systems. Furthermore, to the best of our knowledge, there are no reports in the literature on the successful preparation of a continuous NiW1−xMoxO4 solid solution with a monoclinic structure across the entire compositional range.
Previous experimental and theoretical investigations of solid solutions composed of tungstates26–31 and molybdates32,33 have provided a deep understanding of the structural and electronic property changes, helping to rationalize the design of new optical and photocatalytic materials, which are sometimes absent in the parent materials.
Specifically, Ag2W0.50Mo0.50O428 and α-Ag2W0.75Mo0.25O429 solid solutions have demonstrated that these systems exhibit unique photoluminescence (PL) emissions with higher intensities than those of single-structured, α-Ag2WO4 and β-Ag2MoO4.34 Delving deep into the evolution of the structure and electronic properties when metal cations are substituted during the formation of metal oxide solid solutions, as well as managing the relationship between the crystal structure and PL emissions, is crucial for targeted applications.33,35 Although precise regulation of the spatial distribution of the dopant in the host lattice is an effective method to improve their properties, the experimental determination and the corresponding mechanisms involved in this process are still unclear. Theoretical investigations can greatly aid in paving the way for the rational design of novel materials with optimal composition and enhanced performance. Therefore, it is desirable and necessary to use not only characterization techniques but also advanced quantum-chemical calculation methods to further deepen the understanding of the physiochemical processes occurring during the formation of these complex solid solutions.
The considerations above led us to synthesize complex quaternary NiW1−xMoxO4 (x = 25, 50, and 75) solid solutions using a co-precipitation (CP) method, followed by heat treatment in a conventional oven, without the need for expensive surfactants or toxic solvents.
The synthesized materials were characterized using X-ray diffraction (XRD), Raman and infrared spectroscopy, X-ray fluorescence (XRF), scanning electron microscopy (SEM), ultraviolet-visible (UV-vis) diffused reflectance spectroscopy, and PL spectroscopy. These techniques were employed to evaluate the effects of W6+ substitution by Mo6+ into the NiWO4 crystal structure, as well as its impact on the morphology, energy band structure, and PL emissions. Additionally, density functional theory (DFT) calculations were performed to investigate the geometry, band structure, and density of states (DOS) in detail.
The main aims of the study were twofold: (i) to investigate the local bonding patterns of [NiO6], [WO6], and [MoO6] clusters and unveil the multicentric bonding character during the substitution process in NiW1−xMoxO4 (x = 25, 50, and 75%) solid solutions, and (ii) to model these phenomena in greater detail to gain deep insights into the structure, electronic properties, and PL emissions during the solid solution formation. These findings provide both experimental references and theoretical support for the design of these promising materials for optical applications.
2 Results and discussion
2.1 Structural analysis
The XRD patterns of the as-synthetized samples are presented in Fig. 1a. For both NW and NM, pure phases of their respective materials were obtained, and the diffractograms were analyzed based on the available crystallographic data for NW (ICSD No. 15852)36 and NM (ICSD No. 450142).37 Both NW and NM exhibit a monoclinic crystal structure, with NW crystallizing in the P2/c space group and NM in C2/m. The NW structure comprises each chain of [NiO6] clusters which is corner linked to four chains of [WO6] clusters, and vice versa, creating open channels along the [001] direction. In NM, Ni2+ and Mo6+ cations are also coordinated with six oxygen atoms, forming [NiO6] and [MoO6] clusters, but these clusters are interconnected via edge-sharing. As a result, the three-dimensional (3D) atomic packing in both NW and NM is nearly identical, with individual [NiO6], [WO6], and [MoO6] clusters connected to their neighboring [NiO6] and [MoO6/WO6] clusters through edge-sharing. In other words, in both the NW and NM crystal lattices, the [NiO6] and [MO6] clusters are linked via Ni–O–M bridging links (where M = W6+ or Mo6+).For the NW75 and NW50 samples, only peaks corresponding to the NW phase were detected by XRD. However, in the NW25 sample, some peaks corresponding to the NM phase were also detected, including (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ), (112), (040), (31
), (112), (040), (31![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ), and (421).
), and (421).
Moreover, local stress and strain are generated due to the unit cell volume difference between the P2/c and C2/m phases. In Fig. 1b, changes in full width at half maximum (FWHM) values in the range of 10 to 80° can be observed during the synthesis of solid solutions from NW to NM. A shift in the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11) plane, characteristic of the NW phase, occurs due to the incorporation of Mo6+ cations into the lattice. These shifts are observed at smaller θ values, indicating the expansion of the crystal lattice. Among the analyzed samples, NW75 exhibited the greatest structural expansion, with a θ FWHM value of 0.48°. A 3D representation of the monoclinic structures of both NM and NW is illustrated in Fig. 1c.
11) plane, characteristic of the NW phase, occurs due to the incorporation of Mo6+ cations into the lattice. These shifts are observed at smaller θ values, indicating the expansion of the crystal lattice. Among the analyzed samples, NW75 exhibited the greatest structural expansion, with a θ FWHM value of 0.48°. A 3D representation of the monoclinic structures of both NM and NW is illustrated in Fig. 1c.
The elemental analysis of W and Mo atoms, performed using XRF spectrometry, is presented in Table S1 of the ESI.† The results show that the compositions of both cations closely match the nominal values, confirming the formation of the NW75, NW50, and NW25 solid solutions.
To complement the experimental results, DFT calculations using the B3LYP and HSE06 functionals were performed to determine the changes in lattice parameters and β angle associated with the substitution process of W6+ by Mo6+ cations. An analysis of the results in Table 1 shows good agreement between the theoretical results and the experimental data, as well as consistency with previous experimental and theoretical results reported in the literature. Furthermore, the results indicate that the formation of a solid solution leads to an increase in the a, b, and c lattice parameters and β values, resulting in lattice expansion from NW to NM. These findings are consistent with the shift in the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11) peak observed earlier (see Fig. 1b).
11) peak observed earlier (see Fig. 1b).
| Model | B3LYP | HSE06 | Ref. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | b | c | β | ΔEf | a | b | c | β | ΔEf | ||
| a This work. | |||||||||||
| NW | 4.578 | 5.759 | 4.803 | 87.66 | −0.670 | 4.563 | 5.680 | 4.775 | 87.84 | −0.678 | |
| NW75 | 4.585 | 5.734 | 4.822 | 88.01 | −0.664 | 4.568 | 5.664 | 4.789 | 88.10 | −0.672 | |
| NW50 | 4.590 | 5.714 | 4.840 | 88.26 | −0.658 | 4.572 | 5.649 | 4.802 | 88.33 | −0.665 | |
| NW25 | 4.595 | 5.692 | 4.859 | 88.64 | −0.653 | 4.577 | 5.633 | 4.817 | 88.61 | −0.659 | |
| NM | 9.579 | 8.757 | 7.691 | 113.92 | −0.647 | 9.512 | 8.682 | 7.659 | 114.13 | −0.652 | |
| NWexp | 4.602 | 5.672 | 4.921 | 90.05 | — | 7 | |||||
| NWexp | 4.605 | 5.674 | 4.930 | 89.99 | — | 36 | |||||
| NWtheo | 4.578 | 5.759 | 4.803 | 87.64 | — | 7 | |||||
| NMexp | 9.564 | 8.732 | 7.648 | 114.26 | — | 38 | |||||
| NMtheo | 9.369 | 8.413 | 7.010 | 113.00 | — | 39 | |||||
The formation energy (ΔEf) of the pure materials and the solid solutions was calculated, and the corresponding values are also presented in Table 1. Negative values of ΔEf indicate greater stability of the crystal.40 The pure NW with a more negative ΔEf value exhibits greater stability compared to all solid solutions and pure NM.
In Fig. S1 and Table S2 of the ESI,† the calculated values of the Ni–O, W–O, and Mo–O bond distances, as well as the values of J–T distortion (σJT) for each [NiO6], [WO6] and [MoO6] cluster, which act as J–T active sites, are reported, obtained at the B3LYP level. Analysis of the results indicates that the geometric distortions of these clusters during the formation of solid solutions are minimal, i.e. low values of σJT. There are subtle changes in the local environment around the Ni2+, W6+, and Mo6+ cations. This result was anticipated, as the ionic radius (0.69 Å) and electronegativity (1.8) of the Mo6+ cation are similar to those of W6+ (0.66 Å and 1.7). An increase in the lattice parameter occurs only in NM due to the change in the point symmetry group, from P2/c to C2/m.
In our case, the 3d orbitals of the Ni2+ cation in the octahedral environment of the [NiO6] cluster split into two degenerated sets of orbitals: t2g orbitals (dxz, dyz, and dxy) and eg orbitals (dx2−y2 and dz2). The adjacent [WO6] and [MoO6] clusters induce slight geometrical distortion (corresponding to elongated or compressed octahedra) to minimize the overall energy of the system, i.e. J–T distortion.
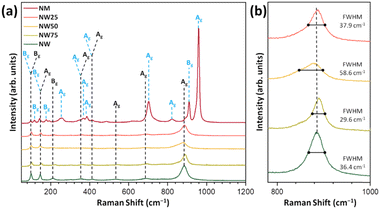
The Raman spectra of NW, NM, and solid solutions are presented in Fig. 2. According to group theory, 36 distinct Raman vibrational modes are present in these structures, of which 18 are expected to be active modes (8Ag + 10Bg). As shown in Fig. 2a, the NW exhibits Raman modes at ≈100, 149, 416, 537, 695, and 885 cm−1. The Bg vibrational mode at 100 cm−1 with a low intensity is associated with the symmetric bending of O–Ni–O.41
The most intense mode at 884 cm−1 (Ag mode) corresponds to the symmetric stretching of the W–O bond in the [WO6] cluster.42 The Raman modes at 100, 140, 255, 368, 385, 704, 824, 911, and 960 cm−1 are associated with NM. The weakly intense mode below 500 cm−1 corresponds to the Raman-active Ni–O bond in the [NiO6] clusters.
Regarding the Mo–O bond in the [MoO6] clusters, the strongest band at 960 cm−1 represents symmetric stretching, while the vibration signals at 824 cm−1 and 811 cm−1 correspond to asymmetric stretching.20
The FWHM values for the most intense Raman mode at 884 cm−1, present in NW and NW75, NW50, and NW25 solid solutions, are 36.4, 29.6, 58.6, and 37.9 cm−1, respectively (see Fig. 2b). Consequently, the NW50 sample exhibits a slight structural disorder in a short-range. The substitution of W6+ by Mo6+ may adjust the distortion of the local environment of the [MoO6] cluster and self-adapt the different structures of solid solutions. The relationship between this structural disorder, the composition of the conduction band (CB), and PL emissions will be discussed in the following sections.
The theoretical Raman spectra obtained at the B3LYP level are presented in Fig. 3a.
As observed experimentally (Fig. 2), the most intense peak in the NW structure, located at 867 cm−1 (Ag mode), shifts with the increasing incorporation of Mo6+ cations. The Raman spectra in the 350–800 cm−1 range are highlighted in Fig. 3b. At 431 cm−1, a shift to a lower wavelength is observed with increasing Mo6+ content, corresponding to the O–Ni–O bending (Ag mode) in pure NW. Meanwhile, at 766 cm−1, the Ag mode associated with the Mo–O stretching in [MoO6] clusters, characteristic of the NM structure, appears only in the NW50 and NW25 solid solutions. These results demonstrate an excellent correlation between the theoretical and experimental Raman spectra.
The infrared spectra are shown in Fig. 4. NW75, NW50, and NW25 solid solutions presented the same spectral profile as the pure NW sample. The Au mode located at around 877 cm−1, corresponds to the symmetric stretching vibrations (O–W–O) in the distorted octahedral [WO6] clusters, while the band at 837 cm−1 is associated with the optical Bu mode. Another low-intensity band at 689 cm−1 can be attributed to the anti-symmetric stretching vibrations in the distorted octahedral [WO6] clusters. The band at 535 cm−1 corresponds to symmetric stretching vibrations (O–W–O–W–O) between [WO6]–[WO6] clusters. Additionally, the symmetric stretching vibrations (–O–Ni–O–) of the distorted octahedral [NiO6] clusters were detected at 470 and 450 cm−1.43
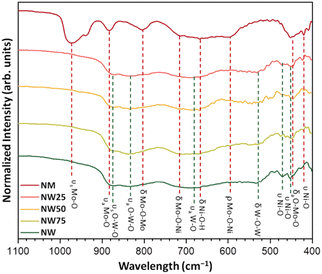 | ||
| Fig. 4 Infrared spectra of NW, NW75, NW50, NW25, and NM samples. The vertical lines indicate the positions and assignation of the active modes. | ||
2.2 Morphological analysis
Fig. 5 shows the morphology and the average particle size distribution of all samples obtained from SEM images. As observed, the NW sample (Fig. 5a) exhibits faceted morphologies: however, with the increasing incorporation of Mo6+ cations, the particles became agglomerated and lost their defined morphology, as seen in Fig. 5(c, e, and g). The pure NW sample has an average size of 97.3 nm, while the NM sample has an average size of 39.4 nm. | ||
| Fig. 5 SEM images and average particle size distribution for (a) and (b) NW, (c) and (d) NW75, (e) and (f) NW50, (g) and (h) NW25, and (i) and (j) NM samples. | ||
For the NW75, NW50, and NW25 solid solutions, the average particle sizes were 39.4, 36.5, and 35.2 nm, respectively. Thus, the formation of the solid solution results in a reduction in particle size. This phenomenon may be attributed to short- and long-range structural changes that increase the system's disorder, ultimately leading to a decrease in particle size.
2.3 Electronic properties, DOS, and PL emissions
The diffuse reflectance spectroscopy graphs are shown in Fig. 6, where the NW and NM samples exhibit band gap energies (Egaps) of 4.42 eV and 3.96 eV, respectively. The Egap values of solid solutions decrease as the Mo6+ content increases (see Fig. 6 and Table 2). The theoretical calculations at the B3LYP and HSE06 levels reveal that the electronic transitions between the valence band (VB) and CB exhibit an indirect band gap, with the corresponding K-points in the Brillouin zone listed in Table 2. From NW to NW25, the indirect transition in the α channel, for both functionals, occurs between the Z-point in the VB and the Y-point in the CB, with the only difference being the K-point in the VB for NM. Additionally, in the β channel, the transition occurs between the Y-point in the VB and a different k-point in the CB, depending on the system. The experimental and calculated Egap values for NW are higher than those for NM.| Model | Exp. | B3LYP | HSE06 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Direct (Γ–Γ) | Indirect | Direct (Γ–Γ) | Indirect | ||||||||||
| Alpha | Beta | Alpha | Beta | Alpha | Beta | Alpha | Beta | ||||||
| a Experimental. b Theoretical. | |||||||||||||
| NW | 4.42 | 4.33 | 3.60 | 3.95 | Z–Y | 3.54 | Y–B | 4.03 | 3.47 | 3.62 | Z–Y | 3.43 | Y–Γ |
| NW75 | 4.25 | 4.03 | 3.35 | 3.59 | 3.26 | 3.81 | 3.26 | 3.36 | 3.19 | ||||
| NW50 | 3.99 | 3.81 | 3.17 | 3.33 | 3.04 | 3.64 | 3.09 | 3.16 | 2.98 | Y–A | |||
| NW25 | 3.91 | 3.81 | 3.08 | 3.27 | 2.97 | Y–Γ | 3.63 | 3.03 | 3.10 | 2.91 | Y–Γ | ||
| NM | 3.96 | 4.29 | 4.48 | 4.24 | Γ–Y | 4.40 | 4.12 | 4.37 | 4.04 | A–Y | 4.25 | Y–C | |
| NWa | 3.0021 | NWb | 3.917 | ||||||||||
| NMa | 2.2338 | ||||||||||||
As the quantity of Mo6+ cations in the solid solution increases, the indirect Egap values decrease, approaching the values observed for NM.
The formation of NiW1−xMoxO4 solid solutions introduces new energy states within the band gap region due to the presence of Mo6+ cations. Consequently, this leads to a shift in the Fermi energy levels and a reduction in the Egap. The decrease in the optical Egap value may be attributed to distortions in the [WO6], [NiO6], and [MoO6] clusters, which promote the creation of intermediary energy states between the VB and CB. These newly formed energy states are reflected in the DOS representation shown in Fig. 8.
The PL spectrum of the as-synthetized samples, shown in Fig. 7a, exhibits a broad emission range spanning from 400 to 650 nm, with an intense blue emission peak located at 450 nm observed for the NW50 sample. These broad emission bands in the visible region are commonly attributed to the recombination of trapped charge carriers,44,45 which is associated with a distinctive multiphoton phenomenon. In this process, multiple energy levels and/or different light emission centers can trap electrons within the band gap.
 | ||
| Fig. 7 (a) PL emissions and (b) CIE chromaticity diagram of the pure NW and NM, and NW75, NW50, and NW25 solid solutions. | ||
As electrons in these intermediate electronic states combine with holes from the VB, this process induces radiative recombination, leading to the appearance of PL emission lines.46,47
The PL emission data of pure NW and NM, as well as the NW75, NW50, and NW25 solid solutions, were used to construct the chromaticity diagram shown in Fig. 7b, to visualize the change in the color emission perceptible to the human eye. This analysis was performed using the coordinates of the Commission Internationale de l’Eclairage (CIE), calculated with Spectralux software.48 The pure NW sample emits in the green region, with a shift toward the blue region as the substitution of W6+ cations by Mo6+ increases up to 50%. In the NW25 sample, the emission shifts to greenish yellow.
Due to the higher presence of MoO6 in the NW25 sample, its characteristics are like those of the pure NM sample, which also emits in the green region. However, the NW25 sample exhibits more efficient energy transfer between [MoO6] and [WO6].49–51
It is well established that the PL spectra of NW are associated with the intrinsic emission of the wolframite structure49,52 and the presence of structural defects (oxygen vacancies in the crystal structure).53 The blue and green emissions may be attributed to the intrinsic [WO6] clusters, i.e., the WO66− complex, with double emission from one and the same center (3T1u–1A1g), while the yellow emission results from recombination of electron–hole pairs localized at oxygen anions, as reported in the ZnWO4 and CdWO4 crystals by Ovechkin et al.54 and Lammers et al.55
Other authors point out the presence of strong electron–phonon coupling, which may account for the blue band, while the transitions of T2u–T2g and T1g–T2g in the WO66− complex are responsible for the appearance of the green and yellow bands.52,56 On the other hand, Harshan et al.41 proposed that the emission peaks in the range of 470–494 nm are related to the intensive transition between the ground state 3A2g and the excited state 3T1 of Ni2+ (3d8) cations in the distorted octahedral [NiO6] cluster.
After detailed analysis of the reported results on the PL emissions of molybdates with monoclinic symmetry, we conclude that the corresponding structures present the local coordination of Mo6+ as four, i.e., a tetrahedral [MoO4] cluster, belonging to the β-phase, as discussed in molybdates such as MgMoO457 and CoMoO4.58,59 In contrast, six oxygen anions surround one Mo6+ cation to render the [MoO6] cluster, as present in the NM crystal lattice, corresponding to the α-phase, which belongs to the C2/m space group.
Based on the above considerations, we argue that the nature of the PL emissions of NW and NM, as well as of the solid solutions, remains unclear. A detailed interpretation of the electronic structures of the solid solutions is made more challenging by the presence of spectral signatures of electronic states associated with [NiO6], [WO6], and [MoO6] clusters in our measurements. The presence of these electronic states leads to electron–hole recombination through intermediate energy levels, resulting in light emission during the PL process. However, the theoretical description of these electronic states, particularly the excited states, is challenging, as it requires high accuracy, which is beyond the scope of the present study.
In our case, we propose that the slight lattice distortions associated with the J–T effect in the 3d8 electronic configuration of Ni2+ cations at the [NiO6] cluster, which is sensitive to the crystal field environment of the adjacent [WO6] and [MoO6] clusters, promote charge transfer among these clusters to modulate the PL emissions. Therefore, taking advantage of the fact that PL emissions are sensitive to the composition of DOS, specifically to the electronic states forming the CB, we conducted systematic atom-level analysis on the orbital overlap between Ni2+ at the [NiO6] cluster and the adjacent [WO6] and [MoO6] clusters.
This orbital hybridization can be considered a signature of the electronic cloud in the CB, which may serve as a guide to understanding and rationalizing the PL emissions throughout the solid solution.
Previously, Evarestov et al.60 showed that in NW, the VB is formed by hybridized O 2p and Ni 3d orbitals, whereas the CB is formed by the empty W 5d orbitals with an admixture of the empty Ni 3d (eg) states at the bottom of the CB. In our case, using the B3LYP functional, detailed analysis of the total DOS in Fig. 8 reveals that the VB is formed by the contributions of O and Ni atoms, while the CB is derived mainly from the lattice former (W and/or Mo atoms), with a smaller contribution from O and Ni atoms.
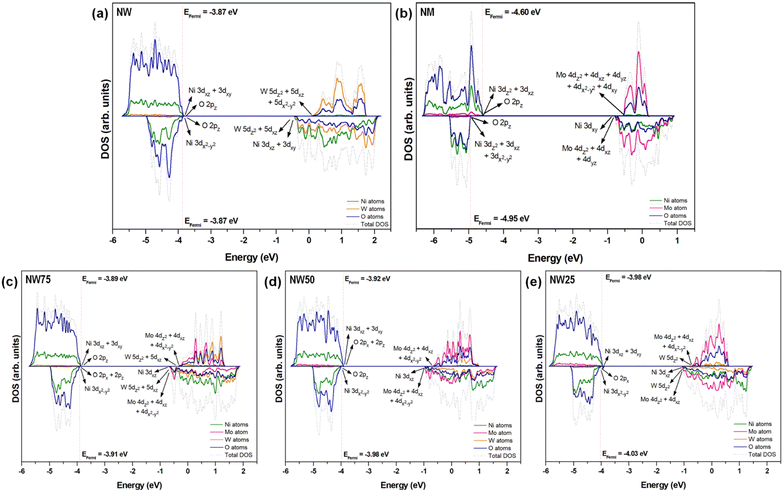 | ||
| Fig. 8 Total DOS projected on Ni, W, Mo, and O atoms at the (a) pure NW and (b) NM and for the (c) NW75, (d) NW50, and (e) NW25 solid solutions. | ||
It is well known that the hybridization between different orbitals plays a crucial role in determining the electronic properties of both NW and MN. Detailed analysis reveals that the top of the VB in the α channel at NW involves the hybridization of Ni 3dxz + 3dxy orbitals and O 2pz orbitals, whereas the bottom of the CB is formed mainly by empty W 5dz2 + 5dxz + 5dx2−y2 orbitals. For the β channel, the VB is formed by Ni 3dx2−y2 orbitals hybridized with O 2pz orbitals, while the CB is composed of the hybridization between W 5dz2 + 5dxz orbitals with Ni 3dxz + 3dxy orbitals. For NM, a similar profile is observed, with the top of the VB composed only of the Ni 3dxy and 3dx2−y2 orbitals in the α and β channels, respectively. Regarding the bottom of the CB, the α channel is composed of empty Mo 4dz2 + 4dxz + 4dx2−y2 orbitals, while at the β channel, there is hybridization between the Mo 4dz2 + 4dxz orbitals with Ni 3dxz orbitals. A more detailed analysis of the partial DOS for the NW (Fig. S2) and NM (Fig. S3) can be found in the ESI.†
During the formation of the NiW1−xMoxO4 solid solutions, small changes at the top of the VB are observed, particularly in the NW25 model, where hybridization between O 2px orbitals and Ni 3dx2−y2 orbitals occurs exclusively in the β channel. The Mo 4d orbitals become significant contributors to the bottom of the CB in both α and β channels. In NW75 and NW50, contributions from the W eg orbitals and Mo 4dyz orbital are observed. The atomic orbital contribution of W atoms in NW25 decreases and is represented by W 5dx2−y2 orbitals, maintaining the same Mo orbital contribution. Furthermore, as the NiW1−xMoxO4 solid solutions form, the Mo 4d orbital contribution to the CB increases at the bottom of this band in both α and β channels. In NW75, the Mo 4dz2 + 4dxz + 4dx2−y2 orbitals and W 5dz2 + 5dxz orbitals become the main components of the CB. On the other hand, in NW25, the W 5dz2 orbital begins to contribute to the bottom of the CB.
An interesting observation is made for the NW50 solid solution: at the bottom of the CB, only the presence of Mo 4dz2 + 4dxz + 4dx2−y2 orbitals is detected, with no contribution from the W 5dz2 orbitals. Therefore, for the solid solutions, the main changes are observed at the CB. The partial DOS projections onto orbitals can be found in the ESI† in Fig. S4–S6. Consequently, this leads to the emergence of spatially extensive hybrid bands at the CB, formed by subtle coupling among the Ni 3d, W 5d, Mo 4d, and O 2p orbitals. The corresponding charge-transfer configurations result from a complex mixing of orbitals, generating an electronic chain along the [NiO6], [WO6], and [MoO6] clusters, thereby enhancing the transfer of photoexcited electrons to modulate the intensity of the PL emissions of the solid solutions. By exploiting previous analysis, our findings discern the assembled J–T effects at the [NiO6], [WO6], and [MoO6] clusters to regulate the PL emissions and boost the orbital hybridization along the Ni–O–W/Mo framework of solid solutions (see Scheme 1).
 | ||
| Scheme 1 Schematic illustration of the [NiO6], [WO6], and [MoO6] clusters, as J–T active sites, which are assembled by orbital hybridization to drive the PL emissions. | ||
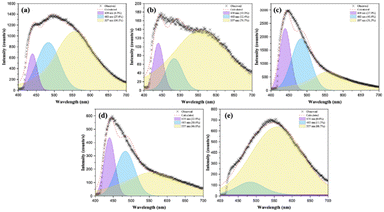
To elucidate the electronic characteristic and the photogenerated charge migration mechanism within the solid solutions, the PL curves were analyzed in detail. The broad emission band was deconvoluted into three Gaussian curves, corresponding to emission peaks centered at 439, 483, and 557 nm (see Fig. 9).
As we know, samples with a higher contribution in the red or yellow regions, characterized by longer wavelengths, resulting from the presence of more defects in the lattice, such as deeper defects (e.g., oxygen vacancies). On the other hand, PL emission in the blue regions, at lower wavelengths, indicates the presence of more shallow defects, such as structural defects, with concomitant changes in the W/Mo–O distances and O–W/Mo–O angles. Indeed, slight structural defects, such as distortions in the local environment of Ni2+, W6+, and Mo6+, can significantly affect the position and intensity of the observed PL emissions (see Fig. 7). Therefore, the NW25 sample exhibits deeper defects in the 557 nm region in the yellow (76.7%), similar to the pure NM sample (88.7%), while the NW50 sample shows more shallow defects at 483 nm in the blue region (40.8%). On the other hand, we can relate the peak at 439 nm to the orbital hybridization among the intra-cluster Ni–O–W/Mo framework at the CB, while the peaks at 483 and 557 nm correspond to the intrinsic emissions of [NiO6] and [WO6]/[MoO6] clusters, respectively. As observed, the first and second parameters exhibit a maximum at NW50, while the contribution of the third is higher at pure NW and NM structures.
In this scenario, the modulation of PL emissions results from the hybridization of Mo 4dz2 + 4dxz + 4dx2−y2 orbitals into W 5dz2 orbitals, thereby perturbing the electronic structure. This behavior plays a pivotal role in defining the electronic structure and the nature of PL emissions. Therefore, subtle changes occurring during the formation of the solid solution impact the Egap values, the composition of the CB, and cluster–cluster electronic transitions, ultimately modulating the PL emissions.
3 Conclusions
The synthesis of solid solutions is an effective strategy for fine-tuning the properties of advanced materials. This combined experimental and theoretical study enhances our understanding of the evolution of the structure, morphology, band gap, and PL from NiWO4, homogeneous NiW1−xMoxO4 (x = 25, 50, and 75%) solid solutions to NiMoO4. These materials were successfully synthesized via the co-precipitation method, followed by heat treatment in a conventional oven.Their characterization was carried out using XRD, Raman, infrared, XRF, UV-vis, and PL spectroscopies, along with DFT calculations. The structural parameters and band gap values obtained using the B3LYP and HSE06 functionals show consistent results.
The main conclusions can be summarized as follows: (i) for x ≤ 50%, the substitution of W6+ by Mo6+ cations resulted in XRD patterns showing only peaks corresponding to the NW phase, while at x = 75%, characteristic peaks of the NM phase emerged alongside those of the NW phase; (ii) SEM images reveal agglomerated particles with no defined morphology, and a reduction in particle as the concentration of Mo6+ cations increases; (iii) DOS analysis indicates that the VB is primarily composed of Ni(3d) and O(2p) states, while the CB is mainly derived from W(5d)/Mo(4d) and O(2p) states; (iv) the formation of NiW1−xMoxO4 solid solutions introduces new energy states within the band gap region due to Mo6+ cations, leading to a shift in Fermi energy levels and a concomitant decrease in the Egap value; (v) the significant enhancement of the PL emission intensity in the blue region at 483 nm of NW50 solid solution is attributed to shallow defects in the lattice and the contribution of 4d Mo orbitals to the CB; (vi) DFT calculations elucidate the role of competing emissions from [NiO6], [WO6] and [MoO6] clusters, establishing a relay mechanism based on an electron transport ladder through the Ni–O–W/Mo framework at the CB. This electronic channel is formed by J–T active sites ([NiO6], [WO6] and [MoO6] clusters), maximizing the orbital overlap of O(2p) with d orbitals from Ni, W, Mo cations, thereby driving the PL emission.
The conceptual framework constructed in this study provides a comprehensive understanding of the multifaceted characteristics of solid solutions. These findings highlight a novel approach for fine-tuning PL emissions by revealing the key hybridization of atomic orbitals within the complex DOS structure at the CB of semiconducting oxides. The diverse alignment patterns of J–T active sites ([NiO6], [WO6] and [MoO6] clusters) offer an in-depth insight into electronic coupling within a three-dimensional ordered structure.
Overall, this work advances our understanding of PL emission in solid solution by disentangling the subtle changes in the electronic structure of [NiO6], [WO6], and [MoO6] coordination environments, which is crucial for optical applications. The proposed model can be extended to other solid solutions based on ternary metal oxides, providing a straightforward framework for rationalizing the relationship between the structure, electronic properties, and PL emissions, thereby guiding the design of solid solutions with tailored optical performance.
4 Experimental and theoretical methods
4.1 Synthesis
The samples were synthesized using the CP method, followed by heat treatment in a conventional oven. We began by synthesizing the pure NW and NM phases. For NW synthesis, 1 × 10−3 mol of Na2WO4·2H2O (99.9%, Sigma-Aldrich) and 1 × 10−3 mol of Ni(NO3)2·6H2O (99%, Sigma-Aldrich) were each diluted in two beakers with 50.0 mL of distilled water. The Ni(NO3)2·6H2O solution was then added to the Na2WO4·2H2O solution, forming a yellow precipitate. The final system was left under magnetic stirring at room temperature for 10 min. After this process, the precipitate was centrifuged, washed several times with distilled water (∼pH 7), and dried in an oven at 60 °C for 12 h. The resulting powder was then placed in a conventional oven at 500 °C for 2 h, with a heating rate of 10 °C min−1. The pure NM phase was synthesized in the same manner as NW, using Na2MoO4 (99.8% purity, Sigma-Aldrich) as the precursor. The same procedure was followed to prepare the NiW1−xMoxO4 (x = 25, 50, and 75%) solid solutions. Variations in the lattice former were implemented at concentrations of 25, 50, and 75% using Na2MoO4. The samples were labeled as NW75, NW50, and NW25 according to the percentage of W6+ cations remaining in the solid solution.4.2 Characterization
The samples were characterized by XRD using a D/Max-2500PC diffractometer (Rigaku, Tokyo, Japan) with Cu Kα radiation (λ = 1.5406 Å) in the 2θ range of 10–80° and a scanning speed of 1° min−1. XRF spectrometry was performed using an EDX-720 (Shimadzu). Raman spectra were recorded with an iHR550 spectrometer (Horiba Jobin-Yvon, Kyoto, Japan) coupled to a silicon charged-coupled-device (CCD) detector and an argon-ion laser (Melles Griot, Rochester, NY USA), operating at 514.5 nm with a maximum power of 200 mW. Fourier-transform infrared spectroscopy (Bruker Vector 22 FTIR, Billerica, MA USA) was used to record the samples’ spectra in the 400–1100 cm−1 range. UV-vis diffuse-reflectance measurements were obtained using a Varian Cary spectrometer model 5G in the diffuse-reflectance mode, with a wavelength range of 200–800 nm and a scan speed of 600 nm min−1. The morphologies of the samples were observed with a SEM operating at 5 kV (Supra 35-VP, Carl Zeiss, Jena, Germany). PL measurements were performed at room temperature by using a 355 nm laser (Cobolt/Zouk) as the excitation source, focused on a 200 μm spot at a constant power of 5 mW. The luminescence signal was dispersed using a 19.3 cm spectrometer (Andor/Kymera) and detected using a silicon CCD (Andor/IdusBU2).4.3 Computational methods and model systems
First-principles calculations for the models NiW1−xMoxO4 (x = 25, 50, and 75%) solid solutions, as well as the pure NW and NM phases, were carried out using DFT with the B3LYP61,62 hybrid functional, as implemented in the CRYSTAL17 program.63 It is well known that the B3LYP functional tends to underestimate the band gap of solid-state materials.64,65 To validate our computational approach, we performed additional calculations using the HSE0666 functional, comparing the optimized structural parameters and band gap values with those obtained from B3LYP. The Ni, W, Mo, and O atoms were described using the 86-411(41d)G, Cora, SC_HAYWSC-311(d31)G, and 6-31d1 bases sets, respectively.67 Regarding the diagonalization of the density matrix, the reciprocal space was sampled using a shrinking factor of 6, generated according to the Monkhorst–Pack scheme. The accuracy of the Coulomb and exchange series evaluation was controlled by five thresholds, set to 10−8, 10−8, 10−8, 10−8, and 10−16.For modelling solid solutions, the NW was represented by a 2 × 1 × 1 supercell, resulting in a model with a 4-unit molecular formula in the structure (Z = 4). From this NW supercell, W6+ cations were substituted by Mo6+ cations according to the experimental data (25, 50, and 75%), as illustrated in Fig. 10. The NM bulk, which has a C2/m structure, was modeled without expansion since its unit cell already contains a 4-unit molecular formula (Z = 4).
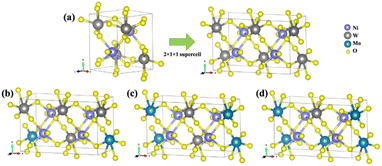 | ||
| Fig. 10 (a) NW bulk model expanded in a 2 × 1 × 1 supercell; (b) NW75 model; (c) NW50 model; and (d) NW25 model. | ||
The formation energy (ΔEf) of the NW75, NW50, and NW25 solid solutions was calculated using the following equation:68–70
 | (1) |
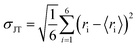 | (2) |
The partial and total DOS of the models were generated along the appropriate high-symmetry directions of the corresponding irreducible Brillouin zone.
Author contributions
A. F. G.: conceptualization, methodology, formal analysis, investigation, writing – original draft, writing – review & editing, and visualization. M. A.: conceptualization, methodology, formal analysis, investigation, writing – original draft, and writing – review & editing. L. K. R.: conceptualization, methodology, formal analysis, investigation, and writing – review & editing. E. O. G.: formal analysis, investigation, and writing – review & editing. M. D. T.: methodology, formal analysis, and writing – review & editing. E. L.: writing – review & editing, supervision, and funding acquisition. J. A.: methodology, writing – original draft, writing – review & editing, supervision, and funding acquisition.Data availability
The data will be made available upon request.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
A. F. G. acknowledges the Generalitat Valenciana (Conselleria de Innovación, Universidades, Ciencia y Sociedad Digital) for the postdoctoral contract (CIAPOS/2021/106). M. A. was supported by the Margarita Salas postdoctoral contract MGS/2021/21 (UP2021-021) financed by the European Union-Next Generation EU and “Fundação de Amparo à Pesquisa do Estado de São Paulo” (FAPESP postdoctoral fellowship, grant # 2023/08525-7). L. K. R. thanks the FAPESP postdoctoral fellowship (grant #2023/12399-7 and #2023/01415-1) and Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, grant #158689/2023-2). E. O. G. thanks Generalitat Valenciana (Conselleria de Innovación, Universidades, Ciencia y Sociedad Digital) for the postdoctoral contract (CIAPOS/2022/162). This work was funded in part by FAPESP (CEPID-finance code #2013/07296-2, and #2022/10340-2), Financiadora de Estudos e Projetos – FINEP, CNPq, and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – CAPES (finance code 001). J. A. acknowledges Ministerio de Ciencia, Innovación y Universidades (Spain) (project PGC2018094417-B-I00), Generalitat Valenciana (Conselleria de Innovación, Universidades, Ciencia y Sociedad Digital – project CIAICO/2021/122) and Universitat Jaume I (UJI-B2022-56) for financially supporting this research.References
- H. Arandiyan and M. Parvari, Braz. J. Chem. Eng., 2009, 26, 63–74 CrossRef CAS.
- J. Vieten, B. Bulfin, P. Huck, M. Horton, D. Guban, L. Zhu, Y. Lu, K. A. Persson, M. Roeb and C. Sattler, Energy Environ. Sci., 2019, 12, 1369–1384 RSC.
- K. Maeda and K. Domen, Chem. Mater., 2010, 22, 612–623 CrossRef CAS.
- P. de Sousa, I. Nogueira, G. Gusmão, S. Gusmão, F. Lopes, B. Sousa, J. C. Sczancoski, A. Gouveia and L. S. Cavalcante, J. Mater. Sci.: Mater. Electron., 2022, 33, 22127–22152 CrossRef CAS.
- H. L. Abubakar, J. O. Tijani, S. A. Abdulkareem, A. Mann and S. Mustapha, Heliyon, 2022, 8, e09964 CrossRef CAS PubMed.
- H. Azevedo, R. A. Raimundo, L. S. Ferreira, M. M. S. Silva, M. A. Morales, D. A. Macedo, U. U. Gomes and D. G. L. Cavalcante, Mater. Chem. Phys., 2020, 242, 122544 CrossRef CAS.
- F. J. O. Rosal, A. F. Gouveia, J. C. Sczancoski, P. S. Lemos, E. Longo, B. Zhang and L. S. Cavalcante, Inorg. Chem. Commun., 2018, 48, 34–40 CrossRef.
- Y. L. Oliveira, A. F. Gouveia, M. J. S. Costa, F. H. P. Lopes, J. C. Sczancoski, E. Longo, G. E. Luz Jr., R. S. Santos and L. S. Cavalcante, Mater. Sci. Energy Technol., 2022, 5, 125–144 CAS.
- R. A. P. Ribeiro, M. C. Oliveira, A. G. de Sousa, M. R. D. Bomio, F. V. Motta, L. Gracia, S. R. de Lazaro, E. Longo and J. Andres, J. Appl. Phys., 2019, 126, 235301 CrossRef.
- S. Balasurya, M. K. Okla, I. A. Alaraidh, W. Soufan, A. A. Al-ghamdi, S. R. Ahamad, M. A. Abdel-Maksoud, H. AbdElgawad, L. L. Raju, A. M. Thomas and S. S. Khan, Chemosphere, 2022, 297, 10 CrossRef PubMed.
- A. M. Sorouri, A. Sobhani-Nasab, M. R. Ganjali, S. Manani, H. Ehrlich, Y. Joseph and M. Rahimi-Nasrabadi, Appl. Mater. Today, 2023, 32, 101819 CrossRef.
- A. Kumar, P. Sharma, G. Sharma, P. Dhiman, M. Shekh, M. Sillanpää and F. J. Stadler, J. Alloys Compd., 2023, 172665 Search PubMed.
- A. Kuzmin, J. Purans, R. Kalendarev, D. Pailharey and Y. Mathey, Electrochim. Acta, 2001, 46, 2233–2236 CrossRef CAS.
- D. Ma, H. Niu, J. Huang, Q. Li, J. Sun, H. Cai, Z. Zhou and J. Wang, Nano Lett., 2024, 24, 814–821 CrossRef CAS PubMed.
- R. Yang, X. F. Guo, K. Song, X. F. Bai, L. H. Jia, X. S. Chen, X. Wang and J. Wang, Ceram. Int., 2021, 47, 11349–11357 CrossRef CAS.
- A. E. Reddy, T. Anitha, C. Gopi, S. S. Rao and H. J. Kim, Dalton Trans., 2018, 47, 9057–9063 RSC.
- T. Xiong, B. Huang, J. Wei, X. Yao, R. Xiao, Z. Zhu, F. Yang, Y. Huang, H. Yang and M.-S. J. T. Balogun, J. Energy Chem., 2022, 67, 805–813 CrossRef CAS.
- P. Sharma, M. Minakshi, J. Whale, A. Jean-Fulcrand and G. Garnweitner, Nanomaterials, 2021, 11, 580 CrossRef CAS PubMed.
- N. A. Lima, L. D. S. Alencar, M. Siu-Li, C. A. C. Feitosa, A. Mesquita, J.-C. M’peko and M. I. B. Bernardi, J. Adv. Ceram., 2020, 9, 55–63 CrossRef CAS.
- A. Rajput, M. K. Adak and B. Chakraborty, Inorg. Chem., 2022, 61, 11189–11206 CrossRef CAS PubMed.
- D. Errandonea, F. Rodriguez, R. Vilaplana, D. Vie, S. Garg, B. Nayak, N. Garg, J. Singh, V. Kanchana and G. Vaitheeswaran, J. Phys. Chem. C, 2023, 127, 15630–15640 CrossRef CAS PubMed.
- C. Liu, Z. He, Y. Liu, R. Chen, M. Shi, H. Zhu, C. Dong and J. Wang, J. Magn. Magn. Mater., 2017, 444, 190–192 CrossRef CAS.
- B. R. Ibiapina, A. E. Lima, L. K. Ribeiro, J. F. Cruz-Filho, A. G. Sales, M. A. Ramos, J. A. Sousa, D. Souza, Y. G. Gobato and F. E. Santos, Environ. Sci. Pollut. Res., 2022, 29, 79343–79356 CrossRef CAS PubMed.
- A. G. Sales, B. R. Ibiapina, G. S. Sales, J. F. Cruz-Filho, A. E. Lima, G. L. da Paz, R. R. Garcia, A. Correa, B. C. Viana and G. O. Gusmão, J. Solid State Chem., 2023, 318, 123773 CrossRef CAS.
- S. K. Ray and J. Hur, J. Environ. Manage., 2021, 278, 111562 CrossRef CAS PubMed.
- W. d S. Pereira, M. M. Ferrer, G. Botelho, L. Gracia, I. C. Nogueira, I. M. Pinatti, I. L. V. Rosa, F. d A. La Porta, J. Andrés and E. Longo, Phys. Chem. Chem. Phys., 2016, 18, 21966–21975 RSC.
- P. F. S. Pereira, C. C. Santos, A. F. Gouveia, M. M. Ferrer, I. M. Pinatti, G. Botelho, J. R. Sambrano, I. L. V. Rosa, J. Andres and E. Longo, Inorg. Chem., 2017, 56, 7360–7372 CrossRef CAS PubMed.
- M. D. P. Silva, R. F. Goncalves, I. C. Nogueira, V. M. Longo, L. Mondoni, M. G. Moron, Y. V. Santana and E. Longo, Spectrochim. Acta, Part A, 2016, 153, 428–435 CrossRef CAS PubMed.
- M. D. Penha, A. F. Gouveia, M. M. Teixeira, R. C. de Oliveira, M. Assis, J. R. Sambrano, F. Yokaichya, C. C. Santos, R. F. Gonçalves, M. Siu Li, M. A. San-Miguel, J. Andrés and E. Longo, Mater. Res. Bull., 2020, 132, 111011 CrossRef CAS.
- I. M. Pinatti, P. F. S. Pereira, M. de Assis, E. Longo and I. L. V. Rosa, J. Alloys Compd., 2019, 771, 433–447 CrossRef CAS.
- P. F. Pereira, C. C. De Foggi, A. F. Gouveia, I. M. Pinatti, L. A. Cabral, E. Guillamon, I. Sorribes, M. A. San-Miguel, C. E. Vergani, A. Z. Simões, E. Z. da Silva, L. S. Cavalcante, R. Llusar, E. Longo and J. Andrés, Int. J. Mol. Sci., 2022, 23, 10589 CrossRef CAS PubMed.
- M. C. Oliveira, J. Andres, L. Gracia, M. de Oliveira, J. M. R. Mercury, E. Longo and I. C. Nogueira, Appl. Surf. Sci., 2019, 463, 907–917 CrossRef CAS.
- E. O. Gomes, L. Gracia, A. A. G. Santiago, R. L. Tranquilin, F. V. Motta, R. A. C. Amoresi, E. Longo, M. R. D. Bomio and J. Andres, Phys. Chem. Chem. Phys., 2020, 22, 25876–25891 RSC.
- A. F. Gouveia, R. A. Roca, N. G. Macedo, L. S. Cavalcante, E. Longo, M. A. San-Miguel, A. Altomare, G. S. da Silva and J. Andrés, J. Mater. Res. Technol., 2022, 21, 4023–4051 CrossRef CAS.
- R. C. Dickson, T. D. Manning, E. S. Raj, J. C. Booth, M. J. Rosseinsky and M. S. Dyer, Phys. Chem. Chem. Phys., 2022, 24, 16374–16387 RSC.
- L. Araújo, M. Costa, B. Sousa, P. de Sousa, R. Monção, A. Araújo, R. de Sousa, F. Santos, R. Santos and L. Cavalcante, J. Energy Storage, 2024, 77, 109999 Search PubMed.
- M. A. Ehsan and A. Khan, ACS Omega, 2021, 6, 31339–31347 Search PubMed.
- L. Yang, J. Wang, Y. Wan, Y. Li, H. Xie, H. Cheng and H. J. Seo, J. Alloys Compd., 2016, 664, 756–763 Search PubMed.
- S. F. Matar, A. Largeteau and G. Demazeau, Solid State Sci., 2010, 12, 1779–1785 CrossRef CAS.
- N. A. Zarkevich, T. L. Tan and D. D. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104203 CrossRef.
- H. Harshan, K. P. Priyanka, A. Sreedevi, A. Jose and T. Varghese, Eur. Phys. J. B, 2018, 91, 287 CrossRef CAS.
- B. Akila, S. Sakthinathan, T.-W. Chiu, J. N. Baby and M. George, ACS Appl. Eng. Mater., 2024, 2, 1663–1671 CrossRef.
- Y. L. Oliveira, M. J. S. Costa, A. C. S. Juca, L. K. R. Silva, E. Longo, N. S. Arul and L. S. Cavalcante, J. Mol. Struct., 2020, 1221, 128774 CrossRef CAS.
- L. De Haart, A. De Vries and G. Blasse, J. Solid State Chem., 1985, 59, 291–300 CrossRef CAS.
- R. Leonelli and J. Brebner, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8649 CrossRef CAS PubMed.
- L. Gracia, J. Andres, V. Longo, J. A. Varela and E. Longo, Chem. Phys. Lett., 2010, 493, 141–146 Search PubMed.
- V. M. Longo, L. S. Cavalcante, M. G. Costa, M. L. Moreira, A. T. de Figueiredo, J. Andrés, J. A. Varela and E. Longo, Theor. Chem. Acc., 2009, 124, 385–394 Search PubMed.
- E. I. Stearns, Commission Internationale de L'Éclairage, Colorimetry. Color Res. Appl., Publication CIE No. 15.2, 78, Central Bureau of the CIE, Gaithersburg, MD, 2nd edn, 1987 Search PubMed.
- N. A. Lima, L. D. Alencar, M. Siu-Li, C. A. Feitosa, A. Mesquita, J.-C. M’peko and M. I. Bernardi, J. Adv. Ceram., 2020, 9, 55–63 Search PubMed.
- C. Macchi, G. M. Petinardi, L. A. Freire, M. S. Castro, C. M. Aldao, T. M. Luiz, F. Moura, A. Z. Simões, H. Moreno and E. Longo, Dalton Trans., 2024, 53, 525–534 RSC.
- M. V. da Silva, D. F. M. de Oliveira, H. S. Oliveira and K. P. F. Siqueiras, Mater. Res. Bull., 2020, 122, 110665 Search PubMed.
- A. Mohammadi, Z. Amouzegar, M. Aminzare, M. Jafari and M. Nasr-Esfahani, Mater. Res. Innovations, 2017, 21, 407–412 CrossRef CAS.
- M. Anicete-Santos, E. Orhan, M. De Maurera, L. Simoes, A. Souza, P. Pizani, E. Leite, J. A. Varela, J. Andrés and A. Beltrán, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165105 Search PubMed.
- A. Ovechkin, V. Ryzhikov, G. Tamulaitis and A. Žukauskas, Phys. Status Solidi A, 1987, 103, 285–290 CrossRef CAS.
- M. Lammers, G. Blasse and D. Robertson, Phys. Status Solidi A, 1981, 63, 569–572 Search PubMed.
- L. Grigorjeva, R. Deych, D. Millers and S. Chernov, Radiat. Meas., 1998, 29, 267–271 Search PubMed.
- A. A. Santiago, M. C. Oliveira, R. A. Ribeiro, R. L. Tranquilin, E. Longo, S. R. de Lazaro, F. V. Motta and M. R. Bomio, Cryst. Growth Des., 2020, 20, 6592–6603 Search PubMed.
- K. Seevakan, A. Manikandan, P. Devendran, A. Baykal and T. Alagesan, Ceram. Int., 2018, 44, 17735–17742 CrossRef CAS.
- R. Wangkhem, K. Khupfu, N. Yaiphaba and N. S. Singh, Phys. Rev. B, 2024, 416353 CrossRef CAS.
- A. Kuzmin, A. Kalinko and R. Evarestov, Open Phys., 2011, 9, 502–509 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- R. Shinde, S. S. R. K. C. Yamijala and B. M. Wong, J. Phys.: Condens. Matter, 2021, 33, 115501 CrossRef CAS PubMed.
- B. G. Janesko, T. M. Henderson and G. E. Scuseria, Phys. Chem. Chem. Phys., 2009, 11, 443–454 RSC.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Zicovich-Wilson, Crystal Basis Sets Library, 2025, https://www.crystal.unito.it/basis_sets.html.
- D. P. Rai, A. Laref, A. Shankar, Sandeep, A. P. Sakhya, R. Khenata and R. K. Thapa, J. Phys. Chem. Solids, 2018, 120, 104–108 Search PubMed.
- D. P. Rai, A. Shankar, Sandeep, M. P. Ghimire, R. Khenata and R. K. Thapa, RSC Adv., 2015, 5, 95353–95359 Search PubMed.
- A. B. Trench, T. R. Machado, A. F. Gouveia, M. Assis, L. G. da Trindade, C. Santos, A. Perrin, C. Perrin, M. Oliva, J. Andres and E. Longo, Appl. Catal., B, 2018, 238, 198–211 CrossRef CAS.
- G. Bakradze, E. Welter and A. Kuzmin, J. Phys. Chem. Solids, 2023, 172, 111052 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Elemental analysis – XRF spectrometry, bond distances and Jahn–Teller distortion, and density of states (DOS). See DOI: https://doi.org/10.1039/d4tc05251j |
| This journal is © The Royal Society of Chemistry 2025 |