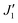Prediction of room-temperature antiferromagnetism in V₂CT₂ (T = Cl, Br, I) MXenes

Abstract

The search for two-dimensional (2D) magnetic materials has attracted considerable attention in both experimental and theoretical research due to their distinctive properties and potential applications in spintronic devices. Although many 2D materials exhibiting magnetic order have been discovered, room-temperature 2D ferromagnetic (FM) materials remain scarce, and 2D materials with antiferromagnetic (AFM) order are even more rarer. In this manuscript, we propose an effective strategy to achieve high Néel temperatures T_c in 2D AFM materials by designing interlayer superexchange coupling. Through first-principles calculations, we identify V₂CT₂ (T = Cl, Br, I) MXenes as dynamically stable materials with strong exchange coupling interactions. To determine their T_c, we developed a Monte Carlo (MC) simulation code, spins2, accelerated with Numba. Our results show that V₂CT₂ MXenes are promising candidates for room-temperature AFM materials, with predicted T_c values of 590, 550, and 420 K for Cl, Br, and I terminations, respectively. Furthermore, we demonstrate that T_c can be tuned linearly by applying strain along the y-axis, offering a versatile approach for tailoring their magnetic properties.

---

1. Introduction

Whether magnetism can exist at finite temperature in 2D is a fundamental problem in condensed matter physics. The Mermin–Wagner theorem¹ states that continuous symmetries cannot be spontaneously broken at finite temperature in 2D for models with short-range interactions between the spins, thus no ferromagnetism and anti-ferromagnetism can occur in the 2D Heisenberg model at finite temperature. However, the spatial asymmetry of the electron cloud introduces magnetic anisotropy, breaking the continuous rotational symmetry of the Hamiltonian and enabling ordered states in 2D at a finite temperature.² This relationship between order and temperature can be described by the classic Ising model,³ where a finite-temperature ferromagnetic phase transition can occur even in a simple 2D square lattice. The critical phenomena of classical magnetism have been extensively studied over many decades, and the fundamental universal properties around criticality are well understood. Magnetism in atomically thin, ideal 2D layers, though, remains an attractive area of research due to its potential applications in spintronics, magnetoelectric and magneto-optic devices.² More recently, due to the experimental discovery of many 2D materials with layer thickness down to a single atom, such as graphene,⁴ phosphorene,⁵ silicone,⁶ hexagonal boron nitride (h-BN)⁷ and transition metal dichalcogenides (TMDs)^8–10etc., as well as due to the long lasting interests in spintronics applications,¹¹ there has been a renewed interest to search for realistic and atomically thin 2D magnetic materials, especially the room temperature 2D magnets, leading to the experimental discovery or theoretical prediction of apparent 2D magnetism in several materials.^12–17 Along this line, in 2018 several authors of this paper conducted a systematic materials informatics search of 2D FM materials¹⁸ from the large experimental Inorganic Crystal Structure Database (ICSD), focusing on the possibility of discovering room-temperature 2D FM materials. This search followed by density functional theory (DFT) calculations to determine the exchange coupling strength and by further Monte Carlo (MC) simulations to study the critical phenomenon, predicted that the 2D Cr₃Te₄ layer to possess a Curie temperature T_c of 2057 K, where the interlayer interactions play a crucial role in achieving this high Curie temperature. Indeed, in 2021, X-ray magnetic circular dichroism measurements confirmed that the monolayer Cr₃Te₄ to have T_c of 344 K.¹⁹ The discrepancy arises because the T_c predicted by the Ising model often needs to be adjusted by a scaling factor of 0.2–0.4 to better estimate the experimental T_c.

High-throughput computational studies have also been conducted to investigate magnetic ordering in 2D materials, leading to the prediction of numerous new 2D magnetic materials.^20–22 During the screening for FM materials, some materials with AFM ordering were also identified. Interestingly, although FM and AFM have similar origins, room-temperature 2D AFM materials are even scarcer than their FM counterparts in these predictions. This scarcity may be due to the magnetic properties associated with AFM orderings being significantly more complex than those of FM materials. In AFM systems, the dominant interactions may extend beyond the nearest-neighbor, with next-nearest-neighbor interactions sometimes being ten times stronger than the nearest-neighbor interactions.²³Table 1 presents a selection of 2D AFM materials with predicted Néel temperatures exceeding 300 K, derived from first-principles calculations and MC simulations. The column ‘M’ indicates the number of metal layers in each monolayer. It should be noted that some of the predicted T_c values in Table 1 might be overestimated due to the use of the Ising model in these simulations. For instance, the 2D monolayer AFM materials MnCaSn and FeTe, which have a square lattice as shown in Fig. S1 (ESI†) and were identified in ref. 18 yield T_c values of 710 and 790 K, respectively, based on the Ising model. While when magnetic anisotropy energies (MAE) are included in the MC simulations using the Heisenberg model, the T_c values decrease to 235 K and 240 K, respectively, as shown in Table S1 (ESI†). The ratio of T_c values from the Heisenberg model to those from the Ising model is approximately 0.3, indicating that Heisenberg model-based MC simulations provide estimates closer to actual results.

Table 1 A list of 2D AFM materials, including their chemical formula, predicted magnetic ground state (G.S.), and Néel temperature (T_c)

	Sample	G.S.	T c (K)	Ref.
M	VPS3	nAFM	570	24
	NiPS3	zAFM	560	24
M 2	Mn2C	AFM-a	720	25
	Ti2C	AFM1	875	26
	Cr2CO1.5F0.5	AFM2	335	27
	V2COF	AFM2	347	27
	Cr2CFCl	AFM1	395	28
	Cr2CHCl	AFM1	430	28
	Cr2CHF	AFM1	380	28
	MnCl	AFM1	766	29
	Cr2CF2	AFM1	675	29
M 3	Hf2VC2F2	Y-AFM	313	30

---

Nevertheless, these predicted monolayers indicate promising structural configurations for achieving high-T_c 2D AFM materials. Transition metals such as Ti, Cr, V, and Mn show potential, with superexchange coupling in these 2D monolayers emerging as an effective mechanism for realizing high-T_c properties, as demonstrated in MXenes.^25,31–36 Recent studies have identified MXenes as a novel family of 2D materials composed of few-atom-thick layers featuring staggered arrangements of transition metals and carbides/nitrides,^37–44 with the adjacent metal layers may exhibit ideal superexchange interaction between half-filled metal atoms mediated by carbon as reported in previous works.^27–29 He et al. investigated the properties of asymmetrically functionalized MXenes (Janus MXenes) such as Cr₂CXX′ (X, X′ = H, F, Cl, Br, OH), discovering their high Néel temperatures, with the electron or hole doping could control the spin carrier orientation.²⁸ Similarly, Niu et al. demonstrated that the AFM configuration for 2D MnCl and Cr₂CF₂ could be controlled by an electric field, highlighting exciting opportunities for achieving nanoscale spintronics.²⁹ However, the above calculations only focused on the nearest and next-nearest interactions, denoted as J₀ and J_a, respectively. The dominant M–C–M interaction remains inconclusive and may lead to deviations in the predicted T_c.

In this work, we investigate MXenes with various transition metals and terminal groups, identifying V₂CT₂ with halogen terminations (T = Cl, Br, I) as having enhanced antiferromagnetic moments and structural stability. The structure of V₂CT₂ MXenes is illustrated in Fig. 1, where black dashed line outlines the primitive cell, the small dark gray spheres denote C atoms, light gray spheres represent V atoms, and green spheres indicate T atoms (F, Cl, Br, or I). A supercell is constructed to determine the spin exchange coupling among magnetic atoms, particularly focusing on the M–C–M superexchange interaction. Additionally, a MC code, spins2, accelerated using Numba⁴⁵ was developed to simulate variations in physical quantities, revealing that V₂CT₂ MXenes with halogen terminations exhibit antiferromagnetic properties with Néel temperatures above room temperature. This study introduces a promising high-T_c 2D AFM material with strain-tunable properties. Additionally, the exchange coupling calculation method and MC simulation code presented here serve as valuable tools for designing and developing future FM and AFM materials for spintronic applications. Moreover, the insights gained provide important reference points for the study of ultra-thin materials.

Fig. 1 Top (a) and side (b) view of the V₂CT₂ MXene.

2. Computational details

The first-principles calculations are carried out based on projector augmented-wave (PAW) potentials⁴⁶ in reciprocal space represented by a generalized gradient approximation (GGA) in DFT as implemented in Vienna ab initio Simulation Package (vasp) codes.^47,48 Due to the non-negligible contribution for the vdW interactions to the total energy of the 2D materials, optPBE-vdW functional is applied,^49,50 and the Hubbard “U” correction within the rotationally invariant DFT+U approach⁵¹ based on relevant previous reports⁵² to properly address the strong correlation of localized electrons in transition metals in these calculations of the exchange energy. Due to the underestimation of energy band gaps through GGA-PBE, the non-local HSE06 hybrid functional^53,54 is also adopted to correct the band gap values.^55,56 Plane-waves with energies up to 550 eV are employed to describe the electronic wave functions, the maximum force on each atom is less than 10⁻⁴ eV Å, and the total energies are converged within 10⁻⁷ eV for the structure optimization and energy calculations. The relationship between magnetic moments on magnetic atoms and the total energy can be determined by Heisenberg model,^23,26 as shown in eqn (1).where A_i denotes the single-ion anisotropy tensor, J_ij represents the exchange coupling tensor, and S_i is the spin operator corresponding to the magnetic metal atom. Generally, A_i and J_ij are represented by 3 × 3 matrices, while S_i is a 3 × 1 column unit vector. In our calculations, the anisotropic exchange along the x, y and z directions, as well as the Dzyaloshinskii–Moriya interaction (DMI), are much smaller than the main diagonal J_ij and can thus be omitted. Consequently, eqn (1) can be simplified to a sum of constant coefficient terms, and the non-zero A_i and J_ij can be achieved separately. The exchange coupling terms in eqn (1) includes interaction terms ranging from nearest-neighbor to long-range interactions. However, only a finite number of terms are required to accurately describe the system because the exchange interactions decay with distance. In this work, we consider intralayer nearest and next-nearest neighbor interactions J_a and J_b, as well as interlayer nearest and next-nearest neighbor interactions J₀ and J₁.

3. Spin model and magnetic coupling

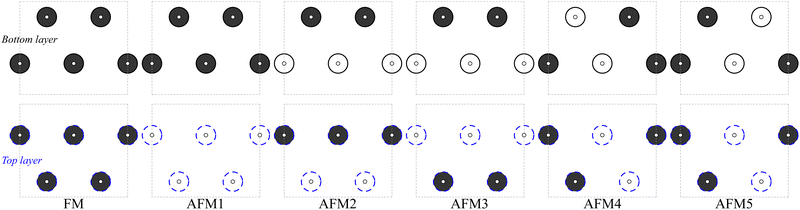
The exchange coupling parameters are determined by analyzing the energy differences between various magnetically ordered states, including FM and several AFM configurations, with the specific equations tailored to the arrangement of magnetic atoms within the material.⁵⁷ The surface terminations on transition metal atoms serve to protect the magnetic properties from external disturbances. Following a similar approach to constructing the magnetic unit cells for MnCaSn and FeTe with a 2D square lattice as shown in Fig. S2 (ESI†), a supercell containing 8 magnetic atoms is employed to capture the magnetic characteristics of V₂CT₂ based on the system's symmetry. The possible magnetic configurations, labeled as FM and AFMs 1–5, are shown in Fig. 2. In this figure, black and white circles denote spin-up and spin-down states, while circles with solid and dashed outlines indicate atoms in the bottom and top layers, respectively.

Fig. 2 The FM and AFM configurations for V₂CT₂ MXene structure. Black and white circles represent spin-up and spin-down, and the circles with solid and dashed line represent top and bottom layer atoms, respectively.

The intralayer nearest and next-nearest neighbor interactions, denoted as J_a and J_b, along with the interlayer nearest and next-nearest neighbor interactions, J₀ and J₁, are illustrated in Fig. 1. Additionally, the magnetic configurations induce changes in the system's symmetry, causing slight variations in the lattice constants of V₂CT₂ along the zigzag (x) and armchair (y) directions, leading to a transition from the 1T to 1T′ phase.⁵⁸ This symmetry shift results in unequal V–V atomic distances along the x and y directions. Furthermore, the application of uniaxial strain introduces additional disparities in atomic distances along these directions. Among these interactions, J₁ is the most significantly affected due to the larger distance between metal atoms mediated by M–C–M superexchange interactions. Thus, alongside J₁, which captures the M–C–M interaction along the y-direction, an additional parameter 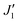is introduced to represent the M–C–M interactions that slightly deflect towards the x-direction. To determine the ground state and exchange interactions, we compare the total energies of various AFM states and calculate the coupling parameters. Similarly to the monolayer MnCaSn or FeTe, which feature a square lattice and checkerboard ground states with total energies described in eqn (S1) (ESI†) and exchange couplings for the nearest J_a, next-nearest J_b, and third-nearest neighbors J_c defined in eqn (S2) (ESI†), the total energies for the V₂CT₂ FM and AFM1-5 configurations are formulated in eqn (2). The intralayer exchange coupling interactions between the nearest J_a, next-nearest J_b, and interlayer exchange coupling interactions between the nearest J₀, next-nearest J₁ and are subsequently expressed in eqn (3). Then take the spin–orbit coupling (soc) induced MAE into consideration, the direction of atomic magnetic moment may prefer to align along a certain axis (easy axis) or plane (easy plane).

Parsing the full Heisenberg model analytically remains a challenge due to its complex exchange coupling and anisotropy tensor, but the reduced Ising model can be analytically solved for simple lattices, as shown in eqn (S3) (ESI†). These analytical solutions are helpful for validating the MC simulation results. To estimate the Curie or Néel temperature of the FM/AFM materials, a MC code, spins2, has been developed using the Metropolis algorithm. In spins2, during each MC step, the energy difference E_β − E_α between old state α and the new state β for every magnetic atom in the periodic lattice is calculated. Transition from the state α to β involves changing the spin 1 to −1 or from −1 to 1, achieved by multiplying the current state by −1 in the Ising model. In contrast, in the Heisenberg model, the new state is obtained by normalizing three independent Gaussian random variable x, y and z as described in eqn (S4) (ESI†), to ensure that the possibility p is uniformly distributed over the sphere. The probability to accept the new state is given by eqn (S5) (ESI†), and the mean magnetization, magnetic susceptibility and specific heat per spin are obtained through statistics analysis and defined in eqn (S6) (ESI†). In the MC simulations, the influence of MAE can be incorporated, with contributions along the easy axis factored into the calculations of average magnetization and susceptibility. To enhance computational efficiency, spins2 leverages Numba to accelerate the spin flip operations, enabling parallelized MC simulations. This optimization significantly reduces computation time and allows for more extensive simulations of large magnetic systems.

4. Results and discussion

The structure of V₂CT₂ (T = F, Cl, Br, I) supercells are first optimized without imposing symmetry restrictions, and the energy difference between FM and AFM magnetic atom arrangements are list in Table 2. Evidently, all V₂CT₂ MXenes exhibit their lowest energy in the AFM2 state, which slightly deviates from a perfect hexagonal lattice. The lattice parameter along the y-axis is reduced by 3.68%, 3.44%, 3.17% and 2.83% for V₂CT₂ (T = F, Cl, Br, I), respectively, compared to that of the primitive cell, leading to the formation of the 1T′ structure, as shown in Table S2 (ESI†). Subsequently, the exchange interactions J_a, J_b, J₀, J₁ and are calculated using eqn (2) and (3), and the anisotropy parameter A is derived from the energy differences of spin orientations along different directions. It is evident that intralayer interactions are generally weaker than interlayer interactions. This is likely attributed to the spatial distribution of d-orbital electrons, which are more prone to interact with each other across interlayer regions, facilitating stronger magnetic coupling between adjacent layers. Compared to V₂COF²⁷ and Cr₂CHCl,²⁸ which have J₀ values of 22.52 and −18.292, and J_a values of −14.17 and 26.487, respectively, V₂CT₂ exhibits significantly higher J values, particularly in interlayer interactions. This enhancement contributes to a higher critical temperature. The J₁ interaction represents a classic superexchange interaction, driven by the Pauli exclusion principle, where the non-magnetic C atom serves as a mediator between two interlayer V atoms. This interaction induces a transition from a ferromagnetic direct exchange J₀ to an antiferromagnetic superexchange J₁, with J₁ displaying the largest absolute value among all the exchange interactions, thus playing a dominant role in defining the overall magnetic behavior.

Table 2 The calculated relative energy per formula unit for V₂CT₂ (T = F, Cl, Br, I). The relative energy for the AFM2 configuration is set to zero and highlighted in bold

(meV)	V2CF2	V2CCl2	V2CBr2	V2CI2
FM	453.4	450.7	407.0	240.2
AFM1	146.7	212.3	214.6	231.7
AFM2	0.0	0.0	0.0	0.0
AFM3	526.5	528.5	501.4	449.5
AFM4	202.7	263.1	251.5	212.7
AFM5	175.5	158.0	136.4	101.6
J 0	27.48	36.26	38.62	55.13
J 1	−118.02	−79.56	−67.79	−56.87
	−58.88	−74.22	−72.14	−56.39
J a	−19.74	−8.69	−7.32	−4.42
J b	15.14	0.29	−0.19	3.02
A z	0.024	0.024	0.023	0.178
A y	0.0	0.0	0.028	0.326
A x	0.026	0.019	0.0	0.0

---

Both AFM1 and AFM2 configurations can accommodate the opposing magnetic moments induced by the antiferromagnetic J₁ interaction, yet the positive J₀ is incompatible with the AFM1 configuration, and it is partially satisfied in AFM2. Similarly, the negative J_a, which typically causes geometric frustration in triangular lattices, is only partially accommodated in a stripe-like arrangement. This partial satisfaction of J_a, along with the influence of J₁ and J₀, further stabilizes the AFM2 configuration as the ground state. Additionally, given the similar atomic environments for the J₁ and interactions, their values are expected to be comparable near equilibrium positions. However, in the case of V₂CF₂, a noticeable discrepancy between J₁ and is observed. This difference may be attributed to a relatively larger J_a in V₂CF₂, leading to spin canting. As a result, the spin ground state of V₂CF₂ may adopt a Y-type AFM or exhibit frustration rather than a co-parallel arrangement, warranting further investigation.

The phonon dispersion curves for V₂CT₂ (T = F, Cl, Br, I) in the AFM2 co-parallel magnetic configuration are presented in Fig. 3. Notably, V₂CF₂ exhibits clear imaginary frequencies around the S and Γ points in the Brillouin zone, further indicating its dynamic instability in the AFM2 co-parallel magnetic configuration. This behavior contrasts with that of the other three V₂CT₂ MXenes (T = Cl, Br, I), which do not show such instability. To verify the stability of the remaining V₂CT₂ (T = Cl, Br, I), ab initio Molecular Dynamics (AIMD) simulations at 300 and 700 K are performed. The structures only undergo minor deformations as shown in Fig. 3(b)–(d), suggesting their thermodynamic stability. The V atoms in V₂CT₂ MXenes have similar magnetic moments of 2.078, 2.143, 2.209 and 2.329μ_B. The number of unpaired electrons appears to correlate with the electronegativity of the halogen elements. While the energy differences between the FM and AFM states show significant variations across the different terminations. Unlike MnCaSn or FeTe, which have their easy axis along the z direction, V₂CF₂ and V₂CCl₂ have their easy axis along the y direction, while V₂CBr₂ and V₂CI₂ along the x direction. This may result from the 3d-orbitals of V being divided into d_yz/d_xz, d_xy/d_x²−y² and d_z² under crystal field, as shown in Fig. 4, with the two unpaired electrons tending to half-occupy the d_xy/d_x²−y² orbital. The band structures and density of states for V₂CT₂ (T = Cl, Br, I) MXenes are presented in Fig. 5, showcasing their semiconducting properties. The sates of halogen terminations gradually increase from Cl to I below the Fermi level, overlapping with V, which may contribute to their stability. With the HSE06 correction, the band gap significantly increases from 1.23 to 1.91 eV for V₂CCl₂, 1.16 to 1.90 eV for V₂CBr₂, and 0.46 to 1.12 eV for V₂CI₂. The optical properties of V₂CT₂ are also investigated using HSE06, with the absorption, reflection, and transmission spectra presented in Fig. S5 (ESI†). Due to the band gap reduction, the absorption, reflection, and transmission peaks of V₂CT₂ shift to the left in the order of Cl, Br, and I, and the spectra exhibit notable differences in the optical properties along the x and y directions.

Fig. 3 The phonon dispersions of V₂CF₂ (a), and the AIMD energy frustration of V₂CCl₂ (b), V₂CBr₂ (c) and V₂CI₂ (d) at 300 and 700 K with the simulation time of 6 ps.

Fig. 4 The electronic occupation of d-orbitals under crystal fields for V₂CT₂ (T = Cl, Br, I) MXenes.

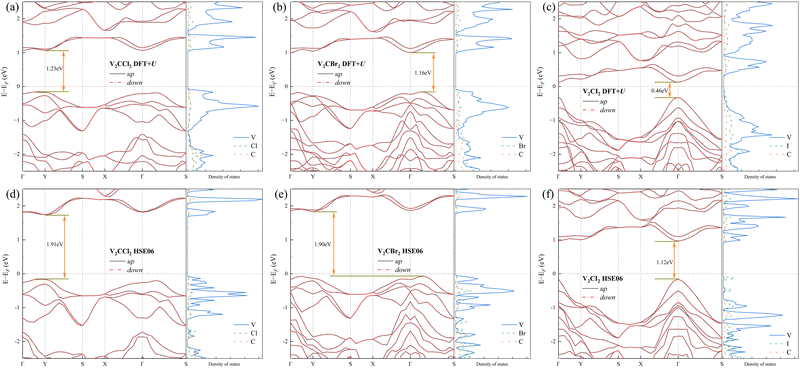Fig. 5 Band structures and density of states for V₂CT₂ (T = Cl, Br, I) MXenes from DFT+U and HSE06 respectively.

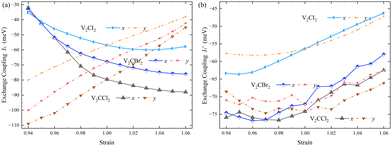
Using the interaction parameters obtained, simulations in spins2 are conducted to study the temperature-dependent changes in specific heat, magnetic properties, and susceptibility for the V₂CT₂ (T = Cl, Br, I) MXenes using the Heisenberg model, as depicted in Fig. 6. Remarkably, the calculated T_c values are found to be 590, 550, and 420 K, respectively, well above room temperature. To better comprehend the impact of atomic distances on exchange couplings and, consequently, on T_c, strains along the x or y-axis are applied. The total energy variation under strains is illustrated in Fig. S6–S8 (ESI†). It is observed that AFM2 arrangements consistently exhibit the lowest energy within the range of strains from 0.94 to 1.06, indicating the stability of these configurations. The variations of J₁ and 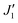along with strains are plot in Fig. 7. Due to the structural characteristics depicted in Fig. 1, stains along the y-axis would affect both J₁ and , whereas strains along the x-axis would impact more significantly than J₁. As a result, the T_c decreases linearly with increasing strain along the y-axis, while a peak is observed with increasing strain along the x-axis. This indicates that lattice deformation induced by strain along the y-axis could be an effective approach to tuning the critical temperature.

Fig. 6 Temperature-dependent changes in specific heat (a), magnetic properties (b), and susceptibility (c) for V₂CT₂ (T = Cl, Br, I) MXenes using the Heisenberg model, and the T_c variation induced by strain along the x or y-axis (d).

Fig. 7 The exchange coupling J₁ (a) and (b) variation under x or y-axis stains.

5. Conclusion

In summary, we present a feasible strategy for designing 2D AFM materials with high Néel temperatures. Based on DFT calculations, the magnetic moments of various MXenes are examined, and the magnetic properties and stability of the identified V₂CT₂ (T = Cl, Br, I) MXenes with AFM2 ground states are thoroughly investigated in this study. Unlike conventional direct exchange interactions, the AFM state for V₂CT₂ MXenes originates from the superexchange interactions between interlayer V atoms. Spin non-collinear calculations are conducted to determine the MAE along different directions, and the methods for calculating spin exchange coupling between interlayer and intralayer nearest and next-nearest neighbor are deduced for the MC simulations aimed at obtaining the Néel temperatures T_c. An efficient Python code, spins2, accelerated with Numba, is developed and made available as a pip-installable package for conducting MC simulations. By utilizing the calculated interactions as input, discrepancies in T_c between Ising and Heisenberg models are discussed. The V₂CT₂ (T = Cl, Br, I) MXenes demonstrate high T_c values of 590, 550, and 420 K, respectively, well above room temperature. This study highlights the promising potential of antiferromagnetic V₂CT₂ MXenes in future spintronic or sensor device applications, while providing valuable insights into the critical temperature through MC simulations for experimental or practical applications in the magnetic 2D materials field.

Author contributions

Kan Luo: conceptualization; data curation; formal analysis; investigation; methodology; project administration; writing – original draft; writing – review & editing. Xianghua Kong: investigation; validation; visualization; writing – review & editing. Shiyu Du: conceptualization; project administration; Hong Guo: conceptualization; funding acquisition; resources; software; supervision; writing – review & editing.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article and its ESI.† The data analysis code spins2 used in this study is publicly available on https://github.com/lkccrr/spins2 and https://pypi.org/project/spins2 for transition temperature simulations.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This research was funded by the Natural Science and Engineering Research Council (NSERC) of Canada, and the Fonds de recherche du Québec-Nature et technologies (FRQNT) of the Province of Quebec (H. G.). We thank financial support by Shenzhen Science and Technology Program (Grant No. RCYX20231211090126026), Shenzhen Natural Science Fund (Grant No. 20220810161616001), and Ningbo Natural Science Fund (Grant No. 20221JCGY010746). The authors would like to thank Bao-huei Huang, Jyun-Jie Jiang, Bing Luo, and Songqi Jia for stimulating discussions. We also thank Digital Research Alliance of Canada and the High Performance Computing Center of McGill University for the computing facilities which made this work possible.

References

1. B. I. Halperin, On the Hohenberg–Mermin–Wagner Theorem and Its Limitations, J. Stat. Phys., 2019, 175(3), 521–529.
2. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals, Nature, 2017, 546(7657), 265–269.
3. S. G. Brush, History of the Lenz-Ising Model, Rev. Mod. Phys., 1967, 39, 883–893.
4. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric Field Effect in Atomically Thin Carbon Films, Science, 2004, 306(5696), 666–669.
5. M. Wu, H. Fu, L. Zhou, K. Yao and X. C. Zeng, Nine New Phosphorene Polymorphs with Non-Honeycomb Structures: A Much Extended Family, Nano Lett., 2015, 15(5), 3557–3562.
6. M. Houssa, A. Dimoulas and A. Molle, Silicene: a review of recent experimental and theoretical investigations, J. Phys.: Condens. Matter, 2015, 27(25), 253002.
7. L. Ci, L. Song, C. Jin, D. Jariwala, D. Wu, Y. Li, A. Srivastava, Z. F. Wang, K. Storr, L. Balicas, F. Liu and P. M. Ajayan, Atomic layers of hybridized boron nitride and graphene domains, Nat. Mater., 2010, 9(5), 430–435.
8. C. Tan and H. Zhang, Two-dimensional transition metal dichalcogenide nanosheet-based composites, Chem. Soc. Rev., 2015, 44, 2713–2731.
9. H. Fang, C. Battaglia, C. Carraro, S. Nemsak, B. Ozdol, J. S. Kang, H. A. Bechtel, S. B. Desai, F. Kronast, A. A. Unal, G. Conti, C. Conlon, G. K. Palsson, M. C. Martin, A. M. Minor, C. S. Fadley, E. Yablonovitch, R. Maboudian and A. Javey, Strong interlayer coupling in van der Waals heterostructures built from single-layer chalcogenides, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(17), 6198–6202.
10. G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano, V. R. Cooper, L. Liang, S. G. Louie, E. Ringe, W. Zhou, S. S. Kim, R. R. Naik, B. G. Sumpter, H. Terrones, F. Xia, Y. Wang, J. Zhu, D. Akinwande, N. Alem, J. A. Schuller, R. E. Schaak, M. Terrones and J. A. Robinson, Recent Advances in Two-Dimensional Materials beyond Graphene, ACS Nano, 2015, 9(12), 11509–11539.
11. I. Choudhuri, P. Bhauriyal and B. Pathak, Recent Advances in Graphene-like 2D Materials for Spintronics Applications, Chem. Mater., 2019, 31(20), 8260–8285.
12. M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan and M. Batzill, Strong room-temperature ferromagnetism in VSe₂ monolayers on van der Waals substrates, Nat. Nanotechnol., 2018, 13(4), 289–293.
13. S. Tian, J.-F. Zhang, C. Li, T. Ying, S. Li, X. Zhang, K. Liu and H. Lei, Ferromagnetic van der Waals Crystal VI₃, J. Am. Chem. Soc., 2019, 141(13), 5326–5333.
14. P. Jiang, C. Wang, D. Chen, Z. Zhong, Z. Yuan, Z.-Y. Lu and W. Ji, Stacking tunable interlayer magnetism in bilayer CrI₃, Phys. Rev. B, 2019, 99, 144401.
15. L. Webster and J.-A. Yan, Strain-tunable magnetic anisotropy in monolayer CrCl₃, CrBr₃, and CrI₃, Phys. Rev. B, 2018, 98, 144411.
16. C. Liu, S. Guan, H. Yin, W. Wan, Y. Wang and Y. Zhang, γ-GeSe: A two-dimensional ferroelectric material with doping-induced ferromagnetism, Appl. Phys. Lett., 2019, 115(25), 252904.
17. D. J. O’Hara, T. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta, D. W. McComb and R. K. Kawakami, Room Temperature Intrinsic Ferromagnetism in Epitaxial Manganese Selenide Films in the Monolayer Limit, Nano Lett., 2018, 18(5), 3125–3131.
18. Y. Zhu, X. Kong, T. D. Rhone and H. Guo, Systematic search for two-dimensional ferromagnetic materials, Phys. Rev. Mater., 2018, 2, 081001.
19. R. Chua, J. Zhou, X. Yu, W. Yu, J. Gou, R. Zhu, L. Zhang, M. Liu, M. B. H. Breese, W. Chen, K. P. Loh, Y. P. Feng, M. Yang, Y. L. Huang and A. T. S. Wee, Room Temperature Ferromagnetism of Monolayer Chromium Telluride with Perpendicular Magnetic Anisotropy, Adv. Mater., 2021, 33(42), 2103360.
20. D. Torelli, H. Moustafa, K. W. Jacobsen and T. Olsen, High-throughput computational screening for two-dimensional magnetic materials based on experimental databases of three-dimensional compounds, npj Comput. Mater., 2020, 6(1), 158.
21. X. Jiang, Q. Liu, J. Xing, N. Liu, Y. Guo, Z. Liu and J. Zhao, Recent progress on 2D magnets: Fundamental mechanism, structural design and modification, Appl. Phys. Rev., 2021, 8(3), 031305.
22. C. M. Acosta, E. Ogoshi, J. A. Souza and G. M. Dalpian, Machine Learning Study of the Magnetic Ordering in 2D Materials, ACS Appl. Mater. Interfaces, 2022, 14(7), 9418–9432.
23. A. Tellez-Mora, X. He, E. Bousquet, L. Wirtz and A. H. Romero, Systematic determination of a materials magnetic ground state from first principles, npj Comput. Mater., 2024, 10(1), 20.
24. B. L. Chittari, Y. Park, D. Lee, M. Han, A. H. MacDonald, E. Hwang and J. Jung, Electronic and magnetic properties of single-layer MPX₃ metal phosphorous trichalcogenides, Phys. Rev. B, 2016, 94, 184428.
25. L. Hu, X. Wu and J. Yang, Mn₂C monolayer: a 2D antiferromagnetic metal with high Neel temperature and large spin-orbit coupling, Nanoscale, 2016, 8(26), 12939–12945.
26. K. Luo, X.-H. Zha, Q. Huang, C.-T. Lin, M. Yang, S. Zhou and S. Du, First-principles study of magnetism in some novel MXene materials, RSC Adv., 2020, 10, 44430–44436.
27. N. C. Frey, A. Bandyopadhyay, H. Kumar, B. Anasori, Y. Gogotsi and V. B. Shenoy, Surface-Engineered MXenes: Electric Field Control of Magnetism and Enhanced Magnetic Anisotropy, ACS Nano, 2019, 13(3), 2831–2839.
28. J. He, P. Lyu, L. Z. Sun, Á. M. García and P. Nachtigall, High temperature spin-polarized semiconductivity with zero magnetization in two-dimensional Janus MXenes, J. Mater. Chem. C, 2016, 4, 6500–6509.
29. Y. Niu, H. Lv, X. Wu and J. Yang, Electric-Field Control of Spin Polarization above Room Temperature in Single-Layer A-Type Antiferromagnetic Semiconductor, J. Phys. Chem. Lett., 2023, 14(17), 4042–4049.
30. J.-J. Zhang, L. Lin, Y. Zhang, M. Wu, B. I. Yakobson and S. Dong, Type-II Multiferroic Hf₂VC₂F₂ MXene Monolayer with High Transition Temperature, J. Am. Chem. Soc., 2018, 140(30), 9768–9773.
31. J. He, P. Lyu and P. Nachtigall, New two-dimensional Mn-based MXenes with room-temperature ferromagnetism and half-metallicity, J. Mater. Chem. C, 2016, 4(47), 11143–11149.
32. G. Wang and Y. Liao, Theoretical prediction of robust and intrinsic half-metallicity in Ni₂N MXene with different types of surface terminations, Appl. Surf. Sci., 2017, 426, 804–811.
33. Y. Wang, S.-S. Wang, Y. Lu, J. Jiang and S. A. Yang, Strain-Induced Isostructural and Magnetic Phase Transitions in Monolayer MoN₂, Nano Lett., 2016, 16(7), 4576–4582.
34. P. Lv, Y.-L. Li and J.-F. Wang, Monolayer Ti₂C MXene: manipulating magnetic properties and electronic structures by an electric field, Phys. Chem. Chem. Phys., 2020, 22, 11266–11272.
35. Q. Gao and H. Zhang, Magnetic i-MXenes: a new class of multifunctional two-dimensional materials, Nanoscale, 2020, 12, 5995–6001.
36. B. Akgenc, E. Vatansever and F. Ersan, Tuning of electronic structure, magnetic phase, and transition temperature in two-dimensional Cr-based Janus MXenes, Phys. Rev. Mater., 2021, 5, 083403.
37. J. Zhang, Y. Chen and X. Wang, Two-dimensional covalent carbon nitride nanosheets: synthesis, functionalization, and applications, Energy Environ. Sci., 2015, 8, 3092–3108.
38. Z. H. Fu, Q. F. Zhang, D. Legut, C. Si, T. C. Germann, T. Lookman, S. Y. Du, J. S. Francisco and R. F. Zhang, Stabilization and strengthening effects of functional groups in two-dimensional titanium carbide, Phys. Rev. B, 2016, 94, 104103.
39. R. M. Ronchi, J. T. Arantes and S. F. Santos, Synthesis, structure, properties and applications of MXenes: Current status and perspectives, Ceram. Int., 2019, 45(15), 18167–18188.
40. K. Luo, X.-H. Zha, Y. Zhou, Q. Huang, S. Zhou and S. Du, Theoretical exploration on the vibrational and mechanical properties of M₃C₂/M₃C₂T₂ MXenes, Int. J. Quantum Chem., 2020, 120(24), e26409.
41. Z. M. Sun, Progress in research and development on MAX phases: a family of layered ternary compounds, Int. Mater. Rev., 2011, 56(3), 143–166.
42. K. Luo, X.-H. Zha, Q. Huang, C.-T. Lin, R. Zhang and S. Du, Theoretical investigations on helium trapping in the Zr/Ti₂AlC interface, Surf. Coat. Technol., 2017, 322, 19–24.
43. W. Feng, C. Q. Xu, S. Cui, H. Hu, G. Q. Zhang and Z. T. Lv, First-principles study of elastic and structural properties of Zr₃Al₃C₅, Eur. Phys. J. B, 2012, 85(11), 391.
44. J. Zhou, X. Zha, F. Y. Chen, Q. Ye, P. Eklund, S. Du and Q. Huang, A Two-Dimensional Zirconium Carbide by Selective Etching of Al₃C₃ from Nanolaminated Zr₃Al₃C₅, Angew. Chem., Int. Ed., 2016, 55(16), 5008–5013.
45. S. K. Lam, A. Pitrou and S. Seibert, Numba: A LLVM-Based Python JIT Compiler, LLVM’15, New York, NY, USA, 2015.
46. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
47. John P. Perdew, J. A. Chevary, S. H. Vosko, Koblar A. Jackson, Mark R. Pederson, D. J. Singh and Carlos Fiolhais, Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
48. J. Hafner, Ab initio Simulations of Materials using VASP: Density-Functional Theory and Beyond, J. Comput. Chem., 2008, 29(13), 2044–2078.
49. J. Klimeš, D. R. Bowler and A. Michaelides, Chemical accuracy for the van der Waals density functional, J. Phys.: Condens. Matter, 2009, 22(2), 022201.
50. J. Klimeš, D. R. Bowler and A. Michaelides, van der Waals density functionals applied to solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
51. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
52. J. He, G. Ding, C. Zhong, S. Li, D. Li and G. Zhang, Cr₂TiC₂-based double MXenes: novel 2D bipolar antiferromagnetic semiconductor with gate-controllable spin orientation toward antiferromagnetic spintronics, Nanoscale, 2019, 11, 356–364.
53. J. Heyd and G. E. Scuseria, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118(18), 8207–8215.
54. J. Heyd and G. E. Scuseria, Erratum: “Hybrid functionals based on a screened Coulomb potential” [J. Chem. Phys. 118, 8207 (2003)], J. Chem. Phys., 2006, 124(21), 219906.
55. S. A. Khandy, K. Kaur, S. Marutheeswaran and I. Islam, Understanding the Ultralow Thermal Conductivity and Strong Anharmonicity of a Lanthanum-Based Germanium Halide Monolayer for Possible Thermoelectric Applications, ACS Appl. Energy Mater., 2024, 7(20), 9279–9288.
56. J. H. Malik, I. Islam, R. Tomar and S. A. Khandy, Electronic structure, photocatalytic and electrochemical performance of chalcogenide quantum dots loaded on reduced graphene oxide: (Cu₂MnSnS₄/rGO), Ceram. Int., 2024, 50(21, Part B), 42886–42894.
57. S. Zhang, R. Xu, N. Luo and X. Zou, Two-dimensional magnetic materials: structures, properties and external controls, Nanoscale, 2021, 13, 1398–1424.
58. Y.-J. Zhang, R.-N. Wang, G.-Y. Dong, S.-F. Wang, G.-S. Fu and J.-L. Wang, Mechanical properties of 1T-, 1T′-, and 1H-MX₂ monolayers and their 1H/1T′-MX₂ (M = Mo, W and X = S, Se, Te) heterostructures, AIP Adv., 2019, 9(12), 125208.

---

Footnote

† Electronic supplementary information (ESI) available: The geometric structures and calculated relative energy for MnCaSn and FeTe; equation to calculate Js with a 2D square lattice; total energy variation under x or y-axis stain for V₂CT₂ MXenes. See DOI: https://doi.org/10.1039/d4tc05199h

---