 Open Access Article
Open Access ArticleOptical and excitonic properties of calcite CaCO3†
Jozef
Janovec
*ab,
Jorge S.
Dolado
 ac and
Andrés
Ayuela
ac and
Andrés
Ayuela
 *ac
*ac
aCentro de Física de Materiales-MPC, CSIC-UPV/EHU, Manuel de Lardizabal 5, 20018 San Sebastián, Spain. E-mail: a.ayuela@csic.es
bDepartment of Advanced Polymers and Materials: Physics, Chemistry and Technology, Faculty of Chemistry, University of the Basque Country (UPV/EHU), Manuel de Lardizabal 3, 20018 San Sebastián, Spain. E-mail: jozef.janovec@ehu.eus
cDonostia International Physics Center (DIPC), Manuel de Lardizabal 4, 20018 San Sebastián, Spain
First published on 4th February 2025
Abstract
Calcite has been successfully used as a substrate or coating material in optical devices, but very little is known about its own optical properties. In this study, we present a comprehensive analysis of the optical properties of CaCO3 calcite, a typical representative of metal carbonates, obtained using the density functional theory (DFT), GW, and Bethe–Salpeter equation (BSE) methods. Our findings demonstrate that the onset of the CaCO3 optical spectrum is characterized by bound excitons, with the excitonic wavefunction primarily localized on the CO3 units. We find that calcite exhibits two different types of excitons: a Frenkel-type exciton centered on the CO3 units, leading to a narrow absorption band, and a more delocalized charge-transfer exciton that contributes more significantly to the optical spectra. The excitons exhibit a strong anisotropy with a larger spatial extent in the xy plane, along the layers of the CO3 molecules. Our results provide insight into the electronic structure and reveal the distinctive optical properties of calcite, with further implications for optical applications and the design of nanodevices, where an accurate description of the dielectric properties is required.
1 Introduction
Calcite, the stable polymorph of CaCO3, is a versatile material with numerous applications in the chemical, paper, food, metallurgical and civil engineering industries, with rich biological and geological resources. CaCO3 is the primary constituent of limestone, which serves as the main source for cement production. Furthermore, calcite is a potential material for carbon capture and storage.1 Additionally, CaCO3 is used in photocatalysis where it appears to enhance the efficiency of photocatalytic materials. For instance, CaCO3 has been shown to improve the photocatalytic performance for the purposes of the air and water purification,2–6 the efficiency of dye-sensitized solar cells,7–9 as well as the UV sensing and the photoluminescence of nanoparticles.10,11The crystal structure of calcite (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) is shown in Fig. 1. The Ca cations occupy pseudo-cubic lattice sites within the oxygen octahedra with planar CO3 groups at the vertices. The lattice parameters of calcite are a = b = 4.99 Å and c = 17.06 Å,12,13 determined by the room temperature X-ray diffraction experiments.
c) is shown in Fig. 1. The Ca cations occupy pseudo-cubic lattice sites within the oxygen octahedra with planar CO3 groups at the vertices. The lattice parameters of calcite are a = b = 4.99 Å and c = 17.06 Å,12,13 determined by the room temperature X-ray diffraction experiments.
 | ||
| Fig. 1 Crystal structure of CaCO3 calcite: (a) primitive rhombohedral computational cell and (b) conventional hexagonal unit cell, which shows the planar arrangement of CO3 structural units. | ||
The CaCO3 polymorphs exhibit large birefringence, which can be attributed to the planar arrangement of the trigonal CO3 groups oriented perpendicular to the z crystallographic axis. Previous density functional theory (DFT)14,15 calculations, using the independent particle approximation (IPA), have already shown the pronounced optical anisotropy.16,17 Despite its technological importance, the optical properties of CaCO3 have not been extensively studied. Several experimental works have reported a strong reflectance within the CO3 plane (ordinary ray), with peaks observed at 7.55 eV and 7.75 eV18 or 8 eV.19 The main spectral feature was attributed to a localized molecular excitation of the CO3 radical.19 On the other hand, most of the scattering experiments do not detect such a pronounced peak at the absorption edge.20–22 Nevertheless, methods such as low-loss electron energy-loss spectroscopy (LEELS) are capable of detecting a separate low-intensity peak at the spectrum onset,23 which suggests a strong dependence of the main peak on the momentum transfer. Optical excitations, with negligible momentum transfer, and low-energy electron methods are able to capture the onset peak, while the higher-energy scattering experiments are not. Therefore a further detailed study is necessary in order to fully understand the high-intensity peak observed in the reflection spectrum. First principles calculations can provide a deeper insight into the origin and characteristics of the spectral features.
Regarding the band gap of CaCO3, there is a scarcity of experimental data available. The measurement of the electronic properties is challenging due to a number of factors. Low-energy probe beams are sensitive to the surface states, defects and charging, while the high-energy beams can induce surface deformation and chemical decomposition.19,20,22,23 The extrapolation of the linear part of the first peak in the light reflection spectrum suggests that the optical band gap of calcite is equal to 7.5 eV.19 The scattering experiments have reported a band gap of 6 eV,20 a value that was later revised to 7.1–7.5 eV.22,23 The ground state DFT calculations have reported an indirect fundamental band gap of approximately 5 eV,16,17,23 a value that is significantly lower than the experimental one. In order to provide a more accurate description of the electronic structure of CaCO3, more sophisticated theoretical approaches must be employed.
In general, the underestimation of the electronic band gap is a common problem of semi-local exchange–correlation potentials such as the generalized gradient approximation (GGA).24 Some improvement can be achieved by using a meta-GGA exchange–correlation such as the strongly correlated SCAN approximation,25 which introduces the dependence on the second derivative of the local density. Beyond DFT, the band gap problem is often addressed using the many-body perturbation theory (MBPT) such as GW approximation,26–30 where the excited electrons (and holes) interact with the surrounding charge and induce a local rearrangement of the electron density. These particles, also known as quasiparticles, interact via a dynamically screened potential W instead of the stronger bare Coulomb interaction used in DFT.26 The screened Coulomb potential is proportional to the frequency dependent dielectric matrix. The GW approach corrects the electronic structure, opens the band gap and reproduces well charged excitations. However, the excitations within the independent quasi-particle approximation (IQPA) are described by the single particle Green's functions. Therefore, similarly to the DFT, the neutral excitations and related absorption optical spectra are reproduced poorly. In order to model a realistic optical spectrum, it is crucial to include many-body interactions.
In order to calculate a precise optical spectrum we need to solve at least a two-body problem, which includes the interaction of excited electrons with holes. The electron–hole (e–h) interaction can be described by the solution of the Bethe–Salpeter equation (BSE).28,31–33 In systems with band gaps, electron excitations can lead to the formation of hydrogen-like bound states, known as excitons. The optical spectrum of excitonic materials exhibits distinct absorption peaks below the energy of direct interband transitions, which are attributed to the finite binding energy of the e–h pairs. In general, the BSE method provides an excellent agreement with experimental spectra thanks to the prediction of distinct exciton peaks, modified transition oscillator strengths and a red-shifted spectral weights with respect to IQPA spectra. Calcite is a potential candidate for the complex excitonic response, hinted by the presence of excitons in its hydrated form Ca(OH)2.34
The aim of the present study is to contribute to a better understanding of the optical and dielectric properties of calcite by including the electron–hole interactions. First we compare the ground state exchange–correlation functionals, specifically GGA and SCAN, which serve as the foundation for the G0W0 calculations. Subsequently, an analysis of the electronic structure and optical spectra is presented. The optical and excitonic properties of calcite are unique and arise from the electronic structure and the planar arrangement of the CO3 groups. We find that the presence of bound excitons, in particular the charge-transfer exciton, plays a crucial role in determining the optical properties. The anisotropy of calcite, both in terms of its optical properties and the nature of the excitons, makes it a promising material for a variety of optical applications.
2 Methods and computational details
We employed the DFT using a plane-wave basis set in combination with the projector augmented wave (PAW) method,35 as implemented in the Vienna Ab-initio Simulation Package (VASP).36,37 The exchange–correlation potential was approximated using GGA, following the Perdew–Burke–Ernzerhof (PBE) parametrization,24 and the meta-GGA SCAN25 functional. The ten atoms computational cell, shown in Fig. 1a, was optimized using the quasi-Newtonian ionic relaxation with the 10−8 eV convergence criterion. The Gaussian smearing method was used for integration over the Brillouin zone (BZ), with the smearing width of 0.05 eV and 0.01 eV for the ground state and the optical spectra calculations, respectively. The BZ was sampled by a 6 × 6 × 6 Γ-centered k-mesh. We used the GW version of PAW potentials including 3s 3p 4s valence electrons for Ca and 2s 2p for C and O. The plane-wave expansion energy cutoff was set to 800 eV for the ground state calculations.The fully frequency-dependent single-shot G0W0 method29 was used with the 500 eV energy cutoff for the plane waves. The cutoff for the response function expansion was set to two-thirds of the plane wave cutoff. The polarizability was calculated on 100 frequency points in combination with 1024 unoccupied bands in the self-energy sum. This setup guaranteed that the GW band gap was converged below 0.1 eV, as shown in Fig. S1 (ESI†).
Within the framework of BSE, the e–h problem is characterized by an effective two-particle Hamiltonian. The BSE transformed into an eigenvalue problem yields
 | (1) |
 , which consists of the attractive, statically screened Coulomb potential and a repulsive bare exchange interaction. The solution of the BSE equation are the eigenvalues Eλ and the e–h wavefunction coefficients Aλcvk, that define the exciton λ. The indices v, c and k run over the valence bands, conduction bands and k-vectors, while v′, c′ and k′ denote a scattered configuration vck → v′c′k′ of an electron and a hole. The coefficients Aλcvk contain information about the spatial localization and can be used to construct the excitonic wavefunction in the basis of the ground state optimized electron–hole orbitals.28,38 The macroscopic dielectric function within the Tamm–Dancoff approximation39,40 is expressed as
, which consists of the attractive, statically screened Coulomb potential and a repulsive bare exchange interaction. The solution of the BSE equation are the eigenvalues Eλ and the e–h wavefunction coefficients Aλcvk, that define the exciton λ. The indices v, c and k run over the valence bands, conduction bands and k-vectors, while v′, c′ and k′ denote a scattered configuration vck → v′c′k′ of an electron and a hole. The coefficients Aλcvk contain information about the spatial localization and can be used to construct the excitonic wavefunction in the basis of the ground state optimized electron–hole orbitals.28,38 The macroscopic dielectric function within the Tamm–Dancoff approximation39,40 is expressed as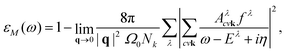 | (2) |
As calculations on dense k-meshes quickly become unmanageable for GW and BSE, we applied a two-step k-averaging approach for the BSE spectra calculations.40 First, we ran a single n × n × n (n3) mesh calculation to obtain the irreducible k-points. In the second step we executed a set of calculations on the m3k-mesh, each of which was shifted according to the irreducible k-points obtained in the first step. To obtain the spectrum we averaged over the dielectric functions calculated in the second step, weighted by the corresponding irreducible k-point weights from the first step. In this way we obtained the dielectric function that effectively corresponds to a (m × n)3k-mesh. For CaCO3 the k-averaging of the dielectric function was performed with m = 6 (each spectrum calculated on 63k-mesh) and n = 3, which corresponds to an average of 12 spectra.
The density of states (DOS), the orbital projection, the crystal orbital Hamilton overlap (COHP)43 bonding analysis and the population analysis were studied using the LOBSTER package.44,45 The COHP divides interatomic interactions into bonding with negative COHP and antibonding with positive COHP. The corrected GW electronic structure was taken as the input for the LOBSTER calculations.
3 Results
3.1 Crystal and electronic structure
The optimized lattice parameters of the conventional unit cell are presented in Table 1. The SCAN method predicts lattice parameters that are in a closer agreement with the experimental results when compared to GGA. Both methods correctly predict the lattice parameter a larger than the experimental one measured at the room temperature, in agreement with the negative thermal expansion coefficient of calcite in the xy plane.12 On the other hand, the c constant is clearly overestimated in GGA, while the SCAN functional correctly predicts the trend of lower c constant. The experimental lattice constants extrapolated to 0 K are a(0 K) = 4.994 Å and c(0 K) = 16.936 Å, using the expansion coefficient from ref. 12. For comparison, the hybrid functionals predict the lattice constants correctly only when used with van der Waals corrections, which reduce the c constant.46| GGA/GGA + G0W0 | SCAN/SCAN + G0W0 | Experiment | ||
|---|---|---|---|---|
| a Conduction band minimum is at three-fourths of the Γ–T distance. | ||||
| Lattice | a [Å] | 5.051 | 5.002 | 4.994 (4.989) |
| c [Å] | 17.217 | 16.821 | 16.936 (17.062) | |
| V [Å 3] | 380.37 | 364.53 | 365.79 (367.78) | |
| Dielectric constant | ε xy ∞ | 3.2/2.8 | 3.0/2.6 | 2.6 |
| ε z ∞ | 2.5/2.2 | 2.4/2.1 | 2.2 | |
| ε xy I | 6.0 | 6.1 | 6.0 | |
| ε x I | 4.7 | 5.7 | 6.1 | |
| BG | F−Γ | 5.03a/7.85 | 6.05a/8.35 | 7.10 |
| Γ−Γ | 5.63/8.20 | 6.35/8.71 | ||
The optical anisotropy of CaCO3 is reflected in the dielectric constants. At low frequencies, the experimental ε0 = ε∞ + εI is equal to 8.64 in the xy polarization and 8.23 in the z direction, which is parallel to the optical axis.47 The electron contribution, derived from far-infrared reflectance measurements, yields ε∞ = 2.63 along the xy plane and 2.17 along the z direction,47 with an almost isotropic ionic dielectric constant εI ≈ 6. The agreement of the dielectric constants calculated using the RPA local field effects is demonstrated in Table 1. The G0W0 approximation brings ε∞ even closer to the experimental values, especially when the starting point is the SCAN calculation.
The SCAN functional increases the band gap of CaCO3, a phenomenon that can be partially attributed to the reduction in lattice constants. The G0W0 correction opens the band gap of the SCAN ground state up to 8.35 eV, compared to the experimental optical gap of 7.1 eV.22,23 All methods agree in predicting an indirect fundamental gap, with the valence band maximum (VBM) positioned at the F (0.5, 0.5, 0.0) point. On the contrary, the conduction band minimum (CBM) calculated by the DFT is located between the Γ and T (0.5, 0.5, 0.5) points, whereas the MBPT calculations indicate that the CBM is located at the Γ point. The hybrid functionals B3LYP and PBE0 predic 7.42 eV and 8.01 eV band gaps.46 The SCAN + G0W0 method predicts similar values without including semiempirical corrections.
A comparison of the SCAN and SCAN + G0W0 band structures is shown in Fig. 2a. The main distinction between the two is the band gap opening and the increased separation between the conduction bands predicted by the G0W0 method. We also study the atom-projected DOS calculated using the LOBSTER tool, shown in Fig. 2b, and the orbital-projected band structures, shown in Fig. 2d–f. The SCAN results are in qualitative agreement with those of the GGA calculations.16,23,48 The valence region can be divided into three sections: (i) the uppermost set of flat bands above −3 eV, composed almost entirely of O 2p orbitals, (ii) the region just below −5 eV is characterized by two DOS peaks, which correspond to hybridized C–O states, and (iii) the DOS peak at −8 eV which arises from the interaction of C–O 2s electrons with the in-plane 2pxy orbitals of O. The lower intensity peak of the double DOS peak, situated just below −5 eV, arises from the overlap of C and O 2pz orbitals, and the second peak, located below −6 eV, exhibits a hybridized 2s–2pxy character. At lower energies, below −20 eV, the Ca 3p states overlap with the O 2s and C 2pxy orbitals, followed by mostly the O 2s orbitals at −25 eV, and the Ca 3s orbitals at −40 eV.
The bottom of the conduction region is characterized by a set of flat C–O pz bands with additional contribution from the s and d orbitals. In the vicinity of the Γ point, these flat bands hybridize with the Ca–O s bands characterized by a larger curvature. The region above 10 eV is predominantly composed of Ca d orbitals, which can be divided into two main DOS peaks. The crystal field splitting results in the formation of degenerate dxy−dx2−y2 orbitals, which together with dz2, give rise to the wider peak observed between 10 and 13 eV. The third set of degenerate dyz−dxz orbitals contributes the most to the peak located at 15 eV. The higher energy conduction bands consist of sp bands with contributions from all atoms.
CaCO3 is a material which exhibits a mixture of ionic and covalent bonding.16,49 The C–O bond is characterized by bonding COHP peaks in the C–O sp energy region, as shown by the orange line in Fig. 2c. The σ bond is formed through the hybridization of the in-plane pxy and s orbitals. Furthermore, most of the C 2pz electrons are concentrated on the flat bands in the energy range between −5 eV and −7 eV. These orbitals overlap with the O pz states to form π bonds. The bonding states are followed by the non-bonding O p region, which is separated from the antibonding π* and σ* states by the band gap.
The second most important interaction indicated by the COHP integrated up to the Fermi level (ICOHP, in units of eV) is the ionic Ca–O bond. As shown by the blue line in Fig. 2c, this bond is around eight times weaker than the C–O bond. The Ca–O interaction contributes to the bonding primarily in the s and pxy valence energy region. The charge redistribution results in the formation of positively charged Ca and C atoms, with a loss of 1.25 and 0.75 electrons per atom, respectively. On the contrary, the O atoms exhibit a −0.67e negative charge, as predicted by the Lowdin charge distribution. In comparison, the previously reported Mulliken population analysis have indicated a positive charge of 1.72/0.55 on the Ca/C atoms and an electron excess of −0.76e on the oxygen.16 The non-bonding O p electrons above −3 eV interact weakly with each other, as shown by the green line in Fig. 2c. This interaction results in the formation of a slightly bonding bond through the pz orbitals and an antibonding interaction of pxy orbitals, which contribute minimally to the overall bonding.
3.2 Optical spectrum
First we compare the spectra calculated using IPA and G0W0 theories with that obtained using the BSE method, as shown in Fig. 3. The optical anisotropy between the two polarization directions is observed at all levels of theory. The onset of the spectra is predominantly formed by the in-plane polarization response, with a negligible contribution from the out-of-plane polarization. The IPA and IQPA (G0W0) spectra exhibit comparable features, with a shift of approximately 3 eV. In both cases, the spectrum begins with a low-intensity peak, followed by the main peak, which has almost a double intensity in the case of IPA. The origin of the peaks can be attributed to the interband transitions and can be visualized in the joint band structure (see Fig. S3, ESI†). In both the IPA and the IQPA approaches, the two peaks at the spectral onset arise mostly from the transitions to the two lowest conduction bands at the Brillouin zone edges.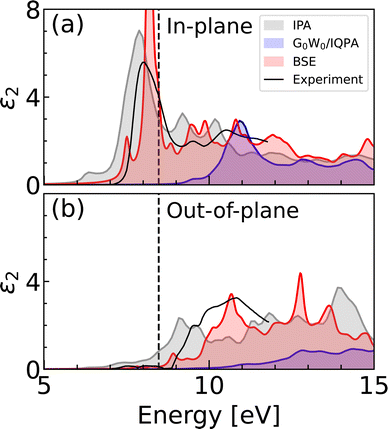 | ||
| Fig. 3 Imaginary dielectric function calculated using SCAN (IPA), SCAN + G0W0 (IQPA) and BSE on top of SCAN + G0W0, compared with experimental data.19 Panels show (a) in-plane polarization corresponding to the CO3 planes, and (b) out-of-plane polarization along the z-axis. Dashed line corresponds to the indirect band gap. The calculated curves were obtained using the 6 × 3 k-mesh averaging, following the notation introduced in Methods section. | ||
The presence of BSE peaks within the band gap indicates the formation of bound excitons, which are observed almost exclusively in the in-plane polarization direction. In addition to the main excitonic peak at 8.2 eV, we report another lower intensity peak at 7.5 eV, which marks the onset of the spectral profile. The available experimental data on the light absorption of calcite is limited and allows for comparison only up to 12 eV. The experimental dielectric function is characterized by a dominant peak in the in-plane polarization, followed by two low-intensity peaks around 10 eV, in agreement with the BSE spectrum. The main experimental peak has been observed to be broader and of lower intensity, which can likely be ascribed to the finite temperature effects. The absence of the small excitonic peak predicted by BSE may also be explained by thermal disorder. The positions of the spectral features in the out-of-plane polarization are in line with the experiment. The real part of the dielectric function is shown in Fig. S4 (ESI†).
 | ||
| Fig. 4 G0W0 + BSE excitonic spectrum. (a) Dielectric function ε2 calculated using 6 × 3 k-mesh averaging (red line), with BSE oscillator strengths (green lines) and dark exciton energies (negative black lines), compared to the experiment.19 (b)–(d) Amplitude of coupling coefficient |Aλcvk|2 summed over all bands projected onto (100) plane of the Brillouin zone, showing the reciprocal space distribution of excitons highlighted in the panel a. (e)–(g) Band structure segments with |Aλcvk|2 represented by the circle size, calculated on 123k-mesh. | ||
We first focus on the peak A, shown in more detail in Fig. 4e. The exciton comprises transitions from the non-bonding O p upper valence bands to the two lowest π* conduction bands. The involved valence bands are primarily composed of O pz states, and the conduction bands are defined by the hybridization of the C–O pz and Ca d orbitals. The topmost flat valence band with O pxy character has a negligible contribution to the formation of the exciton. The exciton is delocalized across the entire Brillouin zone, with a larger contribution along the Γ−T high symmetry path, which is evident from the reciprocal space distribution of  in the (100) BZ cut, as shown in Fig. 4b. The delocalized nature of the exciton A in the k-space is manifested by the fact that the there are no k-points in the Brillouin zone with a negligible contribution to
in the (100) BZ cut, as shown in Fig. 4b. The delocalized nature of the exciton A in the k-space is manifested by the fact that the there are no k-points in the Brillouin zone with a negligible contribution to 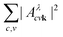 .
.
The main peak B is composed of two excitons with comparable optical strengths, denoted here as B1 and B2. The exciton B1 stems mostly from a single pair of bands that form the band gap edges (Fig. 4f). The exciton develops between a hole in the nonbonding O pxy valence band and an excited electron in the π* band. In contrast to the exciton A, the exciton B1 is delocalized in all k-space directions, except along the Γ−T direction. The excitonic wavefunction shows a disperse character with the highest contribution from k-points situated between the center and vertices of the BZ, as shown in Fig. 4c.
The exciton B2 has a complementary character to the exciton B1. It originates from the transitions between the two topmost valence bands and the second lowest conduction band. Analogously to the peak B1, the contribution from the Γ–T path to the peak B2 is minimal. The largest contribution to |Aλcvk|2 comes from the bands where the exciton B1 has a small amplitude, i.e. close to the BZ faces. The two peaks B1 and B2 taken together are responsible for excitations between the three uppermost valence and the three lowest conduction bands.
Fig. 5 illustrates the excitonic wavefunction in real space with the hole fixed on an oxygen atom. In agreement with the previous analysis, the main excitons are found to be highly confined. The exciton A, as shown in Fig. 5a, is localized exclusively on the CO3 units with negligible in-plane extension. This outcome was expected based on the nearly uniform distribution of the excitonic wavefunction in the reciprocal space. In contrast, the peak B exhibits a somewhat different picture. Both excitons B1 (Fig. 5b) and B2 (Fig. 5c) involve Ca electrons and show a certain degree of delocalization. The anisotropy of the exciton B1, predicted from the wavefunction distribution in the reciprocal space, is evident from the exciton charge density map in real space. The exciton B1 shows a larger degree of spacial extension in the xy plane than in the z direction. Similar observations with lower delocalization in xy plane apply to the exciton B2. Despite the larger delocalization of the B excitons compared to the excion A, both are highly confined, spanning mainly over the nearest Ca atoms and the CO3 units around the hole. The excitons B1 and B2 do not extend over four CO3 planes in the z direction. Based on the presented analysis, the exciton A can be considered the Frenkel molecular type centered on a single CO3 unit. The B excitons, besides being localized mostly on the CO3 units, include contributions from the Ca atoms, which points towards the charge-transfer excitonic character.
 | ||
| Fig. 5 Exciton charge density map in real space of (a) exciton A, (b) exciton B1, and (c) exciton B2. In all cases, the hole is located on the O atom. | ||
The position of excitonic peaks in the spectrum is related to the binding energy Eexc, which results from the e–h interaction. In general, the binding energy is determined by subtracting the exciton energy (Eλ) from the electronic band gap. A determination of the Eexc for a delocalized exciton is problematic. Here we calculated the binding energy as the difference between Eλ and the interband separation at the k-point with the largest value of |Aλcvk|2. The calculated BSE binding energies of the excitons A and B are large, equal to 1.65 eV and 1.05 eV. However, the supercell calculation predicts binding energies lower by 40%, as shown in Fig. S6 (ESI†). Large binding energies of excitons centered on the planar CO3 units agree with the excitons in low-dimensional systems.50
4 Discussion
Although the G0W0 method might seem to overshoot the measured optical band gap, the BSE and experimental dielectric functions coincide with a remarkable precision, as shown in Fig. 6a. The discrepancy with the experimental value can be attributed to the fact that the tabulated experimental band gap corresponds to the optical absorption threshold, which is obtained through an interpolation of the linear part of the first peak observed in an optical spectrum. In the presence of excitons, this method strongly biased and can results in a significant underestimation of the electronic band gap.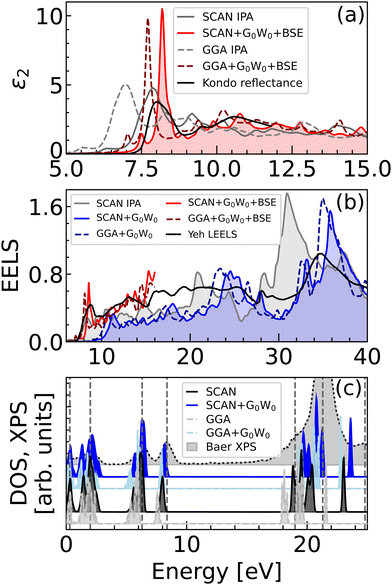 | ||
| Fig. 6 Comparison of optical spectra calculated using GGA, SCAN and G0W0 with the experimental data. (a) Dielectric function,19 (b) electron-loss function (ELF),23 and (c) X-ray photoelectron spectrum,20 with the first peak aligned to zero energy. Both theoretical and experimental ε and ELF curves were averaged over the three polarization directions. | ||
It is noteworthy that the main IPA peak within the SCAN approximation falls on top of the most intense experimental peak, a fact that might ask for a reconsideration of the GW and BSE calculations. This peak arises from transitions that involve multiple higher conduction bands, as shown in Fig. S3a (ESI†). Conversely, the high-intensity peak in the BSE spectrum predominantly includes the band edge transitions and correctly predicts the spectral onset.
Similarly, the experimental electron energy-loss spectroscopy (EELS) data23 in Fig. 6b agrees closely with the energy-loss function (ELF) calculated using G0W0 + BSE on top of SCAN, defined as ELF = Im(−1/ε) = ε2/(ε12 + ε22). The onset of the EELS spectrum is the most accurately approximated using BSE and the plasmon peak around 35 eV is matched by the G0W0 method with better precision than by the IPA calculations, which predict its position at lower energies.
In order to analyze the occupied electronic states, we compare the calculated DOS and the experimental X-ray photoelectron spectroscopy spectrum (XPS) in Fig. 6c. Again, the agreement with the experiment is enhanced when using the GW correction. Both the DFT and G0W0 results agree acceptably with the experimental emission peaks below 10 eV (vertical dashed lines). However, the DFT description of the deeper lying states is innacurate, with energy shifts in the order of several eV. The GW approximation enhances the separation of the lower energy states, which leads to a more precise comparison with the XPS experimental results.
Based on the discussion above, it becomes evident that the DFT band structure of calcite requires corrections, and the overlap of the main ε2 peak calculated using SCAN and the experimental one can be considered coincidental. It can therefore be concluded that the electronic band gap predicted by GW must be reevaluated as an accurate value. The GW band gap corresponds to the description of charged excitations, where an electron is either removed or added to the system, analogous to a photoemission experiment. It may hence be anticipated that there will be an improved agreement between the XPS spectra and the GW spectrum. The description of neutral excitations, such as those observed in light absorption experiments, depends on the electron–hole interaction, as evidenced by the BSE results.
The analysis of excitons in calcite underscores the many-body nature of the electron–hole interaction, emphasized by the interplay between multiple valence and conduction bands forming an exciton. The excitons plotted in Fig. 4 contain contributions from various valence and conduction bands. This mixing is the most evident in the case of the peak A, where most of the valence bands up to −3 eV contribute to the excitonic wavefunction. Indeed, the BSE matrix elements and the spectrum are obtained as the summation over all valence and conduction bands, as indicated in eqn (2). The spectrum of CaCO3 displays a slow convergence with respect to the number of the bands, especially with regard to the position of the main peak. As a result, the optical spectrum is converged after using at least 18 valence and 24 conduction bands.
The main exciton peak in calcite arises from transitions between the O pxy and C–O π* states, as shown in Fig. 4c. Although these transitions are expected to be dipole forbidden, they are optically active due to the hybridization of the lowest conduction band with s and d states. Furthermore, the Γ point may also support a bound exciton, given that the transition from the VBM (eu) to the CBM (a1g) is allowed by symmetry and the joint density of states has a minimum here (the M0 critical point51), as can be seen in Fig. S3 (ESI†). Nonetheless, no bright exciton is found to be localized at the Γ point. The VBM is dispersionless and characterized by non-bonding O pxy states, while the CBM at the Γ point is mainly composed of Ca 4s states. In this case, the minimal overlap between the electron and hole wavefunctions of the Ca and O atoms results in the formation of a dark exciton, situated at 7.8 eV.
The precision of GW and BSE depends largely on the choice of the ground state method. The SCAN structural relaxation predicts a smaller unit cell than the GGA and hybrid functionals.18 The structural optimization using the SCAN approach yields better results than the GGA functional. Moreover, the SCAN functional yields a band gap that is larger than that obtained with the GGA by 1 eV, which brings the calculation closer to the physical picture. The dielectric function obtained by GGA, SCAN, and from the light reflectance experiment are compared in Fig. 6a. The G0W0 + BSE method applied on top of GGA and SCAN functionals predict identical spectral features with comparable intensities. However, the peak positions agree better with experiments when the SCAN ground state was employed. Similarly, the onset of the experimental ELS23 in Fig. 6b is in better agreement with G0W0 + BSE on top of SCAN. Considering the XPS spectra (Fig. 6c), there is a comparable agreement between the GGA + G0W0 and SCAN + G0W0 approaches for the emission peaks below 10 eV; however, the region of higher energies (deeper lying states) is better mimicked by SCAN, especially for the Ca 3p (the main peak above 21 eV) and the O 2s peak (at 25 eV). In conclusion, the SCAN ground state calculation outperforms GGA in terms of accuracy at a comparable computational cost, without the need for empirical or semi-empirical corrections as in the case of commonly used hybrid functionals.
The observed optical anisotropy and unique excitonic character of calcite can be mainly attributed to the CO3 groups and their planar arrangement. Therefore, other isomorphic carbonates can be expected to exhibit similar excitonic behavior, including high localization and long lifetimes. Bandgap engineering can be facilitated by the partial or complete substitution of Ca cations by another element. For example, transition metal carbonates absorb visible light or even become wide-bandgap semiconductors.52 The carbonates that are optically active at lower energies may be of interest for the energy conversion applications, catalysis and others.
5 Conclusions
Our study shows that the DFT is not sufficient to describe the optical properties of calcite and higher levels of theory are necessary to accurately predict the optical spectrum and other excited state properties. The fundamental band gap calculated using SCAN + G0W0 approach equals to 8.35 eV, a value considerably larger than the experimental optical gap. Our BSE calculations explain this discrepancy by the presence of the bound excitons on the onset of the calcite optical spectra. Further analysis revealed two distinct types of excitons: (i) a Frenkel-type exciton, localized on a single CO3 molecule, which is observed as a small peak at the onset of the optical spectrum, and (ii) a charge-transfer exciton which involves the delocalization of electrons on Ca atoms and is represented by the main peak in the optical spectrum. Furthermore, calcite exhibits significant optical anisotropy due to the planar arrangement of the CO3 groups perpendicular to the crystallographic z-axis. Excitons in calcite show a two-dimensional character, with a larger spatial extent in the xy-plane. This anisotropy contributes to the birefringence observed in calcite.Author contributions
Jozef Janovec: investigation, visualization, writing – original draft, writing – review & editing; Jorge S. Dolado: conceptualization, funding acquisition, writing – review & editing; Andrés Ayuela: conceptualization, funding acquisition, project administration, supervision, writing – review & editing.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
Authors declare no conflicts of interest.Acknowledgements
We acknowledge funding from the Spanish Ministry of Science and Innovation (grants no. PID2022-139230NB-I00, and TED2021-132074B-C32), the Gobierno Vasco UPV/EHU (project no. IT-1569-22), the Diputación Foral de Gipuzkoa (Project No. 2023-CIEN-000077-01), the European Commission MIRACLE project (GA 964450), and NaturSea-PV (GA 101084348). Research conducted in the scope of the Transnational Common Laboratory (LTC) Aquitaine-Euskadi Network in Green Concrete and Cement-based Materials. The authors acknowledge the computer resources at MareNostrum and the technical support provided by Barcelona Supercomputing Center (FI-2023-2-0039).References
- G. Goracci, E. Saeed, M. B. Ogundiran, A. Iturrospe, A. Arbe, C. Aymonier and J. S. Dolado, ACS Sustainable Chem. Eng., 2024, 12, 1911–1917 CrossRef CAS PubMed.
- W. Cui, J. Li, L. Chen, H. Wang, J. Sheng, Y. Sun, Y. Zhou and F. Dong, et al. , Sci. Bull., 2020, 65, 1626–1634 CrossRef CAS.
- K. Li, W. Zhou, X. Li, Q. Li, S. A. Carabineiro, S. Zhang, J. Fan and K. Lv, J. Hazard. Mater., 2023, 442, 130040 CrossRef CAS PubMed.
- X. Zhang, X. He, Z. Kang, M. Cui, D.-P. Yang and R. Luque, ACS Sustainable Chem. Eng., 2019, 7, 15762–15771 CrossRef CAS.
- X. Zhang, M. Liu, Z. Kang, B. Wang, B. Wang, F. Jiang, X. Wang, D.-P. Yang and R. Luque, Chem. Eng. J., 2020, 388, 124304 CrossRef CAS.
- C. Qi, H. Chen, X. Chen, C. Chu, X. Mei, W. Lu and N. Li, J. Environ. Sci., 2023, 126, 517–530 CrossRef CAS PubMed.
- J. Y. Kim, S. Lee, J. H. Noh, H. S. Jung and K. S. Hong, J. Electroceram., 2009, 23, 422–425 CrossRef CAS.
- M. Kaur and N. Verma, J. Mater. Sci. Technol., 2014, 30, 328–334 CrossRef CAS.
- S. F. Shaikh, R. S. Mane, Y. J. Hwang and O.-S. Joo, Electrochim. Acta, 2015, 167, 379–387 CrossRef CAS.
- H. Wei, F. He, Y. Li, Q. Zhang, Y. Zhou, H. Yan, R. He, J. Fan and W. Yang, ACS Sustainable Chem. Eng., 2019, 7, 18854–18862 CrossRef CAS.
- J. Qiu, W. Ye, X. Xu, B. Guo, R. Wang, C. Hu, J. Zhuang, H. Dong, G. Hu and Y. Liu, Cryst. Growth Des., 2022, 22, 4357–4365 CrossRef CAS.
- K. K. Rao, S. N. Naidu and K. S. Murthy, J. Phys. Chem. Solids, 1968, 29, 245–248 CrossRef CAS.
- S. M. Antao, I. Hassan, W. H. Mulder, P. L. Lee and B. H. Toby, Phys. Chem. Miner., 2009, 36, 159–169 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- F. M. Hossain, G. E. Murch, I. V. Belova and B. D. Turner, Solid State Commun., 2009, 149, 1201–1203 CrossRef CAS.
- S. Medeiros, E. Albuquerque, F. Maia, E. Caetano and V. Freire, J. Phys. D: Appl. Phys., 2007, 40, 5747 Search PubMed.
- E. Uzan, H. Damany and V. Chandrasekharan, Opt. Commun., 1969, 1, 221–222 CrossRef CAS.
- S.-i Kondo, H. Yamashita and K. Nakamura, J. Phys. Soc. Jpn., 1973, 34, 711–714 CrossRef CAS.
- D. Baer and D. L. Blanchard Jr, Appl. Surf. Sci., 1993, 72, 295–300 CrossRef CAS.
- K. S. Katti, M. Qian, D. W. Frech and M. Sarikaya, Microsc. Microanal., 1999, 5, 358–364 CrossRef CAS PubMed.
- M. Vos, G. Marmitt, Y. Finkelstein and R. Moreh, J. Chem. Phys., 2015, 143, 104203 CrossRef CAS.
- Y.-W. Yeh, S. Singh, G. Cheng, N. Yao, K. M. Rabe, D. Vanderbilt, P. E. Batson, L. Pan, G. Xu and S. Xu, Acta Mater., 2023, 257, 119191 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 Search PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 Search PubMed.
- L. Hedin, Phys. Rev., 1965, 139, A796 Search PubMed.
- M. S. Hybertsen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390 CrossRef CAS.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601 CrossRef CAS.
- M. Shishkin and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035101 CrossRef.
- F. Bruneval, F. Sottile, V. Olevano, R. Del Sole and L. Reining, Phys. Rev. Lett., 2005, 94, 186402 CrossRef.
- M. Rohlfing and S. G. Louie, Phys. Rev. Lett., 1998, 81, 2312 CrossRef CAS.
- W. Hanke and L. Sham, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 4656 CrossRef CAS.
- V. Turkowski, N. Ud Din and T. S. Rahman, Computation, 2017, 5, 39 CrossRef.
- A. Pishtshev, S. Z. Karazhanov and M. Klopov, Solid State Commun., 2014, 193, 11–15 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 Search PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- F. Fuchs, C. Rödl, A. Schleife and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 085103 Search PubMed.
- S. Dancoff, Phys. Rev., 1950, 78, 382 CrossRef.
- T. Sander, E. Maggio and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045209 CrossRef.
- H. Ehrenreich and M. H. Cohen, Phys. Rev., 1959, 115, 786 CrossRef.
- F. Sottile, F. Bruneval, A. Marinopoulos, L. Dash, S. Botti, V. Olevano, N. Vast, A. Rubio and L. Reining, Int. J. Quantum Chem., 2005, 102, 684–701 Search PubMed.
- R. Dronskowski and P. E. Blöchl, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 Search PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS.
- G. Ulian, D. Moro and G. Valdre, Phys. Chem. Chem. Phys., 2021, 23, 18899–18907 RSC.
- L. Long, M. Querry, R. J. Bell and R. W. Alexander, Infrared Phys., 1993, 34, 191–201 Search PubMed.
- M. Brik, Phys. B, 2011, 406, 1004–1012 CrossRef CAS.
- A. J. Skinner, J. P. LaFemina and H. J. Jansen, Am. Mineral., 1994, 79, 205–214 CAS.
- P. Cudazzo, L. Sponza, C. Giorgetti, L. Reining, F. Sottile and M. Gatti, Phys. Rev. Lett., 2016, 116, 066803 CrossRef PubMed.
- B. Velický and J. Sak, Phys. Status Solidi B, 1966, 16, 147–157 CrossRef.
- M. Morukuladi, N. Lethole, M. Masedi, N. Ngoepe and P. Ngoepe, J. Electrochem. Soc., 2022, 169, 020540 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc04921g |
| This journal is © The Royal Society of Chemistry 2025 |

