Large magnetoresistance and thermoelectric properties of a quasi-skutterudite Ca₃Pt₄Sn₁₃ single crystal

Abstract

We conducted a detailed study of the quasi-skutterudite Ca₃Pt₄Sn₁₃ single crystal through measurements of electrical resistivity, Hall effect, specific heat, and thermoelectric properties. The resistivity exhibited metallic behavior from 300 to 2 K. The results of resistivity, the Wilson ratio, and low-temperature magnetic susceptibility indicated non-Fermi liquid behavior in the Ca₃Pt₄Sn₁₃ crystal. Ca₃Pt₄Sn₁₃ crystals showed a large longitudinal magnetoresistance (MR) of up to 200% at 5 T and 2 K for a magnetic field applied along the [110] direction. Combined with first-principles calculation results, we believe that carrier mobility is an important factor contributing to the large MR phenomenon. Meanwhile, we also performed angle-resolved MR (AMR) measurements on the Ca₃Pt₄Sn₁₃ crystal. An eight-fold symmetry in the AMR was observed in the low-temperature region, indicating that Ca₃Pt₄Sn₁₃ could be a potential candidate for valleytronics. Furthermore, the negative slope and linear dependence observed in the Hall resistance indicated electron conductivity, while the thermoelectric power results suggested the presence of hole-like carriers. The different signs of the Hall and Seebeck coefficients could be related to the unique structure of the Fermi surface boundaries in the Ca₃Pt₄Sn₁₃ crystal. In conjunction with the above experimental observations, we found that the carrier mobility, carrier concentration, Hall coefficient, Seebeck coefficient, thermal conductivity, magnetic susceptibility, MR, and AMR all showed significant changes when the temperature dropped below T^*, indicating that they might share a common origin closely related to the T^* phase. The current findings could provide a non-superconducting system to investigate the intrinsic origin of T^* in the Ca₃T₄X₁₃ family.

---

Due to many potential applications in hard drives and magnetic sensors, new large magnetoresistance (MR) materials have attracted significant attention over the last few decades.^1–4 The giant MR (GMR) in magnetic multilayers and colossal MR (CMR) in perovskite-manganites have been widely exploited.^5–7 Recently, an extremely large MR (XMR), up to 10⁶%, without magnetic ions was found in Dirac semimetals, Weyl semimetals, and transition metal dipnictides such as TPn₂ (T = W, Mo, Nb, and Ta; Pn = P, As, Sb, and Bi),^8–13 as well as in rock salt rare-earth compounds like LaBi/Sb, and others.¹⁴ In recent years, the mechanism of XMR has been explored through both theoretical and experimental approaches.^13–16 A few different mechanisms have been proposed for the origin of XMR in materials lacking magnetic ions.¹⁷ They can be summarized as follows: (i) the origin of XMR in DSMs (Cd₃As₂, Na₃Bi, etc.) is related to the unique band structure, which exhibits linear dispersion in momentum space;^18–20 (ii) for LaBi/Sb and the WSMs of WTe₂ and T_d-MoTe₂, electron–hole (e–h) compensation also plays an important role in the formation of XMR;¹⁴ (iii) for TaTe₂ and TaNiTe₅, which have a trivial band structure, the carriers show high mobility at low temperatures.^21,22

R₃T₄X₁₃ series compounds, where R is a rare earth element, Sc, Y, or the alkaline earth metals, Ca or Sr; T is a Group VIII d-electron element; and X is either In, Ge, or Sn, are caged-structure compounds.^23–33 These compounds typically crystallize in the same primitive cubic structure with the space group Pm3̄n and exhibit remarkably different properties depending on the combination of the three elements. Hence, R₃T₄X₁₃ compounds with caged structures have attracted significant attention, as many interesting new phenomena, such as superconductivity, the Kondo effect, and good thermoelectric properties, have been observed. Among these quasi-skutterudite materials, Ca₃Ir₄Sn₁₃ displays an anomaly in the resistivity at T^* ∼ 38 K and a superconducting transition at T_c ∼ 7 K.^23–25 Some studies attributed the anomaly at T^* to ferromagnetic spin fluctuations,²³ while another study proposed a charge-density wave (CDW) scenario at T^*.²⁴ To date, the microscopic origin of T^* and its relationship with superconductivity remains an open issue. Meanwhile, superconductivity around 5 K, accompanied by clear anomalies around T^* ∼ 147 K, has also been observed in a similar compound, Sr₃Ir₄Sn₁₃.^26–28 Both compounds provide a platform to study the relationship between quantum phase transitions and superconductivity. Furthermore, the quasi-skutterudite compound, Y₃Ir₄Ge₁₃, with a large Seebeck coefficient (S), is a promising candidate for thermoelectric devices.²⁹ Owing to the strong hybridization of the localized f-electrons of R ions with the p-electrons of X, Yb₃Os₄Ge₁₃ shows a Kondo effect at low temperatures.³⁰ The R₃T₄X₁₃ series compounds provide a platform to study novel physical phenomena in materials with a cage structure. Therefore, exploring new quasi-skutterudite R₃T₄X₁₃ compounds is of great interest.

Among the R₃T₄X₁₃ family, the alkaline earth metals, Ca and Sr intermetallics, are of particular interest because of their novel properties, such as superconductivity and quantum critical behavior.^23–28 Compared with the rare earth metals, alkaline earth metals, lacking the collective hybridization of localized f-electrons with the conduction electrons, may lead to systems that are easier to understand. For example, the detailed phase diagram of Ca₃Ir₄Sn₁₃ has been studied under applied pressure and chemical changes induced by Sr ion substitution for Ca ions.^31–33 Additionally, materials with large spin–orbital (SO) coupling effects have always attracted significant attention in condensed matter physics.^34–39 Usually, the SO coupling is proportional to the atomic number Z²,³⁷ and exploring materials with larger atomic numbers could lead to stronger SO coupling effects. The controllable SO coupling effect could provide a useful way to study topological insulators, such as Bi₂(Se/Te)₃,³⁶ the quasi-one-dimensional superconductor Nb₂PdS₅,³⁷ the Weyl semimetal WTe₂,^38,39 and others. Therefore, studying and comparing the electrical and thermal transport properties in new quasi-skutterudite compounds with large SO coupling effects will be highly valuable.

In order to further explore the physical properties of quasi-skutterudite Ca₃T₄Sn₁₃-based materials, studied the isovalent substitution effect by introducing Pt onto the Ir site in the Ca₃Ir₄Sn₁₃ system. Compared with the Ir element, the Pt element has a larger atomic number, indicating a stronger SO coupling effect. Subsequently, we performed a detailed investigation of the Ca₃Pt₄Sn₁₃ crystal through measurements of electrical resistivity, specific heat, and thermoelectric properties. It exhibited metallic behavior from 300 K to 2 K. The results of the resistivity, Wilson ratio, and low-temperature magnetic susceptibility indicated that Ca₃Pt₄Sn₁₃ was a non-Fermi liquid system. The MR at T = 2 K with an applied magnetic field of H = 5 T was 200% for H along the [110] direction. Based on the Hall resistance behavior, the origin of the large MR was closely related to the high mobility of the carriers. An eight-fold symmetry in the AMR was observed in the low-temperature region. Both the results of the first-principles calculations and the different signs of the Hall and Seebeck coefficients indicated the presence of a special structure in the Fermi surface boundaries of the Ca₃Pt₄Sn₁₃ system. Furthermore, we found that the mobility of the carriers, carrier concentration, Hall coefficient, Seebeck coefficient, thermal conductivity, magnetic susceptibility, MR, and AMR all showed significant changes when the temperature dropped below T^*.

Ca₃Pt₄Sn₁₃ single crystals were grown using the flux method with Sn element as the self-flux. The starting materials of Ca (99.99%), Pt (99.99%), and Sn (99.999%) were mixed in a molar ratio of 3 : 4 : 93 and placed in alumina ampoules. All operations were performed in a glove box filled with high-purity argon. The alumina ampoules were then seeded into evacuated quartz tubes and heated in a furnace at 1050 °C for 10 h. Subsequently, the tubes were cooled to 600 °C at a rate of 2 °C h⁻¹. The quartz tubes were then inverted and spun rapidly in a centrifuge to separate the Sn flux. Crystals with approximate dimensions of 3 × 2.5 × 2.5 mm³ (shown in Fig. 1(a)) were left in the alumina ampoule. The crystals typically exhibit a larger surface with a clean (110) face. The chemical composition of the crystals was analyzed by energy dispersive X-ray (EDX) spectroscopy using a scanning electron microscope (SEM). X-ray diffraction (XRD) experiments were performed on a PANalytical X’pert diffractometer using Cu K_α1 radiation (λ = 0.15406 nm) at room temperature. A large single crystal with a (110) surface was used for the measurements. Electrical resistivity was measured with the electric current along the (110) surface using a physical property measurement system (Quantum Design, PPMS-9 T, 2 K ≤ T ≤ 400 K, 0 T ≤ H ≤ 9 T). Resistivity was measured in cooling mode using a standard four-probe technique. Thermal conductivity and thermoelectric power measurements were also performed in the PPMS. The specific heat was measured using the thermal relaxation method in the PPMS. First-principles calculations were performed using the Vienna ab initio simulation package (VASP).^40,41 The exchange–correlation potential was described using the Perdew–Burke–Ernerhof (PBE) formula within the generalized gradient approximation (GGA).⁴² The kinetic energy cutoff was set to 500 eV, and the K-point grid was set to 9 × 9 × 9 to sample the irreducible Brillouin zone (BZ). Spin–orbit coupling was included in the calculation.

Fig. 1 (a) Crystal structure of Ca₃Pt₄Sn₁₃; (b) photograph of the Ca₃Pt₄Sn₁₃ single crystal used in this study. The large surfaces are indexed based on XRD measurements. The size is approximately 3 × 2.5 × 2.5 mm³; (c) XRD patterns of the crystal measured on the (100) and (110) surfaces.

The crystal structure of Ca₃Pt₄Sn₁₃ is shown in Fig. 1(a). This structure features a cage-like network, in which one 20-coordinate cage surrounds the Ca atom and another surrounds the Pt atom, while a third cage is centered on an empty position. This configuration provides multiple available positions for the Sn atoms. Fig. 1(b) shows the studied crystal with the large (110) surface. Fig. 1(c) shows the powder XRD pattern of Ca₃Pt₄Sn₁₃, obtained from crushed single crystals. All Bragg reflections could be appropriately fitted based on the Pr₃Rh₄Sn₁₃-type cubic structure (space group: Pm3̄n, No. 223). Fig. 1(d) shows the XRD pattern of the large (110) surface.

Fig. 2(a) presents the temperature dependence of resistivity, ρ(T) for a Ca₃Pt₄Sn₁₃ single crystal at zero magnetic field, measured between 2 K and 320 K with the electrical current I along the (110) surface. It can be seen that the value of ρ(T) increases monotonically with increasing temperature, indicating metallic behavior. The residual resistance ratio (RRR), defined as ρ(300 K)/ρ(2 K), was approximately 21, indicating the high quality of the crystal studied. As shown in the inset of Fig. 2(a), at low temperatures, the ρ(T) followed the equation:

ρ(T) = ρ₀ + AT² (1)

where ρ₀ and A represent the residual resistivity and the coefficient of the T²-term, respectively. Overall, the fitting line matched well with Fermi liquid theory at high temperatures, while it showed a significant deviation from the resistivity data in the low-temperature region, as shown in the inset of Fig. 2(a). To obtain more reliable results, we considered some additional evidence, such as the Wilson coefficient and the low-temperature magnetic susceptibility behavior, to comprehensively determine whether Ca₃Pt₄Sn₁₃ conformed to a Fermi liquid system. The Wilson ratio, R_W, is an effective parameter for evaluating Fermi-liquid behavior. Usually, the values of the R_W ratio for correlated metals with strong spin–orbit coupling lie between 1 and 6.⁴³ This notably high R_W value is an outcome of the strong non-Fermi liquid nature of the compound. For example, high R_W values have been observed in non-Fermi liquid compounds such as SrIrO₃ (R_W ∼ 55)⁴⁴ and Pr₂Ir₂O₇ (R_W ∼ 21.7).⁴⁵ In our case, the Wilson ratio of Ca₃Pt₄Sn₁₃ was evaluated as R_W = π²k_B²χ₀/3μ_B²γ ∼ 9.1, which was larger than that of Ca₃Ir₄Sn₁₃ crystal (R_W ∼ 1.7),²³ indicating that Ca₃Pt₄Sn₁₃ was a possible non-Fermi liquid system. In addition to the Wilson coefficient, the behavior of low-temperature magnetic susceptibility also serves as evidence for determining whether the system is Fermi or non-Fermi liquid. Usually, the magnetic susceptibility, χ, is independent of temperature T in a Fermi liquid system, while in a non-Fermi liquid system, it exhibits characteristics such as χ ∼ −In T or T^−α (α < 1).⁴⁶ For example, the divergence of magnetic susceptibility below 10 K follows a power-law form of χ ∼ T^−α, with α ∼ 0.21 for Pb₂Ir₂O_7−δ⁴⁵ and α ∼ 0.28 for CeRhBi.⁴⁶ Both of these are typical characteristics of a non-Fermi liquid. In our case, the low-temperature magnetic susceptibility fitted well with a power-law form of χ ∼ T^−α, as shown in Fig. S1 (ESI†).⁴⁷ The fitting coefficient α ∼ 0.5 indicated a non-Fermi liquid system for Ca₃Pt₄Sn₁₃. Therefore, by combining the results from resistivity, the Wilson ratio, and low-temperature magnetic susceptibility, we considered that Ca₃Pt₄Sn₁₃ crystal behaved as a non-Fermi liquid system.

Fig. 2 (a) Temperature dependence of resistivity at H = 0 T and 5 T with the electrical current along the (110) surface; inset: fitting result of the low-temperature resistance based on Fermi-liquid theory, ρ = ρ₀ + AT²; (b) temperature-dependent MR under an applied magnetic field of H = 5 T; inset: temperature dependence of d(MR)/dT. T* corresponds to the temperature where the sign of d(MR)/dT changes from positive to negative as temperature decreases; (c) magnetic field (H)-dependent ρ_xx at different temperatures; (d) temperature dependence of MR defined as MR = (ρ_H(9 T) − ρ_H(0 T))/ρ_H(0 T). The lines represent fitting results according to MR ∼ H² and MR ∼ H.

As shown in Fig. 2(b), with an applied magnetic field H = 5 T, at low temperatures, d(MR)/dT was positive. However, as the temperature increased, the sign of d(MR)/dT changed from positive to negative around T^* ∼ 33 K for I along the [110] direction. The origin of MR in Ca₃Pt₄Sn₁₃ differed from that in Gd₃It₄Sn₁₃. In Gd₃It₄Sn₁₃, the MR was related to the magnetic ordering of Gd ions under the applied magnetic field; however, no magnetic order was observed in Ca₃Pt₄Sn₁₃. The origin of MR in Ca₃Pt₄Sn₁₃ is still not clear. Furthermore, the angle-resolved magnetoresistance (AMR) of Ca₃Pt₄Sn₁₃ was investigated, with the relative spatial position relations shown schematically in Fig. S3(a) and S4(a) (ESI†).⁴⁷ When the magnetic field was always perpendicular to the excitation current flow, as shown in Fig. S3 (ESI†), the AMR data exhibited an isotropic symmetry at high temperatures. As the temperature decreased, the curves gradually evolved into an eight-fold symmetry. These features were similar to the multivalley system observed in Ag₃Sn,⁴⁸ which strongly depended on the orientation of the magnetic field, thus indicating that Ca₃Pt₄Sn₁₃ could be a possible candidate for valleytronics. In contrast, the AMR maintained an isotropic symmetry over the entire temperature range when the magnetic field rotated within the bc plane, as shown in Fig. S4 (ESI†).⁴⁷ Some previous studies have proposed magnetic or Lifshitz transition scenarios to explain the changing symmetry.⁴⁸ However, the microscopic origin of these changes remains an open issue.

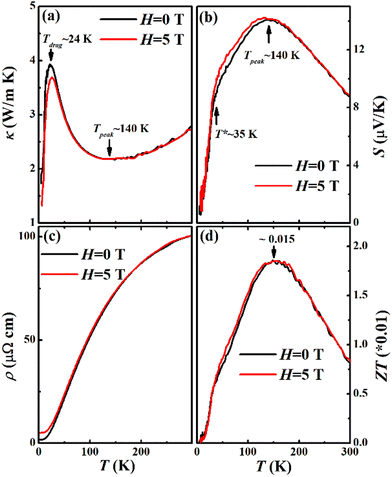
As shown in Fig. 3, we systematically investigated the temperature-dependent thermal conductivity, thermoelectric power, resistivity, and ZT for the Ca₃Pt₄Sn₁₃ single crystal under 0 T and 5 T. Characteristic transitions were clearly observed in the thermal conductivity, thermoelectric power, and ZT curves. However, interestingly, in addition to the large MR at low temperatures, no abnormal behavior was observed in the temperature-dependent resistivity data. To our knowledge, the possible reason is that resistance measurements typically select the optimal path in the system, which may not fully reflect the overall behavior of the sample. Correspondingly, measurements of thermal conductivity and thermoelectric power could be considered thermodynamic measurements, providing more bulk information about the selected crystal. Therefore, it is reliable to conclude that these characteristic transitions were determined from the thermoelectric measurements.

Fig. 3 (a)–(c) Temperature dependence of the thermal conductivity (κ), Seebeck coefficient (S), and resistivity (ρ) at H = 0 T and 5 T, respectively; (d) temperature-dependent calculated ZT under applied magnetic fields of H = 0 T and 5 T.

To obtain more detailed information, we carefully extracted these critical temperature points. Two significant transitions were observed in the thermal conductivity (T_drag = 24 K, T_peak = 140 K) and thermoelectric power (T^* = 35 K, T_peak = 140 K) curves, while only one transition (T = 160 K) was observed in the ZT curve. After careful comparison, we found that although the thermal conductivity and thermoelectric power exhibited completely different evolutionary behaviors, their critical temperature points were almost identical. The maximum value of the merit factor ZT was 0.015 when the temperature was around 160 K. Combining the above results and analysis, we confirm the critical temperature points for these observed transitions, which will provide useful insights into understanding the interesting physical phenomena in the Ca₃Pt₄Sn₁₃ single crystal.

Fig. 4 shows the specific heat, C_p, of the Ca₃Pt₄Sn₁₃ single crystal. At higher temperatures, the value of C_p approached the limiting value of 500 J mol⁻¹ K⁻¹, which was close to the Dulong–Petit limit, C_v = 3nR₀ = 498.8 J mol⁻¹ K⁻¹, where n = 20 is the total number of atoms per formula unit and R₀ is the molar gas constant. Meanwhile, the magnitude of C_p decreased monotonically with decreasing temperature and showed no visible signatures of a structural transition. The inset of Fig. 4 shows the low-temperature specific heat data, C_p/T, plotted as a function of T². It can be fitted by the following formula:

C_p/T = γ + βT² (2)

where γ is the Sommerfeld coefficient and βT² represents the lattice contribution. The fitted values of γ and β were 4.76 mJ mol⁻¹ K⁻¹² and 3.16 mJ mol⁻¹ K⁻¹⁴, respectively. According to the Sommerfeld theory of metals, the coefficient γ can be expressed as a function of the density of states (DOS) at the Fermi energy level as follows:where N(E_F) is the DOS at the Fermi energy level and λ is the electron–phonon coupling constant. Assuming λ = 0, the obtained value of N(E_F) was 2.9 states per eV per f.u. The Debye temperature Θ_D was obtained from the following formula:For Ca₃Pt₄Sn₁₃, n was equal to 20 and β was 3.16 mJ mol⁻¹ K⁻¹; therefore, the calculated Θ_D was approximately 220 K.

Fig. 4 Temperature dependence of the heat capacity C_p. The red line is the fitting result according to eqn (5). The inset shows the T²-dependence of C_p/T. The blue line is the fitting result based on the formula C_p/T = γ + βT², where γ is the Sommerfeld coefficient and β is the phonon heat capacity coefficient.

To understand the behavior of the specific heat, C_p, we performed a detailed analysis of the conduction electron and phonon contributions using:

C_pT = γT + nC^Debye_V(T) (5)

andwhere R is the molar gas constant, Θ_D is the Debye temperature, and n = 20 is the number of atoms per formula unit. Using the obtained values of γ = 4.76 mJ mol⁻¹ K⁻¹ and Θ_D = 220 K, the red line represented the calculated result, which matched the experimental data very well and confirmed that the obtained values of γ and Θ_D were reasonable.

As shown in Fig. 5(b), we systematically performed the temperature-dependent Hall coefficient measurements at various fixed temperature points. The negative slope observed in the Hall resistance indicated that electron-type carriers were dominant in the Ca₃PtSn₁₃ crystal. Interestingly, the thermoelectric power results suggested the presence of hole-like carriers. The difference in the signs of the Hall and Seebeck coefficients has been observed in pure thallium,⁴⁹ bismuth thin film,⁵⁰ Ag₂Se crystal,⁵¹ and others. Some theoretical studies suggest that the inconsistency in the signs of Hall and Seebeck coefficients may be related to the special structure of the Fermi surface boundaries. Because the boundary lines for the sign change of the Hall and Seebeck coefficients did not coincide, it was useful to define a region between them in which the Hall and Seebeck coefficients had different signs. This anomalous region always corresponded to a positive Seebeck coefficient and a negative Hall mobility, as found experimentally.⁵² In our case, to understand their intrinsic origin, we performed first-principles calculations for the Ca₃Pt₄Sn₁₃ crystal, as shown in Fig. S2 (ESI†).⁴⁷ We found a “neck-shaped” behavior in the three-dimensional Fermi surface, as shown in Fig. S2(d) (ESI†).⁴⁷ However, at this stage, whether these “neck-shaped” Fermi surfaces are the microscopic origin of the different signs of the Hall and Seebeck effects remains an open issue. Further in-depth theoretical analysis in the future will clarify this issue.

Fig. 5 (a) Temperature dependence of the Hall coefficient under an applied magnetic field of H = 5 T; (b) field dependence of the Hall resistivity ρ_xy at representative temperatures; (c) and (d) temperature dependence of the carrier density and mobility, respectively, obtained from the fitting of data in (b).

In order to obtain more information, we also extracted the temperature-dependent mobility of the carriers, the carrier concentration, and the hall coefficient R_H, as shown in Fig. 5(a), (c) and (d). All of these extracted data exhibited a rapid increase below a characteristic temperature of ∼35 K, which was almost identical to the low-temperature transition of the Seebeck coefficient. Meanwhile, we found that the MR and AMR also showed significant changes when the temperature was below ∼35 K. On the other hand, the thermal conductivity exhibited a relatively poorer match with the above critical temperatures, showing a phase transition near 24 K. The magnetic susceptibility also showed a kink around 40 K in the zero-field cooling curve, as shown in Fig. S1(b) (ESI†).⁴⁷ Although the starting temperature points may vary due to different measurement methods, their evolutionary behaviors imply that they may share a common origin closely related to the T^* phase. Some previous studies have suggested that the T^* in the Ca₃Ir₄Sn₁₃ superconductor may originate from CDW order or ferromagnetic spin fluctuations,²³ which remains a controversial issue. Based on the current results, we seem to have also encountered a similar situation in the Ca₃Pt₄Sn₁₃ system. Nevertheless, the current findings could provide a non-superconducting system to investigate the intrinsic origin of T^*.

Unlike some Dirac semimetals, the Fermi surface is solely contributed by Dirac cones. We have not found any special electronic structure (near the Fermi surface) or significant compensation mechanisms to support physical mechanisms that could explain the large MR effect, such as the Dirac system, Weyl semimetal system, electric-hole compensation, and so on. In such cases, more fundamental and intrinsic factors of origin will need to be considered. Some studies have pointed out that high carrier mobility, μ, is an essential prerequisite for the observation of large MR.⁵³ In our case, the mobility was almost consistent with the evolutionary behavior of the large MR. Therefore, at the current stage of research, we tend to believe that the high mobility behavior in the low-temperature region is an important factor contributing to the large MR phenomenon in Ca₃Pt₄Sn₁₃. Certainly, more detailed microscopic mechanisms related to the T^* scenarios (associated with the CDW order) need to be verified by further experimental and theoretical studies in the future.

In summary, we have carried out a detailed study of the quasi-skutterudite Ca₃Pt₄Sn₁₃ single crystal through measurements of electrical resistivity, Hall effect, specific heat, and thermoelectric properties. The resistivity exhibited metallic behavior from 300 K to 2 K. The results of the resistivity, Wilson ratio, and low-temperature magnetic susceptibility indicated that Ca₃Pt₄Sn₁₃ was a non-Fermi liquid system. The MR with an applied magnetic field H = 5 T at T = 2 K was 200% for H along the [110] direction. Combining the results of first-principles calculations and the Hall resistance, we tend to consider that the origin of the large MR is closely related to the high mobility of the carriers. Meanwhile, the AMR was also systematically investigated. An eight-fold symmetry AMR observed in the low-temperature region indicated that the Ca₃Pt₄Sn₁₃ crystal could be a possible candidate for valleytronics. The results of the first-principles calculations and the different signs of the Hall and Seebeck coefficients indicated that there was a special structure of the Fermi surface boundaries in the Ca₃Pt₄Sn₁₃ crystal. Furthermore, we found that the mobility of carriers, carrier concentration, Hall coefficient, Seebeck coefficient, thermal conductivity, magnetic susceptibility, MR, and AMR all showed significant changes when the temperature was below T^*, indicating that they might share a common origin. The current findings could provide a non-superconducting Ca₃Pt₄Sn₁₃ system to study the intrinsic origin of T^*.

This work is supported by the National Key Research and Development Program of China (Grant No. 2023YFA1406500), the National Natural Science Foundation of China (No. 11904003, No. 12204487, 12474098, No. 12104011, No. 12274388, No. 12174361, No. 52102333, No. 12104010, and No. 12204004), and the Natural Science Foundation of Anhui Province under contract 1908085MA09.

Data availability

The data supporting the findings of this study can be obtained from the corresponding author upon request.

Conflicts of interest

There are no conflicts to declare.

References

1. C. Shekhar, A. K. Nayak, Y. Sun, M. Schmidt, M. Nicklas, I. Leermakers, U. Zeitler, Y. Skourski, J. Wosnitza and Z. Liu, et al. , Nat. Phys., 2015, 11, 645.
2. J. Hu, J. Liu, D. Graf, S. Radmanesh, D. Adams, A. Chuang, Y. Wang, I. Chiorescu, J. Wei and L. Spinu, et al. , Sci. Rep., 2016, 6, 18674.
3. T. Liang, Q. Gibson, M. N. Ali, M. Liu, R. Cava and N. Ong, Nat. Mater., 2015, 14, 280.
4. N. Zhou, Y. Sun, C. Q. Xu, C. Y. Xi, Z. S. Wang, B. Li and J. J. Feng, et al. , Phys. Rev. B, 2020, 101, 245102.
5. H. Asano, J. Hayakawa and M. Matsui, et al. , Appl. Phys. Lett., 1997, 71, 844.
6. Y. Tomioka, H. Kuwahara, A. Asamitsu and M. Kasai, Appl. Phys. Lett., 1997, 70, 3609.
7. H. Y. Hwang, S. W. Cheong and B. Batlogg, Appl. Phys. Lett., 1996, 68, 3494.
8. L. X. Zhao, J. B. He, D. Chen, S. Zhang, Z. A. Ren and G. F. Chen, Phys. Rev. B, 2019, 99, 205116.
9. R. Singha, A. Pariari, G. K. Gupta, T. Das and P. Mandal, Phys. Rev. B, 2018, 97, 155120.
10. Z. J. Yuan, H. Lu, Y. J. Liu, J. F. Wang and S. Jia, Phys. Rev. B, 2016, 93, 184405.
11. D. S. Wu, J. Liao, W. Yi, X. Wang, P. G. Li, H. M. Weng, Y. G. Shi, Y. Q. Li, J. L. Luo, X. Dai and Z. Fang, Appl. Phys. Lett., 2016, 108, 042105.
12. C. L. Zhang, C. Guo, H. Lu, X. Zhang, Z. J. Yuan, Z. Q. Lin, J. F. Wang and S. Jia, Phys. Rev. B, 2015, 92, 041203.
13. Y. Y. Lv, X. Li, J. L. Zhang, B. Pang, S. S. Chen, L. Cao, B. B. Zhang, D. J. Lin, Y. B. Chen, S. H. Yao, J. Zhou, S. T. Zhang, M. H. Lu, M. L. Tian and Y. F. Chen, Phys. Rev. B, 2018, 97, 245151.
14. S. S. Sun, Q. Wang, P. J. Guo, K. Liu and H. C. Lei, New J. Phys., 2016, 18, 082002.
15. Y. L. Wang, L. R. Thoutam, Z. L. Xiao, J. Hu, S. Das, Z. Q. Mao, J. Wei, R. Divan, A. Luican-Mayer, G. W. Crabtree and W. K. Kwok, Phys. Rev. B, 2015, 92, 180402.
16. Q. Chen, Z. F. Lou, S. N. Zhang, Y. X. Zhou, B. J. Xu, H. C. Chen, S. J. Chen, J. H. Du, H. D. Wang, J. H. Yang, Q. S. Wu, O. V. Yazyev and M. H. Fang, Phys. Rev. B, 2021, 104, 115104.
17. J. Diaz, K. Wang, J. Straquadine, C. Putzke, Q. Yang, B. Yan, S. L. Budko, P. C. Canfield and P. J. W. Moll, Nature Commun, 2024, 15, 4585.
18. D. S. Wu, X. Wang, X. Zhang, C. L. Yang, P. Zheng, P. G. Li and Y. G. Shi, Sci. China: Phys., Mech. Astron., 2015, 58, 1.
19. I. Di Bernardo, J. Collins, W. Wu, J. Zhou, S. A. Yang, S. Ju, M. T. Edmonds and M. S. Fuhrer, Phys. Rev. B, 2020, 102, 045124.
20. Z. K. Liu, B. Zhou, Y. Zhang, Z. J. Wang, H. M. Weng, D. Prabhakaran, S.-K. Mo, Z. X. Shen, Z. Fang, X. Dai, Z. Hussain and Y. L. Chen, Science, 2014, 343, 864.
21. H. X. Chen, Z. L. Li, L. W. Guo and X. L. Chen, EPL, 2017, 117, 27009.
22. J. Y. Hua, Z. X. Dai, X. C. Kana, G. H. Zheng, Z. Chena and Y. Q. Ma, J. Alloys Compd, 2022, 895, 162563.
23. J. H. Yang, B. Chen, C. Michioka and K. Yoshimura, J. Phys. Soc. Jpn., 2010, 79, 113705.
24. K. F. Wang and C. Petrovic, Phys. Rev. B, 2012, 86, 024522.
25. S. Y. Zhou, H. Zhang, X. C. Hong, B. Y. Pan, X. Qiu, W. N. Dong, X. L. Li and S. Y. Li, Phys. Rev. B, 2012, 86, 064504.
26. A. F. Fang, X. B. Wang, P. Zheng and N. L. Wang, Phys. Rev. B, 2014, 90, 035115.
27. C. N. Kuo, H. F. Liu, C. S. Lue, L. M. Wang, C. C. Chen and Y. K. Kuo, Phys. Rev. B, 2014, 89, 094520.
28. C. W. Luo, P. C. Cheng, C. M. Tu, C. N. Kuo, C. M. Wang and C. S. Lue, New J. Phys., 2016, 18, 073045.
29. A. M. Strydom, J. Phys.: Condens. Matter, 2007, 19, 386205.
30. C. L. Yang, X. Wang, X. Zhang, D. S. Wu, M. Liu, P. Zheng, J. Y. Yao, Z. Z. Li, Y.-F. Yang, Y. G. Shi, J. L. Luo and N. L. Wang, Phys. Rev. B, 2015, 91, 075120.
31. D. A. Tompsett, Phys. Rev. B, 2014, 89, 075117.
32. L. S. I. Veiga, J. R. L. Mardegan, M. V. Zimmermann, D. T. Maimone, F. B. Carneiro, M. B. Fontes, J. Strempfer, E. Granado, P. G. Pagliuso and E. M. Bittar, Phys. Rev. B, 2020, 101, 104511.
33. J. Luo, J. Yang, S. Maeda, Z. Li and G. Q. Zheng, Chin. Phys. B, 2018, 27, 7.
34. M. Zeng, D. H. Xu, Z. M. Wang and L. H. Hu, Phys. Rev. B, 2023, 107, 094507.
35. C. Wang, B. Lian, X. M. Guo, J. H. Mao, Z. T. Zhang, D. Zhang, B. L. Gu, Y. Xu and W. H. Duan, Phys. Rev. Lett., 2019, 123, 126402.
36. K. Zollner and J. Fabian, Phys. Status Solidi B, 2021, 258, 2000081.
37. N. Zhou, X. F. Xu, J. R. Wang, J. H. Yang, Y. K. Li, Y. Guo, W. Z. Yang, C. Q. Niu, B. Chen, C. Cao and J. H. Dai, Phys. Rev. B, 2014, 90, 094520.
38. Q. Youa, X. C. Wang, G. F. Chen and Z. D. Zheng, Phys. E, 2017, 88, 87.
39. J. Jiang, F. Tang, X. C. Pan, H. M. Liu, X. H. Niu, Y. X. Wang, D. F. Xu, H. F. Yang, B. P. Xie, F. Q. Song, P. Dudin, T. K. Kim, M. Hoesch, P. Kumar Das, I. Vobornik, X. G. Wan and D. L. Feng, Phys. Rev. Lett., 2015, 115, 166601.
40. J. Taylor, H. Guo and J. Wang, Phys. Rev. B, 2001, 63, 303.
41. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
43. L. E. DeLong, R. P. Guertin, S. Hasanain and T. Fariss, Phys. Rev. B, 1985, 31, 7059.
44. G. Cao, V. Durairaj, S. Chikara, L. E. DeLong, S. Parkin and P. Schlottmann, Phys. Rev. B, 2007, 76, 100402.
45. M. S. Khan, I. Carlomagno, C. Meneghini, P. K. Biswas, F. Bert, S. Majumdar and S. Ray, Phys. Rev. B, 2022, 105, 085137.
46. V. K. Anand, D. T. Adroja, A. D. Hillier, K. Shigetoh, T. Takabatake, J. G. Park, K. A. McEwen, J. H. Pixley and Q. Si, J. Phys. Soc. Jpn., 2018, 87, 064708.
47. See ESI† for the temperature dependent magnetic susceptibility, the first-principles calculations, the polar plot of field angle-resolved resistivity in the ac plane, the polar plot of field angle-resolved resistivity in the bc plane.
48. N. Zhou, Y. Sun, C. Q. Xu, Z. S. Wang, B. Li, J. J. Feng, L. Zhang, X. Z. Xing, Y. F. Zhang, Y. Q. Pan, Y. Meng, X. L. Yi, L. Pi, X. F. Xu and Z. X. Shi, Phys. Rev. B, 2020, 101, 245102.
49. A. T. Burkov and P. P. Konstantinov, Tech. Phys., 2024, 69, 1510.
50. V. A. Komarov, V. M. Grabov, A. V. Suslov, N. S. Kablukova and M. V. Suslov, Semiconductors, 2019, 53, 593.
51. M. Ferhat and J. Nagao, J. Appl. Phys., 2000, 88, 813.
52. M. R. Boon, Phys. Status Solidi B, 1972, 49, K163.
53. N. Xin, J. Lourembam, P. Kumaravadivel, A. E. Kazantsev, Z. Wu, C. Mullan, J. Barrier, A. A. Geim, I. V. Grigorieva, A. Mishchenko, A. Principle, V. I. Falko, L. A. Ponomarenko, A. K. Geim and A. I. Berdyugin, Nature, 2013, 616, 270.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc04812a

---