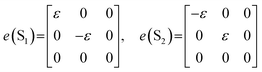Coupling between ferroelasticity and magnetization in two-dimensional organic–inorganic perovskites (C₆H₅C₂H₄NH₃)₂MCl₄ (M = Mn, Cu, Fe)

Abstract

Materials with coexistence of two or more ferroic orders are known as multiferroics. Magneto-elastic multiferroics, where ferromagnetism and ferroelasticity coexist, have been rarely reported previously. We studied the magneto-elastic multiferroic properties of two-dimensional organic–inorganic perovskites having the formulas (PEA)₂MnCl₄, (PEA)₂CuCl₄ and (PEA)₂FeCl₄ (PEA = C₆H₅C₂H₄NH₃). All three exhibited ferroelasticity but the manganese and iron compounds showed canted antiferromagnetism and the copper one showed ferromagnetism. Also, only (PEA)₂FeCl₄ displayed a shift of magnetization when the sample was cooled in a magnetic field from above the magnetic ordering temperature. We propose that the magnetization shift originates from the coupling between ferroelasticity and magnetization via spin–orbit coupling (SOC). This work would shed light on understanding the coupling mechanism between ferroelasticity and magnetization towards the interesting role of SOC in ferroelastic materials.

---

Introduction

Organic–inorganic perovskites have gained worldwide attention for their multiferroic, photovoltaic and semiconducting properties.^1–4 They are composed of organic ammonium cations and metal halide octahedra. While the organic group offers various properties such as elasticity and efficient luminescence, the inorganic parts provide important properties such as thermal stability and magnetic and dielectric properties.^5–7 Recent studies in organic–inorganic perovskites have focused not only on their respective characteristics but also on the interactions between them. Among the organic–inorganic perovskites, two-dimensional organic–inorganic perovskites can be a promising platform for functional material design due to their ability to introduce various sizes of organic cations.^8,9 Recently, these perovskites have been recognised as candidates for multiferroic materials.^10–15

Multiferroic materials exhibit a direct correlation between two or more ferroic orders such as ferromagnetism, ferroelectricity, ferroelasticity and ferrotoroidicity.^1,2,16,17 For example, materials coupling ferromagnetism and ferroelectricity display electric field-induced magnetization and magnetic field-induced electric polarization. Such properties are known as the magnetoelectric effect (ME effect), which has been reported in inorganic perovskites and organic–inorganic hybrid materials.^18–23 The ME effect enables potential applications in high-efficiency memories due to controllable magnetic properties by the electric field without energy dissipation.²⁴ The correlation between magnetic and elastic orders is known as the magnetoelastic effect (MA effect). However, observations of the MA effect are extremely challenging and have been sparsely investigated.^25–27 The MA effect gives rise to the possibility of applications in strain-assisted logic memory and magnetic position sensors.^28,29 Recently, the coupling of crystal symmetry and spin structures has been observed in chiral magnets.³⁰ A crystal without an inversion center generates an asymmetry of the orbital angular momentum due to the non-symmetry of the electric field in the solid, which twists each neighboring spin via spin–orbital coupling (SOC).³¹ This is called the Dzyaloshinskii–Moriya interaction (DMI),^32,33 which is the key to chiral magnetism. Therefore, by extension, the MA effect should be observed in multiferroic materials, given the ability of coherent coupling of crystal symmetry and spin structures in chiral magnets.

We previously reported that the two-dimensional organic–inorganic perovskite (C₆H₅C₂H₄NH₃)₂FeCl₄ (PEA-Fe), composed of a 2-phenylethylammonium cation (PEA) and an FeCl₄²⁻ anion, is a material with ferroelasticity and canted antiferromagnetism (CAF).¹⁴ PEA-Fe underwent a successive structural phase transitions with rotation of the PEA and tilting of the FeCl₆ octahedron (Fig. 1). The reported crystal structures for each phase of PEA-Fe are I4/mmm above 433 K, Bbcm between 433 K and 323 K, and Pbca from 323 K to at least 90 K, with a ferroelastic phase transition from I4/mmm to Bbcm, clearly identifiable by the observation of ferroelastic domains. The magnetic properties of PEA-Fe exhibited CAF below 98 K (T_N). Although ferroelastic and CAF in PEA-Fe were established in previous work, the crystal structure below T_N and the magnetic structure have not been extensively discussed. To investigate the crystal and magnetic structures of two-dimensional organic–inorganic perovskites at liquid helium temperature, neutron diffraction experiments are a powerful tool.³⁴ In this paper, we evaluated the structural and magnetic properties of two-dimensional organic–inorganic perovskites PEA-M (M = Mn, Cu, Fe) by using magnetometry and powder neutron diffraction (PND) techniques to obtain insight into the MA effect. PEA-Mn and PEA-Cu were synthesized to further discuss the MA effect of PEA-Fe. The three compounds are isostructural and show ferroelasticity and ferromagnetism (M = Cu) or CAF (M = Mn, Fe). In PEA-Fe, we discovered a magnetization shift after cooling in a magnetic field from above T_N, and the crystal and magnetic structures down to 2 K were determined by PND measurements. Several models to explain the origin of the magnetization shift will be discussed. The most plausible mechanism is likely associated with the coupling between ferroelasticity and magnetic order, which is similar to the mechanism of chirality-assisted direct coupling between the lattice and magnetic degrees of freedom in chiral magnets.

Fig. 1 Comparison of the (a)–(c) side and (d)–(f) top views of the crystal structures of PEA-M (M = Mn, Cu, Fe) in (a) and (d) Pbca, (b) and (d) Bbcm, and (c) and (f) I4/mmm space groups. MCl₆ units show polyhedra. H atoms are omitted for clarify. Color code: orange, M; gray, C; blue, N; green, Cl.

Experimental

Crystallization

All reagents and solvents were used as purchased.

(C₆H₅C₂H₄NH₃)₂FeCl₄ crystals were prepared as reported previously.¹⁴ The yield was 22%. Elemental analysis: calc. (%) for C₁₆H₂₄N₂FeCl₄: C, 43.47; N, 6.34; H, 5.47. Found: C, 43.66; N, 6.34; H, 5.35.

(C₆H₅C₂H₄NH₃)₂MnCl₄ crystals were prepared using a slow evaporation method. PEA·Cl and MnCl₂·4H₂O were dissolved in methanol according to the molar ratio. After being kept open to air for several days, pale-pink transparent plate-like single crystals were obtained, and the yield was 72%. Elemental analysis: calc. (%) for C₁₆H₂₄N₂MnCl₄: C, 43.56; N, 6.35; H, 5.48. Found: C, 43.68; N, 6.31; H, 5.49.

(C₆H₅C₂H₄NH₃)₂CuCl₄ crystals were prepared by a similar method to that of (C₆H₅C₂H₄NH₃)₂MnCl₄. PEA·Cl and CuCl₂·2H₂O were dissolved in distilled water according to the molar ratio. After several days of slow evaporation, yellow transparent plate-like single crystals were obtained, and the yield was 82%. Elemental analysis: calc. (%) for C₁₆H₂₄N₂CuCl₄: C, 42.73; N, 6.23; H, 5.38. Found: C, 42.56; N, 6.12; H, 5.35.

Characterization

CHN spectroscopy was carried out using a PerkinElmer series II CHNS/O Analyzer 2400 or an Exeter Analytical series CE440 Analyzer. Thermogravimetry and differential thermal analysis (TG-DTA) were performed on a Seiko Instruments SII Exstar TG/DTA 6200 with a temperature range of 293–673 K and a heating rate of 5 K min⁻¹. Differential scanning calorimetry (DSC) measurements were carried out on a Rigaku Thermo plus DSC8230 with a temperature range of 273–453 K and a scanning rate of 5 K min⁻¹. The phase transition temperature was determined from the beginning of the thermal anomaly. Crystal images under polarized light were collected using a Meiji Techno EMZ-5HPOL-2 polarized microscope to evaluate the ferroelastic behavior.

X-ray crystallography

Unit-cell determinations were performed on a Bruker D8-QUEST equipped with a CMOS area detector or a Rigaku XtaLAB Synergy-DW equipped with a HyPix diffractometer. Both employed graphite-monochromated Mo K_α radiation (λ = 0.71073 Å). Using Olex2, the structures were solved with the SHELXS or the SHELXT structure solution programs and refined with the SHELXL refinement package.^35–38 The nonhydrogen atoms were refined with anisotropic thermal parameters, and hydrogen atoms were added and refined using a riding model. Drawings of crystal structures were performed using the VESTA program.³⁹

Stress tests

The stress tests were performed as reported previously.¹⁴ A single crystal was sandwiched between two stainless plates and pressurized by loading the metal in the tube. The stress application device was heated to higher temperature in an oven (AVO-310V, ETTAS).

Magnetic measurements

Dc magnetic susceptibilities were collected using a MPMS-5S, MPMS-7, MPMS-XL7 or MPMS3 superconducting quantum interference device magnetometer (Quantum Design) with temperature and dc field ranges of 2–300 K and −50 to +50 kOe, respectively, for single crystals and powder samples. Powder samples were fixed on gelatin capsules after mixing with a small amount of n-eicosane, while single crystals were fixed on gelatin capsules with quartz cotton. The n-eicosane was added to prevent crystallite torquing during sweeping the magnetic field. The quartz cotton was used to avoid stress due to thermal expansion and contraction of adhesive during heating and cooling processes. Single crystals were indexed using X-ray diffraction prior to or after the measurements. Diamagnetic contributions of the sample holder and sample were corrected by the measurement of the sample holder and calculation of Pascal's constants, respectively.⁴⁰ Temperature dependences of the magnetization were measured in the zero-field-cooled warming (ZFCW) and field-cooled cooling (FCC) processes. In the ZFCW process, the sample was first cooled from 150 K to 2 K in the absence of an external magnetic field, and then measurements were made with increasing temperature under the fixed magnetic field. In the FCC process, the magnetization was recorded in the presence of a fixed applied magnetic field with decreasing temperature to 2 K. Field-sweep measurements were done after the ZFC and FC processes. For the ZFC process, the sample was cooled from 150 to the target temperature under a zero magnetic field, while for the FC process the sample was cooled under a desired magnetic field. For example, the FC process under the ±50 kOe magnetic field is referred to as FC_±50kOe.

Powder neutron diffraction (PND) experiments

PND measurements on PEA-Fe on non-deuterated samples were performed at D20 and D2B, high flux and high-resolution diffractometers, respectively, at the Institut Laue-Langevin (ILL) in France. Powder samples were introduced in a cylindrical vanadium holder of 8 mm in diameter. PND patterns at D20 were collected with λ = 2.41 Å at fixed temperatures of 2, 50, 120, 300, 400 and 460 K using a cryo-furnace. Also, thermo-diffractograms were collected, in each temperature ramp between each of these temperatures (thermodiffractograms). High resolution diffractograms were collected at D2B with λ = 1.594 Å for different fixed temperatures of 10, 300, 400 and 450 K.

Crystalline and magnetic structural parameters at each temperature were determined by Rietveld refinement using the FullProf suite.⁴¹ The raw diffraction data at each temperature are provided in Fig. S1 (ESI†).

Results and discussion

Structural phase transitions

From TG of PEA-Mn and PEA-Cu, weight loss starting from 534 K and 497 K was observed, respectively (Fig. S2, ESI†). DSC curves of PEA-Mn and PEA-Cu showed two endothermic events at 364 K and 415 K, and 340 K and 408 K, respectively, for the heating process. Two exothermic events for PEA-Mn and PEA-Cu were observed at 368 K and 418 K, and 334 K and 409 K, respectively, for the cooling process. The enthalpy changes ΔH and the corresponding of the entropy changes ΔS for PEA-M were obtained as determined from the area under the heat flow vs. the temperature curve and the equation of ΔS = ΔH/T, respectively (Table S1, ESI†). According to the Boltzmann equation of ΔS = R ln(N), where R is the gas constant and N is the variation of the number of disorder positions during the transition, the N values for the low-temperature and high-temperature sides of PEA-Mn and PEA-Cu were calculated to be 2.5 and 1.8, and 1.5 and 2.0, respectively. DSC measurements indicated that two structural phase transitions occurred in PEA-Mn and PEA-Cu.

To further investigate the structural phase transitions, single crystal X-ray structural analyses were performed at 293 K, 393 K, and 433 K for PEA-Mn and PEA-Cu (Tables S2 and S3, ESI†). At 293 K, both compounds crystallized in the Pbca space group where 2 PEA units and the corner-shared inorganic layers of MCl₄²⁻ (M = Cu, Mn) were alternately stacked along the c-axis. The bond lengths between Mn and the bridging Cl ions in MnCl₆ octahedra were 2.5747(8) and 2.5763(8) Å and that between Mn and the non-bridging Cl ions was 2.4827(9) Å. The bond distances between Cu and the bridging Cl ions in CuCl₆ octahedra were 2.2853(10) and 2.9004(10) Å, and the bond distance between Cu and the non-bridging Cl ions was 2.2950(13) Å. Such M–Cl bond lengths are consistent with those reported values in PEA-Mn and PEA-Cu.^42,43 Upon heating, both compounds were kept in an orthorhombic system but had a Bbcm space group. The C₂H₄NH₃ group of the PEA was disordered in two crystallographic equivalent positions. At the highest temperature, the crystal structure changed to a tetragonal system of an I4/mmm space group. In this state, the PEA was fully disordered giving a four-fold symmetry along the c-axis. PEA-Mn and PEA-Cu underwent the same structural phase transformations as PEA-Fe with the increasing temperature (Table S4, ESI†).

According to the DSC data, N was close to two for both structural phase transitions. It indicates that the transition is close to a simple 2-fold order–disorder model. On the basis of our crystallographic data, the energetically equivalent positions of the PEA groups are changed from one to two then to four during consecutive structural phase transitions, allowing plausible N values.

Observations of ferroelastic domains

The structural phase transition from I4/mmm to Bbcm is a ferroelastic phase transition with an Aizu notation of 4/mmmFmmm.⁴⁴ The symmetry element is divided by two through the ferroelastic phase transition, from 16 symmetry elements for I4/mmm to 8 for Bbcm, indicating the appearance of two possible orientation states in the ferroelastic phase. From a microscopic point of view, the formation of ferroelastic domains is one of the effective methods to confirm the ferroelastic behavior. Thus, observations of ferroelastic domains for PEA-Mn and PEA-Cu crystals were carried out by polarizing microscopy along the c-axis (Fig. 2). No ferroelastic domain structures were observed at room temperature in fresh PEA-Mn and PEA-Cu crystals at room temperature. However, when the crystal structure was changed to the I4/mmm space group by heating to 430 K and then cooled to room temperature, the linear ferroelastic domain structures appeared. The ferroelastic domain walls of PEA-Mn and PEA-Cu were parallel and orthogonal to the (110) directions. The appearance of domain structures for both PEA-Mn and PEA-Cu means that these compounds exhibit ferroelasticity, similarly to PEA-Fe. For the ferroelastic state with the species 4/mmmFmmm, there are two orientation states of S₁ and S₂. Then the spontaneous strain tensor e in S₁ and S₂ states is, respectively,⁴⁵
where ε is the element of the e. The magnitude of ε is calculated using the lattice parameters of a and b in the ferroelastic phase.

Fig. 2 Polarized optical microscopy images of different ferroelastic domains in single crystals of (a) and (b) PEA-Mn and (c) and (d) PEA-Cu at room temperature before (a) and (c) and after (b) and (d) heating. Scale bar: 0.5 mm.

With respect to the lattice parameters in the Bbcm phase for PEA-M (M = Mn, Cu, Fe), the magnitudes of ε are 1.5 × 10⁻³, 3.0 × 10⁻³ and 2.6 × 10⁻³, respectively. The spontaneous strain e_s is defined as the following equation.

As a result, the e_s values for PEA-M (M = Mn, Cu, Fe) are 2.1 × 10⁻³, 4.3 × 10⁻³ and 3.6 × 10⁻³, respectively.

To further investigate the ferroelastic properties of PEA-Mn and PEA-Cu, stress tests were performed on the multi-domain ferroelastic crystal (Fig. S3, ESI†). By application of stress at room temperature, the ferroelastic domains of PEA-Mn were moved, while for PEA-Cu, the crystals broke before observation of domain wall motion, similar to PEA-Fe.¹⁴ After thermal treatment up to 373 K under stress, the ferroelastic domains of PEA-Cu were moved. Therefore, the stress tests for both PEA-Mn and PEA-Cu confirmed the ferroelastic behavior of these compounds. In contrast to PEA-Cu and PEA-Fe, the ferroelastic domains of PEA-Mn are mobile at room temperature, which can be attributed to the larger spontaneous strain e_s for PEA-Cu and PEA-Fe compared to PEA-Mn.

Magnetic properties of PEA-M

PEA-Mn showed a magnetic transition at 44.3 K with a rapid increase of the magnetization when the temperature decreased and saturation at low temperatures (Fig. S4, ESI†). The magnetic transition temperature was consistent with that in previous study.⁴² Our experimental results included the magnetic properties of PEA-Mn along all crystallographic axes. The ZFCW and FCC processes exhibited similar magnetization, with values at 2 K for the FCC process of 4.2 emu Oe mol⁻¹ and 6.2 emu Oe mol⁻¹, along the b- and c-axes, respectively. However, along the a-axis, the FCC magnetization reached a value of 31.70 emu Oe mol⁻¹ at 2 K whereas a ZFCW magnetization of 0.48 emu Oe mol⁻¹ at 2 K and a cusp reaching 12 emu Oe mol⁻¹ at 44.0 K were observed. A magnetic hysteresis with a remanent magnetization (M_rem) of 5 × 10⁻³μ_B and a coercive field of 260 Oe was observed when the magnetic field was applied along the a-axis. In the high field region, a linear increase of magnetization was observed, reaching a value of 0.18 μ_B at 50 kOe. This value is much smaller than the theoretical saturated magnetization value of M_sat = gSμ_B = 5μ_B (Mn²⁺, g = 2, S = 5/2). Application of a magnetic field along the b-axis exhibited a linear increase of magnetization, reaching a value of 0.17 μ_B at 50 kOe. Along the c-axis, spin-flop transition was observed around ±35 kOe, which was in agreement with the reported study.⁴² During this spin-flop transition, the easy axis of the antiferromagnetic (AFM) arrangement was altered from the c-axis to the direction perpendicular to the applied field.

For PEA-Cu, observation for the ZFCW and FCC processes was similar (Fig. S4, ESI†). Along all axes, abrupt changes in the magnetization were observed around 9.5 K demonstrating a long-range magnetic order, in agreement with the previous studies.^43,46,47 The magnetic field dependences along all axes were described as soft magnetic behavior with a saturated magnetization of around 1.1 μ_B at 50 kOe, and hysteresis could not be observed in spite of the measurements at a field step of 5 Oe. The experimental saturation value is in good agreement with a value of M_sat = 1 μ_B (Cu²⁺, g = 2, S = 1/2).

For PEA-Fe, a magnetic transition at 98 K with a rapid increase of the magnetization along all axes in both ZFCW and FCC processes was observed (Fig. S4, ESI†). This transition temperature was in good agreement with the reported one.¹⁴ A magnetic hysteresis at 5 K with a M_rem of 0.02 μ_B and a coercive field of 5 kOe was observed when the magnetic field was applied along the a-axis. At 50 kOe, the magnetization reached a value of 0.10 μ_B, which was much smaller than the saturation value of gSμ_B = 6.84μ_B (Fe²⁺, g = 3.42,⁴⁸S = 2). Application of the magnetic field along b- and c-axes exhibited a linear increase of magnetization, reaching values of 0.01 μ_B and 0.08 μ_B at 50 kOe, respectively.

Results from temperature and magnetic field dependency measurements suggested that PEA-Mn and PEA-Fe display CAF with a spin-canted angle θ estimated at 0.05° and 0.17°, respectively, using M_rem = M_sat sin θ.⁴⁹ In comparison to PEA-Mn and PEA-Fe, PEA-Cu displays ferromagnetic (FM) ordering below 9.5 K.

Magnetization shift of PEA-M

The field-sweep measurements after the ZFC process exhibited a symmetric magnetization loop with respect to the origin for PEA-Mn and PEA-Cu. For PEA-Fe, the symmetric magnetization loop was observed along b- and c-axes while not along the a-axis. The shift of the magnetization curve after ZFC reflects on the weak cooling field remaining in the system. In fact, this shift is dependent on the cooling magnetic field (see “Relationship between SOC and the value of magnetization shift” section for details). Therefore, the application of exact ZFC would introduce the absence of the magnetization shift along the a-axis. After the FC process, a similar behavior to that of the ZFC process was observed for PEA-Mn and PEA-Cu (Fig. 3 and Fig. S5, ESI†). In the case of PEA-Fe, a displacement of the magnetization curves was observed, along all axes, after the FC process. To quantify the displacements of the magnetization curve, a shift value (M_Shift) can be defined as (M₊ + M₋)/2, where M₊ and M₋ are the magnetization at +50 and −50 kOe magnetic fields, respectively. Additionally, a shifted field (H_Shift) is calculated using the equation H_Shift = (H₊ + H₋)/2, where H₊ and H₋ correspond to the upper and lower magnetic fields of the magnetization zero point. The values of H_Shift during the FC_±50kOe process were ∓10 kOe along a- and b-axes and only ∓0.5 kOe along the c-axis. The M_Shift values after FC_±50kOe along the a-, b- and c-axes were ±2.04 × 10⁻²μ_B, ±2.7 × 10⁻³μ_B and ±0.8 × 10⁻³μ_B, respectively (Fig. 4). For powder samples, the magnetization shift was also observed for PEA-Fe after FC_±50kOe while not for PEA-Mn and PEA-Cu (Fig. 4 and Fig. S6, ESI†). The field-sweep measurements were also measured at 105 K where PEA-Fe showed paramagnetic, confirming the lack of the magnetization shift (Fig. S7, ESI†). The M_Shift, H_Shift, H₊ and H₋ for PEA-Fe along the a-axis were plotted as a function of the temperature (Fig. S8, ESI†). The H₊ and H₋ became presence below T_N while the M_Shift and H_Shift were observable at least blow 30 K. The increase in M_Shift was accompanied by an improvement in the H_Shift.

Fig. 3 Field dependence of the magnetization of PEA-M, with the magnetic field applied along (top) a-, (middle) b- and (bottom) c-axes at 5 K after ZFC, FC_+50kOe and FC_−50kOe. (a) M = Mn, (b) M = Cu, and (c) M = Fe.

Fig. 4 (a) The values of the magnetization shift for single crystals and powder samples of PEA-M (Mn, Cu and Fe) at 5 K after ZFC, FC_+50kOe and FC_−50kOe. (b) The enlarged figure of (a). The gray bidirectional arrows present in both graphs correspond to the same range.

PND study of PEA-Fe

The thermo-diffractograms collected at D20 for PEA-Fe as the system was heated from 2 K to 460 K allow two structural phase transitions to be observed (Fig. 5). The first one appeared around 340(10) K, where some peaks merged as the temperature was increased and a second one was visible at around 432(5) K. Although our data do not allow a high-quality refinement due to the presence of the incoherent scattering of the H atom, and a high degree of disorder at high temperatures, the space group in each phase has been identified, which corresponds to the Pbca for 2 K < T < 343 K, Bbcm for T in the interval of 343 K < T < 433 K and I4/mmm for 433 K < T, in agreement with the anomalies observed in DSC measurements. The analysis of the thermo-diffractograms allows the thermal evolution of the lattice parameters to be determined as a function of the temperature (Fig. S9, ESI†). The change from tetragonal to orthorhombic was clearly visible at 433 K whereas the change from Bbcm to Pbca was noticed at 343 K as a drastic change in the a- and b-axes. The unit cell volume is decreasing progressively, but not linearly, as temperature decreases and shows two small anomalies at the critical temperatures.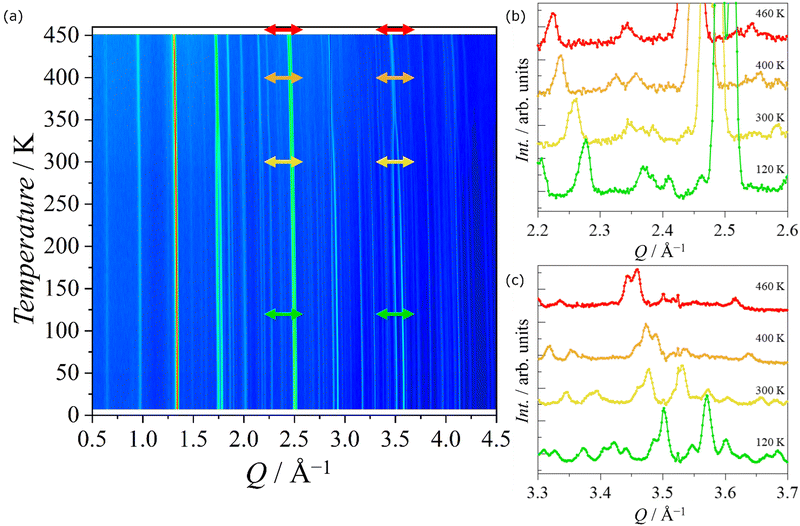

Fig. 5 (a) Thermo-diffractograms measured warming up the PEA-Fe from 2 K to 460 K. (b) and (c) Neutron diffraction patterns of the regions (b) 2.2 < Q < 2.6 Å⁻¹ and (c) 3.3 < Q < 3.7 Å⁻¹ at 120, 300, 400 and 460 K, corresponding to green, yellow, orange and red double-headed arrows in panel (a), respectively. In Table S5 (ESI†), the refinement parameters for different temperatures in the Pbca space group phase below 343 K are given.

The high statistics data collected at fixed temperatures on D20 confirmed that there was no structural phase transition in the range 2 K to 343 K. However, some very small additional peaks were observed at the diffractograms at 2 K and 50 K around Q = 0.9, 1.8 and 2 Å⁻¹ that were not present at the diffractograms measured for T > 100 K and that were indexed with a propagation vector k⃑ = (0,0,0) (Fig. 6a). This suggested the onset of a long-range magnetic order, which was estimated to appear around T = 97(7) K from the thermo-diffractograms data.

Fig. 6 (a) and (b) Refinements of the diffractogram for PEA-Fe at (a) 120 K and (b) 2 K. The red points are the experimental points, the solid black line is the fit, the blue line is the difference between the experimental data and the fit, and the green lines correspond to the hkl positions for the nuclear and magnetic phases. In the inset of panel (a), the subtraction between the high statistics (more than 4 hours) diffractograms collected at 2 K and 120 K in D20 is shown in order to better visualize those small magnetic peaks. The inset in panel (b) represents the fitting curve by using the model Pb′c′a. (c) Magnetic structure of PEA-Fe. Red and blue lines show the (blue) ferromagnetic J_FM and (red) antiferromagnetic J_AFM interactions between neigboring magnetic ions. Yellow arrows indicate the orientation of the magnetic dipoles.

PND measurements of PEA-Fe revealed the absence of the structural phase transition from the ferroelastic Pbca to a higher symmetry space group, suggesting the persistence of ferroelasticity below T_N. The remaining of the ferroelastic phase below the magnetic phase transition temperatures in PEA-Mn and PEA-Cu can be assumed, due to their structural similarity with PEA-Fe.

Magnetic structure analysis of PEA-Fe

To describe the symmetry of the magnetic phase, the irreducible representation theory is employed. For the Fe atom in Wyckoff position 4b of the Pbca space group and propagation vector k⃑ = (0,0,0), the magnetic representation was decomposed as the direct sum of irreducible representations (Irreps) as follows:

Γ_M = 3mΓ⁺₁(1) + 3mΓ⁺₂(1) + 3mΓ⁺₃(1) + 3mΓ⁺₄(1) (1)

which indicated that each 1-dimensional Irreps appears 3 times. In Table 1, the Fourier coefficient for each Irreps was shown. In all the above Irreps, the magnetic moments were allowed to have components (u,v,w) along the a-, b-, and c-axes.

Table 1 Irreps contained in the magnetic representation Γ_M for the Fe atom in the Wyckoff position 4b of the Pbca space group and the propagation vector k⃑ = (0,0,0)

	Fe1	Fe2	Fe3	Fe4
	x,y,z	−x + 1/2, −y, z−1/2	−x, y + 1/2, −z + 1/2	x + 1/2, −y + 1/2, −z + 1
Γ ^+1	(u,v,w)	(−u,−v,w)	(−u,v,−w)	(u,−v,−w)
Γ ^+2	(u,v,w)	(−u,−v,w)	(u,−v,w)	(−u,v,w)
Γ ^+3	(u,v,w)	(u,v,−w)	(−u,v,−w)	(−u,v,w)
Γ ^+4	(u,v,w)	(u,v,−w)	(u,−v,w)	(u,−v,−w)

---

From the magnetization data, we know that the magnetic structure has to be a CAF along the a-axis and the only Irreps that allows a FM component along the a-axis and AFM along the others is Γ⁺₄. The fit of the high statistics diffractogram at 2 K was done with each one of the previous Irreps, and, as was expected, only the Γ⁺₄ was able to fit the peaks shown in the inset of Fig. 6a giving a value of the magnetic moment of 2.6(2) μ_B along the b-axis and zero along the other directions. In fact, the other possible models allowed by the symmetry, described by Γ⁺₁, Γ⁺₂ and Γ⁺₃, failed to reproduce the intensity found experimentally at the magnetic Bragg peak (1 0 1). At this point, it is important to remark that the neutron diffraction experiments are done under zero magnetic field and that the measured magnetic signal, in spite of the high acquisition time, was very small. Therefore, we can conclude that the magnetic structure is the one given by the Γ⁺₄ irreducible representation, where the Fe magnetic moments form a CAF structure along the a-axis. In fact, the structure obtained from the fit is a pure AFM along the b-axis, with no component along the a-axis. However, this is in agreement with our magnetization data, since it is mentioned that the component parallel to the a-axis is around 0.02 μ_B, with a canting angle of around 0.17°. In this case, such a low magnetic component will be undetectable with PND, even with high acquisition times.

The magnetic subgroup which corresponds with the fitted magnetic structure is Pb′c′a (No. 61.4.500), with a transformation matrix given by: (−b, −c, a; 0, 0, 0). The fits of the diffractograms at 120 K in the paramagnetic phase and 2 K in the ordered phase are shown in Fig. 6, respectively, with continuous black lines. The experimental data are the red points whereas the blue line represents the difference between the experimental and the fitted model at each temperature. The most intense magnetic peak is only correctly fitted by considering the model Pb′c′a (the inset in Fig. 6b).

Relationship between SOC and the value of the magnetization shift

Comparing the field cooling effect for PEA-M, only PEA-Fe shows the shift in both the powder samples and single crystals. Such magnetic behavior has been observed in the iron-based 2D perovskite compound (C₂H₅NH₃)₂FeCl₄.¹² The authors tentatively associated the magnetization shift with the interaction of magnetic, electric, and elastic domains. In this study, we considered three possible mechanisms to explain the magnetization shift: a minor loop effect, an exchange bias effect and the interaction between magnetic and elastic orders.

The first possible mechanism to explain the magnetization shift involves minor loops. Minor loops are typically defined as a hysteresis loop without saturation within the applied magnetic field. After cooling under the magnetic field, minor loops appear as shifted hysteresis loops when the maximal external field is too small to completely reverse the magnetization. Saturation of the magnetization of PEA-Fe within an external field of 50 kOe was not achieved, making it difficult to distinguish between magnetization shifts from the minor loop phenomena. To do so, the field dependence magnetization was performed at 5 K after various field cooling (Fig. S10a, ESI†). The value of the magnetization shift was increased and reached in saturation by increasing the cooling field (Fig. S10b, ESI†). The magnetization shift is observed even when the external field is over 1000 times larger than the cooling field, and magnetic behaviors under the field sweep cannot be minor loops. Therefore, the scenario based on the minor loop phenomenon is not suitable.

The second plausible mechanism to explain the magnetization shift involves the coexisting (anti)ferromagnetic and spin glass orders. Such a property is known as the exchange bias.⁵⁰ The exchange bias has been observed in various systems including FM or ferrimagnetic nanoparticles embedded in an AFM matrix, FM/AFM thin film heterostructures and materials with coexistence of (anti)ferromagnetic and spin-glass orders.^50–52 The theory for the exchange bias in their systems has been described as various models such as the uncompensated spins, and the pinning of domain walls at the interface.^53,54 Many materials with the exchange bias exhibit the training effect, i.e., a reduction of the displacement value of the magnetization curve upon repeated measurements without new field cooling. The origin of the training effect is explained as a rearrangement of the AFM domain structures with repetition of field cycles.^55,56 For the powder sample of PEA-Fe, we repeated the magnetic field-sweep measurements six times at 5 K after field cooling under the 50 kOe magnetic field (Fig. S11, ESI†). The magnetization shift was invariant of the number of field cycles, suggesting that the second mechanism also cannot describe the magnetization shift.

The third plausible mechanism to explain the magnetization shift involves the coupling of different ferroic orders. In contrast to the second mechanism, where the behavior is attributed to the interaction between different spin orders, here the behavior is attributed to the interaction between different ferroic orders. ME materials show an electrically controllable hysteresis loops shift, which is attributed to the coupling between magnetic and electric orders.^57,58 Materials with the ME effect tend to have an incommensurate magnetic structure; however, PND experiments on PEA-Fe revealed a commensurate magnetic structure with the propagation vector k⃑ = (0,0,0). In addition, the crystal structure of PEA-Fe below T_N is non-polar (Pbca). From this finding, we assume the absence of the ME effect in PEA-Fe, to explain the magnetization shift, but more studies would be necessary to confirm it. On the other hand, the MA effect to induce the magnetization shift can be investigated. The ferroelastic phase transition from tetragonal to orthorhombic crystal systems induces the distortion of the bridging Cl–Fe–Cl angle as 0.293(3)°, resulting in non-zero DM vectors. The DM vectors in PEA-Fe are aligned antiparallel to each other, which tilts the AFM spins (i.e. CAF appears), while are aligned parallel in chiral magnets (Fig. S12, ESI†).^14,59 DM interactions are due to SOC.³³ An orbital angular momentum is induced by the anisotropic distortion of the crystal during the ferroelastic phase transition, which affects the spin angular momentum via SOC. As a result, magnetic moments, which is a macroscopic measurement of the spin angular momentum, are coupled to crystalline distortion, leading to anisotropy. This phenomenon can be understood as crystalline magnetic anisotropy. This crystalline magnetic anisotropy corresponds to the internal magnetic field for the AFM spin structure,⁶⁰ and the crystalline magnetic anisotropy affects the magnetic domains through magnetic dipole interactions. For the ZFC process, mean magnetization is null because the magnetic anisotropy is non-polarized. As a result, the internal magnetic moment is not induced. For the FC process, due to the magnetostrictive effect, the 50 kOe magnetic field induces a strain in the material. This strain is stabilized or strengthened by the cooling process and become unalterable. This strain induces an extended internal magnetic field, which depends on the strength of the MA effect, strong enough to partially mitigate the external field which induce the magnetization shift. The applied magnetic field and the actual magnetic field are dissimilar and create a shift. The shift between the ZFC and FC processes can be considered as a direct riding of the extended internal magnetic field. Again, our concept for the MA effect is inspired by the chiral magnets exhibiting chirality-induced couplings among lattice, electronic, and magnetic degrees of freedom.^59,61,62

Here, we assess the applicability of the third mechanism in PEA-Fe. In the ferroelastic phase transition from tetragonal to orthorhombic crystal systems, spontaneous strain e_s exists within the layers. In addition, the spin component along the c-axis is absence below T_N. As a result, the coupling of the in-plane configurations of e_s and AFM spins can impose different strengths of the MA effect along the crystallographic axes, leading to anisotropy for M_Shift and H_Shift. Indeed, both M_Shift and H_Shift, after FC, were much smaller along the c-axis than along the a or b-axes. Therefore, the M_Shift and H_Shift along the c-axis can come from the in-plane components of the MA effect, due to a slight misalignment of the crystal. Moreover, the temperature dependence of M_Shift and H_Shift along the a-axis suggests that lower temperature suppresses the thermal fluctuation of the AFM structures, strengthening the association with the induced internal magnetic field, resulting in a larger values of M_Shift and H_Shift. These specific characteristics of PEA-Fe can support the argument about the mechanism of the MA effect.

Our concept suggests that the value of the magnetization shift could be understood as the strength of the coupling between magnetic and elastic orders, i.e., the effect of the strength of SOC. However, it is well known that the SOC constant of the Fe²⁺ ion is smaller than that of the Cu²⁺ ion, indicating that the SOC energy of the Fe²⁺ ion is smaller than that of the Cu²⁺ ion. This is not consistent with our experimental data and discussion about the magnetization shift for PEA-M with ferroelasticity. In general, the strength of the SOC is reflected in that of magnetocrystalline anisotropy for transition metal-based magnets. PEA-Cu exhibits soft magnetic behavior, with the magnetization at 50 kOe along all axes being almost identical. For PEA-Fe, there is the absence of spin–flop transition in the range of the 50 kOe magnetic field, indicating the presence of large magnetocrystalline anisotropy. Thus, we can conclude that the SOC in PEA-Fe is stronger than that in PEA-Cu, which authenticates the explanation for the proposed mechanism of the magnetization shift.

Our study investigates the MA effect in two-dimensional organic–inorganic perovskites. The relationship between the strain and SOC associated with the ferroelastic phase transition can be explained by the Ginzburg–Landau phenomenology. The energy contributing to the magnetic anisotropy depends on both SOC and strain. This has established the role of uniaxial strain in chiral magnets.^63,64 Since anisotropic strain is applied to the crystal during the ferroelastic phase transition, the above interpretation provides knowledge on how the lattice distortion during the ferroelastic phase transition affects the magnetic anisotropy. However, theoretical studies on the interactions between magnetic and elastic domains are required to obtain a deeper insight into the MA effect.

Based on the above research results, the chemical approaches to control the magnetization shift should have the following ways. Firstly, taking into account that the larger the atomic number of the halogen ion, the stronger SOC, the value of the magnetization shift should be increased in bromine- or iodide-based organic–inorganic perovskite compounds. Second, the negative (positive) value of the magnetization shift after cooling in a positive (negative) magnetic field can be observed when the number of d electrons is less than 5 (d < 5) because the sign of the SOC constant is opposite to that for d > 5.⁶⁵ Among d < 5, some Cr²⁺-based organic–inorganic perovskite materials have been reported,⁶⁶ and their magnetization shift should be opposite to that of PEA-Fe. Finally, the magnetization shift of 4d, 5d or 4f magnetic materials can be larger than that of 3d magnetic materials because the SOC tends to be larger with an increasing atomic number.⁶⁷ The presented magnetization shift and its mechanism suggest that PEA-Fe is an important example of multiferroic materials with the MA effect, providing an intriguing role of SOC in ferroelastic materials.

Conclusions

In this study, we investigated the interaction between ferroelasticity and spontaneous magnetization in PEA-M (M = Mn, Cu, Fe) with two-dimensional organic–inorganic perovskite structures. All three compounds show ferroelasticity and magnetic order; in particular, the coexistence of ferroelasticity and CAF is demonstrated in PEA-Fe. More notably, the magnetization curve is shifted by cooling in the magnetic field from above the magnetically ordered temperature. Our comprehensive discussions propose that the magnetization shift is due to the MA coupling, and the strength of the coupling can be controlled by the tuning of SOC.

This work provides an approach to build AFM-based spintronic devices. For example, the spontaneous strain can be used to drive magnons, enabling information transport without magnetic field. Besides, our findings can achieve improved properties in strain-assisted logic memory devices due to the reversible control of the AFM moment. Finally, our study of the MA effect provides an intriguing character in ferroelastic–magnetic materials, invigorating multiferroic research.

Author contributions

N. T.: methodology, investigation, formal analysis, visualization, and writing – original draft preparation. S. A. and Y. N.: methodology and investigation. G. C.: visualization, validation of magnetic properties, and writing. S. N.: methodology and validation. M. P-S., J. A. R-V., and J.C.: investigation, formal analysis, and visualization. K. I.: conceptualization, funding acquisition, and supervision. All authors have given approval to the final version of the manuscript.

Data availability

The thermal, optical and magnetic data are available from the corresponding author, K. I., upon reasonable request. The crystallographic data have been deposited in the Cambridge Crystallographic Data Centre (CCDC) under accession codes: CCDC 2411272–2411280† for PEA-M (M = Mn, Cu, Fe). The neutron data for this article are accessible at the Institut Laue-Langevin (ILL) at https://dx.doi.org/10.5291/ILL-DATA.5-31-2820.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the JSPS Grants-in-Aid for Scientific Research (Grant Numbers 15K13674, 25220803 and 22H02053) and the JSPS Core-to-Core Program “Advanced Research Networks”, SPRING (Grant Numbers JPMJSP2132) from the Japan Science and Technology Agency (JST) and the Advanced Research Infrastructure for Materials and Nanotechnology in Japan (ARIM) of the Ministry of Education, Culture, Sports, Science and Technology (MEXT). Grants No. PID2022-138492NB-I00-XM4, funded by MCIN/AEI/10.13039/501100011033, and No. E11-23R/M4, funded by Diputación General de Aragón (Spain), supported this work. This work was conducted with the facilities in the Natural Science Center for Basic Research and Development (N-BARD) at Hiroshima University (NBARD-00105), and in Institute for Molecular Science (Proposal Number JPMXP1222MS1047b, S21MS1023 and S20MS1029). The MPMS3 SQUID magnetometer used in this paper was installed with the support of WPI-SKCM² at Hiroshima University and the Hiroshima University Regional Core (J-PEAKS). Institut Laue Langevin is acknowledged for beam time granted through proposal number 5-31-2820.

Notes and references

1. C. N. R. Rao and K. Rao, Ferroics, in Solid State Chemistry: Compounds, ed. P. Day and A. K. Cheetham, Oxford University Press, New York, 1992, pp. 281–296.
2. H. Schmid, Multi-ferroic magnetoelectrics, Ferroelectrics, 1994, 162, 317–338.
3. D. B. Mitzi, A Layered Solution Crystal Growth Technique and the Crystal Structure of (C₆H₅C₂H₄NH₃)₂PbCl₄, J. Solid State Chem., 1999, 145, 694–704.
4. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131, 6050–6051.
5. T. Goto, B. Luthi, R. Geick and K. Strobel, Elastic properties of the layer-structure material (CH₃NH₃)₂MnCl₄, J. Phys. C: Solid State Phys., 1979, 12, L303–L307.
6. T. Ishihara, J. Takahashi and T. Goto, Optical properties due to electronic transitions in two-dimensional semiconductors (C_nH_2n+1NH₃)₂PbI₄, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 11099–11107.
7. A. K. Cheetham and C. N. R. Rao, There's Room in the Middle, Science, 1979, 2007(318), 58–59.
8. D. B. Mitzi, Synthesis, Structure, and Properties of Organic-Inorganic Perovskites and Related Materials, in Progress in Inorganic Chemistry, ed. K. D. Karlin, John Wiley & Sons, New York, 1999, pp. 1–121.
9. L. Mao, C. C. Stoumpos and M. G. Kanatzidis, Two-Dimensional Hybrid Halide Perovskites: Principles and Promises, J. Am. Chem. Soc., 2019, 141, 1171–1190.
10. T. Suzuki, M. Yoshizawa, T. Goto, T. Yamakami, M. Takahashi and T. Fujimura, Structural Phase Transition of Layer Compound (C₂H₅NH₃)₂FeCl₄, J. Phys. Soc. Jpn., 1983, 52, 1669–1675.
11. J. Han, S. Nishihara, K. Inoue and M. Kurmoo, On the Nature of the Structural and Magnetic Phase Transitions in the Layered Perovskite-Like (CH₃NH₃)₂[Fe^IICl₄], Inorg. Chem., 2014, 53, 2068–2075.
12. J. Han, S. Nishihara, K. Inoue and M. Kurmoo, High Magnetic Hardness for the Canted Antiferromagnetic, Ferroelectric, and Ferroelastic Layered Perovskite-like (C₂H₅NH₃)₂[Fe^IICl₄], Inorg. Chem., 2015, 54, 2866–2874.
13. B. Huang, B.-Y. Wang, Z.-Y. Du, W. Xue, W.-J. Xu, Y.-J. Su, W.-X. Zhang, M.-H. Zeng and X.-M. Chen, Importing spontaneous polarization into a Heisenberg ferromagnet for a potential single-phase multiferroic, J. Mater. Chem. C, 2016, 4, 8704–8710.
14. Y. Nakayama, S. Nishihara, K. Inoue, T. Suzuki and M. Kurmoo, Coupling of Magnetic and Elastic Domains in the Organic–Inorganic Layered Perovskite-Like (C₆H₅C₂H₄NH₃)₂Fe^IICl₄ Crystal, Angew. Chem., Int. Ed., 2017, 56, 9367–9370.
15. K. Taniguchi, M. Nishio, N. Abe, P. Huang, S. Kimura, T. Arima and H. Miyasaka, Magneto-Electric Directional Anisotropy in Polar Soft Ferromagnets of Two-Dimensional Organic–Inorganic Hybrid Perovskites, Angew. Chem., Int. Ed., 2021, 60, 14350–14354.
16. K. Aizu, Possible Species of Ferromagnetic, Ferroelectric, and Ferroelastic Crystals, Phys. Rev. B, 1970, 2, 754–772.
17. B. B. Van Aken, J.-P. Rivera, H. Schmid and M. Fiebig, Observation of ferrotoroidic domains, Nature, 2007, 449, 702–705.
18. S. V. Kiselev, R. P. Ozerov and G. S. Zhdanov, Detection of Magnetic Order in Ferroelectric BiFeO₃ by Neutron Diffraction, Sov. Phys. Dokl., 1963, 7, 742–744.
19. T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima and Y. Tokura, Magnetic control of ferroelectric polarization, Nature, 2003, 426, 55–58.
20. J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom, U. V. Waghmare, N. A. Spaldin, K. M. Rabe, M. Wuttig and R. Ramesh, Epitaxial BiFeO₃ Multiferroic Thin Film Heterostructures, Science, 2003, 299, 1719–1722.
21. P. Jain, V. Ramachandran, R. J. Clark, H. D. Zhou, B. H. Toby, N. S. Dalal, H. W. Kroto and A. K. Cheetham, Multiferroic Behavior Associated with an Order−Disorder Hydrogen Bonding Transition in Metal–Organic Frameworks (MOFs) with the Perovskite ABX₃ Architecture, J. Am. Chem. Soc., 2009, 131, 13625–13627.
22. A. Stroppa, P. Jain, P. Barone, M. Marsman, J. M. Perez-Mato, A. K. Cheetham, H. W. Kroto and S. Picozzi, Electric Control of Magnetization and Interplay between Orbital Ordering and Ferroelectricity in a Multiferroic Metal–Organic Framework, Angew. Chem., Int. Ed., 2011, 50, 5847–5850.
23. M. Ackermann, D. Brüning, T. Lorenz, P. Becker and L. Bohatý, Thermodynamic properties of the new multiferroic material (NH₄)₂[FeCl₅(H₂O)], New J. Phys., 2013, 15, 123001.
24. M. Fiebig, Revival of the magnetoelectric effect, J. Phys. D: Appl. Phys., 2005, 38, R123–R152.
25. T. Kyômen, A. Sano, Y. Murachi, M. Hanaya, K. Suzuki and M. Ito, Coupling of ferroelasticity and ferromagnetism in La_1−xSr_xCoO₃ twin crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 064402.
26. M. Ramazanoglu, W. Ratcliff, H. T. Yi, A. A. Sirenko, S.-W. Cheong and V. Kiryukhin, Giant Effect of Uniaxial Pressure on Magnetic Domain Populations in Multiferroic Bismuth Ferrite, Phys. Rev. Lett., 2011, 107, 067203.
27. T. Nakajima, S. Mitsuda, T. Nakamura, H. Ishii, T. Haku, Y. Honma, M. Kosaka, N. Aso and Y. Uwatoko, Control of ferroelectric polarization via uniaxial pressure in the spin-lattice-coupled multiferroic CuFe_1−xGa_xO₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 220101.
28. K. Ullakko, J. K. Huang, C. Kantner, R. C. O’Handley and V. V. Kokorin, Large magnetic-field-induced strains in Ni₂MnGa single crystals, Appl. Phys. Lett., 1996, 69, 1966–1968.
29. C. Feng, Y. Li, L. Wang, Y. Cao, M. Yao, F. Meng, F. Yang, B. Li, K. Wang and G. Yu, Giant Strain Control of Antiferromagnetic Moment in Metallic FeMn by Tuning Exchange Spring Structure, Adv. Funct. Mater., 2020, 30, 1909708.
30. Y. Togawa, T. Koyama, K. Takayanagi, S. Mori, Y. Kousaka, J. Akimitsu, S. Nishihara, K. Inoue, A. S. Ovchinnikov and J. Kishine, Chiral Magnetic Soliton Lattice on a Chiral Helimagnet, Phys. Rev. Lett., 2012, 108, 107202.
31. M. Mito, H. Ohsumi, T. Shishidou, F. Kuroda, M. Weinert, K. Tsuruta, Y. Kotani, T. Nakamura, Y. Togawa, J. Kishine, Y. Kousaka, J. Akimitsu and K. Inoue, Observation of orbital angular momentum in the chiral magnet CrNb₃S₆ by soft x-ray magnetic circular dichroism, Phys. Rev. B, 2019, 99, 174439.
32. I. Dzyaloshinsky, A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics, J. Phys. Chem. Solids, 1958, 4, 241–255.
33. T. Moriya, Anisotropic Superexchange Interaction and Weak Ferromagnetism, Phys. Rev., 1960, 120, 91–98.
34. R. D. Willett and E. F. Riedel, A neutron diffraction study of the crystal structures and magnetic studies of (NH₃CH₂CH₂CH₂NH₃)MnCl₄ and (NH₃CH₂CH₂NH₃)FeCl₄: Layer structures with two-dimensional magnetic interactions, Chem. Phys., 1975, 8, 112–122.
35. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341.
36. G. M. Sheldrick, A short history of SHELX, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
37. G. M. Sheldrick, SHELXT – Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8.
38. G. M. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
39. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.
40. G. A. Bain and J. F. Berry, Diamagnetic Corrections and Pascal's Constants, J. Chem. Educ., 2008, 85, 532.
41. J. Rodríguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B, 1993, 192, 55–69.
42. S.-H. Park, I.-H. Oh, S. Park, Y. Park, J. H. Kim and Y.-D. Huh, Canted antiferromagnetism and spin reorientation transition in layered inorganic–organic perovskite (C₆H₅CH₂CH₂NH₃)₂MnCl₄, Dalton Trans., 2012, 41, 1237–1242.
43. A. O. Polyakov, A. H. Arkenbout, J. Baas, G. R. Blake, A. Meetsma, A. Caretta, P. H. M. van Loosdrecht and T. T. M. Palstra, Coexisting Ferromagnetic and Ferroelectric Order in a CuCl₄-based Organic–Inorganic Hybrid, Chem. Mater., 2012, 24, 133–139.
44. K. Aizu, Possible Species of “Ferroelastic” Crystals and of Simultaneously Ferroelectric and Ferroelastic Crystals, J. Phys. Soc. Jpn., 1969, 27, 387–396.
45. K. Aizu, Determination of the State Parameters and Formulation of Spontaneous Strain for Ferroelastics, J. Phys. Soc. Jpn., 1970, 28, 706–716.
46. W. E. Estes, D. B. Losee and W. E. Hatfield, The magnetic properties of several quasi two-dimensional Heisenberg layer compounds: A new class of ferromagnetic insulators involving halocuprates, J. Chem. Phys., 1980, 72, 630–638.
47. G. Park, J. Cho, J.-S. Kim, Y. Kim, J. H. Jung, N. Hur, I.-H. Oh and K.-Y. Kim, Critical behavior of quasi-2D organic-inorganic halide perovskite (C₆H₅CH₂CH₂NH₃)₂CuCl₄ single crystals, Curr. Appl. Phys., 2022, 35, 24–31.
48. T. P. P. Hall, W. Hayes, R. W. H. Stevenson and J. Wilkens, Investigation of the Bonding of Iron-Group Ions in Fluoride Crystals. II, J. Chem. Phys., 1963, 39, 35–39.
49. O. Kahn, Molecular Magnetism, VCH, New York, 1993.
50. W. H. Meiklejohn and C. P. Bean, New Magnetic Anisotropy, Phys. Rev., 1956, 102, 1413–1414.
51. J. Nogués, D. Lederman, T. J. Moran, I. K. Schuller and K. V. Rao, Large exchange bias and its connection to interface structure in FeF₂–Fe bilayers, Appl. Phys. Lett., 1996, 68, 3186–3188.
52. M. Ali, P. Adie, C. H. Marrows, D. Greig, B. J. Hickey and R. L. Stamps, Exchange bias using a spin glass, Nat. Mater., 2007, 6, 70–75.
53. K. Takano, R. H. Kodama, A. E. Berkowitz, W. Cao and G. Thomas, Interfacial Uncompensated Antiferromagnetic Spins: Role in Unidirectional Anisotropy in Polycrystalline Ni₈₁Fe₁₉/CoO Bilayers, Phys. Rev. Lett., 1997, 79, 1130–1133.
54. R. L. Stamps, Mechanisms of exchange bias: partial wall pinning, and fluctuations, J. Magn. Magn. Mater., 2002, 242–245, 139–145.
55. U. Nowak, K. D. Usadel, J. Keller, P. Miltényi, B. Beschoten and G. Güntherodt, Domain state model for exchange bias. I. Theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 014430.
56. J. Keller, P. Miltényi, B. Beschoten, G. Güntherodt, U. Nowak and K. D. Usadel, Domain state model for exchange bias. II. Experiments, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 014431.
57. Y. Tokunaga, Y. Taguchi, T. Arima and Y. Tokura, Magnetic Biasing of a Ferroelectric Hysteresis Loop in a Multiferroic Orthoferrite, Phys. Rev. Lett., 2014, 112, 037203.
58. J. K. H. Fischer, H. Ueda and T. Kimura, Domain switching and exchange bias control by electric field in the multiferroic conical magnet Mn₂GeO₄, Phys. Rev. B, 2020, 102, 054412.
59. J. Kishine and A. S. Ovchinnikov, Theory of Monoaxial Chiral Helimagnet, in Solid State Physics, ed. R. E. Camley and R. L. Stamps, Academic Press, 2015, vol. 66, pp. 1–130.
60. S. Chikazumi, Physics of Ferromagnetism, Magnetic Characteristics and Engineering Application, 1984, vol. 2.
61. J. Kishine, A. S. Ovchinnikov and A. A. Tereshchenko, Chirality-Induced Phonon Dispersion in a Noncentrosymmetric Micropolar Crystal, Phys. Rev. Lett., 2020, 125, 245302.
62. K. Ishito, H. Mao, Y. Kousaka, Y. Togawa, S. Iwasaki, T. Zhang, S. Murakami, J. Kishine and T. Satoh, Truly chiral phonons in α-HgS, Nat. Phys., 2023, 19, 35–39.
63. A. B. Butenko, A. A. Leonov, U. K. Rößler and A. N. Bogdanov, Stabilization of skyrmion textures by uniaxial distortions in noncentrosymmetric cubic helimagnets, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 052403.
64. Y. Nii, T. Nakajima, A. Kikkawa, Y. Yamasaki, K. Ohishi, J. Suzuki, Y. Taguchi, T. Arima, Y. Tokura and Y. Iwasa, Uniaxial stress control of skyrmion phase, Nat. Commun., 2015, 6, 8539.
65. M. Blume, R. E. Watson and R. E. Peierls, Theory of spin–orbit coupling in atoms, II. Comparison of theory with experiment, Proc. R. Soc. London, Ser. A, 1963, 271, 565–578.
66. C. Bellitto and P. Day, Feature article. Organic-intercalated halogenochromates(II): low-dimensional magnets, J. Mater. Chem., 1992, 2, 265–271.
67. M. Blume, A. J. Freeman and R. E. Watson, Theory of Spin-Orbit Coupling in Atoms. III, Phys. Rev., 1964, 134, A320–A327.

---

Footnote

† Electronic supplementary information (ESI) available: Thermogravimetric-differential thermal analysis, differential scanning calorimetry measurement, stress test, magnetic properties, neutron diffraction, and crystallographic data. CCDC 2411272–2411280. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4tc04445b

---