Novel layered As₂Ge with a pentagonal structure for potential thermoelectrics

Abstract

The versatile properties of two-dimensional materials indicate that they have enormous potential for applications in thermoelectrics. In this work, we proposed a novel layered pentagonal-structured As₂Ge crystal and investigated its stability and electronic structure using density functional theory (DFT) calculations. By combining the results of DFT with Boltzmann transport and phonon transport theory, we studied the electronic conductivity, thermal conductivity and thermoelectric transport properties. It was found that the As₂Ge monolayer is a stable layered semiconductor with a wide indirect band gap of 2.43 eV. It exhibits a high electron mobility of up to 7595 cm² V⁻¹ s⁻¹. The n-type monolayer of As₂Ge can achieve a remarkable ZT value as high as 4.36 at 1000 K, and the maximal value of ZT in p-type As₂Ge is predicted to reach 3.5 at 1000 K.

---

1. Introduction

In recent years, the global energy crisis and environmental pollution problems have become increasingly severe, posing a significant challenge to humanity. There are various approaches to tackle these challenges, among which enhancing the development and utilization of new energy sources is crucial for addressing these issues.¹ Thermoelectric devices enable direct conversion between electric energy and heat energy, offering vast prospects for applications. Consequently, extensive attention and research have been devoted to the advancement of high-performance thermoelectric materials.^2–4

The thermoelectric properties of thermoelectric materials are evaluated by the dimensionless quality factor (ZT).^5–8 It can be expressed as ZT = S²σT/κ, where S, σ, T and κ represent the Seebeck coefficient, conductivity, absolute temperature, and thermal conductivity.² A higher value of ZT indicates better thermoelectric performance.⁶ Therefore, high-performance thermoelectric materials should possess a high power factor (PF = S²σ) while simultaneously exhibiting low thermal conductivity.

In 2004, the emergence of graphene sparked significant attention and research on two-dimensional layers.^9–11 Numerous studies have demonstrated that the quantum confinement effect in low-dimensional materials holds potential for enhancing the material's power factor (PF), leading to a higher figure of merit (ZT) compared to bulk materials.^12–15 Additionally, in two-dimensional material systems, it is possible to exhibit remarkably low thermal conductivity characteristics, exemplified by PdSe₂ crystals, SnSe crystals, and SnS crystals.^16–18 Consequently, these two-dimensional materials were regarded as highly promising candidates for high-performance thermoelectric applications.^19–23 Additionally, layered materials typically consist of multiple atomic layers interconnected by weak forces, such as van der Waals interactions, which often result in distinct physical properties along the in-plane and inter-plane directions, leading to thermoelectric anisotropy.²⁴ Comprehending and manipulating this anisotropy can offer valuable insights for enhancing the thermoelectric performance of materials. Recently, a layered pentagonal structure has been explored for potential application of thermoelectrics and some materials with this structure have been reported with possible high-performance, such as penta-PdSe₂,²⁵ penta-silicene and penta-germanene.²⁶ This crumpled pentagonal configuration may contribute to reducing lattice thermal conductivity^25–30 and thus lead to potential high-performance. We considered that germanium with possible sp³ hybridization combines with arsenic to form As₂Ge with a possible pentagonal structure which may have excellent thermoelectric properties.

In this work, we performed density functional theory (DFT) calculations to explore the structural stability and thermal stability of the pentagonal As₂Ge monolayer for possible experimental fabrication. Then the electronic structure and electron transport properties were analyzed based on Boltzmann transport theory with DFT calculations. Using phonon transport theory combined with the DFT results, we simulated the phonon thermal conductivity. Finally, under the constant relaxation time approximation (CRTA), we combined the thermopower with electronic transport and phonon transport to analyze the thermoelectric figure of merit ZT. The findings have predicted that the As₂Ge monolayer exhibits excellent thermoelectric properties, providing crucial theoretical guidance for its potential application in electronic and thermoelectric devices.

2. Calculation methods

The Vienna Ab initio Simulation Package (VASP) was utilized for ab initio calculations based on the DFT within the framework of first principles.³¹ To account for electron–electron interactions, we employed the projected augmented wave (PAW) pseudopotential approach.³² For investigating electronic properties, we adopted the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation³³ as standard exchange–correlation functionals.³⁴ Due to the inherent tendency of the PBE functional to underestimate electronic band gaps, we incorporated the HSE06 hybrid functional to accurately describe them.³⁴ An energy convergence criterion of 10⁻⁸ eV Å⁻¹ was set and a maximum Hellmann–Feynman force threshold of 10⁻⁴ eV Å⁻¹ was ensured during relaxation procedures. Sampling of the Brillouin zone was performed using a Monkhorst–Pack k-point mesh with dimensions of 20 × 20 × 1. Additionally, interlayer interactions in two-dimensional materials were considered to be ignored by introducing a vacuum thickness along the z-axis with a value of 16 Å during calculations.

The thermal stability of the proposed structural model was assessed through ab initio molecular dynamics (AIMD) simulations. The AIMD simulation was conducted at a temperature of 1000 K, employing a time step of 1 fs and total simulation duration of 9 ps. Here, a temperature of 1000 K was selected to investigate the structural stability of the As₂Ge monolayer for the following reasons. First, the properties of thermoelectric materials are typically most pronounced at elevated temperatures, and 1000 K is sufficiently high to examine the variations in the thermodynamic properties of materials under such conditions, thereby providing a comprehensive understanding of the thermal stability of As₂Ge monolayers. Second, from a practical standpoint, 1000 K represents a manageable and frequently utilized high-temperature setting in laboratory environments, offering a robust theoretical foundation for subsequent experimental research on As₂Ge materials.

The BoltzTrap code was utilized for investigating the electron transport characteristics, and a grid of 50 × 50 × 1 k-points sampling was selected to accurately determine transport coefficients such as the Seebeck coefficient.³⁵ The relaxation time was calculated based on the deformation potential theory, which further enabled the determination of conductivity.³⁶

The lattice thermal conductivity was calculated based on the anharmonic phonon–phonon scattering mechanism. The second order (2ND) force constant was obtained using the finite displacement method in the PHONOPY code,³⁷ with a 5 × 5 × 1 k-mesh sampling in a 4 × 4 × 1 supercell. With the ShengBTE code,³⁸ the third order (3RD) force constant was obtained, and the lattice thermal conductivity was calculated using a dense grid of 70 × 70 × 1 q-mesh.

3. Results and discussion

3.1. Structure and stability

The optimized layered crystal structure of As₂Ge, depicted in Fig. 1a, belongs to the space group P4̄21m (numbered 113). Each primitive cell comprises six atoms, with four As atoms surrounding each Ge atom. Thus, each Ge forms chemical bonds with 4 As atoms with sp³ hybridization. Each As interacts with two Ge atoms and one As atom, though the As–As bond may be weak. In this way, according to the electron counting rule, it is possible that As₂Ge is a semiconductor since the valence bands are fully occupied. All the parameters obtained after optimization are presented in Table 1. The lattice constant is a = b = 5.24 Å, the average length of the As–As bond is 2.48 Å, and the average length of the inter-layer Ge–As bond is 2.49 Å. These parameters are similar to those reported for penta-Sb₂X (X = Si, Ge, Sn),³⁰ PdTe₂,³⁹ and Bi₂X (X = Ge, Sn).⁴⁰ Additionally, the effective thickness, h = d + 2r₀ = 5.75 Å, where d represents the separation between the upper and lower As atomic layers (3.09 Å), and r₀ represents the van der Waals radius of an As atom (1.33 Å), considering the quasi-three atomic layer structure.

Fig. 1 (a) Top and side views of the As₂Ge structure and (b) the structure of As₂Ge under the temperature of 1000 K in the process of MD simulation, and (c) the energy changes and (d) changes in average bond lengths for the As₂Ge monolayer over MD simulation.

Table 1 Optimized lattice parameters a and b, bond lengths (d_As–As) and d(Ge–As), and effective thickness (h) for As₂Ge monolayers

System	a = b (Å)	d As–As (Å)	d(Ge–As) (Å)	h (Å)
As2Ge	5.24	2.48	2.49	5.75

---

In order to demonstrate the dynamic stability of the As₂Ge structure, the phonon calculation was conducted on the basis of the finite displacement method with DFT results. The phonon dispersion is analyzed, as illustrated in Fig. S1 (ESI†). Each unit cell consists of six atoms, resulting in 18-branch phonon modes with three acoustic branches and fifteen optical branches spanning from the frequency of zero to 8.5 THz. The absence of imaginary frequencies in the obtained phonon spectrum confirms the dynamic stability of As₂Ge (Fig. S1, ESI†). The mechanical stability is evaluated based on elastic constants. For the As₂Ge monolayer, the calculated elastic constants are, C₁₁ = 38.40 N m⁻¹, C₂₂ = 38.40 N m⁻¹, C₁₂ =8.60 N m⁻¹ and C₆₆ =23.27 N m⁻¹. According to the Born–Huang mechanical stability criterion,⁴¹ it is confirmed that both criterions C₁₁ × C₂₂ − C₁₂² > 0 and C₆₆ > 0 hold true for ensuring the mechanical stability of As₂Ge.

We analyzed the thermal effect on the stability of the As₂Ge structure and AIMD was performed using a 4 × 4 × 1 supercell. It was observed that the system exhibited slight periodic changes at a temperature of 1000 K due to the thermal perturbation of atoms around their equilibrium positions, as depicted in Fig. 1b. However, the system is very stable, seen from the change of energy in Fig. 1c. We didn’t find the flying out of As pairs in the simulation processes. At this high temperature, the fluctuation of the Ge–As bond and As–As bond is less than 0.25 Å, as shown in Fig. 1d. This does not lead to the breaking of bonds and thus structural collapse, indicating the thermodynamic stability of the As₂Ge layer structure.

3.2. Electron transport characteristics

The electronic band structure and corresponding state density of the As₂Ge monolayer were calculated, as illustrated in Fig. 2a. The detailed results of the electronic band structure and corresponding density of states of the As₂Ge monolayer are provided in Fig. S2 (ESI†). The projected density of states indicates that the contributions of As and Ge atoms to the valence and conduction bands are different, with As atoms making the most significant contributions to the valence band maximum (VBM) and conduction band minimum (CBM) compared to Ge atoms. Additionally, the As₂Ge monolayer exhibits a high and sharp total density of states near the Fermi level, suggesting a high Seebeck coefficient for this material. The conduction band minimum is located between the M point and Γ point. This means there are four equivalent points in the Brillouin zone which help to enhance the Seebeck coefficient (Fig. S3a, ESI†). The Seebeck coefficient can be derived from transport theory and represents the contribution of carrier energy distribution to conductivity. According to the Boltzmann transport theory, Seebeck coefficients can be expressed in the quasi-static approximation as follows,
where E is the energy, μ is the chemical potential (Fermi level), σ(E) is the energy-dependent conductivity, f is the Fermi–Dirac distribution function, and T is the absolute temperature. This formula reveals that the Seebeck coefficient directly relates to electron transport properties around the Fermi level (specifically at the top of the valence band and bottom of the conduction band). The valence band maximum is at the X point. We also observe there is maximum value at the M point whose energy level is just 0.17 eV lower than the VBM (Fig. S3b, ESI†). Consequently, after optimizing doping, local states are introduced to influence the Fermi level position thereby enhancing electron transport efficiency and increasing the absolute value of the Seebeck coefficient.

Fig. 2 (a) PBE and HSE band structure of the As₂Ge monolayer and the corresponding partial and total state of density, and (b) the Seebeck coefficient and conductivity related to the relaxion time (σ/τ) of the As₂Ge monolayer for both (c) p-type and (d) n-type as the functions of carrier concentration.

The Fermi level is set above the valence bands, and consistent with the proposed electron occupation based on the electron counting rule discussed above. As₂Ge is a semiconductor as proposed. At the PBE/GGA level, the band gap is determined to be about 1.76 eV. By employing HSE06 correction, the band gap of the As₂Ge monolayer is increased to 2.43 eV. The main difference in the results from HSE06 and PBE is that the conduction bands are shifted rigidly up and thus the band gap is increased. Its nature as an indirect band gap semiconductor is not changed.

To some extent, the electronic structure and electrical conductivity of a material are determined by its bonding type. From the semiconductor characteristics of As₂Ge stated above, the As₂Ge lattice is possibly formed with covalent bonds. In Fig. S4a (ESI†), the change density difference of As₂Ge is plotted. It is evident that the electron cloud density distribution around the Ge atom is relatively uniform along four different directions, and it forms covalent bonds with the neighboring As atom via its four sp³ hybrid orbitals. The electron cloud distribution around the As atom is primarily concentrated in the two sp² hybrid orbitals that constitute the two covalent bonds with two Ge atoms, while the remaining lone electron resides in the p orbital, forming a quasi-sp² hybridization. Thus, there is a strong covalent bond between Ge and As. However, due to the sp² configuration of the As atom perpendicular to the As–As pair, the interaction between As–As is not very strong. In order to understand further the bonding characteristics, we analyzed the crystal orbital Hamilton population (–COHP), as shown in Fig. S4b and c (ESI†). It is clear that a positive value of –COHP under the Fermi level for Ge–As indicates a bonding feature. There is a small part of anti-bonding states between As–As which weaken the interaction between As and As. The calculated –ICOHP values of Ge–As and As–As are 4.21 and 4.19, respectively. Thus, the Ge–As bond is stronger than As–As.

From the view of electronic transport, the thermoelectric properties of a material are directly influenced by the Seebeck coefficient S, conductivity σ, and electron thermal conductivity κ_e. Under the frame of CRTA, we can directly calculate the S by decoupling the σ and S with Boltzmann transport theory. Thermoelectric devices commonly employ two distinct doping types, p-type and n-type, to create p–n junctions, thereby facilitating the application of the thermoelectric effect. The p-type materials generally supply holes through the incorporation of acceptors, whereas the n-type materials furnish electrons via the introduction of donor impurities. By meticulously regulating the type and concentration of dopants, the carrier concentration in both p-type and n-type materials can be fine-tuned to attain varying levels of conductivity and Seebeck coefficient. For layered As₂Ge, we may introduce the dopant with low electronegativity (such as Na between As₂Ge layers) as the donor for the n-type doping and the dopant (which can more easily accept the electrons from the lattice than Ge, such as Ge replaced by Ga and Al) as the acceptor for the p-type doping. For the theoretical analysis here, we just control the chemical potential to modulate the types and concentrations of carriers.

With the dispersion relation of electrons from DFT results, the S values as the function of carrier concentration at 300 K, 500 K, and 700 K are analyzed. As plotted in Fig. 2b, the |S| values of both the p-type and n-type increase with rising temperature. The bipolar effect was not obviously observed due to the large band gap of As₂Ge. Following the increase in concentration, the |S| value decreases whatever the p-type doping or the n-type doping, as has been known well in other semiconductors.^42,43 As we have noticed, the |S| of As₂Ge has a good value under appropriate carrier concentrations. The |S| value can easily reach 400 μV K⁻¹ at the typical temperature (500–700 K) under the carrier concentration of 2 × 10¹² cm⁻² whatever the p-type doping or the n-type.

Similar to the S, we can also calculate the reduced electronic conductivity σ/τ directly by Boltzmann transport theory without considering the scattering mechanism of the electron. In the cases of both p-type doping and n-type doping, the σ/τ values as the function of carrier concentration under different temperatures are shown in Fig. 2c and d. It is clear that the σ/τ increases with the carrier concentration. To further determine σ, we employed deformation potential theory for calculating the relaxation time (τ) and mobility (μ) of carriers.³⁶

The value of τ can be calculated using the parameters obtained from DFT calculations within the framework of deformation potential theory. The relationship between them is given by,

where ħ represents the Planck constant, k_B denotes the Boltzmann constant, C_2D stands for the elastic constant, E_l represents the deformation potential constant, m_d refers to the density of states mass of carrier, and T indicates temperature. To calculate the C_2D, uniaxial strain was employed. The relative variation of the lattice parameter Δa/a₀ ranges from −1% to 1%. By fitting the ratio of the total energy of the system (E) to the applied strain (Δa/a₀) using the formula C_2D = [∂²E/∂(Δa/a₀)²]/S₀ (S₀ is for the basal area of As₂Ge), the C_2D is determined. The E_l can be obtained by calculating the change in the band edge, specifically the first derivative of energy at the top of the valence band and bottom of the conduction band with respect to the strain. The relationship is expressed as E_l = ∂E_edge/∂(Δa/a₀). The m_d is calculated using the formula, , where m* represents the effective mass in the direction of transmission. In this study, the effective mass along both x and y directions is equivalent. The data from the band structure with the edge are extracted for a second fitting to obtain the effective mass with the formula, .

The calculated relevant parameters are presented in Table 2. The temperature dependence of τ is illustrated in Fig. 3. It is observed that the τ decreases by following the increase of temperature. The relaxation time of electrons is larger than that of holes mainly due to the smaller |E_l| and m* of electrons. With the formula, μ = eτ/m*, the carrier mobility can be obtained. It is noticed that the electron mobility is higher and reaches 7595 cm² V⁻¹ s⁻¹. Thus, it is expected the As₂Ge has good conductivity.

Table 2 Calculated effective mass (m*), elastic modulus (C_2D), deformation potential constant (E_l), carrier mobility (μ) and relaxation time (τ) of As₂Ge monolayers

System	Carrier type	E l (eV)	C 2D (J m^−2)	m* (m0)	μ (cm^2 V^−1 s^−1)	τ (fs)
As2Ge	Electron	−0.64	37.83	0.51	7595.08	2000.85
	Hole	−0.90	37.83	0.78	1641.94	727.68

---

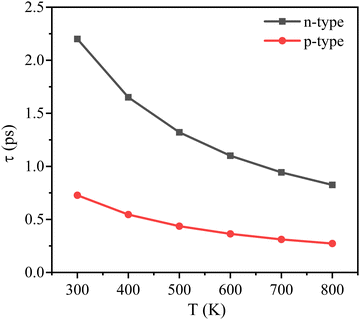Fig. 3 Calculated relaxation times of the As₂Ge monolayer as a function of temperature for the p-type doping and n-type doping.

By putting the values of τ into the σ/τ, we can obtain the electronic conductivity σ. As shown in Fig. 4a and b, the σ follows the typical rule of conductivity in heavily doped semiconductors where the σ increases with the rising of carrier concentration and decreases with the increase of temperature. This behavior of σ following the variation of concentration contradicts that of the |S|. In both p-type and n-type materials, an elevation in doping concentration typically results in an increased carrier concentration, which in turn enhances material conductivity. However, excessively high carrier concentrations, resulting from the Fermi level shifting deeply into the valence bands or conduction bands, lead to a reduction in the Seebeck coefficient. Therefore, the curve of power factor which is expressed as PF = S²σ should have a peak at a certain carrier concentration. As depicted in Fig. 4c and d, it is observed that the n-type doping yields a higher PF than the p-type doping. The power factor (PF) is primarily determined by the Seebeck coefficient (S) and conductivity (σ). Under CRTA, the S is not influenced directly by the phonon spectrum. The conductivity σ is strongly related to electron–phonon coupling, as discussed above regarding the relaxation time (τ). As we have observed in the phonon spectrum in Fig. S1 (ESI†), the acoustic phonon mode and optical phonon mode do not strongly overlap, and thus the scattering effect is not strong. Meanwhile, the phonon velocity is very high in the low-frequency band (discussed in the next part). These characteristics are related to the lattice rigidity of As₂Ge, which is confirmed by its larger elastic modulus value. The higher lattice rigidity typically results in weaker electron–phonon coupling, as evidenced by the longer carrier lifetime observed in Fig. 3. Consequently, carriers exhibit greater mobility (as shown in Table 2), leading to higher conductivity σ in As₂Ge, regardless of whether it is p-type or n-type doped. Therefore, As₂Ge has a higher power factor, and it has a higher lattice thermal conductivity (discussed in the next part). At the temperature of 500 K, the maximum values of PF for p-type and n-type As₂Ge are 0.16 W m⁻¹ K⁻² and 0.21 W m⁻¹ K⁻² at the concentrations of 10¹⁴ cm⁻² and 2 × 10¹³ cm⁻², respectively.

Fig. 4 (a) and (b) Calculated conductivity σ and (c) and (d) power factor PF of the As₂Ge monolayer as functions of carrier concentration for the p-type doping and n-type doping.

3.3. Phonons and lattice thermal transport

In general, phonons serve as the primary carriers in the heat transfer processes. From the phonon band structure, the phonon group velocity of As₂Ge can be calculated. As depicted in Fig. 5a, the optical phonon group velocities exceeding 3 THz are approximately below 1.0 km s⁻¹. We also noticed that the acoustical phonon velocity is a little high and the maximum value reaches about 4.3 km s⁻¹.

Fig. 5 (a) Phonon group velocity, (b) phonon lifetime, (c) anharmonic scattering rate, (d) Gruneisen parameter as the function of frequency, and (e) cumulative lattice thermal conductivity with the mean free path of phonons (MFP) at 300 K, and (f) lattice thermal conductivity with increased temperature.

Prior to computing the lattice thermal conductivity κ_l, the supercell size and the cutoff radius were evaluated for the 3RD force constant. In our calculations, due to the application of periodic boundary conditions, the maximum cutoff radius (r_c) can’t surpass half the lattice length of the supercell. As illustrated in Fig. S6 (ESI†), the outcomes for the 3 × 3 × 1 and 4 × 4 × 1 supercells of the As₂Ge monolayer are similar for the smaller cutoff radius. With the increase in cutoff radius, the κ_l begins to converge. With the 4 × 4 × 1 supercell as a test, it is converged at approximately 11 Å.

For analyzing the lifetime τ_ph, we need to consider the anharmonic action of lattice vibration. From Boltzmann–Peierls theory, κ_l is from the sum of the contribution of all phonon modes, and is expressed as,

where the index λ presents the phonon branch and q is the phonon wave vector. For each phonon mode, the contribution of thermal conductivity is calculated by the formula,

κ_l(λ,q) = C_ph(λ)υ_g,λ(q)²τ_ph(λ,q) (2)

where C_ph(λ, q) and υ_g,λ(q) are obtained from phonon bands with harmonic approximation. The lifetime τ_ph(λ, q) of the phonon mode (λ, q) can be calculated with anharmonic 3RD force constants from density functional perturbation theory. In Fig. 5b and c, we demonstrate the phonon lifetime and anharmonic scattering rate of the As₂Ge monolayer as the function of frequency. Clearly, the lifetime of phonons decreases quickly with an increase in frequency. Above 4 THz, the phonon lifetime is less than 10 ps. This is due to the large scattering rate of phonons in Fig. 5c. By calculating phonon frequencies with the change of volume using the formula, γ = −∂ ln ω/∂ ln υ, we can gain the Grüneisen parameters (γ) to evaluate the magnitude of anharmonic phonon scattering. As shown in Fig. 5d, the value of |γ| at relative low frequency is very large, contributing to the low phonon lifetime, especially for the out-of-plane acoustic (ZA) mode. However, the value of |γ| is not large at the high frequencies, especially for optical modes (OP). At low frequencies, phonons from acoustic branches contribute substantially to thermal conductivity due to their higher velocities and lower scattering rates. In contrast, the contribution of optical branches to thermal conductivity is relatively minor. The average value of γ is 0.36. This value indicates the lattice of As₂Ge can resist high temperature for the application of thermoelectrics.

Fig. 5e illustrates the variation in cumulative lattice thermal conductivity with respect to the mean free path (MFP) of phonons at 300 K. It is found that the most optical phonon modes whose MFPs are less than 100 nm have small contribution to thermal conductivity. The contributed thermal conductivity of all these phonons at 300 K is about 5.5 W m⁻¹ K⁻¹. Fig. 5f presents temperature-dependent values for thermal conductivity in the As₂Ge monolayer. Clearly, following the increase of temperature, the number of phonons increases and thus the scattering rate increases, leading to the decrease of thermal conductivity. By fitting the calculated values of thermal conductivity, the κ_l has a linear relationship with the 1/T. At 800 K, the calculated lattice thermal conductivity of As₂Ge is about 7.78 W m⁻¹ K⁻¹.

3.4. Thermoelectric transport properties

As discussed above, the σ value of As₂Ge is large. Thus, the electron thermal conductivity (κ_e) cannot be ignored. According to the Wiedemann–Franz relationship, the κ_e is directly proportional to the electrical conductivity (σ) through the equation, κ_e = LσT, where L represents the Lorentz number (L = 2.45 × 10⁻⁸ W Ω K⁻²). The variations in κ_e with carrier concentration at temperatures of 300 K, 500 K, and 700 K are depicted in Fig. S5 (ESI†). As we know, the σ decreases quickly with the increase in temperature. Thus, the κ_e does not increases, but decreases following the rising of temperature. The main factor to affect the κ_e is the carrier concentration. With the increase in carrier concentration, the σ increases and thus the κ_e increases. For example, in the n-type As₂Ge, the κ_e can reach about 45 W m⁻¹ K⁻¹ at the electron concentration of 10¹³ cm⁻².

The quality factor ZT serves as a crucial indicator for thermoelectric efficiency. With the power factor and thermal conductivity, we can analyze the ZT value of p-type and n-type As₂Ge. As shown in Fig. 6a and b, we plot the ZT as a function of temperature and carrier concentration. It can be noticed that the ZT will have the optimal value under appropriate temperature and carrier concentration. Consistent with the calculated PF values mentioned above, the n-type doping exhibits higher ZT compared to the p-type doping. At 500 K, the ZT value reaches up to 1.98 for the p-type and up to 2.39 for the n-type. The maximal ZT value of p-type As₂Ge is 3.5 at the carrier concentration of 1.5 × 10¹³ cm⁻² under 1000 K. For the n-type doing, the maximal ZT value is 4.36 at the carrier concentration of 4.5 × 10¹² cm⁻² under 1000 K. The As₂Ge monolayer exhibits good thermoelectric properties compared to several other excellent Ge-based thermoelectric materials, such as GeTe alloys (ZT ∼ 2.4 at 600 K),⁴⁴ GeSe monolayers (ZT = 1.76 at 700 K),⁴⁵ and GeSn/Ge layers (ZT = 1.04 at 600 K).⁴⁶ In summary, the As₂Ge monolayer demonstrates promising potential for thermoelectric applications.

Fig. 6 Calculated ZT values of the As₂Ge monolayer as the functions of carrier concentration and temperature for the (a) p-type doping and (b) n-type doping.

4. Conclusions

In this study, we investigated the structural stability, electronic properties, thermal transport and thermoelectric properties of As₂Ge monolayers by combining DFT calculations with Boltzmann transport and phonon transport theory. It is found that the As₂Ge monolayer exhibits exceptional stability, providing robust theoretical support for experimental feasibility. The analysis of the energy band structure indicates the As₂Ge monolayer is an indirect semiconductor with a band gap of 2.43 eV. The layered As₂Ge has excellent electronic transport properties. The power factor of p-type As₂Ge can reach up to 0.16 W m⁻¹ K⁻² at 500 K, while the maximum value of power factor of the n-type As₂Ge is 0.21 W m⁻¹ K⁻² at 500 K. Combining the excellent power factor with the lower lattice thermal conductivity, the ideal ZT values on As₂Ge are obtained. Our predictions indicate that the maximal ZT value of the p-type doping is 3.5 and that of the n-type doping is 4.36. These findings affirm that the As₂Ge monolayer is a typical semiconductor and that appropriate doping can lead to the potential application of As₂Ge as thermoelectric materials. We expect that these results can offer valuable theoretical insights for experiments of thermoelectrics and electronic devices.

Data availability

Data will be made available upon request.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (Grants No. 2024YFA1207700) and the Natural Science Foundation of Jilin Province, China (Grant No. 20240101320JC).

References

1. Y. Zhou and L. D. Zhao, Adv. Mater., 2017, 29, 1702676.
2. C. Gayner and K. K. Kar, Prog. Mater. Sci., 2016, 83, 330–382.
3. J. He and T. M. Tritt, Science, 2017, 357, 1369.
4. Y. Ouyang, Z. Zhang, D. Li, J. Chen and G. Zhang, Ann. Phys., 2019, 531, 1800437.
5. F. J. DiSalvo, Science, 1999, 285, 703–706.
6. R. Moshwan, L. Yang, J. Zou and Z. G. Chen, Adv. Funct. Mater., 2017, 27, 1703278.
7. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
8. X. Zhang and L.-D. Zhao, J. Mater., 2015, 1, 92–105.
9. D. R. Cooper, B. D’Anjou, N. Ghattamaneni, B. Harack, M. Hilke, A. Horth, N. Majlis, M. Massicotte, L. Vandsburger, E. Whiteway and V. Yu, ISRN Condens. Matter Phys., 2012, 2012, 1–56.
10. G. Fiori, F. Bonaccorso, G. Iannaccone, T. Palacios, D. Neumaier, A. Seabaugh, S. K. Banerjee and L. Colombo, Nat. Nanotechnol., 2014, 9, 768–779.
11. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
12. C. Chang, W. Chen, Y. Chen, Y. Chen, Y. Chen, F. Ding, C. Fan, H. Jin Fan, Z. Fan and C. Gong, Acta Phys.-Chim. Sin., 2021, 37, 2108017.
13. M. S. Dresselhaus, G. Chen, M. Y. Tang, R. G. Yang, H. Lee, D. Z. Wang, Z. F. Ren, J. P. Fleurial and P. Gogna, Adv. Mater., 2007, 19, 1043–1053.
14. K. Kanahashi, J. Pu and T. Takenobu, Adv. Energy Mater., 2019, 10, 1902842.
15. G. Tan, L.-D. Zhao, F. Shi, J. W. Doak, S.-H. Lo, H. Sun, C. Wolverton, V. P. Dravid, C. Uher and M. G. Kanatzidis, J. Am. Chem. Soc., 2014, 136, 7006–7017.
16. C. Chang, M. Wu, D. He, Y. Pei, C.-F. Wu, X. Wu, H. Yu, F. Zhu, K. Wang, Y. Chen, L. Huang, J.-F. Li, J. He and L.-D. Zhao, Science, 2018, 360, 778–783.
17. D. Qin, P. Yan, G. Ding, X. Ge, H. Song and G. Gao, Sci. Rep., 2018, 8, 2764.
18. Q. Tan, L.-D. Zhao, J.-F. Li, C.-F. Wu, T.-R. Wei, Z.-B. Xing and M. G. Kanatzidis, J. Mater. Chem. A, 2014, 2, 17302–17306.
19. R. Fei, A. Faghaninia, R. Soklaski, J.-A. Yan, C. Lo and L. Yang, Nano Lett., 2014, 14, 6393–6399.
20. D. Li, Y. Gong, Y. Chen, J. Lin, Q. Khan, Y. Zhang, Y. Li, H. Zhang and H. Xie, Nano-Micro Lett., 2020, 12, 36.
21. K. Nakamura, Jpn. J. Appl. Phys., 2018, 57, 06HE04.
22. G. Zhang and Y.-W. Zhang, J. Mater. Chem. C, 2017, 5, 7684–7698.
23. T. Zhou, X. Wu, T. Deng, H. Li, Z. Gao and W. Shi, J. Mater. Chem. A, 2023, 11, 15821–15832.
24. X. Liu, J. Gao, G. Zhang and Y.-W. Zhang, Nano Res., 2017, 10, 2944–2953.
25. X. Liu, D. Zhang, H. Wang, Y. Chen, H. Wang and Y. Ni, J. Appl. Phys., 2021, 130, 27413–27422.
26. Y. Zhao, P. Yu, G. Zhang, M. Sun, D. Chi, K. Hippalgaonkar, J. T. L. Thong and J. Wu, Adv. Funct. Mater., 2020, 30, 26033–26040.
27. Z. Gao, Z. Zhang, G. Liu and J.-S. Wang, Phys. Chem. Chem. Phys., 2019, 21, 26033–26040.
28. Y. Shen, D. Ni, Y. Chen, J. Sun and Q. Wang, Phys. Chem. Chem. Phys., 2022, 24, 27413–27422.
29. Y. Wang, N.-D. Chen, C. Yang, Z.-Y. Zeng, C.-E. Hu and X.-R. Chen, Acta Phys. Sin., 2021, 70, 116301.
30. N. Wu, X. Fan, D. J. Singh and W. T. Zheng, J. Mater. Chem. C, 2023, 11, 5156–5166.
31. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186.
32. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
34. Y.-S. Kim, K. Hummer and G. Kresse, Phys. Rev. B, 2009, 80, 035203.
35. G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
36. J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72–80.
37. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
38. W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758.
39. L. Liu, Y. Ji, M. Bianchi, S. M. Hus, Z. Li, R. Balog, J. A. Miwa, P. Hofmann, A.-P. Li, D. Y. Zemlyanov, Y. Li and Y. P. Chen, Nat. Mater., 2024, 23, 1339–1346.
40. M. Lv, N. Wu, X. Fan, W. Zheng and D. J. Singh, Mater. Today Phys., 2024, 49, 101594.
41. S. H. Park, G. Goodall and W. S. Kim, Mater. Des., 2020, 193, 108797.
42. Z. Gao and J.-S. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 14298–14307.
43. X. Yu, W. Jin, J. Pang, J. Zuo, X. Kuang and C. Lu, J. Mater. Chem. A, 2024, 12, 1488–1497.
44. J. Li, X. Zhang, Z. Chen, S. Lin, W. Li, J. Shen, I. T. Witting, A. Faghaninia, Y. Chen, A. Jain, L. Chen, G. J. Snyder and Y. Pei, Joule, 2018, 2, 976–987.
45. X.-L. Zhu, C.-H. Hou, P. Zhang, P.-F. Liu, G. Xie and B.-T. Wang, J. Phys. Chem. C, 2019, 124, 1812–1819.
46. D. Spirito, N. von den Driesch, C. L. Manganelli, M. H. Zoellner, A. A. Corley-Wiciak, Z. Ikonic, T. Stoica, D. Grützmacher, D. Buca and G. Capellini, ACS Appl. Energy Mater., 2021, 4, 7385–7392.

---

Footnote

† Electronic supplementary information (ESI) available: Phonon dispersion of As₂Ge in Fig. S1; band structure and state of density in Fig. S2; constant energy surfaces in Fig. S3; charge density difference and –COHP curves in Fig. S4; electronic thermal conductivity in Fig. S5; and test of cutoff radius and supercell size in Fig. S6. See DOI: https://doi.org/10.1039/d4tc04065a

---