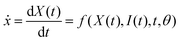Open Access Article
Open Access ArticleNeural ordinary differential equations for predicting the temporal dynamics of a ZnO solid electrolyte FET†
Ankit
Gaurav
a,
Xiaoyao
Song
b,
Sanjeev Kumar
Manhas
a and
Maria Merlyne
De Souza
 *b
*b
aDepartment of Electronic and Communication, Indian Institute of Technology Roorkee, Roorkee, 247667, India
bDepartment of Electronic and Electrical Engineering, University of Sheffield, North Campus, Sheffield S3 7HQ, UK. E-mail: m.desouza@sheffield.ac.uk
First published on 7th December 2024
Abstract
Efficient storage and processing are essential for temporal data processing applications to make informed decisions, especially when handling large volumes of real-time data. Physical reservoir computing provides effective solutions to this problem, making them ideal for edge systems. These devices typically necessitate compact models for device-circuit co-design. Alternatively, machine learning (ML) can quickly predict the behaviour of novel materials/devices without explicitly defining any material properties and device physics. However, previously reported ML device models are limited by their fixed hidden layer depth, which restricts their adaptability to predict varying temporal dynamics of a complex system. Here, we propose a novel approach that utilizes a continuous-time model based on neural ordinary differential equations to predict the temporal dynamic behaviour of a charge-based device, a solid electrolyte FET, whose gate current characteristics show a unique negative differential resistance that leads to steep switching beyond the Boltzmann limit. Our model, trained on a minimal experimental dataset successfully captures device transient and steady state behaviour for previously unseen examples of excitatory postsynaptic current when subject to an input of variable pulse width lasting 20–240 milliseconds with a high accuracy of 0.06 (root mean squared error). Additionally, our model predicts device dynamics in ∼5 seconds, with 60% reduced error over a conventional physics-based model, which takes nearly an hour on an equivalent computer. Moreover, the model can predict the variability of device characteristics from device to device by a simple change in frequency of applied signal, making it a useful tool in the design of neuromorphic systems such as reservoir computing. Using the model, we demonstrate a reservoir computing system which achieves the lowest error rate of 0.2% in the task of classification of spoken digits.
1. Introduction
In recent years, there has been a significant increase of interest in neuromorphic computing, driven by artificial intelligence and novel multi-state devices that mimic biological neural capabilities such as memristors,1 ferroelectric FET,2 and anti-ferroelectric FET.3 Such devices necessitate compact models for device-circuit co-design4 to accelerate the development time of neuromorphic systems. Although most models are based on well-known principles of current continuity and electrostatics, as described by the Poisson equation, some devices can be more complex and not fully simulated by these laws.5 For example, an electrical stimulus in an insulating memristor causes oxygen vacancies or metal ions to move within the switching layer,6,7 causing either short or long term changes to the device resistance, leading to a volatile or non-volatile memory effect.8,9 Several models based on physical principles have been introduced to model this complex behaviour. These models typically include two main components: (1) the switching model, which explains the changes in resistance states, and (2) the conduction model, which describes the current flow in response to an applied voltage. The switching mechanisms are explained by theories of filament growth and rupture,10 ion migration and redox reactions.7,11 Conduction mechanisms are described by Poole–Frenkel emission12 (trap-assisted electron transport in insulators), Schottky emission13 (electric field-induced reduction of the energy barrier for electron emission), and space charge limited current14 (excess charge carriers in poorly conducting materials). Additionally, these devices, display distinctive features including hysteresis, plasticity, negative capacitance, stochasticity, and nonlinearity which add to their complexity.To address this challenge various machine learning models based on multilayer perceptron (MLP) neural networks have been proposed.15–17 In multi-state devices, a single voltage can result in different current values corresponding to low and high resistance states, necessitating a separate model for each state. For instance, researchers have explored two distinct approaches using MLP neural networks to model memristors. One approach involves decoupling the switching and conducting behaviours,17 whereas the second emulates the physical equations governing state variables and current.16 Additionally, some models directly use the state variable as input to the MLP network for accurate predictions.15
In an alternative approach,18 a memristor device model based on long short-term memory (LSTM) was introduced, that treats the device switching and conducting behaviour as a time-series problem. This approach eliminates the need for two separate models, as the LSTM output depends on the previous input and output states.
However, LSTM is limited by its dependency on previously measured signals in the training dataset, necessitating separate models for distinct signal types i.e. sine and random sine variations, which hinders its compactness and practical use in circuit simulations. These approaches result in increased model complexity, due to separate models for switching/conducting behaviour or distinct signal types, and the need for a larger dataset to accurately capture device dynamics. Additionally, these models encounter challenges in continuous time modelling due to their structure consisting of a fixed number of discrete hidden layers. This inflexibility hampers their ability to adjust to changing temporal dynamics, reducing their effectiveness for real-time processing and continuous learning applications of truly neuromorphic systems.
Alternatively, a new family of deep neural network models called neural ordinary differential equations (neural ODEs) was introduced, which offers an effective approach for continuous-time modeling.19 Instead of specifying a discrete sequence of hidden layers as in traditional neural networks, such as MLP, or LSTM, neural ODEs parameterize the derivative of the hidden state using a neural network. Neural ODE models operate at continuous depths, which means they adapt their evaluation strategy to each input dynamically. Unlike fixed-depth architectures, neural ODEs can have varying depths based on the problem at hand. The output is computed using a black-box differential equation solver for any given time t, making them also useful for irregularly sampled data. Moreover, neural ODEs are both parameter–efficient, typically requiring fewer parameters than traditional neural networks, and memory-efficient, because the initial state is sufficient to predict the dynamical state. This efficiency translates to better performance with smaller datasets during training.19
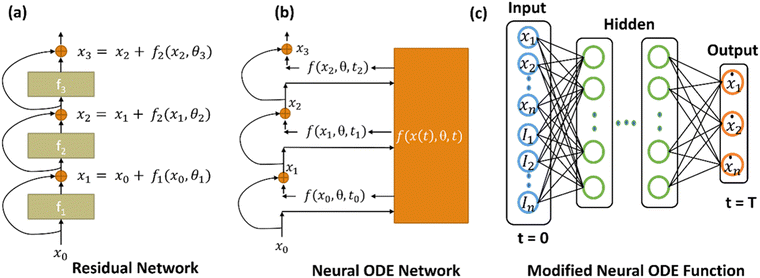
As an example, the transformation of the input state x0 using a discrete sequence of hidden layers as in traditional neural networks vs. neural ODEs is shown in Fig. 1a and b. Consider the transformation of input from x0 to x1 by a residual network (ResNet), as shown in Fig. 1a.
| x1 = x0 + f1(x0,θ1) | (1) |
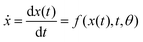 | (2) |
Recently, a new approach was proposed for modeling spintronic devices using a modified neural ODE framework.21 This approach incorporates an embedding theorem, which reconstructs the state space of a dynamical system from a series of observations. By doing so, it addresses the challenge of unknown internal variables and external time-varying inputs by utilizing multiple successive previous states, which is equivalent to information provided by higher-order derivatives:
| X(t) = (x1(t), x1(t − Δtd),…, x1(t − (n − 1)Δtd)) | (3) |
 | (4) |
The general schematic of the modified neural ODE function is shown in Fig. 1c, and the neural ODE network with the new function is shown in Fig. S1 (ESI†). Adding extra dimensions with time delay to the input space allows for learning more complex functions with simpler flows. However, this increases the computational overhead, making the ODE solver work harder due to the added complexity.20 Once trained, the prediction speed of neural ODEs and ANODEs is influenced by model complexity and available computational resources. Generally, they are quite efficient during prediction, as most intensive computations occur during training. Further, to deal with inconsistencies in the data, advanced ODE solvers that are designed for stability and consistency such as Nesterov's accelerated gradient22 can be used. Alternatively, pre-data processing techniques such as interpolation can be applied to fill in gaps in the data.
In a different approach,23 a physics-informed neural ODE was proposed. This method incorporates physical principles into reduced-order models (ROMs) by employing collocation-based loss terms. This strategy notably improves the performance in data-scarce and high-noise environments to predict the behaviour of complex systems viz., acoustics, gas and fluid dynamics, and traffic flows. Similarly in another study,24 a physics-enhanced neural ODE combined partially known mechanistic models (based on physical laws) with universal surrogate approximators (neural networks). This hybrid approach allows for more accurate modelling from limited datasets, particularly applied to industrial chemical reaction systems. Such studies demonstrate the adaptability of neural ODEs in accurately predicting the behaviour of complex systems, even when data is limited.
In this paper, we demonstrate a neural ODE based continuous-time model of an electronic charge-based system. We incorporate time-delay embedding of a single observable and external input in a neural ODE as proposed in ref. 21. Using this approach, we demonstrate that neural ODEs can accurately predict the complex behaviour of a three-terminal, non-filamentary, solid electrolyte-based thin film transistor (SE-FET) with a unique negative differential resistance in its gate current characteristics.7 The model achieves high accuracy in dynamically predicting the performance of the SE-FET after training on a minimal experimental dataset spanning only 240 seconds. Furthermore, we compare the performance of the neural ODE model with a previous conventional physics-based model25 and experimental measurement using distinct input not belonging to the training dataset. Our model is able to predict the temporal dynamics of the SE-FET such as excitatory postsynaptic current (EPSC) measured as the time-dependent channel conductance after the application of a voltage pulse (presynaptic pulse) on the gate electrode, notably, where previous multilayer perceptron and long short-term memory-based models of memristor fail.15–18 Moreover, we show that transient, steady state response, and device-to-device variation can also be predicted using the neural ODE model without training a separate model. Additionally, we demonstrated the SE-FET-based reservoir system using the neural ODE model of the device. The performance of this reservoir system was benchmarked using the standard spoken-digit recognition task.
2. Experimental
2.1 Device fabrication and mechanism
Our bottom-gated SE-FET (W × L = 100 μm × 1.5 μm) is fabricated via RF sputtering at room temperature and fully compatible with BEOL processing. A conducting indium tin oxide with a resistance of 20 Ω square−1 is used as the gate. A 275 nm layer of tantalum oxide (Ta2O5) serves as the bottom gate insulator, and a 40 nm layer of ZnO is sputtered on top as the channel. Aluminium contacts are evaporated over the ZnO to form the top contact. Electrical characterization is performed using Keysight B2902A.The unique redox reaction occurring within the insulator of SE-FET7 defines the device mechanism.26 The accumulation of positively charged vacancies near the channel end of the insulator, induced by a gate voltage, leads to an additional electrolytic capacitance. During the reverse sweep, this capacitance becomes negative25 due to a rapid collapse of the internal electric field in the device, resulting in steep switching as shown in Fig. 2, without any filamentary process. The characteristics of the SE-FET such as hysteresis, plasticity, negative capacitance, short term memory and non-linearity facilitate a broad spectrum of neuromorphic analogue computing applications such as vision, speech recognition, and time series forecasting.27,28 However, modelling the SE-FET gate current characteristics in insulators is challenging due to the inherent differences between insulators and semiconductors, particularly with respect to the behaviour of charge carriers in semiconductors versus insulators.
In semiconductors, the current continuity equation governs the flow of electrons and holes, ensuring charge conservation and accounting for the drift and diffusion of charge carriers under the influence of electric fields and concentration gradients. Conversely, in insulators, the absence of free charge carriers necessitates consideration of alternative phenomena to explain any observed electrical behaviour. These include space charge effects,29 where charge accumulation at interfaces or within the material influences the electric field; Ion generation and movement,30 involving ion migration within the insulator under an electric field; and tunneling,31 a quantum mechanical process where electrons pass through potential barriers, they classically shouldn’t be able to cross. This introduces challenges in conventional TCAD tools, especially when trying to model current continuity at the same time as these other phenomena. We have earlier used a simple point ion model of Mott and Gurney32,33 to define the motion of the ions in the insulator, coupled with a 1D-Poisson model to evaluate the charge in the channel. The rate of change of sheet charge density at the interface was modelled by a balance between the drift and diffusion current densities. However, the model does not include any gate current characteristics, including the unique redox reaction in the gate insulator (Fig. 2) that underlies the sub-60 nm decade−1 steep switching observed during the reverse sweep of the gate bias.25 Therefore, this model is not sufficient to capture the dynamic characteristics of the device.
2.2 Training of the neural ODE model
An experimental single-trajectory dataset consisting of 2400 data points xtrue of IDS (drain to source current) of random input voltages is used for training. The time interval (Δt) between each point is kept the same as in measurement which is 100 ms per data point. The mean squared error (MSE) is used to define the loss function between the actual point (xtrue) and the corresponding predicted point (xpred):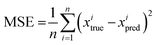 | (5) |
To minimize the loss function, the gradients of the loss with respect to the parameter θ are computed using the adjoint sensitivity method, then θ is updated using the adaptive moment estimation (Adam) optimization algorithm in a supervised manner.
Our neural ODE function is given by eqn (4) (i.e., X(t) = (x1(t),…,x1(t − (n − 1)Δtd)), I(t) = (I1(t),…,I1(t − (n − 1)Δtd))) and consists of a feedforward neural network, as shown in Fig. 1c, with three hidden layers, each featuring 200 neurons, with 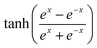 as an activation function. A fourth-order fixed step Runge–Kutta with 3/8 rule is used as the ODE solver to solve this neural ODE function. To prevent overfitting, we use batch sampling without replacement to ensure diversity in the batches. We add dropout layers, which randomly set a fraction of input units to zero during each update in training. This stops the network from becoming overly reliant on specific neurons. Additionally, we initialize weights with a normal distribution to promote stable training. These techniques together make the model more robust and less likely to overfit.
as an activation function. A fourth-order fixed step Runge–Kutta with 3/8 rule is used as the ODE solver to solve this neural ODE function. To prevent overfitting, we use batch sampling without replacement to ensure diversity in the batches. We add dropout layers, which randomly set a fraction of input units to zero during each update in training. This stops the network from becoming overly reliant on specific neurons. Additionally, we initialize weights with a normal distribution to promote stable training. These techniques together make the model more robust and less likely to overfit.
For a clearer visualization, the entire procedure of our technique is laid out in Algorithm 1.
3. Results and discussion
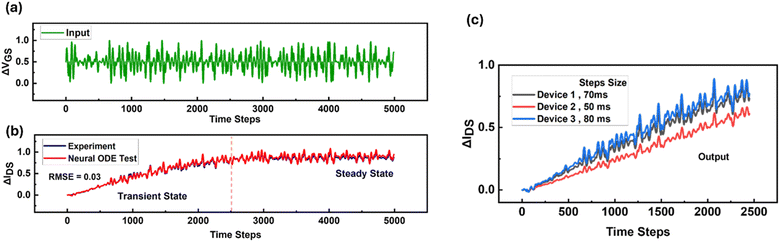
To model the continuous dynamic behaviour of the SE-FET, the neural ODE function is trained using a normalized single-trajectory continuous dataset measured by applying random ΔVGS (gate-source voltage as input) as shown in Fig. 3a. The corresponding measured output i.e. the normalized ΔIDS (drain to source current) (grey line) is used as the target value. The dynamical prediction of the drain current as a function of voltage during training is shown by the red dashed line in Fig. 3b. The data was normalized to reduce training time and improve the accuracy of prediction. An RMS (root mean squared) error of 0.02 or lower is achieved for several previous states ranging from 2 to 10 shown in Fig. 3c and the ΔIDSversus time for all other previous states in Fig. S2 (ESI†). | ||
| Fig. 3 Training and testing of a neural ODE model of the SE-FET. (a) Normalized random voltage (green line), in the form of ΔVGS (gate to source voltage) is applied as input to the neural ODE. (b) The corresponding experimentally measured normalized ΔIDS (drain to source current) (grey line) is used to train the neural ODE for which a low training error of 0.013 (RMSE) is obtained (red dotted line). (c) Training error with respect to iterations for a different set of previous states to that used in training. All achieve a low training error with RMSE ≤ 0.02. (d) and (e) Testing the dynamic characteristics of the SE-FET and comparison with the physics based model25 and experiment. Normalized voltage pulse, in the form of ΔVGS (gate to source voltage) is given as input to the neural ODE. The neural ODE model shows a low prediction error of 0.06 (RMSE) when compared to experiment (blue line). A lack of underlying physics that is not fully captured in,25 leads to discrepancy with experiment as shown by the green line. (f) Testing the normalized excitatory post synaptic current (ΔEPSC) of the neural ODE model compared to experiment.7 The presynaptic pulse widths vary from 20 to 240 ms with 50% duty cycle and consist of 10 normalized gate pulses (ΔVGS = 1) in each case. For this task, a low prediction error of 0.0093 (RMSE) is obtained. | ||
Fig. 3d shows the positive write pulses of +2 V (normalized to ΔVGS = 1) with pulse width of 180 ms continuously repeated 8 times, different from that used in training. For this test, a very low prediction error of 0.06 (RMSE) is achieved as shown in Fig. 3e by the red line. For a lower number of previous states, the error as shown in the Fig. S3 (ESI†) ranges from 0.14–5.68 (RMSE). A higher number of previous states is equivalent to the information provided by higher-order derivatives that leads to better performance albeit for a longer training time.34 On the other hand, our previous physics-based model as shown by the green line in Fig. 3e, fails to capture the dynamics with a prediction error of 0.15 (RMSE). With this new approach (neural ODE), the prediction error is reduced by 60% compared to our physics-based approach25 (see device fabrication and mechanism section). Additionally, our model predicts device dynamics in approximately 5 seconds, compared to nearly an hour using an equivalent computer with a physics-based model. In Fig. 3f, the EPSC response of the device is compared with predicted results with a prediction error of 0.009 (RMSE). The SE-FET, EPSC is measured as the channel conductance changes over time following a voltage pulse applied to the gate electrode. If the EPSC signal persists for a few seconds to tens of minutes, it is analogous to a short-term memory. Conversely, if the EPSC signal endures for several hours to a lifetime, it represents a long-term memory. A stimulus train of different pulse widths (20 to 240 ms) with 50% duty cycle, consisting of 10 normalized gate pulses (ΔVGS = 1) are used in each case. A longer pulse width results in higher EPSC values and extended retention time. Both these characteristics are captured well by the model.
Further, we evaluate the model using an extended input sequence comprising 5000 time steps, with each time step corresponding to 100 ms, consistent with experimental measurements. For this test, the neural ODE accurately captures both the transient and steady-state behaviour of the SE-FET. Remarkably, this is achieved with a low error rate of 0.03 (RMSE), without specifically training the model for steady-state dynamics as shown in Fig. 4a and b. Initially the response of the SE-FET is in transient states up to 2500 times steps which shows a gradual increment in ΔIDS beyond which the device response goes into steady state. Furthermore, experimentally, we find that when different SE-FET devices are subjected to the same input, their responses follow the same trend but only differ in magnitude. We can artificially recreate this behaviour in our model by feeding the same input at different frequencies as shown in Fig. 4c. This is because when we apply input pulses at a lower frequency, the device experiences longer periods of exposure to the signal that results in a higher magnitude and vice versa. To validate this approach, we compare the model output to that of three different SE-FET devices, at (12.5 Hz = 80 ms, 14.28 Hz = 70 ms, and 20 Hz = 50 ms) to emulate the same level of device-to-device variation as in experiment with RMSE = 0.03 or lower (Fig. S4, ESI†). With this simple modification, we can use the model to study any application, with multiple devices including device to device variation without training a separate model of each device.
Table 1 summarizes various machine learning based device models. The previously reported MLP15–17 and LSTM18 based memristor models operate in discrete time, where information flows through a fixed number of layers (depth) during each forward pass. Their depth is determined by the architecture, and it remains constant regardless of the complexity.35 Whereas in neural ODEs, instead of discrete layers, they use continuous-time dynamical systems, allowing a continuous adaptation to their depth implicitly.19 This adaptability makes them suitable for predicting device dynamics across different pulse widths or frequencies using a single trained model. Additionally, the SE-FET devices exhibit short-term memory characteristics, allowing them to switch states from low to high resistance in an analogue manner over time without any input. Thus, continuous-time dynamical systems such as neural ODEs are more effective in capturing the device dynamics and short-term memory. Additionally, whether applied to spintronic21 or SE-FETs, they can be effectively trained with limited experimental data. This makes them valuable for predicting the behaviour of complex systems in environments where data is scarce. In an alternative approach,36 physics-informed neural networks (PINNs) have been used to model system dynamics but differ in how they handle the underlying dynamics. PINNs embed physical laws directly into the training process, using differential equations as constraints. This allows them to model physical systems using both observed data and governing physics equations. Meanwhile, neural ODEs evolve hidden states continuously through a differential equation solver, learning system behaviour solely from data without the need for explicit physical laws. This makes neural ODEs ideal for data-driven applications where the device physics is unknown. In essence, PINNs blend known physics with learning, whereas neural ODEs extract dynamics purely from data.
| Device | Machine learning | Data quantity | Continuous-time modeling | Proposed for | ref. |
|---|---|---|---|---|---|
| TaN/HfO2/Pt memristor | LSTM | Large | Inherently not suited | Process tuning | 18 |
| HfOx memristor | MLP | Moderate | No | HSPICE circuit simulation | 15 |
| Memristor | MLP | Moderate | No | Transient circuit simulation | 17 |
| TaN/HfO2/Pt memristor | MLP | Moderate | No | HSPICE circuit simulation | 16 |
| Spintronic | Neural ODEs | Small | Yes | Efficient alternative to micromagnetic simulations | 21 |
| ZnO/Ta2O5 solid electrolyte FET | Neural ODEs | Small | Yes | Temporal dynamic modeling | This work |
In conclusion, we demonstrate the application of our model in an example of physical reservoir computing (RC). Physical dynamic reservoirs can efficiently process temporal input with low training costs by leveraging the short-term memory of the device for in-memory computation.27 Our framework and process flow of an SE-FET-based reservoir system for the task of recognition of spoken digits is highlighted in Fig. 5. It consists of three sections: input, reservoir, and a readout function. For a specific input, processed via a mask into a temporal signal of time duration (t), is fed into the reservoir, consisting of the neural ODE model of m number of SE-FET devices. The connection between each temporal input to each SE-FET is fixed. The SE-FET responses are sampled continuously such that the output of the present state also depends upon its previous history. The sampled reservoir output nodes S10, S11… are used to train the weights (Wout) of the readout network using logistic regression. Superscript denotes the device number (m), and subscript denotes (n) over all the sample states of a given device. We use this framework to investigate the impact of various reservoir parameters on performance, such as data representation, single vs. multi-device reservoirs, and device variation. Using the model, we perform a standard benchmark task of recognition of isolated spoken-digits using the NIST TI46 database37 which consists of 500 samples.
 | ||
| Fig. 5 Our framework and process flow of the SE-FET-based reservoir system for the classification of spoken digits. | ||
Before feeding the audio file of isolated spoken digits (0–9) into the reservoir as input, it is preprocessed using Lyon's passive ear model based on human cochlear channels (see Supplementary note 1 for methods, ESI†). The preprocessing using Lyon's passive ear model transforms the audio sample into a set of 64-dimensional vectors (corresponding to the frequency channels) with up to 42-time steps. One example representing the original spoken digit waveform of digit 5 is shown in Fig. 6(a) and its preprocessed Cochlea gram by Lyon's passive ear model consisting of 64 channels is shown in Fig. 6(b) where the lower channel number captures the higher frequency components and vice versa. The preprocessed input is then converted into an analog voltage stream by concatenating all 64 channels. The converted analog voltage stream is applied to the SE-FET reservoir in transient states and its response is sampled after every 0.1 second as shown in Fig. 6(c) for spoken digit 5. The procedure is repeated for all 500 samples.
In this implementation, a single device based reservoir achieves an overall mean accuracy of 99.80%. However, a major drawback of a single device-based reservoir is that it takes too much time to process each isolated spoken digit. For example, the input consists of 64 channels with each channel 42 times long. To process one step, it takes 0.1 seconds. Thus, the total time required to process the entire input is (64 × 42 × 0.1) = 268.8 seconds. To resolve this problem, we can use a multi-device-based SE-FET reservoir system consisting of 64 devices, one device per channel processed using different devices in parallel. Each of these 64 devices are assigned to a different input frequency in the range of 10 Hz to 20 Hz to create device to device variation. Each individual channel is fed to devices in parallel, thus reducing the overall time required to process the one isolated spoken digit from 268.8 seconds to (42 × 0.1) = 4.2 seconds. The response of the reservoir for channel numbers 23 and 64 is shown as an example in Fig. 7, similarly, undertaken for all other channels. A multi device based reservoir results in an overall mean accuracy of 99%. Furthermore, for the performance summary of SE-FET based RC under various conditions such as data representation, single vs. multi-device reservoirs see Supplementary note 2 (ESI†).
 | ||
| Fig. 7 The response of neural ODE model based multi-device reservoir for (a) channel number 23 and (b) channel number 64 is shown as an example. | ||
In our recently reported work28 for the same task, each channel was divided into 14 sub-sections mainly due to it being practically impossible to measure 242 different input patterns. This lead to unnecessary addition of a reset pulse in experiment for a reasonable mask length of 3 bits sequence read at a time. Such constraints do not exist in the present work, due to the neural ODE model. We were also able to reduce the time to 4.2 seconds by parallel processing, which was previously more than an hour for a single spoken digit.28 Moreover, with the help of the neural ODE model we were able to simulate reservoir computing in an analog mode without digitizing the input, which removes extra preprocessing to convert analog to digital signal, while preserving the integrity of analog information. Our SE-FET based reservoir computing achieved a lower error rate of 0.2% for a single device reservoir and 1% for multi device reservoir which performs better or on par with earlier published works, which need other physical devices as shown in Table S3 (ESI†).
However, real-world variations of manufacturing defects and environmental changes can be reasonably expected to affect the performance of the model. This can be mitigated by incorporating variations in the training data to simulate these defects and changes, helping the model to generalize better under different conditions. Additionally, implementing anomaly detection algorithms can identify and filter out data points likely caused by these defects or changes, ensuring cleaner data for training. Further, to integrate device degradation into the model will require to gather data reflecting degradation. This could involve collecting data from devices at various stages of their lifecycle to show changes in performance metrics over time. Moreover, creating features that quantify degradation, such as the age of the device or its usage frequency, could be beneficial.
4. Conclusions
This paper demonstrates that neural ODE models can learn complex device physics without explicitly defining any material properties or device physics. We have demonstrated that by using minimal experimental data spanning 240 seconds, the neural ODE can learn and predict the temporal dynamic behaviour of an SE-FET in any given situation with error reduced by 60% in comparison with physics based models. Further, the neural ODEs offer a valuable capability to predict device behaviour across different pulse widths or frequencies. By doing so, they can significantly reduce development time while precisely tuning input parameters in neuromorphic systems. For instance, in reservoir computing a type of neuromorphic systems, for temporal data processing, these models can be used to generate space time dependent features which can be used to train straightforward machine learning algorithms. This adaptability makes the SE-FET based reservoir computing well-suited for flexible edge systems.Author contributions
A. G. and X. S. made equal contributions on modelling and experiment respectively. A. G. drafted the manuscript. S. M. project administration, supervision, and commented on the manuscript. M. S. project administration, supervision, commented and edited the manuscript. All authors technically discussed the results and have given approval to the final version of the manuscript.Data availability
The original contributions presented in the study are included in the article/ESI,† further inquiries can be directed to the corresponding author.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the fund by MHRD-SPARC under grant code No. P436 between the University of Sheffield, UK, and Indian Institute of Technology Roorkee, India. M. De Souza also acknowledges funding from UKRI project APRIL (EP/Y029763/1) and EP/X016846/1, under “new horizons”.References
- S. H. Jo, T. Chang, I. Ebong, B. B. Bhadviya, P. Mazumder and W. Lu, Nano Lett., 2010, 10, 1297–1301 CrossRef CAS PubMed.
- M. Lederer, T. Kämpfe, T. Ali, F. Müller, R. Olivo, R. Hoffmann, N. Laleni and K. Seidel, IEEE Trans. Electron Devices, 2021, 68, 2295–2300 CAS.
- Z. Li, J. Wu, X. Mei, X. Huang, T. Saraya, T. Hiramoto, T. Takahashi, M. Uenuma, Y. Uraoka and M. Kobayashi, IEEE Electron Device Lett., 2022, 43, 1227–1230 CAS.
- J.-C. Liu, T.-Y. Wu and T.-H. Hou, IEEE Trans. Circuits Syst., 2018, 65, 617–621 Search PubMed.
- L. Gao, Q. Ren, J. Sun, S. T. Han and Y. Zhou, J. Mater. Chem. C, 2021, 9, 16859–16884 RSC.
- D. Ielmini and H. S. P. Wong, Nat. Electron., 2018, 1, 333–343 CrossRef.
- P. B. Pillai and M. M. De Souza, ACS Appl. Mater. Interfaces, 2017, 9, 1609–1618 CrossRef.
- G. Zhou, Z. Wang, B. Sun, F. Zhou, L. Sun, H. Zhao, X. Hu, X. Peng, J. Yan, H. Wang, W. Wang, J. Li, B. Yan, D. Kuang, Y. Wang, L. Wang and S. Duan, Adv. Electron. Mater., 2022, 8, 1–33 Search PubMed.
- R. Wang, J.-Q. Yang, J.-Y. Mao, Z.-P. Wang, S. Wu, M. Zhou, T. Chen, Y. Zhou and S.-T. Han, Adv. Intell. Syst., 2020, 2, 2000055 CrossRef.
- U. Celano, L. Goux, A. Belmonte, K. Opsomer, A. Franquet, A. Schulze, C. Detavernier, O. Richard, H. Bender, M. Jurczak and W. Vandervorst, Nano Lett., 2014, 14, 2401–2406 CrossRef CAS PubMed.
- K. Moon, A. Fumarola, S. Sidler, J. Jang, P. Narayanan, R. M. Shelby, G. W. Burr and H. Hwang, IEEE J. Electron Devices Soc., 2018, 6, 146–155 CAS.
- Y.-M. Kim and J.-S. Lee, J. Appl. Phys., 2008, 104, 114115 CrossRef.
- C.-Y. Lin, S.-Y. Wang, D.-Y. Lee and T.-Y. Tseng, J. Electrochem. Soc., 2008, 155, H615 CrossRef CAS.
- Q. Liu, W. Guan, S. Long, R. Jia, M. Liu and J. Chen, Appl. Phys. Lett., 2008, 92, 012117 CrossRef.
- J. Hutchins, S. Alam, A. Zeumault, K. Beckmann, N. Cady, G. S. Rose and A. Aziz, IEEE Access, 2022, 10, 115513 Search PubMed.
- A. S. Lin, P. N. Liu, S. Pratik, Z. K. Yang, T. Rawat and T. Y. Tseng, IEEE Trans. Electron Devices, 2022, 69, 1835–1841 CAS.
- Y. Zhang, G. He, K. T. Tang, Y. Li and G. Wang, IEEE Trans. Comput. Des. Integr. Circuits Syst., 2023, 42, 834–846 Search PubMed.
- A. S. Lin, S. Pratik, J. Ota, T. S. Rawat, T. H. Huang, C. L. Hsu, W. M. Su and T. Y. Tseng, IEEE Access, 2021, 9, 3126–3139 Search PubMed.
- R. Chen, Y. Rubanova, J. Bettencourt and D. Duvenaud, Adv. Neural Inf. Process. Syst., 2018, 6571–6583 Search PubMed.
- E. Dupont, A. Doucet and Y. W. Teh, Adv. Neural Inf. Process. Syst., 2019, 32, 1–20 Search PubMed.
- X. Chen, F. A. Araujo, M. Riou, J. Torrejon, D. Ravelosona, W. Kang, W. Zhao, J. Grollier and D. Querlioz, Nat. Commun., 2022, 13, 1–12 CAS.
- S. W. Akhtar, DOI:10.48550/arXiv.2312.01657.
- A. Sholokhov, Y. Liu, H. Mansour and S. Nabi, Sci. Rep., 2023, 13, 1–13 CrossRef PubMed.
- F. Sorourifar, Y. Peng, I. Castillo, L. Bui, J. Venegas and J. A. Paulson, Ind. Eng. Chem. Res., 2023, 62, 15563–15577 CrossRef CAS.
- A. Kumar, P. Balakrishna Pillai, X. Song and M. M. De Souza, ACS Appl. Mater. Interfaces, 2018, 10, 19812–19819 CrossRef CAS.
- P. Balakrishna Pillai, A. Kumar, X. Song and M. M. De Souza, ACS Appl. Mater. Interfaces, 2018, 10, 9782–9791 CrossRef CAS.
- A. Gaurav, X. Song, S. Manhas, A. Gilra, E. Vasilaki, P. Roy and M. M. De Souza, Front. Electron., 2022, 3, 1–9 Search PubMed.
- A. Gaurav, X. Song, S. K. Manhas, P. P. Roy and M. M. De Souza, 7th IEEE Electron Devices Technol. Manuf., 2023, 9–11 Search PubMed.
- R. I. Frank and J. G. Simmons, J. Appl. Phys., 1967, 38, 832–840 CrossRef CAS.
- C. Liu and A. J. Bard, Nat. Mater., 2008, 7, 505–509 CrossRef CAS.
- C. K. Perkins, M. A. Jenkins, T.-H. Chiang, R. H. Mansergh, V. Gouliouk, N. Kenane, J. F. Wager, J. F. Conley and D. A. Keszler, ACS Appl. Mater. Interfaces, 2018, 10, 36082–36087 CrossRef CAS.
- N. F. Mott and R. W. Gurney, Electronic Processes in Ionic Crystals, Clarendon Press, Oxford, 1940 Search PubMed.
- S. Kim, S. J. Kim, K. M. Kim, S. R. Lee, M. Chang, E. Cho, Y. B. Kim, C. J. Kim, U.-In Chung and I. K. Yoo, Sci. Rep., 2013, 3, 1–6 Search PubMed.
- S. Massaroli, M. Poli, J. Park, A. Yamashita and H. Asama, Adv. Neural Inf. Process. Syst., 2020 DOI:10.48550/arXiv.2002.08071.
- S. Hochreiter and J. Schmidhuber, Neural Comput., 1997, 9, 1735–1780 CrossRef CAS PubMed.
- M. Raissi, P. Perdikaris and G. E. Karniadakis, J. Comput. Phys., 2019, 378, 686–707 CrossRef.
- Texas Instruments-Developed 46-Word Speaker-Dependent Isolated Word Corpus (TI46) NIST Speech Disc 7-1.1. (1991).
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03696d |
| This journal is © The Royal Society of Chemistry 2025 |