Emergence of heavy-fermion behavior and distorted square nets in partially vacancy-ordered Y4FexGe8 (1.0 ≤ x ≤ 1.5)†
Hengdi
Zhao
 a,
Xiuquan
Zhou
a,
Xiuquan
Zhou
 a,
Mohammad
Usman
a,
Ramakanta
Chapai
a,
Mohammad
Usman
a,
Ramakanta
Chapai
 a,
Lei
Yu
b,
Jianguo
Wen
a,
Lei
Yu
b,
Jianguo
Wen
 b,
Hyowon
Park
ac,
Alexios P.
Douvalis
b,
Hyowon
Park
ac,
Alexios P.
Douvalis
 d,
Patricia E.
Meza
d,
Patricia E.
Meza
 e,
Yu-Sheng
Chen
f,
Ulrich
Welp
a,
Stephan
Rosenkranz
e,
Yu-Sheng
Chen
f,
Ulrich
Welp
a,
Stephan
Rosenkranz
 a,
Duck Young
Chung
a and
Mercouri G.
Kanatzidis
a,
Duck Young
Chung
a and
Mercouri G.
Kanatzidis
 *ag
*ag
aMaterials Science Division, Argonne National Laboratory, 9700 South Cass Avenue, Lemont, IL 60439, USA. E-mail: m-kanatzidis@northwestern.edu
bCenter for Nanoscale Materials, Argonne National Laboratory, 9700 South Cass Avenue, Lemont, IL 60439, USA
cDepartment of Physics, University of Illinois Chicago, Chicago, Illinois 60607, USA
dDepartment of Physics, University Ioannina, Ioannina, 45110, Greece
eDepartment of Material Science and Engineering, Northwestern University, Evanston, Illinois 60208, USA
fNSF's ChemMatCARS, the University of Chicago, 9700 South Cass Avenue, Lemont, Illinois 60439, USA
gDepartment of Chemistry, Northwestern University, Evanston, Illinois 60208, USA
First published on 7th November 2024
Abstract
Disorders in intermetallic systems belonging to the CeNiSi2-family are frequently overlooked. Even compounds presumed to be stoichiometric, such as YFeGe2, can be misidentified. Here, we report a series of Y4FexGe8 (1.0 ≤ x ≤ 1.5) compounds and show, using high-resolution synchrotron X-ray diffraction, that they feature asymmetrical structural distortions in the Fe and Ge sites that lead to a superstructure with partially ordered Fe vacancies and distorted Ge square-net in the triclinic crystal system, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with a = 11.4441(3) Å, b = 32.7356(7) Å, c = 11.4456(3) Å, α = 79.6330(10)°, β = 88.3300(10)°, and γ = 79.6350 (10)°. The unit cell is 16 times the conventional orthorhombic cell with the space group Cmcm. We identified the lower and upper limits for Fe in Y4FexGe8 (1.0 ≤ x ≤ 1.5). Our physical property measurements yielded a Sommerfeld coefficient γ = 39.8 mJ mole−1 K−2, a Kadowaki–Woods ratio of 1.2 × 10−5 μΩ cm mole2 K2 mJ−2, and a Wilson ratio of 1.83, suggesting heavy fermion behavior in the absence of f electrons, a rather rare case. Furthermore, we observed strong spin frustration and noted findings indicating possible superconductivity associated with the Fe content.
with a = 11.4441(3) Å, b = 32.7356(7) Å, c = 11.4456(3) Å, α = 79.6330(10)°, β = 88.3300(10)°, and γ = 79.6350 (10)°. The unit cell is 16 times the conventional orthorhombic cell with the space group Cmcm. We identified the lower and upper limits for Fe in Y4FexGe8 (1.0 ≤ x ≤ 1.5). Our physical property measurements yielded a Sommerfeld coefficient γ = 39.8 mJ mole−1 K−2, a Kadowaki–Woods ratio of 1.2 × 10−5 μΩ cm mole2 K2 mJ−2, and a Wilson ratio of 1.83, suggesting heavy fermion behavior in the absence of f electrons, a rather rare case. Furthermore, we observed strong spin frustration and noted findings indicating possible superconductivity associated with the Fe content.
Introduction
The CeNiSi2-type structure1 consists of a wide collection of rare earth or alkaline earth metal (R) transition metal (M) silicides and germanides (X). This structure type comprises two distinct layers: AlB2-type2 [RX] and edge-sharing square pyramidal MX5 slabs. This family further expands its structural diversity with derivatives including non-stoichiometric vacancy disorder on the M site,3–5 superstructures with vacancy ordering,6–8 and even homologous series.9,10 This diversity in intermetallic compounds of the CeNiSi2-family gives rise to rich physics including superconductivity,3,11 heavy fermion behavior,12 and new emerging orders induced by pressure, such as superconductivity.13–15A heavy-fermion system features strong correlations between localized magnetic and conduction electrons through the competition of the Kondo effect and the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction.16–18 Experimentally, a heavy-fermion metal is characterized by a large Sommerfeld coefficient γ arising from the large density of states near the Fermi level, with a typical value ranging from 20 mJ mole−1 K−2 to up to 1600 mJ mole−1 K−2.19 Heavy fermion systems are known to host diverse strong correlated phenomena.19 What is particularly interesting among them is the unconventional superconductivity in the heavy fermion systems, which only appears after the full suppression of an antiferromagnetic phase, suggesting that fluctuations associated with a magnetic quantum critical point play an important role in facilitating superconductivity.20,21 Interestingly, this behavior mirrors that of Fe-based superconductors,22 where unconventional superconductivity can manifest by suppressing the magnetism in Fe via doping.23–27 This can be considered one of the strategies for seeking unconventional high-Tc (critical temperature) superconductors as the cuprates28 also showed interplays between magnetism and superconductivity.29 Therefore, it is of great interest to illustrate whether similar behavior can be hosted beyond the Fe–As and Fe–Se systems, such as in the Fe–Ge system.
YFe2Ge2, analogous to KFe2−xSe2 (Tc = 35 K),30 has shown unconventional superconductivity between 1.4–1.8 K,31–33 which was thought to be related to the magnetism in Fe.34 Therefore, the YFeGe2 system35 can be a candidate for hosting unconventional superconductivity due to its close proximity to YFe2Ge2. Our previous work has shown that vacancy-ordered Ru-deficient Y4RuGe8 in the CeNiSi2-family exhibits superconductivity below 1.3 K.8 Although the synthesis of stoichiometric YFeGe2 was reported,35 its physical properties or the Fe-deficient phases have not been studied. In addition, adjusting the Fe content in this system can be used to tune the Fermi level to induce emerging properties. Therefore, in this work, we report a series of new compounds with the composition of Y4FexGe8 (1 ≤ x ≤ 1.5) crystallizing in a structure related to the CeNiSi2-type with a distorted Ge square-net and partially vacancy-ordered superstructure. Furthermore, we characterized the heavy fermion state of Y4FexGe8 through measurements of electrical transport, heat capacity, and magnetic susceptibility. The extracted Sommerfeld coefficient γ = 39.8 mJ mole−1 K−2, the Kadowaki–Woods ratio of 1.2 × 10−5 μΩ cm mole2 K2 mJ−2, and the Wilson ratio of 1.83, all fall within the typical range of a heavy fermion system. While heavy fermion behavior typically necessitates the presence of f-electrons, discovering instances where this phenomenon arises without them is both rare and fascinating, defying conventional expectations. The first notable exception containing only 3d electrons is the transition metal vanadate, LiV2O4,36 and its heavy-fermion behavior is attributed to some non-Kondo mechanism, such as strong AFM spin fluctuations due to geometrical spin frustration.37–42 In addition to LiV2O4, only a few more exemptions involving 3d/4d electrons have been reported in transition-metal oxides, such as CaCu3Ru4O12,43 Ba4Nb1−xRu3+xO12;44 chalcogenides, for instance, Fe3GeTe2,45 KNi2Se2;46 ferromagnetic superconducting Laves metal ZrZn2,47,48 1T/1H-TaS2 heterostructure,49,50 MoTe2/WSe2 moiré lattice,51 and Fe-based strongly-correlated intermetallic.52–54 The heavy fermion behavior was also theoretically proposed in twisted trilayer graphene55 and magic-angle twisted bilayer graphene.56,57 In addition to the heavy fermion behavior, strong spin frustration and a possible superconducting state in Y4FexGe8 will also be discussed.
Experimental section
General details
Iron powder (Alfa Aesar, 99.998%) and yttrium powder (Lunex, 99.98%) were used as received. Germanium pieces (Plasmaterials, 99.999%) were ground to a fine powder prior to use. Indium shots (Apache Chemicals, 99.999%) were briefly rinsed with dilute HCl to remove a thin layer of oxide impurities on the surface. The handling of all materials was performed in an M-Braun glovebox under an inert Ar atmosphere with O2 and H2O levels below 0.1 ppm.Synthesis
Y4FexGe8 (1.0 < x < 1.5) crystals were grown from molten In. It is advisable to use Y powder rather than chunks or pieces to subdue the formation of Y/Ge binaries. A stoichiometric mixture of Y/Fe/Ge containing 0.25 g of Y, 0.0565 g of Fe, and 0.41 g of Ge was layered under ∼6 g of In flux in an alumina crucible. The alumina was capped with a stainless-steel frit held in place by a quartz support for hot filtration. This assembly was sealed in a 15 mm OD and 13 mm ID fused silica tube evacuated under a 10−4 mbar vacuum. The ampoule containing the charge was placed in a furnace heated at 30 °C h−1 to 1100 °C, dwelled there for 12 h, cooled at 2 °C h−1 to 1000 °C, cooled at 5 °C h−1 from 1000 °C to 800 °C, cooled at 15 °C h−1 from 800 °C to 500 °C, where the ampoule was carefully taken out of the furnace and centrifuged at 2000 rpm for 30 s to separate the crystals from molten In flux. Rod-shaped crystals with the long dimension beyond 3 mm in length were obtained with granular residues on their surface which were removed by soaking the crystals in dilute HCl (4 parts of water to 1 part of conc. HCl) overnight followed by washing them thoroughly with water and acetone. Y4FexGe8 samples with variable x were also prepared using direct combination reaction of the respective elements at 1000–1100 °C, followed by a furnace cooling by turning off the furnace and letting it cool naturally. The direct combination samples were homogenized with intermediate grind and checked with powder X-ray diffraction until a uniform solid solution is reached.Diffraction
Powder X-ray diffraction (PXRD) data were collected using a Rigaku Miniflex X-ray diffractometer with Cu Kα radiation, λ = 1.5406 Å. Laboratory single crystal XRD data were collected using a STOE IPDS diffractometer or Bruker APEX-2 diffractometer with Mo Kα radiation at room temperature. Synchrotron X-ray beam single crystal XRD data were collected at 15-IDD (NSF's ChemMatCARS at the Advanced Photon Source) with a wavelength λ = 0.41328 Å at either room temperature or under liquid nitrogen flow (∼100 K). Single-crystal structures were solved with the ShelXT intrinsic phasing solution method58 and were refined with ShelXL full-matrix least-squares minimization on F2 method59 using Olex260 as the graphical interface.Electron microscopy
Microscopic images were examined on a Hitachi SU-70 SEM field emission scanning electron microscope (SEM), and their elemental compositions were determined by energy dispersive X-ray spectroscopy (EDS) using a BRUKER EDS detector. Transmission electron microscopy (TEM) images and electron diffraction patterns were obtained using the Argonne Chromatic Aberration-corrected TEM (ACAT), which is an FEI Titan 80–300 ST equipped with an image corrector to correct both spherical and chromatic aberration to enable information resolution better than 0.08 nm at 200 keV. TEM samples were prepared by mechanical grinding of single crystals of Y4Fe1.5Ge2 using mortar and pestle, followed by spreading smaller particles onto a copper TEM grid.X-ray photoelectron spectroscopy (XPS)
X-ray photoelectron spectroscopy measurements (XPS) were performed using a Thermo Scientific Nexsa G2 system (monochromated Al Kα radiation, ∼1486.6 eV) at a pressure of ∼6.4 × 10−7 mbar and with an analysis spot size of 50 μm. Samples were charge compensated with a flood gun. To prepare samples for XPS oxidation state analysis and remove surface contamination without Ar beam sputtering, the Y4FexGe8 particles were washed with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 parts by volume HCl
4 parts by volume HCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DI water for 10 minutes. All peaks were charge-corrected to adventitious carbon at 284.8 eV. Peak widths were not allowed to be larger than 3.5 eV.
DI water for 10 minutes. All peaks were charge-corrected to adventitious carbon at 284.8 eV. Peak widths were not allowed to be larger than 3.5 eV.
Mössbauer spectroscopy
57Fe Mössbauer spectra (MS) of a fine powder Y4FexGe8 sample resulted from grinding several crystals in an agate mortar were collected in transmission geometry at room temperature (RT = 300 K) and 11 K using a constant-acceleration spectrometer, equipped with a 57Co(Rh) source kept at RT, in combination with a closed loop gas He Mössbauer cryostat (ARS). Metallic α-Fe at RT was used for the velocity calibration of the spectrometer and all isomer shift (IS) values are given relative to this standard. The experimentally recorded MS were fitted and analyzed using the IMSG code.61Specific heat
Heat capacity measurements from 1.8 to 300 K were performed in a Quantum Design Dynacool Physical Property Measurement System (Dynacool-PPMS). A sample puck with the appropriate amount of Apiezon N grease was first measured as the background. The sample heat capacity was measured afterward by mounting one bar-shaped single crystal (3 mg in weight) on top of the sample puck. The measurement was performed using a time relaxation method.Electrical resistivity
Electrical resistivity measurements from 1.8 K to 300 K were performed in the same Dynacool-PPMS system. We employed a Bluefors LD400 dilution refrigerator for low-temperature magneto-transport measurements. This cryostat is equipped with a -bottom-loading sample transfer system and a 9-1-1 T three-axis magnet, and it reaches sample temperatures as low as 25 mK. The standard four-leads method was used for the electrical transport measurement and the DuPont 4929N-100 silver paint was used to bond gold wires to the sample to ensure optimal electrical and mechanical contacts. A bar-shaped single crystal with the dimension of 2 × 0.3 × 0.2 mm3 was used in the electrical transport measurements.Magnetic susceptibility
The dc-magnetic susceptibility measurements from 1.8 K to 300 K were performed in a superconducting quantum interference device (SQUID) from Quantum Design Magnetic Property Measurement System (MPMS-3). Multiple coaligned bar-shaped single crystals with a total weight of 14.5 mg were used in the magnetic susceptibility measurements shown in the main text and polycrystalline samples were used for the direct combination measurements shown in the ESI.†Result and discussion
Crystal structure
Similar to YFeGe2, the Fe-deficient Y4FexGe8 crystallizes in the orthorhombic space group Cmcm (Fig. 1a and b) with a = 4.1384(2) Å, b = 15.8468(8) Å and c = 4.0178(2) Å for x = 1.44(1), equivalent to a Fe occupancy of 0.360(3) for the CeNiSi2-type (Table 1). A similar ratio of Y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe
Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ge ≈ 4
Ge ≈ 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5
1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 was also confirmed by elemental analysis using energy dispersive X-ray spectroscopy (EDS) as shown in Fig. S1 (ESI†). However, upon a closer examination of the diffraction data, we found a large number of reflections were omitted using the orthorhombic symmetry (4690 reflections in orthorhombic vs. 23
8 was also confirmed by elemental analysis using energy dispersive X-ray spectroscopy (EDS) as shown in Fig. S1 (ESI†). However, upon a closer examination of the diffraction data, we found a large number of reflections were omitted using the orthorhombic symmetry (4690 reflections in orthorhombic vs. 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 reflections collected in triclinic, hence 80% of reflections were omitted). Therefore, we report here a more accurate crystal structure refinement using the space group P
168 reflections collected in triclinic, hence 80% of reflections were omitted). Therefore, we report here a more accurate crystal structure refinement using the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with a = 5.7716(3) Å, b = 8.1916(4) Å, c = 11.5363(5) Å, α = 79.5610(10)°, β = 88.3050(10)°, and γ = 79.5490(10)° in column 3 of Table 1. The refinement of this triclinic cell, two times the volume of the orthorhombic cell, showed meaningful differences in the Ge square-net and Fe layers of the structure as illustrated in Fig. 2a and b for the space groups Cmcm and P
with a = 5.7716(3) Å, b = 8.1916(4) Å, c = 11.5363(5) Å, α = 79.5610(10)°, β = 88.3050(10)°, and γ = 79.5490(10)° in column 3 of Table 1. The refinement of this triclinic cell, two times the volume of the orthorhombic cell, showed meaningful differences in the Ge square-net and Fe layers of the structure as illustrated in Fig. 2a and b for the space groups Cmcm and P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , respectively. A stepwise symmetry reduction caused by Ge and Fe is illustrated in Fig. S2 (ESI†) to show how the ideal orthorhombic space group Cmcm transitions to P
, respectively. A stepwise symmetry reduction caused by Ge and Fe is illustrated in Fig. S2 (ESI†) to show how the ideal orthorhombic space group Cmcm transitions to P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) .
.
 | ||
| Fig. 1 Crystal structures of Y4FexGe8, crystallizing in a CeNiSi2-type structure (space group Cmcm) viewing at (a) the ab-plane and (b) the bc-plane. | ||
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (column 3). More detailed report of the crystal structure can be found in Tables S1 and S2 (ESI) and CCDC (CSD2357729 and CSD2357730)†
(column 3). More detailed report of the crystal structure can be found in Tables S1 and S2 (ESI) and CCDC (CSD2357729 and CSD2357730)†
| Empirical formula | Y4Fe1.44Ge8 | Y4Fe1.44Ge8 |
|---|---|---|
| Crystal system | Orthorhombic | Triclinic |
| Space group | Cmcm |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| Crystal shape and color | Metallic silver | Metallic silver |
| Unit cell dimensions (Å) | a = 4.1384(2) | a = 5.7716(3) |
| b = 15.8468(8) | b = 8.1916(4) | |
| c = 4.0178(2) | c = 11.5363(5) | |
| α | 90° | 79.5610(10)° |
| β | 90° | 88.3050(10)° |
| γ | 90° | 79.5490(10)° |
| Volume (Å3) | 263.49(2) | 527.49(4) |
| Wavelength (Å) | 0.71073 | 0.71073 |
| Z | 1 | 2 |
| Density (g cm−3) | 6.408 | 6.400 |
| Independent reflections | 255 [Rint = 0.0298] | 4508 [Rint = 0.0532] |
| Data k/restraints/parameters | 255/0/19 | 4508/0/150 |
| Goodness-of-fit | 1.135 | 0.946 |
| Final R indices [I > 2σ(I)] | R obs = 0.0138, wRobs = 0.0293 | R obs = 0.0307, wRobs = 0.0749 |
| R indices [all data] | R all = 0.0150, wRall = 0.0298 | R all = 0.1473, wRall = 0.1091 |
In the orthorhombic setting, the Ge square-net undergoes a minor distortion from 90° to 88.285° with a Ge–Ge distance of 2.88450(11) Å; while for the triclinic setting, without any symmetry restrictions, the Ge square-net distort further from rhombi to irregular quadrilaterals resulting in four distinct Ge–Ge distances (Fig. 2b) for each Ge and its four nearest neighbors varying from 2.872(3)–2.901(3) Å, breaking all mirror and glide planes of the space group Cmcm. For the Fe layer, despite only slight variations of Fe occupancies from 0.320(7) to 0.394(9) in the triclinic setting, the Fe atoms shift to off-center sites. Moreover, their thermal displacement parameters exhibit significant elongations along diagonals of the ac-plane; while they resemble flattened spheres along the b-axis in the orthorhombic setting. This suggests that the radius of Fe is too large to allow full occupancy of the square pyramidal centers in the typical CeNiSi2-type structure.
In comparison, Ru in Y4RuGe88 is large enough to cause more pronounced distortions to the Ge square-net leading to chessboard-like patterns with each big square of Ge (3.22–3.24 Å) surrounded by four neighboring smaller highly distorted squares (2.53–2.55 Å). As a result, Ru can only occupy square-pyramidal centers enclosed by big squares leaving neighboring Ru sites completely unoccupied. In Y4RuGe8, the large Ru atoms cause significant Ge square-net distortions, preventing other Ru atoms from occupying adjacent square pyramidal sites. In contrast, Fe atoms form partially ordered vacancies. While Fe atoms also distort the Ge square-net when occupying square pyramidal sites, their smaller size compared to Ru results in a less pronounced distortion (2.872(3)–2.901(3) Å). This reduced distortion does not completely exclude other Fe atoms from adjacent squares, leading to partially ordered Fe vacancies and off-centering of Fe atoms, which breaks all mirror and glide planes in the orthorhombic space group Cmcm. Consequently, in the orthorhombic space group Cmcm, the occupancies for Fe sites increase up to 0.375, which corresponds to Y4Fe1.5Ge8 compared to 0.25 in Y4RuGe8, leading to the partial order of Fe vacancies in Y4FexGe8 (1.0 ≤ x ≤ 1.5). Compared to the disorder in the Ge square-net and Fe layers, there are no meaningful differences between the two space groups for the Y atoms and Ge–Ge zig-zag chains. The Ge–Ge bond distances in the Ge–Ge zig-zag chains are 2.6053(7) Å and 2.601(5)–2.608(4) Å for the orthorhombic and triclinic settings, respectively.
To fully verify the partial order of Fe vacancies in Y4FexGe8 with asymmetrical distortions and a distorted Ge square-net, we conducted high-resolution single crystal diffraction on a similar sample using a synchrotron X-ray source (15-IDD at APS) at 100 K. Although we were able to index an orthorhombic unit cell similar to the one shown in Table 1, extra reflections from a triclinic supercell were also indexed as a = 11.4441(3) Å, b = 32.7356(7) Å, c = 11.4456(3) Å, α = 79.6330(10)°, β = 88.3300(10)°, and γ = 79.6350 (10)°, whose volume is 16 times of the smaller orthorhombic cell (Table S3, ESI†). Hence, we have discovered a new triclinic cell that surpasses the size of the above-described triclinic cell. Compared to the smaller triclinic cell, the lattice constants of this bigger cell double a and quadruple b, leading to a 2 × 4 × 1 supercell. This indicates that the prior refinement overlooked further weak Bragg reflections, which we were able to uncover through synchrotron diffraction. We synthesized precession images from this data collection, and weaker reflections of supercell are clearly seen in the reciprocal lattice that cannot be accounted for using the orthorhombic cell alone, Fig. 2c and d. These extra reflections showed non-integer numbers, usually at ½ and ¼, for H and L indices, suggesting a 2 × 4 supercell in the basal plane of ac compared to the orthorhombic cell. The refinement of the synchrotron data showed further disparities between the occupancies of the Fe sites ranging from 0.08(2) to 0.475(16), whereas the range is between 0.320(7) to 0.385(8) for the smaller triclinic cell. Therefore, this superstructure is likely a result of partial Fe-vacancy ordering.
To fully understand such disorder in Y4FexGe8, we conducted a local structural analysis on nanoscale using high-resolution transmission electron microscopy (HRTEM). Based on the atomic resolution image depicted in Fig. 3a, we were able to match the overall atomic positions in the unit cell easily. However, upon closer examination of the periodicity of the Fe atoms, we discovered an imperfect recurrence of Fe atoms in almost every three vacant sites (Fig. 3b). In addition, such repeat is not precise and lacks long-range periodicity (Fig. 3c). This is further confirmed by electron diffraction along the [101] zone axis (Fig. 3d and e), where superstructure reflections similar to those shown in Fig. 2d and e could be seen. All this evidence suggests that Y4FexGe8 does not exhibit long-range vacancy ordering like Y4RuGe8,8 but instead, Fe creates local disorders leading to asymmetric distortions in the structure. This explains the larger triclinic cells observed that can better account for the structure distortion.
Variation in Fe composition
Although we have seen the spread of x in obtained crystals from x = 1.23(6) to 1.49(1), it is unclear what synthetic conditions led to these differences. Therefore, we carried out direct combination reactions to target different nominal x values from 0.25 to 2.50 by direct reactions of elemental Y, Fe, and Ge at 1000–1100 °C. We performed Rietveld refinement for as-recovered powder samples as shown in Fig. 4a. For the nominal x = 0.25, the sample contained a large number of impurities with less than half being Y4FexGe8 (17% Ge, 41% YGe1.86, and other unidentified impurities). This was not caused by inadequate reaction as less Y4FexGe8 (∼24% vs. 42%) was obtained after further homogenization by grinding and subsequent annealing at 1000 °C for two days. More YGe1.86 and YFe2Ge2 were obtained from further annealing. However, the purity significantly improved for nominal x = 0.50 as we obtained about 90% Y4FexGe8 with about 10% Ge and an unidentified impurity. Similarly, for x = 0.75 and 1.00, we obtained over 90% of Y4FexGe8 with 8–10% of Ge without the 2nd impurity phase. However, for x = 1.50–2.50, we obtained mainly Y4FexGe8 (∼90%) but with an impurity phase of Y2O3. Our in situ diffraction studies of ground Y4FexGe8 crystals loaded in a quartz tube also resulted in Y2O3 at higher temperatures. This suggests that Y2O3 formed from the reaction of Y4FexGe8 with quartz ampoules.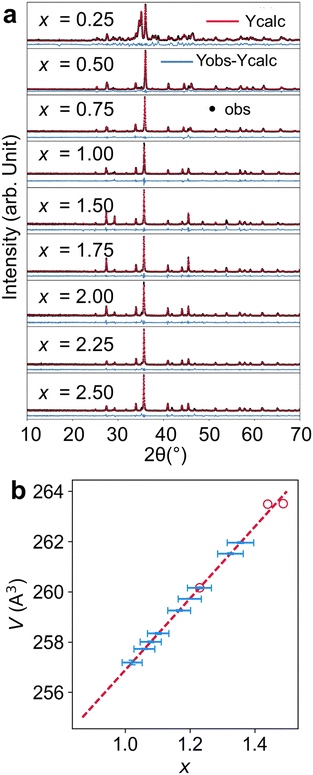 | ||
| Fig. 4 Analysis of direct combination reaction by (a) Rietveld refinement of the PXRD patterns with nominal ratios of x varying from 0.25 to 2.50 and (b) calculated x (blue) based on the fitted x vs. volume modeled from single crystal data (red circle) for each pattern shown in (a). The results are described in Table 2. | ||
Because of the quality of the PXRD data, our Rietveld refinement cannot distinguish small changes in x values as the contributions to the form factor from small variations in Fe is small compared to background noise. However, the trend in unit cell volume determined from our refinement is more reliable. Therefore, we used our single crystal data to obtain x as a function of volume (V) and then used Vegard's law to fit the x values (Table 2). We found the actual x values varied from 1.021(31) to 1.325(40) despite their nominal values changed from 0.25 to 2.50. There appears to be both lower and upper limits for the Fe content based on the fitted volume data. For the smallest nominal x = 0.25, we saw the largest amounts of impurities including unreacted Ge. With increasing nominal x, the fitted x values tend to increase, but appeared to be saturated below x = 1.4. This is consistent with our single crystal data, as we generally obtained crystals with x varying from 1 to 1.5. Therefore, we believe that the stoichiometric YFeGe2 reported in literature35 is likely to be an Fe deficient phase since the reported volume is 261.69 Å3, corresponding to approximately x = 1.34 instead of 4. This is consistent with the upper limit we obtained from our solid-state reactions. Therefore, this evidence demonstrates that the previously reported stoichiometric YFeGe2 was indeed a phase deficient in iron, similar to ours.
| Nominal x | 0.25 | 0.50 | 0.75 | 1.00 | 1.50 | 1.75 | 2.00 | 2.25 | 2.50 |
| V | 257.19 | 257.73 | 258.01 | 259.72 | 258.34 | 259.26 | 260.16 | 261.95 | 261.52 |
| Calculated x | 1.02(3) | 1.06(3) | 1.08(3) | 1.20(4) | 1.10(3) | 1.17(4) | 1.23(4) | 1.36(4) | 1.33(4) |
Fe oxidation state
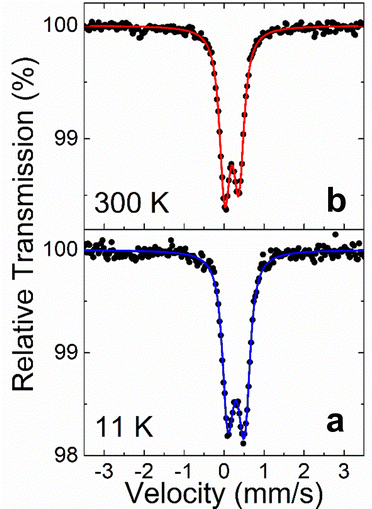
To fully understand the oxidation state of Fe we used 57Fe Mössbauer spectroscopy. The 57Fe MS of the Y4FexGe8 powder sample recorded at RT and 11 K are shown in Fig. 5. These spectra present only quadrupole split contributions, while there is no apparent magnetically split contribution down to 11 K. Although there is no significant change in the shape of the MS between 300 K and 11 K, the spectra possess some broadening and a slight intensity asymmetry in their resonant lines. Thus, one quadrupole split doublet was used to fit both spectra, while an asymmetrical spreading (ΔQS, Gaussian-type) of its quadrupole splitting (QS) values around the central QSC value was allowed. The resulting Mössbauer parameters are listed in Table 3.| IS (mm s−1) | Γ/2 (mm s−1) | QSC (mm s−1) | ΔQS < QSC/ΔQS > QSC (mm s−1) |
|---|---|---|---|
| 0.30 | 0.13 | 0.36 | 0.06/0.04 |
| 0.41 | 0.13 | 0.42 | 0.10/0.05 |
From this table, it is evident that the IS values for the Fe atoms in Y4FexGe8 lie in the range of the values found for crystalline intermetallic as well as amorphous Fe–Ge alloys,62 while the temperature evolution of the IS values between RT and 11 K falls within the expected limits due to the second order Doppler shift.63
The Mössbauer spectroscopy hyperfine parameters values of IS, Γ/2, QSC, asymmetric ΔQS and intensity of spectral resonant lines indicate that there is only one type of neighbor chemical environment for the iron atoms, although this environment involves a slight distribution that could be related to the kind of quasi periodic occurrence of Fe atoms discussed earlier in the crystal structure of Y4FexGe8, as demonstrated by our diffraction (Fig. 2) and electron microscopy data (Fig. 3).
In this crystal structure, the iron atoms occupy square pyramidal positions with 5 Ge atoms as first neighbors. Each pyramid shares its 4 common base-square edges with other 4 neighboring pyramids, while the position of the fifth “apex-Ge” atom in these pyramids is such that the “orientation” of each pyramid is opposite to its first 4 basal-square neighboring pyramids and same with its second 4 neighbor pyramids along the diagonals of the base. So the main interaction of iron is with Ge atoms, along which they seem to form a layered-type structure of orientation-alternating FeGe5 pyramids.
As the Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ge ratio in the Y4FexGe8 phase is 0.18
Ge ratio in the Y4FexGe8 phase is 0.18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 it seems rational to seek resemblance with a Fe–Ge crystalline phase with low iron content as for example in FeGe2, which adopts a tetragonal crystal structure and acquires antiferromagnetic ordering for the iron atoms below TN ≈ 287 K.64,65 The IS values of FeGe2 are quite similar to the ones determined for Y4FexGe8 in this work, indicating a possible resemblance of the electronic configuration for the iron atoms in the latter compound to the former. This configuration is thus referred to as an alloying (Fe0) state.
1 it seems rational to seek resemblance with a Fe–Ge crystalline phase with low iron content as for example in FeGe2, which adopts a tetragonal crystal structure and acquires antiferromagnetic ordering for the iron atoms below TN ≈ 287 K.64,65 The IS values of FeGe2 are quite similar to the ones determined for Y4FexGe8 in this work, indicating a possible resemblance of the electronic configuration for the iron atoms in the latter compound to the former. This configuration is thus referred to as an alloying (Fe0) state.
However, since there is no apparent magnetic transition between RT and 11 K for Y4FexGe8, we could seek a closer resemblance in the Mössbauer spectroscopy hyperfine parameters of iron in this compound with those found in amorphous Fe–Ge compounds of similar compositions. Indeed, the IS, QSC, and ΔQS values resulting from Y4FexGe8 are quite similar to those found for amorphous Fe–Ge compounds in the range of stoichiometries that includes the 0.18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Fe
1 Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ge ratio throughout the total temperature interval between 11 K and RT.62,66,67 Moreover, in these reports there is an important additional experimental result that renders increased resemblance with the current studied Y4FexGe8 phase, which refers to the vanishing magnetic moment of the iron atoms, that is found only for a certain range of low iron concentration and only in the amorphous Fe–Ge system, not the crystalline one. This behavior for the amorphous Fe–Ge compounds is likely associated with the disorder of Fe atoms in the structure akin to that in Y4FexGe8. It was proposed to be associated with the widening of the 3d band of Fe atoms and its strong hybridization with the sp bands of the underlying Ge atom matrix (for relatively low to medium iron atomic concentrations of FexGe1−x, x = 0.01–0.5).
Ge ratio throughout the total temperature interval between 11 K and RT.62,66,67 Moreover, in these reports there is an important additional experimental result that renders increased resemblance with the current studied Y4FexGe8 phase, which refers to the vanishing magnetic moment of the iron atoms, that is found only for a certain range of low iron concentration and only in the amorphous Fe–Ge system, not the crystalline one. This behavior for the amorphous Fe–Ge compounds is likely associated with the disorder of Fe atoms in the structure akin to that in Y4FexGe8. It was proposed to be associated with the widening of the 3d band of Fe atoms and its strong hybridization with the sp bands of the underlying Ge atom matrix (for relatively low to medium iron atomic concentrations of FexGe1−x, x = 0.01–0.5).
X-ray photoelectron spectroscopy (XPS) measurements were also conducted to determine the oxidation state of Fe in Y4FexGe8. The individual samples were washed in an HCl solution to clean the surface of oxidized Fe species, eliminating the need for Ar sputtering. The Fe 2p spectrum in Fig. S4 (ESI†) shows two spin–orbit doublets (2p3/2 and 2p1/2). Although the Fe surface signal is noisy without surface sputtering, only one peak contribution is identifiable for both components. The peak is centered at 707.1 eV and 719.8 eV for 2p3/2 and 2p1/2, respectively.68–70 Studies on FeGe films and other Fe systems conclude that this peak energy corresponds to metallic Fe.70–72
Heavy fermion behavior
Y4FexGe8 is a paramagnetic metal at high temperatures before a superconducting-like transition dominates, which will be discussed later. The magnetic susceptibility at high temperatures is well fitted by a Curie–Weiss law for both crystallographic directions (Fig. 6a). The fits yield a Curie–Weiss temperature, θCW, and an effective moment, μeff, for H//a and H//bc of −55.8 K, 0.87μB per f.u. and −63.1 K, 1.03μB per f.u., respectively with a temperature-independent term χ0 = 0.0011 emu mole−1. The low value of the effective moment is consistent with our results from 57Fe Mössbauer spectroscopy, which is attributed to the strong p–d orbital hybridization between the adjacent Fe and Ge atoms and commonly seen in transition metal intermetallic compounds. However, the system is also strongly correlated, as suggested by the strong antiferromagnetic interactions signaled by the large value of negative θCW. The strong antiferromagnetic interaction is at the heart of the realization of many novel quantum states, such as unconventional superconductivity,22,28 magnetic frustrations,73–75etc. Given the lack of long-range magnetic order down to 1.8 K, the spin of this system can also be considered highly frustrated and warrants future investigations.The resistivity of Y4FexGe8 exhibits a typical metallic behavior with a residual-resistance-ratio (RRR = R250K/R10K) of 1.97 (Fig. 6b). The relatively small RRR ratio may result from scattering related to the large disorder on the Fe-site. A possible consequence of this disorder is the apparent saturation in the temperature dependence of the resistivity near room temperature at a value of 57 μΩ cm. This behavior resembles the approach to the Ioffe–Regel limit observed in disordered systems.76 For example, in A15 compounds (intermetallics with Cr3Si structure type), limiting resistivities of around 100–150 μΩ cm have been reported.76 At temperatures below ∼25 K, the system behaves as a Fermi-liquid77–79 with resistivity following a T2 temperature dependence ρ(T) = ρ0 + AT2, where ρ0 = 27.3 μΩ cm and A = 0.019 μΩ cm K−2 (Fig. 6b inset).
Lastly, heat capacity measured down to 1.8 K reveals no obvious anomalies resembling any transitions (Fig. 6c). The low-temperature heat capacity can be well described by C(T) = γT + βT3 where γ and β is the Sommerfeld coefficient and the Debye constant representing the contribution from electron and phonon, respectively (Fig. 6c inset). The Debye constant β = 0.81 mJ mole−1 K−4 leads to a Debye temperature of 314.5 K, consistent with the observation that the heat capacity approaches the Dulong–Petit limit near room temperature. Meanwhile, the Sommerfeld coefficient, γ, is estimated to be 39.8 mJ mole−1 K−2, which is large even for a metallic system, suggesting enhanced electronic correlation and heavy fermion behavior.
To further explore this enhanced electronic correlation, we carried out DFT calculations for Y4FexGe8 with x = 1.5 using a  supercell of the orthorhombic Cmcm space group structure. We adopt Vienna ab initio simulation package (VASP)80,81 to compute the DFT band structure using the Perdew–Burke–Ernzerhof (PBE)82 correlation energy functional. We used the 8 × 8 × 4 k-mesh along with the energy cutoff of 400 eV for the plane-wave basis. Due to computational limitations, a structure with partial vacancy could not be modeled with DFT. Thus, we used this
supercell of the orthorhombic Cmcm space group structure. We adopt Vienna ab initio simulation package (VASP)80,81 to compute the DFT band structure using the Perdew–Burke–Ernzerhof (PBE)82 correlation energy functional. We used the 8 × 8 × 4 k-mesh along with the energy cutoff of 400 eV for the plane-wave basis. Due to computational limitations, a structure with partial vacancy could not be modeled with DFT. Thus, we used this  supercell with a formula of Y4Fe1.5Ge8 to carry out DFT calculations. The detailed atomic coordinates of the relaxed structure are described in Table S4 (ESI†). Indeed, our DFT calculation displays both flat bands of the Fe 3d state close to the Fermi level (Fig. 7a red color) and the large density of states (DOS) below the Fermi level (Fig. 7c), which is consistent with the large value of γ, suggesting a heavy fermion behavior. The apparent flatness of Fe d bands originates from the small hopping between Fe ions induced by the large in-plane Fe–Fe distance (∼5.77 Å) due to the Fe vacancies. The orbital-resolved DOS shows mostly the Fe 3d and Ge 4p characters below the Fermi level while the Y d state is located at higher energy above the Fermi level. This feature tends to lead to possible electronic instability such as ferromagnetism, known as the Stoner's criterion for magnetism,83 and is consistent with the heavy fermion behavior we observed in this system. Furthermore, the significant hybridization between Fe 3d and Ge 4p orbitals, which is evident in the mixed nature of these states in the band structure near the Fermi level, also has the potential to trigger heavy fermion behavior in the localized Fe d orbitals.
supercell with a formula of Y4Fe1.5Ge8 to carry out DFT calculations. The detailed atomic coordinates of the relaxed structure are described in Table S4 (ESI†). Indeed, our DFT calculation displays both flat bands of the Fe 3d state close to the Fermi level (Fig. 7a red color) and the large density of states (DOS) below the Fermi level (Fig. 7c), which is consistent with the large value of γ, suggesting a heavy fermion behavior. The apparent flatness of Fe d bands originates from the small hopping between Fe ions induced by the large in-plane Fe–Fe distance (∼5.77 Å) due to the Fe vacancies. The orbital-resolved DOS shows mostly the Fe 3d and Ge 4p characters below the Fermi level while the Y d state is located at higher energy above the Fermi level. This feature tends to lead to possible electronic instability such as ferromagnetism, known as the Stoner's criterion for magnetism,83 and is consistent with the heavy fermion behavior we observed in this system. Furthermore, the significant hybridization between Fe 3d and Ge 4p orbitals, which is evident in the mixed nature of these states in the band structure near the Fermi level, also has the potential to trigger heavy fermion behavior in the localized Fe d orbitals.
In addition to the DFT calculation, the heavy fermion is further evidenced by two empirical dimensionless ratios. By examining the Kadowaki–Woods ratio (KWR), we can gain insights into the nature of electron–electron interactions in the material. The Kadowaki–Woods ratio is defined as KWR = A/γ2, where A is the coefficient of the quadratic term in the temperature dependence of electrical resistivity, which is experimentally observed when the electron–electron scattering is dominating over the electron–phonon scattering and γ is the Sommerfeld coefficient accounting electronic contribution to the specific heat. This ratio helps identify the presence of heavy fermion behavior by quantifying the relationship between the electronic specific heat coefficient (γ) and the electrical resistivity (ρ). Empirically, even though both A and γ2 vary by order of magnitude across the materials, their ratio converges to 0.04 × 10−5 μΩ cm mole2 K2 mJ−2 for normal d-band metals and 1.0 × 10−5 μΩ cm mole2 K2 mJ−2 for heavy-fermion systems.19,78,79 Adopting A and γ values estimated above, the KWR of A/γ2 = 1.2 × 10−5 μΩ cm mole2 K2 mJ−2 falls near the value typically seen for a heavy fermion system, providing another evidence reaffirming the heavy fermion behavior in the Y4FexGe8.
In addition, combining magnetic susceptibility and heat capacity results, another informative ratio that can be estimated the is Wilson ratio (WR),84 WR = π2kB2χ0/(3μB2γ), where χ0 is the Pauli magnetic susceptibility and γ is the Sommerfeld coefficient. Both χ0 and γ are related to the electronic density of state near the Fermi surface and the dimensionless Wilson ratio between them reflects the degree of correlations between electrons and spins.85–87 For example, a Wilson ratio greater than unity indicates enhanced electronic correlations, while a ratio close to or less than unity suggests weaker or absence of correlations. Using the Pauli magnetic susceptibility estimated from the high-temperature Curie–Weiss analysis, the WR reaches 1.83, which is close to the value of 2 for strongly correlated systems in contrast to the value of 1 for the non-correlated systems.85–87 Overall, the Wilson ratio analysis strongly indicates that the electrons in Y4FexGe8 are strongly correlated, consistent with the strong antiferromagnetic coupling suggested by the magnetic susceptibility measurements and the heavy fermion state discussed above. It is worth mentioning that strong antiferromagnetic coupling and the absence of a long-range magnetic order were also observed in another heavy fermion metal system FeSi1−xAlx.52 Interestingly, the coexistence of heavy fermion behavior and strong AFM spin fluctuations due to spin frustration resembles the celebrated LiV2O4,37–42 providing Y4FexGe8 as another possible archetype for the study of heavy fermion systems originating from unconventional non-Kondo mechanisms.
Possible superconductivity
We observed a sharp transition near Tc ∼ 3.5 K evidenced in both the magnetic susceptibility (Fig. 8a) and the resistivity (Fig. 8b). In addition, the transition moves to lower temperatures with an increasing magnetic field, an anticipated behavior for a superconductor as the magnetic flux breaks Cooper pairs. However, the low superconducting volume fraction, the non-zero residual resistance, and the lack of heat capacity anomaly all suggest that the superconducting transition observed is not in the bulk. Moreover, the proximity of the observed Tc to the superconducting transition temperature of indium (Tc(In) = 3.4 K) further hinders the justification of the superconducting state in the Y4FexGe8. Therefore, we extended our measurement temperature range down to the milli-Kelvin range.As shown in Fig. 8(d), an additional 64% drop of resistivity is observed between 3 K and 0.05 K with an onset temperature of 2.2 K. This additional resistivity drop comes entirely from the Y4FexGe8 itself as residual indium, if there is any, already becomes a superconductor under this condition and has no resistivity contribution. In addition, the estimated upper critical field of 600 Oe (Fig. 8(d) inset) is also higher than that of indium (Hc(In) = 286 Oe), further highlighting contributions from Y4FexGe8 itself. Similarly, the onset of resistivity drops with an increasing magnetic field, suggesting a superconducting transition onset, but the non-zero residual resistivity and the broad transition once again hinder the claim of bulk superconductivity in the Y4FexGe8. One possible extrinsic explanation of this superconducting-like behavior is that a thin layer of YGe3, which is a superconductor with zero resistivity below 2.2 K,88 intergrow with single crystal Y4FexGe8. However, we deem this scenario unlikely because of the very different way of stacking along the b-axis and a large lattice mismatch along the ac-plane. The broad transition under a zero magnetic field is another piece of evidence that this extrinsic scenario is doubtful. As discussed previously, the wide range of Fe-content, x, has been demonstrated in single- and powder-crystal X-ray diffraction, and its large inhomogeneity even at the atomic level is well established from the above-presented HRTEM studies. Accordingly, we speculate that the Y4FexGe8 might indeed be an intrinsic bulk superconductor but with a Tc highly sensitive to the amount of Fe within its structure. This postulated scenario can explain both the broad transition and non-zero residual resistivity due to the inhomogeneity of Fe across the single crystal of Y4FexGe8 well. In addition, our magnetic susceptibility measurements on the powder samples synthesized via the direct combination method (without the use of indium in the synthesis) also suggest the x-dependent diamagnetic response on the low-Fe side of the phase diagram (Fig. S6, ESI†).
Conclusions
We uncovered a partial order of Fe-vacancies with asymmetrical distortions and distorted Ge square-net in a series of Fe-deficient Y4FexGe8 (1 ≤ x ≤ 1.5) compounds and used solid-state reactions with different Fe ratios to show that the stoichiometric YFeGe2 of the CeNiSi2-type reported in literature belonged to the same Fe-deficient group described in this work. With the use of advanced structural characterizations using X-ray diffraction and high-resolution electron microscopy we probed the limits of Fe content, which does not seem to reach x = 4. Our findings highlight the necessity for more rigorous examination of crystal structures in the CeNiSi2-family, as similar nonstoichiometries and partial occupancies are likely present in most members of this group. Interestingly, Y4FexGe8 exhibits heavy fermion behavior, which is uncommon for a 3d transition metal intermetallic without f electrons. This behavior, combined with strong spin fluctuations, suggests an unconventional non-Kondo mechanism related to spin fluctuation. This discovery opens avenues for exploring heavy fermion systems induced by 3d transition metals through non-Kondo mechanisms related to strong spin fluctuations, particularly in RMX2 and related intermetallic compounds. Moreover, a possible superconductivity that is highly sensitive to the Fe-content also hints at the possibility of unconventional superconductivity. As the RMX2 system is capable of hosting a large number of transition metals across 3d, 4d and 5d elements and adopt tunable distorted structures induced by size effects in the different X = Si, Ge and Sn members of the family, we can expect that they can be leveraged to design strongly electron-correlated systems in which to investigate competing interactions and other emergent phenomena.Author contributions
The work was conceived by H. Z., X. Z., M. U., D.-Y. C., and M. G. K., with input from all authors. H. Z., X. Z., and M. U. carried out the synthesis, lab X-ray diffraction, and elemental analysis. H. Z., X. Z., and Y.-S. C. carried out synchrotron X-ray diffraction and data analysis. H. Z. performed resistivity, magnetization, and heat capacity measurements. L. Y. and J. W. collected and analyzed high-resolution transmission electron microscopy data. P. E. M. collected and analyzed X-ray photoelectron spectroscopy data. H. P. performed first-principle calculations. A. P. D. collected and analyzed Mössbauer Spectroscopy. R. C. and U. W. performed electrical transport down to milli-Kelvin and contributed magnetization measurements. S. R., D.-Y. C., and M. G. K. supervised the project. H. Z., X. Z., D.-Y. C., and M. G. K. wrote the manuscript with input from all authors.Data availability
Additional elemental analysis and X-ray photoelectron spectroscopy, single crystal diffraction data, photoemission yield spectroscopy in air measurement of work function, and additional magnetic susceptibility measurements on powder samples synthesized via direct combination method. Additional crystallographic information files (CIFs): CSD# 2357729 and 2357730.†Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work is primarily supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences, and the Engineering Division. This material is based upon work supported by Laboratory Directed Research and Development (LDRD) funding from Argonne National Laboratory, provided by the Director, Office of Science, of the U.S. Department of Energy under Contract No. DE-AC02-06CH11357. The work (SEM/EDX and TEM) performed at the Center for Nanoscale Materials, a U.S. Department of Energy Office of Science User Facility, was supported by the U.S. DOE, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. Work at the beamline 15-IDD at the Advanced Photon Source (APS) at Argonne National Laboratory was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-06CH11357. NSF's ChemMatCARS Sector 15 is supported by the Divisions of Chemistry (CHE) and Materials Research (DMR), National Science Foundation, under grant number NSF/CHE-2335833 and NSF/CHE-1834750. H. Park acknowledges the computing resources provided by Bebop, a high-performance computing cluster operated by the Laboratory Computing Resource Center at Argonne National Laboratory. XPS measurements were conducted in the EPIC facility of Northwestern University’s NUANCE Center, which has received support from the SHyNE Resource (NSF ECCS-2025633), the International Institute of Nanotechnology (IIN), and Northwestern's MRSEC program (NSF DMR-2308691). We thank Isaiah Gilley for providing photoemission yield spectroscopy in air measurements.References
- O. Bodak and E. Gladyshevsky, Kristallografiya, 1969, 14, 990–994 CAS.
- R.-D. Hoffmann and R. Pöttgen, Z. Kristallogr. - Cryst. Mater., 2001, 216, 127–145 CrossRef CAS.
- G. Venturini, M. François, B. Malaman and B. Roques, J. Less-Common Met., 1990, 160, 215–228 CrossRef CAS.
- H. Bie, A. V. Tkachuk and A. Mar, J. Solid State Chem., 2009, 182, 122–128 CrossRef CAS.
- L. Gustin, L. Xing, M. T. Pan, R. Jin and W. Xie, J. Alloys Compd., 2018, 741, 840–846 CrossRef CAS.
- V. Mykhalichko, R. Kozak and R. Gladyshevskii, Chem. Met. Alloys, 2015, 55–62 CrossRef CAS.
- M. A. Zhuravleva, D. Bilc, R. J. Pcionek, S. D. Mahanti and M. G. Kanatzidis, Inorg. Chem., 2005, 44, 2177–2188 CrossRef CAS.
- J.-K. Bao, H. Zheng, J. Wen, S. Ramakrishnan, H. Zheng, J. S. Jiang, D. Bugaris, G. Cao, D. Y. Chung, S. van Smaalen and M. G. Kanatzidis, Chem. Mater., 2021, 33, 7839–7847 CrossRef CAS.
- A. Weiland, J. B. Felder, G. T. McCandless and J. Y. Chan, Chem. Mater., 2020, 32, 1575–1580 CrossRef CAS.
- T. M. Kyrk, M. Bravo, G. T. McCandless, S. H. Lapidus and J. Y. Chan, ACS Omega, 2022, 7, 19048–19057 CrossRef CAS.
- B. Chevalier, P. Lejay, J. Etourneau and P. Hagenmuller, Mater. Res. Bull., 1983, 18, 315–330 CrossRef CAS.
- W. H. Lee, K. S. Kwan, P. Klavins and R. N. Shelton, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 6542–6545 CrossRef CAS.
- A. M. Alsmadi, H. Nakotte, J. L. Sarrao, M. H. Jung and A. H. Lacerda, J. Appl. Phys., 2003, 93, 8343–8345 CrossRef CAS.
- T. Nakano, M. Ohashi, G. Oomi, K. Matsubayashi and Y. Uwatoko, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 172507 CrossRef.
- Y. Hirose, N. Nishimura, F. Honda, K. Sugiyama, M. Hagiwara, K. Kindo, T. Takeuchi, E. Yamamoto, Y. Haga, M. Matsuura, K. Hirota, A. Yasui, H. Yamagami, R. Settai and Y. Ōnuki, J. Phys. Soc. Jpn., 2011, 80, 024711 CrossRef.
- S. Doniach, Phys. B+C, 1977, 91, 231–234 CrossRef.
- H. v Löhneysen, A. Rosch, M. Vojta and P. Wölfle, Rev. Mod. Phys., 2007, 79, 1015 CrossRef.
- Q. Si and F. Steglich, Science, 2010, 329, 1161–1166 CrossRef CAS PubMed.
- G. R. Stewart, Rev. Mod. Phys., 1984, 56, 755–787 CrossRef CAS.
- N. Mathur, F. Grosche, S. Julian, I. Walker, D. Freye, R. Haselwimmer and G. Lonzarich, Nature, 1998, 394, 39–43 CrossRef CAS.
- B. White, J. Thompson and M. Maple, Phys. C, 2015, 514, 246–278 CrossRef CAS.
- Y. Kamihara, T. Watanabe, M. Hirano and H. Hosono, J. Am. Chem. Soc., 2008, 130, 3296–3297 CrossRef CAS PubMed.
- J. Paglione and R. L. Greene, Nat. Phys., 2010, 6, 645–658 Search PubMed.
- A. D. Christianson, E. A. Goremychkin, R. Osborn, S. Rosenkranz, M. D. Lumsden, C. D. Malliakas, I. S. Todorov, H. Claus, D. Y. Chung, M. G. Kanatzidis, R. I. Bewley and T. Guidi, Nature, 2008, 456, 930–932 CrossRef CAS PubMed.
- D. C. Johnston, Adv. Phys., 2010, 59, 803–1061 CrossRef CAS.
- P. Hirschfeld, M. Korshunov and I. Mazin, Rep. Prog. Phys., 2011, 74, 124508 CrossRef.
- R. M. Fernandes, A. I. Coldea, H. Ding, I. R. Fisher, P. Hirschfeld and G. Kotliar, Nature, 2022, 601, 35–44 CrossRef CAS.
- J. G. Bednorz and K. A. Müller, Z. Phys. B Condens. Matter, 1986, 64, 189–193 CrossRef CAS.
- Z.-H. Cui, H. Zhai, X. Zhang and G. K.-L. Chan, Science, 2022, 377, 1192–1198 CrossRef CAS.
- J. Guo, S. Jin, G. Wang, S. Wang, K. Zhu, T. Zhou, M. He and X. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 180520 CrossRef.
- J. Chen, K. Semeniuk, Z. Feng, P. Reiss, P. Brown, Y. Zou, P. W. Logg, G. I. Lampronti and F. M. Grosche, Phys. Rev. Lett., 2016, 116, 127001 CrossRef PubMed.
- H. Kim, S. Ran, E. D. Mun, H. Hodovanets, M. A. Tanatar, R. Prozorov, S. L. Bud’ko and P. C. Canfield, Philos. Mag., 2015, 95, 804–818 CrossRef CAS.
- Y. Zou, Z. Feng, P. W. Logg, J. Chen, G. Lampronti and F. M. Grosche, Phys. Status Solidi RRL, 2014, 8, 928–930 CrossRef CAS.
- D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 024505 CrossRef.
- V. K. Pecharskii, O. Y. Mruz, M. B. Konyk, P. S. Salamakha, P. K. Starodub, M. F. Fedyna and O. I. Bodak, J. Struct. Chem., 1989, 30, 777–782 CrossRef.
- S. Kondo, D. Johnston, C. Swenson, F. Borsa, A. Mahajan, L. Miller, T. Gu, A. Goldman, M. Maple and D. Gajewski, Phys. Rev. Lett., 1997, 78, 3729 CrossRef CAS.
- O. Chmaissem, J. Jorgensen, S. Kondo and D. Johnston, Phys. Rev. Lett., 1997, 79, 4866 CrossRef CAS.
- V. Eyert, K.-H. Höck, S. Horn, A. Loidl and P. S. Riseborough, Europhys. Lett., 1999, 46, 762 CrossRef CAS.
- J. Matsuno, A. Fujimori and L. Mattheiss, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 1607 CrossRef CAS.
- C. Urano, M. Nohara, S. Kondo, F. Sakai, H. Takagi, T. Shiraki and T. Okubo, Phys. Rev. Lett., 2000, 85, 1052 CrossRef CAS PubMed.
- J. Hopkinson and P. Coleman, Phys. Rev. Lett., 2002, 89, 267201 CrossRef CAS PubMed.
- S. Burdin, D. Grempel and A. Georges, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 045111 CrossRef.
- W. Kobayashi, I. Terasaki, J.-I. Takeya, I. Tsukada and Y. Ando, J. Phys. Soc. Jpn., 2004, 73, 2373–2376 CrossRef CAS.
- H. Zhao, Y. Zhang, P. Schlottmann, R. Nandkishore, L. E. DeLong and G. Cao, Phys. Rev. Lett., 2024, 132, 226503 CrossRef CAS.
- Y. Zhang, H. Lu, X. Zhu, S. Tan, W. Feng, Q. Liu, W. Zhang, Q. Chen, Y. Liu and X. Luo, Sci. Adv., 2018, 4, eaao6791 CrossRef PubMed.
- J. R. Neilson and T. M. McQueen, J. Am. Chem. Soc., 2012, 134, 7750–7757 CrossRef CAS PubMed.
- C. Pfleiderer, M. Uhlarz, S. Hayden, R. Vollmer, H. V. Löhneysen, N. Bernhoeft and G. Lonzarich, Nature, 2001, 412, 58–61 CrossRef CAS.
- S. Yates, G. Santi, S. Hayden, P. Meeson and S. Dugdale, Phys. Rev. Lett., 2003, 90, 057003 CrossRef CAS.
- V. Vaňo, M. Amini, S. C. Ganguli, G. Chen, J. L. Lado, S. Kezilebieke and P. Liljeroth, Nature, 2021, 599, 582–586 CrossRef.
- L. Crippa, H. Bae, P. Wunderlich, I. I. Mazin, B. Yan, G. Sangiovanni, T. Wehling and R. Valentí, Nat. Commun., 2024, 15, 1357 CrossRef CAS.
- W. Zhao, B. Shen, Z. Tao, Z. Han, K. Kang, K. Watanabe, T. Taniguchi, K. F. Mak and J. Shan, Nature, 2023, 616, 61–65 CrossRef CAS.
- J. DiTusa, K. Friemelt, E. Bucher, G. Aeppli and A. Ramirez, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 10288 CrossRef CAS.
- P. Sun, N. Oeschler, S. Johnsen, B. B. Iversen and F. Steglich, Dalton Trans., 2010, 39, 1012–1019 RSC.
- K. Umeo, Y. Hadano, S. Narazu, T. Onimaru, M. A. Avila and T. Takabatake, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 144421 CrossRef.
- A. Ramires and J. L. Lado, Phys. Rev. Lett., 2021, 127, 026401 CrossRef CAS.
- Y.-Z. Chou and S. D. Sarma, Phys. Rev. Lett., 2023, 131, 026501 CrossRef CAS.
- Z.-D. Song and B. A. Bernevig, Phys. Rev. Lett., 2022, 129, 047601 CrossRef CAS PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8 CrossRef PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- A. P. Douvalis, A. Polymeros and T. Bakas, J. Phys.: Conf. Ser., 2010, 217, 012014 CrossRef.
- H. H. Hamdeh, M. R. Al-Hilali, N. S. Dixon and L. S. Fritz, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 2201–2206 CrossRef CAS.
- N. Greenwood and T. Gibb, Mössbauer Spectrosc., 1971, 1–16 Search PubMed.
- J. B. Forsyth, C. E. Johnson and P. J. Brown, Philos. Mag. (1798–1977), 1964, 10, 713–721 CrossRef CAS.
- G. Fabri, E. Germagnoli, M. Musci and V. Svelto, Phys. Rev., 1965, 138, A178–A179 CrossRef.
- O. Massenet and H. Daver, Solid State Commun., 1977, 21, 37–40 CrossRef CAS.
- Y. Endoh, K. Yamada, J. Beille, D. Bloch, H. Endo, K. Tamura and J. Fukushima, Solid State Commun., 1976, 18, 735–737 CrossRef CAS.
- T.-C. Lin, G. Seshadri and J. A. Kelber, Appl. Surf. Sci., 1997, 119, 83–92 CrossRef CAS.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- W. Mi, Y. Liu, E. Jiang and H. Bai, J. Appl. Phys., 2008, 103, 093713 CrossRef.
- G. A. Lungu, N. G. Apostol, L. E. Stoflea, R. M. Costescu, D. G. Popescu and C. M. Teodorescu, Materials, 2013, 6, 612–625 CrossRef CAS PubMed.
- J. Liu, X. Cheng, F. Tong and X. Miao, J. Alloys Compd., 2015, 650, 70–74 CrossRef CAS.
- L. Savary and L. Balents, Rep. Prog. Phys., 2016, 80, 016502 CrossRef PubMed.
- Y. Zhou, K. Kanoda and T.-K. Ng, Rev. Mod. Phys., 2017, 89, 025003 CrossRef.
- C. Broholm, R. Cava, S. Kivelson, D. Nocera, M. Norman and T. Senthil, Science, 2020, 367, eaay0668 CrossRef CAS.
- N. Hussey, K. Takenaka and H. Takagi, Philos. Mag., 2004, 84, 2847–2864 CrossRef CAS.
- L. D. Landau, J. Exp. Theor. Phys., 1957, 3, 920 CAS.
- K. Kadowaki and S. Woods, Solid State Commun., 1986, 58, 507–509 CrossRef CAS.
- A. Jacko, J. Fjærestad and B. Powell, Nat. Phys., 2009, 5, 422–425 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- E. C. Stoner, Proc. R. Soc. London, Ser. A, 1938, 165, 372–414 Search PubMed.
- K. G. Wilson, Rev. Mod. Phys., 1975, 47, 773 CrossRef.
- L. Balents, Nature, 2010, 464, 199–208 CrossRef CAS PubMed.
- T. Usuki, N. Kawakami and A. Okiji, Phys. Lett. A, 1989, 135, 476–480 CrossRef.
- X.-W. Guan, X.-G. Yin, A. Foerster, M. T. Batchelor, C.-H. Lee and H.-Q. Lin, Phys. Rev. Lett., 2013, 111, 130401 CrossRef.
- M. Wei, H. Sung and W. Lee, Phys. C, 2005, 424, 25–28 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2357729 and 2357730. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4tc03601h |
| This journal is © The Royal Society of Chemistry 2025 |