Computational screening of MOX₂ transition metal oxydihalides with M = V, Nb, Ta, Mo, Ru, or Os, and X = Cl, Br, or I

Abstract

Several members of the van der Waals (vdW) layered family of transition metal oxydihalides MOX₂ have been shown to exhibit lattice distortions, leading to interesting electronic properties such as colossal magnetoresistance, ferroelectricity and strong second harmonic generation. Two of these structures have been reported as exfoliated into two-dimensional (2D) materials, out of which one, NbOCl₂, has been shown to have almost layer-independent electronic properties. We here report a computational study of the MOX₂ phases within the compositional space M = V, Nb, Ta, Mo, Ru, or Os, and X = Cl, Br, or I, chosen to cover all experimentally reported three-dimensional (3D) structures within the family. The thermodynamical stability with respect to competing phases and the dynamical stability are considered, and the electronic bandstructure and density of states are evaluated for each MOX₂ structure in both 3D and 2D form. Trends are identified between structures with the same type of distortions. For MOX₂ with M = V, Nb or Ta, a Peierls distortion opens up a wide bandgap at the Fermi level. MoOX₂ also display a Peierls distortion, and while the increased valence renders it conductive, the characteristic features of the bandstructure are still similar to the semiconducting phases. For M = Ru and Os, which are also found conducting, the Peierls distortion is not observed, and the bandstructure and DOS are significantly different from the other considered phases. All 3D phases are shown to be of vdW nature, with very similar properties between their 3D and 2D versions. Analysis of binding energies as well as delamination energies suggest that the investigated 3D phases can all be converted into 2D.

---

1 Introduction

A recent study demonstrates extremely strong non-linear optical response in thin flakes of the van der Waals (vdW) laminated transition metal oxychloride NbOCl₂.¹ This allows for correlated parametric photon pair generation in the material, which renders it promising as a quantum light source. Further, it shows second harmonic generation (SHG) that scales quadratically with flake thickness, and a strong exitonic effect originating from a localized Nb d-electron state at the Fermi level. The exciton energy in NbOCl₂ barely changes going from 3D to a single layer of 2D material, indicating weak interlayer interaction through this lack of layer dependency. The scaling of the SHG contrasts to, e.g., 2D transition metal dichalcogenide WS₂, where the second-harmonic generation is attenuated with increased number of 2D layers.¹ This can be attributed to the non-centrosymmetry of 2D NbOCl₂ being retained also in the 3D form, which is not the case for W₂S.

NbOCl₂ was first reported in 1961,² along with the homeostructural TaOCl₂. These are both members of a larger family of vdW laminated transition metal oxyhalides, which also includes the experimentally observed phases NbOBr₂,³ NbOI₂,^4–6 TaOI₂,⁷ VOCl₂,^8–10 VOBr₂,⁸ MoOCl₂,^4,10–12 RuOCl₂,¹⁰ and OsOCl₂.¹⁰ Two of these, NbOCl₂ and NbOI₂, have been reported as exfoliated into their single layer 2D form, both exhibiting large second harmonic generation.^1,6

Out of this family of phases, it is not only NbOCl₂ which has received interest from the research community, but multiple studies have considered different members of this group of materials and found a number of interesting properties. Following a theoretical prediction of possible large ferroelectric ordering in NbOX₂, X = Cl, Br, or I,^13,14 switchable ferroelectricity was experimentally verified for NbOI₂,¹⁵ and the whole set of NbOX₂ has been suggested as promising for photocatalytic water splitting.¹⁶ MoOCl₂ has also received experimental attention, and has been identified as a metal with colossal magnetoresistance.¹⁷

Hypothetical 2D derivatives of members of the MOX₂-family have also been studied computationally. The V-based phases VOX₂ are all predicted to be multiferroics, with both magnetic and ferroelectric ordering,^18–20 while NbOI₂ is suggested to exhibit ferroelectrically controlled spin helix formation,²¹ which may be important for nano-electronics applications. Also TaOI₂ is proposed to be suitable for applications in valleytronics.²² Other hypothetical compositions which would belong to the MOX₂ family have also been studied and found to exhibit intriguing properties similar to the V- and Nb-based phases.^23–26

This family of vdW-bonded oxyhalides is thus an interesting group of materials, which is why we have chosen to perform a systematic study of its members. In addition to the 10 experimentally reported 3D phases already listed above, we have also considered the 8 hypothetical phases TaOBr₂, VOI₂, and MOX₂ with M = Mo, Ru, or Os, and X = Br, or I, to include all elemental combinations within this compositional space. Since we want to keep the study relevant for potential experimental realization, we only consider phases including transition metal species which have been reported experimentally in this family of phases. The purpose of this study is to assess the possibility for realization of 2D versions of the MOX₂-family members in addition to NbOCl₂ and NbOI₂,^1,6 and to study trends within this family of materials. We consider the ground state structure of each composition and assess the corresponding electronic properties. We find that all the considered MOX₂-structures are likely to be possible to delaminate. They all show very similar electronic structure between 3D and 2D forms, and both semiconducting and conducting behaviours are observed.

2 Results and discussion

2.1 Structure of 3D MOX₂

We have identified the lowest energy non-magnetic structure of the 3D MOX₂ phase for each of the considered compositions. The members of the MOX₂ family are not structurally isomorphic but homeomorphic, with four different prototype structures proposed in experimental studies.¹⁰ The basic prototype structure is reminiscent of the so called 2D perovskites, and is shown in Fig. 1(a). Each layer can be described as consisting of Cl₄O₂ octahedra encasing the transition metal cation. Along the a-direction, these octahedra are corner sharing via the O-atoms, while in the b-direction, they are edge sharing via the X-atoms. Alternatively, the layers can be described as single-atom transition metal chains connected into a sheet by oxygen atoms, and decorated with the respective halogen at the M–M bridge sites. The layers stack by aligning the halogen and oxygen atoms between adjacent layers. For different compositions, the structure undergoes different distortions, and Fig. 1(b) and (c) show the different structures corresponding to each of these distortions. The fourth prototype will be discussed further down.

Fig. 1 Structural schematics of the different structure assumed by the 3D and 2D MOX₂ compositions. Panel (a) shows the highest symmetry structure with space group Immm (no. 71), where the left side of the panel shows the structure from the (100) direction, and the right side from the (010) direction. Panel (b) shows the structure in (a) but with a Peierls distortion of the M-atoms along the b-axis, resulting in a dimerisation of the M-atoms in this direction and reducing the symmetry to space group C2/m (no. 12). In panel (c) the structure is further distorted along the a-axis, resulting in space group C2 (no. 5). Panels (d)–(f) shows the corresponding three structures assumed for the 2D derivatives, where the structures in panels (d) and (e), corresponding to the 3D structure of panels (a), and (b) respectively, both are of space group Pmmm (no. 47), while the structure in panel (f), corresponding to the 3D structure of panel (c), is of space group Pmm2 (no. 25). In panels (d)–(f), the top and bottom of the left side shows the 2D sheets from the (100) and (010) directions, respectively, while the right side shows the (001)/top-direction.

The symmetry of the structures assumed by each composition was found to be determined to the transition metal element. RuOX₂ and OsOX₂ prefer the structure shown in Fig. 1(a) which is of space group Immm (no. 71) and in the following referred to as A₇₁, where the letter refers to the panel of Fig. 1 in which the prototype structure is displayed, and the subscript refers the space group number. Table S1 (ESI†) tabulates energy, lattice parameters and space group of relaxed structures discussed herein.

For TaOX₂ and MoOX₂, a Peierls distortion along the M–M chains (the b-direction indicated in Fig. 1(a)–(c)) causes the M-atoms to form dimers. We refer to this type of distortion as dimerization in the following. This lowers the symmetry from space group Immm to C2/m (no. 12), with the corresponding structure shown in panel (b) of Fig. 1 and referred to as B₁₂. This dimerization is clearly seen comparing panel (a) and (b) of Fig. 1, where the two unequal M–M distances are indicated as L₁ and L₂. The dimerization also causes a distortion of the X-atoms in the z-direction, resulting in two different M–X distances, as opposed to in the A₇₁ structure shown in panel (a). This is indicated by the horizontal dashed lanes in panels (a)–(c) of Fig. 1.

Dimerization of the M-atoms along the b-direction was also observed for the remaining structures, i.e. NbOX₂ and VOX₂, along with an additional pseudo Jahn–Teller (pJT) distortion along the a-axis. The pJT distortion displaces the M-atom along the M–O bond direction, inducing a local dipole moment at each M–O pair which, in turn, leads to ferroelectric properties of these materials, as previously reported.^13,14,18,27 The vertical dashed line in Fig. 1(c) shows how the M-atom of each octahedra is shifted out of the plane of X-atoms, resulting in two different M–O distances denoted l₁ and l₂, as compared to A₇₁ and B₁₂ with undistorted M-atoms residing in the X-atom plane of each octahedra. This structure is of space group C2 (no. 5) and referred to as C₅. This distortion thus breaks the inversion symmetry of the A₇₁ and B₁₂ structures, opening the possibility for second order optical response in these structures.²⁸ The pJT distortion in NbOI₂ is found to be particularly weak, with a very small difference in the two distances l₁ and l₂ and a non-significant energy difference between the B₁₂ and C₅ prototype structures. Nevertheless, we still consider it to be of C₅ structure since it doesn't relax completely into B₁₂ upon relaxation, and because significant second order optical effects have been experimentally proven for the material.²⁹ Table S2 (ESI†) lists the identified structure for each composition in terms of labels as defined by Fig. 1. The energy differences between the different prototype structures for each composition can be found in Table S3 (ESI†), together with an extended discussion of the structural determination. The phonon dispersions for each considered composition in its identified ground state 3D structure can be found in Fig. S1 of the ESI,† showing that the identified structures are all dynamically stable.

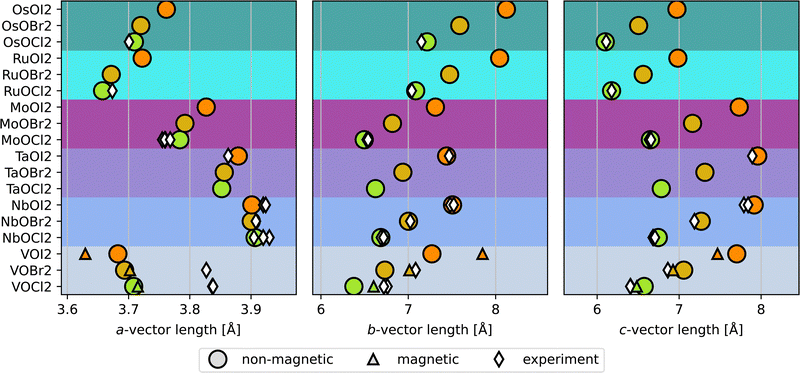
The lattice parameters found for the non-magnetic lowest energy structures are shown by circles in Fig. 2, along with experimental results from previous reports shown by white diamonds.^3–12,30 The lattice vectors refer to the primitive cell of the B₁₂/C₅ prototypes, which contains 8 atoms and one layer in the c-direction (i.e. not the conventional cells shown in Fig. 1). The agreement with experiments is excellent, for all but the VOX₂-phases. These phases have been proposed to exhibit magnetism in previous computational reports.^14,18,19,31 When considering magnetic configurations, the VOX₂ compositions are no longer driven to dimerize, but the M-atoms are evenly distributed along the b-direction, as in the A₇₁ structure. The pJT distortions persist, however, so that the symmetry is reduced from space group Immm to Imm2 (no. 44). Thus the VOX₂ phases are ferroelectric with broken inversion symmetry regardless of the M–M bond Peierls distortion, and the explicit structure is shown in Fig. S2(a) (ESI†). We refer to this structure as FE₄₄ in the following, where FE refers to its ferroelectric nature, and the subscript to the number of the space group it belongs to. Fig. S2(c) (ESI†) shows the antiferromagnetic (AFM) configuration previously reported for 2D VOCl₂ and VOBr₂, which are used in the current work for the 2D units of the 3D magnetic phases. VOI₂ has been reported as ferromagnetic (FM) and we thus also consider FM ordering for this phase. In agreement with previous work, we identify VOCl₂ and VOBr₂ as AFM and VOI₂ as FM. The phonon dispersions for the VOX₂ magnetic structures are shown in Fig. S3 (ESI†), indicating dynamical stability.

Fig. 2 Lattice parameters found for the respective 3D structure of each MOX₂ composition. Circles indicate results from non-magnetic structures, triangles from magnetic structures and white diamonds are data from experimental reports. Lattice vectors are given for the primitive unit cell of the B₁₂/C₅ prototypes.

The lattice parameters corresponding to the magnetic FE VOX₂ are displayed by the smaller triangles in Fig. 2. They agree considerably better with experimental reports for VOCl₂ and VOBr₂ (we have not found any experimental lattice parameters for VOI₂), although the a-parameter, i.e., along the direction of the M–O bond, still does not agree particularly well. Additionally, we find the energy between the C₅ and the magnetic FE structures for VOX₂ to be within 1.5 meV per atom, which is an insignificant energy difference in relation to the approximations employed. Hence, the magnetic FE and non-magnetic C₅ structures are considered as energetically degenerate from the computations presented here. The calculated energies with respect to the corresponding non-magnetic dimerized VOX₂ phases are found in Table S7 (ESI†). Because the structural analysis of the VOX₂ phases is not conclusive in determining the ground state structure, we chose to include both the magnetic and non-magnetic structures in the ensuing discussion.

The preference for dimerization along the M–M bond direction can be linked to the size of the transition metal element, where the dimerizing compositions have consistently larger atomic radii of the transition metal element (M = Nb, Mo, or Ta), than the non-dimerizing compositions (M = Ru, or Os). The atomic radius of V is larger than that of Ru and Os, while smaller than for Nb, Ta and Mo, which may explain why the dimerized and non-dimerized structures are so similar in energy for the VOX₂ phases.

In addition to dynamical stability assessment, the thermodynamical stability of each identified non-magnetic ground state structure was estimated by comparing the energy of each phase with respect to the energy of the set of most competing phases, ΔH_cp, as defined in eqn (S1) (ESI†). Given the energetic degeneracy of the magnetic and non-magnetic VOX₂ structures, only the non-magnetic were considered in this analysis. Competing phases were taken from the Materials Project database.³² All but OsOI₂ was found to have ΔH_cp < 0, indicating thermodynamical stability. The detailed results of these calculations are shown in Fig. S4 and further discussed in the ESI.†

In addition to magnetism, we have also considered the effect of strong correlation by introducing a Hubbard U parameter,³³ for the set of structures NbOX₂, MoOCl₂ and VOCl₂. These were chosen to cover the range of different halogens, and transition metal elements from different periodic groups. No significant change improving the lattice parameters towards experimental values was observed, while for some structures the lattice parameters changed considerably for the worse, as can be seen in Fig. S5 of the ESI.† Given the lack of improved agreement with experiment from inclusion of strong correlation effects, we chose to continue the calculations without +U.

The bonding interactions in MOX₂ phases were analyzed using the LOBSTER code and IpCOHP (integrated projected Crystal Orbital Hamilton Population), focusing on interactions within a 5 Å range. As shown in Fig. S8 (ESI†), the strongest interactions, characterized by the most negative IpCOHP values, correspond to M–O bonds, followed by M–X bonds, both with short bond lengths. Distinct trends in bonding were observed based on structural variations: RuOX₂ and OsOX₂ exhibited symmetric bonding due to their A₇₁ structure, while TaOX₂ and MoOX₂ displayed splitted M–X interactions linked to Peierls distortion in the B₁₂ structure. VOX₂ and NbOX₂ showed distinct interactions due to the distorted C₅ structure.

The total interaction strengths for the 3D MOX₂ phases are summarized in Fig. S9 (ESI†), showing a near 1 : 1 ratio of M–O to M–X contributions. Notably, MOI₂ consistently exhibited the highest M–O to M–X ratio, while MOBr₂ had the lowest.

2.2 Binding energy

It has previously been argued that the pseudo-2D characteristics of 3D NbOCl₂ is related to extremely weak interlayer interactions compared to many other 2D materials,¹ with a reported binding energy of ∼5 meV Å⁻². Thus, we have estimated the binding energy E_b as defined by eqn (1) for all the ground state structures. We have compared these values with binding energies for MOX₂ structures as evaluated elsewhere, as well as with the well known vdW materials BN, MoS₂ and graphite using the random phase approximation (RPA).³⁴E_b is presented for each composition in Fig. 3, where our values are indicated by colored markers. The exact values and corresponding references of earlier work presented in Fig. 3 can be found in Table S8 (ESI†). All values indicated in Fig. 3 are computational estimates of the binding energies, not experimental values. Additionally, we have also considered what we refer to as the delamination energy, E_d, defined by eqn (S2) and shown in Fig. S6 (ESI†). No significant difference between E_b and E_d was observed for the MOX₂ structures.

Fig. 3 Interlayer binding energy E_b. Circles represent data from the present study, with the smaller circles referring to the magnetically ordered VOX₂. Values from previous work evaluated using different exchange–correlation potentials are indicated, as are reference values of the well known vdW materials BN, MoS₂, and graphite.^13,35–37 Additionally, the van der Waals MXene structure Nb₂CS₂ which was recently delaminated into 2D is also indicated.

Within each set of compositions sharing transition metal (but different halogens), there is a very clear trend of increasing E_b for increasing halogen size. This trend is slightly stronger for the Os- and Ru-based compositions, and it is weakest for the Nb- and Ta-based compositions. There is a larger increase in E_b between MOI₂ and MOBr₂ than between MOBr₂ and MOCl₂ within all compositions sharing transition metal, proportional to the total increase within the set. Furthermore, for the compositions with the early transition metals, i.e. V, Nb, Ta and Mo, which assumes one of the dimersized B₁₂ or C₅ structures shown in Fig. 1(b) and (c), the binding energy is clearly lower than for the compositions with the later transition elements Os or Ru, which assumes the non-dimerized A₇₁ structure in Fig. 1(a). This indicates that the dimerization contributes to the weak interlayer interaction in NbOCl₂, as proposed in ref. 1. However, VOX₂ and MoOX₂ show stronger binding energies than NbOX₂ and TaOX₂ even though the structures of all these compositions dimerize, rendering this observation at best partially correct.

The binding energy reported here, and also those given by several previous reports, is in stark contrast with that presented in ref. 1 of ∼5 meV Å⁻², attained using the Perdew–Burke–Ernzerhof (PBE) general gradient approximation (GGA) for the exchange correlation effects.³⁸ PBE does not include vdW effects, which have been shown to be crucial for estimating binding energies in vdW materials,³⁷ and values obtained with this approximation must be considered an underestimate. The range of estimated values for the binding energies as reported here and by earlier studies for any single MOX₂ structure further shows the challenge of accurately estimating E_b. Our estimates for the MOX₂ structures display binding energies lower than that of MoS₂ for most compositions, and they are over all close to that of graphite. Importantly, they are below the estimated value for NbOCl₂,³⁶ which has been realized in 2D form by liquid exfoliation.³⁹ Thus, judging by the estimated binding energies, all MOX₂ structures considered here should be possible to realize in 2D form.

2.3 Structure of 2D MOX₂

The 2D version of each composition has been constructed by separation of the individual layers of the 3D structure, followed by structural relaxation. The schematic 2D structures corresponding to each of the A₇₁, B₁₂ and C₅ structures are shown in Fig. 1(d)–(f), and referred to as D₄₇, E₄₇ and F₂₅, respectively. Detailed information for relaxed non-magnetic 2D structures are tabulated in Table S4 (ESI†). The 2D structure corresponding to FE₄₄ is shown in Fig. S2(b) (ESI†) and is referred to as FE₂₅. All compositions were found to retain the structure of their 2D units upon delamination and structural relaxation, as expected given the vdW nature of these materials and thus weak interlayer interaction. All 2D structures were dynamically stable, with the phonon dispersions shown in Fig. S3 and S7 (ESI†).

Just as for the 3D structures, the energy differences between the magnetic FE₂₅ and the dimerized F₂₅ structures for VOX₂ were insignificant. The F₂₅ was consistently preferred over the FE₂₅ structures for all compositions, by ∼2 meV per atom for VOBr₂ and ∼3.2 and 3.6 meV per atom respectively for VOCl₂ and VOI₂, which makes dimerization more favorable for the 2D structures than for the 3D ones. However, a definite conclusion can still not be drawn, and we continue to consider them as degenerate.

The attained energy differences are found in Table S7 (ESI†), along with a more in depth discussion and summary of earlier work.

The bonding interactions in 2D MOX₂ phases were analyzed using the LOBSTER code and IpCOHP (integrated projected Crystal Orbital Hamilton Population), focusing on interactions up to a 5 Å range. Fig. S10 and S11 (ESI†) show that M–O bonds are the strongest, with the most negative IpCOHP values and shortest bond lengths, followed by M–X bonds. Similar trends in bonding strength and contributions were observed in 3D MOX₂ phases.

The total interaction strengths for 2D phases exhibit a near 1 : 1 ratio of M–O to M–X contributions, consistent with 3D results. Structural variations among the phases, such as distortions and symmetry differences, influence the bonding interactions, as seen in both 2D and 3D systems.

2.4 Electronic structure

For all compositions considered, the electronic properties are very similar between the 3D and 2D phases. We will focus the main discussion on the 2D structures, with the full set of electronic structure data to be found in the ESI,† for both 3D (Fig. S12 and S15) and 2D (Fig. S13 and S14) structures. We have chosen to use the same band path for all 3D and 2D structures respectively, choose as the appropriate band path for the lowest symmetry represented – i.e. C₅ for 3D and F₂₅ for 2D. This allows for straightforward comparison of the band structures between the different materials. For the sake of the following discussion we divide the compositions into three different groups, group V, VI and VIII, where the roman numeral refers to the Group of the periodic table to which the M-element of each phase belongs. The compositions in groups V (M = V, Nb, or Ta) and VI (M = Mo) are those with structures forming dimers along the M–M bond direction, while those of group VIII with M = Ru or Os do not dimerize. In addition, we have the magnetic FE structures for VOX₂, which will be discussed further down.

Fig. 4(a)–(c) show the bandstructures and DOS for the series of 2D NbOX₂ structures, with increasing halogen size going from left to right. These structures are well established in the literature (see e.g., ref. 1 and 40–42), with NbOCl₂ and NbOI₂ reported experimentally in exfoliated form.^1,6 The NbOX₂ structures are all semiconductors. They have an almost flat band just below the Fermi level and a corresponding sharp peak in the DOS, which consist primarily of transition metal d-states with minor contributions from X p-states. This peak has been shown to originate from the dimerization which leads to highly localized molecular-like orbitals in the M–M dimers.^1,26 Below the flat band is another gap in the bandstructure to the rest of the valence bands. The flat band gets closer to the rest of the valence bands as the halogen size increases, but the bandgap remains approximately the same. The dispersion of the flat band increases as it gets closer to the rest of the valence bands, and for the largest halogen, X = I, the flat band merges with the rest of the valence bands.

Fig. 4 Bandstructures and DOS for selected 2D MOX₂ phases. Panel (a)–(c) shows the series of NbOX₂ with increasing halogen size going to the left. Panel (d)–(f) shows the series of TaOX₂ with increasing halogen size going to the left, which show clear similarities to NbOX₂. Panel (g)–(i) shows how the bandstructure for the group VI and VIII MOCl₂ phases, showing how the Fermi level shifts as the number of transition metal valence electrons increases and how the dimerization of the group V and VI structures affects the electronic structure. The grey area in panel (a)–(c) represent the extended band gap when disregarding the flat band at the Fermi level.

There is an evident anisotropy in the electronic structures, which is unsurprising considering the anisotropic nature of the structure itself; the dispersion is relatively low for all bands in the G–Z direction, which corresponds to the direction along the M–M dimers, while it is considerably higher along the other parts of the Brillouin zone path, which run diagonal or parallel to the direction along the M–O bonds.

In panel (d)–(f) of Fig. 4, the series of TaOX₂ structures is shown. The electronic structure of the TaOX₂ phases show striking similarities to the NbOX₂ counterparts, yet little is reported on these compared to NbOX₂. The sharp DOS peak is clearly visible for all TaOX₂, and can be seen to correspond to the almost dispersionless flat band just below the Fermi level. The overall shape of the bandstructures is also very similar between each set of NbOX₂/TaOX₂ sharing halogen species, and the trends noted for the NbOX₂ set of phases applies equally well to the set of TaOX₂.

Fig. 4(g) shows the electronic structure for MoOCl₂. This is a group VI phase, and has thus one more valence electron per formula unit and two per unit cell than the group V structures, which leads to an increased Fermi level compared to the group V phases. However, the electronic structure is still very similar to the NbOX₂ and TaOX₂ phases of panels (a)–(f): the flat band and corresponding peak can be seen at ∼−3 eV, and the bandgap is still evident, although it is now below the Fermi level. Compared to the group V chlorides, the bandgap of MoOCl₂ is considerably smaller, and the flat band shows a higher dispersion which indicates a weaker spatial localization of the localized dimer state than in the group V chlorides. Just as for the group V structures, the bandstructure of MoOCl₂ displays clear anisotropy, with dispersive bands primarily along the direction corresponding to the M–O bonds. Thus, the group VI structures can be expected to be primarily conducting along the direction of the M–O chains. The predicted metallicity of the group VI structures is in agreement with experimental reports.^17,26

For the group V and VI phases, the DOS just below the flat band peak is dominated by X p-states, with contributions from oxygen which diminishes with increasing halogen size. Transition metal d-states dominate the DOS above the Fermi level. The electronic structure data for 2D MoOBr₂, MoOI₂ and non-magnetic VOX₂ is shown in Fig. S13 (ESI†). There it can be seen that also the non-magnetic VOX₂ display electronic structure similar to NbOX₂ and TaOX₂.

The bandstructures for the group VIII phases differ significantly from those of group V and VI, and the signature flat band from the localized dimer state is not evident, although several of the group VIII phases still show a peak in the DOS at around −2 eV. Fig. 4(h) and (i) show the electronic structures for RuOCl₂ and OsOCl₂ respectively, which show similar characteristics. The dispersion in the G–Z direction of the Brillouin zone, i.e. the direction of the M–M bonds, is greater for these phases than for the group V and VI phases. However, the bandstructure exhibits a bandgap in this part of the reciprocal space, so that the structures can be expected to exhibit a highly anisotropic conduction behaviour, just as for the group VI phases. The DOS at the Fermi level is dominated by hybridized states between the transition metal d-electrons and oxygen, further confirming that the materials are conducting along the M–O bonds. As the halogen size increases, the bands get more compressed for the group VIII phases. However, the bandgap along the G–Z-direction of the Brillouin zone remains, and the qualitative features of the group VIII bandstructures are thus well represented by RuOCl₂/OsOCl₂. The electronic structure of the remaining group VIII phases is shown in Fig. S13 (ESI†).

2.4.1 The magnetic VOX₂ structures. In addition to the non-magnetic phases, we also calculated the electronic structure for the magnetically ordered FE₄₄ (3D) and FE₂₅ (2D) VOX₂, displayed in Fig. S14 and S15 of the ESI.† The prototype structures FE₄₄ and FE₂₅ are shown in Fig. S2(a) and (b) in the ESI.† Detailed data of magnetic 3D and 2D structures of VOX₂ is found in Tables S5 and S6 (ESI†), respectively. The antiferromagnetic VOCl₂ and VOBr₂, with the explicit magnetic configuration shown in Fig. S2(c) (ESI†), were found to exhibit large bandgaps of 3.2/3.35 and 2.57/3.02 eV for the 3D/2D structures respectively. The localized state within the bandgap seen for the dimerized structures is not present. The bandstructures attained here are in disagreement with earlier reports,^18,19 where populated bands of strong 2D character are present within the bandgap. However, earlier reports have used a general gradient approximation (GGA) exchange correlation functional to evaluate the bandstructures, which we identify as the reason for this discrepancy. This is discussed further in the ESI† and shown in Fig. S16.

VOI₂, which is ferromagnetic, is found to be a half-metal, with a bandgap of 1.53/1.55 eV for the semiconducting spin channel in the 3D/2D structures. The bandstructures for the conducting spin channel shows clear similarities with the RuOX₂ and OsOX₂ structures, which are also conducting and non-dimerized. The semiconducting spin channel gives a bandstructure that is more similar to the dimerized structures, but without the localized d-electron states.

2.4.2 Bandgap analysis and band widths. The bandgaps predicted for the 3D and 2D phases of each composition are shown in Fig. 5(a), with larger and smaller markers representing 3D and 2D phases, respectively. The M-site element is indicated by the shape of the marker, while the X-site element is indicated by color. The V-based phases, for which there is both the non-magnetic dimerized structures and the magnetic FE₄₄ and FE₂₅ structures, the former is marked by the downwards pointing triangles with black outline, while the latter are marked by upwards pointing triangles and a grey outline. For VOI₂ there are two sets of markers corresponding to the FE₄₄ and FE₂₅ structures, one for each spin channel. The FE₄₄ and FE₂₅ structures of VOCl₂ and VOBr₂ have AFM ordering, and thus their bandstructures are the same for both spin channels. Since the bandstructures of the VOX₂ FE₄₄ and FE₂₅ structures are significantly different from the non-magnetic counterpart owing to the lack of dimerization in the magnetic FE₄₄ and FE₂₅, we consider them only partially for the continued discussion on bandgaps trends for the MOX₂ phases. We have, however, included also the bandgaps of the group VI phases, which are below the Fermi level. The reason for including the group VI phases in this bandgap analysis is that also these structures display the flat band feature originating from the dimerization of the M-atoms.

Fig. 5 Electronic structure trends for 3D and 2D MOX₂. The panels show the bandgap of each structure (a), the extended bandgap of each structure (b), the extended bandgap as a function of the dimer length L₁ normalised by the covalent radius r^M_cov of the respective transition metal M (c), and the width of the flat band as a function of the size of the extended bandgap (d).

Fig. 5(a) shows the bandgap for each considered composition, clearly demonstrating how the bandgap is consistently slightly larger for the 2D phases than for the 3D counterpart. Within each set of structures sharing M-site element, the bandgap decreases with increasing halogen size. However, the decrease is small for NbOX₂ and TaOX₂, while considerably larger for MoOX₂ and VOX₂.

Panel (b) instead shows what we choose to refer to as the extended bandgap, defined as the bandgap found when disregarding the flat band. This is marked for NbOX₂ by the grey area in Fig. 4(a)–(c). The reason for considering the extended bandgap is this: the DOS peak corresponding to the flat band is constituted of M-site d-electrons, as does the lowest conduction bands. Hence, an optical transition from the flat band to the lowest valence band is forbidden, as noted previously.^1,13 However, the second highest valence band, i.e., the band directly below the flat band, primarily comes from X p-states, as can be seen in the DOS. This is true for all of the dimerized structures but MoOI₂ and VOI₂, for which the valence band I p-states are higher in energy than the d-states giving rise to the flat band, as seen in Fig. S12 and S13 (ESI†). For these structures, the extended bandgap is thus the same as the bandgap. Hence, for optical transitions the extended bandgap is of more interest than the bandgap. For instance, the first optical adsorption peak in NbOX₂ is considerably higher in energy than the bandgap value^1,13 due to the bandgap not corresponding to an optically allowed transition. Hence, we consider the extended bandgap for the remainder of this discussion.

In panel (b), we now see an evident linear trend within each set of structures sharing M-site element, with the extended bandgap decreasing as the halogen size increases. We also see a trend within each set of structures sharing the X-site element, with the extended bandgap increasing with increased transition metal size. MoOX₂ do not quite follow this trend, which is unsurprising since the electronic structure is indeed intrinsically different for these structures, given that Mo has more valence electrons than the group V elements, as well as a larger nuclear charge which reduces the size of its orbitals.

In panel (c) the extended bandgap is plotted against the length of the dimers, L₁, normalized by the covalent radius of the corresponding element. L₁ has been proposed to be a suitable measure for the dimerization,¹³ which in turn has been deemed the cause of the opening of a bandgap.^1,26 We see indeed that the extended bandgap is linearly related to the normalized L₁, increasing as the M-atoms get relatively closer to each other. However, we also see that the trends are restricted to within each set of structures sharing the M-site element, and this measure is thus not consistent between M-elements. It is also possible to group the ferroelectric C₅/F₂₅ structures, i.e. NbOX₂ and non-magnetic VOX₂, and the non-ferroelectric B₁₂/E₄₇ structures TaOX₂ and MoOCl₂. These two groups can be approximated to follow two linear parallel trends of increasing extended bandgap with decreasing normalized L₁, indicating that the pJT distortion of NbOX₂ and VOX₂ may also affect the extended bandgap.

Finally, we consider the width of the flat band as a function of the extended bandgap, shown in Fig. 5(d). As the extended bandgap increases, the bandwidth can be seen to decrease as the localization of the dimer state gets more pronounced. However, at an extended bandgap of ∼2.5 eV, this trend flattens and the bandwidth remains largely unchanged. For MoOX₂ and for most of the MOI₂ compositions, the 3D structure has consistently a smaller bandwidth than the 2D, while for MOCl₂, M ≠ Mo the opposite is true, and for MOBr₂ no obvious trend is observed.

2.5 Charge transfer

Understanding the charge distribution in 3D and 2D MOX₂ phases is crucial for characterizing the electronic properties of these materials. By examining Mulliken and Löwdin charges, we gain a deeper insight into the role of electronegativity within these phases. Fig. S17 (3D MOX₂) and S18 (2D MOX₂) (ESI†) reveal a consistent pattern in charge distribution between metals and X elements. X elements (Cl, Br, I) exhibit more negative charges, indicating their tendency to gain electrons, or charge, due to their higher electronegativity.

In contrast, metals show positive Mulliken and Löwdin charges, reflecting their lower electronegativity compared to X and O. This makes metals more prone to donating electrons. The comparison between Mulliken and Löwdin charges further supports these observations. Mulliken charges generally show more negative values across all elements, especially for X elements, suggesting a higher electron density due to their higher electronegativity. On the other hand, Löwdin charges, being less localized, present a more balanced distribution across metals and X elements, indicating a lesser tendency for electron acceptance by X elements compared to Mulliken charges.

Overall, the charge distribution observed in Fig. S17 (3D MOX₂) and S18 (2D MOX₂) (ESI†) aligns with electronegativity of corresponding elements. This trend indicates that X elements, due to their higher electronegativity, are more likely to accept electrons, resulting in more negative charges. Metals, with their lower electronegativity, tend to donate electrons, as reflected in their higher positive charges. This relationship between charge distribution and electronegativity provides valuable insights into the electronic structure and behavior of the compounds studied herein.

3 Computational methods

All simulations were performed within the framework of density functional theory (DFT),^43,44 using the Vienna ab initio Simulation Package (VASP).^45–48 The energy cutoff for the plane wave basis set was set to 400 eV, and the projected augmented wave (PAW) approximation was used to account for the core electrons.^49,50 The exchange–correlation effects were modelled using the van der Waals (vdW) density functional developed by Dion et al.,⁵¹ with the optB86b exchange,^52,53 which has been shown to give accurate equilibrium geometries for weakly bound systems.³⁴ Collinear magnetism was used considering FM and AFM spin configurations for the VOX₂ phases.

The relaxation for the 3D phases was done in two steps. First, a standard relaxation of both the unit cell size and shape, and ionic positions was performed, using the built in minimization procedures of VASP. The convergence criteria were set to 10⁻⁶ eV per atom for the electronic convergence and 5 × 10⁻³ eV Å⁻¹ for the forces between ions in the ionic convergence. This was followed by a second step in which the unit cell length perpendicular to the 2D sheets was optimized externally of VASP, using an energy convergence criteria again of 10⁻⁶ eV per atom. For each adjustment of the unit cell the ionic positions were fully relaxed, using the same criteria as for the first step of the relaxation. Looking for the ground state structure for each composition, different prototype structures were considered. This is explained in more detail in the ESI.†

The 2D structures were also relaxed by optimizing the in-plane cell vectors externally. Each in-plane lattice vector was optimized independently, while the angle between them was kept fixed at 90 degrees. The out-of-plane cell vector was kept fixed and set to give a vacuum spacing of 25 Å. The actual vacuum spacing then changed during relaxation, but remained larger than 24 Å for all structures. Again, the ionic positions were relaxed in each step, with the electronic convergence set to 10⁻⁵ eV per atom and forces between atoms were converged to within 5 × 10⁻³ eV Å⁻¹. The external optimization was terminated when the energy gradient with respect to the lengths of the in-plane cell vectors was less than 2.5 × 10⁻³ eV Å⁻¹.

The k-point sampling for all relaxations was Γ-centered with a density equivalent to 2π·0.016 Å⁻¹. In the case of 2D structures, the out-of-plane direction was only sampled at a single k-point.

The binding energy E_b evaluated for each of the 3D structures relative to the constituent 2D layers is defined as

where E_3D is the energy of the 3D structure, and is the energy of the 2D unit of the 3D structure, i.e. without structural relaxation of the 2D unit, and A is the surface cleavage area.

The phonon dispersions were evaluated for the lowest energy structure of each composition, both for the 3D and 2D structures. For the VOX₂ structures, both the magnetic and non-magnetic versions were considered. Phonopy was used to find the phonon dispersion within the harmonic approximation from a force constant potential (fcp) constructed using hiphive.^54,55 In doing so, a supercell of 4 × 2 × 2 primitive unit cells for the 3D structures and 4 × 2 × 1 for the 2D structures was used to construct five initial supercells, rattled using a Monte Carlo method. For the antiferromagnetic VOCl₂ and VOBr₂ a 2 × 2 × 2 or 2 × 2 × 1 supercell was used for the 3D and 2D structures respectively, since the primitive cell was already a 2 × 1 × 1 supercell to allow for the correct magnetic configuration. The forces between atoms in the rattled supercells were evaluated using VASP, and used to attain an initial fcp by fitting to this data with hiphive. The initial fcp will typically result in phonon dispersions with plenty of negative (imaginary) frequencies, but can be readily improved by constructing additional rattled structures that probes the vibrations corresponding to the supposedly negative (imaginary) frequencies. We chose to rattle five new structure in each such step, until the maximum and minimum frequencies of the phonon dispersion, and the R²-value of the fit had converged. The fitting of the fcp was constructed to obey the Born and Huang sum rules.⁵⁶

The electronic properties were simulated using the hybrid exchange correlation functional HSE06.^57,58 This functional gives a good balance between computational requirements and accuracy. It is designed specifically to give accurate bandgaps, and is thus a popular choice for bandstructure calculations. For the bandstructure calculations, a k-point sampling of 7 × 3 × 3 and 7 × 3 × 1 were used for the 3D structures and the 2D structures of the non-conducting phases, respectively. For the 2D structures of the conducting phases, a k-point grid of 12 × 6 × 1 was used, since they were found to converge more slowly with respect to k-point density than the non-conducting structures. The lower density was used for all 3D structures, due to the considerably increase in computational costs when increasing the k-point density. For the antiferromagnetic structures a k-point grid of 3 × 3 × 3 was used for the 3D structures and 5 × 5 × 1 for the 2D structures.

The DOS was calculated using the LOBSTER code,^59–64 with input prepared using the HSE06 functional, using k-point samplings of 7 × 3 × 3 for 3D structures, 13 × 7 × 1 for the 2D non-magnetic/ferromagnetic structures and 7 × 7 × 1 for the antiferromagnetic structures. The DOS calculations proved more sensitive with respect to k-point sampling which is why a denser k-point grid was used. The LOBSTER code was also used to calculate the integrated projected Crystal Orbital Hamilton Population (IpCOHP), where the calculated band-structure energy is reconstructed into orbital interactions up to a distance of 5 Å, along with Mulliken and Löwdin charges for individual atoms.^59–64

4 Summary and conclusions

We have studied the set of structures MOX₂ with M = V, Nb, Ta, Mo, Ru, or Os, and X = Cl, Br, or I which are homeostructural to the recently delaminated van der Waals phase NbOCl₂. We find that in NbOX₂, TaOX₂, and MoOX₂, the M-atoms form dimers along the M–M bond direction. In NbOX₂ there is an additional distortion along the M–O bond direction, rendering them ferroelectric. For VOX₂, we find two energetically degenerate structures for each composition, one which dimerizes and one with magnetic order and no dimerization. Both of these structures also display the distortion along the M–O bond direction which leads to ferroelectricity. For RuOX₂ and OsOX₂ neither of these distortions occur.

We find that the binding energy of the 3D structure is similar across all compositions, increases with atomic size of the X species, and is smaller for the dimerized structures than for the non-dimerized ones. The binding energies are comparable to other van der Waals laminated structures,^36,37 indicating that all 3D structures can be delaminated into 2D.

We have also studied the electronic structure of the considered MOX₂ phases, establishing RuOX₂, OsOX₂, and MoOX₂ as conducting. The magnetically ordered VOI₂ is found to be a half-metal, which could make it interesting for spintronic applications, and the remaining structures are semiconducting. The electronic structure is highly anisotropic for all structures. The bandgap corresponding to optically allowed transitions is compared between phases, and found to decrease with increasing halogen size. As already observed for a number of structures in this family, the electronic properties remain largely unchanged upon delamination.

We identify the set of TaOX₂ structures as similar to the NbOX₂ structures which has received considerable attention lately,^1,16,40 in that they show nearly identical binding energies and very similar electronic structure. We thus propose the TaOX₂ structures for further studies related to the electronic structure properties, such as for photocatalytic applications. An important difference between the NbOX₂ and TaOX₂ is that TaOX₂ does not break inversion symmetry, rendering it unlikely that these phases would display second order optical effects. On the other hand, the VOX₂ phases lack inversion symmetry regardless of whether they are indeed found to be magnetic or not, and thus they can be expected to exhibit second order optical effects such as SHG, similarly to NbOX₂.

Data availability

The data supporting this article have either been included as part of the ESI† or is publicly available at materialsproject.org.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. R. acknowledge support from the Knut and Alice Wallenberg (KAW) Foundation for a Scholar Grant (2019.0433), from the Göran Gustafsson Foundation for Research in Natural Sciences and Medicine, from the Swedish Foundation for Strategic Research (SSF) (EM16-0004), and from the Swedish Research Council (2019-04233). All simulations have been carried out using the PDC Center for High Performance Computing and the National Supercomputer Centre (NSC), provided by the National Infrastructure for Supercomputing in Sweden (NAISS), partially funded by the Swedish Research Council through grant agreements no. 2022-06725.

Notes and references

1. Q. Guo, X.-Z. Qi, L. Zhang, M. Gao, S. Hu, W. Zhou, W. Zang, X. Zhao, J. Wang, B. Yan, M. Xu, Y.-K. Wu, G. Eda, Z. Xiao, S. A. Yang, H. Gou, Y. Ping Feng, G.-C. Guo, W. Zhou, X.-F. Ren, C.-W. Qiu, S. J. Pennycook and A. T. S. Wee, Nature, 2023, 613, 53.
2. H. Schäfer, E. Sibbing and R. Gerken, Z. Anorg. Allg. Chem., 1961, 307, 163–173.
3. J. Beck and C. Kusterer, Z. Anorg. Allg. Chem., 2006, 632, 2193–2194.
4. H. G. Schnering and H. Wöhrle, Angew. Chem., 1963, 75, 684.
5. J. Rijnsdorp and F. Jellinek, J. Less-Common Met., 1978, 61, 79–82.
6. Y. Fang, F. Wang, R. Wang, T. Zhai and F. Huang, Adv. Mater., 2021, 33, 2101505.
7. M. Ruck, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1995, C51, 1960–1962.
8. H. J. Seifert and J. Uebach, Z. Anorg. Allg. Chem., 1981, 479, 32–40.
9. R. J. Sime, Z. Kristallogr. - Cryst. Mater., 1967, 124, 238–240.
10. H. Hillebrecht, P. J. Schmidt, H. W. Rotter, G. Thiele, P. Zönnchen, H. Bengel, H. J. Cantow, S. N. Magonov and M. H. Whangbo, J. Alloys Compd., 1997, 246, 70–79.
11. P. Zönnchen, G. Thiele, C. Hess, C. Schlenker, H. Bengel, H. J. Cantow, S. N. Magonov, D. K. Seo and M. H. Whangbo, New J. Chem., 1996, 20, 295–300.
12. H. Schäfer and J. Tillack, J. Less-Common Met., 1964, 6, 152–156.
13. Y. Jia, M. Zhao, G. Gou, X. C. Zeng and J. Li, Nanoscale Horiz., 2019, 4, 1113–1123.
14. H. Tan, M. Li, H. Liu, Z. Liu, Y. Li and W. Duan, Phys. Rev. B, 2019, 99, 195434.
15. Z. Chen, Y. Hu, L. Zhang, J. Jiang, R. Hawks and J. Shi, Appl. Phys. Lett., 2021, 119, 033103.
16. L. Pan, Y. L. Wan, Z. Q. Wang, H. Y. Geng and X. R. Chen, J. Appl. Phys., 2023, 134, 085105.
17. Z. Wang, M. Huang, J. Zhao, C. Chen, H. Huang, X. Wang, P. Liu, J. Wang, J. Xiang, C. Feng, Z. Zhang, X. Cui, Y. Lu, S. A. Yang and B. Xiang, Phys. Rev. Mater., 2020, 4, 041001.
18. H. Ai, X. Song, S. Qi, W. Li and M. Zhao, Nanoscale, 2019, 11, 1103–1110.
19. A. Mahajan and S. Bhowmick, J. Phys. Chem. C, 2023, 127, 11407–11418.
20. R. Song, B.-L. Wang, K. Feng, L. Wang and D. D. Liang, Acta Phys. Sin., 2022, 71, 37101.
21. Q. Ye, Y.-H. Shen and C.-G. Duan, Chin. Phys. Lett., 2021, 38, 087702.
22. X. Xu, Z. He, Y. Dai, B. Huang, L. Kou and Y. Ma, Appl. Phys. Lett., 2021, 119, 073101.
23. N. Yang, G. Gou, X. Lu and Y. Hao, Nano Res., 2022, 15, 6779–6789.
24. Q. Yang, D. Wang, Z. Y. Zeng, H. Y. Geng and X. R. Chen, Phys. Rev. B, 2024, 109, 035411.
25. G. Song, C. Zhang, T. Xie, Q. Wu, B. Zhang, X. Huang, Z. Li, G. Li and B. Gao, Phys. Chem. Chem. Phys., 2022, 24, 20530–20537.
26. Y. Zhang, L.-F. Lin, A. Moreo and E. Dagotto, Phys. Rev. B, 2021, 104, L060102.
27. Y. Zhang, L.-F. Lin, A. Moreo, G. Alvarez and E. Dagotto, Phys. Rev. B, 2021, 103, L121114.
28. L. Ye, W. Zhou, D. Huang, X. Jiang, Q. Guo, X. Cao, S. Yan, X. Wang, D. Jia, D. Jiang, Y. Wang, X. Wu, X. Zhang, Y. Li, H. Lei, H. Gou and B. Huang, Nat. Commun., 2023, 14, 5911.
29. I. Abdelwahab, B. Tilmann, Y. Wu, D. Giovanni, I. Verzhbitskiy, M. Zhu, R. Berté, F. Xuan, L. D. S. Menezes, G. Eda, T. C. Sum, S. Y. Quek, S. A. Maier and K. P. Loh, Nat. Photonics, 2022, 16, 644–650.
30. D. Drobot and E. Pisarev, Zh. Neorg. Khim., 1984, 29, 1561–1563.
31. M. Noor-A-Alam and M. Nolan, Nanoscale, 2022, 14, 11676–11683.
32. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
33. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
34. J. Björk and J. Rosen, Chem. Mater., 2021, 33, 9108–9118.
35. J. Zhou, L. Shen, M. D. Costa, K. A. Persson, S. P. Ong, P. Huck, Y. Lu, X. Ma, Y. Chen, H. Tang and Y. P. Feng, Sci. Data, 2019, 6, 1.
36. N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246–252.
37. T. Björkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2012, 108, 235502.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
39. A. Majed, M. Kothakonda, F. Wang, E. N. Tseng, K. Prenger, X. Zhang, P. O. Å. Persson, J. Wei, J. Sun and M. Naguib, Adv. Mater., 2022, 34, 2200574.
40. I. Abdelwahab, B. Tilmann, X. Zhao, I. Verzhbitskiy, R. Berté, G. Eda, W. L. Wilson, G. Grinblat, L. de, S. Menezes, K. P. Loh and S. A. Maier, Adv. Opt. Mater., 2023, 11, 2202833.
41. T. Fu, K. Bu, X. Sun, D. Wang, X. Feng, S. Guo, Z. Sun, Y. Fang, Q. Hu, Y. Ding, T. Zhai, F. Huang and X. Lü, J. Am. Chem. Soc., 2023, 145, 16828–16834.
42. B. Mortazavi, M. Shahrokhi, B. Javvaji, A. V. Shapeev and X. Zhuang, Nanotechnology, 2022, 33, 275701.
43. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864–871.
44. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138.
45. G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
46. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
47. G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558–561.
48. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
49. P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
50. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
51. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
52. A. D. Becke, J. Chem. Phys., 1986, 85, 7184–7187.
53. J. Klimes, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
54. F. Eriksson, E. Fransson and P. Erhart, Adv. Theory Simul., 2019, 2, 1800184.
55. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
56. M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University Press, 1954.
57. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
58. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
59. R. Dronskowski and P. E. Blöchl, J. Chem. Phys., 1993, 97, 8617–8624.
60. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
61. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
62. S. Maintz, M. Esser and R. Dronskowski, Acta Phys. Pol., B, 2016, 47, 1165–1175.
63. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
64. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc02708f

---