Biocompatible NaLn(WO₄)₂ core–shell nanoplatelets for multimodal MRI contrast, NIR imaging, and high sensitivity infrared luminescent ratiometric thermometry

Abstract

Multifunctional nanoprobes combining magnetic resonance imaging (MRI) contrast as well as near infrared (NIR) imaging and thermometry are demonstrated by using quasi-bidimensional core–multishell nanostructures based on the scheelite-like NaLn(WO₄)₂ host (Ln = trivalent lanthanide). These nanostructures are composed of a NaHo(WO₄)₂ core, plus a first shell of Tm,Yb:NaGd(WO₄)₂, and a second shell of Nd,Yb:NaGd(WO₄)₂. Proton nuclear magnetic relaxation dispersion studies and MRI of water dispersions of nanoprobes, whose quasi-bidimensional geometries promote the interaction of Gd³⁺ with water protons, reveal behaviors evolving from a T₁-weighted MR contrast agent (CA) at 1.5 T to a highly effective T₂-weighted MR CA at ultrahigh magnetic fields of 7 T and above, and even a dual T₁/T₂-weighted CA at a clinical 3 T magnetic field. By NIR excitation (λ_EXC ∼ 803 nm) of Nd³⁺, luminescence-based thermometry was accomplished at wavelengths within the second biological transparency window (II-BW) through ratiometric analysis of ⁴F_3/2 → ⁴I_11/2 Nd³⁺ (λ = 1058 nm) and ²F_5/2 → ²F_7/2 Yb³⁺ (λ = 996 nm) emissions. Under a biologically safe excitation of 0.68 W cm⁻², a chemically stable 2 mg mL⁻¹ nanoprobe water dispersion presents absolute, S_A, and relative, S_R, thermal sensitivities as remarkable as S_A = 480 × 10⁻⁴ K⁻¹, and S_R = 0.89% K⁻¹ at 40 °C (313 K), and temperature resolution δ ≈ 0.1 K. Moreover, through efficient Nd³⁺ → Yb³⁺ → Tm³⁺ and Nd³⁺ → Yb³⁺ → Ho³⁺ energy transfers, NIR photoluminescence from Tm³⁺ at ∼1800 nm and Ho³⁺ at ∼2000 nm facilitates in depth imaging. The low nanoprobe cytotoxicity allows NIR biolabeling during cellular temperature measurement.

---

1. Introduction

A current direction in bioimaging utilizes hierarchically built nanostructures combining two or even more imaging modalities as exogenous nanoprobes. Among the imaging techniques now in use, photoluminescence (PL) imaging offers real-time precise subcellular and molecular information with high spatial resolution at the wavelength level, but accessible imaging is shallow, and the resolution degrades with the depth, being whole body imaging not possible. Therefore, clinical use of PL imaging is limited to a few applications such as image-guided surgery on tumors and retinal angiography.^1,2 On the other hand, MRI is currently one of the most powerful imaging technologies in both preclinical research and clinical diagnosis. MRI is able to report physiological and anatomical information with unlimited penetration depth and high soft tissue contrast. However, MRI has long been affected by low sensitivity owing to the mechanism of measuring the relaxation rates of water protons,^3,4 which leads to poor resolution,⁵ and thus the requirement for long scan times. Despite technical advances in recent years,^5,6 the low sensitivity of MRI remains a significant limitation on current clinical examinations. Although MRI has become a popular choice for monitoring magnetically labeled cells,^7,8 its low resolution at the cellular level⁹ has led to the combination with other imaging modalities. By exploiting the complementarity of both MR and PL imaging merged into a single nanoprobe, it will be possible to obtain more complete information from anatomical to molecular levels, required to understand disease mechanisms and drug action.

Conventional exogenous probes employed in PL imaging, such as organic dyes, fluorescent proteins, metal complexes and semiconductor quantum dots, among others, require excitation in the ultraviolet (UV) or blue-green visible spectral ranges.¹⁰ At these wavelengths, the low penetration of light in biological tissues due to either direct absorption by tissue constituents (water, blood, fat etc.) or light scattering by the non-continuous media (typically described by the Rayleigh law as I ∼ λ⁻⁴), seriously limit the potential of these probes for biosensing. Thus, schemes of both excitation and sensing shifted to the near infrared (NIR) are preferred to improve the depth for subcutaneous and in vitro PL-based sensing, simultaneously with reduction of photodamage and improved signal-to-noise ratio through prevention of tissue autofluorescence associated to UV/blue optical excitation.¹¹ These NIR–NIR operating schemes may also profit from the so-called ‘optical biological transparency windows’ (BW) present in biological tissues at defined NIR wavelength ranges, the first, I-BW λ = 700–950 nm, second, II-BW λ = 1000–1400 nm, third, III-BW λ = 1500–1850 nm, and fourth, IV-BW λ = 2100–2300 nm, where the light has lower attenuation.¹² I-BW and II-BW are particularly appropriate for PL-based subcutaneous sensing.¹³

Lanthanide (Ln)-based photoluminescent inorganic crystalline nanoparticles (NPs) are non-photoblinking and non-photobleachable, thus very suitable for long term repetitive PL-based bioimaging.^10,14 Other advantages of Ln-NPs in this field are their narrow emission bandwidths, which ease multiplexed imaging, and their high biocompatibility.^15,16 Among Lns, Nd³⁺ owns a favourable energy level distribution to operate within BWs. It can be pumped efficiently at λ_EXC ∼ 800 nm (I-BW) through the ⁴I_9/2 → ⁴F_5/2,²H_9/2 electronic transition, and monitored at different wavelengths, at λ_EMI ∼ 860–920 nm, ∼1050–1100 nm, ∼1300–1400 nm, and even at ∼2100–2200 nm, Fig. 1a. Under pumping also at λ_EXC ∼ 800 nm, Tm³⁺ allows access to the III-BW, at λ_EMI ∼ 1800 nm, through the ³F₄ → ³H₆ transition, Fig. 1b.

Fig. 1 Schemes of lanthanide energy levels with NIR excited photoluminescence emissions within the optical transparency windows for biological tissues, (a) Nd³⁺, (b) Tm³⁺, (c) Yb³⁺. Curved arrows indicate the energy gaps (×10³ cm⁻¹) between thermally coupled energy levels used for ratiometric thermal sensing.

Interestingly, thermal properties can be contactless tested at the nanometric scale by using also PL Ln-doped NPs,^17–22 being the ratiometric method based on the luminescence intensity ratio (LIR) change of two emissions the most commonly used for temperature sensing. In fact, the intensity changes of the different sub-bands observed for the Nd^{3+ 4}F_3/2 → ⁴I_9/2 transitions under λ_EXC ∼ 800 nm have been studied for thermometric purposes in several hosts, for instance, LaF₃,²³ YAG,²⁴ YVO₄,²⁵ or LiNdP₄O₁₂,^26,27 but the absolute and relative thermometric sensitivities obtained are low due to the small (≈100 cm⁻¹) energy gap between the two Stark sublevels (R₁ and R₂), of the Nd^{3+ 4}F_3/2 multiplet, see Fig. 1a. Larger thermometric sensitivities have been obtained by using the ⁴F_5/2/⁴F_3/2 Nd³⁺ PL intensity ratios, but in this case a more energetic excitation in the visible spectra (⁴I_9/2 → ⁴G_5/2 at λ ∼ 577 nm, i.e. outside the BWs), is required,^28,29 otherwise the overlap between excitation (resonant to ⁴F_5/2) and emission wavelengths increases the LIR noise to non-acceptable levels.

Yb³⁺ is an alternative for NIR excitation (λ_EXC = 930–980 nm), and monitoring (λ_EMI = 980–1050 nm) within the II-BW, based on ²F_7/2 ↔ ²F_5/2 electronic transitions, Fig. 1c. However, the spectrally broader nature of the Yb³⁺ luminescence, and again the small energy gap of the Stark sublevels inside of the excited multiplet impose low limits on the sensitivity and resolution of the thermometric determinations. A more promising thermometric approach is to use the electronic transfer between ⁴F_3/2 Nd³⁺ and ²F_5/2 Yb³⁺ quasi-resonant energy levels.^30–32 In the latter case, the results are greatly dependent on the distance between Nd³⁺ and Yb³⁺, i.e. the Nd³⁺ and Yb³⁺ concentrations.³³ The transfer efficiency is assisted by the absorption or emission of lattice phonons, thus the use of fluoride hosts with small cutoff phonon energy is no longer advantageous. In fact, scheelite-type tetragonal double tungstates NaT(WO₄)₂, T = Y, La, Gd, Lu (or isostructural molybdates), with cutoff phonon energy ħϖ ≈ 920 cm⁻¹, have shown much higher ratiometric sensitivity than the commonly used β-NaYF₄ fluorides for the Yb³⁺-sensitized Er³⁺ PL-based thermometry, even for sensing in the physiological temperature range.^34,35

Regarding MRI, a number of Gd³⁺-based chelates are currently used as T₁-weighted contrast agents (CA),^36–38 due to Gd³⁺ capability to shorten T₁ relaxation times of coordinated and/or nearby water protons, resulting in brighter (positive) contrast generation. On the other hand, NPs of superparamagnetic Fe-containing oxides mainly Fe₃O₄, but also CoFe₂O₄, MnFe₂O₄ and ZnFe₂O₄, are used to shorten T₂ relaxation times in the neighbouring regions, producing darker (negative) contrast in T₂-weighted MR images.^39–42 With the purpose of synergizing the contrast enhancement provided by T₁-weighted images, especially for dynamic contrast-enhanced MRI analyses⁴³ with the detailed morphological information obtained with T₂-weighted images, T₁/T₂ dual-mode CAs for MRI have been developed to yield complementary data, with the additional benefit of a single dose for both imaging modes. These CAs are mainly constructed by combining Gd³⁺-chelates as the bright T₁ CA, and superparamagnetic iron oxide NPs as T₂ CA, in a single nanoprobe.^44,45 However, since Gd³⁺-chelates have optimal performance below 1 T, and superparamagnetic iron oxide NPs saturate their magnetization at ∼1.5 T,^46,47 these dual T₁/T₂ CAs are no efficient in high magnetic field MRI instruments developed to gain higher signal-to-noise ratio, higher speed and higher resolution imaging.^5,6 On the other hand, mild adverse reactions associated to Gd³⁺ deposition, accumulation and retention on tissues and organs after Gd³⁺-chelates administration have been evidenced.⁴⁸ Alternatively, Gd³⁺-based crystalline NPs have demonstrated advantageous T₁-weighted imaging properties compared to small molecule Gd³⁺-chelates,⁴⁹ mostly because they contain a very high density of Gd³⁺ probing centers, thus providing higher T₁ relaxivity and good imaging contrast through lower doses, along with longer circulation times in blood. On the other hand, NPs incorporating Dy³⁺ and Ho³⁺, with high effective magnetic moments (μ_eff = 10.6 and 10.4μ_B, respectively) and short electronic relaxation times (around 0.5 ps), show improved capability to relax water protons when the strength of the external magnetic field increases, thus being suitable T₂ CAs even in high magnetic fields. In fact, some Dy³⁺ and Ho³⁺-containing fluoride and oxide NPs have been already proposed as high field T₂ MRI CAs.^50–55

Unfortunately, in Nd³⁺-sensitized (λ_EXC ∼ 800 nm) Ln-doped NPs, PL quenching occurs through efficient energy back-transfers from Lns to Nd³⁺, due to the closeness of these cations within NPs.^56–58 On the other hand, problems associated with a reduction of the expected contrasts in T₁/T₂ dual-mode CAs are unavoidable if the magnetic Lns of interest, Gd³⁺ for T₁, Ho³⁺ or Dy³⁺ for T₂, are integrated nearby into a single nanoprobe, since magnetic coupling between T₁ and T₂ effects will appear.⁵⁹ The proper separation of optically active Lns in rationally designed core–shell nanostructures, in which Yb³⁺ is also incorporated, is a successful strategy to optimize the Ln PL brightness through the prevention of energy back-transfers to Nd³⁺.^56–58 In these core–shells, Yb³⁺ acts as an efficient energy mediator to facilitate energy transfers from the sensitizer Nd³⁺, lying in the outer shell, to the other Lns. Moreover, core–shell nanostructures offer the possibility of achieving magnetically decoupled T₁/T₂ dual mode contrasts in a single nanoprobe, by separating effects of T₂, Ho³⁺ or Dy³⁺ at the core, and T₁, Gd³⁺ at the shell in contact with water.⁶⁰

To address the challenge of developing multifunctional nanoprobes combining MRI contrast, as well as NIR–NIR PL-related imaging and high sensitivity contactless ratiometric thermometry, herein we present the design, preparation and evaluation of a series of materials from single ultra-small Ln-containing NPs to multilayer core–shell nanostructures, built on double tungstates NaLn(WO₄)₂ with the tetragonal scheelite-like structure.⁶¹ The choice of this double tungstate crystalline phase over commonly studied fluorides^56–58 is based on multiple factors, some of which have already been highlighted in previous studies,^34,35 namely the possibility of preparing individualized NPs with ultra-small sizes, even below 10 nm, without the appearance of competitive phases, its high PL efficiency, which is considerably better retained with respect to the bulk material, and the aforementioned superior thermometric sensitivity. Concerning MRI requirements, the main factor favouring longitudinal relaxivity r₁ is the easy access of water molecules to Gd³⁺ centers at the NPs surface; thus, morphologies with the highest surface-to-volume ratio possible must be sought because they will allow higher r₁ values. From this point of view, the planar, quasi-bidimensional diamond-shaped morphology shown by NPs of NaLn(WO₄)₂ will be better suited to provide high r₁ values than 3D NPs of fluorides, either hexagonal β-NaYF₄ or tetragonal LiYF₄ phases.

The Fig. 2 displays the schematic representation of the nanoprobe system proposed in this study.

Fig. 2 Architecture of the proposed series of planar diamond-shaped nanoparticles and successive core–shell nanostructures based on the scheelite-like double tungstate NaLn(WO₄)₂ host, showing the distribution of incorporated lanthanides.

By choosing Ho³⁺ to provide T₂-MRI contrast, single NaHo(WO₄)₂ NPs will constitute the core, C, of the multi-layered system. The first nanostructure, C@1S, is prepared by using NaHo(WO₄)₂ NPs as seeds, which are coated with a Tm³⁺,Yb³⁺-doped NaGd(WO₄)₂ shell (1S). C@1S is suitable for additional generation of T₁-MRI contrast due to surface–lying Gd³⁺ centers. The confinement of Ho³⁺ and Gd³⁺ in the core and the first shell, respectively, should help weaken the magnetic interaction between T₁ and T₂ CAs, thus avoiding contrast quenching. C@1S were the seeds for the second nanostructure C@1S@2S, resulting from the coating with a Nd³⁺,Yb³⁺-doped NaGd(WO₄)₂ second shell (2S), which in turn will provide the thermometric function. Further, the presence of Yb³⁺ in both the 2S and 1S shells allows the excitation of Tm³⁺ and Ho³⁺ through efficient Nd³⁺ → Yb³⁺ → Tm³⁺ and Nd³⁺ → Yb³⁺ → Ho³⁺ energy transfers, giving rise to NIR PL emissions from Tm³⁺ at ∼1800 nm (within the III-BW, ³F₄ → ³H₆ transition)⁶² and Ho³⁺ at ∼2000 nm (⁵I₇ → ⁵I₈ transition),^63,64 of interest for high penetration NIR optical imaging purposes. The spatial separation between surface-lying Nd³⁺ and Tm³⁺ or Ho³⁺cations minimizes energy back-transfers to Nd³⁺, and thus avoids the quenching of their emissions, even at the high Nd³⁺ doping levels in the nanoprobe. Moreover, the 2S layer is protected from its degradation in diluted water dispersions by further growth of an isostructural optically inert NaGd(WO₄)₂ outermost layer to produce C@1S@2S@i3S, which avoids the quenching of Nd³⁺ and Yb³⁺ PL emissions to be used for LIR thermometry.

TWEEN80, a safe food additive for human consumption,⁶⁵ has been used as surfactant in the procedure to render luminescent double tungstate NPs and core–shell nanostructures dispersible in water. MRI contrast and PL-based thermometric sensing characteristics in proposed nanoprobes were optimized through the evaluation and control of the concentration of incorporated Lns. MRI experiments were performed at 1.5, 3, 7 and 11.7 T by using water-stabilized dispersions of the nanoprobes to determine their behaviours as CAs from clinical up to research magnetic fields. PL spectra of these diluted dispersions were excited under low laser power density, typically 0.68–2.5 W cm⁻², and used for LIR-based thermometry at temperatures within the range of physiological interest. Furthermore, to ascertain the safe use of developed multifunctional nanoprobes for biomedical applications, such as diagnostic imaging and NIR biolabeling during cellular temperature measurement, their metabolic interactions with pre-osteoblastic MC3T3 healthy cells and HeLa human cancer cells have been analyzed in vitro through viability, cytotoxicity and nuclear visualization by DAPI (4′,6-diamidino-2-phenylindole) staining assays.

2. Experimental section

2.1 Chemicals

Lanthanide acetate hydrates (LnAc) Ho(CH₃CO₂)₃·4H₂O (Alfa Aesar, 99.9%), Yb(CH₃CO₂)₃·xH₂O (Sigma-Aldrich 99.95%), Tm(CH₃CO₂)₃·4H₂O (Alfa Aesar, 99.9%), Gd(CH₃CO₂)₃·4H₂O (Strem Chemicals, 99.9%) and Nd(CH₃CO₂)₃·4H₂O, (Strem Chemicals, 99.9%), tungsten hexacarbonyl W(CO)₆ (Acros Organics, 99%) and NaOH were used as reagents in a mixture of oleic acid (OA) (Aldrich, technical grade 90%), 1-octadecene (ODE) (Alfa Aesar, technical grade 90%) and oleylamine (OLE) (Sigma Aldrich, 98%) solvents.

To extract and purify the prepared NPs, n-hexane (LabKem, 99%+) and absolute ethanol (EssentQ, Scharlau) were used. TWEEN 80 (Sigma-Aldrich) and CHCl₃ (Merck, Emprove Essential 99%) were used to transform the oleate-capped hydrophobic prepared nanomaterials into water dispersible ones.

Dulbecco's modified Eagle's medium (DMEM), anti–anti (penicillin–streptomycin), trypsin–EDTA medium, fetal bovine serum (FBS), 4′,6-diamidino-2-phenylindole (DAPI), AlamarBlue®, and CyQUANT™ LDH Cytotoxicity Assay Kit (Thermo Fisher Scientific, Cat. No. C20300) were used in nuclear stain, viability, and cytotoxicity assays of MC3T3 and HeLa cells.

2.2 Prepared nanomaterials

Core NPs, C, with composition NaHo(WO₄)₂, were prepared by coprecipitation synthesis in organic solvents with high boiling points, according to a protocol based on previously described methods,^21,22 which have been adapted to the present case as described below. Shells 1S, 2S and i3S with the following selected compositions:

1S ≡ 8 at% Tm,15 at% Yb:NaGd(WO₄)₂

2S ≡ x at% Nd,20 at% Yb:NaGd(WO₄)₂, x = 20, 30

i3S ≡ NaGd(WO₄)₂

were successively grown over C by seed-mediated processes through similar coprecipitation syntheses, see later. Further, C@1S-b and C@1S-b@2S-b nanostructures were prepared with 1S-b and 2S-b shells with the same compositions than in C@1S and C@1S@2S, respectively but with different thicknesses, that is, while 1S-b was achieved after two consecutive reactions to growth 1S over C, the growth of 2S-b was carried out with a lesser volume of the involved shell precursor, see below.

2.2.1 Synthesis and purification of NaHo(WO₄)₂ NPs (core C). For preparing 1 mmol of NaHo(WO₄)₂ NPs, 5 mL of a previously prepared 0.2 M HoAc solucion in water, 25 mL ODE, 16 mL OA and 16 mL OLE were mixed in a three neck flask and heated at 150 °C (423 K) for 2 h with gentle stirring under N₂ flow at a Schlenk line. Then, after reducing the temperature to 50 °C (323 K), 0.75 mL of 2 M NaOH and 704 mg of W(CO)₆ were added to the above Ho-oleate transparent yellow solution, and the mixture was kept at this temperature for 2 h, with vigorous magnetic stirring under inert N₂ atmosphere, to dissolve W(CO)₆ and achieving complete nucleation of NPs without oxidation of OA. The solution was degassed under vacuum by heating up to 100 °C (373 K) for 15 min, and then the temperature was raised to 295 °C (568 K) at a heating rate of 20 °C min⁻¹ and kept at this temperature during 1½ h with gentle stirring, under reflux and nitrogen flow. The solution is getting darker when the temperature increased, acquiring a deep, dark red color at ∼260 °C (∼533 K), but it becames again light yellow at ∼290 °C (∼563 K). The appearance of the red colour is important, and in fact, the expected scheelite-like NPs are not properly synthesized when this colour was not observed. Finally, the solution was cooled down, and the nanocrystals were collected by centrifugation and washed with a mixture of ethanol and n-hexane in a ratio of 4 : 1 for two times. The result is a yellowish-colored pellet, which can be easily resuspended in n-hexane, yielding a transparent yellow dispersion.

2.2.2 Synthesis and purification of NaHo(WO₄)₂@8 at% Tm:15 at% Yb:NaGd(WO₄)₂ (C@1S). For the preparation of 0.4 mmol of C@1S, 1.54 mL of GdAc, 300 μL of YbAc and 160 μL of TmAc from corresponding 0.2 M solutions in water were firstly mixed in a three-neck flask with 12 mL ODE and 8 mL OA. This solution was heated at 150 °C (423 K) with gentle stirring for 2 h under N₂ flow at the Schlenk line. After cooling down to 50 °C (323 K), 0.3 mL of NaOH 2 M and 281 mg of W(CO)₆ were added to the flask, and this 1S-precursor solution was kept at this temperature for 2 h under strong stirring and N₂ flow. In a different flask, we mixed ∼0.4 mmol of previously prepared C NPs dispersed in n-hexane with 12 mL ODE, 8 mL OA and 8 mL OLE. The two flasks were heated to 100 °C (373 K) under vacuum for 15 minutes or until they are both transparent. Then the temperature of the core solution flask was raised at 295 °C (568 K) at a rate of 20 °C min⁻¹, with gentle stirring, under N₂ flow. When this latter solution reached about 260 °C (533 K), the 1S-precursor mixture was poured into it very slowly, and the resulting solution kept at 295 °C (568 K) during 1½ h. In the reaction leading to the growth of 1S over the core NPs there is no change in the colour of the solution, which maintains a transparent very pale yellow colour. The extraction and purification method was the same as for core NPs, and resulting C@1S NPs were redispersed in n-hexane.

For the preparation of C@1S-b, the described procedure with the 1S-precursor was repeated twice.

NaHo(WO₄)₂@8 at% Tm:15 at% Yb:NaGd(WO₄)₂@20 at% Nd (30 at% Nd):20 at% Yb:NaGd(WO₄)₂ (C@1S@2S), as well as the nanostructure with a further NaGd(WO₄)₂ shell (C@1S@2S@i3S), were prepared following procedures similar to the described above, and all details are included in the ESI.†

2.2.3 Water dispersion of colloidal nanomaterials by ligand-exchange reactions with TWEEN80. To transform the hydrophobic oleate-capped prepared NPs and nanostructures to hydrophilic ones, their surfaces were modified with TWEEN80, a biocompatible surfactant and emulsifier. In a typical process, for each mg of single or core–shell NPs dispersed in n-hexane we used 20 μL of TWEEN80 and 0.2 mL of chloroform CHCl₃, and the closed flask was stirred for 1 h at room temperature. Then 0.3 mL of deionized miliQ water for each miligram of NPs were poured into the flask, and the dispersion was kept under stirring for 3 h in a 70 °C (343 K) water bath. During this time, we left the flask open, the CHCl₃ was evaporated and the NPs were gradually transferred into the hydrophilic system. Some mL of water can be eventually added to prevent the dispersion from drying out. The mixture was centrifuged to remove the excess of TWEEN80, and the obtained pellet was resuspended in a volume of water to yield a NPs concentration of 5 mg mL⁻¹.

This ligand exchange procedure can be also carry out with TWEEN40, but to prevent aggregation of the current ultrasmall NPs, the bigger TWEEN80 ligands were preferred.

2.3 Characterization of nanomaterials: phase, size, morphology and concentration of lanthanides

The phase purity of all synthesized materials, NPs, core–shell nanostructures and polycrystalline solid-state prepared samples, was tested by room temperature powder X-ray diffraction (XRD) analysis performed in a Bruker AXS D-8 advance diffractometer, using Cu K_α radiation. To identify the crystalline phase, the angular range scanned was 2θ = 10–65 deg, with a step size Δ2θ = 0.05 deg and an integration time of 3 s at each step.

The morphology of prepared nanomaterials was studied by transmission electron microscopy using JEOL JEM1010 and JEM3000F microscopes. To obtain evidence of the formation of core–shell designs from described syntheses, concentration profiles of Lns were obtained by combined scanning transmission electron microscopy (STEM) and energy dispersive X-ray spectroscopy (EDX) analyses along a line in individual NPs of the largest nanostructure, C@1S@2S@i3S. For this, a JEOL JEM Arm200cF microscope operated at 200 kV, with corrected spherical aberration in the condensed lens and equipped with an X-EDS Oxford X-MaxN 100 TLE detector with active area of at least 50 mm² and resolution of 129 eV, was used. The thickness of single NPs was measured with a Bruker Multimode AFM Nanoscope III A in contact mode on a mica substrate, and evaluated with the Bruker NanoScope Analysis software.

Hydrodynamic sizes and size distributions of NPs in hexane, as the long-lasting storage medium of prepared oleate-capped NPs and nanostrosctures, and in water dispersions after surface modification with TWEEN80, which were used in proton nuclear magnetic relaxation dispersion studies and MRI analyses as well as in PL NIR nanothermometry, were evaluated overtime by dynamic light scattering (DLS) measurements with a Cordouan Technologies particle size analyzer, model Vasco 2, powered by the NanoQ proprietary software.

Magnetic properties were characterized using a SQUID magnetometer (MPMS-3) from quantum design. 80 to 160 μL of sample solutions were dried inside SQUID capsules with cotton. The magnetization of prepared nanomaterials as a function of the applied magnetic field was measured at 300 K under fields up to ±7 T.

The concentration of Lns in water dispersions was measured by inductively coupled plasma optical emission spectroscopy (ICP-OES) with a PerkinElmer Optima 2100 ICP equipment, after digestion of the samples in HNO₃ and dilution with doubly distilled water.

2.4 Photoluminescence measurements

Down-shifted near infrared (NIR) PL (λ_EMI > 900 nm) was excited with a tunable Ti-sapphire Spectra Physics laser model 3900S. The PL emission was dispersed with a SPEX f = 34 cm spectrometer and detected either with a 77 K cooled Applied Detector Corporation Ge photodiode model 403R with spectral response in the λ = 850 to 1650 nm range or with a 77 K cooled Hamamatsu InAs photovoltaic detector model P7163, with spectral response in the λ = 1500 to 3500 nm range. Optical excitation was modulated with a chopper and the detector signal evaluated in phase with a lockin amplifier.

In all cases, the optical excitation density was kept at low levels (I_EXC = 0.68 W cm⁻² for NPs dispersed in water or I_EXC ≤ 2.5 W cm⁻² for n-hexane dispersions) in order to avoid the heating of samples. Proper optical filters were used to avoid optical harmonics and other undesired light contributions. All spectra were corrected by the instrumental responses. For every measured combination of sample/concentration/temperature at least three acquisitions were performed in order to estimate the measurement error.

Liquid colloidal samples were hold in a 10 × 10 × 50 mm³ glass cuvette, and heated with hot water generated by a Lauda bath model RE-420 with temperature resolution of 0.01 °C. The actual temperature of the dispersion was monitored with a K-type thermocouple immersed in the liquid with a reading accuracy of 0.1 °C. Powdered solid samples were set on the horizontal surface of an Instec hot plate (with nominal resolution of 0.01 °C) and the actual temperature was monitored by a K-type thermocouple buried in the powder with a reading accuracy of 0.1 °C. The emission was collected by a parabolic mirror, and sent to the SPEX monochromator through a two lenses optical system.

2.5 In vitro cellular assays

2.5.1 Viability assays of HeLa and MC3T3 cells exposed to NPs. To assess cell viability in vitro, HeLa (human cervical cancer cell line) and MC3T3 (cell line derived from mice calvarial pre-osteoblasts) cells were seeded into 24-well plates at a density of 20 000 cells and 50 000 cells per well, respectively. The cells were incubated at 37 °C (310 K) in a humidified atmosphere of 5% CO₂ and 95% humidity, using Dulbecco's modified Eagle medium (DMEM) supplemented with appropriate growth factors, antibiotics and glutamine. The cells were allowed to adhere overnight under these controlled conditions. Following this incubation period, the cells were treated with increasing concentrations of C@1S@2S@i3S in the water dispersion, up to 200 μg mL⁻¹, for 24 h. Before the viability assay, both NPs-exposed and control (untreated) cells were washed twice with phosphate-buffered saline (PBS) to remove non-internalized NPs.

Cell viability was quantified using the AlamarBlue® (resazurin-based reagent) assay, a sensitive and non-toxic method suitable for assessing cell metabolism. The AlamarBlue® reagent was added to a 10% working solution in DMEM, and the cells were incubated for 30 minutes at 37 °C (310 K). The principle behind this assay is based on the reduction of the AlamarBlue® reagent by NADH/H⁺ produced by metabolically active, viable cells. The reduced form of the reagent (resorufin) regains aromaticity, and emits very bright orange fluorescence, which can be measured as a direct indicator of cell viability. Thus, after the incubation period, the medium containing the AlamarBlue® reagent was carefully removed, and using a plate reader set, the fluorescence at 590 nm was measured by excitation at 560 nm. The fluorescence intensity correlates directly with the number of viable cells in the sample, providing quantitative data on cell viability. This assay allows for the determination of cell viability without interference from the NPs themselves, ensuring accurate results.

The percentage of viable cells was calculated by normalizing the fluorescence values from treated samples to those of controls, with data presented as the mean ± standard deviation from four independent experiments (N = 4).

2.5.2 Cytotoxicity assays by LDH release of HeLa and MC3T3 cells exposed to NPs. Cytotoxicity was assessed using the CyQUANT™ lactate dehydrogenase (LDH) Assay Kit of Thermo Fisher Scientific, following the manufacturer's instructions. Firstly, the optimized cell density for measurements was calculated for both cell lines. For this, cells were seeded in 96-well plates within the range of 0–1 × 10⁵ cells per well (100 μL) and incubated overnight at 37 °C (310 K) in a humidified atmosphere containing 5% CO₂. For calculating the maximum LDH release, i.e., the maximum cell death that can be measured for each density, 10 μL of lysis buffer was added for three samples at each cellular density. On the other hand, for calculating the spontaneous LDH release of each line, i.e., the minimum of cell death for each cell density, 10 μL of water was added to three samples for each cellular density. After that, all samples were incubated for 45 minutes with 50 μL of the reaction mixture. The plates were kept at room temperature for 30 minutes, and then 50 μL of stop solution was added to the samples. Finally, all plates were measured, and results indicated that the optimized concentration of cells are 5 × 10⁴ cells per well for HeLa cells and 1 × 10⁵ cells per well for MC3T3 cells. In the second step, cells at the optimized cell density for each line were treated with various concentrations of TWEEN80-modified C@1S@2S@i3S water dispersions and incubated for 24 hours (from 0 to 135 μg mL⁻¹). To quantify LDH release, 50 μL of cell culture supernatant was transferred to a new flat-bottom 96-well plate. Subsequently, 50 μL of freshly prepared reaction mixture was added to each well, and plates were incubated for 30 minutes at room temperature, protected from light. Then, the reaction was stopped by adding 50 μL of stop solution per well. Absorbance was measured at λ = 490 nm with a reference wavelength of λ = 680 nm using a TECAN microplate reader. Spontaneous and maximum LDH release controls were included in the assay. The percentage of cytotoxicity was calculated using following the equation: % cytotoxicity = [(experimental − spontaneous)/(maximum − spontaneous)] × 100.

2.5.3 DAPI staining for nuclear visualization. This staining procedure allows for the clear visualization of nuclei, enabling the assessment of cell morphology and nuclear integrity. For nuclear visualization using DAPI, HeLa and MC3T3 cells were prepared in a 24-well plate following the same procedure as in the viability assay. Finalizing the 24 h incubation with C@1S@2S@i3S NPs, the medium was carefully aspirated, and the cells were rinsed twice with PBS to remove any residual medium or non-internalized NPs. The cells were then fixed by adding cold 70% ethanol, followed by incubation at −20 °C (253 K) for 10 min to ensure adequate fixation and preservation of cell morphology. After fixation, the cells were washed 2–3 times with PBS to remove ethanol. Subsequently, the cells were stained with a DAPI solution (1 μg mL⁻¹ in PBS) for 5–10 min at room temperature, protected from light to avoid photobleaching. DAPI specifically binds to the adenine–thymine-rich regions of DNA in the nucleus, resulting in bright blue fluorescence at around λ = 461 nm when excited with a wavelength of λ ∼ 358 nm. After staining, excess DAPI was washed off with PBS, and the cells were imaged by using a fluorescence microscope equipped with a DAPI filter set.

2.6 Relaxivity measurements and MRI imaging

Relaxivities of the different compounds in dispersion at different concentrations (solvent: water HPLC Gradient grade, Fischer Scienctific) were measured at magnetic fields B of: (a) 1.5 T, at 37 °C (310 K), using a benchtop relaxometer Bruker Minispec MQ60 (Bruker Biospin GmbH, Ettlingen, Germany). T₁ relaxation time was measured using an inversion recovery sequence (TR = 0.01–10.000 ms, recycle delay = 2 s, number of scans = 4, TE = 0.05 ms, points for fitting = 20). T₂ relaxation time was measured using the Carr–Purcell–Meiboom–Gill sequence (TR = 10.000 ms, recycle delay = 2 s, number of scans = 8, TE = 0.05 ms, points for fitting = 30.000). Relaxivities r₁ and r₂ were calculated using the least squares curve fitting of R₁ = 1/T₁ and R₂ = 1/T₂ relaxation rates (s⁻¹) versus iron concentration (mmol L⁻¹); (b) B = 7 T, at room temperature, using a horizontal bore Bruker Biospec USR 70/30 MRI system (Bruker Biospin GmbH, Ettlingen, Germany), interfaced to an AVANCE III console, and with a BGA12-S imaging gradient insert (maximal gradient strength 400 mT m⁻¹, switchable within 80 μs), and a 40 mm inner diameter volume coil from Bruker, for RF transmission and reception. For T₁ maps imaging of the phantoms the following parameters were adopted: spin echo saturation recovery using a variable repetition time Bruker's RAREVTR method. Images were acquired at 9 different TR values of 150, 400, 750, 1100, 1500, 2000, 3000, 5000 and 10 000 ms, TE = 8.2 ms, RARE factor 1. For T₂ maps imaging of the phantoms the following parameters were adopted: Bruker's MSME (multi slice spin echo) sequence. The TE values were varied in 64 steps of 5 ms, ranging from 5 ms to 320 ms, and TR 4.8 s; (c) B = 11.7 T, at room temperature, using a horizontal bore Bruker Biospec USR 117/16 MRI system (Bruker Biospin GmbH, Ettlingen, Germany), interfaced to an AVANCE III console, and with a BGA12-S imaging gradient insert (maximal gradient strength 600 mT m⁻¹, switchable within 80 μs), and a 40 mm inner diameter volume coil from Bruker, for RF transmission and reception. For T₁ maps imaging of the phantoms the following parameters were adopted: spin echo saturation recovery using a variable repetition time Bruker's RAREVTR method. Images were acquired at 9 different TR values of 150, 500, 1000, 1500, 2000, 3000, 5000, 8000 and 14 000 ms, TE 5.7 ms, RARE factor 1. For T₂ maps imaging of the phantoms the following parameters were adopted: Bruker's MSME sequence was used. The TE values were varied in 64 steps of 5 ms ranging from 5 ms to 320 ms, and TR 4.8 s.

All the above data were acquired with 3 averages, 280 × 280 points and a field of view of 2.8 cm × 2.8 cm, 3 slices with a slice thickness of 1.0 mm and 1 mm gap between slices. The images were fitted into Levenberg–Margardt method to calculate T₁ and T₂ values using Bruker's Paravision 6.0.1 software.

T₁ and T₂ parametric maps at 3.0 T were acquired in a horizontal bore MR Solutions Benchtop scanner equipped with 48 G cm⁻¹ actively shielded gradients with a 56 mm diameter quadrature bird-cage coil in transmit/receive mode, using MPRAGE (magnetization prepared rapid gradient echo imaging) and MEMS (multi-echo multi-slice) sequences, respectively. Images were acquired with an image matrix of 256 × 252 and FOV of 60 × 60 mm. The following parameters were used for the MEMS sequences: NE = 10 (TE = 0.015, 0.03, 0.045, 0.06, 0.075, 0.09, 0.105, 0.12, 0.135, and 0.15 s), TR = 1400 ms. For the MPRAGE sequences, the parameters were as follows: TI = 11 values (0.275, 0.3, 0.35, 0.45, 0.65, 1.05, 1.85, 3.45, 6.65, 12.45, 26.25 s), TE = 5 ms, TR = 10 s. Image analysis was performed using ImageJ software (https://imagej.nih.gov/ij) and the “MRI analysis calculator” plugin by Karl Schmidt.

3. Results and discussion

3.1 Characterization of nanoparticles and core–shell nanostructures

XRD patterns of C, C@1S, C@1S@2S and C@1S@2S@i3S confirm that they correspond to the tetragonal space group I4̄ scheelite-like crystal phase described for the isostructural NaGd(WO₄)₂ single crystal,⁶¹ with no foreign peaks, see Fig. S1a, b, c and d, respectively, in ESI.† The values of their mean crystalline domain sizes calculated by the Scherrer's equation, d_s, evolved as ∼7 nm, ∼10 nm ∼12 nm and ∼17 nm for C, C@1S, C@1S@2S and C@1S@2S@i3S, respectively, in accordance with the corresponding continuous decrease observed in the width of the Bragg reflections.

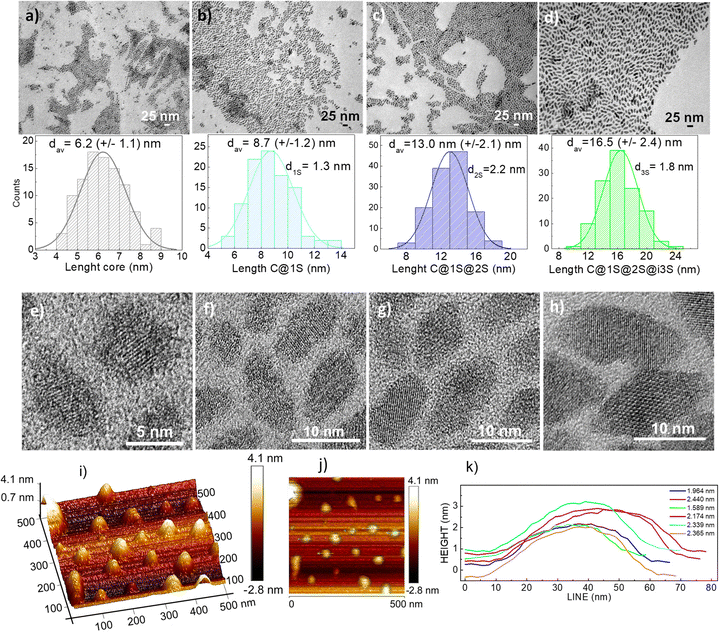
Fig. 3a–d show a panel of representative transmission electron microscopy (TEM) images of these NPs, with statistical histograms for size distribution, and corresponding high magnification images (HRTEM) in Fig. 3e–h reveal their well-defined crystalline characteristics. Diamond-like shape is observed in all cases, with diagonal sizes of ∼6.2 × 4 nm, ∼8.7 × 5 nm, ∼13.0 × 7, and ∼16.5 × 8 nm for C, C@1S, C@1S@2S and C@1S@2S@i3S, respectively, and this size increase would suggest successful growth of 1S, 2S and i3S coating layers, with ∼1.2 nm, ∼2.1 nm and ∼1.7 nm, respectively. These NPs are mostly individualized, highly monodisperse in size, and very thin, see atomic force microscopy (AFM) images for C@1S@2S NPs presented in Fig. 3i and j, whose evaluation indicates thicknesses ranging between 1.6 and 2.5 nm, see Fig. 3k.

Fig. 3 Morphological characteristics of scheelite-like double tungstate-based nanoprobes. TEM images of (a) C, (b) C@1S, (c) C@1S@2S, and (d) C@1S@2S@i3S NPs, with corresponding histograms for nanodiamond largest diagonal size distribution. High-resolution TEM images of (e) C, (f) C@1S, (g) C@1S@2S, and (h) C@1S@2S@i3S NPs. AFM images, (i) and (j), and height profiles, (k), of C@1S@2S NPs.

Qualitative high-angle annular dark field HAADF-STEM images of prepared nanostructures did not provide a complete evidence of contrast differences between the core and shell(s), Fig. 4a shows a typical HAADF image for C@1S. In fact, this was expected since the contrast depends on the atomic number Z, which is very close for Lns distributed in current nanostructures, and the reduced thickness may also minimize the contrast. Therefore, to ascertain the formation of proposed core–shell structures, concentration profiles of Lns in the largest nanostructure, C@1S@2S@i3S, were obtained by STEM-EDX analyses along a line in individual NPs of such material, see Fig. 4b. As it can be seen, the Ho³⁺ ions are well-localized at the central part of the profile, indicating their sole presence at the core. On the other hand, the presence of Gd³⁺ ions has been found to be maximum at the edges of its profile, in accordance with the existence of a stoichiometric Gd³⁺ (i3S) external shell, although the EDX scan indicated also some extended presence to the interior as due to Gd³⁺-containing 2S and 1S shells. The Nd³⁺ profile shows also maxima near the edges, but somewhat displaced to the interior, as expected from Nd³⁺ presence as the major Ln component in 2S. For simplicity, we chose to exclude in this figure the concentration profiles of Yb³⁺, present in 1S (15 at%) and 2S (20 at%), and of Tm³⁺, with very weak concentration (8 at%) in the inner 1S, for better focusing in the characterization of the overall nanostructure.

Fig. 4 (a) HAADF image of NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂ (C@1S); (b) EDX line scan across a single nanoparticle of NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)@30 at% Nd, 20 at% Yb:NaGd(WO₄)₂@NaGd(WO₄)₂ (C@1S@2S@i3S).

Results of the measurement of each Ln concentration in water dispersions of TWEEN80-modified C, C@1S and C@1S@2S NPs by using inductively coupled plasma optical emission spectroscopy (ICP-OES) are included in Table S1 (ESI†). Corresponding Ln concentrations for C@1S-b and C@1S@2S appear in Table S2 (ESI†). These data indicate that detected amounts of Tm³⁺ and Yb³⁺ are lower than expected according to proposed stoichiometries for the syntheses. Table S3 (ESI†) provides the comparison of relationships of interest between the concentrations of Ho, Gd and Nd in the studied nanoprobes.

Mean hydrodynamic sizes, d_DLS, of C, C@1S, C@1S@2S and C@1S@2S@i3S and their size distributions in hexane, the storage medium, and in the water dispersions after surface modification with TWEEN80, used in current MRI and nanothermometry studies, were assessed by overtime DLS measurements, and results can be viewed in Fig. S2–S5 (ESI†). The d_DLS values in hexane are well preserved even 18 months after synthesis, and those in water dispersions, ∼20 nm for C, ∼24 nm for C@1S, ∼29 nm for C@1S@2S, and ∼79 nm for C@1S@2S@i3S, are similar for freshly prepared samples and after five weeks of storage, having polydispersity index (PDI) values typically in the 0.12–0.20 range, indicating that they are satisfactorily water dispersible. It must be taken into account that the morphology of current NPs is not spherical but elongated, with higher aspect ratio when the number of shells increase, and d_DLS results reflect this fact for the very thin C@1S@2S@i3S, whose diffusion will be further hindered, leading to an overestimation of size by DLS.

3.2 Magnetic field dependent MRI contrast properties

To quantitatively evaluate the feasibility of C, C@1S and C@1S@2S nanocrystalline materials as MRI contrast agents (CAs), their longitudinal (r₁) and transverse (r₂) relaxivity values were determined through T₁- and T₂-weighted image acquisitions by using water dispersions of the above nanomaterials. Measurements at current clinical (1.5 T and 3 T) as well as at research (7 T and 11.7 T) magnetic fields have been carried out. Relaxivity values r₁ and r₂ of proposed nanoprobes are calculated by plotting relaxation rates R₁ or R₂ (corresponding to the inverse of the T₁ or T₂ relaxation times) versus the concentration of the Ln responsible for the change in the relaxation. Plots to calculate r₁ and r₂ values at 1.5 T, 7 T and 11.7 T appear in Fig. S6, S7 and S8, respectively, and in Fig. S9 for data at 3 T (ESI†).

The r₁ value of NPs containing Lns other than Gd³⁺ is usually very small when no direct coordination of the Ln to water molecules occurs, and especially at magnetic fields higher than 1 T,⁶⁶ therefore we calculate r₁ values from the concentration of Gd³⁺ in C@1S and C@1S@2S nanostructures. On the other hand, the effect of Gd³⁺ on the r₂ relaxivity of water protons is negligible, being the high anisotropy of the ⁵I₈ ground state of Ho³⁺, and hence the very short relaxation times τ_R of Ho-containing materials, along with its high magnetic moment (10.6μ_B), the main factors leading to an important Curie-spin contribution to the r₂ relaxivity of water protons,⁶⁷ and this effect will increase considerably for ultra-high magnetic fields. Thus, r₂ will be determined from corresponding Ho³⁺ concentrations in the water dispersions of C, C@1S and C@1S@2S. Table 1 shows the r₁, r₂ relaxivity values of water protons caused by C, C@1S and C@1S@2S, and corresponding r₂/r₁ ratios.

Table 1 Longitudinal (r₁) and transverse (r₂) relaxivities (mM⁻¹ s⁻¹), and r₂/r₁ ratios shown by water dispersed NaHo(WO₄)₂ (C), NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂ (C@1S) and NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂@20 at% Nd, 20 at% Yb:NaGd(WO₄)₂ (C@1S@2S) at 1.5 T, 7 T and 11.7 T magnetic fields

	1.5 T			7 T			11.7 T
	r1	r2	r2/r1	r1	r2	r2/r1	r1	r2	r2/r1
	[Gd^3+]	[Ho^3+]		[Gd^3+]	[Ho^3+]		[Gd^3+]	[Ho^3+]
C	—	12.1	—	—	70.5	—	—	84.4	—
C@1S	7.4	13.4	1.8	1.8	155.5	86	1.1	182.7	171
C@1S@2S	6.0	35.8	6.0	0.6	112.8	179	0.6	194.0	353

---

From these values, it is clear that r₁ of C@1S and C@1S@2S are lower than their r₂ at any magnetic field, and that for each material r₁ tends to decrease when the magnetic field increases. On the contrary, the r₂ values show a steady increase with the magnetic field in all cases, and reach maxima of 182.7 and 194.0 mM⁻¹ s⁻¹, for C@1S and C@1S@2S respectively, at 11.7 T. These magnetic field-related evolutions constitute the classical behavior that can be expected for MRI CAs.^68,69

The generation of T₁ contrast is produced by the coupling of the electron spins of the surface lying Gd³⁺ and the nuclear spins of protons of the water in contact. In the current system, r₁ is greater for C@1S than for C@1S@2S, at any field. This fact is, in principle, surprising since: (i) per NP, C@1S@2S offers higher availability of Gd³⁺ centers at the water contact surface; (ii) the ratio between Gd³⁺ and Ho³⁺ concentrations is considerably higher in C@1S@2S (1 : 0.53) than in C@1S (1 : 1.18), see Table S2 (ESI†); (iii) the estimated distances between Ho³⁺ centers at the core and the Gd³⁺ ones in contact with water are also higher in C@1S@2S than in C@1S (the coating thickness of 1S + 2S layers being ∼3.3 nm, compared to ∼1.2 nm coating thickness of 1S), thus (ii) and (iii) suggest that the perturbation caused by the magnetic field of Ho³⁺ would be lessened for C@1S@2S with respect to C@1S. The observed lower r₁ value in the water dispersion of C@1S@2S compared to that of C@1S can be attributed to the additional disturbance that the magnetic field generated by Nd³⁺ centers exerts on the coupling between the spins of neigbouring 2S-Gd³⁺ and the water protons.⁷⁰ This effect, therefore, depends on the number of Nd³⁺ centers, which is related to both the stoichiometry of Nd³⁺ in the 2S layer and the thickness of the layer. An alternative interpretation of the data is supported by considering the surface mechanism of T₁ contrast generation at the macroscopic sample level rather than by individual NP surface area. In this scenario, at equivalent Gd³⁺ concentration, the total surface would be larger for the smaller NPs, C@1S, because the number of these NPs would be larger than that of C@1S@2S. Thus, the reduction of the total available surface in C@1S@2S, combined with the partial substitution of Gd³⁺ by Nd³⁺ ions, may explain the r₁ reduction observed for the C@1S@2S water dispersion.

It is worth noting that at 1.5 T magnetic field, the r₁ value of the C@1S, r₁ = 7.4 mM⁻¹ s⁻¹, exceeds three times the r₁ value determined for the fluoride core–shell counterpart, NaHoF₄@Yb,Tm:NaGdF₄, r₁ = 1.93 mM⁻¹ s⁻¹ (at 1.41 T),⁶⁸ and the comparison between r₁ data is likewise favorable for the C@1S@2S nanostructure. These large r₁ values for NaLn(WO₄)₂-based nanostructures are attributable to the high surface-to-volume ratios derived from their quasi-bidimensional geometry, which facilitate the interaction of Gd³⁺ cations with water protons.

On the other hand, at each measured magnetic field, an increase in r₂ is observed when going from single Ho-containing NPs, C, to nanostructures incorporating Gd³⁺ either in one layer, C@1S, or in two layers, C@1S@2S, see Table 1. According to a classical behavior following the quantum-mechanical outer-sphere theory,⁷¹ and from a oversimplified consideration, larger Ho-containing NPs will present better r₂ because water diffusion around them is slower and the magnetic field from the particle is higher. However, the studied system is not ideal to make this kind of comparison since it is not only the size that changes, but also the composition, which is not spatially uniform, with Ho³⁺ located only at the NPs core, and Gd³⁺ in 1S and 2S outer shells. Instead, it can be considered that the Ho³⁺ Curie-spin contribution to the r₂ relaxivity of water protons should be subjected to a reduction when increasing the number of layers, due to the larger distance between magnetic Ho³⁺ centers at the core and the surface in contact with water. Also, in large NPs and owing to the presence of Gd³⁺ in 1S and 2S shells, lower magnetization, see plots in Fig. S10 (ESI†), and thus lower Curie-spin effect would contribute to the worsening of r₂ values. In fact, these plots of the magnetization vs. the applied magnetic field indicate that, for a same magnetic field, the magnetization decreases as C > C@1S > C@1S@2S. Otherwise, it has been observed in other systems that the interaction between T₁ and T₂ CAs depends on the nanoscale, and that instead of inducing dual T₁/T₂ behaviors, it causes a significant increase in r₂.^68,72,73 Thus, the r₂ increase in C@1S with regards to C can be assigned to Ho³⁺–Gd³⁺ dipolar interactions, given the small concentration of the other paramagnetic Lns at 1S, Table S1 (ESI†). The additional increase observed with C@1S@2S would be due to: (i) the existence of an optimal interaction at somewhat longer distances than with 1S, from the balance between the Ho_core–Gd_1S and Ho_core–Gd_2S interactions, which would result in an increase in r₂, or (ii) the effect of the contribution of additional dipolar interactions between neigbouring Gd³⁺, as these between Gd_1S–Gd_2S, to the Curie-spin effect on r₂. This second possibility has been described in a hybrid compound of Fe₃O₄@SiO₂ NPs that incorporates a Gd³⁺-chelate immobilized inside the channels of SiO₂ pores, to account for the strong increase in r₂,⁷⁴ and is plausible in the present C@1S@2S system, in which a number of Gd³⁺ centers can be similarly considered as confined in the 1S.

The behavior of a CA as T₁, T₂ or dual T₁/T₂ agent in MRI is a consequence of the r₂/r₁ value, being a T₁ CA characterized by low r₂/r₁ ratios, while an efficient T₂ CA will have a high r₂/r₁ ratio. According to Table 1, it can be concluded that C@1S would behave as T₁ CA at 1.5 T (r₁ = 7.4 mM⁻¹ s⁻¹; r₂/r₁ = 1.8), while at high fields both C@1S and C@1S@2S would be efficient T₂ CAs, Fig. 5. Interestingly, C@1S@2S exhibit dual T₁/T₂ behavior already at 1.5 T (r₁ = 6 mM⁻¹ s⁻¹, r₂/r₁ = 6). Thus, it seems relevant to examine the behavior of these nanoprobes at an intermediate magnetic field between 1.5 T and 7 T.

Fig. 5 Evolution of r₂/r₁ at 1.5 T, 7 T and 11.7 T magnetic fields of (a) NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂ (C@1S), squares, and (b) NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂@20 at% Nd, 20 at% Yb:NaGd(WO₄)₂ (C@1S@2S), circles, dispersed in water. Pink, gray and blue symbols are for T₁, dual T₁/T₂ and T₂ behaviors, respectively. Hollow square and hollow circle correspond to r₂/r₁ values of C@1S-b and C@1S-b@2S-b in water dispersions, respectively, measured at 3 T.

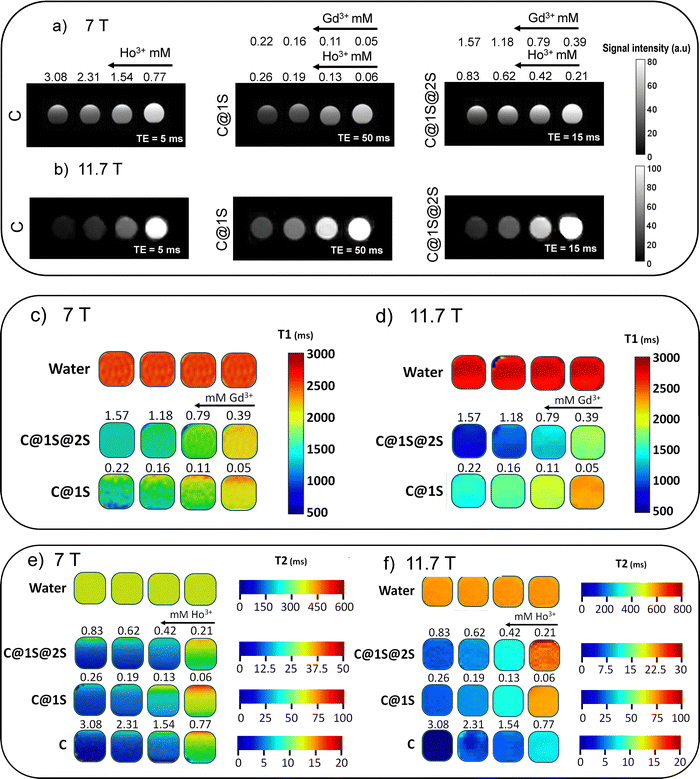
To corroborate the T₂ character of C, C@1S and C@1S@2S at high magnetic fields, T₂-weighted images of their water dispersions at different concentrations were collected at 7 T, Fig. 6a, and at 11.7 T, Fig. 6b. These images show that the three nanoprobes switch from hyper- to hypo-signal intensity with the increase in the concentration.

Fig. 6 T₂-weighted images of C, C@1S and C@1S@2S dispersed in water at (a) 7 T and (b) 11.7 T. T₁-maps of C@1S and C@1S@2S nanoprobes dispersed in water at (c) 7 T and (d) 11.7 T. T₂-maps of C, C@1S and C@1S@2S nanoprobes dispersed in water at (e) 7 T and (f) 11.7 T.

T₁-maps of C@1S and C@1S@2S nanoprobes dispersed in water are shown in Fig. 6c for 7 T magnetic field, and in Fig. 6d for 11.7 T. T₂-maps of C, C@1S, and C@1S@2S are displayed in Fig. 6e for 7 T magnetic field, and in Fig. 6f for 11.7 T. As expected, a linear relation is observed between concentrations of Gd³⁺ and Ho³⁺ and inverse of relaxation times T₁ and T₂, respectively, of protons for all nanoprobes, Fig. S6–S8 (ESI†).

From the above data, the r₁ and r₂ values and their evolution with the magnetic field appear to be closely related to Gd:Ho and Gd:Nd relative concentrations as well as to distances between these magnetic cations according to their distribution into the nanostructure. These two factors are related to the thicknesses of 1S and 2S shells, thus two optimized core–shell nanostructures, C@1S-b, and C@1S-b@2S-b, have been additionally prepared to be evaluated at the intermediate 3 T magnetic field. 1S-b and 2S-b shells have the same composition as 1S and 2S in previously studied nanostructures, but their thicknesses are different. Taking into account the previous results, a greater thickness of the surface shell in C@1S-b will increase the distance between Ho³⁺ and the surface in contact with the water, thus decreasing the magnetic perturbation over surface-lying Gd³⁺, which translates into an increase of r₁. On the other hand, since the presence of Nd³⁺ in the 2S surface shell represents an important disturbance over the coupling of spins of the closest Gd³⁺ with the water protons, to minimize this effect it is desirable a smaller Nd³⁺ content in the surface shell, i.e., a smaller thickness for S-2b. Concentrations of Lns in C@1S-b and C@1S-b@2S-b, measured by ICP-OES, are included in Table S2 (ESI†), and Table S3 (ESI†) shows the comparison of relationships of interest between the concentrations of Ho, Gd and Nd in these optimized nanoprobes with regard to previous C@1S and C@1S@2S ones. The inspection of data in Table S2 (ESI†) reveals the achievement of the above-indicated modifications in both first and second shells of prepared nanoprobes. The relationship of Gd:Ho concentrations is about 33% higher in C@1S-b than in C@1S, and being the nominal stoichiometry of the first shell the same in both samples, it is attributable to a greater shell thickness in C@1S-b.

On the other hand, higher Gd:Nd and Gd:Ho + Nd ratios in C@1S-b@2S-b than in C@1S@2S would mean less disturbance from Ho³⁺ and Nd³⁺ magnetic fields over the coupling of surface Gd³⁺ spins and water protons in C@1S-b@2S-b. Results of measured r₁ and r₂ relaxivities and r₂/r₁ values at 3 T by using water dispersions of C@1S-b and C@1S-b@2S-b are shown in Table 2. The highest measured r₁ has been achieved with C@1S-b@2S-b, r₁ = 10.5 mM⁻¹ s⁻¹, due to its optimized distribution of Gd³⁺ centers. At this magnetic field, the planar geometries of C@1S-b and C@1S-b@2S-b can also explain their high r₁ values when compared to the NaHoF₄@Yb,Tm:NaGdF₄ nanostructure (r₁ = 1.50 mM⁻¹ s⁻¹, at 2.82 T).⁶⁸ Further, r₂/r₁ values indicate that both C@1S-b and C@1S-b@2S-b would behave as dual T₁/T₂ CAs at 3 T magnetic field. Fig. 5 includes the r₂/r₁ values of water dispersed C@1S-b and C@1S-b@2S-b nanoprobes at 3 T.

Table 2 Longitudinal (r₁) and transverse (r₂) relaxivities (mM⁻¹ s⁻¹) and r₂/r₁ ratios shown by core–shell nanostructures NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂ (C@1S-b) and NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂@20 at% Nd, 20 at% Yb:NaGd(WO₄)₂ (C@1S-b@2S-b) dispersed in water at 3 T

	3 T
	r1	r2	r2/r1
	[Gd^3+]	[Ho^3+]
C@1S-b	2.2	33.1	15.0
C@1S-b@2S-b	10.5	70.1	6.7

---

To confirm the dual T₁/T₂ character of C@1S-b and C@1S-b@2S-b nanoprobes at 3 T magnetic field, T₁- and T₂-weighted images of their water dispersions with different concentrations were recorded under this magnetic field, see Fig. 7a–d. Both nanoprobes alter the signal intensity of the contrast of the T₁-weighted images, from dark to gray (C@1S-b), or to light gray (C@1S-b@2S-b), and of T₂-weighted images, from light gray to dark, with Gd³⁺ or Ho³⁺ concentrations, respectively. T₁ and T₂-maps of these C@1S-b and C@1S-b@2S-b water dispersions are presented in Fig. 7e and f. A linear relationship is observed between concentrations of Gd³⁺ and Ho³⁺ and inverse of relaxation times T₁ and T₂, respectively, of protons, for both nanoprobes, Fig. S9 (ESI†).

Fig. 7 T₁-weighted images of water dispersions of (a) C@1S-b, (b) C@1S-b@2S-b. T₂-weighted images of water dispersions of (c) C@1S-b, (d) C@1S-b@2S-b. In all cases the images were acquired at 3 T magnetic field. T₁ maps (e), and T₂ maps (f), of C@1S-b and C@1S-b@2S-b nanoprobes in water dispersions. The images were recorded at 3 T magnetic field.

According to the above results for water dispersions of the series of MRI nanoprobes based on NaLn(WO₄)₂ nanostructures, the optimization of the separation between the Ln responsible for T₁-weighted contrast, Gd³⁺ in the surface layer, and T₂-weighted contrast, Ho³⁺ in the core, provided by the core–shell design, and the control of the relative concentrations of these cations, are critical parameters in the evolution of the behavior as MRI CAs with the magnetic field. Thus, behaviors evolving from a T₁-weighted MR CA at 1.5 T to a highly effective T₂-weighted MR CA at ultrahigh magnetic fields of 7 T and above, and even a dual T₁/T₂-weighted CA at a clinical 3 T magnetic field, have been observed in this studied system. Furthermore, the distinctive quasi-bidimensional geometry of NaLn(WO₄)₂ nanostructures maximizes the surface-to-volume ratio, thereby optimizing the interaction between Gd³⁺ cations on the surface of the nanoprobe and the protons of the water, leading to higher r₁ values than those observed for other bulkier Ln-doped core–shell nanostructures, such as those based on NaLnF₄ fluorides, for magnetic fields up to 3 T.⁶⁸

3.3 Photoluminescence of C@1S@2S nanoprobe within I-, II-, III-, and IV-BWs wavelength ranges

When excited at λ_EXC ∼ 800 nm, through the ⁴I_9/2 → ⁴F_5/2, ²H_9/2 Nd³⁺ transition, C@1S@2S emits light across a wide spectral range spanning the UV, visible and NIR optical regions. However, improved subcutaneous PL sensing requires the use of NIR emissions, mainly within BW wavelength ranges, thus the current interest in C@1S@2S is focused on the evaluation of Nd³⁺, Yb³⁺, and Ho³⁺ NIR PL emissions within these BW ranges.

Fig. 8a shows schemes of electronic configurations of Nd³⁺, Yb³⁺, Tm³⁺ and Ho³⁺, as well as known energy transfer (ET) processes and electronic transitions yielding NIR down-shifted PL emissions. Under NIR excitation at λ_EXC ∼ 800 nm, external 2S-lying Nd³⁺ are pumped to ⁴F_5/2, ²H_9/2 energy levels, and after non radiative relaxation to ⁴F_3/2 level, NIR light is emitted from Nd³⁺ at λ_EMI ∼ 870–930 nm (⁴F_3/2 → ⁴I_9/2, within I-BW), ∼1.06 μm (⁴F_3/2 → ⁴I_11/2, II-BW), ∼1.33 μm (⁴F_3/2 → ⁴I_13/2, II-BW), and at 2–2.15 μm (⁴F_3/2 → ⁴I_15/2, IV-BW), Fig. 8b–d. Moreover, from ⁴F_3/2 Nd³⁺ the energy is transferred to close 2S-Yb³⁺ and to nearby 1S-Yb³⁺, populating the excited ²F_5/2 Yb³⁺ state, from which the excited emitting levels of 1S-Tm³⁺ and C-Ho³⁺ are populated by ET. PL bands peaking at λ_EMI ∼ 1 μm (²F_7/2 → ²F_5/2, Yb³⁺, II-BW), 1.8 μm (³F₄ → ³H₆, Tm³⁺, III-BW), and ∼2.1 μm (⁵I₇ → ⁵I₈, Ho³⁺ IV-BW) have been observed simultaneously in the prepared nanoprobes, Fig. 8b–d. Profiles of the emission cross-sections (σ_EMI) of Tm³⁺ and Ho³⁺ in isostructural NaLn(WO₄)₂ single crystals,^62,75 have been also included in Fig. 8d for help with maxima assignment. Therefore, C@1S@2S would result very suitable for deep tissue NIR optical imaging. It must be noted that the direct excitation of Tm³⁺ at λ_EXC = 795.5 nm, i.e. at the ³H₄ state, does not allow the observation of any Tm³⁺ emission in the PL spectrum of C@1S@2S. This fact points to the decisive role of Nd³⁺ and Yb³⁺ as the sensitizer and energy transmitter elements, respectively, in the mechanism for PL in C@1S@2S nanoprobe.

Fig. 8 (a) Schemes of the electronic configurations of involved trivalent lanthanides and energy transfer processes describing proposed mechanisms for NIR excited (λ_EXC ∼ 800 nm) down-shifted PL emissions (thick black arrows) of Nd³⁺, Yb³⁺, Tm³⁺ and Ho³⁺ in C@1S@2S. (b), (c) and (d) Room temperature luminescence spectra (λ_EXC = 803.4 nm, Ti-sa laser) of C@1S@2S NPs dispersed in CCl₄ (black lines), showing relevant Nd³⁺, Yb³⁺, Tm³⁺ and Ho³⁺ emissions within BWs. Red circles and blue diamonds are the emission cross-sections (σ_EMI) of Tm³⁺ and Ho³⁺, respectively, in the isostructural NaY(WO₄)₂ and NaBi(WO₄)₂ hosts, respectively. The blue continuous line is the Ho³⁺ emission spectrum obtained after substraction of the Nd³⁺ contribution, to be compared with its σ_EMI shape.

3.4 Photoluminescence-based nanothermometry in the II-BW

In order to determine the Nd³⁺ and Yb³⁺ concentrations that optimize the PL-based temperature sensing properties in the NaGd(WO₄)₂ host, as a preliminary step we have evaluated polycrystalline samples prepared by solid-state synthesis (SSS), as well as nanocores (6 × 4 nm) prepared by the coprecipitation route, of NaGd(WO₄)₂ doped with different Nd³⁺ and Yb³⁺ contents. The description of the SSS procedure, prepared compositions, and room temperature XRD patterns for these SSS-samples, Fig. S11, are included in the ESI.†

Upon Nd³⁺ excitation at λ_EXC = 803.4 nm, all these materials show simultaneously Nd³⁺ and Yb³⁺ PL, see Fig. 9a for the x at% Nd, 20 at% Yb:NaGd(WO₄)₂ series of nanocores dispersed in n-hexane. Among the three Nd³⁺ PL emissions from ⁴F_3/2 within I- and II-BWs, the one with the largest emission cross-section is the corresponding to the ⁴F_3/2 → ⁴I_11/2 transition peaking at λ_EMI = 1058 nm,⁷⁶ thus it was selected for the ratiometric comparison with the Yb³⁺ emission peaking at λ_EMI = 996 nm in the evaluation of the temperature sensing potential of C@1S@2S nanoprobes. In this case, a point of concern is the overlap between both PL contributions at λ = 1058 nm, which is particularly critical when the Nd³⁺ PL intensity is low in comparison to the Yb³⁺ one, i.e., when the Nd³⁺ → Yb³⁺ energy transfer is very efficient, as observed for high Yb³⁺ and Nd³⁺ concentrations. To fix this point, the Yb³⁺ contribution at λ_EMI = 1058 nm has been evaluated in each spectrum by extrapolating the shape of the main observed Yb³⁺ emission with the reference emission band profile measured under identical conditions in polycrystalline single doped x at% Yb:NaGd(WO₄)₂, and this contribution was discounted to evaluate the true Nd³⁺ PL intensity.

Fig. 9 (a) Evolution of the PL in the x at% Nd, 20 at% Yb:NaGd(WO₄)₂ series of nanocores dispersed in n-hexane at 20 °C (293 K) upon excitation of Nd³⁺ at λ_EXC = 803.4 nm. (b) Comparison of the spectral distributions at 20 °C (293 K) (black line) and 78 °C (351 K) (red line) of 7.5 at% Nd, 7.5 at%Yb:NaGd(WO₄)₂ polycrystalline SSS sample, λ_EXC = 803.4 nm. The 300 K absorption spectrum of single doped Yb:NaGd(WO₄)₂ is given (hollow circles). (c) Slope of dLIR/dT (being the absolute sensitivity S_A the corresponding |dLIR/dT|) value (black squares), and relative sensitivity S_R (red spheres) of Nd:Yb:NaGd(WO₄)₂ polycrystalline SSS materials as a function of the average Yb–Nd distance in the lattice. (d) Evolution with the Nd concentration of the absolute sensitivity, S_A (points), of x at% Nd, 20 at% Yb:NaGd(WO₄)₂ single nanocores dispersed in n-hexane. The line is a visual help.

In the ratiometric method, the thermometric properties of a material derive from the thermal evolution of the PL intensity ratio (LIR = I₂/I₁) of two emission bands.^77,78 The main thermometric figures of merit of the material are described by the absolute, S_A, and relative, S_R, sensitivities, defined as S_A = |dLIR/dT|, and S_R = S_A/LIR,^77–79 where T is the temperature.

In the present case the emissions come from two different ions, Nd³⁺ and Yb³⁺, thus their relative electronic populations do not follow the Boltzmann law. Nd³⁺ was selected as ion 1, I_1058nm, and Yb³⁺ as ion 2, I_996nm.

For all studied Nd–Yb concentrations, the PL intensity of Yb³⁺ decreases with the temperature while the PL of Nd³⁺ basically remains constant within the temperature range of interest for biomedical applications, Fig. 9b. The as-defined LIR(T) evolution is nearly linear with a negative slope. As an example, Fig. S12 (ESI†) shows LIR(T) for 7.5 at% Nd, 7.5 at% Yb:NaGd(WO₄)₂ SSS sample.

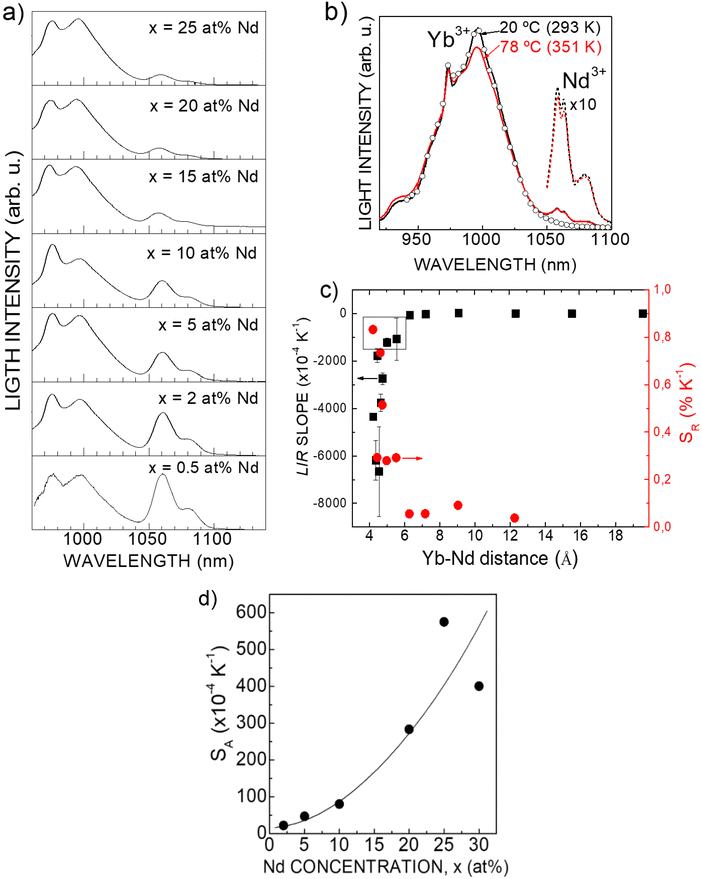
From LIR analyses, the Fig. 9c shows the evolution of S_A and S_R as a function of the Nd–Yb average lattice distance,

where [Yb] and [Nd] are the corresponding Ln densities in cm⁻³. For Nd–Yb distances larger than 7 Å, which correspond to total Nd + Yb concentrations below 10 at% of Gd substitution, the energy transfer Nd³⁺ → Yb³⁺ is little efficient, and the thermometric sensitivities are near to zero. For shorter distances, both S_A and S_R increase enormously, and record values of S_A = 0.67 K⁻¹ are reached for heavily doped samples. Nonetheless, the increase in sensitivity is associated with a decrease of the Nd³⁺ PL intensity, thus a compromise between large sensitivities and confident reproducibility of the measurements must be achieved. In polycrystalline SSS samples such balance is found for a total Nd + Yb concentration in the 15–20 at% range of Gd substitution.

In a next step, PL spectra (λ_EXC = 803.4 nm) of colloidal dispersions in n-hexane of NaGd(WO₄)₂ nanocores doped with 20 at% Yb and Nd concentration ranging from 2 at% to 30 at% were analyzed in the 20 °C–70 °C (293 K–343 K) temperature range. For a given temperature, the intensity distribution of the spectral Nd³⁺ and Yb³⁺ bands resembles those of polycrystalline materials with lower Nd³⁺ and Yb³⁺ concentrations, suggesting that some loss of one or both optically active Ln occurs during the coprecipitation synthesis. In fact, Ln compositional analyses by ICP-OES confirm a lower than nominal Yb³⁺ incorporation in prepared nanomaterials, see Tables S1 and S2 (ESI†). LIR(T) analyses indicated that the highest S_A = 573 × 10⁻⁴ K⁻¹ corresponds to the colloidal dispersion in n-hexane with composition 25 at% Nd, 20 at% Yb:NaGd(WO₄)₂, Fig. 9d.

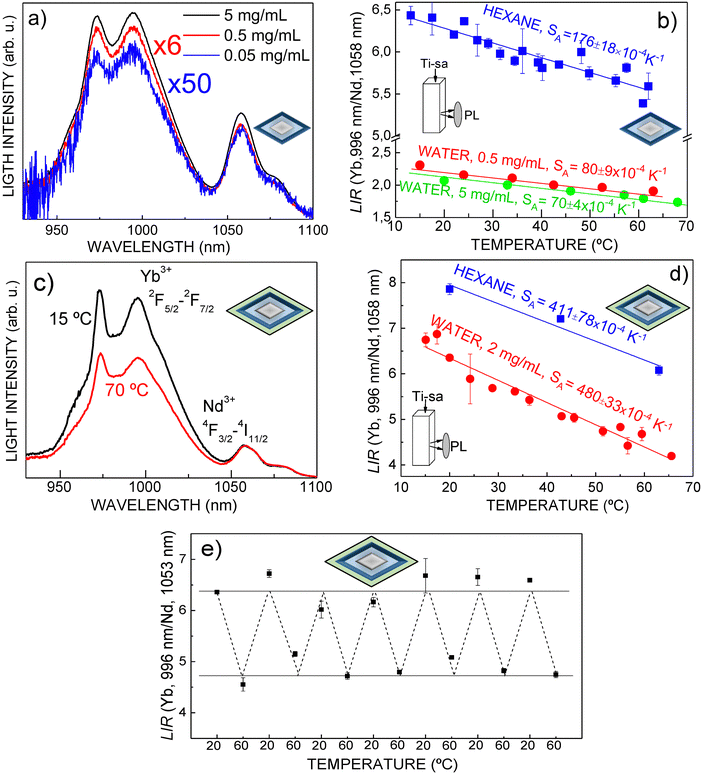
Finally, the LIR(T) characterization of the NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂@20 at% Nd, 20 at% Yb:NaGd(WO₄)₂ (C@1S@2S) nanostructure was carried out in the temperature range of biological interest. Colloidal dispersions in n-hexane, as well as in water with increasing dilution degree, i.e., 5 mg mL⁻¹, 0.5 mg mL⁻¹ and 0.05 mg mL⁻¹, have been used for the PL measurements under Ti-sa excitation at λ_EXC = 803.4 nm. Optical excitation densities of 2.4 W cm⁻² and 0.68 W cm⁻² were used for n-hexane and water dispersions, respectively. Fig. 10a shows the PL distribution at room temperature for the three water dispersions. Obviously the PL signal-to-noise ratio decreases when the dilution increases, but even at the lowest tested concentration, 0.05 mg mL⁻¹, the shape of the spectrum allows the unequivocal determination of a confident LIR value for each measured temperature. Fig. 10b shows the thermal evolution of experimental LIR results in both n-hexane and water colloidal dispersions. It is worth noting that when the nanoprobes are transferred to the water medium the S_A value decreases, see in Fig. 10b the different slopes of LIR(T) for both kinds of colloidal media.

Fig. 10 Thermometric PL response of colloidal dispersions of NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂@20 at% Nd, 20 at% Yb:NaGd(WO₄)₂ (C@1S@2S): (a) PL emissions of dispersions in water with different dilutions, λ_EXC = 803.4 nm, I_E = 0.68 W cm⁻². (b) Comparison of the thermal evolution of the Yb/Nd based LIR in n-hexane, blue squares, I_E = 2.4 W cm⁻², and after transfer to water, red circles, I_E = 0.68 W cm⁻², the symbols are the experimental results and the lines are the linear fits used for calculation of S_A sensitivity. Thermometric PL response of colloidal dispersions of NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂@30 at% Nd, 20 at% Yb:NaGd(WO₄)₂@NaGd(WO₄)₂ (C@1S@2S@i3S): (c) comparison of the spectral distributions at 15 °C (288 K), black line, and at 70 °C (343 K), red line, of the colloidal dispersion in water (2 mg mL⁻¹). (d) Thermometric characterization in n-hexane, blue squares, and in the water dispersion, red circles, I_E = 0.68 W cm⁻², λ_EXC = 803.4 nm, the lines are the linear fits of the experimental results. Values of S_R at 40 °C (313 K) are 0.58% K⁻¹ and 0.89% K⁻¹, for colloidal dispersions in n-hexane and water, respectively. (e) Stability of the PL response upon seven heating/cooling cycles between 20 °C (293 K) and 60 °C (333 K), λ_EXC = 803.4 nm, I_E = 0.68 W cm⁻².

To prevent this undesired degradation of the LIR sensitivity in aqueous/biological media, an additional isostructural undoped NaGd(WO₄)₂ outermost shielding layer was grown on the nanoprobe. Fig. 10c depicts the temperature-dependent (15 °C–70 °C/288 K–343 K) intensity distribution of Yb³⁺ and Nd³⁺ PL bands of a diluted (2 mg mL⁻¹) colloidal water-stabilized dispersion of TWEEN80-modified NaHo(WO₄)₂@8 at% Tm, 15 at% Yb:NaGd(WO₄)₂@30 at% Nd, 20 at% Yb:NaGd(WO₄)₂@NaGd(WO₄)₂ (C@1S@2S@i3S), and Fig. 10d displays the corresponding LIR thermometric characterization. The optically inert NaGd(WO₄)₂ shell induces an efficient enhancement of the thermometric sensitivities in comparison with those of similar nanostructures lacking it, and importantly, the S_A value remains unchanged after transfer from the n-hexane to the diluted water dispersion. The small LIR change upon this transfer is due to the selective optical absorption of water at λ = 995 nm. In both dispersive liquid media, remarkable high S_A= 400–500 × 10⁻⁴ K⁻¹ and S_R = 0.6–0.9% K⁻¹ thermometric sensitivities are determined, specifically S_A = 480 (± 33) × 10⁻⁴ K⁻¹ and S_R = 0.89% K⁻¹ at 40 °C (313 K) in the water dispersion. To further assess the performance for temperature sensing, the stability of the spectral response of the above water dispersed C@1S@2S@i3S nanothermometer was analyzed through seven heating/cooling cycles. No degradation of LIR values occurs, see Fig. 10e. Under the present measurement conditions, a LIR uncertainty value σ_LIR ≈ 0.1% has been established from the observed fluctuations of the mean LIR value for each heating/cooling cycle. From the data collected for water dispersions of C@1S@2S@i3S, the temperature resolution, δT, defined as δT = σ_LIR/S_R,⁷⁹ is ≈0.1 K.

The comparison of luminescent Ln-based nanothermometers performance is carried out through the evaluation of the above-described thermal parameters, i.e., S_A, S_R, δT, and reproducibility in luminescence measurements. However, when nanothermometers are intended for temperature biosensing purposes, other important aspects need to be considered in this assessment. Among these factors the main ones are the wavelength ranges in the excitation–emission operation scheme, the luminescence efficiency at biologically interesting temperatures, which must be high enough to allow keeping low irradiation power densities, and the cellular viability upon nanothermometer intake when in vivo applications are envisaged, which additionally implies the use of highly diluted and stable water dispersions of the nanoprobe. Thus, disregarding the plethora of studied Ln-doped nanothermometers based on visible and I-BW PL emission LIR analyses,^79,80 the comparison for current C@1S@2S@i3S will focused on a handful of described λ ∼ 800 nm-excited thermal sensors similarly operated within the II-BW, through Nd³⁺ (∼1060 nm) and Yb³⁺ (∼1000 nm) LIR measurements,^30–32,81 and even so the comparison is not unequivocal. It should be noted that all issues usually mentioned as hindrances for using S_A as the figure of merit⁸⁰ disappear in the current comparison. Unfortunately, direct S_A values, that would be illustrative of the potential of compared nanothermometers, are not explicitly provided for these systems, and furthermore the normalization of LIR values in reported figures showing LIR vs. T plots does not allow the corresponding S_A estimations.

Regarding S_R results, the highest S_R = 2.1% K⁻¹ is indicated for 808 nm-excited Er,Yb:NaYF₄@Yb, Nd:NaYF₄ (LIR = Nd₁₀₆₀/Yb₉₈₀) nanothermometer at 97 °C (370 K),³¹ but this thermal probe has considerably lower S_R values at biologically interesting temperatures, what required the use of the visible Er₅₂₀/Er₅₄₀ LIR channel to achieve S_R ∼ 1% K⁻¹ for temperature sensing in the 17 °C–37 °C (290 K–310 K) range. Furthermore, LIR measurements were carried out with dried films of prepared NPs, instead of using their colloidal water dispersions. On the other hand, the thermometric performance of the core@multishell system Yb,Tm:SrF₂@Yb:SrF₂@Yb,Nd,Er:SrF₂@Nd:SrF₂ (colloidal water dispersions of ∼27 nm NPs, 1 wt%) is evaluated through Yb₉₈₀/Nd₁₀₆₀ LIR analysis, yielding very high S_R values, up to 1.62% K⁻¹ at 50 °C (323 K), and δT = 1.7 K, but in this case the power density of the 806 nm cw excitation laser diode was 31 W cm⁻²,³² well beyond the limit for biologically safe exposure. For diluted PBS dispersions of simple codoped Nd, Yb:LaF₃ NPs, and two LaF₃-based core–shell nanostructures, one having Nd³⁺ at the core, with Yb³⁺ at the shell, and the other with Yb³⁺ at the core and Nd³⁺ at the shell, the evaluation of S_R (from 790 nm-excited LIR = Nd₁₀₆₀/Yb₁₀₀₀, values obtained under 0.7 W cm⁻² power density) indicated a better performance of the latter core–shell nanostructure, S_R = 0.41% K⁻¹, with regards to simple NPs, S_R = 0.1% K⁻¹, in the physiological range of temperatures, with δT = 1.61 K.³⁰ Similar S_R values are found for Nd³⁺ and Yb³⁺ codoped complexes with pyridine, 3,5 carboxylate (PDC).⁸¹ In this case, the Nd₁₀₅₂/Yb₁₀₀₅ LIR analysis of the complex Gd_1.45Nd_0.40Yb_0.15-PDC yielded S_R values between 0.48% K⁻¹ and 0.439% K⁻¹ in the 25 °C–46 °C (298 K–318 K) range, with δT = 0.08 K.

The above results from NIR–NIR LIR thermometric analyses show that C@1S@2S@i3S behaves as a well-suited nanothermometer for biologically safe operation within the II-BW, exhibiting advantageous thermal sensitivities, S_A = 480 (± 33) × 10⁻⁴ K⁻¹ and S_R = 0.89% K⁻¹ at 40 °C (313 K), and temperature resolution, δT ≈ 0.1 K, with regards to other Yb, Nd-based LIR thermometric systems.

3.5 In vitro assays with cells exposed to core–shell nanoprobes

Establishing the biocompatible nature of developed double tungstate-based nanoprobes in both healthy and cancerous cell lines is a critical step toward validating their potential for intended biomedical applications, such as diagnostic imaging and NIR biolabeling during cellular temperature measurement. For this purpose, HeLa and MC3T3 cells lines were chosen as representative models of human cancer cells and of healthy, non-tumorigenic cells, respectively. In vitro assays of viability by AlamarBlue tests, and cytotoxicity by measuring the catalytic activity of lactate dehydrogenase (LDH), were carried out for these cellular lines by incubation with water dispersions of nanoprobes, at concentrations up to 200 μg mL⁻¹ for viability, and up to 135 μg mL⁻¹ for cytotoxicity, for 24–48 h.

Results of AlamarBlue assays in HeLa cells treated with TWEEN80-modified C@1S@2S@i3S water dispersions are shown in Fig. 11a. After 24 h of the nanoprobe dispersion addition, cell viability is preserved for concentrations of the nanoprobe at least up to 50 μg mL⁻¹. When this concentration reaches 100 μg mL⁻¹, a significant (p < 0.05 Student t-test) reduction in viability to 60% is observed. Interestingly, an enhancement of the AlamarBlue dye reduction appears with increasing nanoprobe doses above 100 μg mL⁻¹, indicating an increase in the metabolism of alive cells. This same effect in metabolic cell activity of living cells has been previously observed in MTT assays with human mesenchymal stem cells (hMSCs) cultured with water dispersions of similar TWEEN80-modified Yb, Er-doped NaGd(WO₄)₂ NPs, and it has been attributed to the TWEEN80 content,³⁴ through its effects on the cellular membrane fatty acid composition.^82–85 Thus, this phenomenon is restricted to cell metabolism, and it does not lead to a cell proliferation increase or overall cell viability, as confirmed by the fluorescence microscopy images shown in Fig. 12a. In any case, the half maximal inhibitory concentration of the nanoprobe, IC₅₀, is even beyond that the most concentrated water dispersion analyzed, 200 μg mL⁻¹.

Fig. 11 Effect of C@1S@2S@i3S water dispersions on cells viability (AlamarBlue assay): (a) HeLa cells, after 24 h incubation compared with control HeLa cells. (b) MC3T3 cells, after 24 h and 48 h incubation compared with control MC3T3 cells. Error bars represent the standard deviation of four independent samples. *p < 0.05 (Student's t-test). Effect of C@1S@2S@i3S water dispersions on cells cytotoxicity (LDH release): (c) HeLa and MC3T3 cells after 24 h incubation.

Fig. 12 Fluorescence microscopy images of HeLa (left block) and MC3T3 (right block) cells stained with DAPI: (a)–(c) untreated HeLa cells; (d)–(f) 24 h HeLa cultured cells with 200 μg mL⁻¹ of C@1S@2S@i3S water dispersion; (g)–(i) untreated MC3T3 cells: (j)–(l) 24 h MC3T3 cultured cells with 200 μg mL⁻¹ of C@1S@2S@i3S water dispersion. Scale bars correspond to 200 μm.

Viability assays conducted in healthy MC3T3 cells revealed their remarkable robustness in the presence of the nanoprobe, Fig. 11b. Even at extended incubation periods, cellular integrity and metabolic activity remained largely unimpaired. For instance, with a nanoprobe concentration of 200 μg mL⁻¹, a significant 85% cell viability was maintained even after a prolonged 48 h incubation period.

To further investigate and confirm the non-toxic effects of C@1S@2S@i3S nanoprobe on both HeLa and MC3T3 cells, cytotoxicity assays by measuring the catalytic activity of lactate dehydrogenase (LDH) were also carried out. This assay is a well-established and reliable method for quantifying cell death. The underlying principle of the LDH assay is based on the cytosolic presence of this enzyme. When the plasma membrane of a cell is damaged or compromised, LDH is released into the cell culture medium. Therefore, the amount of LDH activity detected in the extracellular medium is directly proportional to the number of dead or dying cells. By measuring the extracellular LDH activity, the extent of cytotoxicity induced by a given treatment or condition on the cells can be evaluated accurately. Fig. 11c shows the results of this assay. For both cell lines, the cytotoxicity was almost negligible even at the highest measured concentration, 135 μg mL⁻¹, at 24 h of incubation, with HeLa cells showing a 2.3%, and MC3T3 a 9.7% cytotoxicity.

Fluorescence microscopy using DAPI staining was employed to qualitatively observe the nuclei of viable cells and chromatin condensation at the 24-hour endpoint. Fig. S13 and S14 (ESI†) show the comparison between fluorescence microscopy images of the control (untreated) HeLa and MC3T3 cells and images corresponding to cultured cells with increasingly concentrated nanoprobe water dispersions, and Fig. 12 is a simplified view displaying images of cultured cells only with the highest concentrate nanoprobe dispersion, 200 μg mL⁻¹. The HeLa control sample exhibits a high number of stained nuclei, which represents 100% viability under the established conditions. The presence of intact nuclei, with evenly distributed chromatin, is an indication of healthy cells, and very similar images have been collected for HeLa cells treated during 24 h with a 25 μg mL⁻¹ nanoprobe water dispersion, Fig. S13 (ESI†). In contrast, images of HeLa cells treated with highly concentrated nanoprobe dispersions, 100 μg mL⁻¹ and 200 μg mL⁻¹, exhibit significantly lower levels of stained nuclei, with some cells displaying blue fluorescence brighter than others, due to chromatin condensation, and nuclei shrinkage and fragmentation are also observed, which in all cases indicate cellular apoptosis occurring to some extent. For MC3T3 cell samples, the images indicate that the number of stained nuclei is comparable between the control group and samples for all tested concentrations of the nanoprobe dispersion, suggesting that membrane integrity is not adversely affected by the treatment up to the highest nanoprobe concentration, 200 μg mL⁻¹.

4. Conclusions

Nanoprobes integrating capabilities for magnetic resonance imaging contrast as well as NIR photoluminescence-based imaging and contactless thermometry have been demonstrated through Ln-doped core–shell nanostructures based on the scheelite-like double tungstate NaLn(WO₄)₂ crystal host. The synthesis strategy was the confirmed coating of a NaHo(WO₄)₂ core with shells, the first of Tm,Yb:NaGd(WO₄)₂, and the second of Nd, Yb:NaGd(WO₄)₂, to properly separate the various Lns responsible for the different functionalities of the nanoprobe. Interestingly, these nanostructures offer a large surface-to-volume relationship due to their quasi-bidimensional geometry, which favors T₁-weighted contrast. Furthermore, the surface modification of nanoprobes by coating them with an undoped isostructural crystalline layer and then by the biocompatible emulsifier TWEEN80 facilitates their transfer to water dispersion while preserving their radiative properties.

Results on relaxativity measurements and magnetic resonance imaging of water dispersions of prepared nanoprobes indicate an increase of more than 50 times in r₂/r₁ values and the associated contrast behavior evolution from positive to negative when the strength of the magnetic field increases from 1.5 to 11.7 T. Furthermore, r₂/r₁ = 15 was achieved at 3 T by optimizing the thickness of the first shell, and in this case magnetic resonance imaging demonstrates a dual T₁/T₂-weighted behavior as CA at this clinically relevant magnetic field strength.

By NIR excitation (λ_EXC ∼ 803 nm) of Nd³⁺ in the second shell, contactless thermometry was performed at wavelengths within the II-BW (λ_EMI ∼ 1000–1400 nm) through LIR analysis of the pair of emissions ⁴F_3/2 → ⁴I_11/2 Nd³⁺ (λ_EMI = 1058 nm) and ²F_5/2 → ²F_7/2 Yb³⁺ (λ_EMI = 996 nm). The second shell surface degradation in diluted water dispersions, which leads to Nd³⁺ and Yb³⁺ emissions quenching, is fully avoided by a further coating with an optically inactive NaGd(WO₄)₂ external shell. Absolute, S_A, and relative, S_R, thermal sensitivity values as remarkable as S_A = 480 × 10⁻⁴ K⁻¹, and S_R = 0.89% K⁻¹ at 40 °C (313 K), and temperature resolution δ ≈ 0.1 K, were delivered by chemically stable 2 mg mL⁻¹ water dispersion of the nanoprobe under a biologically safe excitation power density of 0.68 W cm⁻². Moreover, through efficient Nd³⁺ → Yb³⁺ → Tm³⁺ and Nd³⁺ → Yb³⁺ → Ho³⁺ energy transfers, NIR PL emissions from Tm³⁺ at ∼1800 nm (³F₄ → ³H₆ transition, III-BW) and Ho³⁺ at ∼2000 nm (⁵I₇ → ⁵I₈ transition) useful for NIR optical imaging are also observed, being energy back-transfers to Nd³⁺ minimized by the spatial separation between these emitting Lns and Nd³⁺.

The metabolism of HeLa cells treated with water dispersions of the nanoprobe is preserved for concentrations at least up to 50 μg mL⁻¹ in incubations during 24 h, and healthy MC3T3 cells maintain a significant 85% cell viability even after a prolonged 48 h incubation period with a nanoprobe concentration of 200 μg mL⁻¹. Moreover, cytotoxicity levels induced by the nanoprobe are very reduced, 2.3% for HeLa cells and 9.7% for MC3T3 cells, after 24 h incubation with 135 μg mL⁻¹ of the nanoprobe dispersion. Thus, biomedical applications of the developed nanoprobe, in diagnostic imaging and NIR biolabeling during cellular temperature measurement, for example in hyperthermia processes, would be facilitated by its demonstrated safety profile.

Author contributions

C. Alarcón-Fernández: investigation, methodology, writing – original draft, writing – review & editing; C. Zaldo: conceptualization, investigation, methodology, formal analysis, validation, funding acquisition, writing – original draft, writing – review & editing; M. Bañobre-López: investigation, methodology, formal analysis, writing – original draft, writing – review & editing; J. Gallo: investigation, methodology, formal analysis, writing – original draft, writing – review & editing; P. Ramos-Cabrer: investigation, methodology, formal analysis, writing – original draft, writing – review & editing; S. Plaza-García: investigation, writing – original draft, writing – review & editing; A. Ruperti: investigation, writing – review & editing; G. Villaverde: investigation, formal analysis, writing – review & editing; C. Cascales: conceptualization, investigation, formal analysis, validation, funding acquisition, writing – original draft, writing – review & editing.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

Data will be made available upon reasonable request. The data supporting this article have been included as part of the ESI.†

Acknowledgements

This work has been supported by the Ministerio de Ciencia, Innovación y Universidades (MICIU) of Spain under project PID2021-128090OB-C21 funded by MICIN/AEI/10.13039/501100011033, and by ‘ERDF A way of making Europe’, and C. A. F. acknowledges his PhD MICIU grant PRE2019-090446. The National Center for Electron Microscopy (CNME)-Universidad Complutense de Madrid facility, and E. Urones contribution to TEM and STEM-EDX measurements are gratefully acknowledged.

References

1. C. Li, G. Chen, Y. Zhang, F. Wu and Q. Wang, Advanced Fluorescence Imaging Technology in the Near-Infrared-II Window for Biomedical Applications, J. Am. Chem. Soc., 2020, 142(35), 14789–14804.
2. A. Refaat, M. L. Yap, G. Pietersz, A. P. G. Walsh, J. Zeller, B. del Rosal, X. Wang and K. Peter, In vivo fluorescence imaging: success in preclinical imaging paves the way for clinical applications, J. Nanobiotechnol., 2022, 20, 450,  DOI:10.1186/s12951-022-01648-7.
3. J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chemistry of MRI Contrast Agents: Current Challenges and New Frontiers, Chem. Rev., 2019, 119, 957–1057,  DOI:10.1021/acs.chemrev.8b00363.
4. H. Li and T. J. Meade, Molecular Magnetic Resonance Imaging with Gd(III)-Based Contrast Agents: Challenges and Key Advances, J. Am. Chem. Soc., 2019, 141, 17025–17041,  DOI:10.1021/jacs.9b09149.
5. M. E. Ladd, P. Bachert, M. Meyerspeer, E. Moser, A. M. Nagel, D. G. Norris, S. Schmitter, O. Speck, S. Straub and M. Zaiss, Pros and cons of ultra-high-field MRI/MRS for human application, Prog. Nucl. Magn. Reson. Spectrosc., 2018, 109, 1–50,  DOI:10.1016/j.pnmrs.2018.06.001.
6. D. A. Feinberg, A. J. S. Beckett and A. T. Vu, et al., Next-generation MRI scanner designed for ultra-high-resolution human brain imaging at 7 Tesla, Nat. Methods, 2023, 20, 2048–2057,  DOI:10.1038/s41592-023-02068-7.
7. I. de Vries, W. Lesterhuis and J. Barentsz, et al., Magnetic resonance tracking of dendritic cells in melanoma patients for monitoring of cellular therapy, Nat. Biotechnol., 2005, 23(11), 1407–1413,  DOI:10.1038/nbt1154.
8. Y. Ning, I. Y. Zhou and P. Caravan, Quantitative in Vivo Molecular MRI, Adv. Mater., 2024, 36, 2407262,  DOI:10.1002/adma.202407262.
9. J. Yang, M. Yan, Z. Wang, C. Zhang, M. Guan and Z. Sun, Optical and MRI Multimodal Tracing of Stem Cells In Vivo, Mol. Imaging, 2023, 2023, 4223485,  DOI:10.1155/2023/4223485.
10. G. Chen, H. Qiu, P. N. Prasad and X. Chen, Upconversion Nanoparticles: Design, Nanochemistry, and Applications in Theranostics, Chem. Rev., 2014, 114(10), 5161–5214,  DOI:10.1021/cr400425h.
11. N. N. Dong, M. Pedroni, F. Piccinelli, G. Conti, A. Sbarbati, J. E. Ramírez-Hernández, L. Martínez Maestro, M. C. Iglesias-de la Cruz, F. Sanz-Rodriguez, A. Juarranz, F. Chen, F. Vetrone, J. A. Capobianco, J. García Solé, M. Bettinelli, D. Jaque and A. Speghini, NIR-to-NIR Two-Photon Excited CaF₂:Tm³⁺,Yb³⁺ Nanoparticles: Multifunctional Nanoprobes for Highly Penetrating Fluorescence Bio-Imaging, ACS Nano, 2011, 5(11), 8665–8671,  DOI:10.1021/nn202490m.
12. S. L. Jacques, Optical properties of biological tissues: a review, Phys. Med. Biol., 2013, 58, 5007,  DOI:10.1088/0031-9155/58/14/5007 ; see also K. Calabro, Modeling Biological Tissues in LightTools, Synopsis 2020, https://www.synopsys.com/content/dam/synopsys/optical solutions/documents/modeling-tissues-lighttools-paper.pdf.
13. S. Smith, M. Mancini and S. Nie, Second window for in vivo imaging, Nat. Nanotechnol., 2009, 4, 710–711,  DOI:10.1038/nnano.2009.326.
14. S. Wu, G. Han, D. J. Milliron, S. Aloni, V. Altoe, D. V. Talapin, B. E. Cohen and P. J. Schuck, Non-blinking and photostable upconverted luminescence from single lanthanide-doped nanocrystals, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10917–10921,  DOI:10.1073/pnas.0904792106.
15. A. Gnach, T. Lipinski, A. Bednarkiewicz, J. Rybka and J. A. Capobianco, Upconverting nanoparticles: assessing the toxicity, Chem. Soc. Rev., 2015, 44, 1561–1584,  10.1039/c4cs00177j.
16. Y. Sun, W. Feng, P. Yang, C. Huang and F. Li, The biosafety of lanthanide upconversion nanomaterials, Chem. Soc. Rev., 2015, 44, 1509–1525,  10.1039/c4cs00175c.
17. D. Jaque and F. Vetrone, Luminescence nanothermometry, Nanoscale, 2012, 4, 4301–4326,  10.1039/c2nr30764b.
18. C. Zaldo, in Advanced Nanomaterials, Lanthanide-based multifunctional materials: From OLEDs to SIMs, ed. P. Martín-Ramos and M. Ramos-Silva, Elsevier, 2018, ch. 10 DOI:10.1016/B978-0-12-813840-3.00010-7.
19. T. Bai and N. Gu, Micro/Nanoscale Thermometry for Cellular Thermal Sensing, Small, 2016, 12, 4590–4610,  DOI:10.1002/smll.201600665.
20. Q. Wang, M. Liao, Q. Lin, M. Xiong, Z. Mu and F. Wu, A review on fluorescence intensity ratio thermometer based on rare earth and transition metal ions doped inorganic luminescent materials, J. Alloys Compd., 2021, 850, 156744,  DOI:10.1016/j.jallcom.2020.156744.
21. C. Wang, Y. Jin, R. Zhang, Q. Yao and Y. Hu, A review and outlook of ratiometric optical thermometer based on thermally coupled levels and non-thermally coupled levels, J. Alloys Compd., 2022, 894, 162494,  DOI:10.1016/j.jallcom.2021.162494.
22. H. Suo, X. Zhao, Z. Zhang, Y. Wang, J. Sun, M. Jin and C. Guo, Rational Design of Ratiometric Luminescence Thermometry Based on Thermally Coupled Levels for Bioapplications, Laser Photonics Rev., 2021, 15, 2000319,  DOI:10.1002/lpor.202000319.
23. U. Rocha, C. Jacinto, K. U. Kumar, F. J. López, D. Bravo, J. G. Solé and D. Jaque, Real-time deep-tissue thermal sensing with sub-degree resolution by thermally improved Nd³⁺:LaF₃ multifunctional nanoparticles, J. Lumin., 2016, 175, 149–157,  DOI:10.1016/j.jlumin.2016.02.034.
24. A. Benayas, B. Rosal, A. Pérez-Delgado, K. Santacruz-Gómez, D. Jaque, G. A. Hirata and F. Vetrone, Nd:YAG near-infrared luminescent nanothermometers, Adv. Opt. Mater., 2015, 3, 687–694,  DOI:10.1002/adom.201400484.
25. I. E. Kolesnikov, E. V. Golyeva, M. A. Kurochkin, E. Lähderanta and M. D. Mikhailov, Nd³⁺-doped YVO₄ nanoparticles for luminescence nanothermometry in the first and second biological windows, Sens. Actuators, B, 2016, 235, 287–293,  DOI:10.1016/j.snb.2016.05.095.
26. L. Marciniak, K. Prorok, A. Bednarkiewicz, A. Kowalczyk, D. Hreniak and W. Strek, Water dispersible LiNdP₄O₁₂ nanocrystals: New multifunctional NIR–NIR luminescent materials for bio-applications, J. Lumin., 2016, 176, 144–148,  DOI:10.1016/j.jlumin.2016.03.034.
27. Ł. Marciniak, A. Bednarkiewicz, D. Hreniak and W. Strek, The influence of Nd³⁺ concentration and alkali ions on the sensitivity of non-contact temperature measurements in ALaP4O12:Nd3+ (A = Li, K, Na, Rb) nanocrystalline luminescent thermometers, J. Mater. Chem. C, 2016, 4, 11284,  10.1039/c6tc03396b.
28. L. A. O. Nunes, A. S. Souza, L. D. Carlos and O. L. Malta, Neodymium doped fluoroindogallate glasses as highly-sensitive luminescent non-contact thermometers, Opt. Mater., 2017, 63, 42–45,  DOI:10.1016/j.optmat.2016.08.038.
29. X. Tian, X. Wei, Y. Chen, C. Duan and M. Yin, Temperature sensor based on ladder-level assisted thermal coupling and thermal-enhanced luminescence in NaYF4: Nd3+, Opt. Express, 2014, 22, 30333,  DOI:10.1364/OE.22.030333.
30. E. C. Ximendes, W. Querioz Santos, U. Rocha, U. K. Kagola, F. Sanz-Rodríguez, N. Fernández, A. S. Gouveia-Neto, D. Bravo, A. M. Domingo, B. del Rosal, C. D. S. Brites, L. D. Carlos, D. Jaque and C. Jacinto, Unveiling in vivo subcutaneous thermal dynamics by infrared luminescent nanothermometers, Nano Lett., 2016, 16, 1695–1703,  DOI:10.1021/acs.nanolett.5b04611.
31. L. Marciniak, K. Prorok, L. Francés-Soriano, J. Pérez-Prieto and A. Bednarkiewicz, A broadening temperature sensitivity range with a core–shell YbEr@YbNd double ratiometric optical nanothermometer, Nanoscale, 2016, 8, 5037–5042,  10.1039/c5nr08223d.
32. P. Cortelletti, A. Skripka, C. Facciotti, M. Pedroni, G. Caputo, N. Pinna, M. Quintanilla, A. Benayas, F. Vetrone and A. Speghini, Tuning the sensitivity of lanthanide-activated NIR nanothermometers in the biological windows, Nanoscale, 2018, 10, 2568–2576,  10.1039/c7nr06141b.
33. Ł. Marciniak, A. Bednarkiewicz, M. Stefanski, R. Tomala, D. Hreniak and W. Strek, Near infrared absorbing near infrared emitting highly-sensitive luminescent nanothermometer based on Nd³⁺ to Yb³⁺ energy transfer, Phys. Chem. Chem. Phys., 2015, 17, 24315,  10.1039/c5cp03861h.
34. C. Cascales, C. L. Paíno, E. Bazán and C. Zaldo, Ultrasmall, water dispersible, TWEEN80 modified Yb:Er:NaGd(WO₄)₂ nanoparticles with record upconversion ratiometric thermal sensitivity and their internalization by mesenchymal stem cells, Nanotechnology, 2017, 28, 185101,  DOI:10.1088/1361-6528/aa6834.
35. C. Zaldo, M. D. Serrano, X. Han, C. Cascales, M. Cantero, L. Montoliú, E. Arza, V. R. Caiolfa and M. Zamai, Efficient up-conversion in Yb:Er:NaT(XO₄)₂ thermal nanoprobes. Imaging of their distribution in a perfused mouse, PLoS One, 2017, 12(5), e0177596,  DOI:10.1371/journal.pone.0177596.
36. P. Caravan, J. J. Ellison, T. J. McMurry and R. B. Lauffer, Gadolinium(III) chelates as MRI contrast agents: Structure, dynamics, and applications, Chem. Rev., 1999, 99, 2293–2352,  DOI:10.1021/cr980440x.
37. M. Bendszus, A. Laghi, J. Munuera, L. N. Tanenbaum, B. Taouli and H. C. Thoeny, MRI gadolinium-based contrast media: Meeting radiological, clinical, and environmental needs, J. Magn. Reson. Imaging, 2024, 60, 1774–1785,  DOI:10.1002/jmri.29181.
38. K. Dydak, T. Zalewski, M. Kempka, P. Florczak, G. Nowaczyk, Ł. Przysiecka, J. Jagielski, B. Loppinet, M. Banaszak and D. Flak, Nanoassemblies with Gd-chelating lipids (GMO@DTPA-BSA-Gd) as a potential new type of high molecular weight contrast agents, J. Mater. Chem. B, 2024, 12, 12017,  10.1039/d4tb01684j.
39. A. Banerjee, B. Blasiak, E. Pasquier, B. Tomanek and S. Trude, Synthesis, characterization, and evaluation of PEGylated first-row transition metal ferrite nanoparticles as T₂ contrast agents for high-field MRI, RSC Adv., 2017, 7, 38125,  10.1039/c7ra05495e.
40. R. Lapusan, R. Borlan and M. Focsan, Advancing MRI with magnetic nanoparticles: a comprehensive review of translational research and clinical trials, Nanoscale Adv., 2024, 6, 2234–2259,  10.1039/D3NA01064C.
41. A. F. O. Aboushoushah, Iron oxide nanoparticles enhancing magnetic resonance imaging: A review of the latest advancements, J. Sci.:Adv. Mater. Devices, 2025, 10(2), 100875,  DOI:10.1016/j.jsamd.2025.100875.
42. P. Pawar and A. Prabhu, Smart SPIONs for Multimodal Cancer Theranostics: A Review, Mol. Pharmaceutics, 2025, 22(5), 2372–2391,  DOI:10.1021/acs.molpharmaceut.5c00411.
43. M. Behar, K. K. Peck, O. Yildirim, J. Tisnado, A. Saha, J. Arevalo-Perez, E. Lis, Y. Yamada, A. I. Holodny and S. Karimi, T₁-Weighted, Dynamic Contrast-Enhanced MR Perfusion Imaging Can Differentiate between Treatment Success and Failure in Spine Metastases Undergoing Radiation Therapy, Am. J. Neuroradiol., 2023, 44(12), 1451–1457,  DOI:10.3174/ajnr.A8057.
44. Y. Zhuang, Y. Sun, A. Dai, X. Shi, D. Wu, F. Li, H. Hu and S. Yang, Targeted dual-contrast T₁- and T₂ weighted magnetic resonance imaging of tumors using multifunctional gadolinium-labeled superparamagnetic iron oxide nanoparticles, Biomaterials, 2011, 32, 4584–4593,  DOI:10.1016/j.biomaterials.2011.03.018.
45. K. Wang, L. An, Q. Tian, J. Lin and S. Yang, Gadolinium-labelled iron/iron oxide core/shell nanoparticles as T₁–T₂ contrast agent for magnetic resonance imaging, Gadolinium-labelled iron/iron oxide core/shell nanoparticles as T₁–T₂ contrast agent for magnetic resonance imaging, RSC Adv., 2018, 8, 26764,  10.1039/c8ra04530e.
46. P. Caravan, Strategies for increasing the sensitivity of gadolinium based MRI contrast agents, Chem. Soc. Rev., 2006, 35, 512–523,  10.1039/b510982p.
47. E. Terreno, D. D. Castelli, A. Viale and S. Aime, Challenges for molecular magnetic resonance imaging, Chem. Rev., 2010, 110, 3019–3042,  DOI:10.1021/cr100025t.
48. N. Iyad, M. S. Ahmad, S. G. Alkhatib and M. Hjouj, Gadolinium contrast agents-challenges and opportunities of a multidisciplinary approach: Literature review, Eur. J. Radiol. Open, 2023, 11, 100503,  DOI:10.1016/j.ejro.2023.100503.
49. K. B. Ghaghada, M. Ravoori, D. Sabapathy, J. Bankson, V. Kundra and A. Annapragada, New dual mode gadolinium nanoparticle contrast agent for magnetic resonance imaging, PLoS One, 2009, 4(10), e7628,  DOI:10.1371/journal.pone.0007628.
50. Y. Zhang, V. Vijayaragavan, G. K. Das, K. K. Bhakoo and T. T. Y. Tan, Single-phase NaDyF₄:Tb³⁺ nanocrystals as multifunctional contrast agents in high-field magnetic resonance and optical Imaging, Eur. J. Inorg. Chem., 2012, 2044–2048,  DOI:10.1002/ejic.201101203.
51. Y. Feng, Q. Xiao, Y. Zhang, F. Li, Y. Li, C. Li, Q. Wang, L. Shi and H. Lin, Neodymium-doped NaHoF₄ nanoparticles as near-infrared luminescent/T₂-weighted MR dual-modal imaging agents in vivo, J. Mater. Chem. B, 2017, 5, 504–510,  10.1039/C6TB01961G.
52. G. K. Das, N. J. J. Johnson, J. Cramen, B. Blasiak, P. Latta, B. Tomanek and F. C. J. M. van Veggel, NaDyF₄ nanoparticles as T₂ contrast agents for ultrahigh field magnetic resonance imaging, J. Phys. Chem. Lett., 2012, 3, 524–529,  DOI:10.1021/jz201664h.
53. X. Zhang, B. Blasiak, A. J. Marenco, S. Trudel, B. Tomanek and F. C. J. M. van Veggel, Design and regulation of NaHoF₄ and NaDyF₄ nanoparticles for high-field magnetic resonance imaging, Chem. Mater., 2016, 28, 3060–3072,  DOI:10.1021/acs.chemmater.6b00264.
54. E. Gómez-González, C. Caro, D. Martínez-Gutiérrez, M. L. García-Martín, M. Ocaña and A. I. Becerro, Holmium phosphate nanoparticles as negative contrast agents for high-field magnetic resonance imaging: Synthesis, magnetic relaxivity study and in vivo evaluation, J. Colloid Interface Sci., 2021, 587, 131–140,  DOI:10.1016/j.jcis.2020.11.119.
55. E. Gómez-González, C. Caro, N. O. Núñez, D. González-Mancebo, J. D. Urbano-Gámez, M. L. García-Martín and M. Ocaña, Sodium lanthanide tungstate-based nanoparticles as bimodal contrast agents for in vivo high-field MRI and CT, J. Mater. Chem. B, 2024, 12, 11123,  10.1039/d4tb01157k.
56. X. J. Xie, N. Y. Gao, R. R. Deng, Q. Sun, Q. H. Xu and X. G. Liu, Mechanistic investigation of photon upconversion in Nd³⁺-sensitized core-shell nanoparticles, J. Am. Chem. Soc., 2013, 135, 12608–12611,  DOI:10.1021/ja4075002.
57. Y. F. Wang, G. Y. Liu, L. D. Sun, J. W. Xiao, J. C. Zhou and C. H. Yan, Nd³⁺-sensitized upconversion nanophosphors: Efficient in vivo bioimaging probes with minimized heating effect, ACS Nano, 2013, 7, 7200–7206,  DOI:10.1021/nn402601d.
58. J. Shen, G. Y. Chen, A. M. Vu, W. Fan, O. S. Bilsel, C. C. Chang and G. Han, Engineering the upconversion nanoparticle excitation wavelength: Cascade sensitization of tri-doped upconversion colloidal nanoparticles at 800 nm, Adv. Opt. Mater., 2013, 1, 644–650,  DOI:10.1002/adom.201300160.
59. J. Estelrich, M. J. Sánchez-Martín and M. A. Busquets, Nanoparticles in magnetic resonance imaging: From simple to dual contrast agents, Int. J. Nanomed., 2015, 10, 1727–17416,  DOI:10.2147/IJN.S76501.
60. T. H. Shin, Y. Choi, S. Kim and J. Cheon, Recent advances in magnetic nanoparticle-based multi-modal imaging, Chem. Soc. Rev., 2015, 44, 4501–4516,  10.1039/c4cs00345d.
61. C. Cascales, M. D. Serrano, F. Esteban-Betegon, C. Zaldo, R. Peters, K. Petermann, G. Huber, L. Ackermann, D. Rytz, C. Dupre, M. Rico, J. Liu, U. Griebner and V. Petrov, Structural, spectroscopic, and tunable laser properties of Yb³⁺-doped NaGd(WO₄)₂, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 74, 174114,  DOI:10.1103/PhysRevB.74.174114.
62. J. M. Cano-Torres, M. Rico, X. Han, M. D. Serrano, C. Cascales, C. Zaldo, V. Petrov, U. Griebner, X. Mateos, P. Koopmann and C. Kränkel, Comparative study of crystallographic, spectroscopic, and laser properties of Tm in NaT(WO₄)₂ (T = La, Gd, Y, and Lu) disordered single crystals, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 174207,  DOI:10.1103/PhysRevB.84.174207.
63. A. A. Lagatsky, X. Han, M. D. Serrano, C. Cascales, C. Zaldo, S. Calvez, M. D. Dawson, J. A. Gupta, C. T. A. Brown and W. Sibbett, Femtosecond (191 fs) NaY(WO₄)₂ Tm, Ho-codoped laser at 2060 nm, Opt. Lett., 2010, 35, 3027–3029,  DOI:10.1364/OL.35.003027.
64. A. Méndez-Blas, M. Rico, V. Volkov, C. Zaldo and C. Cascales, Crystal field analysis and emission cross sections of Ho³⁺ in the locally disordered single-crystal laser hosts M⁺Bi(XO₄)₂ (M⁺ = Li, Na; X = W, Mo), Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 75, 174208,  DOI:10.1103/PhysRevB.75.174208.
65. US Food&Drug Administration, Code of Federal Regulations Title 21, sec. 172.840, https://www.accessdata.fda.gov/scripts/cdrh/cfdocs/cfcfr/cfrsearch.cfm?fr=172.840.
66. M. Norek and J. A. Peters, MRI contrast agents based on dysprosium or holmium, Prog. Nucl. Magn. Reson. Spectrosc., 2011, 59, 64–82,  DOI:10.1016/j.pnmrs.2010.08.002.
67. S. Liu, T. Tegafaw, H. Yue, S. L. Ho, S. Kim, J. A. Park, A. Baek, M. Y. Ahmad, S. H. Yang, D. W. Hwang, S. Kim, A. Khamis, A. Al Saidi, D. Zhao, Y. Liu, S. W. Nam, K. S. Chae, Y. Chang and G. H. Lee, Paramagnetic ultrasmall Ho₂O₃ and Tm₂O₃ nanoparticles: characterization of r₂ values and in vivo T₂ MR images at a 3.0 T MR field, Mater. Adv., 2022, 3, 5857–5870,  10.1039/d2ma00322h.
68. S. Biju, J. Gallo, M. Bañobre-López, B. B. Manshian, S. J. Soenen, U. Himmelreich, L. Vander Elst and T. N. Parac-Vogt, A magnetic chameleon: Biocompatible lanthanide fluoride nanoparticles with magnetic field dependent tunable contrast properties as a versatile contrast agent for low to ultrahigh field MRI and optical imaging in biological window, Chem. – Eur. J., 2018, 24, 7388–7397,  DOI:10.1002/chem.201800283.
69. P. Caravan, C. T. Farrar, L. Frullano and R. Uppal, Influence of molecular parameters and increasing magnetic field strength on relaxivity of gadolinium- and manganese-based T₁ contrast agents, Contrast Media Mol. Imaging, 2009, 4, 89–100,  DOI:10.1002/cmmi.267.
70. B. Divband, N. Gharehaghaji and M. Takhiri, Effect of Nd doping on MRI relaxitivity of gadolinium oxide nanoparticles, J. Biomed. Phys. Eng., 2020, 10, 580–596,  DOI:10.31661/jbpe.v0i0.2008-1165.
71. H. Du, Q. Y. Wang, Z. Y. Liang, Q. L. Li, F. Y. Li and D. S. Ling, Fabrication of magnetic nanoprobes for ultra high field magnetic resonance imaging, Nanoscale, 2022, 14, 17483–17499,  10.1039/d2nr04979a.
72. N. A. Keasberry, M. Bañobre-López, C. Wood, G. J. Stasiuk, J. Gallo and N. J. Long, Tuning the relaxation rates of dual-mode T₁/T₂ nanoparticle contrast agents: a study into the ideal system, Nanoscale, 2015, 7, 16119–16128,  10.1039/c5nr04400f.
73. J. Gallo, B. I. Harriss, J. Hernández-Gil, M. Bañobre-López and N. J. Long, Probing T₁–T₂ interactions and their imaging implications through a thermally responsive nanoprobe, Nanoscale, 2017, 9, 11318–11326,  10.1039/c7nr01733b.
74. C. C. Huang, C. Y. Tsai, H. S. Sheu, K. Y. Chuang, C. H. Su, U. S. Jeng, F. Y. Cheng, C. H. Su, H. Y. Lei and C. S. Yeh, Enhancing transversal relaxation for magnetite nanoparticles in MR imaging using Gd³⁺-chelated mesoporous silica shells, ACS Nano, 2011, 5, 3905–3916,  DOI:10.1021/nn200306g.
75. X. Han, F. Fusari, M. D. Serrano, A. A. Lagatsky, J. M. Cano-Torres, C. T. A. Brown, C. Zaldo and W. Sibbett, Continuous-wave laser operation of Tm and Ho co-doped NaY(WO₄)₂ and NaLu(WO₄)₂ crystals, Opt. Express, 2010, 18, 5413–5419,  DOI:10.1364/OE.18.005413.
76. A. Méndez-Blas, M. Rico, V. Volkov, C. Zaldo and C. Cascales, Optical emission properties of Nd³⁺ in NaBi(WO₄)₂ single crystal, Mol. Phys., 2003, 101(7), 941–949,  DOI:10.1080/0026897021000046780.
77. S. F. Collins, G. W. Baxter, S. A. Wade, T. Sun, K. T. V. Grattan, Z. Y. Zhang and A. W. Palmer, Comparison of fluorescence-based temperature sensor schemes: Theoretical analysis and experimental validation, J. Appl. Phys., 1998, 84, 4649–4654,  DOI:10.1063/1.368705.
78. S. A. Wade, S. F. Collins and G. W. Baxter, Fluorescence intensity ratio technique for optical fiber point temperature sensing, J. Appl. Phys., 2003, 94, 4743–4756,  DOI:10.1063/1.1606526.
79. A. Nexha, J. J. Carvajal, M. C. Pujol, F. Díaz and M. Aguiló, Lanthanide doped luminescence nanothermometers in the biological windows: Strategies and applications, Nanoscale, 2021, 13, 7913–7987,  10.1039/d0nr09150b.
80. C. D. S. Brites, S. Balabhadra and L. D. Carlos, Lanthanide-Based Thermometers: At the cutting-edge of luminescence thermometry, Adv. Opt. Mater., 2019, 7, 1801239,  DOI:10.1002/adom.201801239.
81. X. Zhou, Y. Wang, H. Wang, L. Xiang, Y. Yan, L. Li, G. Xiang, Y. Li, S. Jiang, X. Tang and X. Zhou, Nd³⁺ and Nd³⁺/Yb³⁺-incorporated complexes as optical thermometer working in the second biological window, Sens. Biosens. Res., 2020, 29, 100345,  DOI:10.1016/j.sbsr.2020.100345.
82. B. B. Zhang and P. C. K. Cheung, A mechanistic study of the enhancing effect of Tween 80 on the mycelial growth and exopolysaccharide production by Pleurotus tuber-regium, Bioresour. Technol., 2011, 102, 8323–8326,  DOI:10.1016/j.biortech.2011.06.021.
83. D. Reitermayer, T. A. Kafka, C. A. Lenz and R. F. Vogel, Interrelation between Tween and the membrane properties and high pressure tolerance of Lactobacillus plantarum, BMC Microbiol., 2018, 18, 72,  DOI:10.1186/s12866-018-1203-y.
84. R. D. Pietersen, I. du Preez, D. T. Loots, M. van Reenen, D. Beukes, G. Leisching and B. Baker, Tween 80 induces a carbon flux rerouting in Mycobacterium tuberculosis, J. Microbiol. Methods, 2020, 170, 105795,  DOI:10.1016/j.mimet.2019.105795.
85. D. Zaręba and M. Ziarno, Tween80™-induced changes in fatty acid profile of selected mesophilic lactobacilli, Acta Biochim. Pol., 2024, 71, 13014,  DOI:10.3389/abp.2024.13014.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis procedure for preparing core–shell nanoprobes C@1S@2S and C@1S@2S@i3S. Characterization of nanomaterials prepared by coprecipitation: room temperature X-ray diffraction patterns. Overtime sizes and size distributions by DLS measurements of nanoprobes in hexane and water solutions. Tables with concentrations of Lns in nanomaterials by ICP-OES. Plots of the magnetization vs. the applied magnetic field for prepared nanoprobes. Plots of R₁ and R₂ vs. [Ln] concentration for r₁ and r₂ calculations. Solid state synthesis of Yb, Nd:NaGd(WO₄)₂ polycrystalline samples, description and characterization. Thermal evolution of LIR Yb/Nd of the polycrystalline sample with composition 7.5 at% Nd, 7.5 at% Yb:NaGd(WO₄)₂, λ_EXC = 803.4 nm. Fluorescence images of HeLa and MC3T3 cells treated with water dispersions of the C@1S@2S@i3S nanoprobe and stained with DAPI. See DOI: https://doi.org/10.1039/d5tb00548e

---