Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
From window panes to bone regeneration: structure, viscosity and bioactivity of soda lime silicate glasses†
Zhaorui
Jin
a,
Daniel R.
Neuville
 *b,
Coraline
Chartier
*b,
Coraline
Chartier
 a,
Pavel
Kachanov
a,
Scott
Kroeker
a,
Pavel
Kachanov
a,
Scott
Kroeker
 c,
Stéphane
Gin
d,
Jincheng
Du
c,
Stéphane
Gin
d,
Jincheng
Du
 *e and
Delia S.
Brauer
*e and
Delia S.
Brauer
 *a
*a
aOtto Schott Institute of Materials Research, Friedrich Schiller University, Lessingstr. 12 (AWZ), 07743 Jena, Germany. E-mail: delia.brauer@uni-jena.de
bGeomat Lab, Institut de Physique du Globe de Paris, CNRS-UPC, 1 rue Jussieu, 75005 Paris, France. E-mail: neuville@ipgp.fr
cDepartment of Chemistry, University of Manitoba, Winnipeg, Manitoba R3T 2N2, Canada
dCommissariat à l’énergie atomique et aux énergies alternatives, DES, ISEC DPME, SEME, University of Montpellier, Marcoule, 30207 Bagnols-sur-Cèze, France
eDepartment of Materials Science and Engineering, University of North Texas, Denton, TX 76207, USA. E-mail: jincheng.du@unt.edu
First published on 8th February 2025
Abstract
Silicate glasses are not only used for everyday items such as windows or drinking glasses. By altering their composition, one can adjust their properties to allow them to become degradable and help to regenerate bone. Here, we investigate how compositional changes from conventional soda lime silicate glasses to low-silica content compositions affect their structure and properties. Results show that silicate network polymerisation, known as network connectivity, controls many properties, including viscosity, which is relevant for processing, and reactivity in aqueous environments. Correlating our data with in vivo results from the literature, we show how changes in silicate network connectivity as represented by their modifier content and non-bridging oxygen concentration, allow us to turn bioinert soda lime silicate glasses into bioactive materials to enhance bone formation.
Introduction
We all use glass in our daily lives, and soda lime silicate glasses are the best-known glass system, as its high silica content compositions are commonly used for everyday articles such as window panes or drinking vessels. But even staying within this well-known ternary system, properties can change dramatically if we change the composition, leading to very different fields of application. The chemically stable glasses used in architecture and household ware are at one end of the compositional range, while towards lower silica contents, the glasses become less chemically durable and can be partially or fully dissolved in aqueous solutions.Because of its common use, the high silica content compositional range has been the focus of most publications characterising their structure and properties through various characterisation techniques (see publication by Neuville1 and references therein). Owing to the increasing crystallisation tendency for compositions of lower silica content (below 60 mol% SiO2), they have been investigated much less often. Low silica content glasses, however, have attracted great interest as biomaterials for several decades now; and while the most well-known bioactive glasses contain small amounts of phosphate,2–4 even simple soda lime silicate glasses do promote in vivo bone formation if the silica content is low.5
Even though this has been known for a number of years, and bioactive glasses have been the focus of structural analyses for nearly as long,6 a systematic investigation of how a decrease in silica content affects atomic arrangement and, thus, causes the change in properties from bio-inert to bio-active, is still lacking. For this reason, we investigated glasses in the system CaO–Na2O–SiO2 with silicate contents between 70 and 50 mol%, combining structural analyses by solid-state nuclear magnetic resonance spectroscopy with viscosity measurements, chemical durability studies and molecular dynamics simulations. In addition, we correlate our findings with those from in vitro and in vivo bioactivity studies in the literature.
Results and discussion
Glass structure
Analysed glass compositions were close to the nominal ones (Table 1). XRD results showed no sharp reflexes, thus confirming the absence of any crystalline phases in the materials (results not shown).| Glass | SiO2 | CaO | Na2O | NC | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| nom. | an. | nom. | an. | nom. | an. | nom. | an. | NMR | MD | |
| Si70 | 70 | 69.4 ± 1.5 | 15 | 15.8 ± 1.4 | 15 | 14.8 ± 0.2 | 3.14 | 3.12 | 3.24 | 3.15 |
| Si65 | 65 | 65.8 ± 1.8 | 17.5 | 17.0 ± 1.7 | 17.5 | 17.2 ± 0.4 | 2.92 | 2.96 | n.d. | 2.93 |
| Si60 | 60 | 60.4 ± 0.6 | 20 | 19.9 ± 0.3 | 20 | 19.7 ± 0.3 | 2.67 | 2.69 | 2.68 | 2.67 |
| Si55 | 55 | 55.8 ± 0.7 | 22.5 | 22.4 ± 0.9 | 22.5 | 21.8 ± 0.3 | 2.36 | 2.42 | n.d. | 2.38 |
| Si50 | 50 | 51.1 ± 0.6 | 25 | 25.0 ± 0.4 | 25 | 23.9 ± 0.6 | 2.00 | 2.09 | 2.19 | 2.02 |
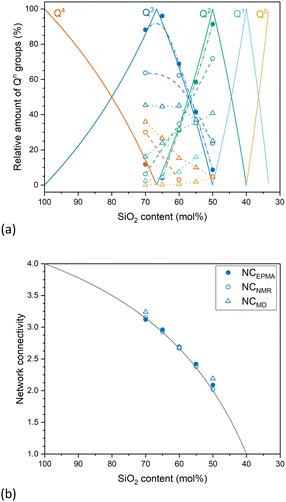
MAS NMR spectra of glasses Si50, Si60 and Si70, shown in Fig. 1, exhibit a broad peak between −60 and −105 ppm, with the maximum position moving to less negative values with decreasing silicate content. This change indicates that the glasses are becoming more depolymerised as expected from compositional changes.7 In silicate glasses, the main building units of the network are SiO4 tetrahedra of silicon atoms surrounded by four oxygens. These tetrahedra are typically referred to as Qn groups, with n being the number of bridging oxygen atoms (BO; ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O–Si
Si–O–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ) connected to the central silicon atom. The deconvolution of the 29Si MAS NMR spectra into Gaussian signals for the different Qn species provided information on the relative amounts of these groups and how they change with SiO2 content (Fig. 1). Results agree with the expected depolymerisation of the silicate network with decreasing silica content, as increasing network modifier contents (here sodium and calcium oxide) turn BO into two non-bridging oxygen atoms each (NBO;
) connected to the central silicon atom. The deconvolution of the 29Si MAS NMR spectra into Gaussian signals for the different Qn species provided information on the relative amounts of these groups and how they change with SiO2 content (Fig. 1). Results agree with the expected depolymerisation of the silicate network with decreasing silica content, as increasing network modifier contents (here sodium and calcium oxide) turn BO into two non-bridging oxygen atoms each (NBO; ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O− M+, where M+ is a modifier cation).
Si–O− M+, where M+ is a modifier cation).
The positions of the peak maxima, the half width at half maximum (hwhm) and intensity of different Qn distributions (I%) are presented in Table 2. The structure of glass Si70, close in composition to window or container glass, is dominated by Q3 species, with Q4 being present to a lesser extent and small amounts of Q2 being found as well, which corresponds to a typical 3D silicate network. With decreasing silica content, the relative amounts of Qn groups with smaller values for n increase, with glass Si50, close to bioactive glass compositions, mostly showing Q2 species, with lesser amounts of Q3 and small amounts of Q1. The structure of Si50 therefore is a weekly cross-linked silicate network, containing significant parts consisting of Q2 chains.
| Si70 | Si65 | Si60 | Si55 | Si50 | ||
|---|---|---|---|---|---|---|
| Q0 | δ (hwhm) | — | n.d. | — | n.d. | — |
| I NMR | — | n.d. | — | n.d. | — | |
| I th | 0 | 0 | 0 | 0 | 0 | |
| I MD | 0.0 | 0.2 | 0.5 | 1.9 | 4.2 | |
| Q1 | δ (hwhm) | — | n.d. | — | n.d. | −67.1 (2.3) |
| I NMR | — | n.d. | — | n.d. | 4.5 | |
| I th | 0 | 0 | 0 | 0 | 0 | |
| I MD | 2.5 | 4.5 | 7.5 | 15.8 | 24.8 | |
| Q2 | δ (hwhm) | −78.2 (4.0) | n.d. | −75.3 (4.9) | n.d. | −74.3 (4.9) |
| I NMR | 6.3 | n.d. | 34.7 | n.d. | 71.8 | |
| I th | 0 | 7.7 | 33.3 | 63.6 | 100 | |
| I MD | 16.2 | 24.0 | 31.6 | 35.2 | 40.9 | |
| Q3 | δ (hwhm) | −87.1 (5.6) | n.d. | −83.9 (5.7) | n.d. | −83.3 (5.5) |
| I NMR | 63.7 | n.d. | 62.3 | n.d. | 23.7 | |
| I th | 85.7 | 92.3 | 66.7 | 36.4 | 0 | |
| I MD | 45.4 | 44.6 | 45.1 | 37.1 | 25.1 | |
| Q4 | δ (hwhm) | −97.7 (6.1) | n.d. | −93.9 (3.6) | n.d. | — |
| I NMR | 30 | n.d. | 3 | n.d. | — | |
| I th | 14.3 | 0 | 0 | 0 | 0 | |
| I MD | 35.9 | 26.6 | 15.3 | 10.0 | 4.9 | |
As the amount of NBO formed, i.e. the depolymerisation of the silicate network, depends on the relative amount of modifier oxides compared to silica,8 one can estimate the relative amounts of Qn groups from the nominal or analysed composition of simple glasses.9 The results of these calculations (both for nominal and analysed compositions) show good agreement with results obtained from MAS NMR experiments (Fig. 2a). Results from MD simulations, while giving the same trend, show a broader distribution of Qn groups, including isolated orthosilicate (Q0) groups for all glasses except Si70, which has been commonly observed with MD simulations.10
Instead of describing glass structure by the relative amounts of each type of Qn group, it is easier to use a single parameter describing the degree of silicate network polymerisation. Network connectivity (NC; Table 1) is one such parameter.11 It describes the average number of BO per SiO4 tetrahedron (the maximum value of 4 corresponding to the fully polymerised network of fused silica), thereby providing an average value of n of all Qn groups present in the glass. In simple soda lime silicate glasses NC is calculated as:
| NC = (4cSiO2 − 2(cNa2O + cCaO))/cSiO2 | (1) |
A decrease in NC corresponds to a depolymerisation of the silicate network, with an NC of 2 describing a chain structure, held together by chain entanglements and ionic bridges between chains rather than by covalent cross-links. This decrease in network connectivity with decreasing silica content is shown in Fig. 2b for nominal and experimental values of the glasses studied here as well as values from MD simulations, all showing a consistent trend.
Soda lime silicate glasses from our MD simulations show network structures similar to our experimental ones, with network connectivity being consistent with 29Si MAS NMR results and theoretical predictions (Table 1). To better visualise the simulated glass network structures, residual network structures are shown in Fig. 3, where the largest covalently connected silicate network units have been removed (modifier cations such as Na+ and Ca2+ were also removed for clarity). For Si70, which has an average NC of 3.15, most of the SiO4 units were in the largest piece of the network structures (Fig. 3a), confirming a highly polymerised silicate network as shown by 29Si MAS NMR results and theoretical predictions. The small amount of small silicate moieties remaining is likely to originate from the broader distribution of Qn groups in MD simulation results. Glass Si60, which has an average NC of 2.67, only shows some branched chains left after removal of the largest network units (Fig. 3b). By contrast, it can be seen that the Si50 glass network structure is highly depolymerised, and the removal of the largest network unit left behind branched moieties as well as chains and islands (Fig. 3c), suggesting a highly disrupted glass network consistent with a network connectivity of 2.02.
 | ||
| Fig. 3 Residual network structure of glasses (a) Si70, (b) Si60 and (c) Si50 obtained from MD simulations after the largest network pieces (and Na+ and Ca2+ cations) were removed. | ||
Another way of characterising the glass network structure is the ring size distribution, shown in Fig. 4a for all glasses. Ring size distributions have a first peak centred at 6-membered rings; peak intensity increases with silica content. Average ring size of the present glasses is relatively constant for glasses Si70, Si65 and Si60; however, for lower silica contents (glasses Si55 and Si50) it decreases rapidly. This is in contrast to NC, which changes more continuously with silica content as shown by 29Si MAS NMR experiments (Fig. 2b) and MD simulation (Fig. 4b).
MD simulations can also give information on the short-range order. In Fig. 4c and d, neutron broadened total correlation function T(r) and major partial contributions as well as partial T(r) and corresponding coordination numbers are presented. Silicon is perfectly four-fold coordinated in all glasses, agreeing with it being present as SiO4 tetrahedra exclusively. Si–O peak distance is 1.61 Å. Ca–O coordination number is 5.8 (peak distance 2.38 Å), while Na–O coordination number is 5.3 with an Na–O peak distance of 2.40 Å, in good agreement with results from neutron diffraction.12 The change with composition is fairly small, indicating that while changing the ratio of network former (SiO2) to network modifiers affects glass structure on a longer range (silicate network connectivity and ring size distributions), its influence on the short-range order is negligible here.
Viscosity, diffusion and thermal properties
Fig. 5a shows the low-temperature viscosity data (around Tg) plotted as a function of temperature. Data were fitted with the Vogel–Fulcher–Tammann (VFT) equation (eqn 2):1 | (2) |
 | ||
| Fig. 5 Viscosity of the glasses as a function of temperature fitted with (a) the Vogel–Fulcher–Tammann and (b) the Adam–Gibbs method. Symbols show experimental data points and dashed lines show fitting. (c) Viscosity of the glasses as a function of network connectivity, plotted for various temperatures. Symbols show values fitted by Adam–Gibbs, and lines are visual guides only. (d) Be/Sconf(Tg) (Table S2, ESI†) plotted as a function of network connectivity. Dashed line is a visual guide only. | ||
The three adjustable parameters, A, B and T1, are listed in Table S1 (ESI†); data and fitted curves are plotted together in Fig. 5a. It is noticeable that the difference in viscosity between glass Si65 and Si70 is smaller than between the other compositions. The fitting curves for all compositions are nearly parallel, suggesting comparable rates in viscosity change.
Combined data of low-temperature and high-temperature viscosity measurements were fitted with the Adam–Gibbs equation (eqn 3):1,13
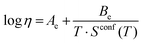 | (3) |
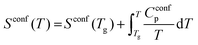 | (4) |
The configurational entropy of the glass remains constant up to the glass transition temperature, Sconf(Tg). Changes in configurational entropy in the melt are associated with configurational heat capacity, Cconfp.1,13,14 For silicates, Cconfp has been described as the difference in heat capacity between the liquid and the glass at transition temperature.15
Besides the decrease in viscosity with increasing temperature, the glasses also show a decrease in viscosity with decreasing silica content (Fig. 5c). This originates from the reduction in network connectivity, i.e. the presence of smaller silica moieties, with lower silica content (illustrated by MD shown in Fig. 3), facilitating movement at a given temperature. Viscosity is closely connected to glass processing at elevated temperatures. With decreasing network connectivity, a given viscosity (as well as Tg, which corresponds to a viscosity of 1012 Pa s, Fig. 7a and b) is reached at lower temperatures, facilitating glass processing. This advantage is counterbalanced, however, by the increase in crystallisation tendency resulting in the typical poor processing shown by bioactive glasses of low silica content and network connectivity.16–18
Toplis plotted Be/Sconf(Tg) over SiO2 content for a series of sodium silicate glasses with varying silica content,19 showing that the ratio remained relatively constant up to 67 mol% SiO2 before increasing steeply. He explained this by differences in viscous flow mechanisms: for SiO2 contents below 67 mol%, one can, on average, expect at least one NBO per silicon, resulting in a constant energy barrier for viscous flow in this range. At larger SiO2 contents, by contrast, the energy barrier can be expected to be higher owing to less NBO being present. In our present study, we also find an increase in Be/Sconf(Tg) with silica content (plotted over network connectivity in Fig. 5d), despite remaining in the compositional region where Toplis found constant values.
The fragility of a glass melt describes how quickly upon cooling its viscosity (plotted as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η) approaches the viscosity of 1012 Pa s, corresponding to Tg. It therefore refers to the slope of the curve log
η) approaches the viscosity of 1012 Pa s, corresponding to Tg. It therefore refers to the slope of the curve log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η vs. Tg/T near Tg. Strong liquids show a linear increase in viscosity with increasing Tg/T (Fig. 6a), while for fragile liquids the curve shows a deviation from the linear line, resulting in a more rapid increase in viscosity nearing Tg.20 With decreasing silica content, i.e. with decreasing network connectivity, the fragility of the glasses in the present study increases (Fig. 6a), as expected.
η vs. Tg/T near Tg. Strong liquids show a linear increase in viscosity with increasing Tg/T (Fig. 6a), while for fragile liquids the curve shows a deviation from the linear line, resulting in a more rapid increase in viscosity nearing Tg.20 With decreasing silica content, i.e. with decreasing network connectivity, the fragility of the glasses in the present study increases (Fig. 6a), as expected.
 | ||
| Fig. 6 (a) Viscosity plotted over Tg/T to display the fragility of the melts. The dashed line represents a strong liquid. (b) Diffusivity calculated from the viscosity data of the glasses in this study together with that of glasses of the nominal molar composition 50SiO2–50CaO (NC50.00), 60SiO2–40CaO (NC60.00) and 60SiO2–40Na2O (NC60.40).1 Results are compared with literature values for a soda lime silicate glass of a related composition (71.7SiO2–12.8CaO–15.5Na2O, mol%), including self-diffusion coefficients of ions in obtained by isotope tracer technique for oxygen (DO; red crosses) by Oishi et al.,21 sodium (DNa+; blue crosses) and calcium (DCa2+; grey crosses) by Johnson et al. (cited and plotted by Oishi et al.21) and diffusivity calculated from the viscosity data (Dη; black crosses) by Oishi et al.21 | ||
Oishi et al.21 experimentally determined the self-diffusion coefficients of oxygen for a soda lime silicate glass of the composition 71.7SiO2–12.8CaO–15.5Na2O (in mol%; given by the authors in weight percentages as 72SiO2–12CaO–16Na2O) from the melt to the solid glass. The authors compared their results with the self-diffusion coefficients of calcium and sodium in the same composition from the literature as well as with the diffusion coefficient calculated from viscosity data using Eyring's relationship.21,22 The authors show that for the soda lime silicate glass (as well as for a soda silicate glass, not shown here) diffusion coefficients calculated from the viscosity show good agreement with self-diffusion coefficients of oxygen, at least in the liquid range (Fig. 6b). This agrees with activation energies for oxygen self-diffusion in the liquid state being close to the activation energies for viscosity for both of these glasses, which the authors interpret as viscous flow being rate-controlled by the diffusion of oxygen ions in these two silicate glasses.21 The authors point out that these are not necessarily free oxygen ions but rather the exchange of oxygen ions between neighbouring silicate units, meaning that their diffusion does not necessarily involve electrical charge transport.
The diffusivity derived from the viscosity data (Fig. 6b) using Eyring's relationship has been calculated for the present glasses (Fig. 6b). Both viscosity and diffusivity pronouncedly change with temperature but in opposite directions. Variation with network connectivity also is in opposite directions, as the diffusivity increases with decreasing network connectivity, i.e. increasing modifier content. Increasing diffusivity (albeit differences being small, Fig. 6b) with increasing modifier content, as observed for the present glasses with constant calcium to sodium ion ratio, can be explained by a decrease in the activation energy for diffusion.9 For comparison, we are also showing diffusivity results from three glasses of nominal composition 50SiO2–50CaO (NC50.00), 60SiO2–40CaO (NC60.00) and 60SiO2–40Na2O (NC60.40).1 Glasses NC50.00 and NC60.00 show very similar values, with differences probably being within the error limits. Comparison of glasses NC60.00 (Ca2+ as modifier only), Si60 (both Ca2+ and Na+ as modifiers) and NC60.40 (Na+ as modifier only), by contrast, clearly shows the influence of the type of modifier cation (or, rather, modifier cation field strength) on diffusivity, with the sodium silicate glass having the highest diffusivity, the corresponding calcium silicate glass the lowest and the mixed soda lime composition lying in between.
The results by Oishi et al. also show that in the soda lime silicate glass oxygen diffusivity is lower than diffusivity of calcium and sodium ions (Fig. 6b).21 They showed this to be opposite to a calcium aluminosilicate slag (40SiO2–20Al2O3–40CaO, in wt%), where oxygen diffusivity was higher than diffusivity of calcium or aluminium. The experimental diffusivity values of the present study, obtained from viscosity data, also are much lower than diffusivity of calcium or sodium ions for compositions related to the present ones published in the literature, including obsidian, diopside, orthoclase and albite glasses (Fig. 6b and Fig. S1, ESI†).21,23,24 This, we interpret as diffusivity in soda lime silicate glasses being rate controlled by the oxygen ions in the silicate network, as described above.
Similar to viscosity, glass transition temperature and dilatometric softening point vary with network connectivity (Fig. 7a). For comparison, Fig. 7b shows the glass transition temperature obtained from viscosity experiments, i.e. the temperature corresponding to a viscosity of 1012 Pa s, which also shows an increase with increasing network connectivity. The thermal expansion coefficient, by contrast, shows a pronounced decrease with increasing network connectivity, owing to lower numbers of modifier ions in the glass vibrating in their oxygen polyhedra.
Correlation with degradation and bioactivity data
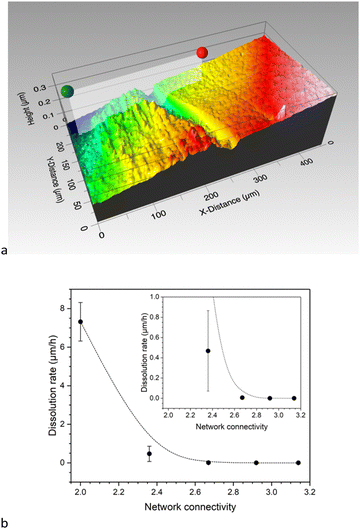
The dissolution behaviour of the glasses has been investigated under very dilute and constant conditions (37 °C, pH 7.45) to prevent solution feedback or precipitation of secondary phases. The glass dissolution rate was obtained from the step height resulting from dissolution of a flat surface and comparing it to a protected, pristine one (Fig. 8a). This method follows a recently published ASTM standard (standard test method for measurement of glass dissolution rate using stirred dilute reactor conditions on monolithic samples, ASTM C1926-23). Again, network connectivity had a pronounced effect: Results show a drastic decrease in dissolution rate from glass Si50 (NC 2.0) to Si55 (NC 2.36), while the remaining glasses show more similar dissolution rates (Fig. 8b). This shows that the more depolymerised glasses, i.e. glasses with lower network connectivity, dissolved faster, as explained in the following.During the corrosion process, a highly connected three-dimensional network provides more resistance to glass corrosion. This trend with network connectivity is related to several factors, including the interaction of water molecules with glass surface features and water diffusion into the glass. Tilocca's molecular dynamics simulations have shown that the depolymerisation of the silicate network by modifiers plays an important role in the interaction between water molecules and glass surfaces.25,26 Modifiers not only act as hydrophilic sites; as Lewis acids they also aid in the dissociation of water molecules. The latter causes fast ion release as well as formation of Si–OH groups. The diffusivity of water molecules at high temperatures also increases with increasing modifier content, as previously shown for sodium silicate glasses,27 which, together with the molecular dynamics simulations, suggests easier water diffusion in the glass with increasing modifier content.
In borosilicate, aluminosilicate and boroaluminosilicate glasses with an overall network connectivity of 3 and above, corrosion rate was shown to increase proportionally with the average ring size.28 This was explained by water molecules diffusing into the glass structures needing to pass through these rings. The larger the average ring size, the easier water molecule diffusion and penetration into the bulk glass, hence the higher the dissolution rate. This model worked well for more connected network structures, e.g. nuclear waste glasses designed for high chemical durability. The present glasses show the opposite trend, however, with average ring size being largest for glasses with the highest network connectivity (Fig. 4b), i.e. for glasses with the lowest solubility (Fig. 8). This suggests that for glasses of low network connectivity, ring size is less important owing to the highly depolymerised silicate network containing chain-like areas in its structure.
Published molecular dynamics simulations have revealed that the depolymerisation of the silicate network in compositions of large modifier contents (Fig. 3), resulting in the presence of small network moieties including chain-like units or rings,29 also plays a critical role in glass dissolution, owing to a lower energetic cost of their release into solution.30 As a result, the initial dissolution rate of the well-known Bioglass 45S54 is several orders of magnitude larger than that of other silicate glasses (including soda lime similar to Si70 and Roman glass) included in a recent review paper.31
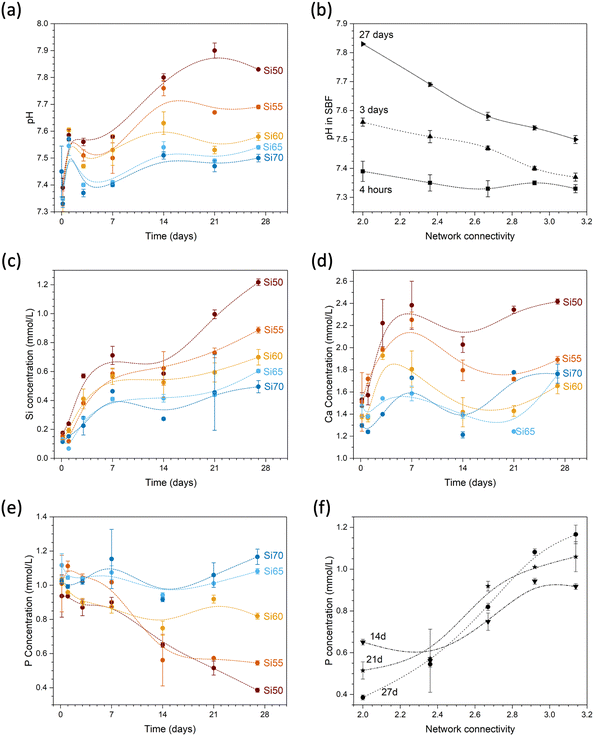
During immersion in simulated body fluid (SBF), pH increased with time (Fig. 9a) as a result of the reaction of water molecules with the glass network and the formation of silanol groups as described above. This pH increase, again, is more pronounced with decreasing network connectivity (Fig. 9b). Silicon concentrations in solution increased with time but also with decreasing silica content and network connectivity, with glass Si50 showing the largest concentrations (Fig. 9c). While the concentrations of soluble silica species in solution depends on various factors including solution pH,32 changes in silica solubility are small in the pH range studied here, i.e. between pH 7.45 and 7.8, and this trend therefore seems to confirm the increased dissolution rate observed in diluted conditions presented above (Fig. 8b).
The effect on solution pH may help us to further understand the high solubility of glass Si50 under very dilute conditions presented above. Although the set-up of the stirred reactor coupon analysis maintains the solution pH constant (as confirmed by measurements), pH changes within the hydrated silicate network may still have played a role here. As shown by computer simulations,33 modifiers provide pathways for water penetration into the network. In addition, non-bridging oxygen anions act as proton acceptors (forming silanol groups), thereby facilitating dissociation of water molecules. The latter will increase the pH locally (and potentially also generally, depending on the conditions), owing to formation of hydroxyl anions.33 It is known that high pH values enable dissolution of the silicate network by nucleophilic attack through hydroxyl anions.34 As these above occur more often in glasses with larger modifier contents, i.e. lower network connectivity,35 a more pronounced pH increase locally36 within the hydrated parts of the silicate network is more likely to occur for Si50 than the remaining glasses. The resulting localised high pH may promote dissolution of the silicate network and, thus, may be the reason for the large difference between glass Si50 and the remaining compositions, and it may be described as an autocatalytic effect promoting glass dissolution.
Calcium concentrations in solution increased rapidly at early time points of immersion (Fig. 9d). Absolute concentrations are also highest for glass Si50; however, as this glass has the highest modifier content, the result is not that meaningful (owing to the inherent calcium concentrations of SBF, normalisation to the amounts present in the glass is difficult). Phosphate concentrations in SBF show an opposite trend: while concentrations for glasses with high silica contents remained relatively constant, concentrations decreased with time for glasses with lower silica contents (Fig. 9e). As a result, concentrations at later time points (shown from 7 days in Fig. 9f) increased with increasing network connectivity. As the glasses studied here are phosphate free, all phosphate in solution originates from the SBF. Fig. 9e shows that the phosphate concentration for glass Si70 (NC 3.14) during immersion remains the same as before immersion, within the error limits. The observed decrease in phosphate content with decreasing NC is therefore related to precipitation of phosphates from solution. SBF is used to test for apatite surface mineralisation in vitro, and its composition not only mimics the concentrations of inorganic components in blood plasma, it is also close to saturation with regard to apatite.37 The apatite forming capacity of soda lime silicate glasses in SBF has been demonstrated by Fujibayashi et al.,5 who investigated the same compositions as studied here: glasses Si50 to Si65 all formed apatite surface layers during immersion in SBF (Fig. 10), with the time point of first apatite detection varying from 12 hours (Si50, NC 2.0) to 21 days (Si65, NC 2.92). Glass Si70 did not form an apatite surface layer within the time period studied (28 days).
 | ||
| Fig. 10 Percentage of new bone formation during animal experiments performed on rabbits (left axis) and first time point of apatite detection during immersion in SBF (right axis); for glass Si70 (NC 3.14) no apatite was detected within the 28-day period investigated (lines are visual guides only. Data plotted from Fujibayashi et al.5). | ||
Fujibayashi also performed in vivo experiments on the soda lime silicate glasses presented here, by implanting granules of the glasses into holes drilled into the femurs of rabbits.5 Subsequently, they quantitatively analysed the amount of new bone ingrowth from the outer edge of the defect towards the centre. Their results at six weeks are plotted in Fig. 10, showing a linear decrease with increasing network connectivity of the glass, representing a change from bioactive at low NC to bio-inactive at high NC. The authors interpreted their results as bone ingrowth among glass particles increasing in proportion to their in vitro apatite-forming capacity, concluding that evaluating apatite formation in SBF is a good screening test for the in vivo bioactivity of materials. However, the relationship shown by Fujibayashi et al. between in vitro apatite precipitation and in vivo bone formation probably may not hold true for all types of glasses, which becomes obvious if one considers glasses containing toxic elements such as barium.
Based on our results on glass structure and other properties, we explain the trends observed both in vitro (besides apatite precipitation also dissolution, ion release and pH changes) and in vivo (formation of new bone) to originate from the differences in silicate network polymerisation as represented by their network connectivity values and ring size distributions. Increasing concentrations of NBO and modifier ions make the glasses more susceptible to water attack,33,35 which can be a disadvantage for more conventional applications of soda lime silicate glasses but also proves to be a great benefit in the area of biomaterials for bone regeneration.
Experimental
Glass synthesis
Glasses in the system CaO–Na2O–SiO2 (Table 1) were prepared by a melt-quench method; reagents Na2CO3, CaCO3 and SiO2 were used as starting materials. Powder of the starting materials was pre-dried at 350 °C for Na2CO3, 500 °C for CaCO3 and 1000 °C for SiO2 overnight. Stoichiometric amounts of powders were thoroughly mixed to make 100 g batch of glass. Glasses were melted in covered platinum crucibles in an electric furnace. Batches were held at 850 °C for 30 min for decarbonation, then the temperature was increased to 1500 °C and held for 3 hours. Afterwards, samples were quenched in a 4 mm height copper mould and transferred to a pre-heated annealing furnace set to 550 °C and cooled to room temperature in the switched-off oven overnight.XRD and compositional characterisation
Glasses were milled into powder and the absence of crystalline phases was tested by powder X-ray diffraction (XRD; Rigaku MiniFlex 300; Cu Kα; 10 to 70°2θ, 1° min−1; measurements performed at room temperature). Glass composition was analysed by electron probe micro-analyzer (EPMA) on bulk samples.Thermal analysis
Dilatometry was performed on cylindric specimens (4 mm in diameter and 20 mm in length) at a heating rate of 5 K min−1 to obtain glass transition temperature (Tg), dilatometric softening point (Ts) and thermal expansion coefficient (α; between 100 and 400 °C).Solid state nuclear magnetic resonance spectroscopy
29Si magic angle spinning nuclear magnetic resonance (MAS NMR) spectra were acquired at 12.5 kHz using a Bruker Avance III 400 MHz NMR spectrometer with an operating field strength of 9.4 T at room temperature. The powder samples in a particle range 38 to 125 μm were filled into a ZrO2 rotor with 4 mm diameter and spun at a spin frequency of 12.5 kHz. The spectra are made up of an accumulation of 2048 scans with a pulse angle of 90° and a recycle delay of 30 s between pulses. Line broadening (LB) equal to 200 Hz was applied for the processing parameter. NMR data were collected and deconvoluted using the software Fityk. Spectra were deconvoluted into Gaussian functions using as few Gaussian curves as necessary and trying to keep peak position and linewidth constant for the same Qn species.Viscosity measurements
High viscosity measurements in the range of 108 to 1013 Pa s were performed using a creep apparatus according to Neuville et al.1,13 on rectangular glass samples (9 mm in height and around 3 mm in width and length). The temperature on top and bottom of the sample was recorded by two Pt–Pt/Rh10% thermocouples separately. A silver cylinder was fixed outside the measurement zone to ensure the temperature difference along the sample remained within 0.3 K throughout. The height change of the samples was measured during compression by means of two linear variable differential transformers located above and below the sample, and the deformation rate of sample was calculated with the height change as a function of time. Dynamic viscosity η (in Pa s) was subsequently calculated as described previously.1,13 The high viscosity measurement for one temperature was repeated more than four times under different applied stress. The calculated viscosity data of different stresses were averaged in the end to ensure accurate results.Low viscosity measurements were performed as described by Neuville1 in a vertical tube furnace. This set-up can measure the viscosity of the glass in the temperature range from 1150 to 1950 K. A tailor-made cylindrical PtRh15% or PtIr10% crucible with a height of 50 mm and an inner diameter of 27 mm was fixed on an alumina tube leading from below to the interior of the furnace. After the glass in the crucible has been heated to a molten state, a rotating cylinder, which with 23° conical extremities, a diameter of 14 mm and a height of 21 mm, was submerged into the melt from the top of the crucible downwards. The viscosity was then calculated by the torque exerted on the rotating cylinder under the force of the melt at different angular velocities as described previously.1 At least five torques with different angular speeds were investigated for each temperature. The viscosity in the range of 104 to 108 Pa s could not be tested with the equipment used here, owing to crystallisation of the glasses studied.13,14
Chemical durability experiments
Dissolution experiments were performed following the SRCA alteration test38 in a large vessel containing 8.8 L of a 0.065 M Tris–HCl solution39 (tris(hydroxymethyl)aminomethane, ≥99.8%, Sigma-Aldrich, and 37% HCl and MilliQ water) at 37 °C and pH 7.45. The solution was mechanically stirred at 60 rpm. The solution was prepared a day before and the pH was adjusted an hour before the beginning of the experiment. Dimensions of the samples were measured prior to immersion. Samples were immersed simultaneously in the same solution for 2 minutes (Si50), 5 minutes (Si55), 2.8 days (Si60) and 6.7 days (Si65 and Si70). The large differences in time are explained by the difference of dissolution rate and the working range of the interferometer (between a few nm and 1 mm step height). Solution pH was measured before and after the measurement. After removing the samples, they were thoroughly rinsed with ethanol and left to dry. The silicone mask was removed and the step height between exposed and protected surface (Fig. 8a) was measured using an interferometer (Profilm3D Optical Profilers, Filmetrics; measurements taken using a PSI laser at 20x magnification). This experiment was performed in duplicate, with 10 measurements per sample; measurements had a repeatability of 0.1 nm. Dissolution rate was calculated according to eqn (5):
 | (5) |
ΔDissolution![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rate = 0.0224 nm t−1. rate = 0.0224 nm t−1. | (6) |
SBF was prepared following the recipe for SBF 10 as published by Helebrant et al.37 using KCl (p.a., Laborchemie Apolda, Germany), NaHCO3 (≥99.5%, Merck, Darmstadt, Germany), NaN3 (≥99%), MgSO4·7H2O (≥99%), KH2PO4 (≥99%), NaCl (≥99.5%), tris(hydroxymethyl)aminomethane (tris, ≥99.9%) (all Carl Roth, Karlsruhe, Germany), CaCl2 solution (prepared using 37% HCl, p.a., Carl Roth, and CaH2, 92%, Thermo Fisher, Germany) and deionised water. The pH was adjusted to between 7.3 and 7.4 at 37 °C by adding 37% HCl. 45 ± 0.1 mg of glass particles was immersed into 30 mL of SBF, i.e. a ratio of 1.5 mg mL−1 as recommended in the literature.40 Samples were incubated in a shaking incubator at 37 °C and 120 rpm (KS 4000i control, IKA, Germany). Duplicate samples were prepared for each time point (4 hours up to 27 days). At the end of each immersion period, pH was tested and particles and solution separated by filtration through narrow-pore filter paper (FiltrakTM 390, Munktell). Solutions were acidified using 65% nitric acid and analysed by inductively coupled plasma optical emission spectroscopy (ICP-OES; 5800 ICP-OES, Agilent, Germany). Calibration standards were prepared by diluting single-element ICP standard solutions (1000 mg L−1, Carl Roth); 5 standard solutions with different concentrations were prepared for each element. Samples were diluted by a factor 10 with deionised water to decrease ion concentrations to the equipment sensitive level.
Molecular dynamics simulations
MD simulations of all the glass compositions were performed to understand the atomic structures of these glasses using a set of partial charge pairwise potential that is known as Teter potential with modification by Du & Cormack41,42 and further expanded by Deng & Du.43,44 The potential has been shown to reproduce well both the short and medium range structures of silicate and phosphosilicate glasses. Based on the glass composition in Table 1, the glass structures were generated by using a simulated melt and quench process. Each glass is represented by around 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms in a cubic simulation cell with dimension according to the experimental density. The initial randomly generated configurations were first melted at 5000 K and then cooled down to 3000 K under the NVT ensemble with a cooling rate of 1 K ps−1. Then it was equilibrated for 200 ps followed by gradual cooling to 300 K under the NPT ensemble at a cooling rate of 1 K ps−1. After equilibration at 300 K under NPT for 100 ps, the structures were collected under NVT and NVE ensemble at 300 K for further structural analysis. Long range Coulombic energies were calculated using the PPPM method and velocity verlet method was used for integration of equation of motion with a time step of 1 fs throughout the simulations. Structural analyses performed include total and partial pair distribution functions, coordination number, Qn distribution, network connectivity and ring size distributions.
000 atoms in a cubic simulation cell with dimension according to the experimental density. The initial randomly generated configurations were first melted at 5000 K and then cooled down to 3000 K under the NVT ensemble with a cooling rate of 1 K ps−1. Then it was equilibrated for 200 ps followed by gradual cooling to 300 K under the NPT ensemble at a cooling rate of 1 K ps−1. After equilibration at 300 K under NPT for 100 ps, the structures were collected under NVT and NVE ensemble at 300 K for further structural analysis. Long range Coulombic energies were calculated using the PPPM method and velocity verlet method was used for integration of equation of motion with a time step of 1 fs throughout the simulations. Structural analyses performed include total and partial pair distribution functions, coordination number, Qn distribution, network connectivity and ring size distributions.
Conclusions
It is well known that glass properties can be changed via the glass composition, and that the properties of soda lime silicate glasses change upon reducing the silicate content. Here, we looked into this effect in more detail, showing that by lowering the silicate content all the way to the region typical for bioactive-type glasses, both physical and chemical properties showed pronounced changes. Some properties, including viscosity or fragility, changed gradually, but dissolution under dilute conditions showed a dramatic increase for the lowest silica content glass. Correlating our data with published literature on animal experiments on the identical glass compositions confirms that network connectivity is a useful parameter when describing bioactive glasses' in vivo bone forming capacity.As in the present system the sodium to calcium ratio was kept constant, property changes were controlled by silicate network structure (network connectivity and ring size distributions), originating from increasing concentrations of non-bridging oxygen atoms with decreasing silica content. Once the modifiers change as well, their relative amounts, field strength or coordination numbers also need to be taken into account to correlate property changes with glass structure.
Taken together, reducing the silica content and, thus, network connectivity allows for turning bio-inactive soda lime silicate glasses into bioactive materials for bone regeneration.
Author contributions
Z. Jin, C. Chartier, P. Kachanov, J. Du: formal analysis, investigation, writing – review & editing. D.R. Neuville: validation, formal analysis, writing – review & editing, funding acquisition. S. Kroeker, S. Gin: validation, formal analysis, writing – review & editing. D. S. Brauer: conceptualization, methodology, validation, formal analysis, resources, writing – original draft, writing – review & editing, supervision, funding acquisition.Data availability
Experimental data are available at https://doi.org/10.5281/zenodo.14767350.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge funding by the German Research Foundation (DFG, Deutsche Forschungsgemeinschaft; research training group RTG 2723, grant 444711651, Project C), the Carl Zeiss Foundation (Funding scheme “Durchbrüche”, Project “Intelligente Substrate: Schaltbare Grenzflächen auf Basis multiresponsiver Hybridmaterialien”) and a joint bilateral PROCOPE exchange project funded by the German Academic Exchange Service (DAAD, grant 57604355), the French Ministry for Europe and Foreign Affairs (MEAE) and the French Ministry of Higher Education and Research (MESR). The authors wish to thank Dr Stefan Kiefer (Institute of Mineralogy, Jena) for EPMA analyses, Hélène Arena (CEA Marcoule) for her help with interferometry measurements and Pengzhu Zhang (Otto Schott Institute) and Leon Lange (NMR Platform, University Jena) for support with solid-state NMR measurements. Coraline Chartier acknowledges an internship at CEA, where she received training on the SRCA method.References
- D. R. Neuville, Chem. Geol., 2006, 229, 28–41 CrossRef CAS.
- A. G. Nowotnick, Z. Xi, Z. Jin, S. Khalatbarizamanpoor, D. S. Brauer, B. Löffler and K. D. Jandt, Adv. Healthc. Mater., 2024, 13(32), e2402001 CrossRef PubMed.
- D. S. Brauer, Angew. Chem., Int. Ed., 2015, 54, 4160–4181 CrossRef CAS PubMed.
- J. R. Jones, D. S. Brauer, L. Hupa and D. C. Greenspan, Int. J. Appl. Glass Sci., 2016, 7, 423–434 CrossRef CAS.
- S. Fujibayashi, M. Neo, H. M. Kim, T. Kokubo and T. Nakamura, Biomaterials, 2003, 24, 1349–1356 CrossRef CAS PubMed.
- M. W. G. Lockyer, D. Holland and R. Dupree, J. Non-Cryst. Solids, 1995, 188, 207–219 CrossRef CAS.
- H. Maekawa, T. Maekawa, K. Kawamura and T. Yokokawa, J. Non-Cryst. Solids, 1991, 127, 53–64 CrossRef CAS.
- C. D. Huang and A. N. Cormack, J. Chem. Phys., 1990, 93, 8180–8186 CrossRef CAS.
- J. E. Shelby, Introduction to glass science and technology, The Royal Society of Chemistry, Cambridge, 2nd edn, 2005 Search PubMed.
- L. Deng, S. Urata, Y. Takimoto, T. Miyajima, S. H. Hahn, A. C. T. van Duin and J. Du, J. Am. Ceram. Soc., 2019, 103, 1600–1614 CrossRef.
- R. G. Hill and D. S. Brauer, J. Non-Cryst. Solids, 2011, 357, 3884–3887 CrossRef CAS.
- L. Cormier, G. Calas and B. Beuneu, J. Non-Cryst. Solids, 2011, 357, 926–931 CrossRef CAS.
- D. R. Neuville and P. Richet, Geochim. Cosmochim. Acta, 1991, 55, 1011–1019 CrossRef CAS.
- M. J. Toplis, D. B. Dingwell and T. Lenci, Geochim. Cosmochim. Acta, 1997, 61, 2605–2612 CrossRef CAS.
- P. Richet, R. A. Robie and B. S. Hemingway, Geochim. Cosmochim. Acta, 1986, 50, 1521–1533 CrossRef CAS.
- F. Döhler, D. Groh, S. Chiba, J. Bierlich, J. Kobelke and D. S. Brauer, J. Non-Cryst. Solids, 2016, 432, 130–136 CrossRef.
- H. Arstila, E. Vedel, L. Hupa and M. Hupa, J. Eur. Ceram. Soc., 2007, 27, 1543–1546 CrossRef CAS.
- H. Arstila, E. Vedel, L. Hupa, H. Ylänen and M. Hupa, Key Eng. Mater., 2004, 254–256, 67–70 CAS.
- M. J. Toplis, Chem. Geol., 2001, 174, 321–331 CrossRef CAS.
- C. A. Angell, J. Non-Cryst. Solids, 1988, 102, 205–221 CrossRef CAS.
- Y. Oishi, R. Terai and H. Ueda, in Mass transport phenomena in ceramics, ed A. Cooper and A. Heuer, Plenum Press, New York, 1975, pp. 297–310 Search PubMed.
- R. Terai and Y. Oishi, Glastech. Ber., 1977, 50, 68–73 CAS.
- A. Jambon and J. P. Carron, Geochim. Cosmochim. Acta, 1976, 40, 897–903 CrossRef CAS.
- K. Roselieb and A. Jambon, Geochim. Cosmochim. Acta, 2002, 66, 109–123 CrossRef CAS.
- A. Tilocca and A. N. Cormack, Proc. R Soc. A, 2011, 467, 2102–2111 CrossRef CAS.
- A. Tilocca and A. N. Cormack, ACS Appl. Mater. Inter, 2009, 1, 1324–1333 CrossRef CAS PubMed.
- M. G. Mesko, P. A. Schader and J. E. Shelby, Phys. Chem. Glasses, 2002, 43, 283–290 CAS.
- J. Du, X. Lu, S. Gin, J. M. Delaye, L. Deng, M. Taron, N. Bisbrouck, M. Bauchy and J. D. Vienna, J. Am. Ceram. Soc., 2021, 104, 4445–4458 CrossRef CAS.
- Y. Xiang and J. C. Du, Chem. Mater., 2011, 23, 2703–2717 CrossRef CAS.
- A. Tilocca, A. N. Cormack and N. H. de Leeuw, Faraday Discuss., 2007, 136, 45–55 RSC.
- S. Gin, J. M. Delaye, F. Angeli and S. Schuller, npj Mater. Degradat., 2021, 5, 42 CrossRef.
- R. K. Iler, The chemistry of silica: solubility, polymerization, colloid and surface properties, and biochemistry, Wiley, New York, 1979 Search PubMed.
- A. Tilocca and A. N. Cormack, J. Phys. Chem. C, 2008, 112, 11936–11945 CrossRef CAS.
- B. C. Bunker, J. Non-Cryst. Solids, 1994, 179, 300–308 CrossRef CAS.
- A. Tilocca and A. N. Cormack, Langmuir, 2010, 26, 545–551 CrossRef CAS PubMed.
- D. Zhang, M. Hupa and L. Hupa, Acta Biomater., 2008, 4, 1498–1505 CrossRef CAS PubMed.
- A. Helebrant, L. Jonášová and L. Šanda, Ceram.-Silik., 2002, 46, 9–14 CAS.
- J. V. Ryan, S. K. Cooley, B. P. G. Parruzot, J. T. G. Reiser, C. L. Corkhill, J. Du, K. Ferrand, S. Gin, M. T. Harrison, Y. Inagaki, C. Lenting, J. S. McCloy, S. Mitsui, M. M. V. Snyder, N. J. Smith, R. M. Asmussen and G. L. Smith, Stirred-reactor coupon analysis: An international round robin study, Pacific Northwest National Laboratory, United States, 2022 Search PubMed.
- D. Groh, F. Döhler and D. S. Brauer, Acta Biomater., 2014, 10, 4465–4473 CrossRef CAS PubMed.
- A. L. B. Maçon, T. B. Kim, E. M. Valliant, K. Goetschius, R. K. Brow, D. E. Day, A. Hoppe, A. R. Boccaccini, I. Y. Kim, C. Ohtsuki, T. Kokubo, A. Osaka, M. Vallet-Regi, D. Arcos, L. Fraile, A. J. Salinas, A. V. Teixeira, Y. Vueva, R. M. Almeida, M. Miola, C. Vitale-Brovarone, E. Vernè, W. Höland and J. R. Jones, J. Mater. Sci., 2015, 26, 115 Search PubMed.
- J. Du and A. N. Cormack, J. Non-Cryst. Solids, 2004, 349, 66–79 CrossRef CAS.
- A. N. Cormack, J. Du and T. R. Zeitler, J. Non-Cryst. Solids, 2003, 323, 147–154 CrossRef CAS.
- L. Deng and J. Du, J. Am. Ceram. Soc., 2018, 102, 2482–2505 CrossRef.
- T. S. Mahadevan and J. Du, in Atomistic Simulations of Glasses - Fundamentals and Applications, ed J. Du and A. N. Cormack, Wiley, Hoboken, NJ, 2022, ch 7 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tb02414a |
| This journal is © The Royal Society of Chemistry 2025 |