Open Access Article
Open Access ArticleAnion-rich solvation structures in high entropy aqueous electrolytes for supercapacitors with enlarged potential windows and superior rate capabilities
Laura
González-Aguilera
a,
José Manuel
Vicent-Luna
 b,
Paula
García-Balaguer
a,
Sofia
Calero
b,
Paula
García-Balaguer
a,
Sofia
Calero
 b,
Rafael M.
Madero-Castro
c,
Encarnación
Raymundo-Piñero
de,
Xuejun
Lu
af,
María C.
Gutiérrez
b,
Rafael M.
Madero-Castro
c,
Encarnación
Raymundo-Piñero
de,
Xuejun
Lu
af,
María C.
Gutiérrez
 a,
M. Luisa
Ferrer
a,
M. Luisa
Ferrer
 *a and
Francisco
del Monte
*a and
Francisco
del Monte
 *a
*a
aInstituto de Ciencia de Materiales de Madrid-ICMM, Consejo Superior de Investigaciones Científicas-CSIC, Campus de Cantoblanco, 28049-Madrid, Spain. E-mail: delmonte@icmm.csic.es; mferrer@icmm.csic.es
bMaterials Simulation and Modelling, Department of Applied Physics and Science Education, Eindhoven University of Technology, 5600MB Eindhoven, The Netherlands
cDepartment of Physical, Chemical, and Natural Systems, Universidad Pablo de Olavide, Ctra. Utrera km. 1, 41013 Seville, Spain
dCNRS, CEMHTI UPR3079, Univ. Orléans, 45071 Orléans, France
eRéseau sur le Stockage Électrochimique de l'Énergie (RS2E), 80039 Amiens Cedex, France
fState Key Laboratory of Chemical Resource Engineering, College of Chemical Engineering, Beijing University of Chemical Technology, Beijing 100029, P. R. China
First published on 8th August 2025
Abstract
The use of aqueous electrolytes as suitable electrolytes for supercapacitors (SCs) largely depends on maintaining a wide operating cell voltage window while ensuring good rate capabilities, thereby achieving high energy and power densities over many cycles. Electrolyte engineering with anion- and/or solvent-rich solvation structures has been recently explored in batteries of any type to enhance the interphase stability at high voltages, typically by the formation of a SEI. This approach has been less explored in SCs to not only extend the range of operational voltage but also balance the inherently distinct electrochemical stability of cations and anions with carbon electrodes. Herein, we prepared electrolytes composed of two ionic liquids with a common cation (e.g., EMIMTFSI and EMIMBF4) in solvent mixtures of H2O, DMSO and CH3CN. We found that the electrolyte with the richest solvation structure (i.e., with many and diverse anions that surrounded the cation) was the most effective at widening the cell voltage at which the electrolyte is capable of operating (e.g., up to 2.2 V). Interestingly, this extremely rich solvation structure also exhibited the best transport properties for different ions that, ultimately, were responsible for an excellent maintenance of the energy density at high power densities.
1. Introduction
Electrolytes are lately playing a capital role in the optimization of electrochemical energy storage (EES) devices, from batteries of any type to supercapacitors (SCs).1–6 Electrolytes are typically composed of salts (e.g., regular ones and also ionic liquids, ILs) dissolved in water, organic solvents, or mixtures thereof. Pure ILs (without any further solvent) have also been used quite commonly taking advantage of their liquid nature. The choice of one type of electrolyte or another is essential for determining the main features of the EES device (e.g., cell voltage, flammability, etc.). Aqueous electrolytes are affordable, safe and environmentally friendly. However, their electrochemical stability window (ESW) is limited to about 1–1.2 V due to electrolyte decomposition caused by the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER) beyond this potential threshold. Organic electrolytes and ILs can achieve ESWs of up to 3.5–4 V, but they are costly and their high flammability and volatility pose significant safety and environmental risks. The challenge lies in finding safe and environmentally friendly aqueous-based electrolytes with large ESWs that provide high cell voltages.In nature, the effect of relatively high content of various biological macromolecular components on different properties of proteins and nucleic acids in vivo (e.g., folding mechanisms or conformational stability) is described as macromolecular crowding7 in which the hydrogen bond (HB) structure of H2O undergoes significant changes. Inspired by this phenomenon in living cells, several authors have applied the concept of molecular crowding to reduce the water activity in aqueous electrolytes and thus suppress water decomposition at voltages exceeding 1.6 V.8–11 For instance, Xie et al. achieved this ‘molecular crowding’ in aqueous electrolytes by addition of high contents of water-miscible poly(ethylene glycol) (PEG) to an aqueous solution of LiTFSI so as to obtain LiTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xPEG
xPEG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1 − x)H2O electrolytes with PEG content (x) ranging from 71% to 100%.8
(1 − x)H2O electrolytes with PEG content (x) ranging from 71% to 100%.8
However, the main characteristic of crowded systems in nature is not having one particular solute at a high concentration but reaching this high concentration by combining many different solutes whose individual concentrations are not really high. This idea somehow links with another emerging concept recently applied to pseudo-concentrated electrolytes, which is the increase of the configurational entropy of the systems that improves the compatibility of salts and solvents to form uniform solutions. This is typically achieved by the combination of multiple salts with a single solvent or/and a single salt with multiple solvents and results in such a diversity in the local interactions between solvents and ions that the solvation structure of ions becomes extremely complex. Non-aqueous high-entropy (HE) electrolytes have been widely used in Li12–15 and Na16–22 metal batteries. In these cases, the complex solvation structure obtained by anion and/or solvent enrichment not only stabilizes the electrode–electrolyte interphase but also improves cycling stability and rate performance. The design of aqueous HE electrolytes has been much less explored with most of the examples dealing with Zn-based electrolytes for Zn-ion batteries (ZIBs), dual-salt batteries and Zn-ion hybrid SCs (ZHSCs).23–25 In these cases, the complex solvation structure was always modified with solvent molecules of different natures (e.g., inert diluents, antisolvents, etc.) and it played the role of controlling the HER on the Zn anode, enhancing Zn2+ transport properties and facilitating Zn2+-intercalation/deintercalation processes. More recently, the use of HE electrolytes in which the controlled addition of CH3CN as a weak-coordinating solvent helped widen the operational voltage window with the subsequent improvement in the energy storage capabilities of SCs has been described.26 Nevertheless, there is still a notable need in the field of SCs for studies exploring the formation of anion-rich solvation structures in aqueous HE electrolytes. Actually, chaotropic anions have been studied based on their capability to limit the fraction of free water in electrolytes.27–30 However, the relationship between the anion-rich solvation structures of HE electrolytes with the ESW and the rate capability of SCs has not yet been fully addressed.
This work aimed to investigate whether balancing the ratio of two chaotropic anions with different sizes and hydrophilic/hydrophobic features (e.g., BF4− and TFSI−) may have a significant effect on the entropic features of the solvation structure of the electrolyte and, eventually, improve their electrochemical stability. Thus, we studied mixtures of two ILs sharing the cation (e.g., EMIMTFSI and EMIMBF4) dissolved in H2O and some additional co-solvents, which were DMSO as a coordinating co-solvent and CH3CN as a weak coordinating one. In particular, we studied mixtures of the type nEMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.5 − n)EMIMTFSI
(1.5 − n)EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN, with n = 1.5, 1.15, 0.94, 0.69, 0.44, 0.2, and 0. The stoichiometry in which ILs and solvents were mixed was selected according to our previous experience with these types of solvent mixtures.31,32 For instance, the deviations from ideality exhibited by liquid mixtures of H2O and DMSO in different properties (viscosity, density, or enthalpy of mixing, among others) reached a maximum for the H2O
1.5CH3CN, with n = 1.5, 1.15, 0.94, 0.69, 0.44, 0.2, and 0. The stoichiometry in which ILs and solvents were mixed was selected according to our previous experience with these types of solvent mixtures.31,32 For instance, the deviations from ideality exhibited by liquid mixtures of H2O and DMSO in different properties (viscosity, density, or enthalpy of mixing, among others) reached a maximum for the H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO mixture with a molar ratio of 2
DMSO mixture with a molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (e.g., 2H2O
1 (e.g., 2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO). Meanwhile, the addition of CH3CN to 2H2O
DMSO). Meanwhile, the addition of CH3CN to 2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO in molar ratios of 3.5 and above has typically resulted in flammable solvent mixtures.26,33 So, in this work, the ternary liquid mixture of choice was 2H2O
DMSO in molar ratios of 3.5 and above has typically resulted in flammable solvent mixtures.26,33 So, in this work, the ternary liquid mixture of choice was 2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN to avoid flammability issues. Moreover, this CH3CN content provided the maximum deviation from ideality of density and viscosity in solvent mixtures with a single IL (e.g., 1.5EMIMBF4
1.5CH3CN to avoid flammability issues. Moreover, this CH3CN content provided the maximum deviation from ideality of density and viscosity in solvent mixtures with a single IL (e.g., 1.5EMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN).33 Finally, the selected IL content provided solutions in the so-called “solvent-in-salt” regime.33 The study of the nEMIMBF4
1.5CH3CN).33 Finally, the selected IL content provided solutions in the so-called “solvent-in-salt” regime.33 The study of the nEMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.5 − n)EMIMTFSI
(1.5 − n)EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN mixtures included the analysis of the mixing behaviour of 1.5EMIMBF4
1.5CH3CN mixtures included the analysis of the mixing behaviour of 1.5EMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN and 1.5EMIMTFSI
1.5CH3CN and 1.5EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN by the determination of the excess of different properties (e.g., density, viscosity and solvent donation) of the resulting mixtures. Moreover, the solvation structure was studied by different spectroscopic tools (NMR, ATR and NIR spectroscopy) and molecular dynamic (MD) simulations. In this regard, we obtained information about the formation or absence of HBs between ions and solvents, enabling us to evaluate the coordinating or non-coordinating nature of each one of the solvents and of the solvation structure of the electrolyte, more specifically of the cation that is common to both IL dilutions (i.e., EMIM+). Furthermore, electrochemical measurements were carried out for the determination of the structure–property-performance relationship of these complex electrolytes in SC cells using porous carbon materials as electrodes.
1.5CH3CN by the determination of the excess of different properties (e.g., density, viscosity and solvent donation) of the resulting mixtures. Moreover, the solvation structure was studied by different spectroscopic tools (NMR, ATR and NIR spectroscopy) and molecular dynamic (MD) simulations. In this regard, we obtained information about the formation or absence of HBs between ions and solvents, enabling us to evaluate the coordinating or non-coordinating nature of each one of the solvents and of the solvation structure of the electrolyte, more specifically of the cation that is common to both IL dilutions (i.e., EMIM+). Furthermore, electrochemical measurements were carried out for the determination of the structure–property-performance relationship of these complex electrolytes in SC cells using porous carbon materials as electrodes.
2. Deviations from ideality
As mentioned in the Introduction, our first objective was to investigate the mixing characteristics of nEMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.5 − n)EMIMTFSI
(1.5 − n)EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN mixtures (Table S1). For this purpose, our initial analysis focused on the deviation from ideality of the excess molar volumes, VE = (χ1M1 + χ2M2)/ρ − (χ1M1/ρ1 + χ2M2/ρ2), where M1 and M2 were the molecular weights of 1.5EMIMBF4
1.5CH3CN mixtures (Table S1). For this purpose, our initial analysis focused on the deviation from ideality of the excess molar volumes, VE = (χ1M1 + χ2M2)/ρ − (χ1M1/ρ1 + χ2M2/ρ2), where M1 and M2 were the molecular weights of 1.5EMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN and 1.5EMIMTFSI
1.5CH3CN and 1.5EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN, respectively. We found negative deviations from ideality in a wide range of compositions (i.e., for molar fractions of 1.5EMIMBF4
1.5CH3CN, respectively. We found negative deviations from ideality in a wide range of compositions (i.e., for molar fractions of 1.5EMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
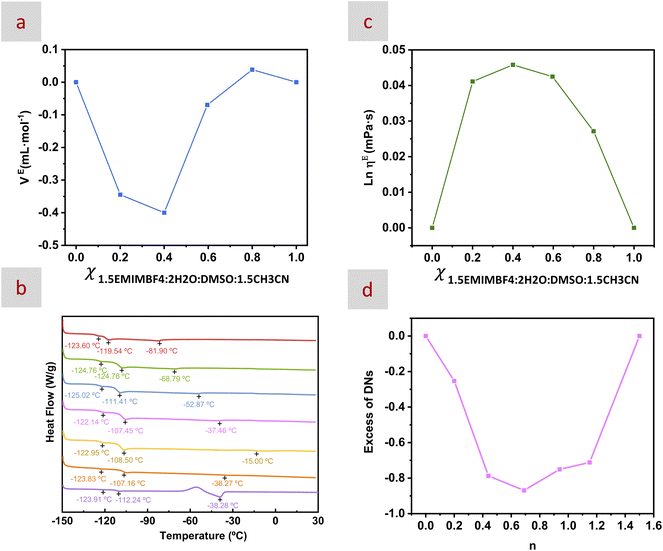
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN of ca. 0.7 and below, see Fig. 1a). Actually, mixtures of H2O, DMSO and CH3CN34 and of hydrophilic salts based on EMIM+,35 including EMIMBF4 in both DMSO and CH3CN36 and in mixtures of H2O and DMSO,19 have also exhibited negative values of excess molar volume. The occurrence of negative values of excess molar volume is usually associated with the formation of strong intermolecular interactions including charge transfer, dipole–dipole interactions, and HBs.37 In our case, this volume contraction on mixing was maximum at n = 0.69 and could be ascribed to the interstitial accommodation of anions within a HB complex structure.
1.5CH3CN of ca. 0.7 and below, see Fig. 1a). Actually, mixtures of H2O, DMSO and CH3CN34 and of hydrophilic salts based on EMIM+,35 including EMIMBF4 in both DMSO and CH3CN36 and in mixtures of H2O and DMSO,19 have also exhibited negative values of excess molar volume. The occurrence of negative values of excess molar volume is usually associated with the formation of strong intermolecular interactions including charge transfer, dipole–dipole interactions, and HBs.37 In our case, this volume contraction on mixing was maximum at n = 0.69 and could be ascribed to the interstitial accommodation of anions within a HB complex structure.
Previous studies have described that volume contractions on mixing coming from interstitial accommodation of solvent molecules within a HB complex structure are typically accompanied by the decrease of the melting point of the mixture.38,39 In our case, the DSC scan of 1.5EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN displayed a transition at −37 °C ascribed to the melting point of EMIMTFSI (Fig. 1b). Actually, the melting point of EMIMTFSI in neat form (without solvents) appears at ca. −15 °C
1.5CH3CN displayed a transition at −37 °C ascribed to the melting point of EMIMTFSI (Fig. 1b). Actually, the melting point of EMIMTFSI in neat form (without solvents) appears at ca. −15 °C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and at ca. −23 °C in 1.5EMIMTFSI
40 and at ca. −23 °C in 1.5EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO.26 None of the other samples studied in this work, neither the double IL mixtures nor the EMIMBF4 mixture, displayed a clear melting point. This trend could be indicating that the TFSI− anion, despite its large size and hydrophobic nature, was interstitially accommodated within the HB complex structure formed by EMIMBF4, H2O, DMSO, and CH3CN.
DMSO.26 None of the other samples studied in this work, neither the double IL mixtures nor the EMIMBF4 mixture, displayed a clear melting point. This trend could be indicating that the TFSI− anion, despite its large size and hydrophobic nature, was interstitially accommodated within the HB complex structure formed by EMIMBF4, H2O, DMSO, and CH3CN.
Moreover, every sample exhibited two weak glass transition temperatures (Tg), one at around −110 °C and another one at around −125 °C (Fig. 1b). The first Tg at around −110 °C has also been observed in mixtures of EMIMBF4 and EMIMTFSI without solvents39 while the second one at around −123 °C has been observed in mixtures of H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO and of H2O
DMSO and of H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH3CN.26 It is worth remembering that the absence of phase transitions such as melting points and crystallization processes is a typical signature of HE electrolytes so the decrease of the Tg could also be of relevance with regard to the eventual utilization of these electrolytes at low temperatures.
CH3CN.26 It is worth remembering that the absence of phase transitions such as melting points and crystallization processes is a typical signature of HE electrolytes so the decrease of the Tg could also be of relevance with regard to the eventual utilization of these electrolytes at low temperatures.
The positive deviations from ideality found in the representation of the excess logarithmic viscosity, obtained from the equation ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ηE = ln
ηE = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η − (χ1
η − (χ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η1 + χ2
η1 + χ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η2), corroborated the occurrence of HBs among the components of these mixtures (Fig. 1c)41 that is typically accompanied by changes in the solvation structure.42 Solute–solvent and solvent–solvent interactions in binary solvent mixtures were studied by 23Na-NMR spectroscopy.43,44 The deviation from ideality of the chemical shift of the 23Na nucleus of dissolved NaClO4 has been used for the determination of the donor numbers (DNs) defined by Gutmann.45 The DN typically accounts for the electron donating properties (donicity) of solvent molecules but its use for ions has also been described.46 Moreover, DNs may reflect the interaction between solvent molecules and ions as molecular fingerprints for the screening of electrolyte additives.47 In our case, we found that the DNs of the nEMIMBF4
η2), corroborated the occurrence of HBs among the components of these mixtures (Fig. 1c)41 that is typically accompanied by changes in the solvation structure.42 Solute–solvent and solvent–solvent interactions in binary solvent mixtures were studied by 23Na-NMR spectroscopy.43,44 The deviation from ideality of the chemical shift of the 23Na nucleus of dissolved NaClO4 has been used for the determination of the donor numbers (DNs) defined by Gutmann.45 The DN typically accounts for the electron donating properties (donicity) of solvent molecules but its use for ions has also been described.46 Moreover, DNs may reflect the interaction between solvent molecules and ions as molecular fingerprints for the screening of electrolyte additives.47 In our case, we found that the DNs of the nEMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.5 − n)EMIMTFSI
(1.5 − n)EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN mixtures exhibited a non-linear evolution along with n, reaching a maximum deviation from ideality at n = 0.69 (Fig. S1 and 1d), as described above for densities and viscosities. Understanding whether this non-linear evolution in the DNs is associated with some specific changes in the solvation structure (e.g., the so-called “preferential solvation”)44 would indeed be of interest. Further details about this matter can be found below (see discussion of the results from MD simulations).
1.5CH3CN mixtures exhibited a non-linear evolution along with n, reaching a maximum deviation from ideality at n = 0.69 (Fig. S1 and 1d), as described above for densities and viscosities. Understanding whether this non-linear evolution in the DNs is associated with some specific changes in the solvation structure (e.g., the so-called “preferential solvation”)44 would indeed be of interest. Further details about this matter can be found below (see discussion of the results from MD simulations).
3. The nature of the HB network
The mixtures were analyzed by 1H NMR spectroscopy (Fig. S2). Increasing the content of EMIMTFSI caused slight downfield shifts (∼0.02–0.04 ppm) in the aliphatic protons of EMIM+ and DMSO, consistent with the more hydrophobic nature of TFSI− (as compared to BF4−) and its preferential interaction with aliphatic chains (Table S2).48,49 Meanwhile, the H2O proton signals shifted upfield as EMIMTFSI content increased from n = 1.5 to n = 0.94 and then downfield from n = 0.94 to 0. Deshielding, reflecting reduced electron density and stronger HB,50,51 indicated that H2O involvement in HB structures was lower in the nEMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.5 − n)EMIMTFSI
(1.5 − n)EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN mixtures than in either 1.5EMIMBF4
1.5CH3CN mixtures than in either 1.5EMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN or 1.5EMIMTFSI
1.5CH3CN or 1.5EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN, reaching a minimum at n = 0.94. This reduction was attributed to the interstitial accommodation of incoming TFSI− anions. Meanwhile, TFSI− and BF4− signals (both 10BF4− and 11BF4− coming from J coupling between 19F with 10B, with spin I = 3 and ca. 20% of natural abundance, and 11B nuclei, with spin I = 3/2 and ca. 80% of natural abundance)52 followed a linear trend, with chemical shifts becoming more negative along with the decrease of n (Table S3).
1.5CH3CN, reaching a minimum at n = 0.94. This reduction was attributed to the interstitial accommodation of incoming TFSI− anions. Meanwhile, TFSI− and BF4− signals (both 10BF4− and 11BF4− coming from J coupling between 19F with 10B, with spin I = 3 and ca. 20% of natural abundance, and 11B nuclei, with spin I = 3/2 and ca. 80% of natural abundance)52 followed a linear trend, with chemical shifts becoming more negative along with the decrease of n (Table S3).
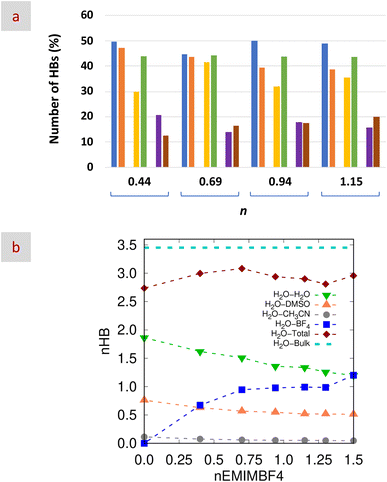
ATR and NIR spectroscopies were used to analyze the mixtures. In the IR spectra (Fig. S4a), bands at ca. 3160, 3120, and 2960 cm−1 were attributed to ν(C4,5–H), ν(C2–H), and ν(alkyl C–H), respectively (Fig. S4b).53 Key TFSI− features included SO2 stretches (at ca. 1275–1400 cm−1), CF3 (at ca. 1194 cm−1), and SNS (at ca. 1059 cm−1). The asymmetric SO2 stretch revealed free TFSI− anions at ca. 1355 cm−1 with a shoulder at ca. 1325 cm−1, both shifting to lower wavenumbers upon coordination.54 In our samples, these bands (at ca. 1355 and 1328 cm−1 for n = 1.15) shifted to smaller wavenumbers as TFSI− content increased (Fig. S4c). Additional bands assigned to BF4− appeared at ca. 997 and 1070 cm−1 with strong absorption, forming a broad single band (Fig. S4d).55 Water bands at ca. 3407 and 3620 cm−1 (Fig. S4b) corresponded to molecules with strong (fully tetrahedral) and weak/incomplete HB, respectively.56
The NIR region further illuminated HB via overtone and combination bands. Water spectra were dominated by ν2 + ν3 (5100–5300 cm−1 → 1887–1941 nm) and ν1 + ν3 (6800–7200 cm−1 → 1389–1471 nm) combinations. These are derived from fundamental OH vibrations in the mid-infrared region (MIR),57 such as the symmetric OH stretching (ν1 at 3520 cm−1), the OH bending (ν2 at 1650 cm−1 → 6061 nm), and the antisymmetric OH stretching (ν3 at 3600 cm−1 → 2778 nm).58 Deconvolution of ν2 + ν3 revealed three components representing different HB strengths, from strong to weak, including an intermediate range of partially disordered tetrahedral structures.59 In our case, the mixture at n = 0.69 showed the lowest contribution from strong HBs (Fig. S5 and Table S4). These NIR results were consistent with those of MD simulations (Fig. 2a and b), reinforcing the described features of the H2O HB network (see further discussion below).
4. Anion-rich solvation structures
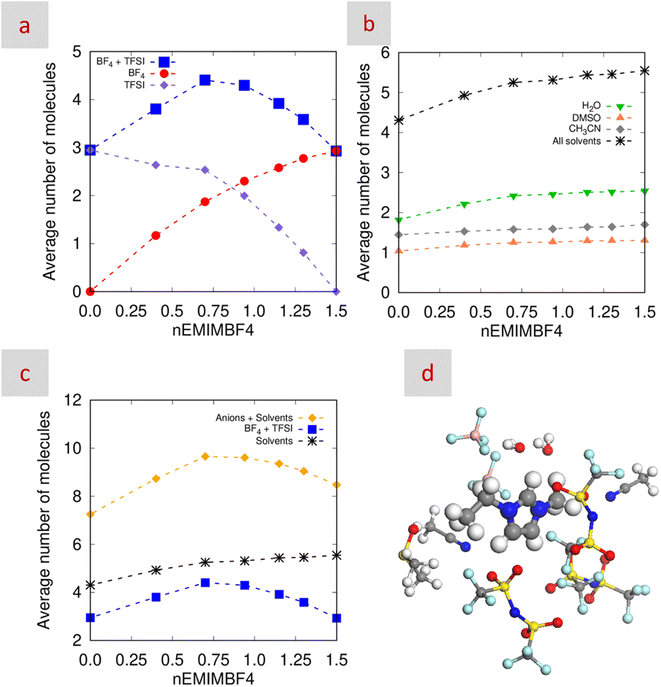
To further investigate the solvation structure in the mixtures, we analyzed the results from MD simulations. Initial analysis focused on the interactions between EMIM+ nitrogen atoms and the most electronegative atoms of the other species, as reflected in the coordination number, cn(r), at ca. 6 Å in the partial radial distribution functions (pRDFs; Fig. S6). As n decreased, interactions with BF4− weakened, while those with TFSI− strengthened, showing a linear trend. Interactions with CH3CN also slightly decreased. In contrast, H2O and DMSO interactions peaked at n = 0.69, deviating from linear behavior.Further insights were gained from trajectory analysis, which provided the average number of molecules (both solvents and anions) surrounding EMIM+ in the first coordination shell as a function of n (Fig. 3). Solvent coordination numbers decreased with decreasing n, likely due to the incorporation of bulkier TFSI− anions (Fig. 3b). As expected, the presence of BF4− and TFSI− followed opposing trends with n (Fig. 3a, red circles and purple diamonds, respectively). Notably, in single-salt mixtures and regardless of whether BF4− or TFSI− was present, the average number of anions surrounding EMIM+ remained at ca. 3, as in neat EMIMBF4 and EMIMTFSI.60 While individual anion coordination did not reveal significant variation, summing the total number of anions around EMIM+ did (Fig. 3a, blue squares). This total increased from ca. 3 for n = 1.5 or 0 to over 4 at n = 0.94 and 0.69, indicating a more complex solvation environment, especially at n = 0.69 (Fig. 3c and d). This supports the defining characteristic of HE electrolytes: an enhanced number and/or diversity of species in the first solvation shell compared to conventional (low-entropy) systems.
In order to investigate the accommodation of CH3CN molecules, we analyzed the interactions between EMIM+ and CH3CN, that were weak according to the pRDF depicted in Fig. S6e. These results confirmed how CH3CN participates in the solvation structure as a weak coordinating solvent disregarding its role as a non-coordinating one. Actually, FT-IR results from previous studies indicated that, as the CH3CN content increases, the interactions among nitrogen atoms were strengthened to a greater extent than those among aliphatic groups.48
Finally, based on the positions of the first peak of the corresponding pRDFs, we found that both BF4− and TFSI− could form HBs with H2O, noticeably stronger for BF4− than for TFSI−.61 Meanwhile, weak interactions were established between CH3CN and CH3CN (Fig. S7) as well as between any of the anions and any of the co-solvents (both DMSO and CH3CN, see Fig. S8). HBs were also formed among the solvent molecules, in particular between H2O and H2O, H2O and DMSO, and H2O and CH3CN. Fig. S9 shows the pRDFs between the hydrogen atoms of water (acting as hydrogen bond donors, HBDs) and the electronegative atoms of H2O, DMSO, and CH3CN (oxygen atoms of DMSO and H2O and the nitrogen atom of CH3CN, acting as hydrogen bond acceptors, HBAs). Fig. S9 also shows the pRDFs between the oxygen atom of the HBD (e.g., H2O) with different HBAs. This set of pRDFs is commonly used to define the geometric criterion for HB formation33,62–64 where the first minimum is located at ca. 3.5 Å for O–O/N pairs and 2.5 Å for H–O/N pairs. pRDFs in Fig. S8 and S9 revealed the formation of HBs of different strengths, strong between H2O and H2O, weak (almost negligible) between H2O and CH3CN, and moderate between H2O and DMSO molecules and between H2O and BF4− anions (Fig. 2b). Actually, the coordination numbers at the first minimum of the H2O–H2O and H2O–DMSO pRDFs were basically unaffected by the formation of HBs between H2O and CH3CN. Interestingly, the total number of HBs obtained for the mixtures was below that obtained for bulk H2O (i.e., 2.75–3.0 and 3.45, respectively) thus revealing the occurrence of some “missing HBs”. This is most likely happening when TFSI− and/or CH3CN molecules (with which the HB formation is negligible), eventually driven by other type of interactions, are located in the proximity of H2O molecules. It is worth noting that the number of strong, moderate and weak HBs obtained from MD simulations that formed the HB network established in the mixture was basically in agreement with that obtained from NIR spectroscopy (Fig. 2a).
5. Transport properties
As compared to regular low-entropy electrolytes, another characteristic of HE electrolytes is the increase in the ionic conductivity, eventually ascribed to the decrease of the cluster size of aggregates (AGGs).12 In this regard, we studied the ionic conductivity of nEMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.5 − n)EMIMTFSI
(1.5 − n)EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN mixtures and the diffusion coefficients of EMIM+, BF4−, TFSI−, H2O, DMSO, and CH3CN (e.g., DEMIM+, DBF4−, DTFSI−, DH2O, DDMSO, and DCH3CN) from pulse-field-gradient spin-echo 19F and 1H NMR (PGSE-NMR) spectroscopy (Tables 1 and S5).
1.5CH3CN mixtures and the diffusion coefficients of EMIM+, BF4−, TFSI−, H2O, DMSO, and CH3CN (e.g., DEMIM+, DBF4−, DTFSI−, DH2O, DDMSO, and DCH3CN) from pulse-field-gradient spin-echo 19F and 1H NMR (PGSE-NMR) spectroscopy (Tables 1 and S5).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.5 − n)EMIMTFSI
(1.5 − n)EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN with n = 1.15, 0.94, 0.69, 0.44, and 0.2
1.5CH3CN with n = 1.15, 0.94, 0.69, 0.44, and 0.2
| n | D (m2 s−1) × 1010 | σ (mS cm−1) | Λ NMR × 103 (S m2 mol−1) | κ = Λ/ΛNMR | |||||
|---|---|---|---|---|---|---|---|---|---|
| EMIM+ | BF4− | TFSI− | DMSO | CH3CN | H2O | ||||
| 1.15 | 2.88 | 3.03 | 2.23 | 3.73 | 6.18 | 7.59 | 39.6 | 7.1 | 0.25 |
| 0.94 | 2.48 | 2.95 | 2.33 | 3.27 | 5.67 | 6.74 | 35.6 | 6.2 | 0.27 |
| 0.69 | 4.02 | 3.18 | 2.59 | 4.87 | 7.61 | 8.12 | 31.2 | 7.8 | 0.20 |
| 0.44 | 2.46 | 2.82 | 1.95 | 3.09 | 5.82 | 6.45 | 28.1 | 5.0 | 0.29 |
| 0.2 | 1.58 | 1.54 | 1.15 | 1.90 | 3.85 | 4.42 | 25.3 | 2.9 | 0.48 |
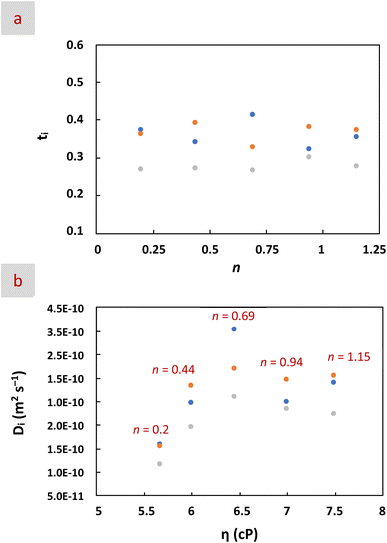
Ionic conductivity increased as viscosity decreased, that is, with increasing n. All diffusion coefficients were in the 10−10 m2 s−1 range, consistent with the values reported for neat EMIMBF4, EMIMTFSI,60,65,66 and their dilutions in CH3CN, H2O, and H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH3CN mixtures (Table 1).26,33,67,68 Ratios of Danion/Dcation near unity suggest coupled ion motion,69 indicative of AGGs (or contact ion pairs, CIPs), where ions diffuse together with other ions (and with solvent molecules in the particular case of CIPs).70 According to the Stokes–Einstein relation (D = kBT/6πηa), diffusion is inversely proportional to the hydrodynamic radius (a).69,71 Thus, based on the Stokes–Einstein relation and the ionic sizes of BF4−, EMIM+ and TFSI− (e.g., 0.229, 0.303 and 0.528 nm, respectively), the expected order of self-diffusion coefficients should be DBF4− > DEMIM+ > DTFSI−.66,72 This trend was observed in all mixtures except at n = 0.69, where DEMIM+ > DBF4− > DTFSI−. Transference numbers (tEMIM+, tBF4− and tTFSI−) followed the same trend, with tBF4− > tEMIM+ > tTFSI− in all mixtures except at n = 0.69 where tEMIM+ > tBF4− (Fig. 4a). Unlike Li-ion batteries, where high cation mobility is preferred, here the similar transference numbers across species (0.41–0.32 for EMIM+, 0.39–0.32 for BF4−, and 0.30–0.26 for TFSI−) support the efficient electric double-layer (EDL) mechanism dominant in SCs. In any case, for HE electrolytes, the hydrodynamic radius has been directly related to the cluster size of ionic AGGs, with high diffusivities of ions leading to small hydrodynamic radii and cluster sizes.12,73–75 Interestingly, as mentioned above, every ion and every solvent molecule reached its respective highest diffusion at n = 0.69 (Fig. 4b), so, in our case, the smallest clusters would be found for this particular mixture.
CH3CN mixtures (Table 1).26,33,67,68 Ratios of Danion/Dcation near unity suggest coupled ion motion,69 indicative of AGGs (or contact ion pairs, CIPs), where ions diffuse together with other ions (and with solvent molecules in the particular case of CIPs).70 According to the Stokes–Einstein relation (D = kBT/6πηa), diffusion is inversely proportional to the hydrodynamic radius (a).69,71 Thus, based on the Stokes–Einstein relation and the ionic sizes of BF4−, EMIM+ and TFSI− (e.g., 0.229, 0.303 and 0.528 nm, respectively), the expected order of self-diffusion coefficients should be DBF4− > DEMIM+ > DTFSI−.66,72 This trend was observed in all mixtures except at n = 0.69, where DEMIM+ > DBF4− > DTFSI−. Transference numbers (tEMIM+, tBF4− and tTFSI−) followed the same trend, with tBF4− > tEMIM+ > tTFSI− in all mixtures except at n = 0.69 where tEMIM+ > tBF4− (Fig. 4a). Unlike Li-ion batteries, where high cation mobility is preferred, here the similar transference numbers across species (0.41–0.32 for EMIM+, 0.39–0.32 for BF4−, and 0.30–0.26 for TFSI−) support the efficient electric double-layer (EDL) mechanism dominant in SCs. In any case, for HE electrolytes, the hydrodynamic radius has been directly related to the cluster size of ionic AGGs, with high diffusivities of ions leading to small hydrodynamic radii and cluster sizes.12,73–75 Interestingly, as mentioned above, every ion and every solvent molecule reached its respective highest diffusion at n = 0.69 (Fig. 4b), so, in our case, the smallest clusters would be found for this particular mixture.
We also estimated the molar conductivity ratio (Λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΛNMR), where Λ is the molar conductivity obtained by electrochemical impedance measurements and ΛNMR is that calculated from the ionic self-diffusion coefficients and the Nernst–Einstein equation.71,76 It is widely assumed that, being the intrinsic NMR time scale (10−9 to 10−10 s) much shorter than those of the conductivity measurements, NMR measurements cannot distinguish ionic AGGs from free ions.77 Thus, the Λ
ΛNMR), where Λ is the molar conductivity obtained by electrochemical impedance measurements and ΛNMR is that calculated from the ionic self-diffusion coefficients and the Nernst–Einstein equation.71,76 It is widely assumed that, being the intrinsic NMR time scale (10−9 to 10−10 s) much shorter than those of the conductivity measurements, NMR measurements cannot distinguish ionic AGGs from free ions.77 Thus, the Λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΛNMR ratio has been taken as an indication of the ionicity.78 For instance, Λ
ΛNMR ratio has been taken as an indication of the ionicity.78 For instance, Λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΛNMR values below unity have been assigned to the presence of not only non-charged AGGs but also ionic ones.78,79 In our case, the good ionicities obtained in the Walden plot depicted in Fig. S10 revealed the preferred presence of ionic AGGs.71,80 Interestingly, the number of AGGs reached a maximum at n = 0.69 (Table 1). Considering that these values come from molar conductivities, the cluster size of the ionic AGGs formed in this latter mixture should be the smallest among all mixtures, as already anticipated by the above-mentioned relationship between the hydrodynamic radius and the diffusion coefficients. Moreover, as mentioned above, the formation of small clusters has been related to the entropic features of HE electrolytes.12 In our case, as revealed by MD simulations, the mixture with n = 0.69 was particularly significant in this regard with a solvation structure with many and diverse anions and molecules around EMIM+.
ΛNMR values below unity have been assigned to the presence of not only non-charged AGGs but also ionic ones.78,79 In our case, the good ionicities obtained in the Walden plot depicted in Fig. S10 revealed the preferred presence of ionic AGGs.71,80 Interestingly, the number of AGGs reached a maximum at n = 0.69 (Table 1). Considering that these values come from molar conductivities, the cluster size of the ionic AGGs formed in this latter mixture should be the smallest among all mixtures, as already anticipated by the above-mentioned relationship between the hydrodynamic radius and the diffusion coefficients. Moreover, as mentioned above, the formation of small clusters has been related to the entropic features of HE electrolytes.12 In our case, as revealed by MD simulations, the mixture with n = 0.69 was particularly significant in this regard with a solvation structure with many and diverse anions and molecules around EMIM+.
6. Electrochemical performance in SCs
At this stage, we proceeded to evaluate the electrochemical response of these mixtures in SC cells. For this purpose, Swagelok cells were assembled with two mesoporous carbons as electrodes and a 0.45 μm PVDF filter paper as a separator (see the Experimental section for further details).33,81 The mesoporous carbons of choice were described in detail in our previous studies31–33 and were selected based on their textural properties with a high surface area (ca. 2681 m2 g−1) and a large contribution of mesopores to the overall porosity with Vmesopores above 70% of the total pore volume and an external surface area of ca. 500–650 m2 g−1 (Fig. S11 and Table S6).In SCs, the energy storage capability of any electrolyte is intimately related to its maximum operating cell voltage. For aqueous electrolytes, this is the voltage range between the highest potential at which irreversible oxidation occurs at the positive electrode (PU) and the lowest potential at which hydrogen production occurs at the negative electrode (PL). As these irreversible reactions are related to the ESW of the electrolyte, it is therefore that the determination of the ESW is of great interest. In this regard, the inherent distinct electrochemical stability of cations and anions with carbon electrodes creates an asymmetry in the potential of the positive and negative electrodes measured at zero voltage (P0 V), situating the P0 V closer to PU than to PL and leaving some unused potential at the negative electrode.82
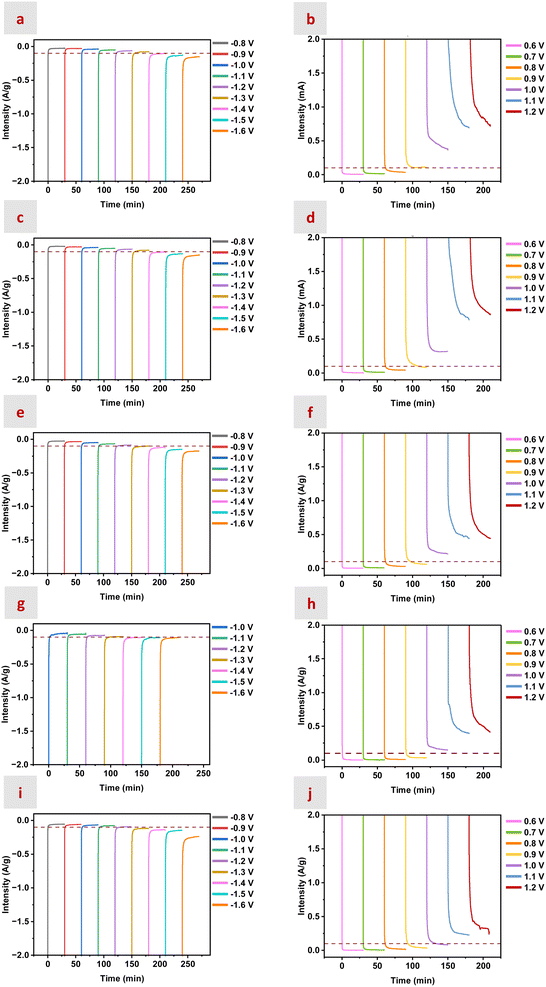
The determination of PL, PU, and P0 V and of the potentials of both the negative and the positive electrodes (denoted as PN and PP, respectively) as a function of the operating voltage (V) was accomplished by the application of three-electrode procedures described elsewhere.83 The determination of PL and PU is critical for the usefulness of an accurate estimation of the ESW. Thus, PL and PU are typically obtained from cyclic voltametry (CV) measurements in either a two- or a three-electrode set-up (Fig. S12–S15). Another option is performing chronoamperometric (CA) measurements at different potentials with a three-electrode set-up. Previous studies using CA categorized the so-called “safe potentials” for current densities below 0.1 A g−1 and/or above −10 μA cm−2.84,85 In our case, we investigated the samples for which the CA curves remained at current densities below 0.1 A g−1 for both positive and negative potentials.
Fig. 5 shows the CA curves obtained at potentials ranging from −0.8 to −1.6 V and from 0.6 to 1.2 V. The application of a threshold of 0.1 A g−1 for the “safe” regime resulted in potential limits (e.g., [PL, PU]) of [−1.2, 0.9], [−1.3, 0.9], [−1.3, 0.9], [−1.3, 0.8], and [−1.3, 0.8] for the nEMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.5 − n)EMIMTFSI
(1.5 − n)EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN mixtures with n = 0.2, 0.44, 0.69, 0.94, and 1.15 (see horizontal lines in red in Fig. 5). It was worth noting that the maximum voltage was limited by PP, with the mixture with n = 0.69 performing the best, likely due to the distinct characteristics of its HB network (i.e., see Fig. 1 and 2, with the mixture with n = 0.69 exhibiting, respectively, the maximum deviation from ideality in excess properties and the lowest number of weak HBs).
1.5CH3CN mixtures with n = 0.2, 0.44, 0.69, 0.94, and 1.15 (see horizontal lines in red in Fig. 5). It was worth noting that the maximum voltage was limited by PP, with the mixture with n = 0.69 performing the best, likely due to the distinct characteristics of its HB network (i.e., see Fig. 1 and 2, with the mixture with n = 0.69 exhibiting, respectively, the maximum deviation from ideality in excess properties and the lowest number of weak HBs).
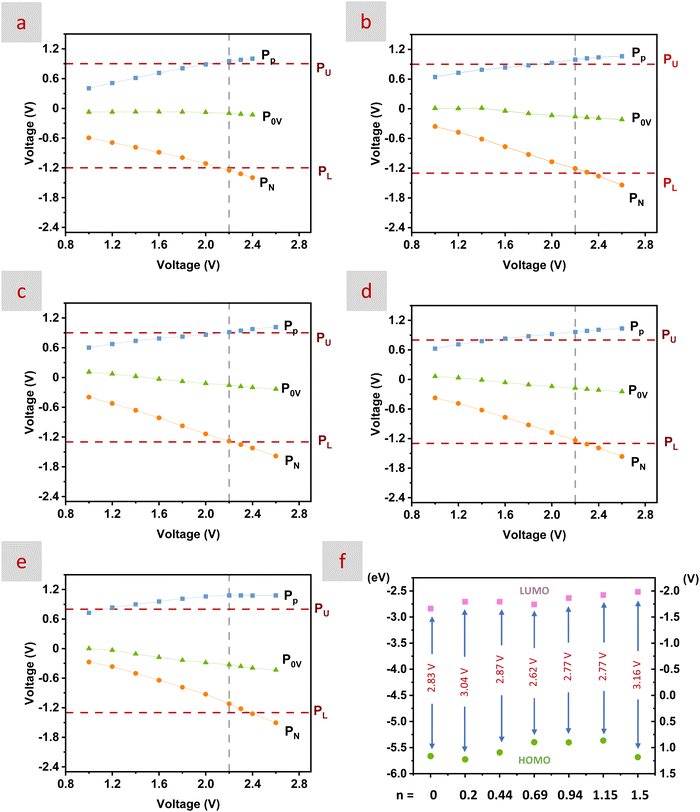
The analysis of Fig. 6 provided some useful information. First, the mixtures with n = 0.2 and 1.15 were disregarded as the best performing ones because the former exhibited narrower potential limits (e.g., [−1.2, 0.9]) and the latter the highest unused potential at the negative electrode and the larger asymmetry between P0 V − PU and P0 V − PL. Meanwhile, irreversible oxidation processes happened in the mixtures with n = 0.44 and 0.94 at less positive potentials than in the mixture with n = 0.69. This latter mixture also exhibited the lowest unused potential at the negative electrode, so, overall, it was the best mixture balancing the distinct electrochemical stability of cations and anions. Moreover, according to the CV and CA measurements depicted above, the ESW of choice for subsequent experiments was 2.2 V.
Based on previous studies identifying the effective oxidation and reduction potentials of the electrolyte with the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energy levels,86,87 we also obtained the HOMO–LUMO energy levels of every mixture following the procedures described elsewhere.88,89 In our case, the lowest LUMO and the narrowest HOMO–LUMO gap were found for the mixture with n = 0.69 (Fig. 6f). This pattern was opposite to that described in most of those previous studies mentioned above but in agreement with other studies describing how the reorganization and subsequent weakening of the interactions among the different components may cause the narrowing of the HOMO–LUMO energy gap.90 Anyway, some authors have recently recommended abandoning the utilization of the HOMO–LUMO energy levels when describing the electrolyte stability.91
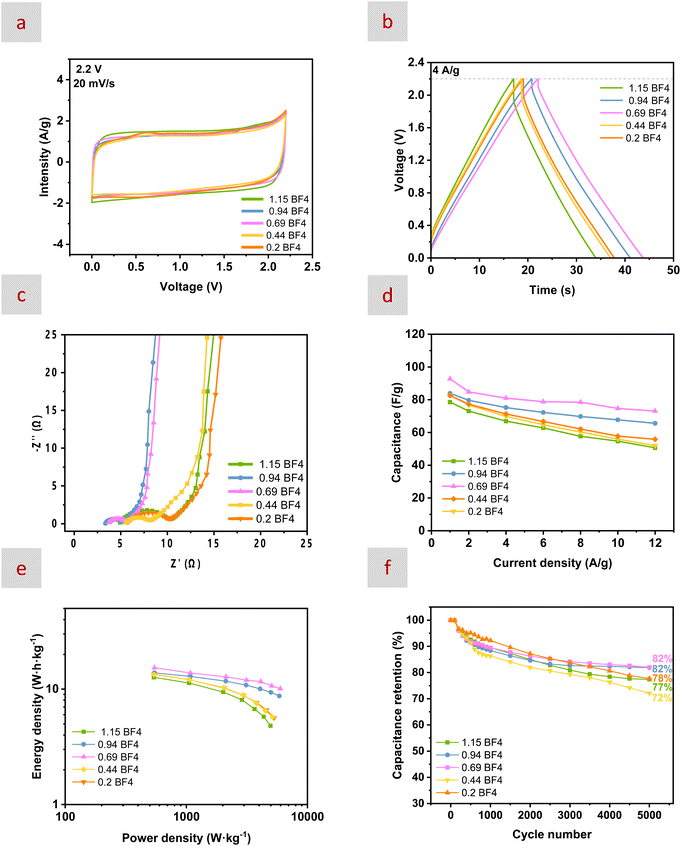
Next, we performed electrochemical impedance spectroscopy (EIS) to begin with the assessment of the electrochemical performance of our mixtures (Fig. S16 and 7c). Despite the in-depth analysis of the results from EIS being rather complicated,92,93 the Nyquist plot of an EDL capacitor measured in a two-electrode configuration typically displays some common features, which are a semicircle at high frequencies, followed by a nonvertical line at intermediate frequencies and then by a nearly vertical line at low frequencies. In this latter region, a slope of 90° is indicative of a purely capacitive system while the decrease of this angle reveals the presence of a charge transfer resistance in parallel to the EDL capacitance. Actually, the occurrence of such a decrease in the angle under the application of a certain potential has been used to study the electrode–electrolyte interphase and determine the cell voltage.94–96 Moreover, the intersection of this nearly vertical line with the x axis provides the internal resistance (Rint_EIS, also named the equivalent series resistance, ESR)93 of the cell. In our case, we observed how the mixture with n = 0.69 displayed the best performance overall, with both the lowest Rint_EIS (as compared to mixtures with n = 1.15, 0.44 and 0.2, Table S6) and the highest verticality (as compared to every mixture, including that with n = 0.94). Actually, the mixture with n = 0.69 exhibited the highest diffusion coefficients for every ion and the best balance among the diffusion transference numbers (Fig. 4) that, respectively, favour ion transport and help prevent charge accumulation and concentration gradients at the interface.
CV and galvanostatic charge/discharge (GCD) curves were also obtained for every mixture. CV was carried out at 25 °C and at scan rates ranging from 10 to 100 mV s−1 (Fig. S17). GCD curves were obtained at current densities ranging from 1 to 12 A g−1 (Fig. S18). The shape of both CV and GCD curves was typical of SCs, quasi-rectangular for CVs and near isosceles for GCDs (Fig. 7a and b). The shape of the CVs obtained at different potentials suggested that the most appropriate ESW for these mixtures was indeed 2.2 V. Interestingly, GCD curves revealed that the mixture with n = 0.69 was the best performing in terms of not only energy storage capabilities but also internal resistances (Rint_IRdrop, determined from the IR drop at the initiation of the current discharge for different current densities, Fig. S19 and Table S7).97 As mentioned above for Rint_EIS, the internal resistance is directly influenced by the diffusion coefficients and transference numbers of the electrolyte. Considering that higher diffusion coefficients and well-balanced transference numbers (Fig. 4) led to lower internal resistance, faster charge transport and better performance, the mixture with n = 0.69 exhibited the best balance between energy and power density as observed in the plot representing specific capacitance versus current density and in the Ragone plot obtained for every mixture (Fig. 7d and e). Finally, the trend followed by the capacitance retentions obtained for the different mixtures after cycling 5000 times at 2.2 V and 3 A g−1 was basically the same as that described above for other electrochemical measurements, following the order n = 0.69 ≈ n = 0.94 > n = 0.2 ≈ n = 1.15 > n = 0.44 (Fig. 7f). The Nyquist plots obtained after cycling revealed different electrolyte deteriorations (Fig. S20), basically aligning with the above-observed capacitance retentions.
7. Conclusions
This work demonstrated how a proper combination of two chaotropic anions with different molecular sizes and hydrophilic/hydrophobic features promoted the formation of anion-rich solvation structures that helped balance the inherently distinct electrochemical stability of cations and anions in SCs. MD simulations allowed identifying the new arrangement of ions and solvent molecules happening in nEMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.5 − n)EMIMTFSI
(1.5 − n)EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN mixtures for which the sum of BF4− and TFSI− anions in the first coordination shell outnumbers those of the single salt mixtures (e.g., 1.5EMIMBF4
1.5CH3CN mixtures for which the sum of BF4− and TFSI− anions in the first coordination shell outnumbers those of the single salt mixtures (e.g., 1.5EMIMBF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN or 1.5EMIMTFSI
1.5CH3CN or 1.5EMIMTFSI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2H2O
2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO
DMSO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5CH3CN). In particular, the number of anions around EMIM+ increased from ca. 3 for both n = 0 and n = 1.5 to ca. 4.5 for n = 0.69 to obtain EMIM+–solvated complexes in the form of a near-10-fold coordination structure (e.g., (BF4−)a(TFSI−)b(EMIM+)(H2O)c(DMSO)d(CH3CN)e, with a + b = 4.5 and c + d + e = 5.2). Spectroscopic analyses (ATR, NIR, and NMR) and MD simulations further confirmed that the HB network of H2O at n = 0.69 is the weakest among all mixtures studied, consistent with the formation of a more disordered, loosely bound structure. This is corroborated by excess property analyses, which showed the greatest deviations from ideality at this composition, and by DN trends, which revealed a high level of complex solvent–solvent and solute–solvent interactions. All these results pointed to the formation of a loose structure that, as revealed by the diffusion coefficients obtained from PGSE-NMR spectroscopy, favours ion mobility minimizing charge accumulation and concentration gradients at the electrode–electrolyte interface. These structural and transport advantages translated directly into superior device performance: the electrolyte with n = 0.69 delivered the lowest internal resistance values (confirmed by both Nyquist plots and IR drops from GCD curves) and the best rate capability among all tested systems. This is particularly notable given the demanding nature of rate performance in SCs, more so than that needed in Li- or Na-metal ion batteries. In summary, the findings demonstrate that HE electrolytes with carefully tuned anion-rich solvation structures (with the mixture with n = 0.69 as the most remarkable example) can simultaneously improve energy storage and power delivery in SCs, positioning them as a promising candidate for next-generation energy storage systems.
1.5CH3CN). In particular, the number of anions around EMIM+ increased from ca. 3 for both n = 0 and n = 1.5 to ca. 4.5 for n = 0.69 to obtain EMIM+–solvated complexes in the form of a near-10-fold coordination structure (e.g., (BF4−)a(TFSI−)b(EMIM+)(H2O)c(DMSO)d(CH3CN)e, with a + b = 4.5 and c + d + e = 5.2). Spectroscopic analyses (ATR, NIR, and NMR) and MD simulations further confirmed that the HB network of H2O at n = 0.69 is the weakest among all mixtures studied, consistent with the formation of a more disordered, loosely bound structure. This is corroborated by excess property analyses, which showed the greatest deviations from ideality at this composition, and by DN trends, which revealed a high level of complex solvent–solvent and solute–solvent interactions. All these results pointed to the formation of a loose structure that, as revealed by the diffusion coefficients obtained from PGSE-NMR spectroscopy, favours ion mobility minimizing charge accumulation and concentration gradients at the electrode–electrolyte interface. These structural and transport advantages translated directly into superior device performance: the electrolyte with n = 0.69 delivered the lowest internal resistance values (confirmed by both Nyquist plots and IR drops from GCD curves) and the best rate capability among all tested systems. This is particularly notable given the demanding nature of rate performance in SCs, more so than that needed in Li- or Na-metal ion batteries. In summary, the findings demonstrate that HE electrolytes with carefully tuned anion-rich solvation structures (with the mixture with n = 0.69 as the most remarkable example) can simultaneously improve energy storage and power delivery in SCs, positioning them as a promising candidate for next-generation energy storage systems.
8. Experimental section
The details of the sample preparation and the details of all the measurements and simulations are described in the SI.Conflicts of interest
The authors have no conflicts of interest.Data availability
Data for this article, including data presented in figures and tables have been included as part of the SI.Experimental procedures, tables with different data (physicochemical properties, NMR chemical shifts, etc.), NMR, ATR and NIR spectra, RDFs from MD simulations, and electrochemical results (CVs, GCDs, Nyquist plots, etc.). See DOI: https://doi.org/10.1039/d5ta04796j.
Acknowledgements
This work was supported by MCIN/AEI/10.13039/501100011033 (TED2021-130372B-C42, TED2021-131812B-I00 and PID2021-123648OB-I00), by “ERDF A way of making Europe” (PID2021-123648OB-I00) and by “European Union Next Generation EU/PRTR” (TED2021-130372B-C42 and TED2021-131812B-I00). Authors also acknowledge the Severo Ochoa Centres of Excellence Program through Grant CEX2024-001445-S. L. G.-A. acknowledges the grant PRE2019-090008 funded by MCIN/AEI/10.13039/501100011033 and “ESF Investing in your future”. P. G.-B. acknowledges the grant PRE2022-101750 funded by MCIN/AEI/10.13039/501100011033 and ESF+. X. L. also acknowledges the National Natural Science Foundation of China (22393961). J. M. V.-L., S. C., and R. M. M.-C. also thank C3UPO for HPC support. The Servicio Interdepartmental de Investigación (SIdI) of the Universidad Autónoma de Madrid and the Thermal Analysis Unit at the Instituto de Ciencia de Materiales de Madrid (ICMM) are acknowledged for helpful assistance with FTIR and NMR spectroscopies and DSC studies, respectively.References
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- A. S. Aricò, P. Bruce, B. Scrosati, J.-M. Tarascon and W. van Schalkwijk, Nat. Mater., 2005, 4, 366–377 CrossRef.
- T. S. Mathis, N. Kurra, X. Wang, D. Pinto, P. Simon and Y. Gogotsi, Adv. Energy Mater., 2019, 9, 1902007 CrossRef CAS.
- Z. Lin, E. Goikolea, A. Balducci, K. Naoi, P. L. Taberna, M. Salanne, G. Yushin and P. Simon, Mater. Today, 2018, 21, 419–436 CrossRef CAS.
- C.-C. Chen and J. Maier, Nat. Energy, 2018, 3, 102–108 CrossRef CAS.
- M. Chen, G. Feng and R. Qiao, Curr. Opin. Colloid Interface Sci., 2020, 47, 99–110 CrossRef CAS.
- L. A. Ferreira, V. N. Uversky and B. Y. Zaslavsky, Mol. BioSyst., 2017, 13, 2551–2563 RSC.
- J. Xie, Z. Liang and Y.-C. Lu, Nat. Mater., 2020, 19, 1006–1011 CrossRef CAS.
- D. Dong, J. Xie, Z. Liang and Y.-C. Lu, ACS Energy Lett., 2022, 7(1), 123–130 CrossRef CAS.
- D. E. Ciurduc, C. de la Cruz, N. Patil, A. Mavrandonakis and R. Marcilla, Energy Storage Mater., 2022, 53, 532–543 CrossRef.
- Q. Nian, W. Zhu, S. Zheng, S. Chen, B.-Q. Xiong, Z. Wang, X. Wu, Z. Tao and X. Ren, ACS Appl. Mater. Interfaces, 2021, 13, 51048–51056 CrossRef CAS.
- S. C. Kim, J. Wang, R. Xu, P. Zhang, Y. Chen, Z. Huang, Y. Yang, Z. Yu, S. T. Oyakhire, W. Zhang, L. C. Greenburg, M. S. Kim, D. T. Boyle, P. Sayavong, Y. Ye, J. Qin, Z. Bao and Y. Cui, Nat. Energy, 2023, 8, 814–826 CrossRef CAS.
- F. Cheng, W. Zhang, Q. Li, C. Fang, J. Han and Y. Huang, ACS Nano, 2023, 17, 24259–24267 CrossRef CAS.
- Q. Wang, C. Zhao, J. Wang, Z. Yao, S. Wang, S. G. H. Kumar, S. Ganapathy, S. Eustace, X. Bai, B. Li and M. Wagemaker, Nat. Commun., 2023, 14, 440 CrossRef CAS PubMed.
- Q. Wang, C. Zhao, F. Wu, S. G. H. Kumar, S. Ganapathy, S. Eustace, X. Bai, B. Li, J. Lu and M. Wagemaker, Adv. Mater., 2023, 35, 2210677 CrossRef CAS.
- M. Mao, X. Ji, Q. Wang, Z. Lin, M. Li, T. Liu, C. Wang, Y.-S. Hu, H. Li, X. Huang, L. Chen and L. Suo, Nat. Commun., 2023, 14, 1082 CrossRef CAS PubMed.
- F. Hu, J. Chen, H. Cao, H. Wang, H. Guo and X. Ouyang, Adv. Funct. Mater., 2025, 35, 2413004 CrossRef CAS.
- C. Yang, X. Liu, Y. Lin, L. Yin, J. Lu and Y. You, Adv. Mater., 2023, 35, 2301817 CrossRef CAS PubMed.
- B. Ge, J. Deng, Z. Wang, Q. Liang, L. Hu, X. Ren, R. Li, Y. Lin, Y. Li, Q. Wang, B. Han, Y. Deng, X. Fan, B. Li, G. Chen and X. Yu, Adv. Mater., 2024, 36, 2408161 CrossRef CAS.
- Y. Zou, B. Zhang, H. Luo, X. Yu, M. Yang, Q. Zheng, J. Wang, C. Jiao, Y. H. Chen, H. Zhang, J. Xue, X. Kuai, H.-G. Liao, C. Ouyang, Z. Ning, Y. Qiao and S.-G. Sun, Adv. Mater., 2024, 36, 2410261 CrossRef CAS.
- H. Lohani, A. Kumar, A. Bano, A. Ghosh, P. Kumari, A. Ahuja, A. Sengupta, D. Kumar, D. T. Major and S. Mitra, Adv. Energy Mater., 2024, 14, 2401268 CrossRef CAS.
- Z. Cheng, Z. Zhang, F. Qiu, Z. Gao, H. Xie, Z. Xu, M. Jia, X. Zhang and H. Zhou, ACS Energy Lett., 2025, 10, 177–184 CrossRef CAS.
- C. Yang, J. Xia, C. Cui, T. P. Pollard, J. Vatamanu, A. Faraone, J. A. Dura, M. Tyagi, A. Kattan, E. Thimsen, J. Xu, W. Song, E. Hu, X. Ji, S. Hou, X. Zhang, M. S. Ding, S. Hwang, D. Su, Y. Ren, X.-Q. Yang, H. Wang, O. Borodin and C. Wang, Nat. Sustain., 2023, 6, 325–335 CrossRef.
- J. Hao, L. Yuan, C. Ye, D. Chao, K. Davey, Z. Guo and S.-Z. Qiao, Angew. Chem., Int. Ed., 2021, 60, 7366–7375 CrossRef CAS PubMed.
- X. Liang, Y. Liang, Y. Gao, W. Qiao, D. Yin, P. Huang, C. Wang, L. Wang and Y. Cheng, Small, 2024, 20, 2408162 CrossRef CAS.
- L. González-Aguilera, J. M. Vicent-Luna, S. Tao, S. Calero, R. M. Madero-Castro, E. Raymundo-Piñero, X. Lu, M. C. Gutiérrez, M. L. Ferrer and F. del Monte, Adv. Funct. Mater., 2024, 34, 2400337 CrossRef.
- K. I. Assaf and W. M. Nau, Angew. Chem., Int. Ed., 2018, 57, 13968–13981 CrossRef CAS.
- D. Reber, R. Grissa, M. Becker, R.-S. Kühnel and C. Battaglia, Anion Selection Criteria for Water-in-Salt Electrolytes, Adv. Energy Mater., 2021, 11, 2002913 CrossRef CAS.
- Z. A. Zafar, G. Abbas, K. Knizek, M. Silhavik, P. Kumar, P. Jiricek, J. Houdková, O. Frank and J. Cervenka, J. Mater. Chem. A, 2022, 10, 2064–2074f RSC.
- A. Tot, L. Zhang, E. J. Berg, P. H. Svensson and L. Kloo, Sci. Rep., 2023, 13, 2154 CrossRef CAS.
- X. Lu, R. J. Jiménez-Riobóo, D. Leech, M. C. Gutiérrez, M. L. Ferrer and F. del Monte, ACS Appl. Mater. Interfaces, 2020, 12, 29181–29193 CAS.
- X. Lu, J. M. Vicent-Luna, S. Calero, M. J. Roldán-Ruiz, R. Jiménez, M. L. Ferrer, M. C. Gutiérrez and F. del Monte, ChemSusChem, 2020, 13, 5983–5995 CrossRef CAS.
- X. Lu, J. M. Vicent-Luna, S. Calero, R. M. Madero-Castro, M. C. Gutiérrez, M. L. Ferrer and F. del Monte, Energy Storage Mater., 2021, 40, 368–385 CrossRef.
- H. A. Zarei, M. Z. Lavasani and H. Iloukhani, J. Chem. Eng. Data, 2008, 53, 578–585 CrossRef CAS.
- C. A. Hall, K. A. Le, C. Rudaz, A. Radhi, C. S. Lovell, R. A. Damion, T. Budtova and M. E. Ries, J. Phys. Chem. B, 2012, 116, 12810–12818 CrossRef CAS PubMed.
- O. Iulian and O. Ciocirlan, J. Chem. Eng. Data, 2012, 57, 2640–26646 CrossRef CAS.
- E. J. González, L. Alonso and A. Domínguez, J. Chem. Eng. Data, 2006, 51(4), 1446–1452 CrossRef.
- V. Agieienko and R. Buchner, J. Chem. Eng. Data, 2019, 64, 4763–4774 CrossRef CAS.
- V. Agieienko and R. Buchner, J. Chem. Eng. Data, 2020, 65, 1900–1910 CrossRef CAS.
- C. L. Bentley, M. Y. Balogun, O. Morales-Collazo and J. F. Brennecke, J. Chem. Eng. Data, 2024, 69(10), 3532–3543 CrossRef CAS.
- H. Zhang, X. Lu, L. González-Aguilera, M. L. Ferrer, F. del Monte and M. C. Gutiérrez, J. Chem. Phys., 2021, 154, 184501 CrossRef CAS PubMed.
- N. López-Salas, J. M. Vicent-Luna, S. Imberti, E. Posada, M. J. Roldán, J. A. Anta, S. R. G. Balestra, R. M. Madero Castro, S. Calero, R. J. Jiménez-Riobóo, M. C. Gutiérrez, M. L. Ferrer and F. del Monte, ACS Sustainable Chem. Eng., 2019, 7, 17565–17573 CrossRef.
- A. R. Harifi-Mood, F. Sharifi and H. R. Bijanzadeh, ChemistrySelect, 2021, 6, 600–608 CrossRef CAS.
- J. Catalán, C. Díaz and F. García-Blanco, J. Org. Chem., 2000, 65, 9226–9229 CrossRef.
- M. Schmeisser, P. Illner, R. Puchta, A. Zahl and R. van Eldik, Chem.–Eur. J., 2012, 18, 10969–10982 CrossRef CAS.
- R. Younesi, G. M. Veith, P. Johansson, K. Edstro and T. Veggea, Energy Environ. Sci., 2015, 8, 1905–1922 RSC.
- H. Luo, Q. Gou, Y. Zheng, K. Wang, R. Yuan, S. Zhang, W. Fang, Z. Luogu, Y. Hu, H. Mei, B. Song, K. Sun, J. Wang and M. Li, ACS Nano, 2025, 19, 2427–2443 CrossRef CAS.
- Y.-Z. Zheng, N.-N. Wang, J.-J. Luo, Y. Zhou and Z.-W. Yu, Phys. Chem. Chem. Phys., 2013, 15, 18055–18064 RSC.
- B. A. Marekha, O. N. Kalugin, M. Bria and A. Idrissi, Phys. Chem. Chem. Phys., 2015, 17, 23183–23194 RSC.
- J. T. Arnold and M. G. Packer, High Resolution Nuclear Magnetic Resonance, McGraw-Hill Book, New York, 1959 Search PubMed.
- M. N. C. Zarycz and C. F. Guerra, J. Phys. Chem. Lett., 2018, 9, 3720–3724 CrossRef CAS.
- K. Hayamizu, S. Tsuzuki, S. Seki and Y. Umebayashi, J. Phys. Chem. B, 2012, 116, 11284–11291 CrossRef CAS.
- S. Cha, M. Ao, W. Sung, B. Moon, B. Ahlström, P. Johansson, Y. Ouchid and D. Kim, Phys. Chem. Chem. Phys., 2014, 16, 9591–9601 RSC.
- Y. Zhang, G. Wan, N. H. C. Lewis, J. Mars, S. E. Bone, H.-G. Steinrück, Ma. R. Lukatskaya, N. J. Weadock, M. Bajdich, O. Borodin, A. Tokmakoff, M. F. Toney and E. J. Maginn, ACS Energy Lett., 2021, 6, 3458–3463 CrossRef CAS.
- S. A. Katsyuba, E. E. Zvereva, A. Vidis and P. J. Dyson, J. Phys. Chem. A, 2007, 111, 352–370 CrossRef CAS PubMed.
- Y. Chen, Y.-H. Zhang and L.-J. Zhao, Phys. Chem. Chem. Phys., 2004, 6, 537–542 RSC.
- M. A. Czarnecki, Y. Morisawa, Y. Futami and Y. Ozaki, Chem. Rev., 2015, 115, 9707–9744 CrossRef CAS.
- Y. Ikemoto, Y. Harada, M. Tanaka, S. Nishimura, D. Murakami, N. Kurahashi, T. Moriwaki, K. Yamazoe, H. Washizu, Y. Ishii and H. Torii, J. Phys. Chem. B, 2022, 126(22), 4143–4151 CrossRef CAS.
- B. Czarnik-Matusewicz and S. Pilorz, Vib. Spectrosc., 2006, 40, 235–245 CrossRef CAS.
- J. L. Trenzado, Y. Rodríguez, A. Gutiérrez, A. Cincotti and S. Aparicio, J. Mol. Liq., 2021, 334, 116049 CrossRef CAS.
- T. Masaki, K. Nishikawa and H. Shirota, J. Phys. Chem. B, 2010, 114, 6323–6331 CrossRef CAS PubMed.
- I. A. Borin and M. S. Skaf, J. Chem. Phys., 1999, 110, 6412–6420 Search PubMed.
- H. Kovacs and A. Laaksonen, J. Am. Chem. Soc., 1991, 113, 5596–5605 CrossRef CAS.
- T. H. G. Saji, J. M. Vicent-Luna, T. J. H. Vlugt, S. Calero and B. Bagheri, J. Mol. Liq., 2024, 401, 124530 CrossRef CAS.
- C. D'Agostino, M. D. Mantle, C. L. Mullan, C. Hardacre and L. F. Gladden, ChemPhysChem, 2018, 19, 1081–1088 Search PubMed.
- K. Hayamizu, Y. Aihara, H. Nakagawa, T. Nukuda and W. S. Price, J. Phys. Chem. B, 2004, 108, 19527–19532 CrossRef CAS.
- V. V. Chaban, I. V. Voroshylova, O. N. Kalugin and O. V. PrezhdoIonic, J. Phys. Chem. B, 2012, 116, 7719–7727 Search PubMed.
- U. Mahanta, D. Kundu, R. P. Venkatesh, S. Sujatha, S. A. Ilangovan and T. Banerjee, Ind. Eng. Chem. Res., 2019, 58, 22741–22753 Search PubMed.
- P. Tan, J. Yue, Y. Yu, B. Liu, T. Liu, L. Zheng, L. He, X. Zhang, L. Suo and L. Hong, J. Phys. Chem. C, 2021, 125, 11838–11847 Search PubMed.
- M. Zanatta, V. U. Antunes, C. F. Tormena, J. Dupont and F. P. dos Santos, Phys. Chem. Chem. Phys., 2019, 21, 2567–2571 Search PubMed.
- L. Sun, O. Morales-Collazo, H. Xia and J. F. Brennecke, J. Phys. Chem. B, 2015, 119, 15030–15039 Search PubMed.
- Y. K. J. Bejaoui, F. Philippi, H.-G. Stammler, K. Radacki, L. Zapf, N. Schopper, K. Goloviznina, K. A. M. Maibom, R. Graf, J. A. P. Sprenger, R. Bertermann, H. Braunschweig, T. Welton, N. V. Ignat'ev and M. Finze, Chem. Sci., 2023, 14, 2200–2214 RSC.
- S. P. Beltran, X. Cao, J.-G. Zhang and P. B. Balbuena, Chem. Mater., 2020, 32, 5973 CrossRef.
- S. C. Kim, X. Kong, R. A. Vilá, W. Huang, Y. Chen, D. T. Boyle, Z. Yu, H. Wang, Z. Bao, J. Qin and Y. Cui, J. Am. Chem. Soc., 2021, 143, 10301 Search PubMed.
- F. Hu, J. Chen, H. Cao, H. Wang, H. Guo and X. Ouyang, Adv. Funct. Mater., 2025, 35, 2413004 Search PubMed.
- L. Sun, O. Morales-Collazo, H. Xia and J. F. Brennecke, J. Phys. Chem. B, 2016, 120, 5767–5776 Search PubMed.
- A. Noda, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2001, 105, 4603–4610 Search PubMed.
- D. R. MacFarlane, M. Forsyth, E. Izgorodina, A. P. Abbott, G. Annat and K. Fraser, Phys. Chem. Chem. Phys., 2009, 11, 4962–4967 RSC.
- H. Tokuda, S. Tsuzuki, M. A. B. H. Susan, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 19593–19600 CrossRef CAS.
- W. Xu, E. I. Cooper and C. A. Angell, J. Phys. Chem. B, 2003, 107(25), 6170–6178 CrossRef CAS.
- M. Sevilla, G. A. Ferrero, N. Diez and A. B. Fuertes, Carbon, 2018, 131, 193–200 CrossRef CAS.
- M. Yu, Y. Lu, H. Zheng and X. Lu, Chem.–Eur. J., 2018, 24, 3639–3649 CrossRef CAS.
- L. Demarconnay, E. Raymundo-Piñero and F. Béguin, Electrochem. Commun., 2010, 12, 1275–1278 CrossRef CAS.
- M. R. Lukatskaya, S.-M. Bak, X. Yu, X.-Q. Yang, M. W. Barsoum and Y. Gogotsi, Adv. Energy Mater., 2015, 5, 1500589 CrossRef.
- K. Kim, Y. Ando, A. Sugahara, S. Ko, Y. Yamada, M. Otani, M. Okubo and A. Yamada, Chem. Mater., 2019, 31(14), 5190–5196 CrossRef CAS.
- S. Sayah, A. Ghosh, M. Baaziz, R. Amine, M. Dahbi, Y. Amine, F. Ghamouss and K. Amine, Nano Energy, 2022, 98, 107336 CrossRef CAS.
- Y. Song, K. Zhang, X. Li, C. Yan, Q. Liu and A. Tang, J. Mater. Chem. A, 2021, 9, 26354–26361 RSC.
- L. Pan, B. Hu, X. Zhu, X. Chen, J. Shang, H. Tan, W. Xue, Y. Zhu, G. Liu and R.-W. Li, J. Mater. Chem. C, 2013, 1, 4556–4564 RSC.
- A. A. Adeniyi, T. L. Ngake and J. Conradie, Electroanalysis, 2020, 32, 2659–2668 CrossRef CAS.
- M. Shakourian-Fard, G. Kamath, S. M. Taimoory and J. F. Trant, J. Phys. Chem. C, 2019, 123, 15885–15896 CrossRef CAS.
- P. Peljo and H. H. Girault, Energy Environ. Sci., 2018, 11, 2306–2309 Search PubMed.
- N. O. Laschuk, E. B. Easton and O. V. Zenkina, RSC Adv., 2021, 11, 27925–27936 Search PubMed.
- B.-A. Mei, O. Munteshari, J. Lau, B. Dunn and L. Pilon, J. Phys. Chem. C, 2018, 122, 194–206 CAS.
- J. P. A. dos Santos, F. C. Rufino, J. I. Y. Ota, R. C. Fernandes, R. Vicentini, C. J. B. Pagan, L. M. Da Silva and H. Zanin, J. Energy Chem., 2023, 80, 265–283 Search PubMed.
- J. Zhao, G. Gorbatovski, O. Oll, T. Thomberg and E. Lust, Electrochim. Acta, 2019, 319, 82–87 CAS.
- X. Wang, T. S. Mathis, K. Li, Z. Lin, L. Vlcek, T. Torita, N. C. Osti, C. Hatter, P. Urbankowski, A. Sarycheva, M. Tyagi, E. Mamontov, P. Simon and Y. Gogotsi, Nat. Energy, 2019, 4, 241–248 CAS.
- C. Lei, F. Markoulidis, Z. Ashitaka and C. Lekakou, Electrochim. Acta, 2013, 92, 183–187 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |