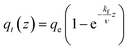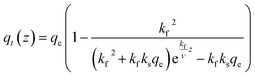Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetics of CO2 adsorption on UTSA-16(Zn) metal–organic framework: thermal, compositional, and geometrical effects†
Sanad
Altarawneh‡
 and
John Luke
Woodliffe‡
and
John Luke
Woodliffe‡
 *
*
Advanced Materials Research Group, Faculty of Engineering, University of Nottingham, Nottingham, NG7 2RD, UK. E-mail: luke.woodliffe1@nottingham.ac.uk
First published on 15th July 2025
Abstract
Capturing CO2 from point sources is a necessary step to limit the negative impacts of climate change. Metal–Organic Frameworks (MOFs), known for their exceptionally high surface areas and porosities, have demonstrated huge promise for environmental pollution control. The next stage of their application requires the design of equipment and materials capable of performing CO2 adsorption optimally and efficiently at scale. However, this requires an in-depth understanding of the kinetics associated with CO2 adsorption on MOFs under different circumstances (different geometries (pellets), compositions and temperatures). We present the first detailed kinetic study of the adsorption of CO2 on MOF UTSA-16(Zn), a strong potential candidate for industrial-scale CO2 capture, in the presence of different polymer binders and at different temperatures. Non-linear regression data fitting confirmed that a mixed order model was most able to describe the adsorption data, suggesting a combined controlling nature of surface adsorption and diffusion. Adsorption rate constants had an Arrhenius temperature dependency, and the calculated temperature independent kinetic parameters (activation energy and pre-exponential factor) allow the calculation of adsorption rates at any required design temperature. A potential reactor design and case study are also presented. The results provide valuable input to inform future design of adsorbent systems for CO2 capture, facilitating the transition of MOFs to industrial scale applications to address urgent environmental challenges.
1. Introduction
Climate change is expected to have a significant negative impact on the environment and our society.1 CO2 capture has been identified as a necessary technology to achieve net-zero emissions limiting the impacts of climate change by capturing CO2 at the source and preventing it from entering the atmosphere.2 The current available technology for this process is known as amine scrubbing, however, large energy requirements for regenerating the amine absorbents have severely limited industrial adoption.3 An alternative class of materials known as Metal–Organic Frameworks (MOFs) have emerged as a promising solution, offering significantly reduced energy demands for regeneration. This reduction in energy is due to CO2 being physically adsorbed to the surface of the materials, rather than bound by chemical bonds as with the amine solvents.4 MOFs contain nodes of metal ions or clusters held together by organic molecules as linkers between the nodes.5 Since the metal ions and organic molecules can be varied, the resulting MOFs demonstrate tuneable properties with high internal surface areas, which can be tailored to a range of applications from gas storage to biomedicine.6–10 MOFs have demonstrated highly beneficial properties for use in CO2 capture applications, including high CO2 capacities and high selectivity for CO2 over other gases such as N2.11 One MOF with strong potential for industrial-scale CO2 capture is UTSA-16(Zn) (UTSA = University of Texas at San Antonio), composed of Zn clusters and citrate linkers (C12H8KO14Zn3).12 In addition to a high CO2 capacity and selectivity, UTSA-16(Zn) has shown high stability to moisture and acid gases, low reagent costs and scalable microwave and continuous-flow synthesis routes.13–15 UTSA-16(Zn) has also found application as a fluorescence detector for SO2,16 and its CO2 capture properties can be further tuned through cation replacement.17Despite the development of scalable synthesis and activation routes for UTSA-16(Zn) and other MOF/MOF composites, they are typically still produced as dry powder formulations.18–21 However, for CO2 capture and other large-scale applications, the powders need to be formed into granules and/or pellets to prevent large pressure drops across packed bed reactors and to improve general handling.22 Pressure compaction has been typically used to form pellets for other materials, however, with MOFs, the pressures can cause the highly porous structures to collapse, resulting in a loss of porosity and gas storage capacity.23 Therefore, binders have been investigated as a solution to hold MOF powders together and provide mechanical stability to the pellets without the need for compaction. In particular, polymer based binders have been effective for producing MOF pellets since they can be easily processed using solvents (without the need for high temperature calcination), have low weights (minimising losses in gravimetric CO2 capacity), are permeable to gases and can form hydrogen bonds to MOFs through polar chemical groups.24,25 Although many studies have explored the impacts of shaping and binders on MOF properties,23,25,26 and others have explored the adsorption kinetics of specific MOFs,27–30 there have been very few in-depth studies on the impact of pelletisation with different binders on the kinetics of CO2 adsorption. The first studies in this area have been produced in the last two years, considering kinetic effects for MOFs Al–BTC (btc = 1,3,5-benzenetricarboxylate), aluminium fumarate (AlFum) and ZIF-8 (ZIF = zeolitic imidazolate framework).31,32 The ZIF-8 study used a binder mixture of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 methylcellulose and bentonite at 20–30 wt%, which was found to significantly improve mechanical strength but caused a loss of surface area and slower CO2 adsorption kinetics due to framework collapse.31 The Al–BTC and AlFum study used sodium alginate, Septon and silica-sol binders, finding that the different binders had varying impacts on CO2 kinetics.32 The impacts on CO2 kinetics from other binders and with different MOFs is still unknown. This underexplored area represents a significant knowledge gap since the kinetics of adsorption will have a large impact on the cycle time for packed bed adsorbers, influencing decisions such as reactor design and operational conditions. Herein, we present a unique study of the kinetics of CO2 adsorption on UTSA-16(Zn) powder and pellets with polyvinyl alcohol (PVA), polyvinyl butyral (PVB) and polyvinylpyrrolidone (PVP) polymer binders. Each of these binders have been used to effectively formulate pellets with different MOFs, but in-depth kinetic analysis is missing for these binders and for UTSA-16(Zn).24,33–38 This study includes isothermal adsorption scans at different temperatures to assess the impact of pelletisation and the various binders on rate constants, activation energies and pre-exponential factors associated with the adsorption phenomenon using a Mixed Order (MO) model rate equation. These results provide researchers and engineers in this field with valuable resource to inform future rational design of UTSA-16(Zn) and other adsorbent formulations for CO2 capture, and enable the improved modelling of packed bed adsorbers to facilitate the transition of MOFs to industrial scale applications.
50 methylcellulose and bentonite at 20–30 wt%, which was found to significantly improve mechanical strength but caused a loss of surface area and slower CO2 adsorption kinetics due to framework collapse.31 The Al–BTC and AlFum study used sodium alginate, Septon and silica-sol binders, finding that the different binders had varying impacts on CO2 kinetics.32 The impacts on CO2 kinetics from other binders and with different MOFs is still unknown. This underexplored area represents a significant knowledge gap since the kinetics of adsorption will have a large impact on the cycle time for packed bed adsorbers, influencing decisions such as reactor design and operational conditions. Herein, we present a unique study of the kinetics of CO2 adsorption on UTSA-16(Zn) powder and pellets with polyvinyl alcohol (PVA), polyvinyl butyral (PVB) and polyvinylpyrrolidone (PVP) polymer binders. Each of these binders have been used to effectively formulate pellets with different MOFs, but in-depth kinetic analysis is missing for these binders and for UTSA-16(Zn).24,33–38 This study includes isothermal adsorption scans at different temperatures to assess the impact of pelletisation and the various binders on rate constants, activation energies and pre-exponential factors associated with the adsorption phenomenon using a Mixed Order (MO) model rate equation. These results provide researchers and engineers in this field with valuable resource to inform future rational design of UTSA-16(Zn) and other adsorbent formulations for CO2 capture, and enable the improved modelling of packed bed adsorbers to facilitate the transition of MOFs to industrial scale applications.
2. Adsorption kinetics
2.1. The rate equation
The degree of CO2 adsorption is usually defined by the normalised molar quantity “qt” which is the molar amount of adsorbed CO2 per unit mass of MOF (mmol_(CO2) g_(MOF)−1); this will be reported as mmol g−1 subsequently. The rate of adsorption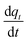 is related to the Arrhenius rate constant k and the adsorption model f(q) as follows:
is related to the Arrhenius rate constant k and the adsorption model f(q) as follows: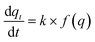 | (1) |
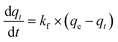 | (2) |
| qt = qe(1 − exp(−kf × t)) | (3) |
Usually, the rate constant is extracted by linear regression using the re-arranged form of eqn (3):
| ln(qe − qt) = ln(qe) − kf × t | (4) |
A plot of ln(qe − qt) against t should yield a straight line with a slope of the PFO rate constant kf.
 | (5) |
 | (6) |
To extract the kinetic rate constant, eqn (6) can be linearised to the following:41
 | (7) |
Such that a plot of  against t yields a straight line with a slope of
against t yields a straight line with a slope of  and an intercept of
and an intercept of  from which the PSO rate constant can be extracted. However, the accuracy of the linear regression approach was shown to be lacking.42,43 Thus, non-linear regression for a more complicated model was used.
from which the PSO rate constant can be extracted. However, the accuracy of the linear regression approach was shown to be lacking.42,43 Thus, non-linear regression for a more complicated model was used.
 | (8) |
Eqn (8) is the general kinetic rate equation which is more capable of describing more complex adsorption systems. However, to solve for the integral form, a more complicated treatment is required. Eqn (8) is considered a Bernoulli ODE. After solving eqn (8), the final solution for the adsorption capacity function can be given as follows:
 | (9) |
Obtaining the values of kf and ks by linear regression is not possible due to the complicated nature of eqn (9). Hence, data fitting against experimental qt values was performed using a non-linear regression approach by iteratively modifying the values of kf and ks for the best fit. From there, values of kf and ks were extracted at different temperatures.
2.2. The rate constant and the Arrhenius function
In addition to kf and ks, it is useful to report the rate of adsorption in terms of temperature independent kinetic parameters: the activation energy (E) and the pre-exponential factor (A). The Arrhenius rate constant can be written as follows:46 | (10) |
Such that R is the universal gas constant (8.314 J mol−1 K−1) and T is the temperature in kelvin. Hence, the rate constant in this work was extracted at different adsorption temperatures of 25, 40, 60 and 80 °C. The values of E and A were then extracted from the linearisation of eqn (10):
 | (11) |
Using the equation above, one can extract E and A from the slope and intercept of the Arrhenius plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k(T) against
k(T) against 
The final kinetic equation in its differential and integral form can be obtained by substituting eqn (10) in eqn (8) and (9):
 | (12) |
 | (13) |
Such that Ef, Es, Af, and As are the activation energy and the pre-exponential factor for the PFO and PSO rate constants, respectively. Eqn (13) is the final equation which shows how the adsorption capacity of the MOF (qt) is related to temperature and time through a series of temperature independent parameters: Ef, Es, Af, and As.
3. Method
3.1. Materials
Reagents were all used as purchased and only deionised water was used. Polyvinyl pyrrolidone (Mw: 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), polyvinyl butyral, polyvinyl alcohol (Mw: 9000–10
000), polyvinyl butyral, polyvinyl alcohol (Mw: 9000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; 80% hydrolysed), potassium hydroxide (86.7%), citric acid monohydrate (≥99.0%), zinc acetate dihydrate (≥99.0%) were purchased from Merck. Ethanol (absolute, SpS grade) was obtained from Scientific Laboratory Supplies LTD, while methanol (≥99.9%) was obtained from Fisher Scientific.
000; 80% hydrolysed), potassium hydroxide (86.7%), citric acid monohydrate (≥99.0%), zinc acetate dihydrate (≥99.0%) were purchased from Merck. Ethanol (absolute, SpS grade) was obtained from Scientific Laboratory Supplies LTD, while methanol (≥99.9%) was obtained from Fisher Scientific.
3.2. Synthesis of MOF UTSA-16(Zn)
The MOF UTSA-16(Zn) was produced in powder form using a continuous flow reactor, custom-built using Vapourtec pumps (R2+/R4, SF-10), Idex fittings and PTFE tubing (OD: 3.2 mm, ID: 1.6 mm). Firstly, two solutions were prepared. One was a solution of Zn(OAc)2·2H2O (0.4 M), citric acid monohydrate (0.44 M) and KOH (1.32 M) in H2O, and the other was pure ethanol. These solutions were pumped at 5 mL min−1 each into an arrowhead mixing tee (ID: 0.79 mm), and the resultant stream heated to 120 °C for 5 minutes residence time through an oil bath heater coil (25 m). The suspension was cooled using a water bath (room temperature) and passed through a back pressure regulator (6 bar). The MOF product suspension was then collected, centrifuged, washed (4× MeOH) and dried (75 °C, overnight). The final UTSA-16(Zn) product was collected in the powder form (12.6 g, 71% yield).3.3. Pelletisation of MOF UTSA-16(Zn)
UTSA-16(Zn) was formulated with different polymer binders and pelletised by extrusion. Pure binder solutions were prepared at 8 wt% by dissolving PVB in 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 EtOH
2 EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (10 mL) and PVA or PVP in 7
H2O (10 mL) and PVA or PVP in 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 EtOH
3 EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (10 mL). Slurries of UTSA-16(Zn) in the polymer binder solutions (8 wt% PVA, PVP and PVB) were then prepared at 1 g mL−1 and extruded using a 5 mL syringe onto Petri dishes. The extrudates were then divided using a knife, dried at 100 °C for 10 minutes after which they were activated in a vacuum oven (120 °C, overnight). Adsorption analysis was performed for the UTSA-16(Zn) MOF powder and pelletised MOF with 8 wt% binders (please refer to the nomenclature in Table 1).
H2O (10 mL). Slurries of UTSA-16(Zn) in the polymer binder solutions (8 wt% PVA, PVP and PVB) were then prepared at 1 g mL−1 and extruded using a 5 mL syringe onto Petri dishes. The extrudates were then divided using a knife, dried at 100 °C for 10 minutes after which they were activated in a vacuum oven (120 °C, overnight). Adsorption analysis was performed for the UTSA-16(Zn) MOF powder and pelletised MOF with 8 wt% binders (please refer to the nomenclature in Table 1).
3.4. Chemical characterisation
4. Results and discussion
4.1. Chemical analysis and MOF characterisation
The MOF UTSA-16(Zn) was synthesised via a continuous flow method as described earlier in Section 3.2, which is reported in detail elsewhere.48Fig. 1A shows the powder XRD pattern for the as-synthesised MOF, demonstrating high crystallinity in close alignment with the calculated pattern produced from the Crystallographic Information File with Mercury software.49 The pattern shows characteristic peaks at 2θ ≈ 7°, 11°, 14° and 16°, matching previous reports.12,14 The MOF crystal structure is also shown to be unaffected by the extrusion pelletisation process (Fig. 1A). FTIR analysis in Fig. 1B supports the expected chemical composition of UTSA-16(Zn) with characteristic symmetric and asymmetric stretching vibrations of carboxylic groups around 1400 and 1580 cm−1, respectively.50 A broad hydrogen bonding peak is also observed around 3400 cm−1 which is assigned to hydroxyl groups. These results match the spectra of UTSA-16(Zn) from previous reports.51 After pelletisation, the chemical structure of the MOF is shown to be unchanged, though the broad hydroxyl peak increased in amplitude due to the hydroxyl groups in the PVA binder (Fig. 1B). SEM and TEM micrographs (Fig. 1C and D) show the MOF particle morphologies, revealing reasonable uniformity of approximately octahedral polyhedra around 50–100 nm. These morphologies are similar to what have previously been observed with different batch synthesis methods.13,154.2. Thermal behaviour and CO2 adsorption isotherms
The CO2 adsorption cycles for powdered MOF (NB-MOF) and MOF pelletised with different binders (PVA, PVB, and PVP) at temperatures of 25, 40, 60 and 80 °C are shown in Fig. 2. Several adsorption–desorption cycles are shown at different temperatures. Clearly, the equilibrium adsorbed amount of CO2 (qe) drops systematically going from 25 °C to 80 °C for all materials; higher temperatures result in lower adsorption capacities. More importantly, however, changing the geometry of the MOF from powder (NB-MOF) to pellets (PVA-P-MOF, PVB-P-MOF, PVP-P-MOF) results in a drop in qe. | ||
| Fig. 2 CO2 adsorption isotherms for (A) NB-MOF, (B) PVA-P-MOF, (C) PVB-P-MOF, and (D) PVP-P-MOF at temperatures of 25, 40, 60 and 80 °C. | ||
To better understand this trend, three replicates for the adsorption isotherms were performed for all the materials, and results of their equilibrium adsorption capacities are summarised in Fig. 3. All pelletised samples showed a drop in the CO2 adsorption capacity of the MOF component compared to the pristine powdered MOF due to several factors. First, binders can cause a pore-blocking effect where they restrict the access of CO2 to active pore sites in the MOF, resulting in a drop in adsorption capacity.24,36,38 In addition, a decrease in capacity may be observed due to the mechanical pressure exerted on the MOF during extrusion pelletisation.23 Finally, the formulation of the material in pellet form results in an overall drop in surface area which adds an additional thickness through which CO2 has to travel before reaching the active site.
 | ||
| Fig. 3 Equilibrium CO2 adsorption capacity of NB-MOF, PVA-P-MOF, PVB-P-MOF, and PVP-P-MOF at different temperatures. | ||
A noticeable variation in equilibrium adsorption capacity can be seen going from one binder type to another. Both PVB-P-MOF and PVP-P-MOF display higher adsorption capacities than that obtained for PVA-P-MOF at all temperatures. This is likely due to the additional pore-blocking nature of PVA compared to PVB and PVP, which has also been observed previously.52
The drop in CO2 capacity of the pellets compared to the powdered MOF starts to diminish at higher temperatures (especially for PVB-P-MOF). This may be assigned to enhanced gas diffusivity at high temperature and/or thermal expansion of the material making more accessible pathways for the gas to reach active sites.
The trend appearing in Fig. 3 suggests that pelletising, while being crucial for development of practical adsorption systems (better material flowability, reduced pressure drop through beds, etc.), can hinder the adsorption capacity of the MOF which can clearly be seen in the case of PVA-P-MOF as an example.
4.3. Kinetics of CO2 adsorption
 | ||
| Fig. 4 Arrhenius plots of PFO rate constants for (A) NB-MOF, (B) PVA-P-MOF, (C) PVB-P-MOF, and (D) PVP-P-MOF against the reciprocal of temperature (units of kf is min−1). | ||
 | ||
| Fig. 5 Arrhenius plots of PSO rate constants for (A) NB-MOF, (B) PVB-P-MOF, and (C) PVP-P-MOF against the reciprocal of temperature (units of ks is g mmol−1 min−1). | ||
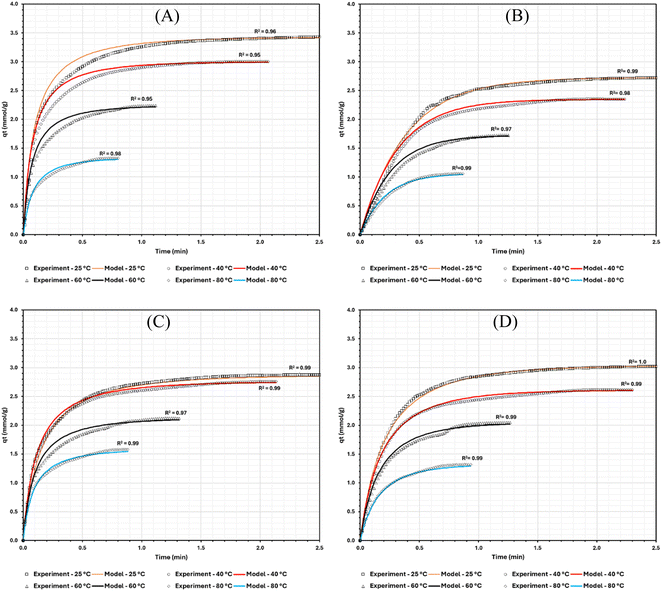
The Arrhenius plots appearing in Fig. 4 and 5 were used to extract the kinetic data reported in Table 2. The data in Table 2 can be used to predict adsorption rates and adsorption progress (qt) when used in conjunction with eqn (12) and (13), respectively. The trend of the activation energy and pre-exponential factor with composition and geometry of the tested materials is summarised in Fig. 6A and B. All the systems exhibited a mixed model (MO) adsorption nature whereby the adsorption rate depends on both PFO and PSO models, except for PVA-P-MOF which only showed a PFO rate dependence (i.e., ks = 0).
| Material | Parametera | Temperature (°C) | E (kJ mol−1) | ln(A)b | |||
|---|---|---|---|---|---|---|---|
| 25 | 40 | 60 | 80 | ||||
| a Units of qe, kf and ks are mmol g−1, min−1 and g mmol−1 min−1, respectively. b Units of Af and As are min−1 and g mmol−1 min−1, respectively. | |||||||
| NB-MOF | q e | 3.2 ± 0.1 | 3.0 ± 0.0 | 2.1 ± 0.1 | 1.4 ± 0.2 | — | — |
| k f | 1.6 ± 0.2 | 2.2 ± 0.3 | 2.5 ± 0.3 | 3.5 ± 0.3 | 11.3 ± 0.7 | 5.1 ± 0.2 | |
| k s | 3.4 ± 1.1 | 3.5 ± 1.1 | 5.2 ± 1.2 | 8.4 ± 1.0 | 15.5 ± 4.0 | 7.3 ± 1.3 | |
| PVA-P-MOF | q e | 2.7 ± 0.0 | 2.3 ± 0.1 | 1.7 ± 0.0 | 1.1 ± 0.0 | — | — |
| k f | 2.7 ± 0.2 | 2.9 ± 0.2 | 3.6 ± 0.2 | 4.8 ± 0.3 | 9.5 ± 0.6 | 4.8 ± 0.2 | |
| k s | 0.0 | 0.0 | 0.0 | 0.0 | N/A | N/A | |
| PVB-P-MOF | q e | 2.9 ± 0.1 | 2.7 ± 0.1 | 2.0 ± 0.1 | 1.4 ± 0.2 | — | — |
| k f | 1.6 ± 0.2 | 1.4 ± 0.1 | 2.0 ± 0.1 | 2.7 ± 0.2 | 9.2 ± 1.9 | 4.1 ± 0.7 | |
| k s | 2.1 ± 0.1 | 2.8 ± 0.2 | 3.7 ± 0.2 | 7.1 ± 1.4 | 17.9 ± 3.4 | 7.9 ± 1.3 | |
| PVP-P-MOF | q e | 3.0 ± 0.1 | 2.6 ± 0.1 | 2.0 ± 0.1 | 1.3 ± 0.0 | — | — |
| k f | 2.2 ± 0.3 | 1.9 ± 0.30 | 2.7 ± 0.3 | 3.7 ± 0.4 | 9.6 ± 1.2 | 4.5 ± 0.5 | |
| k s | 1.2 ± 0.4 | 1.7 ± 0.3 | 1.8 ± 0.5 | 3.0 ± 0.9 | 13.3 ± 2.3 | 5.5 ± 1.0 | |
 | ||
| Fig. 6 (A) Activation energy and (B) pre-exponential factor associated with CO2 adsorption (*units of Af and As are min−1 and g mmol−1 min−1, respectively). | ||
Despite the convoluted behaviour of adsorption (i.e., being governed by PFO and PSO), the significance of the dominant model varies with adsorption progression; this is because the contribution of both kf and ks to the overall adsorption rate (eqn (8)) is weighed by the factors (qe − qt) and (qe − qt)2, respectively. These factors amount to significantly different values depending on the adsorption progress (see Fig. 7A). The (qe − qt)2 factors exhibit much higher values initially, which then dip below the (qe − qt) factors when the adsorption progresses further. This effect is reflected on the adsorption behaviour as presented in Fig. 7B.
At the initial stage of adsorption (<0.5 min), the PSO model fits the data well. However, going towards equilibrium (>1.5 min), the PFO model fits the experimental data more accurately. Such a result is in line with the trends in Fig. 7A showing a dominance of the PSO weighing factor (qe − qt)2 below 0.3 min before PFO starts dominating towards equilibrium. Generally, PFO rate is known to describe diffusion, while PSO rate resembles the adsorption step on active sites.45 Following this, and since at the initial stage more active sites are available, the PSO model would naturally dominate (Fig. 7B). As the adsorption progresses, the active sites become encapsulated within the body of the MOF, which can be considered similar to that described in the Shrinking Core Model (SCM) reported in Levenspiel 1998.53 While the SCM was originally devised for reactive systems (chemical) and not adsorption (physical), the concept still holds since a passive outer layer is formed whether it is a chemical or a physical process. This leads to the PFO model being more representative towards equilibrium adsorption. This behaviour justifies the usage of the MO model where the effect of both PFO and PSO models are convoluted to track the adsorption progress in a more accurate manner.
As previously discussed, PVA-P-MOF is the only system which was entirely described by a PFO model. PVA binder is thus believed to have completely encapsulated the MOF creating a barrier through which the CO2 needs to diffuse. Hence the process was diffusion controlled showing dependence only on the PFO model. This result is in agreement with the equilibrium adsorption capacities reported in Fig. 3, in which PVA-P-MOF showed the lowest adsorption capacity, potentially due to blockage of active sites by the binder resulting in an overall hindrance in adsorption.
The reliability of the extracted kinetic data reported in Table 2 was tested by overlaying it against experimentally obtained values, summarised in Fig. 8. The coefficient of determination (R2) for all the adsorption systems is very close to 1.0 (the lowest R2 was 0.95 in Fig. 8A). This suggests that the extracted kinetic data reported in this work is capable of describing the adsorption systems accurately.
 | ||
| Fig. 8 Data fitting of (A) NB-MOF, (B) PVA-P-MOF, (C) PVB-P-MOF, and (D) PVP-P-MOF adsorption systems using extracted kinetic data appearing in Table 2 (qt is mmol per g_MOF). | ||
 | ||
| Fig. 9 Simulated adsorption rate against conversion generated using the kinetic data in Table 2, eqn (12) and (13) for the adsorption of CO2 on (A) NB-MOF, (B) PVA-P-MOF, (C) PVB-P-MOF, and (D) PVP-P-MOF. | ||
As expected, the adsorption rate drops with conversion for all temperatures due to the saturation of vacant sites in the MOF, resulting in a drop in the driving force (qe − qt) of adsorption. With the exception of PVB-P-MOF, the rate of adsorption at 60 and 80 °C is the lowest (slowest at 80 °C) followed by either 25 or 40° (depending on the material). No clear distinction can be seen between 25 and 40 °C; this is because in some cases, the drop in qe with temperature increase is not large enough to cause the overall rate to drop, while simultaneously the rate constants (kf and ks) are increased at the higher temperature (40 °C). This can be seen in the case of NB-MOF, PVA-P-MOF, and PVB-P-MOF. For PVP-P-MOF, the drop in qe (going from 25 to 40 °C) is large enough, such that even the increase in the rate constants is not enough to compensate for the drop in qe, leading to a slightly faster rate of adsorption at 25 °C. However, as the temperature is increased further to 60 and 80 °C, a significant drop in the overall adsorption rate is observed (with 80 °C exhibiting the slowest rate of adsorption). This is because the drop in qe at such temperatures is very large (see Fig. 3), which diminishes the driving force of adsorption (qe − qt). It is also important to highlight that the drop in the rate of adsorption follows a quadratic nature for all the materials except for PVA-P-MOF, which decays linearly. This is due to PVA-P-MOF being the only material which was completely governed by the linear PFO diffusion model, while the others showed mixed dependence on PFO and PSO (i.e., MO model).
 | ||
| Fig. 10 Geometrical effect on the adsorption rate of CO2 on powdered and pelletised MOF at temperatures (A) 25, (B) 40, (C) 60 and (D) 80 °C. | ||
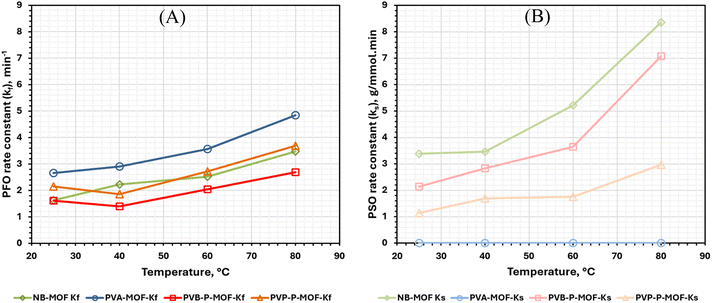 | ||
| Fig. 11 (A) PFO (kf) and (B) PSO (ks) rate constants associated with the adsorption of CO2 on NB-MOF, PVA-P-MOF, PVB-P-MOF, and PVP-P-MOF at different temperatures. | ||
In contrast, PVA-P-MOF exhibits a PSO rate constant of zero and a highest value of PFO rate constant (kf) at all temperatures. This suggests that the adsorption on PVA-P-MOF is majorly diffusion controlled. These results agree with the rates of adsorption appearing in Fig. 10 such that the rate is hindered when the MOF is mixed with binders and shaped into pellets.
5. Example equipment design and application
5.1. Gas–solid molar balance
For a continuous operating process where CO2 is being generated steadily, a possible design for CO2 capture is a counter-current column, where fresh MOF is fed continuously from the top and CO2 carrying gas is fed from the bottom as shown in Fig. 12.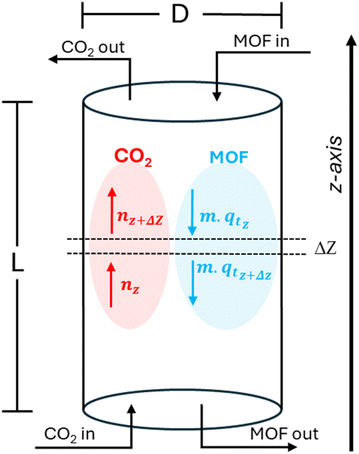 | ||
| Fig. 12 Schematic of a continuous flow adsorption column where fresh MOF is fed at the top and process gas is fed from the bottom. | ||
At the bottom, CO2 is being fed at a rate of N (mol min−1), while at the top fresh MOF (qt = 0) is being fed at a rate of m (kg min−1). At steady state, qt and n molar profiles are developed across the z-axis for a given column diameter (D), MOF flow rate (m), and kinetic parameters kf, ks, and qe (depending on the controlling model). For an infinitesimally small section Δz (where Δz → 0) along the length, a steady state mol balance on CO2 can be performed:
| nz − nz+Δz = mqtz+Δz − mqtz | (14) |
Such that, n is the molar flow rate of CO2 in mol min−1, m is the mass flow rate of fresh MOF in kg min−1 and qt is the adsorbed CO2 on the MOF as defined in previous sections. Dividing both sides with Δz and taking  yields:
yields:
 | (15) |
Eqn (15) is the fundamental equation linking CO2 gradient along the length of the column in the gas phase to the adsorbed CO2 gradient in the solid phase.
5.2. Adsorbed CO2 gradient qt(z)
To be able to solve eqn (15) for the molar gradient of CO2 in the gas phase n(z), the gradient of the adsorbed CO2qt(z) needs to be developed first. appearing in eqn (15) can be linked to the previously developed adsorption rate
appearing in eqn (15) can be linked to the previously developed adsorption rate  as follows:
as follows: | (16) |
Such that  is the MOF velocity travelling down the column and can be denoted to by ν, hence:
is the MOF velocity travelling down the column and can be denoted to by ν, hence:
 | (17) |
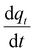 appearing in eqn (17) is what we defined before in Section 2 and can be represented using the PFO, PSO, or MO models (depending on which model fits the adsorption data). For simplicity and for the sake of demonstration, the PFO model will be used in eqn (17) for the treatment here (the derivation for the other models for qt(z) is shown in the ESI†). The final results of qt(z) are all summarised in Table 3. Thus, eqn (17) can be written as follows:
appearing in eqn (17) is what we defined before in Section 2 and can be represented using the PFO, PSO, or MO models (depending on which model fits the adsorption data). For simplicity and for the sake of demonstration, the PFO model will be used in eqn (17) for the treatment here (the derivation for the other models for qt(z) is shown in the ESI†). The final results of qt(z) are all summarised in Table 3. Thus, eqn (17) can be written as follows: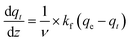 | (18) |
Eqn (18) is a separable ODE which can be written as:
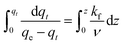 | (19) |
Solving the integral above and with the correct boundary conditions, the final equation yields:
 | (20) |
It is important to highlight that the velocity (ν) of the MOF travelling down the column can be linked to its mass flow rate (m) as follows:
 | (21) |
Such that ρb is the bulk density of the MOF in the column and A is the cross-sectional area of the column.
5.3. Gaseous CO2 gradient n(z)
Using the equations reported in Table 3, one can now solve for the gaseous CO2 gradient along the column. When eqn (17) is substituted in eqn (15), it can now be written in terms of as follows:
as follows: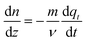 | (22) |
Integrating both sides with the correct boundary conditions, yield:
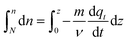 | (23) |
Eqn (23) is the general integral-form which can be used for any controlling model (PFO, PSO, or MO). The rate of adsorption 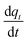 can now be substituted from eqn (2) and (5) or (8) depending on the controlling mechanism. For demonstration, we will substitute the PFO model as follows:
can now be substituted from eqn (2) and (5) or (8) depending on the controlling mechanism. For demonstration, we will substitute the PFO model as follows:
 | (24) |
 | (25) |
Such that ρb, A, kf, and qe are constants. After simplification, n(z) can be written:
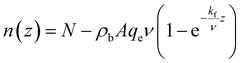 | (26) |
From eqn (26), it is shown that using the kinetic parameters qe and kf (in the case of PFO), one can predict the required MOF feeding speed ν, column area (i.e., diameter), and column length to achieve a certain adsorption target (i.e., to make the CO2 molar flow rate drop from N to a fraction of it or to zero). It is extremely important, however, to note that the term residing next to N in eqn (26) can in some cases yield values higher than N resulting in negative values of CO2 molar flow rate which, in reality, is impossible. Thus, the length of the column (z) must be taken at the point at which the curve of n(z) vs. z intersects with the x-axis (as shown in Fig. 13B and C). The reason for such a behaviour is because the equilibrium capacity qe was reported in this study independently of CO2 concentration in the gas phase; this behaviour, as mentioned before, was out of the scope of the current work and is to be investigated in future study.
can in some cases yield values higher than N resulting in negative values of CO2 molar flow rate which, in reality, is impossible. Thus, the length of the column (z) must be taken at the point at which the curve of n(z) vs. z intersects with the x-axis (as shown in Fig. 13B and C). The reason for such a behaviour is because the equilibrium capacity qe was reported in this study independently of CO2 concentration in the gas phase; this behaviour, as mentioned before, was out of the scope of the current work and is to be investigated in future study.
The same treatment above can be conducted for a PSO or MO systems, however, in that case,  in eqn (23) needs to be substituted for its corresponding model and the value of qt(z) afterwards should be substituted for the controlling model as shown in Table 3.
in eqn (23) needs to be substituted for its corresponding model and the value of qt(z) afterwards should be substituted for the controlling model as shown in Table 3.
5.4. Case study
The exhaust line of a cement production plant typically contains 30 v/v% of CO2 emitted from the burning of fossil fuel combined with the thermal decomposition of calcium carbonate in the calciner. If, for example, we are aiming to treat a branch of that line having a total volumetric flow rate of 1 m3 min−1, the CO2 volumetric flow rate in that branch will be 300 L min−1. If we assume that the gas temperature and pressure in that line were dropped to ambient values (1 atm and 298.15 K), an estimation of CO2 molar flow rate can be done using the ideal gas equation of state: | (27) |
Giving a value of  mol per min CO2.
mol per min CO2.
The molar flow of 12.3 mol min−1 will be assumed to be the initial flow rate (N) entering the adsorption column. For this simulation, the MOF bulk density and the column diameter were fixed at 800 kg m−3 and 0.25 m, respectively. A parametric sweep was done on different typical arbitrary values of the adsorption capacity qe, MOF velocity ν, and rate constant kf as shown in Table 4.
| Parameter | Typical values | |||
|---|---|---|---|---|
| q e (mol kg−1) | 2.5 | 4.0 | 5.0 | 6.0 |
| ν (m min−1) | 0.07 | 0.10 | 0.14 | 0.20 |
| k f (min−1) | 0.5 | 0.3 | 1.0 | 1.5 |
For a certain MOF, if the kinetic analysis revealed that the process is controlled by a PFO model, then the design of the adsorption column will be governed by eqn (26). Results of the simulation using that equation for different parameters are presented in Fig. 13A–C. The values of the first column in Table 4 are fixed when any other parameter is varied. For example, when qe is varied from 2.5 to 6.0 mol kg−1, ν and kf are fixed at 0.07 m min−1 and 0.5 min−1, respectively.
In Fig. 13A, increasing the rate constant kf results in a drop in the column length needed to achieve a certain CO2 molar flow rate value. For instance, to achieve a molar flow rate of 6 mol min−1 (molar flow drop of ∼6.3 mol min−1), a column length of 0.114, 0.171, 0.342, and 0.568 metres are needed for rate constants kf 1.5, 1.0, 0.5 and 0.3 min−1, respectively. Nonetheless, regardless of how much the rate constant value is increased, the final molar flow rate does not change with changing the rate constant and eventually plateaus at the same value (see Fig. 13A). In order for the final molar flow rate value to change, the MOF adsorption capacity qe and/or MOF flow rate ν have to change (this also applies to column diameter and MOF density which were fixed in this treatment). Contrary to the rate constant, increasing both qe and ν causes the final CO2 molar flow rates to decrease. It is important to highlight that when negative CO2 flow rates are encountered, they should be neglected, and the column length should be taken from the intersection point of the curve with the x-axis (see Fig. 13B and C). As mentioned earlier, this behaviour appears since qe in this work was studied independently of CO2 concentration in the gas phase (i.e., the study was conducted in pure CO2). This branch of kinetic effect is to be investigated in future studies. However, the data presented in this work unveils the effect of MOF geometry, binder and temperature effects. It also reports how these parameters can be utilised for adsorption column design which is relevant to industrial needs.
6. Conclusions
In this work, a comprehensive kinetic investigation carried out on the adsorption of CO2 on UTSA-16(Zn) MOF with different solid geometries (powder/pellet), different binders and at different adsorption temperatures (25, 40, 60 and 80 °C). While it is well established that the processing and handling of solid materials is preferred in the pellet form due to several advantages such as lower bulk density, better flowability, and reduced pressure drop in packed beds, the following points need to be kept in mind which were concluded from this work:• Generally, changing the geometry from powder to pellet resulted in a drop in the equilibrium adsorption capacity and the adsorption rate.
• It was confirmed that the adsorption processes are temperature locked (i.e., they are related to activation energy barriers of Ef and Es), whereby the rate constant increases with an increase in temperature. However, the overall adsorption rate can still decrease with an increase in temperature, due to a significant drop in qe at the higher temperatures, leading to a drop in the adsorption driving force (qe − qt).
• Different behaviour was observed when different binders were used. For instance, PVA binder resulted in a drop in both the equilibrium adsorption capacity and the adsorption rate. This led to a change in the kinetic controlling mechanism from a MO model (where both surface adsorption and diffusion control the overall rate) to a PFO model, which is diffusion controlled only.
• The equilibrium adsorption capacity and the rate of adsorption are both affected by the type of the binder; PVB exhibited the highest capacity and adsorption rate followed by PVP and PVA.
The results presented here set a foundation for a better in depth understanding of CO2 adsorption on MOFs and the impacts of pelletisation. Such data can also be used for equipment design (adsorption columns) to estimate optimum diameter, length, and MOFs residence time and/or flow rate to achieve certain adsorption limits as per the analyses reported in Section 5. Future research will extend the investigation to consider the kinetics of adsorption at different CO2 concentrations in a carrier gas (e.g., N2) to account for the equilibrium dependency on CO2 concentration.
Data availability
Data used in this article are available from the University of Nottingham repository, at https://doi.org/10.17639/nott.7546.Author contributions
Sanad Altarawneh: conceptualization, investigation, methodology, validation, formal analysis, visualization, writing – original draft, writing – review & editing. John Luke Woodliffe: conceptualization, funding acquisition, investigation, methodology, validation, visualization, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge and thank the Engineering and Physical Sciences Research Council (EPSRC, grant EP/W524402/1) for funding John Luke Woodliffe's Doctoral Prize Fellowship. The authors also thank the Nanoscale and Microscale Research Centre and the University of Nottingham (UoN) for providing funding and access to SEM (UoN and EPSRC grant EP/L022494/1) and TEM (UoN and EPSRC grant EP/W006413/1) expertise and instrumentation. In particular, the authors thank Michael Fay for TEM support.References
- IPCC, Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, 2014 Search PubMed.
- G. C. C. S. Institute, The Global Status of CCS: 2019, 2019 Search PubMed.
- P. Markewitz, W. Kuckshinrichs, W. Leitner, J. Linssen, P. Zapp, R. Bongartz, A. Schreiber and T. E. Müller, Energy Environ. Sci., 2012, 5, 7281 RSC.
- A. Samanta, A. Zhao, G. K. H. Shimizu, P. Sarkar and R. Gupta, Ind. Eng. Chem. Res., 2012, 51, 1438–1463 CrossRef CAS.
- O. M. Yaghi and H. Li, J. Am. Chem. Soc., 1995, 117, 10401–10402 CrossRef CAS.
- J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504 RSC.
- L. J. Murray, M. Dincă and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294 RSC.
- P. Horcajada, R. Gref, T. Baati, P. K. Allan, G. Maurin, P. Couvreur, G. Férey, R. E. Morris and C. Serre, Chem. Rev., 2012, 112, 1232–1268 CrossRef CAS.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef.
- R. Freund, O. Zaremba, G. Arnauts, R. Ameloot, G. Skorupskii, M. Dincă, A. Bavykina, J. Gascon, A. Ejsmont, J. Goscianska, M. Kalmutzki, U. Lächelt, E. Ploetz, C. S. Diercks and S. Wuttke, Angew. Chem., Int. Ed., 2021, 60, 23975–24001 CrossRef CAS PubMed.
- B. Dziejarski, J. Serafin, K. Andersson and R. Krzyżyńska, Mater. Today Sustain., 2023, 24, 100483 Search PubMed.
- S. B. Peh, S. Xi, A. Karmakar, J. Y. Yeo, Y. Wang and D. Zhao, Inorg. Chem., 2020, 59, 9350–9355 CrossRef CAS.
- S. Gaikwad, S.-J. Kim and S. Han, J. Ind. Eng. Chem., 2020, 87, 250–263 CrossRef CAS.
- J. L. Woodliffe, A.-L. Johnston, M. Fay, R. Ferrari, R. L. Gomes, E. Lester, I. Ahmed and A. Laybourn, Mater. Adv., 2023, 4, 5838–5849 RSC.
- J. L. Woodliffe, J. Molinar-Díaz, R. Clowes, O. H. Hussein, E. Lester, R. Ferrari, I. Ahmed and A. Laybourn, J. Environ. Chem. Eng., 2024, 12, 114167 CrossRef CAS.
- V. B. López-Cervantes, M. L. Martínez, J. L. Obeso, C. García-Carvajal, N. S. Portillo-Vélez, A. Guzmán-Vargas, R. A. Peralta, E. González-Zamora, I. A. Ibarra, D. Solis-Ibarra, J. L. Woodliffe and Y. A. Amador-Sánchez, Dalton Trans., 2025, 54, 1646–1654 RSC.
- M. Sadeghi, F. Esmaeilzadeh, D. Mowla and A. Zandifar, Sep. Purif. Technol., 2024, 338, 126534 CrossRef CAS.
- P. W. Dunne, E. Lester and R. I. Walton, React. Chem. Eng., 2016, 1, 352–360 RSC.
- M. Rubio-Martinez, C. Avci-Camur, A. W. Thornton, I. Imaz, D. Maspoch and M. R. Hill, Chem. Soc. Rev., 2017, 46, 3453–3480 RSC.
- A. Laybourn, A. M. López-Fernández, I. Thomas-Hillman, J. Katrib, W. Lewis, C. Dodds, A. P. Harvey and S. W. Kingman, Chem. Eng. J., 2019, 356, 170–177 CrossRef CAS.
- J. L. Woodliffe, R. S. Ferrari, I. Ahmed and A. Laybourn, Coord. Chem. Rev., 2021, 428, 213578 CrossRef CAS.
- S. M. Iveson, J. D. Litster, K. Hapgood and B. J. Ennis, Powder Technol., 2001, 117, 3–39 CrossRef CAS.
- B. Yeskendir, J.-P. Dacquin, Y. Lorgouilloux, C. Courtois, S. Royer and J. Dhainaut, Mater. Adv., 2021, 2, 7139–7186 RSC.
- J. Zheng, X. Cui, Q. Yang, Q. Ren, Y. Yang and H. Xing, Chem. Eng. J., 2018, 354, 1075–1082 CrossRef CAS.
- V. Ntouros, I. Kousis, A. L. Pisello and M. N. Assimakopoulos, Energies, 2022, 15, 1489–1510 CrossRef CAS.
- Z. Wang, L. Liu, Z. Li, N. Goyal, T. Du, J. He and G. K. Li, Energy Fuels, 2022, 36, 2927–2944 CrossRef CAS.
- J. D. Martell, P. J. Milner, R. L. Siegelman and J. R. Long, Chem. Sci., 2020, 11, 6457–6471 RSC.
- Y. Zhao, H. Ge, Y. Miao, J. Chen and W. Cai, Catal. Today, 2020, 356, 604–612 CrossRef CAS.
- R. Hughes, G. Kotamreddy, A. Ostace, D. Bhattacharyya, R. L. Siegelman, S. T. Parker, S. A. Didas, J. R. Long, B. Omell and M. Matuszewski, Energy Fuels, 2021, 35, 6040–6055 CrossRef CAS.
- Y. Ding, L. Ma, F. Zeng, X. Zhao, H. Wang, X. Zhu and Q. Liao, Energy, 2023, 263, 125723 CrossRef CAS.
- M. Nedoma, H. Azzan, M. Yio, D. Danaci, I. Itskou, A. Kia, R. Pini and C. Petit, Microporous Mesoporous Mater., 2024, 380, 113303 CrossRef CAS.
- B. Singh, M. Kemell, M. J. Heikkilä and T. Repo, Chem. Eng. J., 2025, 505, 159416 CrossRef CAS.
- C. A. Grande, V. I. Águeda, A. Spjelkavik and R. Blom, Chem. Eng. Sci., 2015, 124, 154–158 CrossRef CAS.
- H. Thakkar, S. Eastman, Q. Al-Naddaf, A. A. Rownaghi and F. Rezaei, ACS Appl. Mater. Interfaces, 2017, 9, 35908–35916 CrossRef CAS PubMed.
- M. M. Sadiq, M. Rubio-Martinez, F. Zadehahmadi, K. Suzuki and M. R. Hill, Ind. Eng. Chem. Res., 2018, 57, 6040–6047 CrossRef CAS.
- E. Hastürk, S.-P. Höfert, B. Topalli, C. Schlüsener and C. Janiak, Microporous Mesoporous Mater., 2020, 295, 109907 CrossRef.
- H. Maher, T. H. Rupam, K. A. Rocky, R. Bassiouny and B. B. Saha, Energy, 2021, 238, 121741 CrossRef.
- R. Gaikwad, S. Gaikwad and S. Han, J. Ind. Eng. Chem., 2022, 111, 346–355 CrossRef CAS.
- S. Lagergren, K. Sven. Vetenskapsakad. Handl., 1898, 24, 1–39 Search PubMed.
- Y. Ho, D. A. J. Wase and C. C. F. Forster, Water SA, 1996, 22, 219–224 CAS.
- J. Wang and X. Guo, J. Hazard. Mater., 2020, 390, 122156 CrossRef CAS PubMed.
- K. V. Kumar and S. Sivanesan, J. Hazard. Mater., 2006, 136, 721–726 CrossRef CAS.
- M. I. El-Khaiary, G. F. Malash and Y.-S. Ho, Desalination, 2010, 257, 93–101 CrossRef CAS.
- A. Marczewski, Appl. Surf. Sci., 2010, 256, 5145–5152 CrossRef CAS.
- X. Guo and J. Wang, J. Mol. Liq., 2019, 288, 111100 CrossRef CAS.
- S. Altarawneh, M. Al-Harahsheh, L. Ali, M. Altarawneh, O. H. Ahmed, A. Buttress, C. Dodds and S. Kingman, Chem. Eng. J., 2024, 152873 CrossRef CAS.
- M. G. Plaza, C. Pevida, B. Arias, J. Fermoso, A. Arenillas, F. Rubiera and J. J. Pis, J. Therm. Anal. Calorim., 2008, 92, 601–606 CrossRef CAS.
- J. L. Woodliffe, J. Molinar-Díaz, B. Holland, O. H. Hussein, E. Lester and K. Robertson, Chem. Eng. J., 2025, 503, 158445 CrossRef CAS.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- Q. Xie, F. Li, H. Guo, L. Wang, Y. Chen, G. Yue and D. L. Peng, ACS Appl. Mater. Interfaces, 2013, 5, 5508–5517 CrossRef CAS.
- R. Gaikwad, S. Gaikwad and S. Han, J. Ind. Eng. Chem., 2023, 126, 444–453 CrossRef CAS.
- J. L. Woodliffe, M. Myszczynski, M. Fay, J. Molinar-Díaz, E. Lester and K. Robertson, Chem. Eng. J., 2025, 510, 161641 CrossRef CAS.
- O. Levenspiel, Chemical Reaction Engineering, John Wiley & Sons, 1998 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta03364k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |