Engineering Ru nanoparticle size and metal–support interactions for enhanced catalytic hydrogen combustion

Abstract

Catalytic hydrogen combustion (CHC) plays a crucial role in enhancing the safety and efficiency of fuel cells and electrolysers, thereby promoting the H₂ economy. To increase the catalytic activity of supported metal particles for CHC, the active surface area can be increased through Ru fine dispersion, and intrinsic activity can be enhanced by optimising metal–support interactions (MSIs). In this study, we report the synthesis and CHC performance of highly dispersed Ru sub-nanoparticles on a γAl₂O₃ support with various Ru loadings. A clear correlation between Ru loading and CHC mass activity was identified. The highest mass activity is achieved at 1 wt% Ru, with a yield of 5.7 mmol_H2 mol⁻¹_Ru s⁻¹ at 80 °C. Lower Ru loadings lead to a strong MSI and subsequently to a lower Ru⁰/Ru–O ratio. Further, higher Ru loadings decrease metal dispersion, reducing CHC activity. Operando diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) and density functional theory (DFT) calculations confirmed the role of OH groups as key intermediates in the CHC mechanism over the Ru-γAl₂O₃ catalyst. Our findings highlight the impact of Ru nanoparticle size engineering on CHC mass activity and provide mechanistic insights and design principles for the development of highly active Ru catalysts, showing a way forward to achieve safer, integrated and efficient CHC utilisation.

---

1. Introduction

The ongoing energy and climate crises have accelerated the transition from fossil fuels to H₂ as a sustainable, carbon-free energy carrier, enabling the large-scale integration of renewable energy sources. As an energy vector, H₂ is crucial in driving decarbonization efforts across diverse sectors, particularly in energy conversion^1–4 and power and heat production.^5–7 To maintain safety standards, however, the H₂ concentration in an exhaust must remain below the flammability limit of H₂ in air (4 vol%).^8,9 Although the controlled combustion of residual H₂ is the most effective way to mitigate this risk while improving overall system efficiency, conventional, high-temperature combustion methods introduce several challenges, such as risks of flashback and NO_x emissions.^10,11

Consequently, catalytic H₂ combustion (CHC) has emerged as a promising alternative, enabling the conversion of H₂ to water at temperatures below the autoignition point of H₂.^12,13 This approach is especially relevant in electrolysers and fuel cells, where H₂ crossover significantly compromises safety and efficiency.¹⁴ Particularly in electrolysers operating at high H₂ pressures, a thin layer of Pt catalyst coated on the Nafion membrane is often applied at the anode side.¹⁵ This layer catalyses H₂ combustion in the presence of O₂ and enhances both safety and stack lifetime. In fuel cells, CHC also contributes to improved energy efficiency by increasing the enthalpy of the gas stream before the expansion turbine and ultimately boosting the turbocharger efficiency.¹⁶

In a typical CHC process, the highly exothermic reaction between H₂ and O₂ takes place in the presence of a catalyst, yielding water as the sole product (eqn (1)).

H₂ + ½O₂ → H₂O ΔH_H2^f_O(g) = −241.82 kJ mol⁻¹ (1)

where ΔH_H2^f_O(g) denotes the heat of formation of water vapour at room temperature (RT).

Pt and Pd catalysts are commonly employed in CHC owing to their unique ability to initiate H₂ combustion at RT.^17–20 Nevertheless, thermographic studies have revealed that at low flow rates, water formation below its evaporation temperatures extinguishes the reaction and subsequently decreases the reaction rate.²¹ Therefore, other candidates have been investigated to overcome the limitations associated with Pt and Pd-based catalysts.^22–25 Despite these efforts, most alternative catalysts remain active only above 300 °C, limiting their practical applicability in low-temperature systems.

In addition to the metal catalyst, the support material plays a critical role in CHC activity.^25–27 The Metal-support interaction (MSI) significantly influences the catalytic activity by modulating the charge transfer between the metal catalyst and the support, affecting the metal-O coordination number, the metal nanoparticle (NP) size and dispersion.^26,28,29 Supported monometallic catalysts have shown strong size sensitivity in different catalytic processes.³⁰ Recent advances in single-atom catalysis have further highlighted the importance of optimising MSIs to enhance catalytic activity and stability.³¹ Hence, it is essential to optimise the MSI to achieve high catalytic activity. However, tuning the catalytic activity through MSI regulation remains underexplored in CHC. Recently, it has been shown that by controlling the size of the Cu NPs using different Cu loadings, the Cu–O coordination can be tuned to achieve the highest mass activity at 5 wt% Cu on Al₂O₃ support.³² However, the mass activity only reached 0.009 mol_H2 mol⁻¹_Cu s⁻¹, which is a relatively low mass conversion rate for temperatures as high as 300 °C. This highlights the critical role of MSI in determining catalytic performance, underscoring the need for a deeper understanding of this interaction to achieve high activity at lower temperatures.

Moreover, the rapid kinetics of the CHC process complicate the elucidation of the reaction mechanism. The widely accepted CHC mechanism for Pt and Pd catalysts involves the dissociative adsorption of O₂ and H₂ followed by the formation of H₂O (eqn (2) and (3). If the adsorbed water reaches a sufficient concentration, it can dissociate back to OH (eqn (4)):³³

O_ads + H_ads → OH_ads (2)

2OH_ads + H_ads → H₂O_ads → H₂O_gas (3)

H₂O_ads + O_ads → 2OH_ads (4)

here, OH_ads acts as a key reaction intermediate, indicating that the reaction pathway proceeds through hydroxyl groups.³⁴ IR spectroscopy studies by Zhang et al.^26,32 have provided supporting evidence for this mechanism over a Cu–Al₂O₃ catalyst. However, to develop new catalysts, a deeper understanding of the CHC mechanism requires advanced operando characterisation methods.

Building on these findings and limitations, Ru has emerged as a promising catalyst for initiating CHC at relatively low temperatures, with complete H₂ conversion occurring just above 100 °C.³⁵ This prevents water-induced inhibition and enhances system stability. Nonetheless, further insight into maximising mass activity by tuning the MSI is needed to optimise catalyst loading for practical applications.

In this paper, we describe the design and development of well-dispersed supported Ru NPs and the optimisation of their size to achieve the highest H₂ mass conversion rate. We have synthesised a series of xRu-γAl₂O₃ (x = Ru loading in wt%) catalysts and examined the effect of Ru NPs size on MSI and CHC activity by varying the Ru loading (wt%). Moreover, we investigate the kinetics of the CHC reaction over the xRu-γAl₂O₃ catalyst, identifying a clear trend in the CHC activity and activation energies (E_a), that points to an optimum loading of Ru. To further elucidate the role of OH groups and the CHC mechanism on Ru-γAl₂O₃, operando diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) is performed, complemented by density functional theory (DFT) calculations. Our findings provide guidance for the effective engineering of Ru NPs size and MSIs to achieve high CHC mass activity.

2. Experimental section

2.1. Synthesis of Ru-γAl₂O₃ catalysts

Commercially available γAl₂O₃ pellets (AlfaAesar) are crushed into powder. As described in our previous work, a support pretreatment is employed to enhance the MSI by introducing OH⁻ groups.^36,37 Briefly, the γAl₂O₃ is first heat-treated at 500 °C in air to remove any impurities and then immersed in a 3 M ammonia solution. After filtration, the powder is washed with hot DI water (80 °C) and dried at 120 °C overnight.

The xRu-γAl₂O₃ (x = Ru wt%) catalysts are synthesised through the incipient wetness impregnation method. Ru chloride hydrate (RuCl₃·xH₂O) serves as the metal precursor, and DI water as the solvent. The obtained catalyst is heat-treated at 400 °C for 2 h under forming gas (FG, 5 vol% H₂ in N₂). This reduction temperature is chosen based on results obtained from the H₂ temperature programmed reduction (H₂-TPR) of RuCl₃·xH₂O (Fig. S1†).

Although the reduction process initiates the removal of the chlorine ions, complete removal is hindered by diffusion limitations and/or the strong adsorption of chlorine ions by Ru atoms. To address this, an additional chemical treatment step is performed to remove the chlorine ions using a 3 M ammonia solution, followed by a hot DI water washing procedure.³⁸ Subsequently, pellets with the desired size (250–500 mesh sieve) are formed, and their CHC performance is investigated.

The heat-treatment atmosphere significantly impacts the resulting Ru phase and NP dispersion. An oxidising atmosphere leads to the agglomeration of Ru atoms and the formation of RuO₂. In contrast, a reducing atmosphere stabilises the Ru NPs. Interested readers are referred to section 2 of the (ESI),† which describes the effects of the heat-treatment atmosphere on the phase (Fig. S2†) and particle size (Fig. S3†) of xRu-γAl₂O₃ catalysts.

2.2. Catalyst characterisation

The size and distribution of the Ru NPs are measured by aberration-corrected high-angle annular dark-field scanning transmission electron microscopy (AC-HAADF-STEM) using a Thermo Fisher Scientific Spectra200 system at 200 kV. Elemental maps are obtained by energy dispersive spectroscopy using Super-X detectors. The surface area, pore size, and pore size distribution are analysed by N₂ adsorption/desorption isotherm at −196 °C performed using a Belsorp maxII instrument. H₂ uptake measurements are also conducted using the same instrument at −196 °C. Powder X-ray diffraction (PXRD) is employed to characterise the crystal phases using a Bruker D8 Advance instrument with Cu Kα (λ = 1.54 Å) radiation at 40 kV and 40 mA. To study the reducibility of the catalysts, H₂-TPR is conducted by implementing thermogravimetric analysis coupled with a mass spectrometer (TGA-MS, Netzsch). The surface chemistry of the catalysts is examined by X-ray photoelectron spectroscopy (XPS, Kratos Axis Supra with a monochromated Al Kα X-ray source). The binding energy of the samples is corrected by referencing the binding energy of C 1s to 284.8 eV. The Ru content is confirmed by inductively coupled plasma-mass spectrometry (ICP-QMS, nexION35010, PerkinElmer).

Operando DRIFTS is used to investigate the mechanism of the CHC reaction over Ru-γAl₂O₃ catalysts. The spectra are recorded using a Bruker Tensor27 spectrometer. The setup is equipped with a Praying Mantis high-temperature chamber (Harrick Scientific) and a mercury–cadmium–telluride (MCT) detector. A pellet with the exact size of the chamber (6 mm) is made from the catalyst powder. The exhaust gas is analysed by MS. The same temperature procedure is used for reduction, and the CHC reaction condition is followed in the DRIFTS experiments. The DRIFTS spectra are collected by averaging 38 spectra with 2 cm⁻¹ spectral resolution in the 800–4000 cm⁻¹ range. The reference spectrum is collected on the reduced sample at RT under flowing He. Water and atmospheric compensation were applied for all spectra.

2.3. Catalytic activity tests

A schematic of the experimental setup is presented in Fig. S4.† The CHC performance is evaluated using a fixed-bed reactor. In each test, 100 mg of the catalyst pellets are placed in the middle of a 35 cm stainless steel tube with quartz wool, and the reactor is housed in a furnace (Carbolite Gero). The temperature of the reactor is controlled and monitored using two K-type thermocouples: one attached to the outside of the reactor and one positioned inside the reactor, just before the reaction bed. A gas flow of 20 ml. min⁻¹ is supplied to the reactor using three mass flow controllers (Bronkhorst) for FG, N₂, and synthesised air (80 vol% N₂ and 20 vol% O₂). The total gas hourly space velocity (GHSV) is maintained at 6000 h⁻¹. The exhaust gas composition is analysed by MS (OmniStar 320, Pfeiffer Vacuum). Before introducing the reactive gas, the catalysts are activated (reduced) at 400 °C under FG. After reduction, the system is flushed with N₂ and cooled to RT. Subsequently, the reactive gases are introduced to the reactor at a volume ratio of 4 : 2 : 96 (H₂ : O₂ : N₂). The reactor temperature is then increased to 300 °C with a heating rate of 1 °C min⁻¹. The H₂ conversion and mass conversion rates are calculated using the following equations:^25,32

It is important to note that comparing the CHC activity of the catalysts using eqn (6) is only valid for low H₂ conversions, where the axial change in the reactant concentration can be neglected throughout the catalyst bed. Consequently, we applied the Weisz-Prater Criteria³⁹ to validate the temperature range in which internal and external mass transfers are not critical, and therefore, the calculated rates are not affected by mass transfer limitations.

2.4. DFT calculation

All spin-polarised DFT calculations in this study are performed using the Quantum ESPRESSO (QE) simulation package.^40,41 The generalised gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional is employed,⁴² complemented by the D3BJ dispersion correction scheme to account for dispersion interactions.⁴³ The core electrons are treated using the optimised norm-conserving Vanderbilt (ONCV) pseudopotentials,⁴⁴ and a plane-wave energy cutoff of 480 eV is applied in all calculations. The Brillouin zone is sampled using a 4 × 4 × 1 Γ-centered Monkhorst–Pack grid, but for isolated H₂, O₂, and H₂O molecules, only the Γ-point is used. Methfessel–Paxton smearing⁴⁵ with a width of 0.2 eV is applied for surface/adsorbate systems, whereas a Gaussian smearing method with a narrow width of 0.001 eV is employed for isolated molecules. During geometry optimisations, structures are relaxed until the maximum force on any atom is less than 0.014 eV Å⁻¹.

Frequency calculations are conducted, using phonon calculations based on density functional perturbation theory (DFPT) as implemented in QE, for all atoms within the adsorbates and isolated molecules, and the frequencies of the Ru slab are excluded to improve computational efficiency. The results of these frequency calculations are used to compute thermochemical corrections to the electronic energy (E_DFT) and obtain the Gibbs free energy (G) (eqn (7)).

G = E_DFT + E_ZPE + E_thermal(T) − T × S(T) (7)

in this equation, E_ZPE represents the zero-point energy correction, E_thermal(T) denotes the thermal energy correction at temperature T, and T × S(T) accounts for entropic contributions at temperature T. These corrections are determined using vibrational partition functions for adsorbed species and the total partition functions for gaseous H₂, O₂, and H₂O molecules. Details on the calculation of these correction terms are provided in the ESI8.† All thermochemical calculations are performed at 120 °C. Transition state (TS) searches are conducted using the nudged elastic band (NEB) method implemented in QE, with a force convergence threshold of 0.2 eV Å⁻¹ for TS optimisation.

The Ru (0001) surface is selected for modelling. A 4 × 2 supercell (cell a = 9.1709 Å, cell b = 10.5889 Å) is constructed from the optimised orthogonalized conventional cell of Ru, enabling the exploration of favourable adsorption configurations across various potential sites on the Ru (0001) surface. The slab model comprises three atomic layers because previous studies indicate that this thickness is sufficient to achieve energy convergence with minimal deviation from thicker slabs.⁴⁶ The bottom layer is fixed to simulate the bulk structure, and a vacuum spacing of 15 Å is introduced perpendicular to the surface to minimise slab–slab interactions. Considering that adsorbates are placed on one side of the slab, resulting in an asymmetric unit cell, dipole corrections are applied along the surface-normal direction to account for asymmetry iRASPA software package is used⁴⁷ to visualise the atomistic structures of different states.

3. Results and discussion

3.1. Effects of the Ru NP size and kinetics

The size and distribution of the synthesised xRu-γAl₂O₃ catalysts are presented in Fig. 1. The particle size was determined from the STEM images, and the analysis was conducted based on 100 Ru NPs for each catalyst, revealing well-dispersed Ru NPs in all samples. The results indicate that increasing the Ru loading leads to larger average particle sizes and broader particle size distributions. Among all the catalysts, 0.5Ru-γAl₂O₃ showed the smallest particle size, with a mean value of 0.42 ± 0.06 nm. Conversely, 10Ru-γAl₂O₃ showed the largest particle size, with a mean value of 1.60 ± 0.19 nm. The mean particle sizes of the different catalysts are summarised in Table S1.†

Fig. 1 AC-HAADF-STEM images of (a–e) xRu-γAl₂O₃ catalysts. The scale bar represents 20 nm. The histograms show the size distributions of each catalyst. (f) The mean particle size of xRu-γAl₂O₃ with respect to Ru loading (wt%).

This trend in particle size is further illustrated in Fig. 1f, which shows the relationship between mean particle size and Ru loading. The results indicate that the particle size follows a geometrical correlation in which the size increases as a function of the (Ru loading)^1/3. This trend aligns with the expected behaviour, where a geometric scaling law relates metal mass to particle size in a three-dimensional growth.

As the NP size increases, the surface-to-volume ratio decreases, leading to a corresponding drop in dispersion (D). Herein, D drops by 26.6% for the catalyst series from 0.5Ru-γAl₂O₃ to 10Ru-γAl₂O₃. The details of D calculations are provided in section 4 of the SI. D is later used to calculate the turnover frequency (TOF) over the xRu-γAl₂O₃ catalysts.

To evaluate and compare the catalytic performance of xRu-γAl₂O₃ catalysts during CHC, a reference test condition is established as follows: a 100 mg pellet, a stoichiometric ratio between H₂ and O₂, a gas composition of H₂ : O₂ : N₂ = 4 : 2 : 94 vol%, and a total flow rate of 20 ml min⁻¹ (GHSV = 6000 h⁻¹). A typical H₂ conversion vs. temperature curve obtained for the CHC reaction exhibits a sigmoidal shape. Note that chloride anions poison the catalyst surface (Fig. S5†). As such, this study only considers chlorine-washed catalysts. Section 5 in the ESI† is dedicated to investigating the effect of chlorine ions on the CHC performance and H₂ uptake capacity of the Ru NPs.

Fig. 2a presents the effect of Ru loading on H₂ conversion (X_H2) at temperatures ranging from RT to 300 °C. The CHC activity enhancement is attributed to the increased number of active surface sites in samples with higher Ru loading. However, when H₂ conversion is normalised to the mass of Ru, it becomes evident that the mass activity does not increase proportionally with Ru loading. Fig. 2b shows the H₂ mass conversion rates over Ru, calculated at three different temperatures, 40, 60 and 80 °C. A clear trend in the Ru mass activity is observed for all temperatures, with 1Ru-γAl₂O₃ and 10Ru-γAl₂O₃ showing the maximum and minimum CHC activity, respectively. As the size of the Ru NPs changes, the number of active sites also varies. To investigate the effect of the fraction of surface atoms and include the size effect in the calculations, TOF is calculated using eqn (8) (square points in Fig. 2b).

Fig. 2 (a) Conversion X_H2, (b) mass activity (columns) and TOF (square points), and (c) kinetic parameters (columns as activation energy and square points as frequency factor) of the xRu-γAl₂O₃ catalysts versus Ru loading.

The trend in TOF is similar to the mass activity for all temperatures, confirming that using 1 wt% Ru results in the optimal Ru NP size. Consequently, X_H2 increases with higher Ru loadings at each temperature, whereas CHC mass activity decreases.

The kinetically controlled region is identified to study the kinetics of the CHC reaction over xRu-γAl₂O₃ catalysts. We have applied Weisz-Prater criteria to validate the absence of internal and external mass transfers in the temperature spans 40–80 °C. Using the Arrhenius model, the activation energy (E_a) and the frequency factor (A, pre-exponential factor) are calculated with results summarised in Fig. 2c. Two additional GHSVs (3000 and 12 000 h⁻¹) were tested for 2R-γAl₂O₃ and provided similar E_a, confirming the reliability of the used method to extract the kinetic information and that the kinetic parameters are independent of flow rate and GHSV. The resulting E_a values are summarised in Table S2.†

As can be seen from Fig. 2c, the E_a values are of the same order of magnitude for all xRu-γAl₂O₃ catalysts, with the minimum value of 17.2 kJ mol⁻¹ observed for 1Ru-γAl₂O₃ catalyst.

Variations in the TOF and E_a values demonstrate that changes in the Ru loading influence the Ru NPs' size and their intrinsic catalytic activity, indicating the involvement of additional factors affecting intrinsic activity, such as size-dependent modifications in MSIs. These modifications can alter the xRu-γAl₂O₃ interface, impacting the nature and intrinsic properties of the Ru active sites.

3.2. Evaluation of the physicochemical properties

MSI significantly influences catalytic activity by altering electronic interactions and charge transfer.⁴⁸ To assess changes in MSI with varying Ru particle sizes and determine the reduction properties of the catalysts, H₂-TPR measurements are performed. Fig. 3a displays the normalised ion current of H₂, detected by MS, for all the catalysts. Given that the Ru loading is low in 0.5 and 1Ru-γAl₂O₃, the signals exhibit some noise. Notably, the catalyst with the lowest Ru content, 0.5Ru-γAl₂O₃, displays the highest reduction temperature, indicating the presence of a strong MSI (SMSI). Such strong interactions result in reduced catalytic activity compared to 1Ru-γAl₂O₃, aligning with previous studies, where SMSI hinders the catalytic activity.^49,50 The reason for diminished catalytic activity as a consequence of SMSI is the increase in the metal-O coordination number.³² The higher Ru–O compared to metallic Ru in the case of 0.5Ru-γAl₂O₃ catalyst is further confirmed by the lowest Ru⁰/RuO_x ratio obtained from XPS analysis (Table 1). The SMSI in 0.5Ru-γAl₂O₃ catalyst is consistent with a study by Yan et al.,⁵¹ where they showed that an SMSI is expected at low Ru loadings (<1 wt%) on γAl₂O₃ supports. The origin of MSI is likely the adsorption of positively charged Ru ions on the hydroxylated γAl₂O₃ support during the synthesis procedure.⁵²

Fig. 3 (a) H₂-TPR profiles and (b) PXRD patterns of the xRu-γAl₂O₃ catalysts. The H₂-TPR tests are conducted under FG with a flow rate of 20 ml min⁻¹ and a heating rate of 10 °C min⁻¹.

Table 1 The calculated ratio of Ru⁰ to RuO_x, based on the XPS analysis

Catalyst	0.5Ru-γAl2O3	1Ru-γAl2O3	2Ru-γAl2O3	5Ru-γAl2O3	10Ru-γAl2O3
Ru^0/RuOx	0.8	2.1	1	1.8	1.3

---

The minimum reduction temperature is achieved as the Ru loading increases to 2 wt%. This is an indication of Ru nanocluster formation with lower MSI.⁵¹ Although 2Ru-γAl₂O₃ exhibits the lowest reduction temperature, this does not necessarily correspond to higher mass activity, as seen in the CHC mass activity values (Fig. 2b). This discrepancy arises from the combined effects of weaker MSI and lower catalyst dispersion compared to 1Ru-γAl₂O₃ (Table S1†). Moreover, previous studies have also shown that achieving the highest catalytic activity requires an optimal MSI, which can be tuned by controlling the size of the NPs.^53,54 Therefore, obtaining a high mass activity in CHC necessitates a balance between an optimal MSI and catalyst dispersion, which is achieved with 1Ru-γAl₂O₃ in our case.

Moreover, the TPR peak shifts to higher temperatures for the change in Ru loading from 2 to 10 wt%. This can be explained by the growth of the NPs as measured from the AC-STEM-HAADF images (Fig. 1). Also, the multiple peaks observed in the TPR profile of 5 and 10Ru-γAl₂O₃ are due to the broader size distribution of the Ru NPs.

PXRD measurements are performed to determine the crystallinity and phases present in the catalysts (Fig. 3b). The absence of any sharp metallic Ru peaks confirms the formation of well-dispersed Ru NPs.

To evaluate the influence of the surface area of the 0.5, 1, and 2Ru-γAl₂O₃ catalysts on their catalytic properties, N₂ gas adsorption/desorption measurements are performed. The obtained N₂ adsorption/desorption profiles are shown in Fig. S6a.† The obtained surface areas for the 0.5, 1, and 2Ru-γAl₂O₃ are 222, 216, and 215 m² gr⁻¹, respectively, whereas γAl₂O₃ has a BET surface area of 200 m² gr⁻¹. Similar values were expected because the Ru loading is low. Introducing Ru NPs onto γAl₂O₃ increases the number of pores below 5 nm, which is due to the impregnation of Ru. All three catalysts exhibit similar pore sizes and distributions; thus, the differences in CHC mass activity do not originate from catalyst porosity.

3.3. Evaluation of the electronic properties

XPS measurements are conducted on the reduced catalysts to elucidate the surface chemistry and the state of Ru. The XPS spectra are provided in Fig. 4, revealing the coexistence of metallic Ru (Ru⁰) and oxidised Ru (RuO_x) states in all catalysts. As we later confirmed by DFT calculation, the dissociative adsorption of O₂ on Ru presents no energy barrier. Hence, the presence of the oxide phase after reduction is expected owing to partial surface oxidation, considering that it was exposed to the air.

Fig. 4 XPS Ru 3d spectra of the (a–e) 0.5, 1, 2, 5, and 10 γAl₂O₃ catalysts. The dotted points are experimental data, and the red lines are the fits.

Table 1 shows the calculated ratio between the two Ru states (Ru⁰/RuO_x). Notably, RuO₂ is identified as the predominant Ru oxide phase. The lowest Ru⁰/RuO_x ratio is obtained for 0.5Ru-γAl₂O₃, consistent with its smallest particle size. This results in the maximum number of exposed surface Ru atoms, which are more prone to oxidation upon environmental exposure. In contrast, the highest Ru⁰/RuO_x ratio is observed for 1Ru-γAl₂O₃, consistent with our findings that a 1 wt% Ru loading provides the optimal MSI and Ru NP size, thereby achieving the highest CHC mass activity.

For 2Ru-γAl₂O₃, the weaker MSI facilitates easier oxidation upon exposure to the environment, resulting in a lower Ru⁰/RuO_x ratio. Meanwhile, the 5Ru-γAl₂O₃ catalyst, which has a larger particle size than 2Ru-γAl₂O₃, exhibits fewer exposed Ru atoms and is less susceptible to oxidation. Consequently, a higher Ru⁰/RuO_x ratio is observed owing to the increased proportion of bulk metallic Ru.

3.4. Mechanistic study

3.4.1. Operando DRIFTS. DRIFTS is conducted to investigate the CHC reaction over the 1Ru-γAl₂O₃ catalyst. A pellet of 1Ru-γAl₂O₃ is pressed and placed inside the high-temperature chamber, which is enclosed by a dome with a ZnSe window. The pellet is first reduced under 10 vol% H₂, rest He at 400 °C for 1 h, then flushed with He for 1 h at 400 °C to remove residual H₂. After cooling down to RT under He, a background spectrum is taken. Subsequently, the reactive gas (4 vol% H₂, 2 vol% O₂, and 94 vol% He) is fed to the chamber. Then, the temperature is ramped from RT to 300 °C at 2 °C min⁻¹. The recorded spectra are presented in Fig. 5. We have identified three main regions:

Fig. 5 DRIFTS spectra of 1Ru-γAl₂O₃ catalysts under reactive gas (4 vol% H₂, 2 vol% O₂, and 94 vol% He), from 20 to 300 °C. The reference spectrum (first spectrum from the bottom) is taken on the reduced catalyst at 20 °C.

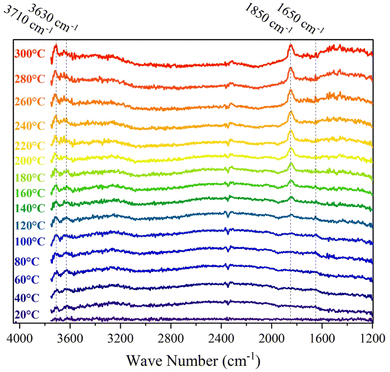
(1) The broad peaks at 3000–3750 cm⁻¹ arise from the stretching of the different types of OH groups formed on the catalyst's surface.^55,56 Based on previous studies,^57–59 the peaks at 3630 and 3710 cm⁻¹ do not correspond to the adsorbed OH on the surface of the γAl₂O₃. As a result, we assign these peaks to the formation of OH species on the Ru NPs.⁵⁵ While the intensity of the peak at 3710 cm⁻¹ increases as the temperature rises, the intensity at 3630 cm⁻¹ decreases.

(2) The small peak around 1650 cm⁻¹ arises from the OH bending of water molecules formed during the reaction.³⁴

(3) A peak around 1830–1890 cm⁻¹ appears at temperatures above 100 °C. It has been shown that oxide materials can give rise to overtone peaks in the 1800–2200 cm⁻¹ range.^60–62 Hadjiivanov et al.⁶⁰ have assigned this peak to the oxidation of Ruⁿ⁺ ions to Ru⁴⁺ in the presence of O₂ in a hydrated RuO_x phase. Thus, we assigned this peak to the formation of RuO_x under the CHC reaction. To evaluate our assignment, we reduced the catalyst and found that this peak vanished as the temperature increased.

From points 1 and 2, we can conclude that even at RT, the catalyst is active toward the CHC reaction, as evidenced by the presence of the aforementioned OH evolution peaks. Moreover, Fig. 2a and 5 indicate that the CHC reaction over the 1Ru-γAl₂O₃ catalyst proceeds through an OH group-involved pathway. This conclusion is supported by the observed increase in peak intensity at 3630 and 3710 cm⁻¹ with rising temperature. DFT calculations are used to further assess this observation and gain more mechanistic insights.

3.4.2. DFT study. Thermodynamically, Ru crystallises in the hcp structure, and owing to its high cohesive and surface energies, it favours growth on {0001} facets.^46,63,64 Ugur et al.⁶⁵ have shown that between 300 and 400 °C, RuO₂ reduction to Ru starts immediately after exposure to H₂. Therefore, in our work, after the activation process at 400 °C, we assume only metallic Ru with {0001} facets are exposed to the reactive gas. We performed DFT to gain more insight into the interaction of Ru NPs with H₂ and O₂, as well as to provide a deeper mechanistic understanding of the role of OH group formation in the CHC reaction.

First, we examine the interactions between the Ru (0001) surface and key atomic and molecular species involved in the reaction process, including H, O, H₂, O₂, OH, and H₂O. Adsorption studies are performed at typical sites - top, bridge, hollow hcp, and hollow fcc - using multiple possible orientations for the H₂, O₂, and H₂O molecules. This enables us to identify the most energetically favourable adsorption configurations for the reactants, products, and intermediates (H, O, and OH) on the Ru (0001) surface. The resulting reaction pathway, Gibbs free energy profiles, and corresponding adsorption configurations for the CHC reaction are shown in Fig. 6. The top and side views of all the states are provided in Table S3.†

Fig. 6 (a) The CHC reaction pathway over the Ru (0001) surface. The simulated cell is expanded 3 times in the x-direction and 2 times in the y-direction for better visualisation. (b) Gibbs free energy profiles and corresponding adsorption configurations at 120 °C.

The interaction between the H₂ molecule and the Ru (0001) surface was modelled as a two-step process involving adsorption and subsequent dissociation. In contrast, O₂ dissociation was found to occur spontaneously, with no Gibbs free energy barrier, making direct dissociation highly favourable. This is consistent with the DRIFTS results, where the oxidation of Ru NPs is evidenced by the appearance of a peak around 1830–1890 cm⁻¹.

Additionally, the Gibbs free energy change for the dissociation of O₂ into oxygen adatoms, combined with the adsorption of H₂ (State0 → State1), is calculated to be −5.4 eV, highlighting the strong binding affinity between oxygen adatoms and the Ru (0001) surface. This is significantly stronger than the Gibbs free energy change of −0.64 eV for the dissociation of H₂ (State1 → State3). The H₂ molecule preferentially adsorbs on the top site of the Ru(0001) surface, aligning parallel to the surface (State1). Once adsorbed, H₂ readily dissociates into two H atoms (State3) with a very low Gibbs free energy barrier of 0.03 eV, demonstrating the surface's high catalytic efficiency for H₂ dissociation. The most energetically favourable site for the dissociated oxygen adatoms is the hollow hcp site, whereas dissociated hydrogen atoms preferentially occupy the hollow fcc sites. These findings are consistent with results obtained in previous computational and experimental studies.^46,66,67 Then, the reaction between oxygen and hydrogen species to form surface OH species (State3 → State5) on the Ru (0001) surface proceeds with an energy barrier of 0.84 eV.

The adsorbed OH species preferentially occupy the hollow fcc site (State5). Hence, during the second transition state (State4), the oxygen and hydrogen adatoms migrate to the nearest hollow fcc site to facilitate the reaction and take on the most stable configuration. Subsequently, H₂O is formed (State5 → State7) through the reaction between OH and hydrogen species, with an energy barrier of 1.01 eV. Unlike OH, the H₂O molecule favours adsorption at the top site. During the third transition state (State6), the OH and hydrogen species move to the nearest top site to form the adsorbed water molecule. This demonstrates the role of formed OH groups on the Ru NPs in the reaction pathway, as we observed by DRIFTS.

The desorption of the H₂O molecule from the Ru (0001) surface (State7 → State8) is slightly endothermic, with an energy change of 0.15 eV, indicating that the water molecule can be readily removed. The calculated energy barriers for the transition states (State2, State4, and State6) reveal that the formation of the H₂O molecule is the rate-determining step in the overall catalytic process on the Ru (0001) surface.

4. Conclusion

We synthesised well-dispersed sub-nano-sized xRu-γAl₂O₃ (x = 0.5, 1, 2, 5, and 10) catalysts through the incipient wetness impregnation method and evaluated their catalytic activity for the CHC reaction. By controlling the Ru particle size through varying Ru loadings, we optimised the MSI and Ru oxidation state to achieve the maximum CHC mass activity. A distinct relationship was identified between the CHC mass activity or turnover frequency (TOF) and Ru nanoparticle (NP) size. The highest CHC mass activity and TOF were achieved with an optimal Ru particle size of 0.75 ± 0.12 nm, corresponding to a 1 wt% Ru loading. At this loading, the catalyst exhibited a maximum mass activity of 5.7 mmol_H2 mol⁻¹_Ru s⁻¹ at 80 °C. Kinetic studies further revealed that the minimum activation energy for the CHC reaction (17.2 kJ mol⁻¹) coincided with the optimal Ru NP size.

Additionally, operando DRIFTS was conducted to investigate the CHC reaction mechanism using the 1Ru-γAl₂O₃ catalyst. The critical role of OH groups as intermediates in the CHC reaction was confirmed, as supported by DFT calculations. These insights provide a comprehensive understanding of the structure–performance relationship and the reaction mechanism, guiding the design of highly efficient Ru catalysts for CHC applications.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

We would like to thank Prof. Christophe Copéret for the discussions on DRIFTS data and Dr Mehrdad Asgari for assistance with DFT calculations. We also thank Interdisciplinary Center for Electron Microscopy (CIME) at EPFL for providing access to microscope facilities.

References

1. G. Anello, G. De Luna, G. De Felice, A. Saker, L. Di Felice and F. Gallucci, Int. J. Hydrogen Energy, 2024, 86, 922–930.
2. T. P. Minyukova and E. V. Dokuchits, Int. J. Hydrogen Energy, 2023, 48, 22462–22483.
3. S. Nuggehalli Sampathkumar, P. Aubin, K. Couturier, X. Sun, B. R. Sudireddy, S. Diethelm, M. Pérez-Fortes and J. Van herle, Int. J. Hydrogen Energy, 2022, 47, 10175–10193.
4. I. Staffell, D. Scamman, A. V. Abad, P. Balcombe, P. E. Dodds, P. Ekins, N. Shah and K. R. Ward, Energy Environ. Sci., 2019, 12, 463–491.
5. G. Li, X. Zhang, Y. Zheng, Y. Zhu, W. Guo and Y. Tang, Int. J. Hydrogen Energy, 2023, 48, 22264–22276.
6. B. Fumey, S. Stoller, R. Fricker, R. Weber, V. Dorer and U. F. Vogt, Int. J. Hydrogen Energy, 2016, 41, 7494–7499.
7. L. V. Hoecke, L. Laffineur, R. Campe, P. Perreault, S. W. Verbruggen and S. Lenaerts, Energy Environ. Sci., 2021, 14, 815–843.
8. L. Gardner, Z. R. Liang, B. Ibeh, M. Hurley, S. Cotosman and J. Murphy, Hydrogen recombiners for non-nuclear hydrogen safety applications, International Conference on Hydrogen Safety, Canada, 2023.
9. W. Yu, X. Yu, S.-T. Tu and P. Tian, Int. J. Hydrogen Energy, 2017, 42, 14829–14840.
10. B. Fumey, T. Buetler and U. F. Vogt, Appl. Energy, 2018, 213, 334–342.
11. L. Hu, F. Chen, Y. Meng and Z. Sang, Int. J. Hydrogen Energy, 2024, 84, 334–343.
12. J. Kim, J. Yu, S. Lee, A. Tahmasebi, C.-H. Jeon and J. Lucas, Int. J. Hydrogen Energy, 2021, 46, 40073–40104.
13. M. van der Spek, C. Banet, C. Bauer, P. Gabrielli, W. Goldthorpe, M. Mazzotti, S. T. Munkejord, N. A. Røkke, N. Shah, N. Sunny, D. Sutter, J. M. Trusler and M. Gazzani, Energy Environ. Sci., 2022, 15, 1034–1077.
14. S. Choi, S.-H. Shin, D.-H. Lee, G. Doo, D. W. Lee, J. Hyun, J. Y. Lee and H.-T. Kim, J. Mater. Chem. A, 2022, 10, 789–798.
15. R.-T. Liu, Z.-L. Xu, F.-M. Li, F.-Y. Chen, J.-Y. Yu, Y. Yan, Y. Chen and B. Y. Xia, Chem. Soc. Rev., 2023, 52, 5652–5683.
16. G. Singer, P. Pertl and A. Trattner, Int. J. Hydrogen Energy, 2025, 106, 1158–1166.
17. G. M. Arzac, O. Montes and A. Fernández, Appl. Catal., B, 2017, 201, 391–399.
18. A. E. Kozhukhova, S. P. Du Preez and D. G. Bessarabov, Int. J. Hydrogen Energy, 2023, 51, 1079–1096.
19. J. Kim, A. Tahmasebi, S. Khoshk Rish, C.-H. Jeon and J. Yu, J. Energy Inst., 2023, 109, 101297.
20. F. Giarratano, G. M. Arzac, V. Godinho, D. Hufschmidt, M. C. Jiménez de Haro, O. Montes and A. Fernández, Appl. Catal., B, 2018, 235, 168–176.
21. I. H. Son, A. M. Lane and D. T. Johnson, J. Power Sources, 2003, 124, 415–419.
22. J. Zhang, Z. Hu, T. Man, Y. Zhao, M. Ding and Z. Guo, Nucl. Eng. Des., 2024, 428, 113481.
23. M. Haruta and H. Sano, Int. J. Hydrogen Energy, 1981, 6, 601–608.
24. Y. Varun, I. Sreedhar and S. A. Singh, J. Environ. Chem. Eng., 2022, 10, 108384.
25. V. M. Shinde and G. Madras, Catal. Today, 2012, 198, 270–279.
26. X. Zhang, N. Fei, K. Sang, W. Chen, G. Qian, J. Zhang, D. Chen, X. Zhou, X. Duan and W. Yuan, Cell Rep. Phys. Sci., 2024, 5(6), 102014.
27. E. Lalik, R. Kosydar, R. Tokarz-Sobieraj, M. Witko, T. Szumełda, M. Kołodziej, W. Rojek, T. Machej, E. Bielańska and A. Drelinkiewicz, Appl. Catal., A, 2015, 501, 27–40.
28. J. Chen, Y. Zhang, Z. Zhang, D. Hou, F. Bai, Y. Han, C. Zhang, Y. Zhang and J. Hu, J. Mater. Chem. A, 2023, 11, 8540–8572.
29. Z. Wang, Z. Mei, L. Wang, Q. Wu, C. Xia, S. Li, T. Wang and C. Liu, J. Mater. Chem. A, 2024, 12, 24802–24838.
30. X. He, F. Dong, W. Han, Z. Tang and Y. Ding, J. Mater. Chem. A, 2024, 12, 7470–7507.
31. H. Li, W. Wang, S. Xue, J. He, C. Liu, G. Gao, S. Di, S. Wang, J. Wang, Z. Yu and L. Li, J. Am. Chem. Soc., 2024, 146, 9124–9133.
32. X. Zhang, K. Sang, W. Chen, J. Zhang, G. Qian, D. Chen, X. Zhou, X. Duan and W. Yuan, Chem. Eng. J., 2024, 485, 149875.
33. S. Völkening, K. Bedürftig, K. Jacobi, J. Wintterlin and G. Ertl, Phys. Rev. Lett., 1999, 83, 2672–2675.
34. S. A. Singh, K. Vishwanath and G. Madras, ACS Appl. Mater. Interfaces, 2017, 9, 19380–19388.
35. Z. Akbari, M. D. Mensi, E. Oveisi, J. Ruffiner, W. Luo, C. D. Koolen and A. Züttel, Int. J. Hydrogen Energy, 2024 DOI:10.1016/j.ijhydene.2024.08.300.
36. C. Li, Q. Sun, F. Cao, W. Ying and D. Fang, J. Nat. Gas Chem., 2007, 16, 308–315.
37. Z. Shahidian, K. Zare and S. M. Mousavi Safavi, Iran. J. Chem. Chem. Eng., 2020, 39, 61–69.
38. V. Mazzieri, F. Coloma-Pascual, A. Arcoya, P. C. L'Argentière and N. S. Fı́goli, Appl. Surf. Sci., 2003, 210, 222–230.
39. M. E. Davis and R. J. Davis, Fundamentals of Chemical Reaction Engineering, Courier Corporation, 2012.
40. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
41. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
44. D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117.
45. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
46. F. Colasuonno and M. Lessio, J. Phys. Chem. C, 2023, 127, 23645–23653.
47. D. Dubbeldam, S. Calero and T. J. H. Vlugt, Mol. Simul., 2018, 44, 653–676.
48. T. W. van Deelen, C. Hernández Mejía and K. P. de Jong, Nat. Catal., 2019, 2, 955–970.
49. S. Zhang, P. N. Plessow, J. J. Willis, S. Dai, M. Xu, G. W. Graham, M. Cargnello, F. Abild-Pedersen and X. Pan, Nano Lett., 2016, 16, 4528–4534.
50. Z. Wang, Z. Mei, L. Wang, Q. Wu, C. Xia, S. Li, T. Wang and C. Liu, J. Mater. Chem. A, 2024, 12, 24802–24838.
51. Y. Yan, Q. Wang, C. Jiang, Y. Yao, D. Lu, J. Zheng, Y. Dai, H. Wang and Y. Yang, J. Catal., 2018, 367, 194–205.
52. B. Yang, X. Chen, L. Guo and L. Zhang, J. Mater. Chem. A, 2024, 12, 19861–19884.
53. G. L. Bezemer, J. H. Bitter, H. P. C. E. Kuipers, H. Oosterbeek, J. E. Holewijn, X. Xu, F. Kapteijn, A. J. van Dillen and K. P. de Jong, J. Am. Chem. Soc., 2006, 128, 3956–3964.
54. Y. Guo, S. Mei, K. Yuan, D.-J. Wang, H.-C. Liu, C.-H. Yan and Y.-W. Zhang, ACS Catal., 2018, 8, 6203–6215.
55. J. Zheng, C. Wang, W. Chu, Y. Zhou and K. Köhler, ChemistrySelect, 2016, 1, 3197–3203.
56. P. Liu, C. Zheng, W. Liu, X. Wu and S. Liu, ACS Catal., 2024, 14, 6028–6044.
57. X. Liu, J. Phys. Chem. C, 2008, 112, 5066–5073.
58. J. Joubert, A. Salameh, V. Krakoviack, F. Delbecq, P. Sautet, C. Copéret and J. M. Basset, J. Phys. Chem. B, 2006, 110, 23944–23950.
59. W. Huang, X. Zhang, A.-C. Yang, E. D. Goodman, K.-C. Kao and M. Cargnello, ACS Catal., 2020, 10, 8157–8167.
60. K. Hadjiivanov, J.-C. Lavalley, J. Lamotte, F. Maugé, J. Saint-Just and M. Che, J. Catal., 1998, 176, 415–425.
61. G. Busca and J. C. Lavalley, Spectrochim. Acta, Part A, 1986, 42, 443–445.
62. Z. Opre, D. Ferri, F. Krumeich, T. Mallat and A. Baiker, J. Catal., 2007, 251, 48–58.
63. Y. Nanba, T. Ishimoto and M. Koyama, J. Phys. Chem. C, 2017, 121, 27445–27452.
64. M. Zhao and Y. Xia, Nat. Rev. Mater., 2020, 5, 440–459.
65. D. Ugur, A. J. Storm, R. Verberk, J. C. Brouwer and W. G. Sloof, J. Phys. Chem. C, 2012, 116, 26822–26828.
66. P. Ferrin, S. Kandoi, A. U. Nilekar and M. Mavrikakis, Surf. Sci., 2012, 606, 679–689.
67. F. Rose, M. Tatarkhanov, E. Fomin and M. Salmeron, J. Phys. Chem. C, 2007, 111, 19052–19057.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta03057a

---