Design of bifunctional bimetallic Fischer–Tropsch synthesis (FTS) catalysts: acid functionalization of TiO₂ support for enhanced product selectivity

Abstract

This study investigates the functionalization of TiO₂ via sulfation to enhance the performance of Fischer–Tropsch synthesis (FTS) catalysts for hydrocarbon production from syngas. Acid-functionalized TiO₂ serves as the support material and is impregnated with iron–cobalt bimetallic nanoparticles as the active phase. This catalyst structure aims to introduce bifunctionality that sustains chain growth and promotes isomerization and hydrocracking by the acid sites during FTS. The introduction of Brønsted and Lewis acid sites is evaluated, and the effects of calcination post-functionalization are quantified in the resulting C₅₊ selectivity and CO conversion. XRD analysis reveals that the functionalization process favors the stabilization of the anatase phase of TiO₂ as a function of SO₄²⁻ ions, resulting in large (>100 nm) particles due to agglomeration. The support's surface chemistry is significantly altered, with the functionalization leading to an oxygen-deficient surface and subsequent calcination removing sulfur-containing compounds, as shown by XPS. The acid site density for the S-doped support is determined to be 4.57 × 10⁻³ mmol_{acid sites} m⁻² post-calcination at 300 °C. Pyridine-DRIFTS indicates a reduction in Brønsted acid species (e.g., surface S–OH) after calcination, with the Brønsted to Lewis acidity (B/L) decreasing from 1.68 pre-calcination to 1.27 post-calcination. FTS reaction testing was performed at 250 °C and 300 psi(g). FTS results show that acid functionalization of TiO₂ followed by a calcination step induces desirable structural and surface chemistry changes on the support which favor the formation of C₂–C₄ hydrocarbons, while maximizing catalyst performance, reaching a CO conversion of 29.0% ± 4.95 and CH₄ selectivity of 3.03% ± 0.33.

---

Introduction

Fischer–Tropsch Synthesis (FTS) catalysis has significantly benefited from technological advances in materials science and engineering. It is a tunable catalytic process through which many hydrocarbon products are synthesized from synthesis gas, gaining prominence for producing transportation fuels.¹ FTS is an important technology for regions which do not have significant petroleum resources, such as South Africa and China. Syngas, consisting primarily of carbon monoxide (CO) and hydrogen (H₂), can originate from any carbon source, but it is primarily produced from the gasification of coal and biomass.^2,3 The complexity of FTS reactions^4,5 and the variability of its product distribution^6,7 have prompted efforts to improve its performance. The material used to support the active phase in a catalyst directly influences FTS performance, influencing parameters such as CO conversion, product distribution, and C₅₊ selectivity.⁸ The support disperses and stabilizes the active metal particles, and metal–support interactions influence reaction kinetics. Similarly, the dispersion of the metal particles depends on the support's textural properties,⁹ such as surface area and porosity. These textural properties have also been identified as important variables impacting the catalyst's sintering rate, leading to catalyst deactivation.¹⁰

The production of valuable hydrocarbon products via FTS can be enhanced by achieving hydrocracking and isomerization reactions after carbon chain formation using acid-functionalized catalysts.¹¹ This approach is appealing, as it can assist in process intensification and facilitate smaller-scale applications of FTS.¹² Studies on the effects of acidity on catalyst behavior and performance using zeolites, such as HZSM-5, have been reported.¹³ The bifunctionality between acid sites and bimetallic FTS catalysts has yet to be reported. Such treatment is hypothesized to enhance FTS performance by providing a suitable environment where exothermic carbon chain growth reactions could coexist with endothermic hydrocracking ones.¹⁴

Titanium dioxide (TiO₂) has been commonly used as a support in FTS catalysts,^15–17 and TiO₂ can be acid-functionalized^18,19 to increase CO conversion as well as selectivity towards gasoline-range hydrocarbon products in FTS.²⁰ Maximizing the yield of long-chain products is favorable, as they can be hydrocracked to produce naphtha (C₅–C₁₀), kerosene, and diesel from waxes and heavy gas oil.²¹ For the applications in this work, it is hypothesized that the nature of the acid sites, either Brønsted or Lewis, plays a crucial role. Their influence on FTS performance has been evaluated for other materials, with recent studies showing that Brønsted acid sites (BAS) are responsible for inducing hydrocracking and isomerization reactions after polymerization.²² The role of BAS and Lewis acid sites (LAS) specifically on acid-treated TiO₂-supported catalysts is not completely understood.²³ Despite this uncertainty, it has been reported that Lewis acid sites play a role in enabling the isomerization of olefin chains in FTS. These secondary reactions include cis–trans isomerization, skeletal rearrangement, and cyclization. LAS are also known for affecting the electron density of neighboring metallic active sites, which has been linked to an increase in hydrogenation rates.²⁴ Therefore, the introduction of these Lewis acid sites is considered a strategic optimization method.

For the active phase in a FTS catalyst, transition metals, including iron (Fe), cobalt (Co), ruthenium (Ru), and nickel (Ni), have been studied.²⁵ Ni is undesirable as it promotes methanation, and Ru is expensive, thus being unfit for large-scale applications. Therefore, Fe and Co are the preferred metals for FTS.²⁶ Iron carbide and metallic cobalt have been identified as iron's and cobalt's most probable active phases, respectively.²⁷ FTS product distribution varies as a function of the active phase and temperature. For low-temperature (200–240 °C) FTS, Fe and Co catalysts favor higher molecular weight products, with Co outperforming Fe.²⁸ Contrarily, at elevated temperatures (250–350 °C), Fe-based catalysts are considered superior due to their lower CH₄ selectivity.²⁹

Catalysts consisting of bimetallic iron–cobalt (FeCo) nanoparticles as the active phase have also been studied.³⁰ FeCo-based catalysts have shown moderate activity, selectivity for heavier hydrocarbons (C₅₊) and increased CO conversion for FTS.^31,32 The particle size and general morphology have been shown to influence activity and selectivity considerably.³³ The influence of a bimetallic active phase on an acid-functionalized TiO₂ support has yet to be studied for FTS applications.

This work demonstrates the synthesis and characterization of acid-functionalized supported bimetallic FeCo catalysts and evaluates their performance in FTS compared with non-acid-functionalized TiO₂-based systems. The proposed acid functionalization and optimization methods assess the impact of introducing Brønsted and Lewis acid sites into the catalyst structure. The methodology introduced in this study is validated by characterization of the catalysts at different points, emphasizing the quantification of acid sites, particle size, catalyst composition, and their effects on FTS catalytic performance.

Experimental

Preparation of acid-functionalized TiO₂ support

The acid functionalization of the TiO₂ support was divided into three main stages: (I) as-manufactured, (II) post-calcination (at 400 °C), and (III) post-acid treatment and final calcination (at 300 °C). Commercial titanium(IV) oxide (TiO₂ Aeroxide^® P25, Acros Organics, ≥99.5% purity) nanopowder was mixed with deionized (DI) water (resistivity of 18.2 MΩ at 25 °C), collected from a Millipore Direct-Q^® 3 UV Water Purification System. For this preparation, 40.0 g of TiO₂ P25 were mixed with 120.0 mL of DI water under magnetic stirring for 2 h. The TiO₂ mixture was transferred onto a watch glass and dried in a VWR Gravity Convection Oven 2.3CF (120 V) at 120 °C for 2 h. The resulting dried powder was calcined in air at 400 °C for 4 h in a single-zone Carbolite Gero Vertical Split Tube (VST) 1200 Furnace. The heating rate was specified at 3 °C min⁻¹, and the TiO₂ was cooled to room temperature inside the furnace. This calcination step was crucial in the removal of surface-bound impurities and contaminants (e.g., adsorbed H₂O) in the as-manufactured TiO₂ support and the enhancement of its crystallinity prior to the impregnation with the active phase.^34,35 After its removal from the vessel, the support precursor was at Stage II of functionalization. The calcined TiO₂ was subsequently acid-treated to introduce potential bifunctional behavior.

The functionalization method herein constitutes a modified version of the experimental protocol introduced by Park et al.³⁶ for TiO₂ nanopowder. For this acid treatment, 5.0 g of the calcined precursor was added to 50 mL of a 1.0 M sulfuric acid solution (H₂SO₄, Mallinckrodt, AR^® grade, 95.7% purity) and stirred at 300 rpm for 6 h. The pH of the acid solution was calculated to be −0.3 (i.e., pH < 1.0), based on the complete dissociation of the 1.0 M H₂SO₄ solution, indicating the strong acidic nature of the solution. If assuming only that the first proton dissociates fully, this pH value is equal to 0. The resulting mixture was then added to 500 mL of DI water and agitated for 30 min, followed by a precipitate-settling period of 90 min. Following dilution with DI water, the pH of the mixture was calculated to be 0.74. The supernatant was decanted, and the precipitated TiO₂ support was washed twice with 500 mL of DI water each time. Following the decantation process and the successive washes with DI water, the acidity was reduced to the range of 3.8–4.0. The precipitate was then dried at 120 °C for 4 h in a VWR Gravity Convection Oven 2.3CF (120 V). The acid-treated TiO₂ was calcined in air at 300 °C for 2 h in a Thermo Scientific Lindberg/Blue M™ 1200 °C Split-Hinge Tube Furnace. The initial heating rate was fixed at 5 °C min⁻¹, with the support cooling down to room temperature in the furnace. This step was named Stage III of the support preparation and functionalization process. The calcined acid-functionalized TiO₂ support was crushed and sieved to pass through 10 and 35 mesh sieves, obtaining particles in the 500–2000 μm range, which were used as the acid-functionalized support material for the catalysts in this work.

Quantification of acid sites on the TiO₂ support via volumetric titration

The acidity of the TiO₂ support at Stage III was determined by measuring the number of total acid sites via volumetric titration. A conventional acid–base titration experimental setup was used (Scheme S2 in the ESI†), with the titrant consisting of a colorless 0.1 N sodium hydroxide solution (NaOH, Thermo Scientific Chemicals), and the titrate was the acid-functionalized TiO₂ as described in the previous section. The volumetric buret was calibrated before the titration experiments (Fig. S3 in the ESI†). A phenolphthalein solution (C₂₀H₁₄O₄, Fisher Chemical, Alcoholic 1.0%) was used as the indicator for the equivalence point in the titrations. The amount of acid-treated TiO₂ in solid form was recorded and then dispersed in 25.0 mL of DI water by magnetically stirring at 300 rpm until the TiO₂ was suspended. This solution was titrated against the NaOH base until it turned from colorless (at pH 8.2) to light pink. The initial and final volumes of NaOH solution used were recorded, and the titrations were performed at least in triplicate.

Characterization of Brønsted and Lewis surface acidity on the TiO₂ support via pyridine-DRIFTS

The surface acidity of the functionalized TiO₂ support was further investigated by determining the type of acid site (Brønsted or Lewis) and their respective amounts. The method introduced herein was a modified version of the protocols by Bortnovsky et al.³⁷ and Bejblová et al.³⁸ for zeolites. Diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) measurements were taken with a Thermo Scientific Nicolet™ iS-50 FTIR spectrometer. The instrument was equipped with a liquid nitrogen-cooled mercury cadmium telluride (MCT) detector and a Praying Mantis™ diffuse reflection accessory (Harrick Scientific Products). Pyridine (C₅H₅N, Thermo Scientific Chemicals, spectrophotometric grade, 99.5+% purity) was used as the probe molecule, and pyridine vapor was transferred to the samples by continuously flowing ultra-high purity N₂ (99.999%) gas through it, as specified by Lu et al.³⁹ for TiO₂/SiO₂ catalysts. The adsorption of pyridine was carried out for 2 h at ambient temperature and pressure conditions to allow for sufficient saturation before transferring the samples to the instrument. A Cole-Parmer mass flow controller 32907-71 (flow range between 0.1 L min⁻¹ and 10 L min⁻¹) was used to control the flow of N₂. For the adsorption, the flow rate was set to 4.0 L min⁻¹. Analogous to the work by Moghaddam et al.,⁴⁰ the samples were purged with pure N₂ flowing at 2.0 L min⁻¹ for 2 h after the adsorption step to remove physisorbed pyridine molecules. The samples were then prepared for spectroscopic measurements by mixing with potassium bromide (KBr, Acros Organics, 98% purity). The corresponding spectra were collected at an optical resolution of 4 cm⁻¹ in the frequency range of 600–4000 cm⁻¹ at room temperature conditions for the acid functionalized support at Stage III pre- and post-calcination. This data was converted to Kubelka–Munk spectra after appropriate baseline corrections. Smoothing was applied with the Savitzky–Golay filter.

Catalyst synthesis

The catalysts were synthesized via wet impregnation of the TiO₂ support with the bimetallic active phase. Samples were prepared and labeled according to the preparation stages for the acid-functionalized support at Stage II (non-functionalized), Stage III (pre-calcination), and Stage III (post-calcination). The catalysts consisted of a bimetallic FeCo active phase. The precursor active metal solutions were co-impregnated and prepared from iron(III) nitrate nonahydrate (Fe(NO₃)₃·9H₂O, Acros Organics, >98.0% purity) and cobalt(II) nitrate hexahydrate (Co(NO₃)₂·6H₂O, Acros Organics, 99.0% purity), respectively. The catalyst synthesis method herein was a modified version of the co-impregnation protocol developed by Duvenhage et al.⁴¹ for non-functionalized TiO₂-supported catalysts. The hydrated Fe and Co salts were dissolved in DI water under magnetic stirring at 500 rpm for 30 min on a Thermo Scientific Cimarec+™ stirring hotplate set to 80 °C. After the dissolution of the nitrate salts, the solutions were added dropwise onto the TiO₂ support on a heat-resistant watch glass. The nominal weight loading for the metals was fixed at 2.0 wt% across all synthesized catalysts, and the Fe : Co ratio was specified as 1 : 1 for Fe and Co, respectively, for all samples. The impregnated materials were dried in a VWR Gravity Convection Oven 2.3CF (120 V). The impregnation protocol was repeated for all samples. For the Stage III (post-calcination) sample, the catalyst was calcined in air at 300 °C for 3 h in a Thermo Scientific Lindberg/Blue M™ 1200 °C Split-Hinge Tube Furnace. The heating rate was fixed to 3 °C min⁻¹, and the sample was left to cool inside the furnace. As proposed in a follow-up study by Duvenhage et al.,⁴² the catalysts were reduced in a 100% H₂ atmosphere at 400 °C for 4 h. The total flow rate of H₂ gas was set to 40 standard cubic centimeters per minute (SCCM) or 8.33 × 10⁻⁷ kg s⁻¹ at 25 °C and 1 atm.

Fischer–Tropsch synthesis (FTS)

The bimetallic catalysts were tested for FTS in an annular packed-bed reactor. An online gas chromatograph-mass spectrometer (GC-MS) (Thermo Fisher Scientific Trace 1310 Gas chromatograph analyzer and an ISQ Single Quadrupole Mass Spectrometer) were used to analyze the hydrocarbon product distribution. As a function of studies by Kasht et al.,⁴³ Cheng et al.,⁴⁴ and Snavely et al.,⁴⁵ the C₁₀₊ product distribution was negligible in this work due to its considerably low yield and the analytical challenges associated in its quantification with the flame ionization detector (FID). Helium (He) was selected as the carrier gas for this process. Following specifications from previous studies on FTS catalysts,³² the reaction was run at 250 °C and 300 psi(g) for 6 h for all samples in this study. The time-on-stream (TOS) was considered sufficient for the initial activity studies for the catalysts in this work, based on previous reports.^46,47 The syngas mixture had an H₂/CO ratio of 2.0 for all experimental runs, with a total gas flow rate of 100 SCCM. The product distribution, C₅₊ selectivity, C₂–C₄ selectivity, and CO conversion GC-MS data were analyzed to assess catalyst performance.

Characterization

Powder X-ray diffraction (XRD) was performed using a Phillips PANalytical X'Pert diffractometer to assess the phase composition and crystallinity of the materials at different points of the synthesis process. The radiation source for the XRD system was a monochromatic Cu-K_α beam of wavelength (λ) 0.154 nm at 50 keV and 10 mA. The Bragg–Brentano geometry was used for all measurements, and 2θ values were obtained in the 20–90° range, with a step size of 0.02. The shifts in diffraction patterns and phase changes were analyzed using the open-source General Structure and Analysis System II (GSAS II) software, and the grain size was calculated according to the Scherrer equation, as discussed in the manuscript. X-ray photoelectron spectroscopy (XPS) was used to assess the acid functionalization treatment on the TiO₂ support. The measurements were taken with a Kratos Axis Ultra DLD X-ray/Ultraviolet photoelectron spectrometer. The instrument had a monochromatic Al K_α X-ray radiation source. The measured binding energies (BEs) were corrected according to the adventitious C 1s peak, commonly found at 284.4 eV.⁴⁸ The data was processed and analyzed with appropriate software, with the elemental composition at the surface being of interest. Surface area measurements were performed via N₂ adsorption–desorption experiments using a Micromeritics 3Flex high-performance gas adsorption analyzer. The samples were pre-activated overnight at 150 °C with a N₂ gas flow using a Micromeritics FlowPrep™ 060 flow degasser. The composition of the bulk catalysts was assessed via X-ray fluorescence (XRF) using an Eagle III Microspot spectrometer. This non-destructive technique was used to measure the actual wt% of the Fe and Co metals in the catalysts after impregnation and reduction. The instrument was set to 40 kV and 750 μA, with a spatial resolution of 0.1 mm. Morphological studies were conducted using a Thermo Fisher Scientific FEI Teneo™ SEM with Trinity™ Detection System, which enabled high-resolution imaging for surface analysis. OriginPro 2024 was used as the scientific graphing and data analysis software for the corresponding figures in this manuscript. As also included in the ESI,† graphical diagrams for experimental processes were created with the Chemix open-source software and molecules were drawn with chemical sketching tools powered by ChemAxon.

Results and discussion

XRD studies assessing crystallographic and microstructural effects of acid-functionalization and calcination on TiO₂ supports

The TiO₂ support precursor is successfully acid-treated to introduce bifunctionality. The relevant phase transitions and crystallographic XRD patterns are assessed by evaluating the support at three stages of preparation [I, II, and III (post-calcination)], as described in the Experimental section. The XRD data is analyzed by performing Rietveld refinement and contrasting to the reference standards in the Crystallography Open Database (COD). The support precursor does not display notable phase transitions between Stages (I) and (II), as shown by the XRD spectra (Fig. S2 in the ESI†). The material shows co-existence of titania as two polymorphs: tetragonal anatase (space group I4₁/amd) and tetragonal rutile (space group P4₂/mnm). The peaks at 2θ = 25.47° and 25.35° for Stages I and II, respectively, were assigned to anatase, and were considered the most prominent peaks in the spectra, denoting the phase's overwhelming majority.

Despite the similarities in XRD spectra between Stages I and II, which was as expected at the specified calcination temperature,⁴⁹ the full width at half maximum (FWHM) values helped elucidate the role of the initial calcination step in the support preparation. The FWHM value decreased from 0.371° in Stage I to 0.312° Stage II for the major anatase peaks. This result denoted the sharpening of the most prominent peak after calcination, which shows successful crystal growth resulting from the partial transition of amorphous TiO₂ into its more crystalline form.⁵⁰ The XRD spectrum for the TiO₂ support precursor at Stage III (post-calcination) is shown in Fig. 1, with the peaks corresponding to the TiO₂ polymorphs labeled.

Fig. 1 XRD spectrum for the TiO₂ support precursor at Stage III, with the anatase and rutile peaks labeled.

Fig. 1 displays crystallographic features different from those found in the TiO₂ precursor at Stage II due to the functionalization process and the final calcination step. A significant result is the absence of the anatase peak at 2θ = 25.35°, which was present at Stage II. This development is attributed to phase transformations resulting from the final calcination step and induced by the acid treatment.⁵¹ The data suggests the presence of a mixed anatase–rutile phase after the final calcination, which agrees with the existing literature.⁵² The peaks found at 2θ = 27.59°, 36.23°, 41.37°, 44.19°, 54.45°, 56.79°, and 64.19° are assigned to TiO₂ in its rutile phase (PDF #00-021-1276)⁵³ in the (110), (101), (111), (210), (211), (220), and (002) planes, respectively. Conversely, the peaks at 2θ = 39.35°, 62.85°, 69.13°, 69.89°, and 76.65° correspond to the (004), (204), (116), (220), and (215) planes of the anatase phase (PDF #00-021-1272).⁵⁴ Table S2 in the ESI† shows the XRD data, including the FWHM (°) and the crystallite size (D_p) values for the acid-functionalized TiO₂ support at Stage III (post-calcination).

The average crystallite size (D_p) for the TiO₂ nanoparticles as a function of the XRD peaks is calculated at 69.27 nm. The average size for the rutile-phase particles is 63.31 nm, with a calculated D_p value of 49.74 nm for its characteristic peak at 2θ = 27.59°. The grain size values calculated for the functionalized rutile are larger than what is typically found in TiO₂ annealed at 400 °C.⁵⁵ Similarly, the average D_p for the anatase nanoparticles is 75.23 nm, with the grain size for its characteristic peak at 2θ = 69.13° being unusually large (>100 nm). This result suggests agglomeration of these nanoparticles during acid treatment of the TiO₂ precursor, leading to larger crystallite sizes, as dictated by electrostatic and van der Waals interactions.⁵⁶ The surface chemistry of the TiO₂ is affected by the acid functionalization, due to the formation of empty spaces via the sulfate ions burning off during the final calcination step, as proposed by Colón et al.⁵⁷ in their study of a sulfated TiO₂ photocatalyst. Further important considerations including the quantification of acid sites and their effects on FTS performance will be discussed in the following sections.

For TiO₂-supported catalysts, studies have demonstrated that crystallite size and phase composition (rutile vs. anatase) significantly impact the dispersion of metal nanoparticles on the support. Smaller crystallite sizes (typically of anatase) promote a high initial dispersion of metal particles. Smaller particles tend to have stronger metal–support interactions (SMSIs), as demonstrated in a study by Bertella et al. for Co and Ru FTS catalysts. In their work, this phenomenon was deemed a consequence of the potential migration of partially reduced TiO_x species onto the metal active sites, “decorating” their surface and masking them. The effects of the SMSIs were found to be directly correlated with the increased surface area of the TiO₂-anatase support.⁵⁸ On the other hand, the development of larger TiO₂ particles, whether from an increase in the rutile's D_p values or calcined anatase, was linked to weaker SMSI effects due to a lesser extent of a lesser extent of TiO_x decoration, thus exposing a higher fraction of the metal surface.⁵⁹ They showed that when SMSIs were strong due to fine-grained anatase TiO₂, the catalyst's activity per gram of the active metal (i.e., Co or Fe) was diminished, despite exhibiting similar initial turnover frequencies (TOFs). Regarding product selectivity, it has been inferred that using larger TiO₂ crystals or rutile phase may favor the formation of higher C₅₊ hydrocarbon products and suppress methanation. Therefore, the considerable D_p value of 69.27 nm calculated for the TiO₂ support in this work may minimize metal–support encapsulation and potentially enhance C₅₊ selectivity. These initial microstructural modifications are essential for evaluating the subsequent acid functionalization, which was hypothesized to introduce additional interactions.

Due to the presence of a mixed rutile–anatase phase in the functionalized TiO₂, the molar proportion of the phases is calculated and evaluated for the two characteristic peaks at Stage III: rutile at 2θ = 27.59° with crystal plane (110), and anatase at 2θ = 69.13° with crystal plane (116). For Stages I and II, the characteristic anatase peaks are identified at 2θ = 25.47° and 2θ = 25.35°, respectively. These peaks correspond to the (101) crystal plane. This specific and prominent anatase peak is absent at Stage III (post-calcination), implying a reduction of this phase. The characteristic rutile peaks for Stages I and II correspond to the same (110) peak, found at 2θ = 27.73° and 2θ = 27.47°, respectively. The quantitative XRD analysis method by Spurr and Myers is used,⁶⁰ according to eqn (1) and (2):

F_R = 1/[1 + 1.265(I_R/I_A)] (1)

F_A = 1 − F_R (2)

where F_R and F_A are the respective quantities of rutile and anatase in the sample and I_R and I_A represent their characteristic peak intensities. The calculated values obtained for the XRD data for the TiO₂ support at all stages of preparation are shown in Table 1.

Table 1 Fraction of rutile and anatase phases in the TiO₂ support precursor at Stages I, II and III (post-calcination)

Stage	FR	FA	FR/FA
I	0.202	0.798	0.253
II	0.185	0.815	0.227
III (post-calcination)	0.160	0.840	0.190

---

XRD analysis is limited in revealing information about the amorphous phase.⁶¹ Therefore, the methods presented in this study consider only two crystalline phases: rutile and anatase, as shown in Table 1. Furthermore, the specifications of TiO₂ Aeroxide® P25 by the manufacturer state a typical composition of 80% anatase and 20% rutile,⁶² as corroborated by the data obtained for the TiO₂ precursor at Stage I. The modest increase of rutile content (and decrease of the anatase phase composition) from Stage I to Stage II shows that the initial calcination did not induce a complete phase transformation between the two phases. This finding agrees with the existing literature, as studies have shown that the anatase-to-rutile transition in TiO₂ nanostructured systems occurs at temperatures above ∼700 °C.⁶³ It is hypothesized that a higher temperature accelerates the transition following the functionalization.

The decrease in rutile content from Stage II to Stage III can be attributed to the acid functionalization process. F_R/F_A decreases from 0.253 in Stage II to 0.190 in Stage III due to the role of the SO₄²⁻ ions in the H₂SO₄ solution, which influenced crystallinity and morphology, favoring anatase phase formation.⁶⁴ The well-documented anatase to rutile transition in TiO₂ as a function of increasing calcination temperature⁶⁵ is contradicted by the results shown in Table 1. As this transition occurs from the surface to the bulk, the impregnation of the precursor with the acid before the final calcination step promotes the stabilization of the anatase phase in the TiO₂ material by delaying the transition process.⁶⁶ For FTS and similar applications, published results are conflicting, with recent studies showing that a higher fraction of rutile leads to desirable CO conversion rates and selectivity for Co-based catalysts.^67,68 Notably, a mixed rutile–anatase phase has been shown to promote enhanced FTS reaction rates.⁶⁹ The potential synergistic effects between an acid-functionalized support and a bimetallic FeCo phase have yet to be studied. Relevant kinetic considerations are presented along with CO conversion and C₅₊ product selectivity data in the following sections of this study.

XPS studies to assess acid functionalization of the TiO₂ support precursor

The surface chemistry and the effects of the acid treatment on TiO₂ in this work are studied with XPS at Stages II and III pre- and post-calcination. As shown in Table S5 in the ESI,† no traceable amount of sulfur was found in the chemical composition of TiO₂ at Stage III (post-calcination).

The O 1s XPS region data reveals minimal differences in peak location for Stages II and Stages III (post-calcination), denoting similar characteristics. Two asymmetric peaks are found in this region (Fig. S5 in the ESI†). The major peak is at 529.51 eV for Stage II and 529.54 eV for Stage III, while the minor peak is at 531.41 eV and 531.04 eV for Stages II and III, respectively. These two components are assigned to O²⁻ in the TiO₂ crystalline complex (metal oxide) for the major peaks and O atoms in hydroxyl (–OH) groups for the minor peaks, as corroborated by the literature for TiO₂.⁷⁰ The peak intensities in the Ti 2p and O 1s regions decreased in magnitude after acid functionalization (Fig. S4 in the ESI†). The integrated peak areas were quantified to assess the effects of the support modification on its surface composition. These results, including the full width at half maximum (FWHM) values in eV and the relative percentages (%) for the relevant peaks as a function of binding energies (BE) in eV are shown in Table 2.

Table 2 XPS data in the O 1s region for the TiO₂ support precursor at Stages II and III (post-calcination)

Stage	Experimental XPS data
	Major peak (O^2− ions)			Minor peak (–OH)
	BE	FWHM	%	BE	FWHM	%
II	529.51	1.2	90.1	531.41	1.0	9.90
III (post-calcination)	529.54	1.4	73.4	531.04	1.6	26.6

---

The main observation from the values shown in Table 2 is the change in relative percentage (%) of O²⁻ ions and hydroxyl (OH) groups from Stage II to Stage III. It is concluded that the acid functionalization treatment favored the formation of these hydroxyl groups, as shown by the increase from 9.9% to 26.6%. The surface of the TiO₂ support is said to be hydroxylated post-functionalization, which can be attributed to the dissociation of H₂O molecules at oxygen vacancies.⁷¹ The acidic conditions in the H₂SO₄ solution promote the formation of these compounds on the support's structure. Titania's surface becomes protonated in low-pH solutions, giving rise to H⁺ being adsorbed and desorbed reversibly.⁷² As a result of this continuous ion exchange, Ti–OH is hypothesized to be formed due to protons attaching to an O atom, as Zhao et al. showed in their study of an acid-treated titania surface.⁷³ These –OH groups are then considered desirable for the applications in this work, as they can act as Brønsted acid sites by donating protons.⁷⁴

In contrast to the elemental composition results in Table S5† for TiO₂ at Stage III post-calcination, the XPS data for its pre-calcined counterpart reveals trace amounts of N and considerable amounts of S but no Ca or Si (Fig. S7 in the ESI†). Notably, the relative atomic percent for O is more significant prior to calcination at 58.4%, compared to the 50.0% value found for the treated sample. The heat treatment procedure successfully removes sulfur-containing compounds introduced in the acid functionalization. This result is attributed to the breakdown of the sulfur-containing species on the material's surface as a function of calcination temperature.⁷⁵

As previously discussed, the O 1s XPS region for the pre-calcined TiO₂ at Stage III displays considerably different features from Stages II and III (post-calcination). This XPS region for the pre-calcined counterpart is notably characterized by a major asymmetric peak that can be dissected into three minor peaks. The deconvolution of the major O 1s peak, as shown in Fig. 2, reveals the presence of a less intense region characterized by a minor peak at a BE of 532.13 eV. This lower-energy peak was assigned to H₂O molecules in the system.⁷⁶ This peak could correspond to SiO₂ due to its proximity to its BE value of 533.1 eV;⁷⁷ however, the elemental analysis in Table S6† further corroborates it as a different compound.

Fig. 2 XPS spectrum of O 1s region, with the metal oxide, OH, and H₂O peaks labeled for TiO₂ at (a) Stage III (pre-calcination) and (b) Stage III (post-calcination).

The three minor O 1s peaks are 1.2–1.6 eV apart. Analogous to the data in Table S5,† the integrated peak areas are used to calculate the relative percentages (%) for the compounds corresponding to the peaks in Fig. 2. The FWHM values are 1.3 eV, 1.5 eV, and 0.8 eV for the metal oxide, OH, and H₂O peaks, respectively, with their corresponding percentages then calculated to be 59.55%, 25.94%, and 14.51%. These values are instrumental in elucidating the role of the acid functionalization process in promoting the growth of an OH and H₂O-abundant layer on the support surface. This development is observed to increase photocatalytic activity in other literature studies, with the presence of hydroxyl groups on the surface promoting charge transfer enhancements.⁷⁸ There is a minimal change in the relative percentage of –OH groups before and after calcination, from 25.94% to 26.6%. Another crucial result of the post-functionalization calcination treatment is the disappearance of the H₂O peak and the successful removal of sulfur-containing compounds. In contrast, Fig. 3 shows the sulfur XPS regions in the TiO₂ support at Stage III (pre-calcination), with the labeled S 2p and S 2s peaks.

Fig. 3 XPS spectrum of the S 2s and S 2p regions, with the peaks labeled for the TiO₂ support at (a) Stage III (pre-calcination) and (b) Stage III (post-calcination).

The relative atomic percent of 5.50% for S, as shown in Table S6,† was a significant result in connecting the role of H₂SO₄ in forming acid sites. Despite the S-doping mechanism of TiO₂ not being well-established, it has been suggested that the uptake of sulfur species is a function of the synthesis method and the operating conditions.⁷⁹ The major S peak shown in Fig. 3 is found at 168.63 eV. This peak can be categorized as a S 2p_3/2 peak, corresponding to SO₄²⁻ ions, with the sulfur atom in a +6 oxidation state (S⁶⁺). A lower peak in the same 2p region would indicate the presence of S⁴⁺ instead.⁸⁰ It can then be inferred that the diprotic H₂SO₄ ionized in the water solution, producing an equilibrium of hydronium and sulfate ions, the latter of which the TiO₂ precursor adsorbed as part of the functionalization process. This finding agrees with existing literature, suggesting that sulfate ions are the predominantly adsorbed species on S-doped TiO₂ catalysts.⁸¹ This introduces acid sites onto the TiO₂ surface, which are hypothesized to be a desirable structural feature for the FTS applications in this work. The presence of the sulfate ions is corroborated by the band in the S 2s region, which was found at a BE of 232.63 eV. Despite the focus of S-species being in the 2p region, this minor 2s peak confirms the presence of SO₄²⁻, which typically shows at 232.7 ± 0.1 eV in this region.⁸²

The XPS data presented in this section reveals crucial information about the electronic state of the support's surface, with a particular focus on Stages II and III (pre- and post-calcination). After functionalization, the S=O bond in the sulfate ions is hypothesized to give rise to Brønsted acid sites by adsorbing H⁺ ions. This effect can be explained by the amplification of the acid strength of the Ti⁴⁺ ion, resulting from the induction effect from the SO₄²⁻ ions.⁸³ Similarly, other functional groups, such as hydroxyls, can contribute to the acidic behavior of the support.⁸⁴ The consequences of the final calcination step on such acid-functionalized supports have not been examined for Fischer–Tropsch synthesis yet in the literature. It is shown that introducing SO₄²⁻ ions on TiO₂ promotes the formation of both Brønsted and Lewis acid sites,⁸⁵ which are discussed in the next section of this study.

Characterization of acid sites on the functionalized TiO₂ via volumetric titration and BET surface area

The acidity of the functionalized TiO₂ support is quantified by determining the number of acid sites via volumetric titration of the precursor against a normalized sodium hydroxide (NaOH) solution. These acid sites on the support at Stage III are calculated according to the reaction between the diprotic sulfuric acid (H₂SO₄) solution used in the functionalization and the alkaline titrant solution shown in eqn (3):

H₂SO₄ + 2NaOH → Na₂SO₄ + 2H₂O (3)

This neutralization reaction between NaOH and H₂SO₄ is assumed to proceed to completion by involving all acid sites on the support and disregarding side reactions and potential impurities. For these results, the acid sites were considered monoprotic, which is a simplification shown in the literature for many other materials.⁸⁶

The results for the aqueous-phase volumetric titration are used to obtain the average number of acid sites on the functionalized TiO₂ support, calculated to be 0.256 ± 0.009 mmol_{acid sites} g_support⁻¹. This reported value represents the total number of acid sites on the material. The acid sites on the TiO₂/SO₄²⁻ solid donated a H⁺ or accepted an electron pair as a function of the titrant and the indicator. This method does not differentiate between acid site types (BAS or LAS) which prompts further characterization using spectroscopic techniques,⁸⁷ which are presented in the subsequent section of this study. Based on the XPS results and the confirmation of acidic character on the support, the two proposed sulfated structural complexes on TiO₂ are shown in Fig. 4.

Fig. 4 Coordinated sulfated TiO₂ (TiO₂/SO₄²⁻) structures, including (a) chelated and (b) bridged complexes.

The acidic properties introduced into the support are a result of the stabilization of the SO₄²⁻ ions on the TiO₂'s surface as a function of open coordination sites on the titanium (Ti) metal. The S=O bonds in the sulfate ions are responsible for the enhancement of both Brønsted and Lewis acidity due to the inductive effect from electronegativity differences with the Ti atoms. It is hypothesized that such acid treatment and calcination modifications induces significant changes in catalytic activity and stability, as shown for comparable support materials like zirconia.⁸⁸

It is hypothesized that the acid-functionalized support in this work is a modified TiO₂ framework involving H⁺ protons that can be donated to a base (Brønsted acid sites), and Ti⁺ atoms that can accept electron pairs (Lewis acid sites).⁸⁹ The successful modification of its structure and the introduction of acid sites is hypothesized to induce a bifunctional character to the system, which corresponds to carbon chain formation followed by isomerization and/or hydrocracking and possible secondary reactions in FTS. Much of the research on bifunctional catalysts has only been conducted on zeolites, thus making the acidic functionalization in this work relevant in FTS and for general catalytic applications.^90–92 Fig. 5 displays a model of a bridged TiO₂/SO₄²⁻ complex, with the Brønsted and Lewis acid sites on the structure.

Fig. 5 Structural model of the bridging TiO₂/SO₄²⁻ support, labeled with the proposed Brønsted and Lewis acid sites.

The surface area of the functionalized support [at Stage III (post-calcination)] is successfully measured with N₂ adsorption/desorption isotherms, and the data is compared to the support prior to acid treatment (at Stage II). The Brunauer–Emmett–Teller (BET) surface area (S_BET) for the non-functionalized precursor is 55.97 m² g⁻¹, and 43.03 m² g⁻¹ for its functionalized counterpart. The acid site density (at Stage III) is calculated at 4.57 × 10⁻³ mmol_{acid sites} m⁻², based on the volumetric titration and N₂ physisorption results. Considering the assumption that one S atom (or sulfate ion) corresponds to one Ti atom prior to calcination, the surface area measurements are important in assessing the elimination of H₂O in the system and the formation of oxygen vacancies resulting from S and OH groups' removal after the final calcination step. The trend shows that S_BET values decrease after functionalization, which are attributed to the successful crystal growth of TiO₂ nanoparticles as a function of the heat treatment. It can be inferred that particle agglomeration played a crucial role, impacted by the final calcination step, as previously reported for titania-based materials.^93,94

Pyridine DRIFTS (Pyr-DRIFTS) for the distribution of Brønsted and Lewis acid sites on the functionalized TiO₂ support

The corresponding FTIR spectra for the sulfated TiO₂ support at Stages III (pre-calcination) and III (post-calcination) are crucial to determining the effects of the acid functionalization of the resulting support material. The successful introduction of sulfate-related species on TiO₂ is corroborated by inspecting their corresponding FTIR peaks. The support at Stage III (pre-calcination) displays four characteristic peaks at wavelengths of 1232.2 cm⁻¹, 1137.9 cm⁻¹, 1049.1 cm⁻¹, and 979.7 cm⁻¹. These peaks are related to two major sulfur-related motions in the functionalized support: vibrations of the S–O bonds and stretching of the S=O bonds.⁹⁵ These four FTIR bands are attributed to asymmetrical motions for the peaks at ∼1226 cm⁻¹ and ∼1049 cm⁻¹ and symmetric vibrations for the ∼1134 cm⁻¹ and ∼979 cm⁻¹ bands.⁹⁶ The identification of these peaks in the 900–1300 cm⁻¹ range corroborates that the sulfur species successfully attached onto the TiO₂'s surface by bonding to Ti⁺ cations after functionalization. Furthermore, the differences between the peak locations and intensities pre- and post-calcination are used to assess the effects of this final heat treatment. For TiO₂ at Stage III (post-calcination), the peaks are found at 1229.4 cm⁻¹, 1136.5 cm⁻¹, 1047.1 cm⁻¹, and 977.5 cm⁻¹. The peaks, which shift towards slightly lower wavenumber values, decrease in intensity after calcination. Calcination favors the removal of these ions from the support via desorption, which relates to changes in the phase composition of the TiO₂ support.⁹⁷

The FTIR spectra also reveals information about the presence of hydroxyl (–OH) groups originating from water introduced in the functionalization. Characteristic peaks at ∼3450 cm⁻¹ are observed for the support, which are assigned to stretching vibrations of the O–H bonds.⁹⁸ For the uncalcined sample, this peak is identified at 3448.2 cm⁻¹, and at 3452.0 cm⁻¹ for its calcined counterpart. A secondary adsorption peak attributed to the bending vibrations of H₂O molecules is found at 1627.7 cm⁻¹ for both samples. The calcined support displays a lower intensity for these peaks in contrast to its uncalcined counterpart, suggesting that a significant amount of H₂O is successfully removed from the support due to calcination.⁹⁹

The use of pyridine (Pyr) as a probe species for DRIFTS allows for the ratio of Brønsted to Lewis acid sites to be determined. Pyridine adsorbs onto the sites, displaying characteristic frequencies, as reported in the literature. When Pyr coordinates to TiO₂, its FTIR peaks are shifted slightly due to its adsorption. Liquid Pyr displays peaks at 1439 cm⁻¹, 1482 cm⁻¹, 1572 cm⁻¹, and 1583 cm⁻¹. The two lower frequencies originate from in-plane C–H deformation modes, and the higher frequency peaks correspond to in-plane deformation modes of the ring found in its chemical structure.^100,101 Fig. 6 shows the FTIR spectra for the support at Stage III in the 1400 cm–1700 cm⁻¹ range.

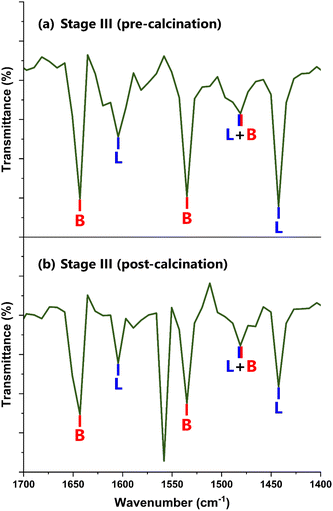Fig. 6 Pyr-DRIFTS spectra of the TiO₂/SO₄²⁻ support at (a) Stage III (pre-calcination) and (b) Stage III (post-calcination).

Fig. 6 confirms the presence of Brønsted and Lewis acid sites on the TiO₂/SO₄²⁻ support complex, which are labeled B and L respectively. The sulfated complex showed an additional peak in this range post-calcination, as shown in Fig. 6(b). This band, found at 1558.2 cm⁻¹, was attributed to the oxidative breakdown of Lewis-bound Pyr molecules into carbonaceous compounds,¹⁰² resulting from the calcination step. The FTIR frequencies for the BAS and LAS on the sulfated TiO₂ support, as shown in Fig. 6, are presented in Table S4 in the ESI.†

The peaks associated with pyridine adsorbed onto the BAS and LAS show the same FTIR bands for both the uncalcined and calcined samples, as elucidated in Table S4.† The common peak for both samples, at 1481.1 cm⁻¹, relates to the total amount of acid sites (Brønsted and Lewis) present in each sample.¹⁰³ The ratio of Brønsted to Lewis acidity (B/L) is calculated according to eqn (4), as introduced by Emeis in a study on pyridine adsorbed on solid acid catalysts:¹⁰⁴

B/L = (A_B × C_L)/(A_L × C_B) (4)

where A_B and A_L represent the areas of the FTIR peaks for Brønsted and Lewis acidity in cm⁻¹ respectively, C_B is the coefficient of Brønsted acidity (188 cm mmol⁻¹), and C_L corresponds to the coefficient of Lewis acidity (142 cm mmol⁻¹).¹⁰⁵

For the acid functionalized TiO₂, the B/L ratio is calculated at 1.68 for the uncalcined support, demonstrating a greater number of Brønsted acid sites than Lewis acid sites. For its calcined counterpart, the B/L ratio is calculated at 1.27. This result shows that the final calcination step had a greater influence on BAS than on LAS. By examining the spectra in Fig. 6, the intensity of the BAS and LAS bands greatly decreased after calcination. This finding suggests a considerable reduction in the total amount of acid sites present in the functionalized and calcined support. The calcination temperature is highlighted as the probable cause for this development, as such harsh conditions are known to reduce specific surface area by damaging its pore structure – and more importantly, prompt the degradation of SO₄²⁻ species.¹⁰⁶ Such modifications are expanded upon further in the following sections.

Catalyst characterization

Following the successful impregnation of the TiO₂ support with a bimetallic FeCo active phase, the crystal structure of the catalysts is evaluated via XRD, after undergoing reduction in an H₂ atmosphere. This reduction in the full hydrogen atmosphere was effective, as evidenced by the XRD data and supporting insights presented in this section. The successful reduction of the Fe and Co active metal species is corroborated by the favorable FTS performance trends observed across the catalytic systems. Moreover, previous relevant studies by van Ravenhorst et al.,¹⁰⁷ Kuznetsov et al.,¹⁰⁸ and Tomić-Tucaković et al.¹⁰⁹ on the reducibility of Co-based catalysts, alongside work by van der Kraan et al.¹¹⁰ and Ji et al.¹¹¹ for Fe-based systems, provided substantial validation for the efficacy of the pure H₂ reduction protocol utilized in this work.

The systems herein are characterized as a function of the titania support at Stages II, III (pre-calcination), and III (post-calcination). As the nominal active metal loading is similar for all samples (2.0 wt%), the focus of the analysis relies on the effects of the acid functionalization and final calcination on the phase composition of the resulting catalysts. Fig. 7 shows the XRD spectra for the synthesized FeCo catalysts supported on TiO₂, following H₂ reduction.

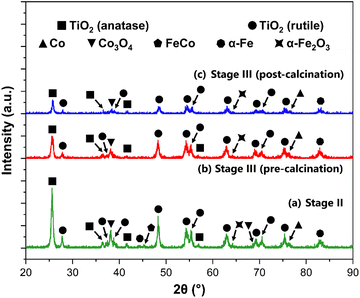Fig. 7 XRD spectra for the functionalized FeCo catalysts, supported on TiO₂ at (a) Stage II, (b) Stage III (pre-calcination), and (c) Stage III (post-calcination), with the peaks labeled.

The XRD spectra for the functionalized catalysts shown in Fig. 7 revealed characteristic peaks corresponding to the rutile and anatase polymorphs of TiO₂. This phase composition for the support material remained unchanged, as shown prior to the impregnation with the bimetallic active phase (Fig. S2 in the ESI†). The strongest reflections pertaining to these titania phases remained unchanged at every stage of support preparation. For Stages II, III (pre-calcination) and III (post-calcination), the characteristic peaks for TiO₂ are at 2θ = 25.59°, 25.53°, and 25.73° for anatase (110), respectively. For rutile (110), the strongest peak reflections are at 2θ = 27.77°, 27.83°, and 27.93°, respectively. By using the Spurr and Myers method, the phase composition of the support in the bimetallic catalysts is calculated, and the fractions of rutile (F_R) and anatase (F_A) are evaluated as a function of the acid functionalization and calcination processes. The results of this analysis are shown in Table 3.

Table 3 Phase composition in the FeCo/TiO₂ catalysts at stages II, III (pre-calcination) and III (post-calcination)

Stage	FR	FA	FR/FA
II	0.301	0.699	0.431
III (pre-calcination)	0.262	0.738	0.355
III (post-calcination)	0.269	0.731	0.368

---

These calculations further corroborate the hypothesis that the acid functionalization process favors the stabilization of the anatase phase, with the catalysts supported on acid-treated TiO₂ (Stage III) displaying a higher fraction of anatase, and a lower fraction of rutile when compared to the Stage III system. The wetness impregnation protocol used to deposit the Fe and Co active phases onto the support does not disrupt this phenomenon, which is discussed earlier in this work. The final calcination step at Stage III does not largely impact the phase composition of the final catalytic systems, as shown by the F_R and F_A values. The fractional content of the anatase phase for the sample supported on the calcined Stage III support was calculated at 0.368, which was only marginally greater than its uncalcined counterpart, at 0.355. Despite the introduction of a bimetallic FeCo active phase being known to increase the rutile fraction in an as-synthesized catalyst,¹¹² the acid functionalization in this work was the main driving force for the corresponding phase composition changes in the support material.

The lack of relatively intense peaks for the Fe and Co species, compared to those of the TiO₂ support, can be attributed to a combination of the low loading of the active metal particles on the TiO₂ surface and the dominant diffraction peaks from the larger TiO₂ crystallites.¹¹³ This phenomenon is further supported by the significant rutile fractions (above 20%), as it has also been shown that the dispersion of a metal phase such as Co is enhanced by the rutile content in the support.¹¹⁴ Jongsomjit et al. demonstrated that CO hydrogenation activity was enhanced for Co/TiO₂ systems by the inclusion of ∼19% rutile in the support. This improvement was attributed to increased support stability, and more importantly associated with weaker SMSIs associated with the rutile phase of TiO₂.¹¹⁵ For Fe-based catalysts, literature is more limited. Nonetheless, Madhusudhan Rao et al. showed in their detailed XPS study on Fe/TiO₂ systems that such systems exhibit SMSI behavior analogous to other Group VIII metals (e.g., ruthenium). Iron oxides can be encapsulated in the TiO₂ support during annealing or lead to interdiffusion mechanisms. These phenomena can result in low apparent dispersion of Fe due to the partial coverage of the reduced TiO₂ surface layer.¹¹⁶

Even with relatively lower intensity Fe and Co peaks, the active species in the bimetallic catalysts are identified in Fig. 7. The resulting peaks are then matched to metallic Co (PDF #00-015-0806)¹¹⁷ and Co₃O₄ (PDF #00-042-1467)¹¹⁸ for the Co phase. For the Fe active phase, α-Fe (PDF #00-006-069)^119,120 and α-Fe₂O₃ (PDF #00-033-0664)¹²¹ are identified. A FeCo alloy peak (PDF #00-048-1818)^122,123 at 2θ = 45.21° is also identified for the non-functionalized bimetallic catalyst supported on TiO₂ (Stage II), with an estimated crystallite size of 89.64 nm. The crystallite size (D_p) of the active species (in nm) for all samples is calculated using the Scherrer equation with the calculated FWHM values from the XRD spectra, as discussed in previous sections. The K constant and λ were set to 0.9 and 0.15406 nm, respectively. The identification of these reflections for the active phases suggests that the reduction was successful in generating the desired active species for FTS applications. Despite initially considering transmission electron microscopy (TEM) for the characterization of these systems, the successful identification of the active metal species via XRD was deemed sufficient. Furthermore, the innate low contrast between FeCo nanoparticles and the TiO₂ support in standard TEM imaging poses a critical limitation for the clear visualization and particle size measurement of these species. Such challenges, due to the proximity in atomic numbers (Z-values) and electron density, have been well-documented in the literature, such an in a study by Nasralla et al. on Fe systems.¹²⁴

The S_BET values for the catalysts were calculated at 49.42 m² g⁻¹, 49.23 m² g⁻¹, and 49.05 m² g⁻¹ for FeCo supported on Stages II, III (pre-calcination), and III (post-calcination) respectively. The minimal level of variability for these values suggests that the overall structural integrity of the support was retained following the acid and heat treatments. The increase from 43.03 m² g⁻¹, which was the calculated S_BET value for the functionalized TiO₂ before impregnation as discussed in previous sections, helped elucidate the role of the sulfate ions in modifying its surface chemistry. This development can be likely attributed to the sulfate groups inducing a partial blockage or restructuring of the pore architecture in the support. The deposition of the active Fe and Co nanoparticles modified TiO₂'s morphological features, which might have caused the exposure of inaccessible sites.

The morphological features of the TiO₂ support at different stages of the acid functionalization process were evaluated by field-emission scanning electron microscopy (FESEM) imaging, as shown in Section 7 of the ESI.† As Fig. S8–S10† indicate, the TiO₂ support was able to retain its overall morphology across Stages II, III (pre-calcination), and III (post-calcination). Despite this development, there was a visible increase in surface roughness and morphological complexity as a function of the acid treatment and its subsequent calcination. These structural changes were consistent with the addition of the sulfate (SO₄²⁻) ions and their thermal decomposition from the final calcination step. While there were alterations to the support material, its integrity was maintained, denoting the prevention of major structural changes. Fig. S11† denotes the general morphology of the as-synthesized FeCo/TiO₂ Stage III (post-calcination) catalyst. These images reveal the presence of irregular clusters and dense superficial features, which suggest agglomeration of nanoparticles. Despite not being able to resolve these nanoparticles in a discrete manner, the apparent clustering behavior observed suggests that the active phase was effectively anchored to the support. As discussed in previous sections, the catalysts' loading was confirmed via XPS (Section 6 of the ESI†).

Catalyst performance: CO conversion and product selectivity for FTS

The catalytic performance of the synthesized bimetallic systems is evaluated for Fischer–Tropsch synthesis (FTS) reactions, as described in the Experimental section. Key FTS parameters analyzed in this study include CO conversion, CH₄ selectivity, and C₅₊ selectivity. These parameters are sensitive to structural modifications and surface chemistry changes induced by the acid functionalization of the TiO₂ support. The catalysts are tested as a function of the TiO₂ functionalization stage: (II) post-calcination (at 400 °C), (III) functionalized pre-calcination, and (III) functionalized post-calcination (at 300 °C). The non-functionalized sample (Stage II) serves as the control catalyst at a nominal 2.0 wt%, with relevant results summarized in Table 4.

Table 4 CO conversion (%), normalized rate of CO consumption (mol_CO s⁻¹ g_FeCo⁻¹), CH₄ selectivity (%), C₅₊ selectivity (%), and C₂–C₄ selectivity for the FeCo/TiO₂ (Stage II) catalysts during FTS

FTS parameter	Experimental value
CO conversion (%)	27.6 ± 6.94
Normalized rate of CO consumption (molCO s^−1 gFeCo^−1)	5.89 × 10^−5 ± 1.62 × 10^−5
CH4 selectivity (%)	4.48 ± 2.47
C5+ selectivity (%)	61.3 ± 3.00
C2–C4 selectivity (%)	34.2 ± 2.08

---

The CO conversion, as shown in Table 4, suggests moderate catalytic activity for FTS. This result is in accordance with other FeCo bimetallic systems in the literature. A 2.0 wt% FeCo/TiO₂ catalyst (1 : 1 Fe : Co ratio) synthesized by Duvenhage et al.¹²⁵ measure a CO conversion of 10.5%. In the same study, for a 4.0 wt% FeCo/TiO₂ catalyst (2 : 2 Fe : Co ratio), the CO conversion increases to 15.8%. Similarly, Arcuri et al.¹²⁶ show that their 4.87 wt% FeCo/SiO₂ catalyst reaches a CO conversion of 2.7% at 1 atm and the same temperature and pressure conditions as the 2.0 wt% catalyst in Table 4. The reported C₂–C₄ selectivity values in Table 4 correspond to a mixture of light hydrocarbons, including paraffins [e.g., ethane (C₂H₆), propane (C₃H₈), butane (C₄H₁₀)], and their olefin counterparts. These compounds were then grouped in accordance with standard reporting practices in FTS literature. While the results in Table 4 are promising for the catalysts introduced in this study, further optimization of the FTS reaction conditions, including temperature, pressure, and H₂ : CO ratio, could enhance performance.

The calculated CH₄ selectivity of 4.48% ± 2.47 indicates a favorable performance trend for these catalysts. As Co-based catalysts tend to favor elevated CH₄ selectivity at higher temperatures,¹²⁷ the selection of low temperature Fischer–Tropsch (LTFT) conditions for these systems is considered appropriate. The non-functionalized catalysts supported on TiO₂ (Stage II) favored chain growth propagation, thereby successfully minimizing undesirable methanation. The low CH₄ selectivity could be attributed to different phenomena, primarily the role of primary olefins competing with methyl groups for surface sites.¹²⁸ This development is further corroborated by the C₅₊ selectivity of 61.3% ± 3.00, which indicates a significant portion of heavier hydrocarbons are produced during the FTS process. The hydrocarbon distribution for this bimetallic catalyst is shown in Fig. 8.

Fig. 8 Product selectivity (%) to C₁–C₉ hydrocarbons for the FeCo catalyst supported on TiO₂ (Stage II).

Despite the considerable amount of heavier paraffins and olefins produced, as denoted by the C₅₊ selectivity, this parameter is notably lower in magnitude than the 72.6% value for the analogous 2.0 wt% FeCo/TiO₂ catalyst (1 : 1 Fe : Co ratio) synthesized by Duvenhage discussed previously. This result can be attributed to the synergy between the Fe and Co active sites in the bimetallic alloy as a function of the calcined TiO₂ at Stage II, which pushes product selectivity towards a lighter hydrocarbon composition. Similarly, there is a slight preference for olefin production, as shown by an olefin selectivity (O_n) of 52.5% ± 2.8, compared to the paraffin selectivity (P_n) of 47.5% ± 2.7. This result suggests that, during FTS, H₂ mobility is slightly reduced, which leads to reduced adsorption rates and therefore a minimization of the hydrogenation of alkenes to alkanes as a function of the bimetallic FeCo active phase.¹²⁹

To determine the catalytic effects of the acid functionalization introduced in this work, three parameters are considered important for catalyst performance and production of lighter olefins and paraffins as a function of hydrocracking: C₅₊ selectivity, C₂–C₄ selectivity, and CO conversion. The mechanism of this desirable hydrocracking during FTS is a function of intermediate carbenium ions (RR′R′′C⁺) formed by the interactions between hydrocarbons and metal/acid sites on the support.¹³⁰ The metal sites dehydrogenate saturated molecules and hydrogenate unsaturated ones, and the acid sites enabled the isomerization or hydrocracking of alkene intermediates.¹³¹ It is hypothesized that the catalyst architecture introduced in this study would increase C₂–C₄ selectivity by cracking the heavier hydrocarbons and decreasing CH₄ selectivity. The FTS results for the FeCo/TiO₂ Stage III (pre-calcination) and FeCo/TiO₂ Stage III (post-calcination) are shown in Table 5.

Table 5 CO conversion (%), Normalized rate of CO consumption (mol_CO s⁻¹ g_FeCo⁻¹), CH₄ selectivity (%), C₅₊ selectivity (%), and C₂–C₄ selectivity for the FeCo/TiO₂ Stage III (pre-calcination) and Stage III (post-calcination) catalysts during FTS

FTS parameter	Experimental value
FeCo/TiO2Stage III (pre-calcination)
CO conversion (%)	16.2 ± 1.61
Normalized rate of CO consumption (molCO s^−1 gFeCo^−1)	3.70 × 10^−5 ± 6.12 × 10^−6
CH4 selectivity (%)	4.80 ± 2.43
C5+ selectivity (%)	55.5 ± 2.17
C2–C4 selectivity (%)	39.6 ± 3.2
FeCo/TiO2Stage III (post-calcination)
CO conversion (%)	29.0 ± 5.0
Normalized rate of CO consumption (molCO s^−1 gFeCo^−1)	6.89 × 10^−5 ± 1.63 × 10^−5
CH4 selectivity (%)	3.03 ± 0.33
C5+ selectivity (%)	60.4 ± 3.3

---

The acid functionalization of the TiO₂ support introduces important metal–support interactions, as evidenced by the catalyst performance of the bifunctional catalysts shown in Table 5. For the FeCo/TiO₂ Stage III (pre-calcination) catalyst, there was a decrease in activity, as denoted by the CO conversion of 16.2% ± 1.61, which represents a 41.3% decrease in catalytic activity compared to the control FeCo/TiO₂ (Stage II) catalyst. This development is attributed to the remaining sulfur in the catalyst, as evidenced by the XPS studies, which induces a partial blockage of the active sites for the carbon chain formation in FTS.¹³² This incorporation of the sulfur atoms into the catalyst's architecture is likely a major contributor to a higher CH₄ selectivity of 4.80% ± 2.43 by hindering CO dissociation and CH coupling. This favors the formation of shorter-chain hydrocarbons and alkanes,¹³³ as shown by the C₂–C₄ selectivity of 39.6% ± 3.2, O_n of 56.47% ± 2.76, and P_n of 43.53% ± 1.95 for this catalytic system. The product distribution results for the FeCo/TiO₂ Stage III (pre-calcination) catalyst, which indicates a tendency to form middle distillates as a function of the induced hydrocracking, are shown in Fig. 9. The chemisorption of sulfur atoms and their role in the deactivation of Fe and Co catalysts has been studied, with Ma et al.¹³⁴ showing that each sulfur atom blocks six surface Fe or Co atoms, as predicted by the sorption theory; thus, corroborating the performance results for the catalysts in this study.

Fig. 9 Product selectivity (%) to C₁–C₉ hydrocarbons for the FeCo catalyst supported on TiO₂ Stage III (pre-calcination).

The final calcination step introduced in the acid functionalization process is considered a favorable optimization technique in the synthesis of the bifunctional catalyst. The FeCo/TiO₂ Stage III (post-calcination) catalyst displayed the optimized performance metrics, as evidenced by its CO conversion of 29.0% ± 4.95 shown in Table 5 and the product distribution in Fig. 10. The calcination temperature specified for this step is hypothesized to be an important variable which affects the sulfur content in the material and the surface area of the support, as shown by Shao et al.¹³⁵ for sulfated TiO₂–SiO₂ catalysts. It has been reported that sulfated TiO₂ catalysts only exhibit higher activities when calcined at temperatures above 500 °C.¹³⁶ The resulting phase evolution of the TiO₂ support at Stage III (post-calcination) is a function of the reduction of Brønsted acid sites. This can be largely attributed to the decomposition of the SO₄²⁻ ions and their removal from the TiO₂, which influences the textural and chemical properties of the support prior to impregnation with the active phase.¹³⁷ The residual Brønsted sites on the support are then attributed to hydroxyl groups remaining on the surface, which are less Brønsted acidic than the sulfate ions, as discussed in previous sections.

Fig. 10 Product selectivity (%) to C₁–C₉ hydrocarbons for the FeCo catalyst supported on TiO₂ stage III (post-calcination).

As shown in Fig. 10, the selectivity towards middle distillates is significant, displaying a C₂–C₄ selectivity of 36.55% ± 2.36 and a C₅₊ selectivity of 60.41% ± 3.24. The slightly greater distribution of heavier hydrocarbons is attributed to the reduced fraction of Brønsted acid sites as a function of the final calcination step. It can then be inferred that the higher proportion of Lewis acid sites has less influence than the Brønsted sites on the hydrocracking process, which is shown for other systems in the literature.^138,139 By considering the kinetic parameters presented in this section, it is concluded that the optimized catalyst is the FeCo/TiO₂ Stage III (post-calcination), which maximizes CO conversion and induces hydrocracking as a function of the surface chemistry and morphological changes. This is further corroborated by the calculation of the normalized average rate of CO consumption (−r̄_CO) for the catalysts, as shown in Section 6 of the ESI,† where the FeCo/TiO₂ Stage III (post-calcination) sample displays the highest rate of CO consumption, at 6.89 × 10⁻⁵ ± 1.63 × 10⁻⁵ mol_CO s⁻¹ g_FeCo⁻¹. For all three samples in this study, catalyst stability as a function of time-on-stream (TOS) is consistent with previously published work on FTS,³² with the catalysts showing no deactivation over the 6 h-time period for each experimental run. TOS performance and catalyst stability data is presented in the ESI.†

For all three catalysts, the chain growth probability (α) was calculated using the Anderson–Schulz–Flory (ASF) distribution model. Although catalysts in the literature have shown critical deviations from this model,^6,140 it remains an important parameter that helps elucidate the extent of chain formation during FTS. For the FeCo/TiO₂ Stage II catalyst, α was 0.704 ± 0.069. For the acid-functionalized samples (FeCo/TiO₂ Stage III), α was estimated at 0.726 ± 0.066 pre-calcination and 0.718 ± 0.024 post-calcination. This increasing trend in α value showcases consistency in the propagation of the hydrocarbon products likely due to the optimized surface properties induced as a function of the acid treatment and final calcination step.

Despite the favorable performance trends displayed by the catalysts in this work, it is critical to emphasize that FTS product distribution is also strongly correlated to reaction temperature and catalyst's active phase, particularly for Co-based systems. For a Co/SiO₂ catalyst, Arslan et al. showed that CO conversion significantly increased from ∼5% at 200 °C to ∼86% at 350 °C (20 bar, H₂/CO = 2.0), highlighting the strong correlation between temperature and activity. Furthermore, the decrease of CO conversion at temperatures above 350 °C was attributed to potential water–gas shift (WGS) activity resulting at elevated temperatures.¹⁴¹ When compared to FTS catalysts reported in the literature, de la Peña O'Shea et al. demonstrated that their FeCo (1 : 2)/SiO₂ (15.0 total wt%) catalyst achieved an optimal CO conversion of ∼60% at 260 °C, while a monometallic Co/SiO₂ (10.0 wt%) specimen exhibited lower activity, which resulted from the lower dispersion of the Co active phase on the support.¹²⁹ For conventional FeCo/TiO₂ systems, Duvenhage et al. also elucidated the influence of reaction temperature on performance and product selectivity. Their Fe : Co (1 : 2)/TiO₂ (5.0 total wt%) catalyst showed an increase in CO conversion from 37.3% at 220 °C to 72.6% at 225 °C to 90.3% at 310 °C. Across this temperature range, C₅₊ selectivity also shifted, from 49.9% to 33.6% to 17.8%, showing that higher temperatures increase the formation of CH₄ and light hydrocarbon products.¹²⁵

Conclusions

The results from this study elucidate the significant effects of introducing acid sites on TiO₂ to impart bifunctionality in a single catalytic material for Fischer–Tropsch synthesis (FTS) reactions. Experimental data shows that acid treatment of the catalyst support with H₂SO₄, followed by a calcination at 300 °C [FeCo/TiO₂ Stage III (post-calcination)], induces significant morphological and microstructural changes that optimized FTS reaction performance at 250 °C and 300 psi(g). With a CO conversion of 29.0% ± 4.95 and a significant shift towards C₂–C₄ products, these catalysts prove to be more adept at inducing hydrocracking reactions than their non-functionalized [FeCo/TiO₂ (Stage II)] and uncalcined [FeCo/TiO₂ Stage III (pre-calcination)] counterparts. This catalyst support optimization sequence begins to address the role of Brønsted and Lewis sites in modifying active sites in an FTS catalyst and their effects on CO activation, carbon chain growth, and olefin modification. A higher number of Brønsted acid sites (e.g., hydroxyl groups) results in a higher level of hydrocracking, compared to a greater number of Lewis acid sites (e.g., unsaturated Ti⁴⁺ sites). Despite this desirable modification, the presence of sulfur-containing species (SO₄²⁻) from acid functionalization poisons the catalyst's active sites and minimizes CO conversion (16.2% ± 1.61). These experimental results highlight the effects of acid sites and support phases on reaction kinetics, further offering a method to optimize overall FTS catalytic efficiency.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Luis C. Caballero: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review and editing. J. Paulo L. Perez: data curation, formal analysis. Michael M. Nigra: conceptualization, funding acquisition, methodology, project administration, resources, supervision, validation, writing – original draft, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the United States Department of Energy (DOE) under award number DE-FE0026825, subaward S000662-DOE as well as DOE award DE-FE0032046. This publication was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessary constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency, thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. This work made use of Nanofab EMSAL shared facilities of the Micron Technology Foundation Inc. Microscopy Suite sponsored by the John and Marcia Price College of Engineering, Health Sciences Center, Office of the Vice President for Research. The authors would also like to acknowledge the University of Utah's Materials Characterization Lab (MCL) for providing their shared facilities to conduct XRD and N₂ adsorption–desorption/BET measurements. We are grateful to Daniel Varga and Sayed Abu Sufyan in the Department of Chemical Engineering for assisting in the interpretation of additional BET studies conducted using Prof. Kevin Whitty's laboratory facilities.

Notes and references

1. S. S. Ail and S. Dasappa, Renewable Sustainable Energy Rev., 2016, 58, 267–286.
2. Y. Cao, Z. Gao, J. Jin, H. Zhou, M. Cohron, H. Zhao, H. Liu and W. Pan, Energy Fuels, 2008, 22, 1720–1730.
3. R. Rauch, J. Hrbek and H. Hofbauer, Wiley Interdiscip. Rev.: Energy Environ., 2014, 3, 343–362.
4. O. R. Inderwildi, S. J. Jenkins and D. A. King, J. Phys. Chem. C, 2008, 112, 1305–1307.
5. A. Y. Khodakov, W. Chu and P. Fongarland, Chem. Rev., 2007, 107, 1692–1744.
6. D. Förtsch, K. Pabst and E. Groß-Hardt, Chem. Eng. Sci., 2015, 138, 333–346.
7. J. Gao, B. Wu, L. Zhou, Y. Yang, X. Hao, J. Xu, Y. Xu and Y. Li, Ind. Eng. Chem. Res., 2012, 51, 11618–11628.
8. A. K. Dalai and B. H. Davis, Appl. Catal., A, 2008, 348, 1–15.
9. M. P. C. Van Etten, M. E. De Laat, E. J. M. Hensen and I. A. W. Filot, J. Phys. Chem. C, 2023, 127, 15148–15156.
10. C. H. Bartholomew, M. Rahmati and M. A. Reynolds, Appl. Catal., A, 2020, 602, 117609.
11. A. Straß-Eifert, L. I. van der Wal, C. Hernández Mejía, L. J. Weber, H. Yoshida, J. Zečević, K. P. de Jong and R. Güttel, ChemCatChem, 2021, 13, 2726–2742.
12. V. Sage, Y. Sun, P. Hazewinkel, T. Bhatelia, L. Braconnier, L. Tang, K. Chiang, M. Batten and N. Burke, Fuel Process. Technol., 2017, 167, 183–192.
13. X. Li, Y. Chen, S. Liu, N. Zhao, X. Jiang, M. Su and Z. Li, Chem. Eng. J., 2021, 416, 129180.
14. G. Yang, C. Xing, W. Hirohama, Y. Jin, C. Zeng, Y. Suehiro, T. Wang, Y. Yoneyama and N. Tsubaki, Catal. Today, 2013, 215, 29–35.
15. F. Morales, F. M. de Groot, P. Glatzel, E. Kleimenov, H. Bluhm, M. Haevecker, A. Knop-Gericke and B. M. Weckhuysen, J. Phys. Chem. B, 2004, 108, 16201–16207.
16. C. Liu, Y. He, L. Wei, Y. Zhang, Y. Zhao, J. Hong, S. Chen, L. Wang and J. Li, ACS Catal., 2018, 8, 1591–1600.
17. N. N. Madikizela-Mnqanqeni and N. J. Coville, Appl. Catal., A, 2007, 317, 195–203.
18. S. K. Mohapatra and M. Misra, J. Phys. Chem. C, 2007, 111, 11506–11510.
19. Z. Yang, W. Xu, B. Yan, B. Wu, J. Ma, X. Wang, B. Qiao, J. Tu, H. Pei, D. Chen and Q. Wu, ACS Omega, 2022, 7, 2474–2483.
20. M. A. M. Motchelaho, H. Xiong, M. Moyo, L. L. Jewell and N. J. Coville, J. Mol. Catal. A Chem., 2011, 335, 189–198.
21. J. Frątczak, H. de Paz Carmona, Z. Tišler, J. M. Hidalgo Herrador and Z. Gholami, Molecules, 2021, 26, 7172.
22. D. Deviana, G. Bae Rhim, Y.-E. Kim, H. Song Lee, G. Woo Lee, M. Hye Youn, K. Young Kim, K. Young Koo, J. Park and D. Hyun Chun, Chem. Eng. J., 2023, 455, 140646.
23. A. P. Kulkarni and D. S. Muggli, Appl. Catal., A, 2006, 302, 274–282.
24. A. L. Lapidus and A. Y. Krylova, Russ. Chem. Rev., 1998, 67, 941–950.
25. V. P. Santos, T. A. Wezendonk, J. J. D. Jaén, A. I. Dugulan, M. A. Nasalevich, H.-U. Islam, A. Chojecki, S. Sartipi, X. Sun, A. A. Hakeem, A. C. J. Koeken, M. Ruitenbeek, T. Davidian, G. R. Meima, G. Sankar, F. Kapteijn, M. Makkee and J. Gascon, Nat. Commun., 2015, 6, 6451.
26. W. D. Shafer, M. K. Gnanamani, U. M. Graham, J. Yang, C. M. Masuku, G. Jacobs and B. H. Davis, Catalysts, 2019, 9, 259.
27. I. C. ten Have and B. M. Weckhuysen, Chem Catal., 2021, 1, 339–363.
28. J. Chai, J. Jiang, Y. Gong, P. Wu, A. Wang, X. Zhang, T. Wang, X. Meng, Q. Lin, Y. Lv, Z. Men and P. Wang, Catalysts, 2023, 13, 1052.
29. H. M. Torres Galvis, J. H. Bitter, C. B. Khare, M. Ruitenbeek, A. I. Dugulan and K. P. de Jong, Science, 2012, 335, 835–838.
30. V. R. Calderone, N. R. Shiju, D. C. Ferré and G. Rothenberg, Green Chem., 2011, 13, 1950–1959.
31. M. Tavares, G. Westphalen, J. M. Araujo Ribeiro de Almeida, P. N. Romano and E. F. Sousa-Aguiar, Frontal Nanotechnol. Res., 2022, 4, 978358.
32. L. C. Caballero, J. S. Brindle, N. P. Ramey, S. A. Sufyan, S. K. Mohanty and M. M. Nigra, J. Mater. Chem. A, 2024, 12, 20975–20989.
33. A. A. Vasilev, M. I. Ivantsov, E. L. Dzidziguri, M. N. Efimov, D. G. Muratov, M. V. Kulikova, N. A. Zhilyaeva and G. P. Karpacheva, Fuel, 2022, 310, 122455.
34. H. Pu, C. Tian and H. Zhang, Sci. Rep., 2024, 14, 31258.
35. H. Lin, J. Long, Q. Gu, W. Zhang, R. Ruan, Z. Li and X. Wang, Phys. Chem. Chem. Phys., 2012, 14, 9468–9474.
36. S.-K. Park and H. Shin, J. Nanosci. Nanotechnol., 2014, 14, 8122–8128.
37. O. Bortnovsky, Z. SobalÍk, B. Wichterlová and Z. Bastl, J. Catal., 2002, 210, 171–182.
38. M. Bejblová, S. I. Zones and J. Čejka, Appl. Catal., A, 2007, 327, 255–260.
39. J. Lu, K. M. Kosuda, R. P. Van Duyne and P. C. Stair, J. Phys. Chem. C, 2009, 113, 12412–12418.
40. A. L. Moghaddam, M. Ghavipour, J. Kopyscinski and M. J. Hazlett, Appl. Catal., A, 2024, 672, 119594.
41. D. J. Duvenhage and N. J. Coville, Appl. Catal., A, 1997, 153, 43–67.
42. D. J. Duvenhage and N. J. Coville, Appl. Catal., A, 2002, 233, 63–75.
43. A. Kasht, R. Hussain, M. Ghouri, J. Blank and N. Elbashir, Am. J. Anal. Chem., 2015, 659–676.
44. S. Cheng, L. An, Z. Li, S. Liu, J. Lv, S. Fan and T. Zhao, Fuel, 2023, 332, 126031.
45. K. Snavely and B. Subramaniam, Ind. Eng. Chem. Res., 1997, 36, 4413–4420.
46. W. Chen, T. F. Kimpel, Y. Song, F.-K. Chiang, B. Zijlstra, R. Pestman, P. Wang and E. J. M. Hensen, ACS Catal., 2018, 8, 1580–1590.
47. F. Platero, A. Caballero and G. Colón, Fuel, 2023, 340, 127528.
48. L. H. Grey, H.-Y. Nie and M. C. Biesinger, Appl. Surf. Sci., 2024, 653, 159319.
49. T. Zhang, K. Li and J. H. Pan, Prog. Nat. Sci.:Mater. Int., 2019, 29, 679–684.
50. X. Jiang, M. Manawan, T. Feng, R. Qian, T. Zhao, G. Zhou, F. Kong, Q. Wang, S. Dai and J. H. Pan, Catal. Today, 2018, 300, 12–17.
51. Z.-G. Zhang, H. Liu, X.-X. Wang, J. Zhang, F.-B. Zhang, R. Li, M. Yu, S. Ramakrishna and Y.-Z. Long, J. Phys. Chem. Solids, 2019, 133, 117–127.
52. N. Wetchakun, B. Incessungvorn, K. Wetchakun and S. Phanichphant, Mater. Lett., 2012, 82, 195–198.
53. A. C. Nkele, U. K. Chime, L. Asogwa, A. C. Nwanya, U. Nwankwo, K. Ukoba, T. C. Jen, M. Maaza and F. I. Ezema, Inorg. Chem. Commun., 2020, 112, 107705.
54. M. Wang, Y. Q. Ma, X. Sun, B. Q. Geng, M. Z. Wu, G. H. Zheng and Z. X. Dai, Appl. Surf. Sci., 2017, 392, 1078–1087.
55. M. J. Uddin, F. Cesano, A. R. Chowdhury, T. Trad, S. Cravanzola, G. Martra, L. Mino, A. Zecchina and D. Scarano, Front. Mater., 2020, 7, 192.
56. D. Zhou, Z. Ji, X. Jiang, D. R. Dunphy, J. Brinker and A. A. Keller, PLoS One, 2013, 8, e81239.
57. G. Colón, M. C. Hidalgo, G. Munuera, I. Ferino, M. G. Cutrufello and J. A. Navío, Appl. Catal., B, 2006, 63, 45–59.
58. F. Bertella, P. Concepción and A. Martínez, Catal. Today, 2017, 296, 170–180.
59. F. Bertella, P. Concepción and A. Martínez, Catal. Today, 2017, 289, 181–191.
60. R. A. Spurr and H. Myers, Anal. Chem., 1957, 29, 760–762.
61. V. A. Lebedev, D. A. Kozlov, I. V. Kolesnik, A. S. Poluboyarinov, A. E. Becerikli, W. Grünert and A. V. Garshev, Appl. Catal., B, 2016, 195, 39–47.
62. A. M. Pennington, A. I. Okonmah, D. T. Munoz, G. Tsilomelekis and F. E. Celik, J. Phys. Chem. C, 2018, 122, 5093–5104.
63. P. C. Ricci, C. M. Carbonaro, L. Stagi, M. Salis, A. Casu, S. Enzo and F. Delogu, J. Phys. Chem. C, 2013, 117, 7850–7857.
64. B. Tian, F. Chen, J. Zhang and M. Anpo, J. Colloid Interface Sci., 2006, 303, 142–148.
65. M. Lal, P. Sharma and C. Ram, Optik, 2021, 241, 166934.
66. V. Collins-Martínez, A. López Ortiz and A. Aguilar Elguézabal, Int. J. Chem. React. Eng., 2007, 5, A92.
67. C. Scarfiello, K. Soulantica, S. Cayez, A. Durupt, G. Viau, N. Le Breton, A. K. Boudalis, F. Meunier, G. Clet, M. Barreau, D. Salusso, S. Zafeiratos, D. P. Minh and P. Serp, J. Catal., 2023, 428, 115202.
68. W. Li, G. Zhang, X. Jiang, Y. Liu, J. Zhu, F. Ding, Z. Liu, X. Guo and C. Song, ACS Catal., 2019, 9, 2739–2751.
69. I. T. Chashechnikova, V. M. Vorotyntsev, A. V. Gette and G. I. Golodets, React. Kinet., Mech. Catal., 1989, 40, 47–51.
70. J.-C. Dupin, D. Gonbeau, P. Vinatier and A. Levasseur, Phys. Chem. Chem. Phys., 2000, 2, 1319–1324.
71. S. Wendt, R. Schaub, J. Matthiesen, E. K. Vestergaard, E. Wahlström, M. D. Rasmussen, P. Thostrup, L. M. Molina, E. Lægsgaard, I. Stensgaard, B. Hammer and F. Besenbacher, Surf. Sci., 2005, 598, 226–245.
72. Z.-S. Wang, T. Yamaguchi, H. Sugihara and H. Arakawa, Langmuir, 2005, 21, 4272–4276.
73. X. Zhao, X. Liu and C. Ding, J. Biomed. Mater. Res., 2005, 75A, 888–894.
74. L. Ding, M. Li, Y. Zhao, H. Zhang, J. Shang, J. Zhong, H. Sheng, C. Chen and J. Zhao, Appl. Catal., B, 2020, 266, 118634.
75. M. Xue, R. Chitrakar, K. Sakane, T. Hirotsu, K. Ooi, Y. Yoshimura, M. Toba and Q. Feng, J. Colloid Interface Sci., 2006, 298, 535–542.
76. G. W. Simmons and B. C. Beard, J. Phys. Chem., 1987, 91, 1143–1148.
77. J. Cañón and A. V. Teplyakov, Surf. Interface Anal., 2021, 53, 475–481.
78. H. Shin, T.-H. Byun, S. Lee, S.-T. Bae and H. S. Jung, J. Phys. Chem. Solids, 2013, 74, 1136–1142.
79. S. Cravanzola, F. Cesano, F. Gaziano and D. Scarano, Catalysts, 2017, 7, 214.
80. T. L. Nguyen, V. Dinh Quoc, T. L. Nguyen, T. T. T. Le, T. K. Dinh, V. T. Nguyen and P. H. Nguyen, J. Nanomater., 2021, 2021, 8873181.
81. F. Wei, L. Ni and P. Cui, J. Hazard. Mater., 2008, 156, 135–140.
82. D. S. Zingg and D. M. Hercules, J. Phys. Chem. A, 1978, 82, 1992–1995.
83. H. Inokawa, T. Ichikawa and H. Miyaoka, Appl. Catal., A, 2015, 491, 184–188.
84. J. Wei, R. Yao, Q. Ge, D. Xu, C. Fang, J. Zhang, H. Xu and J. Sun, Appl. Catal., B, 2021, 283, 119648.
85. Y. Shao, W. Du, Z. Gao, K. Sun, Z. Zhang, Q. Li, L. Zhang, S. Zhang, Q. Liu and X. Hu, J. Chem. Technol. Biotechnol., 2020, 95, 1337–1347.
86. J. Wang, T. Wang, J. G. Burken, C. C. Chusuei, H. Ban, K. Ladwig and C. P. Huang, Chemosphere, 2008, 72, 381–388.
87. M. Yurdakoç, M. Akçay, Y. Tonbul and K. Yurdakoç, Turk. J. Chem., 1999, 23, 319–328.
88. A. A. Kiss, A. C. Dimian and G. Rothenberg, Adv. Synth. Catal., 2006, 348, 75–81.
89. A. Palčić and V. Valtchev, Appl. Catal., A, 2020, 606, 117795.
90. M. G. Valdés, A. I. Pérez-Cordoves and M. E. Díaz-García, Trends Anal. Chem., 2006, 25, 24–30.
91. M. Guisnet, Catal. Today, 2013, 218–219, 123–134.
92. J. Plana-Pallejà, S. Abelló, C. Berrueco and D. Montané, Appl. Catal., A, 2016, 515, 126–135.
93. G.-S. Shao, F.-Y. Wang, T.-Z. Ren, Y. Liu and Z.-Y. Yuan, Appl. Catal., B, 2009, 92, 61–67.
94. J. Zhang, X. Wang, J. Wang, J. Wang and Z. Ji, Chem. Phys. Lett., 2016, 643, 53–60.
95. T. Yamaguchi, T. Jin and K. Tanabe, J. Phys. Chem. A, 1986, 90, 3148–3152.
96. K. Wijaya, A. R. Putri, S. Sudiono, S. Mulijani, A. Patah, A. C. Wibowo and W. D. Saputri, Catalysts, 2021, 11, 1492.
97. J. L. Cheng, J. Y. Mi, H. Miao, B. S. A. Sharifah Fatanah, S. F. Wong and B. K. Tay, Appl. Nanosci., 2017, 7, 117–124.
98. Y. Shao, X. Hu, Z. Zhang, K. Sun, G. Gao, T. Wei, S. Zhang, S. Hu, J. Xiang and Y. Wang, Green Energy Environ., 2019, 4, 400.
99. M. Hamadanian, A. Reisi-Vanani and A. Majedi, Mater. Chem. Phys., 2009, 116, 376–382.
100. B. A. Morrow, I. A. Cody, L. E. Moran and R. Palepu, J. Catal., 1976, 44, 467–476.
101. L. K. Noda, R. M. d. Almeida, N. S. Gonçalves, L. F. D. Probst and O. Sala, Catal. Today, 2003, 85, 69–74.
102. M. M. Mohamed and M. M. Al-Esaimi, J. Mol. Catal. A: Chem., 2006, 255, 53–61.
103. S. Yamaguchi, M. Yabushita, M. Kim, J. Hirayama, K. Motokura, A. Fukuoka and K. Nakajima, ACS Sustain. Chem. Eng., 2018, 6, 8113–8117.
104. C. A. Emeis, J. Catal., 1993, 141, 347–354.
105. N. A. S. Ramli and N. A. S. Amin, Appl. Catal., B, 2015, 163, 487–498.
106. Y. Yu, J. Zhang, C. Chen, C. He, J. Miao, H. Li and J. Chen, J. Environ. Sci., 2020, 91, 237–245.
107. I. K. van Ravenhorst, A. S. Hoffman, C. Vogt, A. Boubnov, N. Patra, R. Oord, C. Akatay, F. Meirer, S. R. Bare and B. M. Weckhuysen, ACS Catal., 2021, 11, 2956–2967.
108. A. N. Kuznetsov, N. F. Kulish and O. T. Nauk, Metall. Topl., 1959, 4, 52–58.
109. B. Tomić-Tucaković, D. Majstorović, D. Jelić and S. Mentus, Thermochim. Acta, 2012, 541, 15–24.
110. A. M. van der Kraan, R. C. H. Nonnekens, F. Stoop and J. W. Niemantsverdriet, Appl. Catal., 1986, 27, 285–298.
111. Q. Ji, D. Li, J. Hu, P. Gao, G. Hou, Y. Liu and D. Deng, Cell Rep. Phys. Sci., 2024, 5, 101826.
112. M. Russo, V. La Parola, M. L. Testa, G. Pantaleo, A. M. Venezia, R. K. Gupta, A. Bordoloi and R. Bal, Appl. Catal., A, 2020, 600, 117621.
113. G. S. G. de Carvalho, M. M. de Siqueira, M. P. do Nascimento, M. A. L. de Oliveira and G. W. Amarante, Heliyon, 2020, 6, e04128.
114. K. Shimura, T. Miyazawa, T. Hanaoka and S. Hirata, Appl. Catal., A, 2013, 460–461, 8–14.
115. B. Jongsomjit, C. Sakdamnuson and P. Praserthdam, Mater. Chem. Phys., 2005, 89, 395–401.
116. P. Madhusudhan Rao, B. Viswanathan and R. P. Viswanath, J. Mater. Sci., 1995, 30, 4980–4985.
117. P. Gurunathan, P. M. Ette, N. Lakshminarasimhan and K. Ramesha, ACS Omega, 2017, 2, 7647–7657.
118. M. Pudukudy and Z. Yaakob, Chem. Pap., 2014, 68, 1087–1096.
119. S. Marzorati, J. M. Vasconcelos, J. Ding, M. Longhi and P. E. Colavita, J. Mater. Chem. A, 2015, 3, 18920–18927.
120. H. D. Omar and J. Nanotechnol, Adv. Mater., 2015, 3, 57–61.
121. Y. Li, Z. Wang and R. Liu, Nanomaterials, 2021, 11, 834.
122. A. Tavasoli, M. Trépanier, R. M. Malek Abbaslou, A. K. Dalai and N. Abatzoglou, Fuel Process. Technol., 2009, 90, 1486–1494.
123. S. Koutsopoulos, R. Barfod, K. M. Eriksen and R. Fehrmann, J. Alloys Compd., 2017, 725, 1210–1216.
124. N. Nasralla, M. Yeganeh, Y. Astuti, S. Piticharoenphun, N. Shahtahmasebi, A. Kompany, M. Karimipour, B. G. Mendis, N. R. J. Poolton and L. Šiller, Sci. Iran., 2013, 20, 1018–1022.
125. D. J. Duvenhage and N. J. Coville, Appl. Catal., A, 2005, 289, 231–239.
126. K. B. Arcuri, L. H. Schwartz, R. D. Piotrowski and J. B. Butt, J. Catal., 1984, 85, 349–361.
127. A. Keunecke, M. Dossow, V. Dieterich, H. Spliethoff and S. Fendt, Front. Energy Res., 2024, 12, 1344179.
128. J. Yang, W. Ma, D. Chen, A. Holmen and B. H. Davis, Appl. Catal., A, 2014, 470, 250–260.
129. V. A. de la Peña O'Shea, M. C. Álvarez-Galván, J. M. Campos-Martín and J. L. G. Fierro, Appl. Catal., A, 2007, 326, 65–73.
130. M. Boronat and A. Corma, Appl. Catal., A, 2008, 336, 2–10.
131. W. Zhao, L. Liu, X. Niu, X. Yang, J. Sun and Q. Wang, Fuel, 2023, 349, 128703.
132. N. N. Madikizela-Mnqanqeni and N. J. Coville, Appl. Catal., A, 2008, 340, 7–15.
133. Y. Daga and A. C. Kizilkaya, Catalysts, 2022, 12, 425.
134. W. Ma, G. Jacobs, G. A. Thomas, W. D. Shafer, D. E. Sparks, H. H. Hamdeh and B. H. Davis, ACS Catal., 2015, 5, 3124–3136.
135. G. N. Shao, R. Sheikh, A. Hilonga, J. E. Lee, Y.-H. Park and H. T. Kim, Chem. Eng. J., 2013, 215–216, 600–607.
136. F. Jiang, Z. Zheng, Z. Xu, S. Zheng, Z. Guo and L. Chen, J. Hazard. Mater., 2006, 134, 94–103.
137. J. M. H. Enríquez, L. A. C. Lajas, R. G. Alamilla, P. G. Alamilla, E. B. Handy, G. C. Galindo and L. A. G. Serrano, Open J. Met., 2013, 3, 34–44.
138. L. Sineva, V. Mordkovich, E. Asalieva and V. Smirnova, Reactions, 2023, 4, 359–380.
139. T. Li, S. Wang, Z. Sun, Y. Wang, J. Su, Y. Lv, L. Zhang, Z. Tao and Y. Yang, ACS Omega, 2024, 9, 36741–36750.
140. X. Liu, A. Hamasaki, T. Honma and M. Tokunaga, Catal. Today, 2011, 175, 494–503.
141. M. Arslan, S. Bepari, R. Abrokwah, N. Mohammad, J. Shajahan and D. Kuila, Top. Catal., 2023, 66, 477–497.

---

Footnote

† Electronic supplementary information (ESI) available: Materials synthesis methods, analysis of XRD data, calibration for volumetric titrations, X-ray photoelectron spectroscopy of TiO₂, elemental composition determination, CO consumption rate calculations, FESEM results, and time-on-stream performance. See DOI: https://doi.org/10.1039/d5ta03026a

---