Boosting the capacity of Mg-stabilized Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ cathodes via particle size control in an emulsion-based synthesis route

Abstract

In this work, the production of ultra-high efficient Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ cathodes synthesized via an emulsion-based organic synthesis route, along with a comprehensive atomic-scale characterization using advanced electron microscopy techniques, is presented. It is demonstrated that increasing the ratio of the surfactant to hydrophobic and hydrophilic components in the emulsion leads to optimized particle size and a significantly more uniform particle size distribution. As a result Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ exhibits superior electrochemical performance, delivering an initial discharge capacity of 260 mA h g⁻¹ and maintaining a discharge capacity of 170 mA h g⁻¹ after 100 cycles, with 99% coulombic efficiency. This enhancement is attributed to the synergistic effect of Mg-induced structural stabilization and the optimization of particle size and distribution. These factors collectively facilitate the accommodation of strain induced by repeated charge–discharge cycles without substantial structural degradation while preserving efficient sodium de-intercalation pathways.

---

Introduction

Energy storage systems based on electrochemical methods are considered a solution to the challenges posed by the highly sought transition away from fossil fuels. Since their development and commercialization in the 1990s, rechargeable lithium-ion batteries (LIBs) have revolutionized the field of portable electronics and played a significant role in the early development of electric vehicles. However, LIBs still face major challenges, including insufficient energy density for the full electrification of automobiles and issues related to the scarcity, cost, and geographic distribution of raw materials.^1,2

Sodium-ion batteries (SIBs) are regarded as promising candidates for large-scale energy storage due to the natural abundance and low cost of sodium, as well as their operational similarities to LIBs.^3,4 Among the most extensively studied cathode materials for SIBs are Prussian blue analogues, polyanionic compounds, and transition metal oxides (TMOs).⁵ The latter are particularly interesting due to their high theoretical specific capacities, especially those with a P2-type or O3-type structure, where “P” and “O” refer to the prismatic and octahedral coordination of Na, respectively, and “2” or “3” indicates the repeating sequence in the stacking order of the oxygen layers.^6,7

The layered P2-type compound Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ has attracted attention due to its greater atmospheric stability and high specific capacity.^8,9 However, the results reported so far remain suboptimal and further research is warranted. This is primarily due to a detrimental phase transition that occurs during charging, in which the material transforms from its original P2 structure to an O2-type structure, due to the sliding of TMO layers when Na⁺ is extracted.^10,11 This transition hinders the accommodation of Na⁺ ions during discharge and leads to volume changes which induce excessive internal stress, potentially causing mechanical failure of the cathode. Additionally, the structure suffers from irreversible oxygen loss at voltages above 4 V, resulting in capacity fading, voltage drop, and consequently, a rapid decline in energy density.¹²

The other stable polymorphic phase that this compound can exhibit is O3. Its main advantage is that, unlike P2, it is not sodium-deficient, resulting in a significantly higher specific capacity.^13,14 However, it has lower atmospheric stability and reduced structural stability, as it undergoes detrimental phase transitions during the charging process.¹⁵ Additionally, the higher sodium content leads to more abrupt volume changes, which generate mechanical stress and, eventually, the formation of microcracks that contribute to cathode degradation.¹⁶

It has been suggested that magnesium doping can offer an effective strategy to improve the structural stability of this material.^17–19 The smaller ionic radius of Mg²⁺ favours the stabilization of the structure and may also form high-density precipitates on the alkali metal layer during high voltage cycling, which can further improve the mechanical strength of the cathode and inhibit crack formation during Na⁺ intercalation processes.²⁰ The use of Mg as a doping agent has been previously explored in similar systems.^12,21 It has been shown that Mg, by substituting Mn in the TM layers, helps mitigate oxygen loss and enhances structural stability. Multi-element doping²² not only retains the benefits of each dopant but also minimizes their respective drawbacks, allowing greater flexibility in tuning the crystal and electronic structures of cathode materials. For this reason, Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ has been studied in this work.

Together with doping, another strategy to stabilise the Na-TMO structure and achieve higher capacities involves particle size control.^23–27 It is considered that a small particle size improves the insertion and extraction kinetics of sodium ions due to a higher surface-to-volume ratio, providing superior initial specific capacity. On the other hand, larger particles are better able to accommodate volume variations associated with lattice parameter changes during charge and discharge cycles, providing better structural stability and greater long-term capacity retention. However, if the particle size is too large, the volumetric changes will not be uniform due to the greater inefficiency in sodium insertion and extraction, leading to cracking and mechanical fatigue. Therefore, possible design strategies should also aim at achieving an optimal particle size, where all aspects are balanced.²⁸

In this sense, emulsion-based synthesis methods provide an effective way for obtaining materials with improved morphology control.^29,30 Microemulsions are systems composed of a mixture of hydrophilic and hydrophobic fluids, stabilized by surfactants to form a thermodynamically stable and isotropic dispersion. When the hydrophobic component constitutes the majority of the system, droplets of the hydrophilic liquid become encapsulated by surfactants, known as reverse micelles, forming nanovessels that permit the synthesis of various nanoparticles.^31,32

While understanding the exact effect that the balance of hydrophobic, hydrophilic and surfactant components has in particular micellar systems is relatively complicated, it is known that varying many factors, such as the nature of solvents, size of the polar headgroup, chain length of the surfactant or temperature, among many others, makes it possible to fine-tune the composition of the microemulsion and hence the size and structure of the reverse micelle^33,34 and, ultimately, the size of the nanoparticles.

Considering all the factors disclosed above, in this work, we have used a variant developed by our research group³⁵ of the emulsion-based method described by F. J. Garcia-Garcia et al.³⁶ This modified method has several advantages over the more conventional ones such as hydrothermal, sol–gel or dry-milling methods: (i) it uses organic precursors, which lead to the production of non-contaminant reaction side-products; (ii) this method has been proven to be faster than conventional dry-milling or sol–gel methods, since the mixing times required to obtain the pre-heat-treatment mixture of oxides is drastically reduced to 5 minutes with the use of a shear mixer, from the extended times ranging from 90 minutes to several hours required in conventional methods such as dry-milling or sol–gel, and (iii) it holds a broad potential for upscaling to industrial levels. More importantly, we show that the size and distribution of Mg-doped Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ particles can be modified by varying the hydrophobic : hydrophilic : surfactant component ratio, leading to an optimum value, which provides first charge capacities very close to the maximum theoretical capacity of Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ and excellent capacity retention up to 100 cycles, related to the structural stability achieved by both doping and optimisation of the particle size and distribution.

The process involves the use of a nonpolar organic liquid that is not miscible with water. In this case, vaseline oil was chosen as it has no known health concerns compared with industrial mineral oils. Since the metal ions used to fabricate Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ have a hydrophilic nature, they can be dissolved in water. Additionally, oleic acid is used as a surfactant, due to its amphipathic nature. It consists of relatively long carbon chains, with a hydrophilic end and a hydrophobic end. When the surfactant is added at a given concentration, reverse micelles are formed. In these micelles, the non-polar ends preferentially orient themselves towards the exterior, while the polar ends point towards the interior of the reverse micelle, in contact with the water containing the metal ions in solution. These micelles act as the foundation for a microemulsion, which is further heat-treated to remove the organic components and ultimately achieve the final Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ particles. Since the size and stability of the reversed micelles formed in the microemulsion will have a direct impact on the final size of the synthesised particles, in this work, we have investigated the effect of varying the concentrations of water, vaseline oil and oleic acid on the size, size distribution, morphology, structure and electrochemical properties of Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ particles.

Materials and methods

Synthesis

Stoichiometric amounts of Na(OCOCH₃)·3H₂O, Mg(OCOCH₃)₂·4H₂O, Ni(OCOCH₃)₂·4H₂O and Mn(OCOCH₃)₂·4H₂O from Sigma Aldrich were mixed with distilled water, oleic acid (Sigma Aldrich, 90%) and vaseline oil (ITW Reagents) in varying proportions inside a Teflon container. The quantities used for each synthesis are summarised in Table 1, which correspond to a synthesis with a high hydrophobic component content (HV), a synthesis with a high-water content (HW), a synthesis with a high oleic acid content (HO), and a final sample synthesised with standard quantities already reported in the literature (ST).³⁶ The mixtures were processed for 5 minutes using a shear mixer operating at 15 000 rpm. To avoid potential decomposition, the resulting emulsion was poured immediately after mixing into an alumina crucible and placed inside an oven with a heating ramp of 5 °C min⁻¹ with a target temperature of 900 °C. It is worth noting that, during the heating ramp, at a temperature of approximately 100 °C, all the H₂O and OH groups were eliminated, and at approximately 450 °C the calcination of the undesired organic groups took place. Finally, once the temperature of 900 °C was reached, the product was left inside the oven for 10 hours and allowed to cool down to room temperature.

Table 1 Mass of the precursors (in grams) used for the synthesis of different samples

Sample	Na Ac	Ni Ac	Mg Ac	Mn Ac	H2O	Oleic acid	Vaseline oil
ST	2.33	1.64	0.32	4.02	5	7	14
HV					5	7	32
HW					32	7	14
HO					5	32	14

---

Electrochemical characterisation

The electrode preparation consisted of mixing the active material (80 wt%), carbon black (10 wt%), and PVDF (polyvinylidene fluoride) (10 wt%) in N-methyl-2-pyrrolidone (Aldrich, 99.5%) to form a homogeneous slurry. This paste was coated on an aluminium current collector and vacuum dried at 120 °C for a minimum of 2 hours to obtain a working electrode loaded with ca. 2.5 mg cm⁻² active material.

The cell assembly was completed using coin-type cells 2032 in an argon-filled Vigor glove box under controlled O₂ and H₂O traces (< 0.1 ppm). For the sodium-ion half-cells, the counter electrode consisted of a metallic sodium disk (Goodfellow, 99.8%). The electrolyte was a 1 mol L⁻¹ solution of NaPF₆ (Aldrich, >99%) and diethylene glycol dimethyl ether (Sigma-Aldrich, 99.7%) as a solvent. Glass fibre disks (GF/A-Whatman) were soaked in this ion-conducting solution and used as separators between electrodes in the half-cell. The electrochemical characterisation of half-cells was conducted on an Ivium-n-Stat battery test system.

Materials characterisation

To study the crystallinity and purity of the samples, X-ray diffraction (XRD) was employed. XRD patterns were scanned at 0.02° s⁻¹ between 10 and 70° (2θ degree) on a Bruker D8 Discover A25 diffractometer equipped with Cu K radiation and a graphite monochromator. Rietveld refinements were performed using the Topas-32v6 software.

To analyse the chemical composition of the samples, wavelength dispersive X-ray fluorescence (XRF) experiments were performed on a Zetium spectrometer equipped with a Rh tube.

To assess the morphology and average size of the synthesized particles, scanning-electron microscopy (SEM) experiments were carried out using a FEI Teneo SEM.

For the analysis of the nanostructure via transmission electron microscopy (TEM) and related techniques, the TEM samples were prepared by dispersing the particles in ethanol, followed by sonication, and drop casting on lacey carbon copper grids. Scanning-transmission electron microscopy (STEM) and energy dispersive X-ray spectroscopy (EDX) were performed using an FEI Talos F200S microscope operating at an accelerating voltage of 200 keV. Further STEM analyses with atomic resolution were carried out using aberration corrected (S)TEM FEI Titan Cubed Themis 60-300 and JEOL ARM200F microscopes and a dedicated Nion UltraSTEM200, all operating at 200 kV. In order to minimize damage and correct for drift and scan distortions, sequences of fast STEM images were recorded and subsequently aligned and averaged using a non-rigid registration algorithm.³⁷ Low-dose integrated differential phase contrast (iDPC) experiments were also performed on the FEI Titan Cubed Themis 60-300 since it is equipped with a four-quadrant segmented detector.

Results and discussion

Fig. 1a shows the XRD patterns of Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ (ST, HO, HW and HV) powder samples. Rietveld refinement (see Section 1 of the ESI†) for figures of merit, unit cell parameters and phase fractions) reveals that all samples primarily crystallize in a hexagonal P2-type phase with space group P6₃/mmc (PDF 04-009-8579) according to the indexed major peaks, indicating that Mg doping does not change the P2 structure of Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ (Table S1†). Smaller amounts of the rhombohedral O3-type phase (PDF 04-016-7123), with space group R3̄m are also present. This was further confirmed via high-resolution STEM (Fig. S4†).

Fig. 1 (a) Rietveld-refined XRD spectra of the Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ particles synthesized using standard conditions (ST), high-vaseline content (HV), high-water content (HW) and high-oleic acid content (HO). At the bottom, simulated spectra of the P2 and O3 crystal structures are presented. (b) Ex situ XRD patterns of the ST, HV, HW and HO samples after full charge and subsequent discharge. At the bottom, simulated spectra of the P2, O3 and O2 crystal structures are presented.

To verify the stabilizing effect of magnesium on the P2 structure, additional XRD patterns were collected after the first charge and during the first discharge (Fig. 1b). Although reflections corresponding to the O2 structure are observed in all cases, it is evident that the P2 (and O3) structure remained predominant during both charge and discharge. This confirms the role of Mg in mitigating the detrimental P2-to-O2 phase transition.

To verify the chemical composition of the particles synthesised via the organic route, XRF measurements were performed (Table S2†). In all cases, the measured values agree well with the expected compositions, considering the instrumental error (5% for Na, Mn, and Ni and 10% for Mg). The homogeneity of the elemental distribution within the particles was assessed using EDX mapping in STEM mode (Fig. S1†).

Secondary electron SEM was used to inspect the size and topography of the fabricated Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂. It can be seen from Fig. 2 that most of the particles have a flat hexagonal pyramid-like shape with edges containing steps due to the laminar structure. A statistical analysis of the particle size distribution (histograms, Fig. S2,† and methodology can be found in Section 3 of the ESI†) allowed us to draw some preliminary conclusions: in the case of the HV sample, a bimodal particle distribution is observed, with more than 70% of the particles having a nanometric size (Fig. 2b), with average values for the longest axis of 205 ± 60 nm, and the rest being much larger, with average values for the longest axis of 2.4 ± 0.9 μm. The HW sample (Fig. 2b) exhibits a similar bimodal behaviour, with average values of 198 ± 60 nm and 2.1 ± 1.0 μm. However, the number of nanometric particles decreases noticeably, and they become less frequently observed in the SEM images.

Fig. 2 SEM micrographs of the Na_0.67Ni_0,27Mg_0,06Mn_0.66O₂ particles synthesized using (a) standard conditions (ST), (b) high-vaseline content (HV), (c) high-water content (HW) and (d) high-oleic acid content (HO).

However, for high concentrations of oleic acid (sample HO, Fig. 2d) a reduction in the average size of particles is observed, together with a much more homogeneous size distribution, following a Gaussian-type curve, with an average value of 1.6 ± 0.7 μm. This difference in particle size and distribution can be attributed to the stabilizing effect that an increased oleic acid concentration has on reverse micellar systems.^38,39 An insufficient concentration of oleic acid (HW and HV) leads to an unstable emulsion, resulting in a separation between the micellar system and water containing dissolved ions, eventually leading to the uncontrolled formation of particles with highly varied sizes. However, the high surfactant concentration in the HO sample results in a microemulsion with much more stable micelles. Although the final particle size is larger than that expected for reverse micelles, this can be attributed to the fact that, during the calcination stage, the surfactant molecules evaporate, and the primary particles that nucleated begin to form union necks between them, which over time lead to the formation of larger particles. However, this size is more uniform, as the greater stability of the emulsion results in a higher similarity in the size and dispersion of the reverse micelles in the microemulsion. This, in turn, ensures that the nucleation of primary particles occurs with equal probability throughout the emulsion and that their growth proceeds at similar rates during the subsequent holding stage at 900 °C.

More importantly, it is confirmed that this difference in particle size distribution has a significant impact on the electrochemical behaviour of the synthesized samples. Fig. 3 shows typical charge and discharge profiles of ST- (Fig. 3a), HV- (Fig. 3b), HW- (Fig. 3c) and HO-Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ (Fig. 3d), respectively, in the voltage window from 2.0 to 4.2 V at 50 mA g⁻¹ in the first cycle. The samples exhibit the first charge capacity of 220 (ST), 219 (HV), 274 (HW) and 323 (HO) mAh g⁻¹. Fig. 3e shows the retention capacity profiles of the samples. It can be observed that the HO sample presents the best retention capacity after 100 cycles, with discharge values of 170 mA h g⁻¹ and a coulombic efficiency of 99%. Rate capability tests were performed cycling between 2 V and 4.4 V vs. Na⁺/Na for kinetics from 0.5 to 10C and returning to 0.5C, as shown in Fig. 3f. All samples show good capacity and capacity retention even at high kinetics such as 10C with a capacity of around 50 mA h g⁻¹, the HO sample showing the best performance at different current densities. When the charge and discharge current densities are reduced from 10C to 0.5C, (1C = 100 mA g⁻¹) the capacity can recover almost 100%, which is a further indication that Mg doping can stabilize the structure of P2-type. Finally, Fig. 3 also shows the cyclic voltammetry curves for the cathodes labelled as ST (Fig. 3g), HV (Fig. 3h), HW (Fig. 3i), and HO (Fig. 3j) at a scan rate of 0.1 mV s⁻¹. All samples exhibit anodic and cathodic bands attributable to the redox couples involved in the process during cycling. At lower voltages, the redox couples located at 2.77/2.67 V (ST), 2.39/2.23 V (HV), 2.39/2.26 V (HW), and 2.38/2.22 V (HO) correspond to the Mn⁴⁺/Mn³⁺ redox process. Additionally, in the voltage range between 3 and 4 V, all cathodes present redox pairs that could be attributed to the Ni²⁺/Ni³⁺ transition. A third contribution is observed at approximately 4.4 V, which could be assigned to oxygen redox couples. These cyclic voltammetry results are consistent with the plateau observed in the corresponding galvanostatic curves.

Fig. 3 Galvanostatic first charge/discharge curve of the (a) ST, (b) HV, (c) HW and (d) HO samples. (e) and (f) Retention capacity profiles over 100 cycles and the rate performance at room temperature of the four samples. (g)–(j) Cyclic voltammograms obtained in the 2–4.4 V potential window with a scan rate of 0.1 mV s⁻¹ of cathodes ST, HV, HW and HO, respectively.

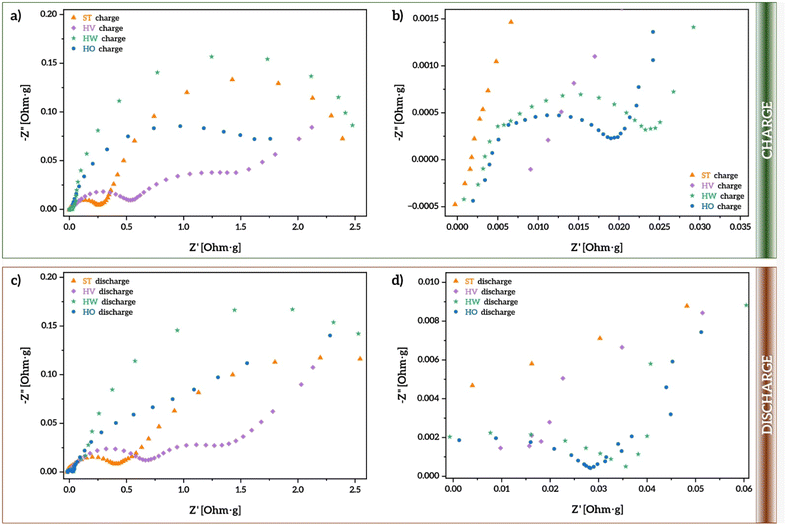
To analyze the impact of the average size and distribution of the particles promoted by the use of different oleic acid–vaseline oil–water ratios on the resistance at the electrode–electrolyte interface during half-cell operation, electrochemical impedance spectroscopy (EIS) spectra were recorded between 1 mHz and 1 MHz, and plotted as Nyquist diagrams (Fig. 4a and c) after the first charge and first discharge, respectively.

Fig. 4 Impedance spectra, represented as Nyquist plots, recorded on ST, HV, HW and HO electrodes subject to (a) the first charge and (c) the first discharge. (b) and (d) display, for clarification, the amplified region corresponding to high frequencies in (a) and (c), respectively.

Their spectra profiles highlight two characteristic semicircles, from which it is possible to directly compare the internal resistances at the electrolyte, the surface layer, and charge-transfer reaction at the electrode/electrolyte interphase. The latter two values are meant to provide information about the kinetic barrier imposed at the electrode interphase. Their spectral profiles also highlight the presence of the Warburg element in series with the charge-transfer resistance, since it is known that these two processes often occur in sequence. In other words, the Na⁺ ions first undergo a charge transfer at the interface, which is followed by the diffusion of the ions into the bulk electrode material. Therefore, the Warburg element would represent the impedance due to Na⁺ ion diffusion. In layered oxides, where diffusion is a critical process, this is important, since Na⁺ ions might need to migrate through interlayer spaces, which could be slow at low frequencies.

From the spectra in Fig. 4, it is evident that all samples present the same electrochemical mechanisms for the charge/discharge. This is somehow expected considering that all have the exact same composition and fabrication methodology. Thus, the main difference among them is in different resistances, which are related to size, in agreement with Fig. 3a–d in which different capacities are obtained. For instance, both charge and discharge spectral profiles revealed that the sample labeled as HV has the highest resistance values, suggesting that the whole process is limited by the internal impedance of the cell. This is in agreement with the predominant faradaic diffusion contribution. This higher resistance is also evidenced by the slightly lower capacitance values obtained for the HV sample in both long cycling and C-rate (Fig. 3e and f).

In contrast, the results clearly show lower resistance values for the HO sample, which was obtained by using a relatively high concentration of surfactant, confirming the reliability of this ratio together with this synthetic procedure to build optimized electro interphases for sodium migration.

Although all samples exhibit considerable capacities, coulombic efficiencies, and retention capabilities due to the stabilizing role of Mg, the HO sample stands out with remarkably high capacities (see Table S3 in the ESI† for a comparison with previously reported results on Mg-doped Na-TMOs). The only difference evident among all samples is the particle size and distribution. The observed trend is that both the average size of the larger particles and the number of smaller particles, which appear to be less electrochemically active, increase at lower oleic acid concentrations. This could explain the difference in specific capacity among various samples. Additionally, to further isolate the effect of particle size on the electrochemical performance of the samples, a Na_0.67Ni_0.27Mg_0,06Mn_0.66O₂ sample was synthesized via a conventional dry milling route for comparison (see the discussion in Section 4 of the ESI†). This conventionally synthesized sample also exhibits a predominantly P2-type structure and a homogeneous elemental distribution comparable to those obtained through our organic synthetic route. However, it presents a larger particle size, with an average value of 3.0 ± 1.1 μm. This result is consistent with the observed trend in which a larger average particle size leads to lower capacities during the first charge and discharge cycles.

It can be therefore concluded that in the HO sample more optimal particle size and size distribution have been achieved—large enough to accommodate the stresses associated with lattice parameter changes during charge and discharge cycles, yet small enough to enable easy and efficient pathways for sodium ion insertion and extraction. To corroborate this hypothesis, more in-depth studies were conducted on the atomic- and nanometric-scale behaviour of the HO sample in different charge states using aberration-corrected STEM techniques.

It is well known that the main mechanisms of capacity loss and, ultimately, structural failure in layered Na-TMOs include the above-mentioned phase transitions, induced by layer gliding, surface restructuring, crack formation, and ion migration to the alkali layers.⁴⁰ The phase transformations, along with the expansion and contraction associated with sodium insertion and extraction, are also responsible for crack formation within the particles.^13,41 Surface restructuring mainly results from interactions between the material and the electrolyte, as well as structural modifications due to oxygen loss.^12,42 Finally, transition metal ions can migrate to nearby layers, occupying Na⁺ vacancies generated during sodium extraction. These transitions are generally irreversible, leading to unexpected capacity loss and structural degradation.⁴³

In order to visualize the structural evolution of the samples with cycling, aberration-corrected STEM measurements were performed on average sized particles of the sample with the best electrochemical properties (HO) and, for comparison, on comparatively larger particles (long axis over 3 μm) of the one synthesized with standard concentrations (ST), both in the pristine state and after the first charge–discharge cycle and 100 charge–discharge cycles. The results are summarized in Fig. 5. In the pristine state, both samples exhibit characteristic stacking of the P2 structure with an ABBA oxygen sequence when observed along the [010] direction (Fig. 5a, e and S4† for all four samples).

Fig. 5 High-resolution STEM image of the HO sample (a) in the pristine state, (b) after 1 cycle and (c) after 100 cycles; of the ST sample (e) in the pristine state, (f) after 1 cycle and (g) after 100 cycles. The inset in (a) represents the P2 modelled structure (transition metals are shown in green, oxygen atoms in red and sodium atoms in yellow). In (d) and (h) are shown low magnification STEM images of the HO and ST particles, respectively, after 100 cycles.

After the first charge cycle, the HO sample (Fig. 5b) retains part of the original P2 structure, although O2 phase domains are observed due to layer slipping during charging, in agreement with the XRD results (Fig. 1b). Additionally, plane bending (∼10°) is observed, attributed to possible electrolyte infiltration, along with a thin surface layer (∼2 nm thick) of disordered rock-salt made of Na-TMOs. These factors likely contribute to the capacity fade observed after the first charge cycle, as they partially block sodium reinsertion by obstructing the channels. In the ST sample, however, this effect is significantly more pronounced (Fig. 4f), where, in addition to a similar plane bending angle, the rock-salt layer is much thicker, around 10 nm.

After 100 charge–discharge cycles, in the HO sample (Fig. 5c), plane bending increases (∼21°), and the thickness of the disordered rock-salt layer grows to approximately 5 nm. Remarkably, however, the material still maintains a layered structure in the bulk. In contrast, in the STEM-visible regions of the ST sample particles (Fig. 5g), a complete transformation into a rock-salt structure has occurred, and in the outermost region, the crystalline order has been entirely lost, leading to irreversible cathode degradation in subsequent cycles.

It is therefore evident that in addition to the stabilizing effect of Mg, particle size plays a critical role, as the HO sample can better accommodate the volume changes associated with sodium extraction and reinsertion without undergoing structural damage as severe as that observed in the ST sample.

This was further confirmed at the microscopic level through conventional STEM measurements on both samples. As can be observed, the HO sample (Fig. 5d) maintains its integrity after 100 cycles, although surface damage with crack initiators appears. However, the ST sample (Fig. 5h) suffers catastrophic damage due to crack formation and propagation, leading to particle pulverization.

Finally, to rule out ion migration to the alkaline metal layer in the HO sample, low-dose iDPC measurements were carried out both in the pristine state and at various charge points. This technique yields an image that is directly interpretable as the projected electrostatic potential. The resulting contrast is roughly proportional to the atomic number Z, which drastically improves the detectability of light elements, such as sodium or oxygen, among heavy ones in the same image.⁴⁴ It has been shown that iDPC-STEM images have a higher signal-to-noise ratio than other STEM techniques.⁴⁵ Additionally, much lower beam currents can be used, since effectively all the electrons that reach the detector plane are collected. These last two aspects are critical in materials sensitive to the electron beam, such as charged particles, since it has been demonstrated in other similar systems that structural changes induced by the electron beam are similar to those produced by charge and discharge cycles, leading to erroneous conclusions.^46,47

Fig. 6 shows reconstructed phase images obtained via iDPC of the sample in the pristine state (Fig. 6a), charged at 3.7 V (Fig. 6b), and charged at 4.2 V (Fig. 6c). In all three cases, the contrast within the sodium layer is homogeneous, although it is lower in the sample charged at a higher voltage due to a higher level of desodiation. Higher contrasts that would correspond to the transition metal migration to adjacent alkaline layers are not observed in any case, further confirming the stabilizing role of Mg within the Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ lattice.

Fig. 6 Low-dose iDPC reconstructed phase image of the HO sample in (a) the pristine state and (b) charged at 3.7 V and (c) 4.4 V. The inset in (a) represents the P2 modelled structure (transition metals are shown in green, oxygen atoms in red and sodium atoms in yellow).

Conclusions

In conclusion, we have shown that an easy and ultrafast emulsion-based synthesis route can be used to fabricate Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ with superior electrochemical properties (260 mA h g⁻¹ first discharge and 140 mA h g⁻¹ after 100 cycles and coulombic efficiency of 99% after 100 cycles). Low concentrations of oleic acid, acting as the surfactant, lead to the formation of unstable emulsions and the subsequent nucleation and growth of particles with uncontrolled size. However, an increase in oleic acid content produces much more stable micelles, which are the origin of particles with optimal size and a narrower particle size distribution. Thus, the synergistic combination of the appropriate size and the stabilizing role of Mg results in particles that can better accommodate volumetric variations induced by charge and discharge cycles while also providing channels through which sodium can be easily extracted and intercalated.

Advanced STEM techniques have confirmed that compared to particles synthesized with lower amounts of surfactants, particles synthesized with higher oleic acid content largely retain the P2 structure after the first charge–discharge cycle and are also capable of maintaining the layered structure and structural integrity after 100 cycles. Moreover, no migration of transition metals to the alkali metal layers is observed during the first charge, which could otherwise cause irreversible capacity loss.

Although further investigation is needed to fully understand the exact mechanism that governs the surfactant ratio–micelle stabilization relationship and to determine the optimal proportions, our research represents an important step toward achieving the rational design of Na_0.67Ni_0.27Mg_0.06Mn_0.66O₂ particles for sodium-ion battery cathodes with optimized sizes through a simple, fast, cost-effective, and industrially scalable synthetic route.

Data availability

Data for this article, including scanning/transmission electron microscopy images and electrochemical data are available at idUS https://hdl.handle.net/11441/161680.

Author contributions

Saúl Rubio: investigation, formal analysis, visualization, writing – review and editing; Eva M. Pérez-Soriano: investigation, writing – review and editing; Cristina Arévalo: investigation, formal analysis, visualization, writing – review and editing; Xiaoqiong Du: investigation, writing – review and editing; Xuyun Guo: investigation, writing – review and editing; Francisco J. Garcia-Garcia: conceptualization, writing – review and editing; Isabel Montealegre-Meléndez: investigation, writing – review and editing; Ana M. Beltrán: investigation, writing – review and editing; Valeria Nicolosi: investigation, resources, writing – review and editing; Juan G. Lozano: conceptualization, investigation, formal analysis, funding acquisition, project administration, writing – original draft, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support was provided by the Grant PID 2020-113108RB-I00 funded by MICIU/AEI/10.13039/501100011033 and, as appropriate, by “ERDF A way of making Europe”, by “ERDF/EU”, by the “European Union” or by the “European Union NextGenerationEU/PRTR”. Financial support was also provided by the Grant CNS2022-135432 funded by MICIU/AEI/10.13039/501100011033 and, as appropriate, by “ESF Investing in your future”, by “ESF+” or by “European Union NextGenerationEU/PRTR”. The authors are also grateful to the Universidad de Sevilla for the use of the research facilities at CITIUS. The authors acknowledge the use of (S)TEM instrumentation provided by the Spanish National Facility ELECMI ICTS (“División de Microscopía Electrónica”, Universidad de Cadiz, DME-UCA), the David Cockayne Centre for Electron Microscopy at the Department of Materials, University of Oxford, and the Advanced Microscopy Laboratory at the Centre for Research on Adaptive Nanostructures and Nanodevices, Trinity College Dublin. V. N. X. D. and X. G. wish to thank the support of the Science Foundation Ireland-funded AMBER Research Centre (Grant No. 12/RC/2278_P2) and the Frontiers for the Future award (Grant No. 20/FFP-A/8950). X. D. would like to thank Marie Skłodowska-Curie Actions Grant Agreement No. 101107396. Furthermore, V. N. and X. G. wish to thank the Advanced Microscopy Laboratory in CRANN for provision of their facilities.

References

1. J. M. Tarascon, Nat. Chem., 2010, 2, 510.
2. J. W. Choi and D. Aurbach, Nat. Rev. Mater., 2016, 1, 1–16.
3. C. Delmas, Adv. Energy Mater., 2018, 8, 1703137.
4. J. Y. Hwang, S. T. Myung and Y. K. Sun, Chem. Soc. Rev., 2017, 46, 3529–3614.
5. C. Shi, L. Wang, X. Chen, J. Li, S. Wang, J. Wang and H. Jin, Nanoscale Horiz., 2021, 7, 338–351.
6. C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85.
7. Y. Gupta, P. Siwatch, R. Karwasra, K. Sharma and S. K. Tripathi, Renewable Sustainable Energy Rev., 2024, 192, 114167.
8. J. Y. Hwang, J. Kim, T. Y. Yu and Y. K. Sun, Adv. Energy Mater., 2019, 9, 1803346.
9. Y. E. Zhu, X. Qi, X. Chen, X. Zhou, X. Zhang, J. Wei, Y. Hu and Z. Zhou, J. Mater. Chem. A, 2016, 4, 11103–11109.
10. P. Wang, Y. You, Y. Yin, Y. Wang, L. Wan, L. Gu and Y. Guo, Angew. Chem., 2016, 128, 7571–7575.
11. J. W. Somerville, A. Sobkowiak, N. Tapia-Ruiz, J. Billaud, J. G. Lozano, R. A. House, L. C. Gallington, T. Ericsson, L. Häggström, M. R. Roberts, U. Maitra and P. G. Bruce, Energy Environ. Sci., 2019, 12(7), 2223–2232.
12. U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin, M. A. Pérez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10(3), 288–295.
13. T. Y. Yu, H. H. Ryu, G. Han and Y. K. Sun, Adv. Energy Mater., 2020, 10, 2001609.
14. B. Xiao, X. Liu, M. Song, X. Yang, F. Omenya, S. Feng, V. Sprenkle, K. Amine, G. Xu, X. Li and D. Reed, Nano Energy, 2021, 89, 106371.
15. B. Xiao, Y. Wang, S. Tan, M. Song, X. Li, Y. Zhang, F. Lin, K. S. Han, F. Omenya, K. Amine, X. Q. Yang, D. Reed, Y. Hu, G. L. Xu, E. Hu, X. Li and X. Li, Angew. Chem., Int. Ed., 2021, 60, 8258–8267.
16. G. L. Xu, X. Liu, X. Zhou, C. Zhao, I. Hwang, A. Daali, Z. Yang, Y. Ren, C. J. Sun, Z. Chen, Y. Liu and K. Amine, Nat. Commun., 2022, 13, 436.
17. Q. Mao, Y. Yu, J. Wang, L. Zheng, Z. Wang, Y. Qiu, Y. Hao and X. Liu, J. Mater. Chem. A, 2021, 9, 10803–10811.
18. Q. C. Wang, J. K. Meng, X. Y. Yue, Q. Q. Qiu, Y. Song, X. J. Wu, Z. W. Fu, Y. Y. Xia, Z. Shadike, J. Wu, X. Q. Yang and Y. N. Zhou, J. Am. Chem. Soc., 2019, 141, 840–848.
19. M. Bomio, P. Lavela, R. L. Tranquilin, F. V. da Motta and J. L. Tirado, J. Electroanal. Chem., 2023, 930, 117157.
20. K. Wang, H. Wan, P. Yan, X. Chen, J. Fu, Z. Liu, H. Deng, F. Gao and M. Sui, Adv. Mater., 2019, 31(46), 1904816.
21. R. Klee, S. Rubio, P. Lavela and J. L. Tirado, J. Alloys Compd., 2025, 1020, 179385.
22. C. Cheng, H. Hu, C. Yuan, X. Xia, J. Mao, K. Dai and L. Zhang, Energy Storage Mater., 2022, 52, 10–18.
23. E. J. Kim, R. Tatara, T. Hosaka, K. Kubota, S. Kumakura and S. Komaba, ACS Appl. Energy Mater., 2024, 7, 1015–1026.
24. N. Yabuuchi, K. Kubota, Y. Aoki and S. Komaba, J. Phys. Chem. C, 2016, 120, 875–885.
25. M. L. Kalapsazova, E. N. Zhecheva, G. T. Tyuliev, D. D. Nihtianova, L. Mihaylov and R. K. Stoyanova, J. Phys. Chem. C, 2017, 121, 5931–5940.
26. E. Stura and C. Nicolini, Anal. Chim. Acta, 2006, 568, 57–64.
27. A. Van Bommel and J. R. Dahn, Electrochem. Solid-State Lett., 2010, 13, A62–A64.
28. X. Yang, L. Zhang, G. Liu, G. Pang, D. Wang, M. Li, C. Li, Z. Liao, Q. Li, C. Zhao, J. Liang, P. Yan, K. Wang, B. Xiao and D. Geng, ACS Appl. Mater. Interfaces, 2024, 16, 40805–40813.
29. A. Pan, D. Choi, J. G. Zhang, S. Liang, G. Cao, Z. Nie, B. W. Arey and J. Liu, J. Power Sources, 2011, 196, 3646–3649.
30. Y. Zhang, W. Zhang, M. Li, Z. Yang, G. Chen and Q. Wang, J. Mater. Chem. A, 2013, 1, 14368–14374.
31. L. Abraham, T. Thomas and M. Pichumani, J. Colloid Interface Sci., 2019, 547, 234–244.
32. R. Ranjan, S. Vaidya, P. Thaplyal, M. Qamar, J. Ahmed and A. K. Ganguli, Langmuir, 2009, 25, 6469–6475.
33. K. Kundu and B. K. Paul, Colloids Surf., A, 2013, 433, 154–165.
34. P. A. Penttila, S. Vierros, K. Utriainen, N. Carl, L. Rautkari, M. Sammalkorpi and M. Osterberg, Langmuir, 2019, 35, 8373–8382.
35. F. J. Garcia-Garcia, S. Rubio, X. Du, X. Guo, J. E. de la Rosa-Melian, E. M. Pérez-Soriano, C. Arévalo, I. Montealegre-Meléndez, A. M. Beltrán, V. Nicolosi and J. G. Lozano, Batteries Supercaps, 2025, e202500213.
36. F. J. García-García, R. Klee, P. Lavela, M. R. D. Bomio and J. L. Tirado, ChemElectroChem, 2020, 7, 3528–3534.
37. L. Jones, H. Yang, T. J. Pennycook, M. S. J. Marshall, S. Van Aert, N. D. Browning, M. R. Castell and P. D. Nellist, Adv. Struct. Chem. Imaging, 2015, 1(8), 1–16.
38. S. Sugiura, S. Ichikawa, Y. Sano, M. Nakajima, X. Q. Liu, M. Seki and S. Furusaki, J. Colloid Interface Sci., 2001, 240, 566–572.
39. L. K. Shrestha, M. Dulle, O. Glatter and K. Aramaki, Langmuir, 2010, 26, 7015–7024.
40. S. Xu, L. Zhao, S. Li and S. Guo, Chem. Commun., 2025, 61, 4147.
41. T. Jin, P. F. Wang, Q. C. Wang, K. Zhu, T. Deng, J. Zhang, W. Zhang, X. Q. Yang, L. Jiao and C. Wang, Angew. Chem., Int. Ed., 2020, 59, 14511–14516.
42. P. Yan, J. Zheng, M. Gu, J. Xiao, J. G. Zhang and C. M. Wang, Nat. Commun., 2017, 8, 14101.
43. X. Zhang, S. Guo, P. Liu, Q. Li, S. Xu, Y. Liu, K. Jiang, P. He, M. Chen, P. Wang and H. Zhou, Adv. Energy Mater., 2019, 9, 1900189.
44. I. Lazić, E. G. T. Bosch and S. Lazar, Ultramicroscopy, 2016, 160, 265–280.
45. E. G. T. Bosch and I. Lazić, Ultramicroscopy, 2015, 156, 59–72.
46. P. Lu, P. Yan, E. Romero, E. D. Spoerke, J. G. Zhang and C. M. Wang, Chem. Mater., 2015, 27, 1375–1380.
47. J. Kim, S. Anand, C. Gilgenbach, I. D. Johnson, M. Murphy, T. Chen, M. Moy, A. Penn, J. Cabana, G. Ceder, B. J. Ingram and J. M. LeBeau, Chem. Mater., 2023, 35, 8455–8463.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta02682b

---