 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural chemistry of the n = 3 Dion–Jacobson phases: controlling polarity and band gap†
Areesha
Ali
a,
Vanessa
Cascos
b,
Faith G.
Pritchard
 c,
Jan R. R.
Verlet
c,
Jan R. R.
Verlet
 c,
Nicole R.
Sutherland
a,
Jack
Woolley
c,
Nicole R.
Sutherland
a,
Jack
Woolley
 d,
James
Lloyd-Hughes
d,
James
Lloyd-Hughes
 d,
Maxim
Avdeev
d,
Maxim
Avdeev
 ef,
Andy
Beeby
c,
Stewart J.
Clark
a and
Emma E.
McCabe
ef,
Andy
Beeby
c,
Stewart J.
Clark
a and
Emma E.
McCabe
 *a
*a
aDepartment of Physics, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: emma.mccabe@durham.ac.uk
bCIEMAT, Department of Energy, Av. Complutense 40, Madrid, 28040, Spain
cDepartment of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK
dDepartment of Physics, University of Warwick, Coventry, CV4 7AL, UK
eAustralian Nuclear Science and Technology Organisation, New Illawarra Road, Lucas Heights, NSW 2234, Australia
fSchool of Chemistry, The University of Sydney, Sydney, NSW 2006, Australia
First published on 12th June 2025
Abstract
The Dion–Jacobson phases are increasingly gaining attention for their photoactivity and potential applications as photocatalysts and sensors, in addition to their polar structures. The structure – composition – property relationships for the n = 3 phases (of general formula A′A2B3O10e.g., A′ = Rb, Cs; A = Ca, Sr, Ba; B = Nb, Ta) are not well understood because of the lack of reliable structural models for this series. Our combined experimental and computational study addresses this by determining and explaining the complex structural chemistry of these materials, and provides a guide to allow structures and properties of new materials to be predicted and understood. We find that both A′ and A cations determine the tilts of BO6 octahedra and hence small A2+ ions tend to give materials with larger band gaps. The polar structures observed for A = Ca phases result from “proper” mechanisms and the role of the second-order Jahn–Teller effect of the B = Nb, Ta cations is discussed.
1. Introduction
Advancing photoactive materials for catalysis and optoelectronic applications requires a deep understanding of their electronic structure (band gaps, edge positions, and density of states), and the ability to strategically tune these properties through structural and compositional engineering. Mastering this control unlocks new possibilities for high-performance materials and transformative technologies. Layered perovskite-related materials including the Dion–Jacobson (DJ) phases have attracted attention due to their promise as photocatalysts,1–6 photovoltaics7–9 and X-ray- and photo-detectors.10,11 DJ phases have significant compositional flexibility, attracting interest for a range of properties (including ionic conductivity12 and ferroelectricity,13–15 in addition to their photoactivity), and giving them huge potential to use composition to tune properties. However, efforts to design DJ materials optimised to specific applications are hampered by the lack of a full understanding of the structure–composition–property relationships in these materials.The Dion–Jacobson phases (of general formula A′An−1B2O3n+1) adopt layered, pseudo-tetragonal crystal structures composed of perovskite blocks n layers thick, separated by A′ cation layers (Fig. 1). As in other families of layered perovskites such as the Aurivillius phases, the B cations are often d0 ions (such as Ti4+, Nb5+, Ta5+ ions) and are located in six-coordinate octahedral sites, whilst the larger A cations (e.g., group 2 or lanthanide ions) are in 12-coordinate sites. The A′ cations in DJ phases are typically much larger (e.g. group 1 ions such as Cs+, Rb+ in inorganic systems, or long “spacer” molecular ions in hybrid systems)16 in more weakly-bound eight-coordinate sites (Fig. 1). The parent structure is tetragonal (of P4/mmm symmetry)17,18 and much analysis (both experimental and computational) is carried out assuming this ideal high symmetry (centrosymmetric) structure,1,3,19 in part due to the difficulty of detecting distortions primarily involving light oxide ions by X-ray diffraction. However, the crystal structures of DJ phases can be tuned by changing their composition, taking advantage of both electronic and geometric factors.20 As for other perovskite families, the DJ phases are susceptible to structural distortions involving rotations of the BO6 octahedra about both in-plane and out-of-plane axes, and to in-plane polar and antipolar displacements.13,20–22 These distortions have been explored for the n = 2 systems both experimentally and in computational studies,13,22,23 but there has not yet been a systematic investigation of these distortions for the triple-layer phases, despite their importance as functional materials,3,4,12 making it hard to predict structures and therefore properties. Building on earlier symmetry analysis of the tilts of BO6 octahedra in n = 3 DJ phases,20,21,24 in this combined experimental and computational study we use second-harmonic generation and neutron powder diffraction to determine the crystal structures for some A′A2B3O10 (A′ = Rb, Cs; A = Ca, Sr, Ba; B = Nb, Ta) n = 3 DJ phases. We find that the A cation size plays a significant role (related to the perovskite tolerance factor)25 in inducing tilts of BO6 octahedra, but the nature of these tilts is also influenced by A′ cation size. Comparison of Nb5+ and Ta5+ phases gives an indication of the balance between geometric and electronic factors in stabilising lower-symmetry structures. Our density functional theory (DFT) calculations are consistent with our experimental results and give an indication of the relative energies of these distortions. We show how this understanding of the structures (and in particular, the magnitude of BO6 tilts) explains trends in band gap observed experimentally (in our work and previously reported5,26), and our understanding of polarity may be useful for designing optimised photoactive materials.
2. Methods
Polycrystalline powders of CsA2Nb3O10 (A = Ba, Sr, Ca) and CsCa2Ta3O10 were prepared by solid–state reaction. Stoichiometric amounts of Cs2CO3 (in 30% excess to account for volatility), BaCO3, SrCO3, CaCO3, Nb2O5 and Ta2O5 were thoroughly ground in an agate mortar with acetone and the mixture was pressed into 10 mm diameter pellets. The resulting pellets were placed in an alumina crucible and heated at 550 °C for 12 h. A subsequent heating in air at 1000 °C for 12 h for CsA2Nb3O10 (A = Sr, Ca) and for CsCa2Ta3O10, or 850 °C for 3 h (A = Ba) was carried out. RbA2Nb3O10 (A = Sr, Ca) were prepared similarly using 30% excess of Rb2CO3 with heating at 550 °C for 12 h followed by grinding and reheating at 1000 °C for 12 h. The initial characterization of the samples was carried out by laboratory X-ray powder diffraction (XRD) using a Rigaku Miniflex utilising Cu Kα radiation (40 kV, 15 mA) and a D/teX Ultra detector.Neutron powder diffraction (NPD) data were collected at room temperature at the Echidna High Resolution Powder Diffractometer27 in the Australian Centre for Neutron Scattering (ACNS), with λ = 2.4395 Å and at 1.6215 Å within the 2θ range from 10 to 165°. About 3 g of sample was contained in a vanadium can and data were collected for ∼two hours per scan. Rietveld refinements28 were carried out using the TopasAcademic software.29 A scale factor and background terms were refined, followed by sample zero point and unit cell parameters. One or more profile parameters to describe the diffraction peak shape were refined, alongside the atomic coordinates for the strongest scattering site (as allowed by symmetry). More atomic coordinates were refined (as allowed by symmetry) as well as remaining profile parameters (assuming a pseudo-Voight peak shape) for stable refinements. Finally, atomic displacement parameters were refined in the final stages of the refinements. ISODISTORT was used for symmetry analysis (including exploring group–subgroup relations) and to describe distorted structures in terms of the parent structure with symmetry-adapted distortion modes applied.24,30
Diffuse reflectance spectra were recorded by grinding each sample with dry NaCl (10% w/w) and placing these mixtures in optical cuvettes and illuminating with a deuterium lamp (OceanOptics DH-2000-S). Non-specular scattered light was collected and the spectrum recorded using an OceanOptics spectrometer (Mayer2000 Pro). A cuvette of ground NaCl was used as a reference. The data were used to calculate the reflectance spectra R(I) and Kubelka–Munk spectra F(R).31
Preliminary second harmonic generation (SHG) measurements were carried out at University of Warwick. Hand-ground powders of each sample (of a wide range of particle sizes) were sealed between glass microscope slides and irradiated with an 800 nm laser and the SHG signal (400 nm) was detected using a photomultiplier tube (PMT), with filters to remove the fundamental. Using the Kurz and Perry powder technique,32 further SHG measurements were carried out in Durham using powders of each sample that were sieved into different particle sizes and then placed into (GPE Secure 55) NMR tubes. While SHG is highly symmetry-dependent, the ISHG efficiency of powders also depends on the particle size and if the particle size is not optimised, a false-negative result may be obtained. Powders were ground into bands of 38–45, 53–65, 65–75, 75–90 & 90–106 μm. A pulsed carbide laser generates the 1028 nm fundamental light at a rate of 150 Hz, with a pulse width of ∼250 fs and this was used to irradiate the samples. The laser (0.2–9.5 mW) passed through a dichroic mirror and was then loosely focused on the sample using a parabolic mirror. The reflected second harmonic light (514 nm) was (again, loosely) collimated by the parabolic mirror, then reflected by the dichroic mirror back to a convex lens and focused to a system of filters to separate out remaining 1028 nm light. An amplified (10 dB) photodiode was used initially to establish SHG activity for each sample relative to a potassium dihydrogen phosphate (KDP) reference, as photodiodes have a large linear dynamic range. A photomultiplier tube (PMT) was used (due to its better sensitivity) to characterise the quadratic relationship between ISHG and laser power for each sample, which confirms that the detected signal was due to a two-photon process. The signal was monitored on an oscilloscope. SHG efficiency below 0.5% KDP are generally characteristic of centrosymmetric materials with quadrupolar interactions, and so this is used as a threshold to avoid false-positive conclusions.32
Electronic structure calculations were performed within the ab initio density functional, plane-wave, pseudo-potential formalism as implemented in the Castep code.33 The electronic wave functions are expanded in a plane wave basis set up to a kinetic energy cut off of ≥1000 eV. Integrations of the Brillouin zone were done with a k-point sampling scheme where the k-points are spaced at 0.05 Å−1. We find this converges total energy differences to greater than 0.5 meV per atom. Our standard DFT calculations use the PBE exchange–correlation functional,34 chosen for its balance between accuracy and computational efficiency making it a widely used choice for DFT calculations. Electron–ion interactions are described using ab initio ultra-soft pseudopotentials based on Vanderbilt′s formalism35 also generated with the PBE functional for consistency. The pseudo-potentials treat some of the semicore states as valence, which is important to obtain accurate electronic structures. In particular, this includes the 5s, 5p and 6s states for Cs; the 4s, 4p and 5s states for Rb; the 3s, 3p and 4s states for Ca; the 4s, 4p and 5s states for Sr; the 5s, 5p and 6s states for Ba; the 4s, 4p, 4d and 5s states for Nb; the 4f, 5s, 5p, 5d and 6s states for Ta, and the 2s and 2p states for O.
3. Results & discussion
3.1 Second harmonic generation tests for A′A2B3O10
Preliminary SHG measurements carried out on hand-ground powder samples containing particles of a range of sizes which suggested some SHG activity for CsCa2B3O10 (B = Nb, Ta) samples (see ESI†). Where ISHG is not tested over multiple particle sizes, only a positive result is conclusive, so the samples were investigated further. Different particle size ranges were tested for the optimum efficiency, and the optimum available particle size for each sample was then used to qualify samples as SHG active (resulting from a non-centrosymmetric structure). The threshold chosen was <0.5% KDP, below which is considered a negative result.36–38 This is in line with contributions from quadrupolar effects or surface contributions measured in related perovskite materials,38 more general estimates of the surface contribution,37 and our own measurements of centrosymmetric NaCl powder (Fig. 2). The photodiode-measured SHG response to a KDP reference is shown in Fig. 2a (left hand axis). On the right axis, the SHG response measured for CsA2B3O10 (A = Ca, Sr, Ba; B = Nb, Ta) samples is shown. All samples showed a quadratic relationship with laser power, suggesting the detected light arose from a two-photon process. ISHG measurements using a PMT (Fig. 2b) revealed moderate SHG activity (>1% that of KDP) for CsCa2Nb3O10 and for RbCa2Nb3O10, weak SHG activity (>0.5% that of KDP) for CsCa2Ta3O10 and negligible SHG activity (comparable to NaCl powder) for <45 μm CsSr2Nb3O10, RbSr2Nb3O10 and CsBa2Nb3O10 (though it was not possible to do a full particle size study for these samples).3.2 Structure refinements for A′A2B3O10
• Rotations of BO6 octahedra about the long axis (Fig. 1b):
- Rotations in adjacent blocks in-phase with one another; described by M3+ irrep (k = ½ ½ 0); symmetry lowered to P4/mbm (note that rotations of B(1)O6 and B(2)O6 octahedra within each block are not constrained to be either in-phase or out-of-phase), Fig. 1b;
- Rotations in adjacent blocks out-of-phase with one another; described by A3+ irrep (k = ½ ½ 0); symmetry lowered to I4/mcm (note that rotations of B(1)O6 and B(2)O6 octahedra within each block are not constrained to be either in-phase or out-of-phase), Fig. 1b;
• Rotations of BO6 octahedra about in-plane axes (Fig. 1c):
- Out-of-phase tilts with tilts in adjacent blocks in-phase with one-another ((a−a−c0) (a−a−c0)); described by M5+ irrep (k = ½ ½ 0); symmetry lowered to Pbmn (cab setting of space group 53, Pmna), Fig. 1c;
- Out-of-phase tilts with tilts in adjacent blocks out-of-phase with one-another ((a−a−c0)–(a−a−c0)); described by A5+ irrep (k = ½ ½ ½); symmetry lowered to Icmm (![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) ba setting of space group 74, Imma), Fig. 1c;
ba setting of space group 74, Imma), Fig. 1c;
- In-phase tilts with tilts in adjacent blocks in-phase with one-another ((a+b+c0) (a+b+c0)); described by X3+ irrep (k = 0 ½ 0); symmetry lowered to Pmmn, Fig. 1c;
• In-plane polar displacements (Fig. 1d):
- Polar displacement along [110] direction of the parent P4/mmm unit cell; described by Γ5− irrep (k = 0 0 0); symmetry lowered to C2mm (![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) ba setting of space group 38, Amm2), Fig. 1d;
ba setting of space group 38, Amm2), Fig. 1d;
As indicated in Fig. 1, we can expect that structural distortions in these DJ phases primarily involve shifts in the oxide positions. However these are very hard (or even impossible) to detect using X-ray powder diffraction (XRPD) for which the scattering of light oxide ions is very weak compared with that of the heavier Rb, Cs, Nb and Ta ions which will dominate the X-ray scattering. XRPD is perhaps the most accessible technique for routine structural characterisation of samples and so most of the phases reported in our study (and closely-related materials) have been reported to adopt the ideal aristotype P4/mmm structure.6,39–42
An early single crystal X-ray diffraction study on CsCa2Nb3O10 indicated a large orthorhombic cell and reported a structure18 very similar to ours determined from NPD analysis (Section 3.2.4), highlighting the advantages of single crystal diffraction over powder, if suitable single crystals are available. A combined computational and experimental study using ssNMR on RbSr2Nb3O10 indicated the P4/mbm model (consistent with ours, Section 3.2.6)43 but there has not been a wider consideration of these structures and the distortions observed to identify structural trends within this family. More recent studies have included phases with smaller A cations as well as ns2 cations and give glimpses of the complex structural chemistry of the n = 3 DJ phases.26,42,44,45 This has motivated our study to explore the structural chemistry of these materials, to understand how it relates to their physical properties, and to identify structural trends to allow structures and therefore properties of n = 3 DJ phases to be predicted.
NPD data for all other phases considered here could not be fitted satisfactorily by the high symmetry P4/mmm model: extra peaks were observed in NPD data indicating larger unit cells, and/or intensities were not well fitted and the models were unphysical (with very distorted polyhedral, and unphysical atomic displacement parameters). This highlights the challenges of structural characterisation using XRPD data40–42 for these perovskite-related materials for which many distortions involve displacements of the light oxide ions (which give relatively weaker scattering of X-rays compared with the heavier cations present). Lower symmetry models allowing rotations of BO6 octahedra were therefore considered to fit our NPD data for all other samples.
Although the hypothetical “SrNbO3” perovskite blocks in CsSr2Nb3O10 again have tolerance factor close to 1 (t = 0.99), the decrease as Ba2+ is replaced by smaller Sr2+ (12-coordinate ionic radii of 1.44 Å and 1.61 Å for Sr2+ and Ba2+, respectively)46 is sufficient to stabilise rotations of the NbO6 octahedra about this out-of-plane axis. Presumably this occurs to optimise bonding within the perovskite layers, and it results in a significant reduction of the in-plane unit cell parameter (3.97705(5) Å for CsBa2Nb3O10 compared with 3.90786(6) Å for CsSr2Nb3O10 (normalised by dividing by √2 for comparison with the P4/mmm model)).
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) b setting of space group 62),18 and so is equivalent to our model in the standard setting, Pnma).18 Subsequently our A5+ + X3+ (+M3+) Pnma model will be referred to in the non-standard Pmcn (bca) setting (to give the long axis along c) for ease of comparison with other structural models. The atomic displacement parameters for sites derived from the same site in the parent P4/mmm structure were constrained to be equal, given the large unit cell which is pseudo-tetragonal. This model allows a complex modulation of NbO6 rotations and gives lower symmetry sites for A2+ cations (four 4c sites of m symmetry in this Pmcn model, compared with the single 4f site of 2mm symmetry for the P4/mbm model described above for CsSr2Nb3O10). This complex structure presumably results from the lower tolerance factor (t = 0.96) for the “CaNbO3” blocks with more significant tilts needed to optimise bonding around the smaller Ca2+ ion. It is striking that the earlier structural study by Dion et al. using single crystal X-ray diffraction18 is in good agreement with our study using NPD data, in contrast with other studies on related materials using X-ray powder diffraction data, highlighting the advantages of single crystal X-ray diffraction compared with XRPD for these systems.
b setting of space group 62),18 and so is equivalent to our model in the standard setting, Pnma).18 Subsequently our A5+ + X3+ (+M3+) Pnma model will be referred to in the non-standard Pmcn (bca) setting (to give the long axis along c) for ease of comparison with other structural models. The atomic displacement parameters for sites derived from the same site in the parent P4/mmm structure were constrained to be equal, given the large unit cell which is pseudo-tetragonal. This model allows a complex modulation of NbO6 rotations and gives lower symmetry sites for A2+ cations (four 4c sites of m symmetry in this Pmcn model, compared with the single 4f site of 2mm symmetry for the P4/mbm model described above for CsSr2Nb3O10). This complex structure presumably results from the lower tolerance factor (t = 0.96) for the “CaNbO3” blocks with more significant tilts needed to optimise bonding around the smaller Ca2+ ion. It is striking that the earlier structural study by Dion et al. using single crystal X-ray diffraction18 is in good agreement with our study using NPD data, in contrast with other studies on related materials using X-ray powder diffraction data, highlighting the advantages of single crystal X-ray diffraction compared with XRPD for these systems.
Given the significant SHG response for this sample (Section 3.1), polar models of Pna21 and Pmn21 symmetries were considered. These models allow the same tilts as the Pmcn model as well an in-plane polarisation (described by the Γ5− irrep) along different in-plane directions (see ESI†). It is hard to confirm either of these polar Pna21 and Pmn21 models from analysis of our diffraction data: the improvement in fit over the Pmcn model was not visible but was noticeable in the fitting statistics for both models. Full details are given in the ESI† and the Pna21 model is illustrated in Fig. 3. Again for ease of comparison between models, the cba setting, P21cn, of space group 33 Pna21 will be used (with polar axis along a and long axis along c), and the cab setting, P21mn, of space group 31 Pmn21 will be used (with polar axis along a and long axis along c).
Two Rb analogues, RbSr2Nb3O10 and RbCa2Nb3O10, were also studied for comparison with the Cs phases to understand the role of the interlayer A′ cations Cs+ and Rb+.
Given the moderate SHG activity measured for RbCa2Nb3O10 (Section 3.1), models allowing for an in-plane polar displacement (described by the Γ5− mode) were also considered. The polar P21 model gave a slight improvement in fit. Refinement details are given in the ESI† and the structure is illustrated in Fig. 4. We note that the polar displacement is relatively small (mode amplitudes of 0.53 Å, 0.77 Å, 0.64 Å and 0.26 Å for M3+, X3+, M5+ and Γ5− modes, respectively), comparable to that refined for CsCa2Nb3O10. However, with a single set of NPD data for RbCa2Nb3O10, the uncertainties in refined positions are nearly three times larger for RbCa2Nb3O10 than for CsCa2Nb3O10, and most sites for the Rb phase refine to positions close to within an uncertainty of the non-polar model, making it hard to confirm this polar distortion from analysis of our NPD data.
3.3 Diffuse reflectance measurements of optical band gap
Diffuse reflectance measurements for these A′A2B3O10 phases showed a decrease in reflectance for λ > 300 nm. The diffuse reflectance spectra after the Kubelka–Munk treatment are shown in Fig. 5. The intercepts of the linear increase in Kubelka–Munk function F = (1 − R)2/2R (where R is the diffuse reflectance) with the energy axis can be used to estimate the optical band gap, and suggest gaps ranging from 3.25 to 3.65 eV for CsA2Nb3O10, with gap increasing with decreasing A cation size. Similar gaps were measured for RbA2Nb3O10 samples. Data for CsCa2Ta3O10 are very noisy but suggest a slightly larger gap than for CsCa2Nb3O10, broadly consistent with the combined experimental and computational study by Zahedi et al.1These results are consistent with the white-off-white colour of the samples, and bandgaps in the visible-UV region of the electromagnetic spectrum.1,49 The low absorption observed for these materials is consistent with their indirect band gaps.50
3.4 Geometry optimisations from density functional theory calculations
Geometry optimisations of possible lower symmetry structures were carried out using DFT and the relative energies of distorted structures with respect to the ideal P4/mmm parent structure are summarised for several compositions in ESI† and Fig. 6. The first observation is that the structures calculated to be low in energy are in good agreement with those determined experimentally from NPD analysis (Section 3.2):• For CsBa2Nb3O10, only very small decreases in energy are calculated for possible distortions, consistent with the P4/mmm experimental model.
• For CsSr2Nb3O10 the single irrep that gives the greatest decrease in energy is M3+ (tilts about the out-of-plane axis, in-phase between blocks), consistent with the P4/mbm experimental mode.
- M3+ and A3+ modes (tilts about the out-of-plane axis, in-phase between blocks and out-of-phase, respectively) give very similar energy decreases, reflecting the weak dispersion (and reduced connectivity between blocks) as reported for CsLn2Ti2NbO10.20
- The X3+ tilts (tilts about an in-plane axis) combined with M3+ tilts give negligible stabilisation over the M3+-only P4/mbm model, and similarly M5+ and A5+ tilts (about in-plane axes) give negligible stabilisations.
• For A′Ca2B3O10 (A′ = Rb, Cs; B = Nb, Ta) the single irreps that give the greatest stabilisation are those that describe rotations about in-plane axes (M5+ for A′ = Rb; A5+ for A′ = Cs), in contrast to the Sr analogues. Tilts about the out-of-plane axis (A3+, M3+) also give some stabilisation.
- Combining the M5+ or A5+ mode with the X3+ mode (which also allows M3+ tilts) gives non-polar models of P21/m symmetry (RbCa2Nb3O10) or Pmcn symmetry (CsCa2B3O10, B = Nb, Ta).
- For both A′Ca2Nb3O10 (A′ = Rb, Cs), there′s a noticeable energy stabilisation by adding an additional in-plane polar distortion (Γ5−) to give polar models of P21 symmetry (RbCa2Nb3O10, energy gain 5 meV per formula unit) or P21cn symmetry (CsCa2Nb3O10, energy gain ∼12 meV per formula unit) compared with the non-polar P21/m or Pmcn models, respectively. The amplitude of the polar distortion from DFT calculations is comparable for these two phases, and consistent with the moderate SHG activity measured for these phases (Section 3.1).
- In contrast, for CsCa2Ta3O10 there′s only a negligible energy decrease (0.2 meV per formula unit) by allowing this additional in-plane polar distortion, and the amplitude of the polar distortion in the DFT-optimised models is negligible. This is consistent with the very weak SHG activity measured for CsCa2Ta3O10 (Section 3.1).
4. Discussion
Exploring trends in the experimentally refined structures gives a deeper understanding of the structural chemistry and physical properties of these systems. Fig. 7 summarises the unit cell parameters for these five compositions. As expected given their ionic radii (eight-coordinate radii are 1.61 Å and 1.74 Å for Rb and Cs, respectively),46 the Rb phases are smaller than the Cs analogues. The long c parameter is much larger for the Cs phases whilst both series have very similar in-plane unit cell parameters, reflecting this in-plane direction being more constrained against compression by the widths of the perovskite blocks. It is striking that the c parameter for CsBa2Nb3O10 (with highest tolerance factor and no octahedral rotations) is smaller than expected compared with other phases, reflecting the reduced height of the CsO layers to give optimal Cs bonding when stacked with the wider (and untilted) “BaNbO3” perovskite blocks.The orthorhombic strain51 (Fig. 7d) is calculated from the normalised in-plane unit cell parameters according to the eqn (1)
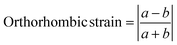 | (1) |
We note that the structures suggested here for CsCa2B3O10 (B = Nb, Ta) are challenging to refine experimentally because of their complexity (particularly for B = Ta with unit cell close to metrically tetragonal) leading to pseudo-symmetry issues and some correlation between refined parameters. The refined models include some irregular octahedra and large distributions of tilts and out-of-centre displacements (see uncertainties in ESI†) and these features are unlikely to give a good representation of the average structure. For comparison between B = Nb, Ta models, the geometry-optimised models from DFT calculations (assuming 0 K) might be more helpful for elucidating trends within this series.
The first observation across all of the lower-symmetry structural models is that the rotations of BO6 octahedra about the long axis (the M3+ rotations) are much larger for the B(1)O6 octahedra in the centre of the perovskite blocks, and are minimal (often negligible) for the B(2)O6 octahedra in the outer layers of the octahedra (see refinement details in the ESI†). Overall, there′s little change in the magnitude of these tilts across these A′A2B3O9 (A′ = Rb, Cs; A = Sr, Ca and B = Nb, Ta) compositions, suggesting that these tilts about the long axis occur to optimise bonding around the A cations. If these M3+ rotations occur to optimise A2+ bonding (e.g. to reduce Sr–O bond lengths for a given Nb–O bond length) there must be some maximum M3+ tilt angle, limited by the A′ = Rb, Cs cation size, beyond which the in-plane unit cell parameters would decrease too much to avoid overbonding of the A′ cations. This might explain the slightly larger M3+ tilts (particularly for the outer Nb(2)O6 octahedra) for the Rb phases compared with their Cs analogues (see ESI†).
These M3+ tilts alone are therefore not sufficient to give good bonding about the smallest A = Ca cations and so additional tilts about in-plane axes are observed for CsCa2B3O10 (B = Nb, Ta) and for RbCa2Nb3O10. These are surprisingly complex, involving two tilt modes to give tilts of different magnitudes through the structure. The experimentally observed models are consistent with those expected from DFT calculations (see Fig. 6 and ESI†): considering single tilts, A5+ and M5+ tilts give the largest energy stabilisations for CsCa2B3O10 and for RbCa2Nb3O10, respectively. This can be understood in terms of the effect of these tilts on the coordination environments of the A′ cations:
• A5+ tilts with k = (½ ½ ½) (to give a model of Icmm symmetry) rotate BO6 octahedra about [110] of the parent structure, with tilts in successive perovskite blocks in opposite directions (Fig. 8). This results in the apical oxide sites above and below a given A′ cation being displaced in the same direction. Presumably this becomes increasingly unfavourable with decreasing size of A′.
• M5+ tilts with k = (½ ½ 0) (to give a model of Pbmn symmetry) again rotate BO6 octahedra about [110] of the parent structure but in this case, the tilts in successive perovskite blocks are in the same directions, and so for these three-layer systems, M5+ tilts cause the apical oxide sites above and below an A′ cation to be displaced in opposite directions, likely to be more electrostatically favourable as the A′ cation (and therefore the distance between apical oxide sites across these layers) get smaller.
The same logic can be applied to the n = 2 DJ phases, noting that for these structures containing an even number of layers of octahedra in the perovskite blocks, the irreps are the other way around:
• A5− (k = (½ ½ ½)) modes describe (a−a−c0)–(a−a−c0) rotations with displacements of apical oxide sites above and below the A′ layer in opposite directions, hence these tilts are favoured for A′ = Rb;15,22,52
• M5− (k = (½ ½ 0)) modes describe (a−a−c0) (a−a−c0) rotations with displacements of apical oxide sites in the same direction, A′ = Cs.15,22,52
The X3+ tilts are more unusual: with k = (0 ½ 0) they describe tilts about [100] of the parent structure, with tilts in successive blocks in the same direction. In our case (with order parameter (a, b) to give a model of Pmmn symmetry) there are unequal tilts about both [100] and [010] of the parent structure, and this distortion breaks sufficient symmetry elements to also allow M3+ rotations about the long axis (hence the large energy stabilisation calculated for this model from DFT, see Fig. 6). These complex models involving multiple tilts are unusual, but are consistent with the large unit cells reported for CsCa2Nb3O10 and RbCa2Nb3O10.18,48 Being able to describe the structures in terms of symmetry adapted distortions helps explain these complex models.
To summarise our findings of rotations of BO6 octahedra in the n = 3 Dion–Jacobson series, slight underbonding of A2+ cations is relieved by rotations about the long axis (e.g., M3+, A3+ tilts), but the extent of these tilts is limited by the size of the A′+ cation (Rb+, Cs+): smaller A2+ ions will therefore induce additional tilts about in-plane axes. Again the A′ size also determines the nature of these tilts: for these odd-layer DJ phases, tilts described by k = (x y 0) (k = (x y ½)) modes give antiparallel (parallel) displacements of apical O(4) ions immediately above and below the A′+ cations and so smaller A′+ cations favour tilts described by k = (x y 0) modes.
Much of the recent work on Dion–Jacobson phases is motivated by their optoelectronic and catalytic activity1–6,8,11 and hence understanding their band gaps and edge positions is critical. The optical band gap increases with decreasing A2+ size (Fig. 5 and ref. 5, 26, 49 and 53), even though electronic structure calculations have shown that A2+ orbitals make negligible contribution to the density of states around the valence band maximum (VBM) and conduction band minimum (CBM).1 We’ve shown that decreasing the A2+ cation size increases the BO6 rotations, reducing the B–O–B angles from 180°. Computational studies (assuming the ideal P4/mmm structure) have shown that the VBM/CBM are predominantly composed of hybridised B 4d/5d and O 2p orbitals.1,50 This hybridisation is likely to be reduced as B–O–B bond angles deviate from 180°, giving more narrow bands and wider band gaps.
Optoelectronic effects such as catalytic activity1 and the photovoltaic effect54 are also reported to be influenced by polarity in the crystal structure. On one hand, the B cation environment may be polar e.g., the B(2) cations may be displaced from the centre of the BO6 octahedra along the long axis towards the A′ layers, lowering the B(2) site symmetry from Oh or D4h to C4v. Our experimental and computational results do not indicate any clear trend in the magnitude of this displacement across the compositions studied.
It is also important to consider any overall polarity in the crystal structure. It is difficult to confirm the loss of inversion symmetry from powder diffraction data55 (particularly for these DJ systems which often have quite subtle polar distortions) and SHG measurements (Section 3.1) are extremely valuable for exploring this aspect of the structure and symmetry.56 Our experimental and computational studies (ESI†) suggest inversion-symmetry-breaking polar distortions of similar magnitudes for CsCa2Nb3O10 and RbCa2Nb3O10. The stronger SHG intensity measured for CsCa2Nb3O10 than for the Rb analogue may reflect need to optimise the particle size for the Rb-containing sample, or the greater hyperpolarizability of Cs–O bonds compared with Rb–O bonds.57
Comparison of the CsCa2Nb3O10 and CsCa2Ta3O10 models and properties is more tricky: the much reduced orthorhombic distortion for CsCa2Ta3O10 compared with the Nb analogue leads to greater uncertainty in the experimentally refined models, and to explore the role the B5+ ions, comparison between the DFT models might be more reliable. The magnitude of M3+ and A5+ tilts (about out-of-plane and in-plane axes, respectively) are similar for both Nb5+ and Ta5+ phases, but the magnitude of the X3+ tilts (also about an in-plane axis) and the polar Γ5− displacement are noticeably smaller for the Ta5+ phase. It should be noted that tilts about in-plane axes (e.g. A5+ and X3+ tilts here, or M5+ tilts) and Γ5− displacements are not coupled by symmetry (as observed for some tilts in hybrid-improper ferroelectric systems),13 and yet the magnitude of these distortions appear to be somewhat correlated in our models. Given the almost identical ionic radii of Nb5+ and Ta5+,46 any differences between these two phases suggests the role of electronic factors, and in particular, the weaker second-order Jahn–Teller effect for 5d0 Ta5+ ion.58
The non-polar Pmcn models (X3+ (+M3+) + A5+) allow anti-polar in-plane displacements (described by Z5+ irreps)24e.g., anti-polar displacements of B(2) ions along the A5+ tilt axis, and our DFT geometry-optimised Pmcn models for CaCa2B3O10 phases have very similar magnitude antipolar distortions (for the overall structures, and for B(2) ions specifically) for both phases, perhaps reflecting the very similar geometric effects for B = Nb, Ta phases. There is little difference in magnitude of the anti-polar Z5+ distortion for the two compositions in the geometry-optimised polar P21cn and P21mn models, but the additional in-plane polar displacement gives a small energy gain for CsCa2Nb3O10, and the magnitude of the displacement is small but non-zero for B = Nb. On the other hand, for B = Ta the polar displacement and the energy gain are both negligible. This polar mode perhaps reflects the additional electronic driving force for lower symmetry (often polar) coordination environments for nd0 cations due to the second-order Jahn–Teller effect, known to be stronger for Nb5+ than for Ta5+.58 The degree of orthorhombic strain seems to be correlated with the strength of this in-plane polar distortion (Fig. 7). The fact that a non-zero SHG activity is measured for CsCa2Ta3O10 (Section 3.1) highlights the sensitivity of this technique and likely indicates very subtle polar distortions (associated with only tiny energy gains, see ESI†) that our powder diffraction techniques (which probe the average structure over long length scales) are barely sensitive to.
It is interesting to consider the relative energies of the various structural distortions discussed above. The energy gains for tilts of BO6 octahedra are always greater than the energies of polar distortions (Fig. 6) for these A′A2B3O10 (A = Ca, Sr, Ba) phases, as observed for A = Ln (lanthanide) phases.20 The energies of these non-polar distortions are also similar to those calculated for the proper ferroelectric CsBi2Ti2NbO10; the key difference is that for CsBi2Ti2NbO10, containing the second-order Jahn–Teller Bi3+ cation, polar and antipolar distortions give much larger energy gains driven by this electronic effect.59 It should be noted that for the A′A2B3O10 (A = Ca, Sr, Ba) phases considered here, any polar nature does not arise from hybrid-improper mechanisms60 (the non-polar tilts described above do not couple to break inversion symmetry), and although the energies associated with polar distortions in A′Ca2Nb3O10 (A′ = Rb, Cs) are small, polarity must arise by proper mechanisms. The difference between CsCa2Nb3O10 and CsCa2Ta3O10 (which must have very similar geometric factors) demonstrates the extent of electronic driving forces to stabilise polar structures in these A = Ca, Sr, Ba phases – significantly reduced compared with the role Bi3+ plays in CsBi2Ti2NbO10 compared with the CsLn2Ti2NbO10 phases,20,59 and consistent with work on related A′Cd2Nb3O10 phases.44
5. Conclusions
Our experimental approach, using second-harmonic generation measurements and neutron powder diffraction, combined with DFT calculations, reveals the range of structural distortions observed for n = 3 DJ phases and allows us to determine the crystal structures and symmetries for several phases. This study shows how the structure is determined by composition: with decreasing size of A2+ cations, BO6 octahedra first tilt about the out-of-plane axis, and then tilt about an in-plane axis, in order to optimise the bonding environment around increasingly small A2+ cations. Larger A′ = Cs cations allow tilts about the in-plane axis to be out-of-phase from block to block, but the repulsion between apical oxide sites means that for smaller A′ = Rb phases, the tilts about the in-plane axis are in-phase from block to block (Fig. 7). These tilt distortions are largely driven by geometric factors. Previous work has highlighted the electronic role of certain A cations (e.g. Bi3+, Cd2+) in stabilising polar phases,44,59 and our comparison here of B = Nb, Ta analogues indicates that the second-order Jahn–Teller effect involving nd0B cations can also play a role (albeit weaker than for ns2 cations) in stabilising polar DJ phases for the more distorted structures RbCa2Nb3O10 and CsCa2Nb3O10. It would be interesting to apply these insights from purely inorganic systems to the hybrid and halide Dion–Jacobson phases,9,16,61 taking into account the additional bonding influences of the molecular cations.62Data availability
The data supporting this article have been included as part of the ESI† as appropriate. Neutron powder diffraction data are available as “Public Experiments” at https://tardis.nbi.ansto.gov.au. Crystallographic data for CsBa2Nb3O10, CsSr2Nb3O10, RbSr2Nb3O10, CsCa2Nb3O10, RbCa2Nb3O10 and CsCa2Ta3O10 will be deposited at the ICSD on acceptance of the manuscript for publication.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank The Leverhulme Trust (RPG-2017-362) for funding. We are grateful to the Royal Society of equipment grant RG130844 and for international exchange scheme IES\R3\170112, and to the EU Cost Action “Towards oxide-based electronics”. We thank the RSC for research fund (R23-4339620653) for equipment for SHG measurements and Warwick seedcorn funding (EP/V007688/1) for supporting preliminary SHG measurements. We acknowledge Durham University for use of their supercomputer services, Hamilton. We are grateful to ANSTO for NPD data. We thank E. Bousquet (Liège) and S. Halasyamani (Houston) for interesting and helpful discussions.References
- E. Zahedi, M. Hojamberdiev and M. F. Bekheet, Electronic, optical and photocatalytic properties of three-layer perovskite Dion–Jacobson phase CsBa2M3O10 (M = Ta, Nb): a DFT study, RSC Adv., 2015, 5(108), 88725–88735, 10.1039/C5RA13763B.
- T. Oshima, T. Yokoi, M. Eguchi and K. Maeda, Synthesis and photocatalytic activity of K2CaNaNb3O10, a new Ruddlesden–Popper phase layered perovskite, Dalton Trans., 2017, 46(32), 10594–10601, 10.1039/C6DT04872B.
- S. A. Kurnosenko, O. I. Silyukov, I. A. Rodionov, Y. P. Biryukov, A. A. Burov and I. A. Zvereva, Synthesis, ion-exchange and photocatalytic properties of layered perovskite-like niobate CsBa2Nb3O10: comparative analysis with related Dion–Jacobson phases AA′2 Nb3O10 (A = K, Rb, Cs; A' = Ca, Sr, Pb), Russ. J. Inorg. Chem., 2023, 68(13), 1903–1912, DOI:10.1134/S0036023623602842.
- J. R. Reddy, S. Kurra, R. Guje, S. Palla, N. K. Veldurthi, G. Ravi and M. Vithal, Photocatalytic degradation of methylene blue on nitrogen doped layered perovskites, CsM2Nb3O10 (M = Ba and Sr), Ceram. Int., 2015, 41(2, Part B), 2869–2875, DOI:10.1016/j.ceramint.2014.10.109.
- O. V. Krasheninnikova, E. V. Syrov, S. M. Smirnov, E. V. Suleimanov, D. G. Fukina, A. V. Knyazev and D. N. Titaev, Synthesis, crystal structure and photocatalytic activity of new Dion–Jacobson type titanoniobates, J. Solid State Chem., 2022, 315, 123445, DOI:10.1016/j.jssc.2022.123445.
- M. Machida, T. Mitsuyama, K. Ikeue, S. Matsushima and M. Arai, Photocatalytic property and electronic structure of triple-layered perovskite tantalates, MCa2Ta3O10 (M = Cs, Na, H, and C6H13NH3), J. Phys. Chem. B, 2005, 109(16), 7801–7806, DOI:10.1021/jp044833d.
- (a) H. Ye, Y. Peng, X. Shang, L. Li, Y. Yao, X. Zhang, T. Zhu, X. Liu, X. Chen and J. Luo, Self-powered visible-infrared polarization photodetection driven by ferroelectric photovoltaic effect in a Dion–Jacobson hybrid perovskite, Adv. Funct. Mater., 2022, 32(24), 2200223, DOI:10.1002/adfm.202200223; (b) L. Wu, G. Li, K. Prashanthan, A. Musiienko, J. Li, T. W. Gries, H. Zhang, H. Köbler, P. Janasik and A. N. S. Appiah, et al., Stabilization of inorganic perovskite solar cells with a 2D Dion–Jacobson passivating layer, Adv. Mater., 2023, 35(42), 2304150, DOI:10.1002/adma.202304150.
- M. R. Aziza, C. W. Chang, A. Mohapatra, C. W. Chu, C. C. Kaun and Y. H. Su, Dion–Jacobson phase perovskite Ca2Nan−3NbnO3n+1 (n = 4–6) nanosheets as high-κ photovoltaic electrode materials in a solar water-splitting cell, ACS Appl. Nano Mater., 2020, 3(7), 6367–6375, DOI:10.1021/acsanm.0c00747.
- H. Fu, Dion–Jacobson halide perovskites for photovoltaic and photodetection applications, J. Mater. Chem. C, 2021, 9(20), 6378–6394, 10.1039/D1TC01061A.
- (a) W. Guo, H. Xu, Q. Fan, P. Zhu, Y. Ma, Y. Liu, X. Zeng, J. Luo and Z. Sun, Centimeter-size single crystal of a polar Dion–Jacobson double perovskite with large mobility-lifetime product toward effective X-ray detection, Adv. Opt. Mater., 2024, 12(17), 2303291, DOI:10.1002/adom.202303291; (b) Q. Fan, Y. Ma, H. Xu, Y. Liu, B. Wang, W. Guo, X. Hu, J. Luo and Z. Sun, Acquiring a newly tailored 2D Dion–Jacobson hybrid perovskite with large structural distortion for efficient crystal array photodetector, Adv. Opt. Mater., 2023, 11(2), 2202277, DOI:10.1002/adom.202202277; (c) P. Wang, X. Li, H. Ye, Q. Guan, Y. Wang, Y. Geng, C. Zhang, H. Li and J. Luo, Durable dielectric switching and photo-responsivity in a Dion–Jacobson hybrid perovskite semiconductor, Inorg. Chem. Front., 2024, 11(8), 2436–2441, 10.1039/D3QI02685J.
- X. Liu, S. Li, Z. Li, Y. Zhang, W. Yang, Z. Li, H. Liu, D. V. Shtansky and X. Fang, Boosted responsivity and tunable spectral response in B-site substituted 2D Ca2Nb3−TaO10 perovskite photodetectors, Adv. Funct. Mater., 2021, 31(20), 2101480, DOI:10.1002/adfm.202101480.
- (a) W. R. Zhang, K. Fujii, E. Niwa, M. Hagihala, T. Kamiyama and M. Yashima, Oxide-ion conduction in the Dion–Jacobson phase CsBi2Ti2NbO10, Nat. Commun., 2020, 11(1), 1224, DOI:10.1038/s41467-020-15043-z; (b) W. R. Zhang, K. Fujii, T. Ishiyama, H. Kandabashi and M. Yashima, Dion–Jacobson-type oxide-ion conductor CsLa2Ti2NbO10 without phase transitions, J. Mater. Chem. A, 2020, 8(47), 25085–25093, 10.1039/d0ta06135b.
- N. A. Benedek, Origin of ferroelectricity in a family of polar oxides: the Dion—Jacobson phases, Inorg. Chem., 2014, 53(7), 3769–3777, DOI:10.1021/ic500106a.
- (a) C. Chen, H. P. Ning, S. Lepadatu, M. Cain, H. X. Yan and M. J. Reece, Ferroelectricity in Dion–Jacobson ABiNb(2)O(7) (A = Rb, Cs) compounds, J. Mater. Chem. C, 2015, 3(1), 19–22, 10.1039/c4tc02136c; (b) S. Pal, R. Nagarajan and S. Uma, Second harmonic generation in the polar A′SmNb2O7 (A′ = Rb, Cs) Dion–Jacobson layered perovskites, Chem. Mater., 2023, 35(3), 1249–1258, DOI:10.1021/acs.chemmater.2c03280.
- Z.-T. Lu, S. Asaki, S. Yoshida, C. Moriyoshi, G. Hasegawa, K. Fujita, V. Gopalan, K. Hayashi and H. Akamatsu, Structural frustration effects by mixed alkali ions in ferroelectric Dion–Jacobson layered perovskites (Cs,Rb)NdNb2O7, J. Mater. Chem. C, 2025, 13(4), 1812–1823, 10.1039/D4TC04190A.
- L. Mao, W. Ke, L. Pedesseau, Y. Wu, C. Katan, J. Even, M. R. Wasielewski, C. C. Stoumpos and M. G. Kanatzidis, Hybrid Dion–Jacobson 2D lead iodide perovskites, J. Am. Chem. Soc., 2018, 140(10), 3775–3783, DOI:10.1021/jacs.8b00542.
- M. Dion, M. Ganne and M. Tournoux, Nouvelles familles de phases MIMII2Nb3O10 a feuillets “perovskites”, Mater. Res. Bull., 1981, 16(11), 1429–1435, DOI:10.1016/0025-5408(81)90063-5.
- M. Dion, M. Ganne and M. Tournoux, Structure cristalline de la perovskite feuilletee ferroelastique Cs Ca2Nb3O10, Rev. Chim. Miner., 1984, 21, 92–103 CAS.
- (a) M. N. H. Liton, M. Roknuzzaman, M. A. Helal, M. Kamruzzaman, A. K. M. F. U. Islam, K. Ostrikov and M. K. R. Khan, Electronic, mechanical, optical and photocatalytic properties of perovskite RbSr2Nb3O10 compound, J. Alloys Compd., 2021, 867, 159077, DOI:10.1016/j.jallcom.2021.159077; (b) M. A. Rehman, Z. U. Rehman, M. Usman, A. A. Ifseisi, J. Fatima, M. E. Assal and A. Hamad, The photocatalytic degradation performance of Dion–Jacobson-type layered perovskites AMCa2Ta3O10 (AM = Rb, Cs): a DFT study, J. Solid State Chem., 2024, 337, 124809, DOI:10.1016/j.jssc.2024.124809.
- V. A. Cascos, J. Roberts-Watts, C. Skingle, I. Levin, W. Zhang, P. S. Halasyamani, M. C. Stennett, N. C. Hyatt, E. Bousquet and E. E. McCabe, Tuning between proper and hybrid-improper mechanisms for polar behavior in CsLn2Ti2NbO10 Dion–Jacobson phases, Chem. Mater., 2020, 32(19), 8700–8712, DOI:10.1021/acs.chemmater.0c03326.
- K. S. Aleksandrov, Structural phase transitions in layered perovskite-like crystals, Kristallographia, 1995, 40, 279–301 CAS.
- T. Zhu, A. S. Gibbs, N. A. Benedek and M. A. Hayward, Complex structural phase transitions of the hybrid improper polar Dion–Jacobson oxides RbNdM2O7 and CsNdM2O7 (M = Nb, Ta), Chem. Mater., 2020, 32(10), 4340–4346, DOI:10.1021/acs.chemmater.0c01304.
- M. E. Strayer, A. S. Gupta, H. Akamatsu, S. Lei, N. A. Benedek, V. Gopalan and T. E. Mallouk, Emergent noncentrosymmetry and piezoelectricity driven by oxygen octahedral rotations in n = 2 Dion–Jacobson phase layer perovskites, Adv. Funct. Mater., 2016, 26(12), 1930–1937, DOI:10.1002/adfm.201504046.
- H. T. Stokes, D. M. Hatch and B. J. Campbell, ISODISTORT, ISOTROPY Software Suite, http://iso.byu.edu/ Search PubMed.
- V. M. Goldschmidt, Die gesetze der krystallochemie, Naturwissenschaften, 1926, 14(21), 477–485, DOI:10.1007/BF01507527.
- E. V. Syrov, O. V. Krasheninnikova, A. V. Knyazev, D. G. Fukina, E. V. Suleimanov, N. S. Volkova, A. P. Gorshkov and S. M. Smirnov, Synthesis, structure, and properties of new Dion–Jacobson compounds A′LnNaNb3O10 (A′ = Cs, Rb, H; Ln = Nd, Pr), J. Phys. Chem. Solids, 2021, 156, 110184, DOI:10.1016/j.jpcs.2021.110184.
- M. Avdeev and J. R. Hester, ECHIDNA: a decade of high-resolution neutron powder diffraction at OPAL, J. Appl. Crystallogr., 2018, 51(6), 1597–1604, DOI:10.1107/S1600576718014048.
- H. Rietveld, A profile refinement method for nuclear and magnetic structures, J. Appl. Crystallogr., 1969, 2(2), 65–71, DOI:10.1107/S0021889869006558.
- (a) TOPAS Academic, General Profile and Structure Analysis Software for Powder Diffraction Data, Bruker AXS, Karlsruhe, Germany, 2012 Search PubMed; (b) A. Coelho, TOPAS and TOPAS-Academic: an optimization program integrating computer algebra and crystallographic objects written in C++, J. Appl. Crystallogr., 2018, 51(1), 210–218, DOI:10.1107/S1600576718000183.
- H. T. Stokes, D. M. Hatch, B. J. Campbell and D. E. Tanner, ISODISPLACE: a web-based tool for exploring structural distortions, J. Appl. Crystallogr., 2006, 39(4), 607–614, DOI:10.1107/S0021889806014075.
- G. Kortüm, W. Braun and G. Herzog, Principles and techniques of diffuse-reflectance spectroscopy, Angew. Chem., Int. Ed. Engl., 1963, 2(7), 333–341, DOI:10.1002/anie.196303331.
- S. K. Kurtz and T. T. Perry, A powder technique for the evaluation of nonlinear optical materials, J. Appl. Phys., 1968, 39(8), 3798–3813, DOI:10.1063/1.1656857.
- (a) S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr., Cryst. Mater., 2005, 220(5–6), 567–570, DOI:10.1524/zkri.220.5.567.65075; (b) M. D. Segall, J. D. L. Philip, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, First-principles simulation: ideas, illustrations and the CASTEP code, J. Phys.: Condens. Matter, 2002, 14(11), 2717, DOI:10.1088/0953-8984/14/11/301.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892–7895, DOI:10.1103/PhysRevB.41.7892.
- J. D. García, F. Gómez, V. Velázquez and B. A. Rodríguez, Bulk second-order optical nonlinearities in centrosymmetric materials, J. Opt. Soc. Am. B, 2022, 39(10), 2582–2588, DOI:10.1364/JOSAB.466210.
- J. I. Dadap, J. Shan and T. F. Heinz, Theory of optical second-harmonic generation from a sphere of centrosymmetric material: small-particle limit, J. Opt. Soc. Am. B, 2004, 21(7), 1328–1347, DOI:10.1364/JOSAB.21.001328.
- T. Wu, B. Yin, Z. Bian, Y. Gao, J. Gu and D. Wang, Insights into the mechanism of the symmetry dependent SHG properties in low dimensional KNbO3 structures, Inorg. Chem. Front., 2023, 10(9), 2689–2696, 10.1039/D2QI02691K.
- M. Hojamberdiev, M. F. Bekheet, E. Zahedi, H. Wagata, Y. Kamei, K. Yubuta, A. Gurlo, N. Matsushita, K. Domen and K. Teshima, New Dion–Jacobson phase three-layer perovskite CsBa2Ta3O10 and its conversion to nitrided Ba2Ta3O10 nanosheets via a nitridation–protonation–intercalation–exfoliation route for water splitting, Cryst. Growth Des., 2016, 16(4), 2302–2308, DOI:10.1021/acs.cgd.6b00081.
- Z.-H. Liang, K.-B. Tang, Q.-W. Chen and H.-G. Zheng, RbCa2Nb3O10 from X-ray powder data, Acta Crystallogr., Sect. E, 2009, 65(6), i44, DOI:10.1107/S1600536809018157.
- V. Thangadurai, P. Schmid-Beurmann and W. Weppner, Synthesis, structure, and electrical conductivity of A′[A2B3O10](A′ = Rb, Cs; A = Sr, Ba; B = Nb, Ta): new members of Dion–Jacobson-type layered perovskites, J. Solid State Chem., 2001, 158(2), 279–289, DOI:10.1006/jssc.2001.9108.
- K. Toda, T. Teranishi, Z.-G. Ye, M. Sato and Y. Hinatsu, Structural chemistry of new ion-exchangeable tantalates with layered perovskite structure: new Dion–Jacobson phase MCa2Ta3O10 (M = alkali metal) and ruddlesden–popper phase Na2Ca2Ta3O10, Mater. Res. Bull., 1999, 34(6), 971–982, DOI:10.1016/S0025-5408(99)00084-7.
- X. Wang, J. Adhikari and L. J. Smith, An investigation of distortions of the Dion–Jacobson phase RbSr2Nb3O10 and its acid-exchanged form with 93Nb solid state NMR and DFT calculations, J. Phys. Chem. C, 2009, 113(40), 17548–17559, DOI:10.1021/jp902318v.
- S. Atri, M. Pokhriyal and S. Uma, Synergistic Influence of d0 (Nb5+) and d10 (Cd2+) cations in stabilizing noncentrosymmetric Dion–Jacobson layered perovskites, A′Cd2Nb3O10 (A′ = Rb, Cs), Inorg. Chem., 2020, 59(12), 8044–8053, DOI:10.1021/acs.inorgchem.0c00291.
- S. Pal, S. Das, R. Nagarajan and S. Uma, Dion–Jacobson A′MiiiNaNb3O10 (A′ = Rb, Cs; M(iii) = Sm, Bi) and RbSmNa2Nb4O13 layered perovskites and their luminescent function, J. Mater. Chem. C, 2022, 10(39), 14675–14685, 10.1039/D2TC03179E.
- R. D. Shannon, Revised effective ionic-radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A, 1976, 32(SEP1), 751–767, DOI:10.1107/s0567739476001551.
- (a) A. J. Tuxworth, E. E. McCabe, D. G. Free, S. J. Clark and J. S. O. Evans, Structural characterization and physical properties of the new transition metal oxyselenide La2O2ZnSe2, Inorg. Chem., 2013, 52(4), 2078–2085, DOI:10.1021/ic302484x; (b) H. Djani, E. E. McCabe, W. Zhang, P. S. Halasyamani, A. Feteira, J. Bieder, E. Bousquet and P. Ghosez, Bi2W2O9: a potentially antiferroelectric aurivillius phase, Phys. Rev. B, 2020, 101(13), 134113, DOI:10.1103/PhysRevB.101.134113; (c) E. A. S. Scott, E. Mitoudi Vagourdi, M. Johnsson, V. Cascos, F. John, D. Pickup, A. V. Chadwick, H. Djani, E. Bousquet and W. Zhang, et al., Bi2CoO2F4–A polar, ferrimagnetic aurivillius oxide-fluoride, Chem. Mater., 2022, 34(21), 9775–9785, DOI:10.1021/acs.chemmater.2c02745.
- J. A. Kurzman and M. J. Geselbracht, Probing octahedral tilting in Dion–Jacobson layered perovskites with neutron powderdiffraction and Raman spectroscopy, MRS Proc., 2007, 988, 9880806 CrossRef.
- Y.-m. Ding, J.-j. Shi, M. Zhang, M. Wu, H. Wang, Y.-l. Cen, W.-h. Guo and S.-h. Pan, Electronic, photocatalytic and piezoelectric properties of n = 3 Dion–Jacobson-type perovskite monolayer A′[A2B3O10], Mater. Res. Express, 2018, 5(9), 096305, DOI:10.1088/2053-1591/aad892.
- I. E. Castelli, K. S. Thygesen and K. W. Jacobsen, Calculated optical absorption of different perovskite phases, J. Mater. Chem. A, 2015, 3(23), 12343–12349, 10.1039/C5TA01586C.
- N. C. Hyatt, I. M. Reaney and K. S. Knight, Ferroelectric-paraelectric phase transition in the $n = 2$ Aurivillius phase Bi3Ti1.5W0.5O9: a neutron powder diffraction study, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(2), 024119, DOI:10.1103/PhysRevB.71.024119.
- V. Yadav, S. Pal and S. Uma, Dion–Jacobson (n = 2) layered perovskites (A′SmTa2O7; A′ = Rb, Cs) as potential ferroelectric materials, J. Phys. Chem. C, 2025, 129(11), 5666–5673, DOI:10.1021/acs.jpcc.4c08181.
- S. Hussain, J. U. Rehman, M. B. Tahir and A. Hussain, First principles calculations of double perovskite RbX2Y3O10 (X = Ca, Ba: YCd, Ta) materials for photocatalytic applications, Int. J. Hydrogen Energy, 2024, 89, 486–495, DOI:10.1016/j.ijhydene.2024.09.355.
- D. Fu, Y. Ma, C.-Y. Su, Z. Chen and D.-W. Fu, Amplification of polarization ratio is observed in monolayer Dion–Jacobson hybrid perovskites, J. Mater. Chem. C, 2023, 11(34), 11492–11499, 10.1039/D3TC01926H.
- IUCr, Friedel's Law, 2021, https://dictionary.iucr.org/Friedel%27s_law, accessed 2021 Search PubMed.
- K. M. Ok, E. O. Chi and P. S. Halasyamani, Bulk characterization methods for non-centrosymmetric materials: second-harmonic generation, piezoelectricity, pyroelectricity, and ferroelectricity, Chem. Soc. Rev., 2006, 35(8), 710–717, 10.1039/B511119F.
- (a) S. H. Patil and K. T. Tang, A simple method for polarizabilities and hyperpolarizabilities of alkali isoelectronic systems, Chem. Phys. Lett., 1998, 295(1), 152–157, DOI:10.1016/S0009-2614(98)00917-8; (b) A. Alejo-Molina, H. Hardhienata and K. Hingerl, Simplified bond-hyperpolarizability model of second harmonic generation, group theory, and Neumann's principle, J. Opt. Soc. Am. B, 2014, 31(3), 526–533, DOI:10.1364/JOSAB.31.000526.
- P. M. Woodward; P. Karen; J. S. O. Evans and T. Vogt, Solid State Materials Chemistry, Cambridge University Press, 2021 Search PubMed.
- E. E. McCabe, E. Bousquet, C. P. J. Stockdale, C. A. Deacon, T. T. Tran, P. S. Halasyamani, M. C. Stennett and N. C. Hyatt, Proper ferroelectricity in the Dion–Jacobson material CsBi2Ti2NbO10: experiment and theory, Chem. Mater., 2015, 27(24), 8298–8309, DOI:10.1021/acs.chemmater.5b03564.
- E. Bousquet, M. Dawber, N. Stucki, C. Lichtensteiger, P. Hermet, S. Gariglio, J. M. Triscone and P. Ghosez, Improper ferroelectricity in perovskite oxide artificial superlattices, Nature, 2008, 452(7188), 732–U734, DOI:10.1038/nature06817.
- J. Gong, M. Hao, Y. Zhang, M. Liu and Y. Zhou, Layered 2D halide perovskites beyond the Ruddlesden–Popper phase: tailored interlayer chemistries for high-performance solar cells, Angew. Chem., Int. Ed., 2022, 61(10), e202112022, DOI:10.1002/anie.202112022.
- T. Liu, N. P. Holzapfel and P. M. Woodward, Understanding structural distortions in hybrid layered perovskites with the n = 1 Ruddlesden-Popper structure, IUCrJ, 2023, 10(4), 385–396, DOI:10.1107/S2052252523003743.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta02587g |
| This journal is © The Royal Society of Chemistry 2025 |








