Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Symmetry-informed graph neural networks for carbon dioxide isotherm and adsorption prediction in aluminum-substituted zeolites†
Marko
Petković
 ac,
José-Manuel
Vicent Luna
ac,
José-Manuel
Vicent Luna
 *a,
Elīza Beate
Dinne
*a,
Elīza Beate
Dinne
 a,
Vlado
Menkovski
a,
Vlado
Menkovski
 bc and
Sofía
Calero
bc and
Sofía
Calero
 *ac
*ac
aMaterials Simulation and Modelling, Department of Applied Physics and Science Education, Eindhoven University of Technology, Eindhoven, Netherlands. E-mail: j.vicent.luna@tue.nl; s.calero@tue.nl
bData and AI, Department of Mathematics and Computer Science, Eindhoven University of Technology, Eindhoven, Netherlands
cEindhoven Artificial Intelligence Systems Institute, Eindhoven University of Technology, Eindhoven, Netherlands
First published on 29th May 2025
Abstract
Accurately predicting adsorption properties in nanoporous materials using deep learning models remains a challenging task. This challenge becomes even more pronounced when attempting to generalize to structures that were not part of the training data. In this work, we introduce SymGNN, a graph neural network architecture that leverages material symmetries to improve adsorption property prediction. By incorporating symmetry operations into the message-passing mechanism, our model enhances parameter sharing across different zeolite topologies, leading to improved generalization. We evaluate SymGNN on both interpolation and generalization tasks, using samples with varying Si/Al distributions from 108 zeolite topologies for interpolation and assessing generalization on two unseen frameworks. SymGNN successfully captures key adsorption trends, including the influence of both the framework and aluminium distribution on CO2 adsorption. Furthermore, we apply our model to the characterization of experimental adsorption isotherms, using a genetic algorithm to infer likely aluminium distributions. Our results highlight the effectiveness of machine learning models trained on simulations for studying real materials and suggest promising directions for fine-tuning with experimental data and generative approaches for the inverse design of multifunctional nanomaterials.
1. Introduction
In recent years, there has been a noticeable increase in atmospheric CO2 levels, with the corresponding rise in greenhouse effects, highlighting the pressing need for effective carbon mitigation strategies. Carbon capture emerges as a viable approach to address this issue,1 and nanoporous materials, specifically zeolites, stand out as promising candidates.2 Zeolites exhibit a notable capacity for gas adsorption, making them well-suited for reducing carbon levels in the atmosphere. This capacity is commonly analyzed through adsorption isotherms, which describe how the amount of CO2 adsorbed varies with pressure and provide insights into the material's efficiency and suitability for carbon capture. Their appeal extends further with attributes such as high thermal stability3 and cost-effectiveness in synthesis when compared to other adsorbents.4Additionally, the extensive variety of synthesizable zeolite topologies,5 each characterized by distinct pore sizes and properties, adds a layer of versatility to their application. Within a zeolite topology, there are multiple possible configurations, as a result of different silicon and aluminium atom arrangements. These configurations can have different CO2 adsorption properties, where the overall trend is that an increase in aluminium atoms leads to better adsorption properties.6 However, for the same Si/Al ratio there can still be a considerable variance in properties such as the heat of adsorption and the adsorption isotherms.
Due to the large configuration space of possible zeolite topologies and Si/Al configurations, experimentally studying each configuration to find structures with desirable properties is impossible. In this context, simulations provide a powerful alternative, enabling the prediction of adsorption properties without the need for extensive synthesis and testing.7–12 However, certain computational methods, particularly classical simulations such as Grand Canonical Monte Carlo (GCMC), require sampling at multiple pressures to generate adsorption isotherms and fully characterize a material's adsorption behavior. This can be computationally expensive, making it challenging to efficiently screen large numbers of candidate structures.
To this end, deep learning (DL) can be a powerful tool for accelerating the discovery and characterization of materials.13–16 For predicting the properties of crystals, several graph neural network (GNN) architectures17–21 and transformer-based models22,23 have been proposed, which operate on atomic types and positions within the unit cell. In addition, generative models have been increasingly explored for the design of novel materials, allowing the discovery of structures with targeted properties.24–27 Furthermore, various DL approaches have been specifically tailored for nanoporous materials, such as zeolites and metal–organic frameworks (MOFs). Some of these methods focus on predicting adsorption behavior across different adsorbates,28–33 while others aim to design new materials with optimized adsorption and structural properties.34,35
Most of these models explicitly respect and leverage the symmetries present in a crystal by being invariant or equivariant to the Euclidean group E(3), as well as the periodic boundary conditions. Each crystal has an associated space group (SG), which is a subgroup of E(3) and determines the equivalent atomic positions within the unit cell. By incorporating this information, geometric constraints can be directly embedded into the neural network architecture. Although several approaches for predicting crystal properties account for space group information, they either neglect symmetries at the unit cell level36 or lack generalizability across materials with different topologies.37 These approaches introduce separate parameters in the GNN for the node and message update functions for nodes/edges, which are considered symmetrically equivalent. Complementary to these efforts, Li et al.38 recently demonstrated that incorporating quantum mechanical descriptors into GNNs can enhance generalizability in chemical property prediction, highlighting the broader value of embedding physical principles into model architectures.
In this work, we introduce SymGNN, a symmetry-informed graph neural network architecture designed to incorporate crystal symmetries into message passing. By leveraging symmetry operations, our model enables more effective parameter sharing across different zeolite topologies, leading to improved generalization. We demonstrate that SymGNN successfully predicts both adsorption isotherms and heats of adsorption for unseen topologies, capturing key adsorption trends by effectively modeling the influence of both the framework structure and the Si/Al distribution on adsorption properties. Finally, we show that our model can be applied to characterize experimental adsorption isotherms by inferring structural properties such as the Si/Al ratio, potentially enhancing materials characterization and analysis.
2. Crystal symmetries
2.1. Unit cell
In crystalline materials, the arrangement of atoms follows a repeating periodic structure, which is described using the Bravais lattice Λ. A Bravais lattice defines the periodic arrangement of points in space, and the structure of the entire crystal can be generated by translating these points along the lattice vectors. Eqn (1) describes the Bravais lattice, where ai are the linearly independent basis vectors of the lattice and mi are their integer multiples. This defines the periodicity of the lattice in a three-dimensional space. | (1) |
From the Bravais lattice, we can define the unit cell U, which represents the smallest repeating unit in the crystal structure. The unit cell can be defined using the basis vectors of the crystal lattice, as shown in eqn (2). Here, xi are the fractional coordinates of the points in space belonging to the unit cell.
 | (2) |
The set of atoms S contained within a unit cell is defined by eqn (3), in which Zi is the atomic number, and xi is the position in fractional coordinates of an atom. By combining the Bravais lattice and the set of atoms in the unit cell, we can fully describe the crystal structure.
| S = {(Zi,xi) | xi∈U} | (3) |
2.2. Space group
Crystals exhibit a high degree of symmetry, which plays a crucial role in determining their physical properties. The symmetry of a crystal can be described mathematically by a space group G. A space group encompasses the full set of symmetry operations that can be applied to the crystal, leaving it invariant. As such, it captures all of the rotational, reflectional, and translational symmetries of the structure.Each element of the space group is a group action g. Each group action consists of a tuple of a linear transformation W and a translation vector t. The elements of a space group act on a position x as shown in eqn (4).
| g·x = Wx + t | (4) |
One important property of space groups is their closure under multiplication. This means that when two elements of the space group are multiplied, the result is another element of the same space group. This closure property is described by eqn (5) and (6).
| W′ = W1W2 | (5) |
| t′ = W2t1 + t2 | (6) |
2.3. Group orbit
The orbit of an atom is the set of all positions which the atom can be mapped to by elements of the space group, and can be formally defined using eqn (7). Atoms that belong to the same orbit are considered to be equivalent under the space group symmetry. The cardinality (or size) of an atom's orbit depends on its position within the crystal. Specifically, an atom located in the least symmetric position will have an orbit that includes all the space group operations, meaning its orbit will have the same cardinality as the space group. In contrast, an atom in a more symmetric position will have a smaller orbit, as some space group operations may map the atom to equivalent positions within the unit cell, reducing the total number of distinct positions in the orbit.| Orbit(x) = {g·x | g∈G} | (7) |
Next, we will define the set of operations that can map each position in an orbit to every other position, except the original position. For orbits with the same cardinality as the space group, this set will coincide with the full set of space group operations, minus the identity operation. However, for smaller orbits (those with fewer positions), some of the space group operations may be redundant as they do not contribute to mapping positions within the orbit. In such cases, the set of operations that maps one position to another will be a proper subset of the full space group. Mathematically, this set of operations is defined in eqn (8).
| Ops(x) = {g ∈G | g·x ∈ Orbit(x) ∧g·x ≠ x} | (8) |
2.4. Generators
To define the generators of the set of operations associated with an orbit, we need to identify the minimal set of operations that, when combined (with repetition) through multiplication, can generate all other operations that map positions within the orbit. These generators are crucial because they form the core operations that preserve the symmetry of the crystal while minimizing redundancy.Mathematically, we define the set of generators, Gen(Ops(x)), as the minimal subset of operations (eqn (9)) such that every operation in Ops(x) can be expressed as a product of elements from this set (eqn (10)). This set of generators can be thought of as the building blocks for the full set of orbit operations.
| Gen(Ops(x)) ⊆ Ops(x) | (9) |
| 〈Gen(Ops(x))〉 = Ops(x) | (10) |
In this equation, 〈S〉 denotes the subgroup generated by the set S. As such, every element g∈Ops(x) can be defined using the generators, as shown in eqn (11).
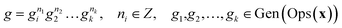 | (11) |
However, there can still be multiple minimal yet distinct sets of generators for a given set of symmetry operations. For example, in the cyclic group of order 4 (C4), both a 90-degree rotation and a 270-degree rotation can independently generate all other elements of C4. To ensure a consistent choice of generators for a given position x, we adopt the generator sets defined for different space groups as provided by the Bilbao Crystallographic Server (BCS).39
3. Methods
3.1. Zeolite frameworks
For this work, we used 108 different zeolite topologies with varying structural features. For each topology, varying configurations of silicon and aluminium atoms were generated, with the lowest Si/Al ratio being 3. The different configurations for each topology were generated using the ZEORAN6 program and the PORRAN program, which is a Python extension of ZEORAN. These programs make use of four different algorithms to place aluminium atoms in an all-silica zeolite. These algorithms place the aluminium atoms either in clusters, chains, uniformly (maximum entropy) or randomly. Depending on the algorithm, the resulting structures may violate the Löwenstein rule (Al–O–Al linkages), which recent studies have shown can occur in practice.40–43 As demonstrated in Romero-Marimon et al.,6 the different aluminium placement algorithms lead to variations in properties such as the heat of adsorption (HOA). While some generated structures may not be (commonly) observed experimentally, their inclusion in the dataset can help a model learn a broader range of configurations, potentially improving robustness and generalization. A more detailed description of the algorithms can be found in the ESI.† Si/Al configurations for the MOR, RHO, MFI and ITW zeolite topologies were taken from Petković et al.30 For the other structures, atomic coordinates for pure silica were taken from IZA,44 following which Si/Al configurations were generated using the aforementioned algorithms. In total, 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 648 structures were generated.
648 structures were generated.
3.2. Computational details
In this study, we investigated the CO2 adsorption isotherm and heat of adsorption (−ΔH). These properties can give us insight into the CO2 adsorption in zeolites. The heat of adsorption can give an indication about the interaction strength between the zeolite and the adsorbate, whereas the isotherm can tell us about the adsorption capacity of a zeolite at different pressures. To calculate the heat of adsorption, simulations using the Widom particle insertion method in the canonical ensemble (NVT) were performed45 for 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. For the CO2 adsorption isotherms, simulations were carried out using the grand canonical ensemble (μVT), where the loading was calculated for a range of pressures between 0.01 and 10
000 cycles. For the CO2 adsorption isotherms, simulations were carried out using the grand canonical ensemble (μVT), where the loading was calculated for a range of pressures between 0.01 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kPA.
000 kPA.
The isotherms were calculated for the MOR, MFI, MEL, TON, and ITW zeolites. These frameworks were selected for isotherm calculations due to the availability of extensive heat of adsorption data from previous studies,30,37 as well as their representation of diverse topological characteristics. To obtain an adsorption isotherm for a single Si/Al configuration of a zeolite, multiple simulations need to be carried out. To generate a large dataset of adsorption isotherms efficiently, some simulations were sped up by using a reduced number of unit cells, depending on the zeolite. We validated this approximation by comparing isotherms varying the Si/Al ratio using full (i.e., the number of unit cells ensures that the simulation box is longer than twice the cutoff in each direction) and reduced simulation boxes of each zeolite. We found that the number of unit cells can be reduced for MOR, MFI, and MEL, without compromising the adsorption results. However, using the reduced simulation box, we found more fluctuations for TON and ITW. Therefore, we use the full simulation box for these two zeolites. The full and reduced number of unit cells and the verification procedure and results of the verification can be found in the ESI.† Finally, we fitted the 2-site Langmuir-Freundlich model (eqn (12)) using RUPTURA,46 which can smooth out possible fluctuations as a consequence of using reduced simulation boxes.
 | (12) |
The RASPA software47 was used to carry out all the simulations. The force field and point charges used for the simulations were taken from Romero-Marimon et al.6 It extends the force field introduced in Garcia-Sanchez et al.,48 by accounting for atoms breaking the Löwenstein rule. For each zeolite configuration, sodium cations were introduced to balance the difference in charge as a result of the aluminium substitutions. The simulations were carried out at room temperature (298 K).
3.3. Dataset
In Fig. 1, the relationship between the proportion of aluminium atoms and the heat of adsorption is visualized. Overall, there is a slight trend for an increasing heat of adsorption with a higher aluminium proportion. However, there is still a significant dependence of the heat of adsorption on both the framework type, as well as the distribution of aluminium atoms within the framework. Sodium cations have been shown to reside close to the aluminium framework atoms,6 and can thus affect the strength of adsorption sites. Furthermore, the geometry of the framework pores also plays a role in the adsorption strength.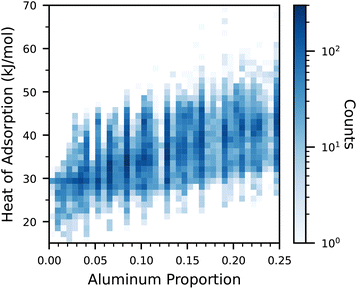 | ||
| Fig. 1 Heat of adsorption for all datapoints as a function of the aluminium proportion. Note that the color is in log-scale. | ||
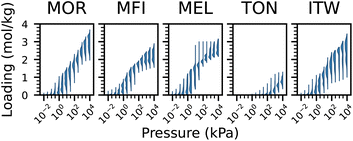
Similarly, the behaviour of the adsorption isotherms is also impacted by the aluminium distribution and the geometry of the material. As can be seen in Fig. 2, the shape of the isotherms can vary greatly between topologies, showing how the geometry of the pores plays a role in the isotherm. Furthermore, there is a significant variance in the isotherms for the same zeolite topology, suggesting that the distribution and ratio of aluminium atoms plays a role. This can be seen in Fig. 3, where the loading for a given pressure and aluminium proportion is shown for each zeolite topology. In general, when increasing the pressure, the loading first increases for structures with a higher aluminium proportion. However, at higher pressures, these structures tend to reach saturation earlier, whereas structures with a lower aluminium proportion tend to achieve a higher loading.
 | ||
| Fig. 3 Loading values for all datapoints with isotherms as a function of the aluminium proportion, at varying pressures. | ||
Using this data, we define two different splits of the data. In the first split, the generalization split, the model is evaluated on the ITW and CHA structures, and trained on the remaining zeolites. As such, the model will not have seen the structure of ITW and CHA. Therefore, we can use this test set to evaluate how well the model has learned how the structure and distribution of aluminium atoms of a zeolite impact its adsorption properties. In the second split, interpolation split, the data is split in training, validation and testing set. For each zeolite, the different configurations are split in an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 between the three sets. Using this test set, we can evaluate how well the model understands the effect of the aluminium distribution within each topology.
10 between the three sets. Using this test set, we can evaluate how well the model understands the effect of the aluminium distribution within each topology.
In our dataset, there is a large class imbalance, with MOR having 4300 samples present in the dataset, and EUO having only 78. To avoid the model overfitting on more prevalent structures, we over- and under-sample the configurations of different zeolites, to ensure the model has seen 250 samples per zeolite during an epoch. The number of structures for each zeolite topology can be found in the ESI.†
4. Symmetry-informed graph neural networks
Several existing GNN architectures36,37 have leveraged crystal symmetries to enhance their performance. These models make use of symmetry-based parameter sharing, where unique node and message update functions are assigned to each set of equivalent nodes and edges that belong to the same orbit. This approach increases the model's expressiveness, as a distinct set of parameters is learned for each (abstract) spatial relationship. This is analogous to how a convolutional neural network learns separate parameters for each pixel within a kernel.However, when trained on a specific set of topologies, these models generally cannot be transferred to a new topology due to the lack of a clear mapping between sets of atomic orbits in different crystals. In Kaba and Ravanbakhsh,36 this challenge was addressed by defining symmetries between unit cells, allowing the model to be fully transferable. This was achieved by constructing a 2 × 2 × 2 supercell, which enabled the model to recognize equivalent relationships across unit cells. However, symmetries within the unit cell itself were not explicitly leveraged, meaning the approach does not take full advantage of all available symmetry information. As a result, while the model generalizes across different crystal topologies, it may not be as efficient or expressive as a model that fully incorporates intra-unit-cell symmetries. Furthermore, the use of a supercell makes training significantly more challenging, as porous materials like zeolites often contain a very large number of atoms, making the process nearly impossible with standard computational resources.
4.1. Symmetry-informed message passing
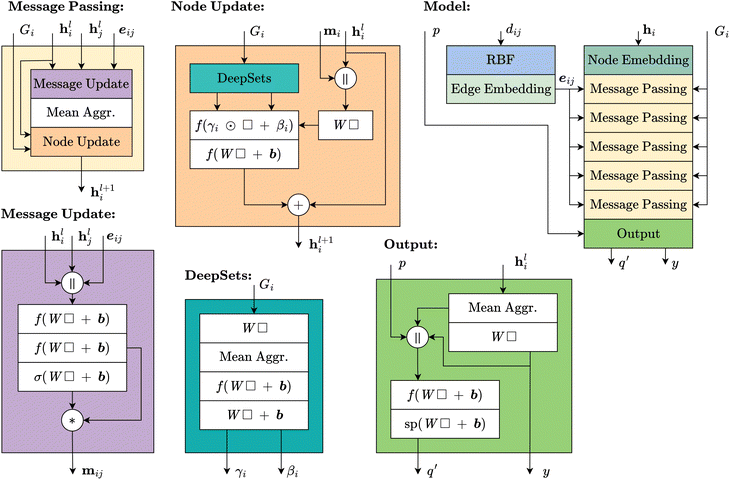
To address these limitations, we introduce symmetry-informed message passing, which explicitly incorporates the generators of the set of symmetry operations into the node update function. By doing so, the model is directly informed about how symmetries act within a given structure, allowing it to distinguish between equivalent and non-equivalent atomic environments in a way that generalizes across different topologies. Unlike previous approaches, which either lack transferability or fail to fully utilize symmetry information, our approach ensures that the model can recognize and leverage shared symmetries while maintaining the flexibility to adapt to new crystal structures.The overall message-passing scheme is defined in eqn (13)–(15). Here, hil represents the embedding of node i at layer l, while eij denotes the embedding of the edge connecting nodes i and j. The set of generators associated with node i, denoted as Gi, encodes the local symmetry properties of the structure. Each message mijl is computed from neighboring nodes and edges using the message function ϕe, while node embeddings are updated through ϕh, the node update function. Unlike standard message-passing approaches, ϕh is explicitly conditioned on Gi, allowing it to capture symmetry-aware representations and adapt its updates based on the geometric context of each node.
| mijl = ϕe(hil,hjl,eij) | (13) |
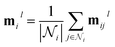 | (14) |
| hil+1 = ϕh(hil,mil|Gi) | (15) |
To condition the node update layer on the generators, we utilize feature-wise linear modulation (FiLM),49 as described in eqn (16) and (17). In the first step, we apply a standard weight multiplication for the node update. Then, we introduce γ and β, which allow the model to adjust the feature values based on the symmetry information of the node. These parameters act as dynamic scaling factors, enabling the model to emphasize or suppress features according to the symmetries inherent in the crystal structure. To compute γ and β, we embed the set of generators using a DeepSets-inspired model.50 Each element of the set of generators is represented by flattening its rotation matrix and concatenating it with the corresponding translation vector. This approach captures the relationships between the generators in a permutation-invariant manner and provides the necessary modulating parameters for the node update.
| γi,βi = DeepSets(Gi) | (16) |
| ϕh(hil,mil|Gi) = γi⊙W(hil∥mil) + βi | (17) |
Fig. 4 compares the utilization of symmetries in symmetry-informed message passing and symmetry-based parameter sharing. While symmetry-based parameter sharing introduces a greater number of distinct parameters, these assignments are specific to each topology and cannot be transferred between zeolites. Consequently, a new model must be trained for each topology. In contrast, symmetry-informed message passing enables certain generator sets to be shared across different zeolites. Furthermore, even when generator sets differ, they may still contain common symmetry operations, further enhancing parameter transferability.
4.2. Model architecture
To address the challenges of predicting adsorption properties in zeolites, we introduce SymGNN, a graph neural network that makes use of symmetry-informed message passing. This approach allows the model to efficiently predict the CO2 heat of adsorption and adsorption isotherms across different zeolite structures by leveraging the inherent symmetries within the zeolite topologies.Since the adsorption isotherm is a function rather than a scalar, and is monotonically increasing with pressure, our model does not predict the loading at a given pressure directly. Instead, it predicts the derivative of the loading with respect to the pressure. Furthermore, rather than predicting the derivative of the loading at discrete pressures, our model predicts the isotherm function itself, similar to the approach used in neural operators. The model takes the final hidden state of the GNN, concatenates it with the pressure and predicted heat of adsorption, and passes it through a multi-layer perceptron (MLP) to produce the loading derivative predictions. To obtain the full isotherm for a given structure, the MLP is evaluated at different pressures. The resulting loading derivatives are then integrated to obtain the true loading.‡ The precision of the predicted isotherm can be controlled by adjusting the number of pressures at which the MLP is evaluated.
A full overview of the SymGNN architecture is provided in Fig. 5. The model consists of 5 symmetry-informed message passing layers, each with hidden states of size 64. Nodes are embedded using a single linear layer, while edges are embedded using radial basis functions (RBF)18 with 64 bins, followed by a linear layer. Messages are self-importance weighted, and aggregated using mean pooling. All linear layers in the message and node update steps are followed by layer normalization.51 The DeepSets modules, which provide the parameters for FiLM in the node update, have an internal hidden state of 32. Throughout the model, the ELU activation function is used. To predict both the heat of adsorption and the loading derivative, mean aggregation is used to obtain a graph-level representation, as adsorption properties are independent of the number of atoms in the unit cell.
4.3. Experiments
As described in Section 3.3, we use two dataset splits: generalization and interpolation. In the generalization split, the model is trained on all topologies except ITW and CHA, which are reserved for evaluation. This experiment assesses how well the model can learn the influence of different zeolite frameworks with varying topological features. ITW has a channel-like structure, while CHA contains cages. The interpolation split, on the other hand, evaluates the model's ability to capture the effect of different aluminium distributions on CO2 adsorption. In both cases, we compare SymGNN against a standard GNN with identical hyperparameters, where the FiLM layer is replaced by a conventional linear layer. In addition, we evaluate our models against ALIGNN20 and Matformer,22 adapting both architectures to also predict the isotherms by replacing their output modules with the same one used in our models (Fig. 5). Due to the large size of zeolite graphs, we reduce the hidden dimensions of these models relative to their default configurations. A detailed summary of all model hyperparameters is provided in the ESI.†All models are trained for 400 epochs, using the AdamW52 optimizer with default weights and a batch size of 128. The models were trained using mean-squared error loss for both the heat of adsorption and loading derivative. During training of GNN and SymGNN, edge dropout53 with a probability of 0.5 is used to regularize the network. Due to the limited amount of isotherm data, the network is initially trained using only the heat of adsorption objective for the first 100 epochs. This approach mimics pre-training strategies used in fields like natural language processing (NLP), where models first learn general patterns before fine-tuning on specific tasks. This phase allows the model to establish the relationship between adsorption properties and framework geometry. In the following 25 epochs, the coefficient for the loading derivative loss is linearly increased from 0 to 1. For loading predictions, we evaluate at 100 logarithmically spaced pressures, ranging from 0.01 kPa to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kPa. A random window of 25 pressures for each structure is used to calculate the loss to reduce overfitting.
000 kPa. A random window of 25 pressures for each structure is used to calculate the loss to reduce overfitting.
To construct a graph representation of a zeolite, we use a binary node encoding, where silicon is represented as 0 and aluminum as 1. This approach is similar to the one used in other crystal GNNs, where each atomic species is assigned a specific embedding to distinguish them in the graph. Undirected edges are drawn between atoms within a radius of 8 Å, while ensuring periodic boundary conditions are respected. Each edge is further annotated with the Euclidean distance between the connected atoms.
We calculate the generators for each atomic position within a given topology. Since the goal is to leverage symmetry operations to inform the GNN about the crystal geometry, atom types are not considered in the calculation. Including them would cause most structures to belong to the least symmetric space group, which would remove any geometric information the generators carry. To determine the generators, we first obtain space group information from the GENPOS program of BCS,39 then algorithmically identify the generators for each atomic orbit within the topology.
4.4. Structure characterization
In experimental settings, the precise atomic structure of a zeolite is often unknown. Determining key structural properties, such as the Si/Al ratio or the specific atomic arrangement within the unit cell, can provide valuable insights into a material's adsorption behavior. To address this, we employ an optimization-based approach to infer likely structures based on adsorption data.We adopt a genetic algorithm (GA)-based approach, where the genes represent the Si and Al atom assignments within the framework.30 Since we work with fixed framework topologies and do not optimize atomic positions, our GA operates exclusively on the distribution of Al and Si atoms within the framework. The algorithm starts with an initial population of 200 candidate structures, initialized randomly. At each iteration, the top 25 structures (elite selection) are preserved, while mutations are applied to both the best 25 and the second-best 25 structures, resulting in 50 structures undergoing modifications per generation. Mutations include local swaps of approximately 5% of the atoms, full permutations of the atom types, and changes that add or remove a single Al atom. The population is filtered to remove symmetrically equivalent structures (structures which can be transformed into one another by a symmetry operation from the space group of the topology), with a 90% probability, allowing high-fitness configurations to appear multiple times while still limiting redundancy. The population is then replenished to 200 candidates to maintain diversity. We do not include crossover operations, as our gene representation, where each gene directly corresponds to an Al atom, does not benefit from traditional crossover mechanisms. In this context, crossover would largely resemble random resampling, a role already fulfilled by our existing mutation strategies. In total, the GA runs for 50 generations, following which we extract the 25 best performing structures.
The fitness function follows the approach from Petković et al.,30 where candidates are evaluated based on their agreement with the experimental isotherm. In addition, the fitness function penalizes unnecessarily introducing aluminium atoms. However, to mitigate potential biases in the model, we introduce an additional term that explicitly evaluates how well the predicted isotherm captures the overall shape of the experimental data. This adjustment helps refine the search towards physically meaningful solutions.
To assess the model's performance in structure characterization, we apply this method to several experimental isotherms from the literature. Specifically, we consider two MFI,54 two MOR,55,56 and one LTA4A57 zeolite, with varying Si/Al ratios. We analyze how well the algorithm can recover the correct structural parameters from the adsorption data. For this experiment, we used the SymGNN model trained on the interpolation data split.
5. Results
5.1. Model performance
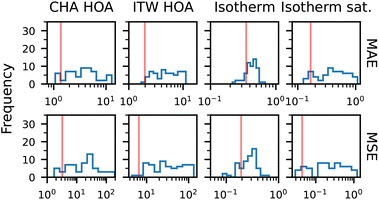
To evaluate the performance of the different models in both interpolation and generalization experiments, we calculate the mean absolute error (MAE) and mean squared error (MSE) across various quantities. These include the heat of adsorption, the full adsorption isotherm, and the isotherm near saturation pressure (the final 10% of the pressure range). The last metric provides insight into how well the model captures variations in loading caused by the framework structure and aluminium distribution. These metrics are summarized in Table 1.| Task | Model | Heat of adsorption | Isotherm | Isotherm sat. | |||
|---|---|---|---|---|---|---|---|
| MAE | MSE | MAE | MSE | MAE | MSE | ||
| Generalization | ALIGNN | 2.07 | 7.20 | 0.23 | 0.10 | 0.32 | 0.15 |
| Matformer | 2.46 | 9.45 | 0.38 | 0.35 | 0.95 | 1.34 | |
| GNN | 2.17 | 7.39 | 0.33 | 0.19 | 0.76 | 0.63 | |
| SymGNN | 1.44 | 3.94 | 0.31 | 0.16 | 0.16 | 0.04 | |
| Interpolation | ALIGNN | 3.01 | 15.13 | 0.16 | 0.08 | 0.29 | 0.21 |
| Matformer | 1.18 | 2.95 | 0.09 | 0.02 | 0.14 | 0.03 | |
| GNN | 1.45 | 3.96 | 0.07 | 0.01 | 0.12 | 0.02 | |
| SymGNN | 1.36 | 3.59 | 0.07 | 0.01 | 0.09 | 0.01 | |
In the interpolation experiment, we observe that ALIGNN performs poorly, likely due to its limited scalability to larger graphs. Matformer achieves higher accuracy than the GNN-based models for predicting the heat of adsorption but underperforms in the isotherm prediction. SymGNN and the regular GNN show more balanced performance across both properties. Since all models have been trained on every topology present in the test set, the focus shifts away from the influence of the zeolite framework and more toward learning how aluminium distribution affects adsorption. As a result, explicitly modeling symmetries provides limited additional benefit in this setting. As shown in Fig. 6, SymGNN performs slightly better than the regular GNN in both heat of adsorption and isotherm predictions.
In contrast, the generalization experiment reveals a decline in performance for all models, especially in terms of full isotherm prediction, where errors increase substantially. However, SymGNN outperforms all baselines across tasks, achieving the lowest mean absolute and mean squared errors for both heat of adsorption and isotherm predictions. Notably, it maintains high accuracy in the saturation region, with a substantial margin over the other models. This indicates that incorporating symmetry information enables better generalization to unseen topologies. To further analyze this, we compare the distributions of the true and predicted isotherms for both SymGNN and the standard GNN, as shown in Fig. 7a and b. The symmetry-informed model captures the overall behavior of the isotherm but increases the loading too early. In contrast, the standard graph neural network predicts isotherms with little variance, producing almost the same isotherm for each structure and severely underestimates the loading at higher pressures. This reduced variability can lead to lower average errors, but at the cost of missing the structure-specific features that are critical for realistic adsorption modeling.
We further evaluate the GNN and SymGNN in the generalization experiment on MOR, MFI, MEL, and ITW, as presented in the ESI.† Both models maintain good predictive performance for isotherms across most structures, but do not always capture the full influence of topology on the heat of adsorption. In particular, we observe a drop in isotherm accuracy for frameworks like TON, whose adsorption behavior differs substantially from the training distribution. These results indicate that while the models generalize well overall, capturing subtle topological effects may require additional training data or further architectural improvements.
Parity plots for the heat of adsorption are shown in Fig. 7f and g. For the SymGNN, we observe a slight overestimation of the heat of adsorption for lower values, whereas the regular GNN tends to underestimate lower values and overestimate higher values. This behavior may be attributed to the distribution of training data, where lower heat of adsorption values are underrepresented, potentially leading to underprediction by the model in those regions. Despite this, SymGNN successfully captures the underlying trends and generalizes well, effectively learning the influence of unseen zeolite topologies on the heat of adsorption.
In the parity plots for loading (Fig. 7h and i), a distinct trend emerges. SymGNN primarily overestimates the loading, whereas the regular GNN overestimates lower loadings but underestimates higher ones. Examining the isotherm predictions for ITW structures with varying Si/Al ratios (Fig. 7c–e), we find that SymGNN accurately captures the overall trend and the correct loading near saturation pressure. In contrast, the regular GNN increases the loading too early and fails to reach the correct saturation pressure. Additionally, SymGNN better captures the influence of aluminium distribution across different pressures (Fig. 8), accurately modeling both the initial increase and subsequent decrease in loading, whereas the regular GNN only captures the decreasing trend. Overall, these results demonstrate that incorporating symmetry improves generalization to unseen zeolite structures, particularly in capturing adsorption trends across different frameworks, despite the model being trained on isotherms from only four other topologies.
 | ||
| Fig. 8 True (black) and predicted distribution of loading values as a function of the aluminium proportion for the symmetry informed (blue) and regular GNN (red) at different pressures. | ||
Table 2 summarizes the computational efficiency of the evaluated models. While ALIGNN and Matformer are significantly more expensive in both training and inference time, the regular GNN and SymGNN offer substantially faster runtimes. SymGNN introduces only a small overhead compared to the regular GNN, with a marginal increase in training and inference time, despite incorporating symmetry-aware message passing. The generator calculation required for SymGNN adds approximately 100 ms per topology, but this step is performed only once and can be further optimized. Overall, SymGNN provides a favorable trade-off between computational cost and improved accuracy, particularly in generalization tasks.
| Model | Parameters (K) | Train/epoch (s) | Inference (ms) |
|---|---|---|---|
| ALIGNN | 790 | 212 | 338 |
| Matformer | 702 | 85 | 120 |
| GNN | 156 | 11 | 79 |
| SymGNN | 190 | 12 | 82 |
5.2. Symmetry utilization analysis
While incorporating symmetry information into the model improves its performance, it is essential to determine whether the model has genuinely learned to leverage these symmetries or if the observed improvements arise from other factors. To this end, we examine whether the generator embedding network assigns distinct γ and β parameters to different sets of generators, indicating that the model differentiates between symmetry elements. Additionally, we analyze how the model's predictions change when substituting the true generators of atoms in a zeolite with an alternative set, testing whether the learned symmetry representations meaningfully influence adsorption behavior. These experiments are carried out on the SymGNN model used in the generalization setting.In total, there are 61 unique sets of generators across all nodes in the dataset. To examine whether the model has learned distinct γ and β parameters for each unique set of generators, we calculate the cosine similarity between these parameters for different generators. Additionally, to assess whether the model has learned to associate similar generator sets with similar parameters, we define two distinct sets of generator pairs. The first set contains pairs (i, j), where Gi ⊂ Gj and |Gj| − |Gi| = 1, meaning one set of generators includes all elements of the other set, plus one additional generator. The second set contains pairs where this condition does not hold.
As shown in Fig. 9, the model has indeed learned distinct γ and β parameters for the different sets of generators across all layers of the network. From the plot, we observe that the parameters of similar generators exhibit higher cosine similarity compared to dissimilar ones, which is also statistically confirmed by the significant difference in cosine similarity between similar and different generators. This indicates that the model has learned a meaningful relationship between the generators, associating similar ones with similar parameter values.
 | ||
| Fig. 9 Cosine similarity for γ and β parameters from similar generators (blue) and different generators (orange), for each message passing layer. | ||
To analyze whether SymGNN bases its predictions on the geometric information provided by the generators, we replace the generators of the nodes in the test set (ITW and CHA), with the generators of nodes from a different zeolite. More specifically, for each orbit of nodes in both topologies, we replace their generators with the same generator from a different zeolite. For each generator replacement, we evaluate the model performance on the modified test set.
In Fig. 10, we observe how the evaluation metrics are impacted when an incorrect set of generators is used for a given topology. Overall, the performance degrades significantly, rendering the model nearly unusable. While there are a few instances where the performance is marginally better, this is likely due to the use of a generator set that is similar to the correct one. In the full isotherm, there are more incorrect generators for which the error is lower, but this can be attributed to an inherent bias in our network when predicting isotherms, as the model performs notably better near saturation pressure. From this, we can conclude that the model indeed leverages the symmetries in the zeolite structures.
5.3. Structure characterization
To assess our model's performance in structure characterization, we examine the aluminium distributions in the generated structures. Fig. 11 compares the predicted distribution of aluminium atoms per unit cell from our genetic algorithm with the true distribution. By generating a range of possible aluminium arrangements, our approach provides additional insight into the material, as real crystals often exhibit variations in their unit cell configurations. In the case of both MFI structures and one of the MOR structures, the predicted aluminium distribution is centered around the true value. However, for the other MOR structure, the model tends to overpredict the aluminium content, while for LTA4A, it underpredicts it. These deviations suggest that while the model captures key trends in aluminium placement, there is still room for improvement in accurately modeling specific cases. One potential reason for these discrepancies is that the experimental isotherms used in this analysis may differ from those generated by simulation, due to factors such as framework defects, cation presence, or adsorbate–framework interactions not fully captured by the training data. These real-world variations may introduce discrepancies that the model is not yet equipped to handle.As observed in the generalization experiment, the model struggles to fully generalize across different zeolite structures. While incorporating the isotherm shape into the fitness function improves performance, it may not completely resolve this limitation. A possible way forward is to increase the diversity of training data by incorporating more isotherms from a wider range of zeolite topologies. Additionally, fine-tuning the model using experimental data could enhance its ability to capture real-world adsorption behavior more accurately. Such improvements could make the model more reliable for structure characterization and broaden its applicability to new materials.
6. Conclusion
In this work, we introduced SymGNN, a symmetry-informed graph neural network capable of accurately predicting adsorption properties in zeolites. Our results demonstrate that incorporating structural information into message passing allows for improved generalization, enabling accurate predictions of both adsorption isotherms and heats of adsorption, even for unseen topologies. Despite being trained on a limited dataset, SymGNN exhibits strong predictive performance. The model effectively learns adsorption trends across different zeolite frameworks and Si/Al distributions, highlighting its robustness even when data is sparse. This makes it a promising approach for studying adsorption in materials where experimental data is limited. Nonetheless, we observe that the model may struggle when encountering adsorption patterns that deviate significantly from the training distribution, or when capturing more subtle topological effects on adsorption properties. These limitations point to potential future improvements, such as incorporating more diverse training data or refining the model to better encode global structural features.A key finding of this work is that a model trained entirely on simulated isotherms can be used to analyze real zeolite structures. By applying SymGNN to experimental adsorption data, we demonstrated its potential for structure characterization, showing that it can infer properties such as the Si/Al ratio from adsorption trends. This suggests that machine learning models trained on computational data can bridge the gap to real-world applications.
One limitation of our study is the restricted availability of adsorption isotherms, both in terms of the number of samples and the diversity of zeolite topologies. While our model performs well across the available data, expanding the dataset to include more topologies and adsorption conditions would likely improve generalization further.
Additionally, the model currently handles idealized zeolite structures, and performance might vary with more complex or larger frameworks, such as those containing defects or larger unit cells. However, the model's design should allow it to scale to larger structures, as the GNN considers local environments with a receptive field that extends periodically, resulting in the complexity scaling linearly with the amount of atoms. While the model may struggle with long-range effects in very large unit cells, techniques like hierarchical GNNs could be explored. For structures with defects, the model could be trained on single unit cells containing defects, as the large graphs can negatively affect the computational complexity of model training. In turn, this model could be applied to supercells containing multiple unit cells with varying defect configurations, as it can combine the local patterns it learns through message passing, making its output independent of the number of atoms in the graph.
Looking ahead, generative models offer an exciting avenue for inverse design, allowing for the discovery of new zeolite structures with tailored adsorption properties. However, while such models have shown promise in MOFs,34 they only operate on a building block level. As such, their application at the atomic level for porous materials remains largely unexplored. Future work could explore how generative models can be combined with physics-informed learning to accelerate zeolite design.
Fine-tuning SymGNN with experimental data presents another promising direction. Incorporating real adsorption measurements into training could further improve both prediction accuracy and structure characterization, helping refine our understanding of real zeolite materials. This approach could also enhance the model's ability to generalize beyond simulated conditions, making it even more applicable to practical adsorption studies. Furthermore, the method is not limited to zeolites and could be applied to other classes of porous materials such as MOFs. Extending SymGNN to these systems would require minimal architectural changes and could open up broader applications in adsorption, separation, and sensing.
Overall, this work highlights the potential of machine learning for adsorption modeling in nanoporous materials. By leveraging structured representations and data-driven learning, models like SymGNN provide a powerful tool for both predictive modeling and material characterization, paving the way for future advances in adsorption science and materials discovery.
Data availability
Data for the zeolite structures and their adsorption properties, as well as the code for the models and experiments, is available at https://doi.org/10.5281/zenodo.15085783. Code for the PORRAN program is available at https://doi.org/10.5281/zenodo.15050435.Author contributions
Conceptualization: M. P., V. M., J. M. V. L., S. C.; data curation: M. P., E. B. D.; formal analysis: M. P.; funding acquisition: V. M., S.C.; investigation: M. P.; methodology: M. P., J. M. V. L.; project administration: V. M., S. C; software: M. P., E. B. D.; resources: S. C.; supervision: J. M. V. L., V. M., S. C.; validation: M. P.; visualization: M. P.; writing – original draft: M. P.; writing – review & editing: M. P, E. B. D., J. M. V. L., V. M., S. C.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work used the Dutch national e-infrastructure with the support of the SURF Cooperative using grant no. EINF-10879.References
- O. Odunlami, D. Vershima, T. Oladimeji, S. Nkongho, S. Ogunlade and B. Fakinle, Results Eng., 2022, 15, 100512 CrossRef CAS.
- S. Kumar, R. Srivastava and J. Koh, J. CO2 Util., 2020, 41, 101251 CrossRef CAS.
- G. Cruciani, J. Phys. Chem. Solids, 2006, 67, 1973–1994 CrossRef CAS.
- A. Khaleque, M. M. Alam, M. Hoque, S. Mondal, J. B. Haider, B. Xu, M. Johir, A. K. Karmakar, J. Zhou and M. B. Ahmed, et al. , Environ. Adv., 2020, 2, 100019 CrossRef.
- T. Derbe, S. Temesgen and M. Bitew, Adv. Mater. Sci. Eng., 2021, 2021, 1–17 Search PubMed.
- P. Romero-Marimon, J. J. Gutiérrez-Sevillano and S. Calero, Chem. Mater., 2023, 35, 5222–5231 CrossRef CAS.
- J. Kim and B. Smit, J. Chem. Theory Comput., 2012, 8, 2336–2343 CrossRef CAS PubMed.
- T. D. Pham, R. Xiong, S. I. Sandler and R. F. Lobo, Microporous Mesoporous Mater., 2014, 185, 157–166 CrossRef CAS.
- W. Kellouai, P. Judeinstein, M. Plazanet, S. Baudoin, M. Drobek, A. Julbe and B. Coasne, Langmuir, 2022, 38, 5428–5438 CrossRef CAS PubMed.
- W. Jeong and J. Kim, J. Phys. Chem. C, 2016, 120, 23500–23510 CrossRef CAS.
- M. Fischer and R. G. Bell, J. Phys. Chem. C, 2013, 117, 24446–24454 CrossRef CAS.
- R. Krishna and J. M. van Baten, J. Membr. Sci., 2010, 360, 323–333 CrossRef CAS.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Chem. Rev., 2020, 120, 8066–8129 CrossRef CAS PubMed.
- Y. Liu, Y. Dong and H. Wu, J. Mater. Chem. A, 2025, 13, 2403–2440 RSC.
- K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza, R. Cohn, C. W. Park, A. Choudhary, A. Agrawal and S. J. Billinge, et al. , npj Comput. Mater., 2022, 8, 59 CrossRef.
- P. Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. van Hoesel, H. Schopmans and T. Sommer, et al. , Commun. Mater., 2022, 3, 93 CrossRef CAS PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 185 CrossRef.
- R. Ruff, P. Reiser, J. Stühmer and P. Friederich, Digital Discovery, 2024, 3, 594–601 RSC.
- K. Yan, Y. Liu, Y. Lin and S. Ji, Adv. Neural Inform. Process. Syst., 2022, 35, 15066–15080 Search PubMed.
- T. Taniai, R. Igarashi, Y. Suzuki, N. Chiba, K. Saito, Y. Ushiku and K. Ono, International Conference on Learning Representations, 2024 Search PubMed.
- T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, International Conference on Learning Representations, 2021 Search PubMed.
- R. Jiao, W. Huang, P. Lin, J. Han, P. Chen, Y. Lu and Y. Liu, Adv. Neural Inform. Process. Syst., 2023, 36, 17464–17497 Search PubMed.
- B. K. Miller, R. T. Chen, A. Sriram and B. M. Wood, Forty-first International Conference on Machine Learning, 2024 Search PubMed.
- D. Levy, S. S. Panigrahi, S.-O. Kaba, Q. Zhu, M. Galkin, S. Miret and S. Ravanbakhsh, AI for Accelerated Materials Design-NeurIPS 2024, 2024 Search PubMed.
- R. Wang, Y. Zhong, L. Bi, M. Yang and D. Xu, ACS Appl. Mater. Interfaces, 2020, 12, 52797–52807 CrossRef CAS PubMed.
- Y. Liu, G. Perez, Z. Cheng, A. Sun, S. C. Hoover, W. Fan, S. Maji and P. Bai, J. Mater. Chem. A, 2023, 11, 17570–17580 RSC.
- M. Petković, J. M. Vicent-Luna, V. Menkovski and S. Calero, ACS Appl. Mater. Interfaces, 2024, 16, 56366–56375 Search PubMed.
- Y. Kang, H. Park, B. Smit and J. Kim, Nat. Mach. Intell., 2023, 5, 309–318 CrossRef.
- P. Chen, R. Jiao, J. Liu, Y. Liu and Y. Lu, J. Chem. Inf. Model., 2022, 62, 5446–5456 CrossRef CAS PubMed.
- Z. Cao, R. Magar, Y. Wang and A. Barati Farimani, J. Am. Chem. Soc., 2023, 145, 2958–2967 CrossRef CAS PubMed.
- X. Fu, T. Xie, A. S. Rosen, T. Jaakkola and J. A. Smith, NeurIPS 2023 AI for Science Workshop, 2023 Search PubMed.
- Y. Kang and J. Kim, Nat. Commun., 2024, 15, 4705 CrossRef CAS PubMed.
- O. Kaba and S. Ravanbakhsh, Adv. Neural Inform. Process. Syst., 2022, 35, 4150–4164 Search PubMed.
- M. Petković, P. Romero Marimon, V. Menkovski and S. Calero, Advances in Intelligent Data Analysis XXII, 2024, pp. 129–140 Search PubMed.
- S.-C. Li, H. Wu, A. Menon, K. A. Spiekermann, Y.-P. Li and W. H. Green, J. Am. Chem. Soc., 2024, 146, 23103–23120 CrossRef CAS PubMed.
- M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, S. Ivantchev, G. Madariaga, A. Kirov and H. Wondratschek, Z. Kristallogr. Cryst. Mater., 2006, 221, 15–27 CrossRef CAS.
- M. Afeworki, D. Dorset, G. Kennedy and K. Strohmaier, Stud. Surf. Sci. Catal., 2004, 154, 1274–1281 CrossRef.
- E. Pavón, F. J. Osuna, M. D. Alba and L. Delevoye, Chem. Commun., 2014, 50, 6984–6986 RSC.
- R. E. Fletcher, S. Ling and B. Slater, Chem. Sci., 2017, 8, 7483–7491 RSC.
- C. J. Heard, L. Grajciar and P. Nachtigall, Chem. Sci., 2019, 10, 5705–5711 RSC.
- C. Baerlocher, L. B. McCusker and D. H. Olson, Atlas of Zeolite Framework Types, Elsevier, 2007 Search PubMed.
- B. Widom, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- S. Sharma, S. R. Balestra, R. Baur, U. Agarwal, E. Zuidema, M. S. Rigutto, S. Calero, T. J. Vlugt and D. Dubbeldam, Mol. Simul., 2023, 1–61 Search PubMed.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101 CrossRef CAS.
- A. Garcia-Sanchez, C. O. Ania, J. B. Parra, D. Dubbeldam, T. J. Vlugt, R. Krishna and S. Calero, J. Phys. Chem. C, 2009, 113, 8814–8820 CrossRef CAS.
- M. Brockschmidt, International Conference on Machine Learning, 2020, pp. 1144–1152 Search PubMed.
- M. Zaheer, S. Kottur, S. Ravanbakhsh, B. Poczos, R. R. Salakhutdinov and A. J. Smola, Adv. Neural Inform. Process. Syst., 2017, 30, 3394–3404 Search PubMed.
- J. L. Ba, J. R. Kiros and G. E. Hinton, arXiv, 2016, preprint, arXiv:1607.06450, DOI:10.48550/arXiv.1607.06450.
- I. Loshchilov and F. Hutter, International Conference on Learning Representations, 2018 Search PubMed.
- Y. Rong, W. Huang, T. Xu and J. Huang, 8th International Conference on Learning Representations, 2020 Search PubMed.
- J. Dunne, M. Rao, S. Sircar, R. Gorte and A. Myers, Langmuir, 1996, 12, 5896–5904 CrossRef CAS.
- J. A. Delgado, M. A. Uguina, J. M. Gómez and L. Ortega, Sep. Purif. Technol., 2006, 48, 223–228 CrossRef CAS.
- D.-i. Kwon, M. Numan, J. Kim, M. Yilmaz, S.-E. Park, H. Ihee and C. Jo, J. CO2 Util., 2022, 62, 102064 CrossRef CAS.
- A. Martin-Calvo, J. Parra, C. Ania and S. Calero, J. Phys. Chem. C, 2014, 118, 25460–25467 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. S1: aluminium placement algorithms example; Fig. S2: number of samples per zeolite topology; Fig. S3: reduced simulation settings validation; Fig. S4: RUPTURA validation; Fig. S5: isotherm distribution from the generalization experiment for MEL, MFI, TON and MOR; Fig. S6: heat of adsorption parity plots from the generalization experiment for MEL, MFI, TON and MOR; Table S1: reduced simulation settings; Table S2: model hyperparameters; Table S3: error from the generalization experiment for MEL, MFI, TON and MOR (PDF). See DOI: https://doi.org/10.1039/d5ta02482j |
| ‡ For numerical stability, both the calculation of the loading derivative and the integration process are performed with respect to the logarithm of the pressure. |
| This journal is © The Royal Society of Chemistry 2025 |