Open Access Article
Open Access ArticlePoly(styrene-co-maleamic acid)-based monoamide covalent adaptable networks†
Aitor
Hernández
 ,
Susanne M.
Fischer
,
Susanne M.
Fischer
 ,
Johan M.
Winne
,
Johan M.
Winne
 and
Filip E.
Du Prez
and
Filip E.
Du Prez
 *
*
Polymer Chemistry Research Group, Centre of Macromolecular Chemistry, Laboratory for Organic Synthesis, Department of Organic and Macromolecular Chemistry, Faculty of Sciences, Ghent University, Krijgslaan 281 S4, Ghent B-9000, Belgium. E-mail: Filip.DuPrez@UGent.be
First published on 11th June 2025
Abstract
This study presents poly(styrene-co-maleamic acid)-based monoamide (PS-MMA) covalent adaptable networks (CANs) as a novel class of high performance dynamic covalent polymer networks. PS-MMA CANs are readily synthesized by crosslinking poly(styrene-co-maleic anhydride) (PSMA) copolymers with secondary diamines, introducing a previously unexplored dynamic monoamide exchange chemistry. By tailoring the amine-to-anhydride ratios, crosslink density and viscoelastic properties were finely adjusted, yielding networks with high thermal stability and reprocessability. The dissociation of monoamides into amines and anhydrides, as observed in high-temperature FT-IR analysis, was validated through Density Functional Theory (DFT) calculations. These calculations revealed an enthalpically favored tendency for amines and anhydrides to re-associate into monoamides, confirming their suitability for thermally triggered dynamics and effective viscosity control at increasing temperatures. Rheological analysis of the PS-MMA CANs showed distinct diamine structure-dependent profiles, where the interplay between the chain entanglements, supramolecular interactions and dynamic dissociative monoamide debonding governed their stress relaxation regimes and macroscopic flow behavior. Notably, such materials exhibited a unique combination of fast dissociative relaxation modes and slower reptation-driven dynamics, enabling precise control over material properties. These networks demonstrated an exceptional thermal resilience, maintaining their integrity and flow properties at temperatures up to 280 °C, surpassing the chemically analogous (and more widely studied) monoester-based CANs. Lastly, chemical recycling experiments further validated the sustainability of PS-MMAs, enabling efficient recovery of PSMA precursors while preserving their functionality.
Introduction
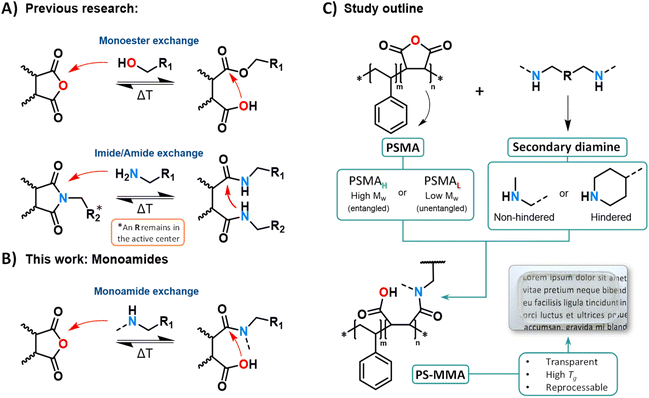
Covalent Adaptable Networks (CANs) are crosslinked polymer materials incorporating dynamic covalent bonds that rearrange when subjected to specific stimuli such as pH changes, light, ultrasonic waves, and most typically by heat.1–3 This unique chemical architecture allows thermally triggered CANs to selectively exhibit the typical macroscopic flow properties of thermoplastics at high temperatures, while maintaining the structure and mechanical properties of thermosets at lower temperatures.4–6 In this context, a series of dynamic covalent chemistries have been developed exploiting neighboring group participation (NGP).7 In that specific case, an internal catalytic effect can be derived from proximity-induced intramolecular covalent interactions, such as ring-closure reactions (e.g., monoester and dicarboximide/amide exchanges), where a fast intermolecular bond exchange is triggered by chemical moieties positioned near the dynamic covalent crosslink (see Scheme 1A).8–15Our research group recently reported polystyrene (PS)-inspired dissociative CANs (PS-MMEs) synthesized via monoesters (Scheme 1A) derived from industrially applied poly-(styrene-co-maleic) anhydride copolymers (PSMAs) and diol-based crosslinkers.16 Such simple, yet functional material design facilitated the creation of NGP-assisted and chemically robust materials without the need for external catalysis while still offering fast flow rates and excellent (re)processability including extrusion and injection molding.16–18 Indeed, the resulting architecture of PSMA-derived monoesters, embedded within the main chain of the copolymer and flanked by two styrene units, greatly improved the thermal resilience of these styrene-rich CANs compared to previous dynamic polyester/anhydride systems. Thus, PSMAs proved to be a polyvalent synthetic handle to develop NGP-enabled CANs with robust chemical structures and could serve as a platform to explore other dynamic cross-linkers to reversibly ring-open and ring-close the maleic anhydride moiety.
The dynamic covalent exchange of amide bonds via NGP was reported in 2021 by two research groups including ours,13,14 where bisamide/dicarboximide equilibria (derived from cyclic anhydrides or dibasic esters) enable an amide bond exchange (Scheme 1A). This would also appear as an interesting alternative chemistry platform to implement in PSMAs, considering the well-known high reactivity of primary amines towards anhydrides.19 However, if the diol crosslinker strategy were to be simply substituted with primary diamines to obtain a bisamide CAN, the resulting PSMA network would entail a design flaw that incurs in reduced flow capability when compared to the earlier mentioned monoester-based design. Indeed, each bisamide pair would contribute to two crosslinking points per anhydride embedded in the PSMA chains (see Scheme 1A).
Then, as the dissociative mechanism is triggered, one of the crosslinking points per amide pair within the PSMA chain would remain part of the dicarboximide, resulting from the dissociative ring-closure of the amides. In this specific architecture, only a fraction of the network could simultaneously dissociate. In turn, this would limit the loss of crosslinking density that the CAN could experience, hence compromising the viscosity drop required to develop adequate flow rates and enable faster (re)processing times at normal PS processing temperatures.20–22 Furthermore, the imide/amide dynamic exchange requires the presence of amide pairs that react to liberate primary amines upon dissociation. In other words, formulations incorporating ratios ‘[NH2]/[anhydride] > 1’ would be needed in order to grant dynamicity to the system.13,14
Additionally, as seen in previous reports, it is certain that the presence of entanglements and elevated network connectivity in CANs synthesized from polymer precursors above their critical entanglement molecular weight (Mc) have a large impact on the networks' rheological properties.16,23–27 According to the Sticky Rouse and Sticky Reptation theory models,28,29 the motion and flow mechanics of chain segments derived from entangled PSMAs (Mw > Mc)30–32 are bound to exhibit chain segment dynamics that are constrained by temporary physical ‘sticky’ supramolecular or dynamic covalent interactions, following a snake-like reptation movement.33–35 This situation leads to flow mechanics involving simultaneous processes where temporary associations continuously break and reform, establishing a complex interplay between entangled chain segment reptation movements, sticky interactions, and the relaxation of mechanical stress.36–38
Starting from this state-of-the-art and from our general interest in the design of amide-containing CANs for reasons of thermal stability and hydrolytic resistance,14,39 the focus of this study was set in using secondary diamines as crosslinkers for the PSMA-embedded cyclic anhydride moieties. With this design strategy, cyclization to the cyclic imide is impossible (Scheme 1B), and at the same time a wide range of entangled CANs can be investigated by crosslinking commercial PSMAs, both below and above their Mc. These materials were expected to retain a CAN-character associated to the NGP effect of the unreacted, pendant carboxylic acid moiety that arises after ring opening. Moreover, as amide bonds are generally more robust than ester bonds, we targeted a straightforward design of several robust, (re)processable polyamide networks with customizable properties. In fact, the resulting reversible so-called ‘amic acids’ or ‘monoamides’ within the poly(styrene-co-maleamic acid) CANs (PS-MMAs) closely resemble the previously studied monoester containing PS-MME CANs in which the ester functionality has been replaced with a tertiary amide that cannot form a dicarboximide (Scheme 1C). Finally, amide dissociation of conformationally restricted amic acid units within low molar mass compounds or crosslinked networks has been reported in strong acidic media40,41 or in the presence of amine catalysts, facilitating carboxylate-mediated reactions enhanced by steric effects.42 Alternatively, the herein reported PS-MMAs were studied as an alternative to imide/amide CANs generated from small molecule monomers to introduce a new class of catalyst-free amide based dissociative CANs.
Experimental procedures
Synthesis of PS-MMA CANs. To a 250 mL or 1000 mL Teflon® beaker immersed in an oil bath and equipped with a magnetic stirrer, 3 mL of THF (or CHCl3) was added per gram of PSMA of commercial name Xibond® 120 (PSMAH) or Xibond® 220 (PSMAL) (Scheme 2A and Table 1). Afterwards, the PSMA beads were slowly poured into the beaker while stirring at room temperature, and the reaction setup was covered with aluminum foil. Once the beads had completely dissolved, targeting adequate stoichiometric ratios, the specified amount of secondary diamine [4,4-trimethylenedipiperidine (DPP) or N,N-dimethyl-1,6-hexanediamine (MeHDA)] (Scheme 2A and Table 1) was quickly added to the beaker at 0.2 g mL−1 in THF (or CHCl3) solutions (Scheme 2B), and the beaker was covered again and kept under constant stirring for 5 min to let the organogel form slowly at room temperature. The resulting transparent gel was heated at 60 °C for 10 min before it was broken into small fragments (diameter <5 mm) inside the same Teflon® beaker with the help of a stainless steel lab spatula. Finally, the remaining solvent was removed by heating gel fragments inside the beaker in an oven at 80 °C for 1 h and then for 4 h under vacuum at 140 °C. PS-MMA CANs were obtained as colorless (for NH/MA eq. ≤ 0.5) to faint yellow ([NH]/[MA] eq. = 1.00), glassy transparent materials. | ||
| Scheme 2 (A) Structure and details of PSMA copolymers (left) and secondary diamine crosslinkers (right) used for the synthesis of the PS-MMAs studied (see Fig. S1† for GPC analysis). (B) Schematic representation of the PS-MMA synthesis method with a representative picture of a PS-MMA material (sample HDP50). | ||
| CANa | PSMA | Crosslinker | [NH]/[MA]eq./eq. | T g (°C) | T d2% (°C) | Swelling ratio (wt%) | Soluble fraction (wt%) |
|---|---|---|---|---|---|---|---|
| a Systematic ABC network labeling code is explained at the beginning of the present subsection. b Glass transition temperature (Tg) obtained from the second heating run measured by DSC (Fig. S3A and B). c Onset temperature after 2% mass loss measured by TGA (Fig. S4A and B). | |||||||
| LMe50 | PSMAL | MeHDA | 0.50 | 127 | 300 | 87 ± 4 | 7.6 ± 2.7 |
| LMe100 | PSMAL | MeHDA | 1.00 | 130 | 296 | 68 ± 3 | 5.0 ± 0.9 |
| LDP50 | PSMAL | DPP | 0.50 | 124 | 313 | 88 ± 5 | 8.7 ± 3.0 |
| HMe10 | PSMAH | MeHDA | 0.10 | 127 | 364 | 166 ± 8 | 6.8 ± 1.5 |
| HMe50 | PSMAH | MeHDA | 0.50 | 132 | 342 | 90 ± 8 | 4.8 ± 0.7 |
| HDP10 | PSMAH | DPP | 0.10 | 124 | 340 | 151 ± 8 | 5.2 ± 1.1 |
| HDP50 | PSMAH | DPP | 0.50 | 124 | 338 | 81 ± 6 | 4.5 ± 1.1 |
Solubility tests at room temperature
Solubility tests were performed on at least six discs, each with a thickness of 2 to 3 mm, prepared from preheated single-pressed samples using a 3 mm diameter puncher. These discs were annealed at 140 °C for 2 h and subsequently allowed to cool gradually. The samples were then immersed in 40 mL acetone for a period of 7 days in 40 mL vials, with the acetone being replaced on the 2nd, 4th, and 6th day, and weighed on the 7th day. The samples were then dried overnight under vacuum at 140 °C. The swelling ratios and soluble fractions were determined using eqn (1) and eqn (2), with m0, ms, and md representing the initial, swollen, and dry masses of the samples, respectively.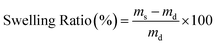 | (1) |
 | (2) |
Density functional theory (DFT) computational details
All calculations were performed using the quantum chemistry software ORCA (version 5.0.2).43 Model compounds of the investigated structures were used in order to reduce the conformational freedom and the computational cost. All structures were optimized using the range-separated double-hybrid functional CAM-B3LYP44 with Grimme's D3 dispersion correction, and the def2-TZVPPD basis set45 was employed for all atoms. A fine numerical integration grid was chosen for accurate energy and gradient evaluations. The conductor-like polarizable continuum model (CPCM)46 was employed with N,N-dimethylformamide (DMF) as the solvent, providing an implicit representation of the matrix environment. Confirmation of the minima, calculation of zero-point vibrational energies and thermal property testing under standard conditions were performed by calculation of analytical normal modes using the rigid-rotor harmonic oscillator (RRHO) approximation. The Nudged Elastic Band (NEB) method47 was employed to locate transition states which were optimized using the abovementioned method. The Hessian matrix was recalculated after every 5th optimization step. All transition states displayed one imaginary frequency and were further confirmed by Intrinsic Reaction Coordinate (IRC) calculations.48Results and discussion
The in-solution synthesis of a series of PS-MMA CANs was performed starting from secondary diamines and two types of PSMA copolymers (Scheme 2A) with molar masses (see Fig. S1† for GPC analyses) either well below (PSMAL, low Mw) or above (PSMAH, high Mw) their expected critical entanglement molecular weight to study its influence on the material flow dynamics. The chosen diamine crosslinkers were incorporated in variable [NH2]/[anhydride] ratios to further evaluate the influence of the tertiary amide architecture and crosslink density on the viscoelastic and rheological properties of the PS-MMAs. As seen in Table 1, the PS-MMAs were labeled following an ABC code in which A stands for the polymer precursor used: ‘L-Series’ (PSMAL) and ‘H-Series’ (from PSMAH); B refers to the diamine crosslinker used: ‘DP’ for the piperidine-based 4,4-trimethylenedipiperidine (DPP) and ‘Me’ for the methylamine-based N,N-dimethyl-1,6-hexanediamine (MeHDA). Lastly, the subscript C (i.e., ‘100’, ‘50’, and ‘10’) states the [NH]/[MA] equivalent percentage ratio as used in the PS-MMAs’ formulation (see Schemes S1, S2, Tables S2 and S3† for further details and formulations).All obtained PS-MMA CANs displayed soluble fractions below 10% (Table 1), elevated glass transition temperatures (i.e., Tg ≥ 120 °C, Fig. S3A and B†), high thermal stability (Td2% > 295 °C, Fig. S4A and B†), as well as exceptional thermal resilience, as evidenced by their good rheological property retention after prolonged exposure to elevated temperatures and excellent reprocessability (vide infra).
Chemical and structural analysis via FTIR
Previous reports on PSMA-derived monoester networks demonstrated difficulties in achieving full conversion of anhydride to ester and carboxylic acid pairs due to kinetically arrested equilibria below the material's Tg.16 This was evidenced by persistent ν (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, anhydride) stretches near 1780 cm−1 in their FTIR spectra.9,16 On the other hand, the FTIR spectra of the LMe100 network ([NH]/[MA] eq. = 1.00, see Table 1) displayed residual anhydride ν (C
O, anhydride) stretches near 1780 cm−1 in their FTIR spectra.9,16 On the other hand, the FTIR spectra of the LMe100 network ([NH]/[MA] eq. = 1.00, see Table 1) displayed residual anhydride ν (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, anhydride) peaks of much lower intensity compared to their homologue monoester networks (Fig. 1), which is ascribed to the higher nucleophilicity of amines towards the anhydrides.19
O, anhydride) peaks of much lower intensity compared to their homologue monoester networks (Fig. 1), which is ascribed to the higher nucleophilicity of amines towards the anhydrides.19
Mild intensity amide I carbonyl signals appeared between 1660 and 1610 cm−1, while intense absorption bands were always observed between 1760 and 1700 cm−1. Even though ν (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) of carboxylic acids generated in both monoesters and monoamides appeared between 1730 and 1700 cm−1, an intense overlapping band between 1760 and 1730 cm−1 suggested a newly acquired carbonyl band associated with the monoamide's amic acid structure (further referred to as Monoamide I).
O) of carboxylic acids generated in both monoesters and monoamides appeared between 1730 and 1700 cm−1, an intense overlapping band between 1760 and 1730 cm−1 suggested a newly acquired carbonyl band associated with the monoamide's amic acid structure (further referred to as Monoamide I).
To further confirm this, a monoamide-containing model compound was synthesized from DPP and succinic anhydride (PP-MMA) (Scheme S4 and Fig. S2†). The FTIR spectrum of PP-MMA (Fig. 1) showcased a partial overlapping pair of peaks, composed of Monoamide I and ν (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, carboxylic acid), centered at 1740 and 1725 cm−1, respectively, matching the values reported in the literature.49 It appears that the molecular architecture of the maleamic acid groups in PS-MMAs leads to strong polar interactions between amide and carboxylic acids groups, resulting in a deviation from standard tertiary amide-related bands (still present in lower intensities). Additionally, a second intense signal was observed at 1585 cm−1, which is also attributed to the maleamic acid group Monoamide II.
O, carboxylic acid), centered at 1740 and 1725 cm−1, respectively, matching the values reported in the literature.49 It appears that the molecular architecture of the maleamic acid groups in PS-MMAs leads to strong polar interactions between amide and carboxylic acids groups, resulting in a deviation from standard tertiary amide-related bands (still present in lower intensities). Additionally, a second intense signal was observed at 1585 cm−1, which is also attributed to the maleamic acid group Monoamide II.
Monoamide dissociation mechanism
To gain further insights, the dissociation equilibrium of PS-MMA networks was evaluated between 100 °C and 200 °C via High Temperature Attenuated Total Reflectance FTIR (HT-ATR-FTIR) spectroscopy to follow changes in the molecular structure as well as assess the presence of intermediate species.In contrast to previous reports on dissociative amide CANs,42 the ‘standard’ Amide I carbonyl band in the HT-FTIR spectra of LMe50 (Fig. 2A) remained unaltered with increasing temperature. In contrast, the carboxylic acid and Monoamide I bands demonstrated a clear decrease, while the intensity of the anhydride signals increased. These observations suggest a ring-closure reaction, where the neighboring carboxylic groups and tertiary amides react to regenerate the original cyclic anhydride.
In order to confirm the reaction mechanism, density functional theory (DFT) calculations, conducted at the CAM-B3LYP/def2-TZVPPD level of theory, have been made to investigate the formation of zwitterionic species during a classic nucleophilic acyl substitution process. This analysis was conducted for two types of aliphatic amines, representing the architecture around the amine groups of DPP and MeHDA: piperidine and dimethylamine (Fig. 2B).
Starting from the dissociated anhydride and amine, the proposed reaction begins with the direct addition of the neutral amine to the anhydride through a first transition state (TS1), resulting in the formation of a zwitterionic intermediate (Int–1). The energy barrier for the transition state involved was calculated to be 14.4 kJ mol−1 higher for the piperidine when compared to the dimethylamine, likely due to the greater steric hindrance imposed by the piperidine's six-membered cycloaliphatic structure. A subsequent proton transfer step then leads to the stabilization of Int–1, and the formation of another intermediate (Int–2). The stabilization energy was determined to be 24.6 kJ mol−1 for piperidine and 13.3 kJ mol−1 for dimethylamine, suggesting that the charge separation in the zwitterion in Int–1 is particularly less stabilized when the cycloaliphatic amine is involved due to the positive charge delocalization restrictions set by its cyclic structure. A stronger acidic character and lower stability of the piperidinium ion compared to dimethylammonium can be reasoned by comparing the pKaH values of dimethylamine's (pKaH = 19) and piperidine's (pKaH = 15) ammonium cations in a non-aqueous medium like acetonitrile.50 Thus, the stronger base is also the most reactive amine.
The transition from Int–2 to the ring-opened structure (Int–3) occurs through a second transition state (TS2), with energy barriers of 67.9 kJ mol−1 for piperidine and 53.3 kJ mol−1 for dimethylamine, respectively. It is noteworthy that the similarity in energy between Int–2 and Int–3 underscores a high degree of reversibility in this step. The final step of the modelled reaction involves another proton transfer, leading to the formation of the monoamide product. Interestingly, in the reaction mechanism involving piperidine, the rate-determining step is the initial addition of the amine to the anhydride, while for dimethylamine, it is the ring-opening of Int–2. Such differences in rate-determining steps can be attributed to the structural and steric variations between the two types of secondary amines. It is noteworthy that the ring closure for the monoesters is expected to be much less endothermic than the corresponding ring closure of the monoamides, which indicates a much higher degree of reversibility in this step.51
Despite the structural and mechanistic similarities between monoesters and monoamides, these results reveal notable differences in their viscoelastic and dynamic properties. In essence, these calculations further highlight the enthalpically favored re-association of dissociated amines to monoamide moieties, pointing to the presence of effectively crosslinked structures at elevated temperatures in monoamide CANs. As seen in the literature, monoester dissociative CANs are prone to experiencing significant modulus and viscosity drops with increasing temperatures due to substantial net-crosslink density losses.16,51 In contrast, monoamides, while still dissociating at higher temperatures, are bound to display a notable exothermic character according to their ΔrG° (ca. +30 kJ mol−1). Such higher reactivity suggests greater re-association rates in MMAs and points to the preservation of network connectivity in PS-MMAs, even at elevated temperatures. Consequently, PS-MMAs are expected to physically behave closer to associative CANs, where their stress relaxation and viscosity drops are likely associated with short-lived bond dissociations. This in turn results in effective network topology rearrangements in response to external mechanical stimuli, rather than in structural losses.
Network rheological assessment
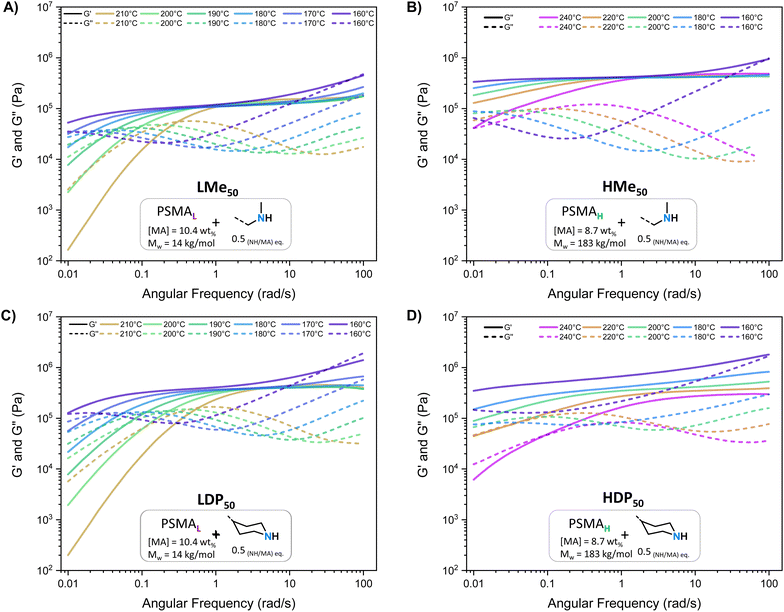
As further discussed below, common features shared between all PS-MMAs include apparent G′ plateaus ( ), typical for efficiently crosslinked networks at intermediate frequencies (see Table 2 for
), typical for efficiently crosslinked networks at intermediate frequencies (see Table 2 for  values at 160 and 200 °C), and a dominant viscous character at low frequencies where G′ < G′′ at high temperatures starting at 180 °C for PSMAL and at 220 °C on PSMAH-derived materials, respectively.22,52,53 However, different
values at 160 and 200 °C), and a dominant viscous character at low frequencies where G′ < G′′ at high temperatures starting at 180 °C for PSMAL and at 220 °C on PSMAH-derived materials, respectively.22,52,53 However, different  evolution profiles were observed when altering the PS-MMA formulations.54
evolution profiles were observed when altering the PS-MMA formulations.54
As deduced from the DFT calculations, the unentangled networks derived from PSMAL (e.g., LMe50 or LDP50, Fig. 3A and C) displayed minimal crosslinking density losses, as evidenced by quasi-invariable 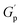 as a function of temperature. In fact, the sole difference observed for this L-Series of networks was the higher plateau moduli recorded for DPP-containing materials as a consequence of their different molecular architecture. Similarly, quasi-invariable
as a function of temperature. In fact, the sole difference observed for this L-Series of networks was the higher plateau moduli recorded for DPP-containing materials as a consequence of their different molecular architecture. Similarly, quasi-invariable  values have also been observed in other dissociative CANs (e.g., imine/amide networks) that display ring-size related entropic factors, which favor the shift of their thermodynamic equilibrium towards the associated state.14
values have also been observed in other dissociative CANs (e.g., imine/amide networks) that display ring-size related entropic factors, which favor the shift of their thermodynamic equilibrium towards the associated state.14
In the case of PS-MMAs, the static  aligns with the conclusions drawn from the DFT calculations (vide supra) and points towards a strong enthalpic driving force that promotes a quick re-association, thereby maintaining a network structure that practically responds like an associative system if analyzed from a practical standpoint.21,22 In the entire H-Series, such invariable
aligns with the conclusions drawn from the DFT calculations (vide supra) and points towards a strong enthalpic driving force that promotes a quick re-association, thereby maintaining a network structure that practically responds like an associative system if analyzed from a practical standpoint.21,22 In the entire H-Series, such invariable  (Table 2) was observed throughout the entire temperature range for the MeHDA-derived HMe50 (Fig. 3B). This network displayed a plateau that was approximately 300 kPa higher than its L-Series counterpart (i.e., LMe50), which is ascribed to the structural reinforcement effect resulting from the additional chain entanglements. However, while the
(Table 2) was observed throughout the entire temperature range for the MeHDA-derived HMe50 (Fig. 3B). This network displayed a plateau that was approximately 300 kPa higher than its L-Series counterpart (i.e., LMe50), which is ascribed to the structural reinforcement effect resulting from the additional chain entanglements. However, while the 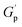 values of the DPP-derived LDP50 and HDP50 above 200 °C did not extensively differ (Fig. 3C and D), at 160 °C, the entire G′ range of HDP50 increased roughly to 250 kPa, similar to the difference observed between the G′ values of LMe50 and HMe50. Interestingly, as the MeHDA crosslinker content was further decreased in the formulation of the less crosslinked HMe10 (Fig. S7A†), the profiles and values of its SAOS curves matched with those of its DPP-based counterpart at all temperatures (HDP10, Fig. S7C†). In other words, the chosen amine crosslinker's structure, parent copolymer, and the subsequent overall network connectivity have a direct impact on the resulting SAOS profile of the PS-MMAs.
values of the DPP-derived LDP50 and HDP50 above 200 °C did not extensively differ (Fig. 3C and D), at 160 °C, the entire G′ range of HDP50 increased roughly to 250 kPa, similar to the difference observed between the G′ values of LMe50 and HMe50. Interestingly, as the MeHDA crosslinker content was further decreased in the formulation of the less crosslinked HMe10 (Fig. S7A†), the profiles and values of its SAOS curves matched with those of its DPP-based counterpart at all temperatures (HDP10, Fig. S7C†). In other words, the chosen amine crosslinker's structure, parent copolymer, and the subsequent overall network connectivity have a direct impact on the resulting SAOS profile of the PS-MMAs.
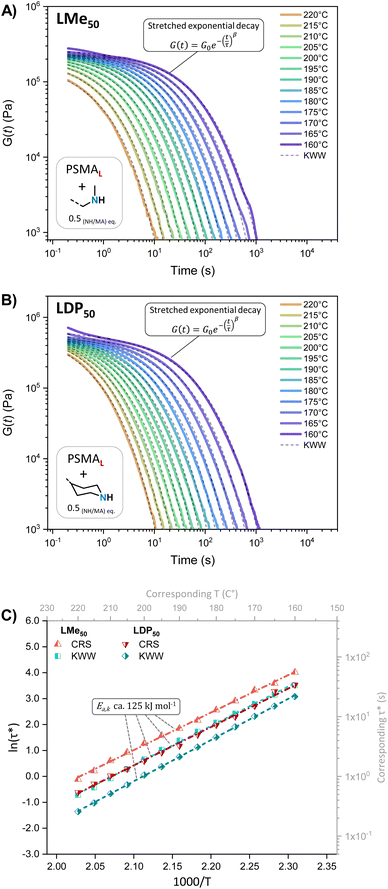
The unentangled L-Series PS-MMA networks consistently exhibited monomodal relaxation profiles across the tested temperature range (i.e., 220 to 160 °C), where the only observable difference was the higher initial G(t) values of LDP50 compared to LMe50 (Fig. 4A and B), mirroring its G′ behavior in SAOS experiments. Their relaxation curves could then be successfully fitted to Kohlrausch–Williams–Watts (KWW) stretched exponential decays (see eqn (3)) with β factors comprised between 0.4 and 0.6 (Table S5†), revealing monomodal relaxation profiles of moderate dispersity with remarkably fast relaxation times (τKWW) beyond 180 °C, i.e., below 10 s (see Fig. 4C or Table S6†).
 | (3) |
 | (4) |
The results obtained suggest homogeneous network structures, where the dynamic bond exchange processes dominate and the influence of entanglements or supramolecular interactions is minimal. Moreover, the relaxation time distributions H(λ) extracted from the continuous relaxation spectra (CRS)16,55–57 of the L-Series, obtained using the PyRespect software developed by Shanbhag,58 also revealed monomodal relaxation time distributions without intense slow relaxation modes (Fig. S11†), corroborating the KWW analyses and yielding similar relaxation times (τ) and activation energies (Ea,k, see eqn (4), ca. 125 kJ mol−1 see Fig. 4C, S12 or Table S6†).
Conversely, the relaxation profiles of the entangled H-Series PS-MMAs (Fig. 5A, B and S13†) deviated from the narrow monomodal behavior observed in the L-Series. Entangled CANs are known to develop slow relaxation modes that intensify at lower temperatures,16 transitioning from monomodal relaxations towards ‘discrete Rouse’29,59multi-regime profiles governed by sticky reptation and Rouse mechanisms as follows: (R–I) initial sticky reptation and Rouse dynamics at lower temperatures that showcase the transition from the glassy state to the rubbery state following power-law decays, (R–II) a rubbery plateau modulus, (R–III) a second power-law decay associated with sticky Rouse and reptation mechanisms, and (R–IV) a terminal mono-exponential decay relaxation.
However, clear differences emerge at a glance when comparing the obtained relaxation curves of HMe50 and HDP50 (see Fig. 5A and B). Despite the fact that both were formulated following the same 0.5 equivalents of amine groups per anhydride crosslinkers (Table 1), HMe50 (Fig. 5A) was only found close to exhibiting a defined power-law decay with ‘G(t) ∼ t−0.44’ at 240 °C, provided that its relaxation curves seem to transition to bimodal exponential decays at decreasing temperatures. This suggests the presence of a second main relaxation mode that is significantly influenced by temperature.
In contrast, the curves of HDP50 (Fig. 5B) mainly transition across the aforementioned ‘discrete-Rouse’ regimes R–II to R–IV, where the R–III with power-law decays is between G240°C(t) ∼ t−1.0 and G(t) ∼ t−0.68. Here, it should be noted that the theoretical ‘G(t) = t−0.5’ slope was ascribed to highly entangled associative models where the influence of net-crosslinking density losses is neglected.37,38,60
Interestingly, reducing the MeHDA crosslinker content ratio [NH]/[MA] from 0.5 to 0.1 in network HMe10 (Fig. S13C†) led to a material exhibiting the same ‘discrete-Rouse’ relaxation profile including the power law decays displayed by its DPP-derived homologue HDP10 (Fig. S13D†) and by the more densely crosslinked HDP50 (Fig. 5B). Thus, in line with the observations made in SAOS experiments, the structure and concentration of the secondary amine crosslinker are confirmed to influence the stress relaxation and viscoelastic profiles of PS-MMAs, which are further addressed in the present section. Still, even though the CRS analyses of both HDP50 and HMe50 (Fig. 5B, D and S1†) revealed similar relaxation times and activation energies (Ea,k,CRS = 117 kJ mol−1, Table 3), the H(λ) function of HMe50 exhibited broader relaxation time distributions and incomplete relaxation at extended times, implying the existence of a slower relaxation mechanism. This bimodal behavior is still consistent with the sticky Rouse and reptation models,36–38 where chain diffusion or reptation events constrained by supramolecular interactions such as hydrogen bonding or polar interactions can dominate relaxation dynamics at longer times.27,59 In view of those results, the whole H-Series was fitted to a two-element KWW (KWWD) decay as follows (eqn (5)):
 | (5) |
| Material | τ 220°C (s) | τ 180°C (s) | E a,k (kJ mol−1) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| CRS | Bond | Rouse | CRS | Bond | Rouse | CRS | Bond | Rouse | |
| a Relaxation times τ at 220 or 180 °C obtained from CRS H(λ) maxima and both bond-driven and Rouse-driven KWWD components, where τbond = τ1 and τRouse = τ2. b Kinetic activation energy (Ea,k), see equation eqn (4), of the stress relaxation of the network calculated from the CRS H(λ) maxima and both bond-driven and Rouse-driven KWWD components. | |||||||||
| HMe10 | 6 | 3 | 2 | 66 | 42 | 24 | 117 ± 1.8 | 126 ± 1.2 | 129 ± 1.4 |
| HMe50 | 4 | 2 | 1 | 51 | 30 | 425 | 117 ± 2.1 | 133 ± 2.6 | 229 ± 5.5 |
| HDP10 | 2 | 1 | 0.4 | 33 | 12 | 7 | 119 ± 3.3 | 130 ± 0.8 | 135 ± 2.3 |
| HDP50 | 2 | 1 | 0.4 | 24 | 14 | 8 | 121 ± 2.9 | 130 ± 1.7 | 132 ± 1.8 |
Surprisingly, the β1 values, found for the faster flowing components of the entire H-Series, were between 0.4 and 0.6 (Table S7†), matching the ranges of the single β found in the monomodal relaxation of the L-Series. In contrast, the value for the second and slower component yielded β2 ranges between 0.2 and 0.3 (Table S8†), which revealed a complex relaxation landscape composed of an exceptionally disperse population of relaxation events. These results indicate that both the apparent bimodal curves of HMe50 and ‘discrete-Rouse’ curves of HMe10, HDP10 and HDP50 can be rationalized as a result of the overlapping of two main disperse relaxation modes (Fig. 5C, D and S14†). The presence of two main relaxation modes has been reported in materials with various exchange reaction mechanisms,61 coexistence of different dynamic chemistries,62,63 or a defined population of catalyzed dynamic crosslinks.10,64 In our case, no other plausible reaction mechanism could be confirmed via DFT calculations. Even though activation energies in the range of those of the slow mode found in HMe50 (ca. 230 kJ mol−1, Fig. 5E) have been reported,39,65,66 such elevated value could also indicate that an additional physical phenomenon is contributing to the flow rate gains at increasing temperatures.
These findings strengthen the hypothesis of a coexistence of both a distribution of faster relaxations that are predominantly driven by fast bond dissociations (τbond = τ1) and a second array of relaxation events governed by the Rouse time of reptating entangled chain strands (τRouse = τ2)28,29 defining the timescale for terminal relaxation in these systems (τTR).67
At the same time, such chain Rouse times can see themselves strengthened by accumulative supramolecular interactions that act as a further layer of intrinsic reptation stickers.26,68,69 Considering that the frictional drag coefficient, associated with the stickers acting over an entangled chain segment undergoing reptation, is proportional to τRouse,29 efficient supramolecular interactions involving amides, carboxylic acids, dissociated amines, or anhydrides are likely to significantly impair these slow relaxation modes (Fig. 6A).59
We then hypothesized that, in a situation where entangled chain segment motions would be significantly restrained by intense reptation phenomena (e.g., in HMe50), the evolution of τRouse would become substantially more pronounced than that of τbond, or in other words: Ea,k,Rouse ≫ Ea,k,bond. Consequently, as temperature decreases, sticky reptation constrained relaxation events would intensify at a much faster rate than bond dissociation-driven relaxations, leading to bimodal relaxation profiles where sticky Rouse relaxation regimes ultimately decouple from faster bond exchange-driven relaxation events free of reptation restrictions. This situation would explain why HMe50, as the only densely crosslinked entangled network derived from the less-hindered amines within the MeHDA crosslinker (Fig. 6B), resulted in stronger supramolecular reptation constraints than its bulkier DPP-derived counterpart (HDP50). Such structure–property relationship not only accounts for the formulation dependence of HMe50's bimodal stress relaxation profile (Fig. 5A) but also elucidates the reason behind the observed higher and invariable 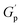 values, as the network elasticity was being reinforced by stronger supramolecular interactions. Therefore, as indicated in Table 3 and Fig. 5E and F, the previously discussed KWWD analysis essentially captured discrete τ and Ea,k of either a dominant ‘bond’ dissociation or ‘sticky Rouse’ reptation restrained flow components. In fact, despite the differences observed on the τbond values across the entire H-Series, all Ea,k,bond values were found to be between 117 and 133 kJ mol−1. Likewise, the Ea,k,Rouse extracted from the three ‘discrete-Rouse’ materials (i.e., HDP50, HDP10 and HMe10, Fig. 5B, C, D and S13†) is in close proximity to the Ea,k,KWW, Ea,k,bond and Ea,k,CRS of the L-Series PS-MMAs (Tables 3 and S6†).
values, as the network elasticity was being reinforced by stronger supramolecular interactions. Therefore, as indicated in Table 3 and Fig. 5E and F, the previously discussed KWWD analysis essentially captured discrete τ and Ea,k of either a dominant ‘bond’ dissociation or ‘sticky Rouse’ reptation restrained flow components. In fact, despite the differences observed on the τbond values across the entire H-Series, all Ea,k,bond values were found to be between 117 and 133 kJ mol−1. Likewise, the Ea,k,Rouse extracted from the three ‘discrete-Rouse’ materials (i.e., HDP50, HDP10 and HMe10, Fig. 5B, C, D and S13†) is in close proximity to the Ea,k,KWW, Ea,k,bond and Ea,k,CRS of the L-Series PS-MMAs (Tables 3 and S6†).
These observations indicate that the power-law regime (found in HMe10, HDP10 and HDP50) seems to root in strong synergies shared between the Ea,k of bond and reptation driven mechanisms. Consequently, the system's main relaxation mechanism follows a smooth transition from bond- to reptation-driven over a given time window. In contrast, HMe50 showed a significant mismatch between its bond and Rouse Ea,k (Table 3), and therefore its relaxation curves adopted two-element bimodal profiles instead of power-law decays following G(t) ∼ t0.5.
In order to confirm the non-covalent or kinetic nature of these observations, benzoic acid (BzOH), p-toluenesulfonic acid (pTSOH), zinc acetate (ZnAc2) or 7-methyl-1,5,7-triazabicyclo(4.4.0)dec-5-ene (MeTBD) were introduced in the formulation of four different HMe50 samples (Table S3 and Scheme S3†) jointly to the PSMAH beads, matching 0.25 equivalents of acid/base per amine group to be used in the formulation. These polar molecules, collectively referred to as ‘external reptation stickers’, were chosen to evaluate their impact on both bond and Rouse relaxation components of HMe50 when doped with mild or strong Brønsted acids (BzOH and pTSOH, respectively), Lewis acids (ZnAc2) or non-nucleophilic organic bases (MeTBD)
These polar compounds, when dispersed in the PS-MMA matrix, are expected to physically interact with polar moieties,70,71 such as the carboxylic acids, amides or amines within the doped HMe50 samples, establishing or stimulating strong polar or ionic interactions. If our initial hypothesis were to be correct, these additional external stickers should only further impair sticky reptation and Rouse mechanisms, leading only to marginal effects on bond-controlled relaxation kinetics. Once the Tg, Td2% and gel contents of the doped HMe50 networks were measured to ensure they shared comparable basic thermal and structural properties to those of neat HMe50 (Tables S4†), their SAOS and stress relaxation behavior were analyzed, following the same methodologies used for the H-Series PS-MMAs (Fig. S8, S17–S20 and Tables S10–S13†).
As expected, the analysis of stress relaxation experiments on those doped HMe50 samples (Fig. S17–S20†) showed that Brønsted/Lewis acid (i.e., BzOH, pTSOH, or ZnAc2) species significantly increased the reptation relaxation times without major effects on their activation energies (Fig. 7A and Table S13†). In contrast and as predicted, the bond-driven and CRS-fitted τ and Ea,k values were not severely affected (Fig. 7B, S20 and Table S13†), with the exception of the ionic ZnAc2, which seemed to have a mild negative effect on the monoamide dissociation equilibrium. The only minor reduction on τRouse values was observed in the PS-MMA doped with basic stickers (i.e., MeTBD), where the base is expected to interfere with polar interactions between carboxylic acids and amides in their vicinity.
 | ||
| Fig. 7 (A) Stress relaxation Arrhenius plots of HMe50 samples doped with external reptation stickers depicting Rouse-driven relaxations extracted from KWWD decay fittings and (B) bond-driven relaxations extracted from KWWD fittings (see Fig. S20† for individual plots). (C) Arrhenius plot of the zero-shear viscosity evolution calculated from creep experiments of the H-Series monoamide PS-MMA networks: HMe50 (diamonds), HDP10 (upright tringles) and HDP50 (inverted triangles) with their PSMAH as reference (circles). | ||
Interestingly, a strong base like MeTBD did not significantly alter any thermodynamic or kinetic parameters, suggesting that PS-MMAs do not follow base-catalyzed mechanisms.42 Additionally, extrinsic acidic stickers consistently decreased the networks' overall crosslink densities, as evidenced by reduced G′ and G0 values (Fig. S8, S17 and Table S10†), as they interfered with the amine crosslinkers during the curing of the PS-MMAs. In fact, the strength of Brønsted acids seemed to greatly influence both their modulus losses and the extent of their effect on network relaxations. Thus, consider that the pKa value of aprotic solvents, such as acetonitrile, and of acyclic aliphatic ammonium salts of secondary amines is 19.50,72 Then, the pKa values of BzOH and pTSOH (i.e., 22 and 8, respectively)50 point to more numerous and stronger ionic acid–amine interactions that occur only in the pTSOH-doped HMe50. Then, pTSOH would lead to notably higher drops in moduli and τRouse when compared to BzOH-doped HMe50 or neat HMe50 PS-MMAs.
 | (6) |
As expected, discrete-Rouse materials such as HDP10 or HDP50 revealed two discrete steady flow regimes ascribed by reptation constrained and reptation-free flow states (Fig. 7C).16 Both of them are evidenced by their two distinct viscous flow activation energies (Ea,ν) in the range of 140 kJ mol−1 for creep Regime I, when affected by Rouse dynamics, and 260 kJ mol−1 for creep Regime II as they enter truly terminal viscous flow. In that terminal regime, PS-MMAs reached Ea,ν values closer to that of non-crosslinked PSMAH on its terminal flow state (Table S14†). HMe50, instead, showed an initial η0 plateau heavily constrained by reptation mechanisms that lead to an extremely low Ea,ν of 22 kJ mol−1, which progressively increased to 155 kJ mol−1 beyond 160 °C. This feature, observed on highly crosslinked and entangled MeHDA-derived PS-MMAs, points towards an exploitable strategy to develop tailorable creep resistant monoamide-CANs.
(Re)processing of PS-MMAs via injection molding
All experiments in the previous section showed that the terminal flow rates and relaxation speeds of the ‘discrete-Rouse’ PS-MMAs greatly exceed those of previously reported PSMA-derived monoester CANs and seemed to be less dependent on crosslink densities. However, if the material processing method were to involve a fast cooling step, the crosslinking density and cooling temperatures were expected to become relevant factors that are necessary to be considered. As seen in the DFT calculations performed (vide supra) and the fast gelation times observed during the synthesis of PS-MMAs, high crosslinking degrees translate into a dense population of amines at stake and excessively fast crosslinking density regeneration upon cooling.A processing technique where this effect can be easily observed is injection molding, where the heated material is forced to flow inside a cooled mold. Therefore, to gain insight into the influence of the crosslink density on these processes, injection molding experiments were performed using a lab-scale injection molding machine operating at an injection pressure of 8 bar with a rectangular mold (63.5 mm × 12.5 mm × 3.15 mm), using the faster flowing ‘discrete-Rouse’ materials HDP50 and HDP10 for this purpose. To ensure that the H-Series PS-MMAs could withstand short-term exposure to air at elevated temperatures (e.g., T = 280 °C; t ≤ 10 min), TGA experiments were performed (Fig. S4D and S5C†). Once the materials' integrity during the processing time was indeed guaranteed, an initial injection experiment was performed using a finely ground HDP50 sample (Φ < 1 mm), preheated at 280 °C for 2 minutes and subsequently injected into a rectangular-bar mold (63.5 mm × 12.5 mm × 3.15 mm) set at 80 °C (Fig. 8A).
As can be observed in Fig. 8A, the injected material experienced severe extrudate melt fracture and incomplete mold filling. Further decreasing the crosslinking density by selecting HDP10 afforded more intense viscosity drops, adequate for the material to at least flow inside the mold before it vitrifies and creates a kind of adhered-particle agglomerate73 (Fig. 8B). Mold temperatures that are much higher than the network's Tg (i.e., mold set at 180 vs. 127 °C for the Tg) created surface distortions due to the thermal history of the material (Fig. 8C).
Finally, decreasing the mold temperature to 140 °C yielded a homogeneous specimen with a uniform surface. However, as can be observed in Fig. 8D, the injection pressure limit, set by the maximum operating pressure of the benchtop setup (8 bar, Fig. S22†), was insufficient to completely evacuate the air originally trapped within the mold before the material's vitrification, leading to small surface deformations near the edges of the sample. Nevertheless, the injected sample's unchanged Tg (Fig. S23A†) and the slow decay of G’ beyond this temperature, as observed via shear DMA analysis (Fig. S23B†), demonstrated the integrity of the PS-MMA CAN and its suitability for high-temperature processing.
Chemical recycling of PS-MMAs
As the last part of this study, we targeted a chemical recycling process with the aim to recovering the PSMAH used in the synthesis of HDP10 (Fig. 9A). After isolation and purification, the recuperated PSMA copolymer could then be potentially repurposed or used again in the synthesis of new PS-MMAs, extending the lifetime of its components beyond that achievable by only physically reprocessing it.With this target in mind, 10 g of ground HDP10 (Fig. 9B1) from pressed plates (190 °C for 10 min and 7 MPa) was dissolved in a mixture of 200 mL of xylene, 30 mL of butyl acetate (nBuOAc), 20 mL of acetic acid 98% (AcOH) and 5 mL of acetic anhydride (Ac2O) set under reflux in a Soxhlet extraction setup at 140 °C (Fig. 9A). During this step, butyl acetate and acetic anhydride were added to trap and separate the dissociated amines by forming tertiary acetamides or ammonium salts that would not regenerate the lost monoamides. After 16 h at reflux, the recycled PSMAH (PSMAH-Rec) was then separated from the obtained solution in xylene (39.2 mg mL−1, Fig. 9B2) by precipitating it using 200 mL of cold methanol.
The obtained yellow polymer was dried at 80 °C for 1 h and at 140 °C for 4 h under vacuum. Lastly, the dry sample was then dissolved again in 100 mL of THF, filtered by gravity, precipitated again using 300 mL of cold diethyl ether and dried using the same conditions as used during the previous step. The precursor PSMA copolymer could be recovered with a 85% yield as an off-yellow transparent amorphous soluble polymer (Fig. 9B3). The recovered PSMAH-Rec displayed comparable structural aspects as assessed by FTIR and 1H-NMR (see Fig. S24 and S25†) when compared to the virgin PSMAH with the exception of the yellow coloration and an increase in the MW from 183 to 345 kg mol−1, as measured by size exclusion chromatography (Fig. S1†). Such molar mass increase has been attributed to PSMA chain couplings triggered by residual diamines that remained within the PSMAH-Rec polymer.
Conclusions
This study successfully explored the design, synthesis, and characterization of poly(styrene-co-maleamic acid) (PS-MMA) covalent adaptable networks (CANs) as a novel class of thermally reprocessable materials based on monoamide dynamic chemistry. By utilizing the reactivity of secondary diamines with PSMA copolymers and controlling the amine-to-anhydride ratio, we developed tunable network architectures that enable fine adjustment of crosslink density, reprocessability, and mechanical properties. The introduction of tertiary amides provided a robust framework for creating CANs with enhanced thermal stability and dynamic behavior.DFT calculations revealed the enthalpically favored re-association of monoamide bonds, aligning with the dissociation behavior observed in High-Temperature FTIR analyses.
The reported findings confirm the unique dissociative exchange chemistry of PS-MMAs. Rheological assessments further demonstrated structure-dependent profiles driven by the interplay of crosslink density, chain entanglements, and amine crosslinker architecture. These networks exhibited a combination of fast dissociation-driven relaxation and slower reptation-driven dynamics, allowing tailored flow and stress relaxation behavior suitable for diverse processing conditions. Thermal analyses confirmed the remarkable resilience of PS-MMAs, maintaining dynamic properties and structural integrity at temperatures up to 280 °C, outperforming conventional CAN systems. Furthermore, chemical recycling experiments showcased the sustainability of PS-MMAs, enabling efficient recovery of their PSMA precursor copolymer while preserving their functionality, underscoring the potential for these networks to integrate into a circular polymer economy and extend the material lifecycle.
In summary, PS-MMAs represent a significant advancement in dynamic covalent polymer networks, combining high-performance mechanical and thermal properties with reprocessability and recyclability. These findings highlight their potential for demanding industrial applications where thermal stability, reprocessability, and sustainability are critical, providing a pathway for environmentally conscious material innovation.
Data availability
The data supporting this article have been included as part of the ESI.† The raw and processed data required to reproduce these findings are available upon request to the corresponding author.Conflicts of interest
The authors have no conflict of interest to declare.Acknowledgements
This project received funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Grant agreement No. 860911 (VITRIMAT). The NMR expertise center (Ghent University) is also acknowledged for providing support and access to NMR infrastructure funded by the Research Foundation – Flanders (I006920N) and the Bijzonder Onderzoeksfonds (BOF.BAS. 2022.0023.01). The authors thank Bernhard De Meyer for providing technical support, Croda and Aurorium (formerly Polyscope) for kindly providing samples that were used in this project. Likewise, the authors express their gratitude to Dr Jérémy Odent and Prof. Dr Jean-Marie Raquez for their assistance during the injection molding tests. Lastly, we acknowledge Loc Tan Nguyen and Dr Adrià Roig for the fruitful discussions held during the duration of this study.References
- C. J. Kloxin, T. F. Scott, B. J. Adzima and C. N. Bowman, Macromolecules, 2010, 43, 2643–2653 CrossRef CAS PubMed.
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Science, 2011, 334, 965–968 CrossRef CAS PubMed.
- M. Podgórski, B. D. Fairbanks, B. E. Kirkpatrick, M. McBride, A. Martinez, A. Dobson, N. J. Bongiardina and C. N. Bowman, Adv. Mater., 2020, 32, 1906876 CrossRef PubMed.
- J. M. Winne, L. Leibler and F. E. Du Prez, Polym. Chem., 2019, 10, 6091–6108 RSC.
- V. Zhang, B. Kang, J. V. Accardo and J. A. Kalow, J. Am. Chem. Soc., 2022, 144, 22358–22377 CrossRef CAS PubMed.
- A. V. Karatrantos, O. Couture, C. Hesse and D. F. Schmidt, Polymers, 2024, 16, 1373 CrossRef CAS PubMed.
- F. Van Lijsebetten, J. O. Holloway, J. M. Winne and F. E. Du Prez, Chem. Soc. Rev., 2020, 49, 8425–8438 RSC.
- O. R. Cromwell, J. Chung and Z. Guan, J. Am. Chem. Soc., 2015, 137, 6492–6495 CrossRef CAS PubMed.
- M. Delahaye, J. M. Winne and F. E. Du Prez, J. Am. Chem. Soc., 2019, 141, 15277–15287 CrossRef CAS PubMed.
- M. Delahaye, F. Tanini, J. O. Holloway, J. M. Winne and F. E. Du Prez, Polym. Chem., 2020, 11, 5207–5215 RSC.
- H. Zhang, S. Majumdar, R. A. T. M. van Benthem, R. P. Sijbesma and J. P. A. Heuts, ACS Macro Lett., 2020, 9, 272–277 CrossRef CAS PubMed.
- M. Podgórski, S. Mavila, S. Huang, N. Spurgin, J. Sinha and C. N. Bowman, Angew. Chem., Int. Ed., 2020, 59, 9345–9349 CrossRef PubMed.
- Y. Chen, H. Zhang, S. Majumdar, R. A. T. M. van Benthem, J. P. A. Heuts and R. P. Sijbesma, Macromolecules, 2021, 54, 9703–9711 CrossRef CAS PubMed.
- F. Van Lijsebetten, Y. Spiesschaert, J. M. Winne and F. E. Du Prez, J. Am. Chem. Soc., 2021, 143, 15834–15844 CrossRef CAS PubMed.
- R. Wink, S. Majumdar, R. A. T. M. van Benthem, J. P. A. Heuts and R. P. Sijbesma, Polym. Chem., 2023, 14, 4294–4302 RSC.
- A. Hernández, T. Maiheu, E. Drockenmuller, D. Montarnal, J. M. Winne and F. E. Du Prez, Chem. Mater., 2024, 36, 7487–7503 CrossRef.
- W. Denissen, M. Droesbeke, R. Nicolaÿ, L. Leibler, J. M. Winne and F. E. Du Prez, Nat. Commun., 2017, 8, 14857 CrossRef CAS PubMed.
- J. L. Self, N. D. Dolinski, M. S. Zayas, J. Read de Alaniz and C. M. Bates, ACS Macro Lett., 2018, 7, 817–821 CrossRef CAS PubMed.
- A. R. Padwa, Y. Sasaki, K. A. Wolske and C. W. Macosko, J. Polym. Sci., Part A: Polym. Chem., 1995, 33, 2165–2174 CrossRef CAS.
- B. R. Elling and W. R. Dichtel, ACS Cent. Sci., 2020, 6, 1488–1496 CrossRef CAS PubMed.
- A. Jourdain, R. Asbai, O. Anaya, M. M. Chehimi, E. Drockenmuller and D. Montarnal, Macromolecules, 2020, 53, 1884–1900 CrossRef CAS.
- O. Anaya, A. Jourdain, I. Antoniuk, H. Ben Romdhane, D. Montarnal and E. Drockenmuller, Macromolecules, 2021, 54, 3281–3292 CrossRef CAS.
- B. J. Adzima, H. A. Aguirre, C. J. Kloxin, T. F. Scott and C. N. Bowman, Macromolecules, 2008, 41, 9112–9117 CrossRef CAS PubMed.
- J. J. Lessard, K. A. Stewart and B. S. Sumerlin, Macromolecules, 2022, 55, 10052–10061 CrossRef CAS.
- I. Mahmad Rasid, A. Rao, N. Holten-Andersen and B. D. Olsen, Macromolecules, 2022, 55, 6056–6066 CrossRef CAS.
- M. Ahmadi, L. G. D. Hawke, H. Goldansaz and E. van Ruymbeke, Macromolecules, 2015, 48, 7300–7310 CrossRef CAS.
- L. M. Fenimore, M. J. Suazo and J. M. Torkelson, Macromolecules, 2024, 57, 2756–2772 CrossRef CAS.
- L. Leibler, M. Rubinstein and R. H. Colby, Macromolecules, 1991, 24, 4701–4707 CrossRef CAS.
- R. G. Ricarte and S. Shanbhag, Macromolecules, 2021, 54, 3304–3320 CrossRef CAS.
- D. J. Plazek and V. M. O'Rourke, J. Polym. Sci., Part A-2, 1971, 9, 209–243 CrossRef CAS.
- M. K. Singh, M. Hu, Y. Cang, H.-P. Hsu, H. Therien-Aubin, K. Koynov, G. Fytas, K. Landfester and K. Kremer, Macromolecules, 2020, 53, 7312–7321 CrossRef CAS PubMed.
- J. Noolandi, G. Slater and G. Allegra, Makromol. Chem., Rapid Commun., 2003, 8, 51–58 CrossRef.
- S. F. Edwards, H. Takano and E. M. Terentjev, J. Chem. Phys., 2000, 113, 5531–5538 CrossRef CAS.
- W. L. Vandoolaeghe and E. M. Terentjev, J. Chem. Phys., 2005, 123, 034902 CrossRef CAS PubMed.
- W. L. Vandoolaeghe and E. M. Terentjev, J. Phys. A: Math. Theor., 2007, 40, 14725–14744 CrossRef CAS.
- S. Wu and Q. Chen, Macromolecules, 2022, 55, 697–714 CrossRef CAS.
- X. Cui, N. Jiang, J. Shao, H. Zhang, Y. Yang and P. Tang, Macromolecules, 2023, 56, 772–784 CrossRef CAS.
- J. Xia, J. A. Kalow and M. Olvera de la Cruz, Macromolecules, 2023, 56, 8080–8093 CrossRef CAS.
- L. T. Nguyen, F. Portone and F. E. Du Prez, Polym. Chem., 2024, 15, 11–16 RSC.
- S. Su, F.-S. Du and Z.-C. Li, Org. Biomol. Chem., 2017, 15, 8384–8392 RSC.
- B. Qin, S. Liu, Z. Huang, L. Zeng, J.-F. Xu and X. Zhang, Nat. Commun., 2022, 13, 7595 CrossRef CAS PubMed.
- J. Zhang, Y. Zhou, S. Ma and F. Zhou, Green Chem., 2024, 26, 3368–3377 RSC.
- F. Neese, Wiley Interdiscip. Rev. Comput., 2012, 2, 73–78 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. Hellweg and D. Rappoport, Phys. Chem. Chem. Phys., 2015, 17, 1010–1017 RSC.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- V. Ásgeirsson, B. O. Birgisson, R. Bjornsson, U. Becker, F. Neese, C. Riplinger and H. Jónsson, J. Chem. Theory Comput., 2021, 17, 4929–4945 CrossRef PubMed.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- F. F. Becker, C. Mukhopadhyay, L. Hackfeld, I. Banik and B. K. Banik, Bioorg. Med. Chem., 2000, 8, 2693–2699 CrossRef CAS PubMed.
- A. Kütt, S. Tshepelevitsh, J. Saame, M. Lõkov, I. Kaljurand, S. Selberg and I. Leito, Eur. J. Org Chem., 2021, 2021, 1407–1419 CrossRef.
- M. Delahaye, J. M. Winne and F. E. Du Prez, J. Am. Chem. Soc., 2019, 141, 15277–15287 CrossRef CAS PubMed.
- T. Maiheu, J. Debuyck, F. Van Lijsebetten, A. Hernández and F. E. Du Prez, Eur. Polym. J., 2024, 210, 112998 CrossRef CAS.
- L. M. Fenimore, B. Chen and J. M. Torkelson, J. Mater. Chem. A, 2022, 10, 1039 RSC.
- H. Y. Song, G. Lee, S. Ahn and K. Hyun, Korea-Aust. Rheol. J., 2023, 35, 69–79 CrossRef.
- L. Porath, J. Huang, N. Ramlawi, M. Derkaloustian, R. H. Ewoldt and C. M. Evans, Macromolecules, 2022, 55, 4450–4458 CrossRef CAS.
- R. G. Ricarte and S. Shanbhag, Polym. Chem., 2024, 15, 815–846 RSC.
- L. E. Porath, N. Ramlawi, J. Huang, M. T. Hossain, M. Derkaloustian, R. H. Ewoldt and C. M. Evans, Chem. Mater., 2024, 36, 1966–1974 CrossRef CAS.
- S. Shanbhag, Macromol. Theory Simul., 2019, 28, 1900005 CrossRef.
- R. G. Ricarte, S. Shanbhag, D. Ezzeddine, D. Barzycki and K. Fay, Macromolecules, 2023, 56, 6806–6817 CrossRef CAS.
- J. Shao, N. Jiang, H. Zhang, Y. Yang and P. Tang, Macromolecules, 2022, 55, 535–549 CrossRef CAS.
- M. Guerre, C. Taplan, R. Nicolaÿ, J. M. Winne and F. E. Du Prez, J. Am. Chem. Soc., 2018, 140, 13272–13284 CrossRef CAS PubMed.
- J. Zhao, Z. Zhang, C. Wang and X. Yan, CCS Chem., 2023, 6, 41–56 CrossRef.
- S. Maes, F. Van Lijsebetten, J. M. Winne and F. E. Du Prez, Macromolecules, 2023, 56, 1934–1944 CrossRef CAS.
- F. Van Lijsebetten, K. De Bruycker, E. Van Ruymbeke, J. M. Winne and F. E. Du Prez, Chem. Sci., 2022, 13, 12865–12875 RSC.
- C. Taplan, M. Guerre and F. E. Du Prez, J. Am. Chem. Soc., 2021, 143, 9140–9150 CrossRef CAS PubMed.
- M. A. Bin Rusayyis, L. M. Fenimore, N. S. Purwanto and J. M. Torkelson, Polym. Chem., 2023, 14, 3519–3534 RSC.
- S. Shanbhag and R. G. Ricarte, Macromol. Theory Simul., 2023, 32, 2300002 CrossRef CAS.
- J. Brassinne, A. Cadix, J. Wilson and E. van Ruymbeke, J. Rheol., 2017, 61, 1123–1134 CrossRef CAS.
- N. Jiang, H. Zhang, P. Tang and Y. Yang, Macromolecules, 2020, 53, 3438–3451 CrossRef CAS.
- C. Schaefer, P. R. Laity, C. Holland and T. C. B. McLeish, Macromolecules, 2020, 53, 2669–2676 CrossRef CAS PubMed.
- P. C. Cai, B. Su, L. Zou, M. J. Webber, S. C. Heilshorn and A. J. Spakowitz, ACS Cent. Sci., 2022, 8, 1318–1327 CrossRef CAS PubMed.
- F. V. Lijsebetten, S. Maes, J. M. Winne and F. E. D. Prez, Chem. Sci., 2024, 15, 7061–7071 RSC.
- Z. Shen, H. Ye, Q. Wang, M. Kröger and Y. Li, Macromolecules, 2021, 54, 5053–5064 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Quick material reference appendix, glossary, reagents, instrumentation and characterization methods, synthetic procedures, GPC analyses, thermal analyses, dynamic mechanical thermal analyses, FT-IR analyses, 1H-NMR analyses, SAOS measurements, stress relaxation measurements and analyses, creep measurements and analyses, single screw extrusion and injection molding experiments, network solubility, and chemical recycling procedures (PDF). See DOI: https://doi.org/10.1039/d5ta02035b |
| This journal is © The Royal Society of Chemistry 2025 |