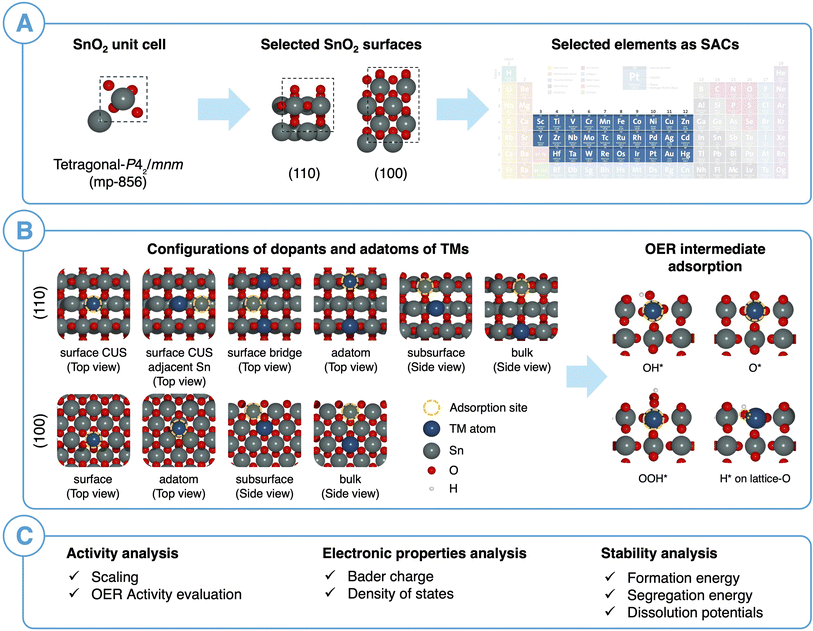
Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Analysis of tin oxide supported transition metal single-atom catalysts for oxygen evolution reaction†
S. A. Keishana
Navodye
and
G. T. Kasun Kalhara
Gunasooriya
 *
*
School of Sustainable Chemical, Biological and Materials Engineering, University of Oklahoma, Norman, OK, 73019 USA. E-mail: kasun.gunasooriya@ou.edu
First published on 13th June 2025
Abstract
Water electrolysis using cost-effective electrocatalysts offers a promising avenue for cheaper green hydrogen production, efficient renewable energy storage, and widespread implementation. In recent years, single-atom catalysts (SACs) supported on acid-stable oxides have emerged as an important class of electrocatalysts due to their ability to maximize the efficiency of precious metal utilization and create well-defined single-site materials with unique electronic properties. Tin oxide (SnO2) is a cheap, acid-stable oxide material with poor OER activity. In this work, we considered 29 SACs corresponding to 3d, 4d, and 5d transition metals with different configurations on SnO2, including surface, subsurface, bulk SACs, and surface-adatoms, using spin-polarized density functional theory calculations for their OER activity and stability. We systematically evaluate the electronic structure trends, the adsorption energy of OER intermediates, OER catalytic activity using both AEM and LOM mechanisms, and the thermodynamic and aqueous stability of these SnO2-supported transition metal SACs (TM-SACs). From a subset of stable TM-SACs, Rh and Pt SACs on the SnO2 surface are identified as the most promising catalysts for experimental validation. Ir-SAC on SnO2(110) also showed comparable activity to state-of-the-art IrO2(110), suggesting significant cost reductions due to lower Ir-loading requirements. Based on these theoretical findings, rational catalyst design principles for next-generation oxide-supported TM-SACs for the OER are established.
1. Introduction
Water electrolysis offers a promising avenue to decarbonize the global energy and chemical sector by converting renewable energy into green hydrogen.1,2 Hydrogen is widely used in the chemical industry for a number of processes, such as ammonia production, methanol and olefin production, and hydrogenation reactions. Water electrolysis consists of two half-cell reactions: the oxygen evolution reaction (OER, 2H2O → O2 + 4e− + 4H+, E0 = 1.23 VRHE) and the hydrogen evolution reaction (HER, 2H+ + 2e− → H2, E0 = 0 VRHE). Extensive studies have shown that the OER is the critical half-cell reaction that governs the overall efficiency of water electrolyzers.1,2 This inefficiency can be attributed to sluggish kinetics, limited aqueous stability resulting dissolution of metal atoms under high oxidative potentials and low pH environments, high cost and scarcity of state-of-the-art OER catalysts (IrO2 and RuO2) further hindering their commercial viability.3 To address this challenge, the rational design and development of stable, active, selective, and cost-effective OER catalysts is imperative.Single-atom catalysts (SACs), consist of isolated, catalytically active atoms embedded within supporting materials, have recently emerged as an important class of electrocatalysts which can integrate the merits of both homogeneous and heterogeneous catalysts.4 SACs have shown great potential for developing highly efficient, low-cost electrocatalysts due to their ability to enhance the utilization of precious metals and create well-defined single-site materials with unique electronic properties.5 While the performance of SACs can be optimized by tailoring the metal atoms, adjacent coordinative dopants, and metal loading, the stability of the support material which host the SACs is crucial in determining the catalytic performance under real operating conditions. The highly oxidative and corrosive reaction environments, especially under OER conditions, significantly reduce material aqueous stability, making most of the materials not suitable for oxygen electrochemical applications and drastically limiting the potential material space as SAC supports.6 In addition to that, electrical conductivity of the support material plays a role in achieving efficient electrochemical reactions.
Tin oxide (SnO2) supported materials have recently attracted a significant interest for oxygen electrochemistry due to its high stability under oxidative conditions and cost effectiveness.7–16 Although SnO2 itself shows poor oxygen electrocatalytic activity, doping is frequently used to enhance the catalytic activity7–16 and electrical conductivity.17,18 For example, Sasaki et al. showed that Pt nanoparticles supported on SnO2 could be used as carbon-free supports for oxygen reduction reaction (ORR) preventing the oxidation-induced support corrosion.8 Oh et al. demonstrated oxidized Ir-nanodendrites supported on antimony doped SnO2 to be more active and highly stable compared to commercial Ir black and Ir/C catalysts.11 Liu et al. demonstrated that IrO2 supported on antimony doped SnO2 nanowires showed superior activity compared to pure IrO2 and good stability for a period of 646 hours.12 Similarly, Bhanja et al. showed that IrO2 nanoparticles supported on mesoporous SnO2 resulted in much lower overpotential of 240 mV at 10 mA cm−2 than the state-of-the-art catalyst IrO2/C with an overpotential of 360 mV.13 Recent theoretical studies by Jimenez-Villegas et al. identified that, out of 16 transition metal (TM) single atoms supported on SnO2(110), single atoms of Mn, Ti and Fe were active and selective for 2e− water oxidation reaction while single atoms of W for 2e− reduction reaction.10 Despite many promising experimental and theoretical studies, a comprehensive and systematic evaluation of TM-SACs on SnO2 surfaces for 4e− OER activity and stability is yet to be explored.
In this work, we use spin-polarized density functional theory (DFT) to understand the electronic structure, OER activity, and thermodynamic and aqueous stability of single atoms of 29 elements corresponding to 3d, 4d, and 5d TMs, supported on SnO2. First, we identified the thermodynamically stable SnO2 facets, SnO2(110) and SnO2(100), based on a comprehensive surface energy calculations analysis and Wulff diagram construction. Ten different configurations of TM-SACs on both surfaces including surface, subsurface, bulk SCAs and surface adatoms were considered for the subsequent activity and stability analysis. Both adsorbate evolving mechanism (AEM) and lattice oxygen mechanism (LOM) were considered in determining the OER activity. The electronic structure modifications of TM-SACs on various configurations on SnO2 were analyzed using density of states (DOS), and Bader charges. We then performed a systematic stability analysis of TM-SACs on SnO2 based on the formation energies and segregation energies to understand the thermodynamic stability and dissolution potentials to evaluate the aqueous stability under realistic OER potentials. Based on both stability and activity analysis, we determined the most promising TM-SAC candidates for experimental validation. Based on these theoretical findings, rational catalyst design principles for next-generation TM-SACs based oxygen electrocatalysts are established.
2. Methods
Periodic spin-polarized DFT calculations were performed using the revised Perdew–Burke–Ernzerhof (RPBE) exchange correlational functional,19 a plane-wave basis set with a cut-off kinetic energy of 500/400 eV for bulk/surface structures, and the projector-augmented wave (PAW) method as implemented in the Vienna Ab initio Simulation Package (VASP version 5.4.4).20,21 PAW pseudopotentials and Hubbard U correction values of 3.25 eV ‘V’, 3.7 eV ‘Cr’, 3.9 eV ‘Mn’, 5.3 eV ‘Fe’, 3.32 eV ‘Co’, 6.2 eV ‘Ni’, 4.38 eV ‘Mo’, 6.2 eV ‘W’ were selected according to the Materials Project (MP) database.22 The electronic convergence criterion was 10−4 eV, while the force criterion for geometry relaxation was 0.05 eV Å−1.The low-index (110) and (100) terminations of tetragonal-SnO2 (mp-856) were selected to model oxide surfaces as these surfaces corresponded to the lowest surface energies (see Section 3.1). SnO2(110) oxide surface was modelled with (2 × 1) with a 4-layer slab while SnO2(100) was modelled with (2 × 2) unit cell with 6-layer slab. In all the slabs, bottom half of the slab in vertical z direction were constrained at the bulk positions, while the top half of the slab and the adsorbed species were fully relaxed. The slabs were separated in the perpendicular z-direction by 15 Å of vacuum, and a dipole correction was applied. To obtain numerically converged results, the Brillouin zone was sampled with (3 × 3 × 1) and (3 × 2 × 1) Γ-centered k-point grids for (110) and (100) surfaces, respectively. All crystal structure manipulations and data analysis were carried out using the Python Materials Genomics package23 and Atomic Simulation Environment (ASE).24 Atomic charges were calculated using Bader analysis as implemented by Henkelman et al.25 Similar to our previous studies,26,27 effective Bader charges were defined as q = Zval − qBader, where Zval is the number of valence electrons and qBader is the computed Bader charge. Crystal orbital Hamiltonian Populations (COHP) calculations were conducted using the Lobster and LobsterPy packages.28 Surface Pourbaix diagrams which show the thermodynamically most favorable surface coverage state as a function of the potential (USHE) and pH, were developed based on the method highlighted by Hansen et al.29
OER catalytic activities of the different surfaces were evaluated based on the theoretical overpotential (η) and limiting potential (UL) based on adsorbate evolving mechanism (AEM) and lattice oxygen mechanism (LOM). The four proton-coupled electron transfer (PCET) reactions under acidic conditions for the 4e− AEM OER mechanism are:
| H2O(l) + * → OH* + (H+ + e−) | (1) |
| OH* → O* + (H+ + e−) | (2) |
| H2O + O* → OOH* + (H+ + e−) | (3) |
| OOH* → O2(g) + * + (H+ + e−) | (4) |
The reaction (1) and (2) are similar for the LOM, while reaction (3) and (4) involve a near-by lattice oxygen according to the following reactions.
| O* + Olattice → O2(g) + Vo | (5) |
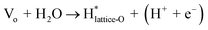 | (6) |
 | (7) |
The computational hydrogen electrode (CHE) was used to express the chemical potential of the proton–electron pair (H+ + e−), which relates chemical potential of the proton–electron pair with chemical potential of gas-phase H2 molecule based on the equilibrium μ[H+] + μ[e−] = 1/2μ[H2(g)] at 0 VRHE (where RHE is the reversible hydrogen electrode).30 The effect of electrode applied potential (URHE) on the free energy of adsorption of the reaction intermediates was then taken into account by shifting the −neURHE term. The free energy of adsorption at a given potential U vs. RHE is given by:
| ΔGCHE(URHE) = ΔGCHE(URHE = 0 V) − neURHE | (8) |
 with respect to the catalyst surface, relative to H2O(g) and H2(g) at U = 0 V and standard conditions (T = 298.15 K, P = 1 bar, and pH = 0). In this equation, ΔEDFT is the difference in DFT calculated electronic energy, ΔEZPE is the difference in zero-point energies,
with respect to the catalyst surface, relative to H2O(g) and H2(g) at U = 0 V and standard conditions (T = 298.15 K, P = 1 bar, and pH = 0). In this equation, ΔEDFT is the difference in DFT calculated electronic energy, ΔEZPE is the difference in zero-point energies,  is the difference in integrated heat capacity from 0 to 298.15 K, ΔS is the change in entropy of the adsorbed species. The values for the current analysis were taken from a previous study by Gunasooriya and Nørskov.6
is the difference in integrated heat capacity from 0 to 298.15 K, ΔS is the change in entropy of the adsorbed species. The values for the current analysis were taken from a previous study by Gunasooriya and Nørskov.6
The theoretical thermodynamic OER overpotential (ηOER), which is a measure of the activity of a catalyst is then defined from Gibbs free energies of reaction (1)–(4) for AEM mechanism (ηOER-AEM):
| ηOER-AEM (V) = max[ΔGOH*, ΔGO* − ΔGOH*, ΔGOOH* − ΔGO*; 4.92 − ΔGOOH*]/e − 1.23 V | (9) |
While the Gibbs free energies of reactions (1), (2), (5)–(7) are used to define the LOM mechanism (ηOER-LOM)
| ηOER-LOM (V) = max[ΔGOH*, ΔGO* − ΔGOH*, 4.92 + ΔGH* − ΔGO*, −ΔGH*]/e − 1.23 V | (10) |
The step with the largest value in eqn (9) for AEM (eqn (10) for LOM) is referred to as the potential-determining step (PDS) for OER. It is important to note that η should not be compared directly with a measured overpotential, since the measured overpotential depends on the current density.1
3. Results and discussion
3.1 Analysis of SnO2 oxide support aqueous stability, surface energy, surface Pourbaix and OER activity
For our analysis, we selected the most stable phase of SnO2 with the P42/mnm space group as the bulk structure (Fig. S1a†) and our DFT optimized lattice parameters (a = b = 4.80 Å and c = 3.24 Å) are in good agreement with experimental literature.17 To determine the aqueous stability of SnO2 under harsh OER operating conditions we constructed a Pourbaix diagram (Fig. 1a) for SnO2 using DFT as implemented in Pymatgen.23,31 Pourbaix diagrams are an invaluable tool for exploring the corrosion profiles of materials as these diagrams show the most stable species as a function of pH and applied electrochemical potential.32 This potential-dependent analysis of materials stability is particularly relevant for understanding how material transformations, such as conversion to other solid species or dissolution, and how stability affects the electrochemical activity and selectivity observed over the potential range. It is worth mentioning that materials aqueous stability is an important yet often overlooked criteria in material design. In addition to the Pourbaix diagrams, we also plotted the most stable phases (Fig. 1b) based on the decomposition free energy (ΔGpbx) of the SnO2 under the potential range of 0–2 V vs. RHE at pH = 0, 7, and 13 representing acidic, neutral and alkaline conditions, respectively. ΔGpbx of SnO2 is 0 above 0.1 V vs. RHE at pH = 0 and within the considered complete potential range at pH = 7 and 13 indicating SnO2 does not undergo dissolution. On the basis of this analysis, we determined that SnO2 is stable in wide range of pH conditions under OER potentials.To determine the most stable surfaces of SnO2, we calculated surface energy for facets up to Miller index of 2. It is important to note that we preserved the SnO2 stoichiometry and used the DFT-optimized lattice parameters while generating surfaces. We considered all the surfaces for a given Miller index (Sn-terminated, O-terminated, combined Sn- & O-terminated) and all the considered surfaces are shown in Fig. S1b†). Surface energy (J m−2) for a given surface was calculated based on eqn (11),
 | (11) |
Based on our calculations of surface energies, we constructed a Wulff diagram to represent the thermodynamically stable crystal shape of SnO2 nanoparticles. As shown in Fig. 2b, nearly the entire surface area of the nanoparticle is comprised of the SnO2(110), SnO2(100) and SnO2(101) surfaces with area fractions of 0.38, 0.28 and 0.34, respectively. The average surface energy of the particle is 0.77 J m−2, and the shape factor of the particle is 5.39. This calculated shape factor serves as a general measure of anisotropy under equilibrium conditions. Based on our surface energy analysis and Wulff construction, we selected the SnO2(110) and SnO2(100) surfaces for OER activity analysis, as these surfaces are the most stable facets with significant surface area fractions.
As shown in Fig. 2c and d, the SnO2(110) surface features two different surface Sn sites: a coordinatively unsaturated (CUS) site with five-coordinated oxygen atoms (5c-M) and a bridge surface site with six-coordinated oxygen atoms (6c-M) and SnO2(100) surface with identical Sn sites. As the coverage of reaction intermediates plays a significant role in influencing the local environment of the active site,33,34 it is important to establish the most relevant surface coverage under the OER reaction conditions to accurately calculate the electrocatalytic activity. Therefore, surface Pourbaix diagrams29 were constructed, considering three extreme coverages – pristine (*), OH*-terminated, and O*-terminated. Our surface Pourbaix diagrams for SnO2(110) and SnO2(100) (Fig. 2e and f) reveal that at standard OER potentials (U = 1.23–1.6 V vs. RHE), the surface coverages were predominantly at the pristine state, indicating that both surfaces weakly adsorb OER intermediates.
Free energy diagrams for OER on both SnO2(110) and SnO2(100) surfaces is shown in Fig. S2a and b.† For SnO2(110), OH*, O* and OOH* exhibit free energies of 1.95, 4.45 and 4.81 eV, respectively, while on the SnO2(100), these values are 2.18, 4.49 and 4.95 eV, respectively. The relatively weak adsorption of OER intermediates leads to significantly high OER overpotentials of 1.26 V for SnO2(110) and 1.08 V for SnO2(100), with limiting potentials of 2.49 V and 2.31 V, respectively. The formation of O* from OH* is the potential determining step for both surfaces. Although O* adsorption strength on both surfaces is nearly same, OH* adsorption is relatively weaker on the SnO2(100) compared to the SnO2(110) resulting lower ΔGO* − ΔGOH* and lower overpotential on SnO2(100). Our results clearly indicate that pristine SnO2 does not exhibit reasonable catalytic activity for OER on both SnO2(110) and SnO2(100) surfaces, despite its highly stable nature under the operating conditions of these reactions. In this context, single-atom catalysis (SACs) presents a promising avenue for introducing isolated active sites for OER, potentially leading to electrocatalysts with lower overpotentials while taking advantage of the superior stability of SnO2 and minimizing the use of transition metals.
3.2 Computational workflow for designing SACs on SnO2 oxide support
Fig. 3 illustrates our computational workflow for evaluating the activity and stability of single transition metal (TM) atom catalysts supported on SnO2. We selected 29 elements corresponding to 3d, 4d, and 5d TMs in the periodic table to serve as our SACs. For each TM, we considered a total of ten different SAC configurations, including surface, subsurface, bulk SACs and surface-adatom arrangements. Specifically, for SnO2(110), we replaced a Sn atom in surface CUS, surface bridge, subsurface (2nd layer), and bulk (3rd layer) with a TM atom while for SnO2(100), we replaced a surface, subsurface and bulk atom with a TM atom. For the surface-adatom configurations, we examined several adsorption sites for single TM atoms on both the SnO2(100) and SnO2(110) surfaces, as shown in Fig. S3 and S4.† Most favorable TM adatom configuration was considered for the subsequent OER intermediates adsorption. The TM atom served as the adsorption site for OER reaction intermediates for all the adatom configurations, surface CUS configuration for SnO2(110) and surface configuration for SnO2(100). For the surface bridge configuration on SnO2(110), a nearby surface Sn-CUS atom was selected as the adsorption site. In the subsurface and bulk SAC configurations, reaction intermediates adsorption on surface Sn sites were considered. Furthermore, we examined the adsorption of reaction intermediates on the Sn-CUS site adjacent to the TM-CUS atom on the SnO2(110) surface to assess the impact of TM SAC on the activity of the surrounding Sn environment.Based on the adsorption free energies of OER intermediates, scaling relations between ΔGOOH*vs. ΔGOH* and ΔGO*vs. ΔGOH* were evaluated. Next, we performed a careful electronic structure analysis of oxide supported SACs by evaluating the density of states (DOS) and Bader charge analysis. This enabled us to understand the adsorption trends of OER reaction intermediates on SACs. Subsequently, thermodynamic stability of SACs was evaluated by using formation energies and surface segregation energies to investigate the synthesizability of SACs supported on SnO2. Additionally, dissolution potentials were calculated to determine the aqueous stability of the SACs at OER potentials. This systematic approach allowed us to analyze both the thermodynamic and the aqueous stability, as well as the catalytic activity of the SACs on SnO2(110) and SnO2(100) surfaces.
3.3 Analysis of adsorption energy trends on oxide supported SACs
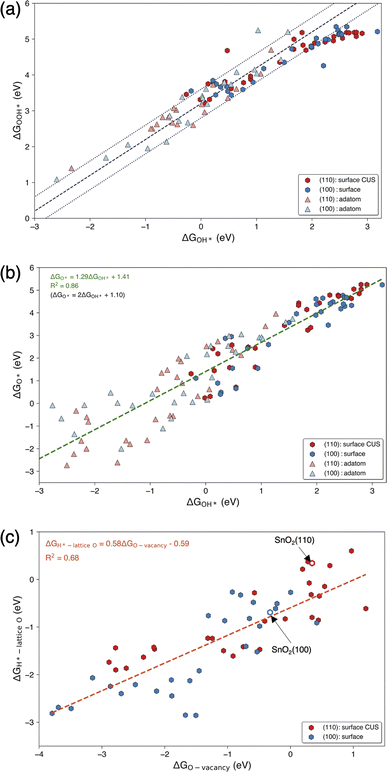
The trends in adsorption free energies of OER intermediates (OH*, O*, and OOH*) for surface and adatom configurations of SACs on SnO2(100) and SnO2(110) are reported in Fig. S5a–c.† As expected, adatoms adsorb reaction intermediates more strongly than the surface SACs on both surfaces. This can be attributed to the lower coordinated oxygen environment where each adatoms bond with 2 or 3 surface oxygen atoms, compared to surface SACs that bond to 4 or 5 oxygen atoms. It is important to note that this increased reactivity of oxide supported adatoms resulted in dissociation of OOH* intermediates and significant structural deformations in some surface-adatom SACs. We observed this behavior for adatoms such as Sc, Ti, Zr, Nb, Tc, Hf, Ta, W, Re, Os and Ir on SnO2(110) and Zr, Nb, Tc, Hf, Ta, W and Re on SnO2(100) which were excluded from our analysis. Considering the trends of OER intermediate adsorption on surface SAC and surface-adatom TMs, it can be identified that free energies of adsorption of OH* and O* go through a minimum as one progresses along each period. This characteristic is evident for both SnO2(100) and SnO2(110) surfaces and has been generally shown for pure metal oxide surfaces.35,36 Fig. S6† shows the trends of adsorption of OER intermediates on the surface Sn site when the SAC is on SnO2(100): subsurface, SnO2(110): subsurface, SnO2(110): surface bridge and SnO2(110): surface CUS configurations. Interestingly, the electronic effect of SAC on neighboring Sn atom is less resulting in a narrow range of adsorption free energies. For instance, ΔGO* is in the range of 3.08–4.86 eV for adsorption of Sn site on SnO2(110): surface CUS compared to the adsorption on SACs (0.24–5.25 eV) on the same surface configuration.Fig. 4(a) and (b) show the linear scaling relationships for ΔGOOH*vs. ΔGOH* and ΔGO*vs. ΔGOH* on TM on surface and adatom sites of SnO2(100) and SnO2(110) surfaces. These SACs adsorb OH* in a wide range of adsorption energies ranging from −3.23 to 3.18 eV, highlighting the diversity of the activity of the SAC TMs on SnO2. As expected, it was observed that the adatoms of early transition metals, Ti, Y, Zr, Nb, Hf, Ta, W, and Re, exhibit strong adsorption energies with ΔGOH* <−1 eV on both surfaces. On the other hand, the majority of weak adsorbing SACs (ΔGOH* > 2 eV), include surface SACs of Sc, Ti, Fe, Co, Ni, Cu, Y, Ag, and the group 12 (Zn, Cd, and Hg) on both surfaces. The scaling relation of ΔGOOH*vs. ΔGOH* follows the universal scaling of ΔGOOH* = ΔGOH* + 3.2 ± 0.4 eV, in agreement with previous studies.1,6,33 The scaling relationship of ΔGO*vs. ΔGOH* shows noticeable scattering when compared to ΔGOOH*vs. ΔGOH* and similar behaviors haven been previously observed on metal oxide surfaces.6 The observed scaling relationship between ΔGO* and ΔGOH* on oxide supported SACs can be expressed as ΔGO* = 1.29ΔGOH* + 1.41 eV, with the R2 value of 0.86. When the slope was fixed at 2, corresponding to the oxygen double bond according to the bond order conservation, a scaling relationship of ΔGO* = 2ΔGOH* + 1.10 was obtained. This intercept (1.10 eV) is considerably higher than the previously observed intercepts of 0.28 and 0.46 eV for metal oxide surfaces indicating O* intermediates adsorb weakly on oxide supported SACs compared to bulk metal oxides.6,33 Considering the scaling relations of individual SAC configurations, as shown in Fig. S7,† all the configurations generally followed the universal scaling of ΔGOOH*vs. ΔGOH*, although slight deviations were noted at very weak ΔGOH* surfaces. Interestingly, the ΔGO*vs. ΔGOH* scaling of individual configurations showed a wide range of values, with the intercepts ranging from 0.12 to 2.02, when the slope is fixed at 2 for the surface and adatom configurations with TM SAC as the adsorption site.
Fig. 4(c) shows the correlation between the free energy of adsorption of H on lattice oxygen (ΔGH*-lattice O) and the free energy of oxygen vacancy formation (ΔGO-vacancy) on the oxide supported SAC surface. Individual ΔGH*-lattice O and ΔGO-vacancy trends with TMs on SnO2(110): surface CUS, and SnO2(100): surface are shown in Fig. S8.† It is important to note that the lattice oxygen atom on which hydrogen is adsorbed and the oxygen atom that is removed to create an oxygen vacancy is the same and located adjacent to the surface SAC (see Fig. S8a and b†). ΔGO-vacancy is much higher on pristine SnO2(110) surface (0.34 eV) compared to SnO2(100) surface (−0.32 eV) due to the presence of highly coordinated oxygen atoms on the (110) surfaces. When comparing the ΔGO-vacancy of surface SAC systems with that of pristine SnO2 surfaces, it is evident that substituting single TM atoms results in a significant variation of ΔGO-vacancy up to 5 eV. This leads to significant differences in TM–O bond strength and oxygen reactivity. Additionally, it can be observed that ΔGH*-lattice O increases with ΔGO-vacancy on both surfaces in agreement with literature.37 A more positive ΔGO-vacancy indicates a stronger TM–O bond and a more unfavorable O-vacancy formation, requiring higher energy to remove an oxygen atom adjacent to a single TM single atom. Based on the bond conservation, H adsorption on that lattice oxygen will be weaker resulting in higher ΔGH*-lattice O.
3.4 Analysis of electronic structure trends on oxide supported SACs
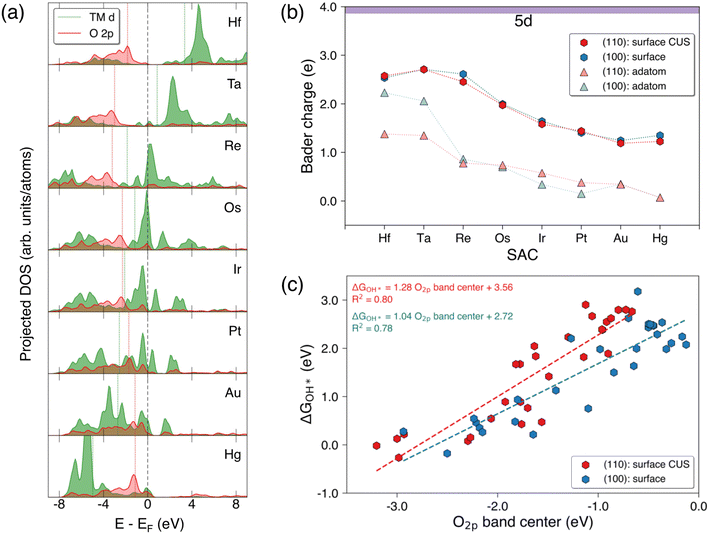
Fig. 5(a) shows the variation in the projected d-band of 5d TM surface SACs and the p-band of the adjacent surface lattice oxygen on the SnO2(110) surface. Generally, the projected d-band center of the TM SACs shifts to more negative values when moving from the left to right along the period similar to the variation of the d-band centers of the pure metals.38 Fig. S9a† shows the projected d-band center of the TM SACs in SnO2(110) and SnO2(100) surface and adatom configurations. The d-band center generally decreases when moving from the left to right along a period and this trend can be observed for all 3d, 4d, and 5d TM SACs for all configurations shown.39 Interestingly, the d-band centers of group 3 (Sc and Y) and group 4 (Ti, Zr and Hf) SACs on SnO2(110): surface CUS and SnO2(100): surface show much higher values compared to the those of adatoms of aforementioned elements on these surfaces. This is a deviation from generally expected trend of having higher d-band center for low-coordinated metal atoms compared to highly coordinated metal atoms. In contrast to the variation observed in the projected d-band center for 5d SACs on SnO2(110): surface CUS, O2p band center of the surface lattice oxygen adjacent to the SAC on SnO2(110) goes through a minimum (Fig. 5a) which is located at the position of Re in 5d indicating a change in bond strengths between the lattice oxygen and the surface SACs. Fig. S10† reveals a similar trend of O2p band center reaching a minimum for surface SACs on SnO2(110) and SnO2(100). Moreover, it is evident that the minimum of O2p band center shifts to more negative values when moving across the 3d, 4d and 5d periods. It is important to note that the similarity in the observed trends for the d-band of the surface SACs and the p-band of the adjacent surface lattice oxygen verify that these trends are broadly applicable to SnO2(100) and SnO2(110).When analyzing the Bader charge variations of surface SAC and surface-adatom configurations of 5d TMs on both SnO2 surfaces (Fig. 5b), we find that the Bader charges for surface SACs are higher than those for surface-adatoms. Surface-adatoms form fewer oxygen bonds with the surface compared to surface SACs resulting in a low-coordinated oxygen environment surrounding the SAC adatom. This leads to lower oxidation states for the surface-adatoms, which in-turn results in reduced Bader charges (more metallic). Fig. S9b† shows similar Bader charge variations for the 3d and 4d TMs. When considering the Bader charge variations for surface SACs, the Bader charge of the TM atom reaches a maximum at group 4 (Ti, Zr and Hf) or group 5 (V, Nb and Ta) SACs (neglecting W), before decreasing as we move further from left to right across a period. A similar trend is observed for surface-adatom TM SACs on both surfaces, where the Bader charge of TM adatom reaches the maximum at group 3 for 3d and group 4 for 4d and 5d. This pattern signifies a decrease in the oxidation state of the TM SACs, which can be generally explained using electronegativity trends. As we move from left to right across a period in the periodic table, the electronegativity of the TM atoms increases. Consequently, the later transition metals are more electronegative, resulting in relatively lower oxidation states for them compared to the earlier transition metals within equivalent oxygen coordination environments.
Fig. 5c shows the correlation between the free energy of OH* adsorption (ΔGOH*) on surface SACs and the O2p band center of the adjacent surface lattice oxygen on the pristine surfaces of SnO2(110) and SnO2(100). The ΔGOH* values on both surfaces correlate well with the O2p band center as demonstrated by an R2 value of ∼0.8 and with a positive gradient. This indicates that an increase in the O2p band center of the adjacent surface lattice oxygen corresponds to a weakening of the OH* adsorption on the TM SAC. Different TM SACs exhibit varying bond strengths between the TM atom and adjacent lattice oxygen on the surface. An increase in O2p band center of the adjacent surface lattice oxygen suggests increased reactivity of that oxygen, resulting in a weaker TM–O bond. Consequently, the adsorption of OH* would also be weaker if the TM–O bond of the surface is already weaker. Furthermore, the O2p band center of adjacent surface lattice oxygen negatively correlates with the free energy of H* adsorption on the same oxygen, as shown in Fig. S11.† The free energies of adsorption of H* on lattice O increase with decreasing O2p band center of adjacent surface lattice oxygen. Similar correlations of adsorption energy of OH* on TM atoms and also H* on lattice oxygen with O2p band center were observed in previous studies.40
3.5 Analysis of OER activities of SnO2 supported SACs
Fig. 6a shows a 2D map of calculated theoretical OER overpotentials (η) based on AEM as a function of ΔGO* − ΔGOH* and ΔGOH* descriptors. It is important to note that the ΔGO* − ΔGOH*, which acts as a measure of the ability of surface adsorbed O* to create and break bonds with hydrogen and oxygen atoms, is widely used as a OER activity descriptor.1,6 Moreover, due to the universal scaling relationship between ΔGOOH* and ΔGOH*, the optimum value for ΔGO* − ΔGOH* descriptor is in the range of 1.5–1.7 eV.1,41 IrO2(110), the current state-of-the-art catalyst for acidic OER1 is indicated in the Fig. 6. Under OER conditions, the surfaces of IrO2 are covered with O* and the IrO2(110) which is the most stable facet, records a theoretical overpotential of 0.57 V under high O* coverage.6 Although a majority of SAC configurations result in higher theoretical overpotentials, interestingly, there are few potential candidates which shows similar or less overpotentials than the IrO2(110) indicating more efficient conversion of H2O to O2. Table S7† shows the summary of highly active SACs which show theoretical AEM overpotentials lower than 0.7 V. Overall, Pd adatom on SnO2(110) shows the highest activity among all the SACs considered in this study with an AEM overpotential of 0.27 V and the OH* → O* + (H+ + e−) step (2nd step) of the OER is the potential determining step. Surface CUS Rh SAC on SnO2(110) (Fig. 6b) shows the lowest theoretical AEM overpotential, 0.32 V, among surface SAC configurations. The potential determining step is the 2nd step similar to Pd adatom on SnO2(110). Rh and Pt SACs of SnO2(100): surface (Fig. 6c and d) result in AEM overpotentials of 0.35 and 0.45, respectively, being next lowest among surface SAC configurations. Rh SAC on SnO2(100): surface shows that H2O + O* → OOH* + (H+ + e−) (3rd step) is the potential determining step while for Pt SAC on SnO2(100): surface, it is the 2nd step. All these highly active SACs resulted in ΔGO* − ΔGOH* values in the range of 1.45–1.70 eV. Additionally, Pt SAC on SnO2(110): surface CUS and also the Pt adatom on SnO2(100) indicate considerably high activities with AEM overpotential values of 0.49 and 0.51 V, respectively. Interestingly, the AEM overpotential of Ir SAC on SnO2(110): surface CUS (Fig. 6e) is 0.64 V indicating a slight activity drop due to the change in the surrounding environment as SAC compared to pristine IrO2(110). It is important to note that the OER intermediates adsorb relatively stronger on Ir SAC on SnO2(110): surface CUS compared to other highly active SACs (Fig. 6b–e and Table S7†). | ||
| Fig. 6 OER activity of the configurations considered in the current study except for the bulk configurations, and free energy diagrams of highly active SACs for OER. (a) Two-dimensional (2D) OER activity plot of theoretical overpotentials (η) based on the AEM for TM adsorption sites explored in this study as a function of ΔGO* − ΔGOH* and ΔGOH*. Note that OER overpotentials were calculated explicitly based on the eqn (9) and subsequent activity plots were constructed based on the scaling relation of ΔGOOH* = 0.77 ΔGOH* +3.36 eV for OER. AEM and LOM free energy diagrams for (b) Rh SAC on SnO2(110): surface CUS, (c) Rh SAC on SnO2(100): surface and (d) Pt SAC on SnO2(100): surface and (e) Ir SAC on SnO2(110): surface CUS. | ||
In addition to evaluating the OER activity through AEM mechanism, we also evaluated the OER activity through LOM mechanism (see Methods) for the surface CUS SACs on SnO2(110) and surface SACs on SnO2(100) (Fig. S12 and Table S8†). Our LOM mechanism activity calculations on adatom structures resulted in significant surface modifications and therefore did not include in our analysis. All the aforementioned surface SACs that showed AEM overpotentials of less than 0.7 V were found to be LOM active, with the exception of the Ir on SnO2(110): surface CUS. The LOM overpotential for Ir on SnO2(110): surface CUS was calculated as 1.89 V, which is significantly higher than its AEM overpotential of 0.64 V. This can be attributed to the potential determining step of the Ir on SnO2(110): surface CUS being the 3rd step, which is sensitive to the free energy of adsorption of H on lattice oxygen in the LOM mechanism. Moreover, H adsorbs relatively weakly on the oxygen atoms adjacent to Ir on SnO2(110) compared to OER intermediates on Ir (see Fig. 6e) resulting an increased overpotential. In contrast, the LOM overpotential for Rh on SnO2(110): surface CUS was 0.42 V, which is only 0.11 V higher than the AEM overpotentials. Only the Rh SAC on SnO2(100): surface showed an improved activity with an LOM overpotential of 0.24 V compared to AEM overpotential of 0.35 V. For all other surface SACs that exhibited AEM overpotentials below 0.7 V, the LOM overpotential remained similar. Based on this analysis, we identified SACs that are highly active for OER, and we will determine the most promising candidate SACs by considering their stabilities.
3.6 Analysis of SACs thermodynamic and aqueous stability
In addition to electrocatalytic activity, both the thermodynamic stability and the aqueous stability of a TM-SAC on SnO2 surface are an essential criterion in developing an OER catalyst. In this study, thermodynamic stability was evaluated by calculating formation and segregation energies while aqueous stability was evaluated by determining dissolution potentials under high OER oxidizing potentials.Formation energies for surface TM-SAC configurations were calculated considering a surface Sn vacancy site on SnO2(100) and SnO2(110) as the initial state according to the reaction (12) while formation energies of surface adatoms were calculated using reaction (13).
 | (12) |
 | (13) |
M(bulk) represents the TM SAC bulk atom and SnN−1O2N (surface) indicates the SnO2 surface with a surface Sn vacancy. The bulk materials tabulated in Table S10† were considered as the references for the TM atoms. We used an arbitrary formation energy tolerance value of 0.5 eV accounting for the accuracy of DFT calculations and surface models used.27 Fig. S13 and Table S9† report the formation energies of surface SAC and surface-adatoms on SnO2(100) and SnO2(110) which follow a similar trend for both SnO2 surfaces. Formation energies of surface SACs are considerably negative and more stable than surface-adatom SACs for all the 29 elements considered. Both, surface bridge and surface CUS configurations on SnO2(110) surface showed similar formation energies. Considering the formation energies of surface-adatom SACs, the early-TMs of group 3 (Sc and Y) and group 4 (Ti, Zr and Hf) form relatively stable adatoms. Formation energies of surface adatoms on both surfaces go through a maximum and decrease when moving from the left to right along 3d, 4d and 5d periods. Group 5–10 TM SACs form unstable surface adatoms on both surfaces with the exception of Ta adatom on SnO2(110) while group 12 (Zn, cd and Hg) TM SACs form stable surface adatoms on both surfaces. Additionally, group 11 TM SACs of Cu and Ag form marginally stable surface adatoms only on SnO2(100). We performed a similar analysis considering the most stable oxide bulk materials tabulated in Table S12† as the references for the TM atoms and a similar trend for relative stabilities between different configurations was observed (see Fig. S14 and Table S11†).
Segregation energies of surface and subsurface SAC configurations were evaluated by calculating the energy requirement for a bulk SAC to migrate to the surface or subsurface according to the following equations.
| Segregation energy(surface-bulk) = EM(surface SAC)SnN−1O2N − EM(bulk SAC)SnN−1O2N | (14) |
| Segregation energy(subsurface-bulk) = EM(subsurface SAC)SnN−1O2N − EM(bulk SAC)SnN−1O2N | (15) |
Bulk and subsurface SACs refer to TM atoms located in the third layer and second layer of a slab, respectively. Based on the above equations, negative segregation energy for surface-bulk indicates that surface SACs are more favorable to remain in the surface position compared to migrating to the bulk while a negative segregation energy for subsurface-bulk indicate that SACs are more favorable to remain in the subsurface position compared to migrating to the bulk. Fig. S15a and b† show the negative segregation energies of surface and subsurface SACs on SnO2(110) and SnO2(100) without any adsorbates on the surfaces. Overall, the surface CUS or surface bridge configurations are more stable than the bulk or subsurface SAC configurations on SnO2(110), while there is no clear trend on SnO2(100). Additionally, for majority of elements on both surfaces, the subsurface SAC configurations are slightly more stable than the bulk SAC. Specific trends indicate that Co, Ni, Cu and Zn (group 9, 10, 11 and 12) in 3d, Ag, Cd (group 11 and 12) in 4d and Au, Hg (group 11 and 12) in 5d elements are highly stable on SnO2(100): surface and SnO2(110): surface CUS configurations. This result can be explained by the fact that these late transition metal atoms are more noble in nature and prefer to have less oxygen bonds to maintain a lower oxidation state. Consequently, the number of oxygen atoms bonded to these SACs are lower on SnO2(100): surface and SnO2(110): surface CUS configurations compared to subsurface and bulk SACs, reinforcing their stability. For Cr in 3d, Mo, Ru, Rh, Pd in 4d and Os, Ir, Pt in 5d, subsurface SAC configuration is the most stable on SnO2(100) although only subsurface SAC configurations of Mo in 4d and Hf in 5d shows the highest stability on SnO2(110). However, this observation can be significantly altered in the presence of adsorbates due to adsorbate-induced segregation.42 Additionally, it was shown that it is possible to segregate Ir towards CUS position on IrxRu1−xO2(110) systems under the presence of OER intermediates.42 We further calculated the adsorbate induced surface segregation of SACs on SnO2(100) and SnO2(110) to determine the most stable configuration of SACs under the reaction conditions. Fig. S16 and Table S14† show the negative surface segregation energies for both surfaces in the presence of a single OH* on the surface clearly indicating that the surface SAC configurations (SnO2(100): surface and SnO2(110): surface CUS) are the most stable configurations for both surfaces except for Hf on SnO2(100) with a slight tendency to be in the bulk. Based on the current analysis, it can be concluded that surface SAC configurations of TMs on SnO2(100) and SnO2(110) are thermodynamically stable under OER reaction conditions.
Dissolution potentials play a critical role in determining the aqueous stability of SACs. SACs with low dissolution potentials would dissolve under reaction conditions, leading to a complete loss of active sites rendering the current strategy of making catalytically active single sites, totally ineffective. The dissolution potential (Udiss) of SACs is calculated based on eqn (16), while the concentration-dependent reduction potential (UM(CM)) is given by eqn (17).43
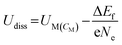 | (16) |
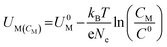 | (17) |
Fig. 7 presents the dissolution potentials of SACs and their corresponding formation energies. A dissolution threshold of 1.23 V vs. RHE was selected as the primary criterion, based on the standard equilibrium potential of the OER reaction. SACs with dissolution potentials below 1.23 V vs. RHE will undergo dissolution and will not withstand under OER conditions. It is important to note that the dissolution potential of SACs must exceed their limiting potential to ensure stability operating conditions. We did not perform dissolution potentials analysis for subsurface and bulk configurations of both surfaces since TM SACs are directly not exposed to the harsh aqueous environment. The dissolution potential analysis reveals that all surface adatom configurations on both SnO2(100) and SnO2(110) fall below the dissolution potential threshold of 1.23 V vs. RHE, with the exception of the Cd and Hg on both surfaces. Conversely, all the surface CUS, surface bridge SACs on SnO2(110) are above the dissolution threshold, except for the Ni SAC on both surface configurations and Mn on SnO2(110): surface CUS. Moreover, all the surface SACs on SnO2(100) are stable except for Ni SAC. All the dissolution data are reported in Tables S15 and S16.† These findings indicate that the adatoms are generally unstable under operating conditions due to their dissolution.
Table 1 shows the most promising SAC candidates with overpotentials less than 0.7 V and are thermodynamic and aqueous stable under OER conditions. Specifically, the formation energies of all these materials are considerably negative and lower than −5 eV indicating that the formation is very favorable. Moreover, dissolution potentials are above 2 V vs. RHE for all the SACs and significantly higher than the lowest limiting potential of either AEM or LOM. This indicates that these materials are stable under OER high operating potentials. Cr on SnO2(110): surface bridge and Re on SnO2(100): subsurface which also showed high activities, (see Table S7†) were excluded since these configurations were not stable based on the segregation analysis. Among most promising SAC candidates, majority of SACs (Rh, Pt and Ir) belong to noble metals while only V and Cr belong to the non-noble metals category. Interestingly, both surface configurations of Rh and Pt are among the most promising SACs having both OER AEM and LOM overpotentials below the state-of-the-art IrO2(110) overpotential value of 0.57 V.6 Additionally, V, Ir and Cr SACs on SnO2(110): surface CUS show AEM overpotentials of 0.61, 0.64 and 0.66 V, respectively. To determine the effect of solvation on OER intermediates and AEM and LOM overpotentials, we further modeled solvation for a selected number of promising TM-SAC candidates using VASPsol45 implicit solvent method. Table S17† summarizes the free energies of O*, OH*, OOH*, and H*-lattice O in the presence of the implicit solvation. Overall, the inclusion of solvation effects resulted in a maximum of 0.14 V stabilization or destabilization of the OER intermediates. Additionally, Table S18† shows the effect of solvation on overpotential based on AEM and LOM pathways. Depending on the potential determining step of the OER, overpotentials on selected SACs were shifted ∼0.08 and ∼0.13 V at the maximum due to solvation for AEM and LOM pathways, respectively. For most of the systems, the change in overpotentials was less than 0.1 V.
| SAC | Configuration | Adsorption site | Formation energy (eV) | Dissolution potential (V vs. RHE) | AEM/LOM overpotential (V) | AEM/LOM limiting potential (V vs. RHE) |
|---|---|---|---|---|---|---|
| Rh | SnO2(110): surface CUS | Rh | −5.94 | 6.18 | 0.32/0.42 | 1.55/1.65 |
| Rh | SnO2(100): surface | Rh | −6.18 | 6.43 | 0.35/0.24 | 1.58/1.47 |
| Pt | SnO2(100): surface | Pt | −5.41 | 3.71 | 0.45/0.45 | 1.68/1.68 |
| Pt | SnO2(110): surface CUS | Pt | −5.17 | 3.59 | 0.49/0.49 | 1.72/1.72 |
| V | SnO2(110): surface CUS | V | −8.66 | 2.97 | 0.61/0.61 | 1.84/1.84 |
| Ir | SnO2(110): surface CUS | Ir | −5.56 | 2.90 | 0.64/1.89 | 1.87/3.12 |
| Cr | SnO2(110): surface CUS | Cr | −6.84 | 2.33 | 0.66/0.66 | 1.89/1.89 |
Recent studies have shown that the LOM mechanism in OER tends to weaken the material stability due to the formation of lattice oxygen vacancies.46 As previously mentioned, all these SAC materials in Table 1 are LOM active except for Ir on SnO2(110): surface CUS. For Ir on SnO2(110): surface CUS, LOM limiting potential is 3.12 V vs. RHE which is significantly higher than its AEM limiting potential of 1.87 V vs. RHE. Hence, Ir on SnO2(110): surface CUS also remains one of the promising catalysts among all analyzed SACs. Summarizing the mechanistic behaviors of promising materials, AEM mechanism dominates well on Ir on SnO2(110): surface CUS while both LOM and AEM are equally active on other SACs supported SnO2.
3.7 Analysis of OER activity on IrO2(110) and Ir on SnO2(110) surface CUS
We further compared the activity and electronic properties of Ir SAC on SnO2(110): surface CUS site and rutile IrO2(110) surface. Fig. 8a and b shows the free energy diagrams for OER on IrO2(110) and Ir SAC supported on SnO2(110): surface CUS. Considering the adsorption free energies, OH*, O* and OOH* intermediates adsorb on IrO2(110) with adsorption strengths of 0.22 eV, 1.51 eV and 3.34 eV at low coverage, respectively, resulting an overpotential of 0.60 V in agreement with previously reported values.47,48 Interestingly, the OER intermediates adsorb slightly stronger on Ir SAC supported on SnO2(110): surface CUS with adsorption strengths of 0.15 eV, 1.45 eV and 3.32 eV for OH*, O* and OOH*, respectively, resulting an overpotential of 0.64 V. Our COHP analysis incorporating all orbital contributions of the 5 Ir–O bonds of Ir CUS active site, resulted in a mean integrated crystal orbital Hamiltonian population (ICOHP) of −3.31 eV and −3.44 eV for IrO2(110) and Ir SAC supported on SnO2(110): surface CUS, respectively. A more negative value of mean ICOHP of Ir SAC supported on SnO2(110): surface CUS indicates that the Ir (SAC)–O bonds are stronger and is in agreement with the relatively stronger adsorption of OER intermediates on the Ir SAC site. Furthermore, the current COHP analysis was extended to analyze t2g and eg resolved COHP of the Ir 5d–O 2p orbital since both bonding and antibonding contributions are highest for the selected orbital. Fig. 8c and d shows the COHP plots of Ir t2g–O 2p and Ir eg–O 2p for IrO2(110) and Ir SAC supported on SnO2(110): surface CUS, respectively. The calculated mean ICOHP of Ir t2g–O 2p are −1.04 eV and −1.12 eV for IrO2(110) and Ir SAC supported on SnO2(110): surface CUS. Considering the Ir eg–O 2p, mean ICOHP are −0.65 eV in IrO2(110) and −0.79 eV Ir SAC supported on SnO2(110): surface CUS. These results show that Ir 5d–O 2p contribution of Ir SAC supported on SnO2(110): surface CUS is slightly stronger compared to IrO2(110). A Bader charge analysis reveals that the oxidation state of Ir is slightly higher in Ir SAC supported on SnO2(110): surface CUS (+1.58 e) compared to IrO2(110) (+1.48 e). Combining the adsorption of OER intermediates and electronic properties of IrO2(110) and Ir SAC supported on SnO2(110): surface CUS, though Ir–O bonds in Ir SAC supported on SnO2(110): surface CUS is slightly stronger and results in slightly lower adsorption free energies of OER intermediates, activity remains almost the same with an increase of AEM overpotential by only 0.04 V compared to pristine IrO2(110). Practical utilization of such Ir SAC supported on SnO2 would result in efficient utilization of precious Ir atoms and therefore, significantly reducing the cost for OER electrocatalysts.4. Conclusions
In summary, we conducted a systematic analysis of SnO2-supported SACs to determine their OER performance by evaluating adsorption of key OER surface intermediates, electronic trends of the OER adsorbates and the surfaces, OER reactivity, thermodynamic stability, and aqueous stability. Our selection of rutile SnO2 as an acid-stable oxide host material was validated through a DFT-constructed aqueous Pourbaix diagram, demonstrating its stability under high potentials across a wide range of pH. Based on our comprehensive surface energy calculations analysis and Wulff diagram construction, we selected both SnO2(110) and (100) surfaces due to their high surface area fractions. This indicates the importance of studying multiple stable facets and not limiting to the most stable facet. Both SnO2 facets were OER inactive with significant overpotentials greater than 1 V. A wide range of ΔGOH* adsorption strengths ranging from −3.2 to 3.2 eV was observed highlighting the diversity of the activity of SnO2-supported SACs. We observed that the ΔGOOH* and ΔGOH* scaling relation remained universal across the SACs considered in this study. We further observed linear scaling relations between ΔGO*vs. ΔGOH* and the correlation between ΔGH*-lattice Ovs. ΔGO-vacancy. We further established that O2p band center of the adjacent surface lattice oxygen on the pristine surfaces correlates linearly with the ΔGOH* values on SnO2-supported SACs indicating that the O2p band center can be used as an alternative descriptor for estimating the adsorption energies of the OER intermediates. As expected, a negative correlation between ΔGH*-lattice O and O2p band center of the adjacent surface lattice oxygen on the pristine surfaces was observed. Our formation energy analysis indicated that only surface-doped SAC configurations are always stable on the SnO2 surfaces and most of the SAC adatoms are unstable. At the same time, all the adatoms except for Cd and Hg undergo dissolution since the dissolution potentials are lower than the standard equilibrium potential of OER. Conversely, surface configurations of SACs are aqueous stable except for Ni on all surface configurations and Mn on SnO2(110): surface CUS. Based on our activity and stability analysis, we identified Rh and Pt SACs on both SnO2(110) and SnO2(100) surfaces with remarkable OER activity enhancement in theoretical AEM and LOM overpotentials. Furthermore, Ir SAC on SnO2(110): surface CUS also showed comparable activity to IrO2(110), suggesting significant cost reductions due to lower Ir-loading requirements. Overall, our findings provide crucial theoretical insights into the design and development of next-generation stable and active OER catalysts for commercial-scale water-splitting.Data availability
Data collected in support of the findings are available in the main text and ESI.† Moreover, the optimized DFT structures and data can be accessed using the link https://github.com/gunasooriya-lab/manuscripts.Conflicts of interest
The authors declare no conflicts of interests.Acknowledgements
The computing for this project was performed at the OU Supercomputing Center for Education & Research (OSCER) at the University of Oklahoma (OU). Financial support from the School of Sustainable Chemical, Biological and Materials Engineering, University of Oklahoma is gratefully acknowledged.References
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Combining Theory and Experiment in Electrocatalysis: Insights into Materials Design, Science, 2017, 355(6321), 146, DOI:10.1126/science.aad4998.
- A. J. Shih, M. C. O. Monteiro, F. Dattila, D. Pavesi, M. Philips, A. H. M. Da Silva, R. E. Vos, K. Ojha, S. Park, O. Van Der Heijden, G. Marcandalli, A. Goyal, M. Villalba, X. Chen, G. T. K. K. Gunasooriya, I. McCrum, R. Mom, N. López and M. T. M. Koper, Water Electrolysis, Nat. Rev. Methods Primers, 2022, 2(1), 84, DOI:10.1038/s43586-022-00164-0.
- J. Kibsgaard and I. Chorkendorff, Considerations for the Scaling-up of Water Splitting Catalysts, Nat. Energy, 2019, 4(6), 430–433, DOI:10.1038/s41560-019-0407-1.
- J. Liu, Catalysis by Supported Single Metal Atoms, ACS Catal., 2017, 7(1), 34–59, DOI:10.1021/acscatal.6b01534.
- L. Liu and A. Corma, Metal Catalysts for Heterogeneous Catalysis: From Single Atoms to Nanoclusters and Nanoparticles, Chem. Rev., 2018, 118(10), 4981–5079, DOI:10.1021/acs.chemrev.7b00776.
- G. T. K. K. Gunasooriya and J. K. Nørskov, Analysis of Acid-Stable and Active Oxides for the Oxygen Evolution Reaction, ACS Energy Lett., 2020, 5(12), 3778–3787, DOI:10.1021/acsenergylett.0c02030.
- S. Geiger, O. Kasian, A. M. Mingers, K. J. J. Mayrhofer and S. Cherevko, Stability Limits of Tin-Based Electrocatalyst Supports, Sci. Rep., 2017, 7(1), 4595, DOI:10.1038/s41598-017-04079-9.
- K. Sasaki, F. Takasaki, Z. Noda, S. Hayashi, Y. Shiratori and K. Ito, Alternative Electrocatalyst Support Materials for Polymer Electrolyte Fuel Cells, ECS Trans., 2010, 33(1), 473–482, DOI:10.1149/1.3484545.
- G. C. Da Silva, S. I. Venturini, S. Zhang, M. Löffler, C. Scheu, K. J. J. Mayrhofer, E. A. Ticianelli and S. Cherevko, Oxygen Evolution Reaction on Tin Oxides Supported Iridium Catalysts: Do We Need Dopants?, ChemElectroChem, 2020, 7(10), 2330–2339, DOI:10.1002/celc.202000391.
- S. Jimenez-Villegas, S. R. Kelly and S. Siahrostami, SnO2-Supported Single Metal Atoms: A Bifunctional Catalyst for the Electrochemical Synthesis of H2O2, J. Mater. Chem. A, 2022, 10(11), 6115–6121, 10.1039/d1ta07562d.
- H.-S. Oh, H. N. Nong, T. Reier, M. Gliech and P. Strasser, Oxide-Supported Ir Nanodendrites with High Activity and Durability for the Oxygen Evolution Reaction in Acid PEM Water Electrolyzers, Chem. Sci., 2015, 6(6), 3321–3328, 10.1039/c5sc00518c.
- G. Liu, J. Xu, Y. Wang and X. Wang, An Oxygen Evolution Catalyst on an Antimony Doped Tin Oxide Nanowire Structured Support for Proton Exchange Membrane Liquid Water Electrolysis, J. Mater. Chem. A, 2015, 3(41), 20791–20800, 10.1039/c5ta02942b.
- P. Bhanja, B. Mohanty, A. K. Patra, S. Ghosh, B. K. Jena and A. Bhaumik, IrO2 and Pt Doped Mesoporous SnO2 Nanospheres as Efficient Electrocatalysts for the Facile OER and HER, ChemCatChem, 2019, 11(1), 583–592, DOI:10.1002/cctc.201801312.
- J. Xu, G. Liu, J. Li and X. Wang, The Electrocatalytic Properties of an IrO2/SnO2 Catalyst Using SnO2 as a Support and an Assisting Reagent for the Oxygen Evolution Reaction, Electrochim. Acta, 2012, 59, 105–112, DOI:10.1016/j.electacta.2011.10.044.
- A. T. Marshall and R. G. Haverkamp, Electrocatalytic Activity of IrO2–RuO2 Supported on Sb-Doped SnO2 Nanoparticles, Electrochim. Acta, 2010, 55(6), 1978–1984, DOI:10.1016/j.electacta.2009.11.018.
- J. Tong, Y. Liu, Q. Peng, W. Hu and Q. Wu, An Efficient Sb-SnO2-Supported IrO2 Electrocatalyst for the Oxygen Evolution Reaction in Acidic Medium, J. Mater. Sci., 2017, 52(23), 13427–13443, DOI:10.1007/s10853-017-1447-1.
- M. Batzill and U. Diebold, The Surface and Materials Science of Tin Oxide, Prog. Surf. Sci., 2005, 79(2–4), 47–154, DOI:10.1016/j.progsurf.2005.09.002.
- H. Oh, H. N. Nong and P. Strasser, Preparation of Mesoporous Sb-, F-, and In-Doped SnO2 Bulk Powder with High Surface Area for Use as Catalyst Supports in Electrolytic Cells, Adv. Funct. Mater., 2015, 25(7), 1074–1081, DOI:10.1002/adfm.201401919.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59(11), 7413–7421, DOI:10.1103/PhysRevB.59.7413.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, APL Mater., 2013, 1(1), 011002, DOI:10.1063/1.4812323.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (Pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319, DOI:10.1016/j.commatsci.2012.10.028.
- A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The Atomic Simulation Environment—a Python Library for Working with Atoms, J. Phys.: Condens. Matter, 2017, 29(27), 273002, DOI:10.1088/1361-648X/aa680e.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36(3), 354–360, DOI:10.1016/j.commatsci.2005.04.010.
- G. T. K. K. Gunasooriya, M. E. Kreider, Y. Liu, J. A. Zamora Zeledón, Z. Wang, E. Valle, A.-C. Yang, A. Gallo, R. Sinclair, M. B. Stevens, T. F. Jaramillo and J. K. Nørskov, First-Row Transition Metal Antimonates for the Oxygen Reduction Reaction, ACS Nano, 2022, 16(4), 6334–6348, DOI:10.1021/acsnano.2c00420.
- M. E. Kreider, G. T. K. K. Gunasooriya, Y. Liu, J. A. Zamora Zeledón, E. Valle, C. Zhou, J. H. Montoya, A. Gallo, R. Sinclair, J. K. Nørskov, M. B. Stevens and T. F. Jaramillo, Strategies for Modulating the Catalytic Activity and Selectivity of Manganese Antimonates for the Oxygen Reduction Reaction, ACS Catal., 2022, 12(17), 10826–10840, DOI:10.1021/acscatal.2c01764.
- R. Dronskowski and P. E. Bloechl, Crystal Orbital Hamilton Populations (COHP): Energy-Resolved Visualization of Chemical Bonding in Solids Based on Density-Functional Calculations, J. Phys. Chem., 1993, 97(33), 8617–8624, DOI:10.1021/j100135a014.
- H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Surface Pourbaix Diagrams and Oxygen Reduction Activity of Pt, Ag and Ni(111) Surfaces Studied by DFT, Phys. Chem. Chem. Phys., 2008, 10(25), 3722–3730, 10.1039/b803956a.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108(46), 17886–17892, DOI:10.1021/jp047349j.
- K. A. Persson, B. Waldwick, P. Lazic and G. Ceder, Prediction of Solid-Aqueous Equilibria: Scheme to Combine First-Principles Calculations of Solids with Experimental Aqueous States, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85(23), 235438, DOI:10.1103/PhysRevB.85.235438.
- M. Pourbaix, Atlas of Electrochemical Equilibria in Aqueous Solutions, Pergamon Press, Oxford, 1966 Search PubMed.
- I. C. Man, H. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3(7), 1159–1165, DOI:10.1002/cctc.201000397.
- J. E. De Vrieze, G. K. K. Gunasooriya, J. W. Thybaut and M. Saeys, Operando Computational Catalysis: Shape, Structure, and Coverage under Reaction Conditions, Curr. Opin. Chem. Eng., 2019, 23, 85–91, DOI:10.1016/j.coche.2019.03.003.
- B. M. Comer, J. Li, F. Abild-Pedersen, M. Bajdich and K. T. Winther, Unraveling Electronic Trends in O* and OH* Surface Adsorption in the MO2 Transition-Metal Oxide Series, J. Phys. Chem. C, 2022, 126(18), 7903–7909, DOI:10.1021/acs.jpcc.2c02381.
- B. M. Comer, N. Bothra, J. R. Lunger, F. Abild-Pedersen, M. Bajdich and K. T. Winther, Prediction of O and OH Adsorption on Transition Metal Oxide Surfaces from Bulk Descriptors, ACS Catal., 2024, 14(7), 5286–5296, DOI:10.1021/acscatal.4c00111.
- S. A. Theofanidis, G. T. K. K. Gunasooriya, I. Itskou, M. Tasioula and A. A. Lemonidou, On-purpose Ethylene Production via CO2-assisted Ethane Oxidative Dehydrogenation: Selectivity Control of Iron Oxide Catalysts, ChemCatChem, 2022, 14(14), e202200032, DOI:10.1002/cctc.202200032.
- A. D. Sison, M. M. N. A. Quaynor, S. A. K. Navodye and G. T. K. K. Gunasooriya, Insights into Segregation and Aggregation in Dilute Atom Alloy Catalysts Using DFT and Machine Learning, ChemCatChem, 2025, 17(7), e202401848, DOI:10.1002/cctc.202401848.
- J. K. Norskov, F. Studt, F. Abild-Pedersen, T. Bligaard, Fundamental Concepts in Heterogeneous Catalysis, 2014, pp. 114–137, DOI:10.1002/9781118892114.ch8.
- L. Giordano, K. Akkiraju, R. Jacobs, D. Vivona, D. Morgan and Y. Shao-Horn, Electronic Structure-Based Descriptors for Oxide Properties and Functions, Acc. Chem. Res., 2022, 55(3), 298–308, DOI:10.1021/acs.accounts.1c00509.
- C. F. Dickens, C. Kirk and J. K. Nørskov, Insights into the Electrochemical Oxygen Evolution Reaction with Ab Initio Calculations and Microkinetic Modeling: Beyond the Limiting Potential Volcano, J. Phys. Chem. C, 2019, 123(31), 18960–18977, DOI:10.1021/acs.jpcc.9b03830.
- I. C. Man, Theoretical Study of Electro-Catalysts for Oxygen Evolution, Technical University of Denmark, 2011 Search PubMed.
- J. Greeley and J. K. Nørskov, Electrochemical Dissolution of Surface Alloys in Acids: Thermodynamic Trends from First-Principles Calculations, Electrochim. Acta, 2007, 52(19), 5829–5836, DOI:10.1016/j.electacta.2007.02.082.
- L. Tang, B. Han, K. Persson, C. Friesen, T. He, K. Sieradzki and G. Ceder, Electrochemical Stability of Nanometer-Scale Pt Particles in Acidic Environments, J. Am. Chem. Soc., 2010, 132(2), 596–600, DOI:10.1021/ja9071496.
- K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, Implicit Self-Consistent Electrolyte Model in PlaneWave Density-Functional Theory, J. Chem. Phys., 2019, 151(23), 234101, DOI:10.1063/1.5132354.
- F.-Y. Chen, Z.-Y. Wu, Z. Adler and H. Wang, Stability Challenges of Electrocatalytic Oxygen Evolution Reaction: From Mechanistic Understanding to Reactor Design, Joule, 2021, 5(7), 1704–1731, DOI:10.1016/j.joule.2021.05.005.
- S. A. K. Navodye and G. T. K. K. Gunasooriya, Acid Electrolyte Anions Adsorption Effects on IrO2 Electrocatalysts for Oxygen Evolution Reaction, J. Phys. Chem. C, 2024, 128(14), 6041–6052, DOI:10.1021/acs.jpcc.3c08103.
- B. Lu, C. Wahl, R. Dos Reis, J. Edgington, X. K. Lu, R. Li, M. E. Sweers, B. Ruggiero, G. T. K. K. Gunasooriya, V. Dravid and L. C. Seitz, Key Role of Paracrystalline Motifs on Iridium Oxide Surfaces for Acidic Water Oxidation, Nat. Catal., 2024, 7(8), 868–877, DOI:10.1038/s41929-024-01187-4.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta01974e |
| This journal is © The Royal Society of Chemistry 2025 |