DOI:
10.1039/D5TA00917K
(Paper)
J. Mater. Chem. A, 2025,
13, 13518-13531
The hydrophilic nature trade-off of supported ionic liquid membranes on CO2/CH4 separation performance†
Received
4th February 2025
, Accepted 24th March 2025
First published on 25th March 2025
Abstract
Biomethane has been highlighted as an energy transition carrier in the quest for a resilient bioeconomy. Advances in its production process are accompanied by the need for new efficient separation methods for purification and carbon capture. However, biogas is fully saturated with water, jeopardising the expected performance of proposed novel materials. In this work, imidazolium-based Supported Liquid Membranes (SLM) with different hydrophilicity levels were proven to separate mixed CO2/CH4 successfully. IL-based SLMs were assessed in terms of stability, transport kinetics, and phase equilibria. Gas diffusion in dry and humid environments was estimated using the time-resolved FTIR-ATR spectroscopy technique. Henry's law constants of CO2 and CH4 and molecular interactions were estimated using the quantum chemical COnductor like Screening MOdel for Real Solvents (COSMO-RS) method. The SLM stability diagram is proposed to represent the effect of the gas water content on the total filled pores as a function of the components' physicochemical properties, support morphology, and operational pressure gradient. Diffusion coefficients of CO2 in the hydrophilic SLMs are substantially altered under wet environments. However, it has been shown that gas solubility mainly dominates the gas separation. The SLM's water sorption increases this effect by further rejecting methane. While the membrane hydrophilicity improves the gas selectivity, its stability diminishes in humid gas processing. The trade-off between the separation performance using highly hydrophilic solvents and the SLM module stability under real and variable conditions of pressure and humidity constrains the technology feasibility. Therefore, its study must be considered in the development and application of SLMs in sustainable biofuel production routes.
Introduction
As the effects of climate change become noticeable faster than our reaction capability, innovation challenges are required beyond adaptation strategies. Facing it compels us to mitigate the current carbon emissions without compromising the ever-growing demand for energy. To withstand the incoming global scenarios, communities and international organisations urge decarbonisation actions, pressing governments to strengthen their policies toward net-zero targets. Among the proposed approaches, transitioning towards a bioeconomy has been advocated as a crucial course for accomplishing the UN's Sustainable Development Goals (SDG).1 Broadly portrayed as the production and conversion of renewable biological resources, bioeconomy includes boosting biomass valorisation, adopting bio-based food, animal feed, and products, and replacing fossil fuels with bioenergy alternatives. Specifically, biogas production by anaerobic digestion of organic feedstocks has shown the potential to cut an important share of global Greenhouse Gas (GHG) emissions as a renewable substitute for natural gas.2 In this line, biomethane refined from biogas is projected to reach 111 billion cubic meters by 2040 only in the European area, i.e., the UE, Norway, Switzerland, and the UK.3
Along with this paradigm change towards bioeconomy, there is a rising interest in more efficient biofuel purification methods, where membrane technology has a starring role. Carbon dioxide, hydrogen sulphide, ammonia, oxygen, nitrogen, and even solid particles are by-products of the anaerobic digestion of biomass, which reduces the fuel quality. Due to the high CO2 content (30–50%), biogas production needs to employ separation methods such as water scrubbing, cryogenic separation, adsorption, or absorption for its purification.4 The need for high energy consumption methods compromises the real effectiveness of the biogas GHG saving. To replace those processes, membrane gas separation has been widely studied in the last decades, presenting major advantages: low energy requirement, selectivity, and simple process design and scale-up. Yet, the purpose of this process is not only to enrich the biofuel quality but also to avert GHG emissions. To prevent CO2 from being released into the atmosphere, carbon capture methods need to be incorporated into industrial activity. Carbon capture has mainly been carried out by chemical absorption using amine-based technologies, processes known for their solvent toxicity and environmental issues. Alternatively, Ionic Liquids (IL) have been proposed as a promising carbon capture media in absorption processes due to their relatively low toxicity, non-flammability, and negligible vapour pressure.5 Such properties lead to an improvement in operation safety and health. Membrane technology can take advantage of novel absorption media by confining such solvents within the inner structure of a thin porous layer in the form of a Supported Liquid Membrane (SLM).6 Here, the semipermeable barrier is the retained solvent rather than the solid matrix, allowing for tuning of the membrane properties for the target application. The process combines the gas absorption and desorption operations into a single stage, attaining a sustainable separation by requiring no solvent regeneration or extra heat input. This hybrid approach offers high selectivity while bringing the solvent requirement to a minimum. In this context, IL-based SLMs have been studied to separate carbon dioxide in mixtures with methane, nitrogen, hydrogen, or hydrogen sulphide and as a gas–liquid contactor for CO2 absorption with aqueous monoethanolamine.7,8 Separation in SLMs is driven by the gas partial pressure gradient following a solution–diffusion mechanism, depicted in Fig. 1, as in the case of polymeric membranes. However, the molecular interaction in the gas–liquid system supported into the pores of the membrane may be more convoluted since additional diffusional effects, chemical complexation, and solvent–solute/solvent–support affinities are involved.
 |
| | Fig. 1 Schematics of the SLM separation principle. A porous support (grey structure) is impregnated with an extraction solvent (light blue) to divide two phases under a transmembrane partial pressure gradient to promote gas transport. Solution-diffusion mechanism throughout an SLM: (a) the gas is absorbed by the solvent from the feed matrix to reach the vapour–liquid equilibrium; (b) then, the gas is diffused across the solvent that fills the support pores; (c) lastly, the gas is desorbed to the receiving stream. | |
Nevertheless, despite its promising features, SLM technology is hindered by its stability, i.e., the support capacity to retain the solvent within the polymer structure over time. Although several configurations and preparation methods have been attempted to improve membrane stability, this issue narrows the lifespan and overall performance of the membrane.9 In an SLM, capillary forces hold the solvent within the membrane pores.10 Hence, its stability depends on the solvent–support affinity and the transmembrane pressure, which might be substantially altered under operational conditions. Gas streams in industrial processes frequently present traces of other compounds that affect the expected membrane performance. Moreover, biogas is fully saturated with water, requiring extra purification steps. According to the membrane nature, moist gas impacts its separation performance differently. Water vapour increases or decreases gas permeabilities due to swelling in rubbery polymers or competitive sorption in glassy polymers, respectively.11 It has also been demonstrated that humidity directly impacts the CO2 flux in molten-salt membranes.12,13 Likewise, ILs are prone to water sorption according to their hydrophilicity. In SLMs, both gas permeability and selectivity are determined by their diffusivity and solubility, which depend at a molecular level on the physicochemical properties and composition of the liquid mixture. However, no systematic studies have been reported to assess the impacts of this phenomenon.
In this work, we address the lack of understanding of the relationship between the stability and viability of IL-based SLMs as gas separation materials by evaluating the gas separation process from a kinetic and thermodynamic standpoint. We prepared SLMs with three imidazolium-based ILs with different degrees of hydrophobicity and performed mixed CO2/CH4 separations. To consider realistic operational conditions, e.g., a wet stream of biomethane mixture, we estimated dry and wet effective gas diffusion coefficients using the time-resolved Fourier Transform Infrared-Attenuated Total Reflectance (FTIR-ATR) spectroscopy technique. Examples of applications of this method range from the determination of multicomponent transport through Nafion® 117 in artificial photosynthesis devices14 to the identification of the CO2 complexation transport in amine-based membranes15 to methanol sorption kinetics characterisation in polybenzimidazole membranes.16 Furthermore, gas solubility in complex systems, such as ILs or [IL + H2O], can be estimated from ab initio quantum chemical methods. Among them, the COnductor-like Screening MOdel for Real Solvents (COSMO-RS) is a fast tool for calculating thermochemical properties and molecular interactions.17 The method has successfully been applied for the vapour–liquid equilibria estimation of CO2 and CH4 in ILs in a wide range of temperatures and pressures,18 as well as for CO2/N2 selectivity inference of IL-based SLMs from computed Henry's Law constants.19
The aspiration of a complete energy transition requires the broadening of technological alternatives for the development of renewable fuel platforms. As such, supported IL membranes are promising candidates for low-energy CO2 separations, with minimal solvent requirements and safe and reliable operating conditions. This work contributes to the development of SLMs based on ILs by evaluating their performance in a working environment, which will help to mature the technology towards sustainable large-scale gas separation applications.
Experimental section
Materials and chemicals
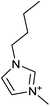
1-Ethyl-3-methylimidazolium methyl-sulfate ([C2min][MeSO4], ≥98.0%) was purchased from Sigma-Aldrich. 1-Butyl-3-methylimidazolium tetrafluoroborate ([C4min][BF4], >98%) and 1-butyl-3-methylimidazolium hexafluorophosphate ([C4min][PF6], >98%) were purchased from Acros Organics. Durapore® hydrophobic PVDF membrane (0.22 μm pore size, 75% porosity, and 125 μm thickness) was purchased from Merck. Carbon dioxide (CO2, 99.8%), methane (CH4, 99.9995%), and helium (He, 99.999%) were acquired from BOC. The chemical structures of ILs are depicted in Table 1.
Table 1 Chemical structure of the ionic liquids used in this work
| Ionic liquid |
Cation |
Anion |
| [C2min][MeSO4] 222.26 g mol−1 |

|

|
| [C4min][BF4] 226.02 g mol−1 |

|

|
| [C4min][PF6] 284.18 g mol−1 |
|

|
Supported liquid membrane preparation and material characterisation
Prior to membrane preparation, ILs were vacuum-dried at 70 °C for 1 hour. Vacuum filtration of 1 ml of the dry IL was carried out on the commercial PVDF membrane support until complete penetration using a sintered glass filter. The remaining solvent on the surface was gently wiped out with tissue paper. As prepared, SLMs were immediately tested for gas permeation to avoid moisture absorption. Water content (wtw/g g−1) in the ILs was measured by Karl Fischer titration using a Metrohm 899 coulometer in dry conditions. Likewise, the water content was measured in the IL sample in wet conditions, i.e., after being exposed to a relative humidity (%RH) of 100% for 1 hour in a closed ambient at room temperature. Dry and wet IL density (ρ/mol m−3) and viscosity (η/mPa s) were measured using an Anton Paar DMA 4500 M densimeter with a Lovis 2000 ME micro viscometer. IL surface tension (γ/mN m−1) and contact angle (θ/°) over the membrane porous support were measured using a Biolin Scientific Theta Lite optical tensiometer at room temperature in dry and wet conditions. Pore sizes (dpore/m) of the commercial PVDF support prior to impregnation were measured by capillary flow porometry using an IB-FT Porolux™ 1000 porometer using Porefil® (19.00 mN m−1) as the wetting liquid. Pore size distribution was determined from the gas flow per cent, assuming a log-normal distribution. SLM stability was assessed by determining the transmembrane pressure (Δp/Pa) needed to empty the support pores according to the Young–Laplace equation (eqn (1)).| | 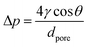 | (1) |
Gas permeability
Mixed CO2/CH4 (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25/sccm
25/sccm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sccm) permeability was tested in a custom-made setup at a constant absolute pressure of 3.01 (±0.07) bar and 1.16 (±0.11) bar for the feed and permeate sides, respectively. The system is composed of a mixer gas circuit with mass flow controllers for the feed gases and permeate sweep gas (He at 10 sccm), a crossflow membrane cell with an effective membrane area of 1.33 cm2, and an in-line permeate autosampler. The membrane cell is kept inside a ventilated oven at a controlled temperature. After 1 hour of equilibration, permeate stream composition was determined by gas chromatography (Agilent 490 Micro GC with a 10 m PPU HI column) as the average of four runs. Sampling was repeated each hour over 3 hours to ensure stability. SLMs were prepared and tested in duplicate. The gas i flux (Ji/mol s−1 m−2) is expressed according to eqn (2) as a function of its permeability (Pi/mol m Pa s−1 m−2), partial pressure gradient (Δpi/Pa), and SLM thickness (L/m). Gas flow rate (qi/mol s−1), i.e., flux times membrane total area (A/m2) as J·A, is calculated from the system's mass balance.
sccm) permeability was tested in a custom-made setup at a constant absolute pressure of 3.01 (±0.07) bar and 1.16 (±0.11) bar for the feed and permeate sides, respectively. The system is composed of a mixer gas circuit with mass flow controllers for the feed gases and permeate sweep gas (He at 10 sccm), a crossflow membrane cell with an effective membrane area of 1.33 cm2, and an in-line permeate autosampler. The membrane cell is kept inside a ventilated oven at a controlled temperature. After 1 hour of equilibration, permeate stream composition was determined by gas chromatography (Agilent 490 Micro GC with a 10 m PPU HI column) as the average of four runs. Sampling was repeated each hour over 3 hours to ensure stability. SLMs were prepared and tested in duplicate. The gas i flux (Ji/mol s−1 m−2) is expressed according to eqn (2) as a function of its permeability (Pi/mol m Pa s−1 m−2), partial pressure gradient (Δpi/Pa), and SLM thickness (L/m). Gas flow rate (qi/mol s−1), i.e., flux times membrane total area (A/m2) as J·A, is calculated from the system's mass balance.| | 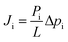 | (2) |
Gas permeability, in Barrer units, and CO2/CH4 selectivity (αi,j/-) are calculated according to eqn (3) and (4), respectively.
| |  | (3) |
| | 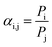 | (4) |
FTIR ATR spectroscopy
Experiments were performed using a Bruker Vertex 70V FTIR vacuum spectrometer coupled with an ATR cell and gas humidifier circuit, following the procedure described by Ferrari et al.20 The setup keeps the gas stream under controlled conditions: pressure: 2.00 (±0.07) bar, temperature: 25.0 and 40.0 (±0.4) °C, and relative humidity: dry gas (from source cylinder) and 20.0 (±2.5)% RH. The ATR cell, depicted in Fig. 2, is composed of a high refractive index crystal of zinc selenide (ZnSe), an electrical heating resistance, and a gap for the continuous crossflow of the gas penetrant. A membrane sample of 5 cm2 is mounted over the ART crystal and kept pressurised to enable the gas penetrant sorption and later diffusion. The IR beam is reflected along the crystal surfaces, generating evanescent waves absorbed by the membrane material, resulting in the IR spectrum detected by the instrument.
 |
| | Fig. 2 Schematic of FTIR-ATR cell and evanescent wave phenomenon. | |
By recording the shifts in the IR spectra over time, the method allows for compound quantification and the identification of chemical interactions. Normal mode vibrations of water, carbon dioxide, and methane, as well as the Infrared spectrums of the pure gases21 and this work SLMs components, are illustrated in Fig. 3. A rapid scan measurement was employed to generate a spectrum as the average of 2 scans with a resolution of 1.29 cm−1. The configuration provides a measurement down to every 0.9 seconds over 1 hour of sampling.
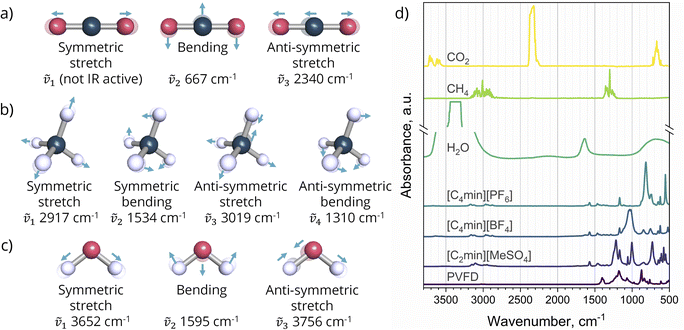 |
| | Fig. 3 Vibrational normal modes at their approximate wavenumbers of: (a) carbon dioxide; (b) methane; (c) water; (d) IR spectrum of pure gases,21 ILs, and support (PVDF membrane) used in this work. | |
Time-resolved Fickian model of diffusion
Experimental FTIR-ATR measurements were used to estimate the gas diffusion coefficient (D/m2 s−1) from the time-resolved Fickian model.22 The change of the gas concentration (C/mol m−3) within the SLM over time (t/s) is described assuming a mass transport governed by Fick's diffusion with constant diffusion coefficient, displayed in eqn (5):| |  | (5) |
The boundary conditions are set based on the initial (C0) and equilibrated (Ceq) concentrations along the membrane thickness, i.e., in the z-axis direction from the top surface to the bottom. The analytical solution to eqn (5) is given in eqn (6), which defines the Fickian concentration profile.
| |  | (6) |
As the gas penetrant is entering the SLM only in one direction (z-axis), the measured ATR absorbance (A/a.u.) can be expressed by eqn (7) as a function of gas concentration at the bottom of the membrane, the molar extinction coefficient (ε/m2 mol−1), and the evanescent wave coefficient (γ/m−1).23
| |  | (7) |
Here,
γ is the reciprocal of the IR beam depth of penetration (
dp/m), which is determined according to
eqn (8) from the ATR crystal refractive index (
nATR/-), membrane refractive index (
nSLM/-), as well as the beam angle of incidence (
θART/°) and wavelength (
λ/m).
24| |  | (8) |
With eqn (6) and (7), it is possible to express the analytical solution by normalising the absorbance (Ā/-) as a function of the initial (A0) and equilibrated (Aeq) absorbances as per eqn (9). The auxiliary functions gn (eqn (10)) and fn (eqn (11)) are defined for the sake of simplicity.
| | 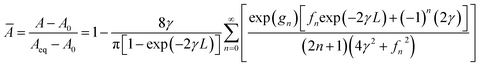 | (9) |
| |  | (10) |
| |  | (11) |
The effective gas diffusion coefficient was fitted to the experimental normalised absorbance using the objective function defined in eqn (12) by minimising the root mean square deviation (RMSD). It is calculated based on the deviation (δj) between the experimental and calculated absorbance, eqn (13), and the number of experimental data points (N) of each [gas – SLM] system. Data fitting was carried out using a MatLab® script developed for this work.
| | 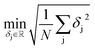 | (12) |
Phase equilibria computation
Based on quantum chemistry and dielectric continuum models in combination with statistical thermodynamics, the COSMO-RS method uses the charge density (σ/e nm−2) on the molecular surface to predict chemical potentials (μ/kJ mol−1) of components within a mixture. The sum of the σ probability distribution is called the “σ-profile” of the molecule: pi(σ), depicted in Fig. 4 for the components modelled in this work. Charge densities in the regions below −0.82 e nm−2 and above 0.82 e nm−2 correspond to the molecule hydrogen bond donor (HBD) and hydrogen bond acceptor (HBA) capacities, respectively, while the charges within them to the non-polar section. This overall property is used to compute the solute chemical potential within a solvent media (s), μsi, according to eqn (14), where μC,si is a combinatorial contribution parameter calculated by the method and μs(σ) the σ-potential, which comprises the mixture affinities in terms of the total interaction energy (electrostatic, hydrogen bonding, and van der Waals interactions) on the surface segments of two molecules in contact.| | | μsi = μC,si + ∫pi(σ)μs(σ)dσ | (14) |
 |
| | Fig. 4
σ-Profiles, molecular geometries, and surface charge densities of the compounds used in this work. | |
From the pure solute chemical potential, μPurei, and μsi is possible to estimate its activity coefficient (γsi/mol mol−1) at a given mixture concentration as a function of the gas constant (R/J K−1 mol−1) and temperature (T/K), as per eqn (15). Gas solubility (S/mol m−3 bar−1) is determined from the vapour–liquid equilibria, eqn (16), by the Henry-law coefficient (Hsi/bar) and solvent density. The method estimates Hsi from the chemical potential at infinite dilution (∞) and the pure gas compound vapour pressure (pSati/bar) according to eqn (17).
| | RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γsi) = μsi − μpurei ln(γsi) = μsi − μpurei | (15) |
| |  | (16) |
| |  | (17) |
Likewise, the method is capable of estimating further properties such as the excess free energy (GEi/kJ mol−1), excess enthalpy (HEi/kJ mol−1), and excess entropy (−TSEi/kJ mol−1) of the mixture, as well as the enthalpy interactions contributions: electrostatics or misfit (MF), hydrogen bonding (HB), and van der Waals forces (vdW), according to eqn (18) and (19), respectively.
| | | HE = HE[MF] + HE[HB] + HE[vdW] | (19) |
Molecular calculations were performed assuming the IL cation–anion pair as a pure component using the COSMOtherm software, version C30, release 18.0.2, at the parametrisation of BP_TZVP_18.
Results and discussion
Mixed CO2/CH4 separation
The performance of membranes for the separation of carbon dioxide from methane varies widely in terms of permeability and selectivity. The trade-off between these parameters in binary systems is described by the pure and mixed gas upper bounds.25–28 It is possible to find polymeric membranes with CO2/CH4 selectivity within a window of 3–10 at CO2 permeabilities of 1000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Barrer under ideal conditions, i.e., single gas testing. Other novel materials, such as Polymers of Intrinsic Microporosity (PIM), can remarkably push the separation performance further.29 However, such results proved to be lesser under practical conditions, i.e., mixed gas testing. In such cases, membranes exhibit lower permeabilities of 10–1000 Barrer without reaching the expected boost in the separation in line with the upper bounds, whereas standard commercial membranes display a higher selectivity of 10–50 at even lower fluxes.26 The 2018 upper bound was built using experimental data of mixed gas separation systems employing polymeric membranes based on, among others, PIMs and polyimides. These materials display a separation performance far exceeding the commercial membranes, e.g., Matrimid®. The approach allows for taking into account penetrant-induced plasticisation and competitive gas sorption effects that are not considered in the ideal selectivity estimation nor considered in the other upper bounds. In this line, IL-based SLMs are a competing alternative to polymeric membranes, demonstrating the same behaviour. Permeability and selectivity measurements of mixed CO2/CH4 separation with the IL-based SLMs studied in this work are presented in Fig. 5, with a performance close to the 2018 mixed-gas upper bound. No solvent leaching or stability issues were observed during the experiments at the transmembrane pressure of 1.86 (±0.14) bar. At 25 °C, the [C2min][MeSO4]-SLM displays a CO2 permeability of 188.2 (±3.6) Barrer and CO2/CH4 selectivity of 25.1 (±0.6). However, at 40 °C, its performance is moved up to 209.0 (±10.5) Barrer while selectivity is not significantly changed (23.7 (±1.7)). Following the upper bound, the same trend is observed for [C4min][BF4]-SLM, with a CO2 permeability of 358.8 (±20.9) Barrer and 436.3 (±22.2) Barrer at 25 °C and 40 °C, respectively, with selectivities of 23.5 (±1.5) and 21.2 (±0.4). Similarly, [C4min][BF4]-based SLMs found in the literature show a worse performance, where the CO2/CH4 selectivity is as low as 9. [C4min][PF6]-SLM exhibits an intermediate CO2 permeability of 253.0 (±16.8) Barrer and 308.4 (±29.1) Barrer at 25 °C and 40 °C, respectively. Conversely, it shows a lower CO2/CH4 selectivity of 15.5 (±0.1) and 14.6 (±1.1), meaning no significant difference within the tested temperatures. Again, others [C4min][PF6]-based SLMs reported in the literature at temperatures from room to 40 °C show different performance. Discrepancies between this work IL-SLMs and similar ones found in the literature can be attributed to the differences in support morphology and the operational conditions, e.g., temperature, and preparation, as well as single or mixed gas measurement. Generally, membrane porosity determines the solvent/support ratio, hence the effective diffusivity, while the support matrix might contribute to the total absorbed gas, thus determining effective solubility. Furthermore, composite membranes, another kind of membrane, have been proposed using the IL as a filler into the polymer matrix to exploit the enhanced mass transfer of solvents without falling on stability issues.30 Nevertheless, this approach differs from SLMs since the polymer has a predominant role in the separation.
000 Barrer under ideal conditions, i.e., single gas testing. Other novel materials, such as Polymers of Intrinsic Microporosity (PIM), can remarkably push the separation performance further.29 However, such results proved to be lesser under practical conditions, i.e., mixed gas testing. In such cases, membranes exhibit lower permeabilities of 10–1000 Barrer without reaching the expected boost in the separation in line with the upper bounds, whereas standard commercial membranes display a higher selectivity of 10–50 at even lower fluxes.26 The 2018 upper bound was built using experimental data of mixed gas separation systems employing polymeric membranes based on, among others, PIMs and polyimides. These materials display a separation performance far exceeding the commercial membranes, e.g., Matrimid®. The approach allows for taking into account penetrant-induced plasticisation and competitive gas sorption effects that are not considered in the ideal selectivity estimation nor considered in the other upper bounds. In this line, IL-based SLMs are a competing alternative to polymeric membranes, demonstrating the same behaviour. Permeability and selectivity measurements of mixed CO2/CH4 separation with the IL-based SLMs studied in this work are presented in Fig. 5, with a performance close to the 2018 mixed-gas upper bound. No solvent leaching or stability issues were observed during the experiments at the transmembrane pressure of 1.86 (±0.14) bar. At 25 °C, the [C2min][MeSO4]-SLM displays a CO2 permeability of 188.2 (±3.6) Barrer and CO2/CH4 selectivity of 25.1 (±0.6). However, at 40 °C, its performance is moved up to 209.0 (±10.5) Barrer while selectivity is not significantly changed (23.7 (±1.7)). Following the upper bound, the same trend is observed for [C4min][BF4]-SLM, with a CO2 permeability of 358.8 (±20.9) Barrer and 436.3 (±22.2) Barrer at 25 °C and 40 °C, respectively, with selectivities of 23.5 (±1.5) and 21.2 (±0.4). Similarly, [C4min][BF4]-based SLMs found in the literature show a worse performance, where the CO2/CH4 selectivity is as low as 9. [C4min][PF6]-SLM exhibits an intermediate CO2 permeability of 253.0 (±16.8) Barrer and 308.4 (±29.1) Barrer at 25 °C and 40 °C, respectively. Conversely, it shows a lower CO2/CH4 selectivity of 15.5 (±0.1) and 14.6 (±1.1), meaning no significant difference within the tested temperatures. Again, others [C4min][PF6]-based SLMs reported in the literature at temperatures from room to 40 °C show different performance. Discrepancies between this work IL-SLMs and similar ones found in the literature can be attributed to the differences in support morphology and the operational conditions, e.g., temperature, and preparation, as well as single or mixed gas measurement. Generally, membrane porosity determines the solvent/support ratio, hence the effective diffusivity, while the support matrix might contribute to the total absorbed gas, thus determining effective solubility. Furthermore, composite membranes, another kind of membrane, have been proposed using the IL as a filler into the polymer matrix to exploit the enhanced mass transfer of solvents without falling on stability issues.30 Nevertheless, this approach differs from SLMs since the polymer has a predominant role in the separation.
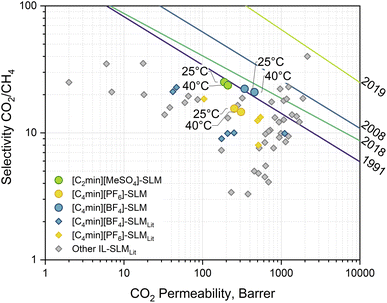 |
| | Fig. 5 Robeson plot of the experimental results (round markers) for mixed gas separation with IL-based SLM at 25 °C and 40 °C with a transmembrane pressure gradient of 1.86 (±0.14) bar. Diamond markers correspond to data on similar IL-based SLMs found in the literature.30–38 Lines correspond to the CO2/CH4 separation upper bounds: 2019 Jansen/McKeown;25 2018 Mixed gas;26 2008 Robeson;27 1991 Robeson.28 | |
On the one hand, the similar non-polar nature of both gases suggests poor affinity with the ions of the ILs. However, the results show a proportional relationship between selectivity and IL hydrophilicity. Solvent-water affinity is given by the alkyl chain length of the imidazolium-cation as well as the IL anion component, decreasing as [MeSO4]− > [BF4]− > [PF6]−.39 These trends can also be observed in the molecule σ-profile (Fig. 4) as the charge density peak intensity is reduced in the non-polar region or shifts toward the HBA region for cation and anion, respectively. On the other hand, CO2 permeability increases with the temperature while the selectivity slightly decreases. This behaviour was also observed for CO2/CH4 separation using an IL-SLM constituted of benzimidazolium-1-acetate.40 There, density functional theory calculations revealed higher favourable complexation energies of CO2, with both anion and cation increasing its absorption. Altogether, this behaviour suggests separation is mainly achieved by rejecting the CH4 by the SLM barrier rather than promoting CO2 transport. The capacity of methane to interact with the solvent is far more deficient than the possible interactions of the oxygen atoms in the carbon dioxide that increase its sorption.
SLM stability diagram
Ensuring the lifespan of modules is required in order to reduce the costs and environmental impact of the membrane technology. The stability of SLMs is commonly described by their performance drop over time or gravimetric measurements before/after use. A real-time non-destructive monitoring methodology has recently been proposed for liquid separation with SLMs.41 However, no predictive modelling of this phenomenon has been developed.
To access the effect of the operational conditions in the biomethane purification using IL-based SLMs, i.e., a water-saturated stream at variable pressure, the impact of water absorption on the physicochemical properties of the solvent was measured. Density, viscosity, surface tension, and contact angle were measured for the dry and wet IL. Results are listed in Table 2. After treating the IL in a closed environment at room temperature and 100% RH, the water content in the solvents shows a massive increase of 35 times for [C2min][MeSO4], 18 times for [C4min][BF4], and 8 times for [C4min][PF6]. This increase agrees with the expected hydrophilicity of the solvents. Only [C2min][MeSO4] shows a density change from dry to wet conditions at 25 °C, with a reduction of 8%. Although water sorption is shown to induce only a minor reduction in the IL density, it has a significant impact on key properties for membrane performance and stability. In liquids, molecular diffusion is inversely proportional to the mixture viscosity. All three ILs viscosities decrease by about 30% and 20% at 25 °C and 40 °C, respectively, suggesting higher overall flux at a high temperature and wet conditions. Furthermore, the magnitude of the change in the IL surface tension and IL/PVDF support contact angle follows the increase in water content. Humidity reduces the cohesive forces within the liquid molecules and intensifies the solid–liquid interfacial energy. As evidenced, solvent properties change in a wet environment, meaning that the SLM stability strongly relies on the processing conditions and will vary with them.
Table 2 Physical properties of the ionic liquids used in this work. Dry: vacuum dried at 70 °C for 1 hour; Wet: sample left open in a closed ambient at room temperature and 100% RH for 1 hour
| Ionic liquid/condition |
|
Water contenta wtw/g g−1 |
Densityaρ/g ml−1 |
Viscosityaη/mPa s |
Surface tensionbγ/mN m−1 |
Contact anglebθ/° |
| RT |
25 °C |
40 °C |
25 °C |
40 °C |
RT |
RT |
|
Standard uncertainty: u(wtw) ≤ 1 × 10−7 g g−1, u(ρ) ≤ 5 × 10−5 g ml−1, and u(η) ≤ 1 × 10−2 mPa s.
Measured at room temperature (RT). Standard deviation (±std) measured over 5 seconds of reading.
|
| [C2min][MeSO4] |
Dry |
2.962 × 10−4 |
1.28022 |
1.26993 |
97.13 |
46.69 |
53.2 (±0.3) |
27.3 (±0.4) |
| Wet |
1.076 × 10−2 |
1.17947 |
1.26917 |
67.22 |
37.76 |
42.0 (±0.1) |
54.3 (±0.5) |
| [C4min][BF4] |
Dry |
3.016 × 10−4 |
1.21217 |
1.20141 |
100.61 |
47.61 |
47.1 (±0.2) |
22.0 (±0.1) |
| Wet |
5.623 × 10−3 |
1.19893 |
1.18825 |
71.22 |
37.74 |
37.4 (±0.2) |
32.3 (±0.1) |
| [C4min][PF6] |
Dry |
3.617 × 10−4 |
1.36356 |
1.35093 |
287.6 |
124.3 |
43.1 (±0.3) |
31.2 (±0.3) |
| Wet |
3.230 × 10−3 |
1.36508 |
1.36508 |
208.1 |
95.25 |
43.6 (±0.1) |
30.0 (±0.3) |
In this work, we propose to assess SLM stability as the material capacity to remain fully impregnated, defined as the total filled pores (porefilled/%) in the Membrane Stability diagram. At the liquid–solid interphase, solvent–support attractive forces can be estimated from the surface tension and contact angle in a pore of a given diameter. Support pore size can be expressed by the log-normal distribution, i.e.,  . The cumulative distribution function (CDF) of the log-normal distribution corresponds to eqn (20), where the log-normal pore size mean (α) and variance (β2) are calculated from the pore size mean (μpore) and variance (σpore2), according to eqn (21) and (22), respectively.
. The cumulative distribution function (CDF) of the log-normal distribution corresponds to eqn (20), where the log-normal pore size mean (α) and variance (β2) are calculated from the pore size mean (μpore) and variance (σpore2), according to eqn (21) and (22), respectively.
| |  | (20) |
| |  | (21) |
| | 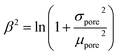 | (22) |
Taking eqn (1) and (20), it is possible to define the SLM stability diagram as per eqn (23), which determines the total filled pores of a solvent–support pair as a function of the transmembrane pressure.
| |  | (23) |
The pore size distribution of the support used in this work and calculated IL-based SLM stability diagrams are shown in Fig. 6. Porometry measurement of the PVDF membrane support shows an average pore size of 0.462 (±0.095) μm. According to the CDF fitting, the smallest pore size is 0.216 μm, agreeing with the supplier specification of 0.22 μm. In the PVDF support, IL-based SLM stability diagrams are proportional to the solvent hydrophilicity. Dry IL-based SLMs stability diagrams follow the trend: [C2min][MeSO4] > [C4min][BF4] > [C4min][PF6], where the maximum pressure gradients, i.e., the Δp at which the curve drops from 100%, are 2.56 (±0.14) bar, 2.36 (±0.03) bar, and 2.00 (±0.10) bar, respectively. However, as the IL absorbs water, the curves are displaced due to a decline of the solvent–support affinity, reducing the pressure gradient tolerance. Moisture absorption alters the capillary forces responsible for retaining the solvent. This effect is more visible for the hydrophilic solvents [C2min][MeSO4] and [C4min][BF4], where the max Δp drops to 1.33 (±0.24) bar and 1.71 (±0.04) bar, respectively. No significant stability reduction is observed for the less hydrophilic [C4min][PF6]. Change in the stability diagram is inversely proportional to the change of the surface tension and contact angle, appearing in the γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ) factor in eqn (23), and pore distribution; hence, higher surface tension plus lower contact angle and pore sizes are desired to favour an SLM capable of operating under an increased pressure gradient to promote the permeate gas flow. However, smaller pores reduce the total solvent in the SLM, hence the expected flux. Conversely, a high porosity led to higher support tortuosity, diminishing the effective diffusion of the gas. The SLM selectivity will remain unaffected if the gas solubility and diffusion coefficient have no significant dependency on the system's operational pressure range. Inversely, operating gas separation at higher temperatures might reduce the solvent surface tension and, therefore, the total filled pores, declining the selectivity. In actual applications, complex feed gas-SLM interactions might arise. Changes in the interfacial properties due to the composition of the gas and liquid mixtures, pressure, and temperature affect not only the fluid mobility but also the interfacial mass transfer.42 Therefore, capillary energies of the [gas mixture + solvent mixture + support] should be further investigated to determine their impact on the process scale-up and long-term stability of SLM modules.
cos(θ) factor in eqn (23), and pore distribution; hence, higher surface tension plus lower contact angle and pore sizes are desired to favour an SLM capable of operating under an increased pressure gradient to promote the permeate gas flow. However, smaller pores reduce the total solvent in the SLM, hence the expected flux. Conversely, a high porosity led to higher support tortuosity, diminishing the effective diffusion of the gas. The SLM selectivity will remain unaffected if the gas solubility and diffusion coefficient have no significant dependency on the system's operational pressure range. Inversely, operating gas separation at higher temperatures might reduce the solvent surface tension and, therefore, the total filled pores, declining the selectivity. In actual applications, complex feed gas-SLM interactions might arise. Changes in the interfacial properties due to the composition of the gas and liquid mixtures, pressure, and temperature affect not only the fluid mobility but also the interfacial mass transfer.42 Therefore, capillary energies of the [gas mixture + solvent mixture + support] should be further investigated to determine their impact on the process scale-up and long-term stability of SLM modules.
 |
| | Fig. 6 (a) Measured pore size (dpore) distribution of and fitted log-normal cumulative distribution function (CDF) (eqn (20)) for a Durapore PVDF membrane (nominal pore size: 0.22 μm); (b) to (d) IL/PVDF-SLM stability diagrams (eqn (23)) at room temperature expressed as a function of the total filled pores after applying a transmembrane pressure. Shaded areas correspond to the error propagation of the experimental standard deviation of contact angle and surface tension measurements. | |
Gas diffusion coefficient
In situ FTIR-ATR spectroscopy was used for the first time to measure the effective gas diffusion in SLMs. ATR absorbance was analysed for the anti-symmetric stretch of CO2, corresponding to the wavenumber of 2340.1 cm−1 (Fig. 3a). No absorbance attributed to the presence of methane has been observed in the IL-based SLMs studied in the work. This suggests a gas absorbance below the technique limit of detection due to the poor CH4 solubility in the ILs. The refractive index and angle of incidence of the ART crystal are nART = 2.49 and θART = 45°, respectively. No experimental values of refractive index for liquid membranes were found in the literature. The refractive index of imidazolium-based ILs ranges from 1.36 to 1.67.43 Likewise, refractive index values within 1.44–1.46 have been reported for pure PVDF polymer.44,45 Hence, for this work, the IL-based SLM refractive index was estimated as a fixed value of nSLM = 1.5, giving an IR evanescent wave dp of 0.74 μm. The experimental absorption data dependency on the gas mass transport can be illustrated in the theoretical solution of eqn (9), as  , plotted in Fig. 7. Given the inputs of the membrane, ATR crystal element, and IR beam wavelength, the codomain surface represents a unique solution for the gas diffusion coefficient in the SLM that can describe the experimental dataset under the Fickian diffusion regime.
, plotted in Fig. 7. Given the inputs of the membrane, ATR crystal element, and IR beam wavelength, the codomain surface represents a unique solution for the gas diffusion coefficient in the SLM that can describe the experimental dataset under the Fickian diffusion regime.
 |
| | Fig. 7 Example of the function codomain of the time-resolved ATR Fickian diffusion model: eqn (9) expressed as D = f(Ā,t), with Ā ∈ (0, 1). The surface was calculated for CO2 absorption in an IL-based SLM at 2340.1 cm−1 (anti-symmetric stretch), showing iso-surface lines of constant gas diffusion coefficient values. Experimental data on gas absorption of the IL-based SLM is fitted to the surface to obtain the effective diffusion coefficient. | |
The fitted effective diffusion coefficients of carbon dioxide in the studied IL-based SLMs present a mean magnitude of 9.3 × 10−11 m2 s−1 with an average RMSD of 2.6%. Results depicted in Fig. 8 show no general trend regarding temperature or gas humidity. Overall, [C4min][BF4]-SLM shows an CO2 diffusion greater than [C2min][MeSO4]-SLM, corresponding to their permeability trend. However, CO2 diffusion is overall lower in [C2min][MeSO4]-SLM and [C4min][BF4]-SLM than the diffusion coefficients in [C4min][PF6]-SLM. Both [C2min][MeSO4]-SLM and [C4min][BF4]-SLM are importantly affected by the humidity of the carbon dioxide stream. Although all three ILs are composed of an imidazolium-cation, their anion counterpart contributes to the CO2-solvent interactions at different levels. Further discussion of this effect on the basis of computed excess energy analysis is given later.
 |
| | Fig. 8 Estimated CO2 diffusion coefficients in IL-based SLMs (bars read to the left) and fitting RSMD (diamond read to the right) at dry gas (from source cylinder) and wet (20.0 (±2.5)% RH) stream conditions. | |
The permeability of CO2 in supported IL membranes has also been modelled using a Fickian model that considers the contribution of Langmuir sorption as in glassy polymer membranes.46 The presence of such Langmuir sites in membranes increases the total gas adsorbed by the material but limits the penetrant mobility compared to the Henry's Laws sites. Observed gas diffusion can also be explained by a facilitated transport regime or CO2-IL complexation. Literature reports evidence of possible carbene formation of the imidazolium cation under CO2 presence.47,48 The carboxylation reaction, depicted in Fig. 9a, is preceded by a cation deprotonation by the anion itself. The complex is further stabilised by a dimerisation sustained by the strong interactions of the carboxylate and imidazolium cations. Similar interactions are formed by hydrogen bonding between the acidified anion (H-[anion]) and another plain anion to maintain the electroneutrality of the mixture. However, fluoroacids, such as fluoroboric acid (HBF4) and hexafluorophosphoric acid (HPF6), are unstable species and do not exist as pure components.49 Therefore, only methoxysulfonic acid (CH4O4S) is likely to be formed and promote the imidazolium complexation within the IL-based SLM, as Fig. 9b depicts. These strong interactions, expected to be involved within the [C2min][MeSO4]-SLM, saturate the liquid phase interactional capacity and generate further polar species within the mixture. This effect controls the CO2 permeability, as the decomplexation stage will limit the overall mass transfer rate yet increases selectivity as the physical sorption of non-polar methane will be diminished.
 |
| | Fig. 9 (a) Imidazolium-2-carboxylate formation (1) and dimerisation stabilisation with an imidazolium-cation (2); (b) methyl sulfate ion – methoxysulfonic acid stabilisation by hydrogen bonding interactions (3). | |
The support effect in the solute transport can be estimated from a pore morphology view. Effective diffusion throughout a porous path in membranes is commonly corrected by the porosity (ε/%) and tortuosity (τ/-). Assuming the pore geometry of the polymeric membrane support resembles interstices between closed-packed spheres, the correction factor can be expressed as per eqn (24).50 The nominal porosity of the PVDF support used in this work has a value of 75%, meaning a correction factor of 0.36. Literature reports CO2 diffusion coefficients values of 5.8 × 10−10 m2 s−1 at 314 K in pure [C2min][MeSO4], 2.7 × 10−10 m2 s−1 at 313.15 K in pure [C4min][BF4], and 2.9 × 10−10 m2 s−1 at 298 K in pure [C4min][PF6].51–53 By taking the support effect into account, values of 2.1 × 10−10, 9.9 × 10−11, and 1.0 × 10−10 m2 s−1 would be expected for the CO2 diffusion coefficient in the [C2min][MeSO4]-SLM, [C4min][BF4]-SLM, and [C4min][PF6]-SLM, respectively. This correction provides values of the diffusion coefficient closer to the values obtained for the IL-based SLMs under their respective conditions. This denotes the importance of the support inner structure for comparing the performance between similar SLMs for gas separation.
| |  | (24) |
Gas solubility
Studied SLMs are composed of three-fourths of solvent, whereas gas solubility in PVDF polymer is negligible compared to the IL. Moreover, gas solubility in neat PVDF polymer has shown a preference for CO2 absorption over methane, with an estimated CO2/CH4 selectivity of 4.5 at low pressure.54 Polymer support selectivity is less than half of the observed in this work for IL-based SLMs (Fig. 5). Therefore, it is reasonable to assume that SLM's capacity to absorb the gases is controlled mainly by the vapour–liquid equilibria, with just a minor contribution of the solid support to the permeability or selectivity.
The gas solubility in SLMs has been estimated from the phase equilibria of gases in ILs using the COSMO-RS method. Computed Henry's law constant of gases in pure and wet (at the water contents listed in Table 2) ILs are displayed in Fig. 10. Results show significantly higher solubilities for CO2, i.e., lower HILi-values, than CH4 in all three IL-based SLMs. Henry's law constants of both gases in the ILs are proportional to temperature. However, CO2 has been shown to be more sensitive to this effect. Conversely, the presence of water in the liquid mixture impacts them differently. While CO2 solubilities in the wet ILs remain almost unaffected, CH4 solubility is significantly decreased. At 25 °C, the aqueous solubility of carbon dioxide, 2.9 g l−1, is several magnitude orders greater than the solubility of methane, 22.15 mg l−1.55 Then, a decline of the methane solubility is expected proportionally to the mixture water content. Nonetheless, notorious is the case of [C4min][BF4], with a largest  -value increase despite its lesser change in water content, from dry to wet conditions, than [C2min][MeSO4]. Results suggest that complex interactions between the IL's ions and water are in play, promoting the rejection of methane. Similar behaviour has been reported for blend membranes composed of poly(vinyl alcohol) and [C2min][DCA], where the IL is completely mixed into the polymer casting solution.56 Commonly, water sorption by polymeric membranes leads to material swelling, which might increase CO2 permeability due to the greater polymer-free volume.57 However, moisture can have a detrimental effect on glassy membranes with high separation performance, such as PIMs. The polymer functional groups responsible for the CO2 solubility become saturated in the presence of water, lowering their interactional capacity. This effect can be reduced by increasing the material hydrophobicity, as it has been shown for highly fluorinated PIMs.58
-value increase despite its lesser change in water content, from dry to wet conditions, than [C2min][MeSO4]. Results suggest that complex interactions between the IL's ions and water are in play, promoting the rejection of methane. Similar behaviour has been reported for blend membranes composed of poly(vinyl alcohol) and [C2min][DCA], where the IL is completely mixed into the polymer casting solution.56 Commonly, water sorption by polymeric membranes leads to material swelling, which might increase CO2 permeability due to the greater polymer-free volume.57 However, moisture can have a detrimental effect on glassy membranes with high separation performance, such as PIMs. The polymer functional groups responsible for the CO2 solubility become saturated in the presence of water, lowering their interactional capacity. This effect can be reduced by increasing the material hydrophobicity, as it has been shown for highly fluorinated PIMs.58
 |
| | Fig. 10 Henry's law constants of CO2 and CH4 in the dry ILs (filled markers) and wet ILs at the water contents listed in Table 2 (empty markers), computed using the COSMO-RS method. | |
Furthermore, mixture interactions can also be identified as the solute–solvent affinity from the activity coefficient at infinite dilution. Computed γs,∞i-values are displayed in Fig. 11. Water-IL affinities decrease (γs,∞i-value increase) as [C2min][MeSO4] < [C4min][BF4] < [C4min][PF6], corresponding to the solvent hydrophilicity, where favourable attractive interactions are observed only for [C2min][MeSO4]. All three studied imidazolium-based ILs show favourable interactions (γs,∞i-value <1) for CO2 while unfavourable interactions (γ-value >1) for CH4. Again, [C4min][BF4] exhibits less affinity with both gases in comparison to the other two ILs. Gas activity coefficients are two orders of magnitude higher in water than in ILs, with slightly bigger repulsive interactions for CO2. However, aqueous solutions of carbon dioxide led to carbonic acid formation, aiding the total amount of dissolved gas, which is not considered in calculations.
 |
| | Fig. 11 Activity coefficients at infinite dilution of the water and gases in the ILs used in this work and gases in aqueous solution, computed using the COSMO-RS method. | |
Both solubility and molecule affinity are a reflection of particular interactional energies within the system. Thermodynamic interactions determine the total deviation from an ideal mixture, quantified by the excess energies and their contributions. The COSMO-RS method has been shown to be capable of successfully estimating the molar excess enthalpies of complex mixtures, such as those containing ILs.59 Excess energies for the systems [gas + IL], [H2O + IL], and [gas + H2O] computed at 25 °C and 40 °C using COSMO-RS are displayed in Fig. 12. The [CO2 + IL] systems show favourable excess energies (negative GE and HE), meaning a spontaneous exothermic dissolution process, while [CH4 + IL] systems show repulsive energies (positive GE and HE). No relevant changes are observed in the trend of excess energies or contributions with the temperature. Overall, the affinity of ILs for CO2 is mainly due to van der Waals forces. Due to the shorter alkyl chain of [C2min][MeSO4], better interstitial accommodation of the molecules raises favourable electrostatic interactions, contributing to improving its affinity for both CO2 and CH4 (Fig. 12a). In the case of [C4min][BF4], all interactions were shown to be repulsive despite a minor contribution of van der Waals forces to the methane dissolution (Fig. 12b), agreeing with the observed high selectivity and Henry's law constants. Likewise, electrostatic repulsion of [C4min][PF6] is observed for both gases (Fig. 12c). This interaction is shown to be responsible for the methane rejection, yet a favourable entropic effect is present. The lesser favourable interactions for CO2 in [C4min][PF6], in addition to its higher energy disorder given by the methane, explain its lower performance as SLM. All studied ILs show repulsive hydrogen bonding interaction with water, which increases along with their hydrophobicity. However, the water affinity of [C2min][MeSO4] is attributed to electrostatic interactions that favour the minimisation of the total energy of the mixture. The observed positive excess entropy in the [H2O + IL] systems, i.e., a negative −TSE value, is a product of an enthalpy-entropy compensation effect: higher repulsive molecular interactions promote a “higher disorder” within the mixture, and vice versa. Lastly, both [gas + H2O] systems show a massive unfavourable deviation from the ideal solution (Fig. 12d). CO2 and CH4 in water have a positive excess free energy and enthalpy, along with negative excess entropy (positive −TSE values). Only favourable van der Waals forces contributions are observed for methane in water, which is in line with the smaller activity coefficient of CH4 than of CO2.
 |
| | Fig. 12 Excess free energy (GE), excess entropy (−TSE), and excess enthalpy (HE) plus its interactional contributions: electrostatic or misfit (MF), hydrogen bonding (HB), and van der Waals forces (vdW), for the binary systems composed of [gas + IL] and [H2O + IL]: (a) [C2min][MeSO4], (b) [C4min][BF4], (c) [C4min][PF6]; and the binary systems composed of (d) [gas + H2O]. Energies were computed using the COSMO-RS method at a solute molar fraction of xgas = 0.001 mol mol−1. | |
On the whole, computed solubilities and excess energies analysis of binary mixtures support the observed performance in mixed CO2/CH4 separation with IL-based SLMs. As discussed above, the outcomes of predicted properties are in line with the notion that gas solubility differences dominate gas separation. The studied ILs show a poor affinity for carbon dioxide yet stronger repulsive interactions with methane. The observed thermodynamic equilibria limit the CO2 permeability and drive the selectivity, a trend potentiated by the presence of water in the mixture.
Conclusion
With performance comparable to polymeric membranes, the studied SLMs formed by a PVDF porous support ILs, [C2min][MeSO4], [C4min][BF4], and [C4min][PF6], show potential for gas separation applications. This piece of work discusses their suitability and trade-off between the SLM nature and capacity for biomethane purification and carbon capture. Higher SLM hydrophilicity offers an improvement in selectivity but decreases the membrane stability in humid gas processing. [C2min][MeSO4]-SLM and [C4min][BF4]-SLM exhibit good transmembrane pressure resistance in dry conditions; however, their stabilities under wet conditions are reduced by 48% and 28%, respectively. Conversely, the hydrophobic [C4min][PF6]-SLM displays less resistance to the pressure but no significant stability changes with the humidity of the gas. The SLM stability diagrams provide a detailed material representation by delimiting the process boundaries and variable operation windows, enabling the behaviour prediction of membrane modules in large-scale applications.
Membrane performance is also affected by the water sorption from the wet gas stream. A humid environment reduces the solvent viscosity, promoting molecule mobility. However, its effect on gas diffusion and solubility depends on further interactions that arise within the mixture. Dissolved water in IL acts by reducing methane absorption capacity with a minor effect on CO2 solubility. Despite the better CH4 solubility in pure [C2min][MeSO4], its complexation ability with CO2 increases the polarity of the mixture even further, improving the methane rejection and, hence, the selectivity. Pure [C4min][BF4] exhibits lower CO2 and CH4 solubilities yet a better CO2 diffusional effect that favours the separation performance. However, it is highly affected by water presence, decreasing carbon dioxide diffusion and methane solubility, meaning a lower CO2 permeability with better selectivity. Although [C4min][PF6] shows the best CO2 diffusional effect, it has strong repulsive interactions with CO2 and a favourable entropic effect for methane dissolution. In consequence, it displays a lower separation performance in comparison to the other two IL-based SLMs. Yet gas diffusion and solubility in [C4min][PF6] are less affected by water sorption, offering a more reliable operation.
This work is an example of the “tailoring” capability of ILs, which is widely advocated in the field. The cation–anion pair and solvent–support can be aligned towards a desired property for the target process. However, as evidenced by this work, they are constrained by the trade-off between the effectiveness and feasibility of their use in real applications. Material development in this context will effectively enhance sustainable separation methods to promote the establishment of a sustainable bioeconomy.
Data availability
Data supporting this article are available in the ESI.†
Author contributions
PLP conceptualisation, investigation, methodology, formal analysis, visualisation and writing original draft; PG investigation and formal analysis; BSM investigation and formal analysis; MGM resources and review & editing; PG review & editing; MCF methodology, resources, review & editing, and supervision; MPP project administration, funding acquisition, resources, review & editing, and supervision.
Conflicts of interest
The authors declare no competing interest.
Acknowledgements
This work was funded by the SynHiSel EPSRC Programme Grant EP/V047078/1. MGM acknowledges Grant PID2022-141965OB-C22 funded by MCIN/AEI/10.13039/501100011033 and by ‘ERDF A way of making Europe’, by the ‘European Union’, as well as the Comunidad Autónoma de Madrid (Spain) for funding through the Multiannual Agreement with the Universidad Politécnica de Madrid in the Excellence Programme for University Professors line (M190020074BMGM), in the context of the V PRICIT (Regional Plan of Research and Technological Innovation).
References
-
U. R. Fritsche, Sustainability Governance of Bioenergy and the Broader Bioeconomy, Darmstadt, 2022 Search PubMed.
-
S. Jain, Global Potential of Biogas, 2019 Search PubMed.
-
S. Alberici, G. Toop, B. Monchen, S. Peeters and J. Peterse, Biogases towards 2040 and beyond, 2024 Search PubMed.
- X. Y. Chen, H. Vinh-Thang, A. A. Ramirez, D. Rodrigue and S. Kaliaguine, RSC Adv., 2015, 5, 24399–24448 Search PubMed.
- V. M. Shama, A. R. Swami, R. Aniruddha, I. Sreedhar and B. M. Reddy, J. CO2 Util., 2021, 48, 101507 CAS.
- P. López-Porfiri, M. González-Miquel and P. Gorgojo, Chem. Eng. J., 2022, 446, 137253 Search PubMed.
- K. Friess, P. Izák, M. Kárászová, M. Pasichnyk, M. Lanč, D. Nikolaeva, P. Luis and J. C. Jansen, Membranes, 2021, 11, 1–58 Search PubMed.
- N. A. Ramli, N. A. Hashim and M. K. Aroua, Sep. Purif. Technol., 2020, 230, 115849 CAS.
-
P. López-Porfiri, M. González-Miquel and P. Gorgojo, in Sustainable Separation Engineering, ed. G. Szekely and D. Zhao, Wiley, 1st edn, 2022, pp. 297–341 Search PubMed.
- J. Wang, J. Luo, S. Feng, H. Li, Y. Wan and X. Zhang, Green Energy Environ., 2016, 1, 43–61 CrossRef.
- E. Lasseuguette, M. Carta, S. Brandani and M. C. Ferrari, Int. J. Greenhouse Gas Control, 2016, 50, 93–99 CrossRef CAS.
- J. A. Penn, W. Hu, I. S. Metcalfe and G. A. Mutch, J. Mater. Chem. A, 2024, 12, 30821–30830 RSC.
- I. S. Metcalfe, G. A. Mutch, E. I. Papaioannou, S. Tsochataridou, D. Neagu, D. J. L. Brett, F. Iacoviello, T. S. Miller, P. R. Shearing and P. A. Hunt, Nat. Energy, 2024, 9 DOI:10.1038/s41560-024-01588-6.
- B. S. Beckingham, N. A. Lynd and D. J. Miller, J. Membr. Sci., 2018, 550, 348–356 CrossRef CAS.
- S. G. Pate, H. Xu and C. P. O'Brien, J. Mater. Chem. A, 2022, 10, 4418–4427 RSC.
- V. Loianno, K. P. Bye, M. Galizia and P. Musto, J. Polym. Sci., 2020, 58, 2547–2560 CrossRef CAS.
- A. Klamt and F. Eckert, Fluid Phase Equilib., 2000, 172, 43–72 CrossRef CAS.
- C. S. Beraldo, X. Liang and L. A. Follegatti-Romero, Chem. Eng. Sci., 2024, 285, 119610 CrossRef CAS.
- M. Gonzalez-Miquel, J. Palomar, S. Omar and F. Rodriguez, Ind. Eng. Chem. Res., 2011, 50, 5739–5748 CrossRef CAS.
- M. C. Ferrari, J. Catalano, M. G. Baschetti, M. G. De Angelis and G. C. Sarti, Macromolecules, 2012, 45, 1901–1912 CrossRef CAS.
-
W. E. Wallace, ‘Infrared Spectra’ by NIST Mass Spectrometry Data Center, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, 2023, Gaithersburg MD, 20899 Search PubMed.
- Y. A. Elabd, M. G. Baschetti and T. A. Barbari, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 2794–2807 CrossRef CAS.
- G. T. Fieldson and T. A. Barbari, Polymer, 1993, 34, 1146–1153 CrossRef CAS.
- N. J. Harrick, J. Opt. Soc. Am., 1965, 55, 851 CrossRef.
- B. Comesaña-Gándara, J. Chen, C. G. Bezzu, M. Carta, I. Rose, M. C. Ferrari, E. Esposito, A. Fuoco, J. C. Jansen and N. B. McKeown, Energy Environ. Sci., 2019, 12, 2733–2740 RSC.
- Y. Wang, X. Ma, B. S. Ghanem, F. Alghunaimi, I. Pinnau and Y. Han, Mater. Today Nano, 2018, 3, 69–95 CrossRef.
- L. M. Robeson, J. Membr. Sci., 2008, 320, 390–400 CrossRef CAS.
- L. M. Robeson, J. Membr. Sci., 1991, 62, 165–185 CrossRef CAS.
- A. B. Foster, J. L. Beal, M. Tamaddondar, J. M. Luque-Alled, B. Robertson, M. Mathias, P. Gorgojo and P. M. Budd, J. Mater. Chem. A, 2021, 9, 21807–21823 RSC.
- L. Martínez-Izquierdo, C. Téllez and J. Coronas, J. Mater. Chem. A, 2022, 10, 18822–18833 RSC.
- T. T. L. Bui, H. T. N. Uong, L. V. Nguyen and N. C. Pham, Chem. Biochem. Eng. Q., 2018, 32, 41–53 CrossRef CAS.
- X. Zhang, Z. Tu, H. Li, K. Huang, X. Hu, Y. Wu and D. R. MacFarlane, J. Membr. Sci., 2017, 543, 282–287 CrossRef CAS.
- H. R. Mahdavi, N. Azizi, M. Arzani and T. Mohammadi, J. Nat. Gas Sci. Eng., 2017, 46, 275–288 CrossRef CAS.
- L. C. Tomá, D. J. S. Patinha, R. Ferreira, H. Garcia, C. S. Pereira, C. S. R. Freire, L. P. N. Rebelo and I. M. Marrucho, ChemSusChem, 2014, 7, 110–113 CrossRef PubMed.
- I. Cichowska-Kopczyńska, M. Joskowska, B. Dębski, J. Łuczak and R. Aranowski, J. Chem., 2013, 2013 DOI:10.1155/2013/980689.
- S. H. Barghi, M. Adibi and D. Rashtchian, J. Membr. Sci., 2010, 362, 346–352 CrossRef CAS.
- P. Scovazzo, J. Membr. Sci., 2009, 343, 199–211 CrossRef CAS.
- Z. Shamair, N. Habib, M. A. Gilani and A. L. Khan, Appl. Energy, 2020, 268, 115016 CAS.
- A. M. O'Mahony, D. S. Silvester, L. Aldous, C. Hardacre and R. G. Compton, J. Chem. Eng. Data, 2008, 53, 2884–2891 Search PubMed.
- Z. Shamair, N. Habib, M. A. Gilani and A. L. Khan, Appl. Energy, 2020, 268, 115016 CAS.
- H. Fukuda and J. Lee, J. Membr. Sci., 2025, 713, 123360 CAS.
- R. Villablanca-Ahues, R. Nagl, T. Zeiner and P. Jaeger, Fluid Phase Equilib., 2023, 570, 113783 CAS.
-
X. Wang and Q. Zhou, Refractive Index of Ionic Liquids, in Encyclopedia of Ionic Liquids, ed. S. Zhang, Springer, Singapore, 2020, DOI:10.1007/978-981-10-6739-6_104-1.
- C. G. Duan, W. N. Mei, W. G. Yin, J. Liu, J. R. Hardy, M. Bai and S. Ducharme, J. Phys.: Condens. Matter, 2003, 15, 3805–3811 CAS.
- N. Enea, V. Ion, A. Moldovan, A. Bonciu and N. D. Scarisoreanu, Coatings, 2020, 10, 1–12 Search PubMed.
- A. Chamoun-Farah, A. N. Keller, M. Y. Balogun, L. M. Cañada, J. F. Brennecke and B. D. Freeman, J. Membr. Sci., 2024, 702 DOI:10.1016/j.memsci.2024.122758.
- N. M. A. N. Daud, E. Bakis, J. P. Hallett, C. C. Weber and T. Welton, Chem. Commun., 2017, 53, 11154–11156 CAS.
- J. X. Mao, J. A. Steckel, F. Yan, N. Dhumal, H. Kim and K. Damodaran, Phys. Chem. Chem. Phys., 2016, 18, 1911–1917 CAS.
- M. Juhasz, S. Hoffmann, E. Stoyanov, K. C. Kim and C. A. Reed, Angew. Chem. Int. Ed., 2004, 43, 5352–5355 CAS.
- S. B. Iversen, V. K. Bhatia, K. Dam-Johansen and G. Jonsson, J. Membr. Sci., 1997, 130, 205–217 CAS.
- Q. Sohaib, M. A. Kazemi, C. Charmette, J. Cartier, M. Younas, A. Azarafza, M. Rezakazemi and J. Sanchez-Marcano, Fluid Phase Equilib., 2022, 563 DOI:10.1016/j.fluid.2022.113581.
- O. B. Emek, E. E. Yildiz, M. Sekerci-Cetin and B. Unlusu, Chem. Eng. Commun., 2021, 208, 233–241 CAS.
- C. Moya, J. Palomar, M. Gonzalez-Miquel, J. Bedia and F. Rodriguez, Ind. Eng. Chem. Res., 2014, 53, 13782–13789 CAS.
- H. Toulhoat and A. D. Bianciotto-Defontaines, Oil Gas Sci. Technol., 2003, 58, 659–665 CAS.
-
S. H. Yalkowsky, Y. He and P. Jain, Handbook of Aqueous Solubility Data, CRC, Boca Raton, Fla, 2nd edn, 2010 Search PubMed.
- M. Klepić, J. C. Jansen, A. Fuoco, E. Esposito, P. Izák, Z. Petrusová, I. F. J. Vankelecom, A. Randová, V. Fíla, M. Lanč and K. Friess, Sep. Purif. Technol., 2021, 270, 118812 Search PubMed.
- J. M. Kolle, M. Fayaz and A. Sayari, Chem. Rev., 2021, 121, 7280–7345 CAS.
- A. Fuoco, B. Satilmis, T. Uyar, M. Monteleone, E. Esposito, C. Muzzi, E. Tocci, M. Longo, M. P. De Santo, M. Lanč, K. Friess, O. Vopička, P. Izák and J. C. Jansen, J. Membr. Sci., 2020, 594, 117460 CrossRef.
- M. Gonzalez-Miquel, M. Massel, A. Desilva, J. Palomar, F. Rodriguez and J. F. Brennecke, J. Phys. Chem. B, 2014, 118, 11512–11522 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Perla
Gavagni
*a,
Perla
Gavagni
 b,
Benjamin S.
Moore
b,
Benjamin S.
Moore
 a,
María
González-Miquel
a,
María
González-Miquel
 ac,
Patricia
Gorgojo
ac,
Patricia
Gorgojo
 ade,
Maria-Chiara
Ferrari
ade,
Maria-Chiara
Ferrari
 f and
María
Pérez-Page
f and
María
Pérez-Page
 *a
*a
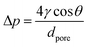
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25/sccm
25/sccm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sccm) permeability was tested in a custom-made setup at a constant absolute pressure of 3.01 (±0.07) bar and 1.16 (±0.11) bar for the feed and permeate sides, respectively. The system is composed of a mixer gas circuit with mass flow controllers for the feed gases and permeate sweep gas (He at 10 sccm), a crossflow membrane cell with an effective membrane area of 1.33 cm2, and an in-line permeate autosampler. The membrane cell is kept inside a ventilated oven at a controlled temperature. After 1 hour of equilibration, permeate stream composition was determined by gas chromatography (Agilent 490 Micro GC with a 10 m PPU HI column) as the average of four runs. Sampling was repeated each hour over 3 hours to ensure stability. SLMs were prepared and tested in duplicate. The gas i flux (Ji/mol s−1 m−2) is expressed according to eqn (2) as a function of its permeability (Pi/mol m Pa s−1 m−2), partial pressure gradient (Δpi/Pa), and SLM thickness (L/m). Gas flow rate (qi/mol s−1), i.e., flux times membrane total area (A/m2) as J·A, is calculated from the system's mass balance.
sccm) permeability was tested in a custom-made setup at a constant absolute pressure of 3.01 (±0.07) bar and 1.16 (±0.11) bar for the feed and permeate sides, respectively. The system is composed of a mixer gas circuit with mass flow controllers for the feed gases and permeate sweep gas (He at 10 sccm), a crossflow membrane cell with an effective membrane area of 1.33 cm2, and an in-line permeate autosampler. The membrane cell is kept inside a ventilated oven at a controlled temperature. After 1 hour of equilibration, permeate stream composition was determined by gas chromatography (Agilent 490 Micro GC with a 10 m PPU HI column) as the average of four runs. Sampling was repeated each hour over 3 hours to ensure stability. SLMs were prepared and tested in duplicate. The gas i flux (Ji/mol s−1 m−2) is expressed according to eqn (2) as a function of its permeability (Pi/mol m Pa s−1 m−2), partial pressure gradient (Δpi/Pa), and SLM thickness (L/m). Gas flow rate (qi/mol s−1), i.e., flux times membrane total area (A/m2) as J·A, is calculated from the system's mass balance.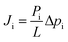

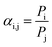





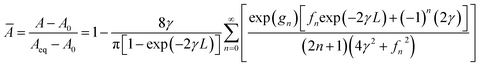


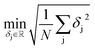

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γsi) = μsi − μpurei
ln(γsi) = μsi − μpurei

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Barrer under ideal conditions, i.e., single gas testing. Other novel materials, such as Polymers of Intrinsic Microporosity (PIM), can remarkably push the separation performance further.29 However, such results proved to be lesser under practical conditions, i.e., mixed gas testing. In such cases, membranes exhibit lower permeabilities of 10–1000 Barrer without reaching the expected boost in the separation in line with the upper bounds, whereas standard commercial membranes display a higher selectivity of 10–50 at even lower fluxes.26 The 2018 upper bound was built using experimental data of mixed gas separation systems employing polymeric membranes based on, among others, PIMs and polyimides. These materials display a separation performance far exceeding the commercial membranes, e.g., Matrimid®. The approach allows for taking into account penetrant-induced plasticisation and competitive gas sorption effects that are not considered in the ideal selectivity estimation nor considered in the other upper bounds. In this line, IL-based SLMs are a competing alternative to polymeric membranes, demonstrating the same behaviour. Permeability and selectivity measurements of mixed CO2/CH4 separation with the IL-based SLMs studied in this work are presented in Fig. 5, with a performance close to the 2018 mixed-gas upper bound. No solvent leaching or stability issues were observed during the experiments at the transmembrane pressure of 1.86 (±0.14) bar. At 25 °C, the [C2min][MeSO4]-SLM displays a CO2 permeability of 188.2 (±3.6) Barrer and CO2/CH4 selectivity of 25.1 (±0.6). However, at 40 °C, its performance is moved up to 209.0 (±10.5) Barrer while selectivity is not significantly changed (23.7 (±1.7)). Following the upper bound, the same trend is observed for [C4min][BF4]-SLM, with a CO2 permeability of 358.8 (±20.9) Barrer and 436.3 (±22.2) Barrer at 25 °C and 40 °C, respectively, with selectivities of 23.5 (±1.5) and 21.2 (±0.4). Similarly, [C4min][BF4]-based SLMs found in the literature show a worse performance, where the CO2/CH4 selectivity is as low as 9. [C4min][PF6]-SLM exhibits an intermediate CO2 permeability of 253.0 (±16.8) Barrer and 308.4 (±29.1) Barrer at 25 °C and 40 °C, respectively. Conversely, it shows a lower CO2/CH4 selectivity of 15.5 (±0.1) and 14.6 (±1.1), meaning no significant difference within the tested temperatures. Again, others [C4min][PF6]-based SLMs reported in the literature at temperatures from room to 40 °C show different performance. Discrepancies between this work IL-SLMs and similar ones found in the literature can be attributed to the differences in support morphology and the operational conditions, e.g., temperature, and preparation, as well as single or mixed gas measurement. Generally, membrane porosity determines the solvent/support ratio, hence the effective diffusivity, while the support matrix might contribute to the total absorbed gas, thus determining effective solubility. Furthermore, composite membranes, another kind of membrane, have been proposed using the IL as a filler into the polymer matrix to exploit the enhanced mass transfer of solvents without falling on stability issues.30 Nevertheless, this approach differs from SLMs since the polymer has a predominant role in the separation.
000 Barrer under ideal conditions, i.e., single gas testing. Other novel materials, such as Polymers of Intrinsic Microporosity (PIM), can remarkably push the separation performance further.29 However, such results proved to be lesser under practical conditions, i.e., mixed gas testing. In such cases, membranes exhibit lower permeabilities of 10–1000 Barrer without reaching the expected boost in the separation in line with the upper bounds, whereas standard commercial membranes display a higher selectivity of 10–50 at even lower fluxes.26 The 2018 upper bound was built using experimental data of mixed gas separation systems employing polymeric membranes based on, among others, PIMs and polyimides. These materials display a separation performance far exceeding the commercial membranes, e.g., Matrimid®. The approach allows for taking into account penetrant-induced plasticisation and competitive gas sorption effects that are not considered in the ideal selectivity estimation nor considered in the other upper bounds. In this line, IL-based SLMs are a competing alternative to polymeric membranes, demonstrating the same behaviour. Permeability and selectivity measurements of mixed CO2/CH4 separation with the IL-based SLMs studied in this work are presented in Fig. 5, with a performance close to the 2018 mixed-gas upper bound. No solvent leaching or stability issues were observed during the experiments at the transmembrane pressure of 1.86 (±0.14) bar. At 25 °C, the [C2min][MeSO4]-SLM displays a CO2 permeability of 188.2 (±3.6) Barrer and CO2/CH4 selectivity of 25.1 (±0.6). However, at 40 °C, its performance is moved up to 209.0 (±10.5) Barrer while selectivity is not significantly changed (23.7 (±1.7)). Following the upper bound, the same trend is observed for [C4min][BF4]-SLM, with a CO2 permeability of 358.8 (±20.9) Barrer and 436.3 (±22.2) Barrer at 25 °C and 40 °C, respectively, with selectivities of 23.5 (±1.5) and 21.2 (±0.4). Similarly, [C4min][BF4]-based SLMs found in the literature show a worse performance, where the CO2/CH4 selectivity is as low as 9. [C4min][PF6]-SLM exhibits an intermediate CO2 permeability of 253.0 (±16.8) Barrer and 308.4 (±29.1) Barrer at 25 °C and 40 °C, respectively. Conversely, it shows a lower CO2/CH4 selectivity of 15.5 (±0.1) and 14.6 (±1.1), meaning no significant difference within the tested temperatures. Again, others [C4min][PF6]-based SLMs reported in the literature at temperatures from room to 40 °C show different performance. Discrepancies between this work IL-SLMs and similar ones found in the literature can be attributed to the differences in support morphology and the operational conditions, e.g., temperature, and preparation, as well as single or mixed gas measurement. Generally, membrane porosity determines the solvent/support ratio, hence the effective diffusivity, while the support matrix might contribute to the total absorbed gas, thus determining effective solubility. Furthermore, composite membranes, another kind of membrane, have been proposed using the IL as a filler into the polymer matrix to exploit the enhanced mass transfer of solvents without falling on stability issues.30 Nevertheless, this approach differs from SLMs since the polymer has a predominant role in the separation.

 . The cumulative distribution function (CDF) of the log-normal distribution corresponds to eqn (20), where the log-normal pore size mean (α) and variance (β2) are calculated from the pore size mean (μpore) and variance (σpore2), according to eqn (21) and (22), respectively.
. The cumulative distribution function (CDF) of the log-normal distribution corresponds to eqn (20), where the log-normal pore size mean (α) and variance (β2) are calculated from the pore size mean (μpore) and variance (σpore2), according to eqn (21) and (22), respectively.

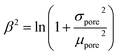

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ) factor in eqn (23), and pore distribution; hence, higher surface tension plus lower contact angle and pore sizes are desired to favour an SLM capable of operating under an increased pressure gradient to promote the permeate gas flow. However, smaller pores reduce the total solvent in the SLM, hence the expected flux. Conversely, a high porosity led to higher support tortuosity, diminishing the effective diffusion of the gas. The SLM selectivity will remain unaffected if the gas solubility and diffusion coefficient have no significant dependency on the system's operational pressure range. Inversely, operating gas separation at higher temperatures might reduce the solvent surface tension and, therefore, the total filled pores, declining the selectivity. In actual applications, complex feed gas-SLM interactions might arise. Changes in the interfacial properties due to the composition of the gas and liquid mixtures, pressure, and temperature affect not only the fluid mobility but also the interfacial mass transfer.42 Therefore, capillary energies of the [gas mixture + solvent mixture + support] should be further investigated to determine their impact on the process scale-up and long-term stability of SLM modules.
cos(θ) factor in eqn (23), and pore distribution; hence, higher surface tension plus lower contact angle and pore sizes are desired to favour an SLM capable of operating under an increased pressure gradient to promote the permeate gas flow. However, smaller pores reduce the total solvent in the SLM, hence the expected flux. Conversely, a high porosity led to higher support tortuosity, diminishing the effective diffusion of the gas. The SLM selectivity will remain unaffected if the gas solubility and diffusion coefficient have no significant dependency on the system's operational pressure range. Inversely, operating gas separation at higher temperatures might reduce the solvent surface tension and, therefore, the total filled pores, declining the selectivity. In actual applications, complex feed gas-SLM interactions might arise. Changes in the interfacial properties due to the composition of the gas and liquid mixtures, pressure, and temperature affect not only the fluid mobility but also the interfacial mass transfer.42 Therefore, capillary energies of the [gas mixture + solvent mixture + support] should be further investigated to determine their impact on the process scale-up and long-term stability of SLM modules.
 , plotted in Fig. 7. Given the inputs of the membrane, ATR crystal element, and IR beam wavelength, the codomain surface represents a unique solution for the gas diffusion coefficient in the SLM that can describe the experimental dataset under the Fickian diffusion regime.
, plotted in Fig. 7. Given the inputs of the membrane, ATR crystal element, and IR beam wavelength, the codomain surface represents a unique solution for the gas diffusion coefficient in the SLM that can describe the experimental dataset under the Fickian diffusion regime.


 -value increase despite its lesser change in water content, from dry to wet conditions, than [C2min][MeSO4]. Results suggest that complex interactions between the IL's ions and water are in play, promoting the rejection of methane. Similar behaviour has been reported for blend membranes composed of poly(vinyl alcohol) and [C2min][DCA], where the IL is completely mixed into the polymer casting solution.56 Commonly, water sorption by polymeric membranes leads to material swelling, which might increase CO2 permeability due to the greater polymer-free volume.57 However, moisture can have a detrimental effect on glassy membranes with high separation performance, such as PIMs. The polymer functional groups responsible for the CO2 solubility become saturated in the presence of water, lowering their interactional capacity. This effect can be reduced by increasing the material hydrophobicity, as it has been shown for highly fluorinated PIMs.58
-value increase despite its lesser change in water content, from dry to wet conditions, than [C2min][MeSO4]. Results suggest that complex interactions between the IL's ions and water are in play, promoting the rejection of methane. Similar behaviour has been reported for blend membranes composed of poly(vinyl alcohol) and [C2min][DCA], where the IL is completely mixed into the polymer casting solution.56 Commonly, water sorption by polymeric membranes leads to material swelling, which might increase CO2 permeability due to the greater polymer-free volume.57 However, moisture can have a detrimental effect on glassy membranes with high separation performance, such as PIMs. The polymer functional groups responsible for the CO2 solubility become saturated in the presence of water, lowering their interactional capacity. This effect can be reduced by increasing the material hydrophobicity, as it has been shown for highly fluorinated PIMs.58












