Mechanical abuse and safety in sodium-ion batteries

Abstract

Sodium-ion batteries (SIBs) are emerging as promising alternatives to lithium-ion batteries (LIBs) because of their low cost and abundant resources. However, their safety and reliability under mechanical abusive loading remain unclear, posing a barrier to further commercialization. In this study, we investigate the mechanical–electrochemical–thermal behavior and underlying mechanisms of SIBs through ball indentation tests. Meanwhile, we develop a multiphysics coupling computational framework—encompassing a 3D mechanical model, a 3D thermal model, an electrochemical model, and an internal short circuit (ISC) model—to gain deeper insights into the internal processes of SIBs. Using this framework, we comprehensively analyze the effects of ball size, battery aspect ratio, and ball loading position, and compare the safety of SIBs and LIBs. Experimental results show that, during ISC, the battery temperature gradually increases, reaching only about 35 °C due to the extremely rapid voltage drop and relatively lower capacity. Parametric studies reveal that using a larger steel ball or a smaller battery aspect ratio delays the ISC trigger and lowers the ISC temperature. Moreover, the computational model demonstrates that SIBs exhibit a slightly later ISC trigger and significantly lower ISC temperatures. Overall, this study lays a solid foundation for understanding SIB behavior and mechanisms under mechanical abuse and provides valuable guidance for designing safer next-generation sustainable batteries.

---

1 Introduction

Sodium-ion batteries (SIBs) have emerged as a promising alternative to lithium-ion batteries (LIBs), particularly for large-scale energy storage applications, due to their abundant and evenly distributed raw materials, cost-effectiveness, and comparable electrochemical performance.^1–5 As the global demand for sustainable and scalable energy storage solutions continues to grow, the development of SIBs is receiving increasing attention.^6–11 However, without understanding their safety and reliability under mechanical abuse conditions, the widespread adoption of SIBs faces big hurdles and challenges.

Safety concerns in energy storage systems often arise from mechanical stresses encountered during manufacturing,¹² transportation,^13,14 and operation.^15,16 Mechanical abuse, such as impact, puncture, indentation, or compression, can compromise the structural integrity of battery components, leading to short circuits, thermal runaway, and even catastrophic failure.^17–19

From an experimental perspective, Wang et al.²⁰ and Zhu et al.²¹ investigated internal battery damage under ball indentation using in situ and ex situ techniques, such as scanning electron microscopy (SEM) and X-ray diffraction (XRD). Their findings revealed that separator failure and electrode cracking are the primary causes of internal short circuits (ISC) in LIBs. Additionally, Li et al.²² accurately measured the contact resistance resulting from ISC, providing critical insights for enhancing battery safety modeling. From a modeling perspective, key contributions include the representative-sandwich model developed to predict ISC under ball indentation^23,24 and homogenized models for LIB behavior under nail penetration and compression.^25,26 Further, a comprehensive computational framework addressing four types of mechanical abuse conditions was introduced by Wang et al.,²⁷ establishing ISC criteria linked to separator failure. Another significant advancement is the multiphysics model based on LS-DYNA, designed for ease of adoption by electric vehicle (EV) manufacturers.²⁸ Fundamental mechanisms triggering ISC under quasi-static and dynamic loading have also been identified in related works.^29–33 From the data-driven modeling perspective, finite element (FE) models combined with machine learning (ML) algorithms have been applied to predict the safety envelope and ISC risk of LIBs under mechanical loading.^34,35 Similarly, ML algorithms have been employed to forecast mechanical behavior and failure during mechanical abuse.³⁶ These approaches underscore the potential of integrating traditional modeling techniques with data-driven methods to improve the accuracy and efficiency of battery safety predictions.

While extensive research has explored the mechanical and thermal safety of LIBs, only a limited number of studies have investigated thermal instabilities in SIB materials, and virtually no work has been done on SIBs under mechanical abuse conditions. For thermally induced ISC in SIBs, Fedoryshyna et al.³⁷ studied the venting behavior of cylindrical SIBs and found that SIBs exhibit lower TR temperatures compared to LIBs, attributed to the absence of gas ignition. Yue et al.³⁸ used accelerating rate calorimetry (ARC) to calculate the TR maximum temperature, revealing that the TR hazard of SIBs with Na_xTMO₂ (NTM) as the cathode lies between that of LIBs with LiFePO₄ (LFP) and LiNi_0.5Co_0.2Mn_0.3O₂ (NCM523) cathodes. Robinson et al.³⁹ also used ARC to demonstrate that SIBs exhibit a slower self-heating rate and TR progression compared to LIBs. However, Li et al.⁴⁰ observed that while SIBs have a slower TR onset, they exhibit more severe TR effects. For electrically induced ISC in SIBs, Xu et al.⁴¹ and Gui et al.⁴² investigated the capacity degradation behavior and cathode performance of SIBs under overcharging, respectively.

This knowledge gap underscores the urgency of investigating how SIBs respond to mechanical abuse and the potential implications for their safe deployment. This study focuses on the behavior and fundamental mechanism of SIBs under mechanical loading. Ball indentation experiments are conducted to evaluate the electrochemical performance, thermal safety, and mechanical integrity of SIBs. Additionally, a three-dimensional multiphysics computational framework is developed. This framework integrates a 3D mechanical model, ISC model, electrochemical model, and 3D thermal model, facilitating an in-depth exploration of the behavior of SIBs under varying ball sizes, aspect ratios, and loading positions. Furthermore, safety comparisons between LIBs and SIBs are performed.

2 Methodology

2.1 Experiment

A commercially available Na_0.97Ca_0.03[Mn_0.39Fe_0.31Ni_0.22Zn_0.08]O₂ layered oxide (NNMF)/hard carbon (HC) sodium-ion pouch cell,⁴³ with a theoretical capacity of ∼220 mA h and manufactured by LiFUN, was selected for model calibration in this paper (Fig. 1(a)). The dimensions of the pouch cell are 30 mm × 18.2 mm × 5.6 mm. The basic information about the battery is summarized in Table 1. The aluminum–plastic battery pouch houses a jellyroll structure consisting of 14 cathode layers, 14 anode layers, and 28 separator layers (Fig. 1(b)). The cathodes and anodes are engineered as sandwich structures, with current collectors double-coated with active material (Fig. 1(c)). The charge and discharge cutoff voltages are 4.0 V and 1.5 V, respectively.

Fig. 1 Internal structure and physical dimensions of (a) sodium ion pouch cell (b) jellyroll, and (c) detailed components of the jellyroll.

Table 1 Basic information about sodium ion battery

Parameters	Value
Theoretical capacity	220 mA h
Reversible capacity	∼200 mA h
Charging cutoff voltage	4.0 V
Discharging cutoff voltage	1.5 V
Cathode active material	Na0.97Ca0.03[Mn0.39Fe0.31Ni0.22Zn0.08]O2 layered oxide
Anode active material	Hard carbon
Cathode & anode current collector	Al
Casing	Al plastic film
Layer number	14

---

Since the batteries we purchased were dry batteries (without electrolyte), we prepared the electrolyte by dissolving 1 m NaPF₆ in a propylene carbonate/ethyl methyl carbonate (PC : EMC = 1 : 1 by volume) mixture, with the addition of 2% fluoroethylene carbonate (FEC). After adding the electrolyte, the batteries were sealed using a Vacuum Sealer (MASK-115-III) in an argon-filled glove box (Vigor SG2400/750TS, H₂O < 0.1 ppm, O₂ < 0.1 ppm). The next critical step was the formation cycle. The batteries underwent three constant current (CC) charge–discharge cycles under a pressure of 0.1 MPa with a current of 10 mA using a charge–discharge instrument (Neware CT-4008) at room temperature. After the formation cycle, the batteries were degassed and resealed within the glove box. Subsequently, a conditional test was conducted for two cycles to determine the initial capacity of the SIBs. In this test, CC charging (22 mA, 0.1C) was applied up to 4 V, followed by constant voltage (CV) charging until the current decreased to 4.4 mA (0.02C). The batteries were then discharged using CC mode (22 mA, 0.1C) down to 1.5 V. The initial capacity was measured to be approximately 196 mA h, as detailed in Table S1.†

The battery was charged to 100% state-of-charge (SOC). The batteries were then positioned on the compression test platform, which was mounted on a mechanical testing machine (SUNS UTM5205X) with a maximum load capacity of 200 kN (Fig. 2(a)). Axial indentation was applied to the center of the battery using a flat indenter. A 1.5 mm diameter steel particle was positioned at the center of the cell (Fig. 2(b)). The loading speed for the ball indentation tests was set at 5 mm min⁻¹ (quasi-static conditions). During the loading process, in situ monitoring of the battery voltage and surface temperature was performed using a digital voltmeter and temperature sensors (Agilent 34970A). Two K-type thermocouples were positioned near the indenter on the battery surface to measure temperature accurately. The dimensions of the indenter are relatively small (Fig. S1†). As a result, it does not come into contact with the K-type thermocouples during the mechanical loading. To ensure precise and stable voltage measurement, nickel sheets were firmly welded to the positive and negative terminals of the cell. During the experiment, the indenter was lowered, driving the ball into the battery under applied pressure.

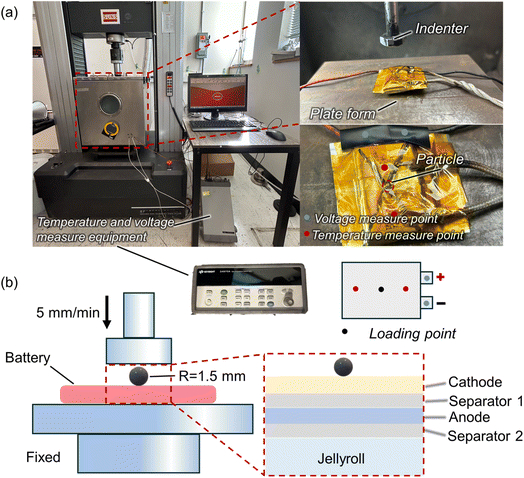Fig. 2 Design of the penetration experiment for a SIB: (a) testing equipment illustration (b) schematic diagrams of experiments and models.

2.2 Computational modeling: multiphysics modeling

A 3D finite element model of a sodium-ion pouch cell was developed in this study. The top four layers were configured individually, in sequence—cathode, separator, anode, separator—to accurately represent the failure of each component, aligning with the actual battery configuration. The remaining layers of the jellyroll were modeled as a homogeneous structure to effectively predict the mechanical response during ball indentation (Fig. 2(b)). To simplify the model, the battery casing was excluded from the modeling with detailed geometry and material properties (Tables S2 and S3†). However, the side surfaces along the length direction are fully constrained to replicate the constraints from the battery casing and the jellyroll winding method.

To comprehensively analyze mechanical deformation, the evolution of internal short circuits, and thermal behavior in SIBs under mechanical abuse, a coupled multi-physics model was developed. This model integrates four sub-models: a 3D mechanical model, an electrochemical model, a short-circuit model, and a 3D thermal model, all implemented on the COMSOL platform (Table S4†).

3D mechanical model. The 3D mechanical model was utilized to predict the mechanical response of batteries during the ball indentation test. The numerical results indicate that the model accurately captures the mechanical behavior observed in the experiments (Fig. 4(a)). The compression and tensile tests conducted on the batteries were used to characterize the elastic modulus and constitutive behavior of the battery materials (Fig. S2†). The SUNS UTM5205X system, with a maximum load capacity of 200 kN, was used for compression tests, whereas the INSTRON 34SC system, with a maximum load capacity of 5 kN, was utilized for tensile tests to suit their respective load requirements. Rectangular specimens measuring 4 mm × 60 mm from the cathode, anode, and separator (machine direction) were prepared for tensile testing, while compression testing was conducted on the complete jellyroll.

The separator material exhibits clear anisotropic behavior, as confirmed by tensile testing. Therefore, an elastoplastic model is employed to represent its mechanical properties. The Hill'48 yield criterion is employed to characterize the anisotropic stress contributions to the yielding behavior of the separator. The associated coefficients are F = 1, G = H = 0.162, L = 0.28, M = N = 1.73.²⁵ The cathode/anode consists of an aluminum foil current collector double-coated with NNMF/HC, modeled as a single integrated component. An isotropic elastic material model is applied to represent the cathode and anode materials, with material parameters derived from tensile tests. Compression tests were performed on the jellyroll at SOC = 0 to determine its constitutive behavior. To simplify the analysis, an isotropic elastic model was utilized. The ball is composed of steel. Its mechanical behavior is modeled using an isotropic elastic material model. Solid elements are employed to represent all battery components in the model. The boundary conditions and loading configurations closely align with those used in the experimental setup. The battery bottom surface is fully constrained, while the top surface is loaded along the Z-axis, corresponding to its thickness direction. This setup mimics the typical loading condition of ball indentation. The penalty function contact method was implemented for the computation.

Electrochemical model. A one-dimensional electrochemical model based on the classical Pseudo-Two-Dimensional (P2D) framework has been developed. This model integrates Fick's laws of diffusion, the Butler–Volmer equation, the Nernst–Planck equation, and charge conservation principles. Additionally, an ISC sub-model is employed to define the boundary conditions for the electrochemical model. It effectively predicts voltage drops and heat generation. The electrochemical model, validated through discharge voltage–time curves at rates of 0.1C and 0.5C, is utilized to predict battery voltage. The computational results show strong agreement with the experimental voltage curves (Fig. S3†).

ISC model. The ISC model is designed to calibrate internal short-circuit resistance and quantify the resulting heat generation. When the strain in the separator reaches the failure criterion, electrical contact occurs in the affected area, leading to a short circuit. In this study, the equivalent plastic strain of the separator is chosen as the criterion for triggering an internal short circuit. The ISC failure mode of sodium-ion batteries remains unidentified. In this study, the ISC resistance is determined by fitting experimental data. Both the discharge current and the heat generated by the ISC are calculated using the ISC resistance.³⁰ With the increase of ball indentation displacement, the contact area between the cell and the ball increases, causing a decrease in resistance.

Thermal model. The thermal model is utilized to predict the heat transfer process in SIBs. Two primary heat sources are considered in the model: short-circuit Joule heat and battery internal resistance Joule heat, both of which are calculated using Ohm's law and Joule's law. The configuration of heat sources and boundary conditions is depicted in Fig. 3(b). Additionally, thermal convection and radiation effects are accounted for on the battery and ball surface. Heat source Q is generated during the progression of the short circuit and the electrochemical reaction. Q includes battery heat Q_cell and ISC heat Q_ISC. It should be noted that due to the lack of experimental data for the thermal parameters of SIBs, accurately determining these parameters for the thermal model is challenging. Therefore, we estimated these parameters (Table S3†) based on available data from LIBs.⁴¹ To ensure the model's accuracy, we calibrated the parameters using ball indentation test data. Additionally, to minimize the impact of parameter estimation on the subsequent discussion, the same thermal parameters were applied to the LIB model in the safety comparison described earlier.

Fig. 3 (a) Coupling strategy and schematic algorithms for the high-level multiphysics model including multiple sub-models. (b) The geometry, boundary conditions, heat source settings, and schematic of an internal short circuit due to mechanical abuse. Detailed variable definitions can be referred to in the Nomenclature.

Coupling strategies. Initially, the mechanical model calculates the equivalent plastic strain of the separator and the ball indentation displacement. The mechanical model operates independently from the other sub-models. In contrast, the electrochemical model, ISC model, and thermal model are fully coupled and interact in real time. Thermal and electrochemical models are linked through the interplay between temperature and heat generation. Heat is generated during the electrochemical reaction, primarily due to the internal resistance of the battery, and is transferred to the thermal model. Simultaneously, the temperature rise caused by heat accumulation influences the electrochemical process by altering transport properties, such as conductivity and diffusion coefficients. These changes, in turn, affect the concentration distribution of the particles.²⁹ The calculated displacement and strain are passed to the ISC model to determine the ISC trigger time and ISC resistance. Once the ISC is triggered, the ISC model computes the ISC current based on the ISC resistance and transfers the ISC current to the electrochemical model to calculate the voltage. Simultaneously, the ISC heat source and electrochemical heat source are computed by the ISC model and the electrochemical model, respectively. These heat sources are then transferred to the thermal model to calculate the temperature (Fig. 3(a)).

3 Results

3.1 Typical results

The typical evolution of a sodium-ion battery behavior under ball indentation is illustrated in Fig. 4(a). For a 100% SOC cell, as the steel ball encounters the pouch wall, the reaction force increases over time during the initial deformation of the battery structure, reaching approximately 530 N at t = 17 s, with a corresponding ball indentation displacement of about 1.4 mm. As the displacement caused by the steel ball progressed, the separator was penetrated upon reaching its mechanical failure strain. At this point, the force sharply drops to 215 N. When the cathode and anode come into direct contact, an ISC is triggered. This results in discharge and heat generation within the cell, causing a sudden voltage drop and a gradual temperature rise. The voltage decreases from 3.8 V to approximately 1.3 V. While the force shows brief recoveries, it continues to decline as the steel ball further compresses the battery. A similar brief recovery is observed in the voltage. After the mechanical loading ceases, the battery voltage stabilizes at approximately 1.1 V (t = 33 s) before gradually decreasing and leveling off at 0.8 V. The short circuit current flowing through the affected area generated Joule heat, causing the measured surface temperature to rise by 8.5 °C and peak at approximately 35 °C (t = 70 s). When t > 70 s, the battery temperature gradually decreases as heat dissipation through convection and radiation exceeds the rate of heat generation (Video 1 in ESI†).

Fig. 4 (a) Comparison between the experimental (dotted lines) and computational (solid lines) results for force (black), voltage (red), and temperature (blue) in battery ball indentation tests, and (b) the physical appearance of the battery and its internal components-cathode, anode, and separator-following the indentation procedure.

It is experimentally challenging to characterize the mechanical–electrochemical–thermal behaviors within a battery, either in situ or ex situ, during the ball indentation process. Therefore, a multiphysics model has been developed to provide deeper insights into phenomena such as internal material deformation and short circuit current. To validate the computational model, computational results were compared with experimental data (Fig. 4(a)). Some deviations in the calculated voltage profiles were observed during the voltage recovery stage, primarily due to the challenge of accurately capturing rapid resistance changes caused by the penetration of battery components (cathode/anode) under mechanical loading, as well as the simplification of the model description. Similar discrepancies in voltage prediction have been reported in other studies,^25,26,31 where achieving a perfect voltage response remains challenging. We may note a comparison between experimental and computational results demonstrates that the model effectively captures voltage variations in the recovery stage, particularly the voltage recovery peaks. Overall, the computation results align well with the experimental data, demonstrating the accuracy of the multiphysics model.

3.2 Analysis: explain the fundamental mechanisms of the behaviors

During the ball indentation process, the battery underwent deformation from 0 s to 17 s, generating strain simultaneously. At around 17 s, the equivalent plastic strain of the separator reached the threshold value of 0.165, triggering an internal short circuit. This event caused the voltage to drop sharply to a lower value (1.1 V) when the short circuit occurred. The abrupt voltage drop led to an instantaneous reduction in the short-circuit current, bypassing the phase of rapid temperature rise. Subsequently, the SIBs discharged at a lower short-circuit current, gradually generating heat and resulting in a steady temperature increase over time.

After the ball indentation experiment, the battery was disassembled to examine its internal mechanical failure. It was observed that the majority of the battery assembly remained intact, with penetration occurring only in a localized area around the indentation. Specifically, the battery components—including the cathode, anode, and separator—near the steel ball's contact layer were penetrated (Fig. 4(b)). Additionally, the size of the indentation holes gradually decreased with each successive layer. The primary cause of the sharp voltage drop was the failure of the separator, which resulted in direct contact between the anode and cathode, triggering an internal short circuit. Additionally, a voltage recovery phenomenon was noted in the experimental results. This recovery occurs because the penetration of the cathode and anode interrupts the internal short circuit, leading to a significant increase in resistance and causing the voltage to rise again. Note that a similar voltage recovery phenomenon has been observed in LIBs, where it is attributed to the melting of the current collector and separator.^31,44 However, this mechanism was not activated in sodium-ion batteries during the ball indentation experiments due to the limited temperature rise in these tests.

4 Discussions

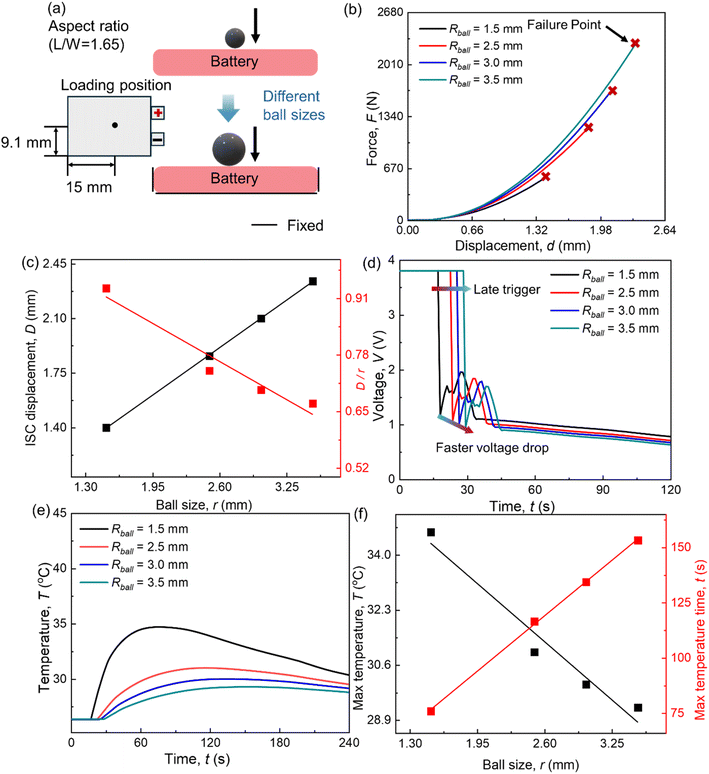
In practical battery applications, high SOC batteries pose more significant safety concerns. Therefore, all discussions in this study are focused on 100% SOC batteries. While safety in larger-format cells is also crucial for battery applications, this study focuses exclusively on the safety of pouch cells. This is due to the inhomogeneities arising from the complex internal structures of larger-format cells and the need for further advancements in thermal runaway modeling. This section examines three critical factors influencing battery safety, i.e., ball size, aspect ratio, and loading position.

4.1 Different ball sizes

The steel ball with a radius of 1.5 mm, battery aspect ratio L/W = 1.65, and loading position L_loading = 15 mm is set as the baseline. To investigate the effect of ball size, three additional radii—2.5 mm, 3 mm, and 3.5 mm—are used (Fig. 5(a)).

Fig. 5 (a) Illustration of the ball indentation test with varying ball sizes, a constant loading position (center), a fixed battery aspect ratio (L/W = 1.65), and fixed boundary conditions (bottom and sides). (b) Computational results showing force–displacement curves for different ball sizes. (c) Voltage–time curves for various ball sizes. (d) ISC displacement and the ratio of ISC displacement to ball size (D/r)-ball size curve. (e) Temperature–time curves for different ball sizes. (f) Maximum temperature and the time to reach a maximum temperature as a function of ball size.

In the mechanical response of the SIB, the reaction force increases with ball size, and a larger ball corresponds to a greater short-circuit trigger displacement (Fig. 5(b)). This is mainly because a larger ball creates a greater contact area with the cell, increasing the load-bearing capacity of the components and resulting in a higher force. Furthermore, the larger contact area leads to a more uniform deformation distribution and less stress concentration, requiring a greater ball indentation displacement for the separator to reach the equivalent plastic strain threshold needed to trigger an internal short circuit. It is observed that the ISC displacement increases linearly with larger ball sizes. This relationship enables a straightforward estimation of the ISC displacement. However, the ratio of ISC displacement to ball size (D/r) decreases almost linearly as the ball size increases (Fig. 5(c)). This suggests that once the ball's size surpasses a certain threshold, the cell's deformation becomes sufficiently uniform, and further increases in ball size exert a weaker influence on the deformation distribution.

In the electrochemical response of the SIB, computational results reveal that the voltage remains stable at 3.8 V until the onset of the ISC. Upon triggering the ISC, the voltage exhibits a sharp decline (Fig. 5(d)). Interestingly, the rate of voltage drop increases with the size of the ball. This occurs because a larger ball generates a more extensive short-circuit contact area, reducing the short-circuit resistance. As a result, the discharge current increases, leading to a more rapid voltage drop.

The temperature results indicate that after the initiation of the ISC, the temperature gradually rises to its peak as the battery discharges, releasing ISC heat and battery heat. Subsequently, the temperature begins to decrease due to heat dissipation through convection and radiation (Fig. 5(e)). The size of the ball significantly impacts the temperature evolution process. Larger balls result in higher peak temperatures and faster temperature rise (Fig. 5(f)). This is primarily because larger balls cause a faster voltage drop and reduced ISC resistance, leading to less overall heat generation. Additionally, larger balls contribute to greater heat dissipation, especially in smaller-sized cells like the one studied here. It is observed that the maximum temperature increases linearly with larger ball sizes, while the time to reach the maximum temperature decreases linearly as the ball size grows. This phenomenon arises because lower ISC temperatures diminish the efficiency of both convection and radiation, resulting in slower heat dissipation. Moreover, these linear relationships can be employed for quick temperature estimation during ISC events. For LIB, the effect of ball size on ISC behavior has been fully explored and explained in detail by Yuan et al.²⁸

4.2 Different aspect ratio

The baseline setup includes a steel ball with a radius of 1.5 mm, a battery aspect ratio of L/W = 1.65 (L_battery = L₀), and a load position fixed at the center of the battery. It is important to note that when analyzing the effect of aspect ratio, the cell thickness remains constant, and the product of the battery's length and width is kept constant (L_batteryW_battery = L₀W₀). To examine the impact of aspect ratio, three additional configurations are considered: L_battery = 0.82L₀, 1.22L₀ and 1.82L₀ (Fig. 6(a)).

Fig. 6 (a) Schematic illustration of ball indentation with varying battery aspect ratios. (b) Computational results depicting force–displacement curves for batteries with different aspect ratios. (c) Voltage–time curves corresponding to various battery aspect ratios. (d) ISC displacement and ISC force as a function of the battery aspect ratio L_battery/L₀. (e) Temperature–time curves for batteries with different aspect ratios. (f) Maximum temperature and the time required to reach it as functions of L_battery/L₀.

In the mechanical response, smaller aspect ratios correspond to larger ISC displacements, resulting in delayed ISC triggering (Fig. 6(b)). This occurs because cells that are closer to a square shape (i.e. L_battery = 0.82L₀) exhibit weaker constraints near the steel ball, leading to more uniformly distributed deformation. Conversely, a longer battery reaches critical strain at lower displacements and experiences severe stress concentrations due to geometric constraints. Additionally, the ISC force decreases with increasing aspect ratio because the separator fails earlier (Fig. 6(c)).

Voltage results reveal that smaller aspect ratio cells experience a faster voltage drop (Fig. 6(d)). The main reason is that, for cells with a smaller aspect ratio, the delayed ISC trigger leads to a larger short-circuit contact area, thereby reducing ISC resistance and raising the discharge current. Interestingly, larger aspect ratio cells exhibit higher temperatures following an ISC, although the time to reach the maximum temperature remains approximately constant at around 75 s (Fig. 6(e) and (f)). This behavior is attributed to smaller aspect ratio cells generating less heat during an ISC due to their faster voltage drop and lower ISC resistance. Moreover, the more square-like geometry of smaller aspect ratio cells provides a larger heat dissipation area, further contributing to lower heat accumulation. Since their ISC temperatures show only minor differences, the time to reach the maximum temperature remains nearly identical because of comparable heat dissipation.

4.3 Different loading positions

The baseline setup consists of a steel ball with a radius of 1.5 mm and a battery aspect ratio of L/W = 1.65 (L_battery = L₀). The steel ball is fixed at W_loading = W₀/2, while L_loading is varied. Note that due to symmetry, only half of the cells are analyzed in this study. To investigate the influence of the loading position, four positions are considered: L_loading = 5 mm, 9 mm, 11 mm and 12.5 mm, as illustrated in Fig. 7(a).

Fig. 7 (a) Schematic illustration of the ball indentation process with varying loading positions. (b) Computational results showing force–displacement curves. (c) Voltage–time curves. (d) Temperature–time curves for batteries under different loading positions.

Changes in the loading position have minimal impact on the mechanical response (Fig. 7(b)). This is primarily due to the strong boundary conditions, which constrain the deformation of the cell, and the relatively small cell size, which exacerbates stress concentration effects. Additionally, for different loading positions, the voltage and temperature profiles remain nearly the same (Fig. 7(c) and (d)). This is mainly because the nearly identical ISC trigger displacements produce similar short-circuit contact areas and ISC resistances, resulting in consistent discharge currents and heat generation across the various loading positions.

Moreover, since the cell's surface area remains constant, its heat dissipation capacity also remains unchanged. As a result, the temperature and voltage profiles exhibit negligible differences across the various loading positions.

4.4 Safety comparison of LIBs and SIBs

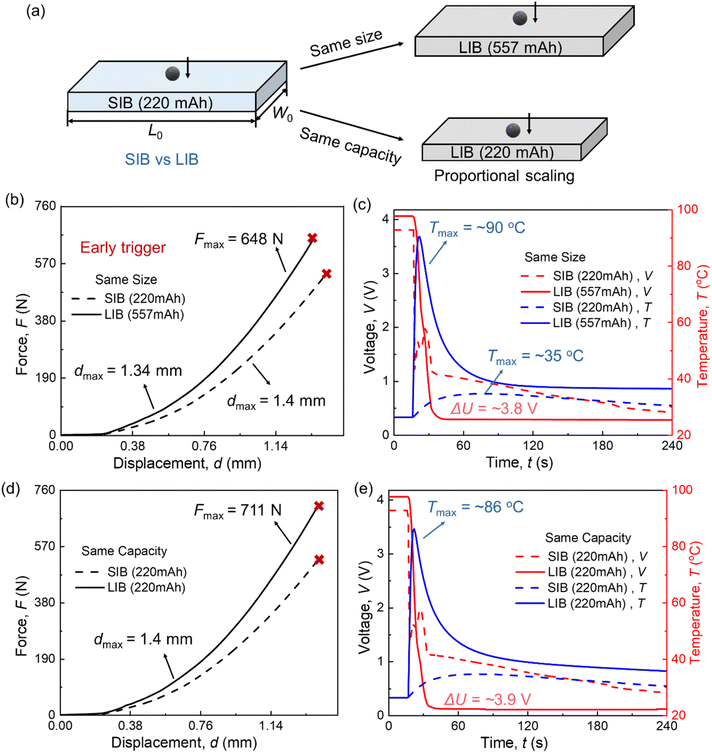
The capacity of LIBs is estimated based on the theoretical capacity of a LiCoO₂ (LCO)–graphite battery based on the size scaling: the dimensions of the scaled-down LIBs are calculated as 22.41 mm × 13.45 mm × 4.18 mm, with a scaling ratio of 0.747. Similarly, LIBs of the same size exhibit a higher capacity, estimated at 557 mA h (Fig. 8(a)). It is assumed that the thickness of each component (cathode, anode, and separator) is identical for both battery types. Additionally, material differences between LIBs and SIBs, such as the current collector, are included. These differences are reflected in the Young's modulus of the cathode, anode, and jellyroll. Furthermore, the baseline conditions remain consistent, including a steel ball radius of 1.5 mm, a centrally located loading position, and an aspect ratio of 1.65.

Fig. 8 Illustrates the comparison between SIB and LIB under various conditions: (a) a schematic illustration of SIB vs. LIB; (b) computational results depicting force–displacement curves for SIB and LIB of the same size; (c) voltage and temperature–time curves for SIB and LIB of the same size; (d) force–displacement curves for SIB and LIB with the same capacity; and (e) voltage and temperature–time curves for SIB and LIB with the same capacity.

Note that since the maximum temperature of SIB in the ISC process in this study is only 35 °C, the thermal runaway of the cell is not considered in the modeling. While for LIBs, the temperature rise in the ISC process is limited, and the main temperature increase is reflected in the thermal runaway process. Therefore, in this study, only the temperature changes caused by the heat production in the ISC process of both batteries are considered.

For LIBs and SIBs of the same size, the ISC force is greater in LIBs (F_max = 648 N) because most lithium-ion components, except for the separator, have a higher Young's modulus compared to sodium-ion components. However, LIBs trigger ISC earlier, at a smaller displacement (d_max = 1.34 mm) in Fig. 8(b). Computational results reveal distinct voltage drop behaviors for high SOC LIBs and SIBs during the ISC process. For LIBs, the voltage decreases from 4.05 V to 0.3 V (ΔU = ∼3.8 V) over approximately 14 seconds. In contrast, for SIBs, the voltage drop from 3.8 V to 1.2 V occurs much faster, lasting only about 1 second in computation (and just 0.45 seconds in experimental results). The primary reason for this behavior is that SIBs possess a lower Young's modulus than LIBs, since both the cathode and anode current collectors in SIBs are made of aluminum (Al). Consequently, during the ball indentation test, SIBs experience more extensive mechanical damage, leading to a faster voltage drop. Additionally, the slower voltage drop in LIBs results in greater heat generation during the ISC process, causing the temperature to rise rapidly to 90 °C. In comparison, the temperature increase for SIBs is more modest, reaching only 35 °C (Fig. 8(c)).

In addition to differences in voltage behavior, the ISC modes also vary between high SOC LIBs and SIBs. In previous studies,³¹ the typical ISC mode for a high SOC LIB involves the voltage dropping to a plateau for a few seconds before eventually falling to 0. In contrast, for a high SOC SIB, the voltage rapidly decreases to a lower value and then gradually declines more slowly over time. This behavior is more similar to the ISC mode observed in low SOC LIBs, highlighting fundamental differences in the electrochemical response of the two battery types during ISC events.

For both cells with the same capacity, the ISC displacement was identical (d_max = 1.4 mm), meaning the ISC was triggered simultaneously. However, the ISC force was higher for the LIB (F_max = 711 N). Additionally, during the ISC process, the LIB exhibited a greater temperature increase, reaching approximately 86 °C, and a larger voltage drop of about 3.9 V, both exceeding those observed in the SIB ISC process.

5 Concluding remarks

Exploring the behaviors and failure mechanisms of SIBs under mechanical loading is crucial for ensuring their safety and reliability. This study conducts ball indentation tests and establishes a multiphysics coupling computational framework to investigate the complex interplay of mechanical, thermal, and electrochemical behaviors in SIBs under mechanical abuse. The framework integrates four sub-models: a 3D mechanical model, an ISC model, a 3D thermal model, and an electrochemical model. To ensure the model's accuracy, ball indentation tests were conducted to validate the computational data, demonstrating that the computational framework effectively predicts the behavior of SIBs.

(1) We observed an extremely rapid voltage drop in SIBs during the ISC event, which explains why SIBs exhibit lower ISC temperatures compared to LIBs. Through post mortem analysis, we identified that the penetration of the cathode/anode caused a voltage recovery phenomenon that is fundamentally different from the similar voltage drop behaviors observed in LIBs, highlighting unique behaviors in SIBs under mechanical abuse.

(2) Results indicate that a larger steel ball results in a delayed ISC trigger, a faster voltage drop, and a lower ISC temperature. Additionally, when the battery shape approaches a square (e.g., with a smaller aspect ratio), the ISC trigger occurs later, and the ISC temperature is slightly lower. However, the loading position has almost no impact on the behavior of SIBs.

(3) We discover that SIBs have a slightly delayed ISC trigger and a significantly lower ISC temperature, demonstrating that SIBs offer greater safety than LIBs under mechanical loading.

By bridging experimental observations with advanced modeling techniques, this work advances the understanding of SIB safety under mechanical abuse conditions. The insights gained and the multiphysics model developed provide a foundation for the development of next-generation SIBs with enhanced safety, reliability, and performance.

Nomenclature

a	Specific surface area of active particle
c	Concentration (mol m^−3)
C p	Heat capacity (J (kg K)^−1)
D	Diffusion coefficient (m^2 s^−1)
E	Young's modulus (MPa)
F	Faraday's constant (9.64853 × 10^4 C mol^−1)
h	Heat transfer coefficient (W (m^2 K)^−1)
I	Current (A)
i	Current density (A m^−2)
j 0	Exchange current density (A m^−2)
j loc	Local current density (A m^−2)
k	Thermal conductivity (W (m K)^−1)
k ^c	Rate constant of cathode
k ^a	Rate constant of anode
Q s	Heat sources (W m^−3)
Q cell	Battery heat (W m^−3)
Q ISC	ISC heat (W m^−3)
q loss	Heat dissipation (W m^−2)
q con	Heat dissipation by conduction (W m^−2)
q rad	Heat dissipation by radiation (W m^−2)
R g	Universal gas constant, 8.314 (J (mol K)^−1)
R	Resistance (Ω)
r	Radial (m)
t	Time (s)
t+	Transfer number
T	Temperature (°C)
T amb	Ambient temperature
V	Voltage (V)
R 0	The initial resistance
R cell	The ohmic internal resistance
E cell	The real-time updated voltage
t ^j	Thickness of jellyroll
w ^j	Width of jellyroll
H ^j	Length of jellyroll
L ^j	Total length after jellyroll expansion
S ^j	Total area of active material
L	Thickness in 1D model

Greek letters

α	Conversion degree (1)
v	Poisson's ratio (1)
ε	Strain (1)
ε z	The through-thickness strain (1)
ε e	Volume fraction
ε Df	Surface emissivity (1)
ρ	Density (kg m^−3)
ϕ	Potential (V)
φ	Efficacy coefficient (1)
η	Overpotential (V)
κ	Electrical conductivity (S m^−1)
σ B–D	Stefan–Boltzmann constant (5.67 × 10^−8 W (m^2 × K^4)^−1)
δ	Thickness in 3D model

Subscripts and superscripts

0	Initial state
amb	Ambient
eff	Effective property
e	Electrolyte
s	Solid
D	Diffusion
c	Cathode
a	Anode
se	Separator
j	Jellyroll
ISC	Internal short circuit
eq	Equilibrium
pc	Cathode current collector
nc	Anode current collector
ps	Cathode active layer
ng	Anode active layer
Al	Aluminum

Data availability

The code for Comsol can be found at https://github.com/BR-UD/Code. The version of the code employed for this study is COMSOL version 6.2.

Author contributions

Bo Rui: methodology, data analysis, and writing – original draft; Shuguo Sun: data analysis and methodology; Xijun Tan: methodology and data analysis; Chanmonirath (Michael) Chak: experimental sample preparation; Lin Ma: methodology, data analysis and writing – review & editing; Jun Xu: conceptualization, methodology, supervision, and writing – review & editing.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

JX acknowledges the support of the startup funding from the University of Delaware. LM acknowledges the support by the US National Science Foundation Award No. 2301719 and ORAU Ralph E. Powe Junior Faculty Enhancement Award.

References

1. C. Vaalma, D. Buchholz, M. Weil and S. Passerini, Nat. Rev. Mater., 2018, 3, 1–11.
2. K. M. Abraham, ACS Energy Lett., 2020, 5, 3544–3547.
3. Y. Fang, L. Xiao, Z. Chen, X. Ai, Y. Cao and H. Yang, Electrochem. Energy Rev., 2018, 1, 294–323.
4. N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682.
5. J. Y. Hwang, S. T. Myung and Y. K. Sun, Chem. Soc. Rev., 2017, 46, 3529–3614.
6. Z. He, Y. Huang, H. Liu, Z. Geng, Y. Li, S. Li, W. Deng, G. Zou, H. Hou and X. Ji, Nano Energy, 2024, 129, 109996.
7. X. Cai, Y. Yue, Z. Yi, J. Liu, Y. Sheng and Y. Lu, Nano Energy, 2024, 129, 110052.
8. Q. Wang, D. Zhou, C. Zhao, J. Wang, H. Guo, L. Wang, Z. Yao, D. Wong, G. Schuck, X. Bai, J. Lu and M. Wagemaker, Nat. Sustainability, 2024, 7, 338–347.
9. Y. Wan, B. Huang, W. Liu, D. Chao, Y. Wang and W. Li, Adv. Mater., 2024, 36, 2404574.
10. X. Lu, S. Li, Y. Li, F. Wu, C. Wu and Y. Bai, Adv. Mater., 2024, 36, 2407359.
11. H. Kim, ACS Mater. Au, 2023, 3, 571–575.
12. R. Li, W. Li, A. Singh, D. Ren, Z. Hou and M. Ouyang, Energy Storage Mater., 2022, 52, 395–429.
13. V. Ruiz, A. Pfrang, A. Kriston, N. Omar, P. Van den Bossche and L. Boon-Brett, Renewable Sustainable Energy Rev., 2018, 81, 1427–1452.
14. Y. Liu, Y. Pan, H. Wang, H. Li, H. Bao, Z. Zhao and B. Liu, Thin-Walled Struct., 2024, 201, 111985.
15. X. Gao, Y. Jia, W. Zhang, C. Yuan and J. Xu, Appl. Mech. Rev., 2022, 74, 060801.
16. B. Liu, Y. Jia, C. Yuan, L. Wang, X. Gao, S. Yin and J. Xu, Energy Storage Mater., 2020, 24, 85–112.
17. D. P. Finegan, E. Darcy, M. Keyser, B. Tjaden, T. M. M. Heenan, R. Jervis, J. J. Bailey, R. Malik, N. T. Vo, O. V. Magdysyuk, R. Atwood, M. Drakopoulos, M. DiMichiel, A. Rack, G. Hinds, D. J. L. Brett and P. R. Shearing, Energy Environ. Sci., 2017, 10, 1377–1388.
18. Y. Xiong, B. Rui, S. Wang, Y. Song, B. Lu and J. Zhang, Int. J. Mech. Sci., 2024, 282, 109641.
19. Q. Wang, P. Ping, X. Zhao, G. Chu, J. Sun and C. Chen, J. Power Sources, 2012, 208, 210–224.
20. H. Wang, S. Simunovic, H. Maleki, J. N. Howard and J. A. Hallmark, J. Power Sources, 2016, 306, 424–430.
21. J. Zhu, X. Zhang, H. Luo and E. Sahraei, Appl. Energy, 2018, 224, 251–266.
22. J. Li, W. Li, J. Song, Y. Chen, L. Wang and J. Xu, J. Electrochem. Soc., 2022, 169, 020505.
23. C. Zhang, S. Santhanagopalan, M. A. Sprague and A. A. Pesaran, J. Power Sources, 2015, 290, 102–113.
24. C. Zhang, S. Santhanagopalan, M. A. Sprague and A. A. Pesaran, J. Power Sources, 2015, 298, 309–321.
25. B. Liu, S. Yin and J. Xu, Appl. Energy, 2016, 183, 278–289.
26. B. Liu, H. Zhao, H. Yu, J. Li and J. Xu, Electrochim. Acta, 2017, 256, 172–184.
27. L. Wang, S. Yin and J. Xu, J. Power Sources, 2019, 413, 284–292.
28. C. Yuan, X. Gao, H. K. Wong, B. Feng and J. Xu, J. Electrochem. Soc., 2019, 166, A1160.
29. H. Li, D. Zhou, M. Zhang, B. Liu and C. Zhang, Energy, 2023, 263, 126027.
30. L. Wang, J. Li, J. Chen, X. Duan, B. Li and J. Li, Appl. Energy, 2023, 351, 121790.
31. B. Liu, Y. Jia, J. Li, S. Yin, C. Yuan, Z. Hu, L. Wang, Y. Li and J. Xu, J. Mater. Chem. A, 2018, 6, 21475–21484.
32. X. Duan, H. Wang, Y. Jia, L. Wang, B. Liu and J. Xu, Energy Storage Mater., 2022, 45, 667–679.
33. H. Li, B. Liu, D. Zhou and C. Zhang, J. Electrochem. Soc., 2020, 167, 120501.
34. Y. Jia, J. Li, C. Yuan, X. Gao, W. Yao, M. Lee and J. Xu, Adv. Energy Mater., 2021, 11, 2003868.
35. W. Li, J. Zhu, Y. Xia, M. B. Gorji and T. Wierzbicki, Joule, 2019, 3, 2703–2715.
36. X. Zhang, L. Gu, X. Yin, Z. Huang, T. Ci, L. Rao, Q. Wang and M. El-Rich, J. Appl. Mech., 2024, 92, 021003.
37. Y. Fedoryshyna, S. Schaeffler, J. Soellner, E. I. Gillich and A. Jossen, J. Power Sources, 2024, 615, 235064.
38. Y. Yue, Z. Jia, Y. Li, Y. Wen, Q. Lei, Q. Duan, J. Sun and Q. Wang, Process Saf. Environ. Prot., 2024, 189, 61–70.
39. J. B. Robinson, D. P. Finegan, T. M. M. Heenan, K. Smith, E. Kendrick, D. J. L. Brett and P. R. Shearing, J. Electrochem. Energy Convers. Storage, 2017, 15, 011010.
40. J. Li, Y. Xie, B. Xu, Q. Gui and L. Mao, J. Phys.: Conf. Ser., 2024, 2914, 012001.
41. B. Xu, J. Li, Y. Xie, Q. Gui, Q. Wu, W. Liu and L. Mao, J. Power Sources, 2024, 623, 235448.
42. Q. Gui, B. Xu, K. Yu, X. Wang, J. Li, Y. Xie, R. Yu, X. Zhou and L. Mao, Chem. Eng. J., 2024, 497, 154732.
43. C. (Michael) Chak, R. Jayakumar, V. Shipitsyn, E. Bass, R. McCloskey, W. Zuo, P. M. L. Le, J. Xu and L. Ma, J. Electrochem. Soc., 2024, 171, 070512.
44. Y. Jia, B. Liu, Z. Hong, S. Yin, D. P. Finegan and J. Xu, J. Mater. Chem. A, 2020, 8, 12472–12484.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta00624d

---