Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Data-driven insights into protonic-ceramic fuel cell and electrolysis performance†
Charlie
Meisel
 *a,
Jake D.
Huang
*a,
Jake D.
Huang
 b,
Long Q.
Le
b,
Long Q.
Le
 c,
You-Dong
Kim
c,
You-Dong
Kim
 a,
Sophia
Stockburger
a,
Sophia
Stockburger
 a,
Zhixin
Luo
a,
Zhixin
Luo
 d,
Tianjiu
Zhu
d,
Tianjiu
Zhu
 e,
Zehua
Wang
e,
Zehua
Wang
 d,
Zongping
Shao
d,
Zongping
Shao
 d,
Ryan
O'Hayre
d,
Ryan
O'Hayre
 a and
Neal P.
Sullivan
*f
a and
Neal P.
Sullivan
*f
aMetallurgical and Materials Engineering Department, Colorado Center for Advanced Ceramics, Colorado School of Mines, Golden, Colorado 80401, USA. E-mail: cmeisel@mines.edu
bInorganic and Analytical Chemistry, University of Münster, Münster, 48149, Germany
cEnergy and Environment Directorate, Pacific Northwest National Laboratory, Richland, Washington 99352, USA
dWestern Australian School of Mines: Minerals, Energy, and Chemical Engineering (WASM-MECE), Curtin University, Perth, Western Australia 6102, Australia
eSchool of Chemical Engineering, The University of Queensland, Brisbane, Queensland 4072, Australia
fMechanical Engineering Department, Colorado Fuel Cell Center, Colorado School of Mines, Golden, Colorado 80401, USA. E-mail: nsulliva@mines.edu
First published on 13th March 2025
Abstract
Cell reproducibility remains a significant challenge for emerging proton-conducting ceramic electrochemical fuel cell and electrolyzer technologies. This study investigates the factors contributing to cell-to-cell performance variation. Gaussian process and random forest regressor machine learning models were utilized to analyze 86 cells for fuel cell performance and 84 cells for electrolysis performance. The study focused on BaCe0.4Zr0.4Y0.1Yb0.1O3−δ (BCZYYb4411) + NiO—BCZYYb4411—BaCo0.4Fe0.4Zr0.1Y0.1O3−δ (BCFZY) material sets for the negatrode, electrolyte, and positrode, respectively. Key processing and morphological parameters impacting performance were identified. The electrolyte thickness to grain size ratio emerged as a critical factor for both fuel cell and electrolysis performance, with maximum gains at ratios ≤1. A NiO particle size threshold of ∼6 μm was identified, below which performance increases markedly. Evaporating organics from the electrolyte spray or positrode application process before sintering may improve performance significantly, but the extent of this improvement remains uncertain. The optimal BCFZY positrode thickness for fuel cell performance is 20–25 μm. Fuel cell performance is primarily influenced by positrode microstructure. Optimizing this microstructure can bring the largest benefit to fuel-cell performance through reduced polarization resistances. In contrast, electrolysis performance is strongly governed by electrolyte microstructure. Improving electrolyte conductivity and reducing ohmic resistance greatly benefits electrolysis performance.
1. Introduction
Hydrogen is poised to play a crucial role in the future green energy economy. Hydrogen offers solutions for decarbonizing industries like steel production, serving as a chemical feed stock for compounds such as ammonia, and functioning as both a fuel and a medium for chemical energy storage.1–4 Consequently, developing devices that efficiently utilize hydrogen as fuel and electrolyze water to generate hydrogen is of paramount importance. Proton-conducting ceramic electrochemical cells (PCCs) emerge as a promising technology for these applications.PCCs operate at intermediate temperatures (350–600 °C),5 offering high efficiencies and oxygen reduction reaction (ORR) capabilities without requiring precious metal catalysts. This temperature range also allows for low stack material costs, crucial for commercialization.6–8 These reversible cells can both generate and consume hydrogen.7,9–12 PCCs are fuel flexible, meaning they can generate electricity from a wide range of chemicals.13 Operated as electrolyzers, PCCs can generate pure, dry hydrogen that can be electrochemically pressurized.14
PCCs are a relatively new technology with a technology readiness level (TRL) of about 4.15 Further development is necessary for PCCs to become commercial devices capable of supplying economically viable hydrogen and/or electricity. High performance is vital for PCC commercialization, with cell performance identified as the most critical parameter in determining stack cost.8 Higher-performing cells allow for the same power output or hydrogen generation with less cell and stacking materials.8
Lab-scale results in literature show promising fuel cell performance, with many cells achieving peak power densities exceeding 1 W cm−2 at 600 °C.5,10,16–25 Additionally, high electrolysis cell water splitting performance has been achieved, with current densities surpassing 0.5 A cm−2 at 500 °C and 1.3 V.10,19,22,24,26
While high reported performances are promising, reproducibility remains a challenge in the PCC field. This issue stems partly from the “champion cell” model, where only the best-performing cells are reported in literature.
A lack of testing standards also contributes to the problem, though standardization efforts are underway in the research community.27 Recently, there have been calls for researchers to provide detailed testing records.28 Fabrication process control can be limited in the research laboratories advancing these early-stage devices. The aforementioned high-performing cells utilize diverse materials, architectures, and processing methods. There is a need to investigate the mechanisms behind high-performing cells to better understand the factors that lead to high performance. A deeper comprehension of which processing variables most-impact performance will accelerate the research and development of PCC devices.
PCC fabrication is complex, involving numerous processing steps with diverse fabrication methods and intricate materials. This complexity likely contributes to significant cell-to-cell and laboratory-to-laboratory variability. The multitude of possible parameters and cell characteristics that could impact performance makes it challenging to discern interrelations using simple statistical regression.
This study takes a novel approach by examining a relatively large experimental dataset consisting of 86 cells, all fabricated in the same laboratory by a single researcher, to better understand which processing parameters and cell characteristics most significantly impact peak power density. Importantly, this dataset represents a full and unbiased collection of cells successfully tested by a single researcher over several years, including both high and low-performance cells. For each cell, 68 processing parameters and cell characteristics are tracked to identify sources of cell-to-cell variability. Machine learning models are employed to unravel the complex interrelationships between these parameters and PCC performance.
Machine learning (ML) models can enable the understanding of the complex interrelationship between processing parameters, cell characteristics, and performance. ML models program computers to optimize a performance criteria based on data or experience.29 These models develop pattern recognition from prior data and attempt to minimize error in future predictions of target values based on unseen input data. Thus, ML models can explain complex phenomena and interrelationships that humans are unable to solve independently.29 In the field of PCCs and solid-oxide cells, ML models have been utilized for materials selection and understanding cell fabrication processes.30,31 We have previously applied ML models to determine which processing parameters most impact negatrode shrinkage and electrolyte grain size.32
This paper implements Gaussian process (GP) and random forest regression (RFR) models to analyze the PCC data. GP models are probabilistic, non-parametric ML tools that predict probability distributions over potential outcomes rather than single target values.33,34 This feature allows GPs to quantify prediction uncertainty, making them robust when dealing with noisy data.33,35 As non-parametric models, GPs can capture complex data patterns and generate confidence intervals for predictions without assuming a fixed number of parameters.34 The computational cost of GPs scales with the cube of the number of observations,33 making them suitable for the small datasets used in this study.
GP models have been applied to adjacent fields, such as solving the distribution of relaxation times,36 and to diverse areas like geostatistics,37 but have not yet been used to analyze PCC performance. The ability of GP models to handle small, noisy, and non-linear data makes them well-suited for PCC device analysis.
Random forest regression (RFR) models predict target values using an ensemble of decision trees. Decision trees are flowchart-like models that recursively split data based on parameter thresholds to minimize prediction error.38 In random forest models, each tree is built using random subsets of parameters and observations,39 decorrelating predictors and improving accuracy. By averaging predictions from multiple trees, random forests reduce overfitting risk while enhancing prediction reliability.39,40 RFR models work with raw feature values, requiring minimal data preprocessing. The ability of RFR to model complex, non-linear relationships with high accuracy makes them well-suited for analyzing PCC data.
Section 3.1 of this study employs GP and RFR models to identify the processing parameters and cell characteristics that most impact PCC fuel cell performance. All data fed into the ML models is from PCCs utilizing BaCe0.4Zr0.4Y0.1Yb0.1O3−δ (BCZYYb4411) electrolytes that were fabricated and tested at the Colorado School of Mines. The models analyze data from 86 PCCs, encompassing 14 parameters (post-initial selection) that encode to 137 features, with peak power density (PPD) as the target variable. Feature importance, averaged over five-fold cross-validation, determines which features most significantly influence PPD prediction. Both GP and RFR models calculate feature importance, with RFR additionally generating partial dependence plots (PDPs) to visualize how key features impact PPD.
In Section 3.2, this process is repeated for electrolysis performance using data from 84 PCCs encompassing 19 parameters (after initial parameter selection) that encode to 164 features. The target value for the electrolysis performance studies is current density (CD) at 1.3 V. Additionally, the PPD and CD data is correlated, using simple regression, with ohmic and polarization resistance (Rp) data from 88 BCZYYb4411 cells fabricated and tested across two universities, as described in Section 3.3.
This study reveals crucial factors for optimizing PCC performance in both fuel cell and electrolysis operation. Evaporating off organics prior to sintering, small electrolyte thickness to grain size ratios, and small NiO particle sizes lead to increased performance. Optimizing the positrode morphology to decrease Rp should be prioritized for fuel cell performance gains. Optimizing the electrolyte microstructure to lower ohmic resistance should be prioritized for electrolysis performance gains. Generally, PCCs with high fuel cell performance exhibit high electrolysis performance, though Rp and ohmic resistance are uncorrelated with fixed material sets.
2. Experimental
2.1 Materials powder fabrication
All cells in this study were fabricated through the solid-state reactive sintering process (SSRS), a method that integrates cell fabrication, phase formation, grain growth, and densification into a single high-temperature sintering step.41–44 This process involves mixing stoichiometric ratios of precursor powders with a sintering aid, then forming them into the desired cell shape and architecture. During subsequent high-temperature sintering, the single-phase ceramic and the negatrode-electrolyte assembly are formed in a single step. SSRS can decrease cell manufacturing costs.8To create the BCZYYb4411 electrolyte powder, stoichiometric precursor powders of BaCO3, CeO2, ZrO2, Y2O3, and Yb2O3 were wet-ball milled for two days in isopropanol with 3 mm yttria-stabilized zirconia (YSZ) spherical milling media. The solution was then dried at 93 °C in a drying oven and milled for one additional day. Precursor supplier, purity, and particle size information can be found in ESI Table S1.†
The negatrode powder was made with stoichiometric ratios of BaCO3, CeO2, ZrO2, Y2O3, Yb2O3, and either of two types of NiO, coarse NiO or fine Type F NiO. Potato starch and corn starch (Alfa Aesar) were used as pore formers. The ratios of electrolyte precursors to NiO to starch were varied from 29 to 36 wt%, ∼47 wt%, and 16–23 wt%, respectively as part of this study. The negatrode powders were wet-ball milled in isopropanol with 5 mm magnesia-stabilized zirconia cylindrical milling media for two days. The solution was dried at 93 °C in a drying oven and then milled for one additional day. The resulting negatrode powder was sieved through a 250 micron mesh to eliminate agglomerates.
The BaCo0.4Fe0.4Zr0.1Y0.1O3−δ (BCFZY) positrode powder was made through sol–gel processing. Stoichiometric ratios of Ba(NO3)2, Co(NO3)2·6H2O, Fe(NO3)3·9H2O, 35 wt% zirconyl nitrate solution in dilute nitric acid, and Y(NO3)3·6H2O were dissolved into DI water while being mixed on a stir plate. Ethylenediaminetetraacetic acid (EDTA) and citric acid monohydrate were added to the solution. The ratio of EDTA to citric acid to metal ions was 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5
1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Ammonium hydroxide was added to the solution in a ratio of 300 mL per 0.1 mol of BCFZY powder. Precursor supplier and purity can be found in ESI Table S2.† The solution was mixed at 250–300 °C until the gel became viscous to the point that the stir bar was not able to move. The gel was dried at 150 °C for 24 hours. The resulting charcoal was calcined at 600 °C for five hours. The calcined powder was then ball milled for one day in isopropanol with a 50
1. Ammonium hydroxide was added to the solution in a ratio of 300 mL per 0.1 mol of BCFZY powder. Precursor supplier and purity can be found in ESI Table S2.† The solution was mixed at 250–300 °C until the gel became viscous to the point that the stir bar was not able to move. The gel was dried at 150 °C for 24 hours. The resulting charcoal was calcined at 600 °C for five hours. The calcined powder was then ball milled for one day in isopropanol with a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio of 3 mm YSZ spheres and 5 mm YSZ cylinders. The isopropanol to media ratio was 2 mL
50 ratio of 3 mm YSZ spheres and 5 mm YSZ cylinders. The isopropanol to media ratio was 2 mL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 g. The milled solution was dried and passed through a 250-mesh sieve to break up agglomerates.
1 g. The milled solution was dried and passed through a 250-mesh sieve to break up agglomerates.
2.2 Cell fabrication
Green negatrode pellets were fabricated by mixing a liquid-binder solution with negatrode precursor powders in a mortar and pestle in concentrations of 10–14 wt%. The liquid-binder solution was composed of 10 wt% polyvinyl alcohol in DI water. The binder-powder mixture was weighed into 2–4 g pellets and pressed in a 2.8 cm (1 1/8 inch) diameter metal die at 52 MPa (7500 lbs) for 10 seconds. This negatrode pellet serves as the mechanical support for the cell.Following dry pressing, the pellet was spray-coated with electrolyte. The electrolyte spray solution was made using 13 wt% BCZYYb4411 precursors, wt% V-006, 2.5 wt% alpha terpineol, 1 wt% polyethylene glycol, 1 wt% polyvinylpyrrolidone, and 80 wt% isopropanol. More information on the polymers used in cell fabrication can be found in ESI Table S3.†
The electrolyte was applied to the green, as-pressed negatrode using a hand sprayer (Master Airbrush model S68) or an automated ultrasonic spray coating system (Sono-Tek Align). The spray nozzle was mounted onto a three-axis translation stage controlled with a microprocessor (Arduino uno R3). Each cell underwent 5–18 layers of electrolyte spray application. The nozzle was positioned approximately 5 cm above the cells. Key spray parameters include spray power (3–5 W), air flow rate (6–8 SLPM), and flow rate of the electrolyte spray solution (0.3–0.9 mL min−1). The air flow helps shape the spray pattern and influences the rate of solvent evaporation. Negatrode and positrode functional layers (NFL and PFL, respectively) were applied to the cells in a similar manner, typically with one or two layers.
The electrolyte-negatrode co-sintering process began with a five-hour binder burnout step at 450 °C. Subsequently, the high-temperature step was carried out at temperatures between 1475 °C and 1550 °C, with holds spanning 0.1 or 5 hours and ramp rates of 3 °C min−1. The cells were placed on setters made from either alumina (AdValue Technology, AL-D-82-6) or yttrium-doped magnesia-stabilized zirconia (MgSZY) with varying degrees of prior usage. All cells were sintered while covered with alumina kiln furniture contaminated with nickel (blue) that allowed for air flow. All cells were sintered in the hot-zone of the furnace. Sintering neighbors were introduced to the furnace environment by placing powders in crucibles positioned a few centimeters from the cells.
The BCFZY precursor powders were mixed into a paste consisting of 2.5 g BCFZY powder, 0.5 g 20% solsperse 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in alpha terpineol, and 0.2 g 5% V-006 in alpha terpineol. The paste was painted onto the sintered electrolyte with a total area of 0.5 cm2. The BCFZY positrode was sintered at 900 °C for five hours with a ramp-rate of 2 °C min−1. Gold contact paste (fuel cell materials, 233
000 in alpha terpineol, and 0.2 g 5% V-006 in alpha terpineol. The paste was painted onto the sintered electrolyte with a total area of 0.5 cm2. The BCFZY positrode was sintered at 900 °C for five hours with a ramp-rate of 2 °C min−1. Gold contact paste (fuel cell materials, 233![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001) diluted with isopopanol, silver contact paste (Vivtek, DAD-87), and silver wires (Alfa Aesar, 0.01 inch diameter, 99.9%) were placed on the electrodes to serve as current collectors and voltage sensors. The research at Colorado School of Mines (Mines) was conducted in a laboratory at an elevation of 1750 m, where the oxygen partial pressure (pO2) is 0.17 atm, compared to 0.21 atm at sea level. All cells analyzed in this paper have the material-sets BCZYYb4411 + NiO—BCZYYb4411—BCFZY.
001) diluted with isopopanol, silver contact paste (Vivtek, DAD-87), and silver wires (Alfa Aesar, 0.01 inch diameter, 99.9%) were placed on the electrodes to serve as current collectors and voltage sensors. The research at Colorado School of Mines (Mines) was conducted in a laboratory at an elevation of 1750 m, where the oxygen partial pressure (pO2) is 0.17 atm, compared to 0.21 atm at sea level. All cells analyzed in this paper have the material-sets BCZYYb4411 + NiO—BCZYYb4411—BCFZY.
2.3 Cell testing
PCC performance was characterized in a custom-built laboratory-scale test stand (ESI Fig. S1†). The cells were heated to 550 °C at 1–3 °C min−1 without gas flow. Reduction occurred at 550 °C with 5 SCCM H2 balanced with 45 SCCM Ar (dry) flowing to the negatrode, and 100 SCCM synthetic air (21 SCCM O2, 79 SCCM Ar) bubbled through water at room temperature flowing to the positrode. Ar was used instead of N2 due to test stand constraints. Cell open circuit voltage (OCV) was recorded during heat-up and reduction. The reduction process lasted 1.5 hours to one day. Post-reduction, H2 concentration was gradually increased to 100% on the negatrode. Then air flow was increased to 200 SCCM. Some earlier tests used 50 or 100 SCCM air flow to the positrode. After increasing the air flow, the cell was left to equilibrate for at least 15 minutes.After equilibration, electrochemical impedance spectroscopy (EIS) was performed potentiostatically with an excitation amplitude of 10 mV. This was followed by a fuel cell mode current–voltage curve (IV-curve) from OCV to 0.4 V at a scan rate of 0.001 A s−1. After a brief rest, an electrolysis IV-curve was obtained from OCV to 1.35–1.5 V at 0.001 A s−1. All performance data was collected at 550 °C using a Gamry Reference 3000 potentiostat with a five-probe setup. EIS data was analyzed to determine ohmic and polarization resistances using software developed by Huang et al.45–47
2.4 Cell characterization
Cell morphology was examined using scanning electron microscopy (SEM, Thermo-Fischer Scientific, Phenom). Electrolyte grain size was quantified by analyzing SEM surface images using ImageJ software. An imageJ macro placed three concentric circles on the sample images; grain size was determined by dividing the number of grain-boundary intersections by the total length of the circles. This process was repeated for three images per sample. Electrolyte and positrode thickness were calculated by measuring the electrolyte at 10 different spots on three different cross-sectional images of the electrolyte of each cell.Particle sizes for negatrode and electrolyte powders were determined using a Microtrac Flowsync laser diffraction analyzer, averaged over three runs with a refractive index of 1.9. The data was analyzed with the Microtrac software.
2.5 Gaussian process machine learning models
Gaussian process (GP) machine learning models were implemented using the GaussianProcessRegressor class from the scikit-learn Python library. A Matérn kernel was chosen for its ability to fit rough data and superior performance in fitting the data in this paper compared to the common radial basis function kernel.48 Kernels calculate dot products in higherdimensional feature spaces, without explicitly mapping data to those spaces. This enables computationally efficient modeling of non-linear relationships between datapoints.48The GP model includes several tunable hyperparameters. The α hyperparameter, which is kernel-independent, quantifies the magnitude of assumed (normally distributed) noise in target value measurements. Meanwhile, the Matérn kernel depends on hyperparameters ν and length scale. The ν parameter controls the GP fitting function's smoothness, with smaller values allowing rougher functions. The lengthscale determines how quickly the correlation between points decays with distance in the input space. Closer points exhibit higher similarity. The lengthscale is automatically tuned using an L-BFGS-B algorithm to maximize the log-marginal-likelihood, a Bayesian metric that inherently balances complexity with goodness of fit (default setting in GaussianProcessRegressor.fit). The lengthscale optimization is constrained to the range between 0.1 and 104.
Prior to modeling, numerical data-parameters underwent Z-score normalization, which adjusts each parameter to a mean of 0 and standard deviation of 1. This process neutralizes scaling differences and aids in handling outliers. Categorical data was encoded using one-hot encoding (OHE), appropriate for nominal data. No encoded parameters were dropped in the OHE process.
After preprocessing, the data was split for cross-validation using the KFold Python class. The parameters were set to n splits = 5 and shuffle = True, with random state optimized through hyperparameter tuning. The random state function was used to seed the randomization of data into training and testing groups, and was tuned so that it was not set arbitrarily.
The hyperparameters α and ν, along with the random state for cross validation, were tuned using the Optuna Python package. Tuning alpha before fitting the model lead to the largest increases in goodness-of-fit than any other hyperparameter. The hyperparameter tuning process for the GP model involved:
1. Optimizing random state for five-fold cross-validation using 150 Optuna trials with values between 0 and 100. The state yielding the lowest negative log-likelihood (NLL) was selected.
2. Optimizing α (range: 10−5–1) in GaussianProcessRegressor using 250 Optuna trials, selecting the value that results in the smallest NLL for the model fit.
3. Testing Matérn kernel ν values (0.5, 1.5, and 2.5), selecting the one that results in lowest NLL for the model fit.
After hyperparameter optimization, feature importance was calculated. This was done using scikit-learn's permutation importance function, with root mean squared error (RMSE) as the error metric. This method assesses each parameter's impact by measuring the effect of its removal from the model. Positive importance indicates that removal worsens the fit, while negative importance suggests potential improvement. To ensure robust results from the small datasets in this paper, feature importance was averaged across all folds of five-fold cross-validation.
To evaluate GP model performance, five-fold cross-validation was employed using the same KFold call as for feature importance. For each fold, RMSE, mean absolute error (MAE), negative loglikelihood (NLL), and R2 values were calculated and averaged. RMSE and MAE measure the magnitude of errors between predicted and observed values, both computed in the target value's units. RMSE penalizes larger errors more heavily. Lower RMSE and MAE values indicate better model fit.
The R2 coefficient, ranging from −∞ to 1, indicates how well the model explains variance in measured target variables. An R2 value of 0.7 indicates that the model can explain 70% of the variance in the target values. Higher R2 values signify better fits. Negative log-likelihood (NLL), tailored for probabilistic models like GP, measures prediction accuracy and confidence of the model in those predictions. Lower (more negative) NLL values are preferred. The standard deviation of the model-predicted values for the NLL calculation was calculated using GaussianProcessRegressor.predict.
Learning curves, which show how model performance changes with training and validation sample sizes, were also used to evaluate goodness-of-fit.49 Additionally, coverage plots were employed to analyze fit quality. These plots display measured target values against model predictions with 95% confidence intervals. The percentage of target values falling within the predicted range is the coverage percentage, with higher percentages being desirable.
2.6 Random forest regressor machine learning models
Random forest regressor (RFR) models were implemented using scikitlearn's RandomForestRegressor class. Four hyperparameters were tuned:1. n estimators: number of trees (estimators) in the model (range: 50– 100).
2. Min samples split: minimum samples required to split an internal node. If a node has below the min samples split it becomes a leaf (end) node (range: 2–10).
3. Min samples leaf: minimum samples required in a leaf node (set to 1 based on early findings).
4. Max features: fraction of total features to consider when looking for the optimal split at each node in the decision tree. It is represented by a fraction (range: 0.1–1).
One-hot encoding (OHE) preprocessing was applied to categorical data, while numerical data remained unprocessed due to random forest models' insensitivity to input feature scaling. RFR models used the same data and random state as their corresponding GP models. The hyperparameters n estimators, min samples split, and max features were concurrently tuned using 500 Optuna trials. The optimal value of min samples leaf was consistently found to be 1 so it was not tuned.
After hyperparameter tuning, feature importance was calculated identically to the GP models and averaged over five-fold cross-validation. Model performance was evaluated using five-fold cross-validation, employing RMSE, MAE, and R2 as predictors. Additionally, an out-of-bag (OOB) score based on R2 was used to assess model fits. OOB score, a performance metric specific to RFR models, estimates model accuracy using data points omitted from each tree's training data set. This provides a reliable measure of the model's generalization to unseen data. Learning curves were also used for model validation.
Partial dependence plots (PDPs) were generated using PartialDependenceDisplay.from_estimator with the trained RFR and parameter training data as inputs. Partial dependence plots are only shown for numerical data columns.
2.7 Parameter selection
Seventy processing parameters, listed and defined in Appendices A and B ESI,† were considered in total. Parameter selection was conducted to ensure an optimal model fit using statistically sound methods. For the BCZYYb4411 models, 29 parameters were removed due to missing values, unique categorical parameters, zero variance, and significant collinearities with other parameters (summarized in ESI Table S4†), leaving 39 viable parameters. Parameter selection was conducted with the GP models rather than the RFR models due to reduced hyperparameter tuning requirements.The hyperparameters for the GP model with 39 parameters were tuned as described in Section 2.5. The 39-parameter model was then fit and the top- and bottom-10 most important features were recorded. Additionally four performance metrics, root mean squared error (RMSE), mean absolute error (MAE), NLL, and R2, were recorded. The feature selection process proceeded as follows:
1. The least important parameter (most negative feature importance, assumed to worsen the fit) was removed.
2. The model was re-fit, and the outcomes were categorized:
• No change in metrics: feature marked as neutral and retained.
• Any of the performance metrics got worse (NLL had to change > |0.005| to be considered significant): feature marked as important and retained.
• Any metrics improved (NLL change > |0.005|): feature marked as noisy and removed.
• Some metrics increased while other decreased: feature marked as mixed and retained.
This process was iterated for all 39 parameters. Once the bottom-10 features were occupied by essential categorical parameters, the remaining parameters were sequentially removed by their listed order. After all parameters were evaluated, neutral parameters were excluded to form the final model.
A crucial assumption of this procedure is that a parameter's impact on the model typically remains consistent, irrespective of other parameters present. This consistency allows for linear parameter selection, eliminating the need to test every possible parameter permutation to achieve the optimal model.
3. Results and discussion
3.1 ML model results on fuel cell performance
This section presents and analyzes the Gaussian process (GP) and random forest regressor (RFR) model results, identifying the processing parameters and cell characteristics that most significantly impact BCZYYb4411 fuel cell performance. All peak power density values were obtained at 550 °C. All cells were fabricated and tested at the Colorado School of Mines (Mines). Additional data were not extracted from the literature, as the model requires all parameters to have values to fit the data. Many of the parameters tracked in this paper go unreported. Two cells were excluded from the model: one due to excessive missing values, and another which had an Rp value exceeding three standard deviations from the mean (ESI Fig. S2†).Initially, 29 parameters were dropped due to zero variance or high collinearity (ESI Table S4, detailed in Appendix B, ESI†). Of the remaining 39 parameters (detailed in Appendix A, ESI†), 25 were removed during the subsequent down-selection process as they either worsened or did not affect the fit (ESI Table S5† summarizes the effect of removal). The final data model incorporates performance data from 86 cells, encompassing 14 parameters encoded to 137 features. These 14 parameters are found in the “model got worse” and “slightly worse” columns of ESI Table S5,† because their removal led to worse model fits. It is crucial to note that ML models demonstrate correlation, not causation. ML-derived information can be valuable in guiding follow-on causation studies.
Fig. 1 illustrates the importance of the 10 most significant features as determined by the GP model. Feature importance indicates the increase in model error if a particular feature is removed. Thus, more important features are stronger predictors of the target value and, if modulated, are likely to significantly impact it. It is noteworthy that feature importance does not capture the directionality of its effect on the target value (i.e., it can positively or negatively impact the target value).
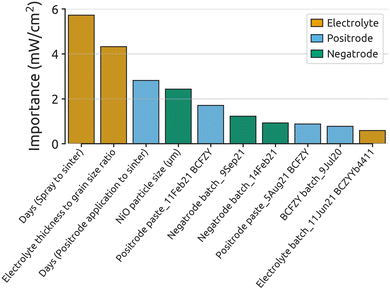 | ||
| Fig. 1 Feature importance results from the GP model. The top 10 most important encoded features, color-coded by the cell layer or process they represent, are displayed. This model analyzed 86 BCZYYb4411 cells and 14 parameters, encoded to 137. A Matérn kernel with a length scale of 919 and ν = 0.5 was used for fitting. Model performance metrics and detailed goodness-of-fit results appear in ESI Table S7 and Fig. S3,† respectively. | ||
Four of the 10 parameters in Fig. 1 relate to the positrode, four to the electrolyte, and three to the negatrode. This distribution underscores the significant role of positrode and electrolyte characteristics in determining fuel cell performance.
Perhaps surprisingly, the parameter days (spray to sinter) has the largest impact on performance. This parameter represents the number of days between spraying the electrolyte and co-sintering the cell. Cells were stored in a desiccator between spraying and sintering, and thus may have experienced organic evaporation (i.e., isopropanol, terpineol and PEG-400 from the spray solution). This could bring beneficial rearrangement of particle packing in the green electrolyte layer and improved interfacial contact between the electrolyte and the negatrode during extended storage. Recent research indicates that higher CO2 content can impede the sintering of BCZY-based perovskites;50 removing organics prior to sintering could therefore help explain the positive impact of the days (spray to sinter) parameter.
Seven of the 86 cells were dried in an oven at 100 °C for a few hours before sintering. However, this categorical feature was dropped from the fuel cell GP model due to its minimal effect, possibly resulting from low variance causing noise in the model fit. A deeper analysis of the days (spray to sinter) data (ESI Table S6†) also suggests that the high importance of this feature may be at least somewhat coincidental, as many of these best cells were also part of the same co-sinter and electrolyte spray batch. However, as the co-sinter and electrolyte spray batch categorical parameters were divided into numerous smaller subgroups (44 and 29, respectively), they yielded low individual impact on the model. ML models typically require thousands to millions of data points for robust results. While these models, based on only 86 cells, provide valuable insights, they are not infallible.
A second important finding in Fig. 1 is the significance of the electrolyte thickness to grain size ratio in predicting fuel cell performance. This aligns with numerous studies showing that grain boundaries are highly resistive51–53 and have higher activation energy for proton motion than the bulk,53,54 due to space charge layer effects and grain boundary disorder.54–59 Electrolyte thickness to grain size ratio is essentially indicative of the number of lateral grain boundaries that a proton is expected to cross. A schematic of electrolyte thickness and grain size measurements can be found in ESI Fig. S4.†
The ratio of electrolyte thickness to grain size is rarely reported in literature when discussing cell performance. The GP model suggests that, using identical materials, this ratio is an impactful parameter in determining peak power density. This finding is noteworthy, given that ORR activity of the positrode is often considered the rate-limiting step in proton-conducting ceramic fuel cell performance.6,60–62 It may help to explain the wide performance variance observed in the literature for cells made with nominally identical positrode materials. Variation across studies in literature may therefore have less to do with the positrode in these cases, and more to do with the grain size and thickness of the electrolyte.
Days (positrode application to sinter) is a significant parameter, but its low variance requires cautious interpretation. Only 4 out of 86 cells had a value of 1 for this parameter, with three of these cells being top performers. Despite low confidence due to limited data, we hypothesize that extended time might improve electrode/electrolyte contact through particle settling or reduced CO2 production during sintering via pre-evaporation of organics.63 While definitive conclusions are precluded, this parameter merits further investigation in future studies.
The final numerical parameter appearing in the top 10 is NiO particle size in the negatrode. This is unexpected, as the negatrode is one of the least studied PCC components due to its similarity to well-researched solid-oxide fuel cell negatrodes.64–66 As will be shown later, the NiO particle size parameter appears to have a threshold effect, leading to a strong boost in performance when the NiO particle size falls below a critical value.
A key insight from Fig. 1 is the prevalence of categorical parameters, such as Positrode paste_11Feb21 BCFZY and Negatrode batch_14Feb21, among the most important features. While partly due to the encoding process, which resulted in many categorical features, we believe this finding also reflects the significant batch-to-batch variation in precursor materials, suspensions, fabrication techniques, and furnace runs. Such variability complicates drawing accurate conclusions from literature in this low-throughput field.
To confirm the findings from Fig. 1, a random forest regressor (RFR) model was applied to the final dataset, with results shown in Fig. 2. The consistency between Fig. 1 and 2 reinforces the initial conclusions, with top features largely maintaining their importance and order across both models. The RFR model supports the unexpected prominence of days (spray to sinter) as the most critical parameter. Additionally, electrolyte thickness to grain size ratio and NiO particle size (μm) continue to be significant predictors of fuel cell performance.
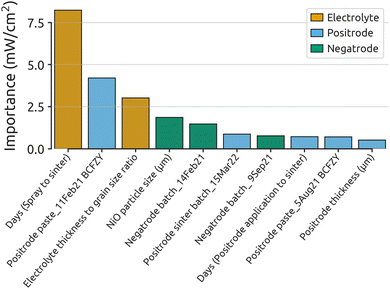 | ||
| Fig. 2 Feature importance results from the RFR model. The top 10 most important features are displayed, color-coded by the cell layer or process they represent. This model analyzed 86 BCZYYb4411 cells and 14 parameters, encoded to 137 features. The hyperparameters used for this model can be found in ESI Table S8.† Model performance metrics can be found in ESI Table S7.† Detailed goodness-of-fit results can be found in ESI Fig. S5.† | ||
Positrode thickness (μm) appears as a new numerical feature in the RFR model, further emphasizing the importance of positrode characteristics and ORR activity on fuel cell performance. It is worth noting that positrode thickness measurements varied considerably for individual cells, introducing noise that may reduce its predictive capability and perceived importance. This may have caused its lower prominence in the GP model.
Fig. 2 emphasizes the importance of positrode features on fuel cell performance. Five of the top 10 most-important features relate to the positrode side of the cell. Two electrolyte features rank among the top three, highlighting the significant impact of electrolyte characteristics. The negatrode contributes two important features, indicating that negatrode microstructure also impacts performance.
The prevalence of categorical parameters, mirroring Fig. 1, underscores that minor cell-to-cell and batch-to-batch differences are major sources of variability in protonic-ceramic fuel cell performance, particularly in regard to the positrode. As the second-most important feature is the positrode paste batch, this suggests that paste rheology strongly affects performance, hinting at the significant impact of positrode microstructure. Although challenging to measure post-sintering, Fig. 2 suggests that the surface area and microstructure of the positrode may be among the largest contributors to cell-to-cell performance variation.
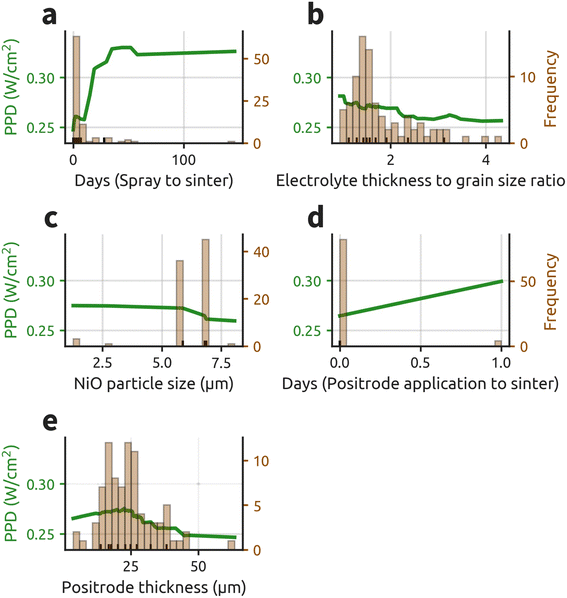
A significant advantage of RFR models is their ability to fit numerical data in its native form, enabling model outputs to retain the original units of the measured values. Consequently, partial dependence plots (PDPs) can be generated from the RFR model in intuitive units, aiding in decision-making. PDPs are valuable as they isolate and display the predicted relationship between a single parameter and the target value. Fig. 3 presents PDPs for every numerical column among the top 10 most important features in the RFR model.
Fig. 3a demonstrates a significant improvement in fuel cell performance with increased time between spraying the electrolyte and sintering, plateauing after 50 days. This trend may be influenced by several high-performing batches sintered 30–50 days post-spraying (ESI Table S6†). Considering grain size is already accounted for, the lower CO2 concentration from less organics in the furnace likely improves the grain boundary characteristics. A plausible explanation is that higher pO2 in the furnace leads to either less defective grain boundaries or a more favorable space-charge layer (higher pO2 → fewer oxygen vacancies → less-positive space charge layer → less-resistive grain boundary). The potential benefits of gradual organic evaporation suggested by these findings warrant further investigation. Additionally, increased CO2 concentration could stymie phase formation and hinder sintering.50,67 No parameters in the model account for phase purity, so perhaps days (spray to sinter) acts as a proxy for phase purity.
Fig. 3b illustrates the PDP for electrolyte thickness to grain size ratio. Substantial performance gains are observed when the electrolyte to grain size ratio drops below two, and again when the ratio reaches unity. Lower average electrolyte thickness and larger average grain size reduce the number of resistive grain boundaries that protons must cross. The significant performance gains observed when the ratio reaches unity likely reflect the attainment of a bamboo-like electrolyte grain structure, which eliminates lateral grain-boundary encounters.51–59 Given the grain size distribution after sintering,58,68 further decreasing this ratio below one may continue to enhance performance.
Fig. 3c exhibits the PDP for NiO particle size in the negatrode precursor powder. Performance increases substantially when NiO particle size falls below six microns. This improvement is possibly due to smaller NiO grains having larger surface area and higher sintering driving force,69 potentially leading to better negatrode densification and improved electrolyte sintering.17 This could enhance conduction pathways for protons and electrons, potentially augmenting the hydrogen oxidation reaction (HOR).70
Additionally, smaller NiO particle sizes will lead to more electrochemically active triple phase boundary area further increasing HOR activity. While HOR is not considered rate-limiting in PCFCs, distribution of relaxation times analysis reveals non-negligible high-frequency resistance associated with negatrode processes such as these.47,71 While porosity is necessary for mass transfer to reaction sites, the 40 vol% change of NiO to Ni upon reduction leads to large amounts of inherent porosity (ESI Fig. S4c†). PCFCs have been fabricated using negatrodes without pore former and have achieved favorable performance.72,73 Performance gains plateau below 6 μm. This threshold may vary with different processing techniques and cell materials but it suggests that there is a critical NiO particle size for significant fuel cell mode performance improvements.
Fig. 3d suggests that waiting a day to sinter the positrode after application could increase performance. Despite low variance in this parameter, we suspect the delay might allow for organics evaporation or favorable particle settling. Both of these effects could enhance the sinterability, morphology and adherence of the positrode.
Fig. 3e indicates an optimal positrode thickness of 20 to 25 μm. This is consistent with previous experimental and computational findings for BCFZY positrodes.74,75 Studies of solid-oxide fuel cell positrodes generally recommend thicknesses between 10 and 35 μm.76–79 Performance improves up to a positrode thickness of 25 microns due to increased ORR reaction sites. However, thicknesses beyond this show decreased performance, likely due mass transfer losses due to the nano-scale structure of the positrode. Additionally, BCFZY's low electronic conductivity can lead to increased resistance losses.80,81
Both the GP and RFR ML models highlight the significant impact of the positrode and electrolyte on fuel cell mode performance. Electrolyte thickness to grain size ratio strongly influences performance and should be reported when comparing cell performances. Although the negatrode has a smaller relative effect, NiO particle size should be kept below 6 μm to maximize cell performance. The time delays between spraying and sintering, and between positrode application and sintering, warrant further investigation. Both delays show surprisingly large performance impacts, but collinearity with a high performing electrolyte spray batch of cells and low variance could be skewing these parameters. Positrode thickness should be maintained at 20–25 microns to maximize ORR activity without excessive electronic resistance.
3.2 Model results on electrolysis performance
This section analyzes BCZYYb4411 electrolysis performance using Gaussian process (GP) and random forest regressor (RFR) models, identifying the processing parameters and cell characteristics with the most significant impact. The models are based on current density values obtained at 550 °C and 1.3 V for 84 cells.Two cells were excluded from the model: one due to excessive missing values, and another which had an ohmic resistance exceeding three standard deviations from the mean (ESI Fig. S6†). The electrolysis model contains two fewer cells than the fuel cell model, as two cells lacked electrolysis performance data.
Parameter selection resulted in the removal of 19 parameters that either worsened the fit or had no effect. ESI Table S9† lists the 39 parameters considered for analysis and the effects of their removal from the model. The final data model incorporates performance data from 84 cells, encompassing 20 parameters encoded to 163 features. These parameters are listed in the “model got worse”, “slightly worse”, and “mixed” columns of ESI Table S5.†
Fig. 4 displays the importance of the 10 most significant features determined by the GP model for electrolysis performance. The similarity between fuel cell and electrolysis feature importances in Fig. 1 and 4, respectively, is notable. This similarity reflects the correlation between fuel cell and electrolysis cell performance, which will be demonstrated later in this study.
 | ||
| Fig. 4 Feature importance results from the GP model on electrolysis performance. The top 10 most important features are displayed, color-coded by the cell layer or process they represent. This model analyzed 84 BCZYYb4411 cells and 20 parameters, encoded to 163 features using a Matérn kernel with a length scale of 29.3 and a ν = 1.5. Model performance metrics and detailed goodness-of-fit results appear in ESI Table S7 and Fig. S7,† respectively. | ||
Electrolyte thickness to grain size ratio was found to have the largest impact on electrolysis performance. This highlights the significant influence of resistive grain boundaries in the electrolyte on proton transport during electrolysis. The effect is more important in the electrolysis model compared to the fuel cell model, emphasizing that electrolyte characteristics have a greater impact on electrolysis performance.
Perhaps surprisingly, the model revealed that absolute humidity during co-sinter (g m−3) strongly affects electrolysis performance. Our previous work showed that this parameter hinders negatrode shrinkage and electrolyte grain growth.32 Its substantial effect on electrolysis performance further underscores the importance of electrolyte characteristics.
Days (spray to sinter) and days (positrode application to sinter) also significantly impact electrolysis performance. As was discussed in the context of the fuel cell model analysis, allowing time for organics to evaporate off the cell likely benefits sintering. The high importance of these factors may be overstated. This potential overestimation stems from the collinearity of days (spray to sinter) with electrolyte spray and co-sinter batches, as well as the limited data for days (positrode application to sinter).
NiO particle size (μm) also emerges as important for electrolysis performance, indicating that the negatrode side of the cell affects electrolysis performance, albeit to a lesser extent than in fuel cell performance. Positrode thickness shows a larger effect on electrolysis performance compared to fuel cell performance, likely due to the increased importance of the positrode electronic conductivity under the higher current densities associated with electrolysis-mode operation.
Comparing the GP models of fuel cell (Fig. 1) and electrolysis (Fig. 4) performance reveals that electrolysis cell performance is more closely tied to electrolyte characteristics. Six of the top 10 most important parameters in the electrolysis GP model relate to the electrolyte or the co-sintering step, which significantly influences electrolyte microstructure. The positrode and negatrode each account for only two parameters among the top 10 features.
The greater importance of electrolyte microstructure in electrolysis performance compared to fuel cell performance likely stems from the asymmetry of chemical species production and transport in these two modes of operation. In fuel cell mode, water vapor generated at the positrode occupies potential ORR reaction sites and negatively impacts reactant mass transport, increasing polarization resistance. This explains why many positrode materials often perform better in electrolysis mode than in fuel cell mode, and also often perform better on oxygen ion conducting electrolytes than on proton-conducting electrolytes at the same temperature.25,82,83
During electrolysis, water vapor consumption at the positrode maintains open reaction sites on the positrode surface. Furthermore, electrolysis operation decreases water vapor partial pressure and increases oxygen partial pressure at the positrode, yielding beneficial thermodynamic and kinetic effects.84 These factors reduce the performance burden on the positrode, making the electrolyte the primary bottleneck for electrolysis performance.
To validate and expand on the conclusions from Fig. 4, we fitted the final dataset using a random forest regressor (RFR) model, with results shown in Fig. 5. While similar to Fig. 4, there are notable shifts in feature importance. Days (positrode application to sinter) dropped out of the top 10, likely due to its low variance (affecting only 4 of 84 cells). Positrode thickness (μm) also shifted out of the top 10, possibly because the RFR model placed higher importance on batch data. The RFR model found days (spray to sinter) relatively more important than the GP model did, while attributing less importance to electrolyte thickness to grain size ratio, again likely due to an emphasis on batch data.
 | ||
| Fig. 5 Feature importance results from the RFR model. The top 10 most important encoded features are displayed, color-coded by the cell layer or process they represent. This model analyzed 84 BCZYYb4411 cells and 20 parameters, encoded to 163 features. The hyperparameters used for this model can be found in ESI Table S8.† Model performance metrics and detailed goodness-of-fit results appear in ESI Table S7 and Fig. S8,† respectively. | ||
Negatrode thickness (mm) appears in the top 10 most important features, a unique occurrence across all four models presented. During parameter selection, its removal led to mixed results, as it improved some error metrics while worsening others. We therefore suspect that the importance of negatrode thickness (mm) is likely due to noise in the data.
The electrolysis RFR model further emphasizes the importance of the electrolyte in electrolysis mode performance. Seven of the top 10 most important parameters relate to the electrolyte or to the negatrode/electrolyte co-sintering process, while none are associated with the positrode.
Fig. 6 shows the partial-dependence plots determined by the RFR model for the numerical columns among the top 10 most important features. Similar to the fuel cell performance PDPs, increasing the delay between spraying and cell sintering to ∼30 days can lead to significant performance gains (Fig. 6a). This effect may be due to collinearity with a high-performing batch of cells. Although, it may also potentially reflect real physical effects associated with the beneficial impact of organics evaporation.
Similar to fuel cell performance, Fig. 6b shows significant electrolysis performance gains by decreasing the electrolyte thickness to grain size ratio, with notable jumps at ratios of two and one. However, for barium-based perovskites with moderate to high zirconium ratios, like BCZYYb4411, electronic leakage can occur at 550 °C.12,71,85–87 Decreased electrolyte thickness has been shown to increase electronic leakage,88–90 potentially explaining why this ratio is more important in electrolysis mode. This might also explain why increasing positrode thickness (μm), a top 10 feature in the GP model (Fig. 4), leads to lower electrolysis performance (ESI Fig. S9†), as thicker BCFZY positrodes increase the cell's electronic resistivity. While some of the observed electrolysis performance gains due to a smaller electrolyte thickness to grain size ratio may stem from (undesirable) electronic leakage, most of the gain is likely the beneficial result of achieving a more favorable electrolyte microstructure. Given its significance, we advise that this ratio should always be reported when disclosing electrolysis performance data.
Fig. 6c shows that electrolysis performance increases with higher relative humidity during co-sintering. This result is unexpected, as higher absolute humidity during co-sintering typically impedes electrolyte grain growth and negatrode shrinkage.32 We hypothesize that higher water content in the furnace during co-sintering could potentially inhibit the formation of amorphous grain boundary layers during electrolyte densification, thereby increasing electrolyte conductivity.91
Interestingly, cells dried in an oven at 100 °C before co-sintering (a top 10 feature in the GP model, Fig. 4) show increased performance compared to undried cells (ESI Fig. S10†). Although this column has low variance (only 4 of 84 cells labeled “yes”), the combination of evaporating organics to lower furnace CO2 concentration and maintaining higher water vapor concentration during sintering might result in electrolyte microstructures that benefit electrolysis performance. To examine the relationship between absolute humidity at co-sinter and fuel cell performance, this parameter is reintroduced to the fuel cell RFR model after its initial exclusion from the GP model. The PDP (ESI Fig. S11†) reveals a moderate but positive correlation between humidity at co-sinter and fuel cell performance.
The increase and subsequent plateau in electrolysis performance shown in Fig. 6d with decreasing NiO particle size (μm) mirrors the fuel cell performance response previously shown in Fig. 3d. The rebound at around 8 μm is likely noise. Counterintuitively, Fig. 6e suggests that thicker negatrodes lead to higher electrolysis performance. Negatrode thickness was dropped from the fuel cell GP model, showed mixed results in the electrolysis GP model, and wasn't among the most important factors in the GP model; therefore we suspect this parameter's apparent importance is likely noise.
The electrolysis ML results on 84 BCZYYb4411 cells indicate that electrolyte characteristics, particularly the electrolyte thickness to grain size ratio, have the largest impact on performance. The negatrode has a minor effect, but NiO particle size should be kept below 6 (μm). The effects of the waiting time between spraying and sintering, and between positrode application and sintering warrant further investigation. Higher humidity during co-sintering may benefit electrolysis performance even though it impedes electrolyte grain growth. Evaporating organics from the cell after spraying (prior to sintering) also appears beneficial to electrolysis performance.
Table 1 summarizes recommendations for improving fuel cell and electrolysis performance. These recommendations are based on insights from the GP and RFR models applied to the 84+ BCZYYb4411 PCC devices discussed both in this section and in Section 3.1.
3.3 Resistance and performance correlations
Electrochemical impedance spectroscopy (EIS) was performed before obtaining fuel cell and electrolysis IV-curves for all button cells in this study. From EIS data, ohmic and polarization (Rp) resistances can be calculated.84 Ohmic resistance is primarily attributed to ionic transport in the electrolyte, although ionic and electronic transport in the electrodes and electrode/electrolyte contact resistances can also contribute.84Rp stems from resistances associated with various electrochemical reaction and mass transport processes at the electrodes.84Plotting ohmic and Rp against fuel cell and electrolysis performance, as shown in Fig. 7, reveals notable trends. The peak power density (PPD) and current density (CD) plots contain data from 88 and 86 BCZYYb4411 cells, respectively. Both data sets were filtered for ohmic and Rp values with Z-scores above 3σ. Each dataset in Fig. 7 was fit with either an exponential function (eqn (1)) or a reciprocal function (eqn (2)). Full fit details can be found in ESI Table S10.† All EIS data was obtained at OCV at 550 °C. EIS data at OCV was used because it is available for all 88 cells.
Plots (a), (b), and (d) in Fig. 7 were best fit with the exponential function, while (c) was best fit with the reciprocal function, with corresponding goodness of fit parameters displayed on each of the plots. Definitions for eqn (1) and (2) are as follows:
y = a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−bx) exp(−bx) | (1) |
 | (2) |
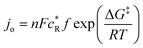 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485C mol−1),
485C mol−1),  is reactant surface concentration (mol cm−2), f is product decay rate, R is the ideal gas constant (J mol−1·k−1), and T is temperature (K). Exchange current density relates to electrode kinetic processes. On the other hand, the reciprocal function, expressed by eqn (2), reflects Ohm's law (eqn (4)):
is reactant surface concentration (mol cm−2), f is product decay rate, R is the ideal gas constant (J mol−1·k−1), and T is temperature (K). Exchange current density relates to electrode kinetic processes. On the other hand, the reciprocal function, expressed by eqn (2), reflects Ohm's law (eqn (4)): | (4) |
Fig. 7b shows that an exponential function more accurately models the relationship between Rp and fuel cell performance, as Rp is linked to electrode processes. Similarly, Fig. 7c illustrates that a reciprocal function most effectively captures the relationship between ohmic resistance and electrolysis performance, since ohmic resistance primarily reflects the resistance of proton motion through the electrolyte.
The goodness-of-fit for PPD vs. Rp and CD vs. ohmic are superior to their counterparts, indicating that Rp better predicts fuel cell performance while ohmic resistance better predicts electrolysis performance. Since Rp mainly derives from electrode processes, while the ohmic resistance largely derives from electrolyte processes, fuel cell performance will benefit most strongly from improving the electrodes and lowering Rp, while electrolysis performance will benefit most strongly from improving the electrolyte and decreasing ohmic resistance. This further substantiates the results from Sections 3.1 and 3.2, where fuel cell mode performance was more strongly tied to the positrode characteristics while electrolysis performance was more strongly dependent on the electrolyte characteristics.
Furthermore, we find that these trends are universal across cells made and tested at two universities: Colorado School of Mines (Mines) and Curtin University (Curtin) in Perth, Western Australia. Although the sample size is small, Curtin cells follow the same trends as Mines cells.
An optimal electrode morphology requires both nanoscale structures to maximize surface area and well-sintered particle networks to enhance ionic conductivity and effective active surface area. Research has demonstrated that increased electrode surface area correlates with improved performance.92–95 Minimal evidence exists for gas transport limitations on performance, suggesting that most electrodes in literature achieve sufficient porosity. Distribution of relaxation time (DRT) analysis indicates that surface diffusion and species dissociation significantly influence polarization resistance.47,71,96
At 550 °C, the average ohmic and Rp values aggregated across all 88 tested cells are roughly even, as shown in ESI Fig. S12.† This indicates that ohmic and Rp contribute approximately equally to performance losses in the cells presented in this paper.
Fig. 8 probes the cross-correlations between fuel cell vs. electrolysis performance and between ohmic and polarization resistance metrics. The fuel cell vs. electrolysis performance comparison (Fig. 8a) reveals moderate correlation (R2 = 0.47), suggesting PCCs with high fuel cell performance likely exhibit high electrolysis performance. On the other hand, Fig. 8b reveals no correlation between ohmic and polarization resistance. While Luo et al. found ohmic and Rp were interrelated when testing different electrode materials due to their effect on electrolyte hydration,97 here we find that these resistances are unrelated when using fixed material sets.
4. Conclusions
This study utilized Gaussian process and random forest regressor machine learning models to identify the key processing and cell morphology parameters that most impact fuel cell and electrolysis performance in protonic-ceramic electrochemical cells. All PCCs in this paper were fabricated using the material sets BCZYYb4411 + NiO—BCZYYb4411—BCFZY for the negatrode, electrolyte, and positrode, respectively. After parameter and cell selection, the fuel cell models analyzed 86 cells with 14 processing parameters (encoded to 137 features), while the electrolysis models examined 84 cells with 20 parameters (encoded to 163 features). Additionally, general correlations between PCC performance and resistance metrics were fit using 86 and 88 cells, respectively.The electrolyte thickness to grain size ratio emerged as a critical factor for both fuel cell and electrolysis performance, with an ideal ratio ≤ 1. Due to its importance in driving performance, we recommend that this parameter be disclosed when reporting PCC results. We identify a critical NiO particle size threshold of ∼ 6 μm, below which performance increases rapidly before plateauing. Evaporating organics from the electrolyte and/or positrode layers before sintering could significantly improve performance, though collinearity and low variance may have influenced the importance of these parameters. For fuel cell mode operation, the optimal BCFZY positrode thickness is 20–25 μm, while for electrolysis, a relative humidity during co-sintering >15% can enhance performance.
Fuel cell performance is primarily influenced by positrode microstructure, with the electrolyte also playing an important role. Reducing Rp should be prioritized for fuel cell performance gains. Conversely, electrolysis performance is strongly governed by electrolyte microstructure, and lowering ohmic resistance should be the focus for improvement. Generally, PCCs with high fuel cell performance likely exhibit high electrolysis performance. However, with a fixed material set, Rp and ohmic resistance vary independently. These findings provide valuable insights for optimizing PCC performance in both fuel cell and electrolysis operation.
Data availability
Raw performance data and open-source code utilizing ML models to analyze the performance data are available online at GitHub: https://github.com/C-Meisel/PCC-performance.Author contributions
Conceptualization, C. M., J. D. H., R. O., and N. P. S.; data curation, C. M.; formal analysis, C. M. and J. D. H.; funding acquisition, R. O. and N. P. S.; investigation, C. M., L. Q. L., Y. K., S. S., Z. L., T. Z., and Z. W.; methodology, C. M. and J. D. H.; resources, Z. S., R. O., and N. P. S.; software, C. M. and J. D. H.; visualization, C. M.; writing – original draft, C. M.; writing – review & editing, C. M., J. D. H., Z. L., R. O., and N. P. S.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. M. was supported by the U.S. Department of Education under a Graduate Assistance in Areas of National Need (GAANN) Fellowship (Grant #P200A210134). R. O. and Y. K. gratefully acknowledge support from the US Army Research Office under grant number W911NF-22-1-0273. C. M. is grateful to Dr Kevin Cannon for training on the particle size analyzer. We appreciate the efforts of Mr Doug Swenning for supplying the relative humidity measurements. We would like to acknowledge Dr Alex Dixon for training on the Phenom SEM. We offer our thanks to Mr Antony Sikorski for feedback on machine learning. We are grateful for technical staff members Dr Roshanak Doroushi and Nathan Tarom for overseeing the laboratories at Curtin University. We would like to acknowledge Mr Tyler Burt for creating the schematics in ESI Fig. S1 and S4.† ChatGPT and Anthropic Claude were used in part to edit this manuscript and to help write the Python code used in for ML model implementation. After using the generative AI tools, the authors reviewed and edited the manuscript and code.References
- D. J. Arent, P. Green, Z. Abdullah, T. Barnes, S. Bauer, A. Bernstein, D. Berry, J. Berry, T. Burrell, B. Carpenter, J. Cochran, R. Cortright, M. Curry-Nkansah, P. Denholm, V. Gevorian, M. Himmel, B. Livingood, M. Keyser, J. King, B. Kroposki, T. Mai, M. Mehos, M. Muratori, S. Narumanchi, B. Pivovar, P. Romero-Lankao, M. Ruth, G. Stark and C. Turchi, Challenges and opportunities in decarbonizing the U.S. energy system, Renewable Sustainable Energy Rev., 2022, 169, 112939, DOI:10.1016/j.rser.2022.112939.
- K. Mazloomi and C. Gomes, Hydrogen as an energy carrier: prospects and challenges, Renewable Sustainable Energy Rev., 2012, 16(5), 3024–3033, DOI:10.1016/j.rser.2012.02.028.
- B. Pivovar, N. Rustagi and S. Satyapal, Hydrogen at scale (H2@Scale): key to a clean, economic, and sustainable energy system, Electrochem. Soc. Interface, 2018, 27(1), 47, DOI:10.1149/2.F04181if.
- Global Hydrogen Review, Technical Report, International Energy Agency (IEA), Paris, 2023 Search PubMed.
- F. Liu, H. Deng, D. Diercks, P. Kumar, M. H. A. Jabbar, C. Gumeci, Y. Furuya, N. Dale, T. Oku, M. Usuda, P. Kazempoor, L. Fang, D. Chen, B. Liu and C. Duan, Lowering the operating temperature of protonic ceramic electrochemical cells to <450 °C, Nat. Energy, 2023, 8(10), 1145–1157, DOI:10.1038/s41560-023-01350-4.
- C. Duan, J. Huang, N. Sullivan and R. O'Hayre, Proton-conducting oxides for energy conversion and storage, Appl. Phys. Rev., 2020, 7(1), 011314, DOI:10.1063/1.5135319.
- C. Duan, R. Kee, H. Zhu, N. Sullivan, L. Zhu, L. Bian, D. Jennings and R. O'Hayre, Highly efficient reversible protonic ceramic electrochemical cells for power generation and fuel production, Nat. Energy, 2019, 4(3), 230–240, DOI:10.1038/s41560-019-0333-2.
- A. Dubois, S. Ricote and R. J. Braun, Benchmarking the expected stack manufacturing cost of next generation, intermediate-temperature protonic ceramic fuel cells with solid oxide fuel cell technology, J. Power Sources, 2017, 369, 65–77, DOI:10.1016/j.jpowsour.2017.09.024.
- S. Choi, T. C. Davenport and S. M. Haile, Protonic ceramic electrochemical cells for hydrogen production and electricity generation: exceptional reversibility, stability, and demonstrated faradaic efficiency, Energy Environ. Sci., 2019, 12(1), 206–215, 10.1039/C8EE02865F.
- M. Choi, D. Kim, T. K. Lee, J. Lee, H. S. Yoo and W. Lee, Interface engineering to operate reversible protonic ceramic electrochemical cells below 500 °C, Adv. Energy Mater., 2024, 2400124, DOI:10.1002/aenm.202400124.
- H. Ding, W. Wu, C. Jiang, Y. Ding, W. Bian, B. Hu, P. Singh, C. J. Orme, L. Wang, Y. Zhang and D. Ding, Self-sustainable protonic ceramic electrochemical cells using a triple conducting electrode for hydrogen and power production, Nat. Commun., 2020, 11(1), 1907, DOI:10.1038/s41467-020-15677-z.
- Z. Luo, Y. Zhou, X. Hu, N. Kane, T. Li, W. Zhang, Z. Liu, Y. Ding, Y. Liu and M. Liu, Critical role of acceptor dopants in designing highly stable and compatible proton-conducting electrolytes for reversible solid oxide cells, Energy Environ. Sci., 2022, 15(7), 2992–3003, 10.1039/D2EE01104B.
- C. Duan, R. J. Kee, H. Zhu, C. Karakaya, Y. Chen, S. Ricote, A. Jarry, E. J. Crumlin, D. Hook, R. Braun, N. P. Sullivan and R. O'Hayre, Highly durable, coking and sulfur tolerant, fuel-flexible protonic ceramic fuel cells, Nature, 2018, 557(7704), 217–222, DOI:10.1038/s41586-018-0082-6.
- H. Malerød-Fjeld, D. Clark, I. Yuste-Tirados, R. Zańon, D. Cataĺan, D. B. Martinez, S. H. Morejudo, P. K. Vestre, T. Norby, R. Haugsrud, J. M. Serra and C. Kjølseth, Thermo-electrochemical produc-tion of compressed hydrogen from methane with near-zero energy loss, Nat. Energy, 2017, 2(12), 923–931, DOI:10.1038/s41560-017-0029-4.
- J. C. Mankins, Tehnology readiness levels, White Paper White paper, NASA, 1995 Search PubMed.
- M. Choi, J. Paik, D. Kim, D. Woo, J. Lee, S. J. Kim, J. Lee and W. Lee, Exceptionally high performance of protonic ceramic fuel cells with stoichiometric electrolytes, Energy Environ. Sci., 2021, 14(12), 6476–6483, 10.1039/D1EE01497H.
- H. An, H.-W. Lee, B.-K. Kim, J.-W. Son, K. J. Yoon, H. Kim, D. Shin, H.-I. Ji and J.-H. Lee, A 5 × 5 cm2 protonic ceramic fuel cell with a power density of 1.3 W cm2 at 600 °C, Nat. Energy, 2018, 3(10), 870–875, DOI:10.1038/s41560-018-0230-0.
- S. Choi, C. J. Kucharczyk, Y. Liang, X. Zhang, I. Takeuchi, H.-I. Ji and S. M. Haile, Exceptional power density and stability at intermediate temperatures in protonic ceramic fuel cells, Nat. Energy, 2018, 3(3), 202–210, DOI:10.1038/s41560-017-0085-9.
- K. Park, H. Bae, H.-K. Kim, I.-G. Choi, M. Jo, G.-M. Park, M. Asif, A. Bhardwaj, K.-S. Lee, Y.-C. Kim, S.-J. Song, E. D. Wachsman and J.-Y. Park, Understanding the highly electrocatalytic active mixed triple conducting NaxCa3–xCo4O9−δ oxygen electrode materials, Adv. Energy Mater., 2022, 13(2), 2202999, DOI:10.1002/aenm.202202999.
- M. Saqib, I.-G. Choi, H. Bae, K. Park, J.-S. Shin, Y.-D. Kim, J. I. Lee, M. Jo, Y.-C. Kim, K.-S. Lee, S.-J. Song, E. D. Wachsman and J.-Y. Park, Transition from perovskite to misfit-layered structure materials: a highly oxygen deficient and stable oxygen electrode catalyst, Energy Environ. Sci., 2021, 14(4), 2472–2484, 10.1039/D0EE02799E.
- K. Bae, D. H. Kim, H. J. Choi, J.-W. Son and J. H. Shim, HighPerformance protonic ceramic fuel cells with 1 $\\mu$m thick Y:Ba(Ce, Zr)O3 electrolytes, Adv. Energy Mater., 2018, 8(25), 1801315, DOI:10.1002/aenm.201801315.
- K. Park, M. Saqib, H. Lee, D. Shin, M. Jo, K. Min Park, M. Hamayun, R. Hyun Kim, S. Kim, K.-S. Lee, R. O'Hayre, M. Choi, S.-J. Song and J.-Y. Park, Water-mediated exsolution of nanoparticles in alkali metaldoped perovskite structured triple-conducting oxygen electrocatalysts for reversible cells, Energy Environ. Sci., 2024, 17(3), 1175–1188, 10.1039/D3EE03510G.
- Z. Luo, X. Hu, Y. Zhou, Y. Ding, W. Zhang, T. Li and M. Liu, Harnessing high-throughput computational methods to accelerate the discovery of optimal proton conductors for high-performance and durable protonic ceramic electrochemical cells, Adv. Mater., 2024, 36(18), 2311159, DOI:10.1002/adma.202311159.
- Z. Luo, Y. Zhou, X. Hu, W. Wang, Y. Ding, W. Zhang, T. Li, N. Kane, Z. Liu and M. Liu, A new class of proton conductors with dramatically enhanced stability and high conductivity for reversible solid oxide cells, Small, 2023, 19(17), 2208064, DOI:10.1002/smll.202208064.
- J. H. Kim, D. Kim, S. Ahn, K. J. Kim, S. Jeon, D.-K. Lim, J. K. Kim, U. Kim, H.-N. Im, B. Koo, K. T. Lee and W. Jung, An universal oxygen electrode for reversible solid oxide electrochemical cells at reduced temperatures, Energy Environ. Sci., 2023, 16(9), 3803–3814, 10.1039/D2EE04108A.
- Z. Luo, Y. Zhou, X. Hu, N. Kane, W. Zhang, T. Li, Y. Ding, Y. Liu and M. Liu, Highly conductive and durable Nb(Ta)-doped proton conductors for reversible solid oxide cells, ACS Energy Lett., 2022, 7(9), 2970–2978, DOI:10.1021/acsenergylett.2c01544.
- 5th Annual Advanced Water Splitting Technology Pathways Benchmarking and Protocols Workshop September 21–22, 2023, https://www.energy.gov/eere/h2awsm/articles/5th-annual-advancedwater-splitting-technology-pathways-benchmarking-and Search PubMed.
- Z. Luo, Z. Wang, T. Zhu, Y. Song, Z. Lin, S. P. Jiang, Z. Zhu and Z. Shao, Performance deviation analysis and reliability improvement during experimental development of lab-scale solid oxide single cells, Energy Environ. Sci., 2024, 17(19), 6873–6896, 10.1039/D4EE02581D.
- E. Alpaydin, Introduction to Machine Learning, MIT Press, 4th edn, 2020 Search PubMed.
- S. Zhai, H. Xie, P. Cui, D. Guan, J. Wang, S. Zhao, B. Chen, Y. Song, Z. Shao and M. Ni, A combined ionic Lewis acid descriptor and machine-learning approach to prediction of efficient oxygen reduction electrodes for ceramic fuel cells, Nat. Energy, 2022, 7(9), 866–875, DOI:10.1038/s41560-022-01098-3.
- W. Shin, Y. Yamaguchi, M. Horie, H. Shimada, K. Nomura and H. Sumi, Machine learning based analysis of metal support co-sintering process for solid oxide fuel cells, Ceram. Int., 2023, 49(22, Part B), 36478–36489, DOI:10.1016/j.ceramint.2023.08.331.
- C. Meisel, J. D. Huang, Y.-D. Kim, S. Stockburger, R. O'Hayre and N. P. Sullivan, Insights on proton-conducting ceramic electrochemical cell fabrication, J. Am. Ceram. Soc., 2025, e20321, DOI:10.1111/jace.20321.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, Adaptive Computation and Machine Learning, MIT Press, Cambridge, Mass, 2006 Search PubMed.
- K. P. Murphy, Machine Learning: A Probabilistic Perspective, MIT Press, 2012 Search PubMed.
- K. Tazi, J. A. Lin, R. Viljoen, A. Gardner, S. T. John, H. Ge, E. Richard and B. I. Turner, A framework for applying gps to real-world data, arxiv, 2023, preprint, arXiv:2307.03093, DOI:10.48550/arXiv.2307.03093.
- N. J. Williams, C. Osborne, I. D. Seymour, M. Z. Bazant and S. J. Skinner, Application of finite Gaussian process distribution of relaxation times on SOFC electrodes, Electrochem. Commun., 2023, 149, 107458, DOI:10.1016/j.elecom.2023.107458.
- A. Sikorski, D. McKenzie and D. Nychka, Normalizing basis functions: approximate stationary models for large spatial data, Stat, 2024, 13(4), e70015, DOI:10.1002/sta4.70015.
- G. James, D. Witten, T. Hastie and R. Tibshirani, Tree-based methods, in An Introduction to Statistical Learning: With Applications in R, Springer Nature, 2021 Search PubMed.
- L. Breiman, Random forests, Mach. Learn., 2001, 45(1), 5–32, DOI:10.1023/A:1010933404324.
- L. Breiman, Bagging predictors, Mach. Learn., 1996, 24(2), 123–140, DOI:10.1007/BF00058655.
- J. Tong, D. Clark, M. Hoban and R. O'Hayre, Cost-effective solid-state reactive sintering method for high conductivity proton conducting yttriumdoped barium zirconium ceramics, Solid State Ionics, 2010, 181(11), 496–503, DOI:10.1016/j.ssi.2010.02.008.
- J. Tong, D. Clark, L. Bernau, A. Subramaniyan and R. O'Hayre, Protonconducting yttrium-doped barium cerate ceramics synthesized by a costeffective solid-state reactive sintering method, Solid State Ionics, 2010, 181(33), 1486–1498, DOI:10.1016/j.ssi.2010.08.022.
- J. Tong, D. Clark, L. Bernau, M. Sanders and R. O'Hayre, Solid-state reactive sintering mechanism for large-grained yttrium-doped barium zirconate proton conducting ceramics, J. Mater. Chem., 2010, 20(30), 6333–6341, 10.1039/C0JM00381F.
- S. Nikodemski, J. Tong and R. O'Hayre, Solid-state reactive sintering mechanism for proton conducting ceramics, Solid State Ionics, 2013, 253, 201–210, DOI:10.1016/j.ssi.2013.09.025.
- J. Huang, M. Papac and R. O'Hayre, Towards robust autonomous impedance spectroscopy analysis: a calibrated hierarchical Bayesian approach for electrochemical impedance spectroscopy (EIS) inversion, Electrochim. Acta, 2021, 367, 137493, DOI:10.1016/j.electacta.2020.137493.
- J. Huang, N. P. Sullivan, A. Zakutayev and R. O'Hayre, How reliable is distribution of relaxation times (DRT) analysis? A dual regression-classification perspective on DRT estimation, interpretation, and accuracy, Electrochim. Acta, 2023, 443, 141879, DOI:10.1016/j.electacta.2023.141879.
- J. D. Huang, C. Meisel, N. P. Sullivan, A. Zakutayev and R. O’Hayre, Rapid mapping of electrochemical processes in energy-conversion devices, Joule, 2024, 8(7), 2049–2072, DOI:10.1016/j.joule.2024.05.003.
- T. Hofmann, B. Schölkopf and A. J. Smola, Kernel methods in machine learning, Ann. Statistics, 2008, 36(3), 1171–1220, DOI:10.1214/009053607000000677.
- T. Viering and M. Loog, The shape of learning curves: a review, IEEE Trans. Pattern Anal. Mach. Intell., 2023, 45(6), 7799–7819, DOI:10.1109/TPAMI.2022.3220744.
- Z. Wang, Z. Luo, H. Xu, T. Zhu, D. Guan, Z. Lin, T.-S. Chan, Y.-C. Huang, Z. Hu, S. P. Jiang and Z. Shao, New understanding and improvement in sintering behavior of cerium-rich perovskite-type protonic electrolytes, Adv. Funct. Mater., 2024, 2402716, DOI:10.1002/adfm.202402716.
- F. Iguchi, N. Sata, T. Tsurui and H. Yugami, Microstructures and grain boundary conductivity of BaZr1−xYxO3 (x = 0.05, 0.10, 0.15) ceramics, Solid State Ionics, 2007, 178(7), 691–695, DOI:10.1016/j.ssi.2007.02.019.
- P. Babilo and S. M. Haile, Enhanced sintering of yttrium-doped barium zirconate by addition of ZnO, 2005 zirconate by addition of ZnO, J. Am. Ceram. Soc., 2005, 88(9), 2362–2368, DOI:10.1111/j.1551-2916.2005.00449.x.
- S. Ricote, N. Bonanos, A. Manerbino, N. P. Sullivan and W. G. Coors, Effects of the fabrication process on the grain-boundary resistance in BaZr0.9Y0.1O3-δ, J. Mater. Chem. A, 2014, 2(38), 16107–16115, 10.1039/C4TA02848A.
- D. R. Clark, H. Zhu, D. R. Diercks, S. Ricote, R. J. Kee, A. Almansoori, B. P. Gorman and R. P. O'Hayre, Probing grain-boundary chemistry and electronic structure in proton-conducting oxides by atom probe tomography, Nano Lett., 2016, 16(11), 6924–6930, DOI:10.1021/acs.nanolett.6b02918.
- C. Kjølseth, H. Fjeld, Ø. Prytz, P. I. Dahl, C. Estourn`es, R. Haugsrud and R. Norby, Space–charge theory applied to the grain boundary impedance of proton conducting BaZr0.9Y0.1O3-δ, Solid State Ionics, 2010, 181(5), 268–275, DOI:10.1016/j.ssi.2010.01.014.
- B. Groß, C. Beck, F. Meyer, T. Krajewski, R. Hempelmann and H. Altgeld, BaZr0.85Me0.15O2.925 (Me=Y, In and Ga): crystal growth, highresolution transmission electron microscopy, high-temperature X-ray diffraction and neutron scattering experiments, Solid State Ionics, 2001, 145(1), 325–331, DOI:10.1016/S0167-2738(01)00927-4.
- Y. Huang, R. Merkle and J. Maier, Effects of NiO addition on sintering and proton uptake of Ba(Zr,Ce,Y)O3-δ, J. Mater. Chem. A, 2021, 9(26), 14775–14785, 10.1039/D1TA02555D.
- Y. Huang, R. Merkle, D. Zhou, W. Sigle, P. A. van Aken and J. Maier, Effect of Ni on electrical properties of Ba(Zr,Ce,Y)O3-δ as electrolyte for protonic ceramic fuel cells, Solid State Ionics, 2023, 390, 116113, DOI:10.1016/j.ssi.2022.116113.
- K. D. Kreuer, Proton-conducting oxides, Annu. Rev. Mater. Res., 2003, 33(1), 333–359, DOI:10.1146/annurev.matsci.33.022802.091825.
- D. Poetzsch, R. Merkle and J. Maier, Oxygen reduction at dense thin-film microelectrodes on a proton-conducting electrolyte: I. considerations on reaction mechanism and electronic leakage effects, J. Electrochem. Soc., 2015, 162(9), F939, DOI:10.1149/2.0951508jes.
- M. Papac, V. Stevanovíc, A. Zakutayev and R. O'Hayre, Triple ionic– electronic conducting oxides for next-generation electrochemical devices, Nat. Mater., 2021, 20(3), 301–313, DOI:10.1038/s41563-020-00854-8.
- A. Grimaud, F. Mauvy, J. M. Bassat, S. Fourcade, L. Rocheron, M. Marrony and J. C. Grenier, Hydration properties and rate determining steps of the oxygen reduction reaction of perovskite-related oxides as H+SOFC cathodes, J. Electrochem. Soc., 2012, 159(6), B683, DOI:10.1149/2.101205jes.
- Q. Wang, M. Zhang, L. Fan and Z. Tao, Balance the conductivity and enhance chemical stability of BaCe0.3Fe0.7O3–δ by tuning A-site cation deficiency, Ceram. Int., 2024, 50(9, Part A), 14631–14636, DOI:10.1016/j.ceramint.2024.01.375.
- J. Zhang, S. Ricote, P. V. Hendriksen and Y. Chen, Advanced materials for thin-film solid oxide fuel cells: recent progress and challenges in boosting the device performance at low temperatures, Adv. Funct. Mater., 2022, 32(22), 2111205, DOI:10.1002/adfm.202111205.
- Z. Gao, L. V. Mogni, E. C. Miller, J. G. Railsback and S. A. Barnett, A perspective on low-temperature solid oxide fuel cells, Energy Environ. Sci., 2016, 9(5), 1602–1644, 10.1039/C5EE03858H.
- C. Sun and U. Stimming, Recent anode advances in solid oxide fuel cells, J. Power Sources, 2007, 171(2), 247–260, DOI:10.1016/j.jpowsour.2007.06.086.
- S. M. Choi, J.-H. Lee, J. Hong, H. Kim, K. J. Yoon, B.-K. Kim and J.-H. Lee, Effect of sintering atmosphere on phase stability, and electrical conductivity of proton-conducting Ba(Zr0.84Y0.15Cu0.01)O3-δ, Int. J. Hydrogen Energy, 2014, 39(13), 7100–7108, DOI:10.1016/j.ijhydene.2014.02.072.
- A. Hinojo, E. Lujan, A. Verdaguer, J. Abella and S. Colominas, Shaping techniques' influence on the electrochemical properties of BaCe0.6Zr0.3Y0.1O3-δ proton conductor, Ceram. Int., 2024, 50(20, Part C), 40249–40260, DOI:10.1016/j.ceramint.2024.05.447.
- M. Rahaman, Ceramic Processing and Sintering, in Materials Engineering, Taylor & Francis Group, Boca Raton, FL, 2nd edn, 2003 Search PubMed.
- P.-C. Cheng, K.-R. Lee, M. Bhavanari, P.-C. Su, N. Osman, S.-W. Lee and C.-J. Tseng, Enhancing protonic ceramic fuel cell performance through nanomilling of BCZY electrolyte powder, Ceram. Int., 2023, 49(19), 32172–32180, DOI:10.1016/j.ceramint.2023.07.188.
- C. Meisel, J. Huang, Y.-D. Kim, R. O'Hayre and N. P. Sullivan, Towards improved stability in proton-conducting ceramic fuel cells, J. Power Sources, 2024, 615, 235021, DOI:10.1016/j.jpowsour.2024.235021.
- B. H. Rainwater, M. Liu and M. Liu, A more efficient anode microstructure for SOFCs based on proton conductors, Int. J. Hydrogen Energy, 2012, 37(23), 18342–18348, DOI:10.1016/j.ijhydene.2012.09.027.
- W. G. Coors and A. Manerbino, Characterization of composite cermet with 68 wt.% NiO and BaCe0.2Zr0.6Y0.2O3-δ, J. Membr. Sci., 2011, 376(1), 50–55, DOI:10.1016/j.memsci.2011.03.062.
- H. Zhu and R. J. Kee, Modeling protonic-ceramic fuel cells with porous composite electrodes in a button-cell configuration, J. Electrochem. Soc., 2017, 164(13), F1400, DOI:10.1149/2.0591713jes.
- C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Readily processed protonic ceramic fuel cells with high performance at low temperatures, Science, 2015, 349(6254), 1321–1326, DOI:10.1126/science.aab3987.
- H. Zhu and R. J. Kee, Modeling distributed charge-transfer processes in SOFC membrane electrode assemblies, J. Electrochem. Soc., 2008, 155(7), B715, DOI:10.1149/1.2913152.
- L. Zhu, L. Zhang and A. V. Virkar, A parametric model for solid oxide fuel cells based on measurements made on cell materials and components, J. Power Sources, 2015, 291, 138–155, DOI:10.1016/j.jpowsour.2015.04.155.
- Z. Shao and S. M. Haile, A high-performance cathode for the next generation of solid-oxide fuel cells, Nature, 2004, 431(7005), 170–173, DOI:10.1038/nature02863.
- Y. Zhang, B. Chen, D. Guan, M. Xu, R. Ran, M. Ni, W. Zhou, R. O'Hayre and Z. Shao, Thermal-expansion offset for high-performance fuel cell cathodes, Nature, 2021, 591(7849), 246–251, DOI:10.1038/s41586021-03264-1.
- Y. Shin, Y.-d. Kim, M. Sanders, S. P. Harvey, M. Walker and R. O'Hayre, Tuning the Co/Fe ratio in BaCoxFe0.8-xZr0.1Y0.1O3-δ, a promising triple ionic and electronic conducting oxide, to boost electrolysis and fuel cell performance, J. Mater. Chem. A, 2022, 10(46), 24839–24853, 10.1039/D2TA03150G.
- Y. Li, Y. Li, M. Singh, Z. Li, X. Hu and L. Fan, Effects of ceria on the oxygen reduction activity and thermal cycling stability of BaCo0.4Fe0.4Zr0.1Y0.1O3−δ cathode for solid oxide fuel cells, ACS Appl. Energy Mater., 2022, 5(11), 14391–14400, DOI:10.1021/acsaem.2c02949.
- M. Liang, Y. Zhu, Y. Song, D. Guan, Z. Luo, G. Yang, S. P. Jiang, W. Zhou, R. Ran and Z. Shao, A new durable surface nanoparticlesmodified perovskite cathode for protonic ceramic fuel cells from selective cation exsolution under oxidizing atmosphere, Adv. Mater., 2022, 34(10), 2106379, DOI:10.1002/adma.202106379.
- H. Gu, M. Xu, Y. Song, C. Zhou, C. Su, W. Wang, R. Ran, W. Zhou and Z. Shao, SrCo0.8Ti0.1Ta0.1O3-δ perovskite: a new highly active and durable cathode material for intermediate-temperature solid oxide fuel cells, Composites, Part B, 2021, 213, 108726, DOI:10.1016/j.compositesb.2021.108726.
- R. O'Hayre, S.-W. Cha, W. Colella and F. B. Prinz, Fuel Cell Fundamentals, John Wiley & Sons, Hoboken, N.J, 2nd edn, 2009 Search PubMed.
- J. Lagaeva, D. Medvedev, A. Demin and P. Tsiakaras, Insights on thermal and transport features of BaCe0.8-xZrxY0.2O3-δ protonconducting materials, J. Power Sources, 2015, 278, 436–444, DOI:10.1016/j.jpowsour.2014.12.024.
- D. Han, X. Liu, T. S. Bjørheim and T. Uda, Yttrium-doped barium zirconate-cerate solid solution as proton conducting electrolyte: why higher cerium concentration leads to better performance for fuel cells and electrolysis cells, Adv. Energy Mater., 2021, 11(8), 2003149, DOI:10.1002/aenm.202003149.
- I. A. Zvonareva, L. R. Tarutina, G. K. Vdovin, J. G. Lyagaeva, A. R. Akhmadeev and D. A. Medvedev, Heavily Sn-doped barium cerates BaCe0.8–xSnxYb0.2O3–δ: correlations between composition and ionic transport, Ceram. Int., 2021, 47(18), 26391–26399, DOI:10.1016/j.ceramint.2021.06.050.
- Y. Okuyama, Y. Harada, Y. Mikami, K. Yamauchi, T. Kuroha, H. Shimada, Y. Yamaguchi and Y. Mizutani, Evaluation of hydrogen ions flowing through protonic ceramic fuel cell using ytterbium-doped barium zirconate as electrolyte, J. Electrochem. Soc., 2023, 170(8), 084509, DOI:10.1149/1945-7111/acef64.
- H. Zhu, S. Ricote and R. J. Kee, Faradaic efficiency in protonic-ceramic electrolysis cells, J. Phys. Energy, 2022, 4(1), 014002, DOI:10.1088/2515-7655/ac3729.
- T. Nakamura, S. Mizunuma, Y. Kimura, Y. Mikami, K. Yamauchi, T. Kuroha, N. Taniguchi, Y. Tsuji, Y. Okuyama and K. Amezawa, Energy efficiency of ionic transport through proton conducting ceramic electrolytes for energy conversion applications, J. Mater. Chem. A, 2018, 6(32), 15771–15780, 10.1039/C8TA05373A.
- H.-S. Kim, H. B. Bae, W. Jung and S.-Y. Chung, Manipulation of nanoscale intergranular phases for high proton conduction and decomposition tolerance in BaCeO3 polycrystals, Nano Lett., 2018, 18(2), 1110–1117, DOI:10.1021/acs.nanolett.7b04655.
- H. Qi, Z. Zhao, B. Tu and M. Cheng, Reaction tuned formation of hierarchical BaCo0.4Fe0.4Zr0.1Y0.1O3-δ cathode, J. Power Sources, 2020, 455, 227971, DOI:10.1016/j.jpowsour.2020.227971.
- M. Shah, P. W. Voorhees and S. A. Barnett, Time-dependent performance changes in LSCF-infiltrated SOFC cathodes: the role of nano-particle coarsening, Solid State Ionics, 2011, 187(1), 64–67, DOI:10.1016/j.ssi.2011.02.003.
- Z. Wang, C. Yang, J. Pu, Y. Tian, J. Wang, F. Ciucci and B. Chi, Insitu self-assembly nano-fibrous perovskite cathode excluding Sr and Co with superior performance for intermediate-temperature solid oxide fuel cells, J. Alloys Compd., 2023, 947, 169470, DOI:10.1016/j.jallcom.2023.169470.
- C. Kim, H. Lee, I. Jang, S. Kim, H. Jung, M. Ryu, J. Kim, D. Lee, H. Yoon, U. Paik and T. Song, BaCo0.4Fe0.4Zr0.1Y0.1O3–δ triple conductor for boosting electrode efficiency for proton conducting fuel cells, Int. J. Hydrogen Energy, 2021, 47(8), 5499–5506, DOI:10.1016/j.ijhydene.2021.11.140.
- K. Akimoto, N. Wang, C. Tang, K. Shuto, S. Jeong, S. Kitano, H. Habazaki and Y. Aoki, Functionality of the cathode–electrolyte interlayer in protonic solid oxide fuel cells, ACS Appl. Energy Mater., 2022, 5(10), 12227–12238, DOI:10.1021/acsaem.2c01712.
- Z. Luo, J. Tang, Z. Wang, G. Yang, T. Zhu, Z. Lin, S. P. Jiang and Z. Shao, First observation of electrode-correlated protonic conductivity of perovskite-type electrolytes and way towards optimization, Energy Environ. Sci., 2024, 17(12), 4115–4125, 10.1039/D4EE00688G.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08326a |
| This journal is © The Royal Society of Chemistry 2025 |