First-principles design of a superior electrocatalyst to Pt for hydrogen production in alkaline media

Abstract

Pt electrocatalysts are known to be surprisingly inactive for the hydrogen evolution reaction (HER) in alkaline media due to their high activation barrier for water decomposition. Despite extensive research over several decades, only a few electrocatalysts with exceptional efficiency and stability have been reported, primarily due to an incomplete understanding of the mechanism and catalyst design principles. Therefore, we investigated the underlying mechanism of the proposed catalyst design for Pt monolayer surface alloy (Pt/W(110)) and nanoparticle (W@Pt) structures, focusing on (i) the surface strain effect and (ii) the ligand effect (charge transfer). Using first-principles calculations, we demonstrated that fabricating Pt nanoparticles increases the H₂O adsorption energy, with lower dissociation energy barrier expected, only shifts the rate-determining step (RDS) to H₂ desorption. When pure Pt structures are modified with W substrates, the dual effects of strain and ligand interactions control the activities of the bulk pseudo-binary Pt/W(110) surface alloy and W@Pt core–shell nanoparticles in the opposite manner. The W@Pt nanoparticles uniformly destabilized all intermediates, increasing the water dissociation activation barrier. In contrast, the Pt/W(110) surface heterogeneously regulated the adsorption intensities of the intermediates, breaking the scaling law of catalysis. We clearly elucidated this heterogeneous behavior in terms of eigenstress-induced surface strain and charge transfer. Our study is expected to provide quantum-mechanical insights into the design of active electrocatalysts by controlling key atomic-level descriptors and addressing the long-standing issue of inactive Pt catalysts in alkaline media.

---

Introduction

Hydrogen is the most abundant element in the universe, accounting for 90% of all atoms. It is also the lightest gas, with the highest gravimetric energy density of 120 kJ g⁻¹.¹ Furthermore, it is also an environmentally friendly and non-toxic gas. These unique properties enable hydrogen gas to play a key role in various chemical reactions from the laboratory to the industrial scale and as a fuel for renewable energy systems and mobile devices. In spite of the attractive aspects, hydrogen production of high purity is difficult in practice because it forms chemically stable mixtures with a wide range of materials (water, hydrides, etc.) or easily smears into bulk crystals.

Over the last several decades, extensive efforts have been made to generate hydrogen gas from hydrolysis through thermochemical, electrochemical, and photovoltaic (or photothermal) pathways. Among these, electrochemical hydrogen production via water decomposition is considered a fully green technology. Developed countries are actively working on designing and optimizing water electrolyzers (WEs).² WEs are largely divided into three different types depending on the working media:^3,4 (i) proton exchange membrane (PEM) WEs, (ii) alkaline WEs, and (iii) anion exchange membrane (AEM) WEs. PEMWEs with high activity in the hydrogen evolution reaction (HER) have been studied for a long time to facilitate their commercialization. However, this has not been successful, mainly due to the instability of the catalysts in acidic media, even for Pt metal and novel transition metal oxides.^5,6 WEs working in an alkaline medium have recently attracted increasing focus, as they allow the use of cost-effective transition metal catalysts for the HER. However, regardless of the decades of study, the system still faces serious challenges in the identification of highly active and stable catalysts other than Pt and in the reduction of system size. Thus, the AEMWE was suggested to operate in an alkaline medium with a polymer membrane, which was designed by taking the benefits of alkaline and PEM systems. A key requirement for AEMWE systems is improved HER catalytic activity and ionic conductivity for industrial-scale commercialization.

In accordance with previous reports, the sluggish HER in alkaline media is caused by the deficiency of a direct proton source, which leads to a more complicated multistep catalytic mechanism than in acidic media. It is noteworthy that even Pt metal is inactive for the HER in alkaline solution because of the substantially high activation energy required to decompose H₂O molecules into H and OH.⁷ This implies that OH molecules do not adsorb on Pt surfaces as effectively as the H atoms do, and the description of HER activity using a single parameter of H adsorption energy would be insufficient. It is essential to precisely control the adsorption behavior of all intermediates along the entire HER pathway, which is difficult to achieve without understanding the accurate catalytic mechanism of various materials and identifying the principles for its control.

It is widely agreed that there is a clear correlation between the catalytic activity and atomic and electronic structures of catalysts employed for the target reaction. This is called the geometric effect⁸ or d-band center energy theory.⁹ Despite well-established theories, few studies have attempted to design highly active HER catalysts as alternatives to Pt metal, and only a few active catalysts with prolonged durability in alkaline solutions have been identified for commercialization. Using first-principles density functional theory (DFT) calculations, we demonstrated the following in this paper: (i) clear elucidation of the underlying mechanism of why nanoparticle construction is not sufficient to increase the HER activity of pure bulk Pt, (ii) identification of two factors (strain and ligand effects) at the atomic and electronic structure levels controlling the HER activity, and (iii) proposal of design principles and selection rules of promising alloying element M with Pt to significantly boost HER activity, surpassing that of Pt bulk and nanoparticles.

Unlike conventional studies, we determined that just the Pt or Pt-M nanoparticles do not actively promote the HER in alkaline media but only shift the RDS of bulk Pt. The two control factors cooperatively worked only for the Pt/W(110) surface, in which a Pt monolayer covered the W(110) plane. To demonstrate the influence of both strain and ligand fields on catalytic activity for the HER, we selected W as the supporting substrate of an active Pt layer. In accordance with the traditional theory, the binding energies of adsorbates with Pt are described by the two factors, which eventually modify the overall catalytic performance. It is difficult, however, to predict the catalytic activity if those variables are coupled with the particle size effect. Therefore, we designed a bulk Pt/W(110) surface and W@Pt nanoparticles to clearly identify a predominant control factor of the catalytic performance and to elucidate its underlying mechanisms. Using DFT calculations, we clearly elucidated the underlying mechanism and proposed unconventional design principles for active electrocatalysts for the HER in alkaline solutions, which can be extended to other targeted catalysts. The rationale of the design is two-fold: (i) decrease Pt loading while maintaining catalytic activity through increased surface area and under-coordinated active sites^10,11 and (ii) develop heterogeneous structures by alloying or ligand fields to induce strain.^12–14 Through first-principles study, we rigorously characterized the interplay of the two factors (strain and ligand fields) for HER catalysts, which are influential for bulk and nanoparticles in a very dissimilar manner.

Computational details

Spin-polarized DFT calculations were performed as implemented in Vienna ab initio simulation package (VASP)¹⁵ for all computations. The interactions between core-valence electrons were described using the projector augmented wave (PAW) pseudopotentials.^16,17 A cutoff energy of 450 eV was applied for the plane wave basis set, with a convergence criteria of 10⁻⁵ eV and 0.04 eV Å⁻¹ for energy and force, respectively. The cutoff value for force was chosen based on test calculations on adsorption energies (Table S1†). The exchange–correlation energy of the electrons was computed using the generalized gradient approximation (GGA) method¹⁸ with Perdew–Burke–Ernzerhof (PBE) functionals.¹⁹ Long-range van der Waals interactions were considered using the DFT-D3 method of Grimme.²⁰ DFT calculations for the nanoparticles were carried out using the Γ-point scheme with a vacuum space of 20 Å to prevent interactions between periodic images. Slab calculations were performed with a dense k-point mesh ensuring at least 1000 k-points per atom and a vacuum space of 15 Å.

The adsorption energy (E_ads) was calculated using eqn (1),

where E_{n adsorbate/surface} is the energy of n (1 for slabs and 6 for nanoparticles) adsorbates on the catalyst surface, E_adsorbate is the energy of the isolated adsorbate, and E_surface is the energy of the clean surface. In the case of ΔE_H*, ΔE_OH*, ΔE_H2O*, and ΔE_H*–OH*, H₂ (g) and H₂O (g) were used as reference states and thermodynamically corrected to account for the liquid state of water.²¹ Adsorption energies of nanoparticles were normalized by adsorbing at all symmetrically equivalent sites of the outermost shell, to avoid undesirable structural distortion by placing the adsorbate only at a single site. The adsorption energy was normalized per adsorption site basis, calculated by averaging over six equivalent sites to mitigate the influence of structural distortions from single-site adsorption. The Gibbs free energy ΔG was computed using eqn (2),

ΔG = ΔE + ΔZPE − TΔS + k_BT ln(10)pH, (2)

where ΔE is the change in total energy, ΔZPE is the change in zero-point energy, and TΔS is the product of temperature (298.15 K) and change in entropy over the reaction. The Gibbs free energy values (G) of the thermodynamic states were corrected for the pH 14 environment by adding k_BT ln(10)pH, where k_B is the Boltzmann constant. Additionally, dielectric constant correction was applied to the systems with the adsorbate to consider the implicit water environment to simulate the aqueous conditions using VASPsol.^22,23 Regarding the electron structure analysis, orbitals were analyzed through the partial density of states (PDOS), and the charge transfer phenomena were examined using the charge density difference plot.

Results and discussion

Model systems

We constructed five model systems (Fig. 1) to study the effects of ligand field and surface strain on the HER catalytic activity by modifying both the bulk and nanoparticle structures. The model systems consisted of two bulk surfaces of the pure Pt(111) surface and Pt/W(110) surface, consisting of a monolayer Pt on the W(110) slab. Additionally, we set up three nanoparticle systems of different sizes and components: pure Pt or W@Pt core–shell configurations. Two differently sized nanoparticles consisting of 55 and 147 atoms were used for the pure Pt system.

Fig. 1 Model systems of Pt(111), Pt/W(110), Pt₅₅, Pt₁₄₇, and W@Pt. Pt and W atoms are represented by yellow and blue solid spheres, respectively.

The active sites for the adsorption of each intermediate were determined using DFT calculations, as illustrated in Fig. S1.† The thermodynamically stable structure of each system was determined using DFT calculations. For the bulk Pt/W surface, we identified that the (110) surface of BCC W (Pt/W(110) surface) was the most stable.²⁴ The structures of Pt₅₅ and W@Pt were optimized by comparing the calculated formation and excess energies of similarly sized icosahedron, decahedron, and cuboctahedron structures (Table S2†). Additionally, we calculated energies for BCC-based W@Pt nanoclusters constructed using the Wulff construction method²⁵ to compare the results with the BCC Pt/W(110) surface. Our DFT calculations indicated that icosahedra were the most favorable shapes for both nanoparticles. This is consistent with the fact that the icosahedron exposes only the most stable (111) surface of the FCC crystal structure and that the outermost Pt shell plays a more significant role than the inner W of the BCC structure. The majority of atoms are Pt because the fraction of surface sites is much greater than the inside of the nanoparticles (42 out of 55 in Pt₅₅ and the W@Pt icosahedron, cuboctahedron, and decahedron and 44 out of 59 in the W@Pt BCC-based cluster).²⁶ Based on these results, we also calculated Pt₁₄₇ of an icosahedron nanoparticle. All the properties of the bulk and nanoparticles were compared to those of a bulk Pt(111) surface, which is the reference model.

HER activity of a pure Pt bulk and nanoparticles

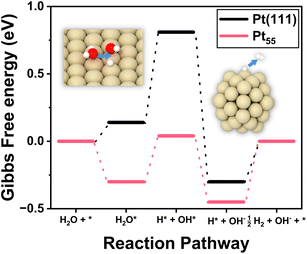
Nanoparticles are the central materials for various electrocatalysts; however, the identification of their ideal structures and compositions for target catalysis is challenging. For electrocatalysis, the conventional Sabatier principle,²⁷ which allows the prediction of catalytic activity using a rather simple descriptor with the scaling law, has been a guideline for searching for optimum materials. However, when catalysts are exposed to aqueous media with non-neutral pH, such as HER catalysts in alkaline or acidic solutions, the catalytic mechanisms are generally much more complicated than the gas-phase reaction under ultra-high vacuum conditions. The scaling law for the adsorption energies of intermediates often does not work, especially in nanoclusters.^28,29 The facets of nanoparticles, even those composed of a single component, consist of highly heterogeneous sites.³⁰ Thus, a comprehensive understanding of the guiding principles for electrocatalytic activity in reactive media is crucial, yet remains a significant challenge for both experiments and computations.

Fig. 2 illustrates the Gibbs free energy diagram calculated for HER catalysis on the Pt₅₅ icosahedral nanoparticles of approximately 1 nm diameter and on the Pt(111) surface. This indicates that there is a strikingly high activation barrier for the dissociation of H₂O molecular bonds into H*–OH* on the Pt(111) surface. This is because the Pt(111) surface adsorbs OH too weakly to cleave the chemical bonds of H₂O. However, it shows that the nanoparticles of Pt₅₅ and Pt₁₄₇ attract all intermediates significantly more strongly (Table S3†) than the Pt(111) surface, as reported previously.^28,31 Interestingly, the RDS of the bulk Pt(111) surface, H₂O bond dissociation, shifted to H₂ adsorbate desorption in Pt₅₅ nanoparticles. The free energy diagram clearly demonstrates that the activation energy for the H₂O dissociation on the bulk Pt(111) surface is at least 0.67 eV (∼65 kJ mol⁻¹). In the Pt₅₅ nanoparticle, the RDS activation energy is about 50 kJ mol⁻¹. This scenario is almost the same as that for the larger Pt₁₄₇ nanoparticles.

Fig. 2 Gibbs free energy diagrams of alkaline HER on the Pt(111) surface and Pt₅₅ nanoparticles. It shows a completely different rate determining step: H₂O bond dissociation into H*–OH* on the bulk Pt(111) surface (left inset) and H₂ desorption on Pt₅₅ nanoparticles (right inset).

In summary, both Pt₅₅ and Pt₁₄₇ stabilize all intermediates of the HER excessively, rendering them incapable as active catalysts, and precise but unequal amounts of control of the intermediate adsorption energies for H₂O and H₂ adsorbates are required to enhance the HER activity in alkaline media.

To control the adsorption energy of individual intermediates, we investigated the surface strain and ligand field effects.³² We achieved it by purposely designing heterogeneous model systems for the bulk Pt/W(110) surface and W@Pt nanoparticles. Both models have larger size element W (1.56 Å, Pt for 1.53 Å)³³ to create tensile strain and different work functions to induce charge transfer. In accordance with conventional theory, it is expected that tensile strain should upshift the d-band center energy of Pt, thereby increasing the binding energy of the intermediates. However, the Fermi energy of W (11.56 eV) is higher than that of Pt (11.32 eV), which facilitates the donation of its electron charge to Pt in the shell since the Fermi energy should be equal under the equilibrium conditions. Our electronic structure calculations demonstrated that the transferred electrons from W filled up the antibonding state of the Pt d-orbital and shifted the PDOS downwards. Thus, charge transfer weakens the binding strength of the adsorbates on the W@Pt surface. Likewise, these two factors are expected to influence the catalyst performance in the opposite manner, which implies that they can serve as effective tools for the precise control of the HER catalytic activity through a fine-tuning process to search for optimal conditions.

HER activity of the Pt/W(110) surface

The Pt/W(110) surface consists of a Pt monolayer on a BCC W(110) surface. Our DFT calculations indicated that it was the thermodynamically most stable structure among the FCC(111), BCC(110), and BCC(001) surfaces (Table S4†).^24,34,35 Owing to the atomic size difference between Pt and W, the Pt/W(110) surface was under tensile strain. Furthermore, the dissimilar electronic structures induce charge transfer from W to Pt. Both the tensile strain and charge transfer influence the adsorption energy of the adsorbates (H₂O, OH, and H) in HER catalysis. It is of interest to characterize which of these is predominant across the varying intermediates. This would lead to the opportunity to fine-tune HER catalysis, and the free energy landscape would be flat (Fig. 3) under optimal conditions.

Fig. 3 Change in bond lengths on the Pt/W(110) surface by intermediate adsorptions: (a) for H₂O, (b) for OH, and (c) for H. (d) Gibbs free energy diagrams of alkaline HER on bulk Pt/W(110) and Pt(111) surfaces.

Khorshidi et al. insisted that the adsorbate should cause eigenstress either in the outward or inward direction by studying CH₂ adsorption on a Cu(110) surface.³⁶ When CH₂ adsorbs on the bridge site, the Cu atoms adjacent to the adsorbate experience positive eigenstress, whereas the four-fold hollow site-adsorbed CH₂ exerts negative eigenstress. Minimization of the potential energy of the system due to stress can be achieved by applying an additional external strain via the formation of a heterostructure similar to the Pt/W(110) surface. As the structure is stabilized, the binding energy is accordingly strengthened and vice versa.

We investigated the HER mechanism on the Pt/W(110) surface under tensile strain. As H₂O adsorbed on the Pt/W(110) surface, the surface Pt atoms were pushed outwards by the positive eigenstress. Additionally, the W substrate expanded the top Pt monolayer. Consequently, the positive eigenstress and the external strain were in the same direction and stabilized the potential energy of the structure, eventually leading to enhanced H₂O adsorption strength. We found that this rationale can explain the trends of the adsorption energies with varying adsorbates on the active sites, even when the strains are in the same direction. The HER intermediates in alkaline media, H₂O, OH, and H, are adsorbed at the atop, long bridge-like hollow sites and atop the Pt surface, respectively. The adsorption energies (Table 1) well agree with the previous report.²⁴ Both the H₂O and OH molecules favor adsorption on the Pt/W(110) surface more than on the Pt(111) surface, and it is notable that OH exhibits a stronger preference for the Pt/W(110) surface than for the Pt(111) surface, whereas the binding strength of H is weaker on the Pt/W(110) surface than on the Pt(111) surface (Table 1).

Table 1 Calculated adsorption energies of alkaline HER intermediates on the bulk Pt(111) and Pt/W(110) surfaces

	Pt(111)	Pt/W(110)
H2O*	−0.46 eV	−0.48 eV
OH*	0.85 eV	0.56 eV
H*	−0.53 eV	−0.28 eV
H*OH*	0.31 eV	0.03 eV

---

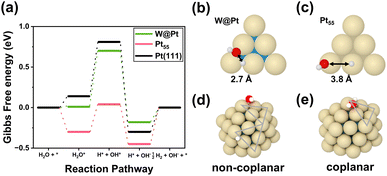
We monitored changes in surface Pt–Pt bond length during adsorption, as shown in Fig. 3. As H₂O molecule adsorbs (Fig. 3a), the surface strain is activated by the eigenstress into only one of the directions (+0.20 Å) to slightly stabilize the H₂O*–Pt/W(110) surface, thus representing a similar adsorption energy to the H₂O*–Pt(111) surface. This implies that the two contradictory factors, tensile strain and charge transfer from W to Pt, offset each other for the H₂O adsorption. In contrast, the bond lengths are significantly elongated (+0.35 Å and +0.25 Å) in the two orthogonal directions of the plane during OH adsorption at the long bridge-like hollow site, as shown in Fig. 3b. An extensively increased adsorption energy by 0.29 eV was ascribed to the fact that the local eigenstress in the positive direction was relieved by the tensile strain on the Pt/W(110) surface. By contrast, the H atom adsorbs on the atop site (Fig. 3c) without evident changes in the bond lengths, indicating that atop is less affected by the strain effect³⁷ and the ligand effect mainly governs the binding behavior. Interestingly, the interplay of these two factors improved the overall HER activity, as shown in Fig. 3d. The adsorption energy calculations on the fixed Pt/W(110) surface upon adsorption of the intermediates are provided in Table S5 and Fig. S2.† The comparison enables us to decouple the effect of adsorbate-induced eigenstress. For H₂O and OH adsorbates, where strain relieves the stress, the fixed surface inhibits the adsorbate-induced change and binding interaction decreases. In the case of the H atom, no difference in adsorption energy between the fixed and relaxed surfaces upon adsorption is observed. The free energy diagram for the HER on the Pt/W(110) surface demonstrated a flatter landscape than that on the Pt(111) surface. It is clear that the two energy barriers of the Pt/W(110) surface for H₂O bond dissociation into H*–OH* and H₂* desorption significantly decreased, resulting in higher HER activity.

In short, the heterogeneous atomic layer in Pt/W(110) beneficially modified the intermediate adsorption characteristics of the Pt(111) surface for HER catalysis: stronger adsorption for OH, weaker adsorption of H, and a marginal change for H₂O. Consequently, these are characterized by a higher HER activity in the free energy diagram.

HER activity of W@Pt nanoparticles

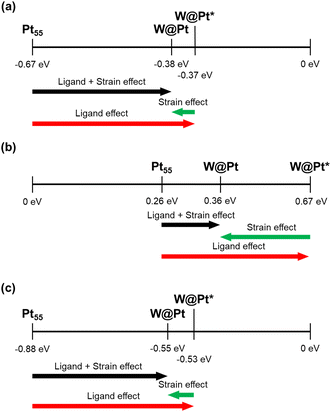
We calculated the HER mechanisms in the W@Pt nanoparticles to determine whether the two factors interact for high HER activity as on the bulk Pt/W(110) surface. DFT calculations indicated that an average bond length over different sites in W@Pt nanoparticle changes only slightly from that of Pt₅₅: edge–edge (+1.11%) and edge–vertex (−1.05%) (Fig. 4a). The Pt–Pt bond lengths in Pt₅₅ featured two distinct peaks: a shorter one for the edge–vertex and a longer one for the edge–edge sites (Fig. 4b). In contrast, the two bimodal peaks were somewhat obscured in the W@Pt nanoparticles, merging into a smooth peak. This is fairly counterintuitive considering that larger W atoms occupy the inner shells of the W@Pt nanoparticles. We ascribed it to the fact that the attractive interaction of Pt–W atoms was stronger in the W@Pt nanoparticles than that of Pt–Pt, which significantly suppressed the tensile strain in the Pt shell. The stronger core–shell binding interaction in W@Pt is shown by the crystal orbital Hamilton population (COHP) in Fig. 4c, Pt–Pt in Pt₅₅ and W–Pt in W@Pt nanoparticles. This also indicates that the strain effect is marginally influential on the HER catalytic activity, which is consistent with the PDOS and charge density difference plot (Fig. 6b–h).

Fig. 4 Bond lengths of Pt–Pt atoms on the surfaces of Pt₅₅ and W@Pt nanoparticles in (a); the grey is for edge–vertex and black for edge–edge atoms. In (b) the bond length distribution in W@Pt and Pt₅₅ nanoparticles is shown and (c) illustrates crystal orbital Hamilton populations (COHP) analysis between the core and shell atoms (Pt–Pt for Pt₅₅ and W–Pt for W@Pt) and the negative values of COHP (–COHP) are on the left and integrated (–ICOHP) on the right.

We decoupled the strain effect from the ligand field effect by constructing W@Pt nanoparticles with the same interatomic bond lengths as Pt₅₅ (W@Pt*). Therefore, the difference in the adsorption energies between the W@Pt and W@Pt* nanoparticles should arise only due to the change in the bond length. However, the d-band center energy shift from Pt₅₅ to W@Pt* is solely caused by the ligand effect. Based on the collective effects of the ligand field theory and surface strain, the effect of interatomic distance change seems smaller for all adsorbates, supporting the aforementioned analysis (Fig. 5). The ligand effect estimated using the amount of charge transfer from W to Pt and the degree of Pt antibonding orbital filling, eventually, is more effective in changing the binding strengths of the adsorbates.

Fig. 5 Net change in adsorption energy, a cumulative result of ligand and strain effects for each intermediate adsorbate, (a) H, (b) OH, and (c) H₂O. W@Pt* denotes the unstrained surface with its geometry restricted to the coordinates of the relaxed Pt₅₅ system to decouple the ligand effect and strain effect.

Our DFT calculations indicate that both H₂O and OH molecules favor the vertices of the Pt₅₅ and W@Pt nanoparticles for chemisorption (Fig. 6a). The component analysis of d-orbitals in the PDOS for the Pt atoms in the vertices of W@Pt (Fig. 6b–g) reveals a downshift of d-band center energies compared to that of Pt₅₅. Three of the five d-orbital components which include the z-direction components (d_z², d_xy, and d_yz) showed the most significant changes in both the center energy and electron density near the Fermi energy. This implies that the nature of the atomic interactions between the core and shell (vertical direction, i.e., the z-component) substantially influenced the PDOS shift and binding energy. The charge density difference plot in Fig. 6h depicts significant charge transfer from W to Pt. In summary, in the W@Pt nanoparticles, the charge transfer from W to Pt predominantly influences the HER catalytic activity over the surface strain in the outermost shell.

Fig. 6 Vertex Pt atom marked in (a). (b) Total d-orbital and the d-orbital component ((c) d_xy, (d) d_x²–d_y², (e) d_z², (f) d_xz and (g) d_yz) partial density of states (PDOS) analyses for the outermost shell Pt atoms located at vertex sites of Pt₅₅ and W@Pt nanoparticles. The charge density difference plot for the W@Pt was in (h) with an isosurface level of 0.01 e Å⁻³.

The Gibbs free energy diagram along the entire HER catalytic pathway on W@Pt unveils several additional insights (Fig. 7a). The adsorption strengths of all intermediates, H₂O, OH, H, and H–OH pairs, became weaker on W@Pt than on Pt₅₅ (Table 2), resulting in an HER activity similar to that of the bulk Pt(111) surface. While the high activation energy problem for H₂ desorption in Pt₅₅ was effectively resolved in the W@Pt nanoparticle by the ligand effect, the RDS was still the same as that of the bulk Pt surface (H₂O bond dissociation). Notably, the adsorption of the H–OH pair is considerably weak. This was attributed to the differences in the adsorption sites of the Pt₅₅ and W@Pt nanoparticles. In the W@Pt nanoparticles, both H and OH are adsorbed at nearby bridge sites in the edges (Fig. 7b), whereas H is adsorbed on the atop site of the edge and OH on the atop site of the vertex (Fig. 7c) in Pt₅₅. Closer adsorption sites allow the easier formation of hydrogen bonds by H–OH, which in turn weakens the binding between the adsorbates and the catalyst surface. Stronger interactions between the H and OH pairs adsorbed on W@Pt were confirmed by the adsorption energies. When H and OH were placed on different facets at a wider distance (Fig. 7d) while maintaining the edge-bridge adsorption sites for both H and OH just as the coplanar adsorption (Fig. 7e), the binding strength with the catalyst surface was reinforced. However, the corresponding configuration does not occur in the HER catalytic pathway, because the closer adsorption sites of the pair of molecules within the same plane are more energetically feasible.

Fig. 7 (a) Gibbs free energy diagrams for the alkaline HER on the W@Pt and Pt₅₅ nanoparticles and the bulk Pt(111) surface. The H*–OH* pair adsorption sites were marked in (b) for W@Pt and Pt₅₅ in (c). Non-coplanar (d) and coplanar (e) adsorption of the H*–OH* pair on the bridge sites in the edges of W@Pt nanoparticles.

Table 2 Calculated adsorption energies of HER intermediates in Pt₅₅ and W@Pt nanoparticles

	Pt55	W@Pt
H2O*	−0.88 eV	−0.55 eV
OH*	0.26 eV	0.36 eV
H*	−0.67 eV	−0.38 eV
H*OH*	−0.40 eV	0.20 eV

---

In summary, the surface Pt–Pt bond lengths did not change tangibly in W@Pt, contradicting the conventional idea that the surface strain should play a key role in controlling the adsorption energy. Instead, the ligand effect manifested by charge transfer from W to Pt drives the filling of antibonding orbitals in the Pt d-orbitals, weakening the binding strength of the adsorbates. This means that simply making smaller nanoparticles of either a pure or core–shell alloy does not enhance the HER activity since the adsorption energy is controlled all uniformly, not specifically for the key intermediate in the RDS.

Conclusion

Through first-principles DFT calculations, we identified that the pseudo-binary Pt/W(110) surface is a more active catalyst for the HER in alkaline media than pure bulk Pt and W@Pt core–shell nanoparticles. The Pt/W(110) surface demonstrates a remarkably low activation barrier for H₂O bond dissociation, producing a proton intermediate in an alkaline medium. We elucidated the underlying mechanism of the dual-mode interplay in activity, including surface tensile strain from atomic size differences and charge transfer between Pt and W due to their unequal work functions. The two factors influenced uniformly for W@Pt nanoparticles, stabilizing all intermediates and resulting in activity similar to that of the bulk Pt(111) surface. It is also noteworthy that the RDS in Pt nanoparticles is not H₂O bond dissociation, but H₂ molecule desorption in the final step of the HER. The mechanism on low activity of the W@Pt nanoparticles arises from the strong interaction between Pt atoms in the shell and W atoms in the core regions, which inhibits structural deformation. This interaction, along with the ligand effect, shifts the adsorbate binding properties, reducing HER efficiency. These two factors were optimized on the Pt/W(110) surface, leading to high catalytic activity for the HER and tuning of the adsorption energy of each intermediate. The framework of this study opens new opportunities for developing highly active catalysts for electrochemical reactions in alkaline media.

Data availability

The data containing additional calculation results for this article have been included in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the National Research Foundation of Korea (2022M3H4A04096482) funded by the Ministry of Science, the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (20214000000090, Fostering human resources training in advanced hydrogen energy industry), and the Technology Innovation Program Development Program (“20022479”, “Development of deuterium oxide localization and deuterium benzene synthesis technology to improve OLED lifetime by 25%”) funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea).

References

1. K. Mazloomi and C. Gomes, Renewable Sustainable Energy Rev., 2012, 16, 3024–3033.
2. Z. Chen, X. Duan, W. Wei, S. Wang and B.-J. Ni, J. Mater. Chem. A, 2019, 7, 14971–15005.
3. M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901–4934.
4. S. A. Grigoriev, V. N. Fateev, D. G. Bessarabov and P. Millet, Int. J. Hydrogen Energy, 2020, 45, 26036–26058.
5. C. C. L. McCrory, S. Jung, I. M. Ferrer, S. M. Chatman, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2015, 137, 4347–4357.
6. R.-T. Liu, Z.-L. Xu, F.-M. Li, F.-Y. Chen, J.-Y. Yu, Y. Yan, Y. Chen and B. Y. Xia, Chem. Soc. Rev., 2023, 52, 5652–5683.
7. J. Guo, J. Liu, X. Zhang, X. Guan, M. Zeng, J. Shen, J. Zou, Q. Chen, T. Wang and D. Qian, J. Mater. Chem. A, 2022, 10, 13727–13734.
8. T. S. Rodrigues, A. G. M. da Silva and P. H. C. Camargo, J. Mater. Chem. A, 2019, 7, 5857–5874.
9. J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943.
10. S. Liu and S. Huang, Int. J. Hydrogen Energy, 2018, 43, 15225–15233.
11. Y. Li, W. Pei, J. He, K. Liu, W. Qi, X. Gao, S. Zhou, H. Xie, K. Yin, Y. Gao, J. He, J. Zhao, J. Hu, T.-S. Chan, Z. Li, G. Zhang and M. Liu, ACS Catal., 2019, 9, 10870–10875.
12. W. Lee, H. Yun, Y. Kim, S. S. Jeon, H. T. Chung, B. Han and H. Lee, ACS Catal., 2023, 13, 11589–11597.
13. X. Zhang, K.-A. Min, W. Zheng, J. Hwang, B. Han and L. Y. S. Lee, Appl. Catal., B, 2020, 273, 118927.
14. L. Zhang and G. Henkelman, ACS Catal., 2015, 5, 655–660.
15. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
16. P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
17. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
18. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
19. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
20. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
21. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
22. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151(23), 234101.
23. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140(8), 084106.
24. J.-H. Meng, C. A. Menning, M. B. Zellner and J. G. Chen, Surf. Sci., 2010, 604, 1845–1853.
25. G. Wulff, Z. Kristallogr. Cryst. Mater., 1901, 34, 449–530.
26. J.-R. Huo, X.-X. Wang, L. Li, H.-X. Cheng, Y.-J. Su and P. Qian, Sci. Rep., 2016, 6, 35464.
27. J. Tymoczko, F. Calle-Vallejo, W. Schuhmann and A. S. Bandarenka, Nat. Commun., 2016, 7, 10990.
28. J. L. C. Fajín, A. Bruix, M. N. D. S. Cordeiro, J. R. B. Gomes and F. Illas, J. Chem. Phys., 2012, 137(3), 034701.
29. B. C. Han, C. R. Miranda and G. Ceder, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 075410.
30. B. H. Kim, J. Heo, S. Kim, C. F. Reboul, H. Chun, D. Kang, H. Bae, H. Hyun, J. Lim, H. Lee, B. Han, T. Hyeon, A. P. Alivisatos, P. Ercius, H. Elmlund and J. Park, Science, 2020, 368, 60–67.
31. J. Marchetti, E. Gonzalez, P. Jasen, G. Brizuela and A. Juan, Surf. Rev. Lett., 2008, 15, 319–327.
32. H. Li, K. Shin and G. Henkelman, J. Chem. Phys., 2018, 149(17), 174705.
33. J. M. Wills and W. A. Harrison, Phys. Rev. B:Condens. Matter Mater. Phys., 1983, 28, 4363–4373.
34. T. E. Madey, K.-J. Song, C.-Z. Dong and R. A. Demmin, Surf. Sci., 1991, 247, 175–187.
35. M. B. Zellner, A. M. Goda, O. Skoplyak, M. A. Barteau and J. G. Chen, Surf. Sci., 2005, 583, 281–296.
36. A. Khorshidi, J. Violet, J. Hashemi and A. A. Peterson, Nat. Catal., 2018, 1, 263–268.
37. H. Li, K. Shin and G. Henkelman, J. Chem. Phys., 2018, 149, 174705.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08250h

---