Open Access Article
Open Access ArticlePtn-Mn(II)Nx and Ptn-Mn(III)Nx are both winning combinations for the durability of these hybrid catalysts in PEM fuel cells: a deep insight into synergism between Pt clusters and MnNx/C sites†
Vassili P.
Glibin
 *a,
Jean-Pol
Dodelet
*a,
Jean-Pol
Dodelet
 *b and
Gaixia
Zhang
*b and
Gaixia
Zhang
 *c
*c
aDepartment of Chemical and Biochemical Engineering, University of Western Ontario, London, Ontario N6A 5B9, Canada. E-mail: vassili.glibin@gmail.com
bInstitut National de la Recherche Scientifique (INRS), Centre Énergie Matériaux Télécommunications, Varennes, Québec J3X1P7, Canada. E-mail: jean-pol.dodelet@inrs.ca
cDepartment of Electrical Engineering, École de Technologie Supérieure (ÉTS), Montréal, Québec H3C 1K3, Canada. E-mail: gaixia.zhang@etsmtl.ca
First published on 24th June 2025
Abstract
In this work, we investigated the influence of a carbon substrate (graphene), doped or undoped, on the adsorption energy, and thus the stability, of Pt(n)-clusters/nanoparticles (NPs) grown on it. For substrate doping, we considered N-doping (graphitic or pyridinic), and carbon doping with MnN(2+2)/C or MnN(4+2)/C sites in the immediate vicinity of Pt(n)-clusters/NPs. These non-noble sites, containing Mn(II) or Mn(III), are also capable of oxygen reduction in fuel cells, similar to Pt(n) nanoparticles. The Pt(n)-graphene interaction is initiated by a Pt atom occupying a single carbon vacancy, forming three Pt–C bonds. The entire Pt(n)-cluster/NP is then built upon this atom. A more negative adsorption energy corresponds to stronger adhesion and enhanced cluster stability. This effect is particularly pronounced when the graphene substrate is doped with Mn(II or III)N(4+2)/C or Mn(II or III)N(2+2)/C sites. We further examined whether a Pt(n)-cluster/NP adjacent to a MnNx/C site could stabilize the latter against demetallation in acidic PEM fuel cell environments. Our findings confirm this hypothesis: Pt(n) effectively stabilizes MnNx/C against demetallation. This effect is especially significant for Mn(II)N(4+2)/C and Mn(II)N(2+2)/C sites, previously shown to undergo spontaneous Mn demetallation. In the presence of Pt(n), the formerly spontaneous demetallation becomes a thermodynamic equilibrium (in a closed thermodynamic environment), improving MnNx/C stability. Despite this stabilization, MnNx sites remain less durable than platinum under PEM fuel cell cathode conditions. This led us to examine what happens to Pt(n) adhesion after Mn demetallation. Our calculations show that the Pt–C bonding energy is minimally affected by the demetallated MnNx sites. Thus, Pt(n) clusters should remain stably anchored even after Mn loss. Finally, beyond these stability insights, we reviewed literature regarding the catalytic performance of Pt(n)-MnNx/C hybrid systems, highlighting how they combine the high activity of Pt with the complementary functionalities of non-noble molecular sites. These findings provide theoretical guidance for designing more robust and efficient hybrid electrocatalysts for fuel cell applications.
1. Introduction
Pt and Pt-based catalysts are considered the best catalysts for the oxygen reduction reaction (ORR) in polymer electrolyte fuel cells (PEMFC). The US Department of Energy (DOE) has set targets for their use. However, given the current success of batteries in LDVs (Light Duty Vehicles), the DOE's new targets now aim to use PEMFCs for MDVs (Medium Duty Vehicles) and especially HDVs (High Duty Vehicles) which, because of the power they require, are less prone to the use of batteries as a source of electrical power.1 Whereas the latest DOE targets for LDVs aimed to reduce the total precious metal loading below 0.125 mgPt cm−2 while maintaining a fuel cell life of 5000 hours, the new HDV targets call for a total precious metal loading of 0.3 mgPt cm−2 while extending the fuel cell life for 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hours. More specifically, at end-of-life (EOL), the PEMFC target that supplies an HDV with electrical power must still produce 275 kWe at 0.7 V with 2.5 atm air, 90 °C coolant exit temperature, and 1.5 cathode stoichiometry. This is a significant demand on platinum, a catalyst that, while effective, faces challenges that can impact its activity and durability.
000 hours. More specifically, at end-of-life (EOL), the PEMFC target that supplies an HDV with electrical power must still produce 275 kWe at 0.7 V with 2.5 atm air, 90 °C coolant exit temperature, and 1.5 cathode stoichiometry. This is a significant demand on platinum, a catalyst that, while effective, faces challenges that can impact its activity and durability.
As far as the catalytic activity of platinum at the cathode of a PEMFC is concerned, about 0.2 V of overpotential must be lost (out of about 1.2 V theoretically available per MEA in open circuit) before a net oxygen reduction current appears.2,3 To explain this, Nørskov et al.2 suggested in 2004 that the ∼0.2 V ORR overpotential could be linked to the strong bonding at high potential of O2 or OH to the Pt surface, rendering the transfer of H+ and electrons impossible. However, the stability of these “poisoning O2 or OH species” decreases by lowering the potential, enabling then the ORR reaction to proceed. The previous explanation of the overpotential has recently been challenged by Z. Wu et al.3 who rather introduced the concept of mixed potential arising at high potential from the oxidation reaction of Pt occurring at the same time as the ORR. In this view, the bottleneck of reducing the overpotential of ORR is obtained by inhibiting Pt oxidation. This explanation was experimentally confirmed by substituting H2O with D2O in acid solution, which resulted in the decrease of Pt oxidation at high potential and an increase, at the same time, in the ORR kinetics.
Regarding the durability of platinum, the metal tends to dissolve when subjected to a potential >0.6 V, affecting the integrity of its electrochemically active surface area (ESCA).4–7 Dissolved platinum will then deposit in the membrane8 and/or redeposit on existing Pt nanoparticles, which may eventually coalesce (Oswald ripening).9,10 Moreover, there are minimum size limits for Pt nanoparticles which means that they dissolve rapidly if they are too small (<0.3 nm in diameter).4,11 Reducing Pt particle size cannot therefore be relied upon to durably increase the ESCA and hence the mass activity of the catalyst. Another way of increasing the mass activity of Pt-based catalysts is to alloy Pt with a non-noble metal such as cobalt, for instance.12–14 However, unless the resulting alloy is an intermetallic or presents a Pt skin that somewhat alleviates the dissolution problems,15–17 the non-noble metal always ends up leaching from the Pt catalyst during the 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hours of durability required for high-duty vehicles.18
000 hours of durability required for high-duty vehicles.18
Again, in the spirit of improving the durability of Pt-based catalysts, a great deal of work has also been carried out on the carbon used to support the metal catalytic sites, to enhance their mutual interaction and thus improve the retention of Pt nanoparticles on the support. Numerous nitrogen-doped carbon supports have been studied for this purpose.19–29 Not only are the catalysts obtained on nitrogen-doped carbon supports more durable than their counterparts on undoped carbon supports, but these experiments also reveal that these more durable catalysts are also more active. Another step towards improved durability has been taken, this time using non-noble catalysts to support the Pt nanoparticles.30–48 This was a logical step to take after doping the carbon with nitrogen, since the sites of the non-noble catalysts are of MeNx-type and embedded in the graphene planes. Here Me is a non-noble metal ion of Fe, Co, Mn, etc. These sites, or more specifically a defect close to each of these sites, can serve as an anchoring point for the Pt nanoparticle. As in the case of nitrogen doping of the carbon support, not only do the non-noble sites improve the retention of the Pt nanoparticles on the support (as shown by the Accelerated Stability Tests; AST), but the resulting interactions, associated with a synergy between Pt nanoparticles and the support, also improve the mass activity of the Pt catalysts.
Recently, using the well-known thermodynamic methods (described in Section 4 in this work), we analyzed the stability towards demetallation of MnNx/C sites in the strongly acidic environment of PEM fuel cells.49 We found that demetallation is a thermodynamically spontaneous reaction for Mn(II)Nx/C, but is equilibrated for X-Mn(III)Nx/C (with X = O2). Although, the oxidation state of Mn in electrocatalysts, determined from XPS (X-ray photoelectron spectroscopy)50 or XANES (X-ray adsorption near edge structure)51 spectra, was always found to be equal to +2, it was shown52 that Mn(II)N4/C electrocatalysts acquire the ability to reduce molecular oxygen only after adsorption of O2 and the transition of Mn2+ to the trivalent state: Mn(III)N4⋯O2. However, as it was suggested in ref. 49, due to the high electrode potential (∼0.95 V vs. RHE) for the pair Mn2+/Mn3+, the thermodynamic stabilization of the Mn(III)N4/C site in contact with O2 or air is limited. Therefore, the Mn species that will prevail in the above XPS or EXAFS spectra are expected to be in the Mn2+ oxidation state.
In this work, studying the association of Pt nanoparticles with nearby Mn(II)Nx/C sites, it will mainly be shown that a Mn(II)Nx/C site associated with a Pt particle enhances the adhesion of this particle to the graphene support. We also find that, conversely, the presence of a Pt particle associated with a Mn(II)Nx/C site stabilizes this Mn(II)Nx/C site in such a way that its demetallation in the acid medium of PEM fuel cells is no longer spontaneous, but rather subject to thermodynamic equilibrium. The combination of Mn(II)Nx/C sites and Pt nanoparticles thus becomes a winning combination for these hybrid catalysts.
The work presented here is divided into three parts. In the first part (Sections 2 and 3), we investigated the influence of a carbon substrate (graphene), doped or undoped, on the adsorption energy (and therefore the stability) of Pt(n)-clusters/nanoparticles (NPs) that have been grown on this substrate. For the doping of the carbon substrate, we considered nitrogen doping, where this atom is substituted for a carbon atom. The nitrogen dopant is either graphitic or pyridinic. We have also considered carbon doping with MnN(2+2)/C or MnN(4+2)/C sites in the immediate vicinity of Pt(n)-clusters/NPs. These non-noble sites have the potential (like Pt(n)) to reduce oxygen in fuel cells, and their manganese ion is either Mn(II) or Mn(III). In the second part of this work (Section 4), we then considered the influence of Pt(n) adsorbed on the carbon substrate on the chemical stability, in the acidic fuel cell environment, of the non-noble MnNx/C sites in the immediate vicinity of the Pt(n)-clusters/NPs adsorbed on graphene. Finaly, after the stability considerations of the first and second parts of this work, we also devoted in the third part (Section 5) a section to reviewing the literature concerning the advantages, for the same Pt(n)-MnNx/C hybrid catalysts, but this time in terms of catalytic activity.
2. Computations and results obtained for the binding (adsorption) energy of Pt clusters and Pt nanoparticles at a single carbon vacancy of graphene and N-doped graphene
In this section, we will first determine the cohesion energy and the electronegativity of isolated Pt clusters and isolated Pt nanoparticles before establishing contact between these Pt clusters/nanoparticles with a single carbon vacancy in a graphene plane. This will be followed by N-doping (either graphitic or pyridinic N doping) in the graphene plane and determining the effect of these dopants onto the adsorption (binding) energy of Pt clusters/nanoparticles.2.1. Determination of the size, the mean coordination number, the cohesion energy, the ionization potential, the electron affinity and the electronegativity of isolated Pt clusters/nanoparticles
An estimation of the size (outer radius R) of Pt metal clusters/nanoparticles was carried out using Section S1, ESI eqn (S1)–(S4).† Then, the mean coordination number, , of Pt atoms in these Pt metal clusters/nanoparticles was obtained using ESI eqn (S5) and (S6).† The cohesion or binding energy, BEPtn, per atom of Pt, the values of ionization potential, IPPtn, and electron affinity, EAPtn, for several sizes of platinum clusters and platinum nanoparticles, were assessed using the formulas presented in Section S2, eqn (S7)–(S17).† The eqn (S16) and (S17)† were used for the calculations of Pt clusters/nanoparticles' ionization potentials and electron affinities. Eqn (S18)† was applied to determine Pt–Pt bond energy values in clusters and nanoparticles of platinum. The results of these calculations are summarized in Table 1. As can be seen from Table 1, the assessed electronegativities of Pt clusters and nanoparticles, χPtn, increase slightly with increasing the number of atoms in Pt clusters/nanoparticles. The mean value of the electronegativity (1.69 eV1/2) is very close in magnitude to the electronegativity of Pt atom, 1.72 eV1/2, in Allen's scale of electronegativity (usually expressed in eV).53 Note that the conversion of χMulliken, (the electronegativity expressed in Mulliken's units, eV) into χPauling, (the electronegativity expressed in Pauling's units, eV1/2), was carried out using Fig. 8 from ref. 54. Considering
, of Pt atoms in these Pt metal clusters/nanoparticles was obtained using ESI eqn (S5) and (S6).† The cohesion or binding energy, BEPtn, per atom of Pt, the values of ionization potential, IPPtn, and electron affinity, EAPtn, for several sizes of platinum clusters and platinum nanoparticles, were assessed using the formulas presented in Section S2, eqn (S7)–(S17).† The eqn (S16) and (S17)† were used for the calculations of Pt clusters/nanoparticles' ionization potentials and electron affinities. Eqn (S18)† was applied to determine Pt–Pt bond energy values in clusters and nanoparticles of platinum. The results of these calculations are summarized in Table 1. As can be seen from Table 1, the assessed electronegativities of Pt clusters and nanoparticles, χPtn, increase slightly with increasing the number of atoms in Pt clusters/nanoparticles. The mean value of the electronegativity (1.69 eV1/2) is very close in magnitude to the electronegativity of Pt atom, 1.72 eV1/2, in Allen's scale of electronegativity (usually expressed in eV).53 Note that the conversion of χMulliken, (the electronegativity expressed in Mulliken's units, eV) into χPauling, (the electronegativity expressed in Pauling's units, eV1/2), was carried out using Fig. 8 from ref. 54. Considering  , reported in the last column of Table 1, two particular regions can be distinguished: (i) the first one highlighted in bold and going from (Pt4 to Pt13 clusters) is a region where the values of Pt–Pt bond energy is practically constant, taking into account the incertitude of the calculations mainly caused by an approximate estimate of the mean coordination numbers; and (ii) the second, where a progressive decrease in binding energies is observed. In the first region, the mean value (1.64 eV) of data highlighted in bold, corresponds to the energy of an ordinary Pt–Pt bond. In the second region, the values of Pt–Pt bond energy are gradually approaching their limit that is the Pt–Pt bond energy in bulk platinum, which is equal (eqn (S18)†) to: 2 × 5.86/12 = 0.98 eV. The extent of the observed regions correlates well with the structural rearrangements in the clusters and nanoparticles of platinum, namely, at cluster size of approximately n = 19 (where a structural transition from triangular clusters to icosahedral ones occurs) and at cluster size of approximately n = 38 (where the structural transition to face-centered cubic-like clusters occurs).55
, reported in the last column of Table 1, two particular regions can be distinguished: (i) the first one highlighted in bold and going from (Pt4 to Pt13 clusters) is a region where the values of Pt–Pt bond energy is practically constant, taking into account the incertitude of the calculations mainly caused by an approximate estimate of the mean coordination numbers; and (ii) the second, where a progressive decrease in binding energies is observed. In the first region, the mean value (1.64 eV) of data highlighted in bold, corresponds to the energy of an ordinary Pt–Pt bond. In the second region, the values of Pt–Pt bond energy are gradually approaching their limit that is the Pt–Pt bond energy in bulk platinum, which is equal (eqn (S18)†) to: 2 × 5.86/12 = 0.98 eV. The extent of the observed regions correlates well with the structural rearrangements in the clusters and nanoparticles of platinum, namely, at cluster size of approximately n = 19 (where a structural transition from triangular clusters to icosahedral ones occurs) and at cluster size of approximately n = 38 (where the structural transition to face-centered cubic-like clusters occurs).55
 , ionization potential (IPPtn), electron affinity (EAPtn), electronegativity (χPtn), binding energy per atom of Pt (BEPtn), and Pt–Pt bond energy
, ionization potential (IPPtn), electron affinity (EAPtn), electronegativity (χPtn), binding energy per atom of Pt (BEPtn), and Pt–Pt bond energy 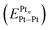 for several platinum clusters and platinum nanoparticles as a function of their size
for several platinum clusters and platinum nanoparticles as a function of their size
| Cluster/nanoparticle and its size/nm | IPPtn/eV eqn (S16) | EAPtn/eV eqn (S17) | χPtn/eV1/2 eqn (S9) | BEPtn/eV eqn (S14) | eqn (S18) | |
|---|---|---|---|---|---|---|
| a Approximately the mean value between data from ESI Table S1 and calculated using ESI eqn (S5). b ESI eqn (S5). c ESI eqn (S6). d ESI eqn (S1) and (S4). | ||||||
| Pt2 | 1 | 8.42 | 1.69 | 1.60 | 1.59 | 3.18 |
| Pt3 | 2 | 8.16 | 2.14 | 1.63 | 2.13 | 2.13 |
| Pt4 | 3 | 7.99 | 2.43 | 1.64 | 2.47 | 1.65 |
| Pt5 | 3.5b | 7.88 | 2.63 | 1.66 | 2.71 | 1.55 |
| Pt6 | 3.6b | 7.79 | 2.78 | 1.66 | 2.90 | 1.61 |
| Pt7 | 3.7b | 7.71 | 2.91 | 1.67 | 3.05 | 1.65 |
| Pt8 | 3.8b | 7.66 | 3.01 | 1.68 | 3.17 | 1.67 |
| Pt9 | 3.9b | 7.60 | 3.10 | 1.68 | 3.27 | 1.68 |
| Pt10/0.9d | 4.2a | 7.56 | 3.17 | 1.69 | 3.36 | 1.60 |
| Pt12/1.0d | 4.2b | 7.49 | 3.29 | 1.69 | 3.51 | 1.67 |
| Pt13/1.1d | 4.3b | 7.46 | 3.35 | 1.70 | 3.57 | 1.66 |
| Pt19/1.2d | 4.9b | 7.33 | 3.57 | 1.71 | 3.84 | 1.57 |
| Pt20/1.2d | 5.0b | 7.31 | 3.60 | 1.71 | 3.88 | 1.55 |
| Pt30/1.4d | 5.9b | 7.19 | 3.81 | 1.72 | 4.13 | 1.40 |
| Pt39/1.5d | 6.8c | 7.12 | 3.93 | 1.73 | 4.27 | 1.25 |
| Pt55/1.6d | 7.3c | 7.04 | 4.08 | 1.74 | 4.45 | 1.22 |
| Pt100/1.9d | 8.4c | 6.91 | 4.29 | 1.75 | 4.70 | 1.12 |
| Pt150/2.3d | 9.3c | 6.84 | 4.41 | 1.76 | 4.85 | 1.04 |
| 1.69 ± 0.08 (the mean value) | ||||||
2.2. Estimation of the adsorption (or binding) energy of a single Pt atom, of a small Pt-cluster and of a nanoparticle at a single graphene vacancy
According to ref. 56: (i) Pt atoms and small Pt clusters appear to be stabilized, and thus rendered immobile by interaction with defects within a graphene lattice and N-dopants, (ii) the specific Pt density obtained with the N-doped graphene samples varied among the locations on the graphene sheets, as a result of the local variations in defects in the graphene lattice, the N-dopant concentration and the N-dopant site distribution.The adsorption (binding) energy of Pt clusters (under standard thermodynamic conditions), as a measure of the adhesion strength, can be assessed by applying the Hess' law commonly used in thermochemistry, namely, as the difference between the formation energy of the complex Ptn/graphene and the energy of Ptn cluster's formation:
| Ead = Ef(Ptn⋯Gr) − Ef(Ptn) | (1) |
The formation energy of a Pt cluster is determined by multiplying its Pt–Pt bond energy (sixth column in Table 1) by the number of atoms in this cluster, assigning a minus sign to the result (because the process of a cluster/nanoparticle formation is accompanied by the release of this energy). The formation energy of a graphene/Ptn complex is calculated by applying the well-known additivity rule for determining standard enthalpies of formation of compounds (that is, more specifically, summing the values of Pt–C and Pt–Pt bonds energy in the complex), and also assigning a minus sign to the result.
A schematic illustration of the Pt2 cluster bound to a single vacancy in graphene is presented in Fig. 1.
 | ||
| Fig. 1 Schematic illustration of Pt2 cluster bound to a single vacancy in the graphene/graphitic surface. | ||
Quantum chemical calculations, carried out in ref. 57, showed that for a Pt atom at a single graphene vacancy, the adsorbate binds to the vacant site by forming three Pt–C bonds. The Pt atom is, however, located out of the graphene plane by about 1.03 Å.
Let us present the procedure to estimate the adsorption energy of small Pt clusters. At first, we started by determining the Pt–C bond energy, a value that was calculated using eqn (S21),† to be equal to 242.7 kJ mol−1 or 2.51 eV (1 eV = 96.485 kJ mol−1) in agreement with the calorimetric value58 of 245 kJ mol−1. Here, the following input data have been used: EPt–Pt= 1.64 eV (158.2 kJ mol−1) (Table 1, the mean value of data highlighted in bold), and χPtn= 1.69 eV1/2 from Table 1; EC–C = 357.3 kJ mol−1 from ref. 59 and χCm = 2.02 eV1/2 (Section S3 in ESI†). Further, by assuming that a single Pt atom forms three Pt–C bonds (Fig. 1), it is found that the adsorption energy, Ead, of a single Pt atom to a single graphene vacancy is equal to −7.53 eV, the value that is in a fairly good agreement with results from quantum chemical calculations (−7.10 eV (ref. 57) and −7.45 eV (ref. 60)). Then, considering the formation energy of −(2 × 1.59 = −3.18 eV) for a Pt2 cluster (Table 1), an Ead value of −(3 × 2.51 + 1 × 1.64 − 3.18) = −5.99 eV was obtained for a Pt2 cluster. Comparing this result with data of quantum chemical calculations of −5.36 (ref. 57) and −6.93 eV,60 one can see that our estimation is in line with the cited values. For Pt3 and Pt4, the values of Ead were found equal to (detail the calculation like above) = −6.06 and (detail the calculation like above) = −7.49 eV, respectively, in a fairly good agreement with data of ref. 60 (Table 2).
| Cluster, size/nm | Number of Pt–Pt bonds in the cluster | Formation energy of the Ptn cluster/eV | Formation energy of the graphene/Ptn complex/eV | Adsorption energy/eV | |
|---|---|---|---|---|---|
| This work | Literature data | ||||
| a The mean value of the adsorption energy for Pt4 to Pt13 is −7.53 ± 0.5 eV. b The clusters' size assessment is given in Section S1.1. | |||||
| Pt2 | 1 | −3.18 | −9.12 | −5.99 | −5.36 (ref. 57) |
| −6.93 (ref. 60) | |||||
| Pt3 | 3 | −6.39 | −12.45 | −6.06 | −4.82 (ref. 57) |
| −6.52 (ref. 60) | |||||
| Pt4 | 6 | −9.88 | −17.37 | −7.49a | −7.27 (ref. 60) |
| Pt7 | 13 | −21.35 | −28.85 | −7.50a | — |
| Pt9 | 18 | −29.43 | −37.05 | −7.62a | — |
| Pt12/1.0b | 26 | −42.12 | −50.17 | −8.05a | — |
| Pt13/1.1 | 28 | −46.41 | −53.45 | −7.04a | −7.29 (ref. 60) |
| −52.48 (ref. 60) | |||||
| −55.16 (ref. 61) | |||||
| Pt19/1.2 | 46 | −72.96 | −79.87 | −6.91 | — |
| Pt30/1.4 | 88 | −123.90 | −131.06 | −7.16 | — |
| Pt35/1.4 | 111 | −147.70 | −154.47 | −6.77 | — |
| Pt38/1.5 | 128 | −161.88 | −169.30 | −7.42 | — |
| Pt39/1.5 | 133 | −166.53 | −174.29 | −7.76 | — |
| Pt100/1.9 | 420 | −470.0 | −478.56 | −8.56 | — |
| Pt150/2.3 | 700 | −727.5 | −736.21 | −8.71 | — |
Considering now larger Pt clusters and Pt nanoparticles, it was assumed that the Pt atom at the vacant site (Fig. 1) anchors the remaining part of the cluster (not shown in Fig. 1) with the help of three Pt–Pt bonds, thus acquiring a coordination number equals to six (one of the typical coordination numbers of Pt in coordination compounds). Beginning from Pt19, in calculations, instead of the Pt–Pt ordinary bond energy value (1.64 eV), the reciprocal mean of 1.64 eV and Pt–Pt bond's energy from the last column of Table 1 was used. For the anchored clusters' residue, the corresponding value of Pt–Pt bond energy from Table 1 was used. This calculation scheme is justified by the following considerations.
In the coordination polyhedron, formed by Pt–Pt and Pt–C bonds, the more ionic Pt–C bonds that are in a trans position to Pt–Pt bonds, experience the so-called trans-effect (well-known in coordination chemistry).62 A consequence of this is an elongation of the more ionic Pt–C bonds (since the electronegativity of a carbon atom (Table 5) is greater than the electronegativity of a Pt atom) and, accordingly, a decrease in their energy. The opposite picture is observed for Pt–Pt-bonds, and these bonds, will be different in their properties from the Pt–Pt bonds in the rest of the cluster. Further, referring to the covalent-ionic resonance theory, Allen63 showed that the energy of a hypothetical bond between A and B atoms is a reciprocal mean of the energy of single homonuclear A–A and B–B bonds (in our case, the Pt atom of the coordination polyhedron plays the role of A and the Pt atoms in the rest of the cluster play the role of B). Thus, it becomes possible to apply the principle of the reciprocal mean for the estimation of the Pt–Pt bond energy in the polyhedron.
The number of Pt–Pt bonds in a cluster/nanoparticle was determined as the quotient of the cluster formation energy value divided by the Pt–Pt bond energy in the cluster (last column in Table 1). The calculation of the adsorption energy (using the data from Table 1) for a Pt30 cluster at a single vacancy graphene is reported in Section S2.5 of ESI† as a typical example.
The results of calculations for several clusters and nanoparticles of platinum in comparison with DFT data are presented in Table 2.
Some conclusions can be drawn from the values of adsorption energy given in Table 2. First, it should be noted that the proposed thermochemical method for estimating the energy of adsorption of clusters makes it possible to predict these values in a fairly good agreement with the data calculated by DFT, despite the large difference in adsorption energies sometimes obtained by DFT between two different works, as seen here for Pt2 and Pt3, for instance (last column of Table 2). Further, it can also be seen that, starting from Pt2 and up to Pt12, a gradual increase in the adsorption energy (from −5.99 to −8.05 eV) is observed. The next region, from Pt13 to Pt35, is characterized by a constant value of adsorption energy (−7.0 ± 0.15 eV), considering the incertitude in the calculations for these Pt clusters. Then, in the region from Pt38 to Pt150, a gradual increase of the adsorption energy (from −7.42 to −8.71 eV) is observed. We suppose that the existence of these regions of adsorption energy reflects the structural rearrangements of platinum clusters, already mentioned in Section 2.1.
2.3. Estimation of the adsorption (binding) energy of a single Pt atom, small Pt-clusters and Pt nanoparticles bound to a graphitic N-doped or to a pyridinic N-doped single vacancy at a graphene/graphitic substrate
The schematic representation in Fig. 2a illustrates the situation when a Pt2 cluster is bound to a single vacancy at a (substitutional or graphitic) N-doped graphene/graphitic substrate. Fig. 2b shows a possible situation occurring when a platinum atom (ion) of a Pt2 cluster in a single vacancy forms one donor–acceptor bond with a pyridinium atom and two bonds with carbon atoms of the graphene/graphitic substrate. This configuration is most likely due to the usually low surface concentration of nitrogen atoms. These structures can be formed as an initial stage in the deposition of platinum nanoparticles from aqueous solutions of platinum compounds using reducing agents. The oxidation state of a central platinum atom is usually equal to +2.The calculations for the structure presented in Fig. 2a were performed in the same way than in the previous case (Section 2.2), except that the electronegativity of a graphitic N-doped graphene (the level of N-doping is 11.1 at%) was calculated using the work function ϕ = 3.25 eV.64 Using Fig. 1 from ref. 65, the electronegativity of the substrate was found to be 1.29 eV1/2. Substituting the latter value into eqn (S21)† yields 245.0 kJ mol−1 (2.54 eV) for EPt–C, which is slightly higher than in the case of a single graphene vacancy (2.51 eV).
The results of the adsorption energy calculations for several Pt clusters and Pt nanoparticles bound to a single vacancy at a N-doped graphene are summarized in Table 3.
| Cluster, size/nm | Number of Pt–Pt bonds in the cluster | Formation energy of Ptn cluster/eV | Formation energy of graphene/Ptn complex/eV | Adsorption energy/eV |
|---|---|---|---|---|
| Pt2 | 1 | −3.18 | −9.26 | −6.08 |
| Pt3 | 3 | −6.39 | −12.54 | −6.15 |
| Pt4 | 6 | −9.88 | −17.46 | −7.58 |
| Pt7 | 13 | −21.35 | −28.94 | −7.59 |
| Pt9 | 18 | −29.43 | −37.14 | −7.71 |
| Pt12/1.0 | 26 | −42.12 | −50.26 | −8.14 |
| Pt13/1.1 | 28 | −46.41 | −53.54 | −7.13 |
| Pt19/1.2 | 46 | −72.96 | −79.93 | −6.97 |
| Pt30/1.4 | 88 | −123.9 | −131.15 | −7.25 |
| Pt39/1.5 | 133 | −166.53 | −174.38 | −7.85 |
| Pt100/1.9 | 420 | −470.0 | −478.65 | −8.65 |
| Pt150/2.3 | 700 | −727.5 | −736.31 | −8.81 |
There are only small changes in adsorption energy in Table 3 (compared with the same in Table 2), as the Pt cluster size increases. The intensity of interactions of Pt clusters/nanoparticles with substitutional N-doped graphene (at a single vacancy) is only slightly stronger compared with that of Pt clusters/nanoparticles bound to a single vacancy at undoped graphene. As in both cases the (Δχ)2 values are close to each other, this leads therefore (eqn (S21)†) to approximately equal ionic contributions to the Pt–C bond energy. To estimate the energy of the Pt–N donor–acceptor bond in the structure of Fig. 2b, we have used eqn (2) (or (S23)†) which is similar to eqn (S21):†
 | (2) |
| Cluster, size/nm | Number of Pt–Pt bonds in the cluster | Formation energy of the cluster/eV | Formation energy of the complex/eV | Adsorption energy/eV |
|---|---|---|---|---|
| Pt2 | 1 | −3.18 | −8.39 | −5.21 |
| Pt3 | 3 | −6.39 | −11.67 | −5.28 |
| Pt4 | 6 | −9.88 | −16.59 | −6.71 |
| Pt7 | 13 | −21.35 | −28.07 | −6.72 |
| Pt9 | 18 | −29.43 | −36.27 | −6.84 |
| Pt12/1.0 | 26 | −42.12 | −49.39 | −7.27 |
| Pt13/1.1 | 28 | −46.41 | −52.67 | −6.26 |
| Pt19/1.2 | 46 | −72.96 | −79.06 | −6.10 |
| Pt30/1.4 | 88 | −123.9 | −130.26 | −6.36 |
| Pt39/1.5 | 133 | −166.53 | −173.49 | −6.96 |
| Pt100/1.9 | 420 | −470.0 | −477.76 | −7.76 |
| Pt150/2.3 | 700 | −727.5 | −735.42 | −7.92 |
Table 4 shows that the dependence of the adsorption energy on the number of atoms in a cluster remains the same as in previous cases. However, the adsorption energy for a series of small clusters is significantly less than in the case of a graphitic N-doped single vacancy graphene. It is only when the size of the cluster increases that this difference gradually decreases, as the values of adsorption energy are then approaching the value of the adsorption energy for a graphitic N-doped graphene. This convergence of adsorption energies is explained by the fact that for large clusters the contribution of the cohesion energy to the adsorption energy begins to prevail.68
3. Effect of Ptn clusters on the energetics of Mn–N and Pt–C bonds in the modelled Pt2-MnNx/C sites
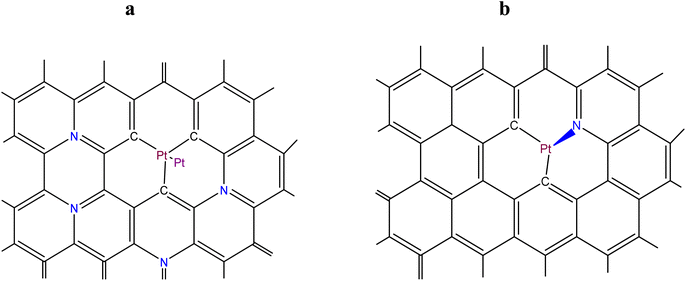
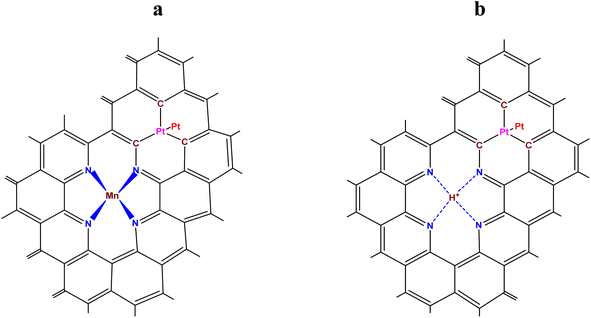
The purpose of the modelling was: (i) to find out, considering the energetics of Pt–C and Mn–N bonds, if there is an interaction (through a system of conjugated π–C–C bonds) between a MnNx site integrated into a graphene or a graphitic surface, and Ptn (n ≥ 2) clusters, located at some distance from the MnNx site on the same surface; and (ii) to estimate the thermodynamic stability in an acid environment at 353 K (the running PEM fuel cell temperature) of the modelled MnNx site in comparison with its stability in absence of the adsorbed Ptn cluster. Fig. 3a shows the hybrid Pt2-MnN(2+2)/C site (as a particular case) in which a Pt2 cluster (adsorbed on a single vacancy) is located in close proximity of a MnN(2+2)/C site (the Mn oxidation states are +2 or +3), while the demetallated form of the hybrid site is depicted in Fig. 3b.Fig. 4a shows the modelled hybrid Pt2-MnN(4+2)/C site (also as a particular case) in which a Pt2 cluster (adsorbed on a single vacancy) is located at some distance from MnN(4+2)/C site (the Mn oxidation states are +2 or +3), while the demetallated form of the hybrid site is depicted in Fig. 4b.
The Sanderson–Boudreaux method (see Section S5 of ESI†) was applied to determine the charge distribution on the atoms of interest and the Pt–C and Mn–N bond energy in the modelled sites. Partial charges on atoms were calculated with eqn (S28).† The fractional ionic character of Pt and Mn atoms was determined using eqn (S29).† The method of Gray and Hercules69 was applied to find the equalized electronegativity, χM, of the modelled sites; namely, the structure shown in Fig. 3a, was considered to consist of Pt2C3 and MnN4C8 groups conjugated to the graphene lattice, Cm. The electronegativity of Pt2, as a chemical group, χg(Pt2), was taken, following the Sanderson principle of the full equalization of electronegativities,59 equal to  , i.e., to the electronegativity of the Pt atom. The same Sanderson principle was equally applied to the determination of χg(Cm) for a graphene or graphitic lattice and Ptn (n > 2) clusters/nanoparticles. An illustrative calculations of charge distribution on atoms, and Pt–C and Mn–N bond energies in the modelled hybrid Pt2-MnIIIN4/C site of Fig. 3a of the main text is detailed in Section S6 of ESI.†
, i.e., to the electronegativity of the Pt atom. The same Sanderson principle was equally applied to the determination of χg(Cm) for a graphene or graphitic lattice and Ptn (n > 2) clusters/nanoparticles. An illustrative calculations of charge distribution on atoms, and Pt–C and Mn–N bond energies in the modelled hybrid Pt2-MnIIIN4/C site of Fig. 3a of the main text is detailed in Section S6 of ESI.†
In the case of the site shown in Fig. 4a, besides the already mentioned chemical groups, the presence of two NC3 groups in the second coordination sphere of Mn was also considered. The bond energies of Pt–C and Mn–N in the modelled hybrid electrocatalytic sites were calculated using ESI eqn (S24), (S28) and (S29).† The input data needed for the calculations are given in Table 5.
| C | N | Pt | Mn(II) | Mn(III) | |
|---|---|---|---|---|---|
| a Calculated with a value of 5.54 eV (Mulliken units) from ref. 70 into eqn (10b) given in ref. 71. b Sanderson electronegativity for di-valent state of Mn taken as the intermediate value between 1.66 (ref. 72) and 2.1.73 c Sanderson electronegativity72 for three-valent state of Mn. d Pt covalent radius74 for coordination number equals to 4. e Covalent radius75 of Mn for di-valent and three-valent states, respectively. f From Table 1 in the main text. g Ref. 74 (Chapter 2, Table 2.3). Here we adopted the incertitude recommended by Gingerich.76 | |||||
| Electronegativity in Sanderson scale,59 unitless | 2.746 | 3.194 | 2.14a | 1.75b | 2.20c |
| Covalent radius, Å (ref. 59) | 0.772 | 0.734 | 1.37d | 1.36e | 1.28e |
| Ordinary homonuclear bond energy59 kJ mol−1 | 357.3 | 156.3 | 158.2f | 121.0 ± 29g | |
The results of the determination of the partial charges on atoms and Pt–C and Mn–N bond energies in the modelled Pt2-MnNx/C hybrid sites (Fig. 3a and 4a, Mn oxidation states are +2 or +3) are summarized in Table 6. It is important to note here that, in view of the above-mentioned Sanderson principle of electronegativity equalization for Pt clusters/nanoparticles, the results of calculations, given in Table 6, are equally applied for hybrid Ptn-MnNx/C sites with n > 2. Note also that the interatomic distance of 2.1 Å for Pt–C was estimated, using the well-known Shoemaker–Stevenson's formula.77 The value of 2.0 Å for the interatomic Mn–N bond distance was borrowed from ref. 49. The results of the calculations of the partial charges on atoms of nitrogen and manganese support the point of view of the authors of the work44 that the MnN4/C sites are centers of specific adsorption of Pt ions formed as a result of electrooxidation of Pt clusters. Apparently, nitrogen atoms carrying a negative charge will adsorb Pt cations, and manganese atoms, carrying a positive charge, will adsorb oxo-anions of Pt (specifically, [Pt6O8]4− units78). Such adsorption may entail the following reactions:
| 2Pt2+ + [Pt6O8]4− = 8PtO | (3) |
| PtO + 2H+ = Pt2+ + H2O | (4) |
| Fig. 3a charge on atoms (in the frame of the Sanderson–Boudreaux method) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| C (Pt–C–N chaine) | C (Pt–C–C chaine) | N (MnN4C8 group) | Pt (Pt2C3 group) | Mn (MnN4C8 group) | |||||
| Mn2+ | Mn3+ | Mn2+ | Mn3+ | Mn2+ | Mn3+ | Mn2+ | Mn3+ | Mn2+ | Mn3+ |
| a The value from Section 2.2. | |||||||||
| −0.015 | −0.013 | −0.043 | −0.042 | −0.171 | −0.142 | +0.172 | +0.174 | +0.406 | +0.242 |
| Fig. 4a charges on atoms (in the frame of Sanderson–Boudreaux method) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| C (Pt–C–C chaine) | N (MnN4C8 group) | N (NC3 group) | Pt (Pt2C3 group) | Mn (MnN4C8 group) | |||||
| Mn2+ | Mn3+ | Mn2+ | Mn3+ | Mn2+ | Mn3+ | Mn2+ | Mn3+ | Mn2+ | Mn3+ |
| −0.038 | −0.055 | −0.165 | −0.148 | −0.106 | −0.098 | +0.179 | +0.180 | +0.411 | +0.246 |
As can be seen from Table 7, the adsorption energy (as a measure of the adhesion strength) of Pt clusters/nanoparticles is significantly larger than in the case of a graphitic N-doped single vacancy graphene and a pyridinic N-doped single vacancy graphene (Section 2.3). The same values will be observed in the case of hybrid Ptn-Mn(II)Nx/C sites, due to the proximity of Pt–C bonds energy to the same in Ptn-Mn(III)Nx/C sites (Table 6).
| Cluster, size/nm | Number of Pt–Pt bonds in the cluster | Formation energy of the cluster/eV | Ptn-Mn(III)N(2+2)/C site Fig. 3a | Ptn-Mn(III)N(4+2)/C site Fig. 4a | ||
|---|---|---|---|---|---|---|
| Formation energy of the complex/eV | Adsorption energy/eV | Formation energy of the complex/eV | Adsorption energy/eV | |||
| Pt2 | 1 | −3.18 | −10.07 | −6.89 | −10.31 | −7.13 |
| Pt3 | 3 | −6.39 | −13.35 | −6.96 | −13.59 | −7.20 |
| Pt4 | 6 | −9.88 | −18.27 | −8.39 | −18.51 | −8.63 |
| Pt7 | 13 | −21.35 | −29.75 | −8.40 | −29.99 | −8.64 |
| Pt9 | 18 | −29.43 | −37.95 | −8.52 | −38.19 | −8.76 |
| Pt12/1.0 | 26 | −42.12 | −51.07 | −8.95 | −51.31 | −9.19 |
| Pt13/1.1 | 28 | −46.41 | −54.35 | −7.94 | −54.59 | −8.18 |
| Pt19/1.2 | 46 | −72.96 | −80.74 | −7.78 | −80.98 | −8.02 |
| Pt30/1.4 | 88 | −123.9 | −131.96 | −8.06 | −132.20 | −8.30 |
| Pt39/1.5 | 133 | −166.53 | −175.19 | −8.66 | −175.43 | −8.90 |
| Pt100/1.9 | 420 | −470.0 | −479.46 | −9.46 | −479.70 | −9.70 |
| Pt150/2.3 | 700 | −727.5 | −737.12 | −9.62 | −737.36 | −9.86 |
Fig. 5 summarizes the changes in adsorption energy for Pt(n) vs. (n) on the graphene carbon support in various structural doping configurations of the carbon support.
 | ||
| Fig. 5 Adsorption energy of several Pt(n)-clusters/NPs bound to: (a) a single graphene vacancy (Table 2; black filled squares); (b) a single vacancy of graphitic N-doped graphene (Table 3; open blue circles); (c) a pyridinic N-doped single vacancy graphene (Table 4; filled blue triangles); (d) a Mn(II) or (III)N(4+2)/C site (Table 7 (4 + 2); filled green triangles) or a Mn(II) or (III)N(2+2)/C site (Table 7 (2 + 2); open green circles). | ||
The more negative the adsorption energy, the more exothermic the adsorption of Pt(n) on graphene, and the better the Pt(n)-cluster/NP will be retained on the graphene plane. Fig. 5 shows that the best cases are represented by the two curves shown in Table 7, which illustrate the effect of the presence of a non-noble MnNx/C site in the vicinity of the Pt(n) cluster/NP. The influence of the substrate on Pt(n) is particularly significant in the case where MnNx/C is either Mn(II or III)N(4+2)/C or Mn(II or III)N(2+2)/C. Fig. 5 also shows various regions in the graph representing the different structural shapes (triangular, icosahedral and face-centered cubic) that Pt(n)-clusters or NPs take on when (n) is increased from 4 to 150 Pt atoms.
Thus, by comparing the bond energy values from the literature for Pt–C and Mn–N and the results of the calculations performed in this work, it can be seen that: (i) an interaction exists between Pt2 or Ptn clusters (n > 2) and MnNx/C and (ii) this interaction is favorable in the sense that a remarkable strengthening of both Pt–C and Mn–N bonds occurs. As consequence, MnNx/C sites increase the adhesion strength of Pt(n) on a carbon substrate (Table 7 and Fig. 5) and, in return, Pt(n) stabilizes MnNx/C towards demetallation in strongly acidic fuel cell media (Section 4). However, even if the presence of Pt nanoparticles near a site such as MnNx/C stabilizes this site towards demetallation, it is well known that such molecular sites do not have the same stability as platinum at the cathode of PEM fuel cells.79 This raises the question of what would happen to the adhesion of Pt(n) on a carbon substrate in the vicinity of a molecular site such as MnNx/C once Mn had left the site. As can be seen in Table 8 (compared with the same from Table 6), the calculations show that demetallation of MnNx/C sites in the vicinity of Pt(n) has very little effect on the energy of the Pt–C bond under the influence of the demetallated forms of the modelled sites (Fig. 3b or 4b). This means that the adhesion of platinum clusters should not undergo changes in these conditions.
| Fig. 3b charges on atoms and Pt–C bond energy (in the frame of the Sanderson–Boudreaux method) | ||||||
|---|---|---|---|---|---|---|
| C (Pt–C–N chain) | C (Pt–C–C chain) | N ([H]+⋯N4C8 group)a | [H]+ ([H]+⋯N4C8 group) | Pt (Pt2C3 group) | Pt–C bond energy, kJ mol−1 | |
| Calculated | Table 6 (Fig. 3a) | |||||
| a The electronegativity of [H+] cation is equal to 6.8 in the Sanderson scale of electronegativity.80 | ||||||
| −0.005 | −0.034 | +0.140 | −0.565 | +0.183 | 269.3 | 270.8 (Mn2+) |
| 270.8 (Mn3+) | ||||||
As can be also seen from Table 8, the hydrogen ion (see Fig. 3b) carries, according to the calculations, a large negative charge of −0.565. This unexpected result is justified if we assume that the lone electron pairs of the nitrogen atoms transfer part of their electron density to the hydrogen ion, so that the rule of electroneutrality for first coordination sphere of the hydrogen ion is fulfilled: 4 × |+0.140| ≅ |−0.565|. Furthermore, one can suppose that platinum cations, formed as a product of the electrochemical corrosion of platinum in the PEM fuel cell4 at a potential >0.6 V, would be adsorbed in the vicinity to the hydrogen ion, leading in the end to the replacement of the hydrogen ion by a platinum ion due to its higher charge and the ability to form four Pt–N donor–acceptor bonds. Then, considering Fig. 4b, we can also suppose that a platinum cation, like a manganese cation, will also be able to form a similar moiety (Pt2-PtN(4+2)/C). Finally, taking into account that “single-pyridinic-nitrogen-atom-anchored single-platinum-atom centers” (ref. 81) are durable and highly active for the oxygen reduction reaction and that the adhesion of platinum clusters should not undergo changes, this all correlates well with the fact that a membrane electrode assembly (MEA) with the Pt/Mn–N–C cathode catalyst, which was able to generate 1.41 A cm−2 at 0.7 V, still retained 1.20 A cm−2 (i.e. 85%) after up to 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 AST's voltage cycles, as mentioned in the literature.45
000 AST's voltage cycles, as mentioned in the literature.45
4. Thermodynamic aspect of the chemical stability of the modelled Ptn-MnNx/C hybrid sites (Mn = Mn2+ or Mn3+)
As it was mentioned in the introduction, the criterium of chemical stability of the MnNx/C sites could be the equilibrium constants of demetallation reactions at temperature of 353 K (the temperature of running PEM fuel cells).The following thermodynamic relation82 was used to calculate the values of equilibrium constants, Kc, of the demetallation reactions (acid leaching of manganese ions) of the MnNx/C sites of Fig. 3a and 4a:
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc = −ΔrG0T/RT Kc = −ΔrG0T/RT | (5) |
| ΔrG0T = ΔrH0298 − TΔrS0298 | (6) |
Equations for the reactions of demetallation of the sites of Fig. 3a are the following:
| Pt2-Mn(II)N(2+2)/C,s + Haq+ = Pt2-(H+)N(2+2)/C,s + Mnaq2+ | (7) |
| Pt2-Mn(III)N(2+2)/C,s + Haq+ = Pt2-(H+)N(2+2)/C,s + Mnaq3+ | (8) |
| ΔrH0298 = [ΔfH0298Mnaq2+ + (−4 × EH+⋯N)] − [ΔfH0298Haq+ + (−4 × EMn–N)] | (9) |
Equations for the reactions of demetallation of the sites of Fig. 4a are the following:
| Pt2-Mn(II)N(4+2)/C,s + 2Haq+ = Pt2-H2N(4+2)/C,s + Mnaq2+ | (10) |
| Pt2-Mn(III)N(4+2)/C,s + 2Haq+ = Pt2-H2N(4+2)/C,s + Mnaq3+ | (11) |
| ΔrH0298 = [ΔfH0298Mnaq2+ + (−2 × EN–H)] − [ΔfH0298Haq+ + (−4 × EMn–N)] | (12) |
A similar equation will be valid when the Mn oxidation state will be +3.
The standard enthalpies of formation and standard entropies of Haq+ and Mnaq2+ and Mnaq3+ ions participating in the acid leaching reactions of manganese ions are tabulated.82 The values of EN–H = 382.3 kJ mol−1 and EH+⋯N = 195.0 ± 6 kJ mol−1 were borrowed from ref. 49. The standard entropies of the frameworks appearing in Fig. 3 and 4 were estimated using the Glasser and Jenkins correlation equation:84
| S0298 (J K−1 mol−1) = 774Vm (nm3 per molecule) + 57 | (13) |
| Ion | ΔfH0298, kJ mol−1 | S 0298, J K−1 mol−1 | S 0298, J K−1 mol−1, of Pt2-MnNx/C sites and their demetallated forms (Mn = Mn2+ and Mn3+) | |||
|---|---|---|---|---|---|---|
| Mn2+ | Mn3+ | Demetallated form | ||||
| a Ref. 82. b The sites of Fig. 3a and b, respectively. c The sites of Fig. 4a and b, respectively. d Table 6, data referred to Fig. 3a. e Table 6, data referred to Fig. 4a. f Ref. 49. | ||||||
| Haq+ | 0a | 0a | 617.1b | 617.1b | 596.5b | |
| 925.4c | 925.4c | 908.4c | ||||
| Bond energy, kJ mol−1 | ||||||
| Mnaq2+ | −220.5 ± 2.1a | −66.9a | Mn–N bond energy, kJ mol−1 | H+⋯N | N–H | |
| Mnaq3+ | −100.4a | −213.4a | 263.2 ± 14d | 227.7 ± 14d | 195.0 ± 6f | 382.3f |
| 262.4 ± 14e | 238.3 ± 14e | |||||
Based on the information presented in Table 9, it was possible to calculate the thermodynamic parameters (ΔrH0298, ΔrS0298, ΔrG0T) of reactions (7), (8), (10) and (11) (Table 10). Considering the values of the Gibbs free energy of the reactions of demetallation in the Table 10, it is important to note that all the hybrid Pt2-Mn(II)Nx/C sites, with divalent manganese, turned out now to be thermodynamically stable, while the same Mn(II)Nx/C sites, in the absence of adsorbed Pt2 cluster, are all thermodynamically instable!49 As can also be seen, the Pt2-Mn(III)N(4+2)/C site with 4 pyridinic N and 2 graphitic N in a hexa-aza configuration should demonstrate an extremely great thermodynamic stability. Although the thermodynamic parameters of Mn leaching reactions given in the Table 10, are referred to the modelled Pt2-Mnx/C sites, these values, due to the fact that Pt atoms do not participate in the Mn leaching reactions and taking into account the above-mentioned Sanderson principle of electronegativities full equalization, will also be valid for the reactions involving the Ptn-Mnx/C sites with n > 2.
| Site and reaction | ΔrH0298, kJ mol−1 | ΔrS0298, J K−1 mol−1 | ΔrG0T at 298 K (in parentheses) and 353 K, kJ mol−1 | K c at 298 K (in parentheses) and 353 K | Mn-ion's equilibrium concentration at 298 K (in parentheses) and 353 K, mol L−1 |
|---|---|---|---|---|---|
| Pt2-Mn(II)N(2+2)/C,s reaction (7) | 52.3 | −87.5 | 83.2 (78.4) | 4.9 × 10−13 (1.8 × 10−14) | 1.1 × 10−12 (3.8 × 10−14) |
| Pt2-Mn(III)N(2+2)/C,s reaction (8) | 30.4 | −234.0 | 113.0 (100.1) | 1.9 × 10−17 (2.8 × 10−18) | 4.1 × 10−17 (6.0 × 10−18) |
| Pt2-Mn(II)N(4+2)/C,s reaction (10) | 64.5 | −83.9 | 94.1 (89.5) | 1.2 × 10−14 (2.0 × 10−16) | 5.4 × 10−14 (9.2 × 10−16) |
| Pt2-Mn(III)N(4+2)/C,s reaction (11) | 88.2 | −230.4 | 169.5 (156.9) | 8.2 × 10−26 (3.2 × 10−28) | 3.8 × 10−25 (1.5 × 10−27) |
Using the values of equilibrium constants, the amount of Mn ions leaching from the modelled electrocatalytic sites in an acid medium in equilibrium conditions can be estimated based on the following facts and assumptions: (i) the experimentally determined activity of H+-ions in Nafion at 353 K is equal to 2.14 (extrapolated value from ref. 86); (ii) the coefficient of activity of Mn-ions, due to the very low value of the equilibrium constant, can be taken equal to 1, meaning that activities of ions are equal to the concentrations of ions; (iii) the activities of the solid phases (Ptn-Mnx/C (n ≥ 2) sites and the corresponding demetallated forms) are equal to 1, by definition. Thus, the expression for the constant of equilibrium, Kc, in terms of activities (or molar concentrations, if the coefficient of activity is equal to 1) has the following form:
(a) referring to the reactions (7) and (8)
 | (14) |
(b) referring to the reactions (10) and (11)
 | (15) |
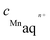 and
and  are the equilibrium concentration (mol L−1) of Mn-ions and activity of hydrogen ions, respectively.
are the equilibrium concentration (mol L−1) of Mn-ions and activity of hydrogen ions, respectively.
Using these equations, the concentrations of interest of Mn-ions (mol L−1) were calculated (Table 10). Although all studied hybrid sites are quite chemically stable, it is nevertheless important to note that, for Mn(III)N(2+2)/C and Mn(III)N(4+2)/C the equilibrium concentrations at 353 K (80 °C) in the absence of Ptn (n ≥ 2) clusters are equal to 8.3 × 10−13 and 8.6 × 10−15 mol L−1, respectively,49 while the equilibrium concentrations of the same sites but with a Pt2 or Ptn (n > 2) clusters are now 4.1 × 10−17 and 3.8 × 10−25 mol L−1, respectively. This means that an important role in ensuring high chemical stability of hybrid sites belongs to two factors, namely, the presence of adsorbed Pt clusters and graphitic nitrogen in the graphene lattice (in the hexa-aza configuration).
5. The use of a doped carbon support (with N or MnNxCy sites) improves the stability of platinum-based catalysts. Is this the only advantage?
So far, we have only considered the influence of N-doping of the carbon support on the stability of Pt catalysts in the highly acidic environment of PEM fuel cells. We have also discovered a reciprocal beneficial influence on the stability of Pt catalysts when these are in the presence, in the same acidic environment, of non-noble metal active sites (such as MnNxCy, or when Mn is replaced by Fe, Co or Ni as in ref. 25 and 26) occupying the same surface area of the carbon support as the Pt nanoparticles. However, the influence of N-doping of the carbon support and/or the presence of non-noble metal sites on the same support, does not stop at the stability of Pt catalysts. There is much more, as N-doping and/or the presence of non-noble metal sites are also responsible for: (i) the distribution of Pt nanoparticles on the carbon substrate and (ii) the significant increase in Pt mass activity for ORR in fuel cells. A detailed explanation of the dopant-induced electronic structure modifications of the carbon surface of Pt catalysts and their implication in PEM fuel cells was given in ref. 21 for the N-doping of HOPG, a highly organized pyrolytic graphite substrate, taken as a model carbon substrate. This explanation is also adaptable to the case where there are also MeNxCy-type non-noble metal sites on the carbon substrate in addition to the N dopants.Let's return now to the case of the Pt catalyst on N-doped HOPG substrate. According to the authors of ref. 21, nitrogen doping the carbon surface increases the density of electron-rich donor surface states just above the Fermi level of HOPG. These surface states are defects that can act as heterogeneous nucleation sites for Pt deposition, increasing therefore the nucleation rate of small Pt nanoparticles that are uniformly distributed on the carbon substrate if it has been uniformly doped with nitrogen. The N-doping of HOPG also increases the ORR catalytic activity of the catalyst. This effect is not simply due to the multiplication of smaller Pt particles instead of fewer larger ones, but it mainly reflects an improvement of the ORR turn-over frequency (ToF) on these particles. The ToF enhancement is indeed induced by some modifications of the d and f bands levels of the supported Pt nanoparticles, as these levels are slightly shifted towards higher energies compared to the d and f band levels of Pt nanoparticles on undoped HOPG.
The slight shift towards higher energy of Pt nanoparticles for Pt catalysts on carbon or also featuring MeNxCy-type sites on the surface of this carbon is experimentally accessible by XPS by measuring the binding energy (BE) at the 4f Pt edge. These spectra are characterized by a 4f7/2 and 4f5/2 doublet (appearing in an 5/3 ratio of peaks) for each of Pt's oxidation states, i.e. Pt(0), Pt(2+), and Pt(4+). The most important Pt state for ORR is Pt(0), which is the Pt metal state on which O2 preferentially adsorbs. Furthermore, it is mainly the BE of Pt(0) 4f7/2 that will provide experimental information on the electronic interactions of Pt with the carbon substrate. It should be noted that the Pt orbitals involved in oxygen reduction are the 5d orbitals, which are of lower energy than the 4f orbitals of Pt which are probed by XPS. This means that changes due to the aforementioned electronic interactions reflected in the BE value for Pt(0) 4f7/2 will be small and of the order of a fraction of an eV (whereas BE for Pt(0) 4f7/2 is between 71 and 72 eV).
The following ref. 21, 22, 24–26, 29, 31, 32, 34–39, 41, 42 and 44–48 have been collected to obtain information about the electronic transfer considered in this section. In these studies, the electro-donation from Pt to the N dopant or to MeNxCy non-noble ORR active sites located on the carbon support, is identified as being the cause for the enhanced catalytic activity of carbon supported Pt nanoparticles on these supports compared to Pt on undoped carbon supports. In XPS this electro-donation from Pt is translated into a positive shift in the BE values of all the Pt 4f peaks. This is because the observed shift in the band levels may increase the bond strength between Pt metal atoms, reducing at the same time the potential of Pt metal to form strong bonds with adsorbed reactants. It is the change in the metal-adsorbate bond strength which is a key factor for an improved catalytic activity. It has indeed been proposed by Hammer and Nørskov87 that the center of the transition metal band affects the ability of a catalyst surface (here the surface of the Pt nanoparticle) to make and break adsorbates bonds (here in ORR, the bonds between *, the catalytic site on Pt, and the sequence of adsorbed ORR intermediates: O2, HOO, O, OH, and H2O) and hence influence the ORR catalytic activity.
The following examples, taken from the list of references mentioned above, illustrate shifts in the BE of the 4f Pt edge that involve Pt electro-donation to the nitrogen doping the carbon support or to non-noble sites that may also be present on the carbon support.
In the first example (Fig. S1†), which shows Pt 4f XPS spectra for Pt nanoparticles on HOPG (Highly Organized Pyrolytic Graphite) and N-HOPG (N-doped HOPG), BE of Pt(0) 4f7/2 = 71.5 eV, while it is 71.9 eV for N-HOPG, i.e., a positive shift of 0.4 eV in BE.21 To obtain credible results, it is important to present the XPS spectrum of a reference carbon (here the spectrum of HOPG). This is a material like the modified carbon (here N-HOPG). Although this may seem obvious, it is not often the case in the literature.
In a second example, it is possible to show the electronic transfer of Pt to a CoNxCy site.36 Fig. S2† shows a superposition of 4 spectra all showing Pt/RGO (RGO = reduced graphite oxide). For the top spectrum, only Pt is predominantly metallic on RGO. The Pt(0) 4f7/2 peak is located at BE = 70.9 eV. This will be the reference. The following three spectra show how the Pt(0) 4f7/2 peak evolves with the addition of more and more CoNxCy sites, which originate from the decomposition of ZIF-67 (a Co and N precursor). We can see that from the penultimate spectrum (3ZIF-67-Pt/RGO), there has been a shift of Pt(0) 4f7/2 from BE = 70.9 eV to BE = 71.4 eV, a positive shift of 0.5 eV due to electronic transfer from the Pt to the carbon support containing the CoNxCy sites.
In a third example, we would like to mention a particular case, that of Fig. S3,† reproduced from ref. 44, which shows the spectra of Pt particles on various non-noble substrates containing MnSA (i.e. MnNxCy sites; SA standing here for single atom), CoNxCy and NiNxCy. The last two spectra are those of Pt@ZIF-NC and Pt@KJ, for which ZIF-NC is the material obtained from the pyrolysis of ZIF-8 (a metal organic framework synthesized by the reaction of zinc nitrate and 2 methyl imidazole). ZIF-NC can be used as a reference for the three catalysts Pt@MnSA-NC, Pt@CoSA-NC and Pt@NiSA-NC. Pt@KJ, where KJ is Ketjenblack 600, a conductive carbon black, can also be chosen as a reference.
If Pt@KJ is chosen as reference. The BE of Pt(0) 4f7/2 for Pt@KJ is 71.5 eV. This means that all the BEs for the other catalysts all have negative shifts with respect to Pt@KJ. This is difficult to explain in the context of this discussion since we rather expect an electron transfer from Pt to the non-noble catalytic sites which are, MnNxCy, CoNxCy, and NiNxCy, respectively, i.e., a positive BE shift from Pt(0) 4f7/2 to the higher energies. The negative shift of BE = 0.45 eV for Pt@ZIF-NC cannot be understood in this context either, since ZIF-NC is an N-doped support (after pyrolysis of ZIF-8), which, as we saw earlier, would rather call for a positive shift with respect to the reference (see Fig. S1†). However, if we consider Pt@ZIF-NC as the reference for all NC catalysts, everything can return to normal. In this case, the addition of further MnNxCy, CoNxCy, and NiNxCy sites on NC will result in a positive shift in the spectrum of Pt(0) 4f7/2, which will transfer its electrons to the three aforementioned sites. In fact, the greatest electron transfer will be to CoNxCy > NiNxCy > MnNxCy, i.e.: 0.27 eV > 0.17 eV > 0.13 eV, respectively.
The situation can be more complex if the nanoparticles do not contain pure Pt but are made from an alloy of Pt with a non-noble metal. When Pt is alloyed with a non-noble metal, the electronic transfer will be in the other direction, from the less noble metal (which will end up more oxidized) to the Pt, and the Pt(0) 4f7/2 shift will be negative, i.e., towards the lower BE energies. However, the Pt alloy particles can also interact with the nitrogen doping the carbon substrate on which they are located, as well as with non-noble sites on the surface of the same carbon substrate. This specific interaction results in a positive shift, i.e., towards the higher binding energy of Pt(0) 4f7/2. The final shift is obtained from the algebraic addition of the two interactions.
This is illustrated in the following example, which shows the dominant effect of a Pt and Fe alloy on the direction of electron transfer.35 Here, Pt@FeSA-N-C is taken as a reference. This catalyst is made from ZIF-8 + the adsorption of an iron precursor, followed by carbonization to give FeSA-N-C (here FeSA means there are FeNxCy sites on N–C). Pt is then added to FeSA-N-C to give Pt@FeSA-N-C. The top spectrum of Fig. S4† shows the XPS spectrum of Pt 4f for Pt@FeSA-N-C. The Pt(0) 4f7/2 peak can be seen at BE = 71.9 eV. The bottom spectrum of the same figure is that of PtA@FeSA-N-C. This material was obtained by heating Pt@FeSA-N-C to obtain an alloy of Pt and Fe (i.e. PtA), while retaining a certain presence of FeSA-NC. We can see that the Pt(0) 4f7/2 peak is now at BE = 71.5 eV, i.e. shifted by 0.4 eV in the negative direction (that of the lower binding energies) due to the dominant presence of the Pt–Fe alloy, for which the Fe in the alloy gives electrons to the Pt, whose BE of the Pt(0) 4f7/2 electrons then decreases.
6. Summary and conclusions
The work presented here is divided into three parts.In the first part, we investigated the influence of a carbon substrate (graphene), doped or undoped, on the adsorption energy (and therefore the stability) of Pt(n)-clusters/nanoparticles (NPs) that have been grown on this substrate. For the doping of the carbon substrate, we considered nitrogen doping, where this atom is substituted for a carbon atom. The nitrogen dopant is either graphitic or pyridinic. We have also considered carbon doping with MnN(2+2)/C or MnN(4+2)/C sites in the immediate vicinity of Pt(n)-clusters/NPs. These non-noble sites have the potential (like Pt(n)) to reduce oxygen in fuel cells, and their manganese ion is either Mn(II) or Mn(III).
In the second part of this work, we then considered the influence of Pt(n) adsorbed on the carbon substrate on the stability, in the acidic fuel cell environment, of the non-noble MnNx/C sites in the immediate vicinity of the Pt(n)-clusters/NPs adsorbed on graphene.
Let us now detail the contents of the first part of this work.
In the first part of this work, the first step was to bring the Pt(n)-clusters/NPs into contact with graphene to determine the influence of the substrate on the adsorption energy between Pt(n) and the carbon substrate. The graphene/Pt(n) interaction is mediated by a platinum atom interacting with three graphene carbon atoms when this Pt atom occupies a carbon single vacancy in the graphene plane. The entire Pt(n)-cluster/NP will be built on this first Pt atom in direct contact with the three carbon atoms in the graphene plane.
Next, if different dopants on the graphene substrate are considered, the adsorption energy values of Pt(n) on these substrates will vary from one type of dopant to another. The results obtained are illustrated in Fig. 5. The reference will be the variation in Pt(n) adsorption energy when the substrate is undoped (Table 2, full black squares in Fig. 5). The curve called (Table 3, open blue circles) refers to the doping of the carbon with a graphitic nitrogen atom in the vicinity of Pt(n), while the curve called (Table 4, full blue triangles) shows how the adsorption energy of Pt(n) varies when one of the 3 carbon atoms holding the Pt in the vacancy is substituted with a pyridinic nitrogen atom. Finally, the two curves named (Table 7 (4 + 2) and Table 7 (2 + 2)) refer to the variation in Pt(n) adsorption energy when the Pt(n)-cluster/NP is in the vicinity of a non-noble MnNx/C site, whether the site is MnN(4+2)/C (Table 7(4 + 2); full green triangles) or MnN(2+2)/C (Table 7 (2 + 2); open green circles). However, there is no difference in the intensity of adsorption energy for the two curves called (Table 7) between Mn(II) or Mn(III) ions.
The more negative the adsorption energy, the more exothermic the adsorption of Pt(n) on graphene, and the better the Pt(n)-cluster/NP will be retained on the graphene plane. Fig. 5 shows that the best cases are represented by the two curves shown in Table 7, which illustrate the effect of the presence of a non-noble MnNx/C site in the vicinity of the Pt(n) cluster/NP. The influence of the substrate on Pt(n) is particularly significant in the case where MnNx/C is either Mn(II or III)N(4+2)/C or Mn(II or III)N(2+2)/C. Fig. 5 also shows various regions in the graph representing the different structural shapes (triangular, icosahedral and face-centered cubic) that Pt(n)-clusters or NPs take on when (n) is increased from 4 to 150 Pt atoms. We found that with an increase in the cluster size, there is a tendency for the adsorption energies to converge, regardless of whether a single vacancy of graphene is N-doped or not. It was explained by the fact that for large clusters the contribution of the cohesion energy to the adsorption energy begins to prevail.
The proposed thermochemical method of calculating adsorption energies of large Pt clusters on both undoped and N-doped graphene substrates, and in the presence of a non-noble MnNx/C site in the vicinity of the Pt(n) cluster/NP is characterized by little computational efforts and an accuracy no worse than that obtained by DFT calculations.
In the second part of this work, we wanted to see whether the effect of Pt(n)-cluster/NP stabilization by a non-noble MnNx/C site was reciprocal, i.e., whether the presence of a Pt(n)-cluster/NP adjacent to a non-noble MnNx/C site also stabilized the MnNx/C towards demetallation in strongly acidic fuel cell media. The answer to this question is: yes, Pt(n) stabilizes MnNx/C back against demetallation of the non-noble site! The stabilization is particularly spectacular for the Mn(II)N(4+2)/C and Mn(II)N(2+2)/C sites for which we had previously determined that demetallation of the Mn(II) sites was a spontaneous reaction, whereas we had found that for the equivalent Mn(III)N(4+2)/C and Mn(III)N(2+2)/C sites (thus having Mn(III) instead of Mn(II)), the demetallation reaction was subject to an equilibrium governed by an equilibrium constant. The presence of a neighboring Pt(n) now drastically transforms the previously spontaneous Mn(II) site demetallation reactions of Mn(II)N(4+2)/C and Mn(II)N(2+2)/C sites into equilibrated reactions. However, even if the presence of Pt nanoparticles near a site such as MnNx/C stabilizes this site towards demetallation, it is well known that such molecular sites do not have the same stability as platinum at the cathode of PEM fuel cells. This raises the question of what would happen to the adhesion of Pt(n) on a carbon substrate in the vicinity of a molecular site such as MnNx/C once Mn had left the site. As can be seen in Table 8 (compared with the same from Table 6), the calculations show that demetallation of MnNx/C sites in the vicinity of Pt(n) has very little effect on the energy of the Pt–C bond under the influence of the demetallated forms of the modelled sites (Fig. 3b or 4b). This means that the adhesion of platinum clusters should not undergo changes in these conditions.
It should be noted that the calculations of the thermodynamic parameters in this second part of the work have only been carried out on the Pt2-MnNx/C hybrid catalyst because the size of Pt(n) is not involved here in the equation for the determination of the electronegativity of Pt(n). This is due to the application of the Sanderson principle of full equalization for the determination of the electronegativity of Pt(n) when calculating the equalized electronegativity of the modelled site. For example, the electronegativity of (Pt2), is equal to  , (or 1/2[χPt]2 = χPt), i. e. to the same electronegativity of Pt atom (2.14 in the Sanderson scale of electronegativity). In the case of Pt100 cluster, the electronegativity of (Pt100) is also equal to the electronegativity of Pt atom, since 1/100[χPt]100 = χPt.
, (or 1/2[χPt]2 = χPt), i. e. to the same electronegativity of Pt atom (2.14 in the Sanderson scale of electronegativity). In the case of Pt100 cluster, the electronegativity of (Pt100) is also equal to the electronegativity of Pt atom, since 1/100[χPt]100 = χPt.
Finaly, in the third part, after defining, in terms of stability, the reciprocal advantages of Pt(n)-cluster/NPs interactions with neighboring MnNx/C sites on the carbon substrate (N-doped or not), we also devoted a section to reviewing the literature concerning the advantages, for the same Pt(n)-MnNx/C hybrid catalysts, but this time in terms of catalytic activity.
The dopant-induced electronic structure modifications of the carbon surface of Pt catalysts are reflected, as calculations showed, in the strengthening of Pt–C and Mn–N bonds (MnNx/C substrates). This may also be named synergy between Pt–C and Mn–N bonds. The same type of calculations, in the frame of Sanderson–Boudreaux method, could also be used as a tool for predicting a possible synergy between Pt–C and other Me–N bonds (where Me = V, Cr, Co, Ni, etc., and eventually also Sn, as examples).
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.References
- HFTO's Hydrogen and Fuel Cell Technologies Office Multi-Year Program Plan; DOE/GO-102024-6266, ENERGY.GOV: U.S., 2024. https://www.energy.gov/sites/default/files/2024-05/hfto-mypp-fuel-cell-technologies.pdf Search PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108(46), 17886–17892, DOI:10.1021/jp047349j.
- Z. Wu, G. Yang, Q. Zhang, Z. Liu and F. Peng, Deciphering the high overpotential of the oxygen reduction reaction via comprehensively elucidating the open circuit potential, Energy Environ. Sci., 2024, 17(10), 3338–3346, 10.1039/d3ee04368a.
- Y. Shao-Horn, W. C. Sheng, S. Chen, P. J. Ferreira, E. F. Holby and D. Morgan, Instability of supported platinum nanoparticles in low-temperature fuel cells, Top. Catal., 2007, 46(3–4), 285–305, DOI:10.1007/s11244-007-9000-0.
- Z. Yang, S. Ball, D. Condit and M. Gummalla, Systematic Study on the Impact of Pt Particle Size and Operating Conditions on PEMFC Cathode Catalyst Durability, J. Electrochem. Soc., 2011, 158(11), B1439–B1445, DOI:10.1149/2.081111jes.
- F. A. De Bruijn, V. A. T. Dam and G. J. M. Janssen, Review: Durability and Degradation Issues of PEM Fuel Cell Components, Fuel Cells, 2008, 8(1), 3–22, DOI:10.1002/fuce.200700053.
- T. Ioroi, Z. Siroma, S. i. Yamazaki and K. Yasuda, Electrocatalysts for PEM Fuel Cells, Adv. Energy Mater., 2019, 9(23), 1801284, DOI:10.1002/aenm.201801284.
- K. Yasuda, A. Taniguchi, T. Akita, T. Ioroi and Z. Siroma, Platinum dissolution and deposition in the polymer electrolyte membrane of a PEM fuel cell as studied by potential cycling, Phys. Chem. Chem. Phys., 2006, 8(6), 746–752, 10.1039/b514342j.
- S. Cherevko, N. Kulyk and K. J. J. Mayrhofer, Durability of platinum-based fuel cell electrocatalysts: Dissolution of bulk and nanoscale platinum, Nano Energy, 2016, 29, 275–298, DOI:10.1016/j.nanoen.2016.03.005.
- D. Y. Chung, J. M. Yoo and Y. E. Sung, Highly Durable and Active Pt-Based Nanoscale Design for Fuel-Cell Oxygen-Reduction Electrocatalysts, Adv. Mater., 2018, 30(42), e1704123, DOI:10.1002/adma.201704123.
- E. F. Holby, W. Sheng, Y. Shao-Horn and D. Morgan, Pt nanoparticle stability in PEM fuel cells: influence of particle size distribution and crossover hydrogen, Energy Environ. Sci., 2009, 2(8), 865–871, 10.1039/b821622n.
- D. D. Papadias, R. K. Ahluwalia, N. Kariuki, D. Myers, K. L. More, D. A. Cullen, B. T. Sneed, K. C. Neyerlin, R. Mukundan and R. L. Borup, Durability of Pt-Co Alloy Polymer Electrolyte Fuel Cell Cathode Catalysts under Accelerated Stress Tests, J. Electrochem. Soc., 2018, 165(6), F3166–F3177, DOI:10.1149/2.0171806jes.
- B. T. Sneed, D. A. Cullen, R. Mukundan, R. L. Borup and K. L. More, PtCo Cathode Catalyst Morphological and Compositional Changes after PEM Fuel Cell Accelerated Stress Testing, J. Electrochem. Soc., 2018, 165(6), F3078–F3084, DOI:10.1149/2.0091806jes.
- R. K. Ahluwalia, D. D. Papadias, N. N. Kariuki, J.-K. Peng, X. Wang, Y. Tsai, D. G. Graczyk and D. J. Myers, Potential Dependence of Pt and Co Dissolution from Platinum-Cobalt Alloy PEFC Catalysts Using Time-Resolved Measurements, J. Electrochem. Soc., 2018, 165(6), F3024–F3035, DOI:10.1149/2.0031806jes.
- M. Gummalla, S. Ball, D. Condit, S. Rasouli, K. Yu, P. Ferreira, D. Myers and Z. Yang, Effect of Particle Size and Operating Conditions on Pt3Co PEMFC Cathode Catalyst Durability, Catalysts, 2015, 5(2), 926–948, DOI:10.3390/catal5020926.
- L. Tong, L. Fan and H.-W. Liang, Platinum intermetallic nanoparticle cathode catalysts for proton-exchange-membrane fuel cells: Synthesis and ordering effect, Curr. Opin. Electrochem., 2023, 39, 101281, DOI:10.1016/j.coelec.2023.101281.
- M. Janssen, P. Weber and M. Oezaslan, Recent advances of various Pt-based catalysts for oxygen reduction reaction (ORR) in polymer electrolyte membrane fuel cells (PEMFCs), Curr. Opin. Electrochem., 2023, 40, 101337, DOI:10.1016/j.coelec.2023.101337.
- D. A. Cullen, K. C. Neyerlin, R. K. Ahluwalia, R. Mukundan, K. L. More, R. L. Borup, A. Z. Weber, D. J. Myers and A. Kusoglu, New roads and challenges for fuel cells in heavy-duty transportation, Nat. Energy, 2021, 6(5), 462–474, DOI:10.1038/s41560-021-00775-z.
- Y. Shao, G. Yin and Y. Gao, Understanding and approaches for the durability issues of Pt-based catalysts for PEM fuel cell, J. Power Sources, 2007, 171(2), 558–566, DOI:10.1016/j.jpowsour.2007.07.004.
- Y. Chen, J. Wang, H. Liu, R. Li, X. Sun, S. Ye and S. Knights, Enhanced stability of Pt electrocatalysts by nitrogen doping in CNTs for PEM fuel cells, Electrochem. Commun., 2009, 11(10), 2071–2076, DOI:10.1016/j.elecom.2009.09.008.
- Y. Zhou, T. Holme, J. Berry, T. R. Ohno, D. Ginley and R. O'Hayre, Dopant-Induced Electronic Structure Modification of HOPG Surfaces: Implications for High Activity Fuel Cell Catalysts, J. Phys. Chem. C, 2010, 114(1), 506–515, DOI:10.1021/jp9088386.
- J. Melke, B. Peter, A. Habereder, J. Ziegler, C. Fasel, A. Nefedov, H. Sezen, C. Woll, H. Ehrenberg and C. Roth, Metal-Support Interactions of Platinum Nanoparticles Decorated N-Doped Carbon Nanofibers for the Oxygen Reduction Reaction, ACS Appl. Mater. Interfaces, 2016, 8(1), 82–90, DOI:10.1021/acsami.5b06225.
- S. Hasegawa, Y. Kunisada and N. Sakaguchi, Diffusion of a Single Platinum Atom on Light-Element-Doped Graphene, J. Phys. Chem. C, 2017, 121(33), 17787–17795, DOI:10.1021/acs.jpcc.7b01241.
- Z. Li, Q. Gao, H. Zhang, W. Tian, Y. Tan, W. Qian and Z. Liu, Low content Pt nanoparticles anchored on N-doped reduced graphene oxide with high and stable electrocatalytic activity for oxygen reduction reaction, Sci. Rep., 2017, 7, 43352, DOI:10.1038/srep43352.
- Z. Song, Y. N. Zhu, H. Liu, M. N. Banis, L. Zhang, J. Li, K. Doyle-Davis, R. Li, T. K. Sham, L. Yang, A. Young, G. A. Botton, L. M. Liu and X. Sun, Engineering the Low Coordinated Pt Single Atom to Achieve the Superior Electrocatalytic Performance toward Oxygen Reduction, Small, 2020, 16(43), e2003096, DOI:10.1002/smll.202003096.
- X. Tong, X. Zhan, Z. Gao, G. Zhang, Y. Xie, J. Tian, H. Ranganathan, D. Li, J. P. Claverie and S. Sun, Effect of the metal-support interaction in platinum anchoring on heteroatom-doped graphene for enhanced oxygen reduction reaction, Chem. Commun., 2022, 58(82), 11519–11522, 10.1039/d2cc03505g.
- E. Hornberger, T. Merzdorf, H. Schmies, J. Hubner, M. Klingenhof, U. Gernert, M. Kroschel, B. Anke, M. Lerch, J. Schmidt, A. Thomas, R. Chattot, I. Martens, J. Drnec and P. Strasser, Impact of Carbon N-Doping and Pyridinic-N Content on the Fuel Cell Performance and Durability of Carbon-Supported Pt Nanoparticle Catalysts, ACS Appl. Mater. Interfaces, 2022, 14(16), 18420–18430, DOI:10.1021/acsami.2c00762.
- A. Chutia, Adsorption of Transition Metal Catalysts on Carbon Supports: A Theoretical Perspective, Johnson Matthey Technol. Rev., 2022, 66(1), 4–20, DOI:10.1595/205651322x16212512135401.
- M. A. Fitzgerald, H. Wang, A. Ly, J. Foster, M. Sorrells, T. Asset, P. Atanassov and S. Pylypenko, Effect of Nitrogen Defects on Pt Nanoparticle Dispersion and Stability Studied by Electron Microscopy Paired with Machine Learning Image Processing for Probing Catalyst–Support Interactions, ACS Appl. Nano Mater., 2023, 6(7), 5313–5324, DOI:10.1021/acsanm.2c05414.
- T. Xie, W. Jung, T. Kim, P. Ganesan and B. N. Popov, Development of Highly Active and Durable Hybrid Cathode Catalysts for Polymer Electrolyte Membrane Fuel Cells, J. Electrochem. Soc., 2014, 161(14), F1489–F1501, DOI:10.1149/2.0961414jes.
- Q. Li, H. Pan, D. Higgins, R. Cao, G. Zhang, H. Lv, K. Wu, J. Cho and G. Wu, Metal-organic framework-derived bamboo-like nitrogen-doped graphene tubes as an active matrix for hybrid oxygen-reduction electrocatalysts, Small, 2015, 11(12), 1443–1452, DOI:10.1002/smll.201402069.
- L. Chong, J. Wen, J. Kubal, F. G. Sen, J. Zou, J. Greeley, M. Chan, H. Barkholtz, W. Ding and D. J. Liu, Ultralow-loading platinum-cobalt fuel cell catalysts derived from imidazolate frameworks, Science, 2018, 362(6420), 1276–1281, DOI:10.1126/science.aau0630.
- J. Ying, J. Li, G. Jiang, Z. P. Cano, Z. Ma, C. Zhong, D. Su and Z. Chen, Metal-organic frameworks derived platinum-cobalt bimetallic nanoparticles in nitrogen-doped hollow porous carbon capsules as a highly active and durable catalyst for oxygen reduction reaction, Appl. Catal., B, 2018, 225, 496–503, DOI:10.1016/j.apcatb.2017.11.077.
- J. Kim, C. Kim, I. Y. Jeon, J. B. Baek, Y. W. Ju and G. Kim, A New Strategy for Outstanding Performance and Durability in Acidic Fuel Cells: A Small Amount Pt Anchored on Fe, N co-Doped Graphene Nanoplatelets, ChemElectroChem, 2018, 5(19), 2857–2862, DOI:10.1002/celc.201800674.
- X. Ao, W. Zhang, B. Zhao, Y. Ding, G. Nam, L. Soule, A. Abdelhafiz, C. Wang and M. Liu, Atomically dispersed Fe–N–C decorated with Pt-alloy core–shell nanoparticles for improved activity and durability towards oxygen reduction, Energy Environ. Sci., 2020, 13(9), 3032–3040, 10.1039/d0ee00832j.
- W. Wu, Z. Zhang, Z. Lei, X. Wang, Y. Tan, N. Cheng and X. Sun, Encapsulating Pt Nanoparticles inside a Derived Two-Dimensional Metal–Organic Frameworks for the Enhancement of Catalytic Activity, ACS Appl. Mater. Interfaces, 2020, 12(9), 10359–10368, DOI:10.1021/acsami.9b20781.
- Z. Qiao, C. Wang, C. Li, Y. Zeng, S. Hwang, B. Li, S. Karakalos, J. Park, A. J. Kropf, E. C. Wegener, Q. Gong, H. Xu, G. Wang, D. J. Myers, J. Xie, J. S. Spendelow and G. Wu, Atomically dispersed single iron sites for promoting Pt and Pt3Co fuel cell catalysts: performance and durability improvements, Energy Environ. Sci., 2021, 14(9), 4948–4960, 10.1039/d1ee01675j.
- F. Xiao, Y. Wang, G. L. Xu, F. Yang, S. Zhu, C. J. Sun, Y. Cui, Z. Xu, Q. Zhao, J. Jang, X. Qiu, E. Liu, W. S. Drisdell, Z. Wei, M. Gu, K. Amine and M. Shao, Fe–N–C Boosts the Stability of Supported Platinum Nanoparticles for Fuel Cells, J. Am. Chem. Soc., 2022, 144(44), 20372–20384, DOI:10.1021/jacs.2c08305.
- L. Huang, M. Wei, R. Qi, C. L. Dong, D. Dang, C. C. Yang, C. Xia, C. Chen, S. Zaman, F. M. Li, B. You and B. Y. Xia, An integrated platinum-nanocarbon electrocatalyst for efficient oxygen reduction, Nat. Commun., 2022, 13(1), 6703, DOI:10.1038/s41467-022-34444-w.
- T. W. Song, C. Xu, Z. T. Sheng, H. K. Yan, L. Tong, J. Liu, W. J. Zeng, L. J. Zuo, P. Yin, M. Zuo, S. Q. Chu, P. Chen and H. W. Liang, Small molecule-assisted synthesis of carbon supported platinum intermetallic fuel cell catalysts, Nat. Commun., 2022, 13(1), 6521, DOI:10.1038/s41467-022-34037-7.
- M. Chen, C. Li, B. Zhang, Y. Zeng, S. Karakalos, S. Hwang, J. Xie and G. Wu, High-Platinum-Content Catalysts on Atomically Dispersed and Nitrogen Coordinated Single Manganese Site Carbons for Heavy-Duty Fuel Cells, J. Electrochem. Soc., 2022, 169(3), 034510, DOI:10.1149/1945-7111/ac58c7.
- Q. Shu, J. Zhang, B. Hu, X. Deng, J. Yuan, R. Ran, W. Zhou and Z. Shao, Rational Design of a High-Durability Pt-Based ORR Catalyst Supported on Mn/N Codoped Carbon Sheets for PEMFCs, Energy Fuels, 2022, 36(3), 1707–1715, DOI:10.1021/acs.energyfuels.1c04306.
- F. Xiao, Q. Wang, G.-L. Xu, X. Qin, I. Hwang, C.-J. Sun, M. Liu, W. Hua, H.-w. Wu, S. Zhu, J.-C. Li, J.-G. Wang, Y. Zhu, D. Wu, Z. Wei, M. Gu, K. Amine and M. Shao, Atomically dispersed Pt and Fe sites and Pt–Fe nanoparticles for durable proton exchange membrane fuel cells, Nat. Catal., 2022, 5(6), 503–512, DOI:10.1038/s41929-022-00796-1.
- Y. Zeng, J. Liang, C. Li, Z. Qiao, B. Li, S. Hwang, N. N. Kariuki, C. W. Chang, M. Wang, M. Lyons, S. Lee, Z. Feng, G. Wang, J. Xie, D. A. Cullen, D. J. Myers and G. Wu, Regulating Catalytic Properties and Thermal Stability of Pt and PtCo Intermetallic Fuel-Cell Catalysts via Strong Coupling Effects between Single-Metal Site-Rich Carbon and Pt, J. Am. Chem. Soc., 2023, 145(32), 17643–17655, DOI:10.1021/jacs.3c03345.
- Y. Zeng, J. Liang, B. Li, H. Yu, B. Zhang, K. S. Reeves, D. A. Cullen, X. Li, D. Su, G. Wang, S. Zhong, H. Xu, N. Macauley and G. Wu, Pt Nanoparticles on Atomic-Metal-Rich Carbon for Heavy-Duty Fuel Cell Catalysts: Durability Enhancement and Degradation Behavior in Membrane Electrode Assemblies, ACS Catal., 2023, 13(18), 11871–11882, DOI:10.1021/acscatal.3c03270.
- X. B. Gao, Y. Wang, W. Xu, H. Huang, K. Zhao, H. Ye, Z. Y. Zhou, N. Zheng and S. G. Sun, Mechanism of Particle-Mediated Inhibition of Demetalation for Single-Atom Catalytic Sites in Acidic Electrochemical Environments, J. Am. Chem. Soc., 2023, 145(28), 15528–15537, DOI:10.1021/jacs.3c04315.
- A. Ly, E. Murphy, H. Wang, Y. Huang, G. Ferro, S. Guo, T. Asset, Y. Liu, I. V. Zenyuk and P. Atanassov, Electrochemical trends of a hybrid platinum and metal–nitrogen–carbon catalyst library for the oxygen reduction reaction, EES Catal., 2024, 2(2), 624–637, 10.1039/d3ey00235g.
- S. Yin, Y. N. Yan, L. Chen, N. Cheng, X. Cheng, R. Huang, H. Huang, B. Zhang, Y. X. Jiang and S. G. Sun, FeN4 Active Sites Electronically Coupled with PtFe Alloys for Ultralow Pt Loading Hybrid Electrocatalysts in Proton Exchange Membrane Fuel Cells, ACS Nano, 2024, 18(1), 551–559, DOI:10.1021/acsnano.3c08570.
- V. P. Glibin, J.-P. Dodelet and G. Zhang, Spontaneous Demetallation of Mn(II)Nx Catalytic Sites in Proton Exchange Membrane Fuel Cell Conditions, ACS Catal., 2024, 14(1), 330–343, DOI:10.1021/acscatal.3c04310.
- T. Chen, Z. Huang, J. Liu, L. Jiang, J. Chu, C. Song and A. Kong, Mn-Pyridine N site-enriched Mn–N–C derived from covalent organic polymer for electrochemical oxygen reduction and capacitive storage, Ionics, 2021, 27, 5229–5239 CrossRef CAS.
- J. Li, M. Chen, D. A. Cullen, S. Hwang, M. Wang, B. Li, K. Liu, S. Karakalos, M. Lucero, H. Zhang, C. Lei, H. Xu, Z. Sterbinsky, D. S. Feng, K. L. More, G. Wang and G. Wu, Atomically dispersed manganese catalysts for oxygen reduction in proton-exchange membrane fuel cells, Nat. Catal., 2018, 1, 935–945 CrossRef CAS.
- T. Stracensky, L. Jiao, Q. Sun, E. Liu, F. Yang, S. Zhong, D. A. Cullen, D. J. Meyers, A. J. Kropf and Q. Jia, Mukerjee. Bypassing formation of oxide intermediate via chemical vapor deposition for the synthesis of an Mn–N–C catalyst with improved ORR activity, ACS Catal., 2023, 13, 14782–14791 CrossRef CAS PubMed.
- J. B. Mann, T. L. Meek, E. T. Knight, J. F. Capitani and L. C. Allen, Configuration Energies of the d-Block Elements, J. Am. Chem. Soc., 2000, 122(21), 5132–5137, DOI:10.1021/ja9928677.
- D. R. Herrick, Connecting Pauling and Mulliken Electronegativities, J. Chem. Theory Comput., 2005, 1(2), 255–262, DOI:10.1021/ct049942a.
- A. Nie, J. Wu, C. Zhou, S. Yao, C. Luo, R. C. Forrey and H. Cheng, Structural evolution of subnano platinum clusters, Int. J. Quantum Chem., 2007, 107(1), 219–224, DOI:10.1002/qua.21011.
- S. Stambula, N. Gauquelin, M. Bugnet, S. Gorantla, S. Turner, S. Sun, J. Liu, G. Zhang, X. Sun and G. A. Botton, Chemical structure of nitrogen-doped graphene with single platinum atoms and atomic clusters as a platform for the PEMFC electrode, J. Phys. Chem. C, 2014, 118(8), 3890–3900 CrossRef CAS.
- C. S. Wang, H. Wang, R. Wu and R. Ragan, Evaluating the Stability of Single-Atom Catalysts with High Chemical Activity, J. Phys. Chem. C, 2018, 122(38), 21919–21926, DOI:10.1021/acs.jpcc.8b06621.
- H. Gross, C. T. Campbell and D. A. King, Metal–carbon bond energies for adsorbed hydrocarbons from calorimetric data, Surf. Sci., 2004, 572(2–3), 179–190, DOI:10.1016/j.susc.2004.08.015.
- R. T. Sanderson, Polar Covalence, Academic Press New York, London; Toronto, 1983 Search PubMed.
- I. Fampiou and A. Ramasubramaniam, Binding of Pt Nanoclusters to Point Defects in Graphene: Adsorption, Morphology, and Electronic Structure, J. Phys. Chem. C, 2012, 116(11), 6543–6555, DOI:10.1021/jp2110117.
- H. Shi, S. M. Auerbach and A. Ramasubramaniam, First-Principles Predictions of Structure–Function Relationships of Graphene-Supported Platinum Nanoclusters, J. Phys. Chem. C, 2016, 120(22), 11899–11908, DOI:10.1021/acs.jpcc.6b01288.
- V. I. Nefedov, Angular dependence of inductive effect and cis—trans influence in coordination compounds, Chem. Phys., 1976, 14(2), 241–254, DOI:10.1016/0301-0104(76)80041-9.
- T. L. Allen, Reciprocal Mean as a Measure of Covalent Bond Energy, J. Chem. Phys., 1957, 27, 810–811, DOI:10.1063/1.1743836.
- N. Dimov, A. Staykov, M. I. M. Kusdhany and S. M. Lyth, Tailoring the work function of graphene via defects, nitrogen-doping and hydrogenation: A first principles study, Nanotechnology, 2023, 34(41), 415001, DOI:10.1088/1361-6528/ac7ecf.
- S. Trasatti, Electronegativity, work function, and heat of adsorption of hydrogen on metals, J. Chem. Soc., Faraday Trans., 1972, 68, 229–236, 10.1039/f19726800229.
- V. M. Yakovlev, New method of the elements' electronegativity assessment, Russ. J. Inorg. Chem., 2002, 47(10), 1644–1646 CAS.
- M. Juhász, S. Takahashi, S. Arulmozhiraja and T. Fujii, Bond energies (Pt–NH3, Pt–Cl) and proton affinity of cisplatin: A density functional theory approach, J. Struct. Chem., 2012, 53, 443–442448, DOI:10.1134/S0022476612030043.
- I. C. Gerber and P. Serp, A Theory/Experience Description of Support Effects in Carbon-Supported Catalysts, Chem. Rev., 2019, 120(2), 1250–1349, DOI:10.1021/acs.chemrev.9b00209.
- R. C. Gray and D. M. Hercules, Correlations between ESCA chemical shifts and modified sanderson electronegativity calculations, J. Electron Spectrosc. Relat. Phenom., 1977, 12(1), 37–53, DOI:10.1016/0368-2048(77)85066-4.
- C. Cardenas, P. Ayers, F. De Proft, D. J. Tozer and P. Geerlings, Should negative electron affinities be used for evaluating the chemical hardness?, Phys. Chem. Chem. Phys., 2011, 13(6), 2285–2293, 10.1039/c0cp01785j.
- M. S. Wilson and S. Ichikawa, Comparison between the geometric and harmonic mean electronegativity equilibration techniques, J. Phys. Chem., 1989, 93(8), 3087–3089, DOI:10.1021/j100345a041.
- R. T. Sanderson, Electronegativity and bonding of transitional elements, Inorg. Chem., 1986, 25(19), 3518–3522, DOI:10.1021/ic00239a040.
- S. S. Batsanov, Refinement of the sanderson procedure for calculating electronegativities of atoms, J. Struct. Chem., 1988, 29, 631–635, DOI:10.1007/BF00748841.
- S. S. Batsanov and A. S. Batsanov, Introduction to Structural Chemistry, Springer Science + Business Media, Dordrecht, 2012 Search PubMed.
- S. S. Batsanov, Dependence of covalent radii on oxidation state of atoms, Russ. J. Inorg. Chem., 2002, 47(7), 1112–1114 CrossRef CAS.
- K. A. Gingerich, Experimental and predicted stability of diatomic metals and metallic clusters, Faraday Symp. Chem. Soc., 1980, 14, 109–125, 10.1039/FS9801400109.
- V. Schomaker and D. P. Stevenson, Some Revisions of the Covalent Radii and the Additivity Rule for the Lengths of Partially Ionic Single Covalent Bonds, J. Am. Chem. Soc., 1941, 63(1), 37–40, DOI:10.1021/ja01846a007.
- B. Kirchhoff, L. Braunwarth, C. Jung, H. Jonsson, D. Fantauzzi and T. Jacob, Simulations of the Oxidation and Degradation of Platinum Electrocatalysts, Small, 2020, 16(5), e1905159, DOI:10.1002/smll.201905159.
- K. Kumar, L. Dubau, F. Jaouen and F. Maillard, Review on the Degradation Mechanism of Metal–N–C Catalysts for the Oxygen Reduction Reaction in Acid Electrolyte: Current Understanding and Mitigation Approaches, Chem. Rev., 2023, 123(15), 9265–9326, DOI:10.1021/acs.chemrev.2c00685.
- R. T. Sanderson, Electronegativities in inorganic chemistry, J. Chem. Educ., 1954, 31(1), 2–7, DOI:10.1021/ed029p539.
- J. Liu, M. Jiao, L. Lu, H. M. Barkholtz, Y. Li, Y. Wang, L. Jiang, Z. Wu, D. Liu, L. Zhuang, C. Ma, J. Zeng, B. Zhang, D. Su, P. Song, W. Xing, W. Xu, Y. Wang, Z. Jiang and G. Sun, High performance platinum single atom electrocatalyst for oxygen reduction reaction, Nat. Commun., 2017, 8, 15938, DOI:10.1038/ncomms15938.
- G. B. Naumov, B. N. Ryzhenko and I. L. V. Khodakovskii, Handbook of Thermodynamic Data, National Technical Information Service; U.S. Geological Survey; U.S. Dept. of Commerce, Springfield, VA, 1974 Search PubMed.
- W. L. Masterton and C. N. Hurley, Chemistry (Principles and Reactions), Harcourt Brace & Company, New York, 2nd edn, 1993, pp. 215–216 Search PubMed.
- L. Glasser and H. D. B. Jenkins, Standard absolute entropies, S°298, from volume or density, Thermochim. Acta, 2004, 414(2), 125–130, DOI:10.1016/j.tca.2003.12.006.
- D. W. Hofmann, Fast estimation of crystal densities, Acta Crystallogr., Sect. B, 2002, 58, 489–493, DOI:10.1107/s0108768101021814.
- M. Umeda, K. Sayama, T. Maruta and M. Inoue, Proton activity of Nafion 117 membrane measured from potential difference of hydrogen electrodes, Ionics, 2013, 19(4), 623–627, DOI:10.1007/s11581-012-0791-z.
- B. Hammer and J. K. Nørskov, Electronic factors determining the reactivity of metal surfaces, Surf. Sci., 1995, 343(3), 211–220, DOI:10.1016/0039-6028(96)80007-0.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08108k |
| This journal is © The Royal Society of Chemistry 2025 |