Optimisation of a P3 phase with superior high voltage reversibility

Abstract

Activation of oxygen anion redox represents an effective method of increasing the specific capacity as well as raising the operating voltage of layered sodium transition metal oxides. However, these reactions are often accompanied by irreversible structural transformations and detrimental side-reactions between the electrolyte and electrode interface which accelerate degradation, thereby impeding their practical application. To optimise the oxygen anion reversibility for practical use and compare the effects of dopants, we investigated Zn- and Ti-substitution both separately and combined in P3-structure Na_0.7Mn_0.75Ni_0.25O₂, assisted by DFT calculations. The Zn-substituted materials, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ present superior cycling stability over the high voltage range 3.8–4.3 V and enhanced rate capability, delivering a reversible capacity of ∼80 mA h g⁻¹ at 500 mA g⁻¹ over the voltage window 2.2–4.3 V compared with 58.6 mA h g⁻¹ for the parent-phase. The improved electrochemical performance of the Zn-substituted materials is attributed to suppression of the P3 to O′3 phase transformation revealed by X-ray diffraction and the lower electronegativity and filled d-band of Zn. The presence of TiO₆ octahedra in the Ti-substituted materials relieves structural distortions/TM ordering, also improving the cycling stability. With Zn/Ti co-substitution these advantages may be combined, as demonstrated by the superior electrochemical performance observed for Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂.

---

Introduction

At present, lithium-ion batteries (LIBs) power most portable electronic devices and more recently facilitated the electrification of vehicles. However, the limited availability of lithium sources and the ever growing demand for energy, make it even more important to develop alternative technologies to LIBs for energy storage devices, especially largescale grid applications.¹ Sodium-ion batteries (SIBs) are considered promising alternatives, based on the widespread distribution, greater abundance and low cost of sodium.^2–4 However, the energy density of SIBs typically remains lower than commercial LIBs, limited by the positive electrode, thus preventing the widespread application of SIBs. Therefore, one of the primary focuses of research lies in enhancing the energy density of positive electrode materials for SIBs.⁵

Layered sodium transition metal oxides, Na_xTM_yO₂ (0.4 ≤ x ≤ 1.0, and TM = transition metal ion(s)) have attracted a great deal of interest as positive electrode materials for SIBs owing to their versatile chemistry, which enables the use of low-cost, abundant elements.² Sodium layered oxides can crystallise in O2, O3, P2 and P3 phases, as well as distorted O′3 and P′2 phases, in which the Na⁺ ions can be accommodated in either octahedral (O) or trigonal prismatic (P) sites, with the number describing the number of TMO₂ slabs in the unit cell with different stacking of the oxygen layers.⁶ However, these materials generally undergo structural transformations upon charge to high voltages, between the P-type and O-type phases, caused by gliding of the TMO₂ layers upon insertion/extraction of Na⁺ ions, which can result in significant unit cell volume changes accompanied by concomitant capacity losses. Substitution of Mn by electrochemically active or inactive elements reduces the concentration of Jahn–Teller active Mn³⁺ ions, thereby suppressing Jahn–Teller distortions, and provides structural stability. Furthermore, substitution of Mn by electrochemically active elements like Ni²⁺ enables the transfer of electrons between the O 2p states and transition metal 3d bands, often via a reductive coupling mechanism, and thus activates oxygen anion redox reactions.^7–10 When electrochemically inactive dopants like Li⁺,^11–13 Mg²⁺,^14,15 and Zn²⁺ are used,^16–18 ionic Li–O, Mg–O and Zn–O bonds form with the electrons localised on the oxygen anions that form O 2p nonbonding orbitals at the top of the valence band upon removal of Na⁺ ions. As a result, additional capacity can be obtained originating from anion redox reactions, which represents an effective method of increasing the energy density of sodium layered oxides.^19,20 Despite this, most anion redox-active materials tend to show a large voltage hysteresis on the initial charge/discharge process, associated with cation migration from the transition metal layers to the alkali metal layers, resulting in oxygen loss with structural changes that lead to severe capacity loss.^17,21–23 Therefore, it is important to stabilise the high voltage phase when Na⁺ ions are removed from the structure to improve the cycling stability.

Thus far, the cyclability of numerous P2-type Na_xTMO₂ materials has been enhanced by metal cation substitution, including for example Li⁺,^13,24 Mg²⁺,^21,25 Zn²⁺,^10,16,26,27 Cu²⁺,^28–30 and Ti⁴⁺.^31–33 Among them, the Zn-substituted phase, P2-Na_2/3Mn_7/9Zn_2/9O₂, exhibited anionic redox activity with no oxygen loss, despite showing evidence of cation migration that resulted in capacity loss. DFT calculations demonstrated that the presence of a nonbonding O 2p state activates the anionic redox activity.³⁴ In addition, substituting Fe²⁺ with Zn²⁺ and Ni²⁺ in the P2-Na_0.67Mn_0.6Fe_0.3−x−yZn_xNi_yO₂ phase greatly improved the electrochemical properties, reduced the polarisation, and stabilised the high-voltage structure.³⁵ The effect of substituting Ni²⁺ with Zn²⁺ ions in P2-Na_0.66Ni_0.33−xZn_xMn_0.67O₂ (x = 0, 0.07, 0.14) has been studied to understand the role of Zn. Overall, the Zn-substituted materials exhibited enhanced electrochemical performance, smoother voltage profiles and suppressed the P2 to P′2 structural transformation compared to the parent-phase P2-Na_0.66Ni_0.33Mn_0.67O₂.^36,37 Wu et al. found that Zn reduces the distortion of the Ni–O bonds of the NiO₆ octahedra upon charge/discharge, thereby providing structural stability.³⁷

Comparatively, there have been fewer studies performed on P3-type materials, even though they require less energy during synthesis compared to P2-type materials, and may exhibit better rate capability because of the larger separation between TMO₂ slabs compared to O3-type materials.^38,39 A previous study has investigated the effects of Zn doping on P3-type Na_0.67Mn_0.9Zn_0.1O₂, which exhibited good cycling performance over the voltage range 1.8–4.3 V owing to its stable framework structure.¹⁸ Other studies have revealed that the partial substitution of Mn with Ti⁴⁺ ions is able to enhance the cycling performance of Na_4/7[□_1/7Mn_6/7]O₂ (where □ represents transition metal vacancies), preserving the P3-type oxygen stacking sequence and showing an ultralow volume change of 0.11% over the first cycle.^40,41 Na_4/7[□_1/7Ti_1/7Mn_5/7]O₂ also reveals no capacity loss when cycled over the voltage range 3.0–4.4 V at 10 mA g⁻¹ after 50 cycles and operates at a higher potential compared to Na_4/7[□_1/7Mn_6/7]O₂, owing to the low electronegativity of Ti, which strengthens the Mn–O bonds, as well as stabilising the adjacent O 2p orbitals, as revealed by DFT calculations.⁴¹

Herein, we have studied the influences of substituting Mn³⁺ by Zn²⁺ and Ti⁴⁺, both in isolation and combined, on the electrochemical performance of P3-type Na_0.70Mn_0.75Ni_0.25O₂. Ex situ powder X-ray diffraction (PXRD) and Raman spectroscopy were used to evaluate the structural evolution of P3-Na_0.7Mn_0.75−x−yNi_0.25Zn_xTi_yO₂ (x = 0, 0.07, 0.1, y = 0, 0.1) over the initial charge/discharge process to understand the effects of Zn²⁺ and Ti⁴⁺ substitution on the structural integrity. Furthermore, the experimental studies were combined with density functional theory (DFT) calculations to understand how Zn²⁺ and Ti⁴⁺ ions influence the structural reversibility and oxygen anion redox reactions. This work further extends our understanding on P3-type sodium-based layered oxides, and develops insights into the effects of dopants on enhancing the oxygen anion redox reversibility.^7,18,41,42

Experimental

Synthesis and characterisation of as-prepared materials

The Na_0.7Mn_0.65−x−yNi_0.25Zn_xTi_yO₂ samples with x = 0, 0.07, 0.1, and y = 0, 0.1 were prepared by a typical sol–gel method. An aqueous solution of citric acid (amount of citric acid equal to the molar equivalent of total transition metals) was added under stirring to an aqueous solution of stoichiometric amounts of NaNO₃ (99.0%, Alfa Aesar), Mn(NO₃)₂·6H₂O (98+%, Alfa Aesar), Ni(NO₃)₂·6H₂O (99%, Acros Organics), Zn(NO₃)₂·6H₂O (≥99.0%, Sigma-Aldrich) and [CH₃CO(O–)CO₂NH₄]Ti(OH)₂ (50 wt% in H₂O, Sigma-Aldrich). The resultant solution was stirred overnight at 80 °C and the water was evaporated by heating at 120 °C for 6 to 8 h to give a powdered precursor. The precursor was ground to a fine powder using a pestle and mortar and calcined at 450 °C for 5 h. The samples were then calcined using a two-step process, they were initially heated to 700–760 °C at a rate of 5 °C min⁻¹ for 3 h and cooled to 500 °C at a rate of 5 °C min⁻¹ and held at 500 °C for 5 h, and finally quenched in air. The as-prepared materials were stored and handled in an argon filled glovebox.

Laboratory powder X-ray diffraction (PXRD) patterns of as-prepared samples were collected on a STOE STADIP diffractometer, using Mo Kα₁ radiation (λ = 0.70930 Å) in the 2θ range, 4.0–53.0° over 40 min per scan with a step size of 0.015° and a time per step of 0.73 s in glass capillaries (0.5 mm diameter), at room temperature. Diffraction data were refined using the Rietveld method using Topas Academic V6.⁴³ Scanning electron microscopy (SEM) and energy dispersive Xray spectroscopy (EDS) analysis were-performed on as-synthesised samples using a Schottky field emission gun scanning electron microscopy (FEG-SEM, FEI Scios dual beam) equipped with an EDAX Octane Plus EDS detector for compositional analysis.

Electrochemical analysis

Positive electrodes were prepared by mixing 80 wt% active material, with 10 wt% super C65 carbon (Imerys) and 10 wt% Solef 5130 binder (modified polyvinylidene fluoride, PVDF, Solvay) in n-methyl-2-polyvinylidene which were cast onto carbon-coated aluminium foil, giving typical cast electrode loadings of ∼2–3 mg cm⁻². Electrodes were prepared in air within 6 h and once dry, punched into 13 mm diameter discs and dried at 80 °C under vacuum overnight. Sodium metal and hard carbon were used as the negative electrodes for the half cell and full cells, respectively. In the fabrication of the full cells, the mass ratio of positive electrode to hard carbon (80% hard carbon, 10% super C65 carbon and 10% Solef 5130 binder, punched into 13 mm diameter discs) negative electrode was roughly 2.2 : 1. The electrolyte used was 1 M NaPF₆ in ethylene carbonate/diethyl carbonate (1 : 1 v/v%, Kishida). CR2032 coin cells were assembled in an argon filled glovebox, with positive and negative electrodes separated by a glass fibre separator (Whatman, GF/F) soaked with electrolyte. Electrochemical measurements were collected in a temperature-controlled environment at 30 °C using a Biologic BCS-805 or Maccor series 4200 battery cyclers.

Material characterisation

For ex situ characterisation by means of PXRD and Raman spectroscopy, positive electrodes were prepared by mixing 80 wt% of active material with 20 wt% super C65 carbon, with no binder and Swagelok type cells were assembled as described above using typical powder electrode loadings of 29 mg cm⁻². Cells were cycled galvanostatically at 25 mA g⁻¹ using a Neware BTS4000 battery cycler at room temperature. Positive electrodes were recovered after cycling in an argon filled glovebox, washed with dry dimethyl carbonate (DMC, Sigma-Aldrich, ≥99%) three times and dried under vacuum at room temperature for 1 h so as to minimise relaxation of the metastable Oⁿ⁻ species (3 ≥ n ≥ 1). Powdered samples were loaded into 0.5 mm glass capillaries in an argon filled glovebox to avoid air exposure. Laboratory PXRD patterns were collected as described above and data were analysed using the Rietveld method using Topas Academic V6.⁴³ Raman spectroscopy measurements were performed with a Renishaw inVia Qontor confocal Raman microscope using a 532 nm laser and 1800 l mm⁻¹ grating from 100 to 1900 cm⁻¹. Static scan measurements were collected using a 50× objective, 5% laser power, and an exposure time of 1 second with 1030 accumulations per measurement. The pristine samples and its mixture with C65 were analysed both in and out of the glass capillaries to observe the contributions from the capillary. The Raman spectra were collected in at least ten different locations per sample to ensure the measurements were reproducible. Wire 5.5 software (Renishaw) was used to remove cosmic rays and correct the baseline of the spectra.

Soft X-ray absorption (SXAS) data were recorded in partial fluorescence yield (PFY) mode at the I21 beamline at Diamond Light Source for the O K edge and Ni L_II- and L_III-edges. The samples were transferred to the RIXS spectrometer using a vacuum transfer suitcase to avoid exposure to air. High resolution resonant inelastic X-ray scattering (RIXS) data were collected from the I21 beamline at Diamond Light Source. Scans at 531.5 eV were recorded at fifteen different sample locations and averaged together. The RIXS map of the O K pre-edge was collected in 0.2 eV increments in excitation energy. All measurements were performed at 20 K to minimise any possible beam damage.

Computational methods

Basic Settings All calculations performed in this work employed density functional theory (DFT) as implemented in the Vienna Ab initio Simulation Package code.^44,45 Interactions between core and valence electrons were described using the projector augmented wave (PAW) method.⁴⁶ Geometry optimisations for all structures were carried out using the PBEsol functional,⁴⁷ a variation of the Perdew–Burke–Ernzerhof (PBE),⁴⁸ generalised-gradient approximation (GGA) functional revised for solids. The electron configurations Na (2p⁶3s¹), Mn (3p⁶3d⁵4s²), Ni (3p⁶3d⁸4s²), Ti (3p⁶3d²4s²), Zn (3d¹⁰4s²) and O (2s²2p⁴) were treated as the valence electrons. Cut-off energy for the plane wave expansion was set to be 500 eV, the value of which is deemed sufficient to converge the total energy to within 0.01 eV per atom. Brillouin zones for all compounds were sampled such that the k-points were converged in an accuracy of the total energy in 0.001 eV per atom. To correct the self-interaction error inherent to the strongly correlated Mn d and Ni d orbitals, PBEsol + U method,^49,50 where the U values of 3.9 and 6.2 eV were applied for Mn and Ni, respectively. All DFT geometry optimisations of model structures were carried out until the forces on all atoms were less than 0.01 eV⁻¹. The magnetic arrangements of Mn and Ni were assumed ferromagnetic for all model structures.

Model structure construction. To assess the P3 to O3 transition behaviour during charge/discharge, it is necessary to obtain the P3- and O3-type structures across the full Na composition range of 0 < x < 1 of Na_xTMO₂. However, experimental P3-type structures are available only for the intermediate region (∼0.3 < x < ∼0.7), whereas O3-type structures are reported near both ends of the composition range (x < ∼0.3 and x > ∼0.7) because of their relative phase stabilities. To obtain the atomic configurations of P3 and O3 phases for the whole Na composition range (0 < x < 1), a model of P3-type NaMnO₂ (R3m) structure was first constructed by gliding part of the TMO₂ slabs of O3 NaMnO₂ (R3̄m, mp-578605) that can be retrieved from Materials Project database.⁵¹ P3-type supercells with 20 formula units were then constructed to depict the chemical compositions to two decimal places (e.g., Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂). In this procedure, the shape of supercells was transformed to simple cubic using the Atomic Simulation Environment to minimise the interatomic interactions with their corresponding periodic images.⁵² The transformation matrix used for generating the supercell structure is .

Atomic configurations of P3-type NaMn_0.65Ni_0.25Ti_0.1O₂, NaMn_0.65Ni_0.25Zn_0.1O₂ and NaMn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ were generated by substituting Mn of NaMnO₂ (R3m) to the target compositions. For the generated structures, differing numbers of Na vacancies were created to model the partially desodiated materials, followed by DFT geometry optimisation. In this calculation, all atomic arrangements arising from symmetry unique Na vacancy sites were considered, the algorithm of which is described by Morgan et al.⁵³ Among numerous atomic arrangements of partially desodiated Na_xMn_0.65Ni_0.25Ti_0.1O₂, Na_xMn_0.65Ni_0.25Zn_0.1O₂ and Na_xMn_0.58Ni_0.25Zn_0.07Ti_0.1O₂, up to eleven lowest electrostatic energy structures were selected per individual Na composition (x = 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0) using the Ewald summation method contained in Pymatgen,⁵⁴ resulting in a total of 645 structures (215 structures for each P3-Na_xTM_yO₂). For the most stable configuration of each chemical formula, O3-type structures were generated by gliding the part of the TMO₂ layers by (−1/3, −2/3, 0), which gives rise to a total of 63 P3-type structures.

Voltage calculation. The subsequent geometry optimisations of the derived structures provide DFT total energies, the values of which were then used to predict theoretical voltage profiles. For the discharge process of layered Na_xTMO₂ with the intercalation of Δx amount of Na (Na_xTMO₂ + ΔxNa → Nax_+ΔxTMO₂), the theoretical voltage (V) can be calculated using the total energies of Na (E_Na), before (E_NaxTMO2) and after sodiation (E_Nax+ΔxTMO2) as follows:

V = (E_NaxTMO2 + ΔxE_Na − E_Nax+ΔxTMO2)/Δx

Here, Na_xTMO₂ and Na_x+ΔxTMO₂ are typically the ground state phases of the convex hull of Na_xTMO₂ and their Na compositions determine the end points of theoretical voltage plateaus. In this study, we calculated theoretical voltages from both the ground state structures and those with different Na arrangements to predict the voltage fluctuations arising from Na diffusion. This was attained by generating the model structures with various Na arrangements (see model structure construction above), followed by calculating the theoretical voltage plateaus using the structures with their total energies close to the ground state structure by less than 0.0259 eV per atom that can be reached by thermal vibration at room temperature.

Results and discussion

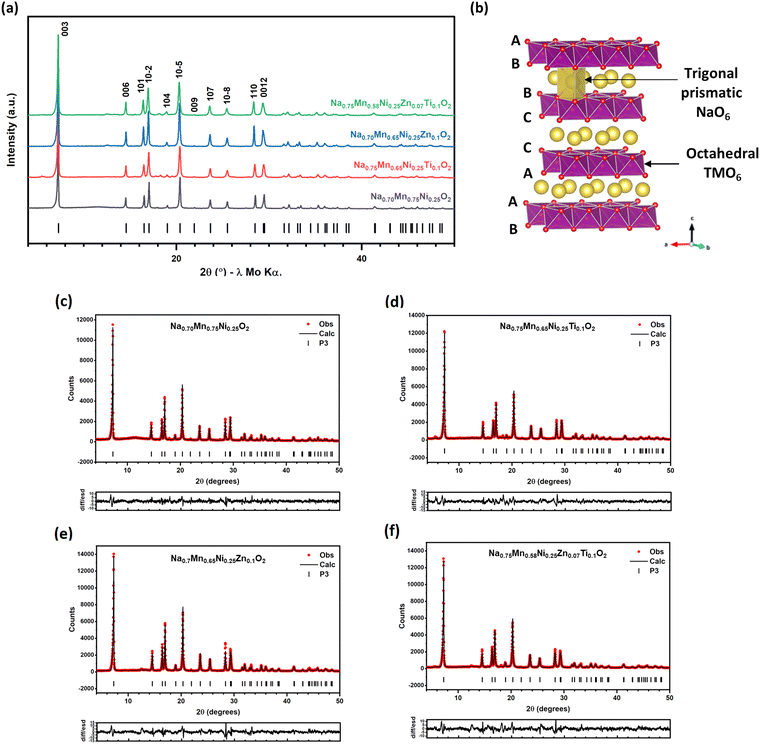
Characterisation of as-synthesised Na_0.7Mn_0.75−x−yNi_0.25Zn_xTi_yO₂

A series of P3-type materials, Na_0.7Mn_0.75Ni_0.25O₂, Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ were prepared by a typical sol–gel method. PXRD patterns of the as-synthesised materials were collected and are presented in Fig. 1(a). The major diffraction peaks can be indexed to a trigonal lattice with space group R3m. Rietveld refinements (Fig. 1(c–f) and Table S1†) were performed, and diffraction peaks are well-fitted using the P3 structural model. Trace impurities were observed in some cases, with a small amount of P2 phase (1.7%) observed in the parent Na_0.7Mn_0.75Ni_0.25O₂ pattern, and an unidentified Ti-containing phase in Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂. The refined unit cell parameters (a = 2.8791(3) Å, c = 16.816(3) Å, V = 120.72(3) ų) for the parent phase, Na_0.7Mn_0.75Ni_0.25O₂ are comparable to those in previous reports.^7,55 Upon substitution of Mn by Ti⁴⁺ and/or Zn²⁺, there are changes in the unit cell volumes, as illustrated in Fig. S2(a).† After substituting 10% of Mn⁴⁺ (ionic radius 0.53 Å) with Ti⁴⁺ (0.605 Å) the unit cell volume increases slightly for Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ (120.86(11) ų) relative to the parent phase Na_0.7Mn_0.75Ni_0.25O₂ (120.72(3) ų).⁵⁶ The larger ionic radius for Zn²⁺ ions (0.74 ų),⁵⁶ results in a greater unit cell volume expansion for Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ (121.49(10) ų) and an even greater unit cell volume increase is observed for Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ (122.02(5) ų). In addition to the unit cell volume expansion, the a unit cell parameter (Fig. S1(b)†) shows a comparable expansion which is correlated with the TMO (TM = transition metal) bond length. Since the refined Na occupancies (Table S1†) for these materials are essentially the same (∼0.63 Na⁺ ions), it is therefore reasonable to attribute the changes in the unit cell volume (Fig. S1(a)†) to the successful incorporation of Ti⁴⁺ and/or Zn²⁺ ions into the P3-Na_xTM_yO₂ phase. Fig. 1(b) illustrates the P3 crystal structure which exhibits the ABBCCA oxygen stacking sequence, consisting of alternating layers of Na⁺ ions which occupy trigonal prismatic sites and TMO₂ layers with the transition metal ions (TM = Mn, Ni, Zn and Ti) occupying octahedral sites. Additional reflections are also apparent in substituted cases, which may arise from ordering in the TM layer and/or sodium/vacancy ordering. Several models exist which describe possible superlattices in the P3 structure and these were tested systematically. For both Na_0.7Mn_0.75Ni_0.25O₂ and Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ the improvements in the fit can be attributed to the increase in the number of variables in the refinement and there are no obvious reflections which may be attributed to superlattice formation. In the Zn-substituted materials, superlattice reflections are apparent and the structures could be refined in the P2₁/c space group – in a model originally developed to describe ordering in Na_0.67NiO₂.⁵⁷ This model contains two different transition metal sites, which for Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ refine with different occupancies and different bond lengths, suggesting that formation of the superstructure is driven by ionic size/charge. We also observe partial ordering of Na/vacancies. A profile refinement in this model for Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ is shown in Fig. S2† with atomic parameters together with selected bond lengths given in Table S2.† Note that since three transition metals share a site they cannot be refined independently, and the Zn occupancies were fixed at values that corresponded to those of the (similarly sized) Ni.

Fig. 1 (a) Laboratory PXRD patterns of as-synthesised Na_0.7Mn_0.75Ni_0.25O₂ (black), Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ (red), Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ (blue), Na_0.7Mn_0.55Ni_0.25Zn_0.07Ti_0.1O₂ (green). Tick marks indicate allowed reflections for the R3m space group. (b) Structural model of the P3-type lattice showing the stacking sequences of the transition metal (TM) layers with NaO₆ trigonal prisms shown as yellow and TMO₆ octahedra shown as purple polyhedra. Laboratory X-ray Rietveld fit of as-synthesised (c) Na_0.7Mn_0.75Ni_0.25O₂, (d) Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, (e) Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂, and (f) Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂. Observed data points are shown in red, with fitted profile in black. Tick marks indicate allowed reflections for the P3 phase.

Fig. S3† shows SEM micrographs for the as-synthesised materials, which exhibit homogenous morphologies. The morphology of Na_0.7Mn_0.75Ni_0.25O₂ (Fig. S3(a)†) shows primary particles approximately 100 nm in size, fused together and the EDS maps show uniform elemental distribution of sodium, manganese, nickel, and oxygen. As-synthesised Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ (Fig. S3(b)†), similarly shows ∼100 nm primary particles, which are round in shape. The elemental maps for Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ show even distribution of most elements but appear to show titanium-rich regions, which may correspond to the unknown impurity observed in the powder XRD patterns but may also be an artefact related to X-ray absorption/fluorescence since these apparent titanium-rich regions coincide with relatively large troughs in the sample surface. Similarly, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ (Fig. S3(c)†) also presents a homogeneous morphology with rounded particles roughly 100 nm in size. It shows largely even elemental distribution other than small zinc-rich regions. As for Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ (Fig. S3(d)†), it exhibits platelet-like shaped particles that are larger in size, ranging from approximately 100 to 200 nm. Again, it appears as though there are titanium-rich regions associated with the topography of the sample since again they coincide with large troughs/holes, whilst the sodium, manganese, nickel, zinc, and oxygen elemental maps show uniform distributions.

Electrochemical properties

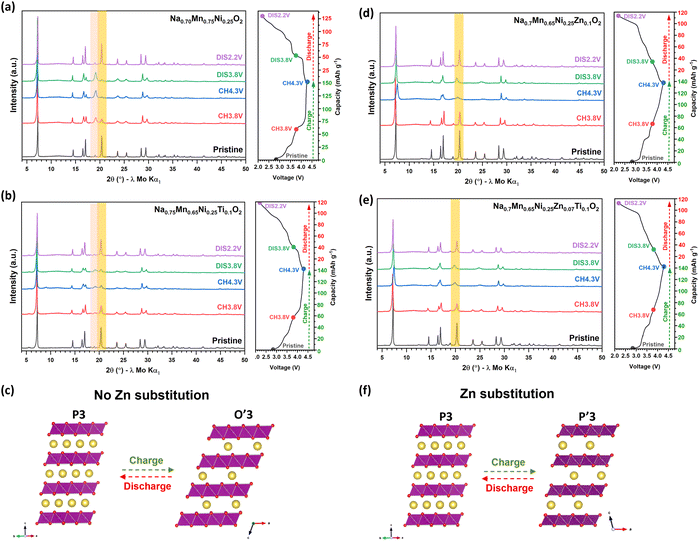
The electrochemical cycling performance of the P3-Na_0.7Mn_0.65−x−yNi_0.25Zn_xTi_yO₂ electrodes was evaluated in sodium-half cells to understand the effects of substituting with Ti⁴⁺ and/or Zn²⁺ ions. Fig. 2(a) and (b) compares the galvanostatic cycling performance of the as-synthesised materials, cycled in the voltage range 2.2–4.3 V vs. Na⁺/Na at rates of 25 and 250 mA g⁻¹, respectively. The discharge capacity of the parent-phase, Na_0.7Mn_0.75Ni_0.25O₂, fades rapidly upon cycling with only 28% of its initial discharge capacity retained after 100 cycles at 25 mA g⁻¹ and at the faster rate of 250 mA g⁻¹ shows a rapid capacity loss over the first ten cycles and stabilises thereafter, maintaining 44% of its initial discharge capacity after 100 cycles. After Ti-substitution, Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, shows an improved capacity retention of 40% at 25 mA g⁻¹ after 100 cycles. As for Zn-substituted Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂, it presents an improved capacity retention of 48% at 25 mA g⁻¹ after 100 cycles. By contrast, Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ reveals superior cycling performance and retains 59% of its initial discharge capacity after 100 cycles at both 25 and 250 mA g⁻¹, thereby demonstrating the stabilising role of Ti and Zn on the cycling stability. In addition, the rate capability of these materials cycled between 2.2–4.3 V at 25, 100, 250 and 500 mA g⁻¹ has been tested. Fig. 2(c) reveals that the Zn-substituted materials, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂, exhibit superior rate performance, and both deliver a reversible capacity of ∼80 mA h g⁻¹ at 500 mA g⁻¹, demonstrating that Zn-substitution has a significant beneficial impact on the electrochemical cycling performance. Similar improvements have also been observed for O3-type NaNi_0.45Zn_0.05Mn_0.4Ti_0.1O₂.⁵⁸

Fig. 2 Galvanostatic cycling performance of Na_0.7Mn_0.75Ni_0.25O₂ (black), Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ (red), Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ (blue) and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ (green), cycled between 2.2–4.3 V at a rate of (a) 25 mA g⁻¹ and (b) 250 mA g⁻¹, showing the discharge capacities. (c) Rate capability of Na_0.7Mn_0.75Ni_0.25O₂ (black), Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ (red), Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ (blue) and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ (green) cycled between 2.2–4.3 V at a current rate of 25, 100, 250 and 500 mA g⁻¹ at 30 °C. Empty and filled symbols represent charge and discharge capacities, respectively.

Fig. 3(a) and (b) shows the galvanostatic charge/discharge curves and corresponding differential capacity versus voltage (dQ/dV) plots, respectively, collected between 2.2–4.3 V at 25 mA g⁻¹. Na_0.7Mn_0.75Ni_0.25O₂ delivers an initial discharge capacity of 127.8 mA h g⁻¹ equivalent to the insertion of 0.50 Na⁺ ions. The initial charge/discharge profile (Fig. 3(a)) exhibits a series of distinct reversible voltage plateaux between 3.0 and 3.8 V associated with the Ni⁴⁺/Ni³⁺/Ni²⁺ redox couples, as well as a reversible extended plateau above 4.0 V, which can be attributed to oxygen anion redox, giving an average initial discharge voltage of 3.51 V.^7,59 However, the oxygen redox activity for Na_0.7Mn_0.75Ni_0.25O₂ deteriorates rapidly and is essentially no longer evident after 30 cycles at 25 mA g⁻¹, consistent with the observed capacity loss (Fig. 2(a)). After Ti-substitution, Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ exhibits a slightly smaller initial discharge capacity of 116.4 mA h g⁻¹ and a comparable charge/discharge profile to Na_0.7Mn_0.75Ni_0.25O₂. It is interesting to note that the dQ/dV plots of Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ reveals two reversible oxidation and reduction peaks beyond 4.1 V at slightly raised redox voltages compared with the other materials, which is consistent with other Ti-substituted systems.^41,60,61 Sodium half-cells of Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ were also cycled between 2.2-4.4 V at 25 mA g⁻¹ and these data are presented in Fig. S4,† which show there is minimal change in the cycling stability over the slightly wider voltage range. Fig. 3(b) shows that the reversibility of the oxygen anion redox activity fades upon cycling, showing only a minimal response after 50 cycles for Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂. In contrast, after Zn-substitution, the charge/discharge profiles for Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ become smoother, suggesting that fewer phase transitions occur, which will be discussed further later. Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ delivers a lower initial discharge capacity of 109.8 mA h g⁻¹ corresponding to the insertion of 0.43 Na⁺ ions and exhibits an average initial discharge voltage of 3.47 V, similar to Na_0.7Mn_0.75Ni_0.25O₂. Furthermore, Fig. 3(b) shows that the high voltage process associated with oxygen anion redox persists even after 50 cycles for both Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂, demonstrating the enhanced oxygen redox stability due to the presence of Zn. Despite this, all materials exhibit a capacity fade, and the voltage profiles (Fig. 2(a)) suggest that this capacity fade occurs at the lower potentials (<3.8 V), associated with the oxidation and reduction of Ni²⁺/Ni³⁺/Ni⁴⁺ ions, indicating that this could be associated with Ni dissolution.^62,63 Future work will involve testing different electrolytes and or binders to suppress this issue.

Fig. 3 (a) Galvanostatic charge/discharge curves and (b) corresponding differential capacity versus voltage plots of Na_0.7Mn_0.75Ni_0.25O₂ (black), Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ (red), Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ (blue) and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ (green) half-cells cycled versus Na⁺/Na at 30 °C between 2.2–4.3 V at a rate of 25 mA g⁻¹.

Fig. S5(a) and (b)† shows the charge/discharge profiles and corresponding dQ/dV plots, respectively, of cells cycled between 2.2–4.3 V at 250 mA g⁻¹. These data show comparable voltage profiles to cells cycled between 2.2–4.3 V at 25 mA g⁻¹ (Fig. 2(a)). Interestingly, Fig. S6(b)† reveals superior oxygen anion reversibility for Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ at 250 mA g⁻¹, consistent with the observed cycling stability shown in Fig. 2(b). Based on these observations, further electrochemical tests were performed to evaluate the effect of Ti and Zn-substitution on the oxygen anion redox reversibility. Cells were cycled galvanostatically between 3.8–4.3 V at 25 mA g⁻¹, where the bulk of the capacity is derived from oxygen anion redox. Over this narrow voltage window (3.8–4.3 V) the materials show reversible anion redox activity (Fig. S6(a–d)†). Fig. S6(e)† shows the galvanostatic cycling performance of the materials, with Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ presenting superior cyclability relative to the other materials.

The electrochemical performance of P3-Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ was evaluated in a sodium full-cell by using Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ as the cathode material and commercial hard carbon as the anode. Fig. 4(a) shows the galvanostatic cycling performance of the Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂‖HC sodium full cell cycled between 1.0–4.3 V at 25 mA g⁻¹ which exhibits a capacity retention of 73% after 50 cycles. Fig. 4(b) shows an initial discharge capacity of 103.0 mA h g⁻¹, with an average discharge voltage of 3.33 V and an initial energy density of 342.5 W h kg⁻¹ based on the active cathode mass.

Fig. 4 (a) Electrochemical performance and coulombic efficiency and (b) galvanostatic charge/discharge profiles based on Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ cycled in a Na ion full cell between 1.0–4.3 V at a rate of 25 mA g⁻¹.

Structural and electronic structural evolution

To understand the effects of Ti and Zn-substitution on the Na⁺ ion insertion/extraction mechanism the structural changes were probed by ex situ PXRD on Na_0.7Mn_0.75Ni_0.25O₂, Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ at various states of charge and discharge over the initial cycle as shown in Fig. 5. High quality diffraction data (e.g., synchrotron data) are required for a detailed structural analysis but several conclusions are possible from qualitative analysis. The ex situ PXRD patterns of Na_0.7Mn_0.75Ni_0.25O₂ (Fig. 5(a)) reveal a reversible phase transformation from P3 to O′3 after charge to 4.3 V, which returns to P3 after discharge to 2.2 V. Characteristic regions of the patterns corresponding to O3 type structures and P3 structures are highlighted in Fig. 5. Upon Na⁺ ion extraction, the PXRD pattern of Na_0.7Mn_0.75Ni_0.25O₂ charged to 3.8 V shows that 70% of the P3 phase (space group R3m) remains and 30% transforms to the O′3 phase (space group C2/m) and after charge to 4.3 V shows complete conversion to the O′3 phase. Extraction of Na⁺ ions from the P3 phase results in increased coulombic repulsion between the Na and TMO₂ layers and the structural transformation via gliding of the TMO₂ layers to O′3 occurs to minimise this repulsion, with Na⁺ ions occupying an octahedral site. Upon subsequent Na⁺ ion insertion, the PXRD pattern after discharge to 3.8 V reveals partial conversion of the O′3 phase to P3 and after discharge to 2.2 V, the P3 phase is restored. These data demonstrate a fully reversible P3 to O′3 phase transformation with a negligible volume change with respect to the pristine phase, which is consistent with previous structural analysis for Na_2/3Mn_2/3Ni_1/3O₂.⁵⁹ The Ti-substituted phase, Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ (Fig. 5(b)), exhibits the same reversible P3 to O′3 phase transformation upon Na⁺ extraction/insertion, but appears to retain more of the P-type layers after charge to 4.3 V. Fig. 5(c) illustrates the P3 → O′3 phase transformation, which shows the gliding of the TMO₂ layers, forming octahedral sites upon Na⁺ ion removal as described by Delmas and co-workers.⁶ This results in the formation of the O′3 phase with stacking faults.

Fig. 5 Ex situ PXRD patterns and the corresponding galvanostatic charge/discharge profiles with the voltage highlighted where the ex situ PXRD measurements were conducted over the initial charge/discharge cycle of (a) Na_0.7Mn_0.75Ni_0.25O₂, (b) Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, (d) Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and (e) Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂. The corresponding structural change (c) without Zn substitution and (f) with Zn substitution. Characteristic regions corresponding to O3 and P3 structure types are highlighted.

As for the Zn-substituted phases, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ (Fig. 5(d)) and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ (Fig. 5(e)), the structure of the samples after charge to 4.3 V were initially fitted using the O′3 structural model with space group C/2m, as previously used for the Na_0.7Mn_0.75Ni_0.25O₂ and Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ materials after charge to 4.3 V. However, less than satisfactory fits were obtained using the O′3 structural model, therefore, refinements were performed using the P′3 structural model with space group C2/m allowing better fits to be achieved. These analyses demonstrate that the presence of Zn²⁺ ions in the TMO₂ layers alleviates the phase transformation to the O′3 phase but results in the formation of the distorted P′3 phase, in which the TMO₂ layers similarly glide but the Na⁺ ions remain in trigonal prismatic sites and the P3 oxygen stacking sequence is maintained, as illustrated in Fig. 5(f). These data agree with the smoother voltage profile curves (Fig. 3) observed for the Zn-substituted materials, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂. Ultimately, the Zn-substituted materials show enhanced structural stability over the high voltage anion redox process, which can be correlated with the superior cycle life (Fig. 2) observed for these materials over the non-Zn-substituted materials.

To probe the redox processes taking place during the first cycle, Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ was used for this study as a representative example of this system, and O K-edge and Ni L-edge XAS spectra were obtained. During charge, a shoulder at 529 eV on the leading edge of the O pre-edge grows in intensity, Fig. 6(a), arising from new hole states associated with Ni oxidation. This is accompanied by gradual oxidation of the Ni ions from +2 towards +4 in the Ni L-edge XAS, Fig. 6(b). On discharge, these changes are reversed, and the spectra resemble those of the pristine material. Although the extent of Na extraction observed on charge for Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ can be accounted for primarily by Ni^2+/4+ redox which reaches an average oxidation state of +3.75 at the top of charge, along with a small contribution from Mn^3+/4+, there also appears to be a change in intensity in the O K-edge at around 531.5 eV. This could indicate oxide ion oxidation is also taking place as this is where absorption intensity arising from molecular O₂ trapped in O-redox cathodes is observed.^64,65 To investigate this possibility, RIXS line scan measurements were performed at this excitation energy and a RIXS map of the pre-edge was obtained, Fig. 6(c) and (d). As shown in Fig. 6(d), there is little change in the RIXS spectra over the first cycle at 8 eV or between 0–2 eV, where emission features for O₂ have been previously observed, and there is no evidence of O₂ in the RIXS map. Instead, the changes in the O K-edge shape likely arise from broadening of the main pre-edge peaks. Overall, the changes indicate minimal contribution of O-redox to the charge compensation mechanism in Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ which can mainly be accounted for by Ni redox. Such a phenomenon occurs because, during charging, the Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ was insufficiently desodiated to cause anionic redox: in order to undergo anionic redox, Na contents x of Na_xTMO₂ should be lower than ∼0.25, but Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ was cycled over 0.28 < x < 0.76 (see Computational investigation section, and Fig. 7 for details).

Fig. 6 (a) O K-edge and (b) Ni L-edge XAS spectra collected in fluorescence yield mode of Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ at different states of charge during the first cycle. (c) RIXS emission spectra collected at an excitation energy of 531.5 eV. (d) RIXS map of the O K-edge pre-edge.

Fig. 7 Correlation between the interlayer distance and P3–O3 transition. (a) Comparison between the calculated (dotted lines) and measured (solid lines) galvanostatic charge/discharge curves, (b) lattice parameters, (c) relative DFT total energies of Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ (red), Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ (blue) and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂. Experimentally measured lattice parameters are indicated as empty symbols in (b). Among all symmetrically unique Na and Ti arrangements, those that can form under thermal vibration energy (0.0259 eV) at room temperature are considered for (a) and (b). Mean and standard deviation of voltages calculated from the selected atomic arrangements are denoted as dotted and vertical black lines in (a), respectively. Relative total energies in (c) are normalised to the lowest energy configuration at the given Na composition.

Raman spectroscopy was further used to examine if peroxide species, O₂²⁻, form as well as study the structural evolution of the materials upon initial charge/discharge. Ex situ Raman spectra were collected at the same states of charge/discharge as those from the PXRD studies (Fig. 5). Raman spectra collected on the pristine materials and after cycling between 2.2–4.3 V for Na_0.70Mn_0.75Ni_0.25O₂, Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ are presented in Fig. S7(a–d),† respectively. These data do not show any additional bands upon cycling in the region where O–O stretches (700–900 cm⁻¹) have been observed for peroxide-containing species (e.g., Li₂O₂, Na₂O₂, H₂O₂ and ZnO₂).⁶⁶ Unfortunately, contributions from the glass capillary are observed at approximately 800 and 1100 cm⁻¹ which are within the same region for O–O stretches (see Fig. S7(b)†) and therefore hinder definitive detection of peroxo O–O bonds. This is consistent with previous ex situ Raman studies on similar TM 3d systems.^66,67 The Raman spectra do however reveal changes upon charge/discharge. The feature at approximately 540 cm⁻¹ appears to evolve upon charging to 4.3 V, which then disappears after subsequent discharge to 2.2 V. In addition, the vibrational frequency of the out-of-plane TM–O stretching mode decreases upon charge and returns to its original position upon discharge to 2.2 V. These changes are indicative of a reversible phase transition and distortions of the oxygen coordination environment around TMs which is consistent with the PXRD analysis (Fig. 5).^14,68

Computational investigation

Electrochemical performance of P3-type layered oxides show a combination of complicated structural evolutions (e.g., P3 to O3 transitions and Jahn–Teller distortion), where all the processes occur during battery cycling. Thus, to understand the enhanced electrochemical performance of Zn- and Ti-substituted P3-type materials, it is crucial to assess the evolution of atomic structures upon charge/discharge. To this end, using first-principles calculations, we computationally modelled the P3-type Zn- and Ti-substituted structures with compositions Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.55Ni_0.25Zn_0.1Ti_0.1O₂, followed by adjusting Na compositions (see Experimental and Fig. S8†). Fig. 7(a) presents the capacity–voltage curves of Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.55Ni_0.25Zn_0.1Ti_0.1O₂ predicted from the model structures (see Methods), superimposed on the first and second cycles of galvanostatic charge/discharge curves. The redox couples responsible for voltage curves were predicted by comparing the projected density of states (Fig. S9†) and were also denoted above each voltage plateau. Overall, redox voltages of all three materials are determined by the Mn^3+/4+ redox couple at high Na contents (x > ∼0.7), whereas Ni^2+/3+/4+ and O^2−/– redox couples dominate the intermediate (∼0.2 < x < ∼0.7) and low Na contents (x < ∼0.2), respectively. Despite the similarity in their redox mechanisms, all three samples undergo different redox reactions because they were cycled over different Na composition ranges. For instance, Na_xMn_0.55Ni_0.25Zn_0.1Ti_0.1O₂ hardly shows oxygen redox because of the high bottom limit of cycling range (Na contents x of 0.28). Rather, it primarily undergoes Ni^2+/4+ redox while displaying a small amount of Mn^3+/4+ redox near the upper limit of x = 0.75, which is well consistent with the XAS results from Zn/Ti co-substituted materials (see Fig. 6). The high Na contents of Na_0.7Mn_0.55Ni_0.25Zn_0.1Ti_0.1O₂ during cycling can also contribute to its enhanced cycling stability, as the remaining Na atoms can act as pillar atoms to suppress structural changes, such as the P3–O3 transition and subsequent TM migration that frequently occurs under Na-deficient conditions. On the other hand, Zn-substituted Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ is cycled over relatively low Na compositions from 0.13 to 0.62, which enables oxygen redox after desodiation. In this regard, the oxygen redox of the Zn-doped sample primarily arises from its lower redox voltages compared to those of Ti-doped sample: due to the relatively low redox voltages, oxygen redox becomes available within the upper voltage window limit of 4.3 V. Hence, understanding the decrease in redox voltages upon Zn-substitution is key to interpreting the superior oxygen redox stability of the Zn-substituted materials, which will be discussed in detail in Fig. 8.

Fig. 8 Interpretation of anionic redox in Zn-doped P3-type cathodes. (a) Schematics of molecular orbitals of M–O and M*–O–X from P3-type Na_x(M, M*, X)O₂, where M and M* are the host transition metals away from and nearby dopants X, respectively.⁷² The substituent Xⁿ⁺ (e.g., Zn²⁺ or/and Ti⁴⁺) is less electronegative than M^m+ (e.g., Mn⁴⁺ and Ni⁴⁺). The redox active orbitals responsible for each redox reaction are denoted as yellow isosurfaces in the insets of (a). (b) Site projected density of states calculated for M–O, M*–O, and X–O bonds of Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ and Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂. Electronegativity of Ti⁴⁺ and Zn²⁺ dopants and the calculated redox voltages of Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ and Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ are indicated on the right side for comparison purposes.

Subsequent examination of the lattice parameters of the partially desodiated materials reveals that, compared with Ti-substituted Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ displays a longer c-axis, especially after being charged to x = 0.25 (see Fig. 7(b) and S9†). The longer c-axis of Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ is attributed to the wider interlayer spacing, rather than the size of the TMO₆ octahedra (Fig. S10†). The larger interlayer spacing of Zn-substituted structures can be rationalised by the relatively low valence state of Zn: sub-valent doping by Zn²⁺ on Mn⁴⁺ (or Ni³⁺, Ni⁴⁺) sites of layered oxides tends to create holes on oxygen atoms, resulting in the stronger electrostatic repulsion between TMO₂ layers and Na⁺ ions.⁶⁹ The wider interlayer distance of the Zn-substituted materials is beneficial in terms of the rate performance, as it can enhance the Na diffusion kinetics. To further assess the effect of lattice parameters on the electrochemical performance, we correlated them with the P3 to O3 transition behaviour. For this purpose, we generated the O3 Na_xTMO₂ structures by gliding TMO₂ layers of the most stable P3 configuration for each chemical formula and compared their relative stability with respect to P3 configurations (see Methods and Fig. 7(c)). These results indicate that the relative stability of the O3 phase is closely related to the c-parameter of the structure. To be specific, O3 phases are relatively more stable for smaller c-parameter, causing the O3 phases to form near both ends of Na compositions (x = ∼0.0 and ∼1.0) for all three samples. This inverse relationship between c-axis and O3 phase stability was manifested particularly in Zn-doped Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ sample, where O3 phases are greatly destabilised after desodiation with larger c-axis. As a result, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ with sub-valent Zn²⁺ become relatively more resistant to the P3 to O3 transition upon charging, as was observed from the PXRD patterns (Fig. 5).

The redox voltage of an element (e.g., Ni, O) can vary depending on the dopants substituted nearby them. This is because the energy of metal–oxygen bonding state can be changed upon doping other elements.⁷⁰ To explain the changes in redox voltages upon elemental substitution of Zn and Ti, we investigated the relative bonding and antibonding states in the model structures. In general, redox voltages are determined by the relative location of σ-bonding and σ*-antibonding orbital of metal–oxygen (M–O) bonds versus Na⁺/Na potential, where bonding and antibonding orbitals determine the anionic and cationic redox voltages, respectively (see the insets and Fig. S9†). Here, the energy separation between two orbitals (ΔE_M–O) is correlated to the electronegativity of M and O. For instance, when dopants (X) with electronegativity lower than the host metal (M) are added, the resulting X–O bonds have relatively higher bond ionicity and the narrower energy separation (ΔE_X–O) between antibonding and bonding state. This is particularly the case for Zn and Ti doping for Mn, since Zn²⁺ and Ti⁴⁺ have lower electronegativity than Mn⁴⁺ (χ_Zn²⁺ = 1.336, χ_Ti⁴⁺ = 1.730, χ_Mn⁴⁺ = 1.912).⁷¹ As a result, doping these elements leads to the shift of X–O bonding states toward Na/Na⁺ potential and lowering the anionic redox voltages. Another important result of doping less electronegative elements is the inductive effect, as illustrated in Fig. 8(a). Owing to the higher bond ionicity of X–O bonds, nearby M*–O bond gains more covalent character than M–O bonds away from dopant X, resulting in a larger energy separation between bonding and antibonding orbitals (ΔE_M*–O). This causes the M*–O antibonding states to shift toward the Na⁺/Na potential, lowering the cationic redox voltages. The decrease in anionic and cationic redox voltages is greater for Zn-substituted materials, since Zn²⁺ has a lower electronegativity than that of Ti⁴⁺. To assess if the above inductive effect theory can be applied to the P3-type materials, electronic states of M–O, M*–O, and X–O bonding are visualised by site projected density of states for Ti- and Zn-substituted materials (Fig. 8(b)). Upon the addition of less electronegative Ti and Zn, the energy separations of M*–O bond (ΔE_M*–O) become greater than that of M–O bond (ΔE_M–O), which is consistent with the inductive effect theory.

The key difference between the density of states of Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ and Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ is the bonding orbital of X–O bonds that determine the anionic redox voltages. Compared to the Ti 3d–O 2p hybrid orbitals of Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, the Zn 3d–O 2p hybrid orbitals of Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ has relatively unstable bonding state, which causes the anionic redox to readily occur in oxygen coordinated by Zn even under low charging voltage. We consider the unstable bonding state of Zn–O bonds to arise from two factors: one is the relatively low electronegativity of Zn versus Ti, which causes the Zn–O bonds to show more ionic character than Ti–O bonds. Another reason is their electronic configuration, where Zn²⁺ has more concentrated 3d orbitals with [Ar]3d¹⁰ than Ti⁴⁺ with [Ar], which greatly destabilises the bonding state of Zn–O hybrid orbitals. Consequently, P3-Na_xMn_0.65Ni_0.25Zn_0.1O₂ presents oxygen redox couples over the voltage range of 2.2–4.3 V with superior redox stability. Although Na_xMn_0.55Ni_0.25Zn_0.1Ti_0.1O₂ also exhibits oxygen redox upon full desodiation (see density of states of Na_xMn_0.55Ni_0.25Zn_0.1Ti_0.1O₂ with x = 0 in Fig. S9†), only minor amount of O in Na_xMn_0.55Ni_0.25Zn_0.1Ti_0.1O₂ participated in the experiments due to the limited cycling range of 0.25 < x < 0.75, where the governing redox reactions are Ni^2+/3+/4+ and Mn^3+/4+ redox couples (see the minimal contribution of O-redox in XAS spectra in Fig. 6). In contrast, owing to its relatively higher anionic redox voltage, Na_xMn_0.65Ni_0.25Ti_0.1O₂ shows only minimal contribution from oxygen redox in the same cycling range of 2.2–4.3 V. Regardless of the type of dopants, all Zn- and Ti-substituted materials show lower redox voltages than the parent-phase Na_0.7Mn_0.75Ni_0.25O₂, as both Zn²⁺ and Ti⁴⁺ have lower electronegativities than Mn⁴⁺ and Ni⁴⁺ (see the inductive effect in Fig. 8(a) and capacity versus voltage plots in Fig. 3(b)). Despite possessing the limitation in oxygen redox stability, Ti-substitution has been reported to be effective for improving structural stability and associated cycling performance of P3-type materials.^40,41 To better assess the influence of Ti-substitution on the structural stability of P3-Na_0.7Mn_0.75Ni_0.25O₂, the volumes of TMO₆ octahedra in the model structures of Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ were compared to each other with respect to the Na composition (Fig. 9). Overall, the octahedra volumes expand during sodiation, where the abrupt stepwise changes occur during the cationic redox reactions of Mn^3+/4+ and Ni^2+/3+/4+, primarily owing to the increase in the ionic radii of transition metals: note that the order of octahedra volumes (V_TMO6) directly follows the Shannon ionic radii (r_M)⁵⁶ for six-coordinated ions such that V_Zn²⁺O6 (r_Zn²⁺ = 0.74 Å) > V_Zn²⁺O6 (r_Ni²⁺ = 0.69 Å) > V_Mn³⁺O6 (r_Mn³⁺ = 0.645 Å) > V_Ti⁴⁺O6 (r_Ti⁴⁺ = 0.605 Å) > V_Ni³⁺O6 (r_Ni³⁺ = 0.6 Å) > V_Mn⁴⁺O6 (r_Mn⁴⁺ = 0.53 Å) > V_Ni⁴⁺O6 (r_Ni⁴⁺ = 0.48 Å). Ti⁴⁺, with its ionic radii being the medium value of all transition metal ions, causes the volumes of Ti⁴⁺O₆ octahedra to lie between those of TMO₆ before and after cationic redox reactions. These TiO₆ octahedra, thanks to their redox-inactive character, are immune to the volumetric changes associated with redox reactions and alleviate the structural changes of adjacent redox-active TMO₆ octahedra.

Fig. 9 (a) Volumes of TMO₆ octahedra of all model structures of (a) Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂, (b) Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and (c) Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ optimised in this study. Representative oxidation states of octahedra are represented on the right side. Redox couples governing the volumetric changes of octahedra are denoted in the coloured area.

The role of redox-inactive Ti⁴⁺ can be better understood by comparing the sequence of the volumetric changes of TMO₆ octahedra. For Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ without the presence of Ti, all the TMO₆ octahedra participate in redox reactions (i.e., Mn^3+/4+O₆, Ni^2+/3+/4+O₆, and Zn²⁺O₆²⁻) and, as a result, multiple redox reactions are correlated and occur simultaneously. To be specific, once all Mn³⁺ are oxidised to Mn⁴⁺ during desodiation from x = 1.0 to 0.7, both NiO₆ and ZnO₆ octahedra shrink upon further desodiation, indicating that Ni⁴⁺/Ni³⁺/Ni²⁺ and O²⁻/O⁻ redox couples occur at the same time. This correlated redox reaction is predicted to proceed over the whole cycling range of Na_xMn_0.65Ni_0.25Zn_0.1O₂ (Fig. 7) and, thus, can reduce its overall cycling stability. In contrast, the Ti-substituted materials, Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ exhibit sequential redox reactions, where MnO₆ shrinks first, followed by NiO₆ (and ZnO₆) during charging. The sequential redox reaction can be explained by the redox-inactivity of Ti⁴⁺; unlike Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ where all redox-active MnO₆, NiO₆, and ZnO₆ octahedra are neighbouring each other, Na_0.7Mn_0.65Ni_0.25Ti_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂ include redox-inactive TiO₆ that separates other TMO₆ octahedra. This can prevent the simultaneous redox reactions of NiO₆ and ZnO₆ octahedra that are in contact with one another, leading to the sequential redox reactions of Mn³⁺/Mn⁴⁺, Ni²⁺/Ni³⁺/Ni⁴⁺, and O²⁻/O⁻ upon charging. The redox-inactive Ti is also considered to be beneficial for disrupting ordering in the transition metal layer due its intermediate ionic size. In this regard, Ti-substitution is an effective method to enhance the cyclability of P3-type layered oxides because TiO₆ octahedra act as mechanical buffers that sustain the layered structure, while suppressing transition metal ordering.

Conclusions

Comparison between experimental and theoretical voltage–capacity profiles revealed that the redox voltages of P3-type materials can also be guided by the inductive effect principle – lower redox voltages for less electronegative TM substituent. Subsequent electronic structural analysis shows that, with the consideration of electron configurations, this principle can be used to activate stable oxygen anion redox. In particular, Zn, owing to its low electronegativity and relatively unstable electron configuration of [Ar]3d¹⁰, enhances the high voltage stability of Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂. Further examination of the model structures revealed another beneficial aspect of Zn as a dopant. With its lower oxidation state, Zn substitution widens the interlayer spacings by enhancing the electrostatic repulsion between TMO₂ layers and Na⁺ cations, contributing to the improved rate performance. In addition, the broader interlayer spacing of Zn-substituted structures destabilise the O3-type phases, which was represented as the suppression of P3 to O3 transition of Na_0.7Mn_0.65Ni_0.25Zn_0.1O₂ and Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂. Ti⁴⁺, on the other hand, remains redox-inactive during cycling because of its stable electronic configuration and relatively higher electronegativity than Zn²⁺. While reducing the theoretical redox capacity of cathodes, Ti and associated TiO₆ octahedra act as mechanical buffers that alleviate structural distortions, improving the cycling stability. The above results show that Ti and Zn, due to their opposite properties, have different impacts on the structural evolution and associated performance of P3-type cathodes. When combined, Zn/Ti dual doping gives rise to a synergetic effect, where Zn provides reversible anionic redox while Ti maintains the cathode structures, as revealed by the superior cycling and rate performance of Na_0.7Mn_0.58Ni_0.25Zn_0.07Ti_0.1O₂. Hence, this study suggests that the combination of dopants with contrasting electronegativity can be a viable approach to achieve the simultaneous improvement in anionic redox stability and cycle performance, which can be a basis for developing advanced layered cathodes for Na-ion batteries.

Conflicts of interest

The authors declare no conflicts of interest.

Data availability

Data for this article, including powder X-ray diffraction data, energy dispersive spectroscopy data, Raman spectra and electrochemical data are available at University of St Andrews Research Portal. https://doi.org/10.17630/682f54f6-f876-42dd-be79-ded023f6fd19.

Acknowledgements

This work was supported by the Faraday Institution (grant number FIRG018). The authors gratefully acknowledge support from the Engineering and Physical Sciences Research Council (EPSRC) Light Element Facility Grants EP/L017008/1, EP/R023751/1 and EP/T019298/1 for funding the acquisition of the scanning electron microscopes and Raman spectrometer. The authors are grateful for the provision of beam time on I21 at Diamond (Proposal Number: MM32023). We gratefully acknowledge technical assistance of the Diamond user support. R. A. H. acknowledges the Royal Academy of Engineering for Research Fellowship funding. Y. C. and D. O. S. are grateful to the Faraday Institution for funding the MICHAEL computing cluster hosted at University College London (UCL), FIRG019. The computations described in this article were performed using the University of Birmingham's BlueBEAR HPC service, the Baskerville Tier 2 HPC service (https://www.baskerville.ac.uk/, funded by the EPSRC and UKRI through the World Class Laboratories scheme (No. EP/T022221/1) and the Digital Research Infrastructure programme (No. EP/W032244/1)), and the Sulis Tier 2 HPC platform hosted by the Scientific Computing Research Technology Platform at the University of Warwick (funded by EPSRC Grant No. EP/T022108/1 and the HPC Midlands+ consortium). Through our membership of the UK's HEC Materials Chemistry Consortium, which is funded by the UK Engineering and Physical Sciences Research Council (EPSRC) (No. EP/L000202, EP/R029431, EP/T022213), this work also used ARCHER2 UK National Supercomputing Services. We are also grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (No. EP/T022213/1, EP/W032260/1, and EP/P020194/1). ARA would like to thank Mr James Steele (University of Cambridge) for helpful discussions.

References

1. M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657.
2. N. Tapia-ruiz, A. R. Armstrong, H. Alptekin, M. A. Amores, H. Au, J. Barker, R. Boston, W. R. Brant, J. M. Brittain, Y. Chen, M. Chhowalla, Y. Choi, S. I. R. Costa, M. C. Ribadeneyra, S. A. M. Dickson, E. I. Eweka, J. D. Forero-saboya, C. P. Grey, Z. Li, S. F. L. Mertens, R. Mogensen, L. Monconduit, D. M. C. Ould, R. G. Palgrave, P. Poizot, A. Ponrouch, S. Renault, E. M. Reynolds, A. Rudola, R. Sayers, D. O. Scanlon, S. Sen, V. R. Seymour, B. Silv, G. S. Stone, C. I. Thomas, M. Titirici, J. Tong, T. J. Wood, D. S. Wright and R. Younesi, J. Phys. Energy, 2021, 3, 031503.
3. J. Y. Hwang, S. T. Myung and Y. K. Sun, Chem. Soc. Rev., 2017, 46, 3529–3614.
4. N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682.
5. A. Rudola, A. J. R. Rennie, R. Heap, S. S. Meysami, A. Lowbridge, F. Mazzali, R. Sayers, C. J. Wright and J. Barker, J. Mater. Chem. A, 2021, 9, 8279–8302.
6. C. Delmas, J. J. Braconnier, C. Fouassier and P. Hagenmuller, Solid State Ionics, 1981, 3–4, 165–169.
7. E. J. Kim, L. A. Ma, L. C. Duda, D. M. Pickup, A. V. Chadwick, R. Younesi, J. T. S. Irvine and A. Robert Armstrong, ACS Appl. Energy Mater., 2020, 3, 184–191.
8. C. Ma, J. Alvarado, J. Xu, R. J. Clément, M. Kodur, W. Tong, C. P. Grey and Y. S. Meng, J. Am. Chem. Soc., 2017, 139, 4835–4845.
9. K. Dai, J. Mao, Z. Zhuo, Y. Feng, W. Mao, G. Ai, F. Pan, Y. Chuang, G. Liu and W. Yang, Nano Energy, 2020, 74, 104831.
10. A. Konarov, H. J. Kim, J. Jo, N. Voronina, Y. Lee, Z. Bakenov, J. Kim and S. Myung, Adv. Energy Mater., 2020, 10, 2001111.
11. X. Rong, J. Liu, E. Hu, Y. Liu, Y. Wang, J. Wu, X. Yu, K. Page, Y. S. Hu, W. Yang, H. Li, X. Q. Yang, L. Chen and X. Huang, Joule, 2018, 2, 125–140.
12. K. Du, J. Zhu, G. Hu, H. Gao, Y. Li and J. B. Goodenough, Energy Environ. Sci., 2016, 9, 2575–2577.
13. R. A. House, U. Maitra, M. A. Pérez-Osorio, J. G. Lozano, L. Jin, J. W. Somerville, L. C. Duda, A. Nag, A. Walters, K. J. Zhou, M. R. Roberts and P. G. Bruce, Nature, 2020, 577, 502–508.
14. U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin, M. A. Pérez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Lu, D. E. McNally, A. V Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10, 288–295.
15. R. A. House, U. Maitra, L. Jin, J. G. Lozano, J. W. Somerville, N. H. Rees, A. J. Naylor, L. C. Duda, F. Massel, A. V. Chadwick, S. Ramos, D. M. Pickup, D. E. McNally, X. Lu, T. Schmitt, M. R. Roberts and P. G. Bruce, Chem. Mater., 2019, 31, 3293–3300.
16. S. Mariyappan, T. Marchandier, F. Rabuel, A. Iadecola, G. Rousse, A. V. Morozov, A. M. Abakumov and J.-M. Tarascon, Chem. Mater., 2020, 32, 1657–1666.
17. X. Bai, M. Sathiya, B. Mendoza-Sánchez, A. Iadecola, J. Vergnet, R. Dedryvère, M. Saubanère, A. M. Abakumov, P. Rozier and J.-M. Tarascon, Adv. Energy Mater., 2018, 8, 1802379.
18. S. F. Linnell, M. Hirsbrunner, S. Imada, G. Cibin, A. B. Naden, A. V Chadwick, J. T. S. Irvine, L. C. Duda and A. R. Armstrong, ChemElectroChem, 2022, 9, e202200240.
19. M. Sathiya, G. Rousse, K. Ramesha, C. P. Laisa, H. Vezin, M. T. Sougrati, M. L. Doublet, D. Foix, D. Gonbeau, W. Walker, A. S. Prakash, M. Ben Hassine, L. Dupont and J. M. Tarascon, Nat. Mater., 2013, 12, 827–835.
20. D. H. Seo, J. Lee, A. Urban, R. Malik, S. Kang and G. Ceder, Nat. Chem., 2016, 8, 692–697.
21. B. Song, E. Hu, J. Liu, Y. Zhang, X. Q. Yang, J. Nanda, A. Huq and K. Page, J. Mater. Chem. A, 2019, 7, 1491–1498.
22. J. Vinckeviciute, D. A. Kitchaev and A. Van Der Ven, Chem. Mater., 2021, 33, 1625–1636.
23. W. E. Gent, K. Lim, Y. Liang, Q. Li, T. Barnes, S. J. Ahn, K. H. Stone, M. McIntire, J. Hong, J. H. Song, Y. Li, A. Mehta, S. Ermon, T. Tyliszczak, D. Kilcoyne, D. Vine, J. H. Park, S. K. Doo, M. F. Toney, W. Yang, D. Prendergast and W. C. Chueh, Nat. Commun., 2017, 8, 1–12.
24. E. De La Llave, E. Talaie, E. Levi, P. K. Nayak, M. Dixit, P. T. Rao, P. Hartmann, F. Chesneau, D. T. Major, M. Greenstein, D. Aurbach and L. F. Nazar, Chem. Mater., 2016, 28, 9064–9076.
25. U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin, M. A. Pérez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10, 288–295.
26. A. Konarov, J. H. Jo, J. U. Choi, Z. Bakenov, H. Yashiro, J. Kim and S. T. Myung, Nano Energy, 2019, 59, 197–206.
27. D. Darbar, M. V Reddy and I. Bhattacharya, Electrochem, 2021, 2, 323–334.
28. W. Kang, Z. Zhang, P. K. Lee, T. W. Ng, W. Li, Y. Tang, W. Zhang, C. S. Lee and D. Y. Wai Yu, J. Mater. Chem. A, 2015, 3, 22846–22852.
29. P. F. Wang, Y. Xiao, N. Piao, Q. C. Wang, X. Ji, T. Jin, Y. J. Guo, S. Liu, T. Deng, C. Cui, L. Chen, Y. G. Guo, X. Q. Yang and C. Wang, Nano Energy, 2020, 69, 104474.
30. W. Zheng, Q. Liu, Z. Wang, Z. Wu, S. Gu, L. Cao, K. Zhang, J. Fransaer and Z. Lu, Energy Storage Mater., 2020, 28, 300–306.
31. M. Zarrabeitia, E. Gonzalo, M. Pasqualini, M. Ciambezi, O. Lakuntza, F. Nobili, A. Trapananti, A. Di Cicco, G. Aquilanti, N. A. Katcho, J. M. López Del Amo, J. Carrasco, M. Á. Muñoz-Márquez and T. Rojo, J. Mater. Chem. A, 2019, 7, 14169–14179.
32. C. Li, C. Zhao, B. Hu, W. Tong, M. Shen and B. Hu, Chem. Mater., 2020, 32, 1054–1063.
33. X. Cao, X. Li, Y. Qiao, M. Jia, F. Qiu, Y. He, P. He and H. Zhou, ACS Energy Lett., 2019, 4, 2409–2417.
34. X. Bai, M. Sathiya, B. Mendoza-Sánchez, A. Iadecola, J. Vergnet, R. Dedryvère, M. Saubanère, A. M. Abakumov, P. Rozier and J.-M. Tarascon, Adv. Energy Mater., 2018, 8, 1802379.
35. H. Xu, J. Zong and X. Liu, Ionics, 2018, 24, 1939–1946.
36. X. Wu, J. Guo, D. Wang, G. Zhong, M. J. McDonald and Y. Yang, J. Power Sources, 2015, 281, 18–26.
37. X. Wu, G. L. Xu, G. Zhong, Z. Gong, M. J. McDonald, S. Zheng, R. Fu, Z. Chen, K. Amine and Y. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 22227–22237.
38. L. Xian, M. Li, D. Qiu, C. Qiu, C. Yue, F. Wang and R. Yang, J. Alloys Compd., 2022, 905, 163965.
39. Y. Shi, Z. Zhang, P. Jiang, A. Gao, K. Li, Q. Zhang, Y. Sun, X. Lu, D. Cao and X. Lu, Energy Storage Mater., 2021, 37, 354–362.
40. Y. Liu, C. Wang, M. Ren, H. Fang, Z. Jiang and F. Li, J. Energy Chem., 2021, 63, 351–357.
41. S. F. Linnell, J. Kim, Y. Choi, M. Hirsbrunner, S. Imada, A. Pramanik, F. Cuesta, D. N. Miller, E. Fusco, B. E. Bode, J. T. S. Irvine, L. C. Duda, O. Scanlon and A. R. Armstrong, J. Mater. Chem. A, 2022, 13–15.
42. E. J. Kim, L. A. Ma, D. M. Pickup, A. V. Chadwick, R. Younesi, P. Maughan, J. T. S. Irvine and A. R. Armstrong, ACS Appl. Energy Mater., 2020, 3, 10423–10434.
43. A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218.
44. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118.
45. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
46. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
47. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
49. V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808.
50. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
51. A. Jain, P. Ong, G. Hautier, W. Chen, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
52. A. H. Larsen, J. JØrgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dulak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. SchiØtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
53. B. J. Morgan, J. Open Source Softw., 2017, 2, 370.
54. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
55. Q. Li, Y. Qiao, S. Guo, K. Jiang, Q. Li, J. Wu and H. Zhou, Joule, 2018, 2, 1134–1145.
56. R. D. Shannon, Acta Crystallogr., 1976, A32, 751–767.
57. X. Wang, L. Yin, A. Ronne, Y. Zhang, Z. Hu, S. Tan, Q. Wang, B. Song, M. Li, X. Rong, S. Lapidus, S. Yang, E. Hu and J. Liu, Nat. Commun., 2023, 14, 1–13.
58. S. Mariyappan, T. Marchandier, F. Rabuel, A. Iadecola, G. Rousse, A. V. Morozov, A. M. Abakumov and J. M. Tarascon, Chem. Mater., 2020, 32, 1657–1666.
59. Y. N. Zhou, P. F. Wang, X. D. Zhang, L. B. Huang, W. P. Wang, Y. X. Yin, S. Xu and Y. G. Guo, ACS Appl. Mater. Interfaces, 2019, 11, S1–S15.
60. K. Kubota, N. Fujitani, Y. Yoda, K. Kuroki, Y. Tokita and S. Komaba, J. Mater. Chem. A, 2021, 9, 12830–12844.
61. H. Yoshida, N. Yabuuchi, K. Kubota, I. Ikeuchi, A. Garsuch, M. Schulz-Dobrick and S. Komaba, Chem. Commun., 2014, 50, 3677–3680.
62. J. Song, K. Wang, J. Zheng, M. H. Engelhard, B. Xiao, E. Hu, Z. Zhu, C. Wang, M. Sui, Y. Lin, D. Reed, V. L. Sprenkle and P. Yan, ACS Energy Lett., 2020, 5, 1718–1725.
63. J. A. Gilbert, I. A. Shkrob and D. P. Abraham, J. Electrochem. Soc., 2017, 164, A389–A399.
64. R. A. House, G. J. Rees, M. A. Pérez-osorio, J. Marie, E. Boivin, A. W. Robertson, A. Nag, M. Garcia-fernandez, K. Zhou and P. G. Bruce, Nat. Energy, 2020, 5, 777–785.
65. R. A. House, J.-J. Marie, J. Park, G. J. Rees, S. Agrestini, A. Nag, M. Garcia-Fernandez, K.-J. Zhou and P. G. Bruce, Nat. Commun., 2021, 12, 2975.
66. K. Luo, M. R. Roberts, R. Hao, N. Guerrini, D. M. Pickup, Y. S. Liu, K. Edström, J. Guo, A. V. Chadwick, L. C. Duda and P. G. Bruce, Nat. Chem., 2016, 8, 684–691.
67. U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin, M. A. Pérez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10, 288–295.
68. Z. Yang, J. Zhong, J. Feng, J. Li and F. Kang, Adv. Funct. Mater., 2021, 31, 2103594.
69. C. Soares, B. Silván, Y.-S. Choi, V. Celorrio, V. R. Seymour, G. Cibin, J. M. Griffin, D. O. Scanlon and N. Tapia-ruiz, J. Mater. Chem., 2022, 10, 7341–7356.
70. Z. X. Huang, K. Li, J. M. Cao, K. Y. Zhang, H. H. Liu, i. Z. Guo, Y. Liu, T. Wang, D. Dai, X. Y. Zhang, H. Geng and X. L. Wu, Nano Lett., 2024, 24, 13615–13623.
71. Z. Li and D. S. Kosov, J. Phys. Chem. B, 2006, 110, 19116–19120.
72. D. A. Kuznetsov, B. Han, Y. Yu, R. R. Rao, J. Hwang, Y. Román-Leshkov and Y. Shao-Horn, Joule, 2018, 2, 225–244.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta07963a

‡ Indicates joint first author.

---