High-throughput computation and machine learning screening of van der Waals heterostructures for Z-scheme photocatalysis

Abstract

Although van der Waals (vdW) heterostructures have shown significant photocatalytic applications, the discovery of high-performance vdW heterostructure photocatalysts is limited by the computational cost in the high-dimensional search space and the complexity of large-scale atomic models. Here, we utilize big-data analysis, high-throughput screening, high-fidelity calculations, and machine learning to discover Z-scheme heterostructure photocatalysts from 11 935 vdW heterostructures, constructed using 155 two-dimensional (2D) semiconductors with diverse structures from our 2DMatPedia database. We first perform high-throughput high-fidelity hybrid functional calculations on the 155 monolayer 2D semiconductors to obtain their high-accuracy band information. Using the explainable descriptor and deep reinforcement learning algorithm, we identify 1062 potential Z-scheme vdW heterostructures. Finally, the best 33 Z-scheme heterostructure photocatalysts from the pool of 1062 candidates are verified and validated through high-fidelity hybrid functional calculations. Among these Z-scheme heterojunctions, our photocatalytic calculations indicate that SnO₂/WSe₂, Bi₂Se₃/VI₂, Bi₂Se₃/Sb, and Bi₂Te₂S/Sr(SnAs)₂ have the best redox abilities. Using machine learning techniques, we further identified 29 new high-potential Z-scheme heterostructures from the pool, making a total of 62 candidates. The combination of high-throughput, descriptor, and machine learning techniques helps to narrow down the candidates of high-performance photocatalytic heterostructures in a very large material space and accelerate the discovery process of Z-scheme photocatalysts in the experiment.

---

Introduction

Photocatalytic technology is one of the most promising sustainable strategies to overcome the challenges of environmental pollution and global fossil fuel depletion.^1,2 Many strategies have been developed to modify the existing photocatalysts or design new photocatalysts. Among these, constructing 2D heterostructures is the most effective way to improve photocatalytic performance.^3,4 Based on the band structure relationship, only the staggered Type-II and its variant Z-scheme heterostructures are suitable for photocatalysis because of their regulated charge transfer mechanism.⁴ Compared to Type-II heterostructures, the Z-scheme heterostructure represents a promising strategy for spontaneously driven chemical reactions through solar energy due to its ability to not only broaden the solar absorption spectrum, but also effectively separate photogenerated electrons and holes on either side of the heterostructure.^5–7 Combining the narrow bandgap semiconductors with the Z-scheme heterostructure mode can also resolve the dilemma in single-material or Type-II photocatalysts that the strong redox ability and a wide light absorption range cannot be achieved simultaneously.^8–11 Thus, exploring a new strategy to discover Z-scheme heterostructures with high efficiency in light utilization and electron–hole separation is crucial.

Currently, the exploration of Z-scheme heterostructures remains confined to traditional methods such as trial-and-error and empirical approaches.¹² Most research efforts are directed towards the investigation of individual Z-scheme heterostructures, such as CdS/SnS₂,¹³ MoSSe/WSeTe,¹⁴ g-C₃N₄/Ti₂CO₂,¹⁵ W₁₈O₄₉/CeO₂,¹⁶ MnO₂/Mn₃O₄,¹⁷ and ZnIn₂S₄/BiVO₄.¹⁸ Clearly, the efficiency of such approaches for identifying new Z-scheme heterostructure photocatalysts is significantly low. Recently, researchers have embarked on the quest for and validation of a couple of Z-scheme heterostructures for photocatalytic applications.^19–21 However, only a few specific types of 2D materials, such as eighteen transitional metal dichalcogenides (TMDs), are used to build vdW heterostructures.²¹ Note that the latest 2D material databases now encompass over 10 000 2D materials,^22,23 which can theoretically assemble into approximately 50 million vdW heterostructures. Navigating through this vast array to pinpoint high-performance heterostructure photocatalysts presents a substantial challenge. This endeavor necessitates the deployment of advanced pre-screening algorithms, effective descriptors, machine-learning methodologies, and high-throughput and high-fidelity calculations.

High-throughput computational design based on a data-driven approach is becoming a novel paradigm in physics, chemistry, and materials science.^24–27 The main aim of the data-driven approach is to maximize the utilization of existing data, thus significantly decreasing computational cost and accelerating the discovery of materials.^25,28 2D vdW functional heterostructures constitute a sub-application field of high-throughput design because of its huge geometric space.^29–31 A series of remarkable, unique characteristics have emerged in hetero-interfaces constructed using two disparate 2D materials, providing great potential in developing solar energy conversion and optoelectronic devices.^32–36 In contrast with the monolayer 2D materials database, a heterostructure database is still unbuilt. This is because the large-scale calculation of heterostructures containing tens of hundreds of atoms using high-level electronic structures methods, such as high-fidelity hybrid functional density functional theory (DFT) or GW many-body perturbation theory, is extremely expensive and requires computational power beyond that which is currently available.^37,38 Fortunately, this obstacle can be partially bypassed using physical models or descriptors that describe the interface and predict the electronic properties of heterostructures based on information concerning 2D materials.²¹ Moreover, utilizing a variety of elemental and material features, machine learning models have shown the capability to enable predictions in the field of materials.^39–41 Therefore, the advanced high-throughput computational design combined with empirical knowledge and machine learning can be an efficient way to narrow down the exploring space and accelerate the discovery of Z-scheme vdW heterostructure photocatalysts from the millions of candidates.

In this work, we performed high-throughput and high-fidelity DFT calculations, explainable descriptors, and machine learning to systematically investigate around 12 000 van der Waals heterostructures formed by 155 2D semiconducting materials and their band alignments. Firstly, we used Hey–Scuderia–Ernzerhof hybrid functional calculations (HSE06) to compute the band gap and band edge position of these 155 2D semiconductors, which can build 11 935 vdW heterostructures theoretically. Secondly, we applied two descriptors, Allen material electronegativity (χ_m) and band offset (ΔV) to screen out the Z-scheme from the 11 935 heterostructures. The descriptors qualitatively enable us to identify 1062 Z-scheme candidates, bypassing the need for expensive HSE calculations on large supercells of heterostructures. Among them, 33 excellent Z-scheme heterostructures with low lattice mismatch ratios (<5%) were further confirmed by HSE calculations as potential candidates for photocatalysis. We further develop a machine learning model to quantitatively explain the relationship between the descriptors (Δχ_m and ΔV) and the interlayer charge transfer (ΔQ) in the heterostructure. Finally, we employed machine learning techniques to screen 1028 previously uncalculated candidates for potential Z-scheme heterojunctions, highlighting its potential in accelerating photocatalyst discovery.

Computational details

The DFT calculations were performed via the Vienna ab initio simulation package (VASP).⁴² The core-electron interaction was described by the frozen-core projector augmented wave (PAW) method.⁴³ The electronic exchange-correlation energy was treated using the generalized gradient approximation in the form of Perdew–Burke–Ernzerhof (GGA-PBE) formalism.⁴⁴ The HSE06 was used to obtain the accurate band gap and alignment.^45,46 The optPBE exchange-correlation energy was employed considering vdW interaction correction.⁴⁷ The plane-wave cutoff energy was 500 eV and the Brillouin zone was integrated using Gamma center grids with a consistent spacing density for all cell sizes (using KSPACING = 0.25 Å⁻¹ for geometric optimization). A vacuum layer of 15 Å in the z-direction was introduced to avoid spurious interactions between the neighboring slabs. For geometry optimization, the convergence criteria of energy and forces acting on each atom were 10⁻⁴ eV and 0.01 eV Å⁻¹. Here, we employed the Jarvis tool developed by K. Choudhary⁴⁸ to automate the construction of the heterojunction, setting the starting interlayer spacing to 3 Å. The atom positions and charge density illustrations were obtained using the VESTA software.⁴⁹ Further analysis was conducted using the post-processing program VASPKIT.⁵⁰ Partial atomic charges were obtained using Bader charge analysis implemented by Henkelman and co-workers.^51–53 Beyond the DFT-based calculations, machine learning effectively establishes semi-quantitative or quantitative relationships between physical parameters describing various 2D materials. We also employed the reinforcement learning-based Physio symbolic regression package,⁵⁴ which leverages physical unit constraints for the analytical inference of physical laws. A simple analytical model for the charge transfer and descriptors was rigorously derived using input parameters.

Results and discussion

Fig. 1a depicts the selection process to identify candidate materials suitable for heterojunction photocatalysts. The process began by extracting 6351 materials from our 2DmatPedia.²³ From this initial pool, 1913 semiconductors were identified based on their PBE band gap, which fell within the 0.5–3 eV range. We applied a top-down stripping approach (2D materials' parents are layered materials in the Inorganic Crystal Structure Database (ICSD)) to ensure that the selected materials could be experimentally synthesized, which reduced the number of candidates to 1034. Further screening was conducted using the criteria of E_exf < 0.26 eV and E_dec < 0.6 eV,²³ where E_exf denotes the exfoliation energy required to separate layers from bulk crystals, and E_dec refers to the decomposition energy that assesses phase stability, identifying 781 materials suitable for easier synthesis in experiments. In the subsequent step, we excluded rare earth and toxic elements to address their limited availability, high costs, and fabrication challenges, resulting in the removal of 172 materials. It is worth noting that we excluded polar 2D materials, reducing the pool to 403 candidates, due to the difficulty in obtaining accurate band edge information affected by shifts in vacuum energy levels caused by material polarity.⁵⁵ Materials with more than ten atoms per unit cell and those with poor structures were excluded. Finally, 155 candidate materials were selected for high-throughput calculations of high-precision HSE06 energy bands and band edge positions (see Text S1 and more details in Data S1†). This rigorous selection process ensures that the identified materials have the necessary properties for efficient heterojunction photocatalysts.

Fig. 1 (a) Illustration of the screening workflow to discover potential 2D candidates from the 2DMatPedia database for photocatalysis. (b) Polar histogram of eight categories, showing their space group and the number of 2D materials involved. Each category presents one representative material with its side view structures. Histograms of (c) HSE band gap and (d) VBM(CBM), respectively. (e) Calculated HSE band gaps and edges respective to the vacuum level of 155 2D materials (see details in Data S1†). The valence band maximum (VBM) is shown in green, and the conduction band minimum (CBM) is in orange. Dashed lines delineate different chemical reaction potentials.

Different from studying a particular type of 2D materials and their heterostructures, such as TMDs,²¹ the screened 155 materials in this work are diverse, including single-element materials, metal oxides, transition metal nitrides, iodides, chlorides, transition metal dichalcogenides, arsenides, as well as structurally complex ternary compounds. These materials can be categorized into nine groups based on their atomic structure and space group, as illustrated in Fig. 1b. The figure also presents the number of structures in each category. The most common structure is P3̄m1, which has 47 variations, and HfS₂ represents this structure. Among the structures investigated, more than 10 materials share the same space group, including P6̄m2 (15), P4/nmm (14), C2/m (12), and Pmmn (10), which represent the structures of GaN, CuI, MoN₂, and SnSe, respectively. Categories with 5 to 10 materials include P222₁ (9), P3̄1m (8) and Pmmm (5) represent the structures of AuO₂F, CrBr₃, and WF₅, respectively. Categories with fewer than 5 materials are grouped in the “other” category, which includes 18 space groups and 35 materials. As can be seen, these 155 2D materials provide a diverse and universal set, which offers sufficient assurance for verifying the reliability of our descriptors and provides diverse datasets for training machine learning models.

After pre-screening 155 2D material candidates, we next conducted high-throughput calculations on the HSE06 band structures of these materials, and the HSE06 band gap distribution is shown in Fig. 1c. As can be seen, the band gap of the majority (126 over 155 materials, 81% of the total) falls within 1.0 to 3.5 eV, an appropriate range for potential photocatalysts. It should be noted that the band gap values calculated using the HSE06 functional are typically higher than those estimated by PBE, as PBE tends to underestimate the band gap. Conversely, calculations performed with HSE06 offer more precise estimations of both the band gap and band edge positions. Fig. 1d illustrates the distribution of their VBM and CBM positions relative to the vacuum level. The VBM positions mainly concentrate in the range of −8 to −4 eV, while the CBM positions are primarily distributed in the range of −6 to −3 eV. From Fig. 1e, we can see that about 115 materials have an oxygen evolution potential lower than −5.67 eV for H₂O/O₂, and 105 materials have a reduction potential higher than −4.44 eV for H⁺/H₂. This suggests that most analyzed 2D materials can perform oxygen or hydrogen evolution reactions. We also compare the VBM and CBM positions with various oxidation-reduction potentials such as H₂O and CO₂, demonstrating that most of them can undergo photocatalytic redox reactions (see details in ESI†). This further confirms the accuracy of our material selection criteria in Fig. 1a.

Although most of the single 2D materials within the 155 candidates show their photocatalytic applications, the single-material photocatalysts suffer a severe problem on having a strong redox ability and wide light absorption range simultaneously, which can be addressed by constructing heterostructures, especially Z-scheme ones. The mechanism of Z-scheme heterostructures is shown in Fig. 2a. When photogenerated electrons are excited to conduction bands (CB) in both semiconducting building blocks of the Z-scheme heterostructure, the photogenerated electron with low CB of oxidation photocatalyst (OP) will recombine with photogenerated holes located in the high valence band (VB) of reduction photocatalyst (RP). Accordingly, the photogenerated electrons and holes accompanied by large redox ability will be well preserved and simultaneously expose good spatial separation in the Z-scheme heterostructure.^56–58

Fig. 2 (a) Scheme of Z-scheme mechanism and two key descriptors, ΔV and Δχ_m. (b) Comparative quantitative analysis of the relationship between interfacial charge transfer ΔQ and the two descriptors. Deep reinforcement learning of φ-SO reveals ΔQ = cΔχ_m × ΔV², which is in good agreement with DFT calculations. (c) Diagram illustrating the high-throughput screening process to discover 2D heterostructures with potentially suitable Z-scheme candidates. Note that of the 34 heterojunctions examined, 33 are confirmed as Z-scheme configurations through high-fidelity DFT calculations.

In accordance with the Z-scheme photocatalytic mechanism (Fig. 2a), the establishment requires two essential characteristics as descriptors. Firstly, a slight band offset is crucial to enhance the migration efficiency of photogenerated electrons from the acceptor and holes from the donor. Thus, a larger value of band offset, ΔV, is an important descriptor for constructing Z-scheme heterostructures. This suggests that electron transfer from the CB of OP to the VB of RP is facilitated, while electron transfer from the CB of RP to the CB of OP is hindered, leading to a Z-scheme carrier-transfer pathway. Additionally, we selected a value of 0.6 eV for ΔV to maximize the inclusion of Z-scheme heterojunctions and minimize the inclusion of non-Z-scheme heterojunctions (see the selection method in ESI†).

Secondly, the presence of a directional interfacial electronic field is the most pivotal evidence for confirming the Z-scheme. A higher magnitude of charge transfer, leading to a more robust built-in electric field, confers distinct advantages to the photocatalytic process.²⁰ Therefore, the direction of charge transfer and the precise band alignment within the heterostructure is paramount in unequivocally identifying a Z-scheme heterostructure within Type-II alignment systems. For these different types of materials, we use the Allen material electronegativity, Δχ_m = χ(OP) − χ(RP), where χ(OP) and χ(RP) are the Allen material electronegativity of the oxidation photocatalyst and reduction photocatalyst, respectively (see details in ESI Text S2†), as another descriptor for predicting charge transfer between interfaces in TMD heterostructures.²¹ A larger value of Δχ_m is expected to correspond to a more definite direction of charge transfer from a material with lower χ_m to one with higher χ_m. If Δχ_m is too small, it may be challenging to accurately determine the electron transfer direction. After careful analysis, we determined that Δχ_m > 0.1 is the most suitable criterion for predicting the charge transfer direction (see Table S1†).

To further elucidate the relationship of these two descriptors in affecting interfacial charge transfer for predicting Z-scheme heterostructure, we employed a physical symbolic optimization algorithm termed φ-SO (see details in ESI Text S3†).⁵⁴ It is essential to emphasize that ΔQ, representing charge transfer between two materials in a heterostructure, is crucial for characterizing the Z-scheme in theoretical calculations. Typically, ΔQ is determined through high-precision DFT calculations of the complex heterostructures. In this study, we innovatively predict ΔQ using machine learning based on two simpler parameters, ΔV and Δχ_m, without needing to construct a heterojunction, significantly enhancing the screening efficiency. This machine learning algorithm leverages deep reinforcement learning to extract and analyze symbolic expressions from physical data, aiming to elucidate the relationship between van der Waals heterojunction interfacial charge transfer (ΔQ) and the two descriptors (ΔV and Δχ_m) we introduced as shown in Fig. 2b. Upon training via φ-SO, we discerned the equation ΔQ = cΔχ_m × ΔV², where c is a constant of 0.29, and its Reward and RMSE metrics are 0.957 and 0.008, respectively. These remarkable results signify that this equation offers a robust predictive power for interfacial charge transfer in heterojunctions. It is worth noting that ΔQ is directly proportional to the square of ΔV, suggesting a more significant impact of ΔV on charge dynamics compared to Δχ_m. Hence, by integrating ΔV and Δχ_m as Z-scheme descriptors, we present a concise framework that not only validates their utility but also enables the prediction of Z-scheme heterostructure only from the electronic structures of two single components before their combination, significantly reducing computational cost.

As depicted in Fig. 2c, we have devised a four-step workflow to discriminate Z-scheme heterostructures from a pool of 11 935 candidates based on their band alignment of two components, as indicated by two descriptors, ΔV and Δχ_m. In the initial step, leveraging Anderson's rule,²¹ we predict that 62963 heterojunctions possess a Type-II band alignment. Proceeding to the second step, we employ ΔV > 0.6 eV as a discriminating criterion, excluding 4803 potential Z-scheme candidates. In the third step, by comparing Δχ_m > 0.10 and assessing the relative values of χ_m, we identify 21062 Z-scheme heterostructures with a definite direction of electron transfer based on discussion above and previous work.²¹ We consider heterojunctions with a lattice mismatch ratio below 5% without cell expansion to determine the most favorable Z-scheme. Ultimately, based on their minimal lattice mismatch ratio, we identify 34 potential Z-scheme heterostructures (see details in Table 1). Our DFT calculations verified 33 out of the 34 analyzed heterojunctions as Z-scheme configurations (see the exception in Table 1), highlighting the robust predictive capability of ΔV and Δχ_m descriptors employed.

Table 1 Heterostructure characteristics, including lattice mismatch (δ), binding energy (E_b) in meV per atom, difference of Allen material electronegativity (Δχ_m), band offset (ΔV) in eV, charge transfer by Bader analysis (ΔQ) in e, and DFT validation for the 34 Z-scheme heterostructure candidates. See detailed DFT calculations on the exception one Bi₂Te₂S/AuI (No. 22) in ESI

	Acceptor/donor	δ	Eb	Δχm	ΔV	ΔQ	Validated	Ref.
1	SnO2/GaN	0.61%	−44.70	0.622	1.949	0.105	Y	—
2	SbBrO/CuI	4.60%	−18.39	0.646	1.604	0.050	Y	—
3	CuClO2/TeRhCl	2.28%	−32.11	0.775	1.557	0.241	Y	—
4	HfS2/Te2W	3.07%	−37.57	0.416	1.386	0.059	Y	—
5	AuClO2/TaI2O	0.20%	−23.28	0.311	1.281	0.159	Y	—
6	PdCl2/SnSe	0.13%	−54.28	0.132	1.085	0.288	Y	—
7	SnS2/Te2Mo	4.33%	−37.82	0.533	0.972	0.055	Y	19
8	Bi2Te2Se/Sr(SnAs)2	3.48%	−38.88	0.194	0.929	0.141	Y	—
9	SnSe2/Te3As2	4.58%	−37.44	0.144	0.789	0.115	Y	—
10	AuO2F/HfTeSe4	0.56%	−31.62	0.899	0.767	0.128	Y	—
11	Bi2TeSe2/Sb	2.64%	−38.93	0.259	2.082	0.081	Y	—
12	NiS2/MoSe2	0.83%	−33.67	0.200	1.821	0.024	Y	62
13	SnO2/WSe2	2.14%	−34.43	1.231	0.767	0.066	Y	—
14	SnO2/ZnO	1.96%	−52.49	0.367	1.949	0.091	Y	63
15	PtO2/MoSe2	4.54%	−36.35	0.200	1.604	0.069	Y	64
16	AuBrO2/TaI2O	0.92%	−36.76	0.266	1.367	0.077	Y	—
17	AuO2F/TeRhCl	4.12%	−32.81	1.022	0.841	0.206	Y	—
18	Bi2Se3/GaGeTe	1.27%	−24.56	0.462	0.793	0.056	Y	—
19	Bi2Se3/GaTe	0.86%	−29.54	0.147	0.637	0.043	Y	65
20	Bi2Se3/Mn(BiTe2)2	3.64%	−17.69	0.242	0.873	0.055	Y	—
21	Bi2Se3/VI2	1.49%	−31.09	0.135	1.345	0.038	Y	—
22	Bi2Te2S/AuI	0.48%	−34.78	0.105	1.126	−0.02	N	—
23	BiBrO/CuI	1.62%	−17.27	0.654	1.662	0.036	Y	66
24	BiIO/CuI	0.48%	−27.66	0.518	1.557	0.012	Y	—
25	BiClO/CuI	2.78%	−17.25	0.735	1.288	0.044	Y	—
26	SnO2/MoSe2	2.14%	−34.70	1.228	1.452	0.063	Y	—
27	NiS2/WSe2	0.83%	−34.34	0.203	1.397	0.031	Y	—
28	Bi2Se3/Sb	0.68%	−38.67	0.323	1.306	0.081	Y	—
29	Sb2TeSe2/Sb	0.12%	−40.27	0.245	0.609	0.085	Y	—
30	SnS2/As	2.08%	−43.06	0.261	0.646	0.050	Y	—
31	Bi2Te2S/Sr(SnAs)2	2.55%	−30.66	0.236	1.056	0.099	Y	—
32	HfS2/Te2Mo	3.20%	−38.71	0.411	1.123	0.055	Y	67
33	Bi2Se3/Te3As2	2.83%	−29.48	0.130	0.699	0.043	Y	—
34	SnO2/WS2	1.60%	−32.92	1.106	1.098	0.037	Y	—

---

To further validate the selected heterostructures for Z-scheme characteristics using empirical descriptors, we performed high-fidelity DFT calculations on all 34 vdW heterostructures. Previous research has demonstrated that stacking configurations minimally influence the electronic structure of vdW heterostructures.⁵⁹ Furthermore, stacking order does not impact the optical response in these systems.⁶⁰ Therefore, we employ the lattice matching method for constructing heterojunctions.^48,61 The 34 heterostructures are shown in Fig. 3, demonstrating their structural diversity and the richness of material types. Firstly, there is a diverse range of space groups, including P3̄m1, P6̄m2, p4/nmm, P2₁/m, P222₁, Pmmm, Pmmn, Pmna, P2/m, and 10 other space groups. Secondly, the material types are also highly varied, encompassing single-element materials (Sb, As), metal oxides (TMOs) such as SnO₂, PtO₂, ZnO, transition metal nitrides (TMNs) like GaN, iodides (AuI, CuI, VI₂), chlorides (PdCl₂), transition metal dichalcogenides (TMDs) including HfS₂, Te₂W, SnSe, SnS₂, Te₂Mo, SnSe₂, NiS₂, MoSe₂, WSe₂, WS₂, MoSe₂, arsenides (Te₃As₂), as well as structurally complex ternary compounds (TrRhCl, SbBrO, BiBrO, BiIO, BiClO, GaGeTe, GaTe, Bi₂Se₃, AuClO₂, AuBrO₂, TaI₂O, Bi₂Te₂S, Sb₂TeSe₂, Bi₂Te₂Se, Sr(SnAs)₂, Mn(BiTe₂)₂, AuO₂F, HfTeSe₄, Bi₂TeSe₂), representing a diverse array of material types. Fig. S35† displays the quantities and categories of materials in two distinct sets of heterostructures. These 1062 Z-scheme heterostructures cover 2124 single components from 153 different monolayer 2D materials. The finally selected 34 heterostructure candidates in Fig. 3 are made of 41 different 2D materials. These findings affirm the reliability and universality of the descriptors applied to 2D materials.

Fig. 3 Structures of 34 heterostructures with <5% lattice mismatch between two materials within a heterostructure. On the left, the space group corresponding to each single material is displayed.

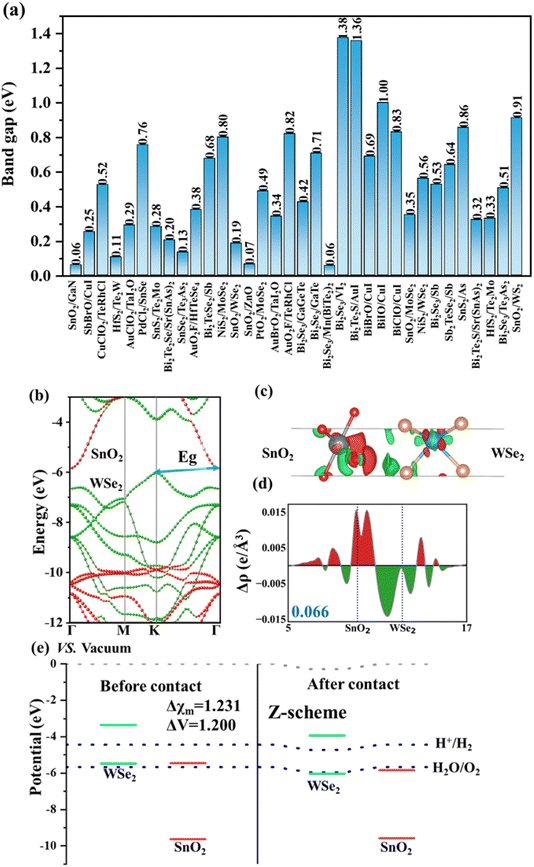
Fig. 4a displays the HSE band gaps for the 34 selected heterostructures, with corresponding electronic structures presented in Fig. S1–S34.† The band gaps range from 0.05 to 1.38 eV. Among the heterostructures, seven have band gaps equal to or less than 0.2 eV: SnO₂/GaN (0.06 eV), HfS₂/Te₂W (0.11 eV), Bi₂Te₂Se/Sr(SnAs)₂ (0.2 eV), SnSe₂/Te₃As₂ (0.13 eV), SnO₂/WSe₂ (0.19 eV), SnO₂/ZnO (0.07 eV), and Bi₂Se₃/Mn(BiTe₂)₂ (0.06 eV). Additionally, there are ten heterostructures with band gaps greater than 0.2 eV but less than 0.5 eV: SbBrO/CuI (0.25 eV), AuClO₂/TaI₂O (0.29 eV), SnS₂/Te₂Mo (0.28 eV), AuO₂F/HfTeSe₄ (0.38 eV), PtO₂/MoSe₂ (0.49 eV), AuBrO₂/TaI₂O (0.34 eV), Bi₂Se₃/GaGeTe (0.42 eV), SnO₂/MoSe₂ (0.35 eV), Bi₂Te₂S/Sr(SnAs)₂ (0.32 eV), and HfS₂/Te₂Mo (0.33 eV). Such small band gaps facilitate the transfer of photogenerated carriers between different materials. Notably, 33 heterostructures exhibit similar electronic structures and demonstrate unidirectional charge transfer, showcasing the characteristic features of Z-scheme heterostructures (see Fig. S1, S21, S23 and S34†). Taking SnO₂/WSe₂ as an example, we show its HSE06 band structures, charge transfer difference, plane-integrated electron density difference along the vertical direction, and band alignment in Fig. 4b–e. As can be seen, the VBM and CBM primarily comprise WSe₂ and SnO₂, respectively. The band structure of this heterostructure displays a staggered band gap. Analysis of charge transfer, plane-integrated electron density difference, and differential charge distribution reveals that electrons accumulate on the SnO₂ side, which has a lower CBM and VBM position compared to WSe₂. Conversely, WSe₂ experiences electron loss. Consequently, charge transfer occurs from WSe₂ to SnO₂, resulting in a transfer of 0.066 e per uc. Additionally, a built-in electric field forms from WSe₂ to SnO₂, indicating a typical Z-scheme behavior. We also examine the rest of the heterostructures which exhibit similar band alignments and built-in field directions, further supporting the screening results of Z-scheme heterostructures. It is noteworthy that over the 34 predicted Z-scheme heterostructures, there is only one exception from our DFT validation, Bi₂Te₂S/AuI (see Table 1 and Fig. S22†). In Bi₂Te₂S/AuI heterostructure, the DFT-based Bader analysis indicates that AuI receives the electron; however, the two simple descriptors suggest that Bi₂Te₂S is the electron recipient. Overall, the 97% prediction accuracy (33 over 34) confirms the high efficiency of the two simple descriptors used in our screening process.

Fig. 4 (a) Calculated band gap of 34 heterostructures by HSE06. Electronic structures of MoSe₂/PtO₂, including (b) HSE06 band structures, (c) differential charge density, (d) plane-integrated charge density difference along the vertical direction, and (e) band alignment. The red and blue regions indicate electron accumulation and depletion, respectively. The isosurface value is set to 0.0002 e Å⁻³. The number labeled in blue is the amount of charge transfer calculated by the Bader approach. The vacuum energy levels on both sides become uneven after contact, leading to distortion in the depicted levels.

Finally, to deeply evaluate the photocatalytic ability of these Z-scheme heterojunctions, we took the redox capability of photocatalytic water splitting as an example and comprehensively considered the band gaps, photogenerated potentials of hydrogen, χ(H₂), (potential difference between CBM and potential of H⁺/H₂) and photogenerated potentials of oxygen, χ(O₂) (the difference between VBM and potential of H₂O/O₂) and the light absorption capacity of 34 Z-scheme heterojunctions, as shown in Table S4.†

It is worth noting that these four heterojunctions all have small band gaps, which are 0.19 eV (SnO₂/WSe₂), 1.38 eV (Bi₂Se₃/VI₂), 0.53 eV (Bi₂Se₃/Sb), and 0.32 eV (Bi₂Te₂S/Sr(SnAs)₂), indicating that the two materials in each heterojunction exhibit efficient charge transfer. Finally, we identified four Z-scheme heterojunctions with powerful redox abilities and strong light absorption capacity, namely SnO₂/WSe₂, Bi₂Se₃/VI₂, Bi₂Se₃/Sb, and Bi₂Te₂S/Sr(SnAs)₂, as shown in Fig. 5. Clearly, we can see that the CBM of WSe₂ (Fig. 5a), VI₂ (Fig. 5b), Sb (Fig. 5c) and Sr(SnAs)₂ (Fig. 5d) is higher than the reduction potential of H⁺/H₂, suggesting that hydrogen evolution reaction (HER) can readily occur on the surface. Specifically, the χ(H₂) for these heterostructures SnO₂/WSe₂, Bi₂Se₃/VI₂, Bi₂Se₃/Sb, and Bi₂Te₂S/Sr(SnAs)₂ are relatively large, i.e., around larger than 0.5 eV. Meanwhile, the VBM of SnO₂ (Fig. 5a), Bi₂Se₃ (Fig. 5b and c), Bi₂Te₂S (Fig. 5d), is lower than the oxidation potential of H₂O/O₂, suggesting that oxygen evolution reaction (OER) can occur on the surface. The χ(O₂) for SnO₂/WSe₂, Bi₂Se₃/VI₂, Bi₂Se₃/Sb, and Bi₂Te₂S/Sr(SnAs)₂ are relatively large, i.e. 3.913, 1.130, 1.117, and 0.477 eV, respectively. Larger values of χ(H₂) and χ(O₂) indicate stronger redox abilities towards HER and OER, which benefit hydrogen generation from water splitting.

Fig. 5 (a) Calculated band alignment and light absorbance of (a) SnO₂/WSe₂, (b) Bi₂Se₃/VI₂, (c) Bi₂Se₃/Sb, and (d) Bi₂Te₂S/Sr(SnAs)₂, respectively. The vacuum energy levels on both sides become uneven after contact, leading to distortion in the depicted levels.

In addition, we analyzed the light absorption capabilities of 2D materials by calculating the light absorption spectrum of all 34 heterostructure candidates (see details in ESI Text S4†). SnO₂/WSe₂ (Fig. 5a) is characterized by pronounced absorption within the visible spectrum, further enhanced by a distinctive peak at 580 nm. Bi₂Se₃/VI₂ (Fig. 5b) exhibits a primary absorption peak at 400 nm, augmented by a secondary peak at 550 nm, demonstrating robust light absorption capabilities. Bi₂Se₃/Sb (Fig. 5c) and Bi₂Te₂S/Sr(SnAs)₂ (Fig. 5d) display significant absorption edges near 600 nm, achieving an absorption intensity of 40%, indicative of strong visible light absorption properties. Upon integrating band gap, photogenerated potentials, and absorbance, we ascertain that these four heterojunctions exhibit superior photocatalytic properties and are thus exemplary candidates for photocatalytic applications. Additionally, the remaining 29 Z-scheme heterojunctions demonstrate substantial photocatalytic potential (Fig. S1–S34†).

Further, to advance the discovery of efficient Z-scheme heterojunctions, we implemented an End-to-End Feed-Forward Network (E2E FFN) machine learning framework, combining both classification and regression models, to systematically screen potential Z-scheme heterojunctions (see details in ESI Text S4†) as shown in Fig. 6. Initially, we processed 11 935 candidate heterojunction combinations through the classification model, successfully identifying 734 heterojunctions that passed the descriptor-based evaluations (Fig. 2c and 6). Following this, the regression model was employed to predict the band edge alignments of these 734 heterojunctions. Using a rigorous selection criterion including the single semiconductor band gap, the heterostructure band gap, the photogenerated potentials of HER (χ(H₂)) and OER (χ(O₂)), and the charge transfer between the heterostructure interface (see Text S4†), we further identified 29 new promising Z-scheme heterojunctions (Table S5†) that were not been captured by the high-throughput DFT calculations in Fig. 2c. These heterojunctions exhibit exceptional properties, including strong light absorption, a Z-scheme charge transfer mechanism, and robust photogenerated potentials for efficient water splitting. This machine learning-driven methodology has greatly accelerated the screening process within a large material space, enabling the discovery of high-performance Z-scheme heterojunctions with minimal computational cost.

Fig. 6 Machine learning screening of high-performance Z-scheme photocatalysts.

Conclusion

In summary, by combining high-throughput screening, high-fidelity calculations, and machine learning on 11 935 vertical vdW heterostructures, we developed an effective and efficient approach to identify the Z-scheme heterostructures before contact. To ascertain precise band structures, the high-precision HSE06 method was employed to compute the band gaps and edge positions of these 155 2D materials, ensuring data reliability and dataset diversity. Our screening results suggest 1062 Z-scheme heterostructure candidates using the Allen material electronegativity and band offset descriptors. Our machine-learning approach in establishing a quantitative relationship between such two descriptors and interfacial charge transfer further strengthens our understanding of the underlying mechanism in the data-driven discovery of Z-scheme heterojunction photocatalysts. Finally, we identified 34 top candidates for Z-scheme heterostructures with lattice mismatch ratios of below 5%, with 33 of them (97%) confirmed by high-fidelity HSE06 calculations as potential photocatalysts. Among these Z-scheme heterojunctions, our photocatalytic calculations indicate that SnO₂/WSe₂, Bi₂Se₃/VI₂, Bi₂Se₃/Sb, and Bi₂Te₂S/Sr(SnAs)₂ exhibit powerful redox abilities for further photocatalytic applications. Finally, leveraging machine learning, we identified 29 new Z-scheme heterojunctions from 1028 previously uncalculated candidates, demonstrating the power of machine learning in accelerating photocatalyst discovery. Our findings not only provide a deeper theoretical insight into Z-scheme photocatalysts but also provide a valuable foundation for subsequent experimental validation and practical applications in photocatalytic water splitting.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Wang Peng for their helpful discussion. This work was supported by the Natural Science Foundation of Chongqing (Grant No. cstc2020jcyj-msxmX0686), the Fundamental Research Funds for the Central Universities (2020CDJ-LHZZ-073), and the National Natural Science Foundation of China (11674042). Xiaoqing Liu acknowledges the financial support from the China Scholarship Council (No. 202106050115). The authors also acknowledge the Centre for Advanced 2D Materials (C2DHPC), High-Performance Computing of the National University of Singapore (HPC@NUS IT), and the National Supercomputing Centre Singapore (NSCC) for providing computing resources. The numerical calculations in this paper have been done on Hefei Advanced Computing Center.

References

1. R. E. Smalley, MRS Bull., 2005, 30, 412–417.
2. M. S. Dresselhaus and I. L. Thomas, Nature, 2001, 414, 332–337.
3. Q. Xu, L. Zhang, J. Yu, S. Wageh, A. A. Al-Ghamdi and M. Jaroniec, Mater. Today, 2018, 21, 1042–1063.
4. J. Low, J. Yu, M. Jaroniec, S. Wageh and A. A. Al-Ghamdi, Adv. Mater., 2017, 29, 1601694.
5. T. Su, Q. Shao, Z. Qin, Z. Guo and Z. Wu, ACS Catal., 2018, 8, 2253–2276.
6. C.-F. Fu, X. Wu and J. Yang, Adv. Mater., 2018, 30, 1802106.
7. P. Zhou, J. Yu and M. Jaroniec, Adv. Mater., 2014, 26, 4920–4935.
8. T. Di, Q. Xu, W. Ho, H. Tang, Q. Xiang and J. Yu, ChemCatChem, 2019, 11, 1394–1411.
9. M. Zhu, Z. Sun, M. Fujitsuka and T. Majima, Angew. Chem., Int. Ed., 2018, 57, 2160–2164.
10. M. Qiao, J. Liu, Y. Wang, Y. Li and Z. Chen, J. Am. Chem. Soc., 2018, 140, 12256–12262.
11. L. Wang, Y. Wan, Y. Ding, S. Wu, Y. Zhang, X. Zhang, G. Zhang, Y. Xiong, X. Wu, J. Yang and H. Xu, Adv. Mater., 2017, 29, 1702428.
12. G. Wang, J. Chang, W. Tang, W. Xie and Y. S. Ang, J. Phys. D: Appl. Phys., 2022, 55, 293002.
13. C. Fu, G. Wang, Y. Huang, Y. Chen, H. Yuan, Y. S. Ang and H. Chen, Phys. Chem. Chem. Phys., 2022, 24, 3826–3833.
14. Z. Zhou, X. Niu, Y. Zhang and J. Wang, J. Mater. Chem. A, 2019, 7, 21835–21842.
15. X. Liu, W. Kang, L. Qi, J. Zhao, Y. Wang, L. Wang, W. Wang, L. Fang and M. Zhou, Phys. E, 2021, 114872.
16. C. H. Shen, X. J. Wen, Z. H. Fei, Z. T. Liu and Q. M. Mu, J. Colloid Interface Sci., 2020, 579, 297–306.
17. S.-T. Li, L. Chang, K. Wang, J. Xie, W. Chen, G.-B. Huang and H. Yin, Chemosphere, 2023, 341, 140117.
18. X. Yan, B. Wang, J. Zhao, G. Liu, M. Ji, X. Zhang, P. K. Chu, H. Li and J. Xia, Chem. Eng. J., 2023, 452, 139271.
19. C.-F. Fu, R. Zhang, Q. Luo, X. Li and J. Yang, J. Comput. Chem., 2019, 40, 980–987.
20. X. Gao, Y. Shen, J. Liu, L. Lv, M. Zhou, Z. Zhou, Y. P. Feng and L. Shen, Catal. Sci. Technol., 2022, 12, 3614–3621.
21. X. Liu, Y.-M. Zhao, X. Zhang, L. Wang, J. Shen, M. Zhou and L. Shen, ACS Catal., 2023, 13, 9936–9945.
22. M. N. Gjerding, A. Taghizadeh, A. Rasmussen, S. Ali, F. Bertoldo, T. Deilmann, N. R. Knøsgaard, M. Kruse, A. H. Larsen, S. Manti, T. G. Pedersen, U. Petralanda, T. Skovhus, M. K. Svendsen, J. J. Mortensen, T. Olsen and K. S. Thygesen, 2D Materials, 2021, 8, 044002.
23. J. Zhou, L. Shen, M. D. Costa, K. A. Persson, S. P. Ong, P. Huck, Y. Lu, X. Ma, Y. Chen, H. Tang and Y. P. Feng, Sci. Data, 2019, 6, 86.
24. S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201.
25. M. C. Sorkun, S. Astruc, J. M. V. A. Koelman and S. Er, npj Comput. Mater., 2020, 6, 106.
26. N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246–252.
27. X. Li, L. Tao, Z. Chen, H. Fang, X. Li, X. Wang, J.-B. Xu and H. Zhu, Applied Physics Reviews, 2017, 4, 021306.
28. Z. Li, Q. Xu, Q. Sun, Z. Hou and W.-J. Yin, Adv. Funct. Mater., 2019, 29, 1807280.
29. A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425.
30. K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, Science, 2016, 353, aac9439.
31. C. Chen, Z. Feng, Y. Feng, Y. Yue, C. Qin, D. Zhang and W. Feng, ACS Appl. Mater. Interfaces, 2016, 8, 19004–19011.
32. Y. Liu, Y. Su, J. Guan, J. Cao, R. Zhang, M. He, K. Gao, L. Zhou and Z. Jiang, Adv. Funct. Mater., 2018, 28, 1706545.
33. B.-X. Zhou, S.-S. Ding, K.-X. Yang, J. Zhang, G.-F. Huang, A. Pan, W. Hu, K. Li and W.-Q. Huang, Adv. Funct. Mater., 2021, 31, 2009230.
34. P. Yao, D. He, P. Zereshki, Y. Wang and H. Zhao, Appl. Phys. Lett., 2019, 115, 263103.
35. I. Shahid, S. Ahmad, N. Shehzad, S. Yao, C. V. Nguyen, L. Zhang and Z. Zhou, Appl. Surf. Sci., 2020, 523, 146483.
36. I. Shahid, A. Ali, J.-M. Zhang, I. Muhammad, I. Ahmad and F. Kabir, Int. J. Hydrogen Energy, 2021, 46, 14247–14258.
37. A. Ratnaparkhe and W. R. L. Lambrecht, Appl. Phys. Lett., 2017, 110, 132103.
38. C. Bhandari, M. van Schilfgaarde, T. Kotani and W. R. L. Lambrecht, Phys. Rev. Mater., 2018, 2, 013807.
39. M. I. Jordan and T. M. Mitchell, Science, 2015, 349, 255–260.
40. Z. Ghahramani, Nature, 2015, 521, 452–459.
41. E. N. Muratov, J. Bajorath, R. P. Sheridan, I. V. Tetko, D. Filimonov, V. Poroikov, T. I. Oprea, I. I. Baskin, A. Varnek, A. Roitberg, O. Isayev, S. Curtalolo, D. Fourches, Y. Cohen, A. Aspuru-Guzik, D. A. Winkler, D. Agrafiotis, A. Cherkasov and A. Tropsha, Chem. Soc. Rev., 2020, 49, 3525–3564.
42. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169.
43. P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
44. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097.
45. J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 124, 154709.
46. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
47. J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2009, 22, 022201.
48. K. Choudhary, K. F. Garrity, S. T. Hartman, G. Pilania and F. Tavazza, Phys. Rev. Mater., 2023, 7, 014009.
49. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658.
50. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
51. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
52. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
53. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
54. W. Tenachi, R. Ibata and F. I. Diakogiannis, Astrophys. J., 2023, 959, 99.
55. J. Y. Seo, S. Shim, J.-W. Lee, B. D. Lee, S. Park, W. B. Park, S. Han, M. Pyo and K.-S. Sohn, J. Mater. Chem. A, 2022, 10, 1831–1839.
56. A. Iwase, S. Yoshino, T. Takayama, Y. H. Ng, R. Amal and A. Kudo, J. Am. Chem. Soc., 2016, 138, 10260–10264.
57. L. Wang, X. Zheng, L. Chen, Y. Xiong and H. Xu, Angew. Chem., 2018, 130, 3512–3516.
58. Z.-F. Huang, J. Song, X. Wang, L. Pan, K. Li, X. Zhang, L. Wang and J.-J. Zou, Nano Energy, 2017, 40, 308–316.
59. J. Linghu, T. Yang, Y. Luo, M. Yang, J. Zhou, L. Shen and Y. P. Feng, ACS Appl. Mater. Interfaces, 2018, 10, 32142–32150.
60. J. F. R. V. Silveira, R. Besse and J. L. F. Da Silva, ACS Appl. Electron. Mater., 2021, 3, 1671–1680.
61. A. Zur and T. McGill, J. Appl. Phys., 1984, 55, 378–386.
62. X. H. H. H. Z. J. Yang Liu, Acta Phys.-Chim. Sin., 2021, 37, 2008030.
63. Y. Yu, B. Yao, B. Cao and W. Ma, Photochem. Photobiol., 2019, 95, 1131–1141.
64. X. Gao, Y. Shen, J. Liu, L. Lv, M. Zhou, Z. Zhou, Y. P. Feng and L. Shen, Catal. Sci. Technol., 2022, 12, 3614–3621.
65. S.-m. Tian, J. Meng, J. Huang and Q.-x. Li, Chin. J. Chem. Phys., 2020, 33, 427–433.
66. B. Liu, X. Hu, J. Yang, C. Yang and Y. Huang, Catal. Sci. Technol., 2023, 13, 504–515.
67. X. Yang, X. Qin, J. Luo, N. Abbas, J. Tang, Y. Li and K. Gu, RSC Adv., 2020, 10, 2615–2623.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta07683d

‡ These authors contributed equally to this work.

---