Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structurally disordered In2Te3 semiconductor: novel insights†
Esteban
Zuñiga-Puelles
 *a,
Ayberk
Özden
*a,
Ayberk
Özden
 b,
Raul
Cardoso-Gil
b,
Raul
Cardoso-Gil
 c,
Christoph
Hennig
c,
Christoph
Hennig
 de,
Cameliu
Himcinschi
de,
Cameliu
Himcinschi
 b,
Jens
Kortus
b,
Jens
Kortus
 b and
Roman
Gumeniuk
b and
Roman
Gumeniuk
 *a
*a
aInstitut für Experimentelle Physik, TU Bergakademie Freiberg, Leipziger Straße 23, 09596 Freiberg, Germany. E-mail: estebanzp1@outlook.com; gumeniuk@physik.tu-freiberg.de
bInstitut für Theoretische Physik, TU Bergakademie Freiberg, Leipziger Straße 23, 09596 Freiberg, Germany
cMax-Planck-Institut für Chemische Physik Fester Stoffe, Nöthnitzer Straße 40, 01187 Dresden, Germany
dHelmholtz-Zentrum Dresden-Rossendorf, Institute of Resource Ecology, Bautzner Landstraße 400, 01328 Dresden, Germany
eThe Rossendorf Beamline at ESRF, CS 40220, 38043 Grenoble Cedex 9, France
First published on 3rd March 2025
Abstract
The crystal structures of low- (α) and high-temperature (β) modifications of In2Te3 are refined for the first time. They crystallize with unique noncentrosymmetric face-centered cubic and half-Heusler arrangements, respectively. Both models are related with each other via a group–subgroup formalism. The small changes in unit-cell volume and entropy at the α → β structural phase transition indicate that it is of 2nd order. The strong structural disorder in α-In2Te3 results in a temperature-dependent behavior of the electrical resistivity similar to that of doped semiconductors (with a well-defined maximum) and extremely low thermal conductivity [κ(T) ≤ 0.7 W m−1 K−1]. Additional reasons for the poor electrical and thermal transport are low charge-carrier concentration and mobility, as well as enhanced phonon scattering at point defects, together with the presence of four-phonon processes and a ‘rattling’ effect. α-In2Te3 is found to be an n-type indirect semiconductor with an energy gap of 1.03 eV. All these physical characteristics are intrinsic properties of a high-quality stoichiometric crystal.
1 Introduction
Indium-based semiconductors play one of the central roles in modern electronic technologies. Revealing often direct band gaps and being easily tunable, they have nowadays become prioritized in comparison with widely used and abundant materials, such as silicon and gallium arsenide. Finding applications in the construction of high- (HT) and low-temperature (LT) transistors,1–8 laser diodes,9–14 optoelectronics,15–19 liquid crystal displays,20–23etc., they are some of the most sought-after objects for investigations. Among the many such materials, In2Te3 attracts special interest due to its potential applications as a catalyst for hydrogen evolution,24 in photodetectors,15–19 in gas sensors,25 as an anode for Li-ion batteries,26 in photovoltaic power generation,27–29 and as an alloying component in thermoelectric (TE) generators.30–35 The development of both latter technologies is of extreme importance with respect to modern attempts in being environmentally friendly. Indeed, In2Te3 doped with Se is shown to reveal a band gap suitable for production of single-junction solar cells. Furthermore, it can be used in tandem solar-cell architectures overcoming the ≈33% efficiency limit.28 Additionally, this chalcogenide finds broad application in TE technology, allowing improvement of the figure-of-merit (zT ≳ 1) of numerous state-of-the-art materials, e.g., SnTe,36 GeTe,37 Bi2Te3,30,31 Sb2Te3,32,33 Ga2Te3,34 InSb,38 and Cu2SnSe4.35 Recent advances in the development of chalcogen-based TE materials, characterized by ultra-low thermal conductivity due to structural defects with lower dimensionality, are highlighted in ref. 39–47.Noteworthily, despite being in focus for such important technological uses, the basic knowledge on In2Te3 seems to still remain questionable, requiring novel insights. In particular, the structural arrangement and nature of the phase transition are less explored. The available structural models for the low-temperature (LT) α-In2Te3 (within space groups F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m, Imm2 and I4mm)48,49 and high-temperature (HT) β-In2Te3 (fcc ZnS prototype)50 were assumed based on the indexing of powder X-ray diffraction patterns, as well as applying group–subgroup crystallographic relations. No structural refinements are known up to now.51,52 Importantly, quantum mechanical calculations performed assuming all these LT-models resulted in metallic properties for α-In2Te3 (material ID: 622511, 1223866 and 1105025),53 whereas those done for β-In2Te3 indicated it to be a semiconductor with a band gap of 1.52 eV.54 These results are contradictory and suggest that the existing structural models are likely to be incorrect.
3m, Imm2 and I4mm)48,49 and high-temperature (HT) β-In2Te3 (fcc ZnS prototype)50 were assumed based on the indexing of powder X-ray diffraction patterns, as well as applying group–subgroup crystallographic relations. No structural refinements are known up to now.51,52 Importantly, quantum mechanical calculations performed assuming all these LT-models resulted in metallic properties for α-In2Te3 (material ID: 622511, 1223866 and 1105025),53 whereas those done for β-In2Te3 indicated it to be a semiconductor with a band gap of 1.52 eV.54 These results are contradictory and suggest that the existing structural models are likely to be incorrect.
The band-gap values obtained for α-In2Te3 from different optical spectroscopic measurements vary in the Eoptg ≈ 0.99–1.22 eV range.55–61 The nature of the transition (i.e., direct/indirect) remains unclear due to the absence of trustworthy structural data. Studies of the temperature dependencies of the Hall55,62 and Seebeck63 coefficients indicated hole- or electron-mediated conduction mechanisms in different samples. These findings agree well with the small homogeneity range reported for α-In2Te3.64–66 However, a relation between the composition and type of conductivity is still less understood. The charge-carrier concentrations at room temperature, of ≈1010 cm−3 for p- and ≈1012 cm−3 for n-type samples as deduced from Hall-effect measurements, are in line with the observed optical band gaps.67 Polycrystalline α-In2Te3 reveals a low thermal conductivity of 1–1.5 W m−1 K−1 in a broad temperature range of 300−700 K.34 However, the underlying physical mechanisms for such an effect have not been elucidated.
In this work, we revisit the structural models of LT and HT polymorphs of In2Te3 by using temperature-dependent high-resolution synchrotron X-ray diffraction. To elucidate the nature of the phase transition, determination of the intrinsic physical and thermodynamic properties, and magnetic, electrical and thermal transport measurements combined with optical and spectroscopic analyses were performed. All these characterization studies were carried out on a well-established high-quality stoichiometric In2Te3 crystal.
2 Experimental section
2.1 Synthesis
The sample was prepared via a solid-state reaction from 5N elemental indium powder and tellurium pieces, cold pressed (5 kN) and mixed in a stoichiometric ratio in an Ar-filled glove-box (MBraun, p(O2/H2O) < 0.1 ppm). The material mixture was placed inside a quartz tube (length ≈ 10 cm with an inner diameter ≈ 12 cm) and sealed under vacuum (<10−5 mbar). The sample was heated in 1 day to 700 C and it was kept at this temperature for 5 hours, then slowly cooled down to 600 C in 5 days and further annealed at this temperature for 5 days. Finally, it was quenched in an ice/water mixture.2.2 Characterization
Temperature-dependent synchrotron powder X-ray diffraction (PXRD) measurements (λ = 0.61996 Å) were performed at beamline BM20 of the European Synchrotron Radiation Facility (ESRF, Grenoble, France).68 The sample was manually powdered and sieved to a grain size of ≤20 μm and then enclosed in a quartz-capillary of 0.3 mm inner diameter under an Ar-atmosphere. Phase analysis was carried out with the WinXpow program suite69 and crystal structure refinements were performed using the WinCSD program package.70A representative sample's surface was analyzed via scanning electron microscopy (SEM) and spectroscopic ellipsometry. Local chemical composition and microstructure analyses were carried out using a SEM-JEOL JSM 7800F microscope equipped with a Bruker Quantax 400, XFlash 6‖30 (silicon drift detector) EDXS spectrometer. The latter confirmed the sample to be single-phase with a chemical composition of In1.9(1)Te3.1(1) determined from 10 randomly selected points (Fig. S1†).
Differential thermal analysis (DTA) with thermogravimetry (TG) was performed on a bulk piece of ≈20 mg, inspected with an optical microscope. The measurement in the temperature range of 300–1000 K with a heating/cooling rate of 10 K min−1 was done using a Netzsch STA 449F3 device.
2.3 Physical properties
Spectroscopic ellipsometry measurements were performed on a polished surface (area >1 cm2), where the final step was done using 0.25 μm diamond powder. The data was recorded at 50°, 55° and 60° incidence angles in the 0.73–6 eV range using an M2000 J.A. Woollam ellipsometer.Non-polarized Raman spectra were recorded with a Horiba LABRAM System-HR-800, with a CCD camera, a 600 grooves per mm grating, a HeNe laser (633 nm), and a 50× objective with a N.A. of 0.5 (calibrated with a Si[111]-standard by use of its 520.6 cm−1 peak). Neon calibration-lamp spectra were recorded after each measurement to track and correct any shift during the Raman measurements. Temperature-dependent Raman spectra and Raman thermal conductivities were obtained with a Linkam THMS-600 cooling–heating stage. The latter was continuously cooled using a liquid-nitrogen vapor-flow and the samples were fixed with silver paste to the stage.
Low-temperature (LT, T ≤ 300 K) magnetic susceptibility [χ(T)], specific heat capacity [cp(T)], charge-carrier concentration [n(T)] and mobility [μ(T)], electrical resistivity [ρ(T)], Seebeck coefficient [S(T)] and total thermal conductivity [κ(T)] measurements were performed with the VSM, HC, VdP-Hall, and TTO modules of a DynaCool-12 from Quantum Design, respectively. The χ(T) and cp(T) measurements were performed on sample pieces of ≈19.5 mg and ≈10 mg, respectively.
The Hall-effect measurements using the Van der Pauw four-probe method were performed on a square-shaped plate of ∼5 × 5 × 0.4 mm3, in contact with platinum wires (25 μm) in a magnetic field of 10 T. Further, n(T) and μ(T) were calculated from the measurements. High-temperature (HT, 300 K ≤ T ≤ 600 K) ρ(T) and S(T) were measured with an ULVAC ZEM-3 device. Both LT and HT ρ(T), S(T) and κ(T) properties were obtained from a bar-shaped sample with dimensions of ∼1.5 × 1.4 × 6.1 mm3. The HT specific heat was measured on a sample piece of ∼36 mg placed inside an Al2O3 crucible using a differential scanning calorimeter, DSC 8500, from PerkinElmer. The heating rate during the measurement was 20 °C min−1.
3 Crystal structure
In order to verify the structural models of low- (LT) and high-temperature (HT) modifications of In2Te3, high-resolution (HR) synchrotron PXRD was performed. Selected 2θ-regions of several obtained PXRD patterns, measured at different temperatures, are depicted in Fig. 1. For T < 870 K, all peaks observed therein could be indexed with a unit-cell parameter (UCP) a ≈ 18.5(2) Å. Further analysis of the extinction conditions indicated a face-centered cubic lattice with possible space groups (SGs) of F23, Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , F432, F
, F432, F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m and Fm
3m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. This finding prompted us to perform Rietveld refinement assuming the structural model proposed for In2Te3.49,71–73 However, it converged with high reliability factors (RI = 0.094, RP = 0.136) as well as with an atomic thermal displacement parameter (Biso) for the In1-atom in the Wyckoff position 24f that is larger by a factor of ≈2 than those of all other crystallographic sites. This latter observation would assume partial occupancy for the 24f site and thus, a deviation from the experimentally confirmed 2
m. This finding prompted us to perform Rietveld refinement assuming the structural model proposed for In2Te3.49,71–73 However, it converged with high reliability factors (RI = 0.094, RP = 0.136) as well as with an atomic thermal displacement parameter (Biso) for the In1-atom in the Wyckoff position 24f that is larger by a factor of ≈2 than those of all other crystallographic sites. This latter observation would assume partial occupancy for the 24f site and thus, a deviation from the experimentally confirmed 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 stoichiometric composition (Fig. S1†). Being derived by solely applying the group–subgroup symmetry reduction to the defective ZnS type, the structural model of α-In2Te3 proposed in the literature needs further analysis. Additional proof based on density functional theory (DFT) calculations hinting towards the wrongness of the structural model is provided in ESI.†
3 stoichiometric composition (Fig. S1†). Being derived by solely applying the group–subgroup symmetry reduction to the defective ZnS type, the structural model of α-In2Te3 proposed in the literature needs further analysis. Additional proof based on density functional theory (DFT) calculations hinting towards the wrongness of the structural model is provided in ESI.†
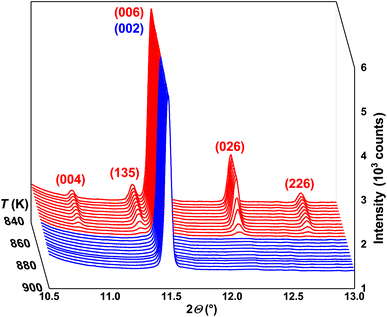 | ||
| Fig. 1 Selected 2θ-region of synchrotron PXRD patterns for 840 K < T < 900 K together with (hkl) indices for LT α- (red) and HT β- (blue) In2Te3. | ||
Therefore, in the next step we tried to deduce the atomic positions in the studied telluride by applying direct methods. The attempt resulted in the same Te2–Te5 positions as reported earlier (cf. Table S2† and data from the ICSD) as well as Te1 at 4c and In at 16e, 24g and 48h, which differed from those found in the literature.49,71–73 Refinement of such a model converged with RI = 0.089, RP = 0.134, the wrong In2.4Te3 composition and the residual electron density (RED) −2.2/+3.7e Å−3. Performed differential Fourier syntheses indicated additional RED at the 4b and 24g Wyckoff positions. The latter one was already known to be occupied by In-atoms in the model derived from the ZnS type. Having now too much In-concentration in the structure, we refined the site occupancy (G) of the crystallographic sites of these atoms. After this step, the values of the RED were already −0.71/+0.91e Å−3. However, refining the atomic displacement parameters (ADPs), we observed an unphysically large value of Biso for Te1 at the 4c position. Shifting it off the center (i.e., assuming this atom to occupy ≈ 25% of a 16e site with x = y = z ≈ 0.02), a reliable ADP could be obtained. The final values of the R-factors, atomic coordinates, Biso and occupancy obtained from the performed refinement are collected in Tables S1 and S2.† The experimental, theoretical and differential profiles corresponding to these are plotted in Fig. 2 (upper panel). The good agreement of the refined and experimental compositions, together with the improvement of the RI-factor by almost 30%, indicate the reliability of the obtained model.
 | ||
| Fig. 2 Synchrotron PXRD patterns and Rietveld refinements for LT α- and HT β-In2Te3 together with peak positions, as well as experimental, theoretical and difference profiles. | ||
Since now the majority of the crystallographic positions shown in Table S2† cannot be derived via group–subgroup relation from the ZnS type, the latter model is obviously inconsistent with the HT β-In2Te3. However, by performing indexing of the PXRD patterns presented in Fig. S2†, we confirmed the earlier reported UCP aHT ≈ aLT/3 ≈ 6.2(1) Å as well as the face-centered cubic lattice with the above-mentioned SGs. Keeping in mind that the klassengleiche transformation with an index of 9 should work during the α → β phase transition in In2Te3, we attempted direct methods, assuming again the SG F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m for HT-modification. There, two In-atoms are localized at 4a and 4b and Te at 4c. Such a structural arrangement corresponds to the MgAgAs half-Heusler type.74 It should also be noted that in the prototype compound, the 4a-, 4b- and 4c-sites are occupied by Mg, As and Ag, respectively, which makes the discussion within the group–subgroup scheme less conclusive (Fig. S3†). Therefore, in the further considerations we refer to the MnPdTe compound, where Pd and Te are at the 4b and 4c sites.75 The R-factors of the refinements performed at different temperatures, the obtained atomic coordinates, and the Biso and occupancy values for HT-β-In2Te3 are shown in Table S3.† The experimental, theoretical and difference profiles for T = 323 K and T = 899 K are depicted in Fig. 2.
3m for HT-modification. There, two In-atoms are localized at 4a and 4b and Te at 4c. Such a structural arrangement corresponds to the MgAgAs half-Heusler type.74 It should also be noted that in the prototype compound, the 4a-, 4b- and 4c-sites are occupied by Mg, As and Ag, respectively, which makes the discussion within the group–subgroup scheme less conclusive (Fig. S3†). Therefore, in the further considerations we refer to the MnPdTe compound, where Pd and Te are at the 4b and 4c sites.75 The R-factors of the refinements performed at different temperatures, the obtained atomic coordinates, and the Biso and occupancy values for HT-β-In2Te3 are shown in Table S3.† The experimental, theoretical and difference profiles for T = 323 K and T = 899 K are depicted in Fig. 2.
The shortest interatomic distances in the structures of α- and β-In2Te3 are collected in Tables S1 and S3.† Both structures are characterized by no bonding In–In and Te–Te contacts. In contrast, the In–Te distances are shortened by ≈5–12% in comparison with the sum of the covalent radii r(In) = 1.5 Å and r(Te) = 1.37 Å.76
The group–subgroup relation scheme between α- and β-In2Te3 modifications is presented in Fig. S3.† As expected, the majority of In- and Te-positions in the LT-polymorph are derived from the largely occupied 4b and 4c sites in the HT-structure. This finding differs from the previously reported model derived from the ZnS type, where both In-positions were deduced from the 4a site. In our case, the 24g position originating from this site is only ≈17% occupied, in agreement with the low occupancy in the HT-polymorph (cf. Tables S2 and S3†). Additionally, the presence of a Te1-atom at 4c in the LT-modification would suggest the initial 4a-site in β-In2Te3 to be occupied with a statistical In/Te mixed site occupancy. However, such a refinement from PXRD data is rather impossible due to the close atomic form factors of indium and tellurium. This problem could be addressed by neutron diffraction on high-quality crystals.77
The In1-atom at 4b in α-In2Te3 can only be derived from the group–subgroup scheme if a 4d position in the HT-polymorph would be occupied (Fig. S3†). The structure arrangement with the (dcba) Wyckoff sequence, SG F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m and a ≈ 6.5(3) Å, is known as the TiCuHg2 type.78 For better visualization, we use in the further discussions its ordered superstructure LiPtMgSb.79 This structural arrangement is obviously not suitable for β-In2Te3, since the 4d-site remained non-occupied therein (i.e., the final values of RED after refinement were −0.14/+0.23e Å−3), which raises a question about the correctness of the proposed group–subgroup scheme in Fig. S3.† However, accounting for G = 0.25 for the In1-atom in the LT-modification, one would expect the 4d site occupancy in β-In2Te3 to be lower than ≈3%, which is again undetectable within the refinement of the PXRD data. Obviously, as mentioned above, to unambiguously solve the crystal structures of α- and β-In2Te3, a temperature-dependent neutron diffraction study is strongly required.
3m and a ≈ 6.5(3) Å, is known as the TiCuHg2 type.78 For better visualization, we use in the further discussions its ordered superstructure LiPtMgSb.79 This structural arrangement is obviously not suitable for β-In2Te3, since the 4d-site remained non-occupied therein (i.e., the final values of RED after refinement were −0.14/+0.23e Å−3), which raises a question about the correctness of the proposed group–subgroup scheme in Fig. S3.† However, accounting for G = 0.25 for the In1-atom in the LT-modification, one would expect the 4d site occupancy in β-In2Te3 to be lower than ≈3%, which is again undetectable within the refinement of the PXRD data. Obviously, as mentioned above, to unambiguously solve the crystal structures of α- and β-In2Te3, a temperature-dependent neutron diffraction study is strongly required.
In Fig. 3, the arrangement of polyhedra in the crystal structures of α- and β-In2Te3, assuming full occupancies of all crystallographic sites, in comparison with the LiPtMgSb type is presented. As is known, not being a centered structure [i.e., no atom at 4b (1/2 1/2 1/2)], ZnS reveals for this site an [□S4]-tetrahedron, [□Zn6]-octahedron and [□Zn8]-cube as the first, second and third coordination spheres, respectively.80 Centering such a unit cell by adding an atom into the 4b Wyckoff position, one would obtain the MgAgAs type (β-In2Te3) with an [In2HTTeHT4]-tetrahedron, [In2HTIn16HT]-octahedron and [In2HTIn2HT12]-cuboctahedron (Fig. S3† and 3b). Adding a further atom at 4d (LiPtMgSb type) results in a [MgPt4Li4]-cube as a first coordination sphere, whereas the second and third ones remain the same as in β-In2Te3 (MgAgAs type) (cf.Fig. 3a and b). Being closely related with both simple prototypes, the α-In2Te3 crystal structure reveals a similar arrangement of polyhedra. As one can see from Fig. 3c, there appears an array of corner-sharing [In5Te44]-tetrahedra (tan) typical for MgAgAs and ZnS types (not shown in Fig. 3a and b). Since the 4d-sites are unoccupied in the HT-modification, the [□Te34]-tetrahedra (red), [□In46]-octahedra (blue) and [□In512]-cuboctahedra (dark grey) remain empty, in contrast to the MgAgAs prototype. The same observation is made for unoccupied [□Te14Te24]-cubes and [□In46]-octahedra surrounding them, which resemble the structural units of the LiPtMgSb arrangement. Also, the third coordination sphere of this empty site is only a [□In24]-tetrahedron (dark grey) (instead of a cuboctahedron, as it is the case for LiPtMgSb), which is due to the unoccupied 16e site derived from the 4b one (Fig. S3†).
 | ||
| Fig. 3 Structural arrangement and comparison of the LiMgPtSb (a), HT β- (b) and LT α- (c) In2Te3 structures. | ||
4 Thermal expansion and atomic motion
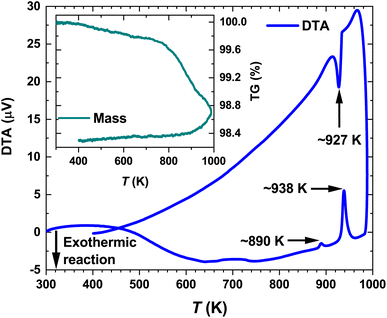
Selected synchrotron PXRD patterns measured in the 100–974 K temperature range are presented in Fig. 1. All of them reveal strong and weak intensities (i.e., Istrong/Iweak ≳ 90) as well as broadened peak bases. The latter has been attributed to diffuse reflections observed in the diffraction patterns of mechanically sorted single crystals from the same long-term-annealed sample. The diffuse scattering by them hampered any further refinements. Thus, we ascribe the broadening in the PXRD patterns to the intrinsic structural disorder rather than to microstructural effects such as, e.g., stacking faults.As the temperature increases, some weak reflections become systematically suppressed (e.g., 004, 135, 026 and 226) until they completely disappear at the transition temperature Tα→β ≈ 865 K (Fig. 1). The strong background increase in the PXRD pattern measured at ∼926 K indicates the beginning of the melting process. It becomes completed at Tmelt ≈ 950 K as no diffraction peaks are observed. These results agree well with our differential thermal analysis (DTA) (see below) and the reported In–Te phase diagrams (Tα→β and Tmelt range between 878–915 K and 938–952 K, respectively).64–66 The small offset between the structurally and thermally determined Tα→β might be attributed to Te-mass losses in the dynamic Ar-flow used during DTA (bulk).
The temperature dependencies of the unit-cell volumes, defined as aLT3 and 27aHT3 for the α and β phases, respectively, are depicted in Fig. 4. The thermal expansion of the LT-modification can be described by a 2nd-order polynomial function in the temperature range of 100–800 K:
| Vα(T) = V0α + V1αT + V2αT2 | (1) |
 | (2) |
 | ||
| Fig. 4 Temperature-dependent unit-cell volume V of α- and β-In2Te3 from 102 K to 974 K together with the fit to eqn (1) (red-dotted line). Inset: Near-phase-transition unit-cell volume variation ΔV estimated at 850 K. | ||
| Parameters | α-In2Te3 |
|---|---|
| Fitted T-range | 100–864 K |
| V 0 (Å3) | 6264(1) |
| V 1 (Å3 K−1) | 0.165(6) |
| V 2 (Å3 K−2) | 5.4(7)× 10−5 |
| α V (10−5 K−1) | 2.8–4.0 |
| γ XRD | 1.5–2.1 |
Unexpectedly, at T ≈ 820 K the UCP of α-In2Te3 starts to decrease, revealing a weak negative thermal expansion (i.e., reduction of the unit-cell volume ΔV ≈ –0.05%) (Fig. 4 inset). Only after the structural transformation is completed at T ≈ 865 K (no superstructural peaks are observed) does the UCP start to increase with temperature again. Such a “negative step” in the a3(T) is in contrast with the behavior of thermal expansion at the SPT (e.g., for the closely related In2S3 (ref. 81) as well as with the classical expectations), where a positive jump in this dependence should be the case.82,83 Nevertheless, an analogous effect has been also observed for TiGePt84 and Zn2−xMgxP2O7.85
Knowing the average speed of sound in α-In2Te3 (vS = 2560 ms−1)86 and the Dulong–Petit limit (cp) we calculate the Grüneisen parameter from the formula γXRD = αvνs2cp−1 (Table 1). The obtained value agrees with those observed for many semiconductors (i.e., γ ≈ 1–2)87 as well as with γ ≈ 2.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88 found for the state-of-the-art thermoelectric material SnTe. All these suggest an enhanced phonon anharmonicity.89
88 found for the state-of-the-art thermoelectric material SnTe. All these suggest an enhanced phonon anharmonicity.89
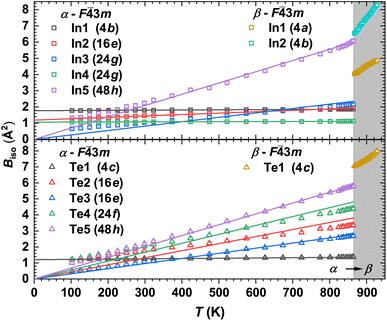
The temperature dependencies of the isotropic atomic displacement parameters (ADPs) for the α- and β phases are shown in Fig. 5. In agreement with the theory proposed in ref. 90, we observe a small Biso dependence on T, together with their displacements upward by a constant value for the strongly statistically disordered sites (Table. S2†). On the other hand, for atoms at almost fully occupied crystallographic positions, the Biso(T) values for T > 400 K are increasing nearly linearly with different slopes, which is a signature of the so-called dynamic disorder.90 The latter is known to be mainly due to thermal motion of atoms, which can be treated as local vibrations of a quantized harmonic oscillator (Einstein model). Hence, for sufficiently high temperatures (i.e., hω ≪ 2kBT), Biso(T) is given as:
 | (3) |
Further, applying the definition of a cage-compound92–94 to α-In2Te3, we assume the Te-atoms form an anionic framework incorporating positively charged In-cations. Such a description can be also justified by the larger electronegativity (Pauling scale) of Te (χTe = 2.10) in comparison to that of indium (χIn = 1.78).76 This concerns the steepest slope of Biso(T) dependence for In5-atoms, which indicates them to potentially be a ‘rattler’.91 Thus, applying eqn (3), a characteristic ΘIn5E = 69(1) K (Fig. 5, upper panel) is deduced.
5 Thermodynamics of the phase transition
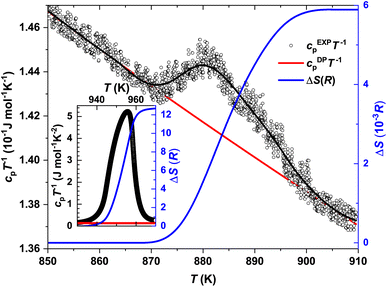
The temperature-dependent differential thermal analysis and thermogravimetry (DTA-TG) curves of α-In2Te3 are presented in Fig. 6. Upon heating, two endothermic peaks corresponding to the α → β phase transition at Tα→β ≈ 890 K and to the melting point at Tmelt ≈ 938 K are observed, in agreement with the reported binary In–Te phase diagram.64–66 On cooling, only the signal at Tmelt ≈ 927 K is present, whereas that corresponding to Tα→β is not observed. One possible explanation for this effect can be found in the TG curve. As one can see from the Fig. 6 inset, the mass loss is ≈0.4 wt% on heating from 400 K up to 800 K. With a further temperature increase up to 1000 K, it becomes ≈1.5 wt%. This indicates the off-stoichiometry of the studied specimen after heating. Additionally, the PXRD patterns measured in a dynamic Ar-flow revealed the peaks corresponding to the α-modification to be broadened and slightly shifted (to higher 2θ values) due to possible Te-losses.The temperature dependencies of the specific heat capacity in the cpT−1(T) representation near the Tα→β and Tmelt transitions are presented in Fig. 7 and the inset therein, respectively. The Tonset–Toffset ranges of both anomalies agree well with the DTA measurements (Table 2). The discrepancies in the assignment of Tmax can be explained by the asymmetries of the peaks in the cpT−1(T) dependencies.
| α → β | Melting | |
|---|---|---|
| T max c p (K) | 882 | 956 |
| T onset c p − Toffsetcp (K) | 865–905 | 923–970 |
| T PXRDα→β (K) | 865 | — |
| T PXRDmelt (K) | — | 950 |
| ΔH (J mol−1) | ∼44.6 | 66× 103 |
| ΔS (J mol−1 K−1) | 4.9 × 10−2 | ∼107 |
| ΔS(R) | 6 × 10−3 | 12.9 |
Further, knowing the Dulong–Petit limit cDPpT−1 (see discussion below) and subtracting it as a peak baseline, we calculated the changes in entropy and enthalpy at the Tα→β and Tmelt transitions (Table 2) using ΔS = ∫cpT−1dT and ΔH = ∫cpdT, respectively. The drastic difference in the obtained ΔS(R) values (where R is the gas constant) would obviously indicate different orders of the transitions.83
To define the α → β structural phase transition in In2Te3 as being of 1st order, the following criteria are expected to be fulfilled: (i) the coexistence of both polymorphs at Tα→β, (ii) a discontinuous change in both unit-cell volume and ΔS, (iii) a sharp symmetric peak in cp(T) and (iv) ρ(T) hysteresis while performing the measurement in the heating and cooling regimes.81,82 The first and last criteria from this list have not been proven up to now, whereas points (ii) and (iii), as is clearly visible from the discussions above, are not fulfilled. Obviously, to unambiguously estimate the order of this transition, some additional studies are required.
6 LT specific heat capacity
The specific heat capacity for α-In2Te3 in the cp/T3(T) representation is depicted in Fig. 8. It reveals a boson peak with a maximum at T ≈ 9 K originating from the minor and major contributions of low-energy acoustic and optical modes, respectively.95 However, in the case of a ‘rattling’ effect, the latter are normally the dominating ones, as has been found for cage compounds.92–94 In these materials, the low-energy optical phonon modes arise from the low-frequency vibrations of weakly-bonded cations incorporated in the anionic framework. Therefore, for the description of the In2Te3 LT specific heat capacity, we applied the combined Debye–Einstein model, given as: | (4) |
 | (5) |
 | (6) |
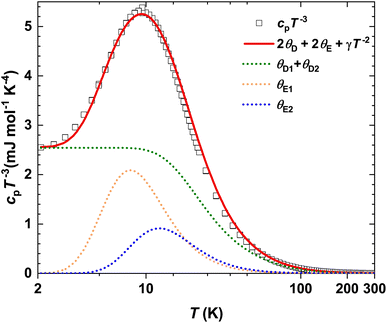 | ||
| Fig. 8 Temperature dependence of specific heat capacity for α-In2Te3 in the cp/T3 representation, including the fit (red line) to eqn (4). The individual contributions from eqn (5) and (6) are shown as dotted lines. | ||
Since the quantity of Debye terms is defined by the number of elemental constituents in the chemical formula (i.e., two for In2Te3) and that of Einstein modes by the amount of ‘rattlers’, we set i = 2 and j = 1 in the preliminary model. Further, accounting for the stoichiometric composition of the studied compound, we find the total number of modes to be Ntot = NDi + NEj = 15. Knowing from the analysis of the Biso(T) dependencies that only In5 could be a ‘rattler’ and thus, having 48-fold site symmetry with a site occupancy G = 0.87 (Table S2†), one could assume NE1 ≈ 3. Then NDi = 12 with ND1 ≈ 3 (for the not-‘rattling’ In-atom) and ND2 = 9 (for Te-atoms) should be the case. However, a model based on this concept failed in the description of the peak in the cp/T3(T) dependence, which is an indication of a much more complex phonon spectrum of the studied α-In2Te3. Such a situation was frequently reported in the literature.98–101 Therefore, in the next attempt of the fitting we assumed an additional ‘rattling’ contribution (i.e., j = 2), which could originate from the In3-atom due to the observed slope in the Biso(T) dependence. Removing all constrains on all NDi and NEj values in the fit, the best description is obtained for a model with ND1 = 4(1), ND2 = 9(1), NE1 = 0.7(1), NE2 = 1.1(2) and thus Ntot = 14.8. The corresponding Debye and Einstein temperatures were ΘD1 = 322(7) K, ΘD2 = 101(5) K, ΘE1 = 39(2) K and ΘE2 = 60(9) K, respectively. Such a result indicates an acceptable description of the phonon spectrum of the anionic framework and a model of the ‘rattling’ motion. Noteworthily, the ΘE2 value correlates well with the In5-atom Einstein temperature ΘXRDE = 69(1) K deduced from the ADP values, whereas ΘE1 is smaller by a factor of ≈3. Obviously, the model given by eqn (4) does not account for the structural disorder and thus, is not providing a complete understanding of the complex phonon spectrum of α-In2Te3.
A similar result (i.e., 2ΘE1 ≈ ΘE2) was obtained for the Sn24P19.4Br8 clathrate (cf. Table 1 in the reference), where two ‘rattlers’ are well established.102 This would again assume a remarkable difference between the Biso(T) dependencies for those atoms (not reported in ref. 102), which makes less sense in the view of the same physical effect (i.e., thermal motion with enhanced amplitudes within the voids with close volumes). This would bring us to a similar conclusion: the consideration of only the cp/T3(T) dependence provides just tentative insights into the ‘rattling’ problem.
Finally, the negligibly small Sommerfeld coefficient of the electronic specific heat capacity γ = 6.2(9) × 10−8 J mol−1 K−2 is in nice agreement with the semiconducting properties of the studied telluride (i.e., γ = 0 for no states at the Fermi level),83 thus indicating a minor metallic impurity (cf. Fig. S5†). The latter is also evidenced by an upturn in the LT diamagnetic susceptibility χ(T) of α-In2Te3 (Fig. S6†).
7 Raman spectroscopy and anharmonic effects
The normalized Raman spectrum for α-In2Te3 recorded at RT, together with the peak fitting, is presented in Fig. 9. Our analysis indicates some additional bands compared with earlier data reported for single-crystal,103 polycrystalline104 and thin-film105 samples (Table 3). The observed differences can be mainly attributed to the resolution of the measurement techniques and performed profile descriptions, since no impurities were detected in our specimen via chemical, structural or spectroscopic analyses. Obviously, to clarify this issue, some theoretical calculations are strongly required, and these would again become hampered by the strongly disordered crystal structure of α-In2Te3.As is known, both the positions of modes in a Raman spectrum and the thermal expansion of a material are mainly related to the so-called anharmonic effects, which are due to the change in frequencies of lattice vibration with temperature.106 Therefore, measurement of T-dependent Raman spectra (Fig. 9 inset) allows the elucidation of underlying harmonic and anharmonic phonon processes. For this purpose, the Klemens–Balkanski model is applied. It defines the peak center W and full-width at half-maximum (FWHM) R of the strongest mode as follows:
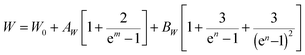 | (7) |
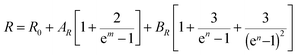 | (8) |
 | ||
| Fig. 10 Klemens–Balkanski analysis of α-In2Te3’s strongest feature for its peak center and FWHM within the 100–300 K range, including independent contributions to eqn (7) and (8), respectively. | ||
To describe the W(T) and R(T) behaviors, both AW,R and BW,R contributions were required (Fig. 10). This indicates the presence of both three-phonon (most common in crystalline materials) and four-phonon processes. However, the latter are contributing only ≈5% in total. Since W and R in α-In2Te3 reveal rather weak T-dependencies, the obtained anharmonic constants are smaller by approximately two-orders of magnitude than those observed for FeS2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 108 or PbCuSbS3.98
108 or PbCuSbS3.98
8 Spectroscopic ellipsometry
The real (ε1) and imaginary (ε2) parts of the dielectric function were calculated (Fig. 11 inset) within a two-phase model (i.e., air/sample) with a determined surface roughness of 9.5(2) nm. The good quality of the sample (i.e., crystallinity, homogeneity and surface) was evidenced by the respective overlaps of ε1 and ε2 for all three incidence angles. The latter was parameterized using five Gaussian oscillators centered at 1.40(1) eV, 2.08(1) eV, 2.66(1) eV, 3.58(1) eV and 4.60(1) eV.The Tauc plot [(αE)1/2vs. E] together with the linear projection to zero absorption is presented in Fig. 11. The s-like shape of the (αE)1/2-plot vs. the photon energy confirms α-In2Te3 to possess an indirect optical band gap with Eoptg = 1.03(1) eV. This value perfectly agrees with the earlier reported one (1.01 eV)55,56 for a single crystal grown using the Bridgman method. On the other hand, the Eoptg values found for both polycrystalline (1.13 eV)57 and amorphous (1.22 eV)58 specimens were slightly larger, which indicates the dependence on the sample microstructure. In this respect, we must again conclude that the crystal studied here is of good quality.
Interestingly, some thin films of α-In2Te3 are reported to possess optical gaps of the same magnitude, however with a direct transition.59–61 Here, we would like to emphasize that in all these works, the estimation of the Eoptg values and their natures was carried out via absorption spectroscopy. Importantly, the elipsometric method is much more sensitive in this respect, since it depends only on the polarization changes after interaction with the sample.109
9 Electrical transport
9.1 Electrical resistivity and Seebeck coefficient
The temperature dependence of the electrical resistivity ρ(T) for In2Te3 is presented in Fig. 12 (left scale). In the LT region, 2–350 K, ρ(T) is varying in a narrow range of ≈7.7–8.7 × 10−2 Ω m, revealing a well-defined minimum at Tmin ≈ 145 K. With a further temperature increase, the electrical resistivity of In2Te3 increases, passes through a maximum centered at Tmax ≈ 450 K and then reveals an activation-like decay. Therefore, in the next step, we applied the Arrhenius approximation for the 2–140 K (green line) and 500–800 K (red line) T-ranges to estimate the values of the corresponding band gaps: | (9) |
As is known, the appearance of two energy gaps (Eg) in the ρ(T) dependence is a signature of a doped semiconductor. In this class of materials, the intrinsic Eg is observed in the HT regime, whereas the LT one represents that between the impurity level and the corresponding band edge [e.g., valence band maximum (VBM) or conduction band minimum (CBM)]. In the T-region in-between, the charge-carrier concentration [n(T)] is considered to remain nearly temperature independent, whereas the mobility [μ(T)] should determine the shape of the ρ(T) curve.110 Noteworthily, the EArr(LT)g value for In2Te3 is lower by at least one order of magnitude than those occurring in doped semiconductors, as well as being much smaller than EArr(HT)g.83 Also, both n(T) and μ(T) (Fig. 13A and B) are nearly T-independent for 150–250 K and for T > 270 K they start to increase and to decrease, respectively. All these observations indicate that despite revealing a ρ(T)-shape similar to that of a doped semiconductor, In2Te3 cannot be considered as belonging to this class of compounds. Additionally, this finding would be in line with the declared purity of the crystal studied here. Obviously, the observed ρ(T)-shape is due to the high number of partially occupied positions in the crystal structure, which possibly can become a source of additional energy levels in close vicinity to the VBM/CBM. Here, we would also like to stress that the origins of such ρ(T) behavior could be of very different natures (e.g., charge density waves,111,112 topological band structures113 or simply remaining unclear114,115).
 | ||
| Fig. 13 Temperature dependency of the charge-carrier concentration n(T) (A) and mobility μ(T) (B) of α-In2Te3 assuming a single band conduction mechanism. | ||
The temperature dependence of the Seebeck coefficient S(T) for In2Te3 is depicted in Fig. 12 (right scale). S(T) is negative in the whole studied T-range indicating electrons to be the dominant charge carriers. Also, n-type conductivity was earlier reported for the here-studied telluride from Hall effect measurements.63 However, there are numerous investigations where p-type transport is detected, namely in single crystals55,56 as well as in thin-films.59,61 Interestingly, in all these cases, a slight In-excess (i.e., In2+xTe3) was found. The off-stoichiometry of In2Te3 would be in line with the In–Te phase diagrams proposed in ref. 64–66.
The Seebeck coefficient of In2Te3 decreases with increasing temperature, revealing a well-defined anomaly centered at Tkink ≈ 450 K, coinciding with the maximum in ρ(T). This might be an indication of a switch or change in charge-carrier scattering mechanisms. However, to shed light on such behavior, HT Hall effect measurements would be strongly required. A further temperature increase leads to the appearance of a broad maximum in |S(T)| at Tmax ≈ 714 K. Such a behavior of |S(T)| allows the estimation of the energy gap by applying the Goldsmid–Sharp formula:116
| ESg = 2e|Smax|Tmax | (10) |
 | (11) |
9.2 Charge-carrier concentration and mobility
The temperature dependence of α-In2Te3’s charge-carrier concentration n(T) and mobility μ(T) are presented in Fig. 13A and B, respectively. They were calculated from the measured Hall coefficients using the RH = (en)−1 and μ = (enρ)−1 equations, which assume a single band conduction mechanism.83 Between 100–250 K, n(T) slightly decreases within the range n ≈ 2.45–2.15 × 1015 cm−3 and then it exponentially increases up to ≈2.8 × 1015 cm−3. In general, the n-magnitude observed here is larger by 3–5 orders of magnitude than those of classical semiconductors (n ≈ 1010–12 cm−3),83 and simultaneously smaller by the same factor (n ≈ 1018 cm−3)118 than the values observed for materials with high thermoelectric (TE) performance. Interestingly, our specimen reveals much larger n at RT in comparison to p- (n ≈ 1010 cm−3)62 and n-type (n ≈ 1012 cm−3)67 single crystals studied earlier. The charge-carrier concentration of ≈1015 cm−3 could be reached in n-In2Te3 only at 556 K.The values of the charge-carrier mobilities [μ(T)] observed in this work (Fig. 13B) are larger by a factor of ≈10 than those previously reported for α-In2Te3 at RT (i.e., 32–70 cm2 V−1 s−1).67 This fact stresses again the strong influence of the structural disorder. Since the μ(T) decrease for T ≳ 250 K is compensated by a simultaneous increase in n(T), a smooth variation (rather than a step-like change) is the case in ρ(T) (Fig. 12).
Further, we analyzed the μ(T)-dependence using the μ ∝ Tm power law. Here, m is an indication of different scattering mechanisms.119,120 Two T-regions were identified within such an approach: (i) μ ∝ T−3/2 for 100–250 K and (ii) μ ∝ T−5/2 for 250–290 K (red and green lines, respectively, in Fig. 13B). m = −3/2 and m = −5/2 stand for scattering of charge carriers on only acoustic or on both acoustic and optical phonons, respectively.
To fully understand the scattering mechanisms in α-In2Te3, we also analyzed its electrical transport properties within the single parabolic band (SPB) model.121 The obtained Pisarenko plot confirmed an excellent agreement between the measured S(n) and the theoretically predicted values (Fig. S7†). Also, a fair agreement is observed for the experimental and simulated μ(n) dependencies for T > 200 K (Fig. S8†), hinting towards the dominance of charge-carrier scattering on the acoustic phonons, as discussed above. Finally, this type of analysis indicates the thermoelectric (TE) power factor [PF(T) = ρ(T)−1S(T)2T] for the studied telluride to be close to the maximal expected semiconducting values (Fig. S9†), which means that its drastic increase (i.e., improvement of the TE efficiency) would be possible only while going towards a metallic type of tuning.
Having the hole mobilities μmin ≈ 210 and 1380 cm2 (V s)−1,55,56 which were reported for p-type single crystals at RT, together with our value μmaj ≈ 225 cm2 (V s)−1 (Fig. 13B), we again analyzed eqn (11). Calculating the μmaj/μmin-ratio to be ∼46/50 or ∼8/50 and assuming A ≈ 1/500, one can conclude that the effective masses  of holes in α-In2Te3 are larger by a factor of 19–60 than those of electrons. The numbers obtained in such a way agree well with the values deduced from theoretical calculations for chemically related In2S3 and its doped variant In2S3−xSex122 as well as InSb.123 All of them also assume the electronic structure of α-In2Te3 to be anisotropic and to be characterized by a flat valence band just below the Fermi level EF, which seems to be in contradiction with the fact that the SPB model fairly describes the electrical transport.83 Obviously, to shed light on this problem, reasonable DFT simulations would be strongly required, which are still a challenge for state-of-the-art approaches, due to the large unit-cell volume and strong structural disorder in the studied telluride. For more details on this topic, see our discussion on the electronic structure calculation of hypothetically ordered α-In2Te3 in the ESI.†
of holes in α-In2Te3 are larger by a factor of 19–60 than those of electrons. The numbers obtained in such a way agree well with the values deduced from theoretical calculations for chemically related In2S3 and its doped variant In2S3−xSex122 as well as InSb.123 All of them also assume the electronic structure of α-In2Te3 to be anisotropic and to be characterized by a flat valence band just below the Fermi level EF, which seems to be in contradiction with the fact that the SPB model fairly describes the electrical transport.83 Obviously, to shed light on this problem, reasonable DFT simulations would be strongly required, which are still a challenge for state-of-the-art approaches, due to the large unit-cell volume and strong structural disorder in the studied telluride. For more details on this topic, see our discussion on the electronic structure calculation of hypothetically ordered α-In2Te3 in the ESI.†
10 Thermal transport
The temperature dependence of the electronic contribution to the thermal conductivity κel(T) is presented in Fig. S10.† It was calculated from the Wiedeman–Franz law: κel = L(T)T[ρ(T)−1], where the Lorenz numbers L(T) (Fig. S10† inset) are obtained from the empirical equation: | (12) |
The phononic contribution (κph) obtained after subtraction of κel(T) from the total thermal conductivity is presented in Fig. 14. It is very low: κph ≤ 0.7 W m−1 K−1 (which is by a factor of ≈2 smaller than that reported for a polycrystalline sample at RT34) and thus indicates α-In2Te3 to possess potential for possible TE applications.125 To understand the underlying individual phonon scattering mechanisms, κph was further analyzed within the modified Debye–Callaway model:126
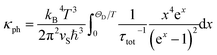 | (13) |
| τtot−1 = τB−1 + τPD−1 + τU−1 | (14) |
 | ||
| Fig. 14 In2Te3 phononic contribution to the thermal conductivity κph together with the fit to eqn (13). Inset: Simulated smallest physically achievable κph by considering a glass-like state. | ||
| Model126 | Fitted parameter | |
|---|---|---|
| τ B −1 | v S/D | D = 7.65(1) × 10−7 m |
| τ PD −1 |

|
Γ = 1.057(1) |
| τ U −1 |
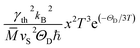
|
γ th = 2.75(2) |
The τB−1 value deduced from the fit to eqn (13) indicates a rather large D = 7650(1) Å crystallite size and thus negligibly small phonon scattering on the grain boundaries in the studied telluride. This finding would be in contradiction with the low κph(T), since large D-values normally imply better conductivity.129 On the other hand, τPD−1 (calculated using the average volume per atom per unit cell ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ) suggests an enlarged point-defect scattering parameter Γ = 1.057(1), which should be the case in strongly disordered structures [reported also for Bi2Te3−xSex nanoplates (Γ = 0.18),130 nanograined Cu2Se (Γ = 0.38)131 and polycrystalline AgBiSe2 (Γ = 1.6)132]. Obviously, higher scattering on point defects compensates for the absence of that on grain boundaries in α-In2Te3. Finally, in the temperature range T ≳ 100 K, τU−1 (calculated using the average atomic mass
) suggests an enlarged point-defect scattering parameter Γ = 1.057(1), which should be the case in strongly disordered structures [reported also for Bi2Te3−xSex nanoplates (Γ = 0.18),130 nanograined Cu2Se (Γ = 0.38)131 and polycrystalline AgBiSe2 (Γ = 1.6)132]. Obviously, higher scattering on point defects compensates for the absence of that on grain boundaries in α-In2Te3. Finally, in the temperature range T ≳ 100 K, τU−1 (calculated using the average atomic mass ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ) dominates the thermal transport. From it, we deduce the average thermal Grüneisen parameter γth = 2.75(2) in agreement with γXRD (Table 1). Our values are similar to those observed for systems [e.g., InTe (γ ≈ 3.3),133 SnTe (γ ≈ 2.1),88 In2Se3 (γ ≈ 5.4),134etc.] with high phonon anharmonicity and thus low κph.
) dominates the thermal transport. From it, we deduce the average thermal Grüneisen parameter γth = 2.75(2) in agreement with γXRD (Table 1). Our values are similar to those observed for systems [e.g., InTe (γ ≈ 3.3),133 SnTe (γ ≈ 2.1),88 In2Se3 (γ ≈ 5.4),134etc.] with high phonon anharmonicity and thus low κph.
Assuming disruption of the long-range order in In2Te3 (i.e., an amorphous or glass-like state) we calculated the minimal possible phononic thermal conductivity κmin(T) of this compound, which is estimated as:
 | (15) |
Calculating the dimensionless TE figure-of-merit zT(T) = PF(T)T[κph(T) + κel(T)]−1 for In2Te3, we found that despite suitable low thermal conductivity, it varies between 10−5–10−2, which is by a few orders of magnitude lower than those observed for state-of-the-art thermoelectric materials.83 This situation is mainly due to the enhanced electrical resistivity caused by low charge-carrier concentration in this compound.
11 Conclusions
The structural models of the low-temperature (LT) α-In2Te3 and high-temperature (HT) β-In2Te3 were obtained by applying direct methods to the high-resolution powder synchrotron X-ray diffraction patterns. Both of them revealed new atomic arrangements and their relationship was explained within the group–subgroup relations. The small jump in the unit-cell volume together with the lowered entropy may indicate a 2nd order for the α → β structural phase transition.The temperature dependence of the electrical resistivity of α-In2Te3 reveals two regions with an activation-like decay and a well-defined maximum. Since the studied crystal is shown to be of a good quality with no impurities, we ascribe these effects to the high structural disorder and do not classify it as a doped semiconductor. This conclusion is additionally corroborated by the nearly temperature-independent behavior of the charge carriers concentration and their mobility. The Seebeck and Hall coefficients for α-In2Te3 are found to be negative in the whole studied T-range, indicating that electrons dominate electrical transport in this material. The analysis performed within the Goldsmid-Sharp approach showed the effective masses of holes to be by a factor of ≈19–60 larger than those of electrons, which assumes the electronic structure of α-In2Te3 to be highly anisotropic and to contain flat valence bands.
The T-dependent evolution of the atomic displacement parameter of the In5-atom at the 48h crystallographic site, combined with the appearance of a boson peak in the specific heat at low temperatures, indicates a ‘rattling’ effect in α-In2Te3. This is obviously one of the reasons for a very low thermal conductivity (κph ≤ 0.7 W m−1 K−1) in this compound. Further analysis performed within the Debye–Callaway model has shown extremely strong phonon scattering on point-defects, whereas temperature-dependent Raman spectroscopy indicated the occurrence of four-phonon decay processes. Both effects are again governing the low κph and nicely agree with the enhanced values of the Grüneisen parameters deduced from differential thermal (γth) and structural (γXRD) analyses. All these findings indicate stronger anharmonicity of phonon processes in α-In2Te3. The simulated minimum κph dependence confirms that the observed thermal conductivity cannot be significantly reduced by, e.g., nanostructuring, and thus it is an intrinsic effect.
Having a sample of an advanced quality (no transport agents were used for its synthesis), we shed light on the interplay between its strong structural disorder and the underlying electrical and thermal transport mechanisms. Obviously, when redistributing the numerous defects by varying the synthesis conditions of α-In2Te3, one can expect some enhancements in charge-carrier density and/or their mobilities, thus improving the electrical transport characteristics. To make such a tuning more predictable, additional theoretical studies concerning electronic and phononic structures are also strongly desired. Undoubtedly, α-In2Te3 is a promising system possessing a remarkable potential with respect to its further investigations.
Data availability
The data supporting this article is included as part of the ESI.†Author contributions
Esteban Zuñiga-Puelles: formal analysis, conceptualization, investigation, methodology, software, validation, visualization, writing – original draft, writing – review & editing. Ayberk Özden: formal analysis, methodology, writing – review & editing. Raul Cardoso-Gil: investigation, writing – review & editing. Christoph Hennig: investigation, writing – review & editing. Cameliu Himcinschi: funding acquisition, project administration, supervision, writing – review & editing. Jens Kortus: investigation, writing – review & editing. Roman Gumeniuk: funding acquisition, project administration, supervision, validation, visualization, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed within the Deutsche Forschungsgemeinschaft (DFG) project 441856638. The DynaCool-12 system was acquired within the DFG Project No. 422219907. The authors thank U. Burkhardt, M. Eckert, S. Kostmann and U. Fischer for metallographic preparation and analyses as well as M. Schmidt and S. Scharsach for the assistance during the DTA/DSC/TG measurements.Notes and references
- L. Viscardi, E. Faella, K. Intonti, F. Giubileo, V. Demontis, D. Prete, V. Zannier, L. Sorba, F. Rossella and A. Di Bartolomeo, Mater. Sci. Semicond. Process., 2024, 173, 108167 CrossRef CAS.
- P. Dodd, M. Melloch, M. Lundstrom, J. Woodall and D. Pettit, IEEE Trans. Electron Devices, 1993, 40, 2141 CrossRef.
- Y. Wang, J. Chi, K. Banerjee, D. Grützmacher, T. Schäpers and J. G. Lu, J. Mater. Chem., 2011, 21, 2459–2462 RSC.
- T. Ashley, M. T. Emeny, D. G. Hayes, K. P. Hilton, R. Jefferies, J. O. Maclean, S. J. Smith, A. W.-H. Tang, D. J. Wallis and P. J. Webber, 2009 IEEE International Electron Devices Meeting (IEDM), 2009, pp. 1–4 Search PubMed.
- T. Ashley, A. Dean, C. Elliott, R. Jefferies, F. Khaleque and T. Phillips, International Electron Devices Meeting. IEDM Technical Digest, 1997, pp. 751–754 Search PubMed.
- K. J. Bachmann, Annu. Rev. Mater. Res., 1981, 11, 441–484 CrossRef CAS.
- J. Ajayan and D. Nirmal, Superlattices Microstruct., 2015, 86, 1–19 CrossRef CAS.
- C. Gutsche, A. Lysov, D. Braam, I. Regolin, G. Keller, Z.-A. Li, M. Geller, M. Spasova, W. Prost and F.-J. Tegude, Adv. Funct. Mater., 2012, 22, 929–936 CrossRef CAS.
- S. Nakamura, Semicond. Sci. Technol., 1999, 14, R27 CrossRef CAS.
- S. Nakamura, M. Senoh, S. ichi Nagahama, N. Iwasa, T. Yamada, T. Matsushita, H. K. H. Kiyoku and Y. S. Y. Sugimoto, Jpn. J. Appl. Phys., 1996, 35, L74 Search PubMed.
- S. Chichibu, A. Abare, M. Mack, M. Minsky, T. Deguchi, D. Cohen, P. Kozodoy, S. Fleischer, S. Keller, J. Speck, J. Bowers, E. Hu, U. Mishra, L. Coldren, S. DenBaars, K. Wada, T. Sota and S. Nakamura, Mater. Sci. Eng. B, 1999, 59, 298–306 CrossRef.
- L. J. Stinson, J. G. Yu, S. D. Lester, M. J. Peanasky and K. Park, Appl. Phys. Lett., 1991, 58, 2012–2014 CrossRef CAS.
- H. Tanaka, Y. Kawamura, S. Nojima, K. Wakita and H. Asahi, J. Appl. Phys., 1987, 61, 1713–1719 CrossRef CAS.
- S. Sassen, B. Witzigmann, C. Wolk and H. Brugger, IEEE Trans. Electron Devices, 2000, 47, 24–32 CrossRef CAS.
- Z. Yang, J. Guo, H. Li, X. Du, Y. Zhao, H. Chen, W. Chen and Y. Zhang, Mater. Des., 2023, 233, 112218 CrossRef CAS.
- Z. Wang, M. Safdar, C. Jiang and J. He, Nano Lett., 2012, 12, 4715–4721 CrossRef CAS PubMed.
- J. Yao, Z. Deng, Z. Zheng and G. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 20872–20879 CrossRef CAS PubMed.
- Z. M. Grushka, P. N. Gorley, O. G. Grushka, P. P. Horley, Y. I. Radevych and Z. Zhuo, ICO20: Materials and Nanostructures, 2006, p. 60291A Search PubMed.
- X. Zhang, W. Sun, Z. Lu, L. Zhang, L. Zhao, J. Ding and G. Yan, Infrared Materials, Devices, and Applications, 2008, p. 68350A Search PubMed.
- J. F. Algorri, N. Bennis, V. U. del Pozo, P. Morawiak, L. R. Jaroszewicz and J. M. S. Pena, Novel Optical Systems, Methods, and Applications XXII, 2019, p. 1110510 Search PubMed.
- P. Yeh and C. Gu, Optics of Liquid Crystal Displays, John Wiley & Sons, 2009, vol. 67 Search PubMed.
- R. S. Datta, N. Syed, A. Zavabeti, A. Jannat, M. Mohiuddin, M. Rokunuzzaman, B. Yue Zhang, M. A. Rahman, P. Atkin and K. A. Messalea, et al. , Nat. Electron., 2020, 3, 51–58 CrossRef CAS.
- Z. Liu, C.-Y. Huang, H. Liu, X. Zhang and C. Lee, Opt. Express, 2013, 21, 6519–6525 CrossRef CAS PubMed.
- X. Yang, A. Banerjee, Z. Xu, Z. Wang and R. Ahuja, J. Mater. Chem. A, 2019, 7, 27441–27449 RSC.
- R. Desai, D. Lakshminarayana, P. Patel and C. Panchal, Sens. Actuators, B, 2005, 107, 523–527 CrossRef CAS.
- S. So, J. Ko, Y. N. Ahn, I. T. Kim and J. Hur, Chem. Eng. J., 2022, 429, 132395 CrossRef CAS.
- A. A. Zahab, M. Abd-Lefdil and M. Cadene, Phys. Status Solidi A, 1990, 119, K35–K39 CrossRef CAS.
- W. Li, X.-F. Cai, N. Valdes, T. Wang, W. Shafarman, S.-H. Wei and A. Janotti, J. Phys. Chem. Lett., 2022, 13, 12026–12031 CrossRef CAS PubMed.
- M. H. Ali, M. A. Al Mamun, M. D. Haque, M. F. Rahman, M. K. Hossain and A. Z. Md. Touhidul Islam, ACS Omega, 2023, 8, 7017–7029 CrossRef CAS PubMed.
- D. Liu, X. Li, P. M. d. C. Borlido, S. Botti, R. Schmechel and M. Rettenmayr, Sci. Rep., 2017, 7, 43611 CrossRef PubMed.
- D. Liu, J. Stötzel, M. Seyring, M. Drüe, X. Li, R. Schmechel and M. Rettenmayr, Cryst. Growth Des., 2016, 16, 617–624 CrossRef CAS.
- S. Vallem, K. V. Bangera and S. G. K., Superlattices Microstruct., 2019, 131, 15–20 CrossRef CAS.
- A. Rosenberg and A. Strauss, J. Phys. Chem. Solids, 1961, 19, 105–116 CrossRef CAS.
- S. Yamanaka, M. Ishimaru, A. Charoenphakdee, H. Matsumoto and K. Kurosaki, J. Electron. Mater., 2009, 38, 1392–1396 CrossRef CAS.
- L. Qu, C. Yang, Y. Luo, Z. Du, C. Li and J. Cui, ACS Appl. Mater. Interfaces, 2022, 14, 45628–45635 CrossRef CAS PubMed.
- G. Tan, W. G. Zeier, F. Shi, P. Wang, G. J. Snyder, V. P. Dravid and M. G. Kanatzidis, Chem. Mater., 2015, 27, 7801–7811 CrossRef CAS.
- H. Sun, X. Lu, H. Chi, D. T. Morelli and C. Uher, Phys. Chem. Chem. Phys., 2014, 16, 15570–15575 RSC.
- Y. Pei and D. T. Morelli, Appl. Phys. Lett., 2009, 94, 122112 CrossRef.
- R. Hanus, R. Gurunathan, L. Lindsay, M. T. Agne, J. Shi, S. Graham and G. Jeffrey Snyder, Appl. Phys. Rev., 2021, 8, 031311 CAS.
- E. S. Toberer, L. L. Baranowski and C. Dames, Annu. Rev. Mater. Res., 2012, 42, 179–209 CrossRef CAS.
- J. He and T. M. Tritt, Science, 2017, 357, eaak9997 CrossRef PubMed.
- A. El Sachat, F. Alzina, C. M. Sotomayor Torres and E. Chavez-Angel, Nanomater., 2021, 11, 175 CrossRef CAS PubMed.
- T. Ghosh, M. Dutta, D. Sarkar and K. Biswas, J. Am. Chem. Soc., 2022, 144, 10099–10118 CrossRef CAS PubMed.
- Y. Zheng, T. J. Slade, L. Hu, X. Y. Tan, Y. Luo, Z.-Z. Luo, J. Xu, Q. Yan and M. G. Kanatzidis, Chem. Soc. Rev., 2021, 50, 9022–9054 Search PubMed.
- H. Han, L. Zhao, X. Wu, B. Zuo, S. Bian, T. Li, X. Liu, Y. Jiang, C. Chen, J. Bi, J. Xu and L. Yu, J. Mater. Chem. A, 2024, 12, 24041–24083 Search PubMed.
- C.-D. Zhou, B. Liang, W.-J. Huang, J.-G. Noudem, X.-J. Tan and J. Jiang, Rare Met., 2023, 42, 2825–2839 CrossRef CAS.
- P. Baskaran and M. Rajasekar, RSC Adv., 2024, 14, 21706–21744 RSC.
- T. Karakostas and N. A. Economou, Phys. Status Solidi A, 1975, 31, 89–99 CrossRef CAS.
- J. Woolley, B. Pamplin and P. Holmes, J. Less Common. Met., 1959, 1, 362–376 CrossRef CAS.
- H. Hahn, W. Klingler and Z. Anorg, Chem, 1949, 260, 97–109 CAS.
- D. Zagorac, H. Müller, S. Ruehl, J. Zagorac and S. Rehme, J. Appl. Crystallogr., 2019, 52, 918–925 CrossRef CAS PubMed.
- S. Gražulis, A. Daškevič, A. Merkys, D. Chateigner, L. Lutterotti, M. Quirós, N. R. Serebryanaya, P. Moeck, R. T. Downs and A. Le Bail, Nucleic Acids Res., 2012, 40, D420–D427 CrossRef PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- A. Vora-ud, C. Thanachayanont, S. Jugsujinda, V. Amornkitbamrung and T. Seetawana, Procedia Eng., 2011, 8, 2–7 CrossRef CAS.
- S. Sen and D. Bose, Solid State Commun., 1984, 50, 39–42 CrossRef CAS.
- A. T. Nagat, M. M. Nassary and H. A. El-Shaikh, Semicond. Sci. Technol., 1991, 6, 979–982 CrossRef CAS.
- O. H. Hughes, P. M. Nikolió, C. J. Doran and S. S. Vujatović, Phys. Status Solidi B, 1975, 71, 105–109 CrossRef CAS.
- S. Ozaki, K. T. K. Takada and S. A. S. Adachi, Jpn. J. Appl. Phys., 1994, 33, 6213–6217 CrossRef CAS.
- R. Desai, D. Lakshminarayana, P. Patel and C. Panchal, J. Mater. Sci., 2006, 41, 2019–2023 CrossRef CAS.
- R. Rousina and G. Yousefi, Mater. Lett., 1990, 9, 263–265 CrossRef CAS.
- V. Sowjanya, K. V. Bangera and G. Shivakumar, Ceram. Int., 2017, 43, 3748–3751 CrossRef CAS.
- S. A. Hussein and A. T. Nagat, Phys. Status Solidi A, 1989, 114, K205–K209 CrossRef CAS.
- V. P. Zhuse, V. M. Sergeeva and A. I. Shelykh, Sov. Phys. Solid State, 1961, 2, 2545–2555 Search PubMed.
- T. B. Massalski and H. Okamoto, Binary Alloy Phase Diagrams, ASM International, 2nd edn, 1990 Search PubMed.
- C.-S. Oh and D. N. Lee, Calphad, 1993, 17, 175–187 CrossRef CAS.
- V. Zlomanov, M. Sheiman and B. Legendre, J. Phase Equilib., 2001, 22, 339–344 CrossRef CAS.
- In2Te3 transport properties: Datasheet from Landolt-Börnstein – Group III Condensed Matter Volume 41E: Ternary Compounds, Organic Semiconductors in SpringerMaterials, Copyright 2000 Springer-Verlag Berlin Heidelberg .
- A. C. Scheinost, J. Claussner, J. Exner, M. Feig, S. Findeisen, C. Hennig, K. O. Kvashnina, D. Naudet, D. Prieur, A. Rossberg, M. Schmidt, C. Qiu, P. Colomp, C. Cohen, E. Dettona, V. Dyadkin and T. Stumpf, J. Synchrotron Radiat., 2021, 28, 333–349 CrossRef CAS PubMed.
- STOE Powder Software, WinXPow (Version 2), Darmstadt, STOE and Cie. GmbH, 2001 Search PubMed.
- L. Akselrud and Y. Grin, J. Appl. Crystallogr., 2014, 47, 803–805 CrossRef CAS.
- S. Sugaike and J. Miner, Pet. Sci., 1957, 2, 63–77 CAS.
- A. Kunjomana and E. Mathai, Mater. Res. Bull., 1991, 26, 1347–1353 CrossRef CAS.
- V. Zhuze, A. Zaslavskii and V. Petrusevich, et al. , Proc. Int. Conf. Phys. Semicond., 1960, 871–881 Search PubMed.
- H. Nowotny and W. Sibert, Int. J. Mater. Res., 1941, 33, 391–394 CrossRef CAS.
- R. Helmholdt and K. Buschow, J. Less-Common Met., 1986, 123, 169–173 CrossRef CAS.
- J. Emsley, The Elements: Oxford University Press, 1998 Search PubMed.
- T. Schröder, T. Rosenthal, S. Grott, C. Stiewe, J. de Boor and O. Oeckler, Z. Anorg. Allg. Chem., 2013, 639, 2536–2541 CrossRef.
- M. Pušelj and Z. Ban, Croat. Chem. Acta, 1969, 41, 79–83 Search PubMed.
- J. Drews, U. Eberz and H.-U. Schuster, J. Less Common. Met., 1986, 116, 271–278 CrossRef CAS.
- M. O'Keeffe and B. G. Hyde, Crystal Structures, Patterns and Symetry, Courier Dover Publications, 2020 Search PubMed.
- P. Wyżga, W. Carrillo-Cabrera, L. Akselrud, I. Veremchuk, J. Wagler, C. Hennig, A. A. Tsirlin, A. Leithe-Jasper, E. Kroke and R. Gumeniuk, Dalton Trans., 2020, 49, 15903–15913 RSC.
- U. Müller, Symmetry Relationships between Crystal Structures: Applications of Crystallographic Group Theory in Crystal Chemistry, Oxford University Press, 2013 Search PubMed.
- R. Gross, A. Marx, D. Einzel and S. Geprägs, Festkörperphysik: Aufgaben und Lösungen, De Gruyter, 2018 Search PubMed.
- S.-V. Ackerbauer, A. Senyshyn, H. Borrmann, U. Burkhardt, A. Ormeci, H. Rosner, W. Schnelle, M. Gamża, R. Gumeniuk, R. Ramlau, E. Bischoff, J. C. Schuster, F. Weitzer, A. Leithe-Jasper, L. H. Tjeng and Y. Grin, Chem. Eur J., 2012, 18, 6272–6283 CrossRef CAS PubMed.
- Y. Kadowaki, R. Kasugai, Y. Yokoyama, N. Katayama, Y. Okamoto and K. Takenaka, Appl. Phys. Lett., 2021, 119, 201906 CrossRef CAS.
- In2Te3 sound velocity, refractive index, dielectric constant: Datasheet from Landolt–Börnstein – Group III Condensed Matter Volume 41E: Ternary Compounds,Organic Semiconductors in SpringerMaterials.
- C. Chang and L.-D. Zhao, Mater. Today Phys., 2018, 4, 50–57 CrossRef.
- T. F. Smith, J. A. Birch and J. G. Collins, J. Phys. C: Solid State Phys., 1976, 9, 4375–4382 CrossRef CAS.
- G. A. Slack, J. Phys. Chem. Solids, 1973, 34, 321–335 CrossRef CAS.
- J. D. Dunitz, V. Schomaker and K. N. Trueblood, J. Phys. Chem., 1988, 92, 856–867 CrossRef CAS.
- B. C. Sales, B. C. Chakoumakos, D. Mandrus and J. W. Sharp, 18th International Conference on Thermoelectrics. Proceedings, ICT’99 (Cat. No. 99TH8407), 1999, pp. 525–530 Search PubMed.
- G. S. Nolas, The Physics and Chemistry of Inorganic Clathrates, Springer Netherlands, 2014 Search PubMed.
- C. Uher, in Recent Trends in Thermoelectric Materials Research I, ed. T. M. Tritt, Elsevier, 2001, vol. 69 of Semiconductors and Semimetals, pp. 139–253 Search PubMed.
- R. Gumeniuk, Handbook on the Physics and Chemistry of Rare Earths, Elsevier, 2018, 54, pp. 43–143 Search PubMed.
- M. Baggioli and A. Zaccone, J. Mater. Phys., 2020, 3, 015004 CrossRef CAS.
- M. Beekman, W. Schnelle, H. Borrmann, M. Baitinger, Y. Grin and G. S. Nolas, Phys. Rev. Lett., 2010, 104, 018301 CrossRef CAS PubMed.
- Y. Ikeuchi, H. Takatsu, C. Tassel, C. M. Brown, T. Murakami, Y. Matsumoto, Y. Okamoto and H. Kageyama, Inorg. Chem., 2019, 58, 6790–6795 CrossRef CAS PubMed.
- E. Zuñiga-Puelles, R. Cardoso-Gil, A. Özden, N. Bulut, V. Svitlyk, C. Himcinschi, J. Kortus and R. Gumeniuk, Phys. Rev. B, 2022, 106, 195201 CrossRef.
- E. Zuñiga-Puelles, A. Özden, V. Pacheco, L. Akselrud, R. Cardoso-Gil, A. Straßheim, P. Wyżga, C. Himcinschi and R. Gumeniuk, J. Alloys Compd., 2024, 976, 173055 CrossRef.
- W. Schnelle, A. Leithe-Jasper, H. Rosner, R. Cardoso-Gil, R. Gumeniuk, D. Trots, J. A. Mydosh and Y. Grin, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 094421 CrossRef.
- R. Gumeniuk, V. Levytskyi, B. Kundys and A. Leithe-Jasper, Phys. Rev. B, 2023, 108, 214515 CrossRef CAS.
- V. V. Novikov, A. V. Matovnikov, N. V. Mitroshenkov, B. I. Kornev, K. S. Pilipenko, M. S. Likhanov and A. V. Shevelkov, Dalton Trans., 2017, 46, 9110–9117 Search PubMed.
- T. D. Golding, P. R. Boyd, M. Martinka, P. M. Amirtharaj, J. H. Dinan, S. B. Qadri, D. R. T. Zahn and C. R. Whitehouse, J. Appl. Phys., 1989, 65, 1936–1941 CrossRef CAS.
- E. Finkman, J. Tauc, R. Kershaw and A. Wold, Phys. Rev. B:Condens. Matter Mater. Phys., 1975, 11, 3785–3794 CrossRef.
- M. Emziane, J. Bernède, J. Ouerfelli, H. Essaidi and A. Barreau, Mater. Chem. Phys., 1999, 61, 229–236 CrossRef CAS.
- X. Gong, H. Wu, D. Yang, B. Zhang, K. Peng, H. Zou, L. Guo, X. Lu, Y. Chai, G. Wang and X. Zhou, Vib. Spectrosc., 2020, 107, 103034 CrossRef CAS.
- M. Balkanski, R. F. Wallis and E. Haro, Phys. Rev. B:Condens. Matter Mater. Phys., 1983, 28, 1928 Search PubMed.
- A. Özden, E. Zuñiga-Puelles, J. Kortus, R. Gumeniuk and C. Himcinschi, J. Raman Spectr., 2023, 54, 84–92.
- Spectroscopic Ellipsometry for Photovoltaics. Volume 1: Fundamental Principles and Solar Cell Characterization, ed. H. Fujiwara and R. W. Collins, Springer, Cham, 2019 Search PubMed.
- R. E. Hummel, Electronic Properties of Materials, Springer Berlin Heidelberg, 2001 Search PubMed.
- L. Krasavin, A. Titov and V. Antropov, Phys. Solid State, 1998, 40, 1962–1964 Search PubMed.
- N. Selezneva, E. Sherokalova, V. Pleshchev, V. Kazantsev and N. Baranov, J. Phys.: Condens. Matter, 2016, 28, 315401 CrossRef CAS PubMed.
- D. Wu, Y. Qian, Z. Liu, W. Wu, Y. Li, S. Na, Y. Shao, P. Zheng, G. Li, J. Cheng, H. Weng and J. Luo, Chin. Phys. B, 2020, 29, 037101 CrossRef CAS.
- R. Gumeniuk, L. Akselrud, K. O. Kvashnina, W. Schnelle, A. A. Tsirlin, C. Curfs, H. Rosner, M. Schöneich, U. Burkhardt, U. Schwarz, Y. Grin and A. Leithe-Jasper, Dalton Trans., 2012, 41, 6299–6309 Search PubMed.
- S. Flipo, H. Rosner, M. Bobnar, K. O. Kvashnina, A. Leithe-Jasper and R. Gumeniuk, Phys. Rev. B, 2021, 103, 195121 Search PubMed.
- H. J. Goldsmid and J. W. Sharp, J. Electron. Mater., 1999, 28, 869–872 CrossRef CAS.
- Z. M. Gibbs, H.-S. Kim, H. Wang and G. J. Snyder, Appl. Phys. Lett., 2015, 106, 022112 CrossRef.
- M. Wolf, R. Hinterding and A. Feldhoff, Entropy, 2019, 21, 1058 CrossRef CAS.
- C. Herring, Phys. Rev., 1954, 96, 1163 CrossRef CAS.
- S. S. Li, in Scattering Mechanisms and Carrier Mobilities in Semiconductors, SpringerNew York, 2006, pp. 211–244 Search PubMed.
- J. Zhu, X. Zhang, M. Guo, J. Li, J. Hu, S. Cai, W. Cai, Y. Zhang and J. Sui, npj Comput. Mater., 2021, 7, 116 CrossRef CAS.
- P. Wyżga, S. Grimm, V. Garbe, E. Zuñiga-Puelles, C. Himcinschi, I. Veremchuk, A. Leithe-Jasper and R. Gumeniuk, J. Mater. Chem. C, 2021, 9, 4008–4019 RSC.
- Y.-S. Kim, K. Hummer and G. Kresse, Phys. Rev. B:Condens. Matter Mater. Phys., 2009, 80, 035203 CrossRef.
- H.-S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506 Search PubMed.
- G. J. Snyder, in Thermoelectric Energy Harvesting, ed. S. Priya and D. J. Inman, Springer US, Boston, MA, 2009, pp. 325–336 Search PubMed.
- T. M. Tritt, Thermal Conductivity: Theory, Properties, and Applications, SpringerNew York, NY, 2005 Search PubMed.
- K. A. Borup, J. De Boor, H. Wang, F. Drymiotis, F. Gascoin, X. Shi, L. Chen, M. I. Fedorov, E. Müller and B. B. Iversena, et al. , Energy Environ. Sci., 2015, 8, 423–435 RSC.
- A. A. Maznev and O. B. Wright, Am. J. Phys., 2014, 82, 1062–1066 CrossRef.
- E. Zuñiga-Puelles, R. Cardoso-Gil, M. Bobnar, I. Veremchuk, C. Himcinschi, C. Hennig, J. Kortus, G. Heide and R. Gumeniuk, Dalton Trans., 2019, 48, 10703–10713 Search PubMed.
- M. Hong, T. C. Chasapis, Z.-G. Chen, L. Yang, M. G. Kanatzidis, G. J. Snyder and J. Zou, ACS Nano, 2016, 10, 4719–4727 CrossRef CAS PubMed.
- J. Chen, T. Liu, D. Bao, B. Zhang, G. Han, C. Liu, J. Tang, D. Zhou, L. Yang and Z.-G. Chen, Nanoscale, 2020, 12, 20536–20542 RSC.
- F. Böcher, S. P. Culver, J. Peilstöcker, K. S. Weldert and W. G. Zeier, Dalton Trans., 2017, 46, 3906–3914 RSC.
- M. K. Jana, K. Pal, U. V. Waghmare and K. Biswas, Angew. Chem. Int. Ed., 2016, 55, 7792–7796 CrossRef CAS PubMed.
- F. Guo, Y. Lyu, M. B. Jedrzejczyk, Y. Zhao, W. F. Io, G. Bai, W. Wu and J. Hao, Appl. Phys. Lett., 2020, 116, 113101 CrossRef CAS.
- D. G. Cahill and R. Pohl, Solid State Commun., 1989, 70, 927–930 CrossRef.
- B. Shan, S. Lin, Z. Bu, J. Tang, Z. Chen, X. Zhang, W. Li and Y. Pei, J. Mater. Chem. A, 2020, 8, 3431–3437 RSC.
- N. Sato, N. Kuroda, S. Nakamura, Y. Katsura, I. Kanazawa, K. Kimura and T. Mori, J. Mater. Chem. A, 2021, 9, 22660–22669 RSC.
- J. Mark, W. Zhang, K. Maeda, T. Yamamoto, H. Kageyama and T. Mori, J. Mater. Chem. A, 2023, 11, 10213–10221 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta06357k |
| This journal is © The Royal Society of Chemistry 2025 |