Formation of lattice vacancies and their effects on lithium-ion transport in LiBO₂ crystals: comparative ab initio studies

Abstract

The monoclinic (m-LBO) and tetragonal (t-LBO) polymorphs of the lithium metaborate (LiBO₂) material have significant potential for technological applications such as solid electrolytes and electrode coatings of lithium-ion batteries. While comparative studies of electronic, ionic, and photonic properties in these polymorphs exist, the role of lattice vacancies in lithium-ion transport in these polymorphs remains unclear. In this study, we employed density functional theory (DFT) to investigate the formation of lattice vacancies and their impacts on the lattice structure, electronic properties, and the lithium-ion migration energy barrier (E_m) in both m-LBO and t-LBO. Our DFT results reveal that boron and oxygen vacancies affect the lithium-ion transport in both the polymorphs, but in different ways. While oxygen vacancies lower E_m in m-LBO, they increase it in t-LBO. In contrast, boron vacancies significantly reduce E_m in both m-LBO and t-LBO, leading to a remarkably enhanced ionic conductivity in both the polymorphs. This enhancement in the ionic conductivity could be due to favorable alterations in the crystal and electronic structures caused by the presence of boron vacancies. This improvement suggests a potential strategy for improving the ionic conductivity of the LiBO₂ material through boron vacancy generation. For example, boron vacancies might be created in the lattice structures of the LiBO₂ material using controlled neutron irradiation.

---

1 Introduction

Lithium metaborate (LiBO₂) is an inorganic compound of lithium, boron, and oxygen, which has drawn increasing attention in both pure and applied research.^1,2 This is due chiefly to its potential applications as an advanced multi-functional material, ranging in use from nuclear reactor material engineering to nonlinear optics,³ to use in lithium-ion batteries (LIBs). In the latter, LiBO₂ belongs to a large family of boron-containing LIB materials^4–6 that exhibit promising characteristics, namely, a stable and effective solid electrolyte interphase (SEI), thermal stability, cost-effectiveness, and environmental friendliness.^3,7–12 The use of LiBO₂ for LIBs includes its potential applications as a solid electrolyte^13–18 and an electrode coating material.^19–23 While solid electrolytes currently hold promise in advanced technologies of LIBs for overcoming limitations of conventional liquid electrolytes such as flammability, leakage, limited electrochemical stability, and dendrite growth, their ionic conductivity needs to be significantly enhanced to approach that of liquid electrolytes (i.e., σ ∼ 10⁻² to 10 S cm⁻¹ (ref. 24)).

Recent experimental studies have demonstrated that LiBO₂ is an effective electrode coating to passivate side reactions in high-voltage LIBs, leading to their improved electrochemical performance.^19–23 Nevertheless, the ionic conductivity of LiBO₂ has been reported to be critically low, of the order of 10⁻⁶ to 10⁻⁵ S cm⁻¹.¹³ Therefore, there has been a surge of interest in the mechanistic understanding of defect formation and how the defects impact lithium migration in the material.^3,7–12,25 Studies intend to shed light on (i) how to improve the ionic conductivity of the LiBO₂ material,¹⁰ and (ii) how to control radiation-induced modifications to its functionalities.^11,12,25 Task (i) focuses on understanding defect chemistry of LiBO₂ to engineer the material for enhanced lithium-ion diffusion.¹⁰ Task (ii) is applied to those LIBs (which consist of LiBO₂ as their solid electrolyte or electrode coating) that operate in extreme environments such as in fission/fusion nuclear reactors or deep-space-exploration spacecraft^10–12,25 where neutrons can transmute boron atoms inside LIB materials via two boron-capturing-neutron reaction (BCNR) pathways.^{10–12,25,26} In these reaction pathways, thermal neutrons absorbed by 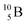produce (1.02 MeV) and (1.78 MeV) with a branching ratio of 94% or produce (0.84 MeV), (1.47 MeV), and γ (0.48 MeV) with a branching ratio of 6%.²⁷ As a result, boron vacancies are created at the original lattice sites of 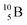(comprising ca. 20% of B atoms), while the products of the reaction pathways, which are energetic particles, can trigger atom displacement cascade processes in crystalline solids, resulting in neutron-induced defects. These range from zero-dimensional defects (i.e., point defects in the form of Frenkel pairs) to three-dimensional ones (volume defects in the form of voids or helium bubbles or clusters of defects).^3,7–12,25 While BCNR is beneficial to neutron detection techniques,²⁶ certain modification techniques of functional materials,²⁸ and cancer treatment,²⁹ whether it is beneficial or detrimental to boron-containing LIBs working in neutron-based environments is still an open question.^11,12,25

Thus, a deeper insight into the role of boron's presence and absence (i.e., boron vacancy) in LIB materials in general, and LiBO₂ in particular, is crucial for both designing and engineering of boron-contained electrode coatings for liquid-electrolyte LIBs or boron-containing solid electrolytes for all-solid-state LIBs with an optimized content of the isotope. Moreover, LiBO₂ is one of the components of SEIs formed on the electrode surface of liquid-electrolyte LIBs assembled with borate-containing liquid electrolytes that have recently been subjected to increasing research interest in the field of liquid electrolytes for LIBs.^4–6 Therefore, investigations of lithium-ion transport in LiBO₂ would also lead to a better understanding of such a borate-based SEI as well as the overall performance of borate-based liquid-electrolyte LIBs.

The monoclinic (m-LBO, α phase) and tetragonal (t-LBO, γ phase) polymorphs are the most commonly studied polymorphs of the LiBO₂ crystals (see Fig. 1 and Table 1 and the detailed description in Section 2). The m-LBO crystal structure is stable at ambient temperature and pressure. In addition, it was reported that ³⁰ baking a hydrated LiBO₂·8H₂O powder at 600 °C enables it to crystallize in the ionic m-LBO polymorph. In contrast, the t-LBO polymorph was reported³⁰ to be stable at high pressures. One notable contrast is that while lithium ions in m-LBO form a two-dimensional network, they are arranged in a three-dimensional network in t-LBO. To explore how these different configurations influence lithium-ion transport in LiBO₂ crystals, Hirose et al.¹³ conducted a comprehensive experimental study on high-density polycrystalline samples of these LiBO₂ polymorphs synthesized under high pressures. The lithium-ionic conductivities of the samples were measured using the a.c. impedance method between 450 and 520 K. They discovered that the intra-grain and total conductivities of t-LBO were of the order 10⁻⁶ to 10⁻⁵ S·cm⁻¹ and 10⁻⁶ S·cm⁻¹, respectively, values that were consistently higher than those of m-LBO across the entire measured temperature range.

Fig. 1 Unit cells of m-LBO (a) and t-LBO (b) polymorphs of the LiBO₂ crystal.

Table 1 Conventional unit cells of LiBO₂ polymorphs

m-LBO (α phase)	t-LBO (γ phase)
Monoclinic (P21/c)	Tetragonal (I4̄2d)
a = 5.77 Å, b = 4.46 Å	a = 4.18 Å, b = 4.18 Å
c = 6.37 Å, α = 90°	c = 6.53 Å, α = 90°
β = 113.56°, γ = 90°	β = 90°, γ = 90°
V = 146.98 Å^3	V = 113.86 Å^3

---

Atom	x (Å)	y (Å)	z (Å)	x (Å)	y (Å)	z (Å)
Li1	2.879	1.256	0.885	2.090	2.090	0.000
Li2	1.617	3.436	2.034	2.090	0.000	1.632
Li3	1.606	0.924	3.805	0.000	0.000	3.265
Li4	0.344	3.104	4.954	0.000	2.090	4.897
B1	4.468	3.587	1.318	0.000	0.000	0.000
B2	0.029	1.407	1.601	0.000	2.090	1.632
B3	3.195	2.952	4.238	2.090	2.090	3.265
B4	−1.244	0.772	4.521	2.090	0.000	4.897
O1	3.247	3.151	1.044	0.666	3.135	0.816
O2	4.667	0.620	1.396	3.514	1.045	0.816
O3	−0.170	2.800	1.523	1.045	1.424	2.449
O4	1.250	0.971	1.875	3.135	2.756	2.449
O5	1.974	3.389	3.963	1.424	3.135	4.081
O6	3.394	1.559	4.315	2.756	1.045	4.081
O7	−1.443	3.739	4.442	1.045	0.666	5.713
O8	−0.023	1.209	4.795	3.135	3.513	5.713

---

While theoretical studies have examined the electronic and vibrational properties of the two polymorphs^15,16 and lithium-ion conductivity in m-LBO,¹⁴ the impact of lattice vacancies on lithium-ion transport remains unknown. The present work is aimed at filling this knowledge gap using density functional theory (DFT) calculations. We investigated the effects of boron and oxygen vacancies on the lattice structure, electronic properties, and lithium-ion migration energy barrier E_m. Our DFT results show that boron and oxygen vacancies affect lithium-ion transport in both polymorphs, but in different ways: oxygen vacancies lower E_m in m-LBO but increase it in t-LBO, while boron vacancies significantly reduce E_m in both m-LBO and t-LBO, leading to an enhanced lithium-ion diffusivity, and hence an enhanced lithium-ionic conductivity, in both polymorphs.

2 Computational methods

We utilized DFT methods, implemented in the Quantum ESPRESSO Package (QE),³¹ to investigate the formation of lithium, boron, or oxygen lattice vacancies and lithium-ion migration in both the m-LBO and t-LBO polymorphs. The Perdew–Burke–Ernzerhof (PBE) generalized-gradient approximation (GGA) was employed.³² The effects of lattice vacancies on the crystal lattice structure, electronic density of states, and lithium-ion transport were then analyzed from our first-principles calculations.

Our DFT calculations were conducted using plane-wave basis sets of pseudopotentials (UPPs): Li.pbe-sl-rrkjus_psl.1.0.0.UPF for lithium, B.pbe-n-rrkjus_psl.1.0.0.UPF for boron, and O.pbe-n-rrkjus_psl.1.0.0.UPF for oxygen.³³ These pseudopotentials have been known for their compatibility with the PBE functionals, ensuring consistency with established theoretical frameworks. Additionally, these pseudopotentials are norm-conserving, accurately representing the core electrons while efficiently capturing the valence electron behavior, crucial for studying lithium-ion diffusion in LiBO₂ with reduced computational expense and increased reliability.³⁴

The atomic positions and lattice parameters of conventional unit cells of the polymorphs were obtained from the database of the Materials Project³⁵ and are shown in Fig. 1 and Table 1. There are 16 ions per unit cell for each polymorph: 4 lithium cations (labeled Li1 to Li4), 4 boron cations (B1 to B4), and 8 oxygen anions (O1 to O8). On the one hand, the m-LBO polymorph possesses the P2₁/c space group, where lithium cations (Li⁺) are coordinated with four oxygen anions (O²⁻) in a 4-coordinate geometry, resulting in Li⁺–O²⁻ bond distances ranging from 1.93 to 1.97 Å. Boron ions (B³⁺) exhibit a trigonal planar coordination with three O²⁻ anions, leading to B³⁺–O²⁻ bond distances spanning 1.33 to 1.41 Å. The compound contains two distinct O²⁻ sites: the first site features a distorted trigonal planar arrangement, where one O²⁻ anion connects to one Li⁺ cation and two equivalent B³⁺ cations, while the second site shows an O²⁻ anion in a 4-coordinate configuration, bonding with three equivalent Li⁺ cations and one B³⁺ cation. On the other hand, the t-LBO polymorph has the I4̄2d space group. Each of the Li⁺ cations is bonded in a 4-coordinate geometry to four equivalent O²⁻ anions. All Li⁺–O²⁻ bond lengths are 1.94 Å. Each of the B³⁺ cations is bonded to four equivalent O²⁻ anions to form corner-sharing BO₄ tetrahedra. All B³⁺–O²⁻ bond lengths are 1.48 Å. Each of the O²⁻ anions is bonded in a 4-coordinate geometry to two equivalent Li⁺ cations and two equivalent B³⁺ cations.³⁵

In the current work, we investigated supercells consisting of one unit cell with a periodic boundary condition in all three dimensions. In the chemical formulae of the defective supercells under investigation, we used the Kröger–Vink notation with the lowercase letter v (instead of the uppercase V to avoid cofusion with the symbol for vanadium) to represent a vacancy in a crystal structure such as 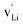, , and respectively for Li, B, and O vacancies whose charges are respectively −1, −3, and +2. Thus, the chemical formulae for the examined supercells are Li₄B₄O₈ (16 atoms and no vacancy) for a pristine nondefective supercell, 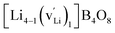(15 atoms, 1 Li vacancy ) for a Li-vacancy supercell, (15 atoms, 1 B vacancy ) for a B-vacancy supercell, and 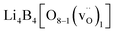(15 atoms, 1 O vacancy for an O-vacancy supercell.)

Selecting supercells of reduced sizes in DFT calculations entails trade-offs between computational efficiency and system representation. However, such supercells allow for a rapid exploration of the localized effects of vacancies on the lithium-ion transport in LiBO₂ and facilitate the study of systems with high or even extremely high concentrations of lattice defects compared to the percolation threshold without losing too much accuracy of the DFT calculations. To illustrate this point, we provide here an example of a previous DFT calculation of the m-LBO polymorph by Islam et al.,¹⁴ who examined the effect of supercell size on the lithium vacancy formation energy in m-LBO. They found that the values of the formation energy of lithium vacancies in 1 × 1 × 1 (i.e., Li₄B₄O₈), 2 × 2 × 2 (i.e., Li₃₂B₃₂O₆₄), and 3 × 3 × 3 (i.e., Li₁₀₈B₁₀₈O₂₁₆) supercells are 663 kJ mol⁻¹ (6.87 eV), 667 kJ mol⁻¹ (6.91 eV), and 673 kJ mol⁻¹ (6.98 eV), respectively. From these results, we estimated that our simulation supercells may suffer a ∼1.5% accuracy loss of the formation energy vs. a significantly more costly 3 × 3 × 3 supercell. This is a reasonable compromise for a fast screening of the many configurations that were sampled in this work as it aims primarily at a quantitative analysis of physics and chemistry of the lattice defects and their effects on the lithium-ion transport. In addition, these supercells serve as valuable benchmark cases for preliminary investigations and provide insights into vacancy-mediated transport phenomena. Therefore, they could guide subsequent studies with large systems or alternative methodologies (e.g., classical molecular dynamics modeling of cascade atomic displacement induced with neutron irradiation) to achieve a comprehensive understanding of defect behavior in lithium-containing materials. Moreover, these supercells are advantageous for modeling the physics and chemistry of interactive lattice defects or of their clusters induced by extremely high-dose neutron radiation such as plasma-facing materials in nuclear fusion reactors, therefore shedding light on the material's response under extreme conditions.

The procedure of our DFT calculations is described briefly as follows.³¹ Firstly, we started our calculations with pristine nondefective supercells for each polymorph. The data of the conventional unit cells of both m-LBO and t-LBO were obtained from the Materials Project (see Table 1). The cutoff energy for the plane wave basis functions of 100 Rydberg (1360 eV) and a 5 × 5 × 5 Monkhorst–Pack k-point mesh to sample the Brillouin zone of the reciprocal space were used for all supercells. The plane wave energy cutoff and k-point mesh density were separately tested in our self-consistent calculations and were also converged to give a total energy within 1 meV per supercell. These initialized calculations were then followed by the optimization of the supercells in which the atomic positions and lattice parameters were fully relaxed using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm³⁶ to minimize the total energy until it converges with an accuracy of better than 1 meV per cell and the force convergence criterion is 0.01 eV Å⁻¹.

Secondly, each of the defective supercells was created by generating a vacancy at a Li, B, or O site in the crystal lattice of its fully relaxed nondefective supercell counterpart. For the m-LBO polymorph, one of Li1, B1, or O1 (see Fig. 1a and Table 1) was respectively removed to form a Li-vacancy, a B-vacancy, or an O-vacancy supercell. For t-LBO, to create these defective supercells, Li1, B3, or O5 (see Fig. 1b and Table 1) was respectively removed. The defective supercells were then fully relaxed to optimize their geometry in the same fashion as those for the nondefective supercells.

Thirdly, the analysis of the effects of the vacancies was performed. The lattice parameters and the volume of each of the supercells were obtained, from which the percentages of the volume change relative to the nondefective supercells were determined. In addition, the formation energy per ion of a supercell of LiBO₂, E_f, was determined as

where E_tot is the total energy of the supercell, m, n, and k are the numbers of Li, B, and O ions in the supercell, and E_Li, E_B, and E_O are respectively the total energy per atom of lithium, of boron, and of oxygen in their solids. In this work, the values E_Li = −202.04 eV (−14.85 Ry), E_B = −85.03 eV (−6.25 Ry), and E_O = −438.78 eV (−32.25 Ry) were respectively obtained from our DFT calculations of the total energies for a body-centered cubic crystal of lithium metal with the Im3̄m space group, a hexagonal crystal of boron with the P6/mmm space group, and a rhombohedral crystal of oxygen molecules with the R3̄m space group. The crystalline solid of oxygen was referenced in order to maintain the consistency and precision in DFT modeling of oxygen vacancies in the solid-state environments of the examined crystalline systems, avoiding challenges such as entropy contributions. The setups of these DFT calculations were similar to those for LiBO₂ described earlier in this section.

The energy of formation of an ionic vacancy X (X = Li⁺, B³⁺, or O²⁻) in a supercell of LiBO₂, E^X_f, was calculated as

E^X_f = E^{X vacancy}_tot − E^perfect_tot + E_X, (2)

where E^{X vacancy}_tot and E^perfect_tot are respectively the total energies of the X-vacancy and perfect supercells, and E_X is the formation energy of ion X in its solid as aforementioned.

To explore the potential migration pathways and determine the corresponding migration energy barriers governing lithium-ion diffusion, we utilized the climbing image nudged elastic band (CI-NEB) method,³⁷ implemented within QE.³¹ The CI-NEB images (7 to 9 images) undergo internal relaxation until the maximum residual force reaches a threshold of less than 0.01 eV Å⁻¹, without altering the volume or cell parameters during optimization.

In the current work, we examined the vacancy-mediated diffusion mechanism,^10,38 where a lithium ion migrates from its initial position (the departure) of a lithium lattice site to its final position (the destination) of the neighboring lattice site of a lithium vacancy. Simultaneously, the vacancy moves in the opposite direction by swapping its site with that of the lithium ion. On its migration pathway, the lithium ion occupies intermediate sites of various energetic levels during the CI-NEB optimization of our DFT calculations. These intermediate sites make the energetic landscape of the pathway quite complex, varying from one migration pathway to another and strongly depending on the type of lattice vacancies. Thus, as one will see in Section 3.3.2 and the Appendix, the intermediate sites of a migration pathway feature mostly higher energies compared to the initial site, resulting in a set of forward-hopping barriers of the lithium-ion migration, {E^f_b} and that of backward-hopping of the lithium-vacancy migration {E^b_b}, with the subscript b denoting barrier and the superscript f (or b) being for forward (or backward). The overall probability of a forward lithium-ion hopping for each specific pathway may be chiefly governed by a rate-determining Arrhenius-type exponential factor exp[−ΔE^f/k_bT], where ΔE^f is the height of the largest forward energy barrier of the lithium ion (i.e., ΔE^f = max{E^f_b}), k_b is the Boltzmann constant, and T is the temperature. Additionally, the backward hopping of the associated lithium vacancy partner may encounter the same or different energy barriers, and a similar hopping probability is associated for this process, with ΔE^f substituted by ΔE^b, the height of the largest backward barrier of the lithium vacancy (i.e., ΔE^b = max{E^b_b}).

In each supercell of a polymorph, there are a certain number of migration pathways that were considered in the current work (see Fig. 2 and 3 and the specification of the pathways in the next paragraph), leading to a set of ΔE^f values (i.e., {ΔE^f}) and that of ΔE^b (i.e., {ΔE^b}), and the fastest lithium-ion migration pathway is the one that possesses the smallest value of ΔE^f, which is assigned to E^f_m (i.e., E^f_m = min{ΔE^f}). Likewise, the fastest lithium-vacancy migration pathway is the one that possesses the smallest value of ΔE^b, which is assigned to E^b_m (i.e., E^b_m = min{ΔE^b}).

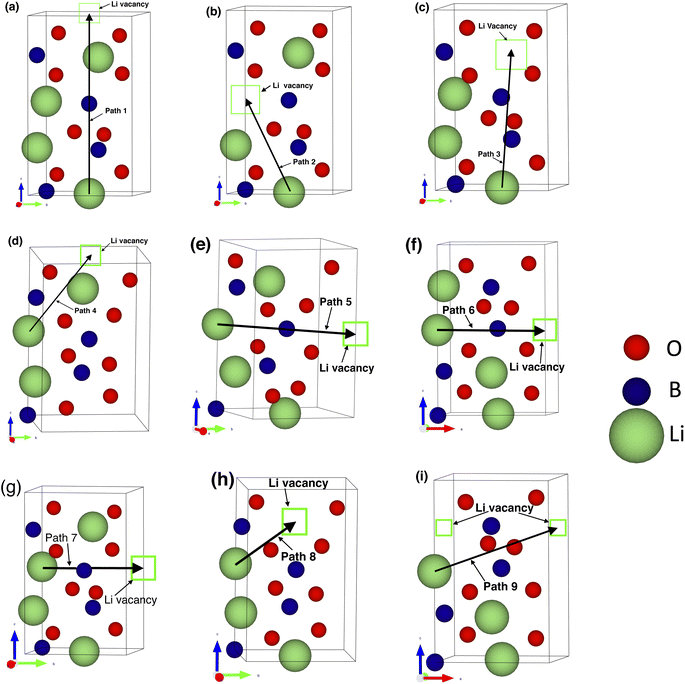
Fig. 2 Li-ion migration pathways investigated in the m-LBO polymorph. (a–f) are for path 1 to path 6.

Fig. 3 Li-ion migration pathways investigated in the t-LBO polymorph. (a–i) for path 1 to path 9.

For each of the two polymorphs of LiBO₂, and each of the four supercells (i.e., the perfect or nondefective, lithium-vacancy, boron-vacancy, and oxygen-vacancy supercells, summing up to 8 supercells in total for both polymorphs), several potential migration pathways were investigated. Specifically, 6 pathways were chosen for the m-LBO polymorph (Fig. 2) and 9 pathways were chosen for the t-LBO polymorph (Fig. 3). The Appendix shows a detailed description of the different pathways, where the energy landscapes for each of the pathways (there are 60 pathways systematically investigated from our DFT calculations for the current work) will be presented for a thorough comprehension of the effects of lattice vacancies on the migration pathways of the lithium ion and its associated partner, the lithium vacancy, in the vacancy-mediated diffusion mechanism. Again, it is worth recalling that in each of the investigated pathways there were 7 to 9 atomic lattice replica (including both the departure and destination as well as the intermediate hopping sites for the lithium ion along the pathway), which were used in our CI-NEB calculations and were referred to as CI-NEB images as aforementioned. Totally, there were up to 540 atomic geometrical configurations used in our DFT calculations for the study of lithium-ion transport. The complete information about these configurations and DFT parameters is provided in the ESI† of this paper.

In each supercell of a polymorph, the lithium-ion (lithium-vacancy) diffusivity is calculated as

with D₀ ≈ a²ν, where a is the hopping distance of the lithium ion from its initial site to its final vacancy site, and ν is the lithium-ion hopping frequency. In eqn (3), E_m = E^f_m for lithium-ion diffusivity and E_m = E^b_m for lithium-vacancy diffusivity (see Table 6). For the sake of simplicity and comparison of the impact of boron or oxygen vacancies on the lithium-ion migration energy barrier and hence the lithium-ion diffusivity, we estimated the same value of D₀ for all of migration pathways by assigning a = 5 Å and ν = 10¹³ Hz, leading to a reasonable D₀ = 2.5 × 10⁻² cm² s⁻¹.³⁹ With this approximation, we can obtain quantitative estimates of how lattice vacancies impact the microscopic local atomic environments of the lattice structure, leading to the modification of the lithium-ion migration energy barrier and hence the modification of the lithium-ion transport quantities (e.g., lithium-ion diffusivity, mobility, and conductivity) by several orders of magnitude. Eqn (3) enables us to determine the lithium-ion mobility and conductivity by using the Einstein–Smoluchowski equation, which relates the diffusivity and mobility of a charged particle (in this case, the positively charged lithium ion or the negatively charged lithium vacancy) and is expressed aswhere μ and q are the mobility of the lithium ion (lithium vacancy) and its charge, respectively (i.e., q = +1.602 × 10⁻¹⁹ C for the lithium ion and q = −1.602 × 10⁻¹⁹ C for the lithium vacancy). The lithium-ion conductivity is then determined as σ = n|q|μ = q²nD/(k_BT), leading to a direct relation between σ and E_m (it is recalled again that E_m = E^f_m is for the lithium ion and E_m = E^f_m is for the lithium vacancy as shown in Table 6) as

As stated previously, n is used to denote the concentration of the lithium ion and its corresponding vacancy that simultaneously participates with it in the hopping-via-vacancy mechanism of lithium-ion diffusion. Thus, the vacancy is set to be one per supercell in this work. To compare our estimated values of σ, we used the same supercell volume of 150 ų, which is the volume of a cubic supercell of 5 Å × 5 Å × 5 Å, for computing the value of n. This approach led to the value of n ≈ 8.0 × 10²¹ cm⁻³. Eqn (5) provides a macroscopic–microscopic relationship, which can be measured experimentally using temperature-dependent electrochemical impedance spectroscopy or modeled theoretically using atomistic modeling tools such as the DFT calculations performed in this work. The values of diffusivity, mobility and conductivity are then estimated at T = 300 K. One should note that since the diffusivity, mobility, and conductivity of the lithium ion are all determined based on the vacancy-induced modification of local atomic and electronic environments along the pathways of lithium-ion migration, this local lithium-ion transport studied in the current work might not necessarily exactly reflect the global intra-grain or inter-grain transport of the lithium ion over a macroscopic scale as vast as several tens or even hundreds of unit cells, where the transport of the lithium ion may be dominantly governed by other mechanisms such as grain boundaries or other types of defects commonly employed by experimenters to account for their measured data of improved ionic conductivity.^1,13,39 However, to some extent, a comprehensive microscopic–macroscopic relationship between the migration energy barrier and the ionic conductivity of the lithium ion as a result of the modification of microscopic and local lattice environments induced with the presence of vacancies could shed more light on a thorough understanding of the effects of defects on the intra-grain ionic conductivity.

3 Results and discussion

3.1 Formation of lattice vacancies in LiBO₂ crystals

Islam et al.¹⁴ conducted a DFT investigation of lithium vacancies in LiBO₂ using the Perdew Wang (PW91) generalized gradient approximation with the projector-augmented wave method (PWGGA-PAWs) implemented in the VASP (Vienna Ab initio Simulation Package) code; they showed that the value of the formation energy is 663 kJ mol⁻¹ (6.87 eV) for a 1 × 1 × 1 supercell of the m-LBO polymorph. They have also attempted to examine both medium (i.e., 2 × 2 × 2) and large (i.e., 3 × 3 × 3) supercells. Yet, they only improved the accuracy of the formation energy by 0.6% and 1.5%, respectively, relative to the 1 × 1 × 1 supercell. Their work did not explore, however, the formation energies of boron and oxygen vacancies in the m-LBO or t-LBO polymorphs. Therefore, we provide here a comprehensive comparison of the formation energy of each of the atomic lattice vacancies in the LiBO₂ material by conducting our ab initio studies for both of the polymorphs in the same setups of our DFT calculations described in detail in Section 2. Again, to minimize our computational cost, we only employed small (i.e., 1 × 1 × 1) supercells. The results are presented in Table 2. It is worth noting from Table 2 that, the value of the formation energy of lithium vacancies in the m-LBO polymorph (α phase) is 5.03 eV (485.32 kJ mol⁻¹), which is 1.84 eV (177.53 kJ mol⁻¹) less than that calculated by Islam et al. This difference is attributed to the different DFT methods and codes used in this work and by Islam et al.¹⁴ (i.e., our PBEGGA-ultrasoft PPs calculated using the QE code versus their PWGGA-PAWs calculated using the VASP). For the sake of a fair comparison, we have fixed the same setup of our DFT calculations for all of the supercells of interest (see Section 2).

Table 2 Formation energy of vacancies in the monoclinic and tetragonal polymorphs of LiBO₂

Polymorph	Vacancy type	Formation energy (eV)
Monoclinic (α phase)	Li vacancy	5.03
	B vacancy	10.28
	O vacancy	5.74
Tetragonal (γ phase)	Li vacancy	4.64
	B vacancy	10.23
	O vacancy	6.49

---

Table 2 presents the values of the formation energy of lithium, boron, or oxygen vacancies in both the m-LBO and t-LBO polymorphs of the LiBO₂ material. Table 2 shows some important points. Firstly, it is energetically more costly to form lithium vacancies in the m-LBO polymorph than in the t-LBO one, which means that the concentration of vacancies at a given temperature is higher in t-LBO than that in m-LBO. In contrast, the formation energy of oxygen vacancies is higher in t-LBO than that in m-LBO. The formation energy of boron vacancies in both polymorphs are the same. Thirdly, the formation energy of vacancies consistently increases from lithium vacancies to oxygen and to boron ones. While the values of the formation energies of lithium and oxygen vacancies in both the polymorphs are considerably high, those of boron vacancies are extremely high, implying that the generation of boron vacancies in the LiBO₂ material is energetically costly and unfavorable thermodynamically. However, if the LiBO₂ material is subjected to a high-dose neutron irradiation, a high concentration of boron vacancies might be achievable, possibly due to the formation of clusters of strongly interactive vacancies. In fact, in experiments on m-LBO polycrystalline samples irradiated with thermal neutrons, recently performed by the authors of the current work at the University of Missouri Research Reactor, evidence of significant dose-dependent changes in the surface microstructure and chemistry due to the formation of neutron-induced defects, such as boron vacancies, was found. This evidence demonstrates that thermal neutron irradiation is a feasible strategy to controllably generate boron vacancies in LiBO₂. The results of these experiments will be published elsewhere.⁴⁰

3.2 Effects of lattice vacancies on lattice structures of LiBO₂ crystals

This subsection presents the results of our ab initio studies of the effects of vacancies in LiBO₂ polymorphs on the crystal lattice and the energy of formation per atom. The latter provides the understanding of the effects of vacancies on the stability of the crystals.

For the sake of comparison between the experimental and theoretical data of the lattice parameters, Table 3 presents the complete data of the lattice parameters of the crystals of both the m-LBO and t-LBO polymorphs theoretically calculated from our current work and the uncomplete data of the parameters reported theoretically by Basalaev et al.¹⁵ and experimentally by Hirose et al.¹³ Our data of the lattice parameters of the LiBO₂ polymorphs were obtained after the supercell of each polymorph was fully relaxed using our PBEGGA-UPP setup in the QE code from the initial inputs shown in Table 1. The data reported by Basalaev et al.¹⁵ were obtained in their DFT calculations using the CRYSTAL code (CRYSTAL14) with a hybrid B3LYP method, including the Becke exchange functional (B3) and the Lee, Yang, and Parr (LYB) correlation method of special points with a 16 × 16 × 16 k-point mesh and a cutoff energy of 40 Ry. Their DFT calculations were obviously computationally demanding and are expected to better simulate the structural properties of experimental samples. We recall that the experimental data reported by Hirose et al.¹³ were obtained from the Rietveld refinement of their synchrotron powder x-ray diffraction measurements of their LiBO₂ samples synthesized under high-pressure conditions. It is worth noting that the relative difference of each of the three lattice parameters, a, b, and c between our theoretical results and Hirose et al.'s experimental values for the m-LBO crystal are −2.39%, +3.22%, and +2.94%, i.e., similar in magnitude to the differences between Basalaev et al.'s theoretical and Hirose et al.'s experimental values, −2.91%, +0.46%, and +0.93%.

Table 3 Comparison of theoretical and experimental lattice parameters for monoclinic LiBO₂ and tetragonal LiBO₂

Parameter	Monoclinic LiBO2 (α phase)			Tetragonal LiBO2 (γ phase)
	Our DFT	Other DFT^a	Other Exp^b	Our DFT	Other DFT^a	Other Exp^b
a Data taken from a theoretical study by Basalaev et al.^15 b Data taken from an experimental study by Hirose et al.^13
a (Å)	5.71	5.68	5.85	4.21	4.16	4.20
b (Å)	4.49	4.37	4.35	4.21	4.16	4.20
c (Å)	6.65	6.52	6.46	6.61	6.33	6.51
α (°)	90	N/A	N/A	90	N/A	N/A
β (°)	110	N/A	115.04	90	N/A	N/A
γ (°)	90	N/A	N/A	90	N/A	N/A

---

In contrast, the comparison for the lattice parameters a and c of the t-LBO crystal is as follows (a = b for a tetragonal crystal): +0.24% and +1.54% for our calculation vs. the experiment, compared to −0.95% and −2.76% for Basalaev et al.'s results. More interestingly, our values of a and c are closer to the experimental ones than Basalaev et al.'s ones. This comparison would reinforce that the norm-reserving pseudopotentials chosen in the current work accurately represented the core electrons while efficiently capturing the valence electron behavior, leading to efficient and reliable modeling of LiBO₂ polymorphs. Overall, the quantitative comparison carried out in this subsection would reveal that the lattice parameters theoretically calculated in the work by Basalaev et al.¹⁵ and in this work by the authors agreed reasonably well with those reported in the experimental work by Hirose et al.¹³ within a tolerable 5%-off accuracy.

Table 4 provides the effect of vacancies on the lattice parameters and the volumes of the conventional unit cells in the crystal polymorphs. As one can see in Table 4, after the fully relaxed optimization of the supercells' geometry in our DFT calculations, some of the lattice parameters were modified. As a result, the volumes of the unit cells of the defective supercells were increased or decreased by 1.5% to 9.8% relative to those of the corresponding nondefective perfect supercells after their geometry optimization. Specifically, the effects of the lattice vacancies on the crystal structure of each polymorph are separately detailed as follows. For the m-LBO polymorph, the tendency of the effect of each type of vacancies on lattice parameters is consistent: lattice vacancies result in the decreased values of both a and b, but an increased value of c. Nevertheless, the overall impact of vacancies on the volume of the unit cell is different: boron vacancies cause the crystal to expand by 1.5% while lithium and oxygen vacancies shrink the crystal by 2.3% and 3.6%, respectively. Yet, the change in the volume of the unit cell of the m-LBO polymorph is still less than 5%. Notably, the effect of boron and oxygen vacancies on the crystal lattice of the t-LBO polymorph is more pronounced, but in the opposite direction: nearly 10% of the volume changes in both oxygen-vacancy (−8.4%) and boron-vacancy (+9.8%) unit cells relative to the perfect unit cell, which is quite remarkable. Finally, while the tendency of lithium vacancies to decrease a and b and to increase c in both polymorphs is similar, lithium vacancies shrink the volume (−2.3%) of the m-LBO crystal, but expand that (+0.3%) of the t-LBO one.

Table 4 Lattice parameters and volumes for nondefective and defective unit cells of the two polymorphs of LiBO₂

Polymorph	Crystal	a (Å)	b (Å)	c (Å)	β (°)	V (Å^3)	ΔV (%)
Monoclinic (α phase)	Perfect	5.71	4.49	6.65	110.0	156.73	0.0
	Li vacancy	5.68	4.36	6.77	111.4	153.05	−2.3
	B vacancy	5.57	4.41	6.92	110.0	159.11	+1.5
	O vacancy	5.66	4.17	6.76	108.4	151.09	−3.6
Tetragonal (γ phase)	Perfect	4.21	4.21	6.61	90	117.16	0.0
	Li vacancy	4.20	4.20	6.66	90	117.48	+0.3
	B vacancy	4.23	4.23	7.19	90	128.65	+9.8
	O vacancy	4.25	4.09	6.39	90	107.35	−8.4

---

Table 5 lists the values of E_f for all of the perfect and defective supercells of interest. These values were determined using eqn (1). One can see from Table 5 that E_f is the same for the nondefective perfect crystals of both polymorphs. However, when a specific ion (either Li⁺, B³⁺, or O²⁻) is removed from the perfect crystals, E_f increases (i.e., less negativity in its value), which suggests that any lattice vacancy likely results in the reduced energetic stability of LiBO₂ crystals. In addition, we considered an additional parameter, ΔE_f, which represents the difference in the energies of formation per ion between the defective supercell and its perfect counterpart: ΔE_f = E^{X vacancy}_f − E^perfect_f, where X is either Li⁺, B³⁺, or O²⁻, and E^perfect_f and E^{X vacancy}_f are the energy of formation per ion for the perfect supercell and defective one, respectively. The higher the value of ΔE_f the less the energetic stability of the defective crystal formation relative to its perfect one. Interestingly, the tendency of the destabilization of crystal formation is energetically similar in both the m-LBO and t-LBO polymorphs. Specifically, the degree of destabilization caused by lattice vacancies follows a distinct order in both the polymorphs: ΔE_f (Li⁺) < ΔE_f (O²⁻) < ΔE_f (B³⁺). This trend suggests that the removal of boron ions has the most pronounced destabilizing effect on the LiBO₂ crystals, followed by oxygen, and lithium has the least destabilizing impact. This trend is consistent with the trend of formation energy of vacancies shown in Table 3 and discussed previously. In summary, the findings of our ab initio studies underscore the nuanced and structure-dependent response of LiBO₂ crystals to specific lattice vacancies, shedding more light on the engineering of defect chemistry to improve the ionic conductivity of LiBO₂ materials.

Table 5 Formation energy per ion (E_f) in supercells and its absolute change (ΔE_f) relative to perfect nondefective supercells for the two polymorphs of LiBO₂. E_f is determined using eqn (1). ΔE_f = E^{X vacancy}_f − E^perfect_f, where X is either Li⁺, B³⁺, or O²⁻, and E^perfect_f and E^{X vacancy}_f are the energy of formation per ion for a nondefective perfect supercell and its X-vacancy counterpart, respectively

Polymorph	Crystal	E f (eV per ion)	ΔEf (eV per ion)
Monoclinic (α phase)	Perfect	−2.45	0.0
	Li vacancy	−2.28	0.17
	B vacancy	−1.93	0.52
	O vacancy	−2.23	0.22
Tetragonal (γ phase)	Perfect	−2.45	0.0
	Li vacancy	−2.30	0.15
	B vacancy	−1.93	0.52
	O vacancy	−2.18	0.27

---

3.3 Effects of lattice vacancies on electronic and ionic conduction of LiBO₂ crystals

Since LiBO₂ has been the subject of both experimental and theoretical studies for its use as a solid electrolyte or an electrode coating of lithium-ion batteries, more insights into how the LiBO₂ material might be engineered to be both a fast lithium-ion conductor and a good electron insulator or conductor in the same material are critically needed from a practical viewpoint.³⁹ From a viewpoint of basic research, a better understanding of the impacts of lattice vacancies on the LiBO₂ material would be essential for the optimization of the LiBO₂ material. This subsection discusses the analysis of the electrical conduction of LiBO₂ polymorphs based on the data obtained from our DFT calculations.

3.3.1 Band gap and electronic insulation. While experimental data of the band gaps E_g of both LiBO₂ polymorphs considered here have not been found in the literature, recent DFT calculations (using a hybrid B3LYP method implemented in the CRYSTAL code) for the band structures of the polymorphs by Basalaev et al.¹⁵ reported that E_g = 7.6 eV and 10.4 eV were obtained for m-LBO and t-LBO, respectively. In addition, Islam et al.¹⁴ reported that a PWGGA-PAW method implemented in the VASP code yielded a lower value of E_g = 5.74 eV for the m-LBO polymorph, and that the defect energy levels of the lithium vacancy occurred in the band gap and were located adjacent to the top of the valence band, implying that the vacancy is capable of acting as an acceptor of electrons to become negatively charged and the lithium-vacancy m-LBO crystal in this case behaves like a (wide-band-gap) p-type semiconductor. However, there have not been any DFT calculations of electronic band structures and density of states (DOS) published for other types of lattice vacancies (i.e., oxygen and boron vacancies) in the m-LBO polymorph and all types of lattice vacancies (i.e., lithium, oxygen, and boron vacancies) in the t-LBO polymorph. In this subsection, we aim at filling this knowledge gap by presenting the effects of all types of vacancies on DOS, from which one might gain deeper insights into how the LiBO₂ material, which functions as an electronic insulator, can be appropriately designed and engineered to meet technical requirements of a desired solid electrolyte or an electrode coating of Li-ion batteries.

The results of our DOS calculations for the perfect (i.e., nondefective) and defective crystals of the LiBO₂ material are presented in Fig. 4 (m-LBO polymorph) and Fig. 5 (t-LBO polymorph). Furthermore, panels 4a and 5a show that the values of the band gap for the respective perfect crystals are E_g = 5.23 eV (m-LBO) and E_g = 7.44 eV (t-LBO). While these values are less than those reported by Basalaev et al.¹⁵ (discussed in the previous paragraph), our results also show that the perfect t-LBO polymorph possesses a wider band gap than its perfect m-LBO counterpart. The smaller values of E_g of our DFT calculations are due to the nature of the GGA method which usually underestimates the band gap. Basalaev et al.¹⁵ used a hybrid B3LYP method which is better at estimating the band gap, but computationally much more costly (which becomes prohibitive given the number of configurations probed in this study).

Fig. 4 Electronic density of states of the m-LBO polymorph. (a) Perfect, (b) Li vacancy, (c) O vacancy, and (d) B vacancy.

Fig. 5 Electronic density of states of the t-LBO polymorph. (a) Perfect, (b) Li vacancy, (c) O vacancy, and (d) B vacancy.

From Fig. 4 and 5, the effect of each of the vacancies on DOS in the m-LBO and t-LBO polymorphs is different. Compared to the perfect m-LBO crystal, the DOS of the Li-vacancy m-LBO crystal (panel 4b) shows the energy levels of lithium defects in the band gap, which are just above and well separated (about 0.8 eV) from the top of the valence band, and behave like acceptor levels. These levels are localized to manifest a sharp peak (rather than a continuous energy band) centered at 4.35 eV below the bottom of the conduction band. The appearance of the defect levels makes the overall band gap effectively narrower (i.e., 4.35 eV versus 5.23 eV). Therefore, the capability of insulating electron conduction is weaker for the lithium-vacancy crystal of the m-LBO polymorph than that of its perfect crystal counterpart. In contrast, for the t-LBO polymorph, lithium vacancies do not change the value of the band gap (panel 5b). The defect levels of the lithium vacancies merge together with the top of the valence band, resulting in an effective valence band whose topmost level is still 7.44 eV apart from the bottom of the conduction band. As a result, the band gap is effectively the same as that of the perfect crystal (i.e., E_g = 7.44 eV), suggesting that the electronic insulation capability of the t-LBO polymorph might not be deteriorated in the presence of lithium vacancies.

The DOS of the boron-vacancy crystals in both polymorphs (panels 4d and 5d) manifests a similar scenario to that of lithium-vacancy crystals, where boron defect energy levels occur in the band gap, close to and separate from the top of the valence band (panel 4d) for the m-LBO polymorph. These defect levels merge together with the valence band (panel 5d) in the t-LBO polymorph. Unlike the lithium-vacancy crystals, the defect energy levels of boron vacancies are broadened to exhibit an overlapping band of the localized levels spanning over approximately a width of 1.0 eV for both polymorphs. For the m-LBO polymorph (panel 4d), the lowest of the defect energy levels of boron vacancies locates nearly 0.4 eV above the top of the valence band while the highest is about 4.18 eV below the bottom of the conduction band. Consequently, the boron vacancies behave like electron acceptors, leading to a reduced effective band gap of E_g = 4.18 eV, lower than that of the Li-vacancy crystal (E_g = 4.35 eV) as seen in panel 4b. This means that boron vacancies reduce the capability of electron insulation of the m-LBO polymorph more than lithium vacancies. In the t-LBO polymorph, the band of the defect levels of boron vacancies merge with the top of the valence band and the band gap gets narrower (E_g = 6.44 eV compared to E_g = 7.44 eV). Similar to the m-LBO polymorph, boron vacancies also tend to degrade the capability of electronic insulation of the t-LBO polymorph. However, the tendency of boron vacancies to delocalize electrons, as discussed below, could electronically facilitate the lithium-ion transport.

The effects of oxygen vacancies on DOS (panels 4c and 5c) are fairly different in the two polymorphs. On the one hand, in the m-LBO polymorph (panel 4c), the defect energy levels of oxygen vacancies are separated into two distinct continuous bands in the band gap with an effective energy gap of E_g = 2.91 eV, which is much narrower than that (E_g = 5.23 eV) of the perfect crystal. The low-energy-level band is approximately 1.2 eV in width and merges with the top of the valence band to create an effective valence band. The high-energy-level band spans as wide as 1.5 eV, the top of which is located 0.8 eV below the bottom of the conduction band, suggesting that the oxygen-vacancy m-LBO crystal likely behaves like an n-type semiconductor in which the oxygen vacancies could be electron donors that when ionized contribute electrons to the conduction band. In terms of the reduction of the band gap, oxygen vacancies tend to degrade the electronic insulation capability of the m-LBO polymorph even more than boron vacancies. On the other hand, in the t-LBO polymorph (panel 5c), the defect energy levels of oxygen vacancies exhibit only one continuous band, which is 0.7 eV separated from the top of the valence band, suggesting that oxygen vacancies behave like electron acceptors in a p-type semiconductor. The defect energy band spans in the band gap toward high energies and makes the band gap shrink to have a narrower band gap of E_g = 4.44 eV, also giving rise to a worsened electronic insulation capability of the t-LBO polymorph.

3.3.2 Lithium-ion transport. This subsection presents our ab initio studies on the effects of lattice vacancies on the lithium-ion transport in both polymorphs of the LiBO₂ material. Only the fastest pathways for both polymorphs of the LiBO₂ material are presented in this subsection. The rest of the pathways are described in detail in the Appendix and in the ESI.†

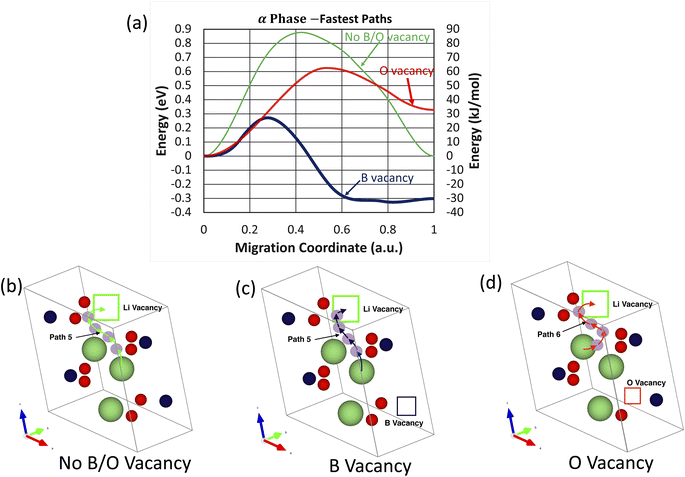
For the six migration pathways under investigation in the m-LBO polymorph, one can see in Fig. 6a that among the three fastest migration pathways, the one in the boron-vacancy crystal has the lowest migration energy barrier. It is suggested from Fig. 6a that the local structure around boron vacancies could facilitate the lithium-ion migration in the m-LBO polymorph of LiBO₂ more efficiently than that of oxygen vacancies, as indicated by the value of E^f_m: E^f_m = 0.88 eV for the crystal with neither oxygen nor boron vacancies, E^f_m = 0.27 eV for the crystal with boron vacancies, and E^f_m = 0.63 eV for the crystal with oxygen vacancies.

Fig. 6 Fastest lithium migration pathways in the m-LBO polymorph.

Atomic visualizations of the fastest migration pathways of the m-LBO polymorph are shown in Fig. 6b–d, from which one can note two remarkable observations: (1) all of the fastest migration pathways are not straight lines, rather curved S-shapes, and (2) while Path 5 is the fastest migration pathway for both the no B/O vacancy and B-vacancy crystals, Path 6 is the fastest pathway for the O-vacancy crystal.

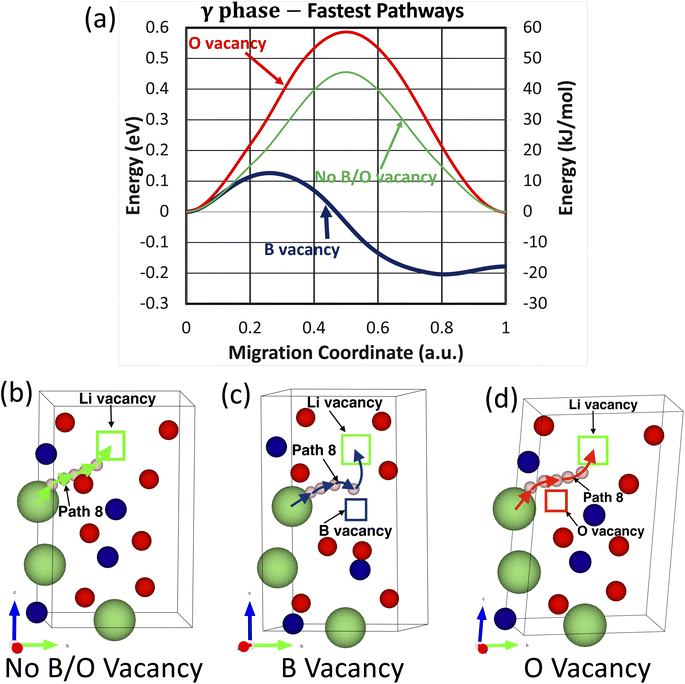
In comparison, of the nine investigated migration pathways in the t-LBO polymorph, Path 8 becomes the fastest migration pathway in the crystals with and without the presence of boron or oxygen vacancies. As shown in Fig. 7a, while oxygen vacancies increase the energy barrier of Path 8 from E^f_m = 0.46 eV to E^f_m = 0.59 eV, boron vacancies substantially reduce the energy barrier from E^f_m = 0.46 eV to E^f_m = 0.13 eV. The atomistic visualization of these fastest migration pathways is shown in Fig. 7b and c. From these considerations, it is apparent that oxygen vacancies inhibit the migration of the lithium ion whereas boron vacancies facilitate it.

Fig. 7 Fastest lithium-ion migration pathways in the t-LBO polymorphs.

The values of E^f_m and E^b_m are respectively shown in Table 6 for the fastest migration pathways of the lithium ion and those of its lithium vacancy partner in each of the investigated crystals. In addition, the diffusivity, mobility, and conductivity of the lithium ion and of the lithium vacancy associated with these values are determined using eqn (3)–(5). The purpose of this investigation is to conduct a quantitative and comparative analysis of the microscopic–macroscopic relationships of the impacts of lattice vacancies on the lithium-ion transport in both the polymorphs of the LiBO₂ material. As shown in Table 6, our DFT calculations have shown that in the crystal without boron and oxygen vacancies, the migration energy barriers E^f_m = E^b_m = 0.88 eV for the fastest pathway are so high that they result in extremely low estimates of diffusivity (D = 1.3 × 10⁻¹⁷ cm² s⁻¹) and ionic conductivity (σ = 7.0 × 10⁻¹³ S cm⁻¹) at 300 K. Both boron and oxygen vacancies lower E_m, but in opposite ways due to their opposite charges: E^f_m = 0.27 eV and E^b_m = 0.60 eV for boron vacancies and E^f_m = 0.63 eV and E^b_m = 0.30 eV for oxygen vacancies, leading to an increased diffusivity, and hence an increased ionic conductivity, by possibly ten orders of magnitude (i.e., D = 5.1 × 10⁻⁷ cm² s⁻¹ and σ = 2.8 × 10⁻² S cm⁻¹ for boron vacancies versus D = 1.5 × 10⁻⁷ cm² s⁻¹ and σ = 8.3 × 10⁻³ S cm⁻¹ for oxygen vacancies). In contrast, compared to m-LBO, the effects of boron and oxygen vacancies on lithium-ion transport in t-LBO are quite different. While oxygen vacancies increase E_m from E^f_m = E^b_m = 0.46 eV to E^f_m = E^b_m = 0.59 eV and inhibit lithium-ion transport, boron vacancies lower E_m considerably to E^f_m = 0.13 eV and E^b_m = 0.33 eV, giving rise to a remarkable enhancement of both the diffusivity (D = 1.4 × 10⁻⁴ cm² s⁻¹) and ionic conductivity (σ = 7.5 × 10⁰ S cm⁻¹), therefore facilitating the very-fast lithium-ion transport.

Table 6 Migration barrier and the corresponding diffusivity, mobility, and conductivity of lithium-ion transport in LiBO₂ crystals at room temperature estimated for the fastest migration pathways by using density functional theory modeling

Crystal		Parameter
		Migration energy (eV)		Diffusivity at 300 K (cm^2 s^−1)		Mobility at 300 K (cm^2 s^−1 V^−1)		Conductivity at 300 K (S cm^−1)
		Forward	Backward	Forward	Backward	Forward	Backward	Forward	Backward
α phase	No B/O vacancy	0.88	0.88	1.3 × 10^−17	1.3 × 10^−17	5.2 × 10^−16	5.2 × 10^−16	7.0 × 10^−13	7.0 × 10^−13
	B vacancy	0.27	0.60	5.1 × 10^− ^7	9.4 × 10^−13	2.0 × 10^− ^5	3.8 × 10^−11	2.8 × 10^− ^2	5.1 × 10^−8
	O vacancy	0.63	0.30	2.8 × 10^−13	1.5 × 10^− ^7	1.1 × 10^−11	6.1 × 10^− ^6	1.5 × 10^−8	8.3 × 10^− ^3
γ phase	No B/O vacancy	0.46	0.46	2.6 × 10^−10	2.6 × 10^−10	1.0 × 10^−8	1.0 × 10^−8	7.0 × 10^−5	7.0 × 10^−5
	B vacancy	0.13	0.33	1.4 × 10^− ^4	4.6 × 10^− ^8	5.5 × 10^− ^3	1.9 × 10^− ^6	7.5 × 10 ^0	2.5 × 10^− ^3
	O vacancy	0.59	0.59	1.4 × 10^−12	1.4 × 10^−12	5.6 × 10^−11	5.6 × 10^−11	7.6 × 10^−8	7.6 × 10^−8

---

Finally, it would be suggested that the favorable impacts of boron vacancies on the crystal and electronic properties, which have been described above, might account for the improved ionic conductivity of the lithium ion in both of the LiBO₂ polymorphs in the presence of boron vacancies. Structurally, boron vacancies lead to an expansion of the lattice volume in LiBO₂ crystals, creating more space for the migration of the lithium ion. This contrasts with oxygen vacancies, which cause lattice contraction. For instance, in the t-LBO polymorph, boron vacancies increase the lattice volume by 9.8%, while oxygen vacancies decrease it by 8.4%. As a result, in most of the examined lithium-ion migration pathways (i.e., Paths 1 to 9), the migration energy barriers are reduced in the presence of boron vacancies, whereas they increase as a result of the formation of oxygen vacancies (see the Appendix and ESI† for further analysis). Electronically, boron vacancies introduce a band of defect-energy levels within the forbidden band of m-LBO, which can facilitate the de-localization of electrons around the boron vacancies. This enhances the lithium-ion transport, as the lithium ion is no longer repelled by a like-charged B³⁺ ion but instead attracted by a negatively charged boron vacancy along its migration pathways. Further investigation of the impacts of lattice vacancies on the band structures of the LiBO₂ polymorphs needs to be conducted in order to provide additional evidence for the observed electron de-localization in the presence of boron vacancies such as the reduced effective mass of the electron at the bottom of the conduction band or that of the electronic hole at the top of the valence band.

4 Conclusions

The m-LBO and t-LBO polymorphs of LiBO₂ (m-LBO and t-LBO) have been extensively studied for their diverse technological applications, including as a solid electrolyte, a solid electrolyte interphase component, and an electrode coating in lithium-ion batteries. Although experimental comparisons of the lithium-ion transport in these polymorphs have been made, focusing on their distinct two-dimensional and three-dimensional lithium–lithium networks, the mechanistic understanding of the formation of lattice vacancies and their effects on the lithium-ion transport remains incomplete.

The primary goals of the current work are (i) to investigate the formation of lithium, boron, and oxygen vacancies at concentrations of ∼8.0 × 10²¹ cm⁻³ and (ii) to analyze the resulting modifications in the lattice structure, electronic density of states, and the lithium-ion migration energy barrier in both polymorphs, focusing on the impact of lattice vacancies on lithium-ion transport. Our findings indicate that the formation energy of lattice vacancies increase from lithium vacancies, to oxygen ones, and then to boron ones. In addition, boron and oxygen vacancies reduce the band gap (E_g) of LiBO₂ crystals by introducing defect levels within the band gap, rendering the material a degenerate semiconductor and deteriorating its electronic insulation characteristics.

Regarding lithium-ion transport, our DFT results show that oxygen vacancies decrease the migration energy barrier (E_m) in m-LBO but increase it in t-LBO. Conversely, boron vacancies significantly reduce E_m in both m-LBO and t-LBO, enhancing diffusivity and ionic conductivity in both polymorphs. This improved ionic conductivity is attributed to the favorable modifications of crystal and electronic structures in the presence of boron vacancies. Our findings suggest that generating boron vacancies could be a viable strategy for improving the ionic conductivity in LiBO₂. One of the methods to generate boron vacancies in LiBO₂ could be using neutron irradiation. Nevertheless, further theoretical calculations of electronic band structures with larger systems and experimental validation of boron vacancy generation by means of neutron irradiation are needed in order to shed more light on the mechanistic understanding of the effects of lattice vacancies on the lithium-ion transport in LiBO₂ crystals.

Data availability

It is officially and firmly stated that the data that support the findings of this study are available from the corresponding authors upon reasonable request. The computational models, parameters, and raw output data generated during the current study have been archived and can be shared with interested researchers to facilitate replication or further exploration of the results.

Author contributions

The contributions of the authors to the current work are as follows: conceptualization: C. W., S. A., T. W. H., Y. X., J. G.; methodology: S. A., H. M. N., C. Z., C. W.; manuscript writing: S. A., C. Z., H. M. N., C. W.; equal contribution to DFT calculations: H. M. N., C. Z., S. A.; manuscript proofreading and reviewing: all authors.

Conflicts of interest

The authors declare no conflicts of interest.

Appendix: investigated pathways of lithium-ion migration in the LiBO₂ material

This appendix presents in detail the energy landscapes of the examined lithium-ion migration pathways in both the polymorphs of the LiBO₂, including the fastest pathways discussed in Section 3.3.2. The atomic visualization of all of the examined migration pathways is provided in the ESI† of this paper.

We recall that in order to examine how the local lattice structure at the oxygen or boron vacancies affects the migration of lithium ion, we chose to investigate various pathways near the vacancy sites of interest (B1 or O1 site for the m-LBO polymorph as labeled in Fig. 1a, and B3 or O5 site for the t-LBO polymorph as in Fig. 1b). Here, 6 migration pathways (Fig. 2) and 9 pathways (Fig. 3) were selected for our search for the optimal migration pathway in each of the examined crystals. The results of the energy landscapes of our CI-NEB calculations for these pathways are depicted in Fig. 8 and 9.

Fig. 8 Energy landscapes of lithium-ion migration pathways in the m-LBO polymorph of the LiBO₂ crystal.

Fig. 9 Energy landscapes of lithium-ion migration pathways in t-LBO polymorphs of the LiBO₂ crystal.

Fig. 8 presents the migration energy landscapes for the 6 pathways (Fig. 2) of interest for crystals without (panel 8a) and with boron (panel 8b) or oxygen (panel 8c) vacancies. These pathways are within the two-dimensional network that includes all of the 4 lithium ions per unit cell of the m-LBO polymorph. As one can see Path 3 is the most prohibitive migration pathway in the m-LBO polymorph under consideration in our current work. For example, for the crystal without boron or oxygen vacancies (panel 8a), on hopping forward from the lithium site Li1 (the departure) to the lithium vacant site at the Li4 position (the destination), a lithium ion take two consecutive jumps: the first one is from the departure to a less stable interstitial site (about 4 eV higher in energy) requiring the overcoming of an extremely high energy barrier of 12 eV, where this intermediate site serves as the “stepping stone” for the lithium ion to make the second jump to the destination, but overcoming a lower barrier of 3.5 eV, and thus the forward migration energy of Path 3 is E^f_m = 12 eV. Along Path 3, the lithium vacancy hops backward from site Li4 to site Li1 and encounters two energy barriers, namely, 7.5 eV and 8.0 eV, resulting in a backward migration energy barrier of E^b_m = 8.0 eV.

Interestingly, both boron and oxygen vacancies modify this “two-stop” migration pathway to “one-stop” pathways with substantially reduced energy barriers, an approximately three times reduction for boron vacancies (4.5 eV vs. 12 eV) as seen in Fig. 8b and two times for oxygen vacancies (5.6 eV vs. 12 eV) as shown in Fig. 8c. Thus, the vacancies are capable of facilitating the lithium-ion migration along Path 3 substantially. Yet, regardless of reduction in the migration energy by both oxygen and boron vacancies, the migration of the lithium ion along Path 3 is of extremely low probability and there are better migration pathways. Due to the migration energy barrier entering into the Arrhenius-type exponential factor, ultimately only the lowest migration energy barrier pathways are significant for the lithium-ion transport.

It is worth noting in Fig. 8a that the migration energy barriers along other migration pathways are quite lower than those of Path 3. These barriers are only a bit more or less than 1 eV. These barriers are lowered by the presence of oxygen vacancies (Fig. 8c) and more substantially by the formation of boron vacancies (Fig. 8b).

Fig. 9 presents the results of our CI-NEB calculations for the nine lithium-ion migration pathways (see also Fig. 3) in the t-LBO polymorph considered to search for the optimal ones. In contrast to the m-LBO polymorph, lithium ions in the t-LBO crystals create a three-dimensional network. For the crystal without boron or oxygen vacancies (Fig. 9a), there are “nonstop” and “multiple-stop” migration pathways of the lithium ion. The “nonstop” pathways refer to those along which the lithium ion only overcomes a single energy barrier to hop from the initial lithium site (i.e., the departure) to the final lithium vacancy site (i.e., the destination). These pathways are Path 2, Path 4, Path 6, Path 7, and Path 8 as shown in Fig. 9a. In contrast, the “multiple-stop” pathways are those along which one or more “stop(s)” (i.e., interstitial site(s)) serve(s) as the “stepping stone(s)” for the lithium ion to make its way from its departure to its destination. As shown in Fig. 9a, the “multiple-stop” pathways are Path 1, Path 3, Path 5 and Path 9. The migration of the lithium ion in the t-LBO polymorph is detailed as follows.

Path 1, which is the most energetically costly pathway, possesses 3 intermediate stops and the destination site with the energy barriers respectively being roughly 5.75 eV, 5.25 eV, 5.75 eV, and 0.0 eV higher than the energy of the departure site. The barriers that the lithium ion overcomes to take intermediate jumps are approximately 6.15 eV, 1.0 eV, 0.75 eV, and 0.2 eV, resulting in E^f_m = 6.5 eV. The presence of boron vacancies causes Path 1 to be modified remarkably (Fig. 9b), highlighting three main features: (i) the energy landscape of Path 1 changes from asymmetric to symmetric; (ii) the number of stops is reduced from 3 to 1; and (iii) the value of E^f_m is reduced from E^f_m = 6.5 eV to E^f_m = 2.34 eV. In contrast, oxygen vacancies (Fig. 9c) still retain the asymmetric and “multiple-stop” nature and the same value of E^f_m = 6.5 eV as Path 1 in the crystal without boron or oxygen vacancies.

Path 3 in the crystal without boron or oxygen vacancies (Fig. 9a) is a symmetric one-stop migration pathway along which the lithium ion takes the first jump over an energy barrier of 6.2 eV on hopping forwards from its departure to an intermediate interstitial site (one stop) 6.66 eV higher in energy that the departure, and then the second jump over a lower energy barrier of 0.5 eV from the intermediate site to the destination, resulting in the migration energy barrier E^f_m = 6.2 eV. The energy landscape of Path 3 has not been changed in the crystal with oxygen vacancies (Fig. 9c); its migration energy barrier is higher (E^f_m = 6.66 eV) than that of the crystal without boron or oxygen vacancies. However, the symmetry of Path 3 is broken in the boron-vacancy crystal (see Fig. 9b); the lithium ion has to jump over an energy barrier as high as 2.5 eV to an interstitial site of almost the same energy as the initial site, and then takes another jump over a lower barrier of 1.7 eV to its destination which is located at a lower energy (about 0.5 eV lower) than the departure, leading to E^f_m = 2.5 eV. Apparently, boron vacancies facilitate the lithium-ion transport along Path 3 while oxygen vacancies inhibit it.

Path 5 also possesses a symmetric and multiple-stop (3 intermediate stops) energy landscape. This landscape is somewhat broken with the presence of oxygen vacancies. The value of E^f_m is a bit lower (E^f_m = 5.1 eV) in the oxygen-vacancy crystal (Fig. 9c) than that (E^f_m = 5.5 eV) in the crystal without boron or oxygen vacancies (Fig. 9a). However, while Path 5 is still symmetric, the number of stops along the pathway is reduced from 3 to 1. Remarkably, boron vacancies reduce the value of E^f_m more than four times, from E^f_m = 5.5 eV to E^f_m = 1.25 eV. Thus, boron vacancies enhance the lithium-ion transport along Path 5 more noticeably than oxygen vacancies.

The energy landscapes of Path 9 in both the crystal without boron or oxygen vacancies and the crystal with oxygen vacancies look quite similar (Fig. 9a and c): they are one-stop migration pathways of the lithium ion, starting with a jump from its departure to an initial site of the same energy level (the only stop) with an energy barrier as low as 0.5 eV, and then another jump from the interstitial site to its destination, encountering a much higher energy barrier, the value of which depends on the crystal with or without boron and oxygen vacancies (E^f_m = 4.0 eV shown in Fig. 9a for the crystal without boron or oxygen vacancies and E^f_m = 6.0 eV shown in Fig. 9c for the crystal with oxygen vacancies). Conversely, the energy landscape of Path 9 is modified dramatically with the presence of boron vacancies in t-LBO. The energy landscape of the pathway becomes an asymmetric two-stop one, and the energy at any point along the pathway is substantially reduced below 2.5 eV. The description of the migration pathway is specified as follows. On hopping forward along Path 9 in the crystal with boron vacancies, the lithium ion takes its first jump from its departure to an interstitial site (the first stop) at an energy level of 1 eV relative to the departure and needs to overcome an energy barrier of approximately 2.1 eV. Next, it jumps from the first interstitial site to the second one with the same energy level as the initial site. On this jump, it needs to overcome another energy barrier of 1.5 eV. Finally, it takes the last jump from the second interstitial site to its destination at an energy level that is 0.4 eV lower than that of the initial site. The energy barrier to overcome for the last jump is approximately 0.75 eV. Overall, the migration energy of the lithium ion migrating along Path 9 in the t-LBO crystal with boron vacancies is E^f_m = 6.0 eV, which is lower than that of the crystal without boron or oxygen vacancies and that of the crystal with oxygen vacancies. Finally, it is worth noting that boron vacancies facilitate lithium transport along Path 9 while the transport is inhibited by oxygen vacancies.

In the crystal without boron and oxygen vacancies of the t-LBO polymorph, the energy landscapes of Path 2 and Path 4, which are nonstop migration pathways of the lithium ion, are respectively the same as shown in Fig. 9a. They are symmetric. The same is seen for the energy landscapes of Path 6 and Path 7. However, they are apparently modified with the presence of either boron (Fig. 9b) or oxygen (Fig. 9b) vacancies. Specifically, in the crystal without boron or oxygen vacancies, Path 2 and Path 4 have the same migration energy barrier of E^f_m = 6.3 eV while Path 6 and Path 7 possess a lower barrier of E^f_m = 5.6 eV. Path 6 and Path 7 still look energetically the same and symmetric in the crystal with boron vacancies even though they are different from those in the crystal without boron or oxygen vacancies. Here boron vacancies lower the value of the migration energy barrier of Path 6 and Path 7 more than twice from E^f_m = 3.5 eV (Fig. 9a) to E^f_m = 1.6 eV (Fig. 9b). In the presence of oxygen vacancies, the energy landscapes of Path 6 and Path 7 are no longer the same and symmetric. The energy barriers in Path 6 and Path 7 are respectively E^f_m = 5.0 eV and E^f_m = 6.0 eV.

Acknowledgements

This work was funded in part by the National Science Foundation Grant No. IIP-2044726 and the University of Missouri Materials Science and Engineering Institute (MUMSEI) Grant No. CD002339. The computation for this work was performed on the high performance computing infrastructure provided by Research Support Services at the University of Missouri, Columbia MO. DOI: https://doi.org/10.32469/10355/97710.

References

1. M. M. Islam, et al., The ionic conductivity in lithium-boron oxide materials and its relation to structural, electronic and defect properties: insights from theory, J. Phys.: Condens. Matter, 2012, 24, 203201.
2. X. Jiang, et al., Anomalous mechanical materials squeezing three-dimensional volume compressibility into one dimension, Nat. Commun., 2020, 11, 5593.
3. I. N. Ogorofnikov, et al., Radiation effects and defects in lithium borate crystals, IOP Conf. Ser.:Mater. Sci. Eng., 2010, 15, 012016.
4. G. Guzman-Gonzalez, et al., Borate-Based Artificial Solid-Electrolyte Interphase Enabling Stable Lithium Metal Anodes, ACS Appl. Mater. Interfaces, 2023, 16(49), 66819–66825.
5. B. Li, et al., A Review of Solid Electrolyte Interphase (SEI) and Dendrite Formation in Lithium Batteries, Electrochem. Energy Rev., 2023, 6, 7.
6. Z. Liua, et al., Functional lithium borate salts and their potential application in high performance lithium batteries, Coord. Chem., 2015, 292, 56–73.
7. D. S. Aidhy, et al., Point defect evolution in Ni, NiFe and NiCr alloys from atomistic simulations and irradiation experiments, Acta Mater., 2015, 99, 69–76.
8. M. Haseman, et al., Neutron irradiation induced defects in oxides and their impact on the oxide properties, J. Appl. Phys., 2021, 129, 215901.
9. Y. You, et al., First-principles investigation of neutron-irradiation-induced point defects in B₄C, a neutron absorber for sodium-cooled fast nuclear reactors, Jpn. J. Appl. Phys., 2018, 57, 055801.
10. G. S. Was, Fundamentals of Radiation Material Science: Metals and Alloys, Springer-Verlag Berlin Heidelberg, 2007.
11. J. Qiu, et al., Effects of neutron and gamma radiation on lithium-ion batteries, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 345, 27–37.
12. C. Tan, et al., Radiation effects on the electrode and electrolyte of a lithium-ion battery, J. Power Sources, 2016, 318, 242–250.
13. E. Hirose, et al., Lithium ionic conductivities of α-LBO₂ with two-dimensional Li-Li networks and γ-LBO₂ with three-dimensional ones synthesized under high pressure, J. Solid State Chem., 2019, 274, 100–104.
14. M. M. Islam, et al., Formation and Mobility of Li Point Defect in LiBO₂: A First-Principles Investigation, J. Phys. Chem. C, 2011, 115, 12343–12349.
15. Y. M. Basalaev, et al., Electronic and Vibrational Properties of LiBO₂ Crystals, Russ. Phys. J., 2019, 61, 1861.
16. S. Zebarjad, et al., Ab-initio Investigation of the Structural Stability, Electronic and Optical Properties of the LiBO₂ Compound by Using the G₀W_O+BSE Approach, Computational Condensed Matter, 2023, 34, e00789.
17. E. Betourne and M. Touboul, Crystallographic data about hydrated and anhydrous lihium momoborates, Powder Diffr., 1997, 12, 155.
18. N. Koga and T. Utsuka, Thermal dehydration of lithium metaborate dihydrate and phase transition of anhydrous product, Thermochim. Acta, 2006, 443, 197–205.
19. S. Gao, et al., Boron Doping and LiBO₂ Coating Synergistically Enhance the High-Rate Performance of LiNi_0.6Co_0.1Mn_0.3O₂ Cathode Materials, ACS Sustainable Chem. Eng., 2021, 9, 5322–5333.
20. Xu-D. Zhang, et al., An effective LiBO₂ coating to ameliorate the cathode/electrolyte interfacial issues of in LiNi_0.6Co_0.2Mn_0.2O₂ solid-state Li batteries, J. Power Sources, 2019, 426, 242–249.
21. Mi Guo, et al., Excellent electrochemical properties of Ni-rich LiNi_0.88Co_0.09Al_0.03O₂ cathode materials co-modified with Mg-doping and LiBO₂-coating for lithium ion batteries, New J. Chem., 2023, 47, 968–2977.
22. B. Ramkumar, et al., LiBO₂-modified LiCoO₂ as an efficient cathode with garnet framework Li_6.75La₃Zr_1.75Nb_0.25O₁₂ electrolyte toward building all-solid-state lithium battery for high-temperature operation, Electrochim. Acta, 2020, 359, 136955.
23. Li Song, et al., Ultrathin and High-Modulus LiBO₂ Layer Highly Elevates the Interfacial Dynamics and Stability of Lithium Anode under Wide Temperature Range, Electrochim. Acta, 2022, 18, 2106427.
24. F. Zheng, Review on solid electrolytes for all-solid-state lithium-ion batteries, J. Power Sources, 2018, 389, 1873.
25. L. Li, et al., Neutron radiation on tin anodes of lithium-ion batteries, Radiat. Eff. Defects Solids, 2018, 173, 1068–1074.
26. M. Takada, et al., Characterization of a real-time neutron detector for boron neutron capture therapy using a thin silicon diode, Radiat. Meas., 2020, 137, 106381.
27. C. A. Maitz, J. D. Brockman, M. Yang, S. Zhang, J. Stannard, D. Volgas and J. M. Gahl, Demonstration of the bactericidal effects of the boron neutron capture reaction, Appl. Radiat. Isot., 2018, 137, 190–193.
28. J. C. Philipps, et al., Polymeric Interlayer Strengthening with Boron Neutron Capture Radiation Treatment for Laminated Glass, Polymers, 2023, 15, 1672.
29. W. H. Jin, et al., A Review of Boron Neutron Capture Therapy: Its History and Current Challenges, International Journal of Particle Therapy, 2022, 9, 71–82.
30. L. Lei, et al., Pressure-induced coordination changes in LiBO₂, J. Solid State Chem., 2009, 182, 3041–3048.
31. P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
33. Ready-to-use files of pseudopotentials for Quantum Espresso Packages weredownloaded from the PSlibraryat https://pseudopotentials.quantum-espresso.org/legacy_tables.
34. D. R. Hamann, M. Schluter and C. Chiang, Norm-Conserving Pseudopotentials, Phys. Rev. Lett., 1979, 43, 1494–1497.
35. Materials Project Database, https://next-gen.materialsproject.org/.
36. R. Fletcher, Practical Methods of Optimization, John Wiley & Sons, New York, 2nd edn, 1987.
37. G. Henkelman and H. Jonsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9978–9985.
38. H. Mehrer, Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-Controlled Processes, Springer-Verlag Berlin Heidelberg, 2007.
39. S. Xu, et al., Lithium transport through lithium-ion battery cathode coatings, J. Mater. Chem. A, 2015, 3, 17248–17272.
40. H. M. Nguyen, C. Ziemke, J. Gahl, Y. Xing, C. Wexler and T. W. Heitmann, Characterization of Lithium Metaborate (LiBO₂) Irradiated with Thermal Neutrons, manuscript in preparation.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta05713a

‡ Authors with equal contributions.

---