Open Access Article
Open Access ArticleCornerstones are the key stones: using interpretable machine learning to probe the clogging process in 2D granular hoppers†
Jesse M.
Hanlan‡
 a,
Sam
Dillavou‡
a,
Sam
Dillavou‡
 a,
Andrea J.
Liu
a,
Andrea J.
Liu
 a and
Douglas J.
Durian
a and
Douglas J.
Durian
 *ab
*ab
aDepartment of Physics & Astronomy, University of Pennsylvania, Philadelphia, PA 19104, USA. E-mail: djdurian@physics.upenn.edu
bDepartment of Mechanical Engineering and Applied Mechanics, University of Pennsylvania, Philadelphia, PA 19104, USA
First published on 16th July 2025
Abstract
The sudden arrest of flow by formation of a stable arch over an outlet is a unique and characteristic feature of granular materials. Previous work suggests that grains near the outlet randomly sample configurational flow microstates until a clog-causing flow microstate is reached. However, factors that lead to clogging remain elusive. Here we experimentally observe over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 clogging events for a tridisperse mixture of quasi-2D circular grains, and utilize a variety of machine learning (ML) methods to search for predictive signatures of clogging microstates. This approach fares just modestly better than chance. Nevertheless, our analysis using linear Support Vector Machines (SVMs) highlights the position of potential arch cornerstones as a key factor in clogging likelihood. We verify this experimentally by varying the position of a fixed (cornerstone) grain, which we show non-monotonically alters the average time and mass of each flow by dictating the size of feasible flow-ending arches. Positioning this grain correctly can even increase the ejected mass by 70%. Our findings suggest a bottom-up arch formation process, and demonstrate that interpretable ML algorithms like SVMs, paired with experiments, can uncover meaningful physics even when their predictive power is below the standards of conventional ML practice.
000 clogging events for a tridisperse mixture of quasi-2D circular grains, and utilize a variety of machine learning (ML) methods to search for predictive signatures of clogging microstates. This approach fares just modestly better than chance. Nevertheless, our analysis using linear Support Vector Machines (SVMs) highlights the position of potential arch cornerstones as a key factor in clogging likelihood. We verify this experimentally by varying the position of a fixed (cornerstone) grain, which we show non-monotonically alters the average time and mass of each flow by dictating the size of feasible flow-ending arches. Positioning this grain correctly can even increase the ejected mass by 70%. Our findings suggest a bottom-up arch formation process, and demonstrate that interpretable ML algorithms like SVMs, paired with experiments, can uncover meaningful physics even when their predictive power is below the standards of conventional ML practice.
Granular flows occur across natural and designed systems at a variety of length scales. Whether the constituent grains are pharmaceuticals,1 pedestrians,2 electron vortices in superconductors3 or agricultural grains,4 the flows are prone to clogging. When the constituent grains pass through an outlet smaller than several grain sizes, a stabilizing arch structure may spontaneously form, preventing further flow. Clogging has been studied extensively in controlled settings (hoppers),5–12 varying parameters such as grain shape, friction, and mechanical stiffness, as well as outlet angle and shape.10,13–16 Nevertheless, signatures of imminent clog formation remain elusive.
There is substantial evidence that flow microstates involving (D/d)n relevant grains near the outlet are sampled randomly until one deterministically leads to a clog.11,12 Here, D/d is the ratio of the outlet diameter to the grain diameter, and n is the dimensionality of the system, indicating that these grains are contained in an area (n = 2) or volume (n = 3) above the outlet, not only in the arch. This model predicts a non-diverging form of average mass ejected per flow event 〈M〉 ∝ exp[(D/d)n], as well as an exponential distribution of ejected masses, both of which match experimental data well.11,12,17–19 Signatures of these clog-forming flow microstates remain unknown, but minimal differences between clogging in air and water suggest that they are primarily determined by grain positions, rather than momenta and contact forces.12
This picture suggests that the structure of clogging microstates is important to the clogging process. Machine learning has been successful in identifying a link between local structure and dynamics in disordered granular systems where particle rearrangements play a key role, such as glassy liquids and granular packings,20 and several types of disordered (granular) solids.21,22 In these works, however, structure was used to predict localized grain-scale rearrangements, which occur frequently throughout the system. In contrast, clogging involves a larger number ∼ (D/d)n of grains, and occurs only once per flow event. This makes the problem both less spatially localized and more difficult to adequately sample.
Here we use machine learning tools to predict clogs from a dataset of over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 flow-to-clogging events obtained using an automated hopper. We analyze positional and momentum flow microstates and find that nonlinear deep learning methods or those that include grain momenta perform only marginally better than linear, grain-position-only methods. All methods completely fail to predict clogging until only a short time prior to clogging (10s of ms, see ESI,† Appendix Predicting Individual Clog Formation), supporting the picture of Poissonian sampling of flow microstates.
000 flow-to-clogging events obtained using an automated hopper. We analyze positional and momentum flow microstates and find that nonlinear deep learning methods or those that include grain momenta perform only marginally better than linear, grain-position-only methods. All methods completely fail to predict clogging until only a short time prior to clogging (10s of ms, see ESI,† Appendix Predicting Individual Clog Formation), supporting the picture of Poissonian sampling of flow microstates.
Within that short time, the predictive accuracy of our simplest model, a linear Support Vector Machine (SVM) given solely positional information, is 58%. This is only marginally higher than random guessing (50%), an unsatisfactory result by prediction and benchmarking standards. Nevertheless, this model identifies the precise location of potential cornerstones of an arch as an important predictor of clogging. We confirm that this correlational observation is causal using experiments with a fixed cornerstone grain. This key grain controls the ejected mass by dictating the range of possible flow-ending arches.
Experimental system & data
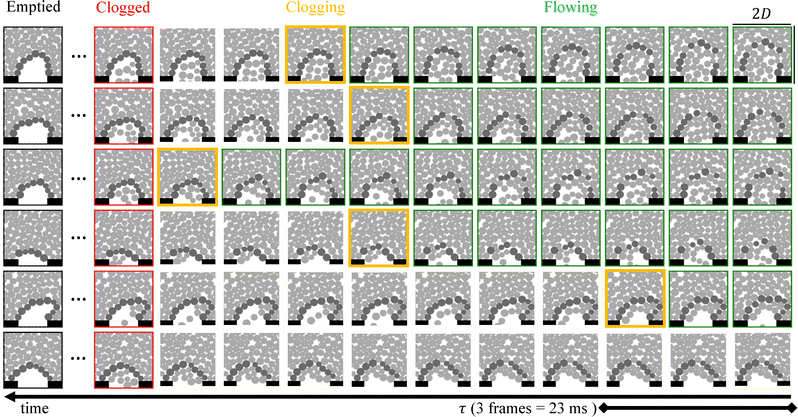
We construct an automated quasi-2D hopper (‘autohopper’), drawn schematically in Fig. 1a, to directly observe the configurations of grains throughout a flow. The transparent vertical hopper is filled with a single layer of tri-disperse discs of diameters dS = 6.0 mm, dM = 7.4 mm, dL = 8.6 mm, which we will refer to as ‘grains’. These grains are laser-cut from anti-static ultra high molecular weight polyethylene (UHMW PE) sheets of mass density ρ = 0.94 g cm−3 and thickness h = 3.18 mm. The spacing between front and rear panes of plexiglass is 4.4 mm so that the grains are free to move but form a monolayer with minimal out of plane displacement. The hopper itself is 22.7 cm wide and 50 cm tall, with fill height of approximately 35 cm.To begin an experiment, an exciter (green in Fig. 1) situated near the outlet vibrates the hopper, dislodging the arch and initiating flow. The grains then flow freely under gravity until a clog spontaneously forms. The region near the outlet is monitored by a digital camera (yellow) at 130 frames per second. The system is considered stably clogged when no grains have exited the hopper for 5 continuous seconds. For each image taken, custom MATLAB code tracks each grain's size (small, medium, large) and location through time to ±σtracking = 0.14 mm precision (0.016dL). This is accomplished prior to starting the next flow, so that tracking data rather than raw video may be written to file to minimize storage requirements. A representation of this process, as well as a stable arch of grains, is shown in Fig. 1b.
Grains that pass through the outlet are directed into a closed loop chute with a blower attached at the base (red in Fig. 1a). An upward airflow recirculates grains to the top of the hopper, removing the need for refilling, and allowing the experiment to continue autonomously without intervention. The air flow is placed sufficiently far and shielded from the outlet such that air currents do not disturb grains in our region of interest, and vents (see Fig. 1a) are placed at the top and sides of the hopper to prevent circulating currents. We perform over 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 experiments in this manner for a single outlet size, D = 3.86dL, and at least one thousand experiments each for D = {3.61, 3.74, 3.98, 4.15}dL, over 7000 total. We additionally perform over 13
000 experiments in this manner for a single outlet size, D = 3.86dL, and at least one thousand experiments each for D = {3.61, 3.74, 3.98, 4.15}dL, over 7000 total. We additionally perform over 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 experiments with a fixed grain and outlet size D = 3.86dL (Fig. 4).
000 experiments with a fixed grain and outlet size D = 3.86dL (Fig. 4).
We confirm a variety of standard granular flow behaviors in ESI,† Appendix Hopper Phenomenology: the distribution of flow events is exponential (Poissonian), the average event size grows exponentially in (D/d)2, and the average discharge rate follows the 2D Beverloo law. The large quantity of data captured with the autohopper presents a wide range of analysis opportunities. For instance, the dataset contains enough flow events to inform a multiplicative noise model that captures the dynamics of the flow rate and the relative stability of arches.23 However, for analysis in this work, we restrict our machine learning dataset to a one outlet size, D = 3.86dL, and use the 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 flows that last at least 0.23 seconds, or 10% of the average flow length. The data for all flows and all outlet sizes is accessible on the Dryad repository.24 We also provide a Python script to automatically create folders of the expected classes described in the following section.25
000 flows that last at least 0.23 seconds, or 10% of the average flow length. The data for all flows and all outlet sizes is accessible on the Dryad repository.24 We also provide a Python script to automatically create folders of the expected classes described in the following section.25
Machine learning analysis
We approach clogging prediction as a classification problem. To do so, we introduce four classes of flow microstates, and construct a labeled dataset as a ground truth. These classes are Flowing, Clogging (flow states leading to a clog), Clogged (a stable arch has formed), and Emptied (all grains have stabilized). By definition these microstates are always experienced in the listed order, though the time spend in each category varies widely. We define these states starting with the emptied state and working backwards. This procedure is described in detail in ESI,† Appendix Labeling and Cleaning Data, and briefly, along with six example flows, in Fig. 2. The three machine learning tasks we attempt are to distinguish Clogging, Clogged, or Emptied microstates from Flowing microstates. We select our definitions to balance the difficulty of the problem; for instance, we want our Clogging states to involve flow so that the problem is not trivial, but not so far before an arch forms that no prediction is possible. We find modifying our definitions by shifting forward or backwards by two frames does not meaningfully affect our results.To be precise, our aim is to use only instantaneous information contained in the microstate (positions, sizes, and momenta of grains) to perform 3 binary classifications to distinguish the Flowing state from the Clogging, Clogged and Emptied states, respectively. Thus, our goal is to produce a binary classification function that takes a microstate Ωi as input, and produces a single number ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) i, which distinguishes between two classes of microstates (e.g.
i, which distinguishes between two classes of microstates (e.g. ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) i > 0 for Clogging, Clogged or Emptied, and
i > 0 for Clogging, Clogged or Emptied, and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) i < 0 for Flowing). We compose a function f with many adjustable parameters
i < 0 for Flowing). We compose a function f with many adjustable parameters  , which we optimize for this purpose using supervised machine learning. Here we assume familiarity with this process, but for an expanded description, see ESI,† Appendix Supervised Machine Learning.
, which we optimize for this purpose using supervised machine learning. Here we assume familiarity with this process, but for an expanded description, see ESI,† Appendix Supervised Machine Learning.
Our trainable functions f in this work are primarily linear Support Vector Machines (SVMs),26 but we also train a Convolutional Neural Network (CNN)27,28 for comparison. We use hinge loss26,29 for the SVMs and crossentropy loss27,28,30 for the CNN, with further training details given in ESI,† Appendices Supervised Machine Learning, SVM Cost Minimization and CNN Reconstruction. We also briefly discuss analysis using Graph Neural Networks (GNNs) in ESI,† Appendix Graph Neural Networks.
In linear SVMs, f takes the form
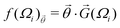 | (1) |
![[G with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0047_20d1.gif) (Ωi) represents a pre-defined feature of microstate i. We have investigated several choices of G and present the most informative, GDG (density grid), below, with other choices described in ESI,† Appendix Alternate Analyses. In short, each GDG measures the grain density in circular windows arranged on a hexagonal grid, as shown in Fig. 3a. More precisely,
(Ωi) represents a pre-defined feature of microstate i. We have investigated several choices of G and present the most informative, GDG (density grid), below, with other choices described in ESI,† Appendix Alternate Analyses. In short, each GDG measures the grain density in circular windows arranged on a hexagonal grid, as shown in Fig. 3a. More precisely, | (2) |
Results
By conventional metrics, our methods perform well separating flowing states from emptied states. However, separating flowing states from either clogged or clogging states proves difficult, reaching classification accuracies only modestly above chance for the latter. Each of these accuracies are listed in Table 1, along with results using other structure functions (GBP), and with added velocity information. We also include results using a far more flexible, nonlinear method, an 830![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 parameter, 35 layer CNN. The details of these additional methods (and several more) are included in ESI,† Appendix Alternate Analyses. Even the most successful method (CNN) is unable to distinguish between Flowing vs. Clogging reliably, with a test accuracy of only 61%. We discuss the limits of such a poor predictor in detail in ESI,† Appendix predicting individual clog formation. Strikingly, accuracies for this task vary by only 4% across these methods. Given this similarity of test accuracy, we focus on the linear SVM that characterizes structure using the density grid. Its simplicity allows us to interpret solutions, and to directly identify structural factors important in clog formation.
000 parameter, 35 layer CNN. The details of these additional methods (and several more) are included in ESI,† Appendix Alternate Analyses. Even the most successful method (CNN) is unable to distinguish between Flowing vs. Clogging reliably, with a test accuracy of only 61%. We discuss the limits of such a poor predictor in detail in ESI,† Appendix predicting individual clog formation. Strikingly, accuracies for this task vary by only 4% across these methods. Given this similarity of test accuracy, we focus on the linear SVM that characterizes structure using the density grid. Its simplicity allows us to interpret solutions, and to directly identify structural factors important in clog formation.
| Method | Clogging (%) | Clogged (%) | Emptied (%) |
|---|---|---|---|
| Linear SVM, GDG | 58 | 70 | 95 |
| Linear SVM, GBP | 57 | 68 | 95 |
| Linear SVM, GDG (+velocity) | 59 | 78 | 99 |
| Convolutional neural network | 61 | 84 | 99 |
The final weights  in the linear SVM have specific spatial importance, that is, they denote the locations in which the presence of a grain correlates with increased likelihood of a given state, for example Clogging. However to understand our solutions, we must visualize not simply the weights, but the average effect this weight has when applied to the training data. Put another way, the features with greatest variance in their contributions σj2 = var[θj × GDGj(Ωi)]trainingset are those with greatest impact on the decision function, and therefore the most important. We plot feature significance αj = sign(qj)σj2 spatially in Fig. 3b–d. A direct comparison between feature weights θ and feature significance α can be found in ESI,† Appendix SVM Cost Minimization.
in the linear SVM have specific spatial importance, that is, they denote the locations in which the presence of a grain correlates with increased likelihood of a given state, for example Clogging. However to understand our solutions, we must visualize not simply the weights, but the average effect this weight has when applied to the training data. Put another way, the features with greatest variance in their contributions σj2 = var[θj × GDGj(Ωi)]trainingset are those with greatest impact on the decision function, and therefore the most important. We plot feature significance αj = sign(qj)σj2 spatially in Fig. 3b–d. A direct comparison between feature weights θ and feature significance α can be found in ESI,† Appendix SVM Cost Minimization.
Despite modest predictive accuracy of the SVM, the feature contributions still give insight into spatial factors of clog formation. First, the prediction of Emptied vs. Flowing states gives an unsurprising feature map in Fig. 3b, where grains (likely falling) in the outlet suggest an emptied state is extremely unlikely. The Clogged vs. Flowing feature significance map in Fig. 3c suggests a relevance of the overall grain density gradient. This may be a means of sensing a slowing flow, occurring at this stage. The fact that velocity information significantly improves the accuracy only of the Clogged prediction fits nicely with this interpretation (see Table 1).
Notably, when predicting clogging states (Fig. 3d) we see high-valued blue and red regions next to each other at the edges of the outlet. This indicates that moving a cornerstone grain slightly to the right or left might change the prediction drastically. These results suggest that the lateral movements of a single grain in this location may have out-sized importance in clog formation. It is this mechanism that we confirm experimentally in the next section. Further discussion of these significance maps, as well as those using the alternative (Behler–Parrinello31) structure functions are included in ESI,† Appendix Alternate Analyses and Fig. S4.
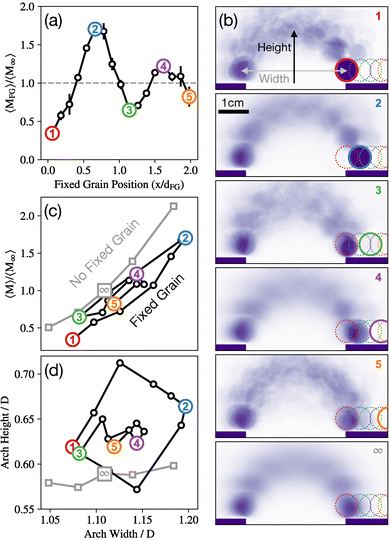
Guided by our machine-learned solutions, we experimentally measure the impact of ‘cornerstone’ grain position. We place a fixed grain (magnet) of diameter dFG = dM on the floor of the hopper near the outlet, as shown by the drawings in Fig. 4a. This grain is held in place by another magnet on the exterior of the hopper. We define its position x to be zero when the grain is centered over the right-hand outlet boundary, and positive when moved to the right (away from the opening). We perform over 7500 experiments with a fixed grain, excluding any flows where we detect any movement of this grain from analysis (fewer than 200).
We find a strong and non-monotonic relationship between the position of the fixed grain x and the resulting average mass flow 〈MFG〉, as shown in Fig. 4a. Strikingly, even when the grain does not obscure the outlet (x > 0.5dFG), its placement may change the average ejected mass by a factor of almost three, including increasing its value above the no fixed-grain case (dashed line in Fig. 4a) by 70%. The mechanisms underlying these effects can be understood by visualizing the average final arch grains at several values of x, as shown in Fig. 4b.
When obscuring the outlet (small x, Fig. 4b1), the fixed grain serves as the cornerstone of the final arches, which are relatively narrow. As x is increased, the region between the cornerstone and outlet becomes excluded space, unable to stably admit another grain, resulting in wider and wider arches (Fig. 4b2) and increased ejected mass. At larger distances from the outlet x > (dFG + dS)/2 ∼ 0.9dFG, the fixed grain allows for free-flowing grains to act as a stable cornerstone, resulting in narrower arches (Fig. 4b3) and reduced ejected mass once again. As x increases further, the fixed grain continues to indirectly dictate cornerstone position, even when it is multiple diameters away from the outlet (Fig. 4b4 and b5). At this stage, the effect of x is reduced, which we attribute to the random availability of differently-sized cornerstones. Overall, we find a clear correlation between average arch width and the average ejected mass, as shown in Fig. 4c. Thus, the non-monotonic dependence of flow rate on fixed grain position x (Fig. 4A) is explained as follows. x affects average arch width non-monotonically due to commensuration effects (Fig. 4B), and arch width monotonically affects average ejected mass 〈M〉. This observation dovetails nicely with the Thomas and Durian model,11 as wider arches require a larger area of grains to cooperate. As a result, there is a smaller likelihood of clogging per sampling time. We find that arches formed in the presence of a fixed grain are slightly wider and significantly taller than those generated without one, as shown in Fig. 4d, perhaps a result of the additional stability of the fixed grain.
Discussion
We have constructed an automated quasi-2D hopper, and performed and analyzed tens of thousands of clogging experiments. By labeling four classes of behavior (Flowing, Clogging, Clogged, Emptied), we cast clogging prediction as a machine learning (ML) classification problem. We have attempted a wide variety of classification methods, including many variations of SVMs, high-dimensional linear regression, several CNNs, and Graph Neural Networks (GNNs). We have also included velocity information, modified the scale of binning of features, and more. Methods not included in the main text are described in detail in ESI,† Appendix Alternate Analyses. CNNs are the most successful (61% prediction accuracy) but are not appreciably better at distinguishing flowing from clogging states than our linear SVM (58% prediction accuracy). Neither of these does much better than random guessing (50%). We note that ML is typically recommended for problems in which data is plentiful. But there are many condensed matter systems like ours, in which phenomena of interest depend on a very large number of relevant microscopic parameters, not all of which are known. For these systems, experimental data is usually far too sparse to cover that high-dimensional space. So perhaps it is not surprising that, by usual prediction or benchmarking standards, we fail to predict imminent clogs. Further, it is possible that the information required to accurately predict clogs is simply not contained in the images fed to our models. This is in contrast to standard ML problems where the information is definitively present (e.g. distinguishing cats and dogs). We note that our model predictions began to achieve their reported accuracy with approximately 10 times less data than was used in this study, potentially suggesting that our dataset provides no useful information beyond that scale.Of course, our numerous attempts do not prove there is no better solution, and we encourage other researchers to try their hand in improving upon our benchmarks. To facilitate such a competition we make our data available at.24 Additionally, we have detailed a variety of alternative analyses on this data and potential pitfalls in ESI,† Appendix Future Directions. One notable pitfall is the imposition of too much coarse-graining, including prematurely enforcing symmetries, even those imposed by the boundary conditions (such as left/right symmetry). In optimization problems it is often helpful to have additional degrees of freedom to find the solution, even if they are ultimately not required.32 We note that our models were trained only on one outlet size, making it prudent for them to ignore the (unchanging) outlet pixels and thus unlikely that any will generalize. However, our physical understanding of the SVM predictions (Fig. 4) suggests that models able to capture cornerstone position relative to the outlet (e.g. a CNN) could predict similarly well across outlet sizes, if provided the right training data.
In this study we ran headlong into another inherent limitation of ML analysis besides its voracious need for data. Because finding good solutions often requires over-parameterization,32 solution weights  typically contain spurious variation; therefore, one can only claim that predictive information is present somewhere in the data. This type of claim is not without its scientific uses,33 however it does not, in itself, provide mechanistic understanding. Moreover, ML analyses (Fig. 3) are correlational, meaning that even high prediction accuracy provides an insufficient basis for any causal claims.
typically contain spurious variation; therefore, one can only claim that predictive information is present somewhere in the data. This type of claim is not without its scientific uses,33 however it does not, in itself, provide mechanistic understanding. Moreover, ML analyses (Fig. 3) are correlational, meaning that even high prediction accuracy provides an insufficient basis for any causal claims.
Despite this, we have uncovered new physics. In particular, by inspecting the features of greatest significance in our simplest method, a linear Support Vector Machine (SVM), we were able to identify that grains in the region immediately adjacent to the outlet are potentially critical to the onset of clog formation. To test this hypothesis directly, we performed a series of experiments with fixed grains in this key position. While many studies have modified outlet width, angle, and/or shape,5,10–16,34,35 or added ‘floating’ obstacles above the outlet,36,37 our experiments are distinct in that they sample a subspace of plausible positional microstates when no fixed grain is present. This allows us to probe the enormously high-dimensional dynamics of clog formation efficiently. For instance, it allows us to make some rare states (e.g. the wide arches in Fig. 4b2), common, and therefore far easier to study. Further, our method allows us to make causal claims about key grains affecting clog formation, which is unlike perturbing or analyzing already-stable arches,23,38,39 where only counterfactual arguments about formation may be made (e.g. were this arch to form differently, it wouldn't clog).
These experiments showed that the position of the ‘cornerstone’ grain has a large effect on ejected mass, potentially increasing it by 70%. Finally, we found that this relationship stems from the cornerstone grain's ability to dictate the size of final arches, and thus the clogging likelihood. Our results suggest a two-step process for clog formation. First, the base grains dictate the available space of stable arches, whose ultimate widths do not vary dramatically (see Fig. 4b). Second, grain microstates are sampled until one forms a clog, with likelihood monotonically decreasing with arch width (see Fig. 4c). The first step (base width) is continually resampled during a flow, resulting in draws from the probability distributions in the second step (arch formation) at width-dependent rates.
Conclusions
These results have implications for practical hopper design, and suggest a rich set of open questions about this and other granular-flow systems. For instance, our system (and others like it) encounters meta-stable arches frequently, only to spontaneously resume flow.23 Might portions of the outlet region be continually finding rigid substructures, only to have them fall apart due to lack of cooperation? Does limiting the subspace of possible arches (Fig. 4b) explain other non-monotonic dependencies in similar systems, such as mass ejected as a function of silo width (not outlet width)?40 In a larger view, what is the relative importance of microstate sampling (finding an arch) vs. arch stability? Further work with multiple fixed grains might prove useful here, by limiting the arch structures available. Such experiments might also allow more detailed investigation of the “second step” discussed above, where perhaps the second layer of grains selected in an arch also obeys an observable probability distribution.In sum, our results give causal insight into clogging, a rare, nonlinear, collective event that is influenced by poorly understood processes like frictional aging.33 This provides a heartening lesson for utilizing machine learning in scientific exploration: even when ML methods fail to make accurate predictions, their ability to find high-dimensional correlations can guide experiments on a broad range of complex phenomena across many fields.
Author contributions
All authors designed research; S. D. performed experiments; J. M. H. and S. D. contributed new analytic tools; J. M. H. and S. D. analyzed data; all authors wrote the paper.Conflicts of interest
There are no conflicts to declare.Data availability
The data for all flows and all outlet sizes is accessible on the Dryad repository at https://doi.org/10.5061/dryad.cvdncjtb5 (link not yet live). We also provide a Python script on Zenodo to automatically create folders of the expected classes at https://doi.org/10.5281/zenodo.10895419 (link not yet live).Acknowledgements
We thank Kieran A. Murphy for helpful discussions. This work was partially supported by NSF grants DMR-1619625, MRSEC/DMR-1720530 and MRSEC/DMR-2309043, and the Simons Foundation grant #327939. SD acknowledges support from the University of Pennsylvania School of Arts and Sciences' Data Driven Discovery Initiative. AJL and DJD thank the Center for Computational Biology at the Flatiron Institute, a division of the Simons Foundation, as well as the Isaac Newton Institute for Mathematical Sciences under the program “New Statistical Physics in Living Matter” (EPSRC grant EP/R014601/1), for support and hospitality while a portion of this research was carried out. Portions of the paper were co-developed in the thesis ‘Interplay Between Structure and Dynamics in Granular Materials and Twisted Strings' by Dr Jesse Hanlan.Notes and references
- R. M. Nedderman, U. Tuzun, S. B. Savage and G. T. Houlsby, Chem. Eng. Sci., 1982, 37, 1597–1609 CrossRef CAS.
- D. Helbing, I. Farkas and T. Vicsek, Nature, 2000, 407, 487–490 CrossRef CAS PubMed.
- C. J. Olson Reichhardt and C. Reichhardt, J. Supercond. Novel Magn., 2013, 26, 2005–2008 CrossRef CAS.
- I. Zuriguel, D. R. Parisi, R. C. Hidalgo, C. Lozano, A. Janda, P. A. Gago, J. P. Peralta, L. M. Ferrer, L. A. Pugnaloni, E. Clément, D. Maza, I. Pagonabarraga and A. Garcimartín, Sci. Rep., 2014, 4, 7324 CrossRef CAS PubMed.
- K. To, P. Y. Lai and H. K. Pak, Phys. Rev. Lett., 2001, 86, 71–74 CrossRef CAS PubMed.
- F. Alonso-Marroquin and P. Mora, Granular Matter, 2020, 23, 7 CrossRef.
- R. Caitano, B. Guerrero, R. Gonzalez, I. Zuriguel and A. Garcimartin, Phys. Rev. Lett., 2021, 127, 148002 CrossRef CAS PubMed.
- A. Janda, I. Zuriguel, A. Garcimartín, L. A. Pugnaloni and D. Maza, Eur. Lett., 2008, 84, 44002 CrossRef.
- A. Janda, I. Zuriguel, A. Garcimartín and D. Maza, Granular Matter, 2015, 17, 545–551 CrossRef CAS.
- A. Hafez, Q. Liu, T. Finkbeiner, R. A. Alouhali, T. E. Moellendick and J. C. Santamarina, Sci. Rep., 2021, 11, 3309 CrossRef CAS PubMed.
- C. C. Thomas and D. J. Durian, Phys. Rev. Lett., 2015, 114, 178001 CrossRef CAS PubMed.
- J. Koivisto and D. J. Durian, Phys. Rev. E, 2017, 95, 032904 CrossRef PubMed.
- T. Pongó, V. Stiga, J. Török, S. Lévay, B. Szabó, R. Stannarius, R. C. Hidalgo and T. Börzsönyi, New J. Phys., 2021, 23, 023001 CrossRef.
- X. Hong, M. Kohne, M. Morrell, H. Wang and E. R. Weeks, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 062605 Search PubMed.
- R. Tao, M. Wilson and E. R. Weeks, Phys. Rev. E, 2021, 104, 044909 CrossRef CAS PubMed.
- K. Harth, J. Wang, T. Börzsönyi and R. Stannarius, Soft Matter, 2020, 16, 8013–8023 RSC.
- K. To, Phys. Rev. E, 2005, 71, 060301 CrossRef PubMed.
- I. Zuriguel, A. Garcimartín, D. Maza, L. Pugnaloni and J. Pastor, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 051303 Search PubMed.
- J. Tang, S. Sagdiphour and R. P. Behringer, AIP Conf. Proc., 2009, 1145, 515–518 CrossRef.
- E. Cubuk, S. Schoenholz, J. Rieser, B. Malone, J. Rottler, D. Durian, E. Kaxiras and A. Liu, Phys. Rev. Lett., 2015, 114, 108001 CrossRef CAS PubMed.
- E. D. Cubuk, R. J. S. Ivancic, S. S. Schoenholz, D. J. Strickland, A. Basu, Z. S. Davidson, J. Fontaine, J. L. Hor, Y.-R. Huang, Y. Jiang, N. C. Keim, K. D. Koshigan, J. A. Lefever, T. Liu, X.-G. Ma, D. J. Magagnosc, E. Morrow, C. P. Ortiz, J. M. Rieser, A. Shavit, T. Still, Y. Xu, Y. Zhang, K. N. Nordstrom, P. E. Arratia, R. W. Carpick, D. J. Durian, Z. Fakhraai, D. J. Jerolmack, D. Lee, J. Li, R. Riggleman, K. T. Turner, A. G. Yodh, D. S. Gianola and A. J. Liu, Science, 2017, 358, 1033–1037 CrossRef CAS PubMed.
- H. Xiao, G. Zhang, E. Yang, R. Ivancic, S. Ridout, R. Riggleman, D. J. Durian and A. J. Liu, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2307552120 CrossRef CAS PubMed.
- D. Hathcock, S. Dillavou, J. M. Hanlan, D. J. Durian and Y. Tu, Phys. Rev. E, 2025, 111, L023404 CrossRef CAS PubMed.
- Data for Cornerstones are the Key Stones, 2024, https://doi.org/10.5061/dryad.cvdncjtb5 (link not yet live).
- Scripts for Cornerstones are the Key Stones, 2024, https://doi.org/10.5281/zenodo.10895419 (link not yet live).
- C. J. Burges, Data Min. Knowl. Discov., 1998, 2, 121–167 CrossRef.
- Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444 CrossRef CAS PubMed.
- Z. Li, F. Liu, W. Yang, S. Peng and J. Zhou, IEEE Trans. Neural Netw. Learn. Syst., 2022, 33, 6999–7019 Search PubMed.
- L. Rosasco, E. D. Vito, A. Caponnetto, M. Piana and A. Verri, Neural Comput., 2004, 16, 1063–1076 CrossRef PubMed.
- P.-T. de Boer, D. P. Kroese, S. Mannor and R. Y. Rubinstein, Annal. Operat. Res., 2005, 134, 19–67 CrossRef.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- R. Schaeffer, M. Khona, Z. Robertson, A. Boopathy, K. Pistunova, J. W. Rocks, I. R. Fiete and O. Koyejo, Double Descent Demystified: Identifying, Interpreting & Ablating the Sources of a Deep Learning Puzzle, 2023.
- S. Dillavou, Y. Bar-Sinai, M. P. Brenner and S. M. Rubinstein, Phys. Rev. E, 2022, 106, L033001 CrossRef CAS PubMed.
- R. Arévalo and I. Zuriguel, Soft Matter, 2015, 12, 123–130 RSC.
- P. A. Gago, M. A. Madrid, S. Boettcher, R. Blumenfeld and P. King, Powder Technol., 2023, 428, 118842 CrossRef CAS.
- D. Gella, D. Yanagisawa, R. Caitano, M. V. Ferreyra and I. Zuriguel, Commun. Phys., 2022, 5, 1–7 CrossRef.
- I. Zuriguel, A. Janda, A. Garcimartín, C. Lozano, R. Arévalo and D. Maza, Phys. Rev. Lett., 2011, 107, 278001 CrossRef PubMed.
- C. Lozano, G. Lumay, I. Zuriguel, R. C. Hidalgo and A. Garcimartín, Phys. Rev. Lett., 2012, 109, 068001 CrossRef PubMed.
- C. Lozano, I. Zuriguel and A. Garcimartín, Phys. Rev. E, 2015, 91, 062203 CrossRef CAS PubMed.
- D. Gella, D. Maza, I. Zuriguel, A. Ashour, R. Arévalo and R. Stannarius, Phys. Rev. Fluids, 2017, 2, 084304 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00367a |
| ‡ J. M. H. and S. D. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |