Pronounced effect of strain biaxiality on high-temperature behavior of strain-crystallizing elastomers

Abstract

We investigate the impact of strain biaxiality on strain induced crystallization (SIC) at elevated temperatures in natural rubber (NR) and synthetic isoprene rubber (IR). By comparing uniaxial (U) and pseudo-planar (P) stretching under different lateral contraction conditions, we find that the upper-limit ambient temperature for SIC-induced reinforcement in the P-geometry is more than 20 °C lower than in the U-geometry. Similarly, the melting temperature of SIC crystallites in the P-geometry is reduced by over 30 °C compared to the U-geometry. These findings demonstrate that finite lateral stretch significantly suppresses both the onset temperature and thermal stability of SIC-induced reinforcement. Our results reveal that strain biaxiality plays a pivotal role in SIC not only at room temperature, as previously recognized, but also under high temperature conditions. These strain biaxiality effects are more pronounced in IR than in NR. Furthermore, elevated-temperature fracture experiments reveal a non-linear crack propagation pattern in the P-geometry: local deformation transitions from planar to pseudo-uniaxial toward the specimen edge, where higher crystallinity forms a barrier. Cracks bifurcate to circumvent these regions, highlighting the critical role of spatial SIC heterogeneity in fracture resistance. Our results offer valuable insights into SIC mechanisms and contribute to the development of SIC-rubber materials with enhanced durability under complex deformation and high-temperature conditions.

---

Introduction

Strain induced crystallization (SIC) has garnered significant attention as an effective toughening mechanism for soft materials.^1–3 The exceptional resistance of natural rubber (NR) against crack growth is primarily attributed to the SIC capability of its constituent cis-1,4-polyisoprene.^4–8 Under strain, significant stress concentration around crack tips causes SIC, and the resulting crystalline region acts as barriers to crack propagation.^9–14 This gives NR and other strain-crystallizing rubbers a notable advantage over non-crystallizing rubbers. Recent studies have further demonstrated that SIC-driven mechanical reinforcement can occur even in polymer gels with high solvent content.^15,16

Most studies on SIC and its toughening effects have focused on uniaxial stretching as the primary deformation mode.^6,17–22 However, uniaxial stretching is only a subset of accessible deformation scenarios.^23–25 Despite its significance, SIC behavior under biaxial stretching has been considerably less explored. Studies using independent biaxial stretching²⁶ or complex deformation scenarios including local biaxial loading²⁷ have commonly reported that, at the same longitudinal stretch, crystallinity decreases as transverse stretch increases. These findings highlight the critical role of orientation anisotropy in the biaxial loading plane, in addition to the total configurational entropy reduction of stretched network strands. Furthermore, comparisons between SIC crystals formed via uniaxial and planar stretching—where lateral contraction is suppressed due to specimen geometry—reveal structural differences: planar-stretching-induced SIC crystals exhibit plane orientation, whereas uniaxial stretching results in cylindrical symmetry.^28,29 Notably, these studies have primarily been conducted at or near room temperature.

Ambient temperature (T) significantly influences SIC, primarily due to its effects on SIC kinetics. This is also practically relevant, as rubber products are often subjected to service conditions well above room temperature. In general, increasing T retards SIC kinetics, reducing the degree of SIC. Previous studies have reported that both the tensile strength and fracture resistance of NR decline with increasing T, and that the mechanical reinforcement associated with SIC disappears at sufficiently high T.^21,22,30,31 These studies also revealed that the threshold strain required for SIC initiation decreases with decreasing T.^21,22 The influence of cross-link density on SIC kinetics has also been examined in terms of the T dependence of crystallite formation and melting behavior.²¹ Additionally, the thermal stability of SIC crystals formed at lower T has been investigated.^32–35 It was shown that, upon heating, the crystalline c-axis contracts while the a- and b-axes expand, resulting in an increased lattice volume and reduced crystallinity. However, most previous studies on the T dependence of SIC have focused exclusively on uniaxial stretching as the triggering mechanism. To the best of the author's knowledge, the effects of strain biaxiality on SIC initiation and crystallite stability at elevated temperatures remain largely unexplored.

In this study, we investigate SIC behavior at high temperatures under uniaxial (U) and pseudo-planar (P) stretching, each with different lateral contraction conditions, for NR and synthetic polyisoprene rubber (IR). In the P-geometry, a sufficiently wide sheet specimen is stretched along its short axis, leading to planar stretching with no lateral contraction in most areas (with no lateral contraction), while regions near free edges experience pseudo-uniaxial stretching. We demonstrate that the maximum ambient temperature at which SIC-induced reinforcement occurs is significantly lower in the P-geometry than in the U-geometry. Furthermore, SIC crystallites formed at room temperature exhibit a substantially lower melting temperature in the P-geometry compared to the U-geometry. These effects of stretching geometry on SIC at elevated temperatures are more pronounced in IR than NR. Interestingly, this strain-biaxiality effect on thermal stability of SIC crystallites leads to a characteristic crack-propagation pattern at fracture in the P-geometry at high temperatures. These results reveal the pronounced suppression effect of lateral stretch on SIC-induced reinforcement and stability at elevated temperatures. Our findings contribute to a more comprehensive understanding of SIC toughening mechanisms and provide insights for designing SIC-reinforced rubber materials capable of withstanding high-temperature conditions.

Experimental section

Materials and sample preparation

Natural rubber (NR; ribbed smoked sheet, RSS#3) and its synthetic analogue, cis-1,4-polyisoprene rubber (IR; IR2200, ENEOS Material Co.), were used to prepare the specimens. Sulfur was used as the cross-linker agent, with a concentration of 1.5 g per 100 g of gum rubber. The vulcanization process followed the method detailed in a previous study.^13,36 Rubber sheet specimens (175 × 20 × 1 mm) were fabricated using a hot press method with a specially designed metal mold at 160 °C. To prevent slippage at the grips, the specimens featured cylindrical bifurcated ends (Fig. 1).

Fig. 1 Schematic illustration of two stretching geometries. (a) Uniaxial stretching (U) geometry: A rectangular specimen is stretched along its long axis, leading to conventional uniaxial deformation. (b) Pseudo-planar stretching (P) geometry: A wide rubber sheet specimen is stretched along its short axis. Due to its width, lateral contraction is suppressed in the central region, leading to a nearly planar deformation. However, regions near the free edges experience partial lateral contraction, resulting in a continuous transition from planar to uniaxial stretching, as shown in Fig. 2.

Stretching geometries and mechanical testing at high temperatures

Two distinct stretching geometries were employed: uniaxial (U) stretching and pseudo-planar (P) stretching. In the P-geometry, wide specimens were stretched along their short (y) axis (Fig. 1), resulting in predominantly planar stretching without lateral shrinkage, except near the free edges. In the U-geometry (conventional uniaxial stretching), rectangular specimens (5 × 20 × 1 mm), cut out from the wide sheets, were employed. Tensile tests were conducted at ambient temperatures ranging from 25 °C to 120 °C using a Shimadzu AGS-X universal tensile tester equipped with a temperature- controlled chamber. The crosshead speed was set at 0.05 mm s⁻¹, corresponding to an initial strain rate of 0.0025 s⁻¹, slow enough to minimize stress relaxation effects during stretching.

To evaluate the thermal stability of the SIC crystals formed at low temperatures, we conducted the following tests. Firstly, the specimens were elongated at 25 °C to a predefined stretch ratio (Λ_y⁰ = 6 or 7) at a sufficiently slow strain rate, ensuring negligible stress relaxation during stretching. The selected Λ_y⁰ values were well beyond the SIC threshold. Subsequently, while maintaining the stretched state at Λ_y⁰, the ambient temperature (T) was increased at a rate of 2 °C min⁻¹. The temperature at which the stretched specimen fractured macroscopically was regarded as the melting temperature of primary SIC crystallites (T_m,SIC), representing the temperature at which the networks with SIC crystals could no longer sustain macroscopic stress.

Strain distribution analysis via digital image correlation (DIC)

2D strain distributions during the P-geometry stretching at 25 °C were characterized using digital image correlation (DIC).³⁷ Random speckle patterns for strain analysis were applied to the sample surface using a water-soluble ink, which does not affect the mechanical properties of rubber specimens. The details of the DIC setup and analysis conditions were provided in previous papers.^12,38

Evaluation of SIC evolution via heat emission measurement

Evolution of SIC during stretching was evaluated at 25 °C by measuring the associated heat emission. The 2D distribution of surface temperature rise (ΔT) was recorded using a SPARK M150 infrared camera (Teplos) at 200 Hz. To minimize heat dissipation effects, the maximum cross-head speed of the tensile tester (15 mm s⁻¹) was employed during these experiments. The ΔT-strain data were converted to adiabatic heat source (s)-strain data using an established method that accounts for heat dissipation and entropy-driven heat emission.^39,40 The degree of crystallinity (χ) was evaluated from the s values associated with SIC excluding minor contributions via entropy-driven heat emission. The protocol for this method is detailed in previous papers^27,39,40 and in the ESI.†

Results and discussion

SIC in the U- and P-geometries at room temperature

Fig. 2a and b present the 2D distributions of local longitudinal (λ_yy) and lateral (λ_xx) principal stretch ratios, obtained via digital image correlation (DIC) at a macroscopic nominal stretch of Λ_y = 7.0 under the P-geometry for the NR specimen. The stretch ratios λ and Λ are defined as the dimensional ratios in the deformed state, with λ = Λ = 1 in the undeformed state. In the observed region, λ_yy is uniform and λ_yx remains nearly zero, indicating negligible shear. The data of λ_yx are shown in Fig. S1 in ESI.† Across the observed area, λ_xx gradually decreases from unity toward values below one as the position shifts from the center to the free edges. This trend is consistently observed at every Λ_y, as shown in the 1D distributions of λ_xx along the central horizontal line (depicted as the yellow dashed line) (Fig. 2b). This variation of λ_xx near the edges reflects a transition in local deformation from planar to pseudo-uniaxial stretching. Furthermore, the 1D distribution of the true strain ratio, defined as μ_yx = −ln λ_xx/ln λ_yy, along the central horizontal line remains unchanged with respect to Λ_y (Fig. 2c). This suggests a stable local deformation distribution throughout stretching. The variation of μ_yx is dominated by a change in λ_xx since λ_yy is uniform across the specimen as shown in Fig. 2a. Notably, μ_yx = 0 corresponds to pure planar stretching with no lateral shrinkage, while μ_yx = 0.5 represents uniaxial stretching in incompressible materials.

Fig. 2 Strain distribution in a NR specimen under P-stretching at a macroscopic stretch of Λ_y = 7. Two-dimensional distributions of (a) longitudinal (λ_yy) and (b) lateral (λ_xx) principal stretch ratios, and (c) true-strain ratio (μ_yx), defined as the ratio of longitudinal to lateral true (Cauchy) strain. The corresponding 1D profiles of λ_yy and λ_xx along the central horizontal line of the specimen as a function of Λ_y.

To investigate the evolution of SIC in each geometry at 25 °C, we measured heat emission during stretching. Fig. 3a shows thermographic images of an NR specimen under P-geometry stretching, while Fig. 3b plots the temperature rise (ΔT) at the central position as a function of Λ_y. A sharp increase in ΔT is observed once Λ_y exceeds the SIC onset threshold (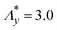 and 2.9 in the U and P geometries, respectively), as determined via wide angle X-ray scattering (WAXS).^12,36 The measured ΔT-Λ_y data are converted into adiabatic heat source (s)-Λ_y relationships, accounting for finite heat dissipation through an established heat diffusion analysis.^27,39,40Fig. 3c illustrates the crystallinity (χ) calculated from these s-λ_yy relationships after excluding minor contributions via entropy drive heat emission (see ESI† for evaluation details). The crystallinity in the P-geometry is lower than in the U-geometry at the same Λ_y, despite their similar 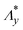values. This indicates that finite lateral stretch suppresses SIC growth relative to the U-geometry. The trend is further supported by the ΔT distributions along the central horizontal line in the P-geometry (Fig. 3d): at a given Λ_y, χ increases as local deformation shifts from planar to pseudo-uniaxial stretching (Fig. 3e and f). It should be noted that the position-dependence of χ at a given Λ_y is governed by that of μ_yx rather than longitudinal local stretch (λ_yy) since λ_yy is constant along the x-axis at each Λ_y (Fig. 2a). Fig. 3g illustrates χ as a function of λ_yy during stretching at the selected positions with different magnitudes of μ_yx, confirming again that χ depends on not only λ_yy but also μ_yx: χ becomes larger with increasing μ_yx at a given λ_yy. The similar trend was observed in the IR specimens. The figures corresponding to Fig. 3b–e for the IR specimens are shown in Fig. 4a–d. These results for the NR and IR specimens indicate that SIC benefits from higher anisotropy in the loading (xy) plane, consistent with trends observed in heterogeneous deformation scenarios²⁷ and WAXS measurements under independent biaxial stretching.²⁶

Fig. 3 Thermal response and SIC in a NR specimen under P-geometry stretching. (a) Thermographic images during P-geometry stretching. (b) Surface temperature rise (ΔT) and (c) degree of crystallinity (χ) as a function of macroscopic stretch (Λ_y) in the U- and P-geometries. The data for the P-geometry were obtained at the central specimen position. The SIC onset stretch for each geometry determined by WAXS tests is indicated. 1D distributions of (d) ΔT and (e) χ along the central horizontal line during P-geometry stretching. Half of the total area is shown due to symmetry. (f) Correlation between χ and the true-strain ratio μ_yx at various positions along the central horizontal line as a function of Λ_y. (g) χ as a function of local longitudinal stretch (λ_yy) at selected positions with different levels of μ_yx.

Fig. 4 Thermal response and SIC in a IR specimen under P-geometry stretching. (a) Surface temperature rise (ΔT) and (b) degree of crystallinity (χ) as a function of macroscopic stretch (Λ_y) in the U- and P-geometries. The data for the P-geometry were obtained at the central specimen position. The SIC onset stretch for each geometry determined by WAXS tests is indicated. 1D distributions of (c) ΔT and (d) χ along the central horizontal line during P-geometry stretching. Half of the total area is shown due to symmetry.

Our earlier study²⁷ employing the same methodology in P-geometry showed that reducing the crosshead speed to 1.5 mm s⁻¹—ten times slower than the current 15 mm s⁻¹—resulted in less than 1% variation in χ at each position, even though the associated ΔT was smaller due to enhanced heat dissipation. This finding indicates that, within the tested range, the strain rate has a negligible influence on SIC. It also confirms that lateral heat transfer between adjacent regions does not significantly impact the localized heat emission detected under our experimental conditions.

Maximum ambient temperature for SIC-induced reinforcement in the U- and P-geometries

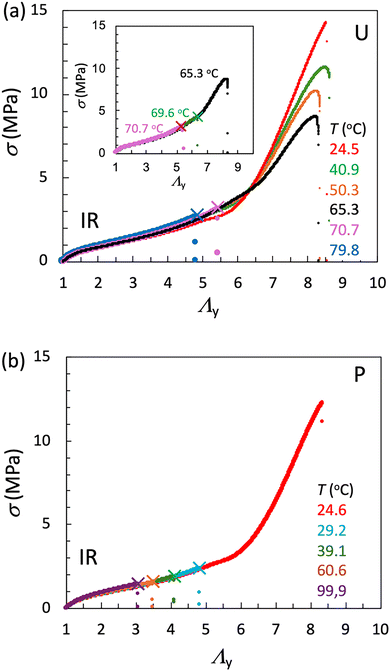
At elevated temperatures, SIC kinetics slow down, diminishing its mechanical reinforcement effect.^21,22,30,31Fig. 5a and b display nominal stress (σ)-Λ_y curves at various ambient temperatures (T) for NR specimens in the U- and P-geometries, respectively. In the U-geometry (Fig. 5a), a pronounced stress upturn due to SIC at high Λ_y is observed up to 85 °C. However, this feature disappears beyond 90 °C, indicating that the upper-limit ambient temperature for SIC-induced reinforcement (denoted as T*) lies between these temperatures. Similar T-dependent behavior for NR or IR was observed in several studies.^{21,22,30,32–34} Notably, the P-geometry exhibits no SIC-induced stress upturn even at 65 °C (Fig. 5b), indicating that T* is over 20 °C lower than in the U-geometry. A similar trend is observed in a vulcanized synthetic isoprene rubber (IR) (Fig. 6a and b), where T* is approximately 65 °C in the U-geometry but only about 30 °C in the P-geometry. This significantly lowering of T* in the P-geometry for both NR and IR confirms that lateral stretch strongly suppresses the evolution of SIC. Furthermore, NR exhibits a higher T* than IR within the same tensile geometry. This difference is likely due to a more stabilized pseudo-network structure formed via inherent functional end group associations in isoprene chains of NR.^{18,20,41–43}

Fig. 5 Stress response under different stretching geometries and ambient temperatures for NR specimens. (a) Nominal stress (σ) as a function of applied stretch (Λ_y) in (a) U- and (b) P-stretching at various ambient temperatures. The insets represent the magnifications of σ-Λ_y curves at moderate stretch values. The temperature at which the SIC-induced stress upturn vanishes corresponds to the maximum ambient temperature for SIC-induced reinforcement (T*). To avoid the data overlapping, the σ-Λ_y curves at T near T* are shown in the insets. Notably, T* in the P-geometry is more than. 20 °C lower than in the U-geometry.

Fig. 6 Stress response under different stretching geometries and ambient temperatures (T) for IR specimens. (a) Nominal stress (σ) as a function of applied stretch (Λ_y) in (a) U- and (b) P-stretching at various ambient temperatures. The insets represent the magnifications of σ-Λ_y curves at moderate stretch values. The temperature at which the SIC-induced stress upturn vanishes corresponds to the maximum ambient temperature for SIC-induced reinforcement (T*). To avoid the data overlapping, the σ-Λ_y curves at T near T* are shown in the insets. Notably, T* in the P-geometry is more than 30 °C lower than in the U-geometry.

In this study, we define T* based on the disappearance of the characteristic stress upturn (strain hardening), which signals the effective onset of SIC-induced mechanical reinforcement. While prior studies^5–7,22,34 have shown that the onset strain for SIC crystallite formation is generally lower than the strain at which the stress upturn appears, the close correlation between these thresholds justifies the use of T* as a practical criterion for the upper temperature limit of SIC-induced reinforcement.

Thermal stability of SIC crystallites in the U- and P-geometries

Thermal stability of SIC crystallites in each stretching geometry was examined via fracture temperature analysis on specimens subjected to high stretch at 25 °C. The specimens were stretched to a predefined stretch ratio at 25 °C in each geometry, and then gradually heated at a controlled rate (2 °C min⁻¹) while maintaining Λ_y = Λ_y0. Fig. 7a plots nominal stress (σ) at Λ_y⁰ = 6 as a function of ambient temperature (T) in the U- and P-geometries for the NR specimen. In general, for amorphous isotropic elastomers, the presence of lateral constraint in the P-geometry leads to a higher σ compared to the U-geometry at the same longitudinal stretch, due to the geometric constraint. However, the results in Fig. 7a do not follow this expectation; σ values in the P-geometry remain comparable to those in the U-geometry. This deviation is attributed to the lower crystallinity in the P-geometry (Fig. 3c). Heating initially causes a slight decrease in σ, counteracting the expected increase from entropic elasticity. This behavior is due to the partial melting of micro-crystallites with lower melting temperatures. The nearly identical σ values observed in both geometries across the examined temperature range appear coincidental. In general, σ in the P-geometry could be smaller than that in the U-geometry if the crystallinity reduction were more pronounced than in the present case.

Fig. 7 Thermal stability at SIC at constant stretch. Nominal stress (σ) at a fixed stretch of Λ_y⁰ as a function of ambient temperature (T) for (a) NR and (b) IR specimens in U- and P-geometries. The heating rate is 2 °C min⁻¹ from 25 °C to a fracture temperature. The arrows indicate the fracture temperature during the heating process.

Continued heating eventually leads to macroscopic fracture at a temperature defined as T_m,SIC, marking the melting of primarily SIC crystallites responsible for bearing load: T_m,SIC is approximately 90 °C in the P-geometry and 109 °C in the U-geometry. Notably, the fracture stretch near T_m,SIC in both geometries is below 4 (see Fig. 5), significantly lower than Λ_y⁰ = 6 used in Fig. 7a. This discrepancy arises because the maximum ambient temperature for SIC reinforcement (T*) is much lower—around 90 °C in the U-geometry and 65 °C in the P-geometry—than T_m,SIC. These results indicates that SIC crystallites effectively sustain macroscopic stress at T < T_m,SIC and Λ_y⁰ = 6. Further verification comes from the swelling experiments in toluene. No change in swelling degree was observed before and after fracture at T_m,SIC, confirming that the fracture results from melting of SIC crystallites rather than network chain scission or thermal degradation.

A similar trend is observed in IR specimens stretched at Λ_y⁰ = 6 and 7 (Fig. 7b). In both cases, T_m,SIC in the P-geometry (50 °C at Λ_y⁰ = 6; 43 °C at Λ_y⁰ = 7) is more than 50 °C lower than in the U-geometry (101 °C at Λ_y⁰ = 6; 96 °C at Λ_y⁰ = 7). At 25 °C, σ values in the P- and U-geometries are similar at Λ_y⁰ = 6, but at Λ_y⁰ = 7, σ in the P-geometry becomes lower—opposite to the expected effect of finite lateral constraint on σ. This reversal further supports the lower crystallinity in the P-geometry at a given Λ_y0. Notably, heating at Λ_y⁰ = 6 results in a slight increase in σ, consistent with entropic elasticity effects. In this case, the entropic elasticity contribution dominates over the reduction from partial SIC melting. The different T dependence of σ between NR and IR at Λ_y⁰ = 6 stems from the higher of IR in both stretching geometries ( and ≈5.1 for the P- and U-geometries in IR, versus and ≈3.0 for NR, respectively), resulting in higher crystallinity in NR at the same Λ_y.

Overall, the results in Fig. 7 highlight a more pronounced effect of lateral stretching on SIC in IR than in NR. The lower sensitivity of high-temperature SIC to strain biaxiality underscores the superior SIC capability of NR relative to IR.

Crack propagation path and SIC melting

Crack propagation in the P-geometry upon fracture at T_m,SIC clearly reveals the influence of SIC crystal melting on fracture behavior (Fig. 8). A characteristic crack propagation pattern was observed in an IR specimen fractured at 50 °C after being initially stretched to Λ_y⁰ = 6 at 25 °C in P-geometry. The crack initiates spontaneously in the planar-stretched central region and propagates nonlinearly toward the free edges. Near the edges, the crack branches into two paths, circumventing regions subjected to pseudo-uniaxial stretching. This behavior reflects the heterogeneous SIC distribution characteristic of P-geometry stretching. As shown in Fig. 3e, χ increases from the planar-stretched central region toward the pseudo-uniaxially stretched edge region. During gradual heating under constant stretch, the finer crystallites in the central region melt first at 50 °C, leading to loss tensile reinforcement and triggering crack initiation. Although the crack propagates toward the edges, these regions retain sufficient crystallinity at 50 °C to resist fracture, causing the crack to split and avoid them. This scenario is further supported by the large difference in ultimate stretch (Λ_max) between the U- and P-geometries at 50 °C (Fig. 6). In P-geometry, Λ_max is below 4, indicating that the material cannot withstand a stretch of Λ_y⁰ = 6. In contrast, Λ_max in U-geometry (∼8) is well above 6, meaning that the pseudo-uniaxially stretched edge regions can still endure the applied stretch. Furthermore, SIC crystallites formed under U-geometry stretching possess significantly higher thermal stability (T_m,SIC ≈ 109 °C) than those formed under P-geometry (T_m,SIC ≈ 50 °C) (Fig. 7). Therefore, the central planar-stretched region becomes the mechanically weakest zone due to its lower crystallinity, lower melting point of SIC crystallites, and reduced stretch tolerance, leading to crack initiation at the center. The underlying mechanism hinges on the markedly higher stretch tolerance of U-geometry, which in turn arises from differences in crystallinity between the two geometries (Fig. 4). While the data in Fig. 4 were obtained at 25 °C, it is reasonable to assume that the qualitative effect of stretching geometry on crystallinity persists across temperatures. This mechanism is schematically illustrated in Fig. 8b.

Fig. 8 Characteristic crack-growth patterns upon fracture of an IR specimen under P-stretching during heating. (a) (Middle) Nonlinear crack propagation path in a specimen stretched to Λ_y⁰ = 6, followed by heating from 25 to 50 °C at fracture. The crack bifurcates near the free edges, avoiding edge regions. (Bottom) Linear crack propagation path in a specimen stretched to Λ_y⁰ = 7, followed by heating from 25 to 43 °C at fracture. The crack propagates straight along the central line. (b) Schematic representation of the mechanism of an edge-localized branched crack. The distribution of strain biaxiality μ_yx in the P-geometry stretching of Λ_y⁰ = 6 obtained by DIC is also shown. Finer SIC crystallites formed in the planar-stretched central region melt first, leading to fracture initiation at the center. The crack then propagates while bypassing higher-crystallinity regions near the pseudo uniaxially stretched edges.

At a higher stretch of Λ_y⁰ = 7 in P-geometry, the IR specimen fractured at 43 °C, and the crack propagated linearly without branching (Fig. 8a, bottom). The absence of crack branching in this case likely stems from two factors: (i) the crack propagates more rapidly due to increased strain energy release rate at this higher stretch level, reducing sensitivity to local crystallinity variations; and/or (ii) the crystallinity gradient between the central and edges may be too small to induce crack branching.

These results demonstrate that finite lateral stretch not only suppresses the onset temperature of SIC-induced reinforcement (T*) but also reduces the thermal stability of the resulting crystallites. Previous studies^26,27 under room temperature conditions have highlighted that the orientation of network strands in the biaxial loading plane plays a key role in governing crystallinity via SIC, alongside the general entropy reduction caused by deformation. Our findings show that this orientation effect remains significant even at elevated temperatures. Although the present study covers only a moderate range of strain biaxiality (from uniaxial to planar stretching), a clear trend is observed: T* decreases with increasing lateral stretch. Moreover, the melting temperature of primary SIC crystallites (T_m,SIC) also decreases as lateral stretch increases. These findings suggest that the degree of strand orientation established during initial deformation is essential not only for promoting SIC but also for preserving the thermal stability of the resulting crystallites.

Conclusion

This study elucidates the significant influences of finite lateral stretch on SIC-induced reinforcement and the thermal stability of SIC crystallites in NR and IR at elevated temperatures. The upper-limit ambient temperature for SIC-induced reinforcement (T*) is more than 20 °C lower under pseudo-planar (P) stretching with finite constraint for lateral contraction than under uniaxial (U) stretching with free lateral contraction, highlighting the significant suppressive effect of lateral constraint on the onset of SIC. Furthermore, the melting behavior of SIC crystallites is highly sensitive to strain biaxiality. The melting temperature of SIC crystals (T_m,SIC) is significantly reduced in the P-geometry compared to the U-geometry, with differences exceeding 30 °C for NR and 50 °C for IR. These results reveal that IR exhibits a higher sensitivity of SIC to strain biaxiality. The influence of strain biaxiality is further manifested in a non-linear crack propagation pattern in the P-geometry. Due to the lateral-stretch gradient near free edges, crack at elevated temperatures initiates in the planar-stretched central region which has lower crystallinity and T_m,SIC, and circumvent the pseudo-uniaxially stretched edge regions which possess higher crystallinity and T_m,SIC. This crack branching behavior underscores the critical role of SIC heterogeneity in fracture resistance. These findings provide valuable insights into the fundamental mechanics of SIC under complex deformation states and offer important implications for the design and high-temperature performance of SIC-based rubber materials.

Author contributions

R. Osumi: experiments and data analysis and writing – original draft, T.-T. Mai: methodology, data analysis, reviewing and editing – original draft. K. Tsunoda: sample preparation, K. Urayama: conceptualization, methodology, supervision, validation and writing – original draft.

Data availability

The data that support the findings of this article have been included in the main manuscript and as part of the ESI† available in the online version of the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was carried out with the support of JST, CREST grant number JPMJCR2091, Japan.

References

1. C. Creton, Macromolecules, 2017, 50, 8297–8316.
2. S. Kohjiya and Y. Ikeda, Chemistry, Manufacture, and Applications of Natural Rubber, Elsevier, 2nd edn, 2021.
3. X. Zhao, X. Chen, H. Yuk, S. Lin, X. Liu and G. Parada, Chem. Rev., 2021, 121, 4309–4372.
4. J. R. Katz, Naturwissenschaften, 1925, 13, 410–416.
5. M. Tosaka, Polym. J., 2007, 39, 1207–1220.
6. B. Huneau, Rubber Chem. Technol., 2011, 84, 425–452.
7. K. Brüning, In situ Structure Characterization of Elastomers during Deformation and Fracture, Springer International Publishing, Cham, 2014.
8. J. Plagge and R. Hentschke, Macromolecules, 2021, 54, 5629–5635.
9. P. Rublon, B. Huneau, E. Verron, N. Saintier, S. Beurrot, A. Leygue, C. Mocuta, D. Thiaudière and D. Berghezan, Eng. Fract. Mech., 2014, 123, 59–69.
10. F. Xiang, K. Schneider and G. Heinrich, Int. J. Fatigue, 2020, 135, 105508.
11. Q. Demassieux, D. Berghezan and C. Creton, Adv. Polym. Sci., 2021, 286, 467–491.
12. R. Osumi, T. Yasui, R. Tanaka, T.-T. Mai, H. Takagi, N. Shimizu, K. Tsunoda, S. Sakurai and K. Urayama, ACS Macro Lett., 2022, 11, 747–752.
13. K. Tsunoda, Y. Kitamura and K. Urayama, Soft Matter, 2023, 19, 1966–1976.
14. T. T. Mai, K. Tsunoda and K. Urayama, J. Mech. Phys. Solids, 2024, 193, 105895.
15. C. Liu, N. Morimoto, L. Jiang, S. Kawahara, T. Noritomi, H. Yokoyama, K. Mayumi and K. Ito, Science, 2021, 372, 1078–1081.
16. K. Hashimoto, T. Shiwaku, H. Aoki, H. Yokoyama, K. Mayumi and K. Ito, Sci. Adv., 2023, 9, eadi8505.
17. J. H. Magill, Rubber Chem. Technol., 1995, 68, 507–539.
18. A. N. Gent, S. Kawahara and J. Zhao, Rubber Chem. Technol., 1998, 71, 668–678.
19. K. Brüning, K. Schneider and G. Heinrich, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 1728–1732.
20. J. Che, C. Burger, S. Toki, L. Rong, B. S. Hsiao, S. Amnuaypornsri and J. Sakdapipanich, Macromolecules, 2013, 46, 4520–4528.
21. N. Candau, R. Laghmach, L. Chazeau, J.-M. Chenal, C. Gauthier, T. Biben and E. Munch, Polymer, 2015, 60, 115–124.
22. N. Candau, R. Laghmach, L. Chazeau, J. M. Chenal, C. Gauthier, T. Biben and E. Munch, Eur. Polym. J., 2015, 64, 244–252.
23. L. R. G. Treloar, The Physics of Rubber Elasticity, Oxford University Press Inc., New York, 3rd edn, 1975.
24. K. Urayama, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 3440–3444.
25. T.-T. Mai, Nihon Reoroji Gakkaishi, 2024, 52, 283–290.
26. X. Chen, L. Meng, W. Zhang, K. Ye, C. Xie, D. Wang, W. Chen, M. Nan, S. Wang and L. Li, ACS Appl. Mater. Interfaces, 2019, 11, 47535–47544.
27. D. Nozaki, T.-T. Mai, K. Tsunoda and K. Urayama, Macromolecules, 2025, 58, 4059–4069.
28. W. Zhou, L. Meng, J. Lu, Z. Wang, W. Zhang, N. Huang, L. Chen and L. Li, Soft Matter, 2015, 11, 5044–5052.
29. R. Tanaka, T. Yasui, H. Takagi, N. Shimizu, N. Igarashi, H. Masunaga, Y. Kitamura, K. Tsunoda, T.-T. Mai, K. Urayama and S. Sakurai, Polym. J., 2024, 56, 753–763.
30. Q. Demassieux, D. Berghezan, S. Cantournet, H. Proudhon and C. Creton, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 780–793.
31. Y. Mouslih, J.-B. Le Cam, B. Ruellan, I. Jeanneau and F. Canevet, Mech. Mater., 2024, 196, 105045.
32. N. Bekkedahl and L. A. Wood, Rubber Chem. Technol., 1941, 14, 347–355.
33. L. A. Wood and N. Bekkedahl, J. Appl. Phys., 1946, 17, 362–375.
34. S. Toki, J. Che, L. Rong, B. S. Hsiao, S. Amnuaypornsri, A. Nimpaiboon and J. Sakdapipanich, Macromolecules, 2013, 46, 5238–5248.
35. R. Tanaka, T. Yasui, Y. Kitamura, K. Tsunoda, H. Takagi, N. Shimizu, N. Igarashi, H. Masunaga, K. Urayama and S. Sakurai, ACS Appl. Polym. Mater., 2024, 6, 2799–2806.
36. T.-T. Mai, T. Yasui, R. Tanaka, H. Masunaga, T. Kabe, K. Tsunoda, S. Sakurai and K. Urayama, Adv. Sci., 2024, 11, 202307741.
37. H. Schreier, J. J. Orteu and M. A. Sutton, Image correlation for shape, motion and deformation measurements: Basic concepts, theory and applications, Springer US, Boston, MA, 1st edn, 2009.
38. T.-T. Mai, K. Okuno, K. Tsunoda and K. Urayama, ACS Macro Lett., 2020, 9, 762–768.
39. J.-B. Le Cam, in Advances in Understanding Thermal Effects in Rubber: Experiments, Modelling, and Practical Relevance, ed. R. S. Gert Heinrich, R. Kipscholl and J.-B. Le Cam, Springer, Cham, 2024, pp. 1–29.
40. J.-B. Le Cam, P.-A. Albouy and S. Charlès, Rev. Sci. Instrum., 2020, 91, 044902.
41. N. Candau, L. Chazeau, J. M. Chenal, C. Gauthier and E. Munch, Phys. Chem. Chem. Phys., 2016, 18, 3472–3481.
42. M. Dixit and T. Taniguchi, Macromolecules, 2024, 57, 2588–2608.
43. M. Dixit and T. Taniguchi, ACS Polym. Au, 2024, 4, 273–288.

---

Footnote

† Electronic supplementary information (ESI) available: Spatial distribution of deformation tensor components in pseudo-planar stretching. Crystallinity evaluation procedure from surface calorimetry. See DOI: https://doi.org/10.1039/d5sm00341e

---