DOI:
10.1039/D5SM00291E
(Paper)
Soft Matter, 2025,
21, 5833-5851
Interpretable machine-learning enhanced parametrization methodology for Pluronics–water mixtures in DPD simulations
Received
19th March 2025
, Accepted 4th June 2025
First published on 19th June 2025
Abstract
Dissipative particle dynamics (DPD) is an incredibly powerful tool for simulating the behavior of structured fluids. However, identifying the appropriate model parameters to accurately replicate physical properties remains a challenge. This study showcases the benefits of integrating machine learning techniques into the top-down parameterization of Pluronic systems. The proposed workflow outlines a data-driven approach to accurately determine model parameters tailored to various Pluronic systems. Gaussian process regression (GPR)-based surrogate models effectively replicate the results of DPD simulations, delivering faster responses that streamline parameter optimization and enable the calibration of Pluronic systems against experimental data. Although DPD simulations provide valuable insight, their high computational cost, due to extensive simulations and post-processing, presents a challenge. The GPR-based surrogate model addresses this by modeling the relationships between input parameters and output properties. SHAP (SHapley additive exPlanations) analysis enhances model interpretability, providing deeper insights into the relationships and causal mechanisms between the input parameters and the predicted properties. The combination of GPR and SHAP analysis provides an interpretable machine learning approach, enabling a more efficient optimization process and reducing the need for exhaustive simulations. This work lays a foundation for generalizing the parameterization process across Pluronic systems and conditions, such as varying temperatures, by incorporating additional DPD model input parameters.
1 Introduction
Pluronics, or poloxamers, are synthetic amphiphilic copolymers with a triblock structure: a central hydrophobic poly(propylene oxide) (PPO) block flanked by two hydrophilic poly(ethylene oxide) (PEO) chains.1 Available in various types, they are highly flexible systems capable of meeting the specific requirements of a wide range of applications. Their versatility, biocompatibility, low toxicity, temperature sensitivity, and self-assembly capabilities make them ideal in numerous fields. These include drug delivery, tissue engineering, bioprinting, and nanomedicine, along with uses in dispersion stabilization, emulsification, lubrication, formulation, and surface modification to improve biocompatibility in medical applications.2,3 They are also commonly applied in the cosmetics industry. The wide range of commercially available Pluronics is due to the flexibility in adjusting the lengths of the PPO and PEO chains. This allows for the customization of their properties and overall molecular weight. They exhibit different behavior and phase diagrams in solution. They can exist in the form of liquids, solids, and pastes. Their molecular weight ranges from 2000 to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, with a PEO content of 10 to 80 wt%. These materials are named using an alphanumeric code that combines a letter and two or three digits.4 The letter represents the physical state at room temperature: L for liquids, P for pastes, and F for flakes. The digits denote the molecular weight and composition. Specifically, the molecular weight of the hydrophobic PO block is calculated by multiplying the first one or two digits by 300, while the hydrophilic EO content (in weight percentage) is determined by multiplying the final digit by 10. Different Pluronics are cataloged according to the molecular weight of the PPO and the PEO contents in the Pluronic grid, reported in Fig. 1. Pluronics are often referred to as EOxPOyEOx, where x and y represent the number of EO and PO units as shown in Fig. 2, respectively. The degree of polymerization of the Pluronic hydrophilic and hydrophobic segments determines its hydrophilic–lipophilic properties. The ratio between the lengths of the EO and PO chains defines the hydrophilic–lipophilic balance (HLB), which quantifies the Pluronic degree of hydrophilicity or lipophilicity.5 The HLB of Pluronic molecules can be calculated using the following equation:6
000 g mol−1, with a PEO content of 10 to 80 wt%. These materials are named using an alphanumeric code that combines a letter and two or three digits.4 The letter represents the physical state at room temperature: L for liquids, P for pastes, and F for flakes. The digits denote the molecular weight and composition. Specifically, the molecular weight of the hydrophobic PO block is calculated by multiplying the first one or two digits by 300, while the hydrophilic EO content (in weight percentage) is determined by multiplying the final digit by 10. Different Pluronics are cataloged according to the molecular weight of the PPO and the PEO contents in the Pluronic grid, reported in Fig. 1. Pluronics are often referred to as EOxPOyEOx, where x and y represent the number of EO and PO units as shown in Fig. 2, respectively. The degree of polymerization of the Pluronic hydrophilic and hydrophobic segments determines its hydrophilic–lipophilic properties. The ratio between the lengths of the EO and PO chains defines the hydrophilic–lipophilic balance (HLB), which quantifies the Pluronic degree of hydrophilicity or lipophilicity.5 The HLB of Pluronic molecules can be calculated using the following equation:6| | 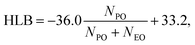 | (1) |
where NPO and NEO refer to the PO and EO block repeating units, respectively.
 |
| | Fig. 1 Pluronic grid. This figure is reproduced from ref. 3. | |
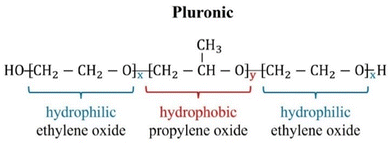 |
| | Fig. 2 Molecular structure of Pluronics. The variables x and y denote the lengths of the PEO and PPO chains, respectively. This figure is reproduced from ref. 3. | |
Depending on factors such as HLB, concentration, temperature, and shear stresses, these materials can exist in aqueous solutions either as individual macromolecules, unimers, or self-assemble into micelles once they surpass the critical micellar concentration (CMC) and the critical micellar temperature (CMT). They can evolve in various microstructures,7,8 which in turn govern the ultimate material properties they exhibit. The CMC represents the concentration threshold at which self-assembly in micelles occurs, which impacts various functionalities, such as drug delivery. Micelles can exhibit a variety of shapes and sizes, typically described by the radius of gyration Rg and the aggregation number As.
Pluronic micelles, widely researched for medical applications, are among the most studied systems for drug delivery.9,10 These micelles can encapsulate hydrophobic drugs within the PPO core, allowing them to be transported throughout the body and to target specific areas, as has recently been done in cancer therapy.11 For these reasons, the micellar phase has been investigated in depth using numerous experimental techniques. For example, the CMC has been studied by surface tension measurements. Micelle characterization is performed by static light scattering or small-angle X-ray and/or neutron scattering.2,12,13 Key properties such as CMC, Rg, and As, which significantly influence functionalities like drug delivery, are determined by factors such as concentrations, temperatures, and the types of Pluronics. Although predicting and controlling these properties is vital for optimizing performance, the experimental campaigns required to explore different conditions, such as composition, concentration, and temperature, are both time-intensive and costly.
Computational tools offer valuable support that enables the efficient and cost-effective exploration of various scenarios. Atomistic simulations, however, face limitations due to the large time and length scales involved, making them unsuitable for studying self-assembly phenomena directly. Coarse-grained (CG) methods, which represent groups of atoms or molecules as single entities called beads, bridge the gap between micro- and macro-scale models.14 These methods operate at scales inaccessible to molecular-level approaches. Among these, dissipative particle dynamics (DPD) is one of the most widely used techniques for such systems. It offers greater computational efficiency and can simulate time and length scales that accurately reproduce the morphologies of diverse systems.15 However, its primary drawback is the challenge of capturing chemical specificity and linking the model to atomic-level structures. These challenges are reflected in the parameterization problem: identifying and transferring the parameters of a CG model, such as DPD, is not straightforward but crucial for accurately representing physical properties. CG model parameters are often neither easily identifiable nor directly transferable across different thermodynamic states. These challenges arise regardless of whether the model is developed by reference to experimental data, top-down coarse-graining (CGing), or by reference to an underlying atomistic model, bottom-up CGing.16,17 In a top-down approach, interaction parameters are typically related to thermodynamic properties or fit to experimental observables. In contrast, bottom-up parameterization derives conservative interactions through structure matching, force matching, or relative entropy methods.
A notable example of bottom-up coarse-graining is multi-scale CGing (force matching),16,17 where the Mori–Zwanzig projection operator method18,19 provides a rigorous framework to determine the CG equations of motion (EoM). These equations, derived from microscopic dynamics, take the form of generalized Langevin equation, which under Markovian approximation reduces to DPD EoM with conservative, dissipative force and random forces whose expressions can be obtained directly from atomistic simulations. Despite its theoretical rigor, this bottom-up approach can be computationally prohibitive, particularly for high molecular weight polymers, where extensive molecular dynamics trajectories are required to inform the DPD model. In such cases, a top-down approach, where parameters are empirically fitted to system-specific properties, remains more practical. In fact, for large macromolecules the identification of DPD interaction parameters is still largely performed relying on this empirical approach.20–22 Furthermore, the simple form of DPD interactions limits the portability of model parameters. As a means of addressing these deficiencies, a new class of DPD variants is emerging with more expressions for forces to capture interactions more realistically, representing an open and active field of research.23 For many practical purposes involving such systems, it may be useful and computationally advantageous to retain the original simple form of linear repulsive forces and fit the parameters to the specific properties of the system under investigation, following a top-down procedure. In this work, we focus on different types of Pluronic systems.
The state-of-the-art approach to treat Pluronic systems, or in general other polymer systems, with DPD is the top-down, following the Flory–Huggins theory. Groot and Warren first presented this approach in their pioneering work.14 In polymer science, established theories connect the χ-parameter to the solubility and the mixing energies of polymeric components.24 These parameters can be obtained through either atomistic simulations or experimental data. Since Flory–Huggins (FH) parameters are experimentally derived, their calculation does not require additional simulations. However, the Flory–Huggins-based mapping procedure has intrinsic limitations, which hinder the accurate quantitative prediction of critical properties, such as the critical micelle concentration (CMC), the micelle radius of gyration (Rg), and the aggregation number (As), especially under varying conditions such as concentration or temperature. Given these limitations, the parameters of a CG model are not universal, hindering dependencies on temperature, composition, and Pluronic types. This dependency cannot be known a priori and need to be investigated for every CG model. The disagreement between experimental results and simulations partly arises from using fixed parameters across different concentrations, temperatures, and Pluronic types. A more flexible model, allowing parameters to vary accordingly, could improve quantitative predictions.
Preliminary work is required to tune and validate these parameters for each system to closely match the experimental results. The adjustment process must account for various itype–jtype interactions (e.g., 1-1, 1-2, 2-2 for a binary system), requiring numerous trial-and-error iterations to find suitable parameters. Indeed, by employing a top-down approach, these can be acquired through multiple iterations of DPD simulations and a systematic comparison with experimental data. However, adjustments are needed to satisfactorily reproduce the physical properties of the system under study. In a top-down parameterization approach, the parameter-tuning task is typically performed through a manual trial-and-error process. This involves using a penalty function that compares the calculated values of selected properties, Ai, with their corresponding target values, ATi, from experiments:
| |  | (2) |
where
θ represents the model parameters. Each evaluation of
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
(
θ) requires running a full DPD simulation, followed by a post-processing step to extract the relevant properties. In addition, for each time variable like temperature or the type of Pluronic change, a new simulation is required, adding complexity to the process. DPD simulations are known to be computationally expensive, making them time-consuming and impractical for high-dimensional optimization tasks. This extensive search through the parameter space is not only labor-intensive and costly but also demands substantial expertise from researchers. Machine learning techniques could potentially streamline this parameter optimization process (
Fig. 3) by reducing the effort and enhancing accuracy.
 |
| | Fig. 3 Typical trial-and-error parameters identification workflow. | |
This work proposes a data-driven approach for parameterizing Pluronic systems. In particular, a reliable data-driven model is developed to accurately surrogate DPD simulations. This model's ability to deliver faster responses facilitates more efficient parameter optimization and enables the calibration of various Pluronic systems against experimental ground truth.
At the heart of this workflow lies the development of an accurate data-driven surrogate model to replace traditional physics-based DPD simulations. The key parameters of the DPD model are identified as input features, and a series of simulations are performed with these features varied within physically meaningful ranges. To ensure physical consistency, the conservative force parameters were varied were varied within ranges that are physically meaningful for DPD modeling of polymer–water systems: aAW from 25 to 30 (with a grid spacing of 1) for the hydrophilic PEO, and aBW from 30 to 44 (with a grid spacing of 2) for the more hydrophobic PPO. These values are consistent with the expected relative solubility behavior of the PEO and PPO in water and prevent excessively strong repulsions that could lead to nonphysical behaviors such as system freezing. For each simulation, physical properties are calculated, creating a dataset in which each sample represents input features paired with their corresponding outcomes. The dataset created by DPD simulations is divided into two subsets: training dataset and validation dataset. The Gaussian process regression (GPR) model is trained on the training dataset, and its performance is evaluated on the validation dataset. The GPR accurately models the relationships between input features and outputs, and once trained, it can make predictions at a much faster rate. However, as a “black-box” machine learning model, it lacks sufficient interpretability. Beyond predictive accuracy and efficiency, understanding why a surrogate model makes a given prediction is crucial. Therefore, we employ SHAP (SHapley additive exPlanations) analysis25 to interpret the outputs of the GPR models designed to predict each physical property. SHAP analysis quantifies each input feature's contribution to a specific prediction, comparing their relative importance and revealing any interactive effects. This combination of a fast and accurate GPR surrogate model and SHAP analysis provides an interpretable machine learning approach to facilitate efficient grid-search optimization of the parameters.
DPD simulations are conducted using the open-source software LAMMPS. Physical observables are extracted through a post-processing workflow involving C++ code and a Python routine. The GPR model is developed, trained and tested using the Python library Scikit learn. SHAP analysis is conducted using the KernelSHAP method from the SHAP library in Python. The grid-search optimization is performed with a dedicated Python script. The outline of the article is as follows. Section 2 provides an overview of the DPD methodology, including the CG model for Pluronic macromolecules and the procedures used to extract physical observables from equilibrium trajectories. Section 3 outlines the data-driven workflow, comprising the creation of datasets from DPD simulations, post-processing routines, the construction of a GPR-based surrogate model, SHAP analysis, and the methodology employed to solve the parameterization problem. Section 4 presents and discusses the results, emphasizing the surrogate model's accuracy, and efficiency, and interpretability in supporting parameter optimization, as well as its potential for generalization across different Pluronic systems and conditions. Finally, the conclusions are summarized in Section 5.
2 Physics-based simulations
2.1 Dissipative particle dynamics
DPD is a particle-based mesoscopic simulation technique, where groups of atoms are projected into a statistically equivalent ensemble of structureless CG particles, referred to as beads.26 In the standard formulation, these beads are considered to have the same size. The beads interact via a mesoscopic force field. The DPD force field consists of variables in reduced units, the so-called DPD units. Typically in DPD, the mass of a single DPD bead, conservative cutoff radius, and thermal energy are taken as, respectively, mass, time, and energy units. The time evolution of each bead can be calculated by the Newton second law as follows:| |  | (3) |
with i = 1,…,N; ri and vi are the position and velocity of the bead i with mass mi, respectively, and N is the number of DPD beads in the system. In the case of a DPD fluid, the force fi acting on the i-th bead is the sum of three pairwise contributions:| | 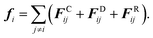 | (4) |
In (4), the sum runs over the indices of beads contained in the closest vicinity of the bead i within a certain cutoff radius rc. The conservative contribution, FCij, is a soft-repulsive force acting between a pair of beads i and j and having the following functional form
| |  | (5) |
where
aij denotes a maximum repulsion between beads
i and
j,
rij = |
rij| = |
ri −
rj| is the separation distance between a pair of beads, and
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij
ij =
rij/
rij is the unit vector of the bead-bead separation distance and
rCc is the cutoff radius for the conservative interactions.
To model chain macromolecules, such as Pluronics, an extra spring force is defined to bind the neighboring beads. The chemical bonds between the monomers are represented using the bead-and-spring model, in which adjacent beads in the polymer chain interact via a harmonic potential, described by the equation:
| | | Eharm = Kb(rij − R0)2, | (6) |
where
R0 is the nominal equilibrium distance and
Kb the harmonic constant. CGing, which involves eliminating degrees of freedom from the system, reduces friction and smooths the free-energy landscape, leading to faster dynamics at the mesoscale level. In DPD, these removed degrees of freedom are effectively reintroduced through pairwise dissipative and random forces. Dissipative and random forces,
FDij and
FRij, respectively, represent the effect of viscosity slowing down the particles motion with respect to each other and of thermal/vibrational energy of the system. They act together as a thermostat. The random and dissipative forces are coupled
via the fluctuation–dissipation theorem (FDT),
27 ensuring sampling from the appropriate probability distribution. In addition, DPD conserves the total momentum. The weight functions for the dissipative force and the stochastic force provide the interaction range for their respective forces and are linked by a relationship necessary to ensure that the system, in the limit of an infinitesimal time step, reaches Gibbs equilibrium, derived from Español and Warren.
27 Obtaining from the simulations an equilibrium distribution corresponding to the Boltzmann distribution of a canonical or Gibbs ensemble is fundamental to relating to the classical relations of thermodynamics in the system under consideration. One of the two weight functions that appear can thus be chosen arbitrarily, and this choice determines the other:
| |  | (8) |
where
kB is the Boltzmann constant and
T is the equilibrium temperature. These conditions ensure that the DPD equations act as a thermostat, and since the algorithm depends on relative velocities and the interactions between particles are symmetric, it is a Galilean-invariant thermostat that preserves hydrodynamics.
28 The conventional functional form for the dissipative and stochastic weight functions is as follows:
| |  | (9) |
2.2 Coarse-grained model and parameters identification
In this work, adhering to the standard approach, the CG factors are selected such that all beads represent almost the same mass and volume14,26,27,29 as shown in Table 1. The mapping scheme adopted is the same as described by van Vlimmeren et al.,30 shown in Fig. 4 for Pluronic L64. The number of monomers clustered into one bead is 4.3 for the ethylene oxide (EO) repeating units and 3.3 for the propylene oxide (PO) repeating units. Based on this scheme, the CG topology of the Pluronic L64 macromolecule results in a chain of 15 beads and is shown in Fig. 4. It can be schematically represented as A3B9A3, where A stands for the CG bead for EO and B for PO. In the Table 2 are reported the coarse-grained topologies of the analyzed Pluronic systems. In the simulations, a third type of beads (W) is considered that represents water molecules, with a corresponding degree of CGing equal to 10.
Table 1 Coarse-grained (CG) beads, molecular volumes of H2O, EO, and PO calculated according to the approach by Durchschlag and Zipper,29 and the corresponding bead volumes expressed in Å3
| CG bead |
Molecular volume (Å3) |
Volume bead (Å3) |
| [H2O]10 |
30 |
300 |
| [CH2CH2O]4.3 |
64.6 |
278 |
| [CH3CHCH2O]3.3 |
96.5 |
318 |
 |
| | Fig. 4 Coarse-grained model of Pluronic L64. | |
Table 2 Coarse-grained topologies of the analyzed Pluronic systems
| Pluronic name |
Composition |
DPD model composition |
| L64 |
EO13PO30EO13 |
A3B9A3 |
| P65 |
EO20PO30EO20 |
A5B9A5 |
| P104 |
EO27PO63EO27 |
A4B18A4 |
| F68 |
EO82PO31EO82 |
A18B9A18 |
The repulsive coefficients for beads of the same type are calculated according to the following relationship:31
| |  | (10) |
where
α is a constant,
κ−1 is the dimensionless bulk modulus at the considered temperature (the inverse of dimensionless compressibility),
ρ is the number density,
kB denotes the Boltzmann constant and
T is the system temperature. This relationship (
eqn (10)) ensures that the compressibility in the simulation model matches the compressibility of the liquid to be studied, correctly describing the density fluctuations as they appear in a molecular liquid. From this condition, the repulsion parameters between equal beads can be fixed. Specifically, this relationship uses the generalized approach
32 extensively tested in our previous work,
31 which incorporates both the simulation temperature
T and the temperature-dependent compressibility
κ in evaluating the repulsive interaction parameter. The repulsion coefficients for beads of different type,
aij, is approximately given by:
14| |  | (11) |
This expression (eqn (11)), suggests that the repulsion parameters between beads representing different species contain an extra-repulsion term, which should be chosen to ensure that different solubilities of the involved species are accurately captured within the DPD model. However, direct transfer of aij values computed from χij between different systems, in this case different Pluronics, is subject to limitations, dictated by different reasons. This problem is commonly known as the parameters portability issue. First, eqn (11) is numerically derived for a specific system.14 Furthermore, the experimental values of χij available in the literature are obtained under specific experimental conditions. A key point is that comparisons with experiments indicate that χij depends on both entropic and energetic contributions. In other words, the behavior of such systems arises from a subtle interplay between entropy and enthalpy.33 However, predicting how entropic effects vary across different systems and incorporating them into a parameter remains a significant challenge. To conclude, while χij and eqn (11) provide a useful starting point for identifying DPD interaction parameters, fine-tuning of aij for a certain system, such as a Pluronic type, remains largely empirical when aiming to fit quantitative experimental targets. For consecutive beads in the chain, two additional parameters are involved: the nominal equilibrium distance R0,ij and the harmonic constant Kb,ij. The choice of the nominal equilibrium distance R0,ij and the harmonic constant Kb,ij for each pair of beads must ensure that the topology of the polymer chains is preserved.
2.3 System observables extraction
In this work, three different physical observables are selected as targets: the micelle aggregation or association number As, the CMC, and the micelle radius Rg. DPD simulations produce trajectories which are analyzed using our in-house software. The trajectory file stores information on all particles, such as their positions or velocities, in regular time intervals. Statistical analysis of these trajectory files allows us to gain valuable insights into the aggregation behavior during simulations, by detecting phenomena such as micelles, aggregates, and other structures. The core of this kind of analysis is a clustering algorithm able to determine if there is any aggregation occurring within the DPD simulation and to calculate various properties of aggregates. The following paragraphs describe how the in-house software we use extracts from DPD simulations each of the three selected target properties.
2.3.1 Aggregation number.
The aggregation or association number, denoted as As, represents the number of chains present within a single aggregate. It is essential to first establish a criterion to establish the belonging of chains to the same aggregate in the simulation. A straightforward and commonly used criterion is that two molecules are considered to be part of the same aggregate if they have at least a specified number of contact pairs. A contact pair is defined as a pair of beads from different molecules that are closer than a given distance. The weight-average aggregation number is defined as| |  | (12) |
where mA,i is the weight of an aggregate i. The weight distribution function of aggregation numbers, Fw, is defined as:| |  | (13) |
where mA,i represents the weight of an aggregate with an association number As = i and NA,i denotes the number of aggregates with that association number. Similarly, the number distribution function of aggregation numbers, Fn, is expressed as:| |  | (14) |
Both of these functions are normalized, so the value of Fw and Fn indicates the fraction of aggregates with a specific mass or aggregation number present in the system.
In this work, 〈As〉w is considered to be compared with experimental data. For simplicity of notation, in the following paragraphs As ≡ 〈As〉w.
2.3.2 Determining the critical micellar concentration.
The CMC is the concentration above which Pluronics macromolecules self-assemble into micelles. Determination of the CMC is not straightforward and depend on the criteria used. Different methods have been presented in the literature. In this work, the CMC is defined as the concentration of sub-micellar aggregates. A cut-off aggregation number is defined to distinguish sub-micellar portion from micellar one. For a system with a concentration, c, above the CMC, the CMC is equal to the concentration of aggregates csm with As below a cut-off association number, As,m. The latter is identified from the number distribution function as done in ref. 34.
2.3.3 Micelle radius from gyration tensor.
The micelle radius, denoted as Rg, is defined as the square root of the mean squared distance of beads in a chain or aggregate from its center of mass, rCM, assuming uniform mass distribution among the particles:| |  | (15) |
where N is the number of particles forming the chain or aggregate. The radius of gyration is calculated using the gyration tensor, S, which describes the second moments of the position vectors of the beads:| |  | (16) |
where rmi stands for the m-th Cartesian coordinate of ri and rCM is the m-th Cartesian coordinate of rCM. The gyration tensor is a symmetric matrix which can be diagonalized:| |  | (17) |
where λx2, λy2 and λz2 are eigenvalues chosen so that λx2 < λy2 < λz2. The eigenvectors indicate the principal axes of the aggregate, while the eigenvalues correspond to the gyration lengths along each principal direction. These eigenvalues can be interpreted as the semi-axes of an equivalent ellipsoid. They are used to calculate various properties, including shape descriptors of the aggregates, such as the radius of gyration:| | | Rg2 = λx2 + λy2 + λz2. | (18) |
Analogously to the aggregation number, the weight-averaged radius of gyration is computed for comparison against experimental data. For simplicity of notation, in the remaining part of the work Rg ≡ 〈Rg〉w.
3 Data-driven approach: methods and computational details
3.1 Dataset creation
The first step involves performing DPD simulations to generate the dataset necessary to train the GPR algorithm. These simulations provide the “ground truth” data for the data-driven model. A portion of data created by simulation is used to train the GPR, and another portion is subsequently used to assess the accuracy of GPR predictions. The workflow comprises two main stages. The first stage is the simulation setup, which involves identifying the key DPD input parameters that govern the accurate reproduction of the target physical properties: micelle gyration radius (Rg), aggregation number (As) and CMC. The second stage is the extraction of these physical properties from simulation trajectories through a structured post-processing routine. These two parts of the workflow are detailed in the subsequent paragraphs. This study investigates four different Pluronics, summarized in Table 3, along with their physiochemical properties.
Table 3 Physiochemical properties of the considered Pluronics3
| Pluronic name |
Composition |
Avg. mol. wt. (g mol−1) |
PO mol. wt. (g mol−1) |
EO content (wt%) |
HLB value |
| L64 |
EO13PO30EO13 |
2900 |
1750 |
40 |
15 |
| P65 |
EO20PO30EO20 |
3400 |
1750 |
50 |
17 |
| P104 |
EO27PO63EO27 |
5900 |
3250 |
40 |
13 |
| F68 |
EO82PO31EO82 |
8350 |
1750 |
80 |
28 |
For each Pluronic, a dataset consisting of 40 data points is created based on DPD simulations, which serve as the “ground truth” for the surrogate model. The number of data points is determined for one Pluronic type and progressively enriched to reduce the uncertainty level. The input features, aBW and aAB, are selected due to their relevance to the system behavior, as will be discussed in Section 3.1.1. These parameters are systematically varied within physically meaningful ranges, whereas other simulation parameters are kept constant, as will be outlined in Section 3.1.1. For each simulation, physical properties are calculated, as will be explained in Section 3.1.2, resulting in a dataset where each sample consists of input features paired with their corresponding outcomes.
3.1.1 Simulations setup and details.
The simulation setup requires the identification of key model parameters that exert the greatest influence on the target properties. This section explains the considerations underlying parameter selection and provides an overview of the simulation details.
All conservative model parameters are summarized in Table 4. The repulsive parameters are denoted as aij and the cutoff distances are represented as rC,ij. The chemical bonds between the monomers that form the polymer macromolecule are represented using the beads and spring model, in which adjacent beads in the polymer chain interact via a harmonic potential. Thus, for consecutive beads in the chain, two additional parameters are involved: the nominal equilibrium distance R0,ij and the harmonic constant Kb,ij. Accounting for all parameters creates a high-dimensional parameter space, making the problem computationally demanding. To address this, we initially restrict the number of parameters by leveraging physical insights. Future work may explore additional parameters to further refine the model. First, since ij-interactions are identical to ji-interactions, redundant parameters below (or above) the diagonal in Table 4 are excluded. Second, as all beads represent almost the same volume, all cutoff distances are assumed equal and set to 1. Third, the repulsive parameter aWW is set to match the isothermal compressibility of water, as is commonly done in DPD simulations. aAA and aBB are assumed equal to aWW as usually done in DPD models. As a result, the remaining adjustable parameters in the table are aAW, aBW, aAB, R0,AA, R0,BB, R0,AB, Kb,AA, Kb,BB, and Kb,AB. All bonded interaction parameters are assumed to be the same (R0 and Kb for all bonds). The assumption is justified by the CG level. In addition, these parameters have a marginal impact on CMC and As. They can slightly influence the shape and compactness of the micelles, and then the Rg. In this work, preliminary simulations are carried out to establish reasonable values of bonded parameters: Kb = 50 and R0 = 0.7 are found to give the desired behavior of the bond–bond distribution function.
Table 4 Conservative interaction parameters for the three species: PEO, PPO, and water
|
|
A (PEO) |
B (PPO) |
W (H2O) |
| A (PEO) |
a
AA;rCc,AA;Kb,AA;R0,AA |
a
AB;rCc,AB;Kb,AB;R0,AB |
a
AW;rCc,AW |
| B (PPO) |
a
BA;rCc,BA;Kb,BA;R0,BA |
a
BB;rCc,BB;Kb,BB;R0,BB |
a
BW;rCC,BW |
| W (H2O) |
a
WA;rCC,WA |
a
WB;rCC,WB |
a
WW;rCC,WW |
Furthermore, aAB is assumed to be equal to aBW, reducing the free parameters to aAW and aBW. These simplifications are reasonable because the self-assembly process is primarily driven by the solubility differences between the hydrophobic and hydrophilic blocks and water.
Thus, aAW and aBW are the key parameters of the DPD model to capture the chosen physical targets. As discussed in Introduction and in Section 2.2, these parameters are expected to be different between different Pluronic types.
All other simulation parameters remain constant. The simulations are conducted in a cubic box with a side length of 40rCc, employing periodic boundary conditions in all directions. The number density is fixed at ρ = 3, and the temperature is set at T = 30 °C. The friction coefficient γ is maintained at a standard value of 4.5.
3.1.2 Post-processing routine.
The post-processing is handled through an automated routine schematized in Algorithm 1, which orchestrates the calculations necessary to derive from the equilibrium trajectories, produced by the DPD simulations, the system observables: CMC, Rg, and As. After the simulation data are converted into a suitable format, the post-processing phase begins by removing water beads from the coordinate file, isolating macromolecules. The post-processing of saved trajectories starts with the identification of Pluronic aggregates. Aggregates are identified on the basis of a predefined minimum distance between beads of different macromolecules and a required number of contacts to classify two macromolecules within the same aggregate. This step is followed by the calculation of the aggregation number distribution. The aggregation or association number, denoted as As, represents the number of chains within a single aggregate. The average aggregation number is then computed over the entire simulation to track its evolution and estimate the equilibration time. Once the equilibration time is obtained, the aggregation number distribution and average aggregation number are recomputed and discarded from the equilibration steps. Specifically, the weight-average aggregation number is computed for comparison with the experimental data. The CMC is then computed as detailed in Section 2.3. Eventually, the weight average Rg is calculated from the gyration tensor, as described in Secion 2.3.
|
Algorithm 1 Automated routine for dataset creation |
|
Input: Interaction parameters aAW, aBW |
|
Run DPD simulation
|
| Convert topology and coordinate files into a format compatible with the post-processing routine |
|
Post-processing routine: |
| • Remove water beads from the coordinate file |
| • Identify aggregates: |
| – Define the minimum distance threshold for two beads from different macromolecules to be considered part of the same aggregate |
| – Establish the minimum number of contacts required between two macromolecules to classify them as belonging to the same aggregate |
| • Compute: |
| – Aggregation number distribution |
| – Average aggregation number |
| – Equilibration time |
| – Aggregation number distribution and average aggregation number (As) discarding equilibration steps |
| – Critical micelle concentration (CMC) |
| – Gyration tensor |
| – Shape descriptors |
| – Gyration radius (Rg) |
|
Output: CMC, As, Rg |
3.2 Surrogate modeling via GPR
Once the dataset for each Pluronic system (e.g., L64 at 30 °C) is generated from the simulations, it is used to construct separate surrogate models for each output property (e.g., Rg, As, CMC). Each model captures the relationship between the respective output property and the input parameters (aAW, aBW). The same process is applied to all four Pluronic systems (L64, P65, P104, F68). To establish these input–output relationships, we employ GPR, a Bayesian machine learning technique that leverages non-parametric modeling through Gaussian processes. It excels in handling small datasets, provides uncertainty estimates for predictions, and offers flexibility through its kernel-based approach, making it well-suited for our regression tasks. The estimated uncertainty, quantified by the confidence intervals 95%, can inform the required size of the training data to achieve a desired level of confidence.
For each Pluronic system, we construct three distinct GPR models of the form y = GP(x), where the input vector x = [aAW,aBW] represents the water-interaction parameters. Each model predicts one of our target properties: Rg, As, or CMC. Using Rg as an example, we will demonstrate the modeling process that is subsequently applied to As and CMC. Consider a training set with Ntrain samples. We can represent the input and output as:
| |  | (19) |
respectively. Here,
xi = [
aAW,i,
aBW,i] represents the input parameters for the
i-th sample from simulation, and
yi is its corresponding output (
Rg,i in this example).
The Gaussian process assumes that the output values Y(X) in any given set of input points X are drawn from a multivariate normal distribution. The Gaussian process is fully characterized by a mean function U(X) and a covariance function, which describes the relationships between input features:
| | | Y(X) ∼ GP(U(X),Σ(X,X)), | (20) |
where
U(
X) ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Ntrain
Ntrain is the mean function, and
Σ(
X,
X) ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Ntrain×Ntrain
Ntrain×Ntrain is the covariance matrix. The covariance function is defined using the radial basis function (RBF) kernel, which measures the similarity between two input points
xi and
xj. The RBF kernel is given by:
| |  | (21) |
where the
θa is the amplitude parameter, and
θl is the length scale, which control the smoothness of the mean function.The GPR model training involves optimizing the kernel hyperparameters by maximizing the log-likelihood function:
| |  | (22) |
where

and

is the determinant of matrix

. Here,
Θ = [
σ,
θa,
θl], which include the noise level
σ and kernel parameters
θa and
θl, are optimized using the L-BFGS quasi-Newton optimization algorithm.
35
Once the GPR model is trained, for any new input x′, the posterior distribution of the output can be obtained as:
| |  | (23) |
where
| |  | (24) |
Here,
û denotes the GPR model's predicted mean value of the output, while the covariance matrix

indicates the prediction confidence and reveals the associated uncertainty of this prediction. The 95% confidence interval is determined from the mean prediction and the standard deviation as: [mean_prediction −1.96× std_prediction, mean_prediction +1.96× std_prediction], where the standard deviation is calculated as the square root of each diagonal element of the covariance matrix.
3.3 SHapley additive exPlanations (SHAP) analysis
In addition to achieving good accuracy, interpretability, understanding why each prediction is made, is also important when building a predictive surrogate model. ML-derived models, like neural networks or GPR models, are often characterized as “black boxes” due to their intricate internal structures, making it difficult to discern the relationships they learn between inputs and outputs. This lack of interpretability can hinder the extraction of actionable knowledge from the constructed surrogate model. To overcome this challenge, a post hoc analysis via SHAP is employed, which seeks an interpretable approximation of the original model through evaluating the additive feature attribution.25
Let f(x) denote the original model that we attempt to interpret, with x the input vector that can belong to a high dimensional space. The goal herein is to explain f locally at a given x. For this, an explanation model g(x′) is sought, whose input vector x′ can be mapped to x using a mapping function hx, i.e., x = hx(x′). The mapping may reduce the dimensionality; x′ can have the same or a lower dimension than x. Mathematically, we can say that g successfully explains the original model f, if we ensure g(z′) ≈ f(hx(z′)), whenever z′ ≈ x′. This gets more intuitive when g is an additive feature attribution model which is defined as:
| |  | (25) |
where
z′ is a binary vector with dimension
M,
i.e.,
z′ = {0,1}
M indicating the presence or absence of a feature;
ϕi ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif)
represents the contribution of feature
i to the output
f(
hx(
z′)); and
ϕ0 is the base value of the model output without any feature's contribution. In particular for our analysis,
f(
x) is the GPR surrogate model with the input vector
x = [
aAW,
aBW]; and
M = 2,
i.e.,
z′ and
hx(
z′) are both two-dimensional vectors. The attribution values
ϕi are referred to as Shapley values (or SHAP values). By the definition and additive nature of
g, Shapley values can effectively quantify how much each input feature contributes to the value of the output.
It has been proved using the co-operative game theory25 that for a given machine learning model f and the additive attribution model g as defined in eqn (25), if f and g satisfy all three properties namely the local accuracy, missingness, and consistency, there exists a unique solution to g, and Shapley values ϕi are given by:
| | 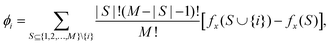 | (26) |
where
S denotes the set of non-zero indexes in
z′, and hence |
S| indicates the number of non-zero indexes in
z′. Here,
f(
hx(
z′)) is denoted by
fx(
S) and called the value function given by
fx(
S) =
f(
hx(
z′)) =
E[
f(
x)|
xS], where
E[
f(
x)|
xS] is the expected value of the function conditioned on a subset
S of the input features. As an example, consider a machine learning model
f with 4 input features
x = (
x1,
x2,
x3,
x4) and let the corresponding interpretation model
g also have 4 feature inputs
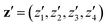
. Let
S = {1,3} which implies
z′ = (1,0,1,0). If we denote the
ith component of
hx(
z′) by
hxi then
fx(
S) is given by
| | | fx(S) = E[f(x)|x1 = hx1, x2 = hx2]. | (27) |
Computing Shapley values directly using eqn (26) is intractable. Inspired from the local interpretable model-agnostic explanations (LIME) method,36 the same Shapely values can be computed by finding an additive feature attribution model g which minimizes the loss function L given by:25
| | 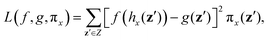 | (28) |
where
Z is the set of all possible
M-dimensional binary vectors
z′; |
z′| is the number of non-zero elements in
z′; and the function π
x(
z′) is defined as:
| | 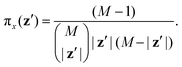 | (29) |
By such, it treats estimating the function
g in
eqn (25) essentially as a weighted linear regression problem. This approach of determining the Shapley values is referred to as Kernel SHAP method,
25 which is adopted in this work for our estimation of Shapley values for the two features [
aAW,
aBW].
3.4 Adaptive grid-search for parameters optimization
The GPR-based surrogate model and SHAP analysis are employed to perform an adaptive grid-search optimization of the parameters. This optimization process addresses a multi-target objective, defined as:| |  | (30) |
where θ = [aAW,aBW] represents the input parameters, and A = [CMC,Rg,As] denotes the output properties of interest with AT representing their target experimental values.
Four different Pluronics, as reported in Table 3, are analyzed in this work. The target experimental values for the output properties are taken from the literature and summarized in Table 5.
Table 5 Experimental values12,13 for the critical micellar concentration (CMC), radii of spherical aggregates (Rg), and aggregation numbers (As) of the considered Pluronics at 30 °C and low concentrations
| Pluronic name |
CMC [wt%] |
R
g [nm] |
A
s
|
| L64 |
2.5 |
2.28 |
10 |
| P65 |
3.2 |
2.27 |
3.8 |
| P104 |
0.002 |
5.36 |
81 |
| F68 |
10 |
2.30 |
3.5 |
The grid-search systematically evaluates combinations of parameter values across a predefined search space to identify the configuration that minimizes the objective function ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (θ). Each evaluation involves querying the GPR surrogate models to estimate the output properties for a given set of input parameters. The optimization employs an adaptive grid-search strategy, which iteratively refines the search space based on the results of previous evaluations. Unlike a traditional grid-search that evaluates all combinations of parameter values in a predefined grid, the adaptive approach dynamically adjusts the resolution and boundaries of the grid to focus on regions of interest where the objective function
(θ). Each evaluation involves querying the GPR surrogate models to estimate the output properties for a given set of input parameters. The optimization employs an adaptive grid-search strategy, which iteratively refines the search space based on the results of previous evaluations. Unlike a traditional grid-search that evaluates all combinations of parameter values in a predefined grid, the adaptive approach dynamically adjusts the resolution and boundaries of the grid to focus on regions of interest where the objective function ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (θ) is minimized. Initially, a coarse grid is defined over the range identified by SHAP analysis in the parameter space, and then the GPR models are used to evaluate
(θ) is minimized. Initially, a coarse grid is defined over the range identified by SHAP analysis in the parameter space, and then the GPR models are used to evaluate ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (θ) at each grid point. Based on these results, regions with low objective values as well as high sensitivity (as revealed from SHAP analysis) are identified, and the grid resolution in these regions is refined iteratively. Each evaluation of
(θ) at each grid point. Based on these results, regions with low objective values as well as high sensitivity (as revealed from SHAP analysis) are identified, and the grid resolution in these regions is refined iteratively. Each evaluation of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (θ) involves querying the GPR surrogate models to estimate the output properties for a given set of input parameters. The process continues until the optimal parameter configuration θopt = [aoptAW,aoptBW] that minimizes the objective function is identified.
(θ) involves querying the GPR surrogate models to estimate the output properties for a given set of input parameters. The process continues until the optimal parameter configuration θopt = [aoptAW,aoptBW] that minimizes the objective function is identified.
4 Results and discussion
4.1 Assessment of the GPR model
In this study, we employ GPR as an effective surrogate model for DPD simulations. GPR demonstrates its capability to provide accurate predictions, successfully capturing the relationships between DPD model input parameters (aAW,aBW) and the resulting properties of the system (CMC, Rg and As). Three different GPR surrogate models are employed, each tailored to predict one of the specific properties of the system based on the two input parameters.
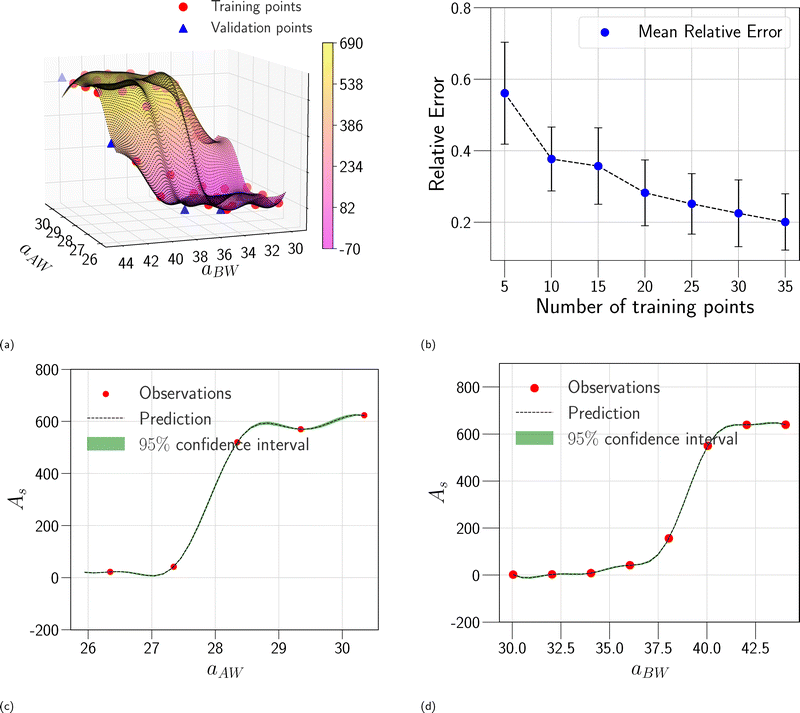
In this section, we assess the training convergence and predictive accuracy of each GPR model, using the Pluronic system L64 for demonstration. To ensure a systematic evaluation, we employ a K-fold cross-validation approach.37 Specifically, with K = 8, we randomly generate eight distinct training-validation splits, each comprising 35 training data points and 5 validation data points. For each fold, we conduct a convergence analysis to evaluate the model's accuracy as the training data size increases. The detailed procedure is as follows: (1) for the first fold, a GPR model is trained using an initial subset of 5 randomly selected data points from the 35 available training samples. The trained model's predictive performance is then quantified by computing the relative L2 error on the 5 validation data points of that fold. This error serves as the initial validation error. (2) Subsequently, a new GPR model is trained using an expanded training set of 10 data points, consisting of the previously used 5 and an additional 5 randomly sampled from the remaining 30 training data points. The validation error is computed again using the same 5 validation data points. (3) This iterative process continues, with 5 new training data points added at each step, until all 35 training data within the fold are utilized. This procedure yields a convergence curve illustrating the evolution of the validation error as the training data size grows. (4) The aforementioned convergence analysis is performed independently for each of the 8 folds. For each training data size considered (5, 10, …, 35), the mean and standard deviation of the validation errors across the 8 folds are then calculated, as shown in Fig. 5b, 6b, and 7b. This rigorous approach provides a comprehensive evaluation of how the trained GPR model's accuracy improves with increasing training data, as evidenced by the consistent decrease in the mean relative error observed with larger training sets. Finally, the ultimate surrogate model is trained using the entire dataset of 40 available data points, leading to further enhanced accuracy. Fig. 5a illustrates the validation result for one of the eight cross-validation folds using the GPR model trained on 35 data points for CMC. The CMC values predicted by the trained GPR model are displayed using a color gradient, with yellow shades indicating higher values and pink shades indicating lower values. The red circles indicate the 35 data points used to train the GPR model, while the continuous surface displays the model predictions across the aAW and aBW input space. Additionally, blue triangles mark the 5 validation data points, allowing for an assessment of the model's predictive accuracy. For the final model trained using all 40 available data, Fig. 5c and d provide detailed views of specific sections of the two-dimensional input space. These plots show slices along the aAW and aBW directions, respectively, to visualize the confidence intervals of the final GPR model. The plots display the predicted CMC values with green regions representing the 95% confidence intervals, where the very thin green regions indicate that the uncertainty of the GPR model is very low and the model represents a reliable regression. By examining these one-dimensional sections, the model's accuracy and robustness are further examined, demonstrating the capability of GPR to effectively capture variations and uncertainties within the input domain. Fig. 6 and 7 present similar analyses and findings for the GPR models of Rg and As, respectively.
 |
| | Fig. 5 GPR surrogate model predictions of CMC. (a) 3D representation of the model predictions as a function of aAW and aBW; (b) convergence plot showing the mean relative error (with standard deviation as error bars) across 8-fold cross-validation, as the number of training points increases. Each fold's convergence analysis was performed independently, and the final values represent the average behavior across folds.(c) Prediction slice along aBW at fixed aAW = 27.346; (d) prediction slice along aAW at fixed aBW = 36.046. | |
 |
| | Fig. 6 GPR surrogate model predictions of Rg. (a) 3D representation of the model predictions as a function of aAW and aBW; (b) convergence plot showing the mean relative error (with standard deviation as error bars) across 8-fold cross-validation, as the number of training points increases. Each fold's convergence analysis was performed independently, and the final values represent the average behavior across folds. (c) Prediction slice along aBW at fixed aAW = 27.346; (d) prediction slice along aAW at fixed aBW = 36.046. | |
 |
| | Fig. 7 GPR surrogate model predictions of As. (a) 3D representation of the model predictions as a function of aAW and aBW; (b) convergence plot showing the mean relative error (with standard deviation as error bars) across 8-fold cross-validation, as the number of training points increases. Each fold's convergence analysis was performed independently, and the final values represent the average behavior across folds. (c) Prediction slice along aBW at fixed aAW = 27.346; (d) prediction slice along aAW at fixed aBW = 36.046. | |
4.2 Interpretation
After assessing the training convergence and predictive accuracy of each GPR surrogate model, we next interpret the output of a GPR model through the results of the SHAP analysis. SHAP values quantify the individual contribution of each DPD model input parameter (aAW or aBW) to a specific prediction of the polymer property (CMC, Rg, or As), effectively revealing how each parameter influences the predicted property. They provide a deeper understanding of the GPR model's behavior and the underlying relationships it captures, moving beyond simple observation to provide insights into the causal mechanisms driving the predicted properties. Using the results of L64 Pluronic system as a demonstration, the SHAP summary plots in Fig. 8 visualize the quantitative impact of each input parameter on the predicted property (the GPR model's output) for all sampled points in the space of (aAW, aBW). In total 400 data points uniformly sampled (as lattice grids) in the space of (aAW, aBW) are used for this calculation. The color gradient represents the magnitude of the input parameter (red for high values, blue for low). The SHAP values not only indicate whether an input parameter pushes the prediction above (positive SHAP value) or below (negative SHAP value) the base value, but also quantify the extent. Here, the base value corresponds to the desired experimental value for each property (see Table 5). Later, it will become evident how this choice of base value greatly enhances the efficiency of the optimization process. The summary plots reveal the varying influences of aAW and aBW on CMC, As, and Rg, respectively. For CMC, higher values of aAW or aBW are associated with negative SHAP values, implying that the DPD model with higher aAW or aBW tends to predict lower CMC values than the target. In contrast, for As, higher aAW or aBW correspond to positive SHAP values, suggesting a tendency to predict higher values As. The impact on Rg is more complicated. Although higher aBW generally leads to higher Rg, the influence of aAW on Rg can depend on other parameters. High aAW typically leads to Rg values exceeding the target, while low aAW results in Rg values both below and above the desired value. This suggests a substantial interaction effect between the two parameters in determining Rg, which will be discussed further later. Furthermore, by taking the average absolute value of the SHAP values for each input parameter, we obtain a bar graph, as shown in Fig. 9. This plot reveals the relative, global importance of each input parameter in determining the predicted property by comparing the two input parameters' overall influences on the model's output. More specifically, aBW plays a significantly more prominent role in determining CMC values compared to aAW. However, both aAW and aBW influence Rg and As, with aBW slightly more influential.
 |
| | Fig. 8 SHAP summary plot for each predicted property: (a) CMC, (b) Rg, and (c) As. The color bar indicates the scaled feature (input parameter) value readings. | |
 |
| | Fig. 9 The relative importance of aAW and aBW for each predicted property, assessed using the average absolute value of the SHAP values, i.e., mean (|SHAP value|): (a) CMC, (b) Rg, and (c) As. | |
Finally, to obtain a deeper insight into the interactions between the two input parameters, we present the SHAP partial dependence plot. Based on the foregoing discussion, a potentially significant interaction between the two input parameters was identified in the determination of Rg. Thus, the SHAP partial dependence plot for Rg is examined, as shown in Fig. 10, from which we can see how the attribution of each parameter depends on the magnitudes of the other parameters. As depicted in Fig. 10a, although high values of aBW can push Rg above its target value, the influence of aBW on Rg is more pronounced when aAW is lower. As aAW decreases, its contribution to Rg shifts from a more monotonic dependence on aBW to a more sensitive and non-linear one, as indicated by Fig. 10b.
 |
| | Fig. 10 SHAP partial dependence plots for Rg: (a) variation of the attribution of aBW with respect to aAW and aBW, and (b) variation of the attribution of aAW with respect to aAW and aBW. | |
These findings validate our intuitive understanding of how the different parameters can affect the predicted property. For instance, aBW is expected to be the most influent parameter in the CMC, since it controls the repulsive force between the hydrophobic block, PPO, and water. The PPO block is the most important factor in the formation of micelles. The tendency of the Pluronic copolymers to associate spontaneously when present in dilute aqueous solutions emanates from the minimization of the contact between their hydrophobic parts and the aqueous polar environment. The micellization of Pluronic copolymers in water is strongly endothermic; it is an entropic gain, which can be attributed to the increased entropy of the water molecules as they are released from the hydrating of the PPO blocks.38 In the DPD model, this tendency is quantified by the repulsive parameter aBW. The higher aBW, the greater the tendency to self-organize into micelles. Furthermore, the presence of PEO makes this effect more pronounced. In addition, aAW has an impact, as it controls the repulsive force between PEO and water. Thus, the higher aAW, the more pronounced the effect of aBW on the CMC value. Specifically, the higher aAW, the lower the predicted CMC. The effects of aAW and aBW on As, are strictly related to the same considerations made for CMC. The higher aAW and aBW, the greater the tendency of macromolecules to self-assemble, and thus the higher the average aggregation number of clusters. In contrast, the effects of aAW and aBW on Rg are less straightforward. Although Rg scales with the aggregation number, as larger aggregates tend to form larger micelles, it is also influenced by the compactness of the structure. The compactness, in turn, depends not only on the number of macromolecules within the aggregate but also on other model parameters and their interactions.
The relationships and causal mechanisms between the input parameters and the predicted properties revealed by the SHAP analysis can also inform the optimization process to efficiently identify optimal parameter values for target properties. Using the analysis presented in Fig. 8, we can narrow down the regions in the parameter space of aAW and aBW where the optimal values may reside. Consider, for example, Fig. 8b. Firstly, we note that the base value corresponding to the experimentally observed Rg from Table 5 is 2.28 nm. This means that at any sampled data point  , the value of Rg is given by:
, the value of Rg is given by:  . Then we observe in Fig. 8b that the negative arm of aAW extends to about −1. If the SHAP value of aBW > 1, then Rg cannot reach the base value 2.28. Hence, the optimal value should occur where aBW ≤ 1. Similarly, the negative arm of aBW extends to about −2.1, so the optimal value cannot occur in the domain where the SHAP value of aAW > 2.1. The data points within these identified regions for aAW and aBW are highlighted as small yellow circles in Fig. 11a. Following the same analysis for CMC and As, we then identify the overlap region where (aAW, aBW) may simultaneously achieve the target values for all three properties, as indicated by green circles in Fig. 11b. It is worth highlighting that this approach assumes that the regions in the (aAW, aBW)-space, where the functions CMC(aAW, aBW), Rg(aAW, aBW), and As(aAW, aBW) match experimental values, are either overlapping or sufficiently close to each other. Given the close relationship between these functions, it is indeed expected that an optimal set of parameters (aAW, aBW) would allow for the simultaneous reproduction of all three target experimental values. For example, it is conceivable that micelles (or supramolecular structures, in general) may exhibit the same CMC and As while differing in compactness, leading to a radius of gyration (Rg) that is either more or less compact than the experimental value, as discussed later in Section 4.3. Furthermore, there may be situations where these regions do not overlap. In such cases, the absence of overlap between the target regions suggests that the parameter space should be expanded, for example, by including other interaction parameters, or that the current model resolution is insufficient to accurately reproduce the experimental behavior.
. Then we observe in Fig. 8b that the negative arm of aAW extends to about −1. If the SHAP value of aBW > 1, then Rg cannot reach the base value 2.28. Hence, the optimal value should occur where aBW ≤ 1. Similarly, the negative arm of aBW extends to about −2.1, so the optimal value cannot occur in the domain where the SHAP value of aAW > 2.1. The data points within these identified regions for aAW and aBW are highlighted as small yellow circles in Fig. 11a. Following the same analysis for CMC and As, we then identify the overlap region where (aAW, aBW) may simultaneously achieve the target values for all three properties, as indicated by green circles in Fig. 11b. It is worth highlighting that this approach assumes that the regions in the (aAW, aBW)-space, where the functions CMC(aAW, aBW), Rg(aAW, aBW), and As(aAW, aBW) match experimental values, are either overlapping or sufficiently close to each other. Given the close relationship between these functions, it is indeed expected that an optimal set of parameters (aAW, aBW) would allow for the simultaneous reproduction of all three target experimental values. For example, it is conceivable that micelles (or supramolecular structures, in general) may exhibit the same CMC and As while differing in compactness, leading to a radius of gyration (Rg) that is either more or less compact than the experimental value, as discussed later in Section 4.3. Furthermore, there may be situations where these regions do not overlap. In such cases, the absence of overlap between the target regions suggests that the parameter space should be expanded, for example, by including other interaction parameters, or that the current model resolution is insufficient to accurately reproduce the experimental behavior.
 |
| | Fig. 11 Confining the search space for aAW and aBW using SHAP analysis. Black circles indicate the data points sampled for performing the SHAP analysis. In (a), the red, blue, and yellow circles represent the data points falling into the regions identified by SHAP analysis for achieving target CMC, As, and Rg, respectively. In (b), the Green circles mark the overlap of these three regions. | |
As such, SHAP analysis can substantially confine the initial search space for the subsequent grid-search optimization. Instead of searching the full parameter space, i.e., 25.9 < aAW < 30.3 and 30 < aBW < 44, we can start our search only in 25.9 < aAW < 29 and 32 < aBW < 36. Besides confining the initial search space, SHAP analysis also guides the refinement of grid searches. In particular, for where SHAP values are sensitive to the other parameter, e.g., at low aAW as indicated by Fig. 10, finer grid searches are needed.
4.3 Optimization results
By leveraging the availability of GPR surrogate models for CMC, Rg and As based on the input parameters of the DPD model, the optimization step is performed using an adaptive grid search method. The average execution time of GPR is 0.001 s. The total execution time to identify the minimum of the penalty function is contingent on the grid resolution. In this analysis, we used an adaptive resolution approach that progressively increases within the area of interest to improve efficiency, as shown in Fig. 12. With the aid of SHAP analysis, this optimization process can be further accelerated, as shown in Fig. 13, where the grid search starts from a smaller space determined by SHAP analysis (as discussed in the previous section). Compared with Fig. 12, we can see that both the iteration count and the execution time per iteration are substantially reduced, highlighting the practical utility of this interpretable ML technique. Finally, the optimal parameter values identified for all Pluronic systems are summarized in Table 6 and visually represented in Fig. 14. The optimal value of aAW increases with increasing percentage content of EO weight and molecular weight of PO. This trend is even more pronounced for aBW. This behavior in the model parameters, aimed at capturing the experimental target, aligns with the considerations discussed in Section 2.2. At a fixed EO content, a higher PO content corresponds to a lower experimental CMC. To achieve a smaller CMC, both aAW and aBW must be increased, with a more significant adjustment required for aBW. Similarly, with a fixed PO content to achieve a smaller CMC, both aAW and aBW must be increased. A comparison of the experimental and computed targets is provided in Fig. 15. It demonstrates a strong correlation between the experimental and simulated CMC values, while the agreement remains good for As. For Rg, some points align well, while others show minor deviations. This suggests that optimization is more effective for CMC and As. The results indicate that the CMC is highly sensitive to the chosen model parameters, which allows us to capture its variation by only adjusting aAW and aBW. In contrast, Rg is influenced by additional parameters that were kept constant in this study, which could be considered in future work.
 |
| | Fig. 12 Adaptive grid search for optimizing L64 parameters, illustrating the progression across different refinement steps. | |
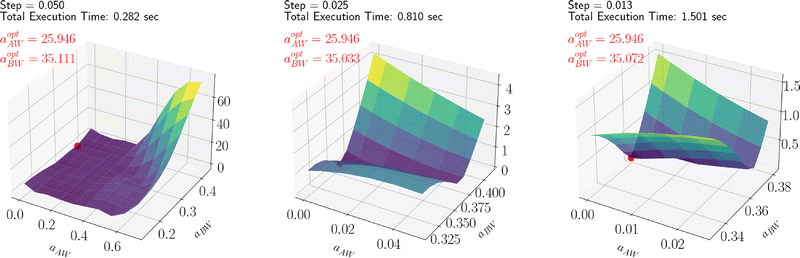 |
| | Fig. 13 SHAP assisted adaptive grid search for optimizing L64 parameters, showing results at different step sizes. | |
Table 6 Optimized DPD model parameters for the considered Pluronics
| Pluronic name |
Composition |
DPD model composition |
a
AW
|
a
BW
|
| L64 |
EO13PO30EO13 |
A3B9A3 |
25.946 |
35.072 |
| P65 |
EO20PO30EO20 |
A5B9A5 |
26.341 |
35.120 |
| P104 |
EO27PO63EO27 |
A4B18A4 |
26.472 |
40.894 |
| F68 |
EO82PO31EO82 |
A18B9A18 |
27.152 |
35.228 |
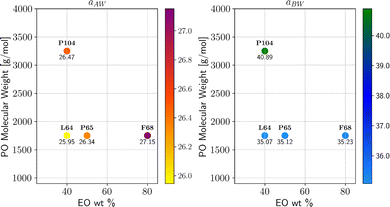 |
| | Fig. 14 Optimized DPD model parameters for the considered Pluronics systems, defined by PO molecular weight and EO content. | |
 |
| | Fig. 15 Comparison of experimental targets and computed results obtained through optimized parameters, for the critical micellar concentration (CMC), radii of spherical aggregates (Rg), and aggregation numbers (As) of the considered Pluronics at 30 °C and low concentrations. | |
5 Conclusions
This study demonstrated that the top-down parameterization of Pluronic systems significantly benefited from the application of interpretable machine learning techniques. The presented workflow outlined a successful data-driven strategy for accurately determining model parameters tailored to different Pluronic systems. In particular, we developed a GPR model as an effective surrogate for DPD simulations. GPR's strength lies in its ability to handle small datasets and provide uncertainty estimates, informing the process of creating sufficient training data for desired confidence levels. By modeling the relationship between input parameters and output properties, the GPR model significantly reduced the need for extensive DPD simulations, enabling fast predictions on the properties of various Pluronic systems and facilitating parameter optimization. Furthermore, a post hoc analysis via SHAP on the GPR model, which seeks an interpretable approximation of the GPR model through evaluating the additive feature attribution, granted deeper insights on how each input parameter impacts the output properties. This in turn allowed for a more informed exploration of the parameter space and, combined with GPR, significantly accelerated the optimization process to determine the optimal DPD model parameters that yield experimentally desired properties for diverse Pluronic systems. The model parameters obtained are specifically tuned to reproduce spherical micelles at certain temperature and concentration, ensuring accurate prediction of key properties such as the critical micelle concentration (CMC), radius of gyration, and aggregation number. It is not intended to capture the full phase diagram or to be directly transferable across different systems. This work laid the groundwork for a general framework aiming to streamline the parameterization process across various Pluronic systems (such as with different EO/PO block lengths and molecular weights) and conditions (such as differing temperatures). The goal is to generalize the parameterization process by incorporating additional DPD model input parameters and extending it to various Pluronic systems and conditions, including differing temperatures. GPR is capable of multi-variate regression, and its performance for high-dimensional surrogate modeling can be further enhanced by coupling it with dimension reduction techniques, such as proper orthogonal decomposition (POD),39,40 to reduce training and prediction costs. The interpretability provided by SHAP analysis will become increasingly valuable for high-dimensional models.
Exploring alternative ML techniques, such as deep neural networks (DNNs), could also be advantageous. DNNs generally demand more training data, and hence careful design of the network architecture and training process is needed to reduce this demand. For instance, inspired by multi-task learning strategies in natural language processing,41 we could partition DNN hidden layers into fixed layers, which learn universal features, and tunable layers, which adapt to specific systems or conditions. This approach would significantly reduce the amount of data needed for training on new systems or conditions. Another promising avenue involves leveraging graph neural networks (GNNs), drawing inspiration from the literature.42,43 By representing the DPD system explicitly as a graph, where individual beads and their pairwise interactions are encoded as nodes and edges (with edge attributes describing interaction parameters), respectively. Such a GNN-based surrogate model could potentially learn more complex relationships and generalize more effectively to unseen Pluronic systems and/or conditions. We can achieve interpretability for the constructed surrogate model by either applying the model-agnostic post hoc SHAP analysis or by building the neural network with intrinsic explainability through generalized additive models44 with structured interactions.45,46
Author contributions
Nunzia Lauriello: conceptualization (equal); data curation (lead); formal analysis (equal); investigation (equal); methodology (equal); software (lead); writing – original draft (lead). Deekshith Naidu Ponnana: formal analysis (supporting); investigation (supporting); methodology (equal); software (equal); writing – original draft (supporting). Zhan Ma: conceptualization (equal); methodology (equal); writing – review & editing (equal). Karel Šindelka: methodology (equal); software (equal); writing – original draft (supporting). Antonio Buffo: conceptualization (equal); supervision (equal); writing – review & editing (equal). Gianluca Boccardo: conceptualization (equal); supervision (equal); writing – review & editing (equal). Daniele Marchisio: conceptualization (equal); funding acquisition (lead); project administration (lead); supervision (equal); writing – review & editing (equal). Wenxiao Pan: conceptualization (equal); funding acquisition (lead); supervision (equal); writing – original draft (supporting), review & editing (equal).
Conflicts of interest
There are no conflicts to declare.
Data availability
The code used can be found online at https://github.com/mulmopro/InterpML-DPD-Param and the corresponding dataset can be accessed https://doi.org/10.5281/zenodo.15040138.
Acknowledgements
Computational resources were provided by HPC@POLITO. We acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources and support. The financial support from ICSC (Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing, funded by European Union – NextGenerationEU) is also gratefully acknowledged. This study was carried out within the “Non-equilibrium self-assembly of structured fluids: a multi-scale engineering problem” project – funded by European Union – Next Generation EU within the PRIN 2022 program (D.D. 104 – 02/02/2022 Ministero dell’Università e della Ricerca). W. P., D. N. P., and Z. M. acknowledge the funding support provided by the US Army Research Office Grant No. W911NF2310256, Defense Established Program to Stimulate Competitive Research (DEPSCoR) Grant No. FA9550-20-1-0072, and Army Research Laboratory contract No. W911NF2320073 under the Center for Extreme Events in Structurally Evolving Materials. This manuscript reflects only the authors’ views and opinions and the Ministry cannot be considered responsible for them. The authors also wish to thank the three anonymous reviewers for their constructive comments and suggestions, which helped improve the quality of the manuscript.
Notes and references
- J. Herzberger, K. Niederer, H. Pohlit, J. Seiwert, M. Worm and F. R. Wurm,
et al., Polymerization of Ethylene Oxide, Propylene Oxide, and Other Alkylene Oxides: Synthesis, Novel Polymer Architectures, and Bioconjugation, Chem. Rev., 2016, 116(4), 2170–2243 CrossRef CAS PubMed
 .
.
- A. V. Kabanov, E. V. Batrakova and V. Y. Alakhov, Pluronic® block copolymers as novel polymer therapeutics for drug and gene delivery, J. Controlled Release, 2002, 82, 189–212 CrossRef CAS PubMed
 .
.
- N. A. D. Spirito, N. Grizzuti and R. Pasquino, Self-assembly of Pluronics: A critical review and relevant applications, Phys. Fluids, 2024, 36, 111302 CrossRef
 .
.
- M. J. Newman, M. Balusubramanian and C. W. Todd, Development of adjuvant-active nonionic block copolymers, Adv. Drug Delivery Rev., 1998, 32(3), 199–223 CrossRef CAS PubMed
 .
.
- D. Y. Alakhova and A. V. Kabanov, Pluronics and MDR Reversal: An Update, Mol. Pharmaceutics, 2014, 11(8), 2566–2578 CrossRef CAS PubMed
 .
.
- K. C. de Castro, J. C. Coco, É. M. dos Santos, J. A. Ataide, R. M. Martinez and M. H. M. do Nascimento,
et al., Pluronic® triblock copolymer-based nanoformulations for cancer therapy: A 10-year overview, J. Controlled Release, 2023, 353, 802–822 CrossRef CAS PubMed
 .
.
- P. Alexandridis and T. A. Hatton, Poly(ethylene oxide)-poly(propylene oxide)-poly(ethylene oxide) block copolymer surfactants in aqueous solutions and at interfaces: thermodynamics, structure, dynamics, and modeling, Colloids Surf., A, 1995, 96, 1–46 CrossRef CAS
 .
.
-
P. Alexandrilis and B. Lindman, Amphiphilic Block Copolymers-Self-Assembly and Applications, Elsevier, 2000 Search PubMed
 .
.
- N. A. Di Spirito, N. Grizzuti, M. Casalegno, F. Castiglione and R. Pasquino, Phase transitions of aqueous solutions of Pluronic F68 in the presence of Diclofenac Sodium, Int. J. Pharm., 2023, 644, 37647976 CrossRef PubMed
 .
.
- A. Pitto-Barry and N. P. E. Barry, Pluronic block-copolymers in medicine: from chemical and biological versatility to rationalisation and clinical advances, Polym. Chem., 2014, 5, 3281–3496 RSC
 .
.
- N. U. Khaliq, J. Lee, S. Kim, D. Sung and H. Kim, Pluronic F-68 and F-127 Based Nanomedicines for Advancing Combination Cancer Therapy, Pharmaceutics, 2023, 15(8), 2102 CrossRef CAS PubMed
 .
.
- G. Wanka, H. Hoffmann and W. Ulbricht, Phase Diagrams and Aggregation Behavior of Poly(oxyethylene)-Poly(oxypropylene)-Poly(oxyethylene) Triblock Copolymers in Aqueous Solutions, Macromolecules, 1994, 27, 4145–4159 CrossRef CAS
 .
.
- A. V. Kabanov, I. R. Nazarova, I. V. Astafieva, E. V. Batrakova, V. Y. Alakhov and A. A. Yaroslavov,
et al., Micelle Formation and Solubilization of Fluorescent Probes in Poly(oxyethylene-b-oxypropylene-boxyethylene) Solutions, Macromolecules, 1995, 28, 2303–2314 CrossRef CAS
 .
.
- R. D. Groot and P. B. Warren, Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation, J. Chem. Phys., 1997, 107(11), 4423–4435 CrossRef CAS
 .
.
- K. Procházka, Z. Limpouchová, M. Štěpánek, K. Šindelka and M. Lísal, DPD Modelling of the Self- and Co-Assembly of Polymers and Polyelectrolytes in Aqueous Media: Impact on Polymer Science, Polymers, 2022, 14(3), 404 CrossRef PubMed
 .
.
- S. Trément, B. Schnell, L. Petitjean, M. Couty and B. Rousseau, Conservative and dissipative force field for simulation of coarsegrained alkane molecules: A bottom-up approach, J. Chem. Phys., 2014, 140(13), 134113 CrossRef PubMed
 .
.
- S. Izvekov and B. M. Rice, Multi-scale coarse-graining of nonconservative interactions in molecular liquids, J. Chem. Phys., 2014, 140(4), 104104 CrossRef PubMed
 .
.
- H. Mori, Transport, collective motion and brownian motion, Prog. Theor. Phys., 1965, 33, 423–455 CrossRef
 .
.
- R. Zwanzig, Transport, collective motion and brownian motion, J. Chem. Phys., 1965, 33, 1338 CrossRef
 .
.
- H. Droghetti, I. Pagonabarraga, P. Carbone, P. Asinari and D. Marchisio, Dissipative particle dynamics simulations of tri-block copolymer and water: Phase diagram validation and microstructure identification, J. Chem. Phys., 2018, 149(18), 184903 CrossRef PubMed
 .
.
- R. Pasquino, H. Droghetti, P. Carbone, S. Mirzaagha, N. Grizzuti and D. Marchisio, An experimental rheological phase diagram of a tri-block co-polymer in water validated against dissipative particle dynamics simulations, Soft Matter, 2019, 15(6), 1396–1404 RSC
 .
.
- A. Prhashanna, S. A. Khan and S. B. Chen, Co-Micellization Behavior in Poloxamers: Dissipative Particle Dynamics Study, J. Phys. Chem. B, 2015, 119(2), 572–582 CrossRef CAS PubMed
 .
.
- J. B. Avalos, M. Lísal, J. P. Larentzos, A. D. Mackie and J. K. Brennan, Generalised dissipative particle dynamics with energy conservation: density- and temperature-dependent potentials, Phys. Chem. Chem. Phys., 2019, 21(45), 24891–24911 RSC
 .
.
-
P. J. Flory, Principles of Chemistry Cap.12, Cornell University Press, Itacha, NY, 1953 Search PubMed
 .
.
-
S. M. Lundberg and S. I. Lee, A Unified Approach to Interpreting Model Predictions, Advances in Neural Information Processing Systems, Curran Associates, Inc., 2017, vol. 30 Search PubMed
 .
.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics, Europhys. Lett., 1992, 19(3), 155–160 CrossRef
 .
.
- P. Español and P. Warren, Statistical mechanics of dissipative particle dynamics, Europhys. Lett., 1995, 30(4), 191–196 CrossRef
 .
.
- M. P. Allen and F. Schmid, A thermostat for molecular dynamics of complex fluids, Mol. Simul., 2006, 33, 21–26 CrossRef
 .
.
- P. Durchschlag and H. Zipper, Calculation of the partial volume of organic compounds and polymers, Prog. Colloid Polym. Sci., 1994, 94, 20–39 Search PubMed
 .
.
-
B. A. C. van Vlimmeren, N. M. Maurits, A. V. Zvelindovsky, G. J. A. Sevink and J. G. E. M. Fraaije, Simulation of 3D Mesoscale Structure Formation in Concentrated Aqueous Solution of the Triblock Polymer Surfactants (Ethylene Oxide) 13(Propylene Oxide)30(Ethylene Oxide)13 and (Propylene Oxide)19(Ethylene Oxide)33(Propylene Oxide)19, Application of Dynamic Mean-Field Density Functional Theory, ACS Publications, 1999, vol. 32, pp. 646–656 Search PubMed
 .
.
- N. Lauriello, M. Lísal, G. Boccardo, D. Marchisio and A. Buffo, Modeling temperature-dependent transport properties in dissipative particle dynamics: A top-down coarse-graining toward realistic dynamics at the mesoscale, J. Chem. Phys., 2024, 161(3), 034112 CrossRef CAS PubMed
 .
.
- P. Vanya, J. Sharman and J. A. Elliott, Invariance of experimental observables with respect to coarse-graining in standard and many-body dissipative particle dynamics, J. Chem. Phys., 2019, 150(6), 064101 CrossRef PubMed
 .
.
- H. Rezaei and H. Modarress, Dissipative particle dynamics (DPD) study of hydrocarbon–water interfacial tension (IFT), Chem. Phys. Lett., 2015, 620, 114–122 CrossRef CAS
 .
.
- K. Šindelka and M. Lísal, Interplay between surfactant selfassembly and adsorption at hydrophobic surfaces: insights from dissipative particle dynamics, Mol. Phys., 2021, 119(15–16), e1857863 CrossRef
 .
.
- D. C. Liu and J. Nocedal, On the limited memory BFGS method for large scale optimization, Math. Prog., 1989, 45, 503–528 CrossRef
 .
.
-
M. T. Ribeiro, S. Singh and C. Guestrin “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD ’16. New York, NY, USA: Association for Computing Machinery, 2016, pp. 1135–1144.
-
G. James, D. Witten, T. Hastie and R. Tibshirani, An Introduction to Statistical Learning: With Applications in R, Springer Texts in Statistics, Springer, New York, 1st edn, 2013 Search PubMed
 .
.
- P. Alexandridis, Amphiphilic copolymers and their applications, Curr. Opin. Colloid Interface Sci., 1996, 1(4), 490–501 CrossRef CAS
 .
.
- Z. Ma, S. Wang, M. Kim, K. Liu, C. L. Chen and W. Pan, Transfer learning of memory kernels for transferable coarse-graining of polymer dynamics, Soft Matter, 2021, 17(24), 5864–5877 RSC
 .
.
- Z. Ma and W. Pan, Data-driven nonintrusive reduced order modeling for dynamical systems with moving boundaries using Gaussian process regression, Comput. Methods Appl. Mech. Eng., 2021, 373, 113495 CrossRef
 .
.
- S. Chen, Y. Zhang and Q. Yang, Multi-task learning in natural language processing: An overview, ACM Comput. Surv., 2024, 56(12), 1–32 Search PubMed
 .
.
- Z. Ma, Z. Ye and W. Pan, Fast simulation of particulate suspensions enabled by graph neural network, Comput. Methods Appl. Mech. Eng., 2022, 400, 115496 CrossRef
 .
.
- A. Aminimajd, J. Maia and A. Singh, Scalability of a graph neural network in accurate prediction of frictional contact networks in suspensions, Soft Matter, 2025, 21, 2826–2835 RSC
 .
.
- R. Agarwal, L. Melnick, N. Frosst, X. Zhang, B. Lengerich and R. Caruana,
et al., Neural additive models: Interpretable machine learning with neural nets, Adv. Neural Inf. Process. Syst., 2021, 34, 4699–4711 Search PubMed
 .
.
- Z. Yang, A. Zhang and A. Sudjianto, GAMI-Net: An explainable neural network based on generalized additive models with structured interactions, Pattern Recogn., 2021, 120, 108192 CrossRef
 .
.
- S. Ibrahim, G. Afriat, K. Behdin and R. Mazumder, GRANDSLAMIN’Interpretable Additive Modeling with Structural Constraints, Adv. Neural Inf. Process. Syst., 2023, 36, 61158–61186 Search PubMed
 .
.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  b,
Karel
Šindelka
b,
Karel
Šindelka
 c,
Antonio
Buffo
a,
Gianluca
Boccardo
a,
Daniele
Marchisio
a and
Wenxiao
Pan
c,
Antonio
Buffo
a,
Gianluca
Boccardo
a,
Daniele
Marchisio
a and
Wenxiao
Pan
 *b
*b
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, with a PEO content of 10 to 80 wt%. These materials are named using an alphanumeric code that combines a letter and two or three digits.4 The letter represents the physical state at room temperature: L for liquids, P for pastes, and F for flakes. The digits denote the molecular weight and composition. Specifically, the molecular weight of the hydrophobic PO block is calculated by multiplying the first one or two digits by 300, while the hydrophilic EO content (in weight percentage) is determined by multiplying the final digit by 10. Different Pluronics are cataloged according to the molecular weight of the PPO and the PEO contents in the Pluronic grid, reported in Fig. 1. Pluronics are often referred to as EOxPOyEOx, where x and y represent the number of EO and PO units as shown in Fig. 2, respectively. The degree of polymerization of the Pluronic hydrophilic and hydrophobic segments determines its hydrophilic–lipophilic properties. The ratio between the lengths of the EO and PO chains defines the hydrophilic–lipophilic balance (HLB), which quantifies the Pluronic degree of hydrophilicity or lipophilicity.5 The HLB of Pluronic molecules can be calculated using the following equation:6
000 g mol−1, with a PEO content of 10 to 80 wt%. These materials are named using an alphanumeric code that combines a letter and two or three digits.4 The letter represents the physical state at room temperature: L for liquids, P for pastes, and F for flakes. The digits denote the molecular weight and composition. Specifically, the molecular weight of the hydrophobic PO block is calculated by multiplying the first one or two digits by 300, while the hydrophilic EO content (in weight percentage) is determined by multiplying the final digit by 10. Different Pluronics are cataloged according to the molecular weight of the PPO and the PEO contents in the Pluronic grid, reported in Fig. 1. Pluronics are often referred to as EOxPOyEOx, where x and y represent the number of EO and PO units as shown in Fig. 2, respectively. The degree of polymerization of the Pluronic hydrophilic and hydrophobic segments determines its hydrophilic–lipophilic properties. The ratio between the lengths of the EO and PO chains defines the hydrophilic–lipophilic balance (HLB), which quantifies the Pluronic degree of hydrophilicity or lipophilicity.5 The HLB of Pluronic molecules can be calculated using the following equation:6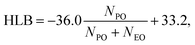



![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (θ) requires running a full DPD simulation, followed by a post-processing step to extract the relevant properties. In addition, for each time variable like temperature or the type of Pluronic change, a new simulation is required, adding complexity to the process. DPD simulations are known to be computationally expensive, making them time-consuming and impractical for high-dimensional optimization tasks. This extensive search through the parameter space is not only labor-intensive and costly but also demands substantial expertise from researchers. Machine learning techniques could potentially streamline this parameter optimization process (Fig. 3) by reducing the effort and enhancing accuracy.
(θ) requires running a full DPD simulation, followed by a post-processing step to extract the relevant properties. In addition, for each time variable like temperature or the type of Pluronic change, a new simulation is required, adding complexity to the process. DPD simulations are known to be computationally expensive, making them time-consuming and impractical for high-dimensional optimization tasks. This extensive search through the parameter space is not only labor-intensive and costly but also demands substantial expertise from researchers. Machine learning techniques could potentially streamline this parameter optimization process (Fig. 3) by reducing the effort and enhancing accuracy.

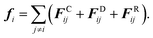

![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij = rij/rij is the unit vector of the bead-bead separation distance and rCc is the cutoff radius for the conservative interactions.
ij = rij/rij is the unit vector of the bead-bead separation distance and rCc is the cutoff radius for the conservative interactions.











![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Ntrain is the mean function, and Σ(X,X) ∈
Ntrain is the mean function, and Σ(X,X) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Ntrain×Ntrain is the covariance matrix. The covariance function is defined using the radial basis function (RBF) kernel, which measures the similarity between two input points xi and xj. The RBF kernel is given by:
Ntrain×Ntrain is the covariance matrix. The covariance function is defined using the radial basis function (RBF) kernel, which measures the similarity between two input points xi and xj. The RBF kernel is given by:

 and
and  is the determinant of matrix
is the determinant of matrix  . Here, Θ = [σ,θa,θl], which include the noise level σ and kernel parameters θa and θl, are optimized using the L-BFGS quasi-Newton optimization algorithm.35
. Here, Θ = [σ,θa,θl], which include the noise level σ and kernel parameters θa and θl, are optimized using the L-BFGS quasi-Newton optimization algorithm.35


 indicates the prediction confidence and reveals the associated uncertainty of this prediction. The 95% confidence interval is determined from the mean prediction and the standard deviation as: [mean_prediction −1.96× std_prediction, mean_prediction +1.96× std_prediction], where the standard deviation is calculated as the square root of each diagonal element of the covariance matrix.
indicates the prediction confidence and reveals the associated uncertainty of this prediction. The 95% confidence interval is determined from the mean prediction and the standard deviation as: [mean_prediction −1.96× std_prediction, mean_prediction +1.96× std_prediction], where the standard deviation is calculated as the square root of each diagonal element of the covariance matrix.

![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) represents the contribution of feature i to the output f(hx(z′)); and ϕ0 is the base value of the model output without any feature's contribution. In particular for our analysis, f(x) is the GPR surrogate model with the input vector x = [aAW,aBW]; and M = 2, i.e., z′ and hx(z′) are both two-dimensional vectors. The attribution values ϕi are referred to as Shapley values (or SHAP values). By the definition and additive nature of g, Shapley values can effectively quantify how much each input feature contributes to the value of the output.
represents the contribution of feature i to the output f(hx(z′)); and ϕ0 is the base value of the model output without any feature's contribution. In particular for our analysis, f(x) is the GPR surrogate model with the input vector x = [aAW,aBW]; and M = 2, i.e., z′ and hx(z′) are both two-dimensional vectors. The attribution values ϕi are referred to as Shapley values (or SHAP values). By the definition and additive nature of g, Shapley values can effectively quantify how much each input feature contributes to the value of the output.
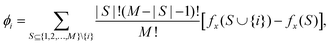
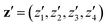 . Let S = {1,3} which implies z′ = (1,0,1,0). If we denote the ith component of hx(z′) by hxi then fx(S) is given by
. Let S = {1,3} which implies z′ = (1,0,1,0). If we denote the ith component of hx(z′) by hxi then fx(S) is given by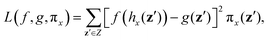
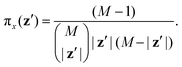

![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (θ). Each evaluation involves querying the GPR surrogate models to estimate the output properties for a given set of input parameters. The optimization employs an adaptive grid-search strategy, which iteratively refines the search space based on the results of previous evaluations. Unlike a traditional grid-search that evaluates all combinations of parameter values in a predefined grid, the adaptive approach dynamically adjusts the resolution and boundaries of the grid to focus on regions of interest where the objective function
(θ). Each evaluation involves querying the GPR surrogate models to estimate the output properties for a given set of input parameters. The optimization employs an adaptive grid-search strategy, which iteratively refines the search space based on the results of previous evaluations. Unlike a traditional grid-search that evaluates all combinations of parameter values in a predefined grid, the adaptive approach dynamically adjusts the resolution and boundaries of the grid to focus on regions of interest where the objective function ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (θ) is minimized. Initially, a coarse grid is defined over the range identified by SHAP analysis in the parameter space, and then the GPR models are used to evaluate
(θ) is minimized. Initially, a coarse grid is defined over the range identified by SHAP analysis in the parameter space, and then the GPR models are used to evaluate ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (θ) at each grid point. Based on these results, regions with low objective values as well as high sensitivity (as revealed from SHAP analysis) are identified, and the grid resolution in these regions is refined iteratively. Each evaluation of
(θ) at each grid point. Based on these results, regions with low objective values as well as high sensitivity (as revealed from SHAP analysis) are identified, and the grid resolution in these regions is refined iteratively. Each evaluation of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (θ) involves querying the GPR surrogate models to estimate the output properties for a given set of input parameters. The process continues until the optimal parameter configuration θopt = [aoptAW,aoptBW] that minimizes the objective function is identified.
(θ) involves querying the GPR surrogate models to estimate the output properties for a given set of input parameters. The process continues until the optimal parameter configuration θopt = [aoptAW,aoptBW] that minimizes the objective function is identified.


 , the value of Rg is given by:
, the value of Rg is given by:  . Then we observe in Fig. 8b that the negative arm of aAW extends to about −1. If the SHAP value of aBW > 1, then Rg cannot reach the base value 2.28. Hence, the optimal value should occur where aBW ≤ 1. Similarly, the negative arm of aBW extends to about −2.1, so the optimal value cannot occur in the domain where the SHAP value of aAW > 2.1. The data points within these identified regions for aAW and aBW are highlighted as small yellow circles in Fig. 11a. Following the same analysis for CMC and As, we then identify the overlap region where (aAW, aBW) may simultaneously achieve the target values for all three properties, as indicated by green circles in Fig. 11b. It is worth highlighting that this approach assumes that the regions in the (aAW, aBW)-space, where the functions CMC(aAW, aBW), Rg(aAW, aBW), and As(aAW, aBW) match experimental values, are either overlapping or sufficiently close to each other. Given the close relationship between these functions, it is indeed expected that an optimal set of parameters (aAW, aBW) would allow for the simultaneous reproduction of all three target experimental values. For example, it is conceivable that micelles (or supramolecular structures, in general) may exhibit the same CMC and As while differing in compactness, leading to a radius of gyration (Rg) that is either more or less compact than the experimental value, as discussed later in Section 4.3. Furthermore, there may be situations where these regions do not overlap. In such cases, the absence of overlap between the target regions suggests that the parameter space should be expanded, for example, by including other interaction parameters, or that the current model resolution is insufficient to accurately reproduce the experimental behavior.
. Then we observe in Fig. 8b that the negative arm of aAW extends to about −1. If the SHAP value of aBW > 1, then Rg cannot reach the base value 2.28. Hence, the optimal value should occur where aBW ≤ 1. Similarly, the negative arm of aBW extends to about −2.1, so the optimal value cannot occur in the domain where the SHAP value of aAW > 2.1. The data points within these identified regions for aAW and aBW are highlighted as small yellow circles in Fig. 11a. Following the same analysis for CMC and As, we then identify the overlap region where (aAW, aBW) may simultaneously achieve the target values for all three properties, as indicated by green circles in Fig. 11b. It is worth highlighting that this approach assumes that the regions in the (aAW, aBW)-space, where the functions CMC(aAW, aBW), Rg(aAW, aBW), and As(aAW, aBW) match experimental values, are either overlapping or sufficiently close to each other. Given the close relationship between these functions, it is indeed expected that an optimal set of parameters (aAW, aBW) would allow for the simultaneous reproduction of all three target experimental values. For example, it is conceivable that micelles (or supramolecular structures, in general) may exhibit the same CMC and As while differing in compactness, leading to a radius of gyration (Rg) that is either more or less compact than the experimental value, as discussed later in Section 4.3. Furthermore, there may be situations where these regions do not overlap. In such cases, the absence of overlap between the target regions suggests that the parameter space should be expanded, for example, by including other interaction parameters, or that the current model resolution is insufficient to accurately reproduce the experimental behavior.


.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.







