Evolution of the structure in a soft binary colloidal mixture during thermodynamic processes of cooling and heating

Abstract

The study of the structural evolution of a material under equilibrium or nonequilibrium thermodynamic conditions is fundamental for understanding its stability and predicting its phase behavior. To the best of our knowledge, the structural transformations induced by different temperature protocols have not been fully understood. This study provides a detailed molecular resolution of the structural evolution occurring in a bidisperse colloidal mixture of soft spheres, as it is subjected to a sequence of controlled thermodynamic processes of heating and cooling. The structural transformations are studied between two equilibrium configurations at different temperatures through extensive molecular dynamics simulations. By exploring the interplay of multiple length and time scales, we uncover how these protocols influence the progression of the colloidal suspension toward thermodynamic equilibrium. Our results show that under fast temperature changes, heating and cooling processes follow distinct thermodynamic pathways toward the corresponding equilibrium configuration because of the emergence of different structural mechanisms, which are discussed here in detail; these distinct pathways are defined as thermodynamic asymmetries that depend strongly on the temperature protocol and the composition of the dispersion. In contrast, for sufficiently slow temperature changes, we identify the condition under which both protocols follow symmetric and reversible pathways.

---

1. Introduction

A thermodynamic system, along with its transitions through various states, can be characterized using either an energy-based or an entropy-based description.¹ This means that the fundamental concepts and relations of both formulations (involving variables or functions of the measurable macroscopic properties) are typically built on a scheme centered on equilibrium states obtained from an extreme principle; energy minimization (dE_S = 0) at a given entropy or entropy maximization (dS_E = 0) at a fixed energy,¹ E and S represent the internal energy and the entropy, respectively, while the subscript indicates that such a parameter remains constant. Choosing the equilibrium approach helps simplify the thermodynamic description whenever the system changes between different states.² This is the standard approach in most Thermodynamics textbooks,^1,2 but it presents limitations, as it cannot describe, for example, the evolution of any thermodynamic system that undergoes a transition between different states, which can lead to the formation of dynamical arrested states or non-equilibrium phases, such as gels and glasses.^3–5

The characteristic time needed to reach equilibrium between different states is called the relaxation time and can vary from one system to another in different orders of magnitude and depends on the thermodynamic protocol employed to induce a state change.² Unless the process is quasi-static, that is, when the change is too slow compared to the characteristic relaxation times,^1,2 nothing guarantees that the thermodynamic process is reversible and symmetric, which means that the thermodynamic pathways from one state to another and vice versa are practically the same.

As mentioned above, it could be the case that the final thermodynamic state is out of equilibrium; an example of this can be observed when the spontaneous evolution process of a system toward its thermodynamic equilibrium state is interrupted by the appearance of favorable conditions for aging or dynamical arrest,⁶ which implies that the system does not quickly stabilize into an equilibrium state but instead displays a behavior that evolves slowly with time and depends significantly on the preparation protocol,^3–5,7 for example, the temperature ramp chosen to heat up or cool down the system.

When analyzing thermodynamic states, whether in equilibrium or not, the temperature T associated with the system under study is crucial, mainly because it is explicitly related to thermal energy.⁸ This is a feature that can be straightforwardly corroborated in colloidal systems, which are excellent model systems that allow us to study fundamental questions related to equilibrium and non-equilibrium transitions,⁹ where the random displacements that characterize colloidal motion originate from the thermal energy, which is of the order of k_BT for each colloidal particle,¹⁰ where k_B is the Boltzmann constant. In the general context of the design of complex materials, temperature also plays a crucial role in processes related to phase transitions or aggregation phenomena, for example, cluster formation,^11,12 gelation,¹³ crystallization,¹⁴ glass transition,⁷ flocculation,^15,16 etc.

Furthermore, changes in temperature can alter the stiffness of soft matter systems, affecting their shear viscosity, shear elastic modulus, and viscoelasticity.^17,18 At the right temperature, complex structures with unique properties can spontaneously form through a process called self-assembly.¹⁹ For example, temperature has been shown to influence the morphology of micelles in copolymer solutions, as transitions from worm-shaped to spherical micelles or vice versa can be generated, depending on whether a heating or cooling protocol is applied.²⁰ Temperature also acts as a factor that modulates the interactions and stability of micelles, since it influences the mobility of surface particles.²¹ At low temperatures, mobility can decrease, favoring the aggregation of structures and affecting the formation of micelles compared to conditions at high temperatures.²¹

Now, given the possible implications and applications that a change in thermodynamic state entails, as well as the fundamental relationships that exist in equilibrium thermodynamics in this regard, we could ask ourselves the following: is it possible to extend them to non-equilibrium conditions to understand, for example, time-dependent transient states during an equilibration process? To address this inquiry, theoretical tools have been developed with the intention of extending the results of equilibrium liquid state theory to non-equilibrium situations,^8,22–27 suggesting that many equilibrium derivations can be understood under steady-state conditions rather than strictly thermodynamic equilibrium, providing a framework for understanding how liquids respond to temporary changes in the thermodynamic conditions underlying the system.²³ It is also necessary to highlight the importance that molecular simulations and experimental techniques have had in complementing the theoretical understanding of phenomena in non-equilibrium liquids, particularly to obtain relevant information with greater detail and molecular resolution.^5,28–40

In this contribution, we consider both monodisperse and bidisperse soft colloidal particles, with the aim of investigating their structural evolution when they undergo a thermodynamic process of heating or cooling between two distinct equilibrium states. We mainly focus on the transient states between the initial and final configurations of the process that occur within the relaxation time.

The radial distribution function (RDF, g(r)) plays a fundamental role in liquid state theory under equilibrium conditions,⁸ and its extension to non-equilibrium states implies a function g(r;t), which is relevant in the study of the properties of the evolving system, vital to unraveling the main features (evolution of the self-assembly process and the transformation of the relevant length scales) of the transient states.²³ Then, we present a comprehensive analysis of instantaneous RDFs. The heating and cooling protocols were implemented using a linear temperature ramp over time, as this is the simplest approach requiring only a single control parameter. This parameter may or may not coincide with the dominant timescale of the system. Linear temperature ramps are commonly employed in experimental setups, particularly with laboratory muffle furnaces, where precise control over heating rates can be achieved.^41,42 Although less common, linear cooling protocols have also been used in some experiments.⁴³ The results were obtained using extensive molecular dynamics simulations, in which the thermal variation was performed by rescaling the colloidal velocities in accordance with the temperature at each given instant of time.

Our results show that during gradual or slow changes in temperature, it is possible to see that the colloidal structure evolves in a quasistatic and reversible manner, exhibiting symmetric behavior when the colloidal dispersion is cooling and heating. In contrast, during fast processes (abrupt transition), the colloidal system goes through a sequence of non-equilibrium states and the symmetry between the cooling and heating processes is broken; however, convergence is maintained in the extreme equilibrium states. These results also show that the methodology used and reported here can be a good tool for studying different temperature protocols or heating and cooling rates, which is of the utmost importance in the development of materials, where heat treatments are necessary to obtain, for example, the desired stoichiometry or phase.

Our findings also reveal that temperature changes in the mixture favor the appearance of certain structures. For example, when the system is heated, the large colloids separate sufficiently so that a small colloid can occupy the gap between them, thus creating a favorable environment for the formation of configurations of the type large–small–large colloid. However, when the mixture is cooled, this type of structure disappears and it is observed that the small colloids are expelled from the space between two large colloids. Then, the way in which the structure evolves in response to the different temperature changes is very important, since within the context of the effective interactions of entropic origin, in particular in hard-core-like colloidal systems, the behavior of the colloids would significantly modulate the form and magnitude of the entropic depletion forces.

The structures formed when the system is heated would imply the appearance of a so-called “entropic gate”⁴⁴ which, as shown in other contributions,^44–46 is very important for the stability of a colloidal mixture. However, when the system is cooled, the structural evolution indicates that this entropic gate tends to disappear. Therefore, our results show that the cooling or heating protocols can also serve as a kind of “entropic switch”; a mechanism that is not exclusive of the size ratio and particle composition, as previous work has shown,^45,46 and drastically modify the effective interactions between colloids towards equilibration. The fact that temperature changes can effect the effective interaction between colloids under nonequilibrium conditions has already been theoretically proposed; see, e.g., ref. 7 and 47, where g(r;t) greatly influences the attraction or repulsion between colloids.

2. Molecular simulation details and temperature protocol

2.1. Interaction potential and molecular dynamics simulations

To explore the influence of distinct length and time scales on structural evolution, we propose a bidisperse system of soft spheres, labeled large (l) and small (s), with diameters σ_l and σ_s, respectively. The size ratio between large and small particles is defined as η = σ_l/σ_s. The interaction between particles is governed by the Weeks–Chandler–Andersen (WCA) potential, which provides a soft repulsive representation⁴⁸where σ_ij = (σ_i + σ_j)/2. The energy scale is set by the parameter ε, which we use as the unit of energy; it has been recently shown that a single parameter ε can be used to describe the static properties of binary and polydisperse colloidal dispersions, see, e.g., ref. 49. Consequently, we define the reduced temperature as T* ≡ k_BT/ε and introduce a reference temperature T_ref such that k_BT_ref = ε, corresponding to T* = 1. The structural evolution of the colloidal dispersion is then studied during the thermodynamic processes of cooling and heating as the temperature varies between a high temperature value (k_BT = 10ε) and a lower temperature value (k_BT = 0.1ε).

Significant differences arise when a soft potential, such as the WCA potential, is employed instead of a hard-sphere potential. First of all, the latter is an athermal potential. In contrast, the softness of the WCA potential allows the particles to reach distances shorter than σ_ij, leading to effective overlap. As the kinetic energy of the particles increases, greater overlaps occur as this energy is transformed into potential energy. This behavior introduces a temperature dependence in the structure of the colloidal system, since the increased kinetic energy allows the exploration of a broader range of thermodynamic states. As expected, in the hard-sphere model, variations in the particle kinetic energy do not induce changes in the structure.⁸

For all simulations, the length, mass, and time scales are given by σ_l, m_l, and , respectively. Both large and small particles are considered to have the same density, so the mass m_s is proportional to m_l in volume. Furthermore, the size ratio is η = 5. The total number of particles is N = N_l + N_s with N_l and N_s being the numbers of large and small particles, respectively. The volume fraction of the α-th species is given by ϕ_α = πσ_α³N_α/6V, while the total volume fraction is ϕ = ϕ_l + ϕ_s. Typical values in our calculations are V^1/3 = 17σ_l, N_l = 4064, and N_s = 127 008. We also consider a monodisperse colloidal dispersion made up of spheres of diameter σ and packing fraction ϕ = 0.4, where N = 32 768 particles were used in the calculations and a simulation box with side V^1/3 = 35σ. We aim to study the evolution from one equilibrium configuration to another, making it crucial to ensure that the colloidal system remains in a liquid phase to avoid the glass transition. In fact, in this work, the chosen packing fractions and the size ratio parameters guarantee that the colloidal dispersion is within the fluid phase of the phase diagram.⁵ Technically speaking, at the highest and lowest temperatures here explored, together with the chosen composition of the mixture, the colloidal dispersion reached its corresponding equilibrium state. This means that we only report the transient non-equilibrium thermodynamic states between the equilibrium ones. All simulations were run on GPUs, using the CUDA extension of the C language.

2.2. Temperature protocol

Simulations are performed in the canonical ensemble NVT, ensuring that both the total number of particles and the simulation box remain constant. At any given time step during the simulation, the instantaneous temperature can be determined from the velocities of all particles using the equipartition theorem,⁵⁰ yielding a temperature T′. To set a new target temperature, the velocities are rescaled accordingly. Specifically, if the desired system temperature is T, the velocities are rescaled by a factor of .

To investigate structural changes induced by temperature variations, a temperature protocol is defined. Suppose that the colloidal system is initially at temperature T₀ and evolves linearly over a period of time t_ramp to a final temperature T_f. In that case, the instantaneous temperature T(t) at time t is given by:

From this point on, it will be understood that all temperatures are expressed in a dimensionless form omitting the *. Equivalently, we define the temperature rate of change as α_ramp = (T_f − T₀)/t_ramp. Alternatively, the change in temperature between successive steps of the simulation can be expressed as T_i+1 = (1 ± δ)T_i, where the minus sign is for a cooling process and the plus sign for a heating process. For fast protocols, the typical values of δ range from 4 × 10⁻⁴ to 4 × 10⁻², whereas for slow protocols, δ is approximately between 1 × 10⁻⁶ and 1 × 10⁻⁴. A more detailed description of the slow and fast protocols is provided in Section 3.

Table 1 presents the characteristic times for the large (τ_l) and small (τ_s) particles at different temperatures. For the monodisperse case, the values are equal to those of large particles τ_l. It can be seen that τ_s is significantly smaller than τ_l, indicating that most of the structural evolution between large particles occurs after the small particles have already relaxed to equilibrium. For fast protocols, the structural evolution takes place on timescales comparable to the characteristic time of large particles. However, during transient states, the system does not evolve according to a single characteristic timescale, neither that of the small nor that of the large particles, since these states are governed by a competition between different time and length scales due to the energetic and structural changes. All these features will be illustrated in the following sections.

Table 1 Temperature and the characteristic time scales of the big, τ_l, and the small, τ_s, colloids. The monodisperse case corresponds to the values of τ_l

T*	τl (τref)	τs (τref)
10.0	0.33	0.005
1.0	1.0	0.017
0.1	3.33	0.05

---

To calculate the instantaneous RDF, we create a histogram of interparticle separations based on the following definition⁸

where 〈⋯〉_T(t) denotes an average over different configurations at temperature T(t).

Fig. 1 presents a flowchart illustrating the calculation of the RDFs as the colloidal dispersion evolves. At each iteration, the system temperature is adjusted according to the temperature protocol, and velocity rescaling is applied to achieve the new target temperature. The system configuration is then evolved using the velocity Verlet algorithm,⁵¹ and the RDF is calculated for the updated configuration. This process is repeated iteratively until the temperature protocol is completed. Furthermore, to ensure sufficient statistical precision, the iterative procedure is applied to multiple independent initial configurations, allowing the average described in eqn (3). For the monodisperse case, approximately 100 initial configurations are used, whereas for the bidisperse case, around 2000 initial configurations are used.

Fig. 1 Flowchart illustrating the iterative process to calculate the RDF using molecular dynamics simulations. At each target temperature, the radial distribution function is computed based on the instantaneous particle positions.

As outlined in eqn (2), this contribution only examines a linear temperature ramp for both heating and cooling purposes. However, the temperature protocol can be designed as a sequence of distinct temperature ramps with varying slopes and durations, allowing for more complex thermal protocols. This case will be published elsewhere.

3. Structural evolution in the monodisperse case: cooling and heating

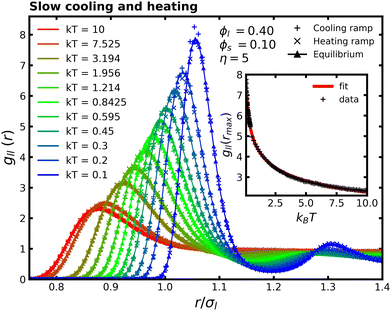
Now, we examine the structural evolution between two equilibrium configurations of a monodisperse colloidal system, with a packing fraction ϕ = 0.40, under different values of t_ramp, see eqn (2). Fig. 2 presents the evolution of the RDF with initial and final temperatures T₀ = 10 and T_f = 0.1, respectively, and cooling time t_ramp = 90.0τ_ref. This relatively slow cooling rate allows the system to relax during the protocol, as t_ramp is much longer than the characteristic timescale of the particles, τ_ref. As the temperature decreases, the position of the first peak shifts to larger interparticle separations, and its amplitude increases, indicating that particles move farther apart while becoming more narrowly distributed around these separations. As the colloidal dispersion cools, the particles lose kinetic energy and there is a transition to lower-energy states, resulting in reduced overlap. Furthermore, as the particles become more separated, they effectively behave as if they have a larger size, resulting in an increased effective packing fraction. This, in turn, leads to a higher amplitude of the first peak.

Fig. 2 Evolution of the RDF for a monodisperse colloidal system with packing fraction ϕ = 0.40 as it undergoes a cooling from an initial temperature T₀ = 10 to a final temperature T_f = 0.1 with a cooling time t_ramp = 90.0τ_ref. Red triangle curve represents the equilibrium state at T = 10, while the blue triangle curve corresponds to the equilibrium state at T = 0.1. The color bar represents the temperature and time corresponding to each color, with red representing the warmer initial periods and green to blue shades indicating the cooler later stages.

Beyond the first peak, the colloidal system exhibits distinct trends. At high temperatures, the RDF rapidly approaches its bulk value immediately beyond the first peak. In contrast, at lower temperatures, the particles become more localized at specific separations, leading to greater structural ordering over longer distances. This enhanced ordering results in a region of reduced particle density, as observed in Fig. 2 in the region r ∈ (1.4, 1.9)σ.

Fig. 3 shows the evolution of the RDF with a much shorter cooling time of t_ramp = 0.25τ_ref, representing a fast cooling protocol. In this case, the rapid temperature drop occurs on a timescale shorter than the characteristic relaxation time τ_ref, preventing the system from fully equilibrated during the cooling process. Even after T_f is reached, the structure continues to reconfigure, which explains the multiple blue curves for g(r) shown in Fig. 3. Similarly to the slow-cooling scenario, the first peak of the RDF shifts to larger distances and increases in magnitude (as indicated by the arrow), reflecting that the particles move farther apart as the system cools.

Fig. 3 Evolution of the RDF for a monodisperse system with packing fraction ϕ = 0.40 during a fast cooling from an initial temperature T₀ = 10 to a final temperature T_f = 0.1 with a cooling time t_ramp = 0.25τ_ref. Red triangle curve represents the equilibrium state at T = 10, while the blue triangle curve corresponds to the equilibrium state at T = 0.1. The color bar represents the temperature and time corresponding to each color. Multiple blue curves are shown as the system continues to evolve after reaching the final temperature.

In contrast to slow cooling, the system first attains intermediate configurations before reaching full equilibrium. In these transient states, the first peak of the RDF is significantly higher and narrower (violet) than in the equilibrium configuration. Over time, the height of the peak decreases as the system gradually relaxes toward equilibrium, as indicated by the black arrow in the inset of Fig. 2.

Under this rapid temperature protocol, energy is extracted from the particles faster than they can reorganize to reduce overlaps. As a result, configurations arise in which particle velocities are significantly lower in magnitude than the forces they experience.

To better illustrate the significance of this imbalance, consider the behavior of the system at equilibrium: the kinetic energy of particles is typically comparable to the energy associated with the interparticle forces. In such cases, collisions can redistribute energy in various directions, reflecting inertial effects. However, when the kinetic energy is much smaller than the potential energy gradients, inertia becomes negligible. In this regime, particle motion is dominated by force directions, leading to highly coordinated dynamics: particles in regions of higher overlap separate more rapidly.

This behavior is evident in the first three blue curves, where a slight shift in the first peak and a narrowing on its left side indicate a stronger reduction in the number of highly overlapped particles compared to those with weaker overlaps. The progressively narrower blue curves that follow result from the same mechanism. Particles with less initial overlap, which must migrate to larger separations to reach the equilibrium low-temperature structure, do so more slowly than those at shorter distances. This variation in particle dynamics generates a local density gradient that is absent in equilibrium configurations.

Fig. 4 illustrates the rapid heating of the RDF with an initial temperature of T₀ = 0.1, a final temperature of T_f = 10 and a heating time of t_ramp = 0.25τ_ref. As the colloidal system heats up, the RDF peak broadens, particularly toward shorter interparticle separations, as particles explore higher-energy configurations, leading to increased overlap. This expansion of accessible thermodynamic states results in a more diffuse structure, causing the first peak to become lower and broader than in the equilibrium configuration at high temperature. After this initial behavior, around t = 0.125τ_ref, the system enters a transient state in which the first peak of the RDF becomes more localized and narrower, but shifted to larger interparticle distances compared to its position at high-temperature equilibrium. Subsequently, it gradually converges to the equilibrium configuration at high temperature, as shown in the inset of Fig. 4.

Fig. 4 Evolution of the RDF for a monodisperse system with packing fraction ϕ = 0.40 during a fast heating from an initial temperature T₀ = 0.1 to a final temperature T_f = 10 with a heating time t_ramp = 0.25τ_ref. Red triangle curve represents the equilibrium state at T = 10, while the blue triangle curve corresponds to the equilibrium state at T = 0.1. The color bar represents the temperature and time corresponding to each color.

When comparing the evolution of the RDF during rapid heating and cooling, we observe that the system follows different structural pathways. Additionally, structural relaxation toward the new equilibrium during heating is approximately three times faster than during cooling. These differences suggest an asymmetry between thermal heating and cooling processes, which will be further studied in the bidisperse case.

4. Evolution of the structure in a binary mixture: cooling and heating effects

In the bidisperse colloidal system, we examine the impact of incorporating smaller particles that introduce distinct length and time scales that influence the structural evolution during both the heating and cooling processes. In all the cases reported here, the packing fraction of the large particles is ϕ_l = 0.40 and the one corresponding to the small particles is ϕ_s = 0.10, with a size ratio of σ_l/σ_s = 5. These parameters ensure that the system remains in the liquid phase.⁵ First, we examine how the structure evolves as a result of slow temperature changes. The temperature protocol consists of two consecutive linear ramps with different cooling rates. The first ramp decreases the temperature from T_A = 10 to an intermediate value T_B = 0.5 over a time interval of t_ramp = 40τ_ref, while the second ramp further cools the system from T_B to T_C = 0.1 over the same duration. This protocol is designed to account for the temperature dependence of the system's relaxation time. In particular, at low temperature T_C = 0.1, the relaxation time of large particles increases to , indicating that the system evolves more slowly. Consequently, the cooling rates are set to α_AB = 0.25T_ref/τ_ref and α_BC = 0.025T_ref/τ_ref, with the second ramp significantly slower to allow adequate relaxation at lower temperatures. The protocol is applied for both the cooling (T_A → T_B → T_C) and heating (T_C → T_B → T_A) processes. Additionally, for certain intermediate temperatures, we calculate the corresponding equilibrium RDF at these specific temperatures for comparison purposes.

Fig. 5 displays the evolution of the RDF between large particles (g_ll(r)). It shows a comparison of the RDF for a range of temperatures during the heating and cooling protocols, together with the equilibrium values. Initially, the colloidal system displays behavior similar to that of the monodisperse case under slow cooling. As the particles lose kinetic energy, the first peak of the RDF shifts to larger interparticle separations, reflecting a reduced overlap between the particles. However, the introduction of smaller particles leads to notable modifications. At lower temperatures, the large particles arrange into a more ordered structure, as evidenced by the pronounced oscillations—maxima and minima—following the first RDF peak. Notably, these additional peaks appear at shorter distances compared to those in the monodisperse case. Moreover, the amplitude of the first RDF peak increases substantially, indicating stronger spatial correlations at specific distances. This enhancement is attributed to the depletion forces generated by the smaller particles, which promote effective attraction among the large particles. Furthermore, variations in RDF at different temperatures suggest that the depletion forces are sensitive to both the temperature and the specific protocol used.⁵² Although the depletion force is stronger at higher temperatures, one could argue that it leads to a higher concentration of first neighbors. However, the rise in kinetic energy of large particles makes it easier for them to escape from the attractive potential well generated by the entropic forces.

Fig. 5 Evolution of the RDF between large particles (g_ll(r)) for a bidisperse colloidal system with packing fractions ϕ_l = 0.40 and ϕ_s = 0.10 with size ratio η = 5. The figure compares RDFs at various temperatures during slow cooling (T_A → T_B → T_C) and heating (T_C → T_B → T_A) protocols, alongside equilibrium values at corresponding temperatures. Here T_A = 10, T_B = 0.5 and T_C = 0.1. Inset shows the height of the first RDF peak as a function of temperature. The data exhibit a power-law decay, indicating that the peak magnitude decreases with increasing temperature. Red line is the power-law fit g_ll(r_max) = 6.625(kT)^−0.1723 − 2.197.

With respect to the evolution of the RDF, the transient states during cooling and heating generally align well with the equilibrium values. However, small deviations from equilibrium are observed at the lowest temperatures during both cooling and heating, indicating that the process is not entirely quasi-static under the current parameter selection. Extending the heating and cooling time frames eliminates these deviations as the system approaches a more quasi-static regime, leading to a closer match with the equilibrium results. The strong agreement between transient states and equilibrium values indicates that implementing temperature changes quasistatically results in transient states that closely approximate equilibrium conditions. This, combined with the consistent correspondence between heating and cooling results across different temperatures during the protocol suggests that the process is reversible and symmetric, i.e., it follows exactly the same thermodynamic pathway.

It is important to clarify that the evolution of the RDF might suggest that the local density of large particles increases at higher temperatures, since the particles appear to be closer—this interpretation can be misleading. By analyzing the inset of Fig. 5, which shows the height of the first peak of the RDF at different temperatures, it becomes clear that the density of the first neighbors of large particles actually decreases with increasing temperature. This behavior is related to a decrease in the effective packing fraction, as discussed in the monodisperse case. We fit the data using a power-law decay of the form g_ll(r_max) = A(k_BT)^−B + C. Although this functional form lacks a direct physical interpretation, it effectively reproduces the overall trend observed in the data throughout the studied temperature range.

As the results from the slow cooling and heating protocols reveal small deviations from equilibrium at the lowest temperatures, we now turn our attention to the structural evolution that arises when the system is subjected to abrupt temperature changes. By examining faster cooling and heating protocols, we aim to uncover the mechanisms driving the emergence of out-of-equilibrium structural transitions and their impact on the progression toward equilibrium.

Fig. 6 illustrates the evolution of g_ll(r) between the initial and final temperatures T₀ = 10 and T_f = 0.1, respectively, with a cooling time t_ramp = 0.25τ_ref. During the cooling ramp, minimal evolution is observed. However, once the colloidal system reaches its final temperature, we observe structural changes that can be divided into three distinct stages, indicated by the arrows in Fig. 6. In the first stage, which spans t ∈ (0.25,0.258)τ_ref, we observe a characteristic transition towards the new equilibrium state, marked by the large particles moving farther apart. In the second stage during t ∈ (0.29,0.35)τ_ref, the height of the first peak in the RDF forms a plateau (see violet and pink curves in Fig. 6), although the peak itself shifts to larger interparticle separations. To clarify this behavior, we refer to Fig. 7, which shows the evolution of the RDF between large and small particles, g_ls(r). Although the overall motion of the small particles initially resembles that observed under slow cooling in the monodisperse case, the inset of Fig. 7 reveals a marked deviation upon reaching the final temperature T_f. Before g_ls(r) settles into equilibrium, its first peak expands to larger separations and decreases in magnitude (violet to pink curves in Fig. 7), indicating that small particles are being “pushed” away from large ones due to their previous overlap caused by abrupt temperature change. This outcome precisely mirrors the effect observed in the monodisperse system under fast cooling (as explained in Section 3), where sudden cooling drives particles apart in response to the repulsive force.

Fig. 6 Evolution of the RDF between large particles (g_ll(r)) for packing fractions ϕ_l = 0.40 and ϕ_s = 0.10 with size ratio η = 5, cooled from T₀ = 10 to T_f = 0.1 with a cooling time t_ramp = 0.25τ_ref. The color bar represents the temperature and time corresponding to each color. Multiple blue curves are shown as the colloidal system continues to evolve after reaching the final temperature.

Fig. 7 Evolution of the RDF between large and small particles (g_ls(r)) for packing fractions ϕ_l = 0.40 and ϕ_s = 0.10 with size ratio η = 5, cooled from T₀ = 10 to T_f = 0.1 with a cooling time t_ramp = 0.25τ_ref. The color bar represents the temperature and time corresponding to each color. Multiple blue curves illustrate the continued evolution of the colloidal system after reaching the final temperature. The inset highlights the evolution of g_ls(r) over the time interval (0.25,0.258)τ_ref, showing the broadening of the first peak to larger interparticle separations.

With the small particles now at greater distances, the large particles have more freedom of movement, which explains the plateau observed at the maximum of the first peak in g_ll(r). In the third stage, as the small particles gradually return to equilibrium, this plateau ends and the system proceeds through a damped progression toward its final equilibrium. The damped behavior reflects how small particles act as a heat bath, producing different dynamics than in rapid monodisperse cooling, where transient states appear with a first peak magnitude greater than the equilibrium value. Although only the evolution of g_ll(r) to t = 1.85τ_ref is shown, the system requires a longer time (approximately t = 3.0τ_ref) to fully achieve the new equilibrium temperature at T = 0.1.

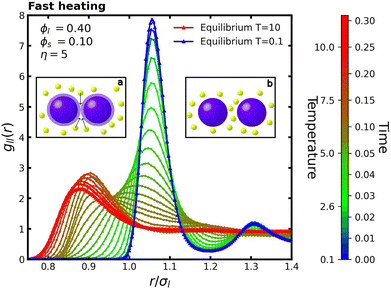
Fig. 8 presents the evolution of g_ll(r) when the colloidal system is rapidly heated from an initial temperature T₀ = 0.1 to a final temperature T_f = 10 with a heating period of t_ramp = 0.25τ_ref. Similarly to the monodisperse case, during the initial phase t ∈ (0.0, 0.05τ_ref), the first peak of g_ll(r) broadens without shifting in position. Subsequently, around r ≈ 0.95σ_l, the RDF curves intersect at different times, indicating a transition in the spacing of large particles from roughly r ≈ 1.08σ_l to r ≈ 0.9σ_l. This reduced spacing is approximately equal to the diameter of the small particles, σ_s, suggesting that this transition is of an entropic nature. However, as discussed in Section 5, it is primarily governed by energetic considerations.

Fig. 8 Evolution of the RDF (g_ll(r)) for large particles in a bidisperse system with packing fractions ϕ_l = 0.40 and ϕ_s = 0.10 with size ratio η = 5, as the temperature is increased from T₀ = 0.1 to T_f = 10 with a heating time t_ramp = 0.25τ_ref. Inset (a) shows the small particles filling the gap left by large particles. Inset (b) illustrates the mechanism known as entropic gate. The color bar represents the temperature and time corresponding to each color.

Notably, the presence of depletants introduces distinct deviations from the monodisperse behavior. In particular, transient states exhibit elevated RDF values beyond the first peak compared to the equilibrium configuration, indicating an increased concentration of large particles at larger separations. As the colloidal system heats up, the increased kinetic energy allows the particles to increase overlap, creating transient gaps between large particles. Due to their shorter timescales, small particles rapidly occupy these newly available spaces, as illustrated in the insets a–b of Fig. 8. In particular, the inset b shows the mechanism known as the entropic gate,^53,54 where a small particle becomes confined between two larger particles. This configuration can promote colloidal stabilization, as it generates a repulsive barrier that forces the large particles apart. Moreover, the strength of this effect can be modulated.⁴⁴

To further investigate this mechanism, we analyze the configurations of the first neighbors of large particles. In Fig. 9a, fully depleted configuration, where two large particles interact without a small particle between them, is shown in green. In contrast, the red configuration indicates the presence of a small particle between the large ones, which is the entropic gate configuration. The latter configuration is particularly important because it creates a potential barrier that must be overcome before large particles reach the potential well induced by the depletion force. We implement this color-coding scheme by assigning each large particle an integer parameter, color_id, initialized to zero. For each first neighbor interaction, color_id is incremented by one for depletion interactions and decremented by one for interactions involving the entropic gate. If color_id is greater than or equal to zero, the particle is colored green; otherwise, it is colored red. This approach ensures that the color of each large particle accurately reflects the dominant interaction type with its surrounding neighbors; see Fig. 9a for illustration purposes.

Fig. 9 (a) Schematic representation of fully depleted configuration (green) and entropic gate configuration (red). (b) Snapshots of a simulation slice showing the color-coded large particles (green or red) and small particles (yellow) at equilibrium. Configurations are presented for low temperature (T = 0.1), where green configurations dominate, and high temperature (T = 10), where red configurations become more prevalent.

In Fig. 9b, we present snapshots of a slice of the simulation box, where large particles are colored green or red, and small particles are yellow. These snapshots depict equilibrium configurations at low (T = 0.1) and high (T = 10) temperatures. At low temperature, green configurations dominate, whereas at high temperature, red configurations become more prevalent. To quantitatively analyze the distribution of colored particles, Fig. 10 shows the percentage of large particles in green or red configurations at different times during the fast heating protocol. Initially, at low temperature, almost 100% of the particles are in green configurations, reflecting aggregation due to depletion forces induced by small particles. During the first 0.05τ_ref, the fraction of green configurations decreases while the red configurations increase, reaching a peak. This corresponds to the mechanism observed in Fig. 8a and b, where small particles occupy the interstitial spaces between large particles. Subsequently, the red configuration fraction decreases before stabilizing at equilibrium, resulting in a final ratio of approximately 60% red to 40% green.

Fig. 10 Percentage of large particles in green (fully depleted) and red (entropic gate) configurations (see Fig. 9a) over time during the fast heating protocol. Over time, the system approaches equilibrium, with red configurations dominating at a ratio of approximately 60% red to 40% green.

This change in local configuration also explains the observed reduction in local density at high temperature, as evidenced by the lower height of g_ll(r_max), even though particles may be closer on average than at low temperature. In the entropic gate configuration, depletants are not required to occupy specific positions between large particles, but can reside within a broader spatial region. Moreover, at higher temperatures, the effective interactions between particles are softer, leading to a more gradual decay of the RDF towards unity as r increases in the high-temperature case.

The predominance of red or green configurations plays a crucial role in assessing colloidal stability. Although colloidal stability has been extensively studied at equilibrium for various interaction types,^55,56 studies on out-of-equilibrium states remain scarce. A higher fraction of green configurations indicates a system prone to aggregation, which can be exploited to drive the self-assembly of colloidal structures. Moreover, the fraction of assembled particles can be fine-tuned by adjusting the temperature. In contrast, a predominance of red configurations suggests a non-aggregating colloidal system, which, due to the entropic gate effect, can be leveraged to prevent particle sedimentation or percolation effectively.

5. Characteristic lengths and density fluctuations

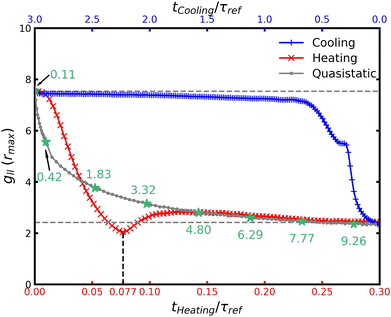
Through both the heating and cooling protocols, the colloidal system undergoes structural reorganization due to changes in its accessible thermodynamic states. These changes can be characterized by the position of the highest peak in the RDF for large particles, denoted r_max, and its respective height, g_ll(r_max). The value of r_max indicates the distance of the most probable interparticle separation, i.e., the distance to the first neighbor layer, making it an appropriate characteristic length to describe structural changes. Fig. 11 presents the evolution of r_max over time for both heating and cooling protocols, together with quasistatic reference results as a function of temperature. As seen in Fig. 11, heating and cooling follow distinct pathways.

Fig. 11 Evolution of the characteristic length scale r_max, representing the position of the highest peak in the RDF for large particles, as a function of time during heating and cooling protocols. The quasistatic results as a function of temperature are also shown for comparison. Each green star on the quasistatic curve describes the equilibrium temperature.

During cooling, there is a rapid initial change in the interparticle distance, which is in accordance with the highly coordinated motion of overlapping. However, once this coordinated behavior has been completed, it starts a much slower evolution with minimal changes in the position of the first peak r_max. In contrast, heating displays a fast change after an initial delay, since the first peak first diffuses as it is broadening, and then starts to move to closer interparticle distances. For times later than 0.10τ_ref, the value of r_max starts to slowly decrease once there are many entropic gate configurations in the system, as observed in Fig. 10, which slow the restructuring of large particles to closer interparticle distances. In addition, we can observe that the heating path is closer to the equilibrium values during this slow evolution, which can be due to being more likely to be a quasi-static evolution.

Furthermore, the difference in r_max between the two extreme temperatures is approximately Δr_max ∼ 0.18σ_l. To estimate this difference, we use eqn (1) to compute the nearest distance r* between two interacting particles at a given temperature, corresponding to the conversion of all kinetic energy into potential energy. For T = 0.1, r* = 1.072, while for T = 10, r* = 0.885. In comparison, the RDF peak positions are r_max = 1.0575 for T = 0.1 and r_max = 0.885 for T = 10. The slight overestimation of r* is due to the neglect of depletion forces that bring large particles closer together, an effect more pronounced at lower temperatures. Despite this overestimation, the difference in characteristic lengths remains consistent: Δr* = 0.187 and Δr_max = 0.18, with the former only 4% higher. This close agreement indicates a strong correlation between these two length-scale variations, implying that the observed changes in characteristic lengths originate from differences in accessible states, i.e., changes in the energetic landscape.

Fig. 12 shows the evolution of the magnitude of the first RDF peak for fast heating and cooling protocols as a function of time. Cooling requires nearly an order of magnitude longer than heating to achieve the new equilibrium configuration. At t = 0.25τ_ref, a plateau emerges (see Fig. 6), where the local density of large particles remains nearly constant. The most significant density fluctuations during cooling occur within the first t = 0.5τ_ref, followed by a slow convergence to equilibrium. This indicates that a rapid temperature decrease may not be optimal for cooling, as it can trap the system in out-of-equilibrium states with slow dynamics, similar to glassy behavior.^7,57,58 In contrast, during heating, the system evolves much faster. The added energy reduces the likelihood of trapping the colloidal dispersion in slow out-of-equilibrium states. After small particles diffuse among large ones, a minimum is observed in the local density around t = 0.77τ_ref, exhibiting higher stability than at T = 10. This time corresponds to the moments immediately after the maximum number of entropic gate configurations (see Fig. 10). This behavior demonstrates the efficiency of fast heating in separating large particles and increasing stability. We again observe that the evolution of the heating is close to the quasistatic evolution after times 0.10τ_ref.

Fig. 12 Evolution of the first peak of the RDF for the fast heating and cooling protocol as a function of time. The quasistatic results as a function of temperature are also shown for comparison. Each green star on the quasistatic curve describes the equilibrium temperature.

It is important to note that the results presented here correspond to a single configuration of the set {ϕ_l,ϕ_s,η}. A systematic study is necessary to explore the different phenomena that might emerge for varying parameter sets. In this work, we use ϕ_l = 0.40 and ϕ_s = 0.10 to avoid introducing an excessive number of small particles into the simulation for each large particle. Lower values of ϕ_s require a higher ratio of N_s/N_l, making it more difficult to obtain sufficient statistical sampling.

6. Conclusions and perspectives

By means of molecular dynamics simulations, we have systematically described the structural transformations observed in a colloidal system subjected to various heating and cooling protocols. By analyzing both monodisperse and bidisperse systems, we elucidated key features that govern the structural evolution towards equilibrium.

For the monodisperse colloidal system, we demonstrated that temperature variations significantly affect the RDF. Specifically, the position of the first peak shifts, decreasing at higher temperatures and increasing at lower temperatures. In addition, the density of the first neighbors increases as the temperature decreases. Under rapid temperature changes, the system deviated from equilibrium, exhibiting transient non-equilibrium configurations, such as particle agglomeration during cooling, before ultimately settling into an equilibrium state. In contrast, during heating, the first peak broadened, and during these transient states, the density of first neighbors was lower than in the high-temperature equilibrium.

In the bidisperse colloidal system, our findings revealed that under quasi-static temperature changes, the structural evolution follows equilibrium configurations. This indicated that for sufficiently slow temperature variations, the structure evolved through reversible and symmetric equilibrium states, as confirmed by the overlap between heating and cooling trajectories. However, under rapid temperature changes, non-equilibrium configurations emerged. During fast cooling, we observed a transient directional motion of small particles away from larger ones, attributed to prior particle overlap and the limited time available for structural reorganization from high- to low-energy states. Despite this, the structural relaxation under rapid cooling was significantly slower compared to the time required for fast heating to reach equilibrium. These observations naturally raise an intriguing question: Is there a cooling protocol that minimizes the time required to reach equilibrium, analogous to the Brachistochrone curve in classical mechanics, or thermodynamic analogous to the so-called Mpemba effect?⁵⁹

In contrast, rapid heating, on the other hand, led to the proliferation of entropic gate configurations, particularly at intermediate temperatures, where their presence was even more pronounced than in the final equilibrium configuration at high temperatures. This phenomenon can be interpreted as an “entropic switch”, highlighting the distinct behavior of the colloidal system under varying thermal conditions. Importantly, this behavior not only offers a potential method to enhance system stability, but it also suggested that periodic temperature protocols could be strategically employed to enhance and stabilize entropic gate configurations, potentially influencing self-assembly mechanisms at non-equilibrium conditions. More broadly, the study of out-of-equilibrium processes opens avenues for discovering new approaches to induce desirable properties in the development of novel materials. These transient states, which enhance specific structures that are absent under equilibrium conditions, provide opportunities for innovation.

Furthermore, our analysis showed that heating and cooling followed distinct structural pathways despite traversing the same temperature range, with heating occurring approximately ten times faster than cooling. This difference was also evident in the evolution of the RDF (Fig. 6 and 8), consistent with previous findings.⁶⁰ The evolution of the interparticle distance through temperature protocols also highlighted the role of kinetic energy in altering the accessible configurational states of particles, leading to scale-dependent effects at high and low temperatures. This behavior confirmed the presence of thermodynamic asymmetries that depend on the applied temperature protocol.

A notable feature in Fig. 11 and 12 was that the heating protocol closely resembled the quasistatic evolution in the final relaxation toward equilibrium, while cooling followed a different pathway. This suggested that the relaxation mechanisms during heating are similar to those of equilibrium relaxation. But more importantly, from these results we observed that the heating and cooling protocols only intersected in the initial and final configurations, i.e., the equilibrium configurations. This behavior was defined as a thermodynamic asymmetry. On the other hand, the lack of correlation between the particle time scales and the global structural evolution suggests the presence of thermodynamic time scales, which govern the system's evolution between equilibrium configurations.

Fluctuations in certain properties of a physical system can lead to intriguing phenomena. For example, fluctuations in electromagnetic fields in a vacuum can induce effective forces between surfaces known as Casimir forces, which may be attractive^61,62 or repulsive.^63,64 Likewise, two solid bodies immersed in a fluid exhibiting density fluctuations experience an effective force that can be attractive or repulsive. When these fluctuations arise near a critical point, they are known as critical Casimir forces.⁶⁵ However, such fluctuations are not limited to near-critical systems: Out-of-equilibrium configurations, such as those with temperature gradients, can also exhibit significant temperature fluctuations.⁶⁶ Based on the density fluctuations observed here, future work will examine their impact on the effective forces acting on larger particles, with the goal of identifying a Casimir-like interaction between large colloids.

Moreover, dimensionality will play a role in achieving thermodynamic equilibrium after a cooling or heating process, since the elimination or addition of translational degrees of freedom reduces or increases, respectively, the kinetic energy and affects the way it is transferred and distributed during particle collisions. Furthermore, the glass transition occurs at different packing fractions depending on dimensionality, underscoring its impact on the thermodynamically accessible states. Thus, dimensionality is another physical parameter that can be explored to design materials with tunable properties through controlled temperature protocols.

Lastly, we identified that variations in local density can induce long-range fluctuations reminiscent of critical phenomena. This suggests that structural heterogeneities arising from thermal cycling could be linked to emergent cooperative behavior in soft-matter systems. Our findings provide new insights into the interplay between thermal history, kinetic constraints, and structural organization, with potential applications in the design of materials with tunable properties through controlled temperature protocols.

Author contributions

MARG, NMSL and RCP conducted the conceptualization and administration of the project. RCP, GPA and JMMA provided the resources and acquired the funding. All authors worked on the investigation and validation. MARG, NMSL and GPA worked on the computer simulations. MARG and NMSL performed a preliminary analysis of the data. MARG and NMSL worked on the methodology, data curation, visualization, and formal analysis. MARG and NMSL wrote the original draft. All authors reviewed and edited the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

The authors confirm that the data supporting the findings of this study are available in the article. The data and the code used to generate the figures are available at the following link: https://github.com/EntropicMaya/structure_evolution.

Acknowledgements

Authors thank the financial support from SECIHTI-Mexico (Grant No. CBF2023-2024-3350). N. M. S.-L. also thanks Conahcyt for financial support (postdoctoral scholarship 2023(1)).

Notes and references

1. H. B. Callen, Thermodynamics and an Introduction to Thermostatistics, John Wiley & Sons, New York, NY, 2nd edn, 1985.
2. W. Nolting, Theoretical Physics 5: Thermodynamics, Springer International Publishing, 2017.
3. C. A. Angell, K. L. Ngai, G. B. McKenna, P. F. McMillan and S. W. Martin, J. Appl. Phys., 2000, 88, 3113–3157.
4. K. L. Ngai, D. Prevosto, S. Capaccioli and C. M. Roland, J. Phys.: Condens. Matter, 2008, 20, 244125.
5. E. Lázaro-Lázaro, J. A. Perera-Burgos, P. Laermann, T. Sentjabrskaja, G. Pérez-Ángel, M. Laurati, S. U. Egelhaaf, M. Medina-Noyola, T. Voigtmann, R. Castañeda Priego and L. F. Elizondo-Aguilera, Phys. Rev. E, 2019, 99, 042603.
6. P. Ramírez-González and M. Medina-Noyola, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061503.
7. R. Peredo-Ortiz, P. F. Zubieta Rico, E. C. Cortés-Morales, G. G. Pérez-Ángel, T. Voigtmann, M. Medina-Noyola and L. F. Elizondo-Aguilera, J. Phys.: Condens. Matter, 2021, 34, 084003.
8. J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, 2nd edn, 1986.
9. J. Dzubiella, H. Löwen and C. N. Likos, Phys. Rev. Lett., 2003, 91, 248301.
10. H. N. Lekkerkerker, R. Tuinier and M. Vis, Colloids and the Depletion Interaction, Springer International Publishing, 2024.
11. N. E. Valadez-Pérez, Y. Liu and R. Castañeda Priego, Phys. Rev. Lett., 2018, 120, 248004.
12. F. Soto-Bustamante, N. E. Valadez-Pérez and R. Castañeda-Priego, et al., J. Chem. Phys., 2021, 155, 034903.
13. J. M. van Doorn, J. Bronkhorst, R. Higler, T. van de Laar and J. Sprakel, Phys. Rev. Lett., 2017, 118, 188001.
14. A. Louhichi, E. Tamborini, N. Ghofraniha, F. M. C. Caton, D. Roux, J. Oberdisse, L. Cipelletti and L. Ramos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032306.
15. M. Mohtadi and P. Rao, Water Res., 1973, 7, 747–767.
16. P. Mpofu, J. Addai-Mensah and J. Ralston, J. Colloid Interface Sci., 2004, 271, 145–156.
17. M. Yoshimoto, S. Kurosawa and M. Tanaka, Chem. Phys., 2019, 523, 87–91.
18. R. Peredo-Ortiz, O. Joaquín-Jaime, L. López-Flores, M. Medina-Noyola and L. F. Elizondo-Aguilera, J. Rheol., 2025, 69, 201–222.
19. S. I. Stupp, R. H. Zha, L. C. Palmer, H. Cui and R. Bitton, Faraday Discuss., 2013, 166, 9.
20. M. J. Greenall and M. J. Derry, Soft Matter, 2024, 20, 3628–3634.
21. C. R. Iacovella, A. S. Keys and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20935–20940.
22. D. J. Evans and G. Morris, Statistical Mechanics of Nonequilibrium Liquids, Cambridge University Press, 1st edn, 2008.
23. O. Joaquín-Jaime, R. Peredo-Ortiz, M. Medina-Noyola and L. F. Elizondo-Aguilera, From equilibrium to non-equilibrium statistical mechanics of liquids, arxiv, 2024, preprint, arXiv:2401.15220, https://arxiv.org/abs/2401.15220.
24. P. Ramírez-González and M. Medina-Noyola, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061503.
25. L. E. Sánchez-Díaz, P. Ramírez-González and M. Medina-Noyola, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052306.
26. P. Ramírez-González and M. Medina-Noyola, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061504.
27. J. M. Olais-Govea, L. López-Flores and M. Medina-Noyola, J. Chem. Phys., 2015, 143, 174505.
28. J. Rouwhorst, C. Ness, S. Stoyanov, A. Zaccone and P. Schall, Nat. Commun., 2020, 11, 3558.
29. P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503.
30. A. P. R. Eberle, N. J. Wagner and R. Castaneda-Priego, Phys. Rev. Lett., 2011, 106, 105704.
31. M. Y. Lin, et al., Nature, 1989, 339, 360.
32. D. J. Koeze and B. P. Tighe, Phys. Rev. Lett., 2018, 121, 188002.
33. E. Del Gado, L. de Arcangelis and A. Coniglio, J. Phys.: Condens. Matter, 1998, 31, 1901.
34. Y. C. Chiew and E. D. Glandt, J. Phys. A: Math. Gen., 1983, 16, 2599.
35. M. C. Grant and W. B. Russel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 2606.
36. K. Broderix, H. Löwe, P. Müller and A. Zippelius, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 63, 011510.
37. P. B. Shelke, V. D. Nguyen, A. V. Limaye and P. Schall, Adv. Mater., 2013, 25, 1499.
38. V. D. Nguyen, S. Faber, Z. Hu, G. H. Wegdam and P. Schall, Nat. Commun., 2013, 4, 1584.
39. M. T. Dang, A. V. Verde, V. D. Nguyen, P. G. Bolhuis and P. Schall, J. Chem. Phys., 2013, 139, 094903.
40. R. Ramírez-Kantun, G. Pérez-Ángel and R. Castañeda-Priego, J. Chem. Phys., 2024, 160, 064505.
41. H. Asoh, K. Nakamura and S. Ono, Electrochim. Acta, 2007, 53, 83–86.
42. M. Sadakane, T. Asanuma, J. Kubo and W. Ueda, Chem. Mater., 2005, 17, 3546–3551.
43. A. Hensel and C. Schick, J. Non-Cryst. Solids, 1998, 235–237, 510–516.
44. N. M. de los Santos-López, G. Pérez-Ángel, J. M. Méndez-Alcaraz and R. Castañeda-Priego, J. Chem. Phys., 2021, 155, 024901.
45. N. M. de los Santos-López, R. C.-P. Gabriel Pérez-Ángel and J. M. Méndez-Alcaraz, J. Chem. Phys., 2022, 157, 074903.
46. N. M. de los Santos-López, M. A. Ramírez-Guízar, G. Pérez-Ángel, J. M. Méndez-Alcaraz and R. Castañeda-Priego, Phys. A, 2024, 655, 130180.
47. P. Mendoza-Méndez, R. Peredo-Ortiz, E. Lázaro-Lázaro, M. Chávez-Paez, H. Ruiz-Estrada, F. Pacheco-Vázquez, M. Medina-Noyola and L. F. Elizondo-Aguilera, J. Chem. Phys., 2022, 157, 244504.
48. J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237.
49. J. Martínez-Rivera, A. Villada-Balbuena, M. A. Sandoval-Puentes, S. U. Egelhaaf, J. M. Méndez-Alcaraz, R. Castañeda-Priego and M. A. Escobedo-Sánchez, J. Chem. Phys., 2023, 159, 194110.
50. W. Greiner, L. Neise and H. Stöcker, Thermodynamics and Statistical Mechanics, Springer, 1995.
51. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford, 1987.
52. M. A. Ramírez-Guízar, N. M. D. L. Santos-López, G. PérezÁngel, J. M. Méndez-Alcaraz and R. Castañeda-Priego, submitted, 2025.
53. Y. Mao, J. Phys. II, 1995, 5, 1761–1766.
54. R. Roth and M. Kinoshita, J. Chem. Phys., 2006, 125, 084910.
55. S. Garciagarcia, S. Wold and M. Jonsson, Appl. Clay Sci., 2009, 43, 21–26.
56. I. Barton, Am. J. Sci., 2019, 319, 737–753.
57. T. Odagaki, J. Matsui and Y. Hiwatari, Phys. A, 1994, 204, 464–481.
58. J. M. Lynch, G. C. Cianci and E. R. Weeks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031410.
59. E. B. Mpemba and D. G. Osborne, Phys. Educ., 1969, 4, 172–175.
60. M. Ibáñez, C. Dieball, A. Lasanta, A. Godec and R. A. Rica, Nat. Phys., 2024, 20, 135–141.
61. H. B. G. Casimir, Proc. K. Ned. Akad. Wet., 1948, 51, 793–795.
62. B. V. Derjaguin, I. I. Abrikosova and E. M. Lifshitz, Q. Rev. Chem. Soc., 1956, 10, 295–329.
63. I. E. Dzyaloshinskii, E. M. Lifshitz and L. P. Pitaevskii, Adv. Phys., 1961, 10, 165–209.
64. J. N. Munday, F. Capasso and V. A. Parsegian, Nature, 2009, 457, 170–173.
65. C. Hertlein, L. Helden, A. Gambassi, S. Dietrich and C. Bechinger, Nature, 2008, 451, 172–175.
66. T. R. Kirkpatrick, J. M. Ortiz de Zárate and J. V. Sengers, Phys. Rev. Lett., 2013, 110, 235902.

---