Microbial biosurfactant hydrogels with tunable rheology for precision 3D printing of soft scaffolds

Abstract

Bio-based surfactants, derived from microbial fermentation, are appealing biocompatible amphiphiles traditionally employed in depollution, pest control, personal care, cosmetics, and medicine, although their potential in biomedical scaffolds remains largely unexplored due to the limited adaptability of their rheological properties for extrusion-based 3D printing. This work demonstrates that microbial biosurfactants can function as low-molecular-weight gelators with facile, tunable rheological functionalities, enabling their integration into additive-free 3D printing processes. A hydrogel, formed by complexing a single-glucose oleyl lipid surfactant with calcium ions, exhibits shear-thinning behavior, viscoelasticity, yield stress, thixotropic response, and elongational properties, all essential for extrusion-based printing. A comprehensive rheological study reveals that the hydrogel's shear-thinning behavior allows controlled extrusion using conventional methods, while its yield stress ensures structural integrity by resisting capillary and gravitational stresses during deposition. Furthermore, the hydrogel demonstrates rapid stress recovery, enabling it to rebuild yield stress post-extrusion and prevent spreading. It's controlled fragility under stretching and shear ensures that structures can be printed without significant deformation, maintaining high fidelity throughout the process. Beyond its printability, the hydrogel exhibits stimuli-responsive functionality, particularly pH sensitivity, unlocking opportunities for 4D printing applications, where material properties evolve dynamically post-fabrication. This work positions biosurfactant-based hydrogels as a sustainable, high-performance material platform, paving the way for the use of this class of molecules for soft material engineering.

---

1. Introduction

Microbial biosurfactants are commonly intended as a class of bio-based amphiphiles produced by a fermentative process. Discovered in the late 1940s in the context of broadening the range of natural antibiotics,^1–4 they became attractive for their potential in soil depollution and emulsification of crude oil. In recent years, microbial surfactants have been described as viable alternatives to petrochemical surfactants for applications in a number of fields, including but not limited to food, pharmaceutics, home and personal care, cosmetics, and agriculture industries.^2,5 This class of molecules provides advantages over synthetic compounds including relatively low toxicity, availability, structure variability, absence of intermediates in their synthesis route, and displaying remarkable, and yet poorly understood, structure-function properties, strongly dependent on pH but also ionic strength, type of counterion, nature of the chemical functional group.^2,6 This vision is shared by the chemical industry worldwide, who started to massively invest in the biosurfactant science and technology field in the past five years or so.⁷

Considered as a mere alternative to synthetic surfactants for a long time,⁸ recent research has demonstrated their potential in the field of colloid and interface science^3,9 including soft matter. It was recently shown, for instance, that specific microbial biosurfactants can form hydrogels by a simple pH variation or by interaction with specific cations, like Ag⁺ or Ca²⁺,^10–14 with distinctive elastic properties.¹¹ Their formation, governed by non-covalent interactions and their responsiveness to external stimuli, make them highly attractive for biomedical applications.¹⁰ This property changes both the perspective and the perception of this class of molecules, positioning them as something different than surfactants, such as low molecular weight gelators (LMWGs).^15–18

Indeed, the design and development of LMWGs for specific applications have garnered tremendous attention in the soft matter field, driven by their broad range of uses spanning biomedicine, food science, and even soft robotics.^19,20 Within this context, microbial LMWGs can emerge as particularly promising candidates, owing to their renewable raw materials, low toxicity, and high biodegradability, making them ideal for sustainable and biocompatible solutions.²¹ These features open opportunities for precise structuring and customization, which could also benefit from the current 3D printing technology, lately applied to LMWG systems.^22–25

In recent decades, 3D printing, particularly additive manufacturing, has seen remarkable advancements, finding applications in nearly every sector, from medicine to advanced technologies, with materials ranging from metals and ceramics to thermoplastics and gels.^22,26–33 Among these, soft hydrogels have emerged as a particularly promising class of materials for 3D printing, offering unique potential for biomedical applications. However, their successful fabrication requires precise control over gelling kinetics, the time-dependent evolution of rheological properties, yield stress, and extrusion parameters, while addressing external forces like gravity and capillary effects. Indeed, this requires a thorough understanding and control of shear-thinning during extrusion, thixotropy, and recovery after solicitation, which must align with the time scales of the printing process.^34–36 These aspects, combined with other critical rheological properties such as low-shear viscosity, elasticity, and characteristic relaxation times, are essential for optimizing the material's performance during additive manufacturing. Thus, significant efforts are still underway to fully understand and optimize the rheological mechanisms involved.^30,31

While 3D additive manufacturing is routinely applied to hard materials such as thermoplastics, ongoing studies are dedicated to exploring its application to hydrogels, particularly bio-sourced polysaccharides like alginate, chitosan, and microfibrillated cellulose.^37–42 These challenges are further amplified when utilizing LMWGs, often due to the difficulty of achieving a strong gel-like material during the printing process and the need to fall into specific windows of pH, temperature, concentration, and cation type. Several strategies have then been explored for printing LMWGs, demonstrating that these materials could serve as promising candidates for 3D-printed hydrogels.^23,25 However, examples are still rare and such an achievement requires a deeper understanding of the dynamic behavior of microbial LMWG gels under mechanical and rheological stresses encountered during the printing process, yet to be explored and optimized.

In this communication, we propose a giant leap in the field of sustainable chemistry, surfactants and LMWG. 3D printing of surfactants, may them be biobased or not, is not known, unless an additive, generally a polymer, is employed as the actual printable gelator.⁴³ We demonstrate here the possibility of performing the additive-free 3D printing of a monounsaturated (C18:1-cis) single-glucose (G) lipid (G-C18:1), a fully bio-sourced glycolipid obtained via microbial fermentation,^44–46 and offering advantages in terms of sustainability, biodegradability, and renewable origin, increasingly important in the development of soft green materials. Additionally, G-C18:1 exhibits a unique multiparametric self-assembly behavior, enabling the formation of different supramolecular structures under mild conditions.⁴⁷ In particular, in the presence of divalent ions and in its micellar phase, it undergoes a sol-to-gel transition.¹¹ For the present work, we select Ca²⁺ for the proof of concept.^11–13 Not only we provide the physicochemical conditions to prepare stable three-dimensional structures of G-C18:1, but we have studied, adapted and tuned the rheological properties (shear-thinning, time-dependent evolution of viscosity, yield stress, elastic and loss moduli, deformation and elongation mechanisms) of the hydrogel across various stages of the printing process, so not to leave any stage of the process uncontrolled. Furthermore, we do not only print cylindrical and bridge-shaped geometries to evaluate their resilience and integrity in three dimensions, but we also evaluate whether or not the known pH-responsivity of the gels is maintained even in their 3D printed form, by exposure to an acidic gaseous environment. We can then anticipate the potential of printed biosurfactant hydrogels even for 4D printing technologies.

2. Experimental

2.1 Materials

The biosurfactant investigated in this study is the monounsaturated glucolipid G-C18:1 (M_w = 460 g mol⁻¹), featuring a β-D-glucose unit covalently bonded to oleic acid, as illustrated in Scheme 1. This molecule is synthesized through the fermentation of the yeast S. bombicola (ΔugtB1), using previously established protocols. G-C18:1 was sourced from Amphistar, Belgium, with lot numbers APS F06/F07, Inv 96/98/99, and was utilized without any further treatment.¹¹ The batch, having a dry matter content of 99.4%, is primarily composed of 99.5% G-C18:1, according to HPLC-ELSD chromatography findings. NMR analysis has been performed on a separate batch of the same compound. Additional chemicals employed in this study include CaCl₂, NaOH (pellets ≥98 wt%), and HCl 1 M, all procured from Sigma-Aldrich. Sodium azide, also obtained from Sigma-Aldrich, was used as an antibacterial for gel conservation. Doubly deionized water is used for the gel preparation.

Scheme 1 (a) Structure of monounsaturated glucolipid, G-C18:1; (b) G-C18:1 micelles form in water at room temperature at pH > 8; (c) Ca²⁺ cross-links the G-C18:1 carboxylate groups and drives the fiber formation; (d) for optimized calcium content, the Ca²⁺-induced self-assembly of G-C18:1 drives hydrogelation.^11–13

2.2 Gel preparation

The G-C18:1 powder is dispersed in deionized water (C = 10 wt%) by vortexing for 1 minute and sonication for 5 minutes. The pH is then set to 8 by adding 5 μL of concentrated NaOH (5 M), with the exact pH fine-tuned to about 10 using microliter quantities of NaOH solutions at a concentration of 1 M, 0.5 M, or 0.1 M.¹³ The solution, initially turbid, becomes clear after around 10 minutes, indicating the G-C18:1 assembly into micelles.^12,48 An aliquot of NaN₃ (0.1 g L⁻¹) is added to the G-C18:1 solution as a preservative to prevent microbial degradation of sugar. Calcium chloride solutions are prepared at different concentrations around 1 M and mixed with the G-C18:1 solution to attain the desired, [CaCl₂]/[G-C18:1] molar ratio. It was previously shown that gelation occurs at about the equimolar amount of positive and negative charges, belonging to calcium ions and carboxylate groups (at pH 10 for G-C18:1), respectively.¹² In this work we employ the notation α = [CaCl₂]/[G-C18:1], with α = 0.3, 0.6 or 0.9. For example, to form a hydrogel [CaCl₂]/[G-C18:1] = 0.9, typically, for a total 1 mL volume, or 195 μL of CaCl₂ (1 M), are added to the complementary volume of 10 wt% G-C18:1. These values were chosen on the basis of previous work¹⁴ with the idea of spanning between under- to over-stoichiometric content of positive charges compared to negative charges of G-C18:1. After the addition of calcium ions, the solution is vigorously stirred for approximately 30 seconds using an IKA MS1 minishaker at maximum power to form self-assembly hydrogels, Scheme 1, and the hydrogels were allowed to rest for 10 minutes post-mixing, followed by an aging period of 48 hours at in the fridge at 4 °C to ensure network stabilization before characterization. The solution is either analyzed using rheometry or stored in the fridge at 4 °C for aging for more than two days.

2.3 Rheological measurements

Rheological measurements were performed using a DHR3 rheometer (TA Instruments), utilized with a cone-plate geometry (diameter: 20 mm) at a controlled temperature of 20 °C. To minimize evaporation, a solvent trap filled with water is employed. Rheological measurements were performed on samples aged for 48 hours in the fridge. First, the amplitude sweep test was conducted to record the storage (G′) and loss (G′′) moduli at a constant frequency of 1 Hz and a strain ranging from 0.01 to 100%. Frequency sweep tests were conducted to measure the storage (G′) and loss (G′′) moduli within the linear viscoelastic regime over a frequency range of 0.01 to 10 Hz. The measurements were performed at a constant strain of 0.1%, a value confirmed to lie within the linear viscoelastic region in the previous analysis. The flow properties of the gel were investigated by measuring the stress (σ) across a shear rate range ([small gamma, Greek, dot above]) from 0.001 to 30 s⁻¹. Adequate time was allowed at each stage of measurement to achieve a pseudo-steady state, enabling the calculation of viscosity (η) using the formula .

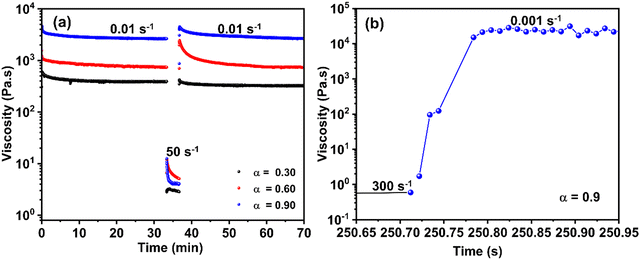
Several models were applied to fit these shear data. The shear stress in the low shear rate regime was fitted using the Herschel–Bulkley model as σ = σ₀ + K[small gamma, Greek, dot above]ⁿ, which σ₀ the yield stress, K the consistency index and n the dimensionless flow index. Far from the low shear rate zone, the shear rate was fitted to a power-law using σ = K[small gamma, Greek, dot above]ⁿ. The thixotropy of the hydrogel was evaluated using the 3iTT test, comprising three intervals. Initially, a shear rate of 0.01 s⁻¹ was applied for 30 min to assess structural stability. Subsequently, the hydrogel underwent a shear rate of 50 s⁻¹ for 3 min to induce structural breakdown. Finally, the shear rate was reduced again to 0.01 s⁻¹ for 30 min to observe structural recovery. Complementary recovery experiments were conducted on an ARES G2 rheometer (TA Instruments) using a 20 mm cone-plate, using 0.001 s⁻¹ for measurement and 300 s⁻¹ for destructuration. Measurements were performed with millisecond sampling. Control experiments conducted on a Newtonian oil allowed estimation of the minimum recovery measurement precision at 40 ms for ARES G2. Therefore, only recovery times exceeding this value were taken into account. Due to the slower response of the DHR3 in this configuration, only long recovery times above 1 s were considered.

2.4 3D printer configuration

The 3D printing apparatus was custom-built, featuring a three-axis motion head, an injection syringe module, and a stationary stage. Displacements of the axes and the operation of the extrusion module are governed by stepper motors. To manage all printer movements, a LabView interface was developed.

Two extrusion processes were employed: one under imposed flow rate and the other under imposed pressure. The extrusion mechanism using an imposed flow rate consisted of either a NORM-JECT syringe with a 9 mm diameter or a HAMILTON syringe with a volume of 5 mL and an internal diameter of 10 mm. During extrusion, the syringe plunger was driven at a controlled speed to regulate the flow rate. Cylindrical stainless-steel nozzles (Nordson EFD) with inner diameters of 0.84 mm, 0.51 mm, and 0.33 mm, and lengths of 0.5 cm or 3.8 cm, were employed for gel deposition.

In other experiments, extrusion was performed under constant pressure using an MFCS-EZ system. The equipment was interfaced with the printer's control program, allowing for precise pressure control ranging from 1 mbar to 2000 mbar, while synchronizing with the nozzle displacement. The flow rate was imposed by controlling the applied pressure throughout the 3D printing process, ensuring synchronization with the nozzle displacement.

For instance, prior to 3D printing, the flow rate for each gel composition was monitored by imposing pressures from 1 mbar to 2000 mbar and measuring the extruded mass using an analytical balance with 0.1 mg precision. The slope of the mass versus time curve was used to determine the flow rate. By applying Poiseuille's law, along with the needle geometry and the imposed pressure, the apparent viscosity and flow index (n) were calculated. For each of these methods, the homogeneity of the extruded fluid was monitored as an indicator of the feasibility of extrusion under constant flow rate and constant pressure conditions. All experiments were conducted at a controlled temperature of 22 °C to ensure consistency in material behavior and reproducibility of the results. Images of the printed material during the printing process were captured using two cameras: one positioned perpendicularly to the printing plane and another placed underneath. Camera calibration was performed using a known scale prior to measurement to ensure accurate distance quantification.

2.5 Printing conditions

The printing process is aimed at creating various geometrical shapes. Several substrates, including glass slides, PVC, and Teflon, were selected to observe how capillary stress deformed the substrate. All substrates were cleaned with deionized water prior to printing.

Printing was conducted under both constant pressure and constant flow rate conditions. However, as constant pressure printing did not allow homogeneous deposition, the most efficient printing was achieved under constant flow rate conditions. Flow rates (Q) ranging from 0.016 mm³ s⁻¹ to 1 mm³ s⁻¹ were tested. The nozzle displacement speed (V_n) was synchronized with the flux rate (Q) and the needle diameter (d_n), following the relationship: . Needles of various diameters (0.84 mm, 0.51 mm, and 0.33 mm) and lengths (0.5 cm and 3.8 cm) were evaluated. Most results presented here were obtained using 0.84 mm diameter needles with lengths of either 0.5 cm or 3.8 cm and a flow rate of 0.55 mm³ s⁻¹.

A custom G-code was developed for each printed structure using a home-built slicer written in Python. These structures included pillars with a diameter of 2 mm and a height of 7.5 mm (15 layers, 0.5 mm per layer), free-suspending beams with a diameter of 1 mm, a hollow cylinder with a diameter of 5 mm, sub-millimetric thick walls, and structures with a height of approximately 10 mm. Additionally, a specific G-code was designed to create the letters “GC”, standing for G-C18:1. For all conditions, the printing process began by depositing a small amount of material away from the intended printing area (approximately 50 mm) to stabilize the flow rate and ensure a steady-state regime before initiating the actual print. This preliminary extrusion, lasting 20 seconds, ensured a constant flow before initiating the designed shape.

2.6 Quantification of the stress involved during printing

The elongational and compressional behavior of the gel during printing was assessed using an analytical balance with a precision of 0.1 mg. Forces were continuously monitored throughout the process, including both fluid extrusion and nozzle retraction. Gel was injected at a constant flow rate of 0.55 mm³ s⁻¹ through a needle with an inner diameter of 0.84 mm and a length of 0.5 cm. The experiment consisted of three phases. First, a known volume of gel (20–100 mg) was deposited at a constant flow rate. Second, injection was halted, and the force was recorded over 1 to 5 minutes to monitor stress relaxation. Third, the nozzle was withdrawn vertically at a constant velocity without extrusion to observe filament stretching. Filament deformation was visualized in situ using a camera, and quantified by image analysis during the retraction phase.

3. Results and discussion

3.1 3D printing of biosurfactant hydrogel

Self-assembled hydrogels from G-C18:1 were obtained by adding calcium ions to a micellar G-C18:1 solution, following a protocol published by us in previous work.^12–14 In particular, rheology, small-angle X-ray scattering (SAXS), cryogenic transmission electron microscopy (cryo-TEM), and isothermal titration calorimetry (ITC) showed fibrillar hydrogels with unusual β-sheet-like domains.¹² Calcium-resolved in situ SAXS was employed to characterize the sol-to-gel transition at concentrations below the gelling conditions,¹⁴ while in situ rheo-SAXS was employed to show the structural resistance of the gel up to about 60 °C and up to 100 s⁻¹.¹³ These studies were used as background information to select the conditions to prepare G-C18:1 hydrogels for the 3D printing.

Printing soft, uncross-linked, hydrogels presents significant challenges due to external forces, gravity stress, and capillary forces. These factors make it particularly difficult to maintain structural integrity under the stresses applied during printing. For instance, as the structure gains height, the pressure on the lower layers increases, often leading to structural collapse. Fig. 1(a) and (b) demonstrates that accurate control of the G-C18:1 hydrogel composition and processing conditions make the printing of this molecule in its surfactant form a realistic possibility. The addition of Ca²⁺ (α = 0.9) to the micellar solution (pH 10) of G-C18:1 (pK_a of 6.5)⁴⁹ allows a good quality 3D printing of the microbial biosurfactant at a concentration of 10 wt%, without the need for additional crosslinking agent or polymer scaffolds. Fig. 1(a)–(d) illustrates that 2 mm diameter hydrogel pillars can achieve and maintain stability at heights of up to 10 mm for this specific composition, with this stability persisting for more than 3 days. When the experiments were repeated on substrates with varying surface energies, such as glass, PVC, and Teflon, comparable stability was consistently observed.

Fig. 1 3D-printed structures using hydrogels prepared from G-C18:1 (10 wt%) with a calcium ratio ([Ca²⁺]/[G-C18:1]) of α = 0.90; (a) and (b) top and side views of five pillars; (c) and (d) images of a hollow cylinder; (e) and (f) top and side views of the letters ‘GC’ (standing for G-C18:1). (g) and (h) Suspended bridge (1 cm in length) immediately after printing (g) and after 20 min (h). Printing was performed using a needle with a 0.84 mm diameter and 0.5 cm length at a flow rate of 0.55 mm³ s⁻¹.

This result is particularly significant, as it provides insights into how a specific combination of rheological and material properties enables such performance in a shear-sensitive, soft gel system. The viscosity of the gel decreases due to its shear-thinning behavior during extrusion, effectively minimizing the pressure drop across the nozzle and ensuring stable flow without instabilities. Upon deposition, the gel demonstrates rapid viscoelastic recovery, restoring its elastic modulus sufficiently to resist potential flow or deformation under applied stresses. To the best of our knowledge, this is the first example of an additive-free printable biosurfactant in particular, but also of a surfactant in general. Previous examples of printable self-assembled hydrogels involve either the use of a polymer⁴³ or established low molecular weight gelators.^23,28

It is also worth noting that the lower layers of the structure do not spread under the applied stresses and are likely able to withstand gravitational pressure, estimated at approximately 100 Pa for a 10 mm high structure, as well as Laplace pressure, calculated to be around 80 Pa for a 2 mm diameter droplet with a surface tension of 40 mN m⁻¹.⁴⁹ These simple assumptions indicate that this biosurfactant-based composition generates a yield stress capable of counteracting the combined forces encountered during deposition on the substrate. This phenomenon is attributed to the stress recovery process occurring within the short timescale between extrusion and deposition, which is in the order of sub-seconds under the experimental conditions explored in this study, as quantified later.

The precision of printing was evaluated by fabricating hollow cylinders with wall thicknesses comparable to the nozzle diameter, as shown in Fig. 1(c) and (d). The results demonstrate that up to a height of 10 mm, these walls remain stable throughout their height and over extended periods of time (days). Notably, the stability of these thin structures, with thicknesses of less than 1 mm, is remarkable, given the stresses induced by stretching and compression during extrusion and nozzle movement. Similar observations were made when printing more complex structures, such as the letters GC, standing for G-C18:1, and demonstrating the capability of this gel composition to respond effectively to multiple 3D constraints (Fig. 1(e) and (f)). Even more remarkable for a surfactant is the successful printing task of a 1 cm long self-standing bridge (Fig. 1(g) and (h)), which illustrates the ability of this gel to be integrated into advanced printing strategies, including the creation of empty cavities or inclusion structures. The printed bridge remained stable over time, showing no signs of structural failure. After 20 minutes, the bridge exhibited shrinkage due to drying, as illustrated in the accompanying images, while maintaining its integrity without breaking (Fig. 1(h)).

3.1.1 Effect of the gel composition. The performance observed during 3D printing strongly depends on the gel composition, particularly on α.¹² Notably, there exists a critical α value beyond which 3D printing produces stable structures both spatially and temporally, as illustrated in Fig. 2. For α = 0.3, even with 10 wt% biosurfactants, the material spreads during extrusion (Fig. 2(a), (b) and Fig. S1(a)–(f) (ESI†)). The extruded fluid appears macroscopically heterogeneous, with millimeter-sized dense biosurfactant regions separated by water-rich domains. Also observed in the confocal image based on their microstructure, Fig. S1g (ESI†). During extrusion, the fluid separates into two phases, with water extruding first, followed by biosurfactant-rich domains. The liquid–solid separation is even more pronounced with longer needles, primarily due to the increased shear stresses and pressure drops associated with Poiseuille flow. Increasing α to 0.6 improves the printing quality and the homogeneity of the gel, reducing the extent of liquid–solid separation and resulting in marginally stable structures (Fig. 2(c), (d) and Fig. S2, ESI†). These structures maintain their integrity up to a certain height but eventually collapse either over time or when the height exceeds a critical limit.

Fig. 2 3D-printed structures using hydrogels prepared from G-C18:1 (10 wt%) with different calcium ratios (α = [Ca²⁺]/[G-C18:1]); (a) and (b) α = 0.30; (c) and (d) α = 0.60; (e) and (f) α = 0.90. Printing was performed using a needle with a 0.84 mm diameter and 0.5 cm length at a flow rate of 0.55 mm³ s⁻¹.

The best performance, in terms of both aqueous phase retention and structural stability, is observed as α settles around 1. In this specific work, α is set at 0.9, although this value is not strict and can be optimized, although always around unity, by the user. The printed structures not only closely match the programmed geometry but they also remain stable over days (Fig. 2(e) and (f)). Extrusion at this composition does not result in phase separation, indicating that the gel is homogeneous, with no liquid–solid separation for any needle length tested. This suggests that the residual pressure from flow resistance is insufficient to induce phase separation.

Overall, at lower α values, the gel structure remains macroscopically heterogeneous, leading to liquid–solid separation under applied pressure.^11,14 As α increases, the gel becomes more homogeneous, better resisting applied pressures, and approaching a more cohesive bulk gel-like structure where osmotic pressure resists water expulsion. This is likely due to the extent of entanglement and connectivity between the Ca²⁺/G-C18:1 fibers, promoted by the carboxylate-Ca²⁺ cross-linking effect for α approaching 1,¹⁴ thus highlighting the importance of tuning α to optimize both the structural integrity and homogeneity of the gel during 3D printing.

3.1.2 Effect of nozzle dimension. Changing the dimensions of the printing nozzles, specifically the needle's diameter, and length, impacts the printing process for this hydrogel. One key manifestation of this effect is the enhanced solid–liquid separation, which becomes more pronounced with increasing needle length (L_n) and decreasing needle diameter (d_n), particularly at low α values. This behavior underscores the hydrogel's sensitivity to applied pressure, quantified by the pressure drop (ΔP) across the needle due to shear-induced wall effects, expressed as: .⁵⁰ For example, for a needle with a diameter of d_n = 0.84 mm and a flow rate of 0.55 mm³ s⁻¹, at viscosity η of 10 Pa s corresponding to the shear rate, ΔP ranges from 3.4 kPa to 26 kPa for L_n between 0.5 cm and 3.8 cm.

This approach offers an approximate estimation of the stress resisting water expulsion. A more quantitative analysis can be achieved by equalizing the applied external pressure to the resisting stresses, which comprise the sum of the osmotic pressure and the elastic modulus of the fibrous network formed within the hydrogel.¹⁴ An open question remains regarding which process is more dominant, but this is beyond the scope of the present work. However, visualization of the gel structure at low α reveals micron-scale heterogeneities, suggesting that resistance to water expulsion is primarily governed by the elastic response of the fibrous network. Additionally, changing the needle length can also modify the conditions required to establish a steady-state flow regime within the needle. The characteristic time for achieving steady flow in a cylindrical needle can be estimated as: where τ is the characteristic time, ρ is the fluid density. Based on the measured viscosity (see below), the steady-state flow regime is established within microseconds to milliseconds, under the experimental conditions, suggesting that the fluid operates under quasi-permanent flow conditions. However, the extent of shear-induced destructuration likely depends on the dimensions of the needle. For example, a longer residence time within the needle, associated with increased length, is expected to amplify destructuration as the material exits the nozzle.

3.1.3 Constant flow rate vs. constant pressure. The 3D printing conditions using constant pressure or constant flow rate were also investigated, as known to be an important processing parameter, particularly for rheo-thickening or rheo-thinning materials. The results here show that constant pressure printing is unsuitable for this heterogeneous system, as the flow rate fluctuates significantly. Periods of high flow occur when low-concentration domains pass through the nozzle, followed by periods of low flow when concentrated regions are extruded. This chaotic transition is more pronounced at lower α values and it decreases as α increases (Fig. S1, ESI†). Even for α approaching 1, this instability persists, making constant pressure printing unviable for 3D fabrication under experimental conditions. It is reasonable to conclude that constant pressure printing should be avoided in this context, particularly under the experimental conditions of this study, due to the inherent instability of the system.

3.2 Rheological properties

3.2.1 Shear-thinning of the gel. The behavior of the hydrogel during the different stages of the 3D printing process is directly linked to its rheological properties during extrusion, but also to the relaxation upon deposition and to the temporal stability under the applied forces. During the extrusion phase, the hydrogel undergoes significant shear, leading to shear-thinning behavior. Under constant flow rate conditions within a cylindrical channel, the shear rate can be estimated using the expression assuming a no-slip boundary condition.⁵⁰ For example, the shear rate ranges from 0.28 s⁻¹ to 17.2 s⁻¹ for a 0.84 mm needle and from 4.7 s⁻¹ to 283 s⁻¹ for a 0.33 mm needle within the flow rates used in this experiment. To better understand the gel behavior during extrusion, its response to shear is further investigated under controlled shear rate conditions using a cone-plate geometry, with shear rates ranging from 10⁻⁴ s⁻¹ to several tens of s⁻¹ (Fig. 3(a) and (b)). Fig. 3(a) and (b) show the evolution of the measured shear stress vs. the shear rate and ·the corresponding viscosity . η of the gel decreases by several orders of magnitude with increasing shear rate, dropping from above 10⁵ Pa s to below 10 Pa s beyond 10 s⁻¹. The calculated η value for 10 s⁻¹ suggests that the gel printing occurs within the laminar flow regime, as indicated by the Reynolds number (Re) , suggesting laminar flow, which ensures controlled material deposition.

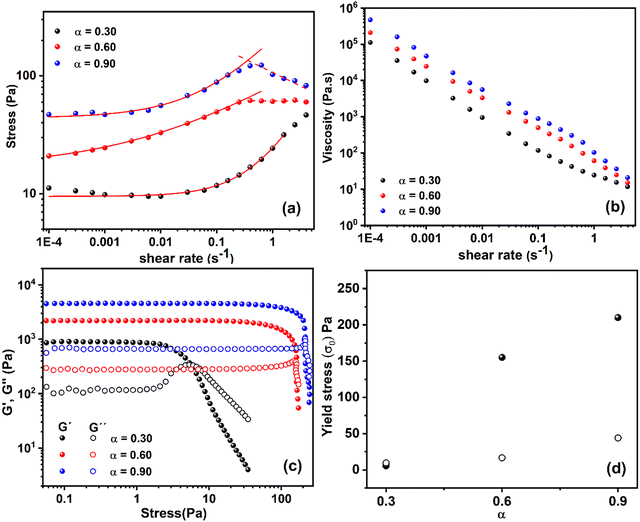Fig. 3 Rheological analysis of hydrogels prepared from G-C18:1 (10 wt%) with different calcium ratios ([Ca²⁺]/[G-C18:1]) of α = 0.3, 0.6, and 0.9 (a) Shear stress vs. shear rate (dots), fitted to the Herschel–Bulkley model for shear rates up to 0.5 s⁻¹ (solid line) and to a power-law model for higher shear rates (dashed line) (b) viscosity, calculated from shear stress, plotted against shear rate. (c) Storage (G′) and loss (G′′) moduli were measured in oscillatory experiments at 1 Hz, plotted against stress for various α (d) Yield stress (σ₀) as a function of α. The σ₀ values are obtained from (●) oscillatory experiments (Fig. 3(c)), defined as the G′ and G′′ crossover, and (○) from the Herschel–Bulkley fit of shear experiments (Fig. 3(a)).

Fig. 3(a) shows that the shear stress remains almost constant or slightly decreases at low shear rates, up to 0.01 s⁻¹, before increasing with rising shear rate. At higher shear rates, the shear stress decreases with increasing shear rate above 0.5 s⁻¹ for α = 0.6 and 0.9, and above 10 s⁻¹ for α = 0.3. This behavior is clearly reflected in the calculated viscosity (Fig. 3(b)), which exhibits a power-law dependence across different shear rate ranges.

The ascending part of the shear stress can be reasonably fitted to the Herschel–Bulkley model (σ = σ₀ + K[small gamma, Greek, dot above]ⁿ), allowing for the determination of the yield stress (σ₀) and the shear index (n). The values of n are estimated to be 0.52, 0.3, and 0.7 for α = 0.9, 0.6, and 0.3, respectively, suggesting shear-thinning behavior since n < 1. These fits σ₀ values of 44 Pa, 16.6 Pa, and 9.5 Pa, and K of 141, 65, and 14.6 for α = 0.9, 0.6, and 0.3, respectively. On the other hand, for α = 0.9 and 0.6, a different behavior emerges beyond 0.5 s⁻¹, deviating from the model. When fitted to a simplified power-law model (σ = K[small gamma, Greek, dot above]ⁿ), n is found to be −0.23 and 0.0 for α = 0.9 and 0.6, respectively, indicating stronger shear-thinning behavior. For α = 0.3, this deviation to stronger shear-thinning behavior occurs above 10 s⁻¹.

These results demonstrate the shear-thinning behavior of this gel beyond 0.01 s⁻¹, consistent with earlier reports.¹³ However, the present results also reveal that shear-thinning occurs in multiple stages, as confirmed by the stress dependence on shear rate shown in Fig. 3(a). The first stage is observed between 0.01 s⁻¹ and 0.5 s⁻¹, while the second stage occurs beyond this range, particularly for α = 0.6 and 0.9, and up to 10 s⁻¹ for α = 0.3. This multi-stage reduction in shear stress suggests that the shear-thinning behavior could be associated with the multiscale alteration of the long-range structure characteristic of G-C18:1 hydrogels. This is likely due to the progressive breakdown of the structure, with each stage affecting a distinct length scale. This mechanism is not seen in rheo-SAXS experiments showing that the nanoscale structure is essentially unchanged when shearing the gel at 0.1 s⁻¹ and at 100 s⁻¹.^12,13 The origin of the shear-thinning behavior is then at the level of the micron-scale heterogeneity.

During the extrusion process, the hydrogel is subjected to stresses that can be quantified by estimating the pressure drop across the channel. As described earlier, prior to the onset of shear-thinning, ΔP for η approaching 10⁵ Pa s could reach several hundred MPa in the case of a 0.84 mm diameter and 3.8 cm long needle. Such pressures are challenging to sustain in a 3D extrusion setup without specialized equipment capable of withstanding this level of structural instability. However, this pressure drop decreases drastically due to the shear-thinning behavior during the establishment of a steady-state flow regime, reducing to just a few kPa at the shear rate of the impression process. This reduced ΔP is manageable within the limits of the tools used for 3D printing. Considering the applied pressure levels and the micro- and macroscopic heterogeneity of the gel, it becomes evident that these pressures contribute to liquid–solid separation. This occurs when osmotic pressure is less dominant compared to the resistance offered by the fibrous network of the gel.

3.2.2 Yield stress and elasticity of the gel

Once deposited on a substrate, external forces such as gravitational force (ρ·g·h) and capillary forces tend to spread the gel. These forces are counteracted by the viscosity, which slows down the spreading process over time. However, for longer-term stabilization of the gel, the yield stress is more effective in preventing flow. The yield stress was determined using two methods: (1) flow measurements at shear rates approaching zero, and (2) oscillatory tests by varying the strain amplitude. The measured shear stress as a function of shear rate, shown in Fig. 3(b), indicates that as the shear rate approaches zero, the stress tends toward a constant value, suggesting the presence of a yield stress. Fitting the initial portion of the shear plot, up to 0.05 s⁻¹ for α = 0.6 and 0.9, and up to 5 s⁻¹ for α = 0.3, to the Herschel–Bulkley model yields an extrapolated value of σ₀, representing the apparent yield stress. This results in values of 44 Pa for α = 0.9, decreasing to 16.6 Pa for α = 0.6 and 9.5 Pa for α = 0.3 (Fig. 3). Yet acquiring true yield stress using shear experiments is challenging in this system, primarily due to the fragile nature of the gel. This is evident from the decrease in measured stress at low shear rates (0.0001 s⁻¹ to 0.001 s⁻¹), indicating that the gel begins to break at these levels of shear. Consequently, the yield stress derived from the Herschel–Bulkley fitting likely underestimates the actual value. This challenge arises because shear tests involve cumulative deformation to achieve a steady-state flow regime, which contributes to gel destruction and further reduces the measured yield stress. In contrast, oscillation experiments overcome this limitation by maintaining the gel within the linear regime, allowing the yield stress to be estimated as the point where the system departs from linearity. This makes oscillation experiments the preferred method for characterizing the yield stress of this gel. Indeed, yield stress measurements using oscillatory tests at 1 Hz across varying strain amplitudes yielded a yield stress of approximately 210 Pa for α = 0.9 (Fig. 3(c) and (d)). This value decreased steadily with decreasing α, reaching 155 Pa at α = 0.6 and 5.6 Pa at α = 0.3 (Fig. 3(d)). Fig. 3(d) highlights the trend of gel yield stress as a function of α and shows that the yield stress approaches zero as α nears 0.3, identifying this fraction as a threshold for developing yield stress in the gel.

The 210 Pa yield stress obtained for α = 0.9 exceeds both the estimated gravitational stress of approximately 100 Pa and capillary stresses of a similar magnitude. This explains the collapse of structures at α = 0.6 and the instability of printed structures at α = 0.3, primarily due to the reduction in yield stress below the applied forces.

This gel exhibits elastic behavior across all α values between 0.9 and 0.3, with the storage modulus (G′) consistently exceeding the loss modulus (G′′) for the investigated frequencies between 0.01 Hz up to 10 Hz, Fig. S4b (ESI†). The phase angle remains below 11°, and both G′ and G′′ increase with α, in line with previously observed trends. However, this elasticity alone is likely insufficient to ensure the structural stability of the printed morphology. For the gel to effectively resist external stresses, it likely requires non-evolutive crosslinking bonds present in sufficient content to produce a yield stress overwhelming external force. The stability observed for α = 0.9 must then be associated with the non-covalently crosslinked networks driven by ionomeric interactions between calcium and gel components, capable of forming non-evolutive networks.¹²

The Young's modulus can be estimated in this case from rheological measurements performed in shear mode. For example, in the case of α = 0.9, the complex modulus G* = (G′² + G′′²)^0.5 reaches about 7000 Pa in the linear regime. Assuming the material is incompressible, the Young's modulus can be approximated by E = 3G*, yielding E ≈ 21 000 Pa.

Entanglements of fiber and crowding may also contribute to structural stability^12,51–53 as classically observed in both carbopol, where swollen particles interact to create a yield stress that increases with concentration, enabling their suitability for 3D printing.^54–56 A similar behavior is noted in hydrogels derived from microfibrillated cellulose, where the crowding of fibrillar structures dominates the dynamics, giving rise to a yield stress suitable for 3D printing.^36,41 By extrapolation, it can be inferred that the fibers formed by the G-C18:1 hydrogel likely maintain their structural integrity, with minimal breaking or recombination, and that this crowding contributes to the gel's stability over time.

3.2.3 Recovery and thixotropy of the gel. The recovery phase of the rheological properties after shear stress in the nozzle plays a critical role in the transition from extrusion to stability on the substrate. This recovery was analyzed using a three-interval thixotropy test (3iTT), which involves a high-shear-rate shearing step followed by recovery at a low shear rate to assess the recovered yield stress.

Fig. 4(a) shows that the hydrogel subjected to a shear rate of 50 s⁻¹ recovers more than 40% of its viscosity within the first second, and then continues to regain its rheological properties over time. Full recovery, however, takes several hours. When the same experiment is repeated on a shorter timescale using the ARES-G2, the gel sheared at 300 s⁻¹ recovers more than 10% of its properties within 72 ms and over 40% after 200 s, Fig. 4(b). This indicates that the extent of recovery is dependent on the applied shear rate and, consequently, on the degree of gel destructuring. Similar recovery patterns are observed for α = 0.6 and α = 0.3, although with lower recovery magnitudes of 24% or less after 200 s.¹⁴

Fig. 4 Plot of the viscosity vs. time illustrating a recovery experiment using the three-interval thixotropy test (3iTT) from (a) measurements using the DHR3 rheometer with a destructuration shear rate of 50 s⁻¹ and a recovery shear rate of 0.01 s⁻¹. (b) Measurements using the ARES G2 rheometer with a destructuration shear rate of 300 s⁻¹ and a recovery shear rate of 0.001 s⁻¹. Experiments were conducted on hydrogels prepared from G-C18:1 (10 wt%) with varying calcium ratios ([Ca²⁺]/[G-C18:1]) of α = 0.3, 0.6, and 0.9.

The recovery dynamics of the gel at α = 0.9 are rapid compared to the deposition time, which occurs on the scale of seconds. During this period, the yield stress recovered within seconds is sufficient to counter external stresses, enabling the gel to maintain structural stability during the 3D printing process. As the height of the printed structure increases, the gravitational stresses also increase, but the recovery process supports these additional forces, ensuring stability. In contrast, at lower calcium fractions (α = 0.6 and α = 0.3), while recovery is rapid, the resulting yield stress is insufficient to counter external stresses, leading to instability during 3D printing. This highlights the critical role of both recovery dynamics and yield stress magnitude in achieving successful 3D printing.

3.2.4 Elongational and compressional behavior of the gel

It is important to note that the mechanical stresses applied during fluid deposition, including the stretching and compression forces induced by the nozzle as it moves across the gel, are essential factors in the 3D printing. These stresses cannot be entirely eliminated by controlling the flow rate and nozzle movement, but they remain as residual forces, which also contribute to the adhesion between successive layers. This process was quantified in Fig. 5 by measuring the forces involved during printing using a precision analytical balance (milligram scale). The force is monitored continuously during both fluid extrusion and the subsequent nozzle retraction without extrusion. During the extrusion phase, the residual force is approximately 3 mN for α = 0.9, corresponding to a residual stress of ∼1000 Pa, which then decreases to around 210 Pa, a value close to the yield stress. This residual stress contributes to the spreading of the structure, but it remains sufficiently moderate relative to the yield stress to preserve the intended morphology of the design. In the final stretching phase of the filament, a tensile force of approximately −1.8 mN is observed, corresponding to a tensile stress of 4000 Pa, calculated using the nozzle diameter of 0.84 mm. Visual observations of the gel's rupture mode reveal that the filament breaks at relatively low strain rates, on the order of a few percent, as shown in the sequence of images in Fig. 5. This low strain at rupture is related to the brittleness of the hydrogel under stretching, a characteristic that is crucial for minimizing sensitivity to nozzle movement during printing. When the strain at rupture is higher, filaments and printed structures deform significantly during nozzle movement, leading to deviations from the intended shape. This progressive departure from the designed structure during 3D printing highlights the importance of the G-C18:1 gel's brittle behavior under stretching and its compressive resistance associated with its yield stress. Together, these properties make the G-C18:1 hydrogel an ideal candidate for 3D printing applications, enabling high structural fidelity and stability.

Fig. 5 Plot of force vs. time during different stages of printing the G-C18:1 hydrogel (10 wt%, α = 0.9). The plot shows the force during the extrusion stage up to 50 s, followed by relaxation after extrusion cessation between 50 s and 110 s, and stretching beyond 110 s. The inset displays a series of images illustrating the hydrogel's behavior during the different stages of the process. Printing was performed using a needle with a 0.84 mm diameter and 0.5 cm length at a flow rate of 0.55 mm³ s⁻¹.

While these measurements provide meaningful insights into the gel's mechanical behavior, directly quantifying linear properties such as the Young's modulus remains challenging due to the material's fragility, it yields below 3% strain (Fig. S4, ESI†), and the presence of additional stress contributions from surface tension.

3.3 Printed structure when exposed to an external stimulus

The evolutive self-assembly properties of a LMWG like G-C18:1 can be also demonstrated in its 3D-printed hydrogel form, possibly paving the way for the use of this molecule in futuristic 4D printing of sustainable, biobased, amphiphiles. This possibility is supported by the gel's rheological sensitivity to external stimuli, notably to acidic conditions and to temperatures in the vicinity of 60 °C, both of which are known to modulate the self-assembled structure.¹³ To explore this potential, we explored the structural evolution of a typical G-C18:1 printed structure when exposed to an external stimulus, pH, known to have an impact on the phase behavior of G-C18:1.⁴⁸ A pillar with consistent shape and dimension as shown in Fig. 1 (diameter, d = 2 mm; height, h = 7.5 mm) served as the experimental subject. The pillar was exposed to HCl vapors by placing it beneath a plastic dome and containing a drop of concentrated hydrochloric acid (HCl 37%). The temporal evolution of the pillar response was systematically tracked through sequential image capture, as depicted in Fig. 6. Remarkably, complete structural disintegration occurred within just 90 seconds, highlighting the gel's pronounced stimuli-responsive behavior. This rapid degradation is attributed to the loss of the fibrillar structure at acidic pH (under pH 5).^14,48 Notably, their propensity for dissolution under mild conditions makes them highly suitable to easy removal, simplifying post-printing processes. Additionally, their utility extends to serving as sacrificial or fugitive inks in the spirit of evolutive 4D printing. This system, as it is currently designed, can lend itself to 4D, but only in one direction for the moment, which limits the applications, certainly, but it could still be useful as sacrificial ink.

Fig. 6 Images illustrating the stimulus response of the G-C18:1 hydrogel (10 wt%, α = 0.9), as the 3D-printed structure progressively collapses over time when exposed to an acidic atmosphere controlled by HCl vapor.

4. Conclusion

This study demonstrates that surfactants of biological origin, essentially developed as replacements to petrochemical surfactants, hide a much higher technological potential, here illustrated in the field of soft printed matter. Our findings show that a micellar solution of the single-glucose oleyl lipid, G-C18:1, can be printed after being physically cross-linked with calcium ions and in the absence of any other reactant or polymeric additive. Ca²⁺ drives the formation of G-C18:1 hydrogels with the yield stress, shear-thinning, and thixotropic properties required for effective 3D printing operations. Long-lasting 3D structures can eventually be stabilized by optimizing the calcium content (α = 0.9) and G-C18:1 concentration (10 wt%).

This work goes one step further compared to other soft printed systems, as it explores the synergy between rheometry and the printing capability. The results reveal that, at the optimal compositional range (α = 0.9, 10 wt%), the gel's shear-thinning behavior significantly reduces viscosity within the nozzle. This enables extrusion with minimal strain under a few kilopascals of pressure, typical conditions compatible with standard syringe-based printing. Additionally, the gel's yield stress is sufficient to counter external forces, and its recovery occurs within a timeframe shorter than the printing deposition time. This rapid recovery ensures that the gel regains its structural integrity during the process. Combined with the gel's unique fragile properties under elongation, these characteristics enable precise fidelity to the intended design during 3D printing, making it an ideal system for hydrogel applications.

External stimuli, particularly pH modification, have a direct impact on these materials’ supramolecular structure. This research not only highlights the innovative potential of biosurfactant-based materials in advancing soft materials engineering but also emphasizes their crucial role in developing sustainable technology solutions for the future.

This hydrogel system shows strong potential as a fugitive ink in biofabrication, where temporary structures are needed to support complex architectures during 3D printing. Such functionality is especially valuable in tissue engineering, where creating perfusable channels or supporting delicate cellular architectures is essential for developing functional biological tissues.

Author contributions

Elizangela Hafemann Fragal: writing – review & editing, writing – original draft, methodology, investigation, formal analysis, data curation, conceptualization. Alexandre Poirier: methodology, formal analysis. Didier Bleses: conception and development of 3D printing equipment. Yan Faria Guimarães Silva: methodology, formal analysis, Niki Baccile: writing – original draft, writing – review & editing, resources, project administration, funding acquisition, conceptualization. Yahya Rharbi: writing – review & editing, writing – original draft, supervision, resources, project administration, funding acquisition, methodology, investigation, formal analysis, data curation, conceptualization.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The Rhéologie et Procédés Laboratory is affiliated with the LabEx Tec 21 (Investissements d’Avenir – Grant agreement no ANR-11-LABX-0030). Additionally, the laboratory is associated with the PolyNat Carnot Institute (Investissements d’Avenir – Grant agreement no ANR-11-CARN-030-01). The authors express their gratitude to Frédéric Hugenell, and Vincent Verdoot for their invaluable assistance in conducting these experiments. The authors would like to thank the ANR program SELFAMPI, grant/award number: 19-CE43-0012-01; for their financial help. Authors also warmly thank Dr. Sophie Roelants, Amphistar, Belgium, for providing the glucolipid G-C18:1.

References

1. D. Kitamoto, T. Morita, T. Fukuoka, M. Konishi and T. Imura, Curr. Opin. Colloid Interface Sci., 2009, 14, 315–328.
2. J. D. Desai and I. M. Banat, Microbiol. Mol. Biol. Rev., 1997, 61, 47–64.
3. N. Baccile and J. Kleinen, Curr. Opin. Colloid Interface Sci., 2024, 101870.
4. G. B. Messaoud, Curr. Opin. Colloid Interface Sci., 2024, 101805.
5. R. D. Ashby, W. N. F. W. M. Zulkifli, A. R. M. Yatim, K. Ren and A. Mustafa, in Applications of Next Generation Biosurfactants in the Food Sector, ed. I. Inamuddin and C. O. Adetunji, Academic Press, 2023, pp. 307–334.
6. I. M. Banat, R. S. Makkar and S. S. Cameotra, Appl. Microbiol. Biotechnol., 2000, 53, 495–508.
7. J. Kleinen, Curr. Opin. Colloid Interface Sci., 2023, 101764.
8. D. Cooper and J. Zajic, Advances in Applied Microbiology, Elsevier, 1980, vol. 26, pp. 229–253.
9. N. Baccile, C. Seyrig, A. Poirier, S. Alonso-de Castro, S. L. Roelants and S. Abel, Green Chem., 2021, 23, 3842–3944.
10. R. K. Mishra, S. Das, B. Vedhanarayanan, G. Das, V. Praveen and A. Ajayaghosh, Supramolecular Gels, 2018, pp. 190–226.
11. A. Poirier, P. L. Griel, J. Perez, D. Hermida-Merino, P. Pernot and N. Baccile, ACS Sustainable Chem. Eng., 2022, 10, 16503–16515.
12. A. Poirier, P. L. Griel, I. Hoffmann, J. Perez, P. Pernot, J. Fresnais and N. Baccile, Soft Matter, 2023, 19, 378–393.
13. A. Poirier, P. L. Griel, T. Bizien, T. Zinn, P. Pernot and N. Baccile, Soft Matter, 2023, 19, 366–377.
14. A. Poirier, P. Le Griel, J. Perez and N. Baccile, J. Phys. Chem. B, 2022, 126, 10528–10542.
15. G. de A. L. e Souza, M. E. Di Pietro and A. Mele, RSC Sustainability, 2023, 2, 288–319.
16. A. M. Patel, V. Bhardwaj and A. Ballabh, Curr. Org. Chem., 2024, 28, 1046–1058.
17. C. Tomasini and N. Castellucci, Chem. Soc. Rev., 2013, 42, 156–172.
18. M. Suzuki and K. Hanabusa, Chem. Soc. Rev., 2009, 38, 967–975.
19. D. K. Smith, Soft Matter, 2024, 2, 10–70.
20. M. De Loos, B. L. Feringa and J. H. van Esch, Eur. J. Org. Chem., 2005, 3615–3631.
21. S. O. Formoso, V. Chaleix, N. Baccile and C. Hélary, Toxicol. Rep., 2024, 101862.
22. F. Andriamiseza, D. Bordignon, B. Payré, L. Vaysse and J. Fitremann, J. Colloid Interface Sci., 2022, 617, 156–170.
23. R. E. Ginesi, J. Doutch and E. R. Draper, Faraday Discuss., 2024 10.1039/D4FD00185K.
24. M. J. Hill and D. J. Adams, Soft Matter, 2022, 18, 5960–5965.
25. M. C. Nolan, A. M. F. Caparrós, B. Dietrich, M. Barrow, E. R. Cross, M. Bleuel, S. M. King and D. J. Adams, Soft Matter, 2017, 13, 8426–8432.
26. A. Chalard, M. Mauduit, S. Souleille, P. Joseph, L. Malaquin and J. Fitremann, Addit. Manuf., 2020, 33, 101162.
27. Z. Chen, Z. Li, J. Li, C. Liu, C. Lao, Y. Fu, C. Liu, Y. Li, P. Wang and Y. He, J. Eur. Ceram. Soc., 2019, 39, 661–687.
28. Q. Yan, H. Dong, J. Su, J. Han, B. Song, Q. Wei and Y. Shi, Engineering, 2018, 4, 729–742.
29. J. Z. Gul, M. Sajid, M. M. Rehman, G. U. Siddiqui, I. Shah, K.-H. Kim, J.-W. Lee and K. H. Choi, Sci. Technol. Adv. Mater., 2018, 19, 243–262.
30. A. D. Valino, J. R. C. Dizon, A. H. Espera Jr, Q. Chen, J. Messman and R. C. Advincula, Prog. Polym. Sci., 2019, 98, 101162.
31. E. Gkartzou, E. P. Koumoulos and C. A. Charitidis, Manuf. Rev., 2017, 4, 1.
32. J. Yu, R. Wan, F. Tian, J. Cao, W. Wang, Q. Liu, H. Yang, J. Liu, X. Liu and T. Lin, Small, 2024, 20, 2308778.
33. R. Wan, S. Liu, Z. Li, G. Li, H. Li, J. Li, J. Xu and X. Liu, J. Colloid Interface Sci., 2025, 677, 198–207.
34. S. Bom, R. Ribeiro, H. M. Ribeiro, C. Santos and J. Marto, Int. J. Pharm., 2022, 615, 121506.
35. A. M. Fuentes-Caparrós, Z. Canales-Galarza, M. Barrow, B. Dietrich, J. Lauger, M. Nemeth, E. R. Draper and D. J. Adams, Biomacromolecules, 2021, 22, 1625–1638.
36. S. Shin and J. Hyun, Carbohydr. Polym., 2021, 263, 117976.
37. J. Li, C. Wu, P. K. Chu and M. Gelinsky, Mater. Sci. Eng., R, 2020, 140, 100543.
38. Z. Chen, D. Zhao, B. Liu, G. Nian, X. Li, J. Yin, S. Qu and W. Yang, Adv. Funct. Mater., 2019, 29, 1900971.
39. X. N. Zhang, Q. Zheng and Z. L. Wu, Composites, Part B, 2022, 238, 109895.
40. K. Varaprasad, C. Karthikeyan, M. M. Yallapu and R. Sadiku, Int. J. Biol. Macromol., 2022, 212, 561–578.
41. Q. Wang, J. Sun, Q. Yao, C. Ji, J. Liu and Q. Zhu, Cellulose, 2018, 25, 4275–4301.
42. A. Ji, S. Zhang, S. Bhagia, C. G. Yoo and A. J. Ragauskas, RSC Adv., 2020, 10, 21698–21723.
43. F. Narciso, S. Cardoso, N. Monge, M. Lourenço, V. Martin, N. Duarte, C. Santos, P. Gomes, A. Bettencourt and I. A. Ribeiro, Colloids Surf., B, 2023, 230, 113486.
44. K. M. Saerens, J. Zhang, L. Saey, I. N. Van Bogaert and W. Soetaert, Yeast, 2011, 28, 279–292.
45. S. Lodens, S. L. Roelants, K. Ciesielska, R. Geys, E. Derynck, K. Maes, F. Pattyn, L. Van Renterghem, L. Mottet and S. Dierickx, Biotechnol. Bioeng., 2020, 117, 453–465.
46. K. M. Saerens, S. L. Roelants, I. N. Van Bogaert and W. Soetaert, FEMS Yeast Res., 2011, 11, 123–132.
47. N. Baccile, A. Poirier, C. Seyrig, P. Le Griel, J. Perez, D. Hermida-Merino, P. Pernot, S. L. K. W. Roelants and W. Soetaert, J. Colloid Interface Sci., 2023, 630, 404–415.
48. N. Baccile, A.-S. Cuvier, S. Prévost, C. V. Stevens, E. Delbeke, J. Berton, W. Soetaert, I. N. Van Bogaert and S. Roelants, Langmuir, 2016, 32, 10881–10894.
49. T. Cui, Y. Tang, M. Zhao, Y. Hu, M. Jin and X. Long, J. Agric. Food Chem., 2023, 71, 2964–2974.
50. F. M. White, Fluid Mechanics, McGraw Hill, 2011.
51. M. Suzuki, S. Owa, H. Shirai and K. Hanabusa, Tetrahedron, 2007, 63, 7302–7308.
52. D. M. Ryan and B. L. Nilsson, Polym. Chem., 2012, 3, 18–33.
53. M. Lescanne, P. Grondin, A. d’Aléo, F. Fages, J.-L. Pozzo, O. M. Monval, P. Reinheimer and A. Colin, Langmuir, 2004, 20, 3032–3041.
54. M. Barreiro Carpio, E. Gonzalez Martinez, M. Dabaghi, J. Ungureanu, A. V. Arizpe Tafoya, D. A. Gonzalez Martinez, J. A. Hirota and J. M. Moran-Mirabal, ACS Appl. Mater. Interfaces, 2023, 15, 54234–54248.
55. J. M. Piau, J. Non-Newtonian Fluid Mech., 2007, 144, 1–29.
56. S. Villata, F. Frascella, C. G. Gaglio, G. Nastasi, M. Petretta, C. F. Pirri and D. Baruffaldi, J. Polym. Sci., 2024, 62, 2259–2269.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00248f

---