Double symmetry breaking in filamentous colloidal tactoids

Abstract

Understanding the dynamics of liquid crystalline tactoids under external forces is of great importance due to their potential applications in optics, medical devices, and displays. However, only recently have tactoids started to be studied systematically under external forces, particularly under extensional flow. Here, we subject tactoids to a shear flow field and study their deformation dynamics under varying conditions of shear and time scales. Using amyloids and nanocellulose to form tactoids from model filamentous colloids with opposite sequences of chirality amplification (left-handed mesoscopic → right-handed cholesteric for amyloids; right-handed mesoscopic → left-handed cholesteric for nanocellulose), we show a complex deformation mechanism in their shape and internal structure under shear flow. When tactoids deform perpendicularly to their long axis, a double symmetry breaking occurs in both their contour shape, with the emergence of a kink, and the orientation of their nematic field. We further show that the mesoscopic chirality of the building blocks directs the position of the kink, with the macroscopic tactoid asymmetry being mirrored when inverting the mesoscopic chirality of the constitutive filamentous colloids, e.g., from the left-handed amyloids to the right-handed nanocellulose.

---

1. Introduction

Chirality is an important and ubiquitous concept in chemistry, biology, materials science, and nanotechnology. Understanding chirality transfer across length scales is of great importance due to its crucial role in the self-assembly of many soft materials.¹ The intrinsic chirality of the colloidal building blocks can affect the macroscopic structure and behavior of systems. Examples include the role of the actomyosin and microtubule networks in symmetry breaking processes during animal development,² the reorientation behavior of self-propelling chiral droplets,³ and spontaneous self-assembly in rotating chiral droplets.⁴ Spontaneous chiral symmetry breaking can, nonetheless, occur even from achiral building blocks in confined liquid crystalline phases when certain conditions are met. This is particularly relevant in liquid crystalline (LC) droplets, also called tactoids, where by the word tactoid we mean “a small anisotropic, birefringent region in a dilute, isotropic solution, consisting of an aggregate of rod-like particles or macromolecules aligned parallel to one another”.⁵ For example, bipolar tactoids formed from achiral chromonic liquid crystals exhibit twisted structures, with equally probable left- and right-handed chirality.⁶ This phenomenon, due to a specific range of elastic constant values, was first hypothesized numerically,⁷ later rationalized on purely theoretical grounds⁸ and further confirmed numerically.⁹ It was also reported that this equal probability of left- and right-handed tactoid occurrence can be disrupted by adding chiral molecules to achiral chromonic LC droplets.¹⁰ Furthermore, even the confining geometry might induce a spontaneous chiral symmetry breaking when some specific conditions are met: a notable case is the emergence of chirality from achiral chromonic liquid crystals confined in cylindrical geometries. This phenomenon is due to the contribution to the free energy of the term associated with saddle-splay deformation, a contribution often neglected in filamentous colloidal systems.^11,12 Importantly, in all the abovementioned cases of spontaneous chiral symmetry breaking, the left- and right-handedness of liquid crystalline structures occurs with equal probability. Therefore, chiral symmetry breaking in confined geometries, e.g., tactoids, is a complex phenomenon that involves several factors, among which are the handedness, physical properties, confining geometry, and interfacial features of the building blocks.

Tactoid formation has been observed in diverse biological and synthetic systems, such as fd viruses,¹³ tobacco mosaic viruses,¹⁴ F-actin,² flagellar filaments,¹⁵ carbon nanotubes,¹⁶ cellulose,¹⁷ and amyloid fibrils.^18–20 In this work, we use amyloid fibrils and sulfated cellulose nanocrystals as representative examples of filamentous colloids with left- and right-handed mesoscopic chirality, respectively, to form liquid crystalline tactoids, and we subject them to a complex shear flow field with a double velocity gradient. We show the emergence of a double symmetry breaking: one feature related to the orientation of the nematic field, whose directors adopt a pseudo-binary distribution, and the other one to the contour shape of the tactoid, with the emergence of a kink whose position can be shown to depend on the mesoscopic chirality of the constitutive filamentous colloid.

The study of heterogeneous complex fluids subjected to various flow fields has been carried out using multiple devices and the most diverse geometries, particularly in microfluidics.^21,22 Recent studies on liquid crystalline systems have applied extensional flow using microfluidic chips to probe various tactoid symmetries.^23–25 Beyond extensional flow, the coupling of flow and chirality has been observed in diverse soft-matter contexts. For instance, Marcos et al. found that shear flow can induce chiral vortices in active filament suspensions,²⁶ Hermans et al. showed that rod-like colloids under steady shear adopt a chiral nematic order,²⁷ and Zhang et al. reported the emergence of chiral nematic patterns in a flowing chromonic liquid crystal.²⁸ These studies demonstrate that external flow can actively bias the handedness of liquid crystalline structures. However, to the best of our knowledge, this is the first time that chiral tactoids have been exposed to a shear flow field exhibiting a double gradient, resulting in a double symmetry breaking, where by double symmetry breaking we mean that both the shape contour and the nematic field have lost all axes of symmetry. Due to the similarity between colloidal liquid crystalline droplets and biological water-in-water systems, such as cell organelles, and the ubiquitous presence of chirality in most of nature's building blocks, this work could improve our fundamental understanding of biological fluids out of equilibrium and may assist in developing new advanced materials and biomedical applications.^29–32

2. Deformation of tactoids using shear flow

To produce tactoids, suspensions of β-lactoglobulin amyloid fibrils (BLG) and sulfated cellulose nanocrystals (CNC) were prepared in the isotropic plus nematic coexistence region (see the Appendix for experimental details). Within this concentration regime, the tactoids spontaneously nucleate and form various anisotropic phases, different in volume and internal structure, as time passes. Here, three types of tactoids were considered. They are characterized by the aspect ratio α = R/r and volume V = r²R, where R and r are the major and minor axes of tactoids, respectively (Fig. 1a). Homogenous tactoids, which are the first phase to form, are spindle-shaped and have the director field always parallel to the long axis of tactoids (Fig. 1a, left column). Their volume is up to 10³ μm³ for BLG and up to 10⁴ μm³ for CNC. Following the growth path, as the volume increases, the configuration of the BLG tactoid changes from homogenous to bipolar, characterized by the director field following the interface of the droplet (Fig. 1a, middle column). Sulfated CNC tactoids do not have the bipolar phase and proceed directly to the uniaxial cholesteric phase. These tactoids are the largest among the three classes studied here and have volumes over 5 × 10⁴ μm³ for BLG and over 10⁴ μm³ for CNC.³³ They are characterized by an ellipsoidal shape and a striped texture resulting from the helical structure of the director configuration (Fig. 1a, right column).

Fig. 1 Internal structure of the tactoids and the experimental setup. (a) Top row: Schematic representation of the director field; middle and bottom rows: liquid crystal-PolScope images of the three classes of BLG tactoids (homogenous, bipolar, and cholesteric) studied here. The colormap (middle row) and the red lines (bottom row) represent the orientation of the director field, where the length of the lines is proportional to anisotropy. (b) Schematic illustration of the shearing system used for tactoid deformation. The system had a lid and a base, with the sample placed in between. The tactoids were investigated in two states, with their long axis both parallel and perpendicular to the shear flow u⃑(h, ρ) in the cell. (c) Structural description of the right- and left-handed cholesteric phases formed from left- and right-handed mesogens for BLG in CNC, respectively.

To date, only the deformation of liquid crystalline tactoids with extensional flow has been studied.²³ Here, to explore the effect of a complex flow field on the structure and shape of tactoids, tactoids based on amyloid and cellulose fibrils were formed inside a shearing cell system, whose geometry is explained in detail in the Appendix. As shown in Fig. 1b, the experimental setup produces a double velocity gradient in the flow field: radial, , and vertical, , where h is the vertical position. However, in the first approximation, we consider the radial gradient negligible, as the velocity difference between the inner side and the outer side of the tactoid is on the order of 10² times smaller than the absolute value of the velocity along the tactoid main axis, . Therefore, the flow velocity was approximated to only have a linear gradient from u(h₀ = 0) = 0 μm s⁻¹ at the fixed lid to u(h_max = 200 μm) = 30 μm s⁻¹ at the rotating base (Fig. 1b). This allows exposing tactoids to constant shear stress, defined as , where μ is the viscosity of the medium (here the isotropic phase), which is considered constant. To ensure the same conditions for all experiments, only the tactoids that were located in the middle plane of the shear cell and isolated from other tactoids were selected for the study. The experiments were performed at a gap size of 200 μm, ensuring that this is ca. 5 times larger than the short axis (2r) of the largest tactoid studied. Once the dispersion concentration is set within the isotropic and nematic coexistence region, homogenous tactoids take minutes to form, bipolar tactoids take hours, and cholesteric tactoids take days; this limits the possibility of forming them inside the shear cell, due to the evaporation of the solution, given that the base and lid of the shear cell cannot be hermetically sealed due to the experimental requirements of the setup. To address this issue, the nematic phase was extruded directly into the isotropic phase, with both phases originating from completely phase separated isotropic and nematic phases, following our previously established procedure.^23–25 Using this method, first 200 μL of the isotropic phase was deposited onto the base, then 2 μL of the nematic phase jet was injected into the isotropic bulk within the observation window area.

3. Double symmetry breaking in BLG tactoids

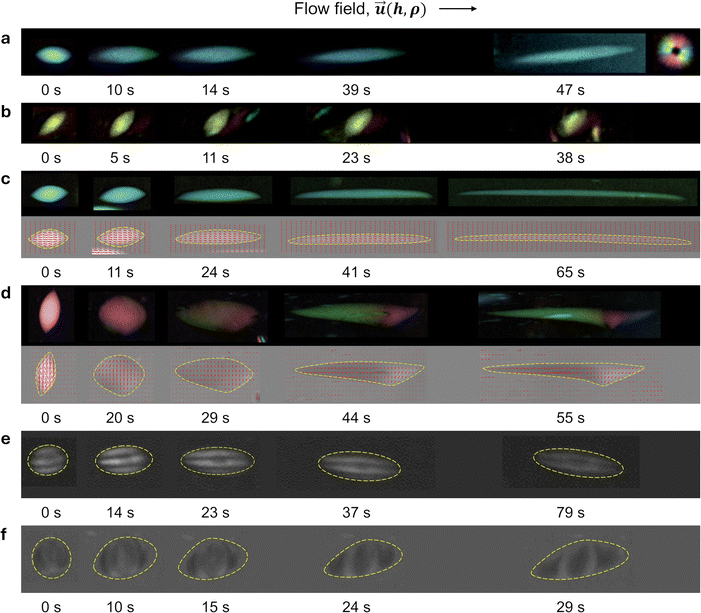
A liquid crystal-based polarizing microscope (PolScope) device was used to observe the changes in the shape and internal structures of tactoids. The initial time, t = 0 s in Fig. 2, corresponds to the moment when the shear stress is applied to tactoids. As shown in Fig. 2, homogenous ((a) and (b)), bipolar ((c) and (d)), and cholesteric ((e) and (f)) tactoids were exposed to shear flow in two configurations: when tactoids are aligned with their long axis parallel ((a), (c) and (e)) and perpendicular ((b), (d) and (f)) to the flow field. Until now, only the deformation of tactoids parallel to the flow field has been studied; however, the experimental setup presented here provides an additional opportunity to study the deformation of tactoids oriented perpendicular to the flow field. For homogenous tactoids, we observe that, for the parallel case, the tactoid gets stretched along the long axis, maintaining a homogenous director configuration (Fig. 2a). When the flow field is perpendicular to the long axis of the tactoid, no significant deformation was observed (Fig. 2b). When bipolar tactoids are subjected to the shear stress along their long axis, the internal director configuration transforms into a homogenous structure (Fig. 2c), similarly to the previous observations in the extensional flow.²³ On the other hand, the bipolar tactoids show complex behavior when they are exposed to shear flow perpendicular to the long axis. The aspect ratio, α, decreases monotonically, as can be seen from Fig. 1a, and the droplet is stretched in the flow direction, with r increasing and R decreasing steadily, and the shape of the deformed tactoid becomes highly asymmetric, unlike the parallel case. As time progresses, the shape exhibits enhanced curvature on one side, and the internal nematic field director rotates, giving rise to a spatially nonuniform reorientation in the proximity of the localized region (the kink) and enhanced splay deformation, as shown in Fig. 2d, where the splay deformation of the nematic field director inside the droplet can clearly be resolved (Fig. 2d, at 55 s). Thus, for bipolar tactoids deformed perpendicularly to the flow field at later stages of the time lapse (e.g., t = 55 s), a double symmetry breaking of the shape and nematic field orientation is observed. A couple of distinctive traits emerge in this double symmetry breaking process. First, for the BLG system, the kink is always formed on the right side of the tactoid relative to the movement direction (top view), which indicates the asymmetric behavior of the tactoid in terms of both the shape and internal structure with respect to the movement direction. This is in sharp contrast to the relatively well-behaving deformation of bipolar tactoids into homogenous tactoid configurations when the flow is applied parallel to the droplet's long axis. Second, according to both the colormap and vectorial representation of the nematic field provided by the PolScope (Fig. 2d), the director field undergoes – on the right side of the tactoid, where the kink is located – rotation in two opposite directions, as evident from the violet vs. green color in the colormap, respectively. This confirms again the double symmetry breaking process, involving both the shape of the tactoid and its internal structure. To further confirm the observed phenomenon, experiments with bipolar tactoids of various volumes (1500–8000 μm³) were repeated for both parallel and perpendicular orientations of the shear flow relative to the main axis of tactoids (10–15 data sets for each), always producing consistent results. We note that the kink formation mechanism is reversible. Once the shear rate is released, the tactoid relaxes back to the ground state (Fig. S2, ESI†). The main quantitative features of the bipolar tactoid deformation by shear flow perpendicular to the long axis of the tactoid are summarized in Fig. 3. Ten tactoids were each observed for about one minute in separate experiments under identical shear flow conditions but with varying volumes (300–2500 μm³). The short axis 2r of tactoids gets stretched over time, and the larger the tactoid, the stronger the observed deformation. The long axis 2R of tactoids monotonically decreases. The aspect ratio of the droplets α undergoes exponential decay: it decreases from values >1, passes through 1 (R = r) and further decreases, indicating consistent stretching of the droplets along the short axis. The normalized area A/A₀ first increases with respect to the initial tactoid area and successively flattens out. To interpret the area change, we consider the volume of tactoids to be constant as the isotropic and nematic phases do not mix. This is explained by the fact that the system minimizes its overall free energy by staying separated into two coexisting phases and it was proven experimentally that the tactoid volume stays nearly constant during deformations occurring over a timescale of a few minutes.²³ Therefore, the increase in the area can be explained by a decrease in the thickness of tactoids due to shear stress. This agrees with the decrease in the long axis 2R of tactoids, as the tactoid axis along h⃑ is also perpendicular to the flow field, u⃑(h, ρ).

Fig. 2 Time-lapse sequence of tactoid deformation under shear flow. Three classes of tactoids were studied here: homogeneous (a) and (b), bipolar (c) and (d), and cholesteric (e) and (f). Two configurations were studied: when the shear flow is parallel ((a), (c) and (e)) and perpendicular ((b), (d) and (f)) to the long axis of tactoids. Images were taken using an OpenPolScope device. The colormap represents the orientation of the direction in the plane (see the inset on the top right row for the orientation map). To deform tactoids with various shapes, volumes and structures, an initial shear force of order 10⁻¹⁰ N was applied. The initial volumes V₀ of the tactoids are (a) 810 μm³, (b) 290 μm³, (c) 2566 μm³, (d) 5020 μm³, (e) 5780 μm³, and (f) 5202 μm³. Systems are BLG in (a)–(d) and CNC in (e) and (f).

Fig. 3 Bipolar amyloid fibril liquid crystalline tactoids under shear flow perpendicular to the long axis. (a) The aspect ratio α = R/r of the droplets decreases from values >1, passes through 1 (R = r) and further decreases, indicating consistent stretching of the droplets along the short axis. (b) The long axis of tactoids in contrast decreases, and the slope is similar for various volumes. (c) The short axis of tactoids gets stretched over time, and the larger the tactoid, the stronger the observed deformation. (d) The normalized area, A/A₀, increases with respect to the initial tactoid area and later flattens out.

4. Effects of flow and mesoscopic chirality on the symmetry breaking process

To understand the mechanisms behind the asymmetric deformation of bipolar tactoids initially aligned perpendicular to the flow direction, we tested the influence of the sense of rotation of the shear cell base. Over small displacements (on the order of 10⁻² mm) compared to the observation radius of 7.5 mm, the flow field is assumed to be translational; however, the rotational component could affect the dynamics of the droplet, leading to its asymmetric stretching. The control experiment is performed by changing the rotation sense of the base disk of the shear cell (Fig. 4a). During counterclockwise (CCW) rotation, the kink (see the schematic sketch of the deformation of the droplet shape represented as a triangle) is formed away from the center of the shear cell, but during clockwise (CW) rotation the kink is formed towards the center. Since the centrifugal force is directed away from the center in both cases, the results show that the asymmetric deformation is not caused by the radial gradient in the flow field. Recent studies hint at the potential of the mesoscopic chirality of the materials in affecting their macroscopic behavior, which could have implications in biomedical applications, drug delivery, and nanomaterials.^4,34,35 Here, we hypothesize that the intrinsic chirality of the filamentous colloidal fibrils may direct the symmetry breaking process during droplet deformation by shear flow. Our starting point is the observation that in bipolar BLG tactoids deformed perpendicularly to the long axis, the symmetry breaking develops in such a way that the formation of the kink always occurs on the right side of the droplet with respect to the flow direction (when viewed from above). To test our hypothesis, we turn our attention to CNC tactoids, as the mesoscopic chirality of CNC is opposite to that of BLG.³⁶ Furthermore, since previous studies show that sulfated CNC nanofibrils do not exhibit the bipolar phase,¹⁹ cholesteric tactoids of both BLG and CNC were examined and compared in the following. As reported in earlier studies, a chirality inversion from the mesogen level to the cholesteric phase is generally observed for both BLG and CNC.^17,18 As shown in Fig. 1c, left-handed mesogens are aligned into right-handed cholesteric phases for BLG, while right-handed fibrils are aligned into left-handed cholesteric phases for CNC.¹⁸ First, as expected, no symmetry breaking was observed when cholesteric tactoids were deformed parallel to the long axis as shown in Fig. 2e for CNC and Fig. S1a (ESI†) for BLG. However, a similar phenomenon is now observed for CNC, but with a reverse effect compared to BLG (Fig. 2c and d), when the flow field is applied perpendicularly to the long axis of CNC tactoids. As already noted, BLG tactoids show double symmetry breaking by developing a pronounced curvature (kink) and a high splay reorientation in the director field on the right side of the droplet with respect to the flow direction for both the bipolar (Fig. 2d) and the cholesteric tactoids (Fig. S1b, ESI†). In contrast, CNC tactoids exhibit a mirror-image response, with the kink occurring on the left side (Fig. 2f), highlighting the crucial role played by the mesoscopic chirality of the mesogens in establishing the macroscopic asymmetry. As a control, we designed an experiment in which droplets based on achiral materials were studied under comparable hydrodynamic conditions (matching capillary numbers) and equal surface tension values.^37,38 To this end, dextran (DEX) droplets in polyethylene glycol (PEG) solutions were deformed using the same shear flow field (details are provided in the Appendix). In this case, no symmetry breaking was observed as shown in Fig. 4b (left panel). Taken together, these results clearly demonstrate that the double symmetry breaking is a result of the combined shear flow field and mesoscopic chirality of the filamentous colloids.

Fig. 4 Control experiments showing the nature of symmetry breaking for tactoids under shear flow. (a) The location of the kink in droplets relative to the flow direction is conserved (CCW = counterclockwise and CW = clockwise). (b) The dextran droplets in polyethylene glycol solution (left panel) were deformed by the same shear field; however, no symmetry breaking was observed in their shape with respect to the direction of the shear flow, comparing to BLG droplets (right panel).

5. Conclusions

To conclude, we examined the deformation of colloidal tactoids of opposite handedness subjected to shear flow with a double velocity gradient. Tactoids produced from β-lactoglobulin amyloid fibrils and cellulose nanocrystals, whose mesogens exhibit opposite mesoscopic chirality, evolve from homogeneous to more complex bipolar and cholesteric configurations as they grow in the isotropic and nematic coexistence region. Under the complex shear flow studied here, bipolar and cholesteric tactoids exhibit a double symmetry breaking: (i) their shape becomes asymmetrically distorted with a localized curvature; (ii) the internal director field reorients in a spatially nonuniform manner. Notably, the macroscopic asymmetric deformation of the tactoids could be mirrored by inverting the mesoscopic chirality of the constitutive filamentous colloids, that is, by switching from the left-handed BLG to the right-handed CNC. Control experiments with achiral dextran droplets confirm that symmetry breaking arises from the intrinsic chirality of the building blocks rather than from hydrodynamic factors alone. We note that the position of the kink does not depend on the presence or absence of macroscopic chirality: the position of the kink is the same for bipolar amyloid tactoids (missing macroscopic chirality) and cholesteric amyloid tactoids (right-handed). This leads us to conclude that it is the mesoscopic chirality that dictates the position of the kink. Future work should extend these conclusions to filamentous colloidal systems, which do not invert chirality across length scales.^39,40 The findings from this work highlight how microscopic chirality can govern macroscopic behavior in liquid crystalline systems. These observations can further improve our fundamental understanding of the effects induced by flow fields in complex colloidal systems and symmetry breaking phenomena in soft matter in general. Finally, these results could also provide new guidelines for the design of advanced chiral materials with anisotropic properties, which may have significant implications in biomedical and material applications.

Author contributions

M. A., H. A., and R. M. conceptualized the project. R. M. supervised the project. M. A. and H. A. designed and performed the experiments and analyzed the data. F. S. contributed to the experiments. M. A., H. A., and R. M. wrote the manuscript. All authors discussed the results and commented on the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data of this study are available at the following link: https://doi.org/10.3929/ethz-b-000741347.

Appendices

Appendix A. Preparation of amyloid fibrils

A 2 wt% solution was prepared by dissolving purified β-lactoglobulin (BLG) in Milli-Q water. Nylon filters (0.45 μm pore size) were used to purify the solution from aggregates. Next, the suspension pH was adjusted to 2 by adding hydrochloric acid. Then, the denaturation of amyloid fibrils was performed by heating the solution in an oil bath at 90 °C for 5 hours, followed by quenching the reaction with an ice bath. The solution was then centrifuged at 3000 RCF for 10 minutes to remove unwanted aggregates. The fibrils were cut into shorter pieces by applying mechanical shear force (kitchen blender). The resulting suspension was purified of unreacted monomers by dialysis using Spectra/Por membranes (MWCO: 100 kDa; Biotec CE Tubing) against 10 L of pH 2 Milli-Q water for 5 days with changing the bath daily. Since the concentration was significantly decreased during the dialysis, the solution was then concentrated by reverse osmosis against a 6 wt% PEG solution (obtained from Sigma-Aldrich, molecular weight: 35 000) using 6–8 kDa Spectra/Por dialysis membranes (Standard RC Tubing).

Appendix B. Preparation of cellulose nanocrystals

A 3 wt% solution of sulfated cellulose nanocrystal (CNC) powder (CelluForce) was obtained by dissolving it in Milli-Q water overnight, followed by sonication for 2 minutes. The solution was then centrifuged at 12 000 RCF for 20 minutes to remove possible aggregates.

Appendix C. Shearing system experiments

To generate the shear flow, a Linkam Shearing System (CSS450) obtained from Linkam Scientific Instruments was used. This microfluidic device consists of two parallel plates, a fixed lid, and a rotating base. The sample was dropped between quartz windows and incorporated into the lid and the base, allowing us to observe it under the microscope. The shearing system allows precise control of parameters such as the gap size (from 5 to 2500 μm) and the angular velocity of the base (from 0.001 to 10 rad s⁻¹). The viewing diameter is 2.8 mm and the radial distance to the center of the quartz windows is 7.5 mm. The lid and the base were cleaned with ethanol solution before placing the sample. In the preset 200 μm gap size and at room temperature, 200 μL of the isotropic solution was deposited with a pipette onto the base, covering the whole area. Next, 2 μL of the nematic solution was injected into the isotropic bulk, approximately at the center of the observation area. The sample was carefully covered with the lid to avoid any air bubble formation, and the lid was attached to the base with lid nuts.

Appendix D. Optical microscopy

Several microscopy setups were used to monitor the experiments: (i) a cross-polarized optical microscope (Zeiss Axio Scope A1), with an attached camera (AxioCam MRc) and various objective lenses: 5× (Achrostigmat), 10×, 20× and 40× (Plan Neofluar), was used to test the composition of the liquid crystalline solution; (ii) an optical microscope (Zeiss Axio Imager M1) coupled with an OpenPolScope⁴¹ system, with an attached camera (Hamamatsu C11440) and various objective lenses: 5× (Plan Neofluar), 10× and 50× (Epiplan Neofluar), was used to conduct the shear flow experiments. The data were analyzed using MicroManager software with OpenPolScope plugins.

Appendix E. Matching the capillary number

To compare the deformation of chiral liquid crystalline nematic droplets with the achiral dextran (DEX) droplets in polyethylene glycol (PEG), the capillary number (Ca) was considered. It is a dimensionless number that captures the balance between viscous forces and surface tension:
where η is the continuous phase viscosity, [small gamma, Greek, dot above] is the shear rate, R is the droplet radius, and γ is the interfacial tension. The molecular weights of dextran and PEG used are M_w (PEG) = 35 kDa and M_w (DEX) = 500 kDa, respectively. Taking the known viscosity and interfacial tension values from the literature, the droplet size and shear rate for the DEX in the PEG system were chosen to closely match the Ca values for the BLG-based liquid crystalline system (nematic droplets in an isotropic continuous phase) (Table 1).

Table 1 Hydrodynamic parameters for the chiral and achiral systems

Parameters	BLG	DEX in PEG
Droplet radius R (μm^3)	15	25
Viscosity η (10^−3 Pa s)	121^23	1.3^42
Shear rate [small gamma, Greek, dot above] (s^−1)	0.3	37.5
Interfacial tension γ (10^−6 N m^−1)	1.1^23	1.5^43
Capillary number Ca (dimensionless)	∼0.5	∼0.81

---

Acknowledgements

We thank T. Schwarz and S. S. Lee from the ScopeM (Scientific Center for Optical and Electron Microscopy of ETH Zurich) for the OpenPolScope installation and for the technical support with polarized optical microscopy and microfluidic experiments. We also thank Q. Sun for providing cellulose nanocrystals.

Notes and references

1. S. M. Morrow, A. J. Bissette and S. P. Fletcher, Nat. Nanotechnol., 2017, 12, 410–419.
2. C. Pohl, Symmetry, 2015, 7, 2062–2107.
3. F. Lancia, T. Yamamoto, A. Ryabchun, T. Yamaguchi, M. Sano and N. Katsonis, Nat. Commun., 2019, 10, 2–9.
4. T. Kajitani, K. Motokawa, A. Kosaka, Y. Shoji, R. Haruki, D. Hashizume, T. Hikima, M. Takata, K. Yazawa, K. Morishima, M. Shibayama and T. Fukushima, Nat. Mater., 2019, 18, 266–272.
5. H. Almohammadi, S. A. Khadem, P. Azzari, Y. Yuan, A. Guerra, A. D. Rey and R. Mezzenga, Rep. Prog. Phys., 2025, 88, 036601.
6. L. Tortora and O. D. Lavrentovich, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5163–5168.
7. R. D. Williams, J. Phys. A: Math. Gen., 1986, 19, 3211–3222.
8. P. Prinsen and P. van der Schoot, J. Phys.: Condens. Matter, 2004, 16, 8835.
9. D. Vanzo, M. Ricci, R. Berardi and C. Zannoni, Soft Matter, 2012, 8, 11790–11800.
10. C. Peng and O. D. Lavrentovich, Soft Matter, 2015, 11, 7257–7263.
11. K. Nayani, R. Chang, J. Fu, P. W. Ellis, A. Fernandez-Nieves, J. O. Park and M. Srinivasarao, Nat. Commun., 2015, 6, 1–7.
12. J. Jeong, L. Kang, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E1837–E1844.
13. Z. Dogic, Phys. Rev. Lett., 2003, 91, 165701.
14. F. C. Bawden, N. W. Pirie, J. D. Bernal and I. Fankuchen, Nature, 1936, 138, 1051–1052.
15. E. Barry, Z. Hensel, Z. Dogic, M. Shribak and R. Oldenbourg, Phys. Rev. Lett., 2006, 96, 1–4.
16. N. Puech, E. Grelet, P. Poulin, C. Blanc and P. Van Der Schoot, Phys. Rev. E, 2010, 82, 020702.
17. G. Nyström, M. Arcari, J. Adamcik, I. Usov and R. Mezzenga, ACS Nano, 2018, 12, 5141–5148.
18. G. Nyström, M. Arcari and R. Mezzenga, Nat. Nanotechnol., 2018, 13, 330–336.
19. M. Bagnani, G. Nyström, C. De Michele and R. Mezzenga, ACS Nano, 2019, 13, 591–600.
20. M. Bagnani, P. Azzari, S. Assenza and R. Mezzenga, Sci. Rep., 2019, 9, 1–9.
21. T. M. Ho, A. Razzaghi, A. Ramachandran and K. S. Mikkonen, Adv. Colloid Interface Sci., 2022, 299, 102541.
22. Y. Schaerli and F. Hollfelder, Mol. BioSyst., 2009, 5, 1392–1404.
23. H. Almohammadi, M. Bagnani and R. Mezzenga, Nat. Commun., 2020, 11, 5416.
24. H. Almohammadi, S. A. Khadem, M. Bagnani, A. D. Rey and R. Mezzenga, Nat. Commun., 2022, 13, 1–10.
25. H. Almohammadi, S. Martinek, Y. Yuan, P. Fischer and R. Mezzenga, Nat. Commun., 2023, 14, 1–9.
26. Marcos, H. C. Fu, T. R. Powers and R. Stocker, Phys. Rev. Lett., 2009, 102, 158103.
27. T. M. Hermans, K. J. M. Bishop, P. S. Stewart, S. H. Davis and B. A. Grzybowski, Nat. Commun., 2015, 6, 5640.
28. Q. Zhang, W. Wang, S. Zhou, R. Zhang and I. Bischofberger, Nat. Commun., 2024, 15, 7.
29. T. P. Knowles and M. J. Buehler, Nat. Nanotechnol., 2011, 6, 469–479.
30. S. J. Woltman, G. D. Jay and G. P. Crawford, Nat. Mater., 2007, 6, 929–938.
31. B. Li, D. Zhou and Y. Han, Nat. Rev. Mater., 2016, 1, 1–13.
32. S. C. Glotzer, Nature, 2012, 481, 450–452.
33. M. Bagnani, P. Azzari, C. De Michele, M. Arcari and R. Mezzenga, Soft Matter, 2021, 17, 2158–2169.
34. M. Rahman, W. H. Almalki, O. Afzal, A. S. Alfawaz Altamimi, S. N. M. Najib Ullah, M. Abul Barkat and S. Beg, Drug Discovery Today, 2023, 28, 103420.
35. X. Chen, Y. Cheng, Q. Pan, L. Wu, X. Hao, Z. Bao, X. Li, M. Yang, Q. Luo and H. Li, ACS Nano, 2023, 17, 3705–3722.
36. I. Usov, G. Nyström, J. Adamcik, S. Handschin, C. Schütz, A. Fall, L. Bergström and R. Mezzenga, Nat. Commun., 2015, 6, 7564.
37. M. Mastiani, S. Seo, S. M. Jimenez, N. Petrozzi and M. M. Kim, Colloids Surf., A, 2017, 531, 111–120.
38. Y. Liu, R. Lipowsky and R. Dimova, Langmuir, 2012, 28, 3831–3839.
39. G. Zanchetta, F. Giavazzi, M. Nakata, M. Buscaglia, R. Cerbino, N. A. Clark and T. Bellini, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17497–17502.
40. E. Grelet and M. M. C. Tortora, Nat. Mater., 2024, 23, 1276–1282.
41. R. Oldenbourg, Nature, 1996, 381, 811–812.
42. S. Kirinčič and C. Klofutar, Fluid Phase Equilib., 1999, 155, 311–325.
43. E. Atefi, J. A. Mann Jr. and H. Tavana, Langmuir, 2014, 30, 9691–9699.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00236b

---