Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Capillary-induced adhesive contact dynamics determines dissipation and flow structure in wetted hydrogel packings
Zohreh
Farmani
 ab,
Jing
Wang
ab,
Jing
Wang
 c,
Ralf
Stannarius
c,
Ralf
Stannarius
 c and
Joshua A.
Dijksman
c and
Joshua A.
Dijksman
 *ab
*ab
avan der Waals-Zeeman Institute, Institute of Physics, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: j.a.dijksman@uva.nl
bPhysical Chemistry and Soft Matter, Wageningen University & Research, Stippeneng 4, 6708 WE Wageningen, The Netherlands
cInstitute of Physics, Otto von Guericke University Magdeburg, Universitätsplatz 2, D-39106 Magdeburg, Germany
First published on 3rd June 2025
Abstract
The bulk response of a granular material is strongly influenced by particle and contact properties, such as friction coefficients, particle softness, lubrication on the contact scale and adhesion between particles. This study explores the bulk flow of wetted hydrogel particles, which are soft but also weakly adhesive due to capillary bridges. This simplified granular material with minimal contact friction reveals key insights in the role of capillary stresses on the macroscopic flow. At the micro-scale, we demonstrate a direct correlation between relative humidity (RH) and liquid bridge size between two wetted hydrogel spheres, with an average rupture distance increasing with humidity. On the macro scale, the wetted hydrogel sphere packings show remarkable flow dissipation and flow behavior in the split-bottom shear cell. We retrieve flow fields of the hydrogel packing with magnetic resonance imaging and measure flow resistance with a rheometric technique. The shear bands for the adhesive hydrogels are much narrower than for dry grain flows. The change in flow resistance due to a change in filling height can be interpreted with a minimization argument, indicating that the flow dissipation is set entirely by the capillary bridge stress: the capillary stress at all filling heights dominates the gravitational stress. We confirm this view by exposing the flowing packing to an external pressure. Beyond a confining stress of 250 Pa, the shear bands become significantly thinner, approaching some plateau at 360 Pa. This underscores the importance of understanding micro-scale interactions in controlling macroscopic hydrogel particle packing behavior.
1 Introduction
Anyone who has ever built a sand castle knows that one needs a bit of water to turn loose sand grains into a good building material. This everyday experience is representative of the general fact that the bulk properties of particulate materials or so-called “bulk solids” are strongly influenced by particle interactions, even if they are very weak. Specifically, in the case of sticky, slightly wet grains, it remains important to comprehend how particle–particle interactions in the presence of liquids affect the intricate mechanics and physics of wet particulate materials.1,2 When wet particles come into contact with each other or with a solid surface, their contact behavior differs significantly from that of dry particles. This disparity arises primarily from the formation of a liquid bridge between wet particles, which introduces distinctive bulk flow characteristics compared to dry systems.3–7 One effect that plays a role is that frictional forces on particle contacts can become substantially larger due to the presence of the normal forces induced by the capillary effects, for example providing the ability to build a sand castle with vertical walls. Liquid bridges form due to contact adhesion or attractive forces arising between (partially deformable) particles upon contact. Various types of liquid bridges, including pendular (low liquid content), funicular (medium liquid content),8 and capillary (high liquid content, particles are completely encapsulated with liquid), have been characterized.9 Liquid bridges also play a vital role in the behavior of particles under compression or indentation,10–12 as they contribute to the particle resistance to deformation by establishing adhesive forces between constituent particles.13 Understanding the mechanisms of contact adhesion provides insights into micro-scale particle behavior14–16 and aids in the design of materials with tailored mechanical properties. The presence of liquid bridges has been shown to significantly influence particle flow, transforming particle behavior from individual grains to clumps.17,18Hydrogel particle packings are distinct from regular particle packings as a result of various differences between the hydrogel material and the typically stiffer materials of which most other granular ensembles are made. Another major difference is that hydrogel–hydrogel contacts have a very low friction coefficient. The actual friction coefficient depends on the hydrogel used, the sliding rate, the normal force and likely other chemical factors.19 The maximum ratio of normal to tangential forces that a hydrogel–hydrogel contact can sustain is typically estimated to be smaller than 0.01. As there are no frictional forces to activate, how do capillary effects change the flow behavior of such low-friction particle packings? The investigation of weakly hydrated (“wetted”) soft particle mixtures is particularly interesting, as the formation of capillary bridges can exert pressures that compete with other stress scales in soft, low-friction particle systems, such as lubrication forces and deformation. How does contact adhesion affect flow and microstructure? To what extent can we quantify the effect of adhesion in soft adhesive grain packing? How is the bulk flow behavior affected by capillary contacts?
We show here that millimeter-sized hydrogel particle packings are strongly affected by capillary necks. Despite the weakness of capillary bridges with respect to gravitational forces, as evidenced by our direct contact measurements, wetted hydrogel particle packings show distinct flow features that sets them apart from their submersed equivalent. Our magnetic resonance imaging (MRI)-based measurements indicate that the quasi-static flow behavior of the packing displays very narrow shear bands and a strong dependence on the flow geometry, suggesting that capillary interactions can generate strong dissipation at the contact level. Further confined flow measurements and rheometer-based dissipation measurements support the unconfined flow geometry-based interpretation in terms of capillary-induced dissipation, providing at once a novel method to probe the role of contact adhesion on the stresses and flow behavior in a slowly flowing granular material. Finally, rate dependent measurements of wetted hydrogel packings reveal a rate dependence that suggests that capillary forces can activate a rate-dependent dissipation mechanism between the hydrogel particles.
2 Liquid bridge mechanics
We first probe the contact mechanics of a capillary neck between two hydrogel particles, to quantitatively establish the adhesive forces on a single hydrogel–hydrogel contact. These contact force measurements are not as trivial as in static, rigid spheres, as hydrogel spheres can absorb water from their bulk into the capillary neck, making the traditional capillary contact models less useful, as they rely on constant liquid bridge volumes.20 Moreover, the hydrogel spheres have relaxation mechanics of their own,21 and an unknown but likely finite contact angle22 that we call θ, all of which may affect capillary neck mechanics. We therefore first explore the contact dynamics of two wet hydrogel spheres separately. We expose the two spheres in contact to various RH environments and contact timescales as they are likely to encounter in the packing of sheared particles.2.1 Setup for capillary adhesion measurements
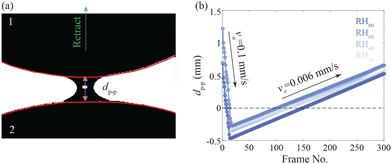
The setup is depicted in Fig. 1. We secured two equally sized hydrogel spheres with 10 mm diameter in holders that covered approximately two-thirds of the spheres. The top holder was connected to a 50 g capacity load cell. We also aligned the particles in the x and y direction. The bottom particle remained fixed to the lab frame, while the top particle was brought into contact with the second sphere and then retracted. During the entire contact process (approach and retraction), we measured the force and displacement. We approached the first particle towards the second particle at a constant velocity va, then allowing for a relaxation period (contact time tc) to ensure particle equilibration. This (probably poroelastic) relaxation time allows for the particles to adjust, redistributing forces and potentially accommodating changes in shape or inter-molecular forces within the particle gel network before measurements during separation. Moreover, during the relaxation period tc, stress redistribution might occur within the particles. In the next step, the first particle was retracted from contact at a velocity vr. All measurements were performed within a chamber in which the relative humidity was controlled. The process was monitored using a camera, allowing us to quantify the properties of the liquid bridge formed between the particles.We systematically varied the relative humidity (RH) and adjusted the contact time tc to study relaxation effects. The approach velocity va and retraction velocity vr were varied to examine the influence of contact (lubrication) dynamics on the magnitude of the inter-particle forces. Additionally, we explored the effect of contact force FM variation on the deformation and rupture distance between the particles.
Fig. 2 illustrates the formation of a liquid bridge during the retraction of the top particle from the bottom one, captured at relative humidities of 20% (Fig. 2a), 40% (Fig. 2b), 60% (Fig. 2c), and 80% (Fig. 2d). We observe changes in the shape, rupture distance, and volume of the liquid bridge as relative humidity increases. We note that the contact angle does not show significant dependence on the RH. From theory,22 we expect a finite contact angle: even though the hydrogel material is superabsorbent and hence likely charged and thus prefers to be surrounded by bulk water, the outer polymer strands on the surface of the sphere will at least partially adsorb on the water–air interface, creating an energy penalty for the wetting of hydrogel surface, leading to finite contact angle. The variation in particle–particle distance throughout the frames is shown in Fig. 3, which is extracted from a single recording of the approaching and retracting particles.
 | ||
| Fig. 2 Liquid bridge captured from particle–particle dynamics just before break-off at (a) RH 20%, (b) 40%, (c) 60%, and (d) 80%. | ||
To analyze the liquid bridge properties, we processed the recorded videos from experiments. The images were converted to grayscale to simplify the processing, and a thresholding technique was applied to segment the dark spheres from the background, resulting in a binarized image. To detect the boundaries of the spheres and calculate the change in distance as they interact, two red circle segments were fitted to the sphere surfaces (Fig. 3a). We calculated the distance between the boundaries of the spheres along the vertical axis (assuming the spheres are aligned vertically). Typical results are shown in (Fig. 3b).
The rupture distance for contacting spheres refers to the separation or retraction distance between their surfaces before rupture. We observed that the rupture distance increases with increasing relative humidity RH due to the increased amount of liquid within the bridge (Fig. 4).
 | ||
| Fig. 4 Rupture distance dp–p as a function of RH = 20, 40, 60, 80%. The error bars represent the standard deviation of triplicate measurements. | ||
Furthermore, when two particles approach and then retract from each other, we measure the force–displacement relationship (Fig. 5). We call the total amount of displacement of the top sphere d. The starting point is always at a finite distance d > 0 from the bottom sphere. Initially, as they approach (red line), the two spheres are separated, and the force is zero. When the top sphere moves downward and touches the bottom sphere, there is a sudden increase in the force, primarily due to the Hertzian elastic response. After the contact point (at d ≈ 1 mm for most experiments), we observe a slight negative force up to d ≈ 1.2 mm, which is followed by a sharp increase in the force until it reaches the maximum contact force or overlap. The small negative dip is a result of a liquid bridge forming.
2.2 Adhesive force dynamics
The experimentally measured force response is the difference between the Hertzian elastic response of the spheres in contact (when there is a contact) and the emerged capillary neck, which establishes itself upon contact and exists until its rupture at finite separation distance. Crucially, we do not know how much liquid the neck extracts out of the sphere: some water may be getting sucked from the sphere due to capillary stresses or imbibed from elsewhere on the surface of the hydrogel sphere. We can hence not disentangle these contributions. The deformation of the sphere, combined with the change in neck volume as the spheres approach, makes it challenging to extract the separate magnitude of these two contributions; such a study would require a separate work. We can, however, establish the capillary adhesive contact force dynamics experimentally.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ based on capillary neck theory. Here, R is the radius of the spheres used in the adhesion tests and γ is the surface tension of the contact liquid, all as specified in Table 1. We gain two insights from this experimental result. First of all, based on the assumption that this force scale is also relevant during elastic (wetted) loading of the contact, Hertz elasticity theory for a sphere yields a maximum Hertz contact pressure p0 of about 2000 Pa. This results comes from the textbook23 relation
θ based on capillary neck theory. Here, R is the radius of the spheres used in the adhesion tests and γ is the surface tension of the contact liquid, all as specified in Table 1. We gain two insights from this experimental result. First of all, based on the assumption that this force scale is also relevant during elastic (wetted) loading of the contact, Hertz elasticity theory for a sphere yields a maximum Hertz contact pressure p0 of about 2000 Pa. This results comes from the textbook23 relation | (1) |
| Particle properties | Settings |
|---|---|
| Diameter 1 (flow tests) (Dp1) | 2–3 mm |
| Diameter 2 (adhesion tests) (Dp2) | 10 mm |
| Density (ρ) | 999 kg m−3 |
| Particle Young's modulus (Ep) | 10 kPa |
| Particles Poisson's ratio (νp) | 0.5 |
| Water density (ρf) | 997 kg m−3 |
| Rotation rate (ω0) | 0.02 rad s−1 |
| Rotation angle (θ) | 10° |
| Strain steps (N) | 7 |
| Split disk radius (mm) | 47.5 |
| Outer fixed plate radius (mm) | 75 |
| Maximum allowed filling height (mm) | 100 |
Second, we can relate the adhesive contact forces to another relevant force scale, namely gravity. The granular Bond number24–27 under gravity is then a helpful concept, which contrasts the maximum attractive force during contact with a single grain's weight.
 | (2) |
3 Flow structure of dense, wetted hydrogel sphere packings
3.1 Split-bottom shear cell, MRI experiments
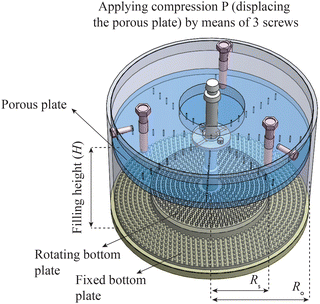
In the context of bulk shear flows, in the so-called split-bottom shear cell (SBSC), extensive studies have examined how various particle and contact properties—such as friction, softness, and adhesion affect the compression of sheared granular materials.6,18,27–31 We use the magnetic resonance imaging (MRI) technique to obtain high-resolution structural and dynamical information of hydrogel packings in the SBSC. Detailed information on the MRI measurement method can be found elsewhere.32 Our focus is on studying the shearing behavior of soft adhesive hydrogels in an SBSC, as this geometry produces well-developed shear bands away from the boundaries of the shear cell.33,34 The hydrogels used here were 2–3 mm in diameter, initially swelled in water and subsequently wetted. Experimental parameters are also provided in Table 1, and the design of the SBSC used in this study can be found elsewhere.35 At the beginning of experiments, our SBSC was filled with a material layer of depth H, and then driven, stepwise, in each step with a constant rotation of an inner bottom disk with a radius of Rs = 47.5 mm. A schematic sketch of the SBSC is shown in Fig. 7. Within the MRI scanner, we performed experiments under two types of applied pressure: (1) shear under constant hydro-static particle pressure (Phyd), which means the flow structure was not confined by a lid, and (2) shear while varying constant confining pressures P from the top boundary, which we refer to as the “confined flow structure”. We provide the results of these different experimental conditions in the two following subsections. In each measurement, step-wise shear with a constant rate of ω0 was applied. We performed the experiments in step-wise mode to allow for imaging after each strain step. In the first set of experiments, the unconfined case, the filling height H and thus the ratio of height to inner disk radius (H/Rs) was varied as a tuning parameter to control the exerted pressure Phyd on the packing. In the second set of experiments, the confined case, an additional pressure source was introduced for every H/Rs through a porous plate placed on top of the packing; the top plate could be positioned at different fixed heights to control the volume of the particle packing. We calibrated the stress exerted separately using a rheometer, where the normal force FN was recorded by displacing the plate in 2 mm increments for a packing with an initial height of 50 mm.To determine the angular velocity fields in a cross section of the SBSC, we employed particle image velocimetry (PIV) of the 3D MRI images. To create smooth PIV fields with high resolution, we assumed axial symmetry of the displacement field. In this approximation, we can obtain the absolute displacement of hydrogel material in the “square donut” space given by a small range in both vertical coordinate h and radial coordinate r, via an image intensity cross-correlation approach. This displacement was calibrated with the simultaneously measured rotation angle of the bottom disk and served as the angular velocity ω(h,r), relative to the rotation rate ω0 of the bottom disk. The data were averaged over 5 strain steps for each H/Rs. We verified that an initial transient was only two strain steps long, it was removed from the analysis. With this approach, we determined the displacement of particles at a given (h,r) from the MRI image stacks.
3.2 Unconfined flow structure
We first probe the flow behavior of unconfined packings, in which only gravity provides the confining stress. Fig. 8a shows a two-dimensional (2D) displacement of particles at a given (h,r) for different filling heights H extracted by PIV from MRI 3D tomograms. In the shallow layers (H = 15 mm), a narrow and nearly vertical shear band is formed between the moving zone above the rotating disk and the static zone. As we increase the filling height and move towards the deeper layers, we observe collapsing of the shear band from vertical to horizontal. There are three distinguishable regions though, (1) a trumpet-like structure in shallow layers (H/Rs = 0.31, 0.42), (2) an intermediate region showing a mixture of trumpet and dome structures (H/Rs = 0.5, 0.59), and (3) a dome-like structure in deep layers (H/Rs = 0.65, 0.95, 1.05). At approximately H/Rs = 0.59 the shear band still reaches the top surface. However, by increasing the fill height by another 3 mm, the particles at the surface become static and a dome with the thickness of few particle layers appears on top of the rotating disk. At H ≈ Rs, we observe a completely closed dome. The phenomenology of the flow fields is very similar to that of dry granular flows and suspensions in the SBSC,36 yet a close look at the flow profiles reveals one essential difference. | ||
Fig. 8 (a) 2D unconfined flow profiles at a given (h,r) extracted from PIV, for adhesive hydrogel packing, in beds of different heights from H = 15 mm to H = 50 mm. (b) Normalized averaged angular velocity profiles for a range of filling heights H = 15 mm  , 20 mm , 20 mm  , 24 mm , 24 mm  , 28 mm , 28 mm  , 31 mm , 31 mm  , 45 mm , 45 mm  , and 50 mm , and 50 mm  . The graph shows the relative rotation speed at height H along a ring of radius r for adhesive hydrogels. For all runs, Rs is 47.5 mm. All the profiles are fitted with an error function (dotted lines), see eqn (3). The slight scatter of the data is due to experimental uncertainty and indicates the typical error on ω. . The graph shows the relative rotation speed at height H along a ring of radius r for adhesive hydrogels. For all runs, Rs is 47.5 mm. All the profiles are fitted with an error function (dotted lines), see eqn (3). The slight scatter of the data is due to experimental uncertainty and indicates the typical error on ω. | ||
By taking a cross-section from 2D profiles of Fig. 8a at a constant h = H/2, we look at the non-dimensional angular velocity profile ω(r)/ω0, defined as the ratio of the time-averaged azimuthal velocity to the driving rate ω0, with a high radial resolution obtained by PIV (Fig. 8b). As usual, we can observe a general trend in the ω(r)/ω0 curves with the three distinguishable regions of shallow, intermediate, and deep layers. From H/Rs = 0.31 (15 mm) to H/Rs = 1.05 (50 mm), the slope of the curves representing the shear bands decreases and the shear band moves inward from totally vertical to horizontal. All profiles fit well with an error function equation established in previous studies:32,34
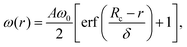 | (3) |
If dissipative mechanisms only play a role in the very narrow shear zones, we can use the torque minimization argument from Unger et al.37 to estimate the transition from vertical to dome-shaped shear bands. The hydrostatic pressure gradient is not an important stress scale in this system, as the gravitational stress ≃ ρgH for a 1 cm layer of wetted hydrogels is about 100 Pa. As eqn (1) showed, the maximum contact stress due to capillarity can exceed that significantly. We find that for the 10 mm diameter hydrogel particles of the microscopic study, the peak Hertz theory contact stress was approximately 2000 Pa; for the smaller spheres used in the flow study, this peak stress increases to >2 kPa as per the scaling in eqn (1). As we also know that the flow is quasistatic and the particles polydisperse38,39 (hence crystallization is unlikely) we can assume that the shear stresses are predominantly set by capillary stresses, which are essentially uniform throughout the packing. The total amount of dissipation is then proportional to the surface area between the static and moving bulk.
To estimate the surface area of the shear zone, we can see that at low fill heights, if the shear zone is perfectly vertical, it resembles a cylinder and the surface area depends linearly on H/Rs (shown as the solid black line in Fig. 9a). At intermediate filling heights, the shear zone collapses and we should approximate the shape of the shear zone as an oblate half-spheroid. With the MRI data at hand, we can estimate the height z = zP of the oblate half-spheroids observed for larger filling heights, by estimating where the normalized angular velocity ω(z = zP) = 1/2. We can then compute the sliding surface areas in the filling height regimes discussed by using the standard equation for the surface S of a paraboloid:40
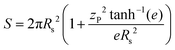 | (4) |
Here,  . The results with estimates for zP(H/Rs) are shown in Fig. 9a. When H/Rs increases, we observe the dome shaped shear zone precisely at the filling height where a cylinder with said filling height would have exceeded the shear surface of the actually observed dome shapes shear band: at approximately 24 mm filling height, a nearly spheroidal shear zone becomes smaller than the cylinder surface area, triggering a system transition. We conclude that the system aims to minimize the shear zone area, influenced by friction coefficient considerations.37,41 We can gain additional evidence for this mechanical picture by measuring the dissipated power as a function of filling height.
. The results with estimates for zP(H/Rs) are shown in Fig. 9a. When H/Rs increases, we observe the dome shaped shear zone precisely at the filling height where a cylinder with said filling height would have exceeded the shear surface of the actually observed dome shapes shear band: at approximately 24 mm filling height, a nearly spheroidal shear zone becomes smaller than the cylinder surface area, triggering a system transition. We conclude that the system aims to minimize the shear zone area, influenced by friction coefficient considerations.37,41 We can gain additional evidence for this mechanical picture by measuring the dissipated power as a function of filling height.
3.3 Confined flow structure
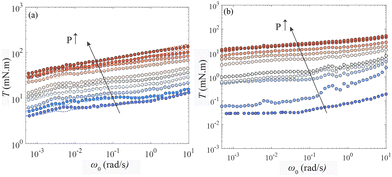
We can get an indication that the nonuniform distribution of pore fluids has a limited effect on the capillary effects by performing flow studies of the hydrogels under confinement of a lid with fixed position. In our confined flow study, we performed a combined set of experiments: step-wise shear experiments followed by a step-wise compression. During the compression steps, we increased the confinement stress on the packing by moving down a porous plate on top of the hydrogel packing. At every compression step, we performed MRI measurements to probe the 3D flow structure and the total compression. We measured the displacement of particles at a given (h,r) using the MRI-PIV methods described above for every compression level P, to be clarified below. We performed a set of MRI measurements of confined packings, at initially constant filling heights of H = 50, 31, and 20 mm. We focus here on the results from the H = 50 mm case, noting that for this case, the fixed compression plate least affects the flow boundary condition at the top, as the surface velocity at this H/Rs is already very small even in the unconfined case. The results for other filling heights are qualitatively consistent. As before, we performed shear over 7 strain steps of 10° at ω0 ≈ 0.02 rad s−1. At P = 0, we observed the shear band in confined to the bulk and forms a dome-shaped structure, as in the unconfined case. By moving down the plate by fixed amounts using the set screws and increasing P, and then performing step-wise shear, the dome becomes flatter, and flow is ever more confined to the rotating plate (Fig. 11).The experimental results of compressed packing have two major consequences: (1) our results suggest that compression above ≈ 360 Pa does not observably change the shape of the profile; the shear band is confined to a shallow layer just above the disk. This indicates that we have reached a plateau region where further increases in confining pressure no longer probe any stress sensitivity in the packing. This limit is interesting as it allows us to probe the effect of confining stress on the packing itself. We also note that (2) during compression, the packing gets submersed into essentially all pore fluid available. The flowing material beyond a stress level of ≈ 250 Pa can be considered a submersed suspension.
4 Discussion
4.1 Micro-scale findings
4.2 Macro-scale findings
5 Conclusion
We conducted microscale and macroscale experiments to investigate the behavior of wetted hydrogel particle packings. Adhesion measurements of the hydrogel particles revealed the systematic presence of capillary bridges under a wide range of loading speeds, maximum forces and contact durations and relative humidity conditions, and allowed to quantify a capillary contact stress scale of about 2 kPa, and establishing the magnitude of the Bond number in our packings. Our study sheds light on the complex interactions between hydrogel particles in which dynamics is set by capillarity, hydrogel swelling and elastic hydrogel properties. Using magnetic resonance imaging (MRI), we investigated the flow structure of hydrogel sphere packings in the SBSC setup. We varied the filling height and pressure applied to the packing, comparing confining pressures to contact pressure scales. We observed the formation of a narrow shear band in the unconfined, yet an even narrower one in the confined flow structure. The filling height had a significant impact on the shape of these bands, yet can be explained with a dissipation minimization principle, similar to such effects in non-adhesive dry particle flows in said geometry. The flow dissipation displayed a non-monotonic filling height effect that can also be rationalized from a shear surface minimalization perspective and may be used for characterization of particle adhesiveness. Our findings provide valuable insights into the flow behavior of adhesive (soft) particle packings and in particular hydrogel materials, offering a foundation for further research and the development of applications in e.g. adhesive powder mixtures and biomaterials.Data availability
Data for this article is available at Zenodo repository with DOI: https://doi.org/10.5281/zenodo.14945583.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement CALIPER no 812638. We acknowledge insightful discussions with Frans Leermakers. Cindy Lübeck and Oliver Speck are acknowledged for making the MRI experiments possible.Notes and references
- T. Li, W. Meng, Y. Wang, A. Valia, R. Jamsandekar, R. Kumar, F. J. Muzzio and B. J. Glasser, Part. Sci. Technol., 2022, 40, 141–150 CrossRef CAS.
- P. Liu, C. Q. LaMarche, K. M. Kellogg, S. Leadley and C. M. Hrenya, AIChE J., 2016, 62, 3529–3537 CrossRef CAS.
- B. Buck, Y. Tang, N. G. Deen, J. Kuipers and S. Heinrich, Chem. Eng. Res. Des., 2018, 135, 21–29 CrossRef CAS.
- H. Shi, R. Mohanty, S. Chakravarty, R. Cabiscol, M. Morgeneyer, H. Zetzener, J. Y. Ooi, A. Kwade, S. Luding and V. Magnanimo, KONA Powder Part. J., 2018, 35, 226–250 CrossRef CAS.
- S. Mandal, M. Nicolas and O. Pouliquen, Phys. Rev. X, 2021, 11, 021017 CAS.
- S. Roy, S. Luding and T. Weinhart, New J. Phys., 2017, 19, 043014 CrossRef.
- A. Gans, B. Dalloz-Dubrujeaud, M. Nicolas and P. Aussillous, Phys. Rev. Lett., 2024, 133, 238201 CrossRef CAS PubMed.
- J.-P. Wang, E. Gallo, B. François, F. Gabrieli and P. Lambert, Powder Technol., 2017, 305, 89–98 CrossRef CAS.
- M. E. D. Urso, C. J. Lawrence and M. J. Adams, J. Colloid Interface Sci., 1999, 220, 42–56 CrossRef CAS PubMed.
- Y. Song and R. Turton, Powder Technol., 2007, 178, 99–108 CrossRef CAS.
- A. Hassanpour and M. Ghadiri, Part. Part. Syst. Charact., 2007, 24, 117–123 CrossRef CAS.
- J. Paul, S. Romeis, J. Tomas and W. Peukert, Adv. Powder Technol., 2014, 25, 136–153 CrossRef CAS.
- S. Luding, Granular Matter, 2008, 10, 235–246 CrossRef.
- C. Thornton, A DEM study. Particle Technology Series, 2015, vol. 24, pp. 21–47 Search PubMed.
- P. G. Rognon, J.-N. Roux, M. Naaim and F. Chevoir, J. Fluid Mech., 2008, 596, 21–47 CrossRef CAS.
- N. Mitarai and F. Nori, Adv. Phys., 2006, 55, 1–45 CrossRef CAS.
- E. L. Chan and K. Washino, Chem. Eng. Res. Des., 2018, 132, 1060–1069 CrossRef CAS.
- S. Roy, S. Luding and T. Weinhart, Procedia Eng., 2015, 102, 1531–1538 CrossRef.
- M. Workamp and J. A. Dijksman, J. Rheol., 2019, 63, 275–283 CrossRef CAS.
- Y. I. Rabinovich, M. S. Esayanur and B. M. Moudgil, Langmuir, 2005, 21, 10992–10997 CrossRef CAS PubMed.
- C. Shakya, J. van der Gucht and J. A. Dijksman, Front. Phys., 2024, 12, 1334325 CrossRef.
- M. Cohen Stuart, W. De Vos and F. Leermakers, Langmuir, 2006, 22, 1722–1728 CrossRef CAS PubMed.
- V. L. Popov et al. , Contact mechanics and friction, Springer, 2010 Search PubMed.
- S. T. Nase, W. L. Vargas, A. A. Abatan and J. McCarthy, Powder Technol., 2001, 116, 214–223 CrossRef CAS.
- V. Richefeu, M. S. El Youssoufi, R. Peyroux and F. Radjai, Int. J. Numer. Anal. Methods Geomech., 2008, 32, 1365–1383 CrossRef.
- E. Koos, Curr. Opin. Colloid Interface Sci., 2014, 19, 575–584 CrossRef CAS PubMed.
- A. Singh, V. Magnanimo, K. Saitoh and S. Luding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022202 CrossRef PubMed.
- D. Faroux, K. Washino, T. Tsuji and T. Tanaka, Phys. Rev. Fluids, 2022, 7, 084306 CrossRef.
- H. Shi, S. Roy, T. Weinhart, V. Magnanimo and S. Luding, Granular Matter, 2020, 22, 1–20 CrossRef.
- Q. Luo, Q. Zheng and A. Yu, Powder Technol., 2017, 314, 121–128 CrossRef CAS.
- S. Roy, S. Luding and T. Weinhart, EPJ Web Conf., 2017, 140, 03065 CrossRef.
- J. Wang, Z. Farmani, J. A. Dijksman, C. Lübeck, O. Speck and R. Stannarius, Granular Matter, 2022, 24, 103 CrossRef.
- D. Fenistein and M. van Hecke, Nature, 2003, 425, 256 CrossRef CAS PubMed.
- D. Fenistein, J. W. van de Meent and M. van Hecke, Phys. Rev. Lett., 2004, 92, 094301 CrossRef PubMed.
- Z. Farmani, N. Ghods, H. Singh, J. Wang, R. Stannarius, S. Radl, D. L. Henann and J. A. Dijksman, Pressure sensitivity in non-local flow behaviour of dense hydrogel particle suspensions, arXiv, 2023, preprint, arXiv:2308.00140 DOI:10.48550/arXiv.2308.00140.
- J. A. Dijksman and M. van Hecke, Soft Matter, 2010, 6, 2901–2907 RSC.
- T. Unger, Phys. Rev. Lett., 2007, 98, 018301 CrossRef PubMed.
- M. Alam and S. Luding, Phys. Fluids, 2003, 15, 2298–2312 CrossRef CAS.
- E. Kurban, D. Vescovi and D. Berzi, Soft Matter, 2025, 21, 2049–2058 RSC.
- F. Olver, D. Lozier, R. Boisvert and C. Clark, The NIST Handbook of Mathematical Functions, Cambridge University Press, New York, NY, 2010 Search PubMed.
- T. Börzsönyi, T. Unger, B. Szabó, S. Wegner, F. Angenstein and R. Stannarius, Soft Matter, 2011, 7, 8330–8336 RSC.
- J. A. Dijksman, E. Wandersman, S. Slotterback, C. R. Berardi, W. D. Updegraff, M. van Hecke and W. Losert, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 060301 CrossRef PubMed.
- Z. Farmani, J. A. Wieringa, J. van Duynhoven and J. A. Dijksman, KONA Powder Part. J., 2024, 2025014 Search PubMed.
- R. Höhler and S. Cohen-Addad, Soft Matter, 2017, 13, 1371–1383 RSC.
- N. Brodu, J. A. Dijksman and R. P. Behringer, Nat. Commun., 2015, 6, 7361 CrossRef PubMed.
- C. Shakya, L. Placidi, A. Misra, L. Kool, A. Lindner, J. Van der Gucht and J. Dijksman, 2025 DOI:10.48550/arXiv.2506.08855.
| This journal is © The Royal Society of Chemistry 2025 |