Directed self-organization of block copolymer micelles on topographic substrates

Abstract

The ability to create complex arrays of organized nanostructures is crucial for many advanced technological applications. An extensively investigated methodology for producing such arrays is the directed self-assembly of block copolymers using topographically patterned substrates, where micron-scale features engraved in the substrate induce nanodomain alignment over macroscopic ranges. Most research thus far concentrated on the formation of ordered surface patterns through microphase separation of block copolymers in thin films. In this work, we demonstrate the utility of block copolymer micelles – soft, self-assembled, non-crosslinked entities – for the preparation of arrays with structural bi-modality. Systematic investigation of the influence of the substrate's topography on the micellar assembly at different concentrations revealed different structural behavior of micelles deposited on the plateaus and in the trenches, which is tunable by the topographic feature dimensions. The potential of this approach for effecting complex superstructures is demonstrated by employing the micelles to organize semiconductor nanorods.

---

Introduction

Ordered nanostructures formed by self-assembly enable organizing functional materials into pre-defined superstructures that are useful for various nanotechnology applications, such as nanoelectronics and photonics.^1–9 A prime example of self-assembling materials that gives rise to ordered nanoscale arrays is block copolymers (BCPs), which are synthetic macromolecules composed of two or more chemically distinct polymer sequences (blocks) of repeat units that are linked together. The inherent incompatibility between the blocks leads to microphase separation and the spontaneous formation of domains with well-defined morphologies (spheres, cylinders, and lamellae depending on the BCP composition), driven by the tendency to minimize the interfacial energy between the incompatible blocks.^10–16

In thin films, BCP domains pack into periodically ordered arrays, which can serve as versatile templates for the assembly of functional nanomaterials in a more elaborate assembly scheme.^{14,15,17–26} Long-range ordering and domain alignment along macroscopic coordinates can be achieved by applying directed self-assembly (DSA) approaches, such as chemoepitaxy and graphoepitaxy, which provide chemical or topographical interfaces on the substrate that guide the BCP domain evolution during phase separation.^16,27–30 Both approaches require the use of top-down, lithographic techniques. The preparation of chemically patterned substrates is rather elaborate whereas the creation of simple topographic features (such as trenches with rectangular profiles) requires only a few processing steps (namely, electron-beam writing into a resist, development, and reactive ion etching).

While most research to date on DSA of block copolymers concentrated on the evolution of ordered structures in continuous films,^28–38 we were intrigued by the following question: how would pre-assembled entities, which are dynamic in nature and could adjust their structure to the environmental conditions, organize on a topographically-patterned substrate? One would expect that the dynamic nature of these entities would lead to non-trivial morphological behavior, where the variables of the topographic pattern could be used for fine-tuning.

Interestingly, block copolymers themselves could provide such dynamic entities: dissolving amphiphilic BCPs in selective solvents gives rise to their self-assembly into micelles, which are usually globular in shape and where the insoluble block forms the core and the soluble block forms the corona.^39–47 Spherical micelles of asymmetric diblock copolymers (where one block is longer than the other) are classified as either “hairy” (starlike) or “crewcut” depending on the relative lengths of the core- and corona forming blocks.^39,43 The fact that these structures are self-assembled but not crosslinked endow them with the ability to respond to environmental changes such as pH, temperature, light, and solvent composition, and thus to use these stimuli to swell/shrink,^48,49 disassemble,⁵⁰ or switch morphology between spherical and cylindrical.⁵¹ This dynamic behavior is useful for applications such as drug delivery.^52–60

When a micellar solution of sufficiently high concentration is cast on a substrate and the solvent quickly evaporates, a monolayer of micelles is formed, where the micelles are spread on the surface in a kinetically trapped structure. Thus, it is interesting to see how the morphology responds to a non-uniform local environment (i.e., the substrate's topography) compared to what is known on annealed block copolymer films that are cast from non-micellar solutions.

Russell et al. investigated BCP micelle organization on topographic substrates.⁶¹ To our knowledge, this is the only work so far that addressed this topic. The main goal was to improve the long-range ordering of micelles by confining them in trenches. This was achieved by casting polystyrene-block-poly(4-vinyl pyridine) (PS-b-P4VP) on grating patterns featuring narrow plateaus. The copolymers consisted of short, core-forming P4VP blocks and long PS blocks, which give rise to hairy micelles in PS-selective solvents. It should be noted, however, that the BCP was cast from a non-selective solvent (i.e., the BCP chains did not assemble into micelles in solution prior to casting), and the micelles were formed in situ only upon annealing the cast film in vapors of a slightly PS-selective solvent. The combination of lateral confinement, the evolution of the micellar structures from a disordered film, and a BCP composition that gives rise to small and hairy micelles (which are expected to be more mobile than crewcut micelles under annealing) enabled achieving long-range ordering of micelles in the trenches after prolonged annealing of a few hours.

In our study, we aimed to explore the morphological changes that micelles, which exist in solution already before casting, undergo when they are deposited on a topographically patterned substrate. Our focus was on the micelle morphology rather than on achieving long-range ordering. Hence, we used crewcut micelles (where the core blocks are longer than the “hairs”), which are supposed to be robust enough to retain their structure under the shear forces acting during spin coating yet dynamic enough to be able to respond to the environmental conditions. We employed an array of patterns with plateaus that are wide enough to accommodate a few micelles across (up to ∼7 multiples of the micelle diameter in solution) and varied the dimensions of the topographic features. Additionally, we investigated the influence of micelle concentration on the resulting structure of the micellar film. The results described below provided insights on the subtle morphological differences between micelles deposited on the plateau and trench regions in films cast from micellar solutions. Lastly, we demonstrate the versatility of our approach by utilizing these subtle differences for obtaining quantum rod superstructures with distinct organizational modes at prescribed locations on the substrate.

Results and discussion

Polystyrene-block-poly(2-vinyl pyridine) copolymer (PS-b-P2VP; M_n 270 kDa, PDI 1.23, f_PS = 0.35; referred to as PS₈₉-b-P2VP₁₈₁) was dissolved in toluene (a PS-selective solvent) to make 0.5 and 1.0 wt% concentration solutions. The crewcut micelles formed consisted of P2VP cores (58 ± 9 nm diameter) and PS corona, with a total diameter in solution measuring 88 ± 9 nm (Fig. S1, ESI†). Micellar solutions were spin-coated over topographically patterned silicon substrates, as illustrated in Fig. 1a and b, and briefly annealed under toluene vapor to locally relax the structures. The arrays of parallel trenches etched into the substrate by electron beam lithography were either shallow (19 or 21 nm-deep) or deep (45 nm), and featured variable widths (Fig. S2, ESI†). These depths were chosen to be shallower or deeper than the deposited micelle height (31 nm).¹⁹

Fig. 1 (a) Cartoon illustrating micelle deposition on topographically patterned substrates and depicting the variables of the topographic features. (b) Cartoon depicting the arrays of parallel trenches on the substrate. (c) Diagram illustrating the parameter space of the study and representative SEM images of micellar PS₈₉-b-P2VP₁₈₁ films cast from 1.0 wt% (i)–(iv) and 0.5 wt% (v)–(viii) toluene solutions, deposited on flat regions of the substrate (i) and (v) or topographically-defined regions (ii)–(iv) and (vi)–(viii), and annealed in toluene vapor. All scale bars represent 500 nm.

The volume of the micelles deposited from a 0.5 wt% solution, modeled as a spherical cap (V = π(h³/6 + (hϕ²)/8), with height h = 31 nm and average diameter ϕ = 89 nm)¹⁹ was 10% larger than the volume of the micelle core (Fig. S1, ESI†). The difference accounts for the “dry” corona blocks covering the cores of the deposited micelles. This suggests that the micelles do not disassemble upon deposition but only undergo a morphological change.

General overview

Fig. 1c provides an overview of the parameter space of the study. The variables include the widths of the plateaus and trenches (w_pl and w_tr), the depths of the trenches (d_tr), and the concentration of the micellar solution. The images presented in Fig. 1c shows that altering these parameters results in distinct structures (see enlarged versions in Fig. S3, ESI†): flattened round micelles (Fig. 1c, images (ii) and (v)–(viii)), a mixed morphology of round and coalesced micelles characterized by the worm-like structure (Fig. 1c, image (i)), and a location-specific, dual morphology consisting of round micelles on the plateaus and worm-like micelles in the trenches (Fig. 1c, images (iii) and (iv)). Additionally, we observed that whereas micelles deposited from 1.0 wt% solution on a flat region of the substrate (a few hundred micrometers from the topographic features) gave rise to both round and worm-like structures (Fig. 1c, image (i)), those deposited on top of the topographic features with 19 nm-deep trenches formed exclusively round structures, both on the plateaus and within the trenches (Fig. 1c, image (ii)).

To explain the substrate-dependent morphological behavior, we must first understand the behavior of micelles when they are deposited on topographically patterned substrates. During spin casting, the liquid layer thins as the solvent evaporates and its surface deforms as its thickness becomes closer to the depth of the trenches. Capillary forces arising from this deformation draw material into the trenches and deplete the amount of material deposited on the plateaus. This behavior was observed with non-micellar BCP films, resulting in the differentiation of the BCP film thickness between the plateaus and the trenches, which subsequently influenced the types of morphologies that developed over these topographic regions upon annealing.^36–38,62

In micellar solutions, the particles on which the immersion capillary forces act are assemblies consisting of hundreds of BCP chains (an average aggregation number of 380 was estimated for the PS₈₉-b-P2VP₁₈₁ micelles).^63,64 As immersion capillary forces depend on the squared radius of the particle,^26,65,66 they are stronger than those acting on individual BCP chains in a non-micellar solution. This means that the differentiation of the amount of deposited material between plateaus and trenches should be considerably enhanced in micellar films than in non-micellar films, leading to sparse micelle deposition on the plateaus and micelle crowding within the confines of the trenches. Hence, under certain conditions the micelles in the trenches may adopt a compact morphology, such as elongated domains, which is manifested as the worm-like morphology (Fig. 1c, images (iii) and (iv)), whereas the micelles sparsely deposited on the plateaus have more available surface to spread on (Fig. 1c, images (vi)–(viii)). Lastly, one should take into account that the hydrophilic silicon substrate (with its native oxide layer) is more compatible with the core (P2VP) blocks, which may promote micelle spreading on the surface to expose their cores to it.

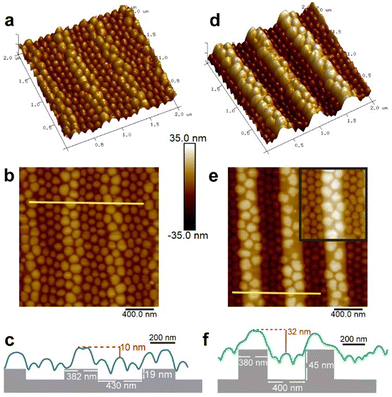
Fig. 2 presents AFM height images and cross-section profiles of micellar structures created on shallow trenches (19 nm) and deep trenches (45 nm), which provide additional insights into the structures of the deposited micelles. Micelles located on the plateaus of the deeper patterns appear more distorted, and the plateaus themselves exhibit a greater amount of exposed regions (Fig. 2d and e) compared to those formed on the plateaus of the shallow patterns (Fig. 2a and b). Additionally, the height difference between the top of the micelles deposited on the plateaus and the top of the micelles localized in the trenches is smaller than the trench depth in both cases (10 and 32 nm compared to d_tr of 19 and 45 nm, respectively; Fig. 2c and f). This suggests that the micelles in the trenches are taller than the micelles deposited on the plateaus.

Fig. 2 AFM images and cross-sections of micelles deposited from 0.5 wt% toluene solution on topographically patterned substrates featuring shallow (19 nm-deep, (a)–(c)) and deep (45 nm-deep, (d)–(f)) trenches. (a) and (d) Three-dimensional renditions, (b) and (e) top view height images, (c) and (f) cross-sectional height profiles corresponding to the yellow lines in (b) and (e) with overlaid illustrations of the substrates depicting the corresponding topographic features and their dimensions. Inset in (e) shows the same region it overlaps at the same magnification with a brighter contrast to facilitate viewing the micelles in the trenches.

Fig. 3 shows SEM images of the annealed micellar structures on shallow and deep topographic patterns with varying lateral dimensions. In Fig. 3a, micelles on shallow and narrow topographic features exhibit consistent “flattened micelle” morphology across the entire pattern. In contrast, Fig. 3d reveals that micelles deposited on deeply etched substrates (with similar lateral feature widths as in Fig. 3a) give rise to a worm-like morphology within the trenches, with the plateaus nearly devoid of material. Aside from this mixed morphology, all other patterns in Fig. 3 demonstrate the morphology of flattened micelles, which appear to the naked eye as relatively uniform in distribution and size. However, quantitative characterization reveals notable differences.

Fig. 3 SEM of micellar PS₈₉-b-P2VP₁₈₁ films cast from 0.5 wt% toluene solutions on topographically defined substrates. The trench depths are 19 nm (a)–(c) and 45 nm (d)–(f). Plateau and trench widths appear at the top right corner of each image.

The differentiating effect of the topography on the density and average diameter of deposited micelles

Extensive quantitative analysis of micelles cast from 0.5 wt% and 1.0 wt% toluene solutions on patterns with varying feature widths, including shallow (19 nm) and deep (45 nm) trenches, was performed in order to gain deeper insights into the behavior of micelles in response to the local environment (see Experimental section and Fig. S5, ESI† for further details). The relative amounts of micelles deposited in each region were quantified as local number-densities, which were calculated using the number of micelles in the selected feature of interest (plateau or trench, counted as demonstrated in Fig. S5a, ESI†) and the total area of that corresponding feature.

Fig. 4 displays the local density values calculated for micelles deposited from the 0.5 wt% solution on the different topographic patterns (denoted as ρ^0.5%). Each data point in the graphs shown in Fig. 4 corresponds to the local density of the micelles deposited on either the plateaus (triangles; ρ_pl^0.5%) or trenches (open squares; ρ_tr^0.5%) on a specific type of pattern (characterized by a unique set of w_pl, w_tr, and d_tr). The data are plotted against the respective widths of the plateaus and trenches in that pattern. This arrangement of data was performed in an attempt to reveal direct correlations (i.e., of the ρ_tr^0.5% to w_tr and of the ρ_pl^0.5% to w_pl) as well as cross-correlations (i.e., influence of the w_pl on the ρ_tr^0.5% and vice versa; depicted as gray data points in Fig. 4). The upper graphs show the dependence of the local micelle densities on w_pl in the shallow and the deep trench cases (Fig. 4a and b, respectively), whereas the bottom graphs show the same data plotted against w_tr (Fig. 4c and d).

Fig. 4 The dependence of local number density of micelles cast from 0.5 wt% toluene solution on the plateau width (a) and (b) and trench width (c) and (d) when deposited on shallow (a) and (c) and deep (b) and (d) trenches. The red dashed lines represent the micelle density values measured on flat regions (56 and 58 micelles per μm² in the shallow and deep trench cases, respectively). Trendlines were calculated by linear regressions for the data aimed at probing direct influence (plateau data in (a) and (b) and the trench data in (c) and (d)), and are provided as a guide to the eye only. Grey datapoints correspond to data aimed at probing cross-correlations.

The first clear observation is that across all analyzed patterns, irrespective of the topographic characteristics of the pattern, the density of micelles deposited in the trenches is always higher than that of micelles localized on the plateaus (i.e., ρ_tr^0.5% > ρ_pl^0.5%). The density of micelles deposited on a flat region of the corresponding sample (ρ_flat^0.5%; marked as dashed red lines in Fig. 4) generally falls between these two sets of data. This density differentiation is caused by the topography-driven capillary forces acting on the micellar solution, which direct the micelles into the trenches. The gap observed between the two data sets in each graph is larger in the deep trenches case (Fig. 4b and d) than in the shallow trenches case (Fig. 4a and c), which is consistent with the stronger capillary forces acting in the case of the deep trench substrates.

Close inspection of the data reveals that the density of deposited micelles on a certain feature is slightly influenced by the width of that feature (blue and green trendlines in Fig. 4). Interestingly, as the plateaus become wider, the density of micelles deposited on it increases (triangles in Fig. 4a and b; positive slopes of the trendlines), approaching the value of ρ_flat^0.5% (56–58 micelles per μm²). This is explained by considering that the immersion capillary forces that “pull” micelles from the plateau into the trench takes place near the plateau edges, where the surface of the liquid layer deforms. In narrow plateaus, the entire surface area of the plateau is dominated by this capillary action. However, as the plateau gets wider, the central part, which is less influenced by the capillary forces acting near the edges, grows in area, and micelles deposited on it experience a similar local environment as in the flat regions of the substrate.

The opposite behavior is noted in the trenches: the density of micelles deposited in wider trenches is lower than in narrower trenches (open squares in Fig. 4c and d; negative slopes of the trendlines). This trend also approaches the value of ρ_flat^0.5%. This is explained in the same terms: the capillary action draws micelles into the trenches causing crowding near the trench walls. As the trench becomes wider, its expanding central area becomes less influenced by this crowding and the local micelle density approaches that of ρ_flat^0.5%.

It is important to note that when the same micelle data were arranged to probe cross-influence (grey symbols in Fig. 4), the micelle density data seemed to be more scattered, and no tangible correlation could be discerned.

The densities of micelles cast from a 1.0 wt% solution measured on a flat region of the substrate are ρ_flat^1.0% = 87–91 micelles per μm². The local density analysis in this case also shows higher densities of micelles deposited in the trenches vs. on the plateaus (ρ_tr^1.0% > ρ_pl^1.0%; see Fig. S6, ESI†).⁶⁷ However, the gaps between the data sets are smaller than those noted in Fig. 4 for micelles cast from a 0.5 wt% solution. Apparently, the increased solution concentration of micelles leads to crowding of the deposited micelles over the entire surface, which does not allow the micelles to deposit sparsely on the plateaus, thus diminishing the density differentiation imparted by the topographic features. Consistent with this explanation is the observation that although a slight influence of w_pl on ρ_pl^1.0% was noted also in the concentrated solution case (triangles in Fig. S6a and b (ESI†); positive slopes of the trendlines), no clear influence of w_tr on ρ_tr^1.0% could be concluded (open squares in Fig. S6c and d, ESI†).

Whereas the relationships between the local micelle densities and the corresponding topographic feature widths provided some insights into the behavior of deposited micelles, additional important information was obtained by correlating the data shown in Fig. 4 to the duty cycle of the plateaus (a reduced parameter of w_pl and w_tr, defined as w_pl/(w_pl + w_tr); Fig. 5).^36,68 The patterns in this study exhibit plateaus that are either equal in width or narrower than the trenches, hence they span the range of 0–0.5 in the duty cycle, where 0.5 represents symmetric patterns (i.e., w_pl = w_tr). Interestingly, for the dilute solution case, we observe positive dependencies both for the ρ_tr^0.5% and ρ_pl^0.5% on the duty cycle (Fig. 5a and b). This means that near-symmetric patterns accumulate more deposited micelles than largely asymmetric patterns. The slopes of the trendlines are steeper for the deep trenches case (Fig. 5b) than for the shallow trenches case (Fig. 5a), which is in accord with the relative strength of the capillary forces.

Fig. 5 The dependence of local number density of micelles cast from 0.5 wt% (a) and (b) or 1.0 wt% (c) and (d) toluene solutions on the duty cycle when deposited on shallow (a) and (c) and deep (b) and (d) trenches. The red dashed lines represent the micelle density values measured on flat regions (56 and 58 micelles per μm² for 0.5 wt% and 87 and 91 micelles per μm² in the shallow and deep trench cases, respectively). Trendlines in (a) and (b) were calculated by linear regressions, their slope values and corresponding standard errors are denoted in red.

The trendlines calculated for the micelles in the trenches in both the shallow and deep trenches intercept the density axis near the value of ρ_flat^0.5% (∼50 micelles per μm²). The trendlines calculated for the micelles on the plateaus, however, intercept at ∼30 micelles per μm² in the shallow trenches case and ∼0 micelles per μm² for the deep trenches. This is consistent with the enhanced depletion of micelles from the plateaus in the latter case, which is characteristic of the enhanced depletion of materials from plateaus in deeply etched gratings where the plateaus are sparse, narrow protrusions.³⁶ The non-zero intercept in the shallow trenches case suggests that the linear relationship may not be valid in the limit of extremely narrow plateaus.

Micelles deposited from concentrated solution exhibit largely scattered ρ^1.0% values without a clear correlation to the duty cycle (Fig. 5c and d). Similar to the low concentration case, the average density ρ_tr^1.0% values in both the shallow and deep trench patterns is ∼100 micelles per μm², which is only slightly higher than ρ_flat^1.0%. The average values of ρ_pl^1.0% in the concentrated solution system are rather high (65–70 micelles per μm²). This is plausible considering that the crowding of micelles deposited from highly concentrated solutions prevents the depletion of micelles from the plateaus.

Analysis of the average micelle diameters provided additional insights on the micelles’ response to the topographic features. Unlike the micelle density data, no clear dependence of the average micelle diameters calculated for each pattern on the widths of the topographic features could be safely concluded (see Fig. S7 and S8, ESI†). However, several interesting conclusions could be made by reviewing the average diameter values shown in Table 1. First, the standard deviation of the average diameters of micelles deposited on flat regions of the substrate are markedly larger (∼2–3-fold) than those of micelles deposited on the topographic features. This observation suggests that the segregation of micelles into distinct regions facilitates obtaining a more uniform distribution of sizes. Second, the data demonstrates that the micelles spread on the plateaus exhibit much larger diameters than those crowded in the trenches. In the 0.5 wt% concentration systems, moving from shallow to deep trenches causes the micelles on the plateaus to spread wider whereas the micelles in the trenches shrink in diameter, approaching the average diameter of the globular micelles in solution (88 ± 9 nm; see Fig. S1, ESI†). This is explained by the larger space available for micelles deposited on the depleted plateaus to spread and thus increase the favourable interaction of their core blocks with the substrate, whereas micelles crowded in the trenches retain their native globular shape even in the deposited state. The opposite trend observed for the micelle height (see Fig. 2c and f) suggests that micelles retain their aggregation number and do not disassemble into smaller micelles upon spreading.

Table 1 Average micelle diameters

	Shallow trenches	Deep trenches
ϕflat^0.5%	99.2 ± 14.1	98.6 ± 13.2
ϕpl^0.5%	110.4 ± 6.9	118.9 ± 11.6
ϕtr^0.5%	97.3 ± 4.4	92.5 ± 5.1
ϕflat^1.0%	87.9 ± 7.8	86.2 ± 8.6
ϕpl^1.0%	93.8 ± 2.5	87.2 ± 3.3
ϕtr^1.0%	83.8 ± 2.7	(Coalesced)

---

The average diameters calculated for the 1.0 wt% solutions are smaller than the corresponding values determined for the 0.5 wt% solution, reflecting the crowding imposed by the high concentration, which does not leave room for the micelles to spread on the surface. Indeed, the average diameters of micelles deposited on a flat region of the substrate are almost identical to their diameter in solution. Yet, it is worthwhile noting that the diameter differentiation imposed by the topographic pattern in the case of the shallow trenches is of a similar extent for both dilute and concentrated solutions (i.e., ϕ_pl is larger than ϕ_tr by 12–14%).

Interestingly, similar diameter differences between micelles deposited on the plateaus and in the trenches were also noted by Russell et al., despite the fact that their micelles assembled only during annealing of the film (which was a non-micellar film when cast).⁶¹ Although that work employed hairy micelles and the casting and annealing solvents were different from toluene, obtaining similar structures through different kinetic pathways (i.e., cast-then-assemble vs. assemble-then-cast) hints that the resulting morphologies represent equilibrium structures of the films when they are saturated with solvent vapor, which become kinetically arrested after solvent evaporation.

Lastly, it is insightful to compare here the dynamic response of the micelles to the substrate topography with that of hard particles (like silica nanoparticles). In the case of hard particles, the topography could only affect the local densities of the deposited entities, but not their shape. Additionally, the rigidity of hard spheres reduces the contact area with the substrate and thus leads to smaller interfacial energy between the particle and the substrate (compared to that of soft, spreadable materials like micelles). Thus, the organization process of hard spheres should be completely dominated by capillary action with negligible influence of the nature of the substrate, where the particles are segregated to the trenches and the plateaus are completely devoid of deposited particles.^9,69 With micelles, on the other hand, the distribution of deposited micelles over the different topographic features is more even, and features a location-specific, bimodal distribution of diameters.

The influence of topographic pattern and micelle concentration on film morphology

The dynamic behavior of the micelles cast from 0.5 wt% solutions prompted us to explore the local morphologies that develop after annealing in films cast from a concentrated micellar solution. Fig. 6 shows SEM images of micelles cast from 1.0 wt% on different patterns and annealed under toluene vapor. Two unexpected types of morphological behavior are observed. First, while micelles deposited from 1.0 wt% solutions on flat regions of the substrate included coalesced, worm-like micelles (Fig. 1c, image (i)), deposition over shallow-topography patterns seems to prevent this coalescence (Fig. 6a–c). However, when the micelles are deposited over deeply etched substrates, the coalescence is enhanced and becomes prevalent regardless of the lateral feature dimensions in the pattern – but occurs only in the trenches, whereas the shape of the micelles deposited on the plateaus remained nearly round (Fig. 6d–f). Hence, the combination of etch depth and solution concentration could be used to either maintain the round micellar structure or to effect a location-specific film morphology.

Fig. 6 SEM images of micellar PS₈₉-b-P2VP₁₈₁ films cast from 1.0 wt% toluene solutions on topographically defined substrates. The trench depths are 21 nm (a)–(c) and 45 nm (d)–(f). Plateau and trench widths appear at the top right corner of each image.

It is interesting to note that despite the coalescence tendency of micelles cast from concentrated solution, micelles cast on shallow topographic patterns indeed retain their shapes better than those cast from dilute solutions onto deeply etched substrates. Visual comparison of the shapes of the micelles in Fig. 6 with those spread on the plateaus in Fig. 2e reveals that the latter are much less round and display a larger size dispersity in ϕ_pl^0.5% (Table 1). The shape retention ability also holds for the micelles deposited from 1.0 wt% solution on the plateaus in deeply etched substrates (Fig. 6e and f), which appear more round than those spread on the plateaus in Fig. 2e, despite the fact that the micelles in the trenches in the former are mostly coalesced. The increased uniformity attests for the limited spreading ability of micelles deposited on the plateaus from the concentrated solution, which is the consequence of the increased crowding of micelles also on the plateaus in this case.

Utilization of micellar films on topographic substrates for assembly: hybrid quantum rod superstructures

The versatility of our approach was demonstrated by applying the assembly principles discovered in this work for assembling quantum rods (QRs) into unique structures. Fig. 7 shows SEM images of the same type of micelles used in the current study, cast from 1.0 wt% toluene solutions that included CdSe-seeded CdS QRs coated with trioctylphosphine oxide QRs, deposited on topographic patterns and annealed for 15 min in toluene vapor. As we have found in a previous study, the presence of QRs prevents micelle fusion (compared to the neat micelles on comparable features in Fig. 1c, image (iv)), owing to surfactant-like behavior of the QRs, which are chemically attracted to the surface of the P2VP cores of the micelles.¹⁹ Interestingly, when a micelles/QRs solution was cast on substrates featuring deep trenches, two types of location-specific organizational behavior were observed: circular arrangements surrounding the micelles on the plateaus,¹⁹ and random QR decoration of the micelles’ tops in the trenches (which often appears as “crowning” the top of the micelle with a circular arrangement of smaller diameter than the diameter of the micelle). The latter behavior is explained by a change in the structure of micelles that are confined in the trenches, where the PS hairs apparently fill the voids between the micelles and force the QRs to migrate to other locations on the micelle surface where the P2VP cores are more exposed.

Fig. 7 SEM image of a film cast on a 45 nm-deep topographic pattern from a 1.0 wt% toluene solution containing PS₈₉-b-P2VP₁₈₁ micelles and CdS quantum rods and annealed in toluene vapor for 15 min. The surface fraction of the quantum rods was 0.13.

Conclusions

The delicate morphological behavior of block copolymer micelles when deposited on topographic substrates emerged from a systematic analysis of their morphology, local density, and size. The trivial outcome is that the capillary forces caused by the deformation of the micellar solution surface near the edges of the topographic features direct micelles into the trenches, causing their depletion from the surfaces of the plateaus. The non-trivial result is the emergence of a bimodal, location-specific distribution of sizes, which under certain conditions translates into the formation of mixed morphologies, where the regions in which each morphology develops are dictated by the topographic pattern used. This result stems from the dynamic behavior of block copolymer micelles, which are self-assembled entities that are soft, deformable, and able to respond to their local environment. It turns out that within the local environment of the micelles one should consider not only the underlying substrate but also the neighboring micelles. Hence, the topography can be used as a differentiation mechanism that induces disparate local number densities of the micelles, which influences their extent of spreading and their coalescence tendency, thus leading to different morphologies in different regions of the substrate in a controlled fashion. One could envisage using more complicated geometries than parallel trenches with uniform widths for the topographic substrates, such as turns, bifurcations, T-junctions, and tapered trenches, which can be produced by lithography in a fully controlled manner, and to place the different types of morphologies according to specific requirements. Fig. S9 (ESI†) shows an example that demonstrates the robustness of the location-specific assembly behavior in non-periodic trench arrays. Capitalizing on this approach and using such platforms for further assembly of functional components such as metal nanoparticles may provide a pathway for the preparation of different types of metasurfaces.

This work highlights the importance of considering the basic characteristics of assembly components and how they influence the self-assembly process. In general, the knowledge that emerges from such investigations helps formulating simple principles that could be useful for designing complex systems from simple building blocks. This was exemplified by the controlled creation of two types of quantum rod superstructures that co-exist on the same substrate. We are currently working on extending the utility of deposited block copolymer micelles as versatile templates for nanoparticle assembly into superstructures that are potentially useful for optical applications.

Materials and methods

Materials

Polystyrene-block-poly(2-vinyl pyridine) copolymer (PS-b-P2VP; M_n 270 kDa, PDI 1.23, f_PS = 0.35; denoted as PS₈₉-b-P2VP₁₈₁, where subscript number denote the M_n values of the respective blocks) was synthesized by standard anionic polymerization using sec-butyllithium in tetrahydrofuran (THF) under nitrogen atmosphere. The molecular weight, size distribution, and polystyrene weight fraction were all determined by gel permeation chromatography (GPC) in THF against PS standards for the PS block and comparison of the ¹H NMR signals for phenyl and pyridine groups, respectively, for the P2VP block.

CdSe-seeded CdS quantum rods coated with trioctylphosphine oxide (TOPO) ligands were received in crude form (batch number 15KL022) from Qlight Nanotech (a Merck subsidiary), dissolved in toluene and purified from excess TOPO by two cycles of centrifugation (3000 rpm for 10 min, and 2000 rpm for 8 min at 15–20 °C) using methanol as an anti-solvent. The QRs measured 24 ± 2 nm in length and 6.3 ± 1 nm in diameter, as determined from SEM images of self-assembled QRs on a SiOx substrate using ImageJ software,⁷⁰ and the grafting density was ca. 2.1 ligand per nm² (∼1000 ligands per QR, calculated from thermogravimetry analysis determination of 16.3 wt% bound TOPO ligands).

Preparation of micellar films

Stock solutions of the copolymers in toluene (2–3.5 wt%) were stirred for 2 h at room temperature and let to equilibrate overnight before use. The BCP solutions were diluted to concentrations of 0.5 and 1.0 wt%. The filtered solutions were spin-coated at 3000 rpm for 30 s onto clean silicon topographically patterned substrates.

For control experiments the solutions were cast on flat “featureless” silicon substrates (covered with ca. 2 nm native oxide; cleaned using NoChromix acid bath (Godax Laboratories)). The films were annealed in closed Petri dishes under saturated atmospheres of toluene vapor for 15 min at room temperature, after which they were quenched by opening the lid and quickly removing the samples.

Topographically patterned substrates with varying feature sizes and trench depths were prepared using electron-beam lithography (Raith eLINE, Dortmund, Germany, and Elionix E-Beam Lithography System, Elionix, Japan ELS-G100) on silicon wafer substrates using a 250 nm-thick PMMA resist (495 kDa, Microchem) followed by cold development (2 min, −5 °C) in the MIBK : IPA (1 : 3) developer solution and reactive ion etching with C₄F₈ and SF₆ (Oxford Instruments Plasma lab System 100). Following etching, substrates were cleaned with acetone, oxygen plasma (Pico plasma asher, Diener, Ebhausen, Germany), and piranha solution, and kept in deionized water until used.

Characterization

Scanning electron microscopy (SEM) images were acquired using extra-high resolution scanning electron microscope Magellan 400 L (ThermoFisher, former FEI) operating at 2 kV and 0.1 nA.

The average micelle diameters and micelle number densities on flat and topographic patterns were quantified by analyzing SEM images of the micellar films using ImageJ software.⁷⁰ A defined rectangular area, a sample highlighted in yellow in Fig. S5a, ESI,† was selected for each analyzed sample. Within this area, all micelles were identified and outlined with ellipses to accurately measure their diameters. The micelle diameters were calculated based on the corresponding circular area measurements. Subsequently, average diameters were computed, and histograms were generated to represent the data (sample histograms are shown in Fig. S5b and c, ESI†). Additionally, the micelle number density was quantified by counting the micelles on each feature in a selected area, as demonstrated in Fig. S5, ESI,† and dividing the count by the corresponding feature area.

Atomic force microscopy (AFM) images for film topography and height profiles were obtained in tapping mode using Dimension Icon XR Scanning Probe Microscope (Bruker).

Cryogenic transmission electron microscopy (Cryo TEM) was used to reveal micelle structure (Fig. S1, ESI†). A drop (2.5 μL) of the micellar solution was deposited on a TEM grid (300 mesh Cu Lacey substrate, Ted Pella, Ltd). Vitrobot Mark IV (FEI) was used to blot the excess liquid in a controlled environment and to vitrify the specimens by a rapid plunging into liquid nitrogen. The vitrified samples were examined at −179 °C using a FEI Tecnai 12 G2 TWIN TEM operated at 120 kV and equipped with a Gatan 626 cold stage. The images were recorded in low-dose mode on a 4 K × 4 K FEI Eagle CCD (charge-coupled device) camera.

Author contributions

The manuscript was written through the contributions of all authors. All authors have approved the final version.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Yael Levi-Kalisman for assistance with the cryo-TEM imaging. R. M. K. thanks the Malvina and Solomon Pollack Scholarship Fund for a doctoral scholarship. This research was funded by the Israel Science Foundation, grant numbers 229/17 and 158/23, and by the Israel Innovation Authority.

Notes and references

1. T. Thurn-Albrecht, R. Steiner, J. DeRouchey, C. M. Stafford, E. Huang, M. Bal, M. Tuominen, C. J. Hawker and T. P. Russell, Adv. Mater., 2000, 12, 787–791.
2. A. A. Kulkarni and G. S. Doerk, Nanotechnology, 2022, 33, 292001.
3. T. H. Park, S. Yu, S. H. Cho, H. S. Kang, Y. Kim, M. J. Kim, H. Eoh, C. Park, B. Jeong, S. W. Lee, D. Y. Ryu, J. Huh and C. Park, NPG Asia Mater., 2018, 10, 328–339.
4. P. Mokarian-Tabari, R. Senthamaraikannan, C. Glynn, T. W. Collins, C. Cummins, D. Nugent, C. O'Dwyer and M. A. Morris, Nano Lett., 2017, 17, 2973–2978.
5. J. Y. Kim, H. Kim, B. H. Kim, T. Chang, J. Lim, H. M. Jin, J. H. Mun, Y. J. Choi, K. Chung, J. Shin, S. Fan and S. O. Kim, Nat. Commun., 2016, 7, 12911.
6. P. A. Mistark, S. Park, S. E. Yalcin, D. H. Lee, O. Yavuzcetin, M. T. Tuominen, T. P. Russell and M. Achermann, ACS Nano, 2009, 3, 3987–3992.
7. C. A. Ross, K. K. Berggren, J. Y. Cheng, Y. S. Jung and J. B. Chang, Adv. Mater., 2014, 26, 4386–4396.
8. M. Stefik, S. Guldin, S. Vignolini, U. Wiesner and U. Steiner, Chem. Soc. Rev., 2015, 44, 5076–5091.
9. S. Jambhulkar, D. Ravichandran, Y. X. Zhu, V. Thippanna, A. Ramanathan, D. Patil, N. Fonseca, S. V. Thummalapalli, B. Sundaravadivelan, A. L. Sun, W. H. Xu, S. Yang, A. M. Kannan, Y. Golan, J. Lancaster, L. Chen, E. B. Joyee and K. A. Song, Small, 2024, 20, 2306394.
10. M. J. Fasolka and A. M. Mayes, Annu. Rev. Mater. Res., 2001, 31, 323–355.
11. W. H. Li, M. J. Liu, F. Qiu and A. C. Shi, J. Phys. Chem. B, 2013, 117, 5280–5288.
12. H. B. Feng, X. Y. Lu, W. Y. Wang, N. G. Kang and J. W. Mays, Polymers, 2017, 9, 494.
13. F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38.
14. H.-C. Kim, S.-M. Park and W. D. Hinsberg, Chem. Rev., 2010, 110, 146–177.
15. J. N. L. Albert and T. H. Epps, III, Mater. Today, 2010, 13, 24–33.
16. J. Bang, U. Jeong, D. Y. Ryu, T. P. Russell and C. J. Hawker, Adv. Mater., 2009, 21, 4769–4792.
17. A. Halevi, S. Halivni, M. Oded, A. H. E. Müller, U. Banin and R. Shenhar, Macromolecules, 2014, 47, 3022–3032.
18. B. J. Kim, J. Bang, C. J. Hawker and E. J. Kramer, Macromolecules, 2006, 39, 4108–4114.
19. R. Muzaffar-Kawasma, M. Oded and R. Shenhar, Materials, 2022, 15, 2949.
20. Q. L. Zhang, S. Gupta, T. Emrick and T. P. Russell, J. Am. Chem. Soc., 2006, 128, 3898–3899.
21. F. Lai, T. Borca-Tasciuc and J. Plawsky, Nanotechnology, 2015, 26, 055301.
22. H. Kang, S. S. Kim, S. Il-Yoo and B. H. Sohn, Adv. Mater. Interfaces, 2019, 6, 1901257.
23. E. Ploshnik, A. Salant, U. Banin and R. Shenhar, Adv. Mater., 2010, 22, 2774–2779.
24. E. Ploshnik, A. Salant, U. Banin and R. Shenhar, Phys. Chem. Chem. Phys., 2010, 12, 11885–11893.
25. J. Diaz, M. Pinna, A. V. Zvelindovsky, I. Pagonabarraga and R. Shenhar, Macromolecules, 2020, 53, 3234–3249.
26. M. J. Pavan and R. Shenhar, J. Mater. Chem., 2011, 21, 2028–2040.
27. S. J. Jeong, J. Y. Kim, B. H. Kim, H. S. Moon and S. O. Kim, Mater. Today, 2013, 16, 468–476.
28. M. A. Morris, Microelectron. Eng., 2015, 132, 207–217.
29. J. Y. Cheng, C. A. Ross, E. L. Thomas, H. I. Smith and G. J. Vancso, Adv. Mater., 2003, 15, 1599–1602.
30. H. Q. Hu, M. Gopinadhan and C. O. Osuji, Soft Matter, 2014, 10, 3867–3889.
31. E. Michman and R. Shenhar, Polym. Adv. Technol., 2017, 28, 613–622.
32. E. Han, H. Kang, C.-C. Liu, P. F. Nealey and P. Gopalan, Adv. Mater., 2010, 22, 4325–4329.
33. I. Bita, J. K. W. Yang, Y. S. Jung, C. A. Ross, E. L. Thomas and K. K. Berggren, Science, 2008, 321, 939–943.
34. R. A. Segalman, H. Yokoyama and E. J. Kramer, Adv. Mater., 2001, 13, 1152–1155.
35. R. Ruiz, H. M. Kang, F. A. Detcheverry, E. Dobisz, D. S. Kercher, T. R. Albrecht, J. J. de Pablo and P. F. Nealey, Science, 2008, 321, 936–939.
36. E. Michman, M. Oded and R. Shenhar, Polymers, 2022, 14, 2377.
37. E. Michman, M. Langenberg, R. Stenger, M. Oded, M. Schvartzman, M. Müller and R. Shenhar, ACS Appl. Mater. Interfaces, 2019, 11, 35247–35254.
38. N. Eren, O. Burg, E. Michman, I. Popov and R. Shenhar, Polymer, 2022, 245, 124727.
39. Y. Mai and A. Eisenberg, Chem. Soc. Rev., 2012, 41, 5969–5985.
40. J. Rodríguez-Hernandez, F. Chécot, Y. Gnanou and S. Lecommandoux, Prog. Polym. Sci., 2005, 30, 691–724.
41. N. S. Cameron, M. K. Corbierre and A. Eisenberg, Can. J. Chem., 1999, 77, 1311–1326.
42. Z. Tuzar, P. Stepanek, C. Konak and P. Kratochvil, J. Colloid Interface Sci., 1985, 105, 372–377.
43. J. F. Gohy, Adv. Polym. Sci., 2005, 190, 65–136.
44. G. Riess, Prog. Polym. Sci., 2003, 28, 1107–1170.
45. G. Riess and C. Labbe, Macromol. Rapid Commun., 2004, 25, 401–435.
46. Y. Q. Lu, J. P. Lin, L. Q. Wang, L. S. Zhang and C. H. Cai, Chem. Rev., 2020, 120, 4111–4140.
47. C. Allen, D. Maysinger and A. Eisenberg, Colloids Surf., B, 1999, 16, 3–27.
48. S. J. Qian, S. Z. Li, W. F. Xiong, H. Khan, J. Huang and W. Q. Zhang, Polym. Chem., 2019, 10, 5001–5009.
49. G. X. Huang, J. Zhu, Z. B. Zhang, W. Zhang, N. C. Zhou and X. L. Zhu, J. Macromol. Sci., Part A:Pure Appl. Chem., 2013, 50, 193–199.
50. Q. A. Jin, G. Y. Liu and J. A. Ji, J. Polym. Sci., Part A:Polym. Chem., 2010, 48, 2855–2861.
51. L. L. Wang, H. Y. Huang and T. B. He, J. Controlled Release, 2013, 172, E54–E55.
52. Y. Matsumura and K. Kataoka, Cancer Sci., 2009, 100, 572–579.
53. D. Sutton, N. Nasongkla, E. Blanco and J. M. Gao, Pharm. Res., 2007, 24, 1029–1046.
54. V. P. Torchilin, Pharm. Res., 2007, 24, 1–16.
55. F. Ahmed and D. E. Discher, J. Controlled Release, 2004, 96, 37–53.
56. Y. P. Li, K. Xiao, J. T. Luo, W. W. Xiao, J. S. Lee, A. M. Gonik, J. Kato, T. A. Dong and K. S. Lam, Biomaterials, 2011, 32, 6633–6645.
57. T. Trimaille and B. Verrier, Pharmaceutics, 2023, 15, 2481.
58. E. Cabane, X. Y. Zhang, K. Langowska, C. G. Palivan and W. Meier, Biointerphases, 2012, 7, 9.
59. M. Nakayama, T. Okano, T. Miyazaki, F. Kohori, K. Sakai and M. Yokoyama, J. Controlled Release, 2006, 115, 46–56.
60. Z. G. Xu, P. Xue, Y. E. Gao, S. Y. Liu, X. X. Shi, M. L. Hou and Y. J. Kang, J. Colloid Interface Sci., 2017, 490, 511–519.
61. S. Park, B. Kim, O. Yavuzcetin, M. T. Tuominen and T. P. Russell, ACS Nano, 2008, 2, 1363–1370.
62. Films cast from a 0.5 wt% solution at a spin rate of 1000 rpm also showed coalesced micelles (not shown) similar to those observed for micelles cast from a 1.0 wt% solution at 3000 rpm, supporting the conclusion regarding the morphology dependence on the amount of deposited material.
63. The aggregation number was calculated as the ratio between the volume of the core (according to the dimensions determined by cryo-TEM, Fig. S1, ESI†) and the volume of a single P2VP block (using ρ_P2VP = 1.115 g mL⁻¹).
64. S. Arichi, M. Yoshida and Y. Ogawa, Bull. Chem. Soc. Jpn., 1975, 48, 1417–1422.
65. P. A. Kralchevsky and K. Nagayama, Adv. Colloid Interface Sci., 2000, 85, 145–192.
66. J. A. Liddle, Y. Cui and P. Alivisatos, J. Vac. Sci. Technol., B, 2004, 22, 3409–3414.
67. Worm-like (coalesced) micelles were treated as a sequence of round micelles in a row in the quantitative analyses.
68. C. I. Lang and D. S. Boning, IEEE Trans. Semicond. Manuf., 2019, 32, 62–69.
69. Y. D. Yin, Y. Lu, B. Gates and Y. N. Xia, J. Am. Chem. Soc., 2001, 123, 8718–8729.
70. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675.

---

Footnote

† Electronic supplementary information (ESI) available: cryo-TEM image and size distribution analysis of the micelles; the library of parallel trench patterns used in the study; enlarged versions of the SEM images; AFM images and cross-sections of micelles deposited from 1.0 wt% toluene solution on topographically patterned substrates; a representative example of the image processing performed for determining the local micelle densities and the average micelle diameters in the plateaus and trenches; analysis of the local number density of micelles cast from 1.0 wt% toluene solution; analyses of the average diameters of micelles cast from 0.5 wt% and 1.0 wt% toluene solutions; SEM images of micelles cast on non-periodic topographic patterns. See DOI: https://doi.org/10.1039/d5sm00152h

---