Low-profile folding mechanism for multi-DoF feedback control

Abstract

Soft structures gain their adaptability from a high number of distributed degrees of freedom (DoF). Integrating reconfigurable robotic systems into these soft structures enables efficient transmission of forces and torques, supporting a wide range of tasks. However, implementing actuation, sensing, and transmission components remains challenging, particularly in optimizing their spatial distribution to achieve effective control over the target structure. In this study, we present an embeddable pneumatic system featuring ultra-thin actuators, with integrable sensors and modular transmissions. The system's ultra-thin profile enables seamless and space-efficient integration onto various surfaces, while its modular design enables flexible reconfiguration to suit different mechanical and control needs. The rolling diaphragm mechanism reduces friction and stress on the joints which are more prone to occur in flat structures. The proposed diaphragm has an aspect ratio of approximately 10 (15 mm 1.4 mm cross-section) and achieves a stroke length up to five times its thickness, extendable through modular connection. An optical sensor module is also introduced to provide precise, low-profile feedback without affecting the mechanical characteristics or flatness of the overall system. We demonstrate the control of folding sequence and angle through feedback control, using compactly embedded components within an origami-inspired surface. This approach leverages the geometric principles of folding to enable complex and reconfigurable structures. The proposed integrable actuator, transmission, and sensor module provides a scalable and customizable foundation for developing large-scale robotic systems with intricate geometries and distributed control, supporting seamless deployment and adaptability.

---

1 Introduction

Soft robotic systems are increasingly recognized for their embedded intelligence, which enables adaptive interaction with dynamic environments. The integration of reconfigurability further augments these capabilities by allowing autonomous modifications to shape, configuration, and mechanical properties, thereby expanding the range of achievable tasks and functionalities.^1–4 Within such systems, distributed control plays a critical role by enabling localized regulation of forces or displacements across multiple spatially distributed points.^5–7

Supporting distributed intelligence requires systematic integration of actuators, sensors, and transmission mechanisms to balance functionality, efficiency, and scalability. Transmissions are important for customizing performance. In multi-point distributed control scenarios, assigning a dedicated actuator to each location is often impractical due to constraints on space, weight, cost, and design complexity. A more flexible approach involves integrating transmission mechanisms that can amplify force, adjust displacement, or redirect motion (e.g., into linear, rotational, or constrained paths), enabling localized control without requiring additional actuators. This modular strategy reduces reliance on custom actuators, simplifies system architecture, and minimizes redundancy. To fully realize the robots reconfigurable potential and adaptability, it is essential to integrate sensors capable of measuring multiple modes of actuation without disrupting the systems kinematics. These sensors provide critical feedback for managing multiple control points and interacting with dynamic environments,⁸ enabling real-time adjustment of motion and control sequences.⁹ Most importantly, preserving overall system performance, efficiency, and design flexibility—especially when deploying multiple components—requires that these elements do not significantly alter the structures intrinsic mechanical properties, such as mass, stiffness, and damping. As the number of control points increases, their cumulative impact can reduce mobility, agility, and energy efficiency, underscoring the need for all components to remain compact and low-profile.

Many reconfigurable robotic systems utilize commercially available actuation methods, such as electromagnetic actuators like motors due to their precise sensing, control capabilities, and well-established analytical models.^3,10 However, motor-driven systems become increasingly complex when managing multiple distributed control points. Their integration often adds bulk, reducing compactness and adversely affecting the robots mechanical properties.^11,12 These constraints have led to the exploration of alternative actuation mechanisms, including smart materials and soft actuators. Smart materials like piezoelectric materials, thermally-driven materials, electroactive polymers, dielectric actuators, and shape memory alloys and polymers (SMA and SMP)^11,13–15 enable compact actuation by directly converting energy into motion. However, their delicate structures and nonlinear behaviors—such as hysteresis and coupled phenomena—present significant challenges for modular integration, sensor embedding, and real-time control in distributed multi-DoF systems.^16–21 Therefore, these materials are often incompatible with conventional transmission mechanisms, limiting mechanical advantage and force amplification. SMA and SMP, while capable of high power density^22–24 are difficult to model and customize due to their nonlinear response.^16,25,26 One notable case is the use of SMA in robotic grippers, which, despite delivering high force in compact volumes, face limitations due to slow thermal response and control hysteresis.²⁷ Soft pneumatic actuators, such as pouches or bellows, offer similar power distribution benefits as conventional pneumatic systems. They offer simple power distribution from a centralized source to distal points via a lightweight fluid delivery system, making them highly suitable for large-area deployment. Unlike traditional piston-cylinder mechanisms, they are lightweight, reducing the mechanical load on the original structure even when multiple actuators are integrated.^28–30 However, their reliance on volume expansion to generate motion constrains their range of movement, compactness, and overall performance, particularly in large-scale applications.^31–33 Unintended expansion can also interfere with seamless actuator integration and pose challenges for optimizing the performance and design of transmission modules. Similar to smart materials, soft pneumatic actuators—particularly those manufactured with elastomers—pose nonlinear modeling challenges, which complicates their integration with conventional transmission and sensing methods.

Beyond the individual functionality of each component, distributability and modularity are critical for effective system integration. In an actuation system with integrable sensing and transmission, modularity enables the accessible and customizable placement of actuation points throughout a multi-DoF reconfigurable robot, enhancing its adaptability to diverse tasks. While much of the existing research in modular robotics has focused on advancing actuator technology and improving connectivity, relatively little attention has been paid to the customizability of each control point, particularly in compact, low-profile designs. A well-developed system that integrates customizable transmission and sensing modules within the actuator framework can significantly enhance the design and deployment of distributed multi-DoF reconfigurable robots.

Here, we present a novel embeddable soft pneumatic system with integrable sensors and transmission modules, designed for surface embedding and reconfigurability to adapt to various tasks (Fig. 1(a) and (b)). Our proposed actuator has an ultra-thin, modular design, allowing for easy integration onto surfaces for distributed control. By configuring multiple actuators and transmission modules in various arrangements, the system can be adapted to meet specific task requirements in terms of force output and position (Fig. 1(c)–(f)). To overcome the shortcomings of the flat structure, such as increased friction and stress concentration at sharp edges, we utilize the concept of the rolling diaphragm. This approach also minimizes friction by creating linear motion through the eversion of the diaphragm and distributes stress caused by pressurization over the diaphragm membrane to prevent air leakage from stress concentration points. We also introduce an optical-based sensor module that can be integrated with the proposed actuator modules to enable embedded sensing. This sensor offers the advantage of a low-profile design while maintaining high accuracy. It is specifically engineered to fit within the actuator without altering its mechanical characteristics, allowing the actuator and sensor to function as a single, unified unit and thereby enabling embedded sensing. The modular design of the actuator, transmission, and sensor enhances flexibility, scalability, and efficient space utilization.

Fig. 1 Comprehensive low-profile robotic control system. (a) Schematic overview of the proposed system components: actuator, sensor, and transmission. (b) Potential application of the proposed distributed control system for complex joint movements. Illustration of various modular assembly configurations. Connection of actuators in (c) series and (d) parallel. Actuator integrated with (e) slider-crank and (f) double-slider transmission module.

The main contributions of this paper are:

• Ultra-thin soft pneumatic module with integrable sensing and customized transmission

• Design optimization and system-level validation of analytical models for actuators, sensors, and transmissions

• Demonstration of a pneumatic system with embedded sensing and reconfigurable transmission for distributed multi-DoF applications, including feedback control

2 Modular pneumatic system with integrable sensing and mechanical transmission

This study introduces an ultra-thin, low-profile modular approach to actuators, transmissions, and sensors, enabling localized and independent adjustments for each distributed point. To achieve a compact design, we present a quasi-2D linear actuator that utilizes a rolling diaphragm. While maintaining the compact and low-profile structure, various transmission modules can be configured in different ways for each control point to accommodate diverse performance requirements, such as actuation mode, range of motion, and force/torque output (Fig. 1(e) and (f)). Performance can also be enhanced by combining actuator units, parallel connections increase force/torque, while series connections extend the range of motion (Fig. 1(c) and (d)). To achieve a low-profile, integrable sensor, we employ an optical-based sensing method that measures changes in relative irradiance, the light intensity incident on a detector which varies with the angle of light travel, allowing us to estimate the linear deformation induced by the actuator. In this chapter, we will discuss the principles and modeling of each component: transmission, actuator, and sensor.

2.1 Design of transmission modules

An actuator typically generates a fundamental movement with one DoF, which is then converted into diverse motion types and patterns through transmission mechanisms such as gears, linkages, or compliant structures. Employing linear actuation as the primary motion facilitates the design of compact and low-profile actuation systems, necessitating transmission mechanisms to transform it into other functional motion types. In this research, a slider-crank mechanism is employed to convert linear motion into rotational motion, while a double-slider mechanism is used to reverse the direction of the output (Fig. 2(a) and (b)). Both transmission mechanisms were designed to preserve compactness and low profile, ensuring compatibility with the actuators flat configuration.

Fig. 2 Transmission mechanisms in flat, low-profile structures. (a) Schematics and (b) images of the transmission modules (slider-crank and double-slider) that convert linear motion into the desired motion and performance. The working video is presented in the Supplementary Video (ESI†). (c) Model diagram of the slider-crank module.

Fig. 2(c) illustrates the slider-crank configuration used with the proposed actuator, where prismatic joint movement is converted into rotational motion through the connecting rod and crank. The range of bending motion, θ, can be determined using the following equations,

The variables are defined in Fig. 2(c). When the actuator delivers an input force F, the resulting output torque at the target bending joint can be expressed as,

T = a × sin(θ + φ)F cos(φ) (2)

The desired range of motion and torque can be achieved by adjusting the stroke, actuator position, connecting rod length, or crank length. However, once the actuator is fabricated, modifying its stroke becomes more complex than adjusting the other parameters. Therefore, the range of motion can be tuned by simply replacing the slider-crank module or repositioning the actuator.

To reverse the direction of motion, allowing the actuator's pushing motion to result in pulling and vice versa, we designed a slider integrated in parallel with existing one inside the actuator, forming a double-slider configuration. To validate the applicability of classical transmission models for tuning performance in low-profile, compact structures, two slider-crank modules of different sizes were fabricated with varying rod and crank lengths.

2.2 Pneumatic actuator with rolling diaphragm

Flat and compact linear motion can be achieved through various actuation methods, such as smart materials mentioned in the introduction. In this research, we chose pneumatic-based linear motion for its ease of modeling, as demonstrated by the classic piston-cylinder model. However, when the pneumatic chamber and piston are designed to be flat, the frictional area becomes significantly larger compared to a cylindrical shape with the same cross-section area. Additionally, sharp corners in flat designs create stress concentrations, increasing the likelihood of leakage. To overcome these limitations and achieve flat actuation, we employ a rolling diaphragm, which enables a flat structure while mitigating these issues.

The mechanism operates based on the eversion driven by the pressure differential, as illustrated in Fig. 3. This eversion allows the diaphragm to extend at the tip, thereby moving the connected piston and generating linear motion. The actuator offers excellent sealing performance and reduced friction due to the rolling diaphragm's ability to create isolated chambers (Fig. S1, ESI†).³⁴ The diaphragm is designed with an eccentric cross-sectional shape to fit within the flat actuator. It is integrated with the guiding structure to facilitate motion in the intended direction and focus the force accordingly.

Fig. 3 Rolling-diaphragm linear actuator. Structure and working principle of the rolling diaphragm-based linear actuator. Actuation is demonstrated in the Supplementary Video (ESI†).

The diaphragm design is primarily influenced by the required stroke, with the maximum stroke being twice the diaphragm's length. For structural stability, the width of the diaphragm should be proportional to its length, ensuring a width-to-stroke ratio equal to or greater than one.³⁵ The sides of the diaphragm are angled to create the necessary space for convolution, enabling smooth rolling motion under pressurization (Fig. S1, ESI†). The chamber that houses the diaphragm, along with the piston attached to its tip, must be at least as long as the diaphragm to accommodate the rolling motion. A restoring force is required to return the diaphragm to its original position. This can be achieved by incorporating additional components, such as a spring, or by antagonistic actuation (Fig. S2, ESI†). If the spring component is not loaded, output force from the actuator can be simplified to F = P × A remaining unaffected by the position of the piston and can be considered constant if the input pressure is fixed.

2.3 Optical linear motion sensing

Managing position and force/torque output from multiple control points—where actuators and transmissions are integrated in diverse configurations—requires sensors that can capture all modes of actuation without interfering with the structural kinematics. This capability is vital for fully utilizing the robots reconfigurability and ensuring adaptability in dynamic environments. Therefore, it is important that the sensors have a similarly low modulus to match the structure and actuators. Various methods have been proposed for low-modulus sensors, particularly in the field of soft robotics, which also demands low-modulus characteristics.³⁶ Liquid conductors and conductive fabrics are commonly used due to their continuous properties and high deformability.³⁷ For example, sensors have been developed using liquid metal within microfluidic channels, carbon ink with piezoresistive effects, and conductive fabric-based using capacitance change.^38–40 However, these methods still encounter limitations stemming from the inherent properties of the sensing medium, such as material leakage, limited lifespan, or signal drift. Another approach for low-modulus sensing is optical-based methods.^41–43 Light can travel through a variety of media, offering a wider range of options for sensing mediums. Even air can serve as a sensing medium through which light can travel. Therefore, we developed a sensor that operates on the principle of limiting the light detection angle based on the position of the reflector, utilizing air as the light transmission medium.

The sensor consists of a stationary part where the light source and detector are located and a moving reflector (Fig. 4(a)). The light emitter and detector are positioned on a plane parallel to the moving reflector, with the remaining portion of the plane being transparent, as shown in Fig. 4(b). This transparent plane ensures that only light reflected along the midline between the emitter and detector reaches the detector, meaning that only a single ray at a specific emission angle reaches the detector while all others escape (Fig. 4(b) and (c)). As the moving reflector approaches the emitter and detector, the emission and incidence angles increase, causing the detected intensity to decrease. In this design, because a light-traveling medium is air, the size-changing of the medium by linear motion does not affect the stiffness and damping of the joint structure. Moreover, it can be fabricated in a flat shape because it only requires a volume, and size of light can travel inside.

Fig. 4 Optical linear position sensor (a) schematic and (b) the working principle of the sensor. (c) Sensor parameters and variations in light travel angle based on reflector position. (d) Circuit diagram of the phototransistor.

The light source and detector used in this research were selected to emit and detect infrared light at a peak wavelength of 850 nm, ensuring robustness against external light. The circuit for the phototransistor was constructed as shown in (Fig. 4(d)), where the measured voltage increases as the light intensity rises. Based on the datasheet, we assume that the current is linearly proportional to the irradiance.⁴⁴ To model the relationship between the position of the reflector and the output voltage, it is necessary to understand how the position affects the amount of light reaching the detector.

First, we assume the emitter and detector are point sources. As shown in Fig. 4(c), the emission and incidence angles (θ_e and θ_d) can be expressed as functions of the position of emitter and detector relative to the center-line l and the distance d between the emitter and detector plane and the reflector plane.

The relative intensity and sensitivity of both the emitter and detector, based on angular displacement, are derived from their datasheets.^44,45 Consequently, the light intensity detected by the sensor when the reflector is positioned at distance d follows the relationship below.

E_detect ∝ I_e,rel(θ)I_d,rel(θ), (4)

where E_detect represents the irradiance detected by the phototransistor, I_e,rel is the relative intensity of the emitter as a function of angle, and I_d,rel is the relative sensitivity of detector as a function of angle. In this case, I_e,rel is equal to I_d,rel that it can be simplified as I_rel². Therefore, the relationship between the normalized output voltage and the position of the reflector can be expressed aswhere V₀ is the voltage at the bottom dead center, V_max is the voltage at the top dead center of the actuator, and C₁ and C₂ are coefficients which should be determined through the calibration.

Our embedded sensor is compact, lightweight, and specifically tailored for seamless integration with the proposed actuator and transmission system. It employs optical sensing with air as the light transmission medium, enabling high sensitivity with minimal mechanical interference. The minimally invasive moving reflector—comprising only a reflective surface on a rod without any electronics—adds negligible mass and disturbance to the system while allowing accurate linear displacement sensing. By coupling the sensor directly to the actuator rather than the joint, it captures actuation-induced displacements even through various transmission configurations, making it well-suited for customizable, multi-DoF control architectures.

3 Characterization of the core components of the system

Accurate characterization is essential to ensure that the analytical model reliably represents real-world performance, allowing for the design of components that meet targeted specifications. Especially, this model is instrumental in optimizing functionality across multiple distributed control points. In this chapter, we focus on validating the analytical model of the actuator, transmission, and sensor (details of data collection in Materials and methods section).

3.1 Static force test for actuator

The model of primary movement is crucial as it influences the performance of the entire mechanism. To reduce force loss due to friction while maintaining a linear relationship between input pressure and output force, even in a flat configuration, we employ a rolling diaphragm. Additionally, the actuator is designed with a constant cross-sectional area, ensuring that the static force output depends only on pressure rather than position. We conducted two experiments to assess the actuator prototype's performance and the model's accuracy to validate the model and design: measuring the blocked force at the bottom dead center and throughout the stroke (Fig. 5(a)). The fabricated actuator prototype for the experiment has dimensions of 30 × 44 × 4 mm and a stroke length of 7 mm (detailed fabrication process in Materials and Methods section and Fig. S1, ESI†). A spring with a spring constant of 0.2 N mm⁻¹ was used to provide restoring force when it is necessary.

Fig. 5 The characterization of the actuator. (a) Schematic of the working range of the actuator. (b) Results of the blocked force experiment at the bottom dead center under increasing pressure. The dotted and dashed line indicates the average, while the shaded region represents the standard deviation. (c) Results of the block force experiment across the entire stroke at a constant pressure of 140 kPa.

The first experiment involved measuring the blocked force without a spring when the actuator's piston was at the bottom dead center to verify the linear relationship between input pressure and output force. This test was repeated ten times across three samples to evaluate the repeatability of both performance and fabrication. The theoretical force output, F = P × A, was presented alongside the experimental data from a single sample in Fig. 5(b). The area in this equation refers to the effective cross-sectional area. The rolling diaphragm includes a convolution region at the bore, located between the piston and cylinder, formed by the diaphragm membrane. The effective area is defined by the inner side of the diaphragm's bending line (Fig. S3, ESI†). Accordingly, the cross-sectional area of this design is 21 mm² (15 mm by 1.4 mm). The results show that the experimental data closely aligns with the model's linearity, with a small offset of approximately 0.25 N. The actuator achieves a maximum force of around 2.7 N at an input pressure of 140 kPa. The blocked force was found to increase linearly with the applied pressure, demonstrating efficient pressure-to-force transfer and the repeatability of the actuator across trials. Also, the variance between samples was low (∼0.11 N), confirming that consistent fabrication can be achievable (the results from the three samples are shown separately in Fig. S4, ESI†). When the pressure applied to the actuator was below 20 kPa, a nearly constant region was observed in the experimental results, indicating that a minimum pressure threshold was required to initiate actuation due to energy loss resulting from the eversion of the diaphragm membrane. The offset in the force graph resulting from this energy loss remained constant across the entire pressure range.

The second experiment was a static force test with varying the piston position to verify that the rolling diaphragm can maintain a constant cross-sectional area. For the actuator to perform consistently and reliably, it is essential that the output force is determined solely by the input pressure and is independent of the piston position. Achieving this requires maintaining a constant effective cross-sectional area, which can be accomplished by limiting the bulging to reduce unwanted expansion. Fig. 5(c) shows the experimental results from a single actuator tested at five different positions, each incremented by 1.5 mm from the bottom dead center. The maximum force at an input pressure of 140 kPa is plotted as a function of the piston position, indicating that it remains consistently around 2.7 N. It is important to limit the stroke to a range where the diaphragm maintains contact with the wall during eversion, ensuring a constant effective cross-sectional area to achieve consistent force when you design the actuator.

3.2 Slider-crank module performance

A comparison of the analytical model of transmission from the previous chapter with experimental data aims to validate that classical transmission models can be applied to optimize performance, even in low-profile, compact structures. To evaluate the range of motion when the actuator is applied to a bending structure using a slider-crank transmission, we measured the bending angle in relation to the displacement of the slider with a motion capture camera (V120:Trio from Optitrack) while actuating a spring-loaded actuator (Fig. 6(a)). The prismatic joint was positioned 18 mm apart from the joint initially. To prevent the actuator from getting stuck in a bi-stable position when the bending angle is at 0 degrees, the slider-crank module was designed with a range of motion between 35 and 180 degrees (a = 4 mm, b = 15 mm). The experiment was conducted three times, and the data from all trials are presented collectively. The results indicated that the relationship between the displacement of the prismatic joint and the bending angle closely resembled the model, with an offset of approximately 10 degrees (Fig. 6(b)). This discrepancy can be attributed to the non-zero thickness of the bending panel and the joint. While we assumed the links and joint had zero thickness, the material of the rigid panel (FR-4 with a thickness of 0.4 mm) necessitated that the joint has a folding length greater than πt for the fully folded state (Fig. S5, ESI†).

Fig. 6 Characterization of transmission modules. (a) Schematic of the slider-crank integrated actuator. (b) Comparison of experimental data and model predictions for the range of motion of the slider-crank integrated actuator. (c) Comparison of experimental data and model predictions for the torque output of the slider-crank integrated actuator.

We measure the output torque of this bending structure and compare it with the analytical model. The torque was measured at different angles (60°, 90°, 120°, and 150°) with both an un-loaded and spring-loaded actuator (Fig. 6(c)). The input pressure was fixed to 140 kPa in all cases and the length of the moment arm was maintained at 24 mm. The force term from the torque model was calculated based on pressure and the force offset measured from the actuator characterization (0.25 N) was deducted. The experimental results were plotted alongside the model predictions, with a root mean square error (RMSE) of 2.15 N for the case without a spring and 2.19 N for the case with a spring. The result shows broadly similar trends between 75° and 135° (Fig. 6(c), RMSE of 0.61 for the case without a spring and 1.19 for the case with a spring). This qualitative agreement supports the models validity in this range. There was a noticeable drop in torque below 60° and above 150°, likely due to joint buckling (Fig. S5, ESI†). As mentioned earlier, the joint in this prototype is a line rather than a point, leading to an excess length that causes buckling, misalignment, and reduced force transmission.

3.3 Calibration and evaluation of the sensor

The model developed in the previous chapter assumes that a single ray, reflected from a specific angle, reaches the detector. As the reflector moves, the incident angle changes, and since irradiance varies with angle, we can determine the reflector's location based on the sensor's signal. Given that light travels through air, we have flexibility in using the space when we design the sensor. The size of the air medium can be determined by the actuator's stroke. In this study, the distance from the center to the emitter and detector, denoted as l, was set to 5 mm, while d was designed to vary between 1 mm and 9 mm to cover the full range of actuation strokes, with a 1 mm safety margin (detailed fabrication process in Materials and Methods section).

To validate the theoretical relationship between the position of the reflector and the voltage output of the phototransistor, we integrated the sensor with the actuator and recorded the absolute displacement of the reflective part alongside the sensor data (Fig. 7(a)). A marker attached to the piston was tracked throughout the single back-and-forth actuation cycle using the motion capture camera to provide ground truth values for comparison. The experimental data was plotted alongside the model (Fig. 7(b)), showing that the sensor output is closely aligned with the calibrated model (RMSE of 0.13 mm). The results demonstrate that the model accurately matches the experimental data, confirming that it can be reliably used to estimate the displacement of the actuator based on sensor values.

Fig. 7 The characterization of sensor. (a) Schematic of sensor integrated actuator with the definition of variable. (b) Comparison between the sensor model and experimental data.

4 Multi-DoF feedback control performance

In this section, we demonstrate how each module can be assembled to perform a range of tasks by employing various configurations of transmission, including changes in the number and arrangement of components. Then, we implement the proposed module on the origami structure to enable feedback control of the folding joints. Origami is an art of paper folding. This approach in design allows flat two-dimensional structures to transform into complex three-dimensional forms.^3,46–48 The flat design of the proposed actuators and sensors aligns naturally with the planar geometry of origami patterns, making it well-suited to preserve the intrinsic advantages of origami-based systems—such as compactness and lightweight structure. Furthermore, this configuration enhances the functional range of origami joints, enabling transitions from fully folded to fully opened states. We demonstrate that the integration of these actuators allows for precise control over the folding sequence at multiple actuation points, as well as real-time adjustment of joint angles for effective shape reconfiguration.

4.1 Customization of performance through multi-module connections and transmission design adjustments

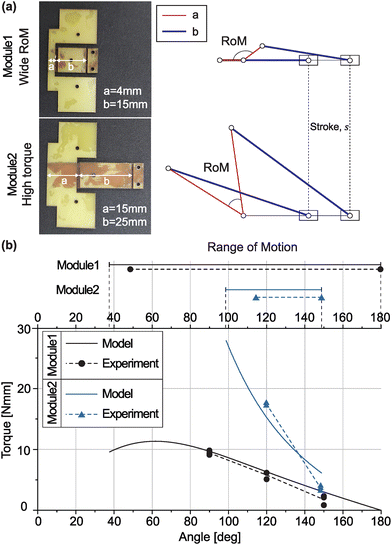
The proposed actuators and sensors are designed to be assembled in various configurations as needed. We first tested the performance programmability through multi-module combinations by experimenting with both parallel and series configurations of modules. For the parallel setup, we measured the blocked force at the bottom dead center (Fig. S6(A) and (B), ESI†). When the actuator was connected in parallel, the slope of input pressure to output force was 0.02 N kPa⁻¹ for a single actuator, 0.04 N kPa⁻¹ for two actuators, and 0.06 N kPa⁻¹ for three actuators (Fig. S6(C), ESI†). This result shows that the output force increased linearly with the number of actuators in parallel, while the resulting displacement remained constant. On the other hand, actuators connected in series (Fig. S6(D) and (E), ESI†) provided an increased stroke while maintaining the same maximum force (with a stroke of 7 mm for a single actuator and 21 mm for three actuators, Fig. S6(F), ESI†). In this experiment, we attached a double-slider transmission to the actuator to change the pushing motion of the actuator to the pulling motion (Fig. S6(D), ESI†).

To validate the ability to modify performance using transmission accessories, we tested the capability of the slider-crank module to achieve different ranges of motion and output torque with the same actuator by comparing two types of slider-crank configurations (Fig. 8(a)). Module 1 is designed to provide a wider range of motion, while Module 2 is optimized for high torque. Fig. 8(b) shows the results for the range of motion in both cases, based on three independent tests for each case. While both cases exhibited some deviation from the model due to the non-zero thickness of the origami structure, we were able to confirm that the range of motion could be controlled by only changing the transmission module, as predicted by the model. Fig. 8(b) also presents the torque results for the two cases, and the experimental data closely followed the model (RMSE of 0.79 N mm for Module 1 and 3.25 N mm for Module 2). This demonstrates that adjusting the rod lengths can modify the torque output, which can be designed using the model.

Fig. 8 Validation of performance variation according to configuration changes. (a) A comparison of different slider-crank designs, illustrating the relationship between stroke length and range of motion for each case: Module 1 is optimized for a wide range of motion, whereas Module 2 is designed for higher torque output. (b) Influence of slider-crank design parameter variations on both range of motion and torque performance.

In conclusion, all components are modular, providing significant assembly potential. We have confirmed that a parallel connection of the actuators enhances output force (magnification), while a series connection increases output stroke (extension). Additionally, the transmission allows for efficient adjustments of actuation mode and performance within a compact configuration. Both the actuator and transmission closely adhere to traditional classical models, despite having flat structures, allowing for easy design of the required performance, even with multiple distributed control points, through the model.

4.2 Distributed and feedback control for a box-shaped origami structure

We fabricated a box-shaped origami structure and installed the actuator to control each side of the box, as illustrated in Fig. 9(a). Sequential actuation is crucial in origami or structures with multiple distributed control points as it prevents interference between them, and, depending on the sequence, enables the structure to achieve different configurations. Initially, the box was in a folded state due to the spring force when no pressure was applied. We applied equal pressure of 90 kPa to all actuators to form the box shape, and then sequentially adjusted the opening and closing of each side. The pressure was first reduced to 0 kPa to fold the sides, then increased to 120 kPa to fully open the box. As shown in Fig. 9(a), we could control the folding sequence by switching the pressurizing channels. Additionally, a sensor was integrated with the actuator to facilitate closed-loop feedback control by providing sensor feedback aimed at achieving a specific folding angle. As shown in Fig. 9(b) we could effectively control the folding angle of the origami joint to the desired position using feedback control while maintaining compact structure.

Fig. 9 The integration of the proposed systems to the box-shaped origami structure with multi-DoF. (a) Sequential transformation of the box from fully folded to fully opened states. (b) Feedback control of the angle using the embedded sensor. The demonstration video can be found in Supplementary Video (ESI†).

5 Conclusion

We presented a compact, flat pneumatic actuation system based on a rolling diaphragm, integrated with modular transmission and sensor components for use in reconfigurable robotic structures. The surface-embedded actuator design enhances spatial efficiency and supports distributed control by minimizing energy loss and maintaining a linear input-output force relationship, which simplifies modeling. The rolling diaphragm structure was selected to address the challenges that arise when designing a flat pneumatic actuator, balancing the trade-off between friction and sealing in a pressurized chamber. Transmission modules, such as the slider-crank mechanism, convert linear motion into customizable outputs, such as torque and range of motion, while preserving compactness and supporting model-based performance prediction. Experimental validation confirmed that performance can be tuned by adjusting transmission parameters or actuator arrangements, parallel connections increased force output, while series connections extended stroke length. Our embedded optical sensor enables a versatile and scalable approach to distributed control in robotic systems by combining a compact, lightweight, and flat form factor with the inherent advantages of optical sensing. By using air as the light transmission medium and a minimally invasive reflector, the sensor achieves seamless integration and accurate displacement sensing across diverse transmission configurations without compromising system dynamics or modularity. Closed-loop control was demonstrated on an origami-inspired structure, where sensor feedback successfully regulated joint angles. Overall, the proposed module can be easily customized to meet specific performance requirements, such as actuation mode, range of motion, and force/torque output, by leveraging the model and implementing classical transmission. This enables each control point to be independently tuned and arranged across the surface of the structure in various shapes and scales. In practical applications, we expect the module to be most effective in mesoscale systems, where compactness, modularity, and adaptability are essential. However, its design principles are inherently scalable, enabling application across a broad range of system sizes. At the microscale, it can be integrated into surgical tools that demand high precision, compact end-effectors, and enhanced dexterity. At larger scales, the module is suitable for robotic manipulators operating in constrained or extreme environments—such as space—where deployability is vital. Additionally, its modular and reconfigurable architecture makes it well-suited for shape-morphing mobile robots that require structural transformation and environmental adaptability. Overall, the proposed approach offers a versatile foundation for developing reconfigurable robotic systems with embedded sensing across various scales and diverse application domains.

Materials and methods

Fabrication of rolling diaphragm actuator (Fig. S1, ESI†)

We fabricated the rolling diaphragm of the actuator using TPU-coated fabric and a laser sealing method to ensure precise and reliable manufacturing. A laser focused 5 mm away from the focal point, followed a predesigned path to melt the TPU and seal the two fabric layers together. While a wider sealing line strengthens the seal, it also increases resistance to the diaphragm's rolling motion. To balance these factors, we limited the sealing line thickness to 1 mm and aligned it vertically to the rolling edge. After completing the process, we inverted it and connected it to the chamber to minimize the impact of the sealing edge on the rolling motion. To prevent leakage, the diaphragm connects to the chamber through a clamping design, providing a tight seal. The cylinder part, where the diaphragm attaches, and the piston, which connects to the diaphragm's end, were fabricated using laser cutting and layer stacking methods. To minimize friction between the piston and its guiding structure, we reduced the contact area and applied a low-friction coating (Teflon tape, SK-02 AD SW from High-tech-flon) to the surfaces.

Fabrication of optical sensor

We selected a light source and detector designed to emit and detect infrared light at a peak wavelength of 850 nm (emitter: VSMY1850, phototransistor: TEMT7100X01, both from VISHAY). These components were mounted on an optically transparent acrylic plate. To enhance reflectivity, we coated the interior walls with reflective silver paste (ELCOAT from CANS), leveraging silvers high reflectance for wavelengths above 700 nm, which aligns with the emitters wavelength range.⁴⁵

Data acquisition

The proposed sensor signal, along with the force sensor signal (load cell 651AL from KYOTO) and the pressure sensor signal (ISE30A-01-C from SMC), was recorded using the NI myRIO-1900 DAQ (from NATIONAL INSTRUMENTS) at a sampling rate of 1 kHz.

Author contributions

H. J. contributed to the conceptualization, writing, experimentation, investigation, and analysis; J. K. provided supervision, funding acquisition, and writing; and J. P. contributed to supervision, conceptualization, and writing.

Data availability

The main text or ESI† contains all the data.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. J. Seo, J. Paik and M. Yim, Annu. Rev. Control Robot. Auton. Syst., 2019, 2, 63–88.
2. H. Gu, M. Möckli, C. Ehmke, M. Kim, M. Wieland, S. Moser, C. Bechinger, Q. Boehler and B. J. Nelson, Nat. Commun., 2023, 14, 1263.
3. C. H. Belke and J. Paik, IEEE/ASME Trans. Mechatron., 2017, 22, 2153–2164.
4. S. Hauser, M. Mutlu, P.-A. Léziart, H. Khodr, A. Bernardino and A. J. Ijspeert, Rob. Auton. Syst., 2020, 127, 103467.
5. S. Wu, Y. Hong, Y. Zhao, J. Yin and Y. Zhu, Sci. Adv., 2023, 9, eadf8014.
6. F. Zuliani and J. Paik, Smart Mater. Struct., 2022, 31, 115023.
7. Q. He, R. Yin, Y. Hua, W. Jiao, C. Mo, H. Shu and J. R. Raney, Sci. Adv., 2023, 9, eade9247.
8. G. Qiao, G. Song, W. Wang, Y. Zhang and Y. Wang, Int. J. Adv. Robot. Syst., 2014, 11, 47.
9. A. Firouzeh, Y. Sun, H. Lee and J. Paik, IEEE/RSJ International Conference on Intelligent Robots and Systems, 2013, pp. 4937–4944.
10. S. S. R. Chennareddy, A. Agrawal and A. Karuppiah, J. Robot., 2017, 5013532.
11. Z. Yoder, E. H. Rumley, I. Schmidt, P. Rothemund and C. Keplinger, Sci. Robot., 2024, 9, eadl3546.
12. P. J. White and M. Yim, IEEE/RSJ International Conference on Intelligent Robots and Systems, 2007, pp. 2773–2778.
13. M. G. Atia, A. Mohammad, A. Gameros, D. Axinte and I. Wright, Adv. Sci., 2022, 9, 2203217.
14. L. Ning, C. Limpabandhu and Z. T. H. Tse, Soft Robot., 2024, 11, 2–20.
15. V. Vallem, E. Roosa, T. Ledinh, S. R. Nadimi, A. Kiani and M. D. Dickey, Soft Matter, 2022, 18, 9291–9298.
16. N. El-Atab, R. B. Mishra, F. Al-Modaf, L. Joharji, A. A. Alsharif, H. Alamoudi, M. Diaz, N. Qaiser and M. M. Hussain, Adv. Intell. Syst., 2020, 2, 2000128.
17. C. Zhang, P. Zhu, Y. Lin, Z. Jiao and J. Zou, Adv. Intell. Syst., 2020, 2, 1900166.
18. M.-S. Kim, J.-K. Heo, H. Rodrigue, H.-T. Lee, S. Pané, M.-W. Han and S.-H. Ahn, Adv. Mater., 2023, 35, 2208517.
19. R. Neuhaus, N. Zahiri, J. Petrs, Y. Tahouni, J. Siegert, I. Kolaric, H. Dahy and T. Bauernhansl, Front. Built Environ., 2020, 6, 95.
20. S. Ahmed, E. Arrojado, N. Sigamani and Z. Ounaies, Behavior and Mechanics of Multifunctional Materials and Composites, 2015, pp. 29–41.
21. S. Zhou, Y. Li, Q. Wang and Z. Lyu, Cyborg Bionic Syst., 2024, 5, 0105.
22. T. Chen, O. R. Bilal, R. Lang, C. Daraio and K. Shea, Phys. Rev. Appl., 2019, 11, 064069.
23. Q. Zhao, W. Zou, Y. Luo and T. Xie, Sci. Adv., 2016, 2, e1501297.
24. P. Motzki, F. Khelfa, L. Zimmer, M. Schmidt and S. Seelecke, IEEE/ASME Trans. Mechatron., 2019, 24, 293–303.
25. O. Perera, R. Liyanapathirana, G. Gargiulo and U. Gunawardana, Sens. Actuators, 2024, 524.
26. D. Kumar, J. Daudpoto and B. S. Chowdhry, Mater. Res. Express, 2020, 7, 073001.
27. J.-H. Lee, Y. S. Chung and H. Rodrigue, Sci. Rep., 2019, 9, 11251.
28. M. A. Robertson, O. C. Kara and J. Paik, Int. J. Robot. Res., 2021, 40, 72–85.
29. R. Drury, V. Sencadas and G. Alici, Soft Matter, 2022, 18, 1911–1919.
30. Z. Zhakypov, M. Mete, J. Fiorentino and J. Paik, 2nd IEEE International Conference on Soft Robotics (RoboSoft), 2019, pp. 814–820.
31. M. A. Robertson, H. Sadeghi, J. M. Florez and J. Paik, Soft Robot., 2017, 4, 23–32.
32. M. S. Xavier, C. D. Tawk, A. Zolfagharian, J. Pinskier, D. Howard, T. Young, J. Lai, S. M. Harrison, Y. K. Yong, M. Bodaghi and A. J. Fleming, IEEE Access, 2022, 10, 59442–59485.
33. M. Mete, H. Jeong, W. D. Wang and J. Paik, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2314901121.
34. A. Gruebele, S. Frishman and M. R. Cutkosky, IEEE Robot. Autom. Lett., 2019, 4, 1478–1484.
35. Yumpu.com, Diaphragm Design Manual - Simrit, 2009.
36. C. Hegde, J. Su, J. M. R. Tan, K. He, X. Chen and S. Magdassi, ACS Nano, 2023, 17, 15277–15307.
37. X. Wang, R. Guo and J. Liu, Adv. Mater. Technol., 2019, 4, 1800549.
38. J.-B. Chossat, Y.-L. Park, R. J. Wood and V. Duchaine, IEEE Sens. J., 2013, 13, 3405–3414.
39. H. Sun, X. Fang, Z. Fang, L. Zhao, B. Tian, P. Verma, R. Maeda and Z. Jiang, Microsyst. Nanoeng., 2022, 8, 111.
40. A. Atalay, V. Sanchez, O. Atalay, D. M. Vogt, F. Haufe, R. J. Wood and C. J. Walsh, Adv. Mater. Technol., 2017, 2, 1700136.
41. C. To, T. L. Hellebrekers and Y.-L. Park, 2015 IEEE/RSJ international conference on intelligent robots and systems (IROS), 2015, pp. 5898–5903.
42. T. Kim, S. Lee, T. Hong, G. Shin, T. Kim and Y.-L. Park, Sci. Robot., 2020, 5, eabc6878.
43. K. C. Galloway, Y. Chen, E. Templeton, B. Rife, I. S. Godage and E. J. Barth, Soft Robot., 2019, 6, 671–684.
44. Silicon Phototransistor in 0805 Package.
45. High Speed Infrared Emitting Diodes, 850 nm, Surface Emitter Technology.
46. D. Rus and M. T. Tolley, Nat. Rev. Mater., 2018, 3, 101–112.
47. Z. Zhakypov and J. Paik, IEEE Trans. Robot., 2018, 34, 151–165.
48. S. Felton, M. Tolley, E. Demaine, D. Rus and R. Wood, Science, 2014, 345, 644–646.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00143a

---