Open Access Article
Open Access ArticleElectronic interactions of a quatertiophene-based surfactant at the liquid/gas interface
Changwoo
Bae
 a,
Kamatham
Narayanaswamy†
b,
Hisham
Idriss
b,
Ludivine
Poyac
b,
Indraneel
Sen
c,
Sébastien
Richeter
a,
Kamatham
Narayanaswamy†
b,
Hisham
Idriss
b,
Ludivine
Poyac
b,
Indraneel
Sen
c,
Sébastien
Richeter
 b,
Sébastien
Clément
b,
Sébastien
Clément
 b,
Anne-Laure
Biance
b,
Anne-Laure
Biance
 *a,
Samuel
Albert
*a,
Samuel
Albert
 *a and
Oriane
Bonhomme
*a and
Oriane
Bonhomme
 a
a
aUniversite Claude Bernard Lyon 1, CNRS, Institut Lumière Matière, UMR5306, F69100 Villeurbanne, France. E-mail: anne-laure.biance@univ-lyon1.fr; samuel.albert@univ-lyon1.fr
bICGM, Univ Montpellier, CNRS, ENSCM, Montpellier, France
cWasabi Innovations Ltd, Sofia 1784, Bulgaria
First published on 16th April 2025
Abstract
We report the synthesis of a functional molecule, a quatertiophene-based surfactant, which can both adsorb at the water/gas interface (surface active molecule) and aggregate through π−π stacking interactions. We assess then the ability of this molecule to create these functionalities at interfaces. This interfacial functional aggregation, characterized here in situ for the first time, is probed thanks to Langmuir trough experiments and spectrometric ellipsometry. These results pave the way to the design of new water based optoelectronic devices.
1 Introduction
The design of new organic materials that can assemble at the nanoscale is a crucial step towards the construction of the next generation of advanced functional materials for nanoscale electronics and optoelectronic devices such as organic field effect transistors (OFETs), organic light emitting diodes (OLEDs) and sensors.1,2 As the performance of the device depends on both the optoelectronic properties and nanoscale morphology, which are inherently interconnected, control over their self-assembly at the nanoscale is of paramount importance. To achieve this, chemists can utilize a wide range of non-covalent interactions, such as hydrogen bonding, van der Waals interactions, electrostatic forces, and π–π interactions, which can be tuned through structural modifications.3,4 Consequently, there is a growing research focus on conjugated organic materials, particularly on developing strategies to optimize their intramolecular conformation and intermolecular electronic coupling through structurally programmed non-covalent assembly.4–6In the self-assembly process of these specifically designed organic materials, the nature of solvent (polarity, dipole moment, protic/aprotic nature, dielectric constant) is a key parameter for tuning the intermolecular interactions between the organic units.7,8 While thin films of organic materials are typically formed using organic solvent, designing molecules capable of self-assembly in water while retaining their optoelectronic properties presents a great challenge.9,10
Achieving such self-assembly in water offers the possibility of using a sustainable and biocompatible solvent. More interestingly, it will be a first step for coupling ionic, specifically protonic, and electronic transport. This coupling is generally achieved thanks to electrochemical processes at electrodes. In the specific case of interfacial processes, this coupling has also been reported in the case of electrokinetic water transport in the vicinity of van der Waals materials such as graphene.11,12 We explore here an alternative route, by designing a new functional molecule that can at the same time assemble at interfaces and bear these electronic properties.
To this aim, we designed an amphiphilic π-conjugated molecule built upon a quaterthiophene backbone allowing the presence of π–π stacking intermolecular interactions, and three ethylene glycol chains to facilitate water solubility.13 We measure the surface pressure of the liquid–gas interface as a function of the molecular area of the molecule at interface, thanks to Langmuir trough experiments. We demonstrate that it tends to adsorb at interfaces and is surface-active. Analysis of the curves with surface equations of state allows us to define two regimes of interaction and to evidence that aggregation occurs when the interfacial layer is dense enough. To go further, we characterize the aggregation properties of this so-called electronic surfactant directly in situ, when they are located at interfaces. Hence, we probe the spectroscopic properties of the molecular assembly directly at the liquid–air interface thanks to a new dedicated spectrometric ellipsometry technique. A shift of some absorption bands when the molecular area is decreased allowed us to get, for the first time, a signature of the formation within the molecular layer of some interfacial molecular complexes in which electron delocalization can occur.
2 Materials and methods
2.1 Surfactant synthesis
1H and 13C{1H} NMR spectra are recorded on Bruker 400 MHz Avance III HD and 500 MHz Avance III spectrometers at 298 K. Deuterated solvents CDCl3 (Sigma-Aldrich, 99.8%) and dimethyl sulfoxide-d6 (DMSO-d6) (Avantor, >99.0%) are used as received. 1H and 13C{1H} NMR spectra are calibrated using the relative chemical shift of the residual non-deuterated solvent as an internal standard. Chemical shifts (δ) are expressed in ppm. Abbreviations used for NMR spectra are as follows: s, singlet; d, doublet; t, triplet; m, multiplet.
High resolution mass spectra (HRMS) are recorded on a Bruker MicroTof QII instrument in positive/negative modes.
2.1.3.1 Synthesis of compound 2. (5′-Bromo-2,2′-bithiophen-5-yl)methanol (355 mg, 1.290 mmol) is placed into a two-neck 100 mL round bottom flask under argon with anhydrous tetrahydrofuran (THF) (20 mL). The solution is cooled to 0 °C with an ice bath. Sodium hydride (60% dispersed in mineral oil) (33 mg, 1.360 mmol, 1.1 eq.) is added and the mixture is stirred for ninety minutes. Then, a solution of compound 1, whose structure is reported in Fig. 2 (784 mg, 1.190 mmol, 0.9 eq.) in 15 mL of anhydrous THF is added dropwise and the mixture is stirred at room temperature for 24 hours. The reaction is followed by TLC using CH2Cl2 as eluent. Once the reaction is finished, the solvent is evaporated, CH2Cl2 is added and the organic phase is washed with water (3 × 25 mL). The organic phases are gathered, dried over MgSO4 and the solvent is evaporated under reduced pressure. The resulting crude mixture is purified by flash column chromatography on silica gel using gradient elution CH2Cl2/MeOH (98
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to 90
2 to 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (v
10 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v)) leading to compound 2 as a yellow/brownish oil (335 mg, 66%).
v)) leading to compound 2 as a yellow/brownish oil (335 mg, 66%).
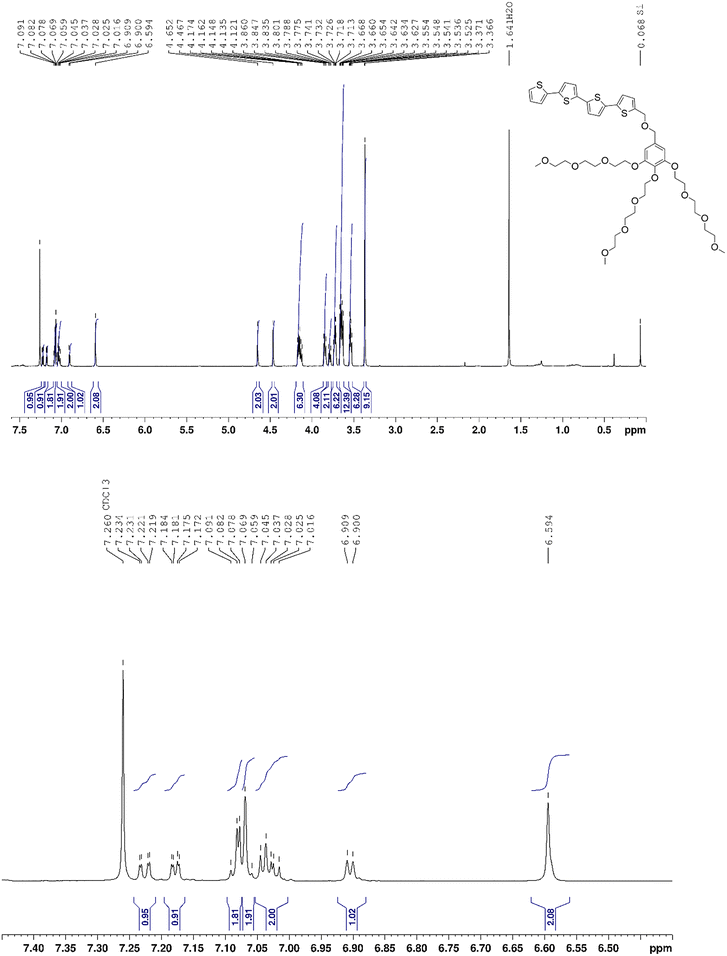
1H NMR (400 MHz, CDCl3) δ = 6.97 (d, 1H, 3JH–H = 3.6 Hz), 6.96 (d, 1H, 3JH–H = 3.8 Hz), 6.89 (d, 1H, 3JH–H = 3.9 Hz), 6.88 (dt, 1H, 3JH–H = 3.6 Hz, 4JH–H = 0.6 Hz), 6.58 (s, 2H), 4.63 (br. s, 2H), 4.55 (br. s, 2H), 4.14 (m, 6H), 3.85 (br. d, 2H 3JH–H = 4.4 Hz), 3.83 (br. d, 3JH–H = 4.8 Hz, 2H), 3.79 (br. d, 1H, 3JH–H = 4.4 Hz), 3.78 (br. d, 1H 3JH–H = 5.0 Hz), 3.72 (m, 6H), 3.65 (m, 12H), 3.54 (m, 6H), 3.37 (s, 9H) ppm.
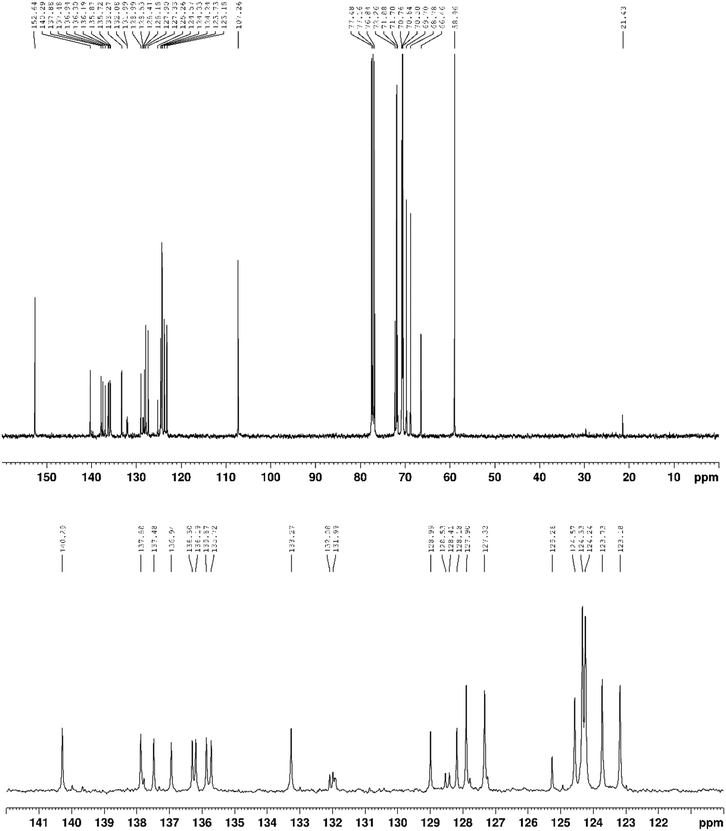
13C{1H} NMR (100 MHz, CDCl3) δ 152.8, 140.7, 139.0, 138.0, 137.0, 133.3, 130.8, 127.4, 123.9, 123.6, 111.1, 107.4, 72.4, 72.0, 71.9, 70.9, 70.8, 70.7, 70.6, 69.8, 68.9, 66.5, 59.2 ppm.
HRMS (ESI+): m/z calcd for C37H55BrO13S2+ [M]+: 851.2334 Da, found: 851.2336 Da.
2.1.3.2 Synthesis of compound 3. Compound 2 (270 mg, 0.317 mmol, 1 eq.), 2,2′-bithiophen-5-yl(trimethyl)stannane (147 mg, 0.447 mmol, 1.4 eq.) and tetrakis(triphenylphosphine)palladium (15 mg, 0.012 mmol, 0.04 eq.) are placed into a two-neck 100 mL round bottom flask and flushed with argon. Then, anhydrous toluene (25 mL) is added. The solution is stirred at reflux 24 hours and the reaction is followed by TLC using CH2Cl2/MeOH (98
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (v
2 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v)) as eluent. Once the reaction is finished, the solvent is evaporated. CH2Cl2 (30 mL) is added and the organic phase is washed with water (3 × 20 mL). All organic phases are gathered, dried over MgSO4 and the solvent is evaporated under reduced pressure. The resulting crude mixture is purified by column chromatography on silica gel using CH2Cl2/MeOH (98
v)) as eluent. Once the reaction is finished, the solvent is evaporated. CH2Cl2 (30 mL) is added and the organic phase is washed with water (3 × 20 mL). All organic phases are gathered, dried over MgSO4 and the solvent is evaporated under reduced pressure. The resulting crude mixture is purified by column chromatography on silica gel using CH2Cl2/MeOH (98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to 90
2 to 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (v
10 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v)) as eluent leading to compound 3 as a yellow/brownish oil (260 mg, 87%).
v)) as eluent leading to compound 3 as a yellow/brownish oil (260 mg, 87%).
1H NMR (400 MHz, CDCl3): δ 7.23 (dd, 1H, 3JH–H = 5.1 Hz, 4JH–H = 1.1 Hz), 7.18 (dd, 1H, 4JH–H = 1.0 Hz, 3JH–H = 3.6 Hz), 7.08 (m, 2H),7.08 (br. s, 2H), 7.03 (m, 2H), 6.90 (d, 1H, 3JH–H = 3.6 Hz), 6.59 (s, 1H), 4.65 (s, 1H), 4.47 (s, 1H), 4.15 (m, 7H), 3.85 (t, 5H, 3JH–H = 5.0 Hz), 3.79 (t, 2H, 3JH–H = 5.2 Hz), 3.73 (m, 7H), 3.65 (m, 14H), 3.54 (m, 7H), 3.37 (2 br s, 9H), 1.64 (s, 9H) ppm.
13C{1H} NMR (100 MHz, CDCl3) δ 152.6, 140.3, 139.7, 137.9, 137.5, 137.3, 136.9, 136.3, 136.2, 135.9, 135.7, 133.3, 132.1, 132.0, 131.9, 131.9, 129.0, 128.5, 128.4, 128.2, 127.9, 127.8, 127.3, 127.2, 125.3, 124.6, 124.3, 124.2, 123.7, 123.2, 107.3, 77.5, 77.4, 76.8, 72.3, 71.9, 71.7, 70.8, 70.6, 70.5, 69.7, 68.8, 66.5, 59.0, 21.4 ppm.
C,H,S analysis. Anal. calcd for C45H60O13S4: C, 57.67; H, 6.45; S, 13.57. Found: C, 57.44; H, 6.62; S, 13.64.
HRMS (ESI+): m/z calcd for C45H60O13S4+ [M+]: 937.2989 Da, found: 937.2994 Da.
UV-vis (H2O): λmax (log(ε)), 357 nm (4.3), 411 nm (3.8), 440 nm (3.56).
2.2 Bulk characterization methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000× and 30
000× and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000× with defocus ranging from 1.8–2.5 μm.
000× with defocus ranging from 1.8–2.5 μm.
2.3 Molecules at interfaces
The molecular layer is deposited on deionized water (18.2 MΩ cm at the exit of the deionized machine PURELAB flex, ELGA, 1 MΩ cm after a few minutes at ambient atmosphere) placed in a Langmuir–Blodgett trough (KSV NIMA Medium), composed of a Teflon tank with two motorized barriers positioned at the water–gas level, allowing for adjustment of the surface area, A, accessible to the surfactants at the liquid–gas interface. First, the Teflon tank is filled with ultrapure water, and a paper Wilhelmy plate is hung on a force sensor to measure the surface pressure at the interface (Fig. 1). Then, a given volume of the surfactant chloroform solution is dispensed cautiously thanks to a glass syringe (Hamilton) on top of the water–air interface. Great care to minimize the dissolution into the bulk water is required. The amount of volume dispensed each time was approximately 1 μL dropwise. A small correction factor (less than 15%) is added when computed the molecular area of 3 to correct uncertainties on the deposited volume and on the surfactant concentration in chloroform. This factor is constant for a run of experiments and allow to collapse both adsorption isotherm, ellipsometry data and UV-vis absorption spectra.
 | (1) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) . The values of this complex ratio depend on the angle of incidence of the light, the thickness of the deposited layer and the complex optical index (namely the refractive index and the extinction coefficient) of the layer as a function of the wavelength through a nonlinear relation. Obtaining the properties of the layer from the ellipsometry measurements requires a model and data inversion procedure. Such procedure is developed on thin solid layer deposited on a solid substrate18,19 or in the commercial software from Woollam. However, it is still challenging to perform it on liquid interfaces where roughness, fluctuations or heterogeneities must be considered.20–22 Moreover, when considering a monolayer of molecular thickness, large uncertainties remain during the inversion and no quantitative result can be obtained.23 Taking into account these effects is out of the scope of this study, so we will only analyse here directly the evolution of the raw ellipsometry data.
. The values of this complex ratio depend on the angle of incidence of the light, the thickness of the deposited layer and the complex optical index (namely the refractive index and the extinction coefficient) of the layer as a function of the wavelength through a nonlinear relation. Obtaining the properties of the layer from the ellipsometry measurements requires a model and data inversion procedure. Such procedure is developed on thin solid layer deposited on a solid substrate18,19 or in the commercial software from Woollam. However, it is still challenging to perform it on liquid interfaces where roughness, fluctuations or heterogeneities must be considered.20–22 Moreover, when considering a monolayer of molecular thickness, large uncertainties remain during the inversion and no quantitative result can be obtained.23 Taking into account these effects is out of the scope of this study, so we will only analyse here directly the evolution of the raw ellipsometry data.
The ellipsometry and Langmuir trough techniques are coupled, as depicted in Fig. 1, to discuss the evolution of the optical properties (namely Ψ and Δ) in relation with the adsorption isotherms (namely surface pressure and surface concentration).
3 Surfactant synthesis and bulk characterizations
3.1 Surfactant synthesis
The synthetic route to the amphiphilic quaterthiophene, noted 3, is described in Fig. 2. Compound 3 is prepared in two steps starting from precursor 1. First, the etherification condensation reaction of precursor 1 with (5′-Bromo-2,2′-bithiophen-5-yl)methanol in THF at room temperature (RT) for 24 hours produces compound 2 in 66% yield. Finally, the quaterthiophene (compound 3) is synthesized in 87% yield by a palladium-catalyzed Stille cross-coupling reaction between 5-trimethylstannyl-2,2′-bithiophene and compound 2. The full reaction protocol and characterizations of compound 3 are detailed in Section 2.1.3. Compounds 2 and 3 have been fully characterized by 1H NMR, 13C{1H} NMR, and high-resolution ESI-MS (see Appendix 1).3.2 Optical properties and aggregation behavior
To determine the critical micellar concentration (CMC) of the obtained amphiphilic quaterthiophene (compound 3) in water, the intensity of scattered light is measured at various concentrations. For concentrations below the CMC, the intensity of scattered light is very low and stable. However, exceeding the CMC results in an abrupt increase in scattered light intensity due to the formation of surfactant aggregates at these concentrations. This phenomenon is based on the principle that large particles scatter light much more efficiently than small molecules. According to this, the CMC value of compound 3 is found to be of the order of 0.008 mM as depicted in Appendix 1 (see Fig. 15). This value is rather low compared to side-chain functionalized oligothiophenes,24,25 probably due to the strong hydrophobic character brought by the presence of the non-decorated four thiophene units.The morphology of the aggregates formed by the amphiphilic quaterthiophene (compound 3) is then examined using cryo-transmission electron microscopy (cryo-TEM). Typical morphologies obtained for samples prepared in deionized water at 0.05 mM, a concentration 10 times higher than the CMC, are depicted in Fig. 3. Large vesicular assemblies, generally unilamellar, with diameters ranging from 63–657 nm and an average diameter of 159 nm, are observed, as previously reported13 for a quaterthiophene bearing a triethylene glycol polar chain in position 2. The size distribution histogram is reported in Appendix 1, Fig. 14. The objects gradually merged over time, forming large and complex structures that became less visible as the measurements progressed.
The UV-visible absorption spectra of the compound are measured in DMSO, water and chloroform as shown in Fig. 4. The UV-visible absorption spectrum of compound 3 in DMSO displays a broad band lacking distinct fine structures at λmax = 404 nm, indicating the presence of multiple conformers in solution. This absorption is attributed to a twisted anti conformation, deviating 30° from planarity, similar to what is observed and calculated for other unsubstituted oligothiophenes.26,27 A similar absorption profile is observed in chloroform. In water, a blue-shifted absorption of λmax = 357 nm is noticed compared to the absorption in DMSO, which may be due to the aggregation order of the oligothiophene chromophores in such solvent, namely formation of H-aggregates as already found for oligothiophenes with linear end groups.13,28
 | ||
| Fig. 4 UV-visible absorption spectra of compound 3 at 0.05 mM in DMSO (dashed black line), 0.05 mM in water (blue line), and at 0.92 mM in chloroform (red line). | ||
4 Aggregation properties at interfaces
4.1 Langmuir trough experiments
 | ||
| Fig. 5 Evolution of the surface pressure Π as a function of the molecular area for compound 3 at the air/water interface at 21 °C. The evolution is obtained from different sets of experiments, where molecular area is corrected. Data are fitted by a combination of eqn (3) and (4), with parameters given in Table 1. Inset: Same data, with colored circles that corresponds to the point at which ellipsometry measurements were performed (Fig. 6). | ||
For that, we first assume that regime 1 corresponds to a classical compressible monolayer, using a modified Volmer model.30,32,33 This model is compatible with the high reproducibility of the compression/decompression cycles of the interfacial layer in this regime, consistent with the absence of strong intermolecular interactions. This model assumes that the surfactants can be considered as hard disks, with no long-range interactions. These hypotheses are softened, by introducing a 2D monolayer compressibility ε, which modifies the excluded area per molecule as a function of the surface pressure, as
| α = α0(1 − εΠ), | (2) |
 | (3) |
This regime is valid at large surface area, until the above-mentioned kink is observed, at a critical pressure noted Πc. This kink is the signature of a phase transition that we attribute to the formation of aggregates at interfaces.13,31
In regime 2, the pressure–area isotherm can be modeled by an equation of state that considers aggregation of the molecules,31 described in Appendix 2. Single surfactant molecules are then in equilibrium with aggregates of n surfactants. In this case, the equation of states reads:
 | (4) |
 | (5) |
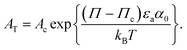 | (6) |
 is a pressure that accounts for interactions between the aggregates at low surface area. Note that
is a pressure that accounts for interactions between the aggregates at low surface area. Note that  and Π* have different values, as they account for distinct phenomena.
and Π* have different values, as they account for distinct phenomena.
Such a refined model, using both eqn (3) and (4) is required to fit all the data, and a satisfying agreement is achieved (see Fig. 5). The fitting procedure is detailed in Appendix 2. The fitting parameters are given in Table 1 and discussed below.
The molecular area occupied by one monomer α0 is found to be around 1 nm2, which can be compared to the size of the hydrophobic part of compound 3. Compound 3 hydrophobic part consists in four thiophenes' group, with sizes around 0.383 nm,34 and three C–C bonds, of length 0.154 nm. A rough estimation of this area is then given by A = (0.154 × 3 + 0.383 × 4) × 0.383 nm2, which results in 0.76 nm2, very comparable to α0, though a bit smaller. It shows that when they are not interacting, single molecules tend to be planar at the interface. In this dilute regime, the interactions between monomers are very small, as shown by the very small value of Π*. The compression factor ε is in the range of commonly observed factors with these types of insoluble molecules.33 The critical area at which aggregation occurs Ac is a little bit less than the area of one monomer α0, showing that a change of conformation of the molecule at the interface must occur before aggregation. This is confirmed by the fact that a compression factor needs to be introduced in the Volmer modified regime.
In the aggregated regime, the aggregates are more compact than the free monomers, as shown by the value of εa, which is larger than 0. This compaction is quite important (εa ≃ 0.6) demonstrating a strong reorganization of the molecules at interface, a signature of specific oriented interactions, among which electronic delocalization or so-called π–π interactions are good candidates. The typical area per molecule in the aggregate is εa/n = α0(1 − εa) ≈ 37.5 Å2 (corresponding to the area at which the collapse appears on Fig. 5): it is sligthly larger than the largest measured cross section of one thiophene group,13 probably due to the presence of the three ethylene glycol chains. It tends to confirm that the electronic surfactant does not have all its thiophene group along the interface in regime 2.
To confirm these findings at a molecular scale, we probe the surface by spectrometric ellipsometry, which gives some qualitative information of the optical response of the monolayers, and can be correlated to the absorption band of the amphiphilic quaterthiophene.
4.2 Spectroscopic ellipsometry
Fig. 6 reports the spectra of the amplitude Ψ (top) and phase Δ (bottom) performed on the air/water interface covered by compound 3 at different stages of the surface compression. For a non-absorbing compound at the interface, only variations of Δ are expected. A clear signature of the adsorption of compound 3 is observed both on Ψ and Δ. Both the amplitude of the bands of the spectra and their shape change with the surface compression.
 | ||
| Fig. 6 Spectroscopic ellipsometry measurements performed at different stage of the surface compression. The blue curves are performed in the dilute regime (regime 1), the red ones in the aggregated regime (regime 2), and the gray ones when the monolayer collapses. The curve color corresponds to the point colors on insert of Fig. 5. | ||
At Brewster angle, for surfactants that do not interact with light, the ellipticity coefficient ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) is a signature of surfactant adsorption: it becomes more and more negative when surfactants get adsorbed at air/water interface as the hydrocarbon chain have a negative contribution in this parameter.36 A direct link between this coefficient and the surfactant concentration is not possible without independent calibration. However, it appears that for single chain cationic surfactants,
is a signature of surfactant adsorption: it becomes more and more negative when surfactants get adsorbed at air/water interface as the hydrocarbon chain have a negative contribution in this parameter.36 A direct link between this coefficient and the surfactant concentration is not possible without independent calibration. However, it appears that for single chain cationic surfactants, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) evolves linearly with the surface concentration.36 We adopt the same approach even if we do not work at Brewster angle to discuss the ellipsometry data collected. We then first analyse the signature of surfactant adsorption far from resonance (absorption peaks) i.e. at 620 nm for example: the evolution of the ellipsometry ratio
evolves linearly with the surface concentration.36 We adopt the same approach even if we do not work at Brewster angle to discuss the ellipsometry data collected. We then first analyse the signature of surfactant adsorption far from resonance (absorption peaks) i.e. at 620 nm for example: the evolution of the ellipsometry ratio ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) is plotted as a function of the surface concentration Γ = 1/as on Fig. 7, top. At small molecular area (regime 1 on Fig. 5), one recovers a linear decrease of
is plotted as a function of the surface concentration Γ = 1/as on Fig. 7, top. At small molecular area (regime 1 on Fig. 5), one recovers a linear decrease of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) as a function of the surface concentration. This is in agreement with observations of the adsorption isotherms: the surfactants behave as independent molecules, with almost no interaction.
as a function of the surface concentration. This is in agreement with observations of the adsorption isotherms: the surfactants behave as independent molecules, with almost no interaction.
 | ||
| Fig. 7 Evolution of the ellipticity coefficient with the surface concentration respectively (top) far from adsorption band at 620 nm and (bottom) at the adsorption band in water i.e. at 404 nm. The vertical grey line corresponds is equivalent to Ac (see Table 1), i.e. the beginning of the interacting-regime identified on the adsorption isotherm. | ||
At the molecular area Ac, where there is a kink in the adsorption isotherm, the slope of the ellipticity as a function of the surface concentration changes: this is also a signature that the surfactant interaction begins. A new linear regime is observed, which is a signature of a change in the effective optical index of these interacting entities. The collapse regime identified in the adsorption isotherm is confirmed by the optical signal: there is no more evolution of the ellipticity ratio indicating that there is no more evolution of the surface concentration.
Interestingly, the behavior close to the absorption band of the surfactant dispersed in chloroform, namely 404 nm, is very different, as illustrated in Fig. 7, bottom. The linear evolution of the ellipticity ratio is recovered in the dilute regime but the intermediate regime is not monotonous. Looking to the spectral signature of the ellipsometry data shown in Fig. 6, one can observe that the dip in Ψ around 404 nm progressively shifts and transforms into a peak at shorter wavelengths, typically around 350 nm, aligning closely with the absorption peak observed when the surfactant is dispersed in bulk water as shown in Fig. 4. If a direct comparison between the UV-vis absorption spectra and the ellipsometry measurements is not possible, this trend tends to highlight a shift in the absorption band under compression. Simultaneously, a new peak appears around 275 nm probably due to the appearance of a new band of adsorption. All these modifications indicate once again the appearance of aggregates on the air/water interface, but also prove the electronic nature of the interactions.
5 Conclusion
In this work, we describe the synthesis of an amphiphilic conjugated molecule possessing aggregation properties at the interface. To ensure amphiphilic features, we decorated a quaterthiophene that should allow intermolecular electronic delocalization, with three ethylene glycol chains, that should ensure its amphihilic properties. The characterization of this compound demonstrates its bulk aggregation behavior in water. Signature of the aggregation process at the interface has also been observed thanks to adsorption isotherm, in which two distinct regimes can be identified, a signature of a 2D phase transition. A model that considers the formation of aggregates closely matches the data, and an analysis of the fitting parameters is in good agreement with the fact that specific directional interactions exist between the molecules in the aggregates, to allow compaction of the molecules. This aggregation is also confirmed by optical characterization at the interface, thanks to ellipsometric spectroscopy. Even if this technique does not allow us to get the direct spectroscopic properties of the surfactant monolayer, analysis of the signal intensity at various wavelengths shows specific transitions when aggregation occurs (peak shift), which are compatible with electronic delocalization due to π−π interactions.This work offers many perspectives in the design and characterization of functional surfactants at interfaces. Various similar molecules, differing in the thiophene backbone or the length of ethylene glycol chains, can be optimized to get the best molecular assembly in the aggregates. Spectroscopic ellipsometry is a powerful tool to characterize spectroscopic properties of the interface, but also requires fundamental theoretical work to analyze the signal to get optical index of the monolayer, taking into account the presence of interface fluctuations. Finally, interfacial conductivity measurements are required to probe the real efficiency of these functional molecules.
Author contributions
C. Bae: methodology, investigation, formal analysis, visulaization, writing – review & editing. K. Narayanaswamy: methodology, investigation. H. Idriss: investigation. L. Poyac: investigation, writing – review & editing, validation. I. Sen: project administration, funding acquisition. S. Richeter: formal analysis, supervision. S. Clément: conceptualization, formal analysis, supervision, writing – review & editing, project administration, funding acquisition. A.-L. Biance: conceptualization, formal analysis, methodology, supervision, writing – original draft, project administration, funding acquisition. S. Albert: investigation, formal analysis, methodology, visualization. O. Bonhomme: conceptualization, formal analysis, methodology, supervision, writing – original draft, project administration.Data availability
Data, including Ellipsometry, Langmuir trough and UV Vis spectrum, and python codes for Langmuir trough fitting are available at https://doi.org/10.5281/zenodo.15131079.Conflicts of interest
There are no conflicts to declare.Appendices
Appendix 1 Surfactant synthesis: compounds characterizations
1H NMR spectrum, 13C{1H} NMR spectrum and high resolution ESI-TOF (positive mode) mass spectrum of compound 2 are reported in Fig. 8, 9 and 10 respectively. Similarly, 1H NMR and 13C{1H} NMR spectra and high resolution ESI-TOF (positive mode) mass spectrum of compound 3 are reported in Fig. 11–13.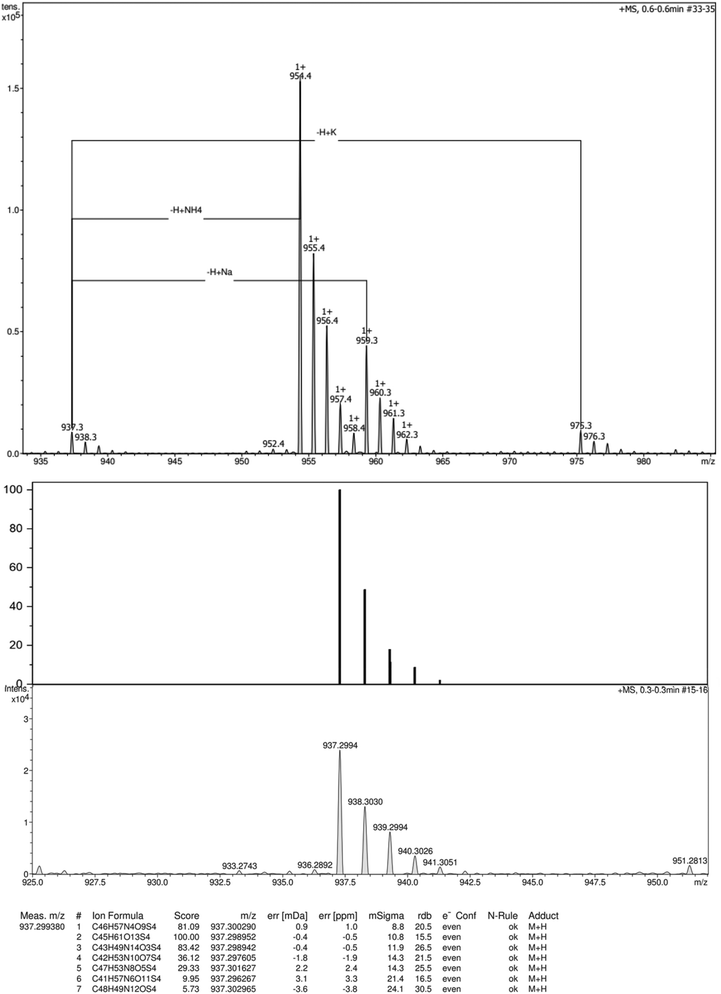 | ||
| Fig. 13 High-resolution ESI-TOF (positive mode) mass spectra (top), theorical and experimental isotopic profiles (bottom) of compound 3. | ||
Appendix 2 Equation of state for the aggregated phase
We consider that two phases coexist at the interface in equilibrium: one phase, with single surfactant molecules, in coexistence with some 2D monodisperse aggregates of n surfactant molecules. The chemical potential of each component at interface reads37μi = μ0i + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fixi − γαi, fixi − γαi, | (7) |
| dΠ = Γ1dμ1 + Γadμa, | (8) |
 | (9) |
 a cohesion pressure, α0 the molecular area of a monomer and αa the molecular area of the aggregate.
a cohesion pressure, α0 the molecular area of a monomer and αa the molecular area of the aggregate.
 | ||
| Fig. 14 Size distribution histograms of the amphiphilic quaterthiophene 3 obtained from the cryo-TEM images analysis. | ||
 | ||
| Fig. 15 Intensity of scattered light (in kilo counts per second) obtained for various concentrations of 3 prepared in deionized water, in a smi-log-plot. Lines are guide for the eyes. | ||
Considering that the chemical potential of the aggregates is equal to the one of the monomers (because they are at equilibrium), one can first link the adsorption amount of monomers and aggregates such as:
| Γa = Γ1(Γ1/ΓT)n−1, | (10) |
We also assume that monomers and aggregates are in equilibrium, so the local concentration of monomers is given by ΓT. In the case of a small numbers of aggregates, this results in Γ1 ≃ ΓT. However, when the number of aggregates is larger, the surface free of aggregates is reduced by a factor β:
 | (11) |
Finally, we consider that monomers in aggregates can occupy a different surface compared with the one occupied by the free monomer. We thus define a parameter εa such as:
| αa = nα0(1 − εa), | (12) |
Knowing that the physically observable value of the area occupied by 1 mole of monomers in the surface layer as can be defined as: as = 1/Γs where Γs = Γ1 + nΓa, one can obtain:
 | (13) |
More information can be obtained on At from eqn (7): the aggregation equilibrium nμs1 = μsn results in
 | (14) |
An−1T = Kn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{(Πnεaα0/kBT)}, exp{(Πnεaα0/kBT)}, | (15) |
AT(Π) = Ac![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{[(Π − Πc)εaα0/kBT]}, exp{[(Π − Πc)εaα0/kBT]}, | (16) |
Combining eqn (13) and (16) results in eqn (4) of the main text. These quantities can be used to fit the Π–as isotherms.
The experimental isotherm was fitted on the form aS = f(Π) to ensure a good convergence of the fitting procedure. For that, the fitting function was defined by part. For pressure below Πc, the critical pressure indicated on Fig. 5, the equation aS = f(Π) derived from eqn (3) was used. For pressure above Πc, the equation aS = f(Π) derived from eqn (4) was used. The two functions are computed such as they both have a pressure equal to Πc when the molecular is equal to Ac. No limitation was applied for the different fit parameters. Standard Python package SciPy and corresponding curvefit function was used for the procedure.
Acknowledgements
This work was financially supported by the European Union's Horizon 2020 Research And Innovation Program (PROGENY no. 899205) and French National Research Agency (ANR-20-CE09-0025 Soft Nanoflu and ANR-21-CE30-0007 Solstice). We thank the platform Nanoptec at iLM and Christophe Moulin for technical support.Notes and references
- K. Ariga, M. Nishikawa, T. Mori, J. Takeya, L. K. Shrestha and J. P. Hill, Sci. Technol. Adv. Mater., 2019, 20, 51–95 CrossRef CAS PubMed.
- D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440 CrossRef CAS PubMed.
- C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191–2201 RSC.
- W. J. Mullin, S. A. Sharber and S. W. Thomas III, J. Polym. Sci., 2021, 59, 1643–1663 CrossRef CAS.
- Y. Yamamoto, Sci. Technol. Adv. Mater., 2012, 13, 033001 CrossRef PubMed.
- C.-A. Palma, M. Cecchini and P. Samor, Chem. Soc. Rev., 2012, 41, 3713–3730 RSC.
- Y. Xi, C. M. Wolf and L. D. Pozzo, Soft Matter, 2019, 15, 1799–1812 RSC.
- A. K. Maerz, D. A. Fowler, A. V. Mossine, M. Mistry, H. Kumari, C. L. Barnes, C. A. Deakyne and J. L. Atwood, New J. Chem., 2011, 35, 784–787 RSC.
- S. Bai, S. Debnath, N. Javid, P. W. Frederix, S. Fleming, C. Pappas and R. V. Ulijn, Langmuir, 2014, 30, 7576–7584 CrossRef CAS PubMed.
- P. P. Syamala and F. Würthner, Chem. – Eur. J., 2020, 26, 8426–8434 CrossRef CAS PubMed.
- N. Kavokine, M.-L. Bocquet and L. Bocquet, Nature, 2022, 602, 84–90 CrossRef CAS PubMed.
- M. Lizée, A. Marcotte, B. Coquinot, N. Kavokine, K. Sobnath, C. Barraud, A. Bhardwaj, B. Radha, A. Niguès and L. Bocquet, et al. , Phys. Rev. X, 2023, 13, 011020 Search PubMed.
- L. Jiang, R. C. Hughes and D. Y. Sasaki, Chem. Commun., 2004, 1028–1029 RSC.
- Y. Wei, Y. Yang and J.-M. Yeh, Chem. Mater., 1996, 8, 2659–2666 CrossRef CAS.
- T. Daou, G. Pourroy, J.-M. Greneche, A. Bertin, D. Felder-Flesch and S. Begin-Colin, Dalton Trans., 2009, 4442–4449 RSC.
- J. A. van Haare, M. van Boxtel and R. A. Janssen, Chem. Mater., 1998, 10, 1166–1175 CrossRef CAS.
- D.-R. Coulson, L. Satek and S. Grim, Inorg. Synth., 1972, 13, 121–124 CrossRef.
- M. Gilliot, Thin Solid Films, 2012, 520, 5568–5574 CrossRef CAS.
- M. Gilliot, Opt. Commun., 2018, 427, 477–484 CrossRef CAS.
- R. Boubekri, M. Gross, M. In, O. Diat, M. Nobili, H. Möhwald and A. Stocco, Langmuir, 2016, 32, 10177–10183 CrossRef CAS PubMed.
- J. Meunier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 061601 CrossRef CAS PubMed.
- A. Ng, C. H. Li, M. K. Fung, A. B. Djurišič, J. A. Zapien, W. K. Chan, K. Y. Cheung and W.-Y. Wong, J. Phys. Chem. C, 2010, 114, 15094–15101 CrossRef CAS.
- K. Hinrichs and K.-J. Eichhorn, Ellipsometry of functional organic surfaces and films, Springer, 2018, vol. 52 Search PubMed.
- D. Janeliunas, R. Eelkema, B. Nieto-Ortega, F. J. R. Aguilar, J. T. L. Navarrete, L. van der Mee, M. C. Stuart, J. Casado and J. H. van Esch, Org. Biomol. Chem., 2013, 11, 8435–8442 RSC.
- P. van Rijn, D. Janeliunas, A. M. Brizard, M. C. Stuart, G. J. Koper, R. Eelkema and J. H. van Esch, New J. Chem., 2011, 35, 558–567 RSC.
- N. DiCésare, M. Belletête, M. Leclerc and G. Durocher, Chem. Phys. Lett., 1998, 291, 487–495 CrossRef.
- N. DiCésare, M. Belletête, A. Donat-Bouillud, M. Leclerc and G. Durocher, Macromolecules, 1998, 31, 6289–6296 CrossRef.
- A. Kreyes, S. Ellinger, K. Landfester, M. Defaux, D. A. Ivanov, A. Elschner, T. Meyer-Friedrichsen and U. Ziener, Chem. Mater., 2010, 22, 2079–2092 CrossRef CAS.
- C. Ybert, W. Lu, G. Möller and C. M. Knobler, J. Phys. Chem. B, 2002, 106, 2004–2008 CrossRef CAS.
- V. M. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779 CrossRef CAS.
- V. Fainerman and D. Vollhardt, J. Phys. Chem. B, 1999, 103, 145–150 CrossRef CAS.
- V. Fainerman, R. Miller and V. Kovalchuk, Langmuir, 2002, 18, 7748–7752 CrossRef CAS.
- Y. Timounay, A. Pannwitz, D. M. Klein, A.-L. Biance, M. E. Hoefnagel, I. Sen, A. Cagna, M. Le Merrer and S. Bonnet, Langmuir, 2022, 38, 9697–9707 CrossRef CAS PubMed.
- T. Bjornholm, D. R. Greve, N. Reitzel, T. Hassenkam, K. Kjaer, P. Howes, N. Larsen, J. Bogelund, M. Jayaraman, P. Ewbank and R. McCullough, J. Am. Chem. Soc., 1998, 120, 7643–7644 CrossRef CAS.
- A. S. Klymchenko, J. Nanosci. Lett., 2013, 3, 21 Search PubMed.
- T. Battal, G. C. Shearman, D. Valkovska, C. D. Bain, R. C. Darton and J. Eastoe, Langmuir, 2003, 19, 1244–1248 CrossRef CAS.
- J. A. V. Butler and J. P. Kendall, Proc. R. Soc. London, Ser. A, 1932, 135, 348–375 CAS.
Footnote |
| † Now at: Department of Chemistry, SRM University – AP, Amaravathi, Andhra Pradesh, India 522 240. |
| This journal is © The Royal Society of Chemistry 2025 |