 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Shock-induced dispersion patterns of powder with diverse physical properties†
Jaehun
Yoo
ab,
Ji Hoon
Kim
b and
Daegyoum
Kim
 *a
*a
aDepartment of Mechanical Engineering, KAIST, Daejeon 34141, Republic of Korea. E-mail: daegyoum@kaist.ac.kr
bAgency for Defense Development, Daejeon 34060, Republic of Korea
First published on 17th April 2025
Abstract
Under the strong pressure pulse induced by a shock wave, powders exhibit specific instability and dispersion patterns that develop into jets over time. We experimentally investigate how the physical properties of particles affect the dispersion of powders in both the compaction and subsequent expansion phases. Our investigation uses a laboratory-scale Hele–Shaw cell device and nano-energetic materials to generate the pressure pulse. Depending on the initial radius of the powder, distinct jetting patterns are initiated by instability in either the inner or outer boundary of the powder. The degree of particle cohesion also influences the instability, and its relationship with the morphology of the finger structure at the inner boundary is quantitatively assessed. The permeability of the powder, which depends on particle size, is another important factor determining the instability of the powder layer during the compaction phase and its inward flow in the expansion phase. Based on the experimental results, a scaling analysis is performed to identify the characteristic time scale of temporal changes in the outer boundary of the powder. The findings presented in this paper offer novel insights for improved predictions of shock-induced particle dispersion in industrial processes.
1 Introduction
Powders are highly susceptible to external forces due to the small size and mass of their constituent particles. This often results in pressure-induced flow, as observed in various natural phenomena.1–5 When subjected to a pressure pulse generated by a shock wave propagating radially from a central point, powders exhibit outward dispersion. Investigations into the high-speed dispersion characteristics of particles under shock-induced pressure have typically followed one of two primary experimental methods. The first method involves large-scale, open-field experiments using highly explosive materials. In these experiments, the jet formation process is identified conceptually, and several key aspects can be analyzed, including the jet structure, particle terminal velocity, and pressure mitigation effect induced by particles.6–11 This approach is a straightforward and reliable means of demonstrating the rapid dispersion of a substance, but has the disadvantage that processes involving explosives happen very fast and do not allow for accurate observation of the internal dispersion process, such as shock wave propagation in the early stage of dispersion. The use of explosives also requires a relatively large space.The second method, which allows for relatively accurate analysis at the laboratory scale, was devised to resolve the issues arising from the use of explosives. By simplifying the experimental conditions to be semi-two-dimensional with a transparent Hele–Shaw cell, particle clusters can be observed, enabling real-time measurements of the particles' behavior in the very early stage of dispersion. In this setup, pressure is usually applied using compressed gas,12–16 or generated by the detonation of hydrogen and oxygen to mimic the effect of explosives.17
To explain the cause of specific dispersion patterns, previous studies have employed some form of flow instability that occurs at the interface between two fluids with a density difference, such as the Rayleigh–Taylor instability or Richtmyer–Meshkov instability.18–21 This approach is preferable to particle-based methods because the instability observed in fluids resembles that observed in powder. In a dilute powder system, instability phenomena can be successfully explained using fluid dynamics approaches. However, recent studies have shown that the dispersion of powder, particularly dense ones, does not exhibit characteristics associated with fluid flow instabilities, and the application of traditional instability models has often yielded inconsistent results.7,15 To address this problem, several approaches have been explored with the aim of identifying the unique instabilities that arise in granular materials. Instead of relying on conventional instability models, a continuum theory based on shock tube experimental results has been used to analyze particle behaviors.22 Additionally, particle dynamics have been examined through highly detailed particle-based analyses within confined regions.23 The instability dynamics have also been investigated by employing a coarse-grained compressible computational fluid dynamics-discrete parcel method to capture the interactions between particles and a surrounding fluid.24,25
Previous studies have focused on explaining the specific jet formation processes12–15 and developing general models for the dispersion behavior of granular media.22,24–26 However, they have not fully incorporated potentially critical factors such as the intrinsic material properties of granular particles and the initial conditions of the system. Hence, the effects of such factors remain unclear. Although certain instability phenomena and patterns have been observed alongside dispersion, further analysis is required to understand the complex interactions between individual particles and shock waves, especially considering multiple variables. Many studies have relied on numerical simulations that simplify the dispersion scenarios to reduce computational load.27,28 Thus, there is a pressing need for foundational particle-based experimental research that comprehensively examines the intrinsic properties of powder and elucidates the granular instability mechanism.
This paper describes experiments focusing on three key variables: the initial radius, cohesion, and individual particle size of the powder. The aim is to determine how the dispersion characteristics of the powder are affected by these variables. A Hele–Shaw cell system is used along with nano-energetic materials (nEMs) as a pressure source to simulate explosive dispersion at the laboratory scale. For experiments involving cohesion as a variable, particles coated with nano-sized fumed silica are adopted, allowing the cohesion to be modified while maintaining other particle properties. To vary the particle size, the particles are sorted using standard sieves for a powder material with low cohesion. Qualitative and quantitative analyses regarding differences in dispersion patterns, with respect to the variables, reveal dispersion mechanisms that could not be easily identified in previous studies.
In Section 2, the fabrication process and characterization methods of the nEMs and powder are explained, and the experimental powder dispersion apparatus is described. Section 3.1 presents the characterization results of the prepared materials. The effects of three powder variables, namely the radius of the powder, cohesion, and particle size, on both the dispersion patterns and underlying dispersion mechanisms are examined in Sections 3.2–3.4. Section 3.5 explains a scaling analysis in which we generalize temporal changes in dispersion radius for different powder conditions. Finally, a summary of this study and suggestions for future research are provided in Section 4.
2 Experimental setup
2.1 Preparation of nEMs, flour, and silica sand
We conducted experiments in which nEMs were employed to induce pressure within a Hele–Shaw cell apparatus. These nEMs are composites consisting of a metal (fuel) and a metal oxide (oxidizer), and are characterized by high reactivity. For the fabrication of the nEMs in the present study, micro-sized aluminum powder, nano-sized copper oxide (CuO), and Viton B were used as the fuel, oxidizer, and binder, respectively. The characterization of the nEMs was performed using a scanning electron microscope (SEM). Detailed fabrication and characterization procedures were reported in our previous study.29Commercially available soft wheat flour was used to examine cohesion as a variable. Because of the broad range of particle sizes in this flour, it was necessary to limit the particle size to a specific value. For this purpose, a 75-μm sieve (ASTM no. 200) and a sieve shaker (Ro-Tap sieve shaker, JISCO Inc.) were employed. The particles filtered through the sieve served as the basic experimental flour. Nano-sized hydrophobic silica (K-T30, OCI Co., Ltd) was prepared for subsequent coating (0.2 wt%, 0.67 wt%, 1 wt%, 1.5 wt%) of the flour particles. An acoustic mixer (LabRAM II, Resodyn Acoustic Mixers, Inc.) was used for the physical mixing necessary in the coating process; the mixing conditions were 60 g with a mixing time of 3 min.
For the experiments involving silica sand, in which the particle size was considered as a variable, the sand was categorized into three main particle sizes based on the mesh table of ASTM standard sieves (Table 1). The smallest group consisted of particle diameters of 45–53 μm, the medium-sized particles measured 125–150 μm, and the largest ones ranged from 250–300 μm. Each powder was sieved for 30 min using the sieve shaker employed for flour preparation.
| Size (μm) | 300 | 250 | 212 | 180 | 150 | 125 | 106 | 90 | 75 | 63 | 53 | 45 |
| Mesh | 50 | 60 | 70 | 80 | 100 | 120 | 140 | 170 | 200 | 230 | 270 | 325 |
To examine the microstructure, composition, and size of the flour sample, a SEM-energy dispersive X-ray spectroscopy (SEM-EDX, Quanta 650 FEG, FEI Co.), a particle size analyzer (PSA, Mastersizer 3000, Malvern Panalytical, Ltd), and a morphological analyzer (Morphologi 4, Malvern Panalytical, Ltd) were employed. The flowability of the flour powder was characterized with a powder rheometer (FT4, Freemantechnology, Ltd).
2.2 Hele–Shaw cell apparatus and data analysis
A Hele–Shaw cell apparatus with the nEMs as the pressure-generating matter was constructed as shown in Fig. 1(a). The apparatus was mainly divided into three sections covering pressure generation, shock wave propagation, and material dispersion. The nEMs were placed in the pressure-generation section, with a tungsten-based heating wire positioned to instigate the reaction of the nEMs. The wire was heated using a DC power supply, with a voltage of 20 V and a current of 8 A applied to the heating coil. Shock-induced pressure was generated when the nEMs reacted under the heating of the coil. A small chamber made of steel (thickness: 10 mm) was designed for the pressure-generation section, and a closure was made with O-rings and flanges to prevent pressure leakage. The shock wave propagation section consisted of a tube with inner diameter 10 mm and length 250 mm. The pressure propagated upwards to the material dispersion section, which was made of black anodized aluminum. A donut-shaped region of powder was placed in this section, with an initial outer radius Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 ranging from 22.5–45 mm and an initial inner radius Rin
0 ranging from 22.5–45 mm and an initial inner radius Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 of 10 mm. To enable observation, a transparent acrylic plate of diameter 500 mm was mounted 4 mm above the material dispersion section.
0 of 10 mm. To enable observation, a transparent acrylic plate of diameter 500 mm was mounted 4 mm above the material dispersion section.
 | ||
| Fig. 1 (a) Hele–Shaw cell apparatus and (b) time-series of gauge pressure measured by five pressure sensors. | ||
A high-speed camera (Phantom V2640, Vision Research Inc.) was installed facing downwards at the transparent plate to capture the particle dispersion process at 0.1-ms intervals. Five pressure sensors (113B26, PCB Electronics Inc.) were attached to the tube and transparent plate to measure the pressure at corresponding positions [Fig. 1(a)]. The pressure data were acquired by a DAQ device (DEWE-2600, DEWETRON GmbH.). The pressure measurements from the five sensors are presented in Fig. 1(b). In our experiments, the amount of nano-energetic material was deliberately adjusted to achieve gauge pressures between approximately 50 kPa and 250 kPa. However, because the pressure was generated dynamically by the reaction, actual pressure varied to some extent among experimental trials. Nevertheless, the main phenomena presented in this study can be generalized for each experimental condition. The pressures in this range correspond to conditions that induce shock waves. After high pressure propagates to the material dispersion section and is applied to the compacted powder particles, the pressure gradually decreases as the inner particle region expands. Eventually, the pressure on the material dispersion section drops below atmospheric pressure, generating a rarefaction wave that moves towards the center.
Powder was first sieved to obtain a desired range of particle size. A guide plate with a height of 4.5 mm to produce an annular powder layer was placed on the lower plate of the Hele–Shaw cell apparatus and carefully aligned. In addition, a small inner ring that defines Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 was plugged to prevent powder accumulation at the center. Next, the sieved powder was evenly sprinkled over the annular region, and a leveling tool was used to level the powder so that it filled the space up to the height of the guide plate, 4.5 mm. Although the target filling height was 4 mm, a 0.5 mm buffer was provided to compensate for any slight underfilling. Once the powder was uniformly distributed, the guide plate was removed, and the upper plate of the Hele–Shaw cell apparatus was secured with screws to complete the setup.
0 was plugged to prevent powder accumulation at the center. Next, the sieved powder was evenly sprinkled over the annular region, and a leveling tool was used to level the powder so that it filled the space up to the height of the guide plate, 4.5 mm. Although the target filling height was 4 mm, a 0.5 mm buffer was provided to compensate for any slight underfilling. Once the powder was uniformly distributed, the guide plate was removed, and the upper plate of the Hele–Shaw cell apparatus was secured with screws to complete the setup.
Temporal changes in the outer and inner radii of the powder boundaries were estimated from the images captured by the high-speed camera. Typically, boundary extraction methods such as the Canny edge detector30 are used for this purpose. However, these methods were insufficient for accurate recognition of the internal and external dispersion of the powder under instability. Additionally, while the deep learning-based holistically-nested edge detection technique31 effectively detects changes in the outer diameter, it cannot successfully recognize irregular internal shapes of the powder. To address these boundary detection challenges, we employed a semi-automatic boundary extraction procedure using CVAT.32 Each frame of the high-speed video was annotated with OpenCV's intelligent scissors tool, which determines an optimal path around irregular shapes based on local image gradients and a cost function.33 This semi-automatic boundary extraction method has been widely used in the image segmentation field,34–36 which offers a reliable balance between automated processing and human supervision for complex image analysis. This procedure yielded polygonal outlines of irregular internal shapes, ensuring consistent and reliable detection of their boundaries across different experimental trials.
3 Results and discussion
3.1 Characterization results of powder
SEM and EDX were used to analyze whether the hydrophobic nano silica particles were effectively coated on the surface of the flour. The SEM image in Fig. 2 demonstrates that the surface of the flour powder particles was indeed coated with the silica particles, and the EDX analysis confirms the presence of silicon across the entire area. Thus, the powder prepared by the acoustic mixer was uniformly coated with the silica particles.From the PSA data, the particle size distribution and volume-based median particle size (D50) were obtained. As shown in Fig. 3, the median particle sizes of the flour samples do not differ significantly between the silica-coated and uncoated samples, both having D50 in the range 27–30 μm. Moreover, the silica sand samples are clearly categorized into three groups of particle sizes under the use of specific sieves.
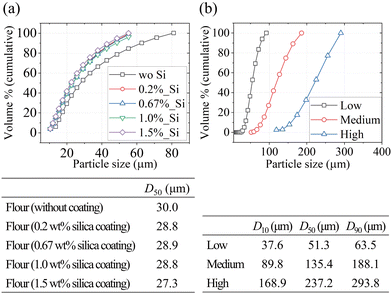 | ||
| Fig. 3 Particle size distribution and median particle size (D50) of (a) flour samples and (b) silica sand samples. | ||
The cohesion of the powder samples was evaluated by measuring a flow function coefficient (FFC) with a powder rheometer (FT4, Freeman technology, Ltd) (Table 2). An FFC value greater than 10 signifies high flowability, whereas a value less than 2 signifies that the powder is cohesive.37 According to this categorization, both the non-coated and 0.2 wt% coated flour samples exhibit cohesive behavior. As the amount of coating material increases, the flowability improves, with the FFC value eventually reaching a plateau; this trend has previously been observed in pharmaceutical research.38 As a dimensionless parameter for cohesion, we consider the Bond number Bog, which is defined as the ratio of the sample's cohesive force to its weight. This parameter has been widely used to assess cohesion in studies of granular materials.39–41 The Bond number was estimated from the measured FFC (Table 2) using the fitting equation proposed by Siliveru et al.:42
| FFC = α(Bog)−β (α: 53.7, β: 0.4) | (1) |
| Sample | FFC | Estimated Bog |
|---|---|---|
| Flour (without coating) | 2 | 3910 |
| Flour (0.2 wt% silica coating) | 3 | 1180 |
| Flour (0.67 wt% silica coating) | 6 | 178 |
| Flour (1.0 wt% silica coating) | 14 | 31 |
| Flour (1.5 wt% silica coating) | 11 | 54 |
Additionally, the flowability of silica sand with medium fraction (D50 = 135 μm) was measured, yielding an FFC value of 119. which is far above the threshold value of 10 to indicate good flowability. This result confirms that the silica sand used in our experiments exhibits excellent flow characteristics.
Previous studies showed that improving particle sphericity could reduce inter-grain friction and interlocking, producing more homogeneous velocity fields under divergent loadings.43,44 In our study, however, nano-scale silica coating minimally affects particle shape, so changes in flow dynamics by silica coating are primarily due to cohesion rather than sphericity or friction. To quantitatively evaluate the effect of the coating on particle sphericity, we measured HS (high sensitivity) circularity for flour and coated flour samples. HS circularity is defined as the ratio of the circumference of a perfect circle having the same projected area to the actual perimeter of the particle and was determined using a morphological analyzer. Our measurements yielded mean values of 0.78, 0.75, and 0.70 for uncoated, 1 wt% coated, and 1.5 wt% coated flours, respectively, indicating that the nano-scale coating leads only to a minor decrease in HS circularity instead of significantly affecting overall particle sphericity.
3.2 Dispersion patterns by radius ratio
The dispersion type or characteristics of powder vary according to its overall size or amount. The initial outer radius Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 determines the overall size directly related to the total mass of the sample, while the initial inner radius Rin
0 determines the overall size directly related to the total mass of the sample, while the initial inner radius Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 is set to create a central void that enables pressure loading on the powder ring from the center and resultant instability at the inner boundary of the power. Accordingly, the radius ratio R* = Rout
0 is set to create a central void that enables pressure loading on the powder ring from the center and resultant instability at the inner boundary of the power. Accordingly, the radius ratio R* = Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0/Rin
0/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 indicates the degree of resistance or inertial effect experienced when pressure is applied from the central void. In our study, R* is 2.25, 3.0, and 4.5. Sequential snapshots of dispersion are shown in Fig. 4 under the different R* conditions with respect to dimensionless time t*. Here, t* is the ratio of physical time to the time at which a rarefaction wave starts to propagate (tshock). The rarefaction wave is first observed when high-speed imaging captures the initial disruption (fracturing) of the compacted powder layer at its outer boundary. This visible disruption serves as a clear indicator of the transition from compaction (densification under shock loading) to expansion (dilation with increased volume and decreased density) of the bulk powder, providing a more direct physical reference than the pressure sensor readings taken further inside. The dimensionless pressure p* represents the ratio of the maximum gauge pressure pmax, measured at pressure sensor #5 [Fig. 1(a)], to the reference atmospheric pressure. The dimensionless variables are expressed as
0 indicates the degree of resistance or inertial effect experienced when pressure is applied from the central void. In our study, R* is 2.25, 3.0, and 4.5. Sequential snapshots of dispersion are shown in Fig. 4 under the different R* conditions with respect to dimensionless time t*. Here, t* is the ratio of physical time to the time at which a rarefaction wave starts to propagate (tshock). The rarefaction wave is first observed when high-speed imaging captures the initial disruption (fracturing) of the compacted powder layer at its outer boundary. This visible disruption serves as a clear indicator of the transition from compaction (densification under shock loading) to expansion (dilation with increased volume and decreased density) of the bulk powder, providing a more direct physical reference than the pressure sensor readings taken further inside. The dimensionless pressure p* represents the ratio of the maximum gauge pressure pmax, measured at pressure sensor #5 [Fig. 1(a)], to the reference atmospheric pressure. The dimensionless variables are expressed as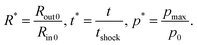 | (2) |
 | ||
| Fig. 4 Sequential snapshots of powder dispersion for flour with R* = 2.25, 3.0, and 4.5; see ESI.† Only one quarter of the powder is presented to clearly show the details of morphology. | ||
In addition to these dimensionless variables, the packing fraction ϕp, which is defined as the ratio of the bulk density to the particle density, is evaluated at the initial state to represent how densely the powder is initially loaded.
In Fig. 4, three distinct dispersion patterns of the powder can be observed. To distinguish the difference in the three patterns, the schematics of powder dispersion with respect to time, corresponding to Fig. 4, are illustrated in Fig. 5; the arrows in this figure represent the jet directions. For R* = 2.25, instability first occurs at the inner boundary of the powder because of the inhomogeneous distribution of particles. This instability causes variations in the pressure difference (Δp) between the inner and outer boundaries of the compacted powder layer. These variations emerge along the circumferential direction of the inner boundary due to different radial distances of points on the inner boundary from the center. Furthermore, uneven radial distances between the inner and outer boundaries of the powder result in the particles having different radial accelerations along the circumferential direction, exacerbating the existing Δp and strengthening the instability. In addition to the variations in Δp along the circumferential direction, a rarefaction wave can further amplify heterogeneities in local velocity within force chains, thereby intensifying the instability, according to Xue et al.25
 | ||
| Fig. 5 Simplified schematics of three particle dispersion types for different R* conditions: (a) R* = 2.25, (b) R* = 3.0, and (c) R* = 4.5. | ||
The instability does not develop into distinct fingers, which are typically observed as intermediate structures for R* = 3.0. Instead, the instability directly develops into outward-facing jets from the inner boundary, depicted as the arrows in Fig. 5(a-i). These jets sequentially affect the outer boundary of particles, and the jetting pattern of the inner boundary quickly turns into the pattern of the entire region in the rarefaction wave phase (t* > 1.0). During this stage, the compacted layer no longer maintains its geometry because the rarefaction wave disrupts its integrity, allowing localized penetration of the outward jets from the inner boundary. This phenomenon is driven by circumferential variations in Δp [Fig. 5(a-ii)].
When R* = 3.0, distinct jets are generated from the unstable inner boundary of the layer. Particles near the inner boundary form discrete inner fingers in the radial direction, and a significantly compacted layer appears between adjacent figures [Fig. 5(b-i)]. Thereafter, the rarefaction wave causes the compacted layer to lose its compaction, and the outer boundary continues to grow while the inner boundary becomes stationary. The compacted layer structure is eventually disrupted. However, the fingers, which do not belong to the compacted layer, are less affected by the rarefaction wave. Thus, the fingers maintain their outward momentum and eventually penetrate the compacted layer, as depicted in Fig. 5(b-ii), forming the outward jets of the inner boundary. These jets become prevalent in the entire powder domain, and similar patterns can be observed at the outer boundary. Chestnut burr-like patterns finally appear [Fig. 5(b-iii)].
In the case of R* = 4.5, the dispersion pattern differs from those of R* = 2.25 and 3.0. The relatively thick samples (i.e., greater R*) mean that the initial instability leads to the formation of negligible inner fingers [Fig. 5(c-i)]. The thick compacted layer reduces the pressure differences along the inner boundary, despite the presence of the initial instability. Consequently, outward jets do not develop at the inner boundary. Instead, outward jets occur at the outer boundary; these are relatively small, regular in shape, and form in large numbers, in contrast to the jets at the inner boundary for R* = 2.25 and 3.0 [Fig. 5(c-ii)]. Furthermore, the increase in the total mass of powder in the large-R* condition yields a lower dispersion velocity, causing the dispersion process to terminate with the powder occupying a relatively small area within the Hele–Shaw cell, instead of fully spreading out. These observations are consistent with the recent findings of Miao et al.,45 which indicate that the case of large R* often exhibits subdued instabilities at the inner boundary but more complex patterns along the outer boundary, highlighting how R* can redistribute the dominant instability modes.
After qualitatively identifying the differences in dispersion patterns, we now analyze the temporal changes in the dimensionless outer radius Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and inner radius Rin/Rin
0 and inner radius Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 of the powder over dimensionless time t* (Fig. 6); the subscript 0 indicates a value at t* = 0. The inner and outer radii were determined by measuring the distance from the center to the inner and outer boundaries of the powder in an image, and then averaged along the circumference to obtain a representative value at each time frame. Rout/Rout
0 of the powder over dimensionless time t* (Fig. 6); the subscript 0 indicates a value at t* = 0. The inner and outer radii were determined by measuring the distance from the center to the inner and outer boundaries of the powder in an image, and then averaged along the circumference to obtain a representative value at each time frame. Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 increases monotonically for all cases, but the rate of increase differs by a factor of 5 between the smallest and largest values of R*.
0 increases monotonically for all cases, but the rate of increase differs by a factor of 5 between the smallest and largest values of R*.
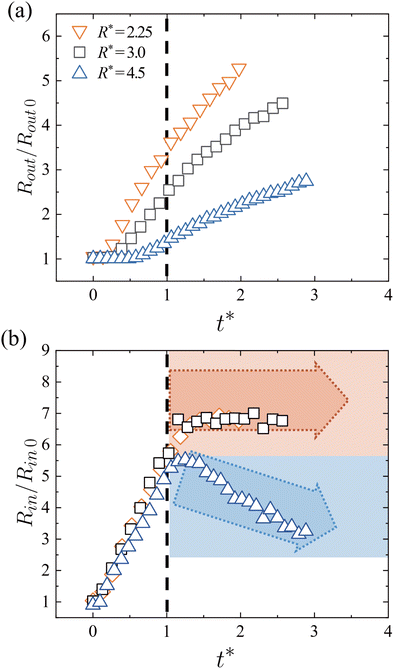 | ||
Fig. 6 Time histories of (a) powder outer radius Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and (b) powder inner radius Rin/Rin 0 and (b) powder inner radius Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 for different R* conditions. 0 for different R* conditions. | ||
In contrast, Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 exhibits a similar rate of increase up to t* = 1.0, regardless of the total mass or radius of the powder region. Before t* = 1.0, the compaction of the particles is dominated by a shock wave from the center; note that t* = 1.0 is equivalent to t=tshock, the time at which the rarefaction wave starts following the shock wave. For t* < 1.0, the particles are displaced by a similar amount after they are exposed to the shock wave at the inner boundary of the powder, resulting in similar Rin/Rin
0 exhibits a similar rate of increase up to t* = 1.0, regardless of the total mass or radius of the powder region. Before t* = 1.0, the compaction of the particles is dominated by a shock wave from the center; note that t* = 1.0 is equivalent to t=tshock, the time at which the rarefaction wave starts following the shock wave. For t* < 1.0, the particles are displaced by a similar amount after they are exposed to the shock wave at the inner boundary of the powder, resulting in similar Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 values despite the steep growth in Rin/Rin
0 values despite the steep growth in Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 from 1.0 at t* = 0 to 4.0–6.0 at t* = 1.0. However, after t* > 1.0, the behavior of Rin/Rin
0 from 1.0 at t* = 0 to 4.0–6.0 at t* = 1.0. However, after t* > 1.0, the behavior of Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 depends on R*. For R* = 2.25 and 3.0, the expansion of the inner boundary ceases, leading to a stationary boundary profile. For R* = 4.5, the inner boundary exhibits an inward flow towards the center (local movement of fluid and particles toward the center), indicating a center-directed motion driven by the rarefaction wave. With the higher mass, the displacement of the inner boundary up to t* = 1.0 remains relatively small. Thus, the influence of negative pressure propagating towards the center during t* > 1.0 is amplified, producing a notable decline in Rin/Rin
0 depends on R*. For R* = 2.25 and 3.0, the expansion of the inner boundary ceases, leading to a stationary boundary profile. For R* = 4.5, the inner boundary exhibits an inward flow towards the center (local movement of fluid and particles toward the center), indicating a center-directed motion driven by the rarefaction wave. With the higher mass, the displacement of the inner boundary up to t* = 1.0 remains relatively small. Thus, the influence of negative pressure propagating towards the center during t* > 1.0 is amplified, producing a notable decline in Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. To find a dimensionless parameter that better describes the trends of the outer radius, a scaling analysis that accounts for the effects of the input conditions on the force balance of the particles is necessary; this is discussed in Section 3.5.
0. To find a dimensionless parameter that better describes the trends of the outer radius, a scaling analysis that accounts for the effects of the input conditions on the force balance of the particles is necessary; this is discussed in Section 3.5.
3.3 Dispersion patterns by cohesion
We now explore the dispersion patterns produced at various levels of cohesion, one of the major properties of powder. Three distinct dispersion patterns can be identified in uncoated and coated flours for R* = 3.0 (Fig. 7; see Table 2 for details of the flours and Bond number Bog). For R* = 2.25 and 4.5, the fingers at the inner boundary of the powder do not form or are very weak, as discussed in the previous section. Because changes in cohesion primarily affect the characteristics of the fingers, the results for these two R* conditions are not considered in this section. | ||
| Fig. 7 Sequential snapshots of powder dispersion for flour with Bog = 3910, 1180, 178, and 54 (R* = 3.0); see ESI.† | ||
In Fig. 7, the condition of Bog = 3910 is equivalent to R* = 3.0 in Fig. 4. Fingers are initially generated by the instability at the inner boundary. As a rarefaction wave propagates, these fingers evolve into outward jets (movement of jets away from the center), influencing the outer boundary of the powder and resulting in the formation of chestnut burr-like patterns. The conditions of Bog = 1180 and 178 under the same R* = 3.0 exhibit weaker finger formation at the inner boundary than Bog = 3910, and Bog = 178 demonstrates a more stable dispersion pattern than Bog = 1180. This result is because of the mechanism similar to Saffman–Taylor instability, in which cohesion provides a viscosity-like effect; as Bog becomes smaller, cohesive forces decrease, and the instability at the inner boundary is mitigated. Consequently, after t* = 1.0, the instability at the inner boundary under low Bog conditions is too weak to influence the outer boundary, yielding a more circular dispersion pattern of the outer boundary compared to Bog = 3910.
In contrast to the previous conditions, the dispersion pattern is irregular for Bog = 54. Although distinct fingers are formed, their morphology differs from that of Bog = 3910, where the fingers are uniformly distributed along the circumferential direction and their shapes are consistently rectangular. For Bog = 54, the arrangement of the fingers becomes irregular in the circumferential direction, and their shapes and sizes vary significantly. Moreover, powder at the inner boundary tends to flow towards the center due to the rarefaction wave, disrupting the boundary of the compacted powder layer and filling the inner blank area of the powder.
The temporal changes in the powder outer radius Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 for all Bog values are similar before the formation of the rarefaction wave at t* = 1.0 (Fig. 8). However, after t* = 1.0, the rate of increase in Rout/Rout
0 for all Bog values are similar before the formation of the rarefaction wave at t* = 1.0 (Fig. 8). However, after t* = 1.0, the rate of increase in Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 depends on Bog. For the low-Bog condition, the outward propagation speed of particles at the outer boundary gradually decreases over time because the outward particle momentum is hindered by the inner flow towards the center. The powder inner radius Rin/Rin
0 depends on Bog. For the low-Bog condition, the outward propagation speed of particles at the outer boundary gradually decreases over time because the outward particle momentum is hindered by the inner flow towards the center. The powder inner radius Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 shows more pronounced variations in the rarefaction wave phase. With Bog = 3910, the inner radius remains almost constant over time, whereas the inner radius decreases over time with the lower values of Bog due to the strong inner flow towards the center. The inward movement of the inner boundary (Rin/Rin
0 shows more pronounced variations in the rarefaction wave phase. With Bog = 3910, the inner radius remains almost constant over time, whereas the inner radius decreases over time with the lower values of Bog due to the strong inner flow towards the center. The inward movement of the inner boundary (Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) does not follow a strictly monotonic trend with respect to Bog at a certain time after t* = 1.0. When cohesion becomes weaker (when Bog decreases from 3910), negative pressure by the rarefaction wave can temporarily overcome the cohesive forces, driving the powder towards the center and producing a notable inward shift of the inner boundary and smaller Rin/Rin
0) does not follow a strictly monotonic trend with respect to Bog at a certain time after t* = 1.0. When cohesion becomes weaker (when Bog decreases from 3910), negative pressure by the rarefaction wave can temporarily overcome the cohesive forces, driving the powder towards the center and producing a notable inward shift of the inner boundary and smaller Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. However, under conditions of significantly weaker cohesion (Bog = 54 and 31), surface roughness and instability effects become more pronounced at the inner boundary, which eventually disrupt the inward flow. The overall inward movement of the powder is attenuated or masked by the development of strong instability patterns, having the greater Rin/Rin
0. However, under conditions of significantly weaker cohesion (Bog = 54 and 31), surface roughness and instability effects become more pronounced at the inner boundary, which eventually disrupt the inward flow. The overall inward movement of the powder is attenuated or masked by the development of strong instability patterns, having the greater Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 than Bog = 178.
0 than Bog = 178.
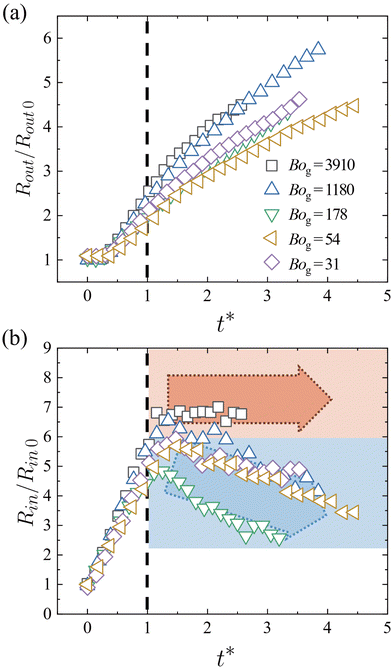 | ||
Fig. 8 Time histories of (a) powder outer radius Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and (b) powder inner radius Rin/Rin 0 and (b) powder inner radius Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 for different Bog conditions (R* = 3.0). 0 for different Bog conditions (R* = 3.0). | ||
The schematics in Fig. 9 distinguish the initial types of fingers between the high Bog of 3910 and low Bog of 54. Fingers form at the inner boundary in both conditions, but the causes of finger formation are different. For the high Bog, certain pores are formed among grouped particles due to agglomeration. As the particles begin to disperse under pressure, the pressure difference Δp between the inner and outer boundaries varies along the circumferential direction of the inner boundary, depending on the level of agglomeration, and fingers eventually form with relatively regular intervals and shapes.46,47 However, under the low-Bog condition, the influence of gravity is relatively strong because of the reduced cohesive forces, and finger formation originates from the irregular initial arrangement of particles under gravity. In the initial particle configuration, weak cohesive forces allow gravity to disturb the powder layer. This creates a bumpy surface and results in increased surface roughness within the powder layer, as exemplified within the red circle in Fig. 9.
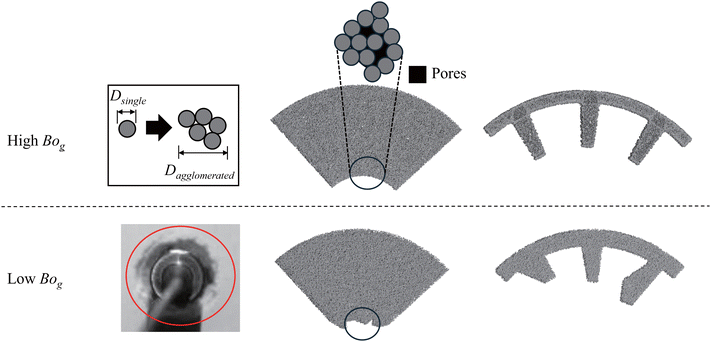 | ||
| Fig. 9 Simplified schematics illustrating differences in finger morphology at the inner boundary between high- and low-Bog conditions. | ||
To quantify the geometry of the fingers, we define the intensity κ, complexity ξ, and area difference ψ:
 | (3) |
The time frame for the quantification of these parameters is set at t* = 1.0 for each condition. Based on the parameters described in Fig. 10(a), the intensity κ is the ratio between the average length of the fingers, 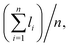 and the average thickness of the compacted powder layer, havg. Complexity ξ represents the ratio of the total complexity of polygons forming the fingers and the total number of the fingers, n. Complexity is determined by first approximating each finger as a polygon via the boundary extraction procedure; see Fig. 17 in Appendix for a sample image of the extracted finger polygons. Here, complexityi denotes the number of vertices in the i-th polygon (finger), such that higher vertex counts indicate more intricate and irregular shapes. Averaging these values over all n fingers provides a quantitative measure of the overall irregularity of the inner boundary.
and the average thickness of the compacted powder layer, havg. Complexity ξ represents the ratio of the total complexity of polygons forming the fingers and the total number of the fingers, n. Complexity is determined by first approximating each finger as a polygon via the boundary extraction procedure; see Fig. 17 in Appendix for a sample image of the extracted finger polygons. Here, complexityi denotes the number of vertices in the i-th polygon (finger), such that higher vertex counts indicate more intricate and irregular shapes. Averaging these values over all n fingers provides a quantitative measure of the overall irregularity of the inner boundary.
 | ||
| Fig. 10 (a) Definitions of l, h, complexityi, and Ai in eqn (3). (b) Intensity κ, (c) complexity ξ, (d) area difference ψ for different Bog conditions. The error bars indicate the standard deviation. | ||
Similarly, ψ represents relative area difference, 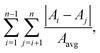 averaged over all pairs of the fingers,
averaged over all pairs of the fingers,  . According to Fig. 10(b)–(d), the highest Bog (= 3910) exhibits the highest mean intensity κ, which is correlated with strong finger formation. The lowest values of Bog (= 31, 54) produce the highest mean values for complexity ξ and area difference ψ, which correspond to irregular finger shapes.
. According to Fig. 10(b)–(d), the highest Bog (= 3910) exhibits the highest mean intensity κ, which is correlated with strong finger formation. The lowest values of Bog (= 31, 54) produce the highest mean values for complexity ξ and area difference ψ, which correspond to irregular finger shapes.
We next examine the fundamental reasons for the variations in finger shapes and their contribution to the overall dispersion characteristics in each condition. The powder properties are quantified in terms of the agglomeration ratio AR and roughness CV (Fig. 11), defined as
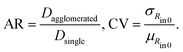 | (4) |
Here, AR is an experimentally quantified measure of the extent to which the particles agglomerate, and its definition is taken from a previous study.38 To obtain AR, the diameters of agglomerated and single particles should be measured; Dagglomerated and Dsingle are depicted in Fig. 9. To measure a single particle diameter, laser diffraction analysis was performed (Fig. 3). Because laser diffraction cannot be applied to agglomerated particles, an optical-based device, BeVision D2 (Bettersize Instrument Ltd), was used to capture each agglomerated particle freely falling under gravity. Although the powder was sieved at 75 μm, the particle size was distributed in a certain range, causing some variations in both single-particle and agglomerate measurements. CV represents the degree of powder surface irregularity, and its definition is adopted from an earlier study.41 The inner radii of the powder in all radial directions were extracted from an image of the initial state, as explained in Section 2.2. The standard deviation of the inner radii, σRin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, was then divided by the average of the inner radii, μRin
0, was then divided by the average of the inner radii, μRin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, to obtain CV.
0, to obtain CV.
The agglomeration ratio AR and roughness CV are plotted with respect to Bog in Fig. 11. With increasing Bog, AR tends to increase while CV tends to decrease. These opposite trends indicate that distinct patterns are formed when Bog is either low or high. However, the shapes of these patterns differ between the two extreme values of Bog (see the upper images in Fig. 11). A high value of AR leads to the formation of intensive and regular fingers, while a high value of CV indicates that the fingers have an enhanced degree of irregularity. Under moderate values of Bog, both CV and AR are relatively low, reducing the strength of the fingers. Thus, the outward jets at the inner boundary, which evolve from the fingers, are weak and do not distinctly impact the overall pattern, as depicted in Fig. 7.
3.4 Dispersion patterns by particle size
To investigate how particle size affects the dispersion pattern, silica sand is selected to minimize the interference of cohesion on the results. Three different particle size distributions, characterized by D50 (as described in Section 2.1), is considered. The low cohesion of the silica sand prevents the powder from maintaining its original vertical boundaries, leading to collapse in the initial state. With a relatively small initial powder radius, this collapse becomes more prominent, making it difficult to determine the boundaries accurately; thus, the condition of R* = 2.25 is not considered in this section. Fig. 12 shows the differences in the dispersion patterns between the lowest and highest D50 cases for R* = 3.0. For the lowest D50 (= 51 μm), the initial instability leads to the formation of weak fingers at the inner boundary, indicating the weak individual strength of the instability. After t* = 1.0, the fingers generate small outward jets at the inner boundary, but the inner boundary eventually stagnates due to a reversal in the pressure direction. These outward jets do not dominate the patterns of the outer boundary, resulting in distinguishable dispersion patterns between the inner and outer boundaries. For D50 = 237 μm, the dispersion pattern is markedly different. The fingers at the inner boundary, which are typically observed for R* = 3.0, are largely absent, and the outward jets at the inner boundary do not form. Additionally, even after the pressure reversal at t* = 1.0, the compacted particle cluster retains its initial momentum and continues to disperse outwards. For the condition of R* = 4.5 (not shown in Fig. 12), unstable patterns barely form in the inner region, regardless of particle size. Following the propagation of the rarefaction wave, flow towards the center is observed along the inner boundary.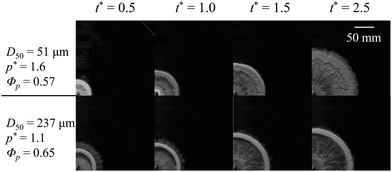 | ||
| Fig. 12 Sequential snapshots of powder dispersion for silica sand with D50 = 51 and 237 μm (R* = 3.0); see ESI.† | ||
Regarding the temporal changes in the powder outer radius Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, the rate of increase for R* = 4.5 is much lower than for R* = 3.0 [Fig. 13(a)]. This is consistent with the behavior of flour in Fig. 6(a), despite the different degrees of cohesion. The trend of Rout/Rout
0, the rate of increase for R* = 4.5 is much lower than for R* = 3.0 [Fig. 13(a)]. This is consistent with the behavior of flour in Fig. 6(a), despite the different degrees of cohesion. The trend of Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 does not show significant differences across the three D50 conditions. The effects of particle size are more pronounced for the powder inner radius Rin/Rin
0 does not show significant differences across the three D50 conditions. The effects of particle size are more pronounced for the powder inner radius Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. For R* = 3.0, although Rin/Rin
0. For R* = 3.0, although Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 increases monotonically, its rate of change becomes greater at higher values of D50 after the formation of a rarefaction wave [Fig. 13(b)]. Under R* = 4.5, the inner boundary stagnates due to the influence of the rarefaction wave just after t* = 1.0. Thereafter, flow towards the center gradually develops on the inner boundary.
0 increases monotonically, its rate of change becomes greater at higher values of D50 after the formation of a rarefaction wave [Fig. 13(b)]. Under R* = 4.5, the inner boundary stagnates due to the influence of the rarefaction wave just after t* = 1.0. Thereafter, flow towards the center gradually develops on the inner boundary.
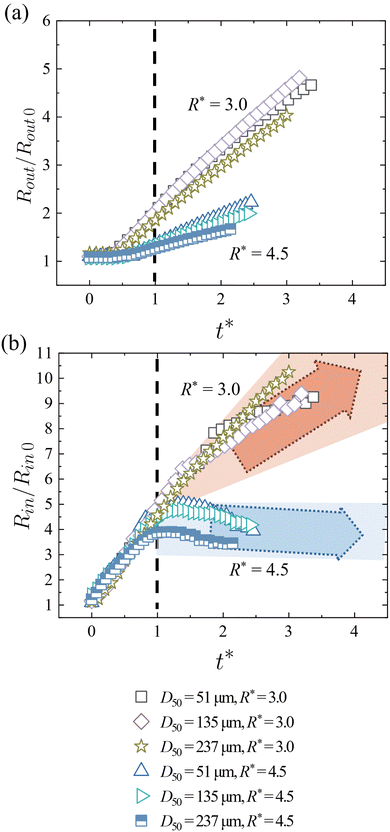 | ||
Fig. 13 Time histories of (a) powder outer radius Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and (b) powder inner radius Rin/Rin 0 and (b) powder inner radius Rin/Rin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 for different D50 conditions of silica sand (R* = 3.0 and 4.5). 0 for different D50 conditions of silica sand (R* = 3.0 and 4.5). | ||
The underlying mechanisms for the sensitivity of the inner boundary pattern to the particle size are detailed in Fig. 14, which corresponds to R* = 3.0. In this figure, the dashed red arrows indicate the direction and amount of gas infiltration, while the solid arrows represent the direction of dispersion. Initially, the particles of the low-D50 condition occupy the space densely, having a greater number of small voids, while the particles of the high-D50 condition create larger and more interconnected voids. When pressure is applied to disperse the particles, a substantial force acts on the particles, leading to similar dispersion behavior for both the low- and high-D50 conditions because of the high degree of compaction. However, during the transition to a rarefaction wave, the high-D50 particles tend to maintain the compacted powder layer, with their larger voids allowing smoother gas flow. In contrast, the low-D50 particles create significant flow resistance, which limits gas movement between particles. This restricted gas flow reduces the rate of expansion of the inner boundary under the influence of the inward-propagating rarefaction wave, while facilitating outward particle dispersion from the outer boundary. These different responses in the two boundaries gradually loosen the compacted layer, ultimately leading to the breakdown of its compressed structure. A similar phenomenon occurs when R* = 4.5. In this case, gas permeability is reduced by the larger powder radius, and the inner boundary is influenced by the rarefaction wave for all particle sizes.
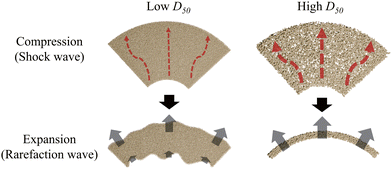 | ||
| Fig. 14 Simplified schematics illustrating the effects of particle size on powder permeability between low- and high-D50 conditions (R* = 3.0). | ||
The abovementioned phenomenon is related to the permeability of the voids. The permeability across the powder is obtained from the Kozeny–Karman equation:48
 | (5) |
 | (6) |
The permeability of the larger particle size is notably greater. This increase in permeability creates additional pathways for gas to permeate through the powder. As a result, Δp between the inner and outer boundaries decreases, reducing the influence of pressure on the particles. That is, the change in permeability associated with particle size is a critical factor in determining the interaction with the gas during the dispersion process. Miao et al.45 also discussed how variations in particle diameter influence compacted powder dispersal through interstitial gas infiltration. In line with the previous study, our Kozeny–Karman approach [eqn (5)] shows that the increase in D50 enlarges gas pathways and modifies local pressure distributions, providing a complementary perspective on how particle size affects the behavior of the compacted powder. In addition to the permeability-based mechanism, we recognize that gravity and friction become more influential as particle diameter increases. Since particles move considerably during dispersion, inertia also affects the dynamics in large-particle cases. In this work, we focused on the Kozeny–Karman approach to simply highlight the influence of permeability, but the roles of gravity, friction, and inertia should be examined in future studies, particularly for large particles.
3.5 Scaling analysis for powder outer boundary
The specific time tshock defined in eqn (2) represents the instant at which significant changes in particle dynamics begin to occur, marking the transition from compaction to expansion of the bulk powder; this time can be obtained from experiments. The changes in the outer and inner radii with respect to the dimensionless time t* = t/tshock do not exhibit consistent trends across different conditions, indicating that t* does not sufficiently characterize the dispersion process (Fig. 6, 8 and 13). In this section, to establish a universal dimensionless time that accounts for properties such as the initial powder radius, particle density, and applied pressure, a simple scaling analysis is performed for the outer boundary Rout of the powder. Note that only the outer boundary is considered because the inner boundary undergoes complicated interactions, including the formation of fingers, jets, and inward flow. The initial instability at the inner boundary eventually affects the outer boundary, and Rout predominantly dictates the degree of large-scale powder dispersion, which mean the governing influence of Rout on the overall dispersion performance.In previous shock tube experiments,49–55 scaling analysis was conducted for a vertically falling particle curtain dispersed by a shock wave. Given that powder dispersion induced by a shock wave in a Hele–Shaw cell resembles that in a shock tube, the pressure-based scaling relationship proposed for the shock tube51 is adopted because of its relevance to the pressure measurements in our experiments. This relationship is then modified to account for the radial conditions specific to the Hele–Shaw cell experiments. Accordingly, a simplified force balance equation for our model can be written as
 | (7) |
Here, pmax is the maximum pressure, which is identical to the variable used in eqn (2), h is the height of the powder, ϕp is the volume fraction, and ρp is the particle density. The area of the inner boundary, where the applied pressure is distributed, is incorporated in the left-hand side of the equation. The dynamic behavior of the powder is described in terms of its mass and the acceleration of the outer radius. When eqn (7) is reformulated into the dimensionless form of d2(Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0)/d(t/τt)2 = 2, the dimensionless time is expressed as
0)/d(t/τt)2 = 2, the dimensionless time is expressed as
 | (8) |
Here, τt is the theoretical characteristic time derived from the simplified force balance.
If eqn (8) is used without modification, temporal changes in Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 with respect to t/τt exhibit inconsistent results, similar to those observed with t/tshock in the previous sections. This is primarily due to variations in the mass or radius of the powder bed. While eqn (7) accounts for the balance of the dominant forces acting on particles, the different configurations between the shock tube and Hele–Shaw cell experiments lead to divergent outcomes in the trends of Rout/Rout
0 with respect to t/τt exhibit inconsistent results, similar to those observed with t/tshock in the previous sections. This is primarily due to variations in the mass or radius of the powder bed. While eqn (7) accounts for the balance of the dominant forces acting on particles, the different configurations between the shock tube and Hele–Shaw cell experiments lead to divergent outcomes in the trends of Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. In shock tube experiments,51 particles can initially form a dense configuration, but a compaction phase does not occur because the domain is not confined by external forces. Thus, particles at the outer boundary move immediately as the shock wave propagates through the particle bed. Furthermore, because the shock tube has a constant cross-sectional area along the propagation direction, the variations in pressure applied on the surface area of the particle bend are negligible.
0. In shock tube experiments,51 particles can initially form a dense configuration, but a compaction phase does not occur because the domain is not confined by external forces. Thus, particles at the outer boundary move immediately as the shock wave propagates through the particle bed. Furthermore, because the shock tube has a constant cross-sectional area along the propagation direction, the variations in pressure applied on the surface area of the particle bend are negligible.
By contrast, in our Hele–Shaw cell experiments, particles can be in a compacted phase. Therefore, changes in the outer boundary do not occur immediately upon the imposition of pressure. Instead, the particles undergo a compaction phase in which only the inner boundary changes, while the particles near the outer boundary remain almost stationary. Once the maximum compaction condition is achieved, the pressure affects the outer particles, causing them to disperse outwards [Fig. 15]. As a shock wave propagates outwards, its strength decreases radially with increasing distance from the center and weakens due to energy dissipation caused by interactions with the particles. Energy dissipation in this type of powder system is primarily driven by particle collisions, frictional sliding, and plastic deformation at contact points during compaction.56,57 In addition, as gas penetrates through the porous medium, the pressure decreases significantly due to the infiltrating gas absorbing energy.58 As the initial outer radius of the powder becomes larger, these effects create a greater attenuation of pressure while passing through the powder, leading to a lower pressure at the outer boundary (t1 frame in Fig. 15). Consequently, the degree of outward dispersion (i.e., the outward displacement of the outer boundary, δb) becomes weaker (t2 frame in Fig. 15).
 | ||
| Fig. 15 Schematics comparing the compaction and expansion of powder between low- and high-R* conditions. | ||
Under the processes described above, the instant at which the outer boundary begins to expand depends on R*. To reflect this dependency in eqn (8), a decay factor proportional to 1/(R*)2 is introduced into the pressure term [eqn (9)]. The decay factor accounts for the radial expansion-induced energy dissipation and pressure attenuation. Because our experiments were conducted in a quasi-two-dimensional environment, a term proportional to the square of the radial distance (R*)2 is considered for the decay factor. With this correction, a new dimensionless time ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) (= t/τm) is defined as follows:
(= t/τm) is defined as follows:
 | (9) |
Compared with t*(= t/tshock) in previous sections, the curves of Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 exhibit consistent trends versus
0 exhibit consistent trends versus ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) across all experimental conditions considered in this study (Fig. 16). In addition to the plot with respect to
across all experimental conditions considered in this study (Fig. 16). In addition to the plot with respect to ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) in Fig. 16(b), the plot with respect to t/τt from eqn (8) is also presented in Fig. 16(a). In Fig. 16(a), an increase in R* leads to a reduction in the slope of the scaled data, suggesting that the radial expansion and associated energy dissipation are not fully captured by eqn (8); for example, under the conditions of Bog = 3910, the slope becomes notably smaller as R* increases from 2.25 to 4.5. By contrast, Fig. 16(b) reveals improved collapse across different R* values, emphasizing the importance of including R* for time scaling. Some discrepancies, which appear in the later phase, are likely due to factors such as cohesion and particle size. These factors are not included in the current scaling analysis because they are difficult to apply directly to the above force balance equation. Nevertheless, the discrepancies do not significantly affect the overall consistency. In particular, conditions with the same material properties but varying R* exhibit more consistent trends. Incorporating the factors identified as potential sources of these discrepancies to improve the scaling relationship remains a subject of future work.
in Fig. 16(b), the plot with respect to t/τt from eqn (8) is also presented in Fig. 16(a). In Fig. 16(a), an increase in R* leads to a reduction in the slope of the scaled data, suggesting that the radial expansion and associated energy dissipation are not fully captured by eqn (8); for example, under the conditions of Bog = 3910, the slope becomes notably smaller as R* increases from 2.25 to 4.5. By contrast, Fig. 16(b) reveals improved collapse across different R* values, emphasizing the importance of including R* for time scaling. Some discrepancies, which appear in the later phase, are likely due to factors such as cohesion and particle size. These factors are not included in the current scaling analysis because they are difficult to apply directly to the above force balance equation. Nevertheless, the discrepancies do not significantly affect the overall consistency. In particular, conditions with the same material properties but varying R* exhibit more consistent trends. Incorporating the factors identified as potential sources of these discrepancies to improve the scaling relationship remains a subject of future work.
 | ||
Fig. 16 Time histories of powder outer radius Rout/Rout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 with respect to modified dimensionless time: (a) t/τt in eqn (8) and (b) 0 with respect to modified dimensionless time: (a) t/τt in eqn (8) and (b)![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) in eqn (9), for all experimental conditions. in eqn (9), for all experimental conditions. | ||
4 Concluding remarks
In this study, the dispersion characteristics of densely packed powder have been examined experimentally using a Hele–Shaw cell with nEMs as the pressure-generating source. By varying three primary parameters (initial powder radius, cohesion, and particle size), distinct dispersion patterns were identified. A low initial radius of the powder leads to instability, inducing outward jets at the inner and outer boundaries. Under an intermediate initial radius, finger-like structures emerge at the inner boundary and dominate the dispersion patterns of the powder. In contrast, a high initial radius creates weak instability at the inner boundary, which fades quickly, resulting in the outward jets forming primarily from the outer boundary. Low cohesion induces instability from the roughness of the inner boundary, while high cohesion causes instability through particle agglomeration and pore formation at the inner boundary, producing either irregular or regular jet patterns. Larger particle sizes retain the compacted layer formation without instability at the inner boundary during dispersion. A scaling analysis implementing both the force balance equation and the pressure decay factor revealed that the proposed time scale successfully characterizes temporal variations in the outer boundary of the powder.Although some novel dispersion mechanisms have been revealed, the two-dimensional experimental setup limits the applicability of our results to actual dispersion phenomena in three-dimensional space. To better simulate natural dispersion scenarios, future research should be extended to experiments under various open-field conditions. Particle-based numerical models based on our experimental data will deepen the understanding of the complex dispersion process and particle interactions. These efforts will improve control strategies for powder dispersion, which hold substantial potential in industrial applications such as optimizing fire suppression systems.
Author contributions
Jaehun Yoo: conceptualization, methodology, investigation, visualization, writing – original draft. Jihoon Kim: methodology, investigation, writing – original draft. Daegyoum Kim: supervision, writing – review & editing.Data availability
Due to the nature of the project, the data presented in the article constitute the sole source of available information, and no additional data are available.Conflicts of interest
There are no conflicts to declare.Appendix
A Appendix
Fig. 17 is a sample image of the extracted finger polygons described in Section 3.3, which demonstrates the application of the boundary extraction procedure for measuring complexity.Acknowledgements
This work was supported by a grant from the Korean Government (Defense Acquisition Program Administration), funded from 2019 to 2023.Notes and references
- A. W. Woods, Rev. Geophys., 1995, 33, 495–530 CrossRef.
- A. G. Dastidar, P. R. Amyotte and M. J. Pegg, Fuel, 1997, 76, 663–670 CrossRef CAS.
- G. S. Collins, H. J. Melosh and R. A. Marcus, Meteorit. Planet. Sci., 2005, 40, 817–840 CrossRef CAS.
- M. B. Planes, E. N. Millán, H. M. Urbassek and E. M. Bringa, Astron. Astrophys., 2017, 607, A19 CrossRef.
- T. Liu, B. Cao, X. Liu, T.-P. Sun and X. Cheng, Soft Matter, 2020, 16, 1323–1332 RSC.
- D. L. Frost, Y. Grégoire, O. Petel, S. Goroshin and F. Zhang, Phys. Fluids, 2012, 24, 091109 CrossRef.
- A. Milne, E. Floyd, A. Longbottom and P. Taylor, Shock Waves, 2014, 24, 501–513 CrossRef.
- F. Zhang, R. Ripley, A. Yoshinaka, C. Findlay, J. Anderson and B. Von Rosen, Shock Waves, 2015, 25, 239–254 CrossRef.
- D. L. Frost, J. Loiseau, B. J. Marr and S. Goroshin, AIP Conf. Proc., 2017, 1793, 120020 CrossRef.
- J. Loiseau, Q. Pontalier, A. Milne, S. Goroshin and D. Frost, Shock Waves, 2018, 28, 473–487 CrossRef.
- Q. Pontalier, J. Loiseau, S. Goroshin and D. Frost, Shock Waves, 2018, 28, 489–511 CrossRef.
- V. Rodriguez, R. Saurel, G. Jourdan and L. Houas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 063011 CrossRef CAS PubMed.
- V. Rodriguez, R. Saurel, G. Jourdan and L. Houas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 043013 CrossRef CAS PubMed.
- V. Rodriguez, R. Saurel, G. Jourdan and L. Houas, Shock Waves, 2017, 27, 187–198 CrossRef.
- K. Xue, K. Du, X. Shi, Y. Gan and C. Bai, Soft Matter, 2018, 14, 4422–4431 RSC.
- K. Xue, P. Han, K. Du, Y. Gan, Z. Wang and C. Bai, Soft Matter, 2020, 16, 1498–1517 RSC.
- K. Xue, X. Shi, J. Zeng, B. Tian, P. Han, J. Li, L. Liu, B. Meng, X. Guo and C. Bai, Phys. Fluids, 2020, 32, 084104 CrossRef CAS.
- S. Ukai, K. Balakrishnan and S. Menon, Phys. Fluids, 2010, 22, 104103 CrossRef.
- P. Vorobieff, M. Anderson, J. Conroy, R. White, C. R. Truman and S. Kumar, Phys. Rev. Lett., 2011, 106, 184503 CrossRef PubMed.
- K. Balakrishnan, Phys. Fluids, 2014, 26, 043303 CrossRef.
- M. Anderson, P. Vorobieff, C. Truman, C. Corbin, G. Kuehner, P. Wayne, J. Conroy, R. White and S. Kumar, Shock Waves, 2015, 25, 107–125 CrossRef.
- K. Kandan, S. N. Khaderi, H. Wadley and V. Deshpande, J. Mech. Phys. Solids, 2017, 109, 217–240 CrossRef CAS.
- H. Mo, F.-S. Lien, F. Zhang and D. Cronin, Shock Waves, 2018, 28, 559–577 CrossRef.
- J. Li, K. Xue, J. Zeng, B. Tian and X. Guo, J. Fluid Mech., 2022, 930, A22 CrossRef CAS.
- K. Xue, L. Miu, J. Li, C. Bai and B. Tian, J. Fluid Mech., 2023, 959, A17 CrossRef CAS.
- P. Han, K. Xue and C. Bai, Phys. Fluids, 2021, 33, 023309 CrossRef CAS.
- A. N. Osnes, M. Vartdal and B. Pettersson Reif, Shock Waves, 2018, 28, 451–461 CrossRef.
- R. B. Koneru, B. Rollin, B. Durant, F. Ouellet and S. Balachandar, Phys. Fluids, 2020, 32, 093301 CrossRef CAS.
- J. Yoo, J. H. Kim and D. Kim, Powder Technol., 2024, 443, 119935 CrossRef CAS.
- J. Canny, IEEE Trans. Pattern Anal. Mach. Intell., 1986, 679–698 CAS.
- S. Xie and Z. Tu, Proc. IEEE Int. Conf. Comput. Vis., 2015, pp. 1395–1403 Search PubMed.
- B. Sekachev, M. Nikita and Z. Andrey, URL, 2019, https://github.com/openvinotoolkit/cvat.
- E. N. Mortensen and W. A. Barrett, Proceedings of the 22nd annual conference on Computer graphics and interactive techniques, 1995, pp. 191–198.
- D. Stalling and H.-C. Hege, Proceedings of 4th Freiburger Workshop Digitale Bildverarbeitung in der Medizin, Freiburg, 1996, pp. 32–36.
- A. Mishra, A. Wong, W. Zhang, D. Clausi and P. Fieguth, 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2008, pp. 3083–3086.
- J. Jin and X. Tong, 2023 4th International Conference on Computer Vision, Image and Deep Learning (CVIDL), 2023, pp. 175–179.
- R. Davé, S. Kim, K. Kunnath and S. Tripathi, Adv. Powder Technol., 2022, 33, 103836 CrossRef.
- S. Kim, M. Cheikhali and R. N. Davé, Pharm. Res., 2022, 39, 3079–3098 CrossRef CAS PubMed.
- L. J. Jallo, M. Schoenitz, E. L. Dreizin, R. N. Dave and C. E. Johnson, Powder Technol., 2010, 204, 63–70 CrossRef CAS.
- L. J. Jallo, Y. Chen, J. Bowen, F. Etzler and R. Dave, J. Adhes. Sci. Technol., 2011, 25, 367–384 CrossRef CAS.
- A. Abramian, P.-Y. Lagrée and L. Staron, Soft Matter, 2021, 17, 10723–10729 RSC.
- K. Siliveru, C. Jange, J. Kwek and R. Ambrose, J. Food Eng., 2017, 208, 11–18 CrossRef.
- K. Xue, L. Sun and C. Bai, Phys. Rev. E, 2016, 94, 022903 CrossRef CAS PubMed.
- K. Xue, H. Cui, K. Du, X. Shi, Y. Gan and C. Bai, Powder Technol., 2018, 336, 220–229 CrossRef CAS.
- L. Miao, J. Li and K. Xue, J. Fluid Mech., 2024, 999, A46 CrossRef CAS.
- D. Kadau, G. Bartels, L. Brendel and D. E. Wolf, Phase Trans., 2003, 76, 315–331 CrossRef CAS.
- M. Sonzogni, J.-M. Vanson, K. Ioannidou, Y. Reynier, S. Martinet and F. Radjai, Soft Matter, 2024, 20, 5296–5313 RSC.
- P. C. Carman, Trans. Inst. Chem. Eng., 1937, 15, 150–166 CAS.
- Y. Ling, J. Wagner, S. Beresh, S. Kearney and S. Balachandar, Phys. Fluids, 2012, 24, 113301 CrossRef.
- J. L. Wagner, S. J. Beresh, S. P. Kearney, B. O. Pruett and E. K. Wright, Phys. Fluids, 2012, 24, 123301 CrossRef.
- T. G. Theofanous, V. Mitkin and C.-H. Chang, J. Fluid Mech., 2016, 792, 658–681 CrossRef CAS.
- E. P. DeMauro, J. L. Wagner, L. J. DeChant, S. J. Beresh and A. M. Turpin, J. Fluid Mech., 2019, 876, 881–895 CrossRef CAS.
- K. A. Daniel and J. L. Wagner, Int. J. Multiphase Flow, 2022, 152, 104082 CrossRef CAS.
- J. L. Wagner, K. Daniel, C. Downing, T. W. Grasser and K. P. Lynch, AIAA Scitech Forum, 2023, p. 2303 Search PubMed.
- J. Capecelatro and J. L. Wagner, Annu. Rev. Fluid Mech., 2024, 56, 379–403 CrossRef.
- Z. Zhao, C. Liu and B. Brogliato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031307 CrossRef PubMed.
- F. Federico, AIP Conf. Proc., 2013, pp. 1206–1209 Search PubMed.
- J. Li, K. Xue, B. Tian, M. Xiang, L. Miao and J. Chen, Phys. Fluids, 2024, 36, 096137 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01541j |
| This journal is © The Royal Society of Chemistry 2025 |



