Predicting and parameterizing the glass transition temperature of atmospheric organic aerosol components via molecular dynamics simulations

Abstract

Atmospheric aerosols contain thousands of organic compounds that exhibit an array of functionalities, structures and characteristics. Quantifying the role of these organic aerosols in climate and air quality requires an understanding of their physical properties. A key property determining their behavior is the glass transition temperature (T_g). T_g defines the phase state of aerosols, which in turn influences crucial aerosol processes. Molecular Dynamics (MD) simulations were implemented to predict T_g of a range of atmospheric organic compounds. The predictions were used to develop a T_g parameterization. The predictions and the parameterization link T_g with molecular characteristics such as the type and number of functional groups present in the molecule, its architecture, as well its carbon and oxygen content. The MD simulations suggest that T_g is sensitive to the functional groups in the organic molecule with the following order: –COOH > –OH > –CO. This trend is maintained even when more than one of these functional groups is present in a molecule. Molecular structure was also found to play a significant role. Cyclic structures exhibited consistently higher predicted T_g values compared to linear counterparts. T_g, as expected, increased as the number of carbon atoms increased. The parameterization was evaluated using a leave-one-out approach, providing insights into the contributions of various molecular features.

---

1. Introduction

Secondary organic aerosol consists of thousands of complex organic compounds, most of which remain un-investigated or even unidentified.¹ These organic compounds exhibit an array of functionalities including alcohols, acids, ketones, etc. and also often feature a combination of such functional groups. Quantifying the physicochemical properties of these compounds is a scientifically challenging task. Organic aerosols (OA) are not always liquid, as was previously assumed;² instead, they can also be glassy,^2,3 or semi-solid.^4,5 Deciphering the phase state of organic compounds is crucial for gaining insight into a variety of atmospheric processes. For example, the presence of a solid or glassy phase state can reduce the rate of heterogeneous chemical reactions, preclude water uptake, change the atmospheric lifetime of particles as well as influence their long-range transport.

The glass transition temperature (T_g) is a key property for the determination of the ambient aerosol phase state. Over the years, various definitions of T_g have been suggested, with the one widely accepted connecting it to viscosity. Specifically, T_g is defined as the temperature at which the zero shear rate viscosity reaches the value of 10¹² Pa s.^6–8T_g can be determined by several experimental approaches. However, the discrepancies in these approaches can be significant.⁹ Common approaches for measuring T_g involve monitoring properties such as the thermal heat capacity over a relevant temperature range and identifying an abrupt change in the property. However, synthesis and purification of atmospheric organic compounds remain highly laborious tasks, which underlines the essential role of computational approaches for T_g prediction.

Over the years, efforts have been made to predict the glass transition temperature of atmospheric organic compounds. These efforts range from semi-empirical equations such as the Boyer–Kauzmann rule (often referred to also as the Boyer–Beaman rule),^10–12 to T_g parameterizations,^13,14 and more recently, to the use of machine learning algorithms.^15,16T_g is sensitive to the thermal history of the system under study and the approach used to analyse the measurements. If these two factors are unknown, it is difficult to verify and reproduce results.^9,10 Furthermore, the development of T_g parameterizations and machine learning algorithms requires an extensive dataset of T_g values of relevant organic compounds with the range of functionalities and complex structures encountered in the atmosphere. However, the compounds which have been studied experimentally are often limited to small molecules, such as alcohols, a few carboxylic acids and some hydroxy acids. The complexity of the atmospheric organic compounds far exceeds that of these simple compounds, with a lot of the OA components having multiple different functional groups and exhibiting intricate structural architectures.^17,18 Therefore, the need for more robust datasets to support predictive approaches is becoming increasingly apparent.

The first atmospherically relevant T_g parameterization was developed by Shiraiwa et al. (2017)¹³ based on the compound's molecular weight and O : C. A refinement of the method was introduced by DeRieux et al. (2018)¹⁴ incorporating atomic and bond contributions, but neglecting structural and functional group effects. The influence of functional group on T_g has been widely documented.^19–21 Moreover, functional groups have been shown to significantly affect the viscosity of organic compounds,^19,22 a property closely associated with T_g. The structure of a compound is known to affect T_g.^21,23 However, existing efforts do not include the structure as a feature in the available parameterizations.

In this work, we use molecular dynamics (MD) simulations to create a dataset of glass transition temperatures of atmospherically relevant organic compounds and to develop a new parameterization of T_g. MD simulations can bypass some of the difficulties encountered in experimental studies. Simultaneously, they offer insights at the molecular level, thus they represent a valuable tool for understanding physicochemical OA properties.^21,24–26 MD simulations have been widely used in polymer science to predict the T_g of a variety of polymers.^27–30 However, similar efforts to apply MD simulations to investigate the T_g of atmospherically relevant organic compounds are rare; one of them was reported recently by our team.²¹ That preliminary effort is extended here to include more organic compounds with diverse and multiple functional groups, and different structural architectures.

The compounds selected for this study were chosen based on their atmospheric relevance and the availability of experimental data, enabling the comparison of the MD predictions as well as the evaluation of the predictive performance of the developed parameterization. Our efforts focus on expanding our understanding of how functional groups, their interactions, carbon chain length, molecular architecture, O : C ratio and molecular weight influence T_g. The T_g parameterization derived from our atomistic MD simulations can eventually improve the accuracy of atmospheric model predictions. It aims to fill an important gap in the existing literature and pave the way for a deeper understanding of a key physicochemical property of organic compounds and its role in atmospheric processes.

2. Methodology

2.1 Simulation details

The materials and processes simulations platform (MAPS)³¹ was used to build all the organic molecules and initial configurations for the systems of interest. The systems were composed of 2000 molecules placed in a cubic box, with the initial box size estimated according to the density of each organic species at ambient temperature and pressure. The latest version of all-atom OPLS (optimized potentials for liquid simulations) force field was implemented (OPLS/2020).^32,33 The LigParGen platform^34,35 was used as a generator of “personalized” atomic charges for each compound under study. The systems were subjected to potential energy minimization to avoid atom overlaps present in the initial configuration. Following this, the systems were equilibrated at a relatively high temperature, well above each compound's melting point. Equilibration was confirmed by monitoring changes in density and the time autocorrelation function of the unit end-to-end distance vector for each compound. All simulations were performed with periodic boundary conditions applied in all spatial dimensions. The isothermal–isobaric (NpT) statistical ensemble was implemented, utilizing the Nosé–Hoover thermostat–barostat³⁶ for pressure and temperature control and the velocity-Verlet algorithm³⁷ for the integration of the microscopic equations of motion with a 1 fs timestep. The simulations were conducted using the open-source large-scale atomic/molecular massively parallel simulator (LAMMPS).³⁸

A common approach for determining T_g is to monitor volumetric, mechanical and structural properties during cooling simulations.^39–41 We selected a temperature range based on each compound's melting point to perform stepwise cooling simulations. Each simulation step lasted 2 ns at each temperature, followed by stepwise reduction of 20 K before the next simulation step. The properties monitored were the density and the energy due to non-bonded interactions. Only the final nanosecond was used in post-processing. The properties of interest were analysed as a function of temperature to identify any abrupt changes in slope, and a bilinear fit was used to identify T_g. To ensure the reproducibility of our results, we conducted each simulation three times, starting from different initial configurations. The T_g determination protocol used in this work is detailed in Siachouli et al. (2024).²¹

2.2 Systems examined

The examined organic compounds had different architecture (linear/non-linear), length of carbon chain and type, number and co-existence of functional groups present. In the group of linearly structured compounds we extended our previous study²¹ by considering alcohols and carboxylic acids with a longer carbon chain length. Specifically, we examined linear alcohols with nine carbon atoms in their main backbone, including 1-nonanol (1 hydroxyl group), 1,2-nonanediol (2 hydroxyl groups), and 1,2,9-nonanetriol (3 hydroxyl groups). We then investigated linear alcohols with twelve carbon atoms in the backbone, namely 1-dodecanol (1 hydroxyl group) and 1,2-dodecanediol (2 hydroxyl groups). Similarly, we examined carboxylic acids with nine carbon atoms in the backbone, including nonanoic acid (1 carboxyl group) and azelaic acid (2 carboxyl groups). For the case of the twelve-carbon atom chain length, we examined dodecanoic (1 carboxyl group) and dodecanedioic acid (2 carboxyl groups).

Cyclic compounds were selected based on the same reasoning for alcohols and carboxylic acids. The groups of cyclo-alcohols investigated had six and nine carbon atom rings. For the six-carbon ring case, we examined cyclohexanol (1 hydroxyl group), 1,2-cyclohexanediol (2 hydroxyl groups) and 1,2,3-cyclohexanetriol (3 hydroxyl groups). For the nine-carbon ring compounds, we investigated only cyclononanol (1 hydroxyl group) due to the lack of available experimental melting points for other compounds in this category. In addition to the compounds already examined in our previous work, we also considered two monocarboxylic acids with ring-like structures: cyclopentanecarboxylic acid and cycloheptanecarboxylic acid.

Linear and cyclic compounds with carbonyl functional groups were included in the study. For ketones, the investigation focused on linear compounds such as 2-propanone (1 carbonyl group – 3 carbon atoms), 2-hexanone (1 carbonyl group – 6 carbon atoms) and 2-nonanone (1 carbonyl group – 9 carbon atoms). The corresponding cyclic ketones studied were cyclopropanone (1 carbonyl group – 3 carbon atoms), cyclohexanone (1 carbonyl group – 6 carbon atoms) and cyclononanone (1 carbonyl group – 9 carbon atoms). The case of diacetyl (2 carbonyl groups – 4 carbon atoms) was also investigated. For aldehydes, propanal (1 carbonyl group – 3 carbon atoms), hexanal (1 carbonyl group – 6 carbon atoms) and nonanal (1 carbonyl group – 9 carbon atoms) were studied.

Finally, we examined compounds containing multiple functional groups, combining the carboxyl, hydroxyl and carbonyl groups already considered. For hydroxyl/carboxyl groups we considered lactic acid (1 hydroxyl, 1 carboxyl and 3 carbon atoms) and tartronic acid (1 hydroxyl, 2 carboxyl and 3 carbon atoms). For the hydroxyl/carbonyl group combination, we considered hydroxy acetone (1 hydroxyl, 1 carbonyl and 3 carbon atoms) and dihydroxy acetone (2 hydroxyl groups, 1 carbonyl group and 3 carbon atoms). Lastly, the combination of carboxyl/carbonyl groups was considered by investigating linear compounds with an increasing carbon chain length, namely, pyruvic acid (1 carboxyl, 1 carbonyl and 3 carbon atoms), 5-oxohexanoic acid (1 carboxyl, 1 carbonyl and 6 carbon atoms) and 6-oxononanoic acid (1 carboxyl, 1 carbonyl and 9 carbon atoms). The same compounds with the addition of one carboxyl group to their structure were also considered, i.e., oxomalonic acid (2 carboxyl, 1 carbonyl and 3 carbon atoms) and 2-oxoadipic acid (2 carboxyl, 1 carbonyl and 6 carbon atoms). The study of multifunctional organic compounds aims to develop an understanding of the combined effect of the coexistence of multiple functional groups and their interactions.

2.3 T _g parameterization

The T_g parameterization developed in this work aims to link the structure of an organic compound to its glass transition temperature. A property of interest for a given compound can be predicted based on contributions of its structural fragments, which can be systematically determined.⁴² This approach is commonly known as the group contribution (GC) method and has been widely used to predict properties of organic compounds such as viscosity,^43–45 boiling point,^19,46 liquid vapor pressure and enthalpy of vaporization.⁴⁷ We developed a parameterization for predicting T_g based on contributions of carbon atoms, oxygen atoms, functional groups and molecular structure. The proposed parameterization is formulated as follows:

T_g = A + n_cC_c + n_oC_o + n_funcC_func + n_archC_arch (1)

where n_c, n_o, and n_func denote the number of carbon atoms, oxygen atoms and functional groups, respectively, while n_arch takes the value of 0 if the compound is linear and the value of 1 if the compound has a cyclic structure. C_c, C_o, C_func and C_arch are the specific contributions of carbon atoms, oxygen atoms, functional groups and structure to T_g. The use of atomic, bond, group and structural contributions ensures that our parameterization takes into account sufficient information about the compound of interest. Furthermore, by incorporating these contributions the molecular weight and oxygen to carbon (O : C) ratio are indirectly included. The influence of both parameters has been examined in past studies.^13,14,48

3. Results

3.1 Insights from the MD simulations

3.1.1 Linear compounds.
Ketones/aldehydes. The T_g of aldehydes increases as their carbon chain length increases (Fig. 1). Furthermore, aldehydes have consistently lower predicted T_g values compared to the corresponding ketones. Aldehydes, due to the presence of a hydrogen atom attached to the carbonyl functional group, tend to have lower steric hindrance compared to ketones, thereby allowing for more flexibility. Additionally, the lack of that hydrogen in the carbonyl group of ketones could possibly allow them to form more tight molecular packing compared to aldehydes which ultimately could contribute to a higher T_g. Moreover, the case of the di-ketone (diacetyl) shows that the existence of a second carbonyl group can lead to higher predicted T_g even for small molecules that contain only four carbon atoms.

Fig. 1 T _g of ketones and aldehydes as a function of the number of carbon atoms present in the molecule, from the MD-based density predictions: (a) linear compounds and (b) cyclic compounds.

Alcohols. Addition of carbon atoms along the main backbone increases the T_g of alcohols (Fig. 2). The increasing trend of T_g with carbon chain length is smooth for mono-hydroxyl compounds. The addition of a second hydroxyl group results in an increase in T_g, but with a non-linear dependence of T_g on the number of carbon atoms. Interestingly, there appears to be a plateau in the predicted T_g for diols and triols after six carbons. The compounds containing three hydroxyl groups consistently show a higher predicted T_g compared to compounds of the same carbon chain length but with fewer hydroxyl groups. Overall, the primary factor driving the increase in T_g is the presence of additional hydroxyl groups. While a longer carbon chain further increases T_g, this effect seems to saturate at long enough chains, suggesting that there may be a limit to the impact of carbon chain length on T_g for alcohols.

Fig. 2 T _g of alcohols as a function of the number of carbon atoms present in the molecule, from the MD-based density predictions: (a) linear compounds and (b) cyclic compounds.

Carboxylic acids. The mono-carboxylic acids show a steady increase in T_g that – similarly to the case of alcohols – reaches a plateau for longer carbon chains (Fig. 3). The smaller mono-carboxylic acid (propionic acid) has a T_g of approximately 160 K whereas dodecanoic acid has a T_g of 200 K, indicating a moderate increase with the addition of carbon atoms. Di-carboxylic acids exhibit a significantly higher T_g compared to mono-carboxylic acids, indicating the impact of the addition of a carboxyl group. The smallest investigated di-carboxylic acid (malonic acid) has a predicted T_g equal to 275.3 K and dodecanedioic acid a predicted T_g of 316.3 K. The addition of carbon atoms above the sixth does not lead to a significant increase in T_g. Finally, the tri-carboxylic acids have the highest predicted T_g, further highlighting the importance of the number of functional groups compared to the addition of carbon atoms.

Fig. 3 T _g of carboxylic acids as a function of the number of carbon atoms present in the molecule, from the MD-based density predictions: (a) linear compounds and (b) cyclic compounds.

Overall, T_g seems to be primarily sensitive to the type and number of functional groups and secondarily to the length of the carbon chain. Carbonyls consistently lead to lower predicted T_g than hydroxyls, regardless of the size of the carbon chain length. Furthermore, the addition of carboxyl groups has a higher impact on T_g compared to the addition of hydroxyl groups. The sensitivity trend (–COOH) > (–OH) > (–C=O) can be attributed to the enhanced ability of carboxyl groups to form hydrogen bonds compared to hydroxyls, and of hydroxyls compared to carbonyls. Carboxyl groups, with both a hydroxyl and a carbonyl, form stronger hydrogen bonding networks, resulting in a more significant impact on T_g. Hydroxyl groups, while capable of hydrogen bonding, form weaker networks compared to carboxyls. Carbonyl groups, with their lower hydrogen bonding potential, seem to have the least influence on T_g compared to the other two functional groups.

3.1.2 The effect of molecular structure/architecture.
Ketones/aldehydes. The compounds considered in this section are divided into two groups, linear ketones and cyclic ketones. In both groups, T_g increases with the addition of carbon atoms. The range of T_g values for linear ketones increases from approximately 110 K for 2-propanone up to almost 180 K for 2-nonanone. Cyclic ketones have a higher predicted T_g than their linear counterparts. Their T_g is characterized by a more stable, increasing trend, while linear ketones exhibit a steeper increase in their T_g with the addition of carbon atoms (Fig. 1). Although linear ketones show a steeper increase in T_g, cyclic ketones have consistently higher predicted T_g values. This can be attributed to the fact that linear ketones have more conformational flexibility due to their open-chain structure compared to the rigid ring-like structure of cyclic ketones. The rigid ring structure can also facilitate close-packing and intermolecular interactions that enhance the hydrogen bonding potential for cyclic ketones compared to linear ones.
Alcohols. Similarly to ketones and cycloketones, alcohols with a cyclic structure have a higher predicted T_g than their linear counterparts with the same number of hydroxyl groups and carbon atoms. Again, the rigid ring-like structure enables a closer packing and an enhanced hydrogen bond network which, combined, can lead to higher T_g. For both groups, the number of hydroxyl groups plays a dominant role in determining T_g, with more hydroxyl groups leading to higher T_g. Regarding the longest chains (those with nine carbon atoms), both linear and cyclic alcohols seem to converge toward similar T_g values, indicating that at higher chain lengths, the influence of hydroxyl groups dominates T_g.
Carboxylic acids. Based on their structure, the investigated carboxylic acids can be divided into linear and cyclic. The linear mono-carboxylic acids exhibit the lower predicted T_g (Fig. 3). Comparing hexanoic acid (a linear mono-carboxylic acid) to its cyclic counterpart (cyclopentanecarboxylic acid) reveals a significant difference in T_g of approximately 30 K. The trend is similarly seen in the case of linear/cyclic di-carboxylic acids, with cyclic structures having consistently higher T_g.

The structural influence on T_g is particularly pronounced for the case of carboxylic acids. Unlike carbonyl or hydroxyl compounds where structural differences between linear and cyclic forms have a notable but nevertheless small effect, the carboxyl group influences significantly the compound's T_g when considering cyclic structures. This observation emphasizes the pronounced sensitivity of the carboxyls to changes in molecular conformation.

3.1.3 Multifunctional organic compounds.
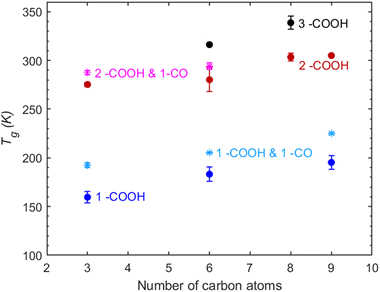
Co-existence of carbonyl and carboxyl functional groups. The compounds containing one carbonyl and one carboxyl group have a slightly higher predicted T_g compared to mono-carboxylic acids (Fig. 4). The difference in T_g remains more or less constant regardless of the carbon chain length, suggesting that carbonyls have a slight and yet consistent contribution to that of the carboxyl group. The difference between the di-carboxylic acids and their corresponding compounds with an extra carbonyl group is similar to that seen in mono-carboxylic acids and compounds containing one carbonyl and one carboxyl group. The overall increase of the T_g by the addition of a carbonyl group in a compound with an existing carboxylic acid is small. The tri-carboxylic acids remain the compounds with the higher predicted T_g regardless of the carbon chain length.

Fig. 4 T _g predictions for multifunctional organic compounds containing carboxyl and carbonyl groups, as a function of the number of carbon atoms along the main carbon chain. Compounds with only carboxyl groups are also included for comparison.

Co-existence of carbonyl–hydroxyl and carboxyl–hydroxyl functional groups. Hydroxyacetone is predicted to have a T_g similar to that of 1,2-propanediol, showing that the addition of a carbonyl group in an alcohol can lead to a significant increase in T_g. However, di-hydroxyacetone exhibits a lower T_g than 1,2,3-propanetriol, indicating that the effect of additional hydroxyl groups is more impactful than that of carbonyls. This supports the conclusion that carbonyls contribute less than hydroxyls to the increase of T_g.

Lactic acid contains one hydroxyl and one carboxyl group; however, it has a slightly higher predicted T_g compared to 1,2,3-propanetriol (Fig. 5). This observation suggests that the combination of a hydroxyl and a carboxyl group may yield a synergistic effect that elevates T_g. Furthermore, tartronic acid, with its two carboxyl groups, exhibits the highest predicted T_g. The addition of a second carboxyl group appears to lead to significant structural changes that can possibly enhance intermolecular interactions which in turn cause an increase in the T_g.

Fig. 5 T _g predictions of multifunctional organic compounds containing hydroxyl–carbonyl groups and hydroxyl–carboxyl, as a function of the number of functional groups. Compounds with only hydroxyl groups are also included for comparison.

These findings emphasize the importance of functional group interactions in determining T_g. The trends that have been observed in compounds comprised solely of carbonyls, hydroxyls and carboxyls remain similar in the multifunctional compounds.

3.1.4 The effect of molecular weight and oxygen to carbon ratio. Molecular weight (M) is a parameter commonly associated with the glass transition temperature and widely used as a T_g predictive indicator. An increase of molecular weight of an organic compound can be achieved by either increasing its carbon atoms and/or by adding oxygen atoms. Our predicted T_g values are positively correlated (R² ≈ 0.46) with molecular weight (Fig. 6). Compounds with higher molecular weight are generally larger and tend to have extensive intramolecular interactions that hinder their mobility, compared to low molecular weight compounds, thereby leading to higher T_g values. The correlation between higher T_g and higher molecular weight is encountered for all classes of compounds and is more prominent in those containing one type of functional group (Fig. S1–S4, ESI†).

Fig. 6 MD-predicted T_g as a function of the molecular weight for all the compounds considered in this study.

We have analyzed our results to detect whether correlations between T_g and molecular mass M proposed in the literature for molecular (non-polymeric) and polymeric glass formers⁴⁹ apply also to the small organic compounds studied here. Namely, Novikov and Rössler (2013)⁴⁹ proposed a correlation between T_g and molecular mass M of the form T_g ∝ M^α, with α = 0.51 ± 0.02 for molecular and short-chain length (i.e., low molecular weight) polymers (also called oligomers). Novikov and Rössler have also found that subclasses of molecular glasses with homologous chemical structure exhibit a similar universal correlation but with significantly lower scatter. Motivated by this study, we considered the entire dataset as well as subcategories based on the type of functional group (Fig. S5–S9, ESI†) and analyzed the dependence of the MD-predicted T_g values with M. The alcohols and carboxylic acids were found to agree well with the correlation proposed by Novikov and Rössler for α = 0.50 and α = 0.51, respectively. For carbonyls and multifunctional compounds, on the other hand, the best correlation was found for α = 0.42 and α = 0.43, respectively. If one considers the entire dataset, then the best correlation requires α = 0.62 indicating a stronger dependence of the glass transition temperature on molecular weight across the dataset. Interestingly the multifunctional compounds exhibit a lower value of α, suggesting a more complex interplay between molar mass and glass transition temperature when multiple functional groups coexist in the molecule.

The oxygen to carbon ratio (O : C) is another parameter commonly used as an indicator of T_g. The O : C ratio indicates the degree of oxygenation of a compound, and a higher O : C ratio tends to lead to a higher T_g. In our study (Fig. 7) the correlation between O : C ratio and T_g is weak (R² ≈ 0.18). While T_g generally increases with an increasing O : C ratio (Fig. 7), there are several instances where compounds with a high O : C ratio exhibit a lower T_g compared to others with lower O : C. A characteristic example is malonic acid (O : C ≈ 1.33, T_g = 275.3 K) compared to tricarballylic acid (O : C ≈ 0.75, T_g = 338.7 K). A detailed analysis of the O : C ratio for each compound category can be found in Section S2 of the ESI.†

Fig. 7 MD-predicted T_g values as a function of the O : C ratio for all the organic compounds considered in this study.

3.2 Evaluation of the parameterization

3.2.1 Comparison of parameterization with MD predictions. The parameterization developed was trained based on the results of the MD simulations.

Most parameterization predictions are within 10% of the MD values, with only a few of them exceeding this range (Fig. 8). Compounds exceeding the 10% include 1-propanol, 1,2-hexanediol, cyclohexanediol, tricarballylic acid, 2,2-dimethylsuccinic acid, diacetyl and pinonaldehyde. Therefore, the proposed T_g parameterization generalizes the results obtained from the MD simulations. Moreover, it could be used to extend the results of the MD simulations to a broader range of compounds within the interval of those included in the training dataset.

Fig. 8 Comparison of the T_g values predicted from the MD simulations with those from the proposed parameterization. The solid line is the 1 : 1 curve while the dashed black line indicates the ±10%, and the dashed red line represents the ±20% deviations from 1 : 1.

Robustness of the parameterization and limitations. The robustness of the T_g parameterization was evaluated using a leave-one-out approach, where each compound was removed and then the contributions were re-evaluated. The procedure was repeated for the removal of all the compounds considered in the dataset. Deviations of each parameter's contribution (e.g., carbons, carboxyls, hydroxyls, etc.) were monitored using a tolerance threshold of 5% from the contribution value extracted upon the training of the parameterization with the full dataset. The tolerance threshold was implemented to point out which compounds stand out and drive the contributions considered (Fig. S10–S16, ESI†).

Removal of triols increased the contribution of hydroxyl groups. The T_g of triols with longer carbon chain length was found to reach a plateau, meaning that the removal of such compounds reduces this effect. The carbonyl contribution increased upon the removal of hydroxyl and carboxyl functional groups, but decreased when multifunctional compounds containing carbonyl groups, or compounds composed solely of carbonyl groups, were removed. Finally, the contribution of cyclic structures increased with the removal of linear compounds and decreased when cyclic compounds with a high T_g were removed.

Overall, the compounds that were under-represented in the developed dataset had a notable impact on the variation of each contribution parameter upon their removal. For example, diacetyl, as the only diketone in the dataset, altered the carbonyl contribution's variation by more than 5% compared to its value in the full dataset. Carbonyl compounds were under-represented in our dataset due to limited experimental input. Moreover, most multifunctional compounds contain carbonyl groups alongside hydroxyl or carboxyl groups, making the carbonyl contribution's behaviour closely linked to that of other functional groups, and therefore difficult to interpret independently. To improve the dataset, measurements such as melting and boiling points are needed for compounds containing only carbonyl groups and for compounds with complex structures and functional groups similar to aldehydes or cis-pinonic acid.

3.2.2 Comparison with measurements.
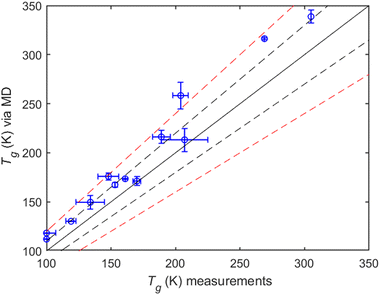
MD simulations compared to measurements. All MD predictions are within 20% of the measured values (Fig. 9). Most of the compounds included in the comparison are small alcohols, with average T_g values taken from Rothfuss et al. (2017). MD predictions for T_g perform relatively well, with a normalized mean error (NME) of 12.4%, a normalized mean bias (NMB) of 12.4% and R² = 0.79.

Fig. 9 MD-predicted T_g values against available experimental data. The solid line depicts the 1 : 1 curve while the dashed black line indicates the ±10%, and the dashed red line represents the ±20% deviations from 1 : 1.

It should be noted that although available measurements of experimental T_g's are rather limited (Table S1, ESI†), one can still indirectly estimate them from viscosity data (given that such data are available). An example is provided by the relatively recent work of Fu et al. (2021)⁵⁰ for 1-dodecanol and 1,12-dodecanediol. We fitted the reported viscosity data in that work to the Vogel–Fulcher–Tammann (VFT) equation:

where A, B, T₀ are fitted parameters, and we estimated T_g as the temperature for which the value of η becomes equal to 10¹² Pa s. The so-extracted T_g values are 165 K for 1-dodecanol and 200 K for 1,12-dodecanediol (Fig. S17, S18 and Section S4, ESI†). The corresponding MD predictions of our work are 187.6 K for 1-dodecanol and 259.5 K for 1,12-dodecanediol, showing a 13% and a 29% deviation, respectively. In the literature,^51,52 an analysis of the variation of the transport properties (e.g., structural relaxation time or viscosity) with respect to temperature of a relatively large number of fragile structural glass-forming liquids has also demonstrated a remarkable degree of universality. While eqn (2) exhibits divergence of the transport properties at T → T₀ (the ideal glass transition temperature), several authors proposed alternative expressions where the dynamic properties stay finite for all temperatures T > 0.^51–59

T _g parameterization compared to measurements. The parameterization developed in this work was compared to the available T_g measurements (Fig. 10(a)). There is a moderately good agreement (NME ≈ 19.6%, NMB ≈ 19.6%, R² ≈ 0.52) with a slight but consistent overprediction of T_g. This overprediction is mainly due to the fact that the MD simulations themselves exhibit an at least 10% overprediction of the measured values. One reason for this is the rather fast cooling rates implemented in the MD simulations due to computational constraints. In an effort to correct for this bias we implement a 0.9 scaling factor to account for the combined overprediction of both the MD simulations and the parameterization. The parameterization takes now the following form:

T_g = 0.9(A + n_cC_c + n_oC_o + n_OHC_OH + n_COOHC_COOH + n_CO + n_ringC_ring) (3)

where the various coefficients have the following values: A = 65.15 K, C_c = 6.57 K, C_o = 29.98 K, C_OH = 20.68 K, C_COOH = 23.58 K, C_CO = −5.93 K and C_ring = 28.48 K, thus leading to

T_g = 0.9(65.15 + n_c6.57 + n_o29.98 + n_OH20.68 + n_COOH23.58 − n_CO5.93 + n_ring28.48) (4)

Fig. 10 Comparison of the T_g values predicted from the proposed parameterization, with (a) original version and (b) the 0.9 scaling factor, with measurements. The solid line is the 1 : 1 curve while the dashed black line indicates the ±10%, and the dashed red line represents the ±20% deviations from 1 : 1.

The scaling factor as expected reduces the overprediction (Fig. 10(b)), particularly at lower T_g values, which are mostly associated with alcohols – compounds that exhibited the highest deviations when comparing MD simulations with measurements. The implementation of the scaling factor improves the performance of the parameterization (NME ≈ 8.9%, NMB ≈ 7.6%, R² ≈ 0.87), making it more reliable for predicting T_g – especially in the case of low T_g compounds.

The effect of cooling rate. A major impediment in comparing experimental studies with molecular simulations regarding properties such as T_g is the cooling rate implemented in the latter, which is several orders of magnitude larger than the typical one characterizing experimental protocols.³⁰ The higher T_g values predicted via MD simulations are therefore qualitatively consistent with the expectation that measurements at a high cooling rate should lead to a higher T_g value. Bridging the gap between measured and simulated T_g values requires calculating the shift of T_g due to a high cooling rate. 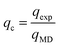A system specific equation^30,60 based on the Williams–Landel–Ferry (WFL)⁶¹ equation iswith being the ratio of experimental and simulated cooling rates, R the ideal gas constant and Δh the apparent activation energy associated with structural relaxation. We calculated the T_g shift for 1-propanol using the average reported experimental value¹⁹ of T_g = 100 K and the value of Δh = 97487.2 J mol⁻¹.⁶² The resulting dT_g was found to be 21.72 K. Based on this, the expected T_g (MD) would be 121.7 K, which is very close to the (average) value of 118.2 K that came out from our simulations (Table S1, ESI†).

3.2.3 Comparison with other parameterizations. There are two available parameterizations for atmospheric organic compounds that consider CH and CHO compounds. The first, introduced by Shiraiwa et al. (2017),¹³ uses the molecular weight and the O : C ratio to predict T_g for compounds with molar mass up to 450 g mol⁻¹. A refinement of the Shiraiwa et al. (2017) parameterization was later introduced by DeRieux et al. (2018),¹⁴ extending the previous work to include higher molar mass compounds, up to 1100 g mol⁻¹. The predicted T_g values from the DeRieux et al. parameterization are in good agreement with the experimental T_g values. The predictions are falling within ±10% of the measurements and none exceeding the ±20% error (Fig. S19, Section S5, ESI†). However, the experimental data used in this comparison were already part of the training set for the DeRieux et al. (2018) parameterization, therefore good agreement was to be expected.

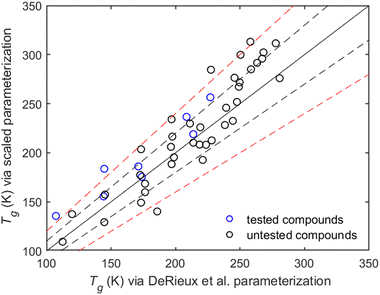
The limitations of T_g parameterizations such as those by Shiraiwa et al. (2017) and DeRieux et al. (2018) are due to the lack of available experimental data to train them. The datasets used for both parameterizations primarily consist of experimental T_g data for small compounds, such as alcohols or small acids,¹⁹ and do not include the effect of different functional groups or that of molecular architecture. DeRieux's parameterization generally agrees mostly within 10% with our parameterization for compounds at low temperatures. However, for compounds with a predicted T_g above 250 K, the two parameterizations exceed the 10% difference (Fig. 11). The compounds that have a higher predicted T_g than 250K are mostly multifunctional or non-linear organic compounds that have not been experimentally investigated and therefore have not been used as input in the past parameterizations. The increasing difference between the two parameterizations at higher temperatures underlines the importance of enriching the current datasets. To refine T_g parameterizations and include more complex compounds, methods such as MD simulations, as implemented in this work, are useful.

Fig. 11 Comparison of the developed parameterization with that by DeRieux et al. (2018). The compounds shown are divided in two categories: (i) blue for the compounds that are experimentally tested, and (ii) black for untested compounds both experimentally and DeRieux's parameterization. The solid line is the 1 : 1 curve while the dashed black line indicates the ±10%, and the dashed red line represents the ±20% deviations from 1 : 1.

4. Conclusions

MD simulations were carried out to investigate the glass transition temperature of atmospherically relevant organic compounds. Two properties were monitored to predict T_g, density and non-bonded potential energy. The two methods agree well within 7% with each other. The MD predictions are within 20% of available experimental measurements while the parameterization is following the MD within 10% of agreement. The scaled parameterization agrees mostly within 10% of the available measurements.

The T_g of aldehydes increases smoothly as the carbon chain length increases; however, their T_g is consistently lower compared to those of ketones with the same carbon atom number. This can be attributed to the flexibility of aldehydes due to an attached hydrogen to their carbonyl group, while ketones can exhibit comparatively tighter packing at the molecular level, contributing to a higher T_g.

Alcohols’ T_g shows a linear increase for mono-hydroxyl compounds upon the addition of carbon atoms. However, in the case of additional hydroxyl groups the increase of T_g seems no longer to be linear. On longer carbon chain, a plateau is reached in the increase of T_g. This plateau of T_g is observed in alcohols with nine carbon atoms or more. The addition of hydroxyl groups has a much more significant effect on T_g than the carbon chain length, marking hydroxyl functionality the primary factor of the two influencing T_g.

In the case of carboxylic acids, the compounds with the most carboxyls show a higher T_g compared to mono- or di-carboxylic acids, which highlights the dominant role of the carboxyl group. The plateau effect of T_g for longer carbon chains that was seen in alcohols is also present in carboxylic acids. The functional group hierarchy for T_g sensitivity is (–COOH) > (–OH) > (–C=O). A key factor for this sensitivity can be the enhanced ability of carboxyl groups to form stronger hydrogen bonds, which ultimately increases T_g. Overall, the number and type of functional groups, particularly carboxyl and hydroxyl groups, tend to have a stronger effect on T_g than the length of the carbon chain.

Cyclic compounds have higher predicted T_g compared to their linear counterparts, a fact that can be attributed to the rigidity imparted by a non-aromatic carbon ring. A similar behaviour is encountered in the case of cyclic alcohols. The structural effect is particularly important in the case of carboxyl groups.

When both carboxyl and hydroxyl groups are present within a compound, the T_g tends to be higher than for the respective compounds with only one type of functional group. This can be attributed to the synergistic effect of the hydrogen bonding networks formed between the carboxyl and hydroxyl groups. Conversely, the combination of carbonyl with a hydroxyl or carboxyl group results in a relatively lower increase in T_g. Such interactions underline the importance of functional group synergy, where the presence of multiple functional groups can enhance or moderate the sensitivity of T_g to the addition of more functional groups.

The molecular weight was found to have a clear, positive correlation with T_g. The O : C ratio was found to have no significant influence, given the several examples of compounds (e.g., malonic acid, oxomalonic, lactic acid, etc.) with high O : C ratio but comparatively low predicted T_g value.

Overall, the limitations primarily involve compounds with complex structures and multiple functional groups. Compounds such as diketones with cyclic structure and multifunctionality were under-represented in the dataset and are needed to improve the parameterization. Experimental data of melting and boiling point for such compounds are needed to guide the MD simulations. Using a lower stepwise cooling rate could help account for the scaling factor.

Author contributions

PS contributed to the design of the study, conducted the simulations, analysed the results, developed the parameterization, and wrote the paper. VGM contributed to the design of the study, the analysis of the results and the writing of the paper. SNP was responsible for the design and coordination of the study and the synthesis of the results.

Data availability

All software programs used in this study are referenced throughout the Methodology and Results sections of this work. Data files for all simulated systems are available in the Zenodo repository, accessible through the C-STACC community records, https://zenodo.org/communities/c-stacc_group/records?q=&l=list&p=1&s=10&sort=newest.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the Atmospheric Nanoparticles, Air Quality, and Human Health (NANOSOMs) research project co-funded by the Stavros Niarchos Foundation (SNF) and the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the 5th Call of “Science and Society” Action Always strive for excellence – Theodoros Papazoglou” (Project Number: 11504). The authors acknowledge the computational time granted by the Greek Research & Technology Network (GRNET) in the national HPC facility ARIS under project GlaSOA III (pr015029).

References

1. A. H. Goldstein and I. E. Galbally, Environ. Sci. Technol., 2007, 41, 1514–1521.
2. A. Virtanen, J. Joutsensaari, T. Koop, J. Kannosto, P. Yli-Pirilä, J. Leskinen, J. M. Mäkelä, J. K. Holopainen, U. Pöschl, M. Kulmala, D. R. Worsnop and A. Laaksonen, Nature, 2010, 467, 824–827.
3. B. Zobrist, C. Marcolli, D. A. Pedernera and T. Koop, Atmos. Chem. Phys., 2008, 8, 5221–5244.
4. L. Renbaum-Wolff, J. W. Grayson, A. P. Bateman, M. Kuwata, M. Sellier, B. J. Murray, J. E. Shilling, S. T. Martin and A. K. Bertram, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8014–8019.
5. M. Song, P. F. Liu, S. J. Hanna, Y. J. Li, S. T. Martin and A. K. Bertram, Atmos. Chem. Phys., 2015, 15, 5145–5159.
6. C. D. Cappa, E. R. Lovejoy and R. Ravishankara, Direct, 2008, 105, 18687–18691.
7. C. Marcolli, B. Luo and T. Peter, J. Phys. Chem. A, 2004, 108, 2216–2224.
8. Y. Cheng, H. Su, T. Koop, E. Mikhailov and U. Pöschl, Nat. Commun., 2015, 6, 1–7.
9. O. Mazurin and Yu. V. Gankin, Glass transition temperature: problems of measurements and analysis of the existing data, Strasbourg, France, 2007.
10. O. V. Mazurin, Glass Physics and Chemistry, 2007, vol. 33, pp. 22–36.
11. P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259.
12. D. Champion, M. Le Meste and D. Simatos, Trends Food Sci. Technol., 2000, 11, 41–55.
13. M. Shiraiwa, Y. Li, A. P. Tsimpidi, V. A. Karydis, T. Berkemeier, S. N. Pandis, J. Lelieveld, T. Koop and U. Pöschl, Nat. Commun., 2017, 8, 1–7.
14. W. S. W. DeRieux, Y. Li, P. Lin, J. Laskin, A. Laskin, A. K. Bertram, S. A. Nizkorodov and M. Shiraiwa, Atmos. Chem. Phys., 2018, 18, 6331–6351.
15. T. Galeazzo and M. Shiraiwa, Environ. Sci. Atmos., 2022, 2, 362–374.
16. G. Armeli, J. H. Peters and T. Koop, ACS Omega, 2023, 8, 12298–12309.
17. A. Kołodziejczyk, P. Pyrcz, K. Błaziak, A. Pobudkowska, K. Sarang and R. Szmigielski, ACS Omega, 2020, 5, 7919–7927.
18. A. Kołodziejczyk, P. Pyrcz, A. Pobudkowska, K. Błaziak and R. Szmigielski, J. Phys. Chem. B, 2019, 123, 8261–8267.
19. N. E. Rothfuss and M. D. Petters, Environ. Sci. Technol., 2017, 51, 271–279.
20. M. Nakanishi and R. Nozaki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 3–7.
21. P. Siachouli, K. S. Karadima, V. G. Mavrantzas and S. N. Pandis, Soft Matter, 2024, 20, 4783–4794.
22. J. W. Grayson, E. Evoy, M. Song, Y. Chu, A. Maclean, A. Nguyen, M. A. Upshur, M. Ebrahimi, C. K. Chan, F. M. Geiger, R. J. Thomson and A. K. Bertram, Atmos. Chem. Phys., 2017, 17, 8509–8524.
23. K. Li, G. Jiang, F. Zhou, L. Li, Z. Zhang, Z. Hu, N. Zhou and X. Zhu, Polym. Chem., 2017, 8, 2686–2692.
24. K. S. Karadima, V. G. Mavrantzas and S. N. Pandis, Atmos. Chem. Phys., 2019, 19, 5571–5587.
25. K. S. Karadima, V. G. Mavrantzas and S. N. Pandis, Phys. Chem. Chem. Phys., 2017, 19, 16681–16692.
26. P. G. Mermigkis, K. S. Karadima, S. N. Pandis and V. G. Mavrantzas, ACS Omega, 2023, 8, 33481–33492.
27. S. Napolitano, E. Glynos and N. B. Tito, Reports Prog. Phys., 2017, 80, 036602.
28. G. Tsolou, V. A. Harmandaris and V. G. Mavrantzas, J. Nonnewton. Fluid Mech., 2008, 152, 184–194.
29. O. Alexiadis, V. G. Mavrantzas, R. Khare, J. Beckers and A. R. C. Baijon, Macromolecules, 2008, 41, 987–996.
30. N. J. Soni, P. H. Lin and R. Khare, Polymer, 2012, 53, 1015–1019.
31. Scienomics SARL, version 3.4.2, MAPS platform, France, 2015.
32. M. M. Ghahremanpour, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2022, 126, 5896–5907.
33. W. L. Jorgensen, M. M. Ghahremanpour, A. Saar and J. Tirado-Rives, J. Phys. Chem. B, 2024, 128, 250–262.
34. L. S. Dodda, J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 3864–3870.
35. L. S. Dodda, I. C. De Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336.
36. William G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
37. M. P. Allen and D. J. Tildesley, Computer Simulation of liquids, Oxford University Press, New York, 1991.
38. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
39. Q. Yang, X. Chen, Z. He, F. Lan and H. Liu, RSC Adv., 2016, 6, 12053–12060.
40. K. K. Bejagam, C. N. Iverson, B. L. Marrone and G. Pilania, Phys. Chem. Chem. Phys., 2020, 22, 17880–17889.
41. C. Wen, B. Liu, J. Wolfgang, T. E. Long, R. Odle and S. Cheng, J. Polym. Sci., 2020, 58, 1521–1534.
42. R. Gani, Curr. Opin. Chem. Eng., 2019, 23, 184–196.
43. S. R. S. Sastri and K. K. Rao, Chem. Eng. J., 1992, 50, 9–25.
44. J. Marrero-Morejón and E. Pardillo-Fontdevila, Chem. Eng. J., 2000, 79, 69–72.
45. N. R. Gervasi, D. O. Topping and A. Zuend, Atmos. Chem. Phys., 2020, 20, 2987–3008.
46. S. E. Stein and R. L. Brown, J. Chem. Inf. Comput. Sci., 1994, 34, 581–587.
47. J. F. Pankow and W. E. Asher, Atmos. Chem. Phys., 2008, 8, 2773–2796.
48. T. Koop, J. Bookhold, M. Shiraiwa and U. Pöschl, Phys. Chem. Chem. Phys., 2011, 13, 19238–19255.
49. V. N. Novikov and E. A. Rössler, Polymer, 2013, 54, 6987–6991.
50. Y. Fu, X. Meng, X. Liang and J. Wu, J. Chem. Eng. Data, 2021, 66, 712–721.
51. Y. S. Elmatad, D. Chandler and J. P. Garrahan, Glass, 2009, 2, 5563–5567.
52. Y. S. Elmatad, D. Chandler and J. P. Garrahan, J. Phys. Chem. B, 2010, 114, 17113–17119.
53. E. A. Di Marzio and A. J. M. Yang, J. Res. Natl. Inst. Stand. Technol., 1997, 102, 135–157.
54. V. V. Ginzburg, Soft Matter, 2020, 16, 810–825.
55. J. C. Mauro, Y. Yue, A. J. Ellison, P. K. Gupta and D. C. Allan, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19780–19784.
56. J. Zhao, S. L. Simon and G. B. McKenna, Nat. Commun., 2013, 4, 1–6.
57. G. B. McKenna and J. Zhao, J. Non. Cryst. Solids, 2015, 407, 3–13.
58. H. Yoon and G. B. McKenna, Sci. Adv., 2018, 4, 1–8.
59. O. V. Laukkanen and H. H. Winter, J. Non. Cryst. Solids, 2018, 499, 289–299.
60. C. T. Moynihan, A. J. Easteal, J. Wilder and J. Tucker, J. Phys. Chem., 1974, 78, 2673–2677.
61. M. L. Williams, R. F. Landel and J. D. Ferry, J. Am. Chem. Soc., 1955, 77, 3701–3707.
62. S. B. Dake and R. V. Chaudhari, J. Mol. Catal., 1986, 35, 119–129.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01533a

---