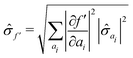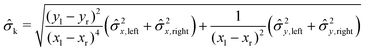Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
In situ error analysis in contact angle goniometry†
Heikki A.
Nurmi
 *,
Gentrit
Zenuni
,
Sakari
Lepikko
,
Reetta
Saine
,
Maja
Vuckovac
*,
Gentrit
Zenuni
,
Sakari
Lepikko
,
Reetta
Saine
,
Maja
Vuckovac
 and
Robin H. A.
Ras
and
Robin H. A.
Ras
 *
*
Department of Applied Physics, School of Science, Aalto University, Konemiehentie 1, Espoo, Finland. E-mail: heikki.nurmi@aalto.fi; robin.ras@aalto.fi
First published on 28th February 2025
Abstract
Contact angle goniometry is a valuable tool for characterising surface wetting properties in various application areas such as petrochemistry, coatings, and medicine. The accuracy of goniometer measurements is often unknown and underappreciated, yet the errors can be large enough to affect or invalidate the interpretation of measurement. In addition, goniometer measurement errors are typically estimated after the measurement by the variance of the measured data, without considering the instrumental uncertainties in the analysis or in the setup. Here, we present a method for estimating these intrinsic measurement errors for each frame in situ and validate it against a commercial contact angle goniometer. We evaluate the method using synthetic images of a droplet with set contact angles. Our results highlight the need for in situ error estimates in goniometer measurements, as the errors can be larger than generally estimated ones. The presented in situ error estimation method could be implemented using contact angle goniometer software to aid the user during the tuning of the instrument and analysis of the contact angle data.
1. Introduction
Wetting describes the interaction between a solid and a liquid, which is relevant in many fields of science and technology.1–6 Typically, this interaction is characterised by the internal angle a sessile droplet forms on a solid (Fig. 1). This angle is called a contact angle7 and is typically measured with a contact angle goniometer. Often researchers measure only the “static contact angle” and then characterise the wetting properties by the mean value of repeated measurements and estimate the error with the variance of the data i.e. the amount of spread in the data.8–12 We define the “static contact angle” as a contact angle of a droplet placed on a surface without a specific protocol aiming for a specific contact angle. “Unfortunately, this [static contact angle] is a meaningless measurement, since there is a random element involved in the process of drop landing – that is, the contact [angle] can be any value within the range of advancing and receding contact angels [sic]; therefore, this contact angle is not useful for any analysis (Marmur et al. 2017)”.7 With a specific protocol producing repeatable results, the static contact angle can provide rough information about wetting in a fast and simple manner.13 However, the static contact angle lacks information about the wetting origin and droplet mobility over surfaces, and it does not fully describe the surface wetting properties.14 The meaningful contact angles are the advancing, receding, and most stable contact angles. However, their analysis is more complicated and demand a careful protocol and/or specific setup.15,16 Even when following these protocols, the measurement errors can be larger than 2° due to different focus, lighting conditions, edge detection, baseline location, and operator skill – especially in the case of superhydrophobic surfaces.17–21 In comparison, it should be noted that companies providing commercial goniometers proclaim an error of 0.1° or similar for the whole measurement range. Even though measuring with a contact angle goniometer seems deceptively simple, the method has pitfalls and great care needs to be taken to gain meaningful data.17,18,20–23In addition to the commercial contact angle analysis software, scientists have shared their tools for contact angle analysis, which aim to improve the accuracy of the analysis using more suitable theoretical models for fitting24,25 or using different fitting schemes.26–29 However, these pieces of software lack error analysis tools to predict the uncertainty due to the setup and image analysis for each frame of the analysis video. The error analysis possible for these pieces of software is to analyse the mean and standard deviation of multiple measurements. In practical applications, it is paramount that the measurement uncertainty of contact angle can be estimated, as the measurement only estimates the real value of the contact angle instead of obtaining the real value.
Here, we first implement a Canny-like edge detector30,31 and Harris corner detector.32,33 The Canny edge detector calculates the sum magnitude of x- and y-directional gradients in the image to detect edges. The Harris corner detector uses the gradients in x- and y-directions in tandem with their cross correlation to detect edges and corners. Then, we use the edge strength and Harris measure distributions to propagate the uncertainty of the edge and contact point measurement to the contact angle. We call this error analysis for each frame “in situ error analysis” in contrast to the error analysis via the mean and standard deviation of repeated measurements. In general, we recommend in situ error estimation with all contact angle measurement methods. However, the details of error estimation will vary depending on the methods used. Then, the contact angle analysis method can estimate the intrinsic uncertainty of the measurement, which would allow better comparison of data between research groups.
2. Theory
The contact angle is measured from a 2D droplet silhouette from an image when the droplet edge and baseline can be found. Then, a model (e.g. Young–Laplace, elliptical, or polynomial) is fitted to the edge points, and the tangent of that model is calculated at the baseline height. Some models such as machine learning34 and masking27,29 detect the contact angle directly from the pixel data based on their own methodology. There are good arguments for selecting a specific model, however each model has its limitations. For example, the Young–Laplace model assumes non-deformed and rotational symmetry,35 which in many cases does not hold, e.g. a needle in a droplet36 and sliding droplet.37 In comparison, the polynomial model is agnostic about the physics of the droplet,38 which omits known details of the droplet in modelling, e.g. symmetry between the droplet and its reflection and the continuity of the droplet edge.39 In addition, the different models and fitting methods can have different contact angle ranges and cases where they are more accurate, e.g. low, medium or high contact angles or an advancing/receding droplet and sliding droplet. For this article, we selected the polynomial model for the ease of error propagation and its capability of measuring the left and right contact angles separately. The shown method for error propagation can be implemented for Young–Laplace, elliptical or similar fitting based models, while for the masking and machine learning models a more suitable error analysis scheme needs to be used, e.g. the Bayesian statistical model for error estimation.The error propagation explored in this article follows the logic of having a function g(xi) with non-correlated xi parameters and how its error can be propagated by calculating the Taylor expansion of the function.
 | (1) |
 | (2) |
2.1. Droplet edge detection
The droplet edge is detected with a Canny-like edge detector, which calculates the sum of the magnitude gradients in x- and y-directions.30,31 The edge points are detected for the left and right sides separately and for each row as the maximum of the edge matrix. The error is estimated in the x-direction as the full width at half maximum (FWHM), while in the y-direction it is assumed to be exact, as the selected row of pixels is exactly known. For the purposes of error propagation, we use FWHM of the detected edge and contact point to estimate the error. We assume that the distribution of the edge/corner strength is close enough to a Gaussian distribution that the connection between the FWHM and standard deviation of the Gaussian distribution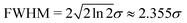 holds. The practical application of this is in the analyseEdge function of the analysis code.†
holds. The practical application of this is in the analyseEdge function of the analysis code.†
The gradient is calculated with a convolution between the grayscale image matrix and the gradient kernels Kx and Ky.
 , where °x means element-wise power. The points near the edge of the image are then removed, as they contain edge-effect data. The maximum of each of the rows corresponds to the edge of the droplet and the FWHM was calculated for each row separately (Fig. 2a). Edge points of the droplet too close to the edge of the image (1% of height/width) are omitted from the analysis.
, where °x means element-wise power. The points near the edge of the image are then removed, as they contain edge-effect data. The maximum of each of the rows corresponds to the edge of the droplet and the FWHM was calculated for each row separately (Fig. 2a). Edge points of the droplet too close to the edge of the image (1% of height/width) are omitted from the analysis.
2.2. Droplet contact point detection
The contact points between the droplet and the surface are found with a Harris corner detector.32,33 The practical application of the detector is found in the function analyseBaseline.† The detector first calculates the gradient matrices Ix and Iy and then the autocorrelation matrices , B = Ix ⊙ Iy, and
, B = Ix ⊙ Iy, and  , where ⊙ is element-wise multiplication. Then, a convolution from each of these autocorrelation matrices is calculated with a Gaussian kernel to smoothen out noise. The corner strength matrix R is then calculated from these convoluted autocorrelation matrices as
, where ⊙ is element-wise multiplication. Then, a convolution from each of these autocorrelation matrices is calculated with a Gaussian kernel to smoothen out noise. The corner strength matrix R is then calculated from these convoluted autocorrelation matrices as| R = A ⊙ C − B°2 − κ(A + C)°2 | (3) |
2.3. Contact angle analysis using the polynomial tangent method
The contact angle and its error are calculated from the detected edge and contact points and their errors. We fit a line to contact points to estimate the baseline and its slope k and angle of inclination α and then fit a polynomial to a subset of edge points to estimate the contact angle at the estimated intersection point between the polynomial and the baseline. The practical application of this is in the functions FitCA and findIntersectAndCA.†The polynomial is fitted to the left and right sides independently, which allows us to measure non-rotationally symmetric droplets, e.g. pinned or sliding droplets. The edge points for fitting are above the contact point at maximum 100 points in total. The maximum number of points was limited, since we noticed that too many points caused the polynomial to converge incorrectly to the edge points. Due to this issue, we also omitted the points above the widest part of the droplet in cases where the contact point is below the widest part, i.e. θ > 90°. This removed the duplicate values above and below the widest part of the droplet, which caused issues with fitting the polynomial. This selection of points was then used to fit the 4th degree polynomial with normalised x values,
 | (4) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) is the mean of the x-coordinates, and σx is the standard deviation of the x-coordinate.
is the mean of the x-coordinates, and σx is the standard deviation of the x-coordinate.
The contact angle was calculated at the estimated intersection point between the baseline and the polynomial fit to the edge to gain theoretically subpixel accuracy for the contact point. The intersection point was estimated by calculating the difference between the line and the polynomial near the identified contact point. The point having the smallest difference was then selected as the intersection point (xI). This way an estimate of the intersection point can be found even if there is no intersection between the polynomial and the baseline, as there is no guarantee that the polynomial and line will intersect. In addition, this is computationally cheaper than finding the zero point of the difference of the polynomial and baseline function, especially in the case when there is no intersection. As a sanity check, we limited the size of the difference to be smaller than 20 pixels (0.04 mm with the used calibration value), and if the size was larger, we considered the fitting to have failed and omitted the data as outliers. Typical failure mode for these cases is finding some stronger corner, such as dirt on the surface, in the image than the corner from the contact point of the droplet; more details can be found in the ESI.† The contact angle was then calculated from the differential of the polynomial (f′) at the estimated intersection point.
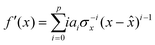 | (5) |
 | (6) |
2.4. In situ error propagation
The in situ error of the contact angle was estimated from the errors of the edge and contact points. The error of the edge points was included in the polynomial fit by including the inverse of the edge error as the fitting weight. The tangent was calculated as the differential of the normalised polynomial eqn (5), and the error estimated via the total differential with respect to the regression parameters ai.Then, the 95% confidence interval (CI) for the regression parameters ai was used to estimate the standard error of the tangent of the polynomial
 . The 95% CI of the regression parameter ai is connected to the standard error (
. The 95% CI of the regression parameter ai is connected to the standard error (![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ai) via Gaussian distribution's 97.5 percentile point by relation CI = 1.96
ai) via Gaussian distribution's 97.5 percentile point by relation CI = 1.96![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) .
.
The standard error for the baseline slope was calculated based on the FWHM of the left and right contact points.
This allows us to calculate the in situ standard error of the contact angle θ.
 | (7) |
3. Experiments & methods
3.1. Goniometer data
We obtained the data from previous research and performed new measurements for validating the analysis method. The measurements were done using a Biolin Scientific OneAttension Theta goniometer and the measurement videos were exported to be analysed with our software. The used surfaces had a variety of contact angles from θ < 10° to θ > 160°: from θ < 10° to θ ≈ 110° were silicon wafers coated with octyltrichlorosilane (OTS) self-assembled monolayers41 with varying coverage degrees to obtain different contact angles, from ≈60° to ≈90° silicone nanofilaments on silicon wafers,42 from ≈70° to ≈120° silicon micropillars with fluoropolymers,42 and from ≈135° to ≈165° nanorough copper.43–45The OTS measurement data (goniometer and video) were obtained from Lepikko et al.41 and the contact angle analysis was done on the video data and compared to the goniometer measurements.
The details of making the rest of the samples can be found in the ESI.† The measurements were done following the protocol developed by Huhtamäki et al.15 and are given in detail in the ESI.†
3.2. Generation of synthetic images of a droplet
In addition to the experimental data, we generated synthetic images of a droplet with varying contact angles to further validate the analysis (Fig. 3). These synthetic images are computer-generated images mimicking real droplets. This gives the benefit of knowing exactly the contact angle of the droplet. The images of a droplet were generated by calculating the spherical cap having a volume of 5 μl and contact angles from 1° to 179°. This allowed us to have correctly proportioned droplet images to each other compared to generating the droplet with a constant height, radius, or baseline length. The area within the calculated spherical cap was set to 1 and the area outside set to 0 with a calibration value of 2 × 10−3 mm px−1. This calibration value was selected to generate images with a resolution of roughly 1984 pixels by 1264 pixels, which is the resolution used in the goniometer. This generated a logical black and white image of a droplet, which was padded with 200 pixels and rotated with some angle (between −5° and 5°) to simulate a tilted surface and the area generated in this rotation was filled. The simulated rotation was used to analyse the effect of misalignment between the sample surface and the camera.† This rotated image was then blurred with a Gaussian filter and a background gradient added to the image (to simulate the surface of a substrate). | ||
| Fig. 3 A synthetic image of a droplet and its reflection generated with the spherical cap model. (a) Black and white binary image of a synthetic droplet and its reflection. The inset shows the pixelation of the edge. (b) Combination of the background gradient and blurred droplet image to create a synthetic image of a droplet. The binary image is blurred and added to a background gradient to create a grayscale image of a droplet. More images of synthetic droplets with varying contact angles can be found in the ESI.† | ||
The synthetic images of a droplet were generated using the supplementary code, specifically, the functions createDroplet and createImage.† The used binary images are included in the ESI.† The blurring, padding and rotation were added to these binary images at the same time as they were analysed with the script analyseSyntheticDrops.
4. Results & discussion
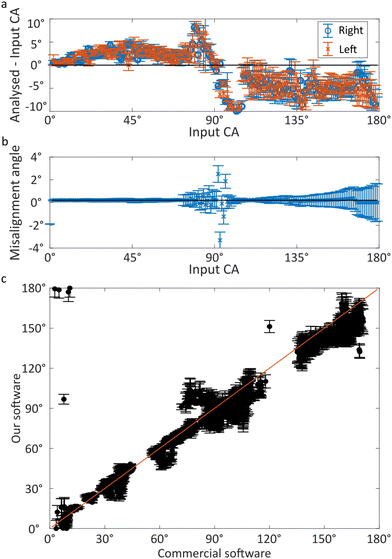
The contact angle analysis described above results in images of a droplet with an overlay of the detected edge and baseline and the fitted polynomial and its tangent at the baseline height (Fig. 4). The error bars of the detected edge are typically so small (around 2 pixels) that they are not visible in the full image. These small errors still propagate enough uncertainty for the regression parameters in the polynomial to cause significant errors in the estimated contact angle. In comparison, the contact points setting up the baseline have more visible errors (around 5 pixels), which typically have a smaller effect on the measured contact angle. For context, some methods state subpixel accuracy for their edge measurements; however, they do not report the uncertainty of their measurements.38,40 Thus, the true accuracy of subpixel methods might not really be subpixel and their accuracy could be more aligned with the accuracy we state here, i.e. around 2 pixels.26,27,34 The estimated error from the baseline is ∼100 times smaller compared to the error from the polynomial in many of our measurements. This is estimated based on a comparative size of the terms in eqn (7). However, the uncertainty of the intersection point is contained within the uncertainty of the polynomial, which explains the typical observation that the baseline location can cause large errors.17–20We validate our software against synthetic images of a droplet and experimental images from a commercial contact angle goniometer (Fig. 5). The analysis of the synthetic images of a droplet with a misalignment of 0.1° (Fig. 5a) shows agreement between the known contact angle and the analysed contact angle. Our software struggles to analyse contact angles in the range between 80° and 120°; however, in our experience this is a typical issue with many goniometry measurements using automated baseline detection. This struggle is because finding the correct baseline location is problematic due to poor detection of contact points, since the droplets and their reflection practically form a nearly perfect circle without any clear contact points to detect as edges. This is shown in the ESI.† The error bars are small (median 1.3°), which implies that the contact angle values and errors are estimated correctly.
We analysed the rotated synthetic images to check the effect of a tilted substrate in experimental images. The analysed misalignment angle in an example case with a misalignment of 0.1° (Fig. 5b) shows that the misalignment is accurately detected, except near 90°. Also, the estimated error increases between the contact angle values 120° and 179° from estimated errors of ±0.3° to ±1.5°. We also performed further analysis of synthetic images of a droplet with varying misalignment angle and these results are shown in the ESI.† These results show that the baseline detection works with varying misalignment angles in a synthetic image up to ±5°, which was the largest used misalignment angle. This amount of misalignment is larger compared to what we have experienced while measuring contact angles.
The experimental measurements from the commercial goniometer do not have any error estimates to which we could compare the measurements of our software. However, the device has a stated error of 0.1° for the whole measurement range. For comparison, we calculated the difference between the commercial device's and our software's results mean error of 1.5° with a standard deviation of 1.9° and the difference between the known contact angle of the synthetic images and our software's results with a mean of 1.6° and a standard deviation of 0.9°. Here, we have excluded points having a difference larger than 10°, difference between the left and right contact angles larger than 10° or measured contact angles outside 0°–180° as outliers. From the commercial software, the data points between 0° and 1° and above 180° were removed as outliers, as the values were clearly incorrect, e.g. 6 × 10−128° and 4 × 10252°. These means and standard deviations show that the results from synthetic images of a droplet have smaller variation due to their inherently fewer imperfections.
Typically, the error estimates using the commercial goniometer (or open-source methods) are based on the variation between multiple measurements, e.g. repeated measurements or measurements at different locations. In addition, commercial companies state a constant error value for the whole measurement range around 0.1°, which does not agree with the practical variance observed by many researchers.17–21 This way of estimating errors does not take into account the uncertainties from the image analysis, i.e. edge and contact point detection accuracy, which affects lighting, camera focus, etc. Although there are no in situ error estimates for the contact angle analysis from the commercial goniometer to compare with our method, the measured contact angle values from the commercial goniometer agree well with the analysis from our software (Fig. 5c). The only areas with variation between the two methods are specific experiments with low contact angles or near 90° based on the commercial goniometer. This can be explained by the contact points being hard to find in the low and near 90° values. The cluster at (0° and 180°) is due to the contact angles overflowing from 0° to 180° in our software. This then causes inherently a large uncertainty for both methods, explaining the variation. However, our software can predict this insensitivity, and the error bars increase in size, which shows the uncertainty the software has at this range. This ability to predict the uncertainties and insensitivities would be important when measuring non-standard droplets such as particle covered droplets, where the uncertainties are likely much larger due to a thicker surface.46,47 In comparison, the commercial goniometer does not have in situ error estimations or error flags, and the measurement accuracy is solely estimated based on the skill of the operator. Even when a highly skilled operator uses the goniometer, there are differences in the measured contact angles.20,21 With the in situ error estimations from our software, we can estimate the uncertainty of the analysis objectively for each frame of the analysis video. However, this is still not a complete analysis of errors; more robust protocols and detailed exploration of the effect of focus, lighting, and other experimental parameters are needed. For this development, the in situ error estimates are a crucial tool to grade the effects and finding the optimal values for the experimental parameters and finding the critical steps needing improvement in the protocols. When protocols considering more of the experimental parameters are developed, and researchers follow these protocols, the results of contact angle goniometer measurements could become truly comparable between research groups.
When there is uncertainty in the measurement of a contact angle, whether it affects the interpretation of the contact angle or not, it also affects the interpretation of contact angle hysteresis (CAH), i.e. the difference of advancing and receding contact angles (Δθ = θadv−θrec). If the assumed error is small (as the commercial and open-source methods do implicitly), the hysteresis can be incorrectly interpreted as small and we would expect to see, e.g. a small sliding angle and low adhesion. However, even a small uncertainty of 1° causes an increased uncertainty to the hysteresis by a factor of  when the errors from advancing and receding contact angles are assumed equal. This increase in error remains if we use the actual errors, and then it depends on the actual values of the error estimates as
when the errors from advancing and receding contact angles are assumed equal. This increase in error remains if we use the actual errors, and then it depends on the actual values of the error estimates as  . This error in hysteresis makes it impossible to interpret that the hysteresis is lower than the estimated error. One way to circumvent this problem is to use other techniques to measure the hysteresis, e.g. sliding angle or friction/adhesion force, which have higher accuracy in measuring the hysteresis in terms of the difference of cosines, i.e. Δcos
. This error in hysteresis makes it impossible to interpret that the hysteresis is lower than the estimated error. One way to circumvent this problem is to use other techniques to measure the hysteresis, e.g. sliding angle or friction/adhesion force, which have higher accuracy in measuring the hysteresis in terms of the difference of cosines, i.e. Δcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = cos
θ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θrec − cos
θrec − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θadv. Also, when estimating the adhesion or slipperiness of the surface, the contact angle and hysteresis in terms of cosines are more relevant than the pure contact angles, as the cosine versions are usually used in the equations instead of the hysteresis.48–50
θadv. Also, when estimating the adhesion or slipperiness of the surface, the contact angle and hysteresis in terms of cosines are more relevant than the pure contact angles, as the cosine versions are usually used in the equations instead of the hysteresis.48–50
5. Conclusions
We have included in situ error estimation in contact angle analysis, which commercial and open-source contact angle analysis has previously omitted. This method is a first step in developing a full error analysis in contact angle goniometry, as in situ error analysis is a crucial tool in exploring and characterizing the effect of experimental parameters of the instrument. The method was validated against commercial goniometer measurements and synthetic images of a droplet. The measured values of contact angles had good agreement with the commercial goniometer and simulated droplets with most values being within error bars. We also found a similar insensitivity with our method between 80° and 120° due to difficulties in finding contact points of the near circular droplet, which we have also experienced with the commercial goniometer with varying fitting methods. However, our analysis can correctly identify this insensitivity, which is seen with increased in situ error estimates. Previous methods do not offer similar in situ error estimations or flags to predict when the fit might be less trustworthy. For commercial contact angle goniometers, the companies typically proclaim a constant error value of 0.1° or similar; however, the correctness of such values is questionable, as the details of their error analysis is not explained in their materials.For increased reproducibility and comparability, we recommend such in situ error estimation with all future contact angle measurements. Practically, this means including the errors of the edge and baseline measurements and/or any other input errors in the analysis and propagating the error estimations into the contact angle measurement. Furthermore, the selection of the used method (polynomial, Young–Laplace, machine learning, or mask) and measurement protocol need to be considered mindfully, as different methods have different strengths, weaknesses, and ranges where they are accurate. The “static contact angle” does not contain meaningful information in wetting characterisation, as at best it is meaningless and at worst the measurement can give incorrect results leading to flawed decisions in research and development. Using error estimations, mindfully selecting the analysis methods, and the measurement protocol would increase the reproducibility of the contact angle measurements and enable more accurate comparisons between measurements from different research groups, which is currently challenging.
Author contributions
HAN worked on conceptualization, formal analysis, methodology, project administration, validation, visualization, and writing – original draft. HAN and GZ wrote software. HAN, GZ, SL, RS and MV did the investigation. RHAR did funding acquisition, resources, and supervision. HAN, MV and RHAR contributed to writing – review & editing.Data availability
Analysis code. The used analysis codes are shared as a separate supplementaryCodes.zip file. Raw data. The measurement videos from the commercial goniometer can be requested from the authors separately. Binary images. The used binary images are shared as a separate syntheticDroplets.zip file in the ESI.† Each file name has the contact angle of the simulated droplet, e.g., the file having the droplet with contact angle 15 has the name BWCA15. Goniometer data. The goniometer data are shared as a separate goniometerData.zip file.Conflicts of interest
All authors declare that they have no conflicts of interest.Acknowledgements
This work was carried out under the Research Council of Finland Center of Excellence Program (2022–2029) in Life-Inspired Hybrid Materials (LIBER) (project number 346109) and the Research Council of Finland's Proof of Concept Funding (project number 359419). The authors acknowledge Ville Jokinen for making silicon micropillar samples and Tommi Huhtamäki for making silicone nanofilament samples. HAN thanks Juuso Korhonen for the detailed discussions on the error analysis.References
- S. S. Latthe, R. S. Sutar, V. S. Kodag, A. Bhosale, A. M. Kumar, K. Kumar Sadasivuni, R. Xing and S. Liu, Prog. Org. Coat., 2019, 128, 52–58 CrossRef CAS.
- K. Sefiane, M. E. Shanahan and M. Antoni, Curr. Opin. Colloid Interface Sci., 2011, 16, 317–325 CrossRef CAS.
- F. Tarpoudi Baheri, M. Rico Luengo, T. M. Schutzius, D. Poulikakos and L. D. Poulikakos, J. Test. Eval., 2022, 50, 999–1008 CrossRef.
- G. Barati Darband, M. Aliofkhazraei, S. Khorsand, S. Sokhanvar and A. Kaboli, Arabian J. Chem., 2020, 13, 1763–1802 CrossRef CAS.
- M. Fromel, D. M. Sweeder, S. Jang, T. A. Williams, S. H. Kim and C. W. Pester, ACS Appl. Polym. Mater., 2021, 3, 5291–5301 CrossRef CAS.
- A. Marmur, Curr. Opin. Colloid Interface Sci., 2021, 51, 101388 CrossRef CAS.
- A. Marmur, C. D. Volpe, S. Siboni, A. Amirfazli and J. W. Drelich, Surf. Innovations, 2017, 5, 3–8 CrossRef.
- M. Ruzi, N. Celik and M. S. Onses, Food Packag. Shelf Life, 2022, 32, 100823 CrossRef CAS.
- M. Zaman Khan, J. Militky, M. Petru, B. Tomková, A. Ali, E. Tören and S. Perveen, Eur. Polym. J., 2022, 178, 111481 CrossRef CAS.
- M. A. Q. Siddiqui, S. Ali, H. Fei and H. Roshan, Earth-Sci. Rev., 2018, 181, 1–11 CrossRef.
- P. Ragesh, V. Anand Ganesh, S. V. Nair and A. S. Nair, J. Mater. Chem. A, 2014, 2, 14773–14797 RSC.
- I. S. Bayer, Adv. Mater. Interfaces, 2020, 7, 2000095 CrossRef CAS.
- S. M. Lößlein, R. Merz, D. W. Müller, M. Kopnarski and F. Mücklich, Sci. Rep., 2022, 12, 19389 CrossRef PubMed.
- D. Daniel, M. Vuckovac, M. Backholm, M. Latikka, R. Karyappa, X. Q. Koh, J. V. I. Timonen, N. Tomczak and R. H. A. Ras, Commun. Phys., 2023, 6, 152 CrossRef CAS.
- T. Huhtamäki, X. Tian, J. T. Korhonen and R. H. A. Ras, Nat. Protoc., 2018, 13, 1521–1538 CrossRef PubMed.
- F. J. M. Ruiz-Cabello, M. A. Rodríguez-Valverde and M. A. Cabrerizo-Vílchez, Adv. Colloid Interface Sci., 2014, 206, 320–327 CrossRef CAS PubMed.
- K. Liu, M. Vuckovac, M. Latikka, T. Huhtamäki and R. H. A. Ras, Science, 2019, 363, 1147–1148 CrossRef CAS PubMed.
- M. Vuckovac, M. Latikka, K. Liu, T. Huhtamäki and R. H. A. Ras, Soft Matter, 2019, 15, 7089–7096 RSC.
- J. Zimmermann, S. Seeger and F. A. Reifler, Text. Res. J., 2009, 79, 1565–1570 CrossRef CAS.
- V. Konduru, Static and dynamic contact angle measurement on rough surfaces using sessile drop profile analysis with application to water management in low temperature fuel cells, MS thesis, Michigan Technological University, 2010.
- H.-J. Butt, I. V. Roisman, M. Brinkmann, P. Papadopoulos, D. Vollmer and C. Semprebon, Curr. Opin. Colloid Interface Sci., 2014, 19, 343–354 CrossRef CAS.
- A. Krishnan, Y.-H. Liu, P. Cha, R. Woodward, D. Allara and E. A. Vogler, Colloids Surf., B, 2005, 43, 95–98 CrossRef CAS PubMed.
- H. Y. Erbil, Surf. Sci. Rep., 2014, 69, 325–365 CrossRef CAS.
- M. J. Orella, M. E. Leonard, Y. Román-Leshkov and F. R. Brushett, SoftwareX, 2021, 14, 100665 CrossRef.
- S. Srinivasan, G. H. McKinley and R. E. Cohen, Langmuir, 2011, 27, 13582–13589 CrossRef CAS PubMed.
- R. Akbari, F. Ambrosio, J. D. Berry and C. Antonini, J. Colloid Interface Sci., 2025, 678, 1075–1086 CrossRef CAS PubMed.
- R. Akbari and C. Antonini, Adv. Colloid Interface Sci., 2021, 294, 102470 CrossRef CAS PubMed.
- M. J. Wood, D. G. K. Aboud, G. Zeppetelli, M. B. Asadi and A.-M. Kietzig, Phys. Fluids, 2023, 35, 1–9 Search PubMed.
- D. Biolè and V. Bertola, Colloids Surf., A, 2015, 467, 149–156 CrossRef.
- J. Canny, IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, PAMI-8, 679–698 Search PubMed.
- D. Vikram Mutneja, J. Electr. Electron. Syst., 2015, 04, 1–5 Search PubMed.
- C. Harris and M. Stephens, Procedings of the Alvey Vision Conference 1988, 1988, pp. 1–23 Search PubMed.
- J. Sánchez, N. Monzón and A. Salgado, Image Process. Line., 2018, 8, 305–328 CrossRef.
- D. G. Shaw, R. Liang, T. Zheng, J. Qi and J. D. Berry, Langmuir, 2024, 40, 16757–16770 CrossRef CAS PubMed.
- J. S. Allen, J. Colloid Interface Sci., 2003, 261, 481–489 CrossRef CAS PubMed.
- E. Albert, B. Tegze, Z. Hajnal, D. Zámbó, D. P. Szekrényes, A. Deák, Z. Hórvölgyi and N. Nagy, ACS Omega, 2019, 4, 18465–18471 CrossRef CAS PubMed.
- S. F. Chini and A. Amirfazli, Colloids Surf., A, 2011, 388, 29–37 CrossRef CAS.
- A. Bateni, S. S. Susnar, A. Amirfazli and A. W. Neumann, Colloids Surf., A, 2003, 219, 215–231 CrossRef CAS.
- A. F. Stalder, G. Kulik, D. Sage, L. Barbieri and P. Hoffmann, Colloids Surf., A, 2006, 286, 92–103 CrossRef CAS.
- E. Atefi, J. A. Mann and H. Tavana, Langmuir, 2013, 29, 5677–5688 CrossRef CAS PubMed.
- S. Lepikko, Y. M. Jaques, M. Junaid, M. Backholm, J. Lahtinen, J. Julin, V. Jokinen, T. Sajavaara, M. Sammalkorpi, A. S. Foster and R. H. A. Ras, Nat. Chem., 2024, 16, 506–513 CrossRef CAS PubMed.
- V. Liimatainen, M. Vuckovac, V. Jokinen, V. Sariola, M. J. Hokkanen, Q. Zhou and R. H. A. Ras, Nat. Commun., 2017, 8, 1798 CrossRef PubMed.
- M. Junaid, H. A. Nurmi, M. Latikka, M. Vuckovac and R. H. A. Ras, Droplet, 2022, 1, 38–47 CrossRef.
- Q. Pan, H. Jin and H. Wang, Nanotechnology, 2007, 18, 355605 CrossRef.
- F. Zhang, W. B. Zhang, Z. Shi, D. Wang, J. Jin and L. Jiang, Adv. Mater., 2013, 25, 4192–4198 CrossRef CAS PubMed.
- H. Liu, X. Pang, M. Duan, Z. Yang, T. P. Russell and X. Li, Adv. Mater., 2024, 37, 2413862 CrossRef PubMed.
- X. Li, X. Pang, H. Jiang, M. Duan, H. Liu, Z. Yang, Y. Xi and T. P. Russell, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2302907120 CrossRef CAS PubMed.
- M. E. Schrader, Langmuir, 1995, 11, 3585–3589 CrossRef CAS.
- C. G. L. Furmidge, J. Colloid Sci., 1962, 17, 309–324 CrossRef CAS.
- H.-J. Butt, J. Liu, K. Koynov, B. Straub, C. Hinduja, I. Roismann, R. Berger, X. Li, D. Vollmer, W. Steffen and M. Kappl, Curr. Opin. Colloid Interface Sci., 2022, 59, 101574 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01509f |
| This journal is © The Royal Society of Chemistry 2025 |