Open Access Article
Open Access ArticlePhysical scaling for predicting shear viscosity and memory effects of lithium-ion battery cathode slurries†
Yoshita
Gupta‡
 ,
Qingsong
Liu‡
,
Qingsong
Liu‡
 and
Jeffrey J.
Richards
and
Jeffrey J.
Richards
 *
*
Department of Chemical and Biological Engineering, Northwestern University, Evanston, IL 60208, USA. E-mail: jeffrey.richards@northwestern.edu
First published on 22nd January 2025
Abstract
Lithium-ion battery cathodes are manufactured by coating slurries, liquid suspensions that typically include carbon black (CB), active material, and polymer binder. These slurries have a yield stress and complex rheology due to CB's microstructural response to flow. While optimizing the formulation and processing of slurries is critical to manufacturing defect-free and high-performance cathodes, engineering the shear rheology of cathode slurries remains challenging. In this study, we conducted simultaneous rheo-electric measurements on 3 wt% CB suspensions in N-methyl-2-pyrrolidone containing various loadings of active material NMC811 and polyvinylidene difluoride. Accounting for the changes in the infinite shear viscosity, the yield stress, and the medium viscosity due to the presence of NMC and polymers, we defined the differential relative viscosity. This differential relative viscosity, Δηr, is a measure of the distance from the infinite shear rate, where carbon black agglomerates are fully broken down. We find that Δηr collapses all flow curves regardless of formulation with an empirical relationship Δηr = 2.18Mn−0.92f, indicating a quantitative prediction of the flow curve of cathode slurries across a wide range of formulation space. We then used electrical conductivity to identify and quantify shear-induced structure memory, evidenced in the ratio of the under-shear conductivity over the post-shear quiescent conductivity. We find that similar to the changes in the yield stress, increasing NMC concentration increases memory retention, and in contrast, the addition of PVDF erases memory effects. Our findings here will provide valuable insight into engineering the formulation and processing conditions of lithium-ion battery cathodes.
Introduction
Lithium-ion batteries (LIBs) play a central role in transitioning our society to a sustainable future reliant on renewable energy.1 With an increasing demand for LIBs, an improved understanding of the manufacturing processes aiming to produce high-performance and defect-free porous electrodes2–6 is needed. In particular, the rheology of cathode slurry, which is a liquid suspension of active material (AM), polymer binder (PB), and carbon black (CB), remains challenging to predict. The rheology of the cathode slurry plays a key role in determining battery performance because the slurry is deposited at high speed onto a current collector. Cathode slurry formulations with the right rheology flow easily out of the coater head and solidify rapidly after coating to form a uniform film.4,6–8 To achieve this, slurries must have a low viscosity at high shear rate, a high viscosity at low shear rate, and a sufficient yield stress to prevent sedimentation of the solid slurry components. At the same time, the porosity of the carbon black binder domain is determined in part by the detailed flow conditions encountered during the coating operation. Linking this complex flow to microstructure remains nontrivial as the CB agglomerates in cathode slurry evolve under flow.9–11CB's rich rheological behavior originates from its hierarchical structure.9,10 At the nanoscale, CB's primary particles (∼10 nm) are fused into primary aggregates (∼100 nm) through covalent bonds. These primary aggregates then form agglomerates due to attractive interactions in the slurry. When suspended in a solvent and exceeding a critical volume fraction, these agglomerates form a percolated network that gives the slurry a yield stress.12 A comprehensive understanding of the agglomerate structural evolution in Newtonian fluids has recently emerged and summarized in a review paper.11 In particular, Hipp et al.9,10 showed that the rheology of CB in Newtonian fluids can be demarcated into two regions: the weak flow region and the strong flow region. When the stress response is below the yield stress, CB agglomerates densify and sediment, and this structural evolution yields a rheopectic response over a long timescale.10,13 Within this weak flow region, CB might also form anisotropic structures such as vorticity-aligned agglomerates when subjected to confinement.14–18 In the strong flow region where the stress response is above the yield stress, Hipp et al.9 and Bauland et al.19 revealed that CB agglomerates undergo self-similar breakup in response to increasing hydrodynamic force using scattering methods. Previous studies have shown that the fluid Mason number (Mnf),20–23 the dimensionless ratio of the hydrodynamic forces acting on the agglomerate and the cohesive force binding them together, can accurately predict the agglomerate size of CB, and therefore the rheology in the strong flow region regardless of the CB or the solvent types.24
The shear rheology of CB suspensions added with other slurry components has also been extensively studied due to their relevance to battery manufacturing. For example, Bauer and Notzle25 demonstrated the critical role of polyvinylidene difluoride (PVDF), a common polymer binder, in forming a gelling network that prevents the aggregation and sedimentation of active material particles. Using simultaneous rheo-electric measurements, Liu and Richards26 demonstrated that PVDF is non-absorbing to CB, and it only enhances the breakup of CB agglomerates via increasing the medium viscosity. This observation is consistent with that reported by Sung et al.4 who showed that PVDF is not absorbed to either CB or active material NMC. Furthermore, Ouyang et al.6 showed that overall solid content is a critical factor in controlling the rheology of LIB slurries. They observed that with increasing solid contents, slurries displayed a higher viscosity but reduced thixotropy.
While much has been reported on slurry shear rheology, rationalizing and predicting the flow curves based on formulation characteristics remains challenging due to the lack of a unified framework that reveals individual components’ contributions to rheology. To address this challenge, we conducted rheo-electric measurements on a series of slurry samples containing CB, PVDF, and NMC811 (LiNi0.8Mn0.1Co0.1O2). To elucidate the roles of NMC and PVDF in modifying the flow curves of these slurries, we fixed the weight percentage of CB in the liquid phase of the suspensions. By first varying the NMC loading, we determined the infinite shear viscosity where CB agglomerates are fully broken down and showed that it only depends on the composition of NMC and CB and is enhanced linearly by the PVDF solution viscosity. The yield stress, which depends on the cohesive bonds formed by CB, decreases and recovers with increasing NMC and PVDF loadings respectively. To account for the changes in the yield stress and the medium viscosity, we defined a relative differential shear viscosity, Δηr, as the measure of the distance from the infinite shear viscosity, where carbon black agglomerates are fully broken down. Using this definition, we collapsed the flow curves of slurries containing various loadings of PVDF and NMC using the fluid Mason number. We further extracted the carbon-phase conductivity from simultaneous rheo-electric measurements and revealed that the conductivity scales with the yield stress, which strongly suggests that the number of bonds between CB agglomerates might have been modified rather than the strength of these cohesive bonds. Finally, we identified that these slurries exhibit shear-induced memory effects that depend on the NMC and PVDF loading.
Methods and materials
Materials
The polyvinylidene difluoride (PVDF) variants Kynar 741 (batch 20C6072) and Kynar 761 (batch 20C3014), were supplied by Arkema (King of Prussia, PA). Solvent N-methyl-2-pyrrolidone (NMP) (ACS reagent, ≥99.0%, density = 1.028 g mL−1, viscosity = 0.00165 Pa s) was obtained from Sigma-Aldrich (St. Louis, MO). Super-C65 carbon black (CB) (batch 29719AA) was sourced from MSE Supplies (Tucson, AZ). Lithium Nickel Manganese Cobalt Oxide – NMC 811 (LiNi0.8Mn0.1Co0.1O2, density = 4.78 g cm−3) was used as active material (NMC); purchased from MSE Supplies (Tucson, AZ), batch number 19622C7.Sample preparation
CB-NMC suspensions were prepared by blending the dry powders of CB and NMC, followed by the addition of a known amount of NMP to form a suspension of known total solids fraction. For PVDF-CB-NMC slurries, a PVDF solution was prepared separately by dissolving a measured mass of PVDF powder in a specified volume of NMP, heating it on a hot plate at 80 °C for 3–4 hours, and then keeping it on a roller plate until complete dissolution was visually confirmed.26 The PVDF solution was then added to the blended CB and NMC dry powder. Both mixtures were processed in a planetary mixer (Thinky AR-100) at 2000 rpm for 7 minutes. To achieve the desired solid weight percentage, additional NMP was added, and the samples were subjected to another round of mixing at 2000 rpm for 12 minutes. Immediately after the final mixing, the samples were loaded into a rheometer to ensure the analyzed composition matched the prepared mixture.Rheo-electric measurements
A strain-controlled rheometer (ARES-G2, TA Instruments, New Castle, DE) with a dielectric Couette geometry (inner diameter = 26 mm, outer diameter = 27 mm, truncation gap = 0.5 mm) was used for rheological measurements.26–29 The rheometer was equipped with a forced convection oven for temperature control and was maintained at 25 °C. Fomblin oil was used as a solvent trap to prevent NMP evaporation during the experiment. The impedance data was measured using an impedance analyzer (E4990A, Keysight Technologies, Santa Rosa, CA) at a voltage amplitude of 500 mV over a frequency range of 20 Hz to 10 MHz. Rheo-electric measurements were conducted using9 a setup that modified the standard protocol used by Hipp et al.9 and Liu et al.26 to measure the changing microstructure of CB under shear. After preparing the samples in the planetary mixer, a conditioning protocol was implemented. In this protocol, samples were subjected to a high shear rate of 2500 s−1 for 160 seconds, followed by a low shear rate of 100 s−1 for 160 seconds. This alternating cycle was repeated 22 times. We found this conditioning step to be necessary as it produces reproducible impedance and rheology after many cycles as shown in Fig. S1–S3 (ESI†).Once adequately conditioned, a three-step rheo-electric measurement was performed at different shear rates. The protocol involved pre-shearing at 2500 s−1 for 160 seconds, followed by shearing at the specific shear rate (between 1 to 2500 s−1) intended for measurement for 160 seconds, and ending with measuring properties in the quiescent state 0 s−1 for 210 seconds (the electric measurement starts after 50 seconds of resting). This three-step process was repeated to get a measurement of the flow curve for each shear rate. At each shear rate, the maximum stress value recorded during the experiment is used to create self-similar flow curves, generated by carbon black suspensions.9,17,26 These values are then fitted to the Herschel–Bulkley model9,30,31 given by eqn (1)
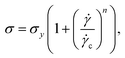 | (1) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , σy is the yield stress of the suspension beyond which the suspension starts to flow,
, σy is the yield stress of the suspension beyond which the suspension starts to flow, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c is the critical shear rate, n is the power law index which determines the relationship between stress and shear rate. When n = 1, suspension behaves Newtonian once the yield stress is exceeded and suspension is shear thinning for n < 1.
c is the critical shear rate, n is the power law index which determines the relationship between stress and shear rate. When n = 1, suspension behaves Newtonian once the yield stress is exceeded and suspension is shear thinning for n < 1.
The raw impedance data were measured during both the shear and post-shear steps over a frequency range of 20 Hz to 10 MHz and all impedance data was corrected using short and open circuit measurements to correct for the capacitance of the open cell and the resistance and stray inductance of the cables.32 We then converted the corrected impedance, Z* to the complex permittivity, ε*(ω), using eqn (2),
| ε*(ω) = Ccell/(2πiZ*fε0) = ε′ − iε′′, | (2) |
Results and discussion
We first explored the impact of active material NMC811 concentration on the self-similar flow curves9,17,26 of Super C65 carbon black (CB) suspensions in n-methyl pyrrolidone (NMP) containing increasing amounts of dissolved PVDF 741 (LP) and PVDF 761 (HP), linear PVDF polymers with molecular weight of 354.3 and 681 kg mol−1 respectively. NMC811 is made of polydisperse non-Brownian particles, with an average diameter of 6.8 ± 2.8 μm.33 The CB loading was fixed at 3 wt% in the suspension phase consisting of NMP, PVDF, and CB. Fig. 1a shows the viscosity (η) versus shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) for CB suspensions containing no NMC as a function of PVDF molecular weight and concentration. This data, reproduced from the study by Liu and Richards,26 showed shear thinning due to the breakup of CB agglomerates and an expected increase in viscosity at high shear rates with increasing polymer concentration and molecular weight (Reproduced from Liu and Richards26 with permission from the Society of Rheology (SOR)). To assess the impact of NMC on the rheology, suspensions of CB in NMP were formulated with increasing NMC concentration in the absence of PVDF. The resulting flow curves are shown in Fig. 1b. Increasing NMC weight percent reduces the viscosity across all shear rates. At the highest shear rates tested, the suspensions exhibit an almost Newtonian response, suggesting that it has reached the infinite shear limit, which is usually not observed in pure CB suspensions.9 Further, in comparison to the base carbon black suspension, the shear viscosity decreases with increasing NMC concentration. To observe the effect of PVDF, flow curves were measured that incorporated 10 wt% and 20 wt% NMC while varying the concentration and molecular weight of PVDF in the base CB suspension. The results are shown in Fig. 1c and d for 10 wt% NMC and 20 wt% NMC respectively. In both cases, the addition of polymer increases the viscosity across all shear rates, with the highest concentrations tested approaching the flow curve for the base suspension but never exceeding it.
) for CB suspensions containing no NMC as a function of PVDF molecular weight and concentration. This data, reproduced from the study by Liu and Richards,26 showed shear thinning due to the breakup of CB agglomerates and an expected increase in viscosity at high shear rates with increasing polymer concentration and molecular weight (Reproduced from Liu and Richards26 with permission from the Society of Rheology (SOR)). To assess the impact of NMC on the rheology, suspensions of CB in NMP were formulated with increasing NMC concentration in the absence of PVDF. The resulting flow curves are shown in Fig. 1b. Increasing NMC weight percent reduces the viscosity across all shear rates. At the highest shear rates tested, the suspensions exhibit an almost Newtonian response, suggesting that it has reached the infinite shear limit, which is usually not observed in pure CB suspensions.9 Further, in comparison to the base carbon black suspension, the shear viscosity decreases with increasing NMC concentration. To observe the effect of PVDF, flow curves were measured that incorporated 10 wt% and 20 wt% NMC while varying the concentration and molecular weight of PVDF in the base CB suspension. The results are shown in Fig. 1c and d for 10 wt% NMC and 20 wt% NMC respectively. In both cases, the addition of polymer increases the viscosity across all shear rates, with the highest concentrations tested approaching the flow curve for the base suspension but never exceeding it.
To go beyond qualitative comparison, we fit the Herschel–Bulkley (HB) model to the stress-shear rate relationship as summarized in Fig. 2a–d. We analyzed the flow behavior up to a shear rate of 700 s−1, where we aim to capture the power-law regime explained by HB fits of the flow curves. This range of shear rates was chosen because the Herschel-Bulkley model cannot describe the rheological behaviors of some samples at high shear rates, where the viscosity reaches the infinite shear limit. The solid lines are overlaid on the experimental data and the fits show excellent agreement with the experimental rheology, indicating that the fluids all exhibit a yield stress. The impact of NMC on the flow curve in the absence of PVDF is shown in Fig. 2b. With increasing NMC concentration, the stress decreases across all shear rates tested including a dramatic decrease in the apparent yield stress. The impact of polymer addition is noteworthy, as PVDF universally increases the stress across all tested shear rates for a fixed NMC concentration, as shown in Fig. 2c and d. HP induces larger stress increases compared to LP at the same PVDF concentration for both NMC loadings, which is consistent with Fig. 2a.26 However, unlike in Fig. 2a where PVDF plays little role in the apparent yield stress, the addition of PVDF to the underlying CB-NMC suspension dramatically increases the apparent yield stress.
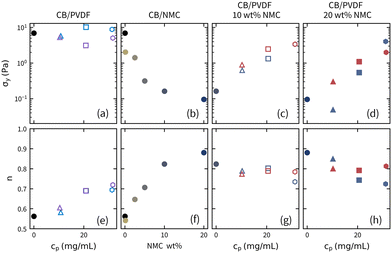
The results of the HB model fits are summarized in Fig. 3 and Table S1 (ESI†). The yield stress, σy, and power-law index, n, from the HB-model are summarized as a function of NMC weight percentage, and PVDF concentration, cp, in Fig. 3. As seen in Fig. 3a, the addition of PVDF to CB suspensions has a subtle and non-monotonic impact on the yield stress, but systematically increases the power-law index. Liu and Richards26 attributed the increased power-law index to the higher suspending medium viscosity and assumed that the yield stress was independent of polymer concentration and molecular weight due to the lack of adsorption of PVDF to CB. In contrast, when NMC is added to the CB suspensions without PVDF, the σy decreases from 10 Pa to <0.2 Pa (Fig. 3b) and the n increases from 0.6 to 0.9 (Fig. 3c), indicating that higher NMC concentrations exhibited diminished shear thinning. However, as shown in Fig. 3c, d and g, h, increasing polymer concentration restores the yield stress and n back toward the base carbon black suspension at the same solution composition. It is also notable that the increase in yield stress and decrease in power-law index is not a strong function of molecular weight.
To quantify the changes in viscosity in the high shear limit, a linearization, log(η) vs. 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , was constructed to extrapolate to the infinite shear viscosity (η∞), where the viscosity becomes independent of shear rate. As the infinite viscosity is only dependent on the sample composition, predicting its value from the details of the formulation can be used to approximate the high-shear viscosity. An example, shown in the inset of Fig. 4a, demonstrates that linear extrapolation to the ordinate yields an estimate for η∞. This procedure was repeated for all suspensions and the results for CB-NMC suspensions are shown in Fig. 4a.
, was constructed to extrapolate to the infinite shear viscosity (η∞), where the viscosity becomes independent of shear rate. As the infinite viscosity is only dependent on the sample composition, predicting its value from the details of the formulation can be used to approximate the high-shear viscosity. An example, shown in the inset of Fig. 4a, demonstrates that linear extrapolation to the ordinate yields an estimate for η∞. This procedure was repeated for all suspensions and the results for CB-NMC suspensions are shown in Fig. 4a.
In bimodal mixture suspensions34–36 containing particles with two different sizes, when smaller particles are added to a matrix of larger particles, the smaller particles fill the voids between the larger particles, resulting in a reduced viscosity due to the change in the maximum packing volume fraction. The suspensions in Fig. 4a show a notable reduction in viscosity to 20 wt% NMC, aligning with previous findings where smaller particles efficiently pack between larger particles. However, previous publications only varied the weight ratio of the two sizes of particles without changing the total solid contents. Beyond 20 wt% NMC, the viscosity begins to increase. A similar inflection has also been previously reported by Chang et al.,37 Shapiro et al.38 and Pednekar et al.39 and is typical of bimodal suspensions when they surpass the optimal packing fraction. At higher loading of large particles, the suspension becomes densely packed or crowded, leading to increased particle interactions and higher viscosity. Therefore, while the systems tested here seem to follow the trends observed in literature, such behaviors might not necessarily be fully explained by previous studies on bimodal mixture suspensions as both the ratio and the total solid content are varied in our suspensions.
We define the relative infinite shear viscosity of the CB-NMC suspensions in neat NMP as η0Pr,∞, a ratio of infinite shear viscosity without PVDF, η0P∞, to the viscosity of NMP, ηNMP. We find that η0Pr,∞ = η0P∞/ηNMP decreases as a function of NMC weight percentage, consistent with qualitative trends from Fig. 1b. We also determined η∞ for all the PVDF containing suspensions, which is presented in Fig. 4b and plotted versus the product ηmη0Pr,∞, where ηm is the medium viscosity, or the viscosity of PVDF in NMP solution. As shown by the dashed line in Fig. 4b, η∞ is quantitatively predicted by this relationship. This finding suggests that the infinite shear viscosity is primarily a function of NMC wt% for a given CB wt% in the suspension and that the polymer contributes predictably via increasing the medium viscosity. This dependence can therefore be determined for a given NMC and CB type, and the infinite shear viscosity estimated from the underlying polymer solution viscosity.
To understand how the CB agglomerates behave under varying shear conditions and PVDF-NMC compositions, we employ the fluid Mason Number,
Mnf = 6πϕCB2ηm![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /σy /σy | (3) |
| Δηr = (η − η∞)/ηm | (4) |
The results of this physical scaling reveal that the addition of NMC and PVDF has nontrivial effects on the yield stress, and therefore allows the slurry suspensions to achieve a wide range of Mnf under the same tested shear rates. To further investigate the origin of the modified yield stress in different formulations, rheo-electric measurements were performed. Helal et al.43 found that the electronic conductivity of CB is strongly linked to the storage modulus achieved in different CB volume fractions or shear histories. We therefore hypothesize that similar phenomena can be observed among LIB formulations that possess different yield stress values. As shown in Fig. S5 (ESI†), we fit a specified frequency range of permittivity data with an equivalent circuit model, which includes a constant phase element in series with a Cole–Cole equation and an ideal resistor in parallel.44 From the fitted conductivity, we obtain the carbon-phase electronic conductivity, κ, under the assumption that the ionic conductivity is negligible. We anticipate that the changes in yield stress come from the number of bonds formed by the CB agglomerates instead of the cohesive force between them. Within CB suspensions, electrons are transported through the conductive network formed by CB agglomerates that are in contact and near proximity.12,26,43,45 For suspensions at rest, the magnitude of electronic conductivity for CB suspensions at the same volume fraction reflects the number of cohesive bonds formed among CB agglomerates while the strength of the bonds has no impact on the electron transport. In Fig. 5b, the post-shear conductivity at 2500 s−1 is shown versus the fitted yield stress from flow curves. In this plot, there is a clear trend of increasing conductivity with increasing yield stress, with a scaling of κpost-shear ∼ σy0.61. This physical scaling is consistent with that observed in pure CB suspensions at different volume fractions by Helal et al.43 When NMC is absent, the carbon phase conductivity remains similar at different polymer loadings, corresponding to almost unchanged yield stress values, as shown in the upper right corner of the plot. When NMC is added to CB suspensions, the decrease in conductivity is coupled with decreased yield stress. On the other hand, the addition of polymers to those suspensions restores the yield stress, and therefore the high conductivity in the carbon phase. Together, all the experimental evidence here suggests that the presence of NMC diminishes CB's ability to agglomerate and reduces the number of bonds within the suspensions, while the addition of PVDF to suspensions containing NMC and CB restores such ability. It should be noted that such coupling between the yield stress and the electrical conductivity will only be valid if CB is the only contributor to both properties. A recent study by Jiang et al.46 showed that when large-sized fillers were added to attractive colloidal gel, the yield stress would be modified significantly once the filler volume fraction exceeds 20%. We therefore expect that for a large loading of NMC, the power-law scaling we observe in electrical conductivity might be invalid.
The link between conductivity of the carbon black network and the yield stress shown in Fig. 5b is determined post-shear, where measurements are made in the quiescent state following steady shearing at the same shear rate for all suspensions. This illustrates the important role of formulation in determining the electrical and mechanical properties of the liquid slurry subjected to strong flow. However, the formulation is not sufficient to predict the properties of cathode slurries as it is well-established that pre-shear stress or shear history can dictate the quiescent properties of carbon black gels,43,45,47 and therefore can induce memory effects where the quiescent properties mimic the under-shear properties. It should be noted that the memory effects discussed here are distinctly different from the memory in transient thixotropic responses discussed by Jamali and McKinley.48 Here, the memory effects originate from CB's ability to form a percolated network upon the cessation of flow. Shear memory effects, such as those observed by Ovarlez et al.,47 imply that cathode slurry electrical properties are potentially a function of shear history as well. To illustrate shear memory effects in cathode slurries, we compared two suspensions that have identical flow curves in the Mnf framework, as shown in the upper panel in Fig. 6a. The first sample is a 3 wt% carbon black suspension in a 3 wt% LP solution without NMC. The second sample is a 3 wt% carbon black suspended in neat NMP containing 2.5 wt% NMC. In the lower panel of Fig. 6a, we plot the conductivity of both samples under shear and post-shear as a function of Mnf. In both cases, the post-shear conductivity is higher than the conductivity during shear across all Mnf, and the conductivity under shear decreases with increasing Mnf. This is consistent with the increasing breakup of CB agglomerates with increasing shear intensity, which after cessation of shear reform a percolated network with closer and more conducting pathways. For the first sample, the post-shear conductivity recovers to the same value regardless of the shear condition, confirming that there is no shear memory in this sample in the strong flow region. In contrast, the second sample shows evidence of shear memory as the post-shear conductivity matches closely that measured during shear. Compared to the neat CB sample, the NMC sample has a lower yield stress, and the LP sample has a higher medium viscosity, which by coincidence results in a similar range of Mnf for two different samples. Therefore, we speculate that the memory effects are correlated to the yield stress, as such effects are not observed in the LP sample. To test this hypothesis, we then calculated the ratio, κshear/κpost-shear, for all formulations tested at 2500 s−1, as shown in Fig. 6b. For samples showing strong memory effects, we expect this value to be close to 1. We observe that for samples exhibiting a low yield stress, κshear/κpost-shear is very close to one. As the yield stress of the sample increases, κshear/κpost-shear decreases, indicating diminished memory retention. This observation further confirms that the yield stress is a direct indication of CB's ability to agglomerate in different formulations, and it is a strong indicator of the memory effects. As memory effects in colloidal gels are an emerging topic with great theoretical and practical interest,49–51 we anticipate that the memory effects of LIB slurry can be tuned by modifying the yield stress by changing the NMC and polymer loadings.
Conclusions
In this study, we conducted simultaneous rheo-electric measurements on a wide range of LIB slurry formulations to reveal a unified framework that can quantitatively describe their shear rheology under industrially relevant processing conditions. We measured the flow curves of 3 wt% CB suspensions containing various loadings of NMC811 and PVDF and observed changes in the infinite shear viscosity, the yield stress, and the medium viscosity. Accounting for these changes, we successfully collapsed the differential relative viscosity that only depends on the CB agglomeration with the fluid Mason number, with an empirical power-law scaling of Δηr = 2.18Mn−0.92f. We then investigated the origin of the changing yield stress among different slurry formulations by extracting the shear and post-shear conductivity using the electric measurements. We observed a power-law scaling between the yield stress and the conductivity, which suggests that the changes in the yield stress are likely due to variations in the number of bonds rather than the strength of CB agglomerates. This power-law scaling confirms the role of NMC in decreasing the yield stress via frustrating CB's ability to form agglomerates and that of PVDF in mitigating such effects. Finally, we investigated the memory effects in LIB slurries by comparing the post-shear and shear conductivity. We observed a strong correlation between the yield stress and the memory effects, as displayed in the deviation between the shear and post-shear conductivity.This fluid Mason number framework provides a unified picture of how polymer binders and active materials particles modify the shear rheology of CB suspensions for lithium-ion battery cathode slurry applications. The finding here suggests that the flow curve of slurries containing CB can be predicted and rationalized with the fluid Mason number using the power-law scaling provided the infinite shear viscosity of a given CB/NMC composition is known or measured separately. This framework has the potential to help optimize and engineer slurry formulations and processing conditions. We also anticipate that such a framework can be extended to any suspensions containing attractive colloidal gels and other interacting or non-interacting components. Finally, the memory effects observed in LIB slurries indicate that the microstructure, and therefore the relevant macroscopic properties, can be carefully tuned by modifying the formulations and the processing history to achieve optimal performance for the manufactured functional cathodes.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award No. DE-SC-0022119. The rheo-electric measurement setup is based upon work supported by the National Science Foundation under Grant No. (CBET-2047365). Q. L. acknowledged that this research was supported in part by an appointment to the Oak Ridge National Laboratory GRO Program, sponsored by the U.S. Department of Energy and administered by the Oak Ridge Institute for Science and Education. Q. L. gratefully acknowledges the support from the Ryan Fellowship and the International Institute for Nanotechnology at Northwestern University. We thank Jeffrey Lopez and Willa Brenneis for discussions on the impedance data fitting.Notes and references
- B. Nykvist and M. Nilsson, Nat. Clim. Change, 2015, 5, 329–332 CrossRef.
- S. L. Morelly, N. J. Alvarez and M. H. Tang, J. Power Sources, 2018, 387, 49–56 CrossRef CAS.
- J. K. Mayer, L. Almar, E. Asylbekov, W. Haselrieder, A. Kwade, A. Weber and H. Nirschl, Energy Technol., 2020, 8, 1–11 Search PubMed.
- S. H. Sung, S. Kim, J. H. Park, J. D. Park and K. H. Ahn, Materials, 2020, 13, 1–11 Search PubMed.
- W. B. Hawley and J. Li, J. Energy Storage, 2019, 26, 100994 CrossRef.
- L. Ouyang, Z. Wu, J. Wang, X. Qi, Q. Li, J. Wang and S. Lu, RSC Adv., 2020, 10, 19360–19370 RSC.
- J. H. Park, S. H. Sung, S. Kim and K. H. Ahn, Ind. Eng. Chem. Res., 2022, 61, 2100–2109 CrossRef CAS.
- Z. Wang, T. Zhao and M. Takei, J. Electrochem. Soc., 2019, 166, A35–A46 CrossRef.
- J. B. Hipp, J. J. Richards and N. J. Wagner, J. Rheol., 2021, 65, 145–157 CrossRef CAS.
- J. B. Hipp, J. J. Richards and N. J. Wagner, J. Rheol., 2019, 63, 423–436 CrossRef CAS.
- J. J. Richards, P. Z. Ramos and Q. Liu, Front. Phys., 2023, 11, 1–11 Search PubMed.
- J. J. Richards, J. B. Hipp, J. K. Riley, N. J. Wagner and P. D. Butler, Langmuir, 2017, 33, 12260–12266 CrossRef CAS PubMed.
- A. Zaccone, D. Gentili, H. Wu, M. Morbidelli and E. Del Gado, Phys. Rev. Lett., 2011, 106, 138301 CrossRef PubMed.
- C. O. Osuji and D. A. Weitz, Soft Matter, 2008, 4, 1388–1392 RSC.
- A. S. Negi and C. O. Osuji, Rheol. Acta, 2009, 48, 871–881 Search PubMed.
- Z. Varga, V. Grenard, S. Pecorario, N. Taberlet, V. Dolique, S. Manneville, T. Divoux, G. H. McKinley and J. W. Swan, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 12193–12198 CrossRef CAS PubMed.
- Y. Wang and R. H. Ewoldt, J. Rheol., 2022, 66, 937–953 CrossRef CAS.
- C. O. Osuji, C. Kim and D. A. Weitz, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2008, 77, 8–11 CrossRef PubMed.
- J. Bauland, L.-V. Bouthier, A. Poulesquen and T. Gibaud, J. Rheol., 2024, 68, 429–443 CrossRef CAS.
- R. C. Sonntag and W. B. Russel, J. Colloid Interface Sci., 1986, 113, 399–413 CrossRef CAS.
- Z. Varga and J. W. Swan, J. Rheol., 2018, 62, 405–418 CrossRef CAS.
- A. P. R. Eberle, N. Martys, L. Porcar, S. R. Kline, W. L. George, J. M. Kim, P. D. Butler and N. J. Wagner, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2014, 89, 1–5 CrossRef PubMed.
- D. Xie, H. Wu, A. Zaccone, L. Braun, H. Chen and M. Morbidelli, Soft Matter, 2010, 6, 2692–2698 RSC.
- J. B. Hipp, P. Z. Ramos, Q. Liu, N. J. Wagner and J. J. Richards, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2403000121 CrossRef CAS PubMed.
- W. Bauer and D. Nötzel, Ceram. Int., 2014, 40, 4591–4598 CrossRef CAS.
- Q. Liu and J. J. Richards, J. Rheol., 2023, 67, 647–659 CrossRef CAS.
- J. K. Riley, J. J. Richards, N. J. Wagner and P. D. Butler, Soft Matter, 2018, 14, 5344–5355 RSC.
- J. J. Richards and J. K. Riley, Curr. Opin. Colloid Interface Sci., 2019, 42, 110–120 CrossRef CAS.
- P. Z. Ramos, C. C. Call, L. V. Simitz and J. J. Richards, J. Colloid Interface Sci., 2023, 634, 379–387 CrossRef CAS PubMed.
- A. Z. Nelson and R. H. Ewoldt, Soft Matter, 2017, 13, 7578–7594 RSC.
- W. H. Herschel and R. Bulkley, Kolloid-Z., 1926, 39, 291–300 CrossRef.
- J. J. Richards and J. K. Riley, Curr. Opin. Colloid Interface Sci., 2019, 42, 110–120 CrossRef CAS.
- Q. Liu, W. Brenneis, G. Nagy, M. Doucet, J. Lopez and J. J. Richards, J. Mater. Chem. A, 2024, 12, 33114–33124 RSC.
- J. S. Chong, E. B. Christiansen and A. D. Baer, J. Appl. Polym. Sci., 1971, 15, 2007–2021 Search PubMed.
- A. J. Poslinski, M. E. Ryan, R. K. Gupta, S. G. Seshadri and F. J. Frechette, J. Rheol., 1988, 32, 751–771 CrossRef CAS.
- C. D. Cwalina and N. J. Wagner, J. Rheol., 2016, 60, 47–59 CrossRef CAS.
- C. Chang and R. L. Powell, Phys. Fluids, 1994, 6, 1628–1636 CrossRef CAS.
- A. P. Shapiro and R. F. Probstein, Phys. Rev. Lett., 1992, 68(9), 1422–1425 CrossRef CAS PubMed.
- S. Pednekar, J. Chun and J. F. Morris, J. Rheol., 2018, 62, 513–526 CrossRef CAS.
- R. C. Sonntag and W. B. Russel, J. Colloid Interface Sci., 1987, 115, 390–395 CrossRef CAS.
- J. F. Brady and G. Bossis, J. Fluid Mech., 1985, 155, 105–129 CrossRef.
- B. M. Guy, J. A. Richards, D. J. M. Hodgson, E. Blanco and W. C. K. Poon, Phys. Rev. Lett., 2018, 121, 128001 CrossRef CAS PubMed.
- A. Helal, T. Divoux and G. H. McKinley, Phys. Rev. Appl., 2016, 6, 1–19 Search PubMed.
- F. Kramer, Broadband Dielectric Spectroscopy, 2003.
- A. Narayanan, F. Mugele and M. H. G. Duits, Langmuir, 2017, 33, 1629–1638 CrossRef CAS.
- Y. Jiang, Y. Cui, Y. Li, Z. Liu, C. Ness and R. Seto, J. Rheol., 2025, 69, 35–44 CrossRef CAS.
- G. Ovarlez, L. Tocquer, F. Bertrand and P. Coussot, Soft Matter, 2013, 9, 5540–5549 RSC.
- S. Jamali and G. H. McKinley, J. Rheol., 2022, 66, 1027–1039 CrossRef CAS.
- T. Larsen, J. R. Royer, F. H. J. Laidlaw, W. C. K. Poon, T. Larsen, S. J. Andreasen and J. C. Christiansen, Rheol. Acta, 2024, 63, 283–289 CrossRef CAS.
- I. Sudreau, S. Manneville, M. Servel and T. Divoux, J. Rheol., 2022, 66, 91–104 CrossRef CAS.
- M. Das and G. Petekidis, J. Chem. Phys., 2022, 157, 234902 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01493f |
| ‡ Y. G. and Q. L. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |