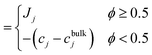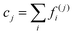Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Shear-induced dynamics of an active Belousov–Zhabotinsky droplet†
Shreyas A.
Shenoy
 ,
KVS
Chaithanya‡
,
KVS
Chaithanya‡
 and
Pratyush
Dayal
and
Pratyush
Dayal
 *
*
Polymer Engineering Research Lab (PERL), Department of Chemical Engineering, Indian Institute of Technology Gandhinagar, Gandhinagar, 382355, India. E-mail: pdayal@iitgn.ac.in
First published on 19th February 2025
Abstract
Controlled navigation of self-propelled active matter in complex biological environments has remained a significant challenge in engineering owing to a multitude of interactions that persist in the process. Active droplets, being some of the several synthetic active matters, have garnered significant attention owing to their ability to exhibit dynamic shape changes, self-sustained motion, interact with external stimuli such as flows, and mimic biological active matter. Here, we explore the dynamics of a self-propelled active droplet powered by the oscillatory Belousov–Zhabotinsky (BZ) reaction in the presence of a shear flow. We adapt a multicomponent lattice Boltzmann method (LBM) in conjunction with the phase-field model to simulate the droplet's interaction with the surrounding fluid. We unravel the collective effect of droplet deformation, reaction kinetics, and strength of the surrounding shear flow on droplet dynamics. Our findings depict that the shear flow disrupts the initial isotropic surface tension, and produces concentration nucleation spots in the droplet. The asymmetry thus generated produces Marangoni flow that ultimately propels the droplet. Our findings provide valuable insights into the mechanisms governing active droplet behavior and open new avenues for designing controllable synthetic active matter systems with potential applications in microfluidics, targeted delivery, and biomimetic technologies. In addition, our framework can potentially be integrated with the physics-informed machine learning framework to develop more efficient mesh-free methods.
1. Introduction
The intricate interplay between mechanical and chemical (phoretic) forces poses a significant challenge in biological and synthetic active matter.1 In this context, synthetic swimmers that mimic biological systems, such as active droplets, have been developed and studied2–10 in an attempt to account for the biological, physical and chemotactic coupling. Recently, approaches like physics-informed machine learning (PIML) have emerged as powerful tools, integrating the model equations that govern physics with machine learning, to capture diverse behaviors in active matter systems.11 On the other hand, the lattice Boltzmann method (LBM) remains a popular approach due to its computational efficiency and inherent ability to handle multiphase flows and chemical transport in complex geometries, making it particularly suited for studying active droplet dynamics under diverse conditions.12 Together, insights from LBM can complement PIML-based frameworks by providing robust and detailed understanding of underlying mechanisms, enabling more accurate and versatile modeling strategies. While most studies on active droplets have focused on quiescent environments,13–15 real-world scenarios often involve dynamic external flows,16 such as shear flow, which not only influences droplet dynamics but also introduces a symmetry-breaking mechanism critical for self-propulsion in active matter.2 Here, we investigate the impact of shear flow on the dynamics and self-propulsion of active droplets powered by the oscillatory Belousov–Zhabotinksy (BZ) reaction,17,18 aiming to navigate the droplet in the fluid that surrounds it. Our findings present ways to control the locomotion of active droplets offering avenues for their application in microfluidics and drug delivery applications.19 Moreover, the approach presented in this work can be integrated with the PIML framework11 to increase the computational efficiency significantly as it eliminates the need for mesh-based computations.A fundamental aspect of active matter research is the process of self-propulsion, which is prevalent in both biological and synthetic systems.20–23 The synthetic systems often rely on chemical reactions, interfacial dynamics, or external energy inputs to generate asymmetry in physicochemical properties at their surface and achieve directed motion.4,24–27 For instance, solid Janus particles coated with two different metals use asymmetry in surface chemistry where one side catalyzes chemical reactions such as decomposition of hydrogen peroxide, whereas the other side remains inert.28 The subsequent asymmetry generates local gradients in concentration or temperature, generating diffusiophoretic forces that propel the particles through the surrounding fluid at speeds ranging from 10–500 μm s−1.29 On the other hand, liquid based active droplets employ Marangoni flow30 – an interfacial flow from lower to higher surface tension – to achieve directed motion. In reaction-driven active droplets, chemical reactions alter the surfactants’ activity at the droplet interface.4,26 Consequently, the interfacial tension either increases or decreases dynamically,31 creating surface tension gradients that generate Marangoni flows along the interface, enabling the droplet to propel itself through the surrounding medium.
In this work, we focus our attention on active droplets driven by the BZ reaction owing to several advantages. The inherent asymmetry associated with the BZ reaction facilitates self-propulsion with minimal external intervention,32 allowing the corresponding oscillations and flows to persist for longer durations compared to other systems. Moreover, active BZ droplets are not constrained by the loss of mass observed in solubilization-driven droplets due to the continuous consumption and generation of reactive species. Furthermore, the tuneability of the BZ reaction kinetics to external stimulus such as light offers mechanisms to control the droplet's motion. For instance, light with spatially varying luminosity has been used to control the motion of an active droplet driven by a photosensitive BZ reaction.33 In addition, the swimming speed of the droplet is shown to be enhanced in the presence of Ceria nanoparticles (CeNPs) due to the enhancement of oscillation frequency of the BZ reaction by the nanoparticles.34 Moreover, the BZ reaction displays a plethora of dynamic behaviors35 making the BZ droplet an interesting candidate to study active matter dynamics. By applying PIML to BZ droplets, one can explore the transition from individual droplet motion to collective dynamics in active BZ droplets, which is a fascinating problem that yet remains unexplored. PIML incorporates physical laws as constraints within the learning process, reducing the reliance on computationally expensive simulations and enabling accurate modeling of complex systems like multi-droplet dynamics while maintaining physical correspondence.36 Lastly, the resemblance of dynamics of several biological processes, such as adenosine monophosphate signaling in slime molds, for instance, to that of BZ reaction,37 makes the BZ droplet a suitable candidate to delve into the large-scale cellular flows observed in biological systems.38
Several external stimuli ranging from magnetic, thermal, and concentration fields, have been employed to control the motion of active matter.39–42 Numerous experimental and simulation-based studies have been conducted to explore the interaction of aforementioned fields with surrounding fluid flows, drawing inspiration from various biological systems.7,32,43–45 Though mesh-based techniques such as the finite difference method (FDM),46 finite element method (FEM),47 and finite volume method (FVM)48 have been used previously, meshless tools such as physics-informed neural networks (PINNs) have emerged in recent times integrating physics-based information with machine learning in attempts to capture the plethora of behaviour observed in active matter. Nonetheless, LBM has continuously garnered attention due to various reasons that have been mentioned previously.
One of the earliest numerical models to simulate active BZ droplets employed LBM to reveal a strong correlation between the droplet's swimming speed and the chemical waves propagating within it.49 Our previous findings identified key parameters influencing droplet dynamics and classified its motion into two distinct types: sustained and decayed.50 The influence of an external stimulus such as an external flow on BZ droplet dynamics, however, remains unexplored and poses a fascinating problem statement due to several reasons. In the presence of shear flow, the internal mechanisms of droplet propulsion are directly coupled with the external deformation and solute transport, significantly altering the droplet's behavior. Moreover, shear flows deform droplets, alter reactant distributions at their surface, and introduce spatiotemporal variations in forces that propel them.51–53 The interaction between the shear flow and chemical activity introduces complex feedback mechanisms that make the dynamics of BZ droplets unique compared to passive systems. For instance, while passive droplets deform and align according to viscous and capillary forces, active droplets exhibit additional complexities due to their internally driven flows.5,51,54 Studies have shown that under moderate shear, solubilization-driven active droplets can exhibit asymmetric migration and oscillatory motion due to the interplay between internal Marangoni forces and external shear.2 Here, we investigate shear-induced asymmetry generation in an active BZ droplet and unravel the types of droplet motion based on the interaction between the shear flow and chemical field. The interplay has profound implications for understanding natural systems, such as the motion of cells in blood flow or vesicles in capillary channels, and for designing synthetic swimmers in microfluidic environments.19
In this article, we numerically investigate the shear-induced droplet deformation, solute distribution, and concentration asymmetry generation, leading to diverse droplet behaviors. Fig. 1 shows an immiscible, neutrally buoyant droplet of radius R0 placed at the center of a channel in which a shear flow is imposed by moving the top wall at a speed of Vw in the positive x-direction. The reaction is contained in the droplet and thus, the concentrations of the active species inside the droplet fluctuate periodically in accordance with the BZ reaction, whereas they relax towards constant values in the bulk. The surrounding fluid flow generates inhomogeneity in the concentration, thereby producing Marangoni flow and propelling the droplet at a speed of Vd. By systematically varying the shear rate and solute parameters, we reveal transitions between steady and oscillatory migrations in the BZ droplet. These findings provide critical insights into the coupling of internal chemical oscillations with external hydrodynamic forces and open avenues for designing bioinspired active systems capable of navigating complex flow environments. Through this work, we aim to address key questions about the role of shear flow in driving emergent behaviors, thus contributing to the broader understanding of active matter in dynamic fluidic contexts.
2. Methodology
Here, we present the model equations governing the dynamics of the active BZ droplet. Specifically, in our current framework, the motion of the fluid, both inside the droplet and its surroundings, is described by the velocity field (u). The regions inside and outside the droplet are identified using the local concentration (ϕ) of the droplet's fluid that serves as the phase field variable. In other words, the interface between the droplet and the surrounding fluid is tracked using ϕ, which varies smoothly along the interface but has the value 1 inside the droplet and 0 elsewhere. On the other hand, the oscillatory BZ reaction, taking place inside the droplet, is captured using concentrations, c1 and c2 of the two key species, known as the activator and oxidized catalyst, respectively.2.1. Phase-field modelling and hydrodynamics
The phase field variable ϕ used to track the droplet phase evolves as55 | (1) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) = ∇ϕ/|∇ϕ| is the outward-pointing unit normal vector at the droplet interface. Across the interface (r = r0), ϕ varies smoothly as49
= ∇ϕ/|∇ϕ| is the outward-pointing unit normal vector at the droplet interface. Across the interface (r = r0), ϕ varies smoothly as49 | (2) |
| ∇·u = 0, | (3) |
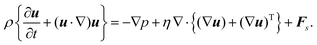 | (4) |
| Fs = μϕ∇ϕ | (5) |
| μϕ = μbulk + μint = 2βϕ(ϕ − 1)(2ϕ − 1) − κ∇2ϕ | (6) |
2.2. The BZ reaction
As time progresses, the activator and oxidized catalyst concentrations fluctuate periodically inside the droplet; these changes are governed by the coupled convection–diffusion equations49 | (7) |
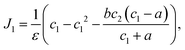 | (8) |
| J2 = c1 − c2 | (9) |
κ = κ0 {1 + Δκ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tanh(ζ(c1 − cref1))}. tanh(ζ(c1 − cref1))}. | (10) |
Here, the coupling parameters50 Δκ and ζ determine how rapidly κ changes when c1 is perturbed about its reference value cref1. It is to be noted, however, that the above equation offers a simplistic mechanism to couple the kinetics of the BZ reaction with hydrodynamics, while still capturing several experimental properties observed in BZ droplets.49,50 Moreover, as the chemical oscillations driven by the periodic oxidation and reduction of the catalyst induce oscillations in c1 between high (c1 = cmax1) and low (c1 = cmin1) values, the reference value is chosen to be cmin1. The tanh profile in eqn (10), along with the condition |Δκ| < 1, ensures that the parameter κ, and in turn the surface tension σ, are always positive. Furthermore, the chemical potentials of the two species are given by49
 | (11) |
| μ2 = γ2c2 | (12) |
Here, γ1 and γ2 are the activity coefficients of species 1 and 2, respectively. The second term on the RHS in eqn (11) represents the contribution of preferential sorption of species 1 to the chemical potential.49 The chemical potential μ2, however, remains unaltered as species 2 exhibits no sorption at the droplet interface.49
2.3. Lattice Boltzmann method
We use the two-fluid multicomponent LBM to solve the governing equations of our system, which are given by eqn (1), (3), (4) and (7). We employ four probability distribution functions fi(j) (j = 1, 2, 3, 4), on a two-dimensional rectangular lattice of spacing Δx, to capture the spatiotemporal changes in concentrations c1 and c2, phase field variable ϕ, and hydrodynamic pressure p, respectively. The generalized expression for the evolution of all four distribution functions is given by the Bhatnagar–Gross–Krook (BGK) approximated LB equation | (13) |
Here the subscript i denotes the lattice direction, and ei refers to the lattice velocity which is chosen such that eiΔt links a lattice site to all its nearest neighbors. The lattice velocity defined as per the D2Q9 scheme, is given by
 | (14) |
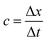 is determined using the length and time scale, Δx and Δt, respectively. The terms fi(j),eq and Si(j) in eqn (13) denote, respectively, the equilibrium distribution function and the source term for a particular fi(j). Furthermore, the term τj in eqn (13) represents the relaxation time that determines the diffusive property
is determined using the length and time scale, Δx and Δt, respectively. The terms fi(j),eq and Si(j) in eqn (13) denote, respectively, the equilibrium distribution function and the source term for a particular fi(j). Furthermore, the term τj in eqn (13) represents the relaxation time that determines the diffusive property  , where cs2 = c2/3 is the speed of sound. Specifically, the diffusivities of species 1 and 2 are represented by N1 and N2, mobility for phase-field variable (M) by N3 and momentum diffusivity (ν) by N4. Additional details of the LB implementation are summarized in Table 2 (see Appendix A).
, where cs2 = c2/3 is the speed of sound. Specifically, the diffusivities of species 1 and 2 are represented by N1 and N2, mobility for phase-field variable (M) by N3 and momentum diffusivity (ν) by N4. Additional details of the LB implementation are summarized in Table 2 (see Appendix A).
The calculations are conducted on a finite Cartesian grid representing a channel bounded by moving walls in the y-direction while extending infinitely in the x-direction. Specifically, periodic boundary conditions in the x-direction simulate the infinite channel length, whereas a mid-grid bounce-back scheme with a correction term for wall velocity incorporates the wall presence in the y-direction. Furthermore, the no-flux boundary condition is applied to reactive species (both 1 and 2), and the neutral wetting behavior (i.e. a contact angle of 90°) and no-slip condition are enforced for the phase field variable and fluids, respectively.50
2.4. Choice of parameters
The lattice Boltzmann simulations are performed on a domain of length 2000 units and a height of 240 units, with a droplet of 60 lattice units placed within it. The ratio of channel height to droplet diameter is chosen to be 4 such that excessive confinement effects on the droplet are avoided while maintaining the physical relevance of the results.50 The densities of both the fluids are taken as unity to minimize the effect of buoyancy; and the interface mobility M and the kinematic viscosity of the fluid ν are chosen as 1/6 and 1/3 by setting the relaxation times for the phase field parameter (τ3) and fluid (τ4) to 1.00 and 1.50, respectively.50 Furthermore, the relaxation times for advection-diffusion equations, τ1 and τ2, are chosen as 0.800 and 0.503, respectively; these values correspond to the diffusivities of c1 and c2 as 0.100 and 0.010. The parameters associated with the chemical potentials, γ1 and γ2, are equally set to 0.05.49 The BZ reaction parameters from the Oregonator model are chosen based on the standard recipe,50,56 which correspond to the sustained chemical oscillations, as ε = 0.0152, a = 0.001, and b = 0.550. We map all the specified parameters to physical units using a length scale of 1/60 mm and a time scale of 5/54 ms. Hence, for instance, a wall speed of 0.005 in lattice units corresponds to a speed of 9/10 mm s−1, typically observed in BZ droplets.34 Furthermore, we use the viscosity of water as a reference to map the other quantities into their corresponding physical units, and present them in Table 1.| Parameter | LB units | Physical units |
|---|---|---|
| Lattice spacing Δx | 1 | 1/60 mm |
| Unit time step Δt | 1 | 5/54 ms |
| Viscosity ν | 1/3 | 10−3 Pa s |
| Droplet diameter D | 60 | 1 mm |
| Surface tension σ | 0.06 | 1 mN m−1 |
3. Results and discussion
In this section, we discuss our simulation results depicting droplet's behavior under various flow conditions. First, we analyze the effect of surrounding fluid flow on droplet's motion in the absence of Marangoni flow in Section 3.1. Subsequently in Section 3.2, we explore the flow-induced droplet's dynamics by enabling Marangoni flow via the coupling of concentration c1 and surface tension of the droplet. Finally, we conclude our work by depicting droplet's motion when subjected to temporary shear flows.3.1. Droplet dynamics in the absence of Marangoni flow
Fig. 2 shows the generation of inhomogeneity in the distribution of c1 (the nucleation site) at the droplet interface due to the flow of the surrounding fluid. Here, we explore the shear-induced BZ droplet dynamics in the absence of Marangoni flow {Δκ = 0 in eqn (10)} to demonstrate the role of shear flow in producing asymmetry in the concentration at the droplet interface. In particular, Fig. 2(a) illustrates the decomposition of the total flow visualized in the droplet's frame of reference into the extensional and rotational components. The extensional component of the fluid velocity is given by E·r, where r is the position vector, the tensor is the symmetric part of the velocity gradient tensor ∇u, whereas the rotational component is calculated as Ω·r with
is the symmetric part of the velocity gradient tensor ∇u, whereas the rotational component is calculated as Ω·r with  being the antisymmetric part of ∇u.57 Furthermore, the compressional axis intersects the droplet's interface at the ‘poles’ as shown. Initially, a droplet of uniform concentration is placed at the center of a channel of 2000 × 240 dimensions, and a shear flow is applied by moving the wall at y = H (see Fig. 1) at a speed of Vw = 5.0 × 10−3; however, only an area of 120 × 120 is shown in every timed snapshot in Fig. 2(b), in the droplet's frame of reference. The contour colors correspond to the concentration of c1, with red and blue corresponding to the respective reduced and oxidized states of the catalyst; the droplet outline is marked in magenta. Moreover, the white curves with arrows indicate the extensional component of the fluid velocity in the droplet's frame whereas the white arrow inside the droplet indicates the instantaneous direction of droplet's motion at its center, i.e., the orientation vector. Note that only the extensional flow is shown since, the other component of fluid velocity – the rotational flow – induces mixing throughout the droplet,58 making it uninformative in locating asymmetry. It is important to note, however, that the rotational component of the imposed shear flow is always present, unlike the time-varying nature of the Marangoni flow. Together, these flows influence the propagation of chemical waves emanating due to the BZ reaction, as we shall demonstrate in the subsequent sections. Furthermore, the internal streamlines have been omitted for clarity and the droplet's internal region is represented by its orientation vector. Let us now examine the evolution of the concentration field in the droplet's vicinity with time in the presence of shear flow.
being the antisymmetric part of ∇u.57 Furthermore, the compressional axis intersects the droplet's interface at the ‘poles’ as shown. Initially, a droplet of uniform concentration is placed at the center of a channel of 2000 × 240 dimensions, and a shear flow is applied by moving the wall at y = H (see Fig. 1) at a speed of Vw = 5.0 × 10−3; however, only an area of 120 × 120 is shown in every timed snapshot in Fig. 2(b), in the droplet's frame of reference. The contour colors correspond to the concentration of c1, with red and blue corresponding to the respective reduced and oxidized states of the catalyst; the droplet outline is marked in magenta. Moreover, the white curves with arrows indicate the extensional component of the fluid velocity in the droplet's frame whereas the white arrow inside the droplet indicates the instantaneous direction of droplet's motion at its center, i.e., the orientation vector. Note that only the extensional flow is shown since, the other component of fluid velocity – the rotational flow – induces mixing throughout the droplet,58 making it uninformative in locating asymmetry. It is important to note, however, that the rotational component of the imposed shear flow is always present, unlike the time-varying nature of the Marangoni flow. Together, these flows influence the propagation of chemical waves emanating due to the BZ reaction, as we shall demonstrate in the subsequent sections. Furthermore, the internal streamlines have been omitted for clarity and the droplet's internal region is represented by its orientation vector. Let us now examine the evolution of the concentration field in the droplet's vicinity with time in the presence of shear flow.
Fig. 2(b) illustrates the progression of redox cycle via the initiation of the nucleation site that is formed at the lower pole of the droplet's compressional axis (t = 330![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200). With time, this site sets up an oxidizing chemical wave inside the droplet (t = 331
200). With time, this site sets up an oxidizing chemical wave inside the droplet (t = 331![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400). As the wave progresses, a second traveling wave originates at the upper pole of the compressional axis and merges with the first wave (t = 332
400). As the wave progresses, a second traveling wave originates at the upper pole of the compressional axis and merges with the first wave (t = 332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200), gradually expanding across the entire droplet (t = 334
200), gradually expanding across the entire droplet (t = 334![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400). A reducing chemical wave then begins in the vicinity of the lower pole of the compressional axis (t = 339
400). A reducing chemical wave then begins in the vicinity of the lower pole of the compressional axis (t = 339![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400) and expands outwards, fully reduces the droplet and the cycle repeats (t = 341
400) and expands outwards, fully reduces the droplet and the cycle repeats (t = 341![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). The crucial observation here is that the nucleation occurs along the droplet's compressional axis ‘poles’, during each redox cycle. The symmetric component of the fluid velocity (extensional flow) dictates the location of nucleation site generation, as illustrated in Fig. 2(b). The fluid flow outside the droplet generates an internal flow in the droplet, both of which carry the species 1 towards the droplet interface along the compressional axis. The extensional flow advects the species along the compressional axis, and a region of higher extensional-velocity gradient is observed at the lower end of the droplet. The advection, in addition to the weaker (total) flow strength at the lower end in comparison to the upper end of the droplet's compressional axis, results in a higher amount of accumulation of species at the droplet's lower end. Consequently, a nucleation site at the droplet's lower pole is produced at an earlier instant than that on the upper pole, as evident in Fig. 2(b). It is worth noting that, although the droplet is fully reduced at the end of the oxidation–reduction cycle, the subsequent oxidation takes place via an off centric nucleation, thereby producing concentration gradients at the droplet interface. Thus, the shear flow is able to generate sustained asymmetry in the concentration, which is crucial for the self-propulsion of active droplets2 (see Movie S1 in the ESI†). Building upon the qualitative effect of shear flow on generation of chemical gradients at the droplet interface, we explore the effect of Marangoni flow on the dynamics of the droplet by coupling the concentration and surface tension {Δκ ≠ 0 in eqn (10)}.
000). The crucial observation here is that the nucleation occurs along the droplet's compressional axis ‘poles’, during each redox cycle. The symmetric component of the fluid velocity (extensional flow) dictates the location of nucleation site generation, as illustrated in Fig. 2(b). The fluid flow outside the droplet generates an internal flow in the droplet, both of which carry the species 1 towards the droplet interface along the compressional axis. The extensional flow advects the species along the compressional axis, and a region of higher extensional-velocity gradient is observed at the lower end of the droplet. The advection, in addition to the weaker (total) flow strength at the lower end in comparison to the upper end of the droplet's compressional axis, results in a higher amount of accumulation of species at the droplet's lower end. Consequently, a nucleation site at the droplet's lower pole is produced at an earlier instant than that on the upper pole, as evident in Fig. 2(b). It is worth noting that, although the droplet is fully reduced at the end of the oxidation–reduction cycle, the subsequent oxidation takes place via an off centric nucleation, thereby producing concentration gradients at the droplet interface. Thus, the shear flow is able to generate sustained asymmetry in the concentration, which is crucial for the self-propulsion of active droplets2 (see Movie S1 in the ESI†). Building upon the qualitative effect of shear flow on generation of chemical gradients at the droplet interface, we explore the effect of Marangoni flow on the dynamics of the droplet by coupling the concentration and surface tension {Δκ ≠ 0 in eqn (10)}.
3.2. Droplet dynamics with Marangoni flow
In Fig. 3, we investigate the time-varying active droplet dynamics under identical conditions as in Fig. 2, but in the presence of Marangoni flow resulting from a positive coupling between concentration c1 and surface tension {Δκ = 0.3 in eqn (10)}, at two different flow strengths. In particular, Fig. 3(a) qualitatively illustrates the role of various internal flows in determining droplet dynamics through their influence on determining the location of nucleation. Fig. 3(b) shows the evolution of the concentration and extensional velocity field in the vicinity of the droplet at two different flow strengths over a redox cycle. Note that we perform the analysis at a fixed |Δκ|, and detailed study on the role of Δκ in droplet dynamics is available in our previous work.50Fig. 3(a)–(c) illustrate the interplay of three fundamental flow types within the droplet that influence the droplet dynamics, namely (a) extensional (b) Marangoni and (c) diffusive flows. Specifically, the first image indicates the extensional velocity component which induces nucleation sites in the droplet. These initial nucleation sites, having higher concentration c1, increase the local surface tension (recall that Δκ > 0), which generates Marangoni flow towards the sites, as shown in Fig. 3(b). Furthermore, Fig. 3(c) depicts the diffusive flow generated from a region of high c1 to a region of low c1, i.e., away from the nucleation site. It is important to note that the Marangoni flow may oppose or assist the diffusive flow depending upon the nature of the surface tension–concentration coupling. When Δκ = 0, the Marangoni flow is absent as discussed previously; however, in this particular case where Δκ > 0, the Marangoni flow tends to assist diffusive flow in homogenizing the concentration inside the droplet, and thereby results in the generation of chemical waves that emerge from the droplet core50 as shown in Fig. 3(d).
In Fig. 3(e), we show the concentration field evolution near the droplet for two different flow strengths of the surrounding fluid over a redox cycle. In particular, the top panel in Fig. 3(e) depicts the droplet's behavior at a low shear flow strength (Vw = 5.0 × 10−3). In contrast, the bottom panel depicts the droplet's behavior at a higher shear flow strength (Vw = 2.0 × 10−2), keeping the coupling parameter constant, i.e., Δκ = 0.3. Though the top and bottom panels indicate the droplet's behavior in shear flows of different strengths, the concentration fields inside them show similar evolution. As a consequence of the homogenization of species 1, a nucleation spot arises close to the droplet's center (t = 328![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800), and then expands outwards in all directions as an oxidizing wavefront (t = 329
800), and then expands outwards in all directions as an oxidizing wavefront (t = 329![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400). The oxidizing wavefront contacts the interface; consequently, Marangoni flow is induced at the interface (t = 330
400). The oxidizing wavefront contacts the interface; consequently, Marangoni flow is induced at the interface (t = 330![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200) from a region of lower c1 to a region of higher c1. In other words, the droplet is pushed away from the point of initial contact between the chemical wave and the interface.50 Meanwhile, the reduction cycle begins at the droplet core (t = 333
200) from a region of lower c1 to a region of higher c1. In other words, the droplet is pushed away from the point of initial contact between the chemical wave and the interface.50 Meanwhile, the reduction cycle begins at the droplet core (t = 333![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800), which expands outwards (t = 338
800), which expands outwards (t = 338![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200). Finally, the droplet becomes fully reduced (t = 339
200). Finally, the droplet becomes fully reduced (t = 339![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200), and the subsequent redox cycle begins via the nucleation in the vicinity of the droplet's center. One of the key observations here is that the droplet's motion in the y-direction differs notably as the strength of shear flow increases, as evident from the orientation vector indicated inside the droplet contours. In particular, the droplet shows an increase in its y-directional motion as the wavefront contacts the droplet's interface (t = 143
200), and the subsequent redox cycle begins via the nucleation in the vicinity of the droplet's center. One of the key observations here is that the droplet's motion in the y-direction differs notably as the strength of shear flow increases, as evident from the orientation vector indicated inside the droplet contours. In particular, the droplet shows an increase in its y-directional motion as the wavefront contacts the droplet's interface (t = 143![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400; t = 146
400; t = 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). The difference in droplet's motion is a consequence of the asymmetric contact of chemical wave generated by the nucleation site, with the droplet interface. As the droplet is carried horizontally by the shear flow, an off-centric, oxidizing chemical wave is generated inside the droplet. The chemical wave is distorted by the droplet's internal flows, and thus, contacts the droplet's interface at the upper end along the compressional axis earlier than at the lower end. Consequently, a Marangoni flow is set up in a direction that propels the droplet away from the point of contact between the chemical wave and the droplet interface.50 Though the effect is less evident at lower flow strengths (see Movie S2 in the ESI†), the asymmetry increases with increasing flow strengths due to larger droplet deformations and stronger internal flows (see Movie S3 in the ESI†) that advect the chemical species away from the center along the compressional axis inside the droplet. Thus, the droplet's motion differs in terms of its orientation as the strength of the shear flow is varied. Hence, a control over the droplet's lateral migration can be achieved solely by varying the strength of the surrounding fluid flow when Δκ > 0, as we shall later show via the droplet's trajectory. Experimentally, a similar control over the droplet's motion can be realized using microfluidic channels with controlled shear flow, where the variations in flow strength can be used to alter the nature of droplet's motion. For instance, several experiments have reported oscillatory motion of an active droplet controlled by varying the strength of the imposed flow, even demonstrating the capability of rheotactic trapping of the droplet.2,59
000). The difference in droplet's motion is a consequence of the asymmetric contact of chemical wave generated by the nucleation site, with the droplet interface. As the droplet is carried horizontally by the shear flow, an off-centric, oxidizing chemical wave is generated inside the droplet. The chemical wave is distorted by the droplet's internal flows, and thus, contacts the droplet's interface at the upper end along the compressional axis earlier than at the lower end. Consequently, a Marangoni flow is set up in a direction that propels the droplet away from the point of contact between the chemical wave and the droplet interface.50 Though the effect is less evident at lower flow strengths (see Movie S2 in the ESI†), the asymmetry increases with increasing flow strengths due to larger droplet deformations and stronger internal flows (see Movie S3 in the ESI†) that advect the chemical species away from the center along the compressional axis inside the droplet. Thus, the droplet's motion differs in terms of its orientation as the strength of the shear flow is varied. Hence, a control over the droplet's lateral migration can be achieved solely by varying the strength of the surrounding fluid flow when Δκ > 0, as we shall later show via the droplet's trajectory. Experimentally, a similar control over the droplet's motion can be realized using microfluidic channels with controlled shear flow, where the variations in flow strength can be used to alter the nature of droplet's motion. For instance, several experiments have reported oscillatory motion of an active droplet controlled by varying the strength of the imposed flow, even demonstrating the capability of rheotactic trapping of the droplet.2,59
In Fig. 4, we perform a similar analysis to that in Fig. 3, but for a negative coupling of concentration and surface tension {Δκ = −0.3 in eqn (10)}, i.e., Fig. 4(a)–(e) have a one-to-one correspondence with Fig. 3(a)–(e). In particular, Fig. 4(a)–(d) provide a qualitative picture of the droplet's internal flows and Fig. 4(e) portrays the evolution of the concentration and extensional velocity field in the droplet's vicinity.
Fig. 4(a)–(d) depict the several internal flows that persist inside the droplet. Unlike Fig. 3(b), here, we observe a reversal in the direction of Marangoni flow which is the key difference that maintains the inhomogeneity inside the droplet. Consequently, the nucleation sites emerge at the droplet interface along the compressional axis. This behavior is also clearly evident in Fig. 4(e) which depicts the evolution of concentration field in the droplet's vicinity, obtained by imposing shear flows of two different strengths over a redox cycle. Similar to Fig. 3(e), the top panel in Fig. 4(e) illustrates the droplet's behavior at a low shear flow strength (Vw = 0.005) whereas the bottom panel depicts the droplet's behavior at a higher shear flow strength (Vw = 0.020), at Δκ = −0.3.
In Fig. 4(e), unlike that in the case of positive Δκ (Fig. 3(e)), we observe a nucleation site that starts at the lower end of the droplet interface along the compressional axis (t = 326![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200). Consequently, a Marangoni flow is set up at the interface in the regions where the wavefront contacts the interface. Shortly, a second nucleation site emerges at the droplet's upper end, which again sets up Marangoni flow at the interface but in an opposite direction (t = 327
200). Consequently, a Marangoni flow is set up at the interface in the regions where the wavefront contacts the interface. Shortly, a second nucleation site emerges at the droplet's upper end, which again sets up Marangoni flow at the interface but in an opposite direction (t = 327![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). These wavefronts propagate inside the droplet and merge (t = 328
000). These wavefronts propagate inside the droplet and merge (t = 328![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600), subsequently bringing the droplet to a reduced state. Furthermore, the reduction cycle begins inside the droplet (t = 335
600), subsequently bringing the droplet to a reduced state. Furthermore, the reduction cycle begins inside the droplet (t = 335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400) that shortly sets up the Marangoni flow in a direction opposite to that during the oxidation cycle (t = 326
400) that shortly sets up the Marangoni flow in a direction opposite to that during the oxidation cycle (t = 326![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200). The droplet is then fully reduced (t = 340
200). The droplet is then fully reduced (t = 340![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), and a subsequent redox cycle begins via the nucleation at the interface. Though the qualitative evolutions of concentration fields are similar at lower and higher shear flow strengths, an interesting difference in the droplet deformation is observed in the above two cases. At lower shear flow strengths (top panel), the droplet initially deforms and aligns itself in the compressional axis direction; however, this deformation disappears as the concentration gradient at the interface diminishes. Thus, the droplet shows a motion that alternately elongates along the direction of the compressional axis and regains its initial shape (see Movie S4 in the ESI†). At higher shear flow strengths, however, the droplet shows deformation that switches between compressional and extensional axes. In particular, during the propagation of oxidizing wavefront, the droplet stretches and aligns along the compressional axis though it later reorients and aligns itself along the extensional axis. Thus, the droplet exhibits a ‘wobbly’ motion, with a repeated switching between the two orientations (see Movie S5 in the ESI†). In addition, the droplet's motion switches periodically in the y-direction, as indicated by the orientation vector, which is oriented in the negative y-direction during the oxidizing wave propagation, and switches to the positive y-direction subsequently, as the reducing wave initiates. Moreover, at a higher shear flow strength, the droplet also shows increased motion in the y-direction indicated by the increase in proximity of droplet's orientation vector to the y-direction.
000), and a subsequent redox cycle begins via the nucleation at the interface. Though the qualitative evolutions of concentration fields are similar at lower and higher shear flow strengths, an interesting difference in the droplet deformation is observed in the above two cases. At lower shear flow strengths (top panel), the droplet initially deforms and aligns itself in the compressional axis direction; however, this deformation disappears as the concentration gradient at the interface diminishes. Thus, the droplet shows a motion that alternately elongates along the direction of the compressional axis and regains its initial shape (see Movie S4 in the ESI†). At higher shear flow strengths, however, the droplet shows deformation that switches between compressional and extensional axes. In particular, during the propagation of oxidizing wavefront, the droplet stretches and aligns along the compressional axis though it later reorients and aligns itself along the extensional axis. Thus, the droplet exhibits a ‘wobbly’ motion, with a repeated switching between the two orientations (see Movie S5 in the ESI†). In addition, the droplet's motion switches periodically in the y-direction, as indicated by the orientation vector, which is oriented in the negative y-direction during the oxidizing wave propagation, and switches to the positive y-direction subsequently, as the reducing wave initiates. Moreover, at a higher shear flow strength, the droplet also shows increased motion in the y-direction indicated by the increase in proximity of droplet's orientation vector to the y-direction.
The alternation in the droplet's orientation in the y-direction is mainly influenced by the chemical waves that persist inside the droplet. In particular, as the oxidizing wave initiates at a nucleation site at the droplet interface, the resultant Marangoni flow propels the droplet in the direction of this nucleation spot due to the negative coupling between surface tension and the concentration. Consequently, the droplet orients in a direction close to the vicinity of the compressional axis during its motion. Subsequently, the droplet becomes fully oxidized during which its motion is primarily dominated by the surrounding fluid flow and orients in the vicinity of the positive x-axis. The oxidized state, however, is short-lived in comparison to the timespan of a redox cycle (see Fig. S1, ESI†), and shortly, the reducing wavefront emerges. Consequently, a Marangoni flow is generated in a direction opposite to the earlier flow, and the droplet's orientation switches back to the positive y-direction. The droplet, however, remains oriented in the positive x-direction due to the shear flow in the surrounding fluid despite the alternating orientation between positive and negative y-directions, as discussed. Moreover, the droplet deformation observed above is primarily influenced by two competing factors: inhomogeneity in interfacial tension and the surrounding fluid flow. At the nucleation site along the compressional axis, the interfacial tension decreases due to the negative coupling effect (eqn 10). Consequently, the droplet deforms along the compressional axis to achieve a balance in the stresses at the interface. On the other hand, the surrounding shear flow deforms the droplet along the extensional axis.60,61 At lower shear strengths, the deformation induced by the external flow is less pronounced, and the droplet primarily elongates along the compressional axis. As the shear strength increases, the flow-induced deformation becomes more dominant, causing the droplet to elongate alternately along the compressional and extensional axes, resulting in an alternating deformation pattern.
To summarize, a shear flow in the surrounding fluid breaks the symmetry in the concentration distribution at the droplet's interface, thereby generating a Marangoni flow that propels the droplet. In addition, the interplay of shear flow strength and concentration–surface tension coupling governs the droplet's behavior. For a positive coupling, weak shear flows produce minimal orientation changes in the droplet due to insignificant flow-induced deformation and an almost-isotropic chemical wave propagation. Stronger flows, however, cause droplet deformation and chemical wave distortion, resulting in interfacial tension gradients and significant orientation changes due to Marangoni forces. In contrast, negative coupling sustains interfacial tension asymmetry, leading to substantial orientation changes at both low and high flow strengths. The complex interplay discussed above results in oscillatory droplet motion and will be detailed in the subsequent section.
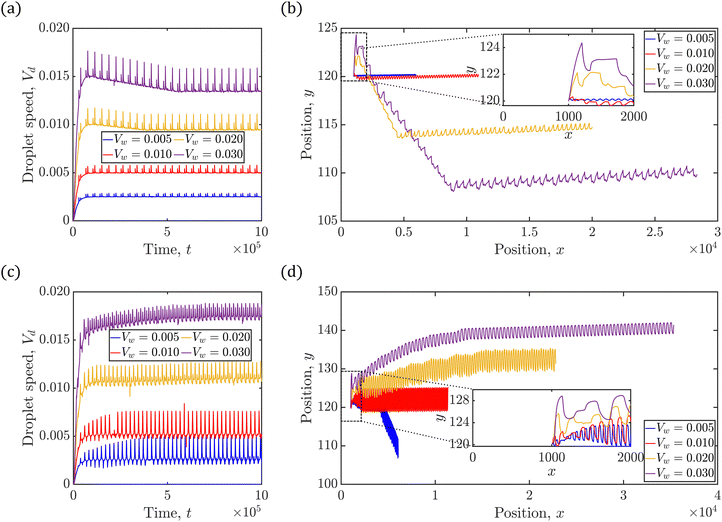
Fig. 5(a)–(d) demonstrate the impact of varying shear flow on the droplet dynamics in terms of its trajectories and swimming speeds, at positive and negative Δκ values, with |Δκ| = 0.3. In particular, Fig. 5(a) and (b) depict respectively, the swimming speed and trajectories of the droplet when Δκ = 0.3, whereas Fig. 5(c) and (d) correspond to that at Δκ = −0.3 Also, the trajectories are simulated for 2 × 106 timesteps with the inset highlighting the initial motion of the droplet. Furthermore, the swimming speeds are shown for 1 × 106 timesteps, since the trend in the swimming speed qualitatively remains unchanged beyond that duration.
We begin our discussion with Fig. 5(a), where the droplet exhibits time-periodic oscillations in its swimming speed irrespective of the strength of the surrounding fluid flow. The swimming speed shows fluctuations characterized by intervals of rapid acceleration followed by deceleration, about a base value. Furthermore, these acceleration–deceleration ‘peaks’ are observed in pairs that correspond to the redox cycle of the BZ reaction (see Fig. S1, ESI†). The resultant droplet trajectories are “wave-like” in nature, and are shown in Fig. 5(b). In particular, at lower strengths of surrounding fluid flow, the droplet moves near the channel centerline, exhibiting oscillatory trajectories of low amplitudes. In contrast, the oscillations in the droplet trajectories show higher amplitudes at higher flow strengths. It is an interesting observation that unlike a passive droplet (see Fig. S2, ESI†), the BZ droplet exhibits motion away from the moving wall, just by increasing the strength of the shear flow. In addition, at higher shear flow strengths, the BZ droplet even exhibits a ‘tumbling’ motion indicated by the significant change in its trajectory.
The oscillations observed in the swimming speed of the droplet in Fig. 5(a) arise from the chemical waves generated inside the droplet. When shear flow is applied in the channel, the droplet is advected by the surrounding fluid, leading to a monotonic increase in its speed during the initial phase. An oxidizing chemical wave is generated shortly inside the droplet, which induces Marangoni flow upon reaching the droplet's interface. Consequently, a rapid increase in the droplet's swimming speed is observed until the oxidizing wave fully forms and the interface completely oxidizes. Once the wave fully develops, the droplet's acceleration ceases, and it primarily moves by the shear flow. Shortly thereafter, a reducing chemical wave is generated due to BZ reaction, which again produces the Marangoni flow at the interface upon its contact. The droplet again accelerates as long as the interface remains partially oxidized, maintaining the Marangoni flow, and deceleration occurs once the droplet is fully reduced. As a result, the droplet exhibits paired oscillations in its swimming speed, synchronized with the redox cycle of the BZ reaction.
The trends observed in droplet trajectories in Fig. 5(b) are explained based on two key factors: the position of the nucleation site generated at the beginning of each redox cycle and the direction of the Marangoni flow generated as the oxidizing and reducing chemical wavefronts contact the droplet interface. Recall that the oxidizing chemical wave generated near the droplet's center (off-centric) is distorted by the droplet's internal flow, and thus, the wave contacts the droplet's interface at the upper end along the compressional axis earlier than at the lower end (Fig. 3(e)). Thus, a Marangoni flow ensues in a direction that propels the droplet away from the point of contact between the oxidizing wavefront and the droplet interface.50 As a consequence, the droplet starts to move downwards along the direction of the compressional axis, in the meanwhile the oxidizing wavefront contacts the droplet at the lower end generating flow in opposite direction of droplet's current motion. Shortly after, the Marangoni flow corresponding to the reduction cycle begins, which moves the droplet in the positive y-direction. These periodic fluctuations in the trajectories manifest as sudden changes in direction of droplet's motion, resembling ‘peaks’ in the trajectories. Furthermore, the generation of the off-centric nucleation site that is closer to the upper end of the droplet interface (see Fig. 3(e)) at higher shear flow strengths results in delay between the opposing flows mentioned earlier, thereby producing a net motion in the negative y-direction with every redox cycle inside the droplet. As time progresses, however, the nucleation sites originate closer to the droplet's center, thereby reducing the delay between the two opposing Marangoni flows, thereby significantly reducing the net motion of the droplet in the y-direction that manifests as a sudden change in the droplet's trajectory. In short, the BZ droplet exhibits an interesting ‘wave-like’ trajectory controlled by altering the strength of the shear flow in its surrounding.
For the value of Δκ = −0.3, in Fig. 5(c) and (d), we still observe oscillations in the droplet's swimming speed and trajectories. A clear difference in the droplet's motion, however, is evident in the characteristic nature of oscillations in its swimming speeds and the direction of lateral migration of the droplet. In particular, at lower strengths of surrounding fluid flow and unlike Fig. 5(a), the droplet in Fig. 5(c) exhibits crest–trough pairs in its swimming speed about a base value. As the flow strength increases, however, the troughs in the swimming speed shift upwards and appear as shorter crests. As far as the droplet's motion is concerned, the trajectories in Fig. 5(d) show a transition in its direction of lateral motion from a negative to a positive y-direction. The two key differences in motion arise from the pattern of chemical wave propagation which dictates the orientation of the droplet's Marangoni flow components with the shear flow of the surrounding fluid. Unlike the case of positive Δκ, here the oxidizing wavefronts originate at the droplet “poles” along the compressional axis (see Fig. 4(e)), generating a Marangoni flow with a positive component in the x-direction, aligned with the shear direction at both high and low shear strengths. Thus, a crest in the swimming speed is observed, corresponding to this oxidizing chemical wave. The emergence of subsequent reducing chemical waves, however, depends on the shear flow strength. At lower shear flow strengths, the subsequent reducing waves generated along the compressional axis produces a Marangoni flow with a negative component in the x-direction, opposing the surrounding shear flow. Consequently, a trough in the droplet's swimming speed is observed as the droplet decelerates. In contrast, at higher shear flow strengths, the droplet is deformed and rotated by the surrounding fluid, causing the reducing chemical wavefront to emerge at the lower end of the extensional axis. The subsequent Marangoni flow, therefore, has a velocity component in the positive x-direction giving rise to a second crest in the droplet's swimming speed at higher shear rates. On the other hand, the oscillations in droplet trajectories along the channel centerline at lower shear flow strengths arise due to the opposing flows produced during the redox cycles, as discussed above. As the strength of shear flow increases, however, the droplet's net motion in y-direction switches from a negative to positive value due to the increased deformation induced by the surrounding shear. Thus, we demonstrate a control over the droplet's motion by varying the strength of the shear flow, which has been a primary objective of several researchers in the past.11,33,62–64
In Fig. 6, we investigate the droplet's motion in terms of its swimming speed, when the droplet is subjected to a temporary shear flow. In particular, shear flows of varying strengths are imposed initially in the channel and are stopped after 105 timesteps. Fig. 6(a)–(d) show the subsequent droplet's swimming speed. In particular, Fig. 6(a) and (b) show the droplet's swimming speed at lower Δκ values of 0.3 and −0.3 respectively, whereas Fig. 6(c) and (d) show the droplet's swimming speed at higher Δκ values of 0.6 and −0.6 respectively. The insets show the droplet's swimming speed for a duration of 2.5 × 105 timesteps. When Δκ is 0.3, the droplet's motion ceases once the shear flow is terminated, as indicated by the O(10−5) swimming speeds in Fig. 6(a). Upon changing the Δκ value to −0.3, +0.6, or −0.6, however, the droplet continues to move despite the cessation of the initial flow as indicated by the O(10−3) and O(10−4) swimming speeds in Fig. 6(b)–(d). In other words, the droplet's motion comes to a stop upon the removal of surrounding fluid flow when the surface tension–concentration coupling is weakly positive whereas, the droplet continues to move when the coupling is negative or stronger. Once the surrounding fluid comes to a halt, the asymmetry in the concentration at the interface eventually ceases due to the homogenization of concentration within the droplet at Δκ = 0.3. Furthermore, the deformations in the droplet that are generated at higher strengths of shear flow are eventually counterbalanced by the surface tension forces, and the droplet regains its original shape. As a consequence, the chemical waves that are generated at the droplet center contact the interface symmetrically across the droplet periphery, despite the presence of initial asymmetry by droplet deformations, thereby terminating its motion (Fig. 3(e)). In contrast, at a Δκ value of −0.3, the gradients in the concentration at the interface persist due to the opposing internal flows50 and thus, sustain the droplet's motion despite the absence of a surrounding fluid flow at later times. In addition, the Marangoni stresses at the interface increase as |Δκ| is increased, leading to significant droplet deformations. The deformations are sustained even in the absence of background flow due to the periodic nature of BZ reaction, and thus, result in persistent asymmetry in the interfacial tension. Marangoni stresses are, therefore, continuously generated at the droplet's interface at higher |Δκ| values, sustaining the droplet's motion. In essence, the presence of a temporary flow in the surrounding fluid disrupts the initial isotropic interfacial tension, and promotes self-propulsion of the droplet under controlled environments (here, by varying Δκ).
 | ||
| Fig. 6 Swimming speeds of the droplet when subjected to temporary shear flows of varying strengths when (a) Δκ = 0.3, (b) Δκ = 0.3, (c) Δκ = 0.6, and (d) Δκ = −0.6. The insets are shown for clarity. | ||
We thus achieve self-propulsion of the droplet by disrupting the isotropic interfacial tension via the means of surrounding fluid flow and tuning the strength of coupling between the concentration and surface tension. Our work demonstrates that a simple shear in the surrounding fluid for brief periods is sufficient to generate self-propelled locomotion in active BZ droplets for longer periods, making them excellent candidates for emulating the behaviors observed in biological active matter systems.
4. Conclusions
Using numerical simulations, we investigate the dynamics of an active BZ droplet under shear flow, revealing the significance of chemical kinetics and internal flows in propelling the droplet. In particular, using the LBM and phase-field model, we adapt a framework that captures the interplay between reaction kinetics, Marangoni flow, and external shear forces, demonstrating the role of these factors in regulating and directing droplet motion. Specifically, we illustrate how shear flow induces concentration nucleation spots at the droplet's interface, producing asymmetries in interfacial tension that ultimately lead to directed propulsion. Previous studies have explored several external stimuli, such as electric fields, light, and temperature gradients, to achieve directional control over droplet motion. On the other hand, our results highlight that the location of asymmetry generation can be controlled by tuning the surfactant properties, one of which is the coupling parameter (Δκ) that represents the sensitivity of the surface tension to changes in concentration of activator (c1). In particular, our findings reveal that the direction of Marangoni flow is strongly dependent on the sign of Δκ, which plays a crucial role in the droplet's swimming speed. Additionally, we elucidate that varying the shear strength alters the droplet's cross-stream migration, and thus provides a straightforward and effective means to control the droplet's motion, offering a flexible strategy for manipulating droplet dynamics. Our simulations reveal that upon increasing the coupling strength (higher |Δκ|), the active BZ droplet exhibits a sustained motion despite being subjected to shear rate for a small initial time interval. Thus, our findings provide a comprehensive understanding of the role of internal flows and surfactant properties that govern the hydrodynamic behavior of the active droplet. We envisage that the implications of our work offer pathways to manipulate the motion of active droplets in various applications, including microfluidics, biophysical systems, and emulsion processing. Needless to say that the LBM and phase-field approach presented here can be harnessed to develop mesh-free computations provided they are integrated with the PIML framework.Author contributions
Shreyas A. Shenoy: conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization, writing – original draft, and writing – review & editing. K. V. S. Chaithanya: conceptualization, methodology, software, and writing – review & editing. Pratyush Dayal: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, and writing – review & editing.Data availability
The data that support the findings of this study are available within the article and its ESI.†Conflicts of interest
The authors declare no conflict of interest.Appendix A: Lattice Boltzmann implementation details
The equilibrium distribution function fi(j),eq and the source term Si(j)in eqn (13) are given in Table 2. , χ = 1,
, χ = 1,  ,
,  and
and 
Acknowledgements
We acknowledge the funding support from DST-SERB (grant no. CRG/2022/002977), MoE India (grant no. MIS/PMRF/CL/PD/202223/097), and IIT Gandhinagar.References
- M. Kumar, A. Murali, A. G. Subramaniam, R. Singh and S. Thutupalli, Nat. Commun., 2024, 15, 4903 CrossRef CAS PubMed.
- P. Dwivedi, A. Shrivastava, D. Pillai and R. Mangal, Phys. Fluids, 2021, 33, 082108 CrossRef CAS.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- S. Herminghaus, C. C. Maass, C. Krüger, S. Thutupalli, L. Goehring and C. Bahr, Soft Matter, 2014, 10, 7008–7022 RSC.
- R. Kree and A. Zippelius, Phys. Fluids, 2023, 35, 042002 CrossRef CAS.
- P. Dwivedi, A. Shrivastava, D. Pillai, N. Tiwari and R. Mangal, Soft Matter, 2023, 19, 3783–3793 RSC.
- M. Schmitt and H. Stark, EPL, 2013, 101, 44008 CrossRef.
- S. Michelin, Annu. Rev. Fluid Mech., 2023, 55, 77–101 CrossRef.
- I. Lavi, N. Meunier, R. Voituriez and J. Casademunt, Phys. Rev. E, 2020, 101, 022404 CrossRef CAS PubMed.
- R. Singh, E. Tjhung and M. E. Cates, Phys. Rev. Res., 2020, 2, 032024 CrossRef CAS.
- C. Casert and S. Whitelam, Nat. Commun., 2024, 15, 9128 CrossRef CAS PubMed.
- T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva and E. M. Viggen, The Lattice Boltzmann Method, Springer International Publishing, Cham, 2017 Search PubMed.
- P. Ramesh, B. V. Hokmabad, D. O. Pushkin, A. J. T. M. Mathijssen and C. C. Maass, J. Fluid Mech., 2023, 966, A29 CrossRef CAS.
- H. Kitahata, N. Yoshinaga, K. H. Nagai and Y. Sumino, Chem. Lett., 2012, 41, 1052–1054 CrossRef CAS.
- N. J. Suematsu, Y. Mori, T. Amemiya and S. Nakata, J. Phys. Chem. Lett., 2016, 7, 3424–3428 CrossRef CAS PubMed.
- G. Junot, N. Figueroa-Morales, T. Darnige, A. Lindner, R. Soto, H. Auradou and E. Clément, EPL, 2019, 126, 44003 CrossRef CAS.
- I. R. Epstein and K. Showalter, J. Phys. Chem., 1996, 100, 13132–13147 CrossRef CAS.
- R. J. Field and R. M. Noyes, J. Chem. Phys., 1974, 60, 1877–1884 CrossRef CAS.
- H.-D. Xi, H. Zheng, W. Guo, A. M. Gañán-Calvo, Y. Ai, C.-W. Tsao, J. Zhou, W. Li, Y. Huang, N.-T. Nguyen and S. H. Tan, Lab Chip, 2017, 17, 751–771 RSC.
- H. C. Berg, Annu. Rev. Biophys. Bioeng., 1975, 4, 119–136 CrossRef CAS PubMed.
- P. Dwivedi, D. Pillai and R. Mangal, Curr. Opin. Colloid Interface Sci., 2022, 61, 101614 CrossRef CAS.
- A. Baskaran and M. C. Marchetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 011920 CrossRef PubMed.
- M. Morozov and S. Michelin, J. Chem. Phys., 2019, 150, 044110 CrossRef PubMed.
- M. Majidi, M. A. Bijarchi, A. G. Arani, M. H. Rahimian and M. B. Shafii, Int. J. Multiphase Flow, 2022, 146, 103846 CrossRef CAS.
- J. L. Moran, P. M. Wheat and J. D. Posner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 065302 CrossRef CAS PubMed.
- S. Thutupalli and S. Herminghaus, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 91 CrossRef PubMed.
- E. Tjhung, D. Marenduzzo and M. E. Cates, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12381–12386 CrossRef CAS PubMed.
- Z. Jalilvand, H. Haider, J. Cui and I. Kretzschmar, Langmuir, 2020, 36, 6880–6887 CrossRef CAS PubMed.
- B. Jurado-Sánchez, S. Sattayasamitsathit, W. Gao, L. Santos, Y. Fedorak, V. V. Singh, J. Orozco, M. Galarnyk and J. Wang, Small, 2015, 11, 499–506 CrossRef PubMed.
- L. E. Scriven and C. V. Sternling, Nature, 1960, 187, 186–188 CrossRef.
- T. Tanabe, T. Ogasawara and N. J. Suematsu, Phys. Rev. E, 2020, 102, 023102 CrossRef CAS PubMed.
- H. Kitahata, Prog. Theor. Phys. Suppl., 2006, 161, 220–223 CrossRef CAS.
- S. J. S. Jamaluddin, K. Khaothong, M. R. Tinsley and K. Showalter, Chaos, 2020, 30, 083143 CrossRef CAS PubMed.
- D. J. P. Kumar, C. Borkar and P. Dayal, Langmuir, 2021, 37, 12586–12595 CrossRef CAS PubMed.
- V. Rajput and P. Dayal, J. Chem. Phys., 2021, 155, 064902 CrossRef CAS PubMed.
- A. B. Buhendwa, S. Adami and N. A. Adams, Mach. Learn. Appl., 2021, 4, 100029 Search PubMed.
- J.-L. Martiel and A. Goldbeter, Biophys. J., 1987, 52, 807–828 CrossRef CAS PubMed.
- A. Vasilyev and I. A. Drummond, Cell Adhes. Migr., 2010, 4, 353–357 CrossRef PubMed.
- C. Jin, B. V. Hokmabad, K. A. Baldwin and C. C. Maass, J. Phys.: Condens. Matter, 2018, 30, 054003 CrossRef PubMed.
- P. Mandal, G. Patil, H. Kakoty and A. Ghosh, Acc. Chem. Res., 2018, 51, 2689–2698 CrossRef CAS PubMed.
- Y. Xiong, H. Yuan and M. Olvera de la Cruz, Soft Matter, 2023, 19, 6721–6730 RSC.
- S. Auschra, A. Bregulla, K. Kroy and F. Cichos, Eur. Phys. J. E:Soft Matter Biol. Phys., 2021, 44, 90 CrossRef CAS PubMed.
- K. V. S. Chaithanya and S. P. Thampi, Soft Matter, 2019, 15, 7605–7615 RSC.
- K. V. S. Chaithanya and S. P. Thampi, J. Phys. D: Appl. Phys., 2020, 53, 314001 CrossRef CAS.
- E. Tjhung, A. Tiribocchi, D. Marenduzzo and M. E. Cates, Nat. Commun., 2015, 6, 5420 CrossRef CAS PubMed.
- G. Volpe, S. Gigan and G. Volpe, Am. J. Phys., 2014, 82, 659–664 CrossRef.
- R. F. Ausas, C. G. Gebhardt and G. C. Buscaglia, Commun. Nonlinear Sci. Numer. Simul., 2022, 108, 106213 CrossRef.
- N. Kruk, J. A. Carrillo and H. Koeppl, J. Comput. Phys., 2021, 440, 110275 CrossRef.
- K. Furtado, C. M. Pooley and J. M. Yeomans, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 046308 CrossRef CAS PubMed.
- K. V. S. Chaithanya, S. A. Shenoy and P. Dayal, Phys. Rev. E, 2022, 106, 065103 CrossRef CAS PubMed.
- G. Soligo, A. Roccon and A. Soldati, Meccanica, 2020, 55, 371–386 CrossRef.
- F. S. Hakimi and W. R. Schowalter, J. Fluid Mech., 1980, 98, 635 CrossRef.
- S. Frijters, F. Günther and J. Harting, Soft Matter, 2012, 8, 6542 RSC.
- N. Yoshinaga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012913 CrossRef PubMed.
- A. Fakhari and D. Bolster, J. Comput. Phys., 2017, 334, 620–638 CrossRef CAS.
- J. J. Tyson and P. C. Fife, J. Chem. Phys., 1980, 73, 2224–2237 CrossRef CAS.
- L. G. Leal, Advanced Transport Phenomena, Cambridge University Press, 2007 Search PubMed.
- R. Chabreyrie, D. Vainchtein, C. Chandre, P. Singh and N. Aubry, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 036314 CrossRef CAS PubMed.
- R. Dey, C. M. Buness, B. V. Hokmabad, C. Jin and C. C. Maass, Nat. Commun., 2022, 13, 2952 CrossRef CAS PubMed.
- K. Sarkar and W. R. Schowalter, J. Fluid Mech., 2001, 436, 207–230 CrossRef CAS.
- M. K. Mulligan and J. P. Rothstein, Phys. Fluids, 2011, 23, 022004 CrossRef.
- S. Liu, S. Shankar, M. C. Marchetti and Y. Wu, Nature, 2021, 590, 80–84 CrossRef CAS PubMed.
- M. Yamada, H. Shigemune, S. Maeda and H. Sawada, RSC Adv., 2019, 9, 40523–40530 RSC.
- S. Kitawaki, K. Shioiri, T. Sakurai and H. Kitahata, J. Phys. Chem. C, 2012, 116, 26805–26809 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01464b |
| ‡ Present address: School of Life Sciences, University of Dundee, Dundee, DD1 4HN, UK. |
| This journal is © The Royal Society of Chemistry 2025 |