Knotting and adsorption of end-grafted active polymers†
Yi-Fan
Shen
and
Meng-Bo
Luo
 *
*
School of Physics, Zhejiang University, Hangzhou 310027, China. E-mail: luomengbo@zju.edu.cn
First published on 4th February 2025
Abstract
The adsorption of end-grafted active polymers is significantly influenced by the presence of knots in the polymer. In this study, the adsorption of end-grafted active polymers composed of an active head and an end-grafted passive chain is investigated using Langevin dynamics simulations. The relationship between knots and adsorption is checked by varying the rotational inertia J of the active head. The effect of the active head becomes more pronounced at larger J as the rotational persistence time of the active force on the active head is increased by increasing J. As a result, the adsorption of the active polymer is hindered and the critical surface attraction strength is increased with rising J. The results are primarily attributed to an increased probability of polymer knots Pknot with increasing J. The presence of knots leads to an obvious decrease in the number of adsorbed monomers. Furthermore, we find that the knotting process is slower than the adsorption and the influence of the knotting on the adsorption is relatively weaker than the surface attraction strength. Our simulation results reveal that the increase in the rotational persistence time can increase the probability of knotting and thus weaken the adsorption of active polymer.
1. Introduction
When a polymer chain is located near an attractive surface, it will be adsorbed on the surface at a sufficiently large surface attraction strength or a sufficiently low temperature.1,2 Critical adsorption is a fundamental phenomenon in polymer science, characterized by a sharp change in the number of adsorbed monomers on a solid surface.1 The critical adsorption is also accompanied by a change in polymer conformation.2 This unique property is crucial for understanding and developing new materials for various applications, such as drug delivery, environmental remediation, and advanced functional coatings.3–5 It is crucial to understand the physical factors that affect the adsorption of polymer chains.6–8Active matter, which possesses the capability to convert chemical energy or other forms of energy into mechanical motion, has garnered significant attention due to unique functionality and potential applications.9–14 Biopolymers such as actin filaments, bacterial motility proteins, and microtubules can be viewed as active polymers constructed of active units.15,16 Some biological systems, such as spermatozoa, bacilli, and spirochetes, have elongated organisms and can move with the help of active parties in their bodies.17 Active polymers have been an important model for studying the behaviors of active biopolymers.18–20 In experiments, active polymers can be obtained by linking passive polymer-like DNAs or proteins to catalytic Janus particles21 or linking self-propelling centimeter-sized disks by rubber chains or springs.22,23 Active polymers are of considerable interest due to their ability to adapt to environmental changes, perform biochemical reactions, and respond to external stimuli.10,24–26 Stimuli-responsive active polymers are regarded as smart polymers with potential applications.
Active matter exhibits a wide range of emergent non-equilibrium phenomena, therefore theoretical studies of which often require computer simulations.27,28 The active polymer models are designed to be composed wholly or partially of active units. The active forces of active units can be either independent or dependent, with the direction of the active forces either random or aligned along the tangential direction.10,29,30 Recently, active polymer models with an active particle at the head were also proposed.17,31 Enhanced diffusion was observed for all kinds of active polymer models.11,19,25 Active polymer models were also proposed by introducing local active fluctuations.26 Active polymers with random, independent active forces can be even regarded as passive polymers in a hotter environment as the active forces provide an extra fluctuation.32 The rotation of the active force is characterized by the rotational persistence time τR. The diffusion is enhanced by increasing τR of active particles.33,34 In other words, the increase in τR enforces the effect of the active force.33,35,36 Meanwhile, the adsorption of active polymers with random or tangential activity was influenced by the active force.37,38 It is interesting to explore the effects of the non-equilibrium dynamics of active matter on adsorption.
The role of the active force on the adsorption was studied for a special active polymer model composed of an active head and a sequential end-grafted passive chain.39 The adsorption of the active polymer is hindered, and the effect of the active force increases proportionally to the square of the active force. The obstruction of the adsorption is accompanied by the occurrence of knotting in the active polymer.39 It was suggested that the knotting was dependent on τR of the active head as τR increased with increasing the active force.39 So, it is worthwhile to reveal the effect of τR on the adsorption while keeping the active force constant.
In this study, the effect of the rotational inertia on the critical adsorption of end-grafted active polymers on an attractive surface is investigated using Langevin dynamics (LD) simulations. Increasing the rotational inertia of the active head, τR is increased, that enhances the effect of the active force. We find that increasing the rotational inertia inhibits the adsorption of active polymers and discover that the inhibition of adsorption stemmed from the increase of knotted active polymers. The presence of knots leads to a significant decrease in the number of adsorbed monomers. As a result, the critical surface attraction strength is raised by increasing the rotational inertia.
2. Model and simulation method
Detailed models and simulation methods are described in our previous paper.39 Here we only give a brief description. A standard bead-spring polymer model is adopted.40 The active polymer of length N consists of one active Langevin particle (labeled 1) at the head and an end-grafted passive flexible polymer with N − 1 passive beads (labeled from 2 to N). Bead-bead pairwise interactions are a repulsive Weeks–Chandler–Anderson (WCA) potential with interaction strength ε. Bonded beads in the passive polymer experience a standard finitely extensible non-linear elastic (FENE) potential with elastic coefficient KF = 30ε/σ2 and maximum bond length R0 = 1.5σ. The active head experiences a self-propulsion force Fa = Fan. Here, n is a unit vector that points from the center of the active bead as shown in Fig. S1 in the ESI.† The active head and passive beads both have a diameter of σ and a mass of m. The terminal passive bead, labeled N, is grafted to an attractive surface positioned at z = 0. Periodic boundary conditions are adopted along the x and y directions. The polymer–surface interaction is described by the Lenard-Jones (LJ) 9-3 potential41 | (1) |
A flexible polymer model is adopted, that is, bending and torsional energy aren't considered. The influence of bending energy on the adsorption of non-active polymer chains was previously studied. It was found that bending energy shifts the critical adsorption point, but the physical mechanism remains the same and can be explained by the energy–entropy balance.42 However, when the polymer chain's contour length greatly exceeds the persistence length, the polymer with bending energy behaves like a flexible polymer. So, the flexible polymer is the most basic polymer model.
Our simulations employ implicit solvents and ignore hydrodynamic interactions. The translational movement of the active head and passive beads is described by the translational Langevin equation33,43
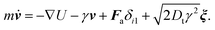 | (2) |
The dynamics of the direction of the active force, n, is determined by33,43
| ṅ = ω × n. | (3) |
 | (4) |
In this work, the restricted rotating active polymer (RRAP)31 is adopted for the end-grafted active polymer. In the RRAP chain, the first passive bead is connected to the edge of the active head opposite the direction of the active force. The FENE potential45
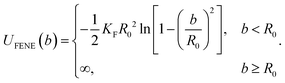 | (5) |
The dynamics of the polymer are achieved by using the LD simulation method with the velocity-Verlet algorithm. Standard LJ units are used to express the physical quantities involved in our system. We set the mass and size of polymer monomers as unity, i.e., m = σ ≡ 1. And the bead–bead pairwise interaction strength is also set as unity, ε ≡ 1. The unit of time is τ0 = (mσ2/ε)1/2. The time step for the velocity-Verlet algorithm is set as 0.005τ0. Simulations are performed at the temperature kBT = ε = 1. We set the friction coefficient γ = 1, so we have Dt = 1 and Dt/Dr = 1/3.
The LD simulation process for the end-grafted active polymer chains is described in the following two main steps. (1) Initial system: generating an end-grafted active polymer chain by a step-by-step growing method. The terminal passive bead is fixed at z = 0.8584 above the surface, which corresponds to the minimum of the surface potential. The initial direction of the active force, n, is set arbitrarily from the center of the first passive bead to that of the active head. The initial conformation of the active polymer chain is coil-like; (2) simulated annealing: increasing the surface attraction strength εPS slowly from 0.05 with a non-adsorbed state to 3 with a strongly adsorbed state. At each εPS, we run for a period of teq for the polymer chains to reach a steady state and tsta to obtain the statistical properties of the polymer chains. The final polymer conformation at the previous εPS is used as the initial polymer conformation of the next εPS. Our simulation results are averaged over 2000 independent samples. The statistical errors are quite small as they are typically less than 2%.
3. Results and discussion
3.1. Adsorption of active polymer
The adsorption of the active polymer of length N = 65 is simulated at constant temperature T = 1. With the increase in the surface attraction strength εPS, the mean number of adsorbed monomers, 〈M〉, increases. A monomer located close to the surface with a distance smaller than 1.22σ is defined as an adsorbed monomer. At z = 1.22σ, the attraction energy is about −0.5εPS. However, the grafted monomer is not counted in 〈M〉. Simulations are carried out for different rotational inertias from J = 0.1 to 50. The value of active force Fa = 5 is used for most simulations. It was found that the active force of Fa = 5 affects the adsorption of the active polymer chain obviously.39 In the study of the adsorption of the active polymer, the simulated annealing process is adopted by slowly increasing εPS from 0.05 to 3.For the J = 0.1 case, simulation results show that it is easy for the active polymer to reach a steady state. We have compared the results for different simulation times with tsta = 5000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, respectively, for every εPS. While teq = 2000 is fixed. Fig. 1 shows the variation of the fraction of adsorbed monomers φ = 〈M〉/N with εPS at Fa = 5. We find the simulation results are roughly independent of tsta. This implies that the simulation times teq = 2000 and tsta = 5000 are already sufficiently long for J = 0.1. The increase in φ with increasing εPS is consistent with the snapshots shown in Fig. 1. More beads are adsorbed at large εPS. However, at εPS = 3, a few beads adjacent to the active heads are desorbed due to the active force.
000, respectively, for every εPS. While teq = 2000 is fixed. Fig. 1 shows the variation of the fraction of adsorbed monomers φ = 〈M〉/N with εPS at Fa = 5. We find the simulation results are roughly independent of tsta. This implies that the simulation times teq = 2000 and tsta = 5000 are already sufficiently long for J = 0.1. The increase in φ with increasing εPS is consistent with the snapshots shown in Fig. 1. More beads are adsorbed at large εPS. However, at εPS = 3, a few beads adjacent to the active heads are desorbed due to the active force.
 | ||
| Fig. 1 Plots of the fraction of adsorbed monomers φ versus the surface attraction strength εPS for the active polymer chains with different simulation time tsta. Polymer length N = 65, rotational inertia J = 0.1, and active force Fa = 5. Two insets show snapshots of the active polymer at εPS = 0.5 and 3. Red, tan, blue, and pink beads represent the active head, grafted bead, adsorbed beads, and non-adsorbed beads, respectively. The grey plane represents the attraction surface. The same symbols are used for the snapshots in Fig. 2 and 6. | ||
Similar simulations are performed for the J = 50 case with tsta = 5000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and with the same teq = 2000. Simulation results of φ versus εPS are presented in Fig. 2. The increase in φ with increasing εPS is also consistent with the snapshots shown in Fig. 2. However, the values of φ are dependent on tsta, indicating that the time for reaching a steady state would be longer than the present simulation time for the large J case. The reason why it is very slow to reach a steady state is the slow knotting process in the chain, which will be discussed later. The inset of Fig. 2 presents a knotted polymer at εPS = 3. Because the polymer monomers at the knotted parts aggregate densely, the adsorption is thus decreased. The values φ of J = 50 are smaller than that of J = 0.1 (Fig. 1), especially in the large εPS region. The evolution of knotting depends on the value of J. As J increases, the time required for the chain to form a knot also increases. For J = 50, this time might exceed the limits of this study.
000 and with the same teq = 2000. Simulation results of φ versus εPS are presented in Fig. 2. The increase in φ with increasing εPS is also consistent with the snapshots shown in Fig. 2. However, the values of φ are dependent on tsta, indicating that the time for reaching a steady state would be longer than the present simulation time for the large J case. The reason why it is very slow to reach a steady state is the slow knotting process in the chain, which will be discussed later. The inset of Fig. 2 presents a knotted polymer at εPS = 3. Because the polymer monomers at the knotted parts aggregate densely, the adsorption is thus decreased. The values φ of J = 50 are smaller than that of J = 0.1 (Fig. 1), especially in the large εPS region. The evolution of knotting depends on the value of J. As J increases, the time required for the chain to form a knot also increases. For J = 50, this time might exceed the limits of this study.
 | ||
Fig. 2 Plots of the fraction of adsorbed monomers φ (a) and the derivative dφ/dεPSversus the surface attraction strength εPS for the active polymer chains with different simulation time tsta. Polymer length N = 65, rotational inertia J = 50, and active force Fa = 5. The curves in (b) are fits of eqn (6) and (7). Fitting parameters are  A = 0.385, d = 0.68, and c = 1.75 for tsta = 5000, and A = 0.385, d = 0.68, and c = 1.75 for tsta = 5000, and 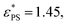 A = 0.354, d = 0.67, and c = 1.60 for tsta = 20 A = 0.354, d = 0.67, and c = 1.60 for tsta = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Two insets show snapshots of the active polymer at εPS = 0.5 and 3. 000. Two insets show snapshots of the active polymer at εPS = 0.5 and 3. | ||
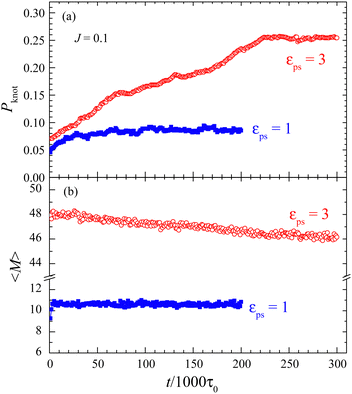
We have calculated the probability of knotted polymers, Pknot, over all simulated samples and simulation times. All polymer conformations are divided into knotted and unknotted conformations. The probability Pknot is the fraction of knotted conformations. In the present study, we use the simulation method to figure out the knots in polymer chains. To this end, we apply a sufficiently large artificial stretching force on the active bead. The force is directed vertically outward from the surface to stretch the polymer chain. The unknotted conformations will be fully stretched to their fullest extent, while knotted ones will resist such complete elongation as shown in Fig. S2 in the ESI.† With this method, we can distinguish between a knotted polymer and an unknotted one. At the final εPS = 3, Pknot is about 0.532 for tsta = 5000 while it is about 0.766 for tsta = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The increase in Pknot reduces the number of adsorbed monomers. Thus we find that the adsorption of the active polymer is of time-dependence, especially for large J. We have also checked the knotted and unknotted conformations by using the KymoKnot software package,46 which identifies knots based on the Alexander determinants. Due to the presence of the surface, to obtain accurate knotting results, it is needed to artificially extend several chain beads downward from the grafted end. These two methods obtain roughly the same value of Pknot.
000. The increase in Pknot reduces the number of adsorbed monomers. Thus we find that the adsorption of the active polymer is of time-dependence, especially for large J. We have also checked the knotted and unknotted conformations by using the KymoKnot software package,46 which identifies knots based on the Alexander determinants. Due to the presence of the surface, to obtain accurate knotting results, it is needed to artificially extend several chain beads downward from the grafted end. These two methods obtain roughly the same value of Pknot.
The critical surface attraction strength 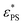 for the end-grafted active polymer is estimated by calculating the place of the maximum variation of dφ/dεPS. Following the method described previously, the variation of dφ/dεPS with εPS is fitted by a Gaussian function39
for the end-grafted active polymer is estimated by calculating the place of the maximum variation of dφ/dεPS. Following the method described previously, the variation of dφ/dεPS with εPS is fitted by a Gaussian function39
 | (6) |
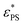 and by an exponential decay function
and by an exponential decay function | (7) |
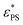 . Here A, d, and c are fitting parameters. At
. Here A, d, and c are fitting parameters. At  the derivative dφ/dεPS reaches the maximum with the value of A. From these two fittings, we estimate
the derivative dφ/dεPS reaches the maximum with the value of A. From these two fittings, we estimate  and 1.45 ± 0.05 for tsta = 5000 and 20
and 1.45 ± 0.05 for tsta = 5000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, respectively. Here the error bar is estimated from the simulation data. Although
000, respectively. Here the error bar is estimated from the simulation data. Although 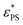 decreases with increasing tsta, the change in
decreases with increasing tsta, the change in  is quite small. We would like to point out that there is no physical basis for eqn (6) and (7) at present. These equations incorporate data that are distant from
is quite small. We would like to point out that there is no physical basis for eqn (6) and (7) at present. These equations incorporate data that are distant from  instead of a single point of maximum dφ/dεPS. As a result, the error associated with
instead of a single point of maximum dφ/dεPS. As a result, the error associated with  is reduced since the data in the vicinity of
is reduced since the data in the vicinity of 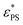 are subject to significant statistical errors as shown in Fig. 2b.
are subject to significant statistical errors as shown in Fig. 2b.
The same simulated annealing process is performed for different rotational inertia of the active head by setting teq = 2000 and tsta = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.  are estimated using eqn (6) and (7). Fig. 3a shows the relationship between
are estimated using eqn (6) and (7). Fig. 3a shows the relationship between  and J for active polymers of N = 33 and 65 at Fa = 5. Within the range of our simulation parameters, the monotonical increase of
and J for active polymers of N = 33 and 65 at Fa = 5. Within the range of our simulation parameters, the monotonical increase of  with J can be approximately expressed as
with J can be approximately expressed as
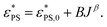 | (8) |
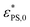 is the critical surface attraction strength for infinitely small J. The higher value of
is the critical surface attraction strength for infinitely small J. The higher value of  for the shorter polymer is due to the finite size effect.42
for the shorter polymer is due to the finite size effect.42
 | ||
Fig. 3 (a) Plot of the critical adsorption attraction strength  versus the rotational inertia of the active head J for the active polymers with length N = 33 (blue solid squares) and 65 (red open circles) and active force Fa = 5. The solid lines are fits of eqn (8) with versus the rotational inertia of the active head J for the active polymers with length N = 33 (blue solid squares) and 65 (red open circles) and active force Fa = 5. The solid lines are fits of eqn (8) with 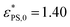 , B = 0.081, β = 0.25 for N = 33 and , B = 0.081, β = 0.25 for N = 33 and  , B = 0.042, β = 0.50 for N = 65. (b) Plot of the fraction of adsorbed monomers φ* at , B = 0.042, β = 0.50 for N = 65. (b) Plot of the fraction of adsorbed monomers φ* at  versus J. versus J. | ||
The monotonic increase of  with J indicates that a higher J enhances the effect of the active force. This observation is consistent with the finding that active forces lead to an increase in the effective temperature.47 The exponent β represents the dependence of
with J indicates that a higher J enhances the effect of the active force. This observation is consistent with the finding that active forces lead to an increase in the effective temperature.47 The exponent β represents the dependence of 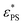 on J. A larger value of β indicates a stronger dependence of
on J. A larger value of β indicates a stronger dependence of  on J. It is interesting to see the polymer of N = 65 has a larger value of β than that of N = 33, implying that
on J. It is interesting to see the polymer of N = 65 has a larger value of β than that of N = 33, implying that 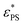 of N = 65 may exceed that of N = 33 at sufficiently large J. This anomaly can be understood through the knots in the polymer chain. The probability of knots in the polymer chain increases with N. For example, we have Pknot = 0.210 for N = 33 and Pknot = 0.766 for N = 65 at εPS = 3. The larger value of Pknot results in a more obvious increase in
of N = 65 may exceed that of N = 33 at sufficiently large J. This anomaly can be understood through the knots in the polymer chain. The probability of knots in the polymer chain increases with N. For example, we have Pknot = 0.210 for N = 33 and Pknot = 0.766 for N = 65 at εPS = 3. The larger value of Pknot results in a more obvious increase in  for a longer polymer chain. Therefore we have a larger value of β for a longer active polymer. For even longer polymer chains, there may be multiple knots in the chains.48
for a longer polymer chain. Therefore we have a larger value of β for a longer active polymer. For even longer polymer chains, there may be multiple knots in the chains.48
The increase of  with J at fixed Fa is similar to the result that
with J at fixed Fa is similar to the result that  increases with increasing Fa for fixed J = 0.1.39 Therefore, an increase in J enhances the effect of the active force. Similarly, less monomers are adsorbed at large Fa or large J. At the same time, the adsorption of a polymer chain is related to the variation of its conformation, especially knots in the polymer chain.39 One main reason is that knotted polymers with less adsorbed monomers are formed when Fa is applied.
increases with increasing Fa for fixed J = 0.1.39 Therefore, an increase in J enhances the effect of the active force. Similarly, less monomers are adsorbed at large Fa or large J. At the same time, the adsorption of a polymer chain is related to the variation of its conformation, especially knots in the polymer chain.39 One main reason is that knotted polymers with less adsorbed monomers are formed when Fa is applied.
The fraction of adsorbed monomers φ* at  is plotted in Fig. 3b for the active polymers with length N = 33 and 65 and active force Fa = 5. φ* is roughly a constant at small J. The reason is that at
is plotted in Fig. 3b for the active polymers with length N = 33 and 65 and active force Fa = 5. φ* is roughly a constant at small J. The reason is that at  a portion of the monomers must be adsorbed to balance the loss of entropy upon adsorption. The decrease of φ* with increasing N is consistent with the previous results φ* ∝ Nϕ−1 with the crossover exponent ϕ < 1,1i.e., a smaller fraction of the adsorbed monomers is required for longer polymer chains. The physics for the increase of φ* at large J is not clear yet.
a portion of the monomers must be adsorbed to balance the loss of entropy upon adsorption. The decrease of φ* with increasing N is consistent with the previous results φ* ∝ Nϕ−1 with the crossover exponent ϕ < 1,1i.e., a smaller fraction of the adsorbed monomers is required for longer polymer chains. The physics for the increase of φ* at large J is not clear yet.
3.2. Relation between polymer knot and adsorption
It is important to understand the effect of polymer knots on the adsorption. Because of the evolution of polymer knots, we need to know how long to fulfill the knots in the polymer or reach the steady state. To this end, the evolution of polymer knots is investigated.For the J = 0.1 case, the evolutions of Pknot and 〈M〉 over time at εPS = 1 and 3 are presented in Fig. 4. The initial states at time t = 0 for the simulation are the obtained steady states at very small εPS = 0.05. Then we quench the system to εPS = 1 and 3 and record the evolution at every 1000τ0. This simulation method is named direct simulation in this work. We find that both Pknot and 〈M〉 first increase with time and then roughly saturate at a sufficiently long simulation time. That means that the steady states can be reached if the simulation time is long enough. Moreover, it is easier for 〈M〉 to saturate as the change in 〈M〉 is much smaller over the simulation time. This can explain why the simulation results of φ = 〈M〉/N shown in Fig. 1 are roughly independent of tsta for J = 0.1. Fig. 4 also shows that the time for the system to reach a steady state becomes longer at large εPS, this is consistent with a small deviation in the simulation results of φ at large εPS. For the same reason, it is better to adopt the simulated annealing method in the study of the adsorption of the active polymer. Although the saturated values of Pknot and 〈M〉 are close to the annealing results of Pknot = 0.0814 and 〈M〉 = 10.61 for εPS = 1 and Pknot = 0.2543 and 〈M〉 = 46.43 for εPS = 3, longer simulation times are required for the direct simulation.
For the J = 50 case, two simulation methods are used for the temporal evolution of Pknot and 〈M〉. In addition to the direct simulation used for the J = 0.1 case, we also extend the simulation time by using the conformations obtained during the annealing simulations, which we call extended simulation. For the extended simulation, the surface attraction strength εPS is kept constant. The results are presented in Fig. 5 for both direct and extended simulations. The probability of knotted polymers Pknot increases with time, indicating that it is hard for the active polymer to reach a steady state at large J. 〈M〉 is roughly a constant independent of time at εPS = 1, whereas it decreases with increasing time at εPS = 3. This is consistent with the results obtained by annealing simulations shown in Fig. 2, where 〈M〉 decreases when τsta is increased and such a decrease is more significant at large εPS. Fig. 5 also shows that 〈M〉 is of less time dependence than Pknot. At εPS = 1, although Pknot increases with time, 〈M〉 is roughly a constant. Therefore, it is easier to estimate the critical attraction strength  from the variation of 〈M〉. We find that Pknot is about 0 at the very beginning of the direct simulation, indicating that the initial polymers are almost unknotted.
from the variation of 〈M〉. We find that Pknot is about 0 at the very beginning of the direct simulation, indicating that the initial polymers are almost unknotted.
The active polymer is adsorbed strongly at εPS = 3 much higher than  . It is interesting to see that, from Fig. 5c and d, the changes in Pknot and 〈M〉 with time for the extended simulations are quite small at εPS = 3 from the simulated annealing process with teq = 2000 and tsta = 20
. It is interesting to see that, from Fig. 5c and d, the changes in Pknot and 〈M〉 with time for the extended simulations are quite small at εPS = 3 from the simulated annealing process with teq = 2000 and tsta = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. This means that the adsorbed active polymer almost reaches its steady state at εPS = 3 even for the largest J = 50 in the present study. To understand the effect of rotational inertia on the knotting, the probability of knotted polymers, Pknot, is calculated for different J at εPS = 3. Pknot is calculated from the conformations obtained in the annealing process with teq = 2000 and τsta = 20
000. This means that the adsorbed active polymer almost reaches its steady state at εPS = 3 even for the largest J = 50 in the present study. To understand the effect of rotational inertia on the knotting, the probability of knotted polymers, Pknot, is calculated for different J at εPS = 3. Pknot is calculated from the conformations obtained in the annealing process with teq = 2000 and τsta = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The dependence of Pknot on J is presented in Fig. 6a. We find Pknot increases sharply at small J and roughly saturates at large J. This is only correct for small active force Fa, long polymer chain, and relatively small J. We can expect that, when J or Fa is infinitely large or N is small, the end-grafted chains will be stretched straight. The straightened chains are not conducive to knotting. For instance, we find Pknot ≈ 0.210 for a short chain of length N = 33 for J = 50 and Fa = 5. Therefore, the knotting probability Pknot will decrease eventually at a sufficiently large J. So, in this work, we adopt a relatively weak active force (Fa = 5) and a relatively long polymer chain (N = 65).
000. The dependence of Pknot on J is presented in Fig. 6a. We find Pknot increases sharply at small J and roughly saturates at large J. This is only correct for small active force Fa, long polymer chain, and relatively small J. We can expect that, when J or Fa is infinitely large or N is small, the end-grafted chains will be stretched straight. The straightened chains are not conducive to knotting. For instance, we find Pknot ≈ 0.210 for a short chain of length N = 33 for J = 50 and Fa = 5. Therefore, the knotting probability Pknot will decrease eventually at a sufficiently large J. So, in this work, we adopt a relatively weak active force (Fa = 5) and a relatively long polymer chain (N = 65).
The variations of 〈M〉 with J are presented in Fig. 6b for both knotted and unknotted polymers. 〈M〉 of knotted polymers is always smaller than that of unknotted polymers. Therefore, combined with the result that Pknot increases with J, the overall value 〈M〉 averaged over all polymers decreases with increasing J. In short, large J causes more knotted polymers, resulting in reduced adsorption of the active polymer.
〈M〉 increases slowly with J for the unknotted polymers, indicating that the increase in J helps the adsorption of the unknotted polymers. Comparing the snapshots shown in Fig. 6c of J = 0.1 and in Fig. 6e of J = 50, we find the active polymer is more stretched at large J = 50. The mean square end-to-end distance 〈R2〉 increases from about 525.9 at J = 0.1 to about 870.9 at J = 50. Such a change in the conformation is similar to the conformation change from a flexible polymer to a rigid polymer. It is known that a rigid polymer is more easily adsorbed to the surface due to the less conformational entropy of the rigid polymer.42 Therefore, it is reasonable to find that the stretched polymer of large J has a large 〈M〉.
Whereas for the knotted polymers, we find 〈M〉 first decreases rapidly with the increase of J, from 〈M〉 = 41 at J = 0.1 to 〈M〉 = 36 at J = 20, and then slightly increases with J. This non-monotonic behavior might be also related to the change in the polymer conformation. Comparing the snapshots shown in Fig. 6d of J = 0.1 and in Fig. 6f of J = 50, we find a loose knot at J = 0.1 and a tight knot at J = 50. This implies a tight knot decreases the adsorption. While at large J, the unknotted part of the polymer is stretched. 〈R2〉 increases from about 241.1 at J = 0.1 to about 388.3 at J = 50. For the same reason as described for the unknotted polymer, the stretch of the polymer strengthens the adsorption of the polymer at large J.
We have investigated which part of the polymer is less adsorbed at large J. To this end, we have calculated the mean adsorption probability, Pads, for every monomer. The results are presented in Fig. 7a for the active polymer chain at Fa = 5 for the strong adsorption case with εPS = 3. The values of Pads are calculated from a total of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 polymer conformations. The decrease in Pads close to the active head is consistent with the snapshots shown in Fig. 1 and 2. The values of Pads at J = 0.1 are larger than those at J = 50, except for the monomers close to the active head. On average, monomers at J = 50 are less adsorbed, consistent with a larger
000 polymer conformations. The decrease in Pads close to the active head is consistent with the snapshots shown in Fig. 1 and 2. The values of Pads at J = 0.1 are larger than those at J = 50, except for the monomers close to the active head. On average, monomers at J = 50 are less adsorbed, consistent with a larger  at J = 50. In other words, a large J enhances the active force to retard the adsorption of the active polymer.
at J = 50. In other words, a large J enhances the active force to retard the adsorption of the active polymer.
To understand the effect of the rotation inertia, the values of Pads for unknotted and knotted polymers are investigated and the results are presented in Fig. 7b and c. For unknotted polymers, values of Pads are almost independent of J, except for the monomers close to the active head. Therefore, the effect of J on the adsorption is mainly reflected in the conformation of knotted polymers. The significant decrease in Pads of knotted polymers near the grafted end is due to that knots appear close to the grafted end. The probability that a bead is part of a knotted region, calculated from the KymoKnot software package, is plotted in Fig. S3 in the ESI.† It is consistent with the snapshots shown in Fig. 6d and f. Thus, we can conclude that knots significantly decrease the adsorption. Whereas the values of Pads near the active head are slightly larger at J = 50 for both knotted and unknotted polymers, due to the stretch of polymer as shown in Fig. 6e and f.
At a sufficiently long simulation time, the probability of knotted polymers Pknot is eventually saturated for J = 0.1 as shown in Fig. 4. However, the saturation is slow for J = 50 as shown in Fig. 5. For both cases, we find the number of adsorbed monomers saturates fast or changes small. That is, although the knotting of polymer is changed obviously with time, the adsorption property is less dependent on the simulation time. So the critical adsorption point can be still estimated accurately with limited simulation time.
In Fig. 5, we find Pknot increases with time for the active polymer at surface attraction strength εPS = 1 and 3. It is interesting to know if Pknot will be saturated over time for J = 50. To this end, the evolution of Pknot with simulation time is investigated by suddenly changing εPS. Two types of simulations are performed for the active polymer with J = 50 at Fa = 5. One is that we suddenly increase εPS from 1 to 3, while the other is that we suddenly decrease εPS from 3 to 1. Here εPS = 1 is below  for J = 50 at Fa = 5 while εPS = 3 is above
for J = 50 at Fa = 5 while εPS = 3 is above  . The initial states for both simulations are the simulated polymer conformations obtained from the simulated annealing process with τsta = 20
. The initial states for both simulations are the simulated polymer conformations obtained from the simulated annealing process with τsta = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
The evolution of Pknot and 〈M〉 are presented in Fig. 8. The value of Pknot increases with time when εPS is increased from 1 to 3, while it decreases with time when εPS is decreased from 3 to 1. Results show that the adsorption of the active polymer above  is conducive to the knotting of the polymer, whereas the desorption below
is conducive to the knotting of the polymer, whereas the desorption below  is conducive to the unknotting of the polymer. The decrease in Pknot with time when εPS is decreased from 3 to 1 implies that Pknot will be saturated when the simulation time is elongated.
is conducive to the unknotting of the polymer. The decrease in Pknot with time when εPS is decreased from 3 to 1 implies that Pknot will be saturated when the simulation time is elongated.
For both cases, Pknot changes slowly with time, indicating that the process of knotting and unknotting is slow. It would take a very long time to reach the annealing results Pknot = 0.334 for εPS = 1 and Pknot = 0.766 for εPS = 3. However, we find that 〈M〉 changes sharply in the initial stage and then changes slowly with time. Because of the slow evolution of Pknot, we find the saturation values of 〈M〉 in the narrow time window shown in Fig. 8b slightly deviate from the annealing results with 〈M〉 = 8.07 for εPS = 1 and 〈M〉 = 40.03 for εPS = 3. Our results show that, although the knotting will decrease the adsorption amount 〈M〉, the value of 〈M〉 is mainly determined by the surface attraction strength.
We would like to point out that the main reason for the change in 〈M〉 shown in Fig. 8 is the change in the surface attraction strength εPS. When εPS increases, 〈M〉 increases; conversely, 〈M〉 decreases. At this time, the influence of the change in Pknot on 〈M〉 is secondary. To see the influence of Pknot on 〈M〉, we perform a simulation by keeping εPS unchanged while varying the value of J. Starting from the steady state of J = 50, we suddenly reduce the value of J to 0.1 and see the variation of Pknot and 〈M〉 with time. The results are presented in Fig. S4 in the ESI.† We can see that the decrease in Pknot over time is accompanied by an increase in 〈M〉, which is consistent with the conclusion that the existence of knots reduces adsorption.
3.3. Rotational persistence time of the active head
Finally, we discuss the effect of rotational inertia on the rotational persistence time of the active head. We have calculated the dynamical orientational correlation function| C(t) = 〈n(t0)n(t + t0)〉 | (9) |
During the rotational persistence time τR, the active particles can be considered as moving straightly along the direction of Fa in time τR, which increases the diffusion of active particles.33 Enhanced diffusive behavior was also observed for active polymers.11,19,25,31 The evolutions of C(t) of the active head with time t are simulated for active polymers in a dilute solution. The results are presented in Fig. 9a for active polymers with length N = 65 at the active force Fa = 5. The decay of C(t) of the active polymer differs from that of active particles. We find the decay of C(t) should be expressed by a double exponential decay function
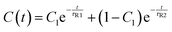 | (10) |
 | ||
| Fig. 9 Evolutions of the dynamical orientational correlation function C(t) with time t for the active polymer in a dilute solution (a) and for the end-grafted active polymer on a repulsive surface (b). Polymer length N = 65, rotational inertia J = 0.1 and 50, and active force Fa = 5. The double-logarithmic plot (Fig. S5, ESI†) is presented in the ESI.† | ||
| J | τ R1 | τ R2 |
|---|---|---|
| 0.1 | 2.2 ± 0.2 | 18 ± 1 |
| 0.2 | 2.2 ± 0.2 | 19 ± 1 |
| 0.5 | 2.4 ± 0.2 | 20 ± 1 |
| 1 | 2.4 ± 0.2 | 20 ± 1 |
| 2 | 3.5 ± 0.2 | 24 ± 2 |
| 5 | 5.5 ± 0.5 | 37 ± 2 |
| 10 | 8.5 ± 0.5 | 55 ± 5 |
| 20 | 10.5 ± 0.5 | 67 ± 5 |
| 30 | 11.0 ± 0.5 | 74 ± 5 |
| 50 | 12.5 ± 0.5 | 80 ± 5 |
The reason for the two rotational persistence times is not straightforward. The smaller one τR1 might represent the rotation of the active head in the polymer chain and the larger one τR2 might be related to the rotation of the entire polymer chain. Because of the limitation on the rotation of the active head, the large-scale rotation is limited by the rotation of the entire chain. We find that the rotation of the entire chain, characterized by the self-correlation function of the end-to-end vector, is much slower than the rotation of the active head. For example, the relaxation time of the end-to-end vector is about 630 for a free polymer chain of length N = 65 in the dilute solution, see Fig. S6 in the ESI.† For comparison, the double-logarithmic plot of Fig. 9 can be found in the ESI† (Fig. S5). The log–log behavior emerges at the moderate range of time. However, in the short-time region, the double exponential decay function is better.
The rotation of the active head has also been checked for a general case when the active polymer is end-grafted on a repulsive surface. We set zc = 0.8584 and εPS = 1 in eqn (1). Evolutions of C(t) with t for the active polymer of length N = 65 with rotational inertia J = 0.1 and 50 are presented in Fig. 9b. The magnitude of the active force is Fa = 5. For the end-grafted polymer chains, the decay of C(t) can be still expressed by the double exponential decay function as eqn (9). Analogue to the active-polymers in a dilute solution, a large J results in a slow rotation of the active head for the end-grafted active-polymers. However, it is interesting to find that τR1 and τR2 are reduced when the active polymer is end-grafted on a repulsive surface. For the end-grafted active polymer, we have τR1 = 0.47 and τR2 = 6.2 for J = 0.1, and τR1 = 2.7 and τR2 = 16.7 for J = 50. The reduction in the rotational persistence times may be due to the larger polymer conformation and thus smaller spatial constraints on the active head.
Simulation results show that the rotational persistence times of the active head increase with increasing J. The increase in the rotational persistence times enforces the effect of the active force. Our results imply that the increase in the rotational persistence times could strengthen the knotting but weaken the adsorption.
The rotational inertia, active force, and restriction of the active bead are considered in the present active polymer model. These three factors make the rotational behavior of the active head rather complicated. Therefore, in this work, we only qualitatively explain that the rotational persistence times increase with the increase of inertia, without a quantitative discussion. The rotational behavior of the active head is worthy of further study.
4. Conclusions
The adsorption of end-grafted active polymers on an attraction surface has been studied by Langevin dynamics simulation. The active polymers are composed of only one active particle at the head and an end-grafted flexible passive chain. The active head experiences an active force of magnitude Fa. In this work, the rotational inertia J of the first active head is varied. We vary the surface attraction strength εPS to investigate the adsorption of the active polymer. We find that the critical surface attraction strength for the active polymer increases with increasing J as . The increase of
. The increase of  is related to the knotting of the active polymer.
is related to the knotting of the active polymer.
Due to the stretch of the active force, knotted polymers are observed especially at high εPS and high J. We find that knotted polymers are less adsorbed than unknotted ones. As the probability of knotted polymers Pknot is increased with increasing J, the mean number of adsorbed monomers 〈M〉 is reduced when J is increased. As a result, the knotting of the active polymer raises the value of  . Moreover, the knotting process is relatively slow, both 〈M〉 and Pknot evolve over simulation time. However, 〈M〉 demonstrates less sensitivity to time changes compared to Pknot. Therefore, simulation on 〈M〉 is less sensitive to the simulation time.
. Moreover, the knotting process is relatively slow, both 〈M〉 and Pknot evolve over simulation time. However, 〈M〉 demonstrates less sensitivity to time changes compared to Pknot. Therefore, simulation on 〈M〉 is less sensitive to the simulation time.
The effect of the active head becomes more pronounced at larger J as the rotational persistence times are increased by increasing J. Our simulations reveal that the increase in the rotational persistence times can enhance knotting and weaken polymer adsorption. The ability of active polymers to exhibit inertia-sensitive adsorption may become a candidate for the future development of adaptive, smart polymer surfaces.
The present model active polymer might be achieved in experiments by linking DNA to Janus particles. To observe knotting in experiments, flexible long chains with moderate forces are preferred. Single-stranded DNA (ssDNA) molecules are considered to be flexible with a Kuhn length σ ≈ 1.6 nm and a pair-wise energy ε ≈ 11.5 kJ mol−1.51 Here, σ ≈ 1.6 nm in ssDNA corresponds to two bases with a mass of about m = 650 g mol−1.51 Then, the units of force ε/σ is about 120 pN, and that of rotational inertia mσ2 is about 2.76 × 10−44 kg m2. Double-stranded DNA (dsDNA) molecules are of finite stiffness and much longer dsDNA molecules are needed to observe the same knotting effect. Furthermore, using attractive surfaces for the active polymer is also helpful for knotting.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
This work is supported by the National Natural Science Foundation of China under grant no. 11974305.References
- E. Eisenriegler, K. Kremer and K. Binder, Adsorption of polymer chains at surfaces: scaling and Monte Carlo analyses, J. Chem. Phys., 1982, 77, 6296–6320 CrossRef.
- R. Descas, J. U. Sommer and A. Blumen, Static and dynamic properties of tethered chains at adsorbing surfaces: a Monte Carlo study, J. Chem. Phys., 2004, 120, 8831–8840 CrossRef CAS PubMed.
- K. Besteman, J. O. Lee, F. G. M. Wiertz, H. A. Heering and C. Dekker, Enzyme-coated carbon nanotubes as single-molecule biosensors, Nano Lett., 2003, 3, 727–730 CrossRef CAS.
- P. Y. Zhu, D. Q. Feng, M. Yasir, W. L. Song, M. A. Hafeez, C. Zhang and L. Liu, Enhanced antifouling capability of PDMS/Cu2O-anchored Fe-based amorphous coatings, Surf. Coat. Technol., 2023, 475, 130192 CrossRef CAS.
- Y. Ji, H. Wang, X. Li, P. Zhao, Q. Wang, R. Li and V. Vandeginste, Effect of anionic polyacrylamide polymer on frost heave mitigation and its implication for frost-susceptible soil, Polymers, 2023, 15, 2096 CrossRef CAS PubMed.
- T. Sintes, K. Sumithra and E. Straube, Adsorption of semiflexible polymers on flat, homogeneous surfaces, Macromolecules, 2001, 34, 1352–1357 CrossRef CAS.
- H. P. Hsu and K. Binder, Effect of chain stiffness on the adsorption transition of polymers, Macromolecules, 2013, 46, 2496–2515 CrossRef CAS.
- A. Milchev and K. Binder, How does stiffness of polymer chains affect their adsorption transition?, J. Chem. Phys., 2020, 152, 064901 CrossRef CAS PubMed.
- Y. G. Tao and R. Kapral, Self-propelled polymer nanomotors, ChemPhysChem, 2009, 10, 770–773 CrossRef CAS PubMed.
- R. E. Isele-Holder, J. Elgeti and G. Gompper, Self-propelled worm-like filaments: spontaneous spiral formation, structure, and dynamics, Soft Matter, 2015, 11, 7181–7190 RSC.
- V. Bianco, E. Locatelli and P. Malgaretti, Globulelike conformation and enhanced diffusion of active polymers, Phys. Rev. Lett., 2018, 121, 217802 CrossRef CAS PubMed.
- H. Löwen, Active colloidal molecules, Europhys. Lett., 2018, 121, 58001 CrossRef.
- L. Caprini, U. M. B. Marconi, A. Puglisi and A. Vulpiani, Active escape dynamics: the effect of persistence on barrier crossing, J. Chem. Phys., 2019, 150, 024902 CrossRef PubMed.
- E. Locatelli, V. Bianco and P. Malgaretti, Activity-induced collapse and arrest of active polymer rings, Phys. Rev. Lett., 2021, 126, 097801 CrossRef CAS PubMed.
- F. Burla, Y. Mulla, B. E. Vos, A. Aufderhorst-Roberts and G. H. Koenderink, From mechanical resilience to active material properties in biopolymer networks, Nat. Rev. Phys., 2019, 1, 249–263 CrossRef.
- K. Krásniewska, S. Galus and M. Gniewosz, Biopolymers-based materials containing silver nanoparticles as active packaging for food applications–A review, Int. J. Mol. Sci., 2020, 21, 698 CrossRef PubMed.
- L. Natali, L. Caprini and F. Cecconi, How a local active force modifies the structural properties of polymers, Soft Matter, 2020, 16, 2594–2604 RSC.
- D. Sarkar, S. Thakur, Y. G. Tao and R. Kapral, Ring closure dynamics for a chemically active polymer, Soft Matter, 2014, 10, 9577–9584 RSC.
- A. Ghosh and N. S. Gov, Dynamics of active semiflexible polymers, Biophys. J., 2014, 107, 1065–1073 CrossRef CAS PubMed.
- R. G. Winkler and G. Gompper, The physics of active polymers and filaments, J. Chem. Phys., 2020, 153, 040901 CrossRef CAS PubMed.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Microscopic artificial swimmers, Nature, 2005, 437, 862–865 CrossRef CAS PubMed.
- E. Zheng, M. Brandenbourger, L. Robinet, P. Schall, E. Lerner and C. Coulais, Self-oscillation and synchronization transitions in elastoactive structures, Phys. Rev. Lett., 2023, 130, 178202 CrossRef CAS PubMed.
- T. L. Xu, C. R. Qin, B. Tang, J. C. Gao, J. Zhou, K. Chen, T. H. Zhang and W. D. Tian, Constrained motion of self-propelling eccentric disks linked by a spring, J. Chem. Phys., 2024, 161, 064905 CrossRef CAS PubMed.
- J. Yan, M. Han, J. Zhang, C. Xu, E. Luijten and S. Granick, Reconfiguring active particles by electrostatic imbalance, Nat. Mater., 2016, 15, 1095–1099 CrossRef CAS PubMed.
- S. K. Anand and S. P. Singh, Conformation and dynamics of a self-avoiding active flexible polymer, Phys. Rev. E, 2020, 101, 030501(R) CrossRef PubMed.
- S. Dutta, A. Ghosh and A. J. Spakowitz, Effect of local active fluctuations on structure and dynamics of flexible biopolymers, Soft Matter, 2024, 20, 1694–1701 RSC.
- M. Das, C. F. Schmidt and M. Murrell, Introduction to active matter, Soft Matter, 2020, 16, 7185–7190 RSC.
- M. R. Shaebani, A. Wysocki, R. G. Winkler, G. Gompper and H. Rieger, Computational models for active matter, Nat. Rev. Phys., 2020, 2, 181–199 CrossRef.
- R. G. Winkler, J. Elgeti and G. Gompper, Active polymers-emergent conformational and dynamical properties: a brief review, J. Phys. Soc. Jpn., 2017, 86, 101014 CrossRef.
- S. M. Mousavi, G. Gompper and R. G. Winkler, Active Brownian ring polymers, J. Chem. Phys., 2019, 150, 064913 CrossRef PubMed.
- H. X. Hu, Y. F. Shen, C. Wang and M. B. Luo, Dynamics of a two-dimensional active polymer chain with a rotation-restricted active head, Soft Matter, 2022, 18, 8820–8829 RSC.
- J. Smrek and K. Kremer, Small activity differences drive phase separation in active-passive polymer mixtures, Phys. Rev. Lett., 2017, 118, 098002 CrossRef PubMed.
- H. Löwen, Inertial effects of self-propelled particles: from active Brownian to active Langevin motion, J. Chem. Phys., 2020, 152, 040901 CrossRef PubMed.
- L. L. Gutierrez-Martinez and M. Sandoval, Inertial effects on trapped active matter, J. Chem. Phys., 2020, 153, 044906 CrossRef CAS PubMed.
- A. R. Sprenger, L. Caprini1, H. Löwen and R. Wittmann, Dynamics of active particles with translational and rotational inertia, J. Phys.: Condens. Matter, 2023, 35, 305101 CrossRef CAS PubMed.
- H. X. Hu, Y. F. Shen and M. B. Luo, Translocation of two-dimensional active polymers through nanopores using Langevin dynamics simulations, J. Chem. Phys., 2024, 160, 184902 CrossRef CAS PubMed.
- G. Q. Feng and W. D. Tian, Desorption of a flexible polymer with activity from a homogeneous attractive surface, Macromolecules, 2023, 56, 2542–2550 CrossRef CAS.
- G. Q. Feng and W. D. Tian, Scaling behavior for the detachment of a self-propelling filament from an attractive surface, J. Chem. Phys., 2023, 158, 164901 CrossRef CAS PubMed.
- M. B. Luo and Y. F. Shen, Langevin dynamics simulations for the critical adsorption of end-grafted active polymers, Soft Matter, 2024, 20, 5113–5121 RSC.
- K. Kremer and G. S. Grest, Dynamics of entangled linear polymer melts: a molecular dynamics simulation, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- A. Chremos, E. Glynos, V. Koutsos and P. J. Camp, Adsorption and self-assembly of linear polymers on surfaces: a computer simulation study, Soft Matter, 2009, 5, 637–645 RSC.
- X. Yang, F. Wu, D. D. Hu, S. Zhang and M. B. Luo, Simulation of the critical adsorption of semi-flexible polymers, Chin. Phys. Lett., 2019, 36, 098202 CrossRef CAS.
- E. A. Lisin, O. S. Vaulina, I. I. Lisina and O. F. Petrov, Motion of a self-propelled particle with rotational inertia, Phys. Chem. Chem. Phys., 2022, 24, 14150–14158 RSC.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Active particles in complex and crowded environments, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- M. Bulacu and E. van der Giessen, Effect of bending and torsion rigidity on self-diffusion in polymer melts: a molecular-dynamics study, J. Chem. Phys., 2005, 123, 114901 CrossRef PubMed.
- L. Tubiana, G. Polles, E. Orlandini and C. Micheletti, Kymoknot: a web server and software package to identify and locate knots in trajectories of linear or circular polymers, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 72 CrossRef PubMed.
- F. Schmidt, H. Šípová-Jungová, M. Käll, A. Würger and G. Volpe, Non-equilibrium properties of an active nanoparticle in a harmonic potential, Nat. Commun., 2021, 12, 1902 CrossRef CAS PubMed.
- J. X. Li, S. Wu, L. L. Hao, Q. L. Lei and Y. Q. Ma, Activity-driven polymer knotting for macromolecular topology engineering, Sci. Adv., 2024, 10, eadr0716 CrossRef CAS PubMed.
- Y. F. Du, H. J. Jiang and Z. H. Hou, Study of active Brownian particle diffusion in polymer solutions, Soft Matter, 2019, 15, 2020–2031 RSC.
- A. R. Sprenger, S. Jahanshahi, A. V. Ivlev and H. Löwen, Time-dependent inertia of self-propelled particles: the Langevin rocket, Phys. Rev. E, 2021, 103, 042601 CrossRef CAS PubMed.
- Y. Zhang, H. Zhou and Z.-C. Ou-Yang, Stretching single-stranded DNA: interplay of electrostatic, base-pairing, and base-pair stacking interactions, Biophys. J., 2001, 81, 1133–1143 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01355g |
| This journal is © The Royal Society of Chemistry 2025 |