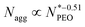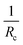Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modulating melting points in micellar cores: influence of the corona chain length on the core confinement in binary mixed block copolymer micelles†
Szymon Mikołaj
Szostak
 a,
Nico
König
a,
Lutz
Willner
a,
Nico
König
a,
Lutz
Willner
 b and
Reidar
Lund
b and
Reidar
Lund
 *a
*a
aDepartment of Chemistry, University of Oslo, NO-0315 Oslo, Norway. E-mail: reidar.lund@kjemi.uio.no
bCentre for Neutron Science (JCNS-1), Forschungszentrum Jülich GmbH, 52425 Jülich, Germany
First published on 7th February 2025
Abstract
Self-assembly of polymers with crystallizable blocks may lead to micelles with ordered, gel-like or crystalline cores. Here we investigate binary mixtures of n-alkyl-poly(ethylene oxide), Cn-PEOx (n = 28, x = 3–20 kDa) and study their self-assembly to gain insight into the effect of confinement on the core-crystallization and micellar structure. By employing identical core block length but varying corona block lengths, the size of the core can be tuned by variation of the block ratios. The micelles were characterized by small-angle X-ray scattering (SAXS) to gain insight into the overall and internal structure, including aggregation number, core size, and density distribution of the corona. SAXS curves from examined samples showed a characteristic pattern of spherical core–shell micelles but with broader corona distribution in the binary mixtures as compared to the neat samples. The structural parameters of the micelles were extracted from the SAXS data by employing a spherical core–shell model with dual density profiles in the core. We found that the aggregation number decreases as PEO length increases following a power law predicted in the literature. Furthermore, the melting point and melting enthalpy of crystalline alkyl cores were closely inspected by densitometry and differential scanning calorimetry (DSC). Correlating the core radius obtained from SAXS, we found that the melting point depression caused by the self-confinement in the micellar core can be described by the Gibbs–Thomson equation. These results show that the micellar structure and phase transition of the semicrystalline core can be easily tuned through blending diblock copolymers with different corona block lengths.
1. Introduction
The self-assembly of amphiphilic block copolymers in aqueous solution to form micellar nanoparticles has been one of the most extensively studied topics in colloidal science.1,2 A growing number of potential biomedical applications, particularly drug delivery,3–5 highlights the demand for structural information at nano resolution,6,7 which combines with the corresponding performance from biological assessments to help establish the structure–property relationships.Micelles designed for in vivo use need to be tested in a mimetic biological milieu, which generally means aqueous solutions. In this context, small-angle X-ray scattering (SAXS) is a powerful tool to determine the shape, size, size distribution, and internal structure of self-assembling systems in aqueous environments.8,9 SAXS is capable of delivering structural information of dimensions between 1 and 100 nm by quantifying electron density differences at the nanoscale. Through variation of the molecular composition, molecular weight, and solvent, the nature and strength of intermolecular forces and consequently the self-assembled structures can be varied, i.e. in a bottom-up strategy.10,11
N-Alkyl-poly(ethylene oxide) (Cn-PEO), a class of relatively simple but important amphiphilic diblock copolymers, can self-assemble into micelles of core–shell structure in water with a semicrystalline alkyl core and a hydrated PEO corona. This micellar system can be used as a model system due to its simplicity and low polydispersity. We previously found that the aggregation number increased quadratically with the alkyl block length and decreased in a power-law dependence with an exponent of −0.51 on the PEO block length for single-component Cn-PEO micelles,12 showing that the micellar structure can be tuned by varying the core and corona block lengths. Blending block copolymers of different lengths, on the other hand, represents a handy and efficient way to alter the micellar structure.13–18 Recently, we systematically investigated binary mixed micelles formed by blending Cn-PEO with various alkyl block lengths at constant PEO block length and observed that the mixed micelles exhibited structural properties that perfectly interpolate those of single-component micelles.19 However, it has not been investigated how mixed PEO block lengths will affect the structural parameters of the equilibrium micelles at a fixed alkyl block length. For commonly used hydrophobic blocks of amphiphilic diblock copolymers, e.g. polycaprolactone, poly(L-lactide), being semicrystalline, core crystallization is a well-known determinant factor to the microstructure20,21 and equilibrium exchange kinetics of the formed micelles,22,23 thereby affecting the loading capacity and stability of the micelles in drug delivery.24 For micellar systems with crystalline cores, the temperature can be used as an external stimulus to control the melting-crystallization phase transition in the core, which enables control of the drug release mode.25–27 For instance, upon heating through responsive co-loaded cargo or directly raising the temperature, crystalline cores transiting to the molten state can potentially make the loaded drug release faster.28 Our previous study on Cn-PEO micelles29 showed that the crystalline core exhibits a melting point depression that can be satisfactorily described by the Gibbs–Thomson equation. Thus this soft self-confined structure follows the same behaviour as hard confined systems such as ordinary liquids in mesoscopic pores.30 Further research showed that the mixed micelles formed by binary mixtures of Cn-PEO with various alkyl block lengths also nicely followed the Gibbs–Thomson law, similar to the single-component counterpart although the melting points are additionally affected by the mixing of components in the core.19 One intriguing approach to alter the core confinement is to utilise Cn-PEOx polymers with binary corona block length mixtures, thereby modulating the confinement and corresponding melting points.
In the present work, we address the effects of binary corona block lengths on the micellar structure and core crystallization using mixed micelles from blends of C28-PEOx polymers with different PEO lengths (MW ranging from ∼3 kDa to ∼20 kDa) at various ratios. Given that the alkyl block is monodisperse and the PEO blocks synthesized by controlled anionic polymerization also exhibit very low polydispersity (Mw/Mn ≤ 1.05), this system is well suited for assessing the effects of the corona block length. The mixed micelles were prepared via a co-solvent protocol. SAXS was employed to determine the structural parameters. Differential scanning calorimetry (DSC) and densitometry were carried out to observe the phase transition of the alkyl core influenced by the blending protocol.
2. Experimental
2.1 Polymer synthesis and characterization
Poly(ethylene oxide)-mono-n-alkyl ethers (poly(ethylene oxide)-mono-n-octacosyl ether), C28-PEOx (x = 3, 5, 10, 20 kg mol−1), were synthesized by living anionic ring-opening polymerization as reported in our previous work.12 In brief, 1-octacosanol (C28H57OH) was mixed in a ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 with its corresponding potassium-1-alkoxide (C28H57O−K+) functioning as the initiator. The polymerizations were carried out in toluene at 95 °C under high vacuum. The molecular weight and polydispersity of the resulting polymers were determined by size exclusion chromatography (SEC) and the results are shown in Table 1.
20 with its corresponding potassium-1-alkoxide (C28H57O−K+) functioning as the initiator. The polymerizations were carried out in toluene at 95 °C under high vacuum. The molecular weight and polydispersity of the resulting polymers were determined by size exclusion chromatography (SEC) and the results are shown in Table 1.
 of C28-PEOx polymers
of C28-PEOx polymers
2.2 Sample preparation
Single-component micelles as reference were prepared by dissolving dry C28-PEOx copolymer powder in degassed Millipore Type I water to make a 5 mg mL−1 solution. The solutions were heated and shaken at 60 °C for 4 hours to ensure equilibrium. Then the solutions were cooled down to room temperature overnight while being continually shaken. For binary mixed micelles, mixtures of C28-PEOx with two different PEO lengths in desired ratios were first dissolved in chloroform (a good solvent for both blocks) to achieve homogeneous mixing. The solvent was then removed under nitrogen flow and a series of dry homogeneous polymer blends was obtained. These blends were then dissolved in water and processed as in the abovementioned procedures for the pure micelles.There are seven mixed samples named with the following nomenclature: C28-PEO3/5 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 denotes a mixture of C28-PEO3 and C28-PEO5 in a mass ratio of 1
1 denotes a mixture of C28-PEO3 and C28-PEO5 in a mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, C28-PEO5/20 1
1, C28-PEO5/20 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 denotes a mixture of C28-PEO5 and C28-PEO20 in a mass ratio of 1
4 denotes a mixture of C28-PEO5 and C28-PEO20 in a mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, etc. For SAXS measurements at BM29 samples were diluted to concentration 2.5 mg mL−1 or 1.25 mg mL−1 to prevent radiation damage.
4, etc. For SAXS measurements at BM29 samples were diluted to concentration 2.5 mg mL−1 or 1.25 mg mL−1 to prevent radiation damage.
2.3 Density measurements
Polymer density in solution was measured with an Anton Paar DMA 5001 density meter. The densities of water, PEO, and micelle solutions were measured in a temperature range from 15 to 65 °C at a heating rate of 0.25 °C min−1. The average density of the copolymer ρpol in aqueous solution was calculated based on the water density ρH2O, the solution density ρpol, the mass of the polymer mpol, the mass of water mH2O, polymer mass fraction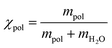 using the following equation:
using the following equation: | (1) |
2.4 Differential scanning calorimetry (DSC)
The melting/freezing point Tm/Tf and the melting/freezing enthalpy ΔHm/ΔHf were determined by DSC. In detail, the heat capacity during heating or cooling runs was measured with a Nano DSC device (TA Instruments) at a polymer concentration of ∼5 mg mL−1 and a scan rate of 2 °C min−1 from 15 °C to 75 °C and 75 °C to 15 °C. Samples were measured in heat-cool–heat-cool mode, the data were baseline-corrected by subtracting the contribution of solvent (water) using the NanoAnalyze Software (TA Instrument). Tm/Tf was determined from the maximum peak temperature and ΔHm/ΔHf was determined from the integral area of the transition peak in the heat capacity curves from the second heat-cool run.2.5 Small angle X-ray scattering (SAXS) experiments
SAXS measurements were conducted at beamline BM29 at the European Synchrotron Radiation Facility in Grenoble, France31 and on a Bruker NanoStar instrument (RECX, University of Oslo, Norway). A photon wavelength of λ = 1 Å (BM29) and λ = 1.54 Å (NanoStar) was used. The scattering intensity was recorded as a function of the wave vector defined as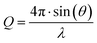 with the scattering angle 2θ, at the polymer concentration of ∼5 mg mL−1. The available Q vector range varies from 0.006–0.5 Å−1 (BM29) to 0.01–0.3 Å−1 (NanoStar). The scattering intensity was corrected by subtracting the scattering contributions from the water and the empty cell and normalized to the absolute intensity with water. Measurements at BM29 were performed using an autosampler at 20 °C, the exposure was split into 10 frames lasting 1 s to avoid radiation damage and averaged if no systematic deviation was detected. Water was measured before and after the sample and averaged. Temperature SAXS measurements were performed at NanoStar, with measurement time 3600 s, heating rate between measurements 5 °C min−1 + 1800 s equilibration time, temperatures T ∈ {20; 30; 40; 45; 50; 55; 60}
with the scattering angle 2θ, at the polymer concentration of ∼5 mg mL−1. The available Q vector range varies from 0.006–0.5 Å−1 (BM29) to 0.01–0.3 Å−1 (NanoStar). The scattering intensity was corrected by subtracting the scattering contributions from the water and the empty cell and normalized to the absolute intensity with water. Measurements at BM29 were performed using an autosampler at 20 °C, the exposure was split into 10 frames lasting 1 s to avoid radiation damage and averaged if no systematic deviation was detected. Water was measured before and after the sample and averaged. Temperature SAXS measurements were performed at NanoStar, with measurement time 3600 s, heating rate between measurements 5 °C min−1 + 1800 s equilibration time, temperatures T ∈ {20; 30; 40; 45; 50; 55; 60}
2.6 Scattering model
The data were analyzed by fitting model for core–shell micelles.12,19 In a preceding publication on Cn-PEO micelles,32 it was established that the micellar core assumes a prolate ellipsoid configuration with an axial ratio of below the melting temperature, subsequently converting into a more spherical conformation with an axial ratio of
below the melting temperature, subsequently converting into a more spherical conformation with an axial ratio of  above the melting point. Additionally, the core is surrounded by a thin layer of dehydrated PEO. The study implemented small angle neutron scattering (SANS) with contrast matching of the PEO chains to isolate the signal from the micellar core. In the present case, where SAXS is the sole method of analysis, determination of the core shape is precluded by the overlap of the signal at large Q with other scattering contributions from the shell. In order to circumvent overparameterization, we have assumed monodispersity of the micelles, spherical alkyl core shape and uniform hydration of PEO chain. Consequently, the core radius is to be regarded as an average radius.
above the melting point. Additionally, the core is surrounded by a thin layer of dehydrated PEO. The study implemented small angle neutron scattering (SANS) with contrast matching of the PEO chains to isolate the signal from the micellar core. In the present case, where SAXS is the sole method of analysis, determination of the core shape is precluded by the overlap of the signal at large Q with other scattering contributions from the shell. In order to circumvent overparameterization, we have assumed monodispersity of the micelles, spherical alkyl core shape and uniform hydration of PEO chain. Consequently, the core radius is to be regarded as an average radius.
In the scattering model the core consisting of alkyl chains is considered to be homogenous, solvent-free sphere of a radius Rc with scattering amplitude
 | (2) |
 | (3) |
 | (4) |
| Vs = Vs1·fshort + Vs2·(1 − fshort) | (5) |
The radial density distribution function for the corona was chosen to have the following form:
 | (6) |
In addition, the blob scattering, originating from the corona chain scattering was calculated using33,34
 | (7) |
| Ic(Q) = (ρc − ρ0)2Nagg2Vc2Ac(Q)2 | (8) |
 | (9) |
| Icross(Q) = 2(ρs − ρ0)(ρc − ρ0)Nagg2VsVcAs(Q)Ac(Q) | (10) |
| Iblob(Q) = (ρs − ρ0)2NaggVs2B(Q) | (11) |
 | (12) |
 | (13) |
3. Results and discussion
3.1 Confirming the formation of binary mixed micelles
First, we hypothesize the formation of mixed micelles instead of a simple mixture of two single-component micelle populations. To assess this, we compare the SAXS curves obtained from mixtures with the fractional mass-weighted linear combinations of measured scattering data of the individual components at 20 °C. If they coincide, there is no intermixing between the two components. Instead, two populations of single-component micelles form independently. In contrast, a deviation between the two curves indicates that mixed micelles containing both component copolymers are formed. The SAXS profile of C28-PEO3/20 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 was selected as a representative example, where the difference in PEO block lengths is the largest between all samples. As shown in Fig. 1a, the experimental data of C28-PEO3/20 1
7 was selected as a representative example, where the difference in PEO block lengths is the largest between all samples. As shown in Fig. 1a, the experimental data of C28-PEO3/20 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 and the linear combination of scattering intensities from C28-PEO3 and C28-PEO20 do not superpose, which confirms our hypothesis.
7 and the linear combination of scattering intensities from C28-PEO3 and C28-PEO20 do not superpose, which confirms our hypothesis.
However, an analogous system of mixed C18-PEOx micelles was reported to segregate into single-component micelles at a low temperature, i.e., below the freezing point of the C18 chains. The was interpreted as the discrepancy in freezing temperatures of the C18 core blocks of the two copolymers.36 Yet, Vuorte et al. could not reproduce the effect in coarse-grained molecular simulations. They observed a tendency for an uneven distribution of the two copolymers in the micelles, but no clearly distinct populations. It has to be noted, though, that the phase transition of the alkyl chains – which Plazzotta et al. cite as the cause of the segregation – cannot be emulated in their computational model.37 In contrast, our present study focuses on a longer C28 alkyl chain which showed a different behavior at 20 °C, well below the melting point (will be shown in the following). At this temperature, C28 blocks are semi-crystalline, yet we still observed mixed micelles. This might be due to the use of longer alkyl chain as well as the entropic gain arising from mixing PEO corona blocks in terms of thermodynamics.
3.2 Extracting the micellar density profile and corona conformation
Fig. 1 shows the SAXS profiles of binary mixed micelles and single-component micelles in water (polymer volume fraction 0.25 vol%) measured at 20 °C. SAXS curves of all samples have characteristic features of spherical micelles: a high intensity at low Q, a steep intensity decay at intermediate Q, and a slowly decaying weak intensity at high Q. Detailed structural parameters were obtained by fitting the data using the spherical core-dual shell model presented in Section 2.6. The best fits are depicted with solid lines in Fig. 1, and the key structural parameters are summarized in Table 2. Effects of the mean number of ethylene oxide repeat units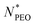 on structural properties will be discussed later. A list of all structural parameters determined for all the samples is presented in Table S1 (ESI†) (BM29 data) and Table S2 (ESI†) (NanoStar data) in ESI.† Additionally, after the determination of structural parameters, we calculated the density profiles for all micelles, showing the changes in the convoluted density of the core and shell depending on the distance from the center of the micelle. We could observe the general trend of the decrease in core diameter as the PEO chain length increased. If we compare the same polymer C28-PEO5 in different mixed micelles (Fig. 2) we observe the decrease in the density of the micellar shell at the border between core and shell when
on structural properties will be discussed later. A list of all structural parameters determined for all the samples is presented in Table S1 (ESI†) (BM29 data) and Table S2 (ESI†) (NanoStar data) in ESI.† Additionally, after the determination of structural parameters, we calculated the density profiles for all micelles, showing the changes in the convoluted density of the core and shell depending on the distance from the center of the micelle. We could observe the general trend of the decrease in core diameter as the PEO chain length increased. If we compare the same polymer C28-PEO5 in different mixed micelles (Fig. 2) we observe the decrease in the density of the micellar shell at the border between core and shell when  increases. When we look closely at the micelles C28-PEO5 and C28-PEO 3/5 1
increases. When we look closely at the micelles C28-PEO5 and C28-PEO 3/5 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 that exhibit the same outer radius, we observe that mixed micelles are more compressed close to the micellar core, whereas PEO chains in pure micelles are more stretched and have a higher density close to the micellar surface. The density profiles for samples C28-PEO5, C28-PEO 3/5 1
1 that exhibit the same outer radius, we observe that mixed micelles are more compressed close to the micellar core, whereas PEO chains in pure micelles are more stretched and have a higher density close to the micellar surface. The density profiles for samples C28-PEO5, C28-PEO 3/5 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, C28-PEO 5/10 1
1, C28-PEO 5/10 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and C28-PEO 5/20 1
1 and C28-PEO 5/20 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are presented in Fig. 2, density profiles for sample C28-PEO 3/10 1
1 are presented in Fig. 2, density profiles for sample C28-PEO 3/10 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at different temperatures are presented in Fig. 3b, whereas other density profiles are presented in Fig. S1 (ESI†).
1 at different temperatures are presented in Fig. 3b, whereas other density profiles are presented in Fig. S1 (ESI†).
 of each sample and the most important structure parameters extracted from SAXS spectra using model fit analysis
of each sample and the most important structure parameters extracted from SAXS spectra using model fit analysis
| Sample | N agg | R m,1 [Å] | R m,2 [Å] | R c [Å] | D 1 [Å] | D 2 [Å] | D [Å] | |
|---|---|---|---|---|---|---|---|---|
| Note: Rm,1 – inner micelle radius, Rm,2 – outer micelle radius, Rc – C28 core radius, D1 – thickness of inner PEO shell, D1 = Rm,1 − Rc, D2 – thickness of outer PEO shell, D2 = Rm,2 − Rm,1, D – thickness of PEO shell, D = Rm,2 − Rc. | ||||||||
| C28-PEO3 | 53 | 150 | 88 | 29 | 59 | |||
C28-PEO3/5 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
72 | 147 | 84 | 115 | 29 | 55 | 31 | 86 |
C28-PEO3/10 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
89 | 129 | 82 | 142 | 28 | 54 | 60 | 114 |
| C28-PEO5 | 105 | 111 | 115 | 27 | 88 | |||
C28-PEO5/10 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
143 | 111 | 132 | 151 | 26 | 106 | 19 | 125 |
C28-PEO5/10 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
162 | 116 | 140 | 162 | 27 | 113 | 22 | 135 |
C28-PEO5/20 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
177 | 88 | 108 | 185 | 24 | 84 | 77 | 161 |
| C28-PEO10 | 218 | 73 | 164 | 23 | 141 | |||
C28-PEO3/20 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 7 |
256 | 69 | 119 | 220 | 22 | 97 | 101 | 198 |
C28-PEO5/20 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
288 | 77 | 100 | 195 | 23 | 77 | 95 | 172 |
| C28-PEO20 | 485 | 42 | 229 | 19 | 210 | |||
 | ||
| Fig. 2 Density profiles of the micelles of C28-PEO5 in one-component and mixed micelles, red line denotes core density, blue line denotes shell density. | ||
 | ||
Fig. 3 (a) SAXS curves of C28-PEO3/10 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as a function of temperature ranging from 20 °C to 60 °C at 0.5 vol% polymer concentration. Solid lines represent the model fits. Temperature scans of other samples can be found in Fig. S2 and S3 in the ESI.† (b) The density profile of core (red) and shell (blue) as a function of micelle radius of C28-PEO3/10 1 1 as a function of temperature ranging from 20 °C to 60 °C at 0.5 vol% polymer concentration. Solid lines represent the model fits. Temperature scans of other samples can be found in Fig. S2 and S3 in the ESI.† (b) The density profile of core (red) and shell (blue) as a function of micelle radius of C28-PEO3/10 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 micelles at 20 °C (solid line) and 60 °C (dotted line). 1 micelles at 20 °C (solid line) and 60 °C (dotted line). | ||
We also investigated the structure at various temperatures in the range of 20–60 °C. Representative scattering profiles of the C28-PEO3/10 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sample are displayed in Fig. 3a with corresponding density profiles presented in Fig. 3b. The scattering intensity at low Q slightly decreased with increasing temperature, which can be attributed to the change of density of the PEO blocks and water and thereby loss in contrast. The micelles maintained a spherical shape reflected in the features of SAXS curves over the tested temperatures. We also observed an abrupt increase in intensity at intermediate Q between 50 and 55 °C, indicating a significant decrease in core electron density. This phenomenon was also found in our previous works on the Cn-PEO micelle system.19,29 Note that a sudden change in density is an implication of a first-order phase transition. Scattering curves of all other samples presented in Fig. S2 and S3 (ESI†) show a similar intensity dependence on temperature. The behavior of phase transition will be further elucidated later in the manuscript.
1 sample are displayed in Fig. 3a with corresponding density profiles presented in Fig. 3b. The scattering intensity at low Q slightly decreased with increasing temperature, which can be attributed to the change of density of the PEO blocks and water and thereby loss in contrast. The micelles maintained a spherical shape reflected in the features of SAXS curves over the tested temperatures. We also observed an abrupt increase in intensity at intermediate Q between 50 and 55 °C, indicating a significant decrease in core electron density. This phenomenon was also found in our previous works on the Cn-PEO micelle system.19,29 Note that a sudden change in density is an implication of a first-order phase transition. Scattering curves of all other samples presented in Fig. S2 and S3 (ESI†) show a similar intensity dependence on temperature. The behavior of phase transition will be further elucidated later in the manuscript.
3.3 Effects of mixed PEO block length on micellar structure
The self-assembly of block copolymers and other macromolecules in solution is regulated both by thermodynamic and kinetic factors. When molecular exchange between micelles is rapid (faster than the experimental time scale), thermodynamic control dominates, and the system obtains the energetically most favorable equilibrium structure. Otherwise, so-called kinetically trapped states may occur. Based on our previous kinetic study on Cn-PEO systems,23 the structure of C28-PEO micelles prepared under the conditions in this work is under thermodynamic control and thus in equilibrium.As shown in Fig. 4a, the Nagg shows a strong dependence on  and decreases with increasing
and decreases with increasing  . Overall, the observed decrease of Nagg can be qualitatively rationalized by a shift of the balance between enthalpic and entropic contributions with the growing corona block. To be specific, the self-assembled micellar structure highly depends on the balance of enthalpic gain of minimizing the area of interfacial contact between the hydrophobic core block and the corona/solvent environment as well as the conformational entropic loss arising from the stretching of the polymer chains when confined into micelles. In other words, the enthalpic gain favors the micellization while the entropic loss counterbalances it. In this case, as PEO length increases, stretching of PEO blocks to a greater extent in the coronal domain impedes the aggregation of the alkyl chains and therefore leads to a smaller aggregation number.
. Overall, the observed decrease of Nagg can be qualitatively rationalized by a shift of the balance between enthalpic and entropic contributions with the growing corona block. To be specific, the self-assembled micellar structure highly depends on the balance of enthalpic gain of minimizing the area of interfacial contact between the hydrophobic core block and the corona/solvent environment as well as the conformational entropic loss arising from the stretching of the polymer chains when confined into micelles. In other words, the enthalpic gain favors the micellization while the entropic loss counterbalances it. In this case, as PEO length increases, stretching of PEO blocks to a greater extent in the coronal domain impedes the aggregation of the alkyl chains and therefore leads to a smaller aggregation number.
The scaling laws for starlike micelles proposed by Halperin38 predict that the aggregation behavior should be close to independent of the corona chain length. Apart from a weak logarithmic dependence on the corona-forming chain, the aggregation number solely depends on the core block. The scaling laws, however, assume the limit Ncorona ≫ Ncore, which is not true in our case. Another scaling law and the model taking into account both soluble and insoluble blocks was suggested by Zhulina et al.39 They introduced a weak logarithmic dependence Nagg ∝ (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N)−6/5 in the limit of long corona chains. In the literature, it was found that the logarithmic scaling describes well the behavior of micelles with high
N)−6/5 in the limit of long corona chains. In the literature, it was found that the logarithmic scaling describes well the behavior of micelles with high 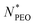 values,12 but in our experiment, we observed high deviation for micelles with shorter PEO chains. The prediction is presented in Fig. 4a as a red line. The dependence between Nagg and
values,12 but in our experiment, we observed high deviation for micelles with shorter PEO chains. The prediction is presented in Fig. 4a as a red line. The dependence between Nagg and  for short PEO chains can be also described with a pseudo mean-field phase approximation proposed by Nagarajan and Ganesh.40 Our results are in agreement with these theoretical predictions, we observed the scaling of
for short PEO chains can be also described with a pseudo mean-field phase approximation proposed by Nagarajan and Ganesh.40 Our results are in agreement with these theoretical predictions, we observed the scaling of  . The previous work from Willner et al.41 on a poly(ethylene-propylene)-block-poly(ethylene oxide) (PEP-b-PEO) micelle system with a fixed PEP core block length showed Nagg in the region of
. The previous work from Willner et al.41 on a poly(ethylene-propylene)-block-poly(ethylene oxide) (PEP-b-PEO) micelle system with a fixed PEP core block length showed Nagg in the region of  larger than 1000 did remain constant as predicted by Halperin. But in the region of
larger than 1000 did remain constant as predicted by Halperin. But in the region of  ranging from 150 to 750, Nagg showed a perfect agreement with the Nagarajan and Ganesh empirical scaling law
ranging from 150 to 750, Nagg showed a perfect agreement with the Nagarajan and Ganesh empirical scaling law 
The core radius Rc as a function of  is depicted in Fig. 4b. We can see that Rc decreases with increasing
is depicted in Fig. 4b. We can see that Rc decreases with increasing 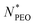 , we observed scaling
, we observed scaling  that is in agreement with
that is in agreement with  predicted by Nagarajan and Ganesh. Note that as the alkyl block is highly hydrophobic, the alkyl core is assumed to be devoid of solvent. According to the theory developed by Tanford,42 the value of Rc relates to the chain configuration in the core domain. Assuming n-alkanes with a fully extended all-trans conformation, the maximal possible length can be calculated as
predicted by Nagarajan and Ganesh. Note that as the alkyl block is highly hydrophobic, the alkyl core is assumed to be devoid of solvent. According to the theory developed by Tanford,42 the value of Rc relates to the chain configuration in the core domain. Assuming n-alkanes with a fully extended all-trans conformation, the maximal possible length can be calculated as
| lCn,max = 1.53 + 1.265(n − 1) [Å] | (14) |
| lCn,flex = 1.53 + 0.925(n − 1) [Å] | (15) |
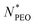 range unravels that the alkyl blocks adopt a rather flexible conformation when
range unravels that the alkyl blocks adopt a rather flexible conformation when 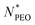 is smaller than 160, while at a larger
is smaller than 160, while at a larger  , a collapsed conformation can be speculated for alkyl blocks. This is in line with the finding that the core-related enthalpic contribution to the micellar free energy is less significant for large
, a collapsed conformation can be speculated for alkyl blocks. This is in line with the finding that the core-related enthalpic contribution to the micellar free energy is less significant for large  .
.
Fig. 4c displays the corona thickness D extracted from SAXS plotted as a function of  . Corona thickness shows a power-law dependence on
. Corona thickness shows a power-law dependence on  with an exponent of 0.58 ± 0.02 in single-component micelles, which matches the theoretical prediction D ∝ N3/5 from the scaling theory for the starlike micelle.38D values of binary mixed micelles also follow a very similar power law with the exponent 0.53 ± 0.08, but the corona is thicker in comparison to single-component micelles (for the same
with an exponent of 0.58 ± 0.02 in single-component micelles, which matches the theoretical prediction D ∝ N3/5 from the scaling theory for the starlike micelle.38D values of binary mixed micelles also follow a very similar power law with the exponent 0.53 ± 0.08, but the corona is thicker in comparison to single-component micelles (for the same  ). That may be explained by the specific structure of mixed micelles where the diameter of the entire micelle depends on the length of the longest PEO chains that are pointing out of the micelle above the shorter ones. Addition of shorter PEO decreases
). That may be explained by the specific structure of mixed micelles where the diameter of the entire micelle depends on the length of the longest PEO chains that are pointing out of the micelle above the shorter ones. Addition of shorter PEO decreases  but doesn’t change significantly outer radius of micelle. Corona thickness as a function of longer component of the micelles is presented in Fig. 4d. As a result, outer shell has lower PEO fration than single component micelles. We could observe the phenomenon in our system, samples C28-PEO3/5 1
but doesn’t change significantly outer radius of micelle. Corona thickness as a function of longer component of the micelles is presented in Fig. 4d. As a result, outer shell has lower PEO fration than single component micelles. We could observe the phenomenon in our system, samples C28-PEO3/5 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and C28-PEO5 have the same outer radius, whereas pairs of C28-PEO5/10 1
1 and C28-PEO5 have the same outer radius, whereas pairs of C28-PEO5/10 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 & C28-PEO10 and C28-PEO3/20 1
1 & C28-PEO10 and C28-PEO3/20 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 & C28-PEO20 have very similar outer radii.
7 & C28-PEO20 have very similar outer radii.
3.4 Melting-freezing transition in the alkyl core
Density as a function of the temperature of C28-PEOx mixed or pure micelles is shown in Fig. 5a. The curves are arranged in the graph in order of the decreasing mean length of the PEO block from top to bottom. It should be pointed out that the density transition is becoming progressively weaker at larger is due to a lower mass fraction of the alkyl block in the whole copolymer at a fixed polymer concentration. There is a clear hint of discontinuity in polymer density upon heating, which indicates an abrupt decrease in the density of alkyl blocks since PEO homopolymer does not exhibit any discontinuity (Fig. S4, ESI†). This discontinuity confirms again the first-order phase transition of the alkyl blocks. As shown in Fig. 5a, the transition temperature slowly shifts towards a lower value with increasing
is due to a lower mass fraction of the alkyl block in the whole copolymer at a fixed polymer concentration. There is a clear hint of discontinuity in polymer density upon heating, which indicates an abrupt decrease in the density of alkyl blocks since PEO homopolymer does not exhibit any discontinuity (Fig. S4, ESI†). This discontinuity confirms again the first-order phase transition of the alkyl blocks. As shown in Fig. 5a, the transition temperature slowly shifts towards a lower value with increasing  . The results of molar heat capacity Cp from DSC endothermic measurements are shown in Fig. 5b (heating) and Fig. S5 (ESI†) (cooling). The melting point Tm of the alkyl blocks determined through the peak of the derivative of the density and melting/freezing point Tm/Tf determined from the DSC peak temperature are plotted in Fig. 6a, whereas the values of corresponding enthalpies ΔHm/ΔHf are plotted in Fig. 6b. It is worth noting that the micelle samples from polymer mixtures only exhibit a single melting transition upon heating in both density and DSC measurements, strengthening the hypothesis of the formation of mixed micelles rather than two separate populations of single-component micelles. The DSC curve of C28-PEO3/20 1
. The results of molar heat capacity Cp from DSC endothermic measurements are shown in Fig. 5b (heating) and Fig. S5 (ESI†) (cooling). The melting point Tm of the alkyl blocks determined through the peak of the derivative of the density and melting/freezing point Tm/Tf determined from the DSC peak temperature are plotted in Fig. 6a, whereas the values of corresponding enthalpies ΔHm/ΔHf are plotted in Fig. 6b. It is worth noting that the micelle samples from polymer mixtures only exhibit a single melting transition upon heating in both density and DSC measurements, strengthening the hypothesis of the formation of mixed micelles rather than two separate populations of single-component micelles. The DSC curve of C28-PEO3/20 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, which displays well-separated peaks for the pure micelles of each component (centered at 57 °C and 45 °C, respectively), exhibits a single peak at 49 °C. This finding provides compelling evidence in support of the formation of mixed micelles. We observed a broadening of the peak of C28-PEO20 in both the heating and cooling runs. This effect is indicative of a decrease in the domain size and a larger surface-to-volume ratio, which result in a smaller degree of cooperativity of the liquid. A similar effect has been previously observed for water,43 alkanes,44 and in our earlier publication.29 As evidenced by extant literature, tightly packed PEO chains have the potential to crystallize even when dissolved in a solvent. In a previous experiment, analyzing the structure of C28-PEO micelles,32 the presence of a very thin (less than 1 nm) dry layer of PEO coating the hydrophobic C28 micellar core was proved using a combination of NMR, SAXS and SANS. The effect is only discernible by employing contrast variation SANS to isolate the core scattering. However, no heat flow consistent with ordered PEO was identified by DSC. This may indicate that either the layer is amorphous or the contribution to the measured signal is simply too small.
7, which displays well-separated peaks for the pure micelles of each component (centered at 57 °C and 45 °C, respectively), exhibits a single peak at 49 °C. This finding provides compelling evidence in support of the formation of mixed micelles. We observed a broadening of the peak of C28-PEO20 in both the heating and cooling runs. This effect is indicative of a decrease in the domain size and a larger surface-to-volume ratio, which result in a smaller degree of cooperativity of the liquid. A similar effect has been previously observed for water,43 alkanes,44 and in our earlier publication.29 As evidenced by extant literature, tightly packed PEO chains have the potential to crystallize even when dissolved in a solvent. In a previous experiment, analyzing the structure of C28-PEO micelles,32 the presence of a very thin (less than 1 nm) dry layer of PEO coating the hydrophobic C28 micellar core was proved using a combination of NMR, SAXS and SANS. The effect is only discernible by employing contrast variation SANS to isolate the core scattering. However, no heat flow consistent with ordered PEO was identified by DSC. This may indicate that either the layer is amorphous or the contribution to the measured signal is simply too small.
In our system, the melting and freezing enthalpies decrease with increasing  (Fig. 6b). The decrease in enthalpy reflects a decreasing packing order or crystallinity χc. In general, the crystallinity can be estimated on the basis that the melting enthalpy is proportional to crystallinity.45 Therefore, we can qualitatively know that χc of C28 blocks in C28-PEOx micelles decreases as
(Fig. 6b). The decrease in enthalpy reflects a decreasing packing order or crystallinity χc. In general, the crystallinity can be estimated on the basis that the melting enthalpy is proportional to crystallinity.45 Therefore, we can qualitatively know that χc of C28 blocks in C28-PEOx micelles decreases as  increases from the monotonous decrease trend of the ΔHmvs.
increases from the monotonous decrease trend of the ΔHmvs. curve in Fig. 6b. The crystallinity χc is calculated by dividing the melting enthalpy of the alkyl core by that of the fully crystallized bulk C28 alkane/octacosane (100.0 kJ mol−1),46 yielding χc between 36% and 31%.
curve in Fig. 6b. The crystallinity χc is calculated by dividing the melting enthalpy of the alkyl core by that of the fully crystallized bulk C28 alkane/octacosane (100.0 kJ mol−1),46 yielding χc between 36% and 31%.
The relatively low χc compared to the bulk alkane undoubtedly correlates with the confinement of alkyl blocks in the micellar core of merely a few nanometers in radius. Given that Rc is inversely proportional to  as demonstrated above, we know that χc is proportional to Rc. It can be intuitively understood by imagining the difficulty of molecular chain packing within a curved nanodomain. The smaller the Rc, the higher the curvature, and consequently the greater the difficulty to pack in a crystalline state. Additionally, in this self-confined micellar system, one chain-end of the alkyl block is tethered to the core–corona interface as a result of the covalent binding with the PEO corona block, which gives rise to the moderate restriction on chain mobility and consequently a reduction in the χc.47,48 In a previous study,32 which involved extended nuclear magnetic resonance (NMR) analysis, it was found that above the melting transition, the core blocks of the Cn-PEO micellar system were liquid-like, with low but finite orientational order, in agreement with the persistent asphericity of the core. However, in the region below the melting transition, the system displayed remarkably elevated relaxation rates, suggesting the presence of a rotator-like phase characterized by predominantly all-trans chain conformation and reorientations occurring within the range of milliseconds to microseconds. Studies on micellar systems from other diblock copolymers like poly(ε-caprolactone)-b-poly(ethylene oxide),49 polymethylene-b-poly(acrylic acid)50 and polystyrene-b-poly(4-vinylpyridine)51 have provided more examples on confinement effects.
as demonstrated above, we know that χc is proportional to Rc. It can be intuitively understood by imagining the difficulty of molecular chain packing within a curved nanodomain. The smaller the Rc, the higher the curvature, and consequently the greater the difficulty to pack in a crystalline state. Additionally, in this self-confined micellar system, one chain-end of the alkyl block is tethered to the core–corona interface as a result of the covalent binding with the PEO corona block, which gives rise to the moderate restriction on chain mobility and consequently a reduction in the χc.47,48 In a previous study,32 which involved extended nuclear magnetic resonance (NMR) analysis, it was found that above the melting transition, the core blocks of the Cn-PEO micellar system were liquid-like, with low but finite orientational order, in agreement with the persistent asphericity of the core. However, in the region below the melting transition, the system displayed remarkably elevated relaxation rates, suggesting the presence of a rotator-like phase characterized by predominantly all-trans chain conformation and reorientations occurring within the range of milliseconds to microseconds. Studies on micellar systems from other diblock copolymers like poly(ε-caprolactone)-b-poly(ethylene oxide),49 polymethylene-b-poly(acrylic acid)50 and polystyrene-b-poly(4-vinylpyridine)51 have provided more examples on confinement effects.
T
m shifts 12 °C towards a lower temperature with an increase in  (Fig. 6a). It has been fairly well documented that the Tm depression in the confined domain is associated with the finite size effect, termed as the Gibbs–Thomson effect.52,53 We know that the surface-to-volume ratio of the material is greatly enhanced upon nanoconfinement. The effect stems from the excess energy of the formation of the surface. Our previous studies23,29 on other Cn-PEO micellar systems have revealed a melting point depression ΔTm proportional to the inverse of Rc, which could be described by the generalized Gibbs–Thomson equation
(Fig. 6a). It has been fairly well documented that the Tm depression in the confined domain is associated with the finite size effect, termed as the Gibbs–Thomson effect.52,53 We know that the surface-to-volume ratio of the material is greatly enhanced upon nanoconfinement. The effect stems from the excess energy of the formation of the surface. Our previous studies23,29 on other Cn-PEO micellar systems have revealed a melting point depression ΔTm proportional to the inverse of Rc, which could be described by the generalized Gibbs–Thomson equation
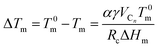 | (16) |
 as shown in Fig. 6c. It should be mentioned that the apparent degree of crystallinity is rather low suggesting partially crystalline core chains and that the core radius is not necessarily the right measure of the domains. However, an apparent low value of χc from DSC, which is essentially a measure of mobility might be affected by other effects. First, our earlier combined NMR and SANS investigations have indicated that the core is in an ordered “rotator phase” rather than a monoclinic phase.32 This would imply that the reference enthalpy of fusion is not that of the fully crystalline bulk phase. Secondly, the self-assembly and connectivity to the PEO might increase mobility such that the measured enthalpy of fusion is lowered. Thus, it is likely that the core radius represents the domain size. We can see that data set from both the pure micelles and the mixed micelle nicely follow the trend expected from the Gibbs–Thomson equation. Extrapolation of the graph to
as shown in Fig. 6c. It should be mentioned that the apparent degree of crystallinity is rather low suggesting partially crystalline core chains and that the core radius is not necessarily the right measure of the domains. However, an apparent low value of χc from DSC, which is essentially a measure of mobility might be affected by other effects. First, our earlier combined NMR and SANS investigations have indicated that the core is in an ordered “rotator phase” rather than a monoclinic phase.32 This would imply that the reference enthalpy of fusion is not that of the fully crystalline bulk phase. Secondly, the self-assembly and connectivity to the PEO might increase mobility such that the measured enthalpy of fusion is lowered. Thus, it is likely that the core radius represents the domain size. We can see that data set from both the pure micelles and the mixed micelle nicely follow the trend expected from the Gibbs–Thomson equation. Extrapolation of the graph to  corresponds to the infinite Rc and T0m of the bulk material. We find the value of T0m = 79 °C that is close to melting temperature of 1-octacosanol (Tm = 83 °C),54 which is the precursor polymerized to yield C28PEO. In a published work reporting on fully crystallized polymer samples, extrapolation of the melting line to the infinitely large domain (bulk, where Rc−1 = 0) do indeed yield the expected T0m as expected from the Gibbs–Thomson equation.55,56
corresponds to the infinite Rc and T0m of the bulk material. We find the value of T0m = 79 °C that is close to melting temperature of 1-octacosanol (Tm = 83 °C),54 which is the precursor polymerized to yield C28PEO. In a published work reporting on fully crystallized polymer samples, extrapolation of the melting line to the infinitely large domain (bulk, where Rc−1 = 0) do indeed yield the expected T0m as expected from the Gibbs–Thomson equation.55,56
The freezing points determined by the molar heat capacity-temperature curves from the DSC cooling run (Fig. S5, ESI†) show a small shift to a lower temperature from 48 to 44.5 °C upon increasing  (Fig. 6a). Tf is always lower than Tm as shown in Fig. 6a, termed as undercooling, which is in line with a well-known fact that freezing typically takes place at a lower temperature than melting as a result of the kinetic barrier associated with the formation of nuclei for crystallization.57 Additionally, in this scenario, nanodomains are spatially too small to place any macroscopic impurities to act as nuclei. Thus, the nucleation mechanism undoubtedly switches from heterogeneous nucleation (usually for the bulk macromolecules) to surface or homogeneous nucleation.58 For instance, a dramatic decrease in Tf of the poly(ε-caprolactone) (PCL) core blocks from 28 °C to −17 °C has been documented for micelles self-assembled from PCL-b-PEO copolymers compared with the bulk PCL, while the Tm of PCL cores was ca. 54 °C, which the authors considered as surface nucleation.49 In another study, where homogenous nucleation of n-alkanes was investigated, the difference between Tm and Tf of pure n-C28H58 was equal 14 °C.59 Considering the relatively small differences between Tm and Tf of the alkyl core observed in this work, i.e., low undercooling effect, surface nucleation mechanism is the more likely mechanism.58 It should be pointed out that the core radii in the current system are one order of magnitude smaller than those in the publication of Mai et al.49 Interestingly, the gap between Tm and Tf is narrowing with
(Fig. 6a). Tf is always lower than Tm as shown in Fig. 6a, termed as undercooling, which is in line with a well-known fact that freezing typically takes place at a lower temperature than melting as a result of the kinetic barrier associated with the formation of nuclei for crystallization.57 Additionally, in this scenario, nanodomains are spatially too small to place any macroscopic impurities to act as nuclei. Thus, the nucleation mechanism undoubtedly switches from heterogeneous nucleation (usually for the bulk macromolecules) to surface or homogeneous nucleation.58 For instance, a dramatic decrease in Tf of the poly(ε-caprolactone) (PCL) core blocks from 28 °C to −17 °C has been documented for micelles self-assembled from PCL-b-PEO copolymers compared with the bulk PCL, while the Tm of PCL cores was ca. 54 °C, which the authors considered as surface nucleation.49 In another study, where homogenous nucleation of n-alkanes was investigated, the difference between Tm and Tf of pure n-C28H58 was equal 14 °C.59 Considering the relatively small differences between Tm and Tf of the alkyl core observed in this work, i.e., low undercooling effect, surface nucleation mechanism is the more likely mechanism.58 It should be pointed out that the core radii in the current system are one order of magnitude smaller than those in the publication of Mai et al.49 Interestingly, the gap between Tm and Tf is narrowing with  and almost closes at
and almost closes at  (the corresponding Rc = 19 Å). As illustrated in Fig. 4a, Nagg monotonously decreases with increasing
(the corresponding Rc = 19 Å). As illustrated in Fig. 4a, Nagg monotonously decreases with increasing  , i.e., thus, there are fewer alkyl chains in the core. It may become easier to arrange in an ordered manner in the case of fewer alkyl chains as the overall degree of freedom of the chains in one core is smaller.
, i.e., thus, there are fewer alkyl chains in the core. It may become easier to arrange in an ordered manner in the case of fewer alkyl chains as the overall degree of freedom of the chains in one core is smaller.
4. Conclusion
In summary, we have investigated the structure of mixed micelles formed in water from binary C28-PEOx mixtures with different PEO corona block lengths at a polymer volume fraction of 0.25 vol% by SAXS. The micelles were prepared by a co-solvent approach. The SAXS profiles of the tested samples exhibited typical features of spherical core–shell micelles and could be perfectly fitted by a spherical core-dual shell model. Decrease of Nagg and Rc were observed with increasing the mean corona block length. The Nagg scaled as
at a polymer volume fraction of 0.25 vol% by SAXS. The micelles were prepared by a co-solvent approach. The SAXS profiles of the tested samples exhibited typical features of spherical core–shell micelles and could be perfectly fitted by a spherical core-dual shell model. Decrease of Nagg and Rc were observed with increasing the mean corona block length. The Nagg scaled as  which is consistent with the theoretical prediction of
which is consistent with the theoretical prediction of  . A closer inspection of radial density profiles revealed that in micelles with the same outer radius, mixed micelles are characterized by higher density at the core–shell interface and lower at the shell–solvent interface in comparison to one-component micelles, which suggests more stretched PEG conformation in case of one-component micelles.
. A closer inspection of radial density profiles revealed that in micelles with the same outer radius, mixed micelles are characterized by higher density at the core–shell interface and lower at the shell–solvent interface in comparison to one-component micelles, which suggests more stretched PEG conformation in case of one-component micelles.
One single-phase transition of the alkyl core from binary polymer mixtures was observed upon heating in both the density and DSC measurements, confirming the formation of mixed micelles. Calculations based on melting enthalpy data from DSC revealed that the apparent crystallinity of the alkyl core decreased from 36% to 31% as the  increased from 53 to 485. However, as was found in our earlier work,32 the ordered phase in the confined core resembles more a “rotator phase” rather than a monoclinic phase typical for n-octacosane at low temperature.60 Interestingly we found that the melting point could be modulated and finely tuned through co-assembly of polymers with different PEO length. Tm decreased with an increase in
increased from 53 to 485. However, as was found in our earlier work,32 the ordered phase in the confined core resembles more a “rotator phase” rather than a monoclinic phase typical for n-octacosane at low temperature.60 Interestingly we found that the melting point could be modulated and finely tuned through co-assembly of polymers with different PEO length. Tm decreased with an increase in  and the reduction with respect to the bulk C28 alkane was proportional to
and the reduction with respect to the bulk C28 alkane was proportional to  as predicted by the Gibbs–Thomson equation. The work thus shows how confinement effects induced by self-assembly play an important role in determining the phase behaviour of micelles which may be of importance e.g. applications for solubilization of drug delivery. This study not only provides important insight into the basic physical chemistry, but also shows how the nature of the core in micellar systems can be manipulated by simple co-assembly strategies, either with the shell block length as shown in this work or using binary core block lengths as a previous work.19
as predicted by the Gibbs–Thomson equation. The work thus shows how confinement effects induced by self-assembly play an important role in determining the phase behaviour of micelles which may be of importance e.g. applications for solubilization of drug delivery. This study not only provides important insight into the basic physical chemistry, but also shows how the nature of the core in micellar systems can be manipulated by simple co-assembly strategies, either with the shell block length as shown in this work or using binary core block lengths as a previous work.19
Author contributions
Szymon M. Szostak: data curation, formal analysis, investigation, validation, visualization, Nico König: formal analysis, investigation, software Lutz Willner: conceptualization, methodology, resources, supervision, Reidar Lund: conceptualization, data curation, methodology, project administration, software, resources, supervision, funding aquistion, all authors: writing – review and editing.Data availability
Small angle X-ray scattering data for this article, are available at European Synchrotron Radiation Facility repository at https://doi.org/10.15151/ESRF-ES-1602273227. The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We indebted to Dr Shanshan Chen (Sun Yat-sen University) for the preliminary study and report. We are grateful the Norwegian Research Council (Project No. 315666, RL). We kindly acknowledge the provision of SAXS beamtime at BM29 at ESRF (Grenoble, France) and thank Dr Petra Pernot and the PSCM lab for support during the SAXS experiment. We also acknowledge the Norwegian national infrastructure for X-ray diffraction and scattering (RECX) at the University of Oslo (Norway) for SAXS beamtime. We would like to thank Bente A. Breiby (Department of Pharmacy, University of Oslo) for performing the nanoDSC experiments.References
- K. Letchford and H. Burt, Eur. J. Pharm. Biopharm., 2007, 65, 259–269 CrossRef CAS PubMed.
- U. Tritschler, S. Pearce, J. Gwyther, G. R. Whittell and I. Manners, Macromolecules, 2017, 50, 3439–3463 CrossRef CAS.
- A. Rösler, G. W. M. Vandermeulen and H. A. Klok, Adv. Drug Delivery Rev., 2012, 64, 270–279 CrossRef.
- A. M. Bodratti and P. Alexandridis, Expert Opin. Drug Delivery, 2018, 15, 1085–1104 CrossRef CAS PubMed.
- F. Xu, H. Li, Y. L. Luo and W. Tang, ACS Appl. Mater. Interfaces, 2017, 9, 5181–5192 CrossRef CAS PubMed.
- C. Li, C. C. Tho, D. Galaktionova, X. Chen, P. Král and U. Mirsaidov, Nanoscale, 2019, 11, 2299–2305 RSC.
- K. Liu, X. Wang, X. Li-Blatter, M. Wolf and P. Hunziker, ACS Appl. Bio Mater., 2020, 3, 6919–6931 CrossRef CAS PubMed.
- R. Lund, L. Willner and D. Richter, Adv. Polym. Sci., 2013, 259, 51–158 CrossRef CAS.
- T. Li, A. J. Senesi and B. Lee, Chem. Rev., 2016, 116, 11128–11180 CrossRef CAS PubMed.
- X. Ye, Z. W. Li, Z. Y. Sun and B. Khomami, ACS Nano, 2016, 10, 5199–5203 CrossRef CAS PubMed.
- R. S. Tu and M. Tirrell, Adv. Drug Delivery Rev., 2004, 56, 1537–1563 CrossRef CAS PubMed.
- T. Zinn, L. Willner, R. Lund, V. Pipich, M. S. Appavou and D. Richter, Soft Matter, 2014, 10, 5212–5220 RSC.
- A. B. Ebrahim Attia, Z. Y. Ong, J. L. Hedrick, P. P. Lee, P. L. R. Ee, P. T. Hammond and Y. Y. Yang, Curr. Opin. Colloid Interface Sci., 2011, 16, 182–194 CrossRef CAS.
- A. P. Lindsay, R. M. Lewis, B. Lee, A. J. Peterson, T. P. Lodge and F. S. Bates, ACS Macro Lett., 2020, 9, 197–203 CrossRef CAS PubMed.
- K. T. Oh, T. K. Bronich and A. V. Kabanov, J. Controlled Release, 2004, 94, 411–422 CrossRef CAS PubMed.
- D. Zhao, Y. Ma, E. Wang and T. P. Lodge, Macromolecules, 2019, 52, 4729–4738 CrossRef CAS.
- Y. Sun, R. Tan, Z. Ma, D. Zhou, J. Li, D. Kong and X. H. Dong, Giant, 2020, 4, 100037 CrossRef.
- Y. Sun, R. Tan, Z. Ma, Z. Gan, G. Li, D. Zhou, Y. Shao, W. Bin Zhang, R. Zhang and X. H. Dong, ACS Cent. Sci., 2020, 6, 1386–1393 CrossRef CAS PubMed.
- N. König, L. Willner and R. Lund, Soft Matter, 2019, 15, 7777–7786 RSC.
- Z. X. Du, J. T. Xu and Z. Q. Fan, Macromolecules, 2007, 40, 7633–7637 CrossRef CAS.
- C. Secker, A. Völkel, B. Tiersch, J. Koetz and H. Schlaad, Macromolecules, 2016, 49, 979–985 CrossRef CAS.
- T. Zinn, L. Willner, V. Pipich, D. Richter and R. Lund, ACS Macro Lett., 2015, 4, 651–655 CrossRef CAS PubMed.
- N. König, L. Willner, V. Pipich, T. Zinn and R. Lund, Phys. Rev. Lett., 2019, 122, 078001 CrossRef PubMed.
- X. Zhuo, T. Lei, L. Miao, W. Chu, X. Li, L. Luo, J. Gou, Y. Zhang, T. Yin, H. He and X. Tang, J. Colloid Interface Sci., 2018, 529, 34–43 CrossRef CAS PubMed.
- J. Dai, Z. Alaei, B. Plazzotta, J. S. Pedersen and I. Furó, J. Phys. Chem. B, 2017, 121, 10353–10363 CrossRef CAS PubMed.
- Y. Deng, J. Ling and M. H. Li, Nanoscale, 2018, 10, 6781–6800 RSC.
- A. L. Glover, S. M. Nikles, J. A. Nikles, C. S. Brazel and D. E. Nikles, Langmuir, 2012, 28, 10653–10660 CrossRef CAS PubMed.
- O. R. Monaghan, P. H. H. Bomans, N. A. J. M. Sommerdijk and S. J. Holder, Polym. Chem., 2017, 8, 5303–5316 RSC.
- T. Zinn, L. Willner and R. Lund, Phys. Rev. Lett., 2014, 113, 238305 CrossRef PubMed.
- M. Alcoutlabi and G. B. McKenna, J. Phys.: Condens. Matter, 2005, 17, R461 CrossRef CAS.
- M. D. Tully, J. Kieffer, M. E. Brennich, R. Cohen Aberdam, J. B. Florial, S. Hutin, M. Oscarsson, A. Beteva, A. Popov, D. Moussaoui, P. Theveneau, G. Papp, J. Gigmes, F. Cipriani, A. Mccarthy, C. Zubieta, C. Mueller-Dieckmann, G. Leonard and P. Pernot, J. Synchrotron Radiat., 2023, 30, 258–266 CrossRef PubMed.
- N. König, L. Willner, G. Carlström, T. Zinn, K. D. Knudsen, F. Rise, D. Topgaard and R. Lund, Macromolecules, 2020, 53, 10686–10698 CrossRef PubMed.
- C. Svaneborg and J. S. Pedersen, Phys. Rev. E, 2001, 64, 010802 CrossRef CAS PubMed.
- J. S. Pedersen and C. Svaneborg, Curr. Opin. Colloid Interface Sci., 2002, 7, 158–166 CrossRef CAS.
- D. J. Kinning and E. L. Thomas, Macromolecules, 1984, 17, 1712–1718 CrossRef CAS.
- B. Plazzotta, J. Dai, M. A. Behrens, I. Furó and J. S. Pedersen, J. Phys. Chem. B, 2015, 119, 10798–10806 CrossRef CAS PubMed.
- M. Vuorte, J. Määttä and M. Sammalkorpi, J. Phys. Chem. B, 2018, 122, 4851–4860 CrossRef CAS PubMed.
- A. Halperin, Macromolecules, 1987, 20, 2943–2946 CrossRef CAS.
- E. B. Zhulina, M. Adam, I. Larue, S. S. Sheiko and M. Rubinstein, Macromolecules, 2005, 38, 5330–5351 CrossRef CAS.
- R. Nagarajan and K. Ganesh, J. Chem. Phys., 1989, 90, 5843–5856 CrossRef CAS.
- L. Willner, A. Poppe, J. Allgaier, M. Monkenbusch, P. Lindner and D. Richter, Europhys. Lett., 2000, 51, 628 CrossRef CAS.
- C. Tanford, The hydrophobic effect: formation of micelles and biological membranes, J. Wiley, 2nd edn, 1980 Search PubMed.
- S. Jähnert, F. Vaca Chávez, G. E. Schaumann, A. Schreiber, M. Schönhoff and G. H. Findenegg, Phys. Chem. Chem. Phys., 2008, 10, 6039–6051 RSC.
- D. Wang, Y. Dong, W. Sun, N. Lu and X. Lan, Chem. Thermodyn. Therm. Anal., 2021, 3–4, 100019 CrossRef.
- R. J. Young and P. A. Lovell, Introd. to Polym., 3rd edn, 2011, pp. 1–653 Search PubMed.
- U. Domanska and D. Wyrzykowska-Stankiewicz, Thermochim. Acta, 1991, 179, 265–271 CrossRef CAS.
- S. Nakagawa, H. Marubayashi and S. Nojima, Eur. Polym. J., 2015, 70, 262–275 CrossRef CAS.
- S. Nojima, Y. Ohguma, K. I. Kadena, T. Ishizone, Y. Iwasaki and K. Yamaguchi, Macromolecules, 2010, 43, 3916–3923 CrossRef CAS.
- B. Mai, Z. Li, R. Liu, S. Feng, Q. Wu, G. Liang, H. Gao and F. Zhu, J. Polym. Res., 2013, 20, 1–8 CAS.
- H. C. Lu, Y. Xue, Q. L. Zhao, J. Huang, S. G. Xu, S. K. Cao and Z. Ma, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 3641–3647 CrossRef CAS.
- C. Göbel, C. Hils, M. Drechsler, D. Baabe, A. Greiner, H. Schmalz and B. Weber, Angew. Chem., Int. Ed., 2020, 59, 5765–5770 CrossRef PubMed.
- M. Perez, Scr. Mater., 2005, 52, 709–712 CrossRef CAS.
- S. Sen, S. H. Risbud and M. H. Bartl, Acc. Chem. Res., 2020, 53, 2869–2878 CrossRef CAS PubMed.
- L. Martínez, E. Uribarri and A. Laguna, Arch. Pharm. Pharm. Med. Chem., 1999, 332, 439–441 CrossRef.
- G. Strobl, Prog. Polym. Sci., 2006, 31, 398–442 CrossRef CAS.
- P. H. Chen, S. J. Lin, J. C. Tsai, U. S. Jeng and A. C. Su, Macromolecules, 2020, 53, 3059–3070 CrossRef CAS.
- F. C. Meldrum and C. O’Shaughnessy, Adv. Mater., 2020, 32, 2001068 CrossRef CAS PubMed.
- R. M. Michell, I. Blaszczyk-Lezak, C. Mijangos and A. J. Müller, Polymer, 2013, 54, 4059–4077 CrossRef CAS.
- M. J. Oliver and P. D. Calvert, J. Cryst. Growth, 1975, 30, 343–351 CrossRef CAS.
- X. Wang, Y. Wei, D. Zhang, X. Lan, F. Han and X. Z. Lan, Thermochim. Acta, 2020, 690, 178687 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01303d |
| This journal is © The Royal Society of Chemistry 2025 |