 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Biomimetic swarm of active particles with coupled passive-active interactions†
Amir
Nourhani
 abc
abc
aDepartment of Mechanical Engineering, University of Akron, Akron, Ohio 44325, USA
bBiomimicry Research and Innovation Center, University of Akron, Akron, Ohio 44325, USA
cDepartments of Biology, University of Akron, Akron, Ohio 44325, USA. E-mail: amir.nourhani@gmail.com
First published on 3rd March 2025
Abstract
We study the universal behavior of a class of active colloids whose design is inspired by the collective dynamics of natural systems such as schools of fish and flocks of birds. These colloids, with off-center repulsive interaction sites, self-organize into polar swarms exhibiting long-range order and directional motion without significant hydrodynamic interactions. Our simulations show that the system transitions from motile perfect crystals to solid-like, liquid-like, and gas-like states depending on noise levels, repulsive interaction strength, and particle density. By analyzing swarm polarity and hexatic bond order parameters, we demonstrate that effective volume fractions based on force-range and torque-range interactions explain the system's universal behavior. This work lays a groundwork for biomimetic applications utilizing the cooperative polar dynamics of active colloids.
Biological microswimmers and active colloids convert environmental energy into self-propulsion in fluids.1 These entities constitute active suspensions that can self-organize into complex, unpredictable patterns.2–5 Initial studies on dense bacterial suspensions6–10 and active biological materials11–15 revealed turbulent-like behavior with large-scale mixing and significant density and velocity fluctuations due to long-range hydrodynamic interactions. Artificial particles have been engineered with controlled properties like size, shape, and propulsion mechanisms.16–20 In many systems, weak short-range interactions and particle contacts drive collective dynamics, leading to cluster formation or motility-induced phase separation,21–28 including in systems with phoretic interactions.29–31 Large-scale directional flow from spontaneous symmetry breaking has been observed in systems modeled by Vicsek model,32 perception-driven alignment,33 and clustering-spreading-adaptive strategies.34 Experimentally, large-scale directional flow is seen in only a few synthetic systems, primarily driven by hydrodynamic interactions35–40 or electric-field induced interactions.41,42
One of the lasting challenges in microrobotics and active matter is designing microswimmers that can self-organize and cooperatively perform directional motion. In this paper, we address this challenge and study the universal behavior of a class of active colloids inspired by Nourhani et al.'s experimental realization of particles with off-center repulsive interaction sites43 and the collective dynamics observed in natural systems such as schools of fish, herds of deer, and flocks of birds. Similar to the animals mentioned above, these microparticles avoid aggregation and spontaneously generate system-scale polar swarms, exhibiting long-range order and coherent directional collective motion, even with negligible hydrodynamic interactions. This capability positions them as a transformative platform for biomimetic applications, overcoming current barriers in utilizing microswimmer swarms for transport and engineering purposes driven by cooperative behavior.
In a simplified phenomenological model of a school of fish, as shown in Fig. 1(a), animals avoid collisions by moving into free space while aligning with neighbors through effective torques. To replicate this in active colloids, their structure must avoid contact and generate aligning torques. This can be achieved by incorporating additional medium-to-long-range off-center repulsive interaction sites. An experimental example is Janus particles43 moving in a plane containing magnetic moments oriented perpendicular to the plane of motion, as depicted in Fig. 1(b) and demonstrated in the Supplementary video BiomimeticSwarm.m4v (ESI†). The use of self-phoretic Janus particles in our demonstrations is exemplary; however, the aligning mechanism based on off-center repulsive interaction sites presented here is independent of the self-propulsion mechanism. For instance, self-propulsion can also be achieved through acoustic actuation44,45 or other mechanisms.1,46
In microswimmers, placing these sites off-center creates passive torques about the active particle centers, aligning the direction of motion so that when particles approach each other, the torque bends their trajectories apart. The emergent coupled passive-active interactions lead to polar alignment from the coupling of activity with passive torques, independent of hydrodynamic interactions and mechanism of motion.
To intuitively understand coupled passive-active interactions, consider passive colloidal spheres with strong central repulsive interaction sites in a two-dimensional arrangement. As shown in Fig. 2(a), these particles repel each other, forming a triangular crystalline structure.47,48 If we design passive particles with off-center interaction sites43 and place them in the same setup, as shown in Fig. 2(b), the interaction sites align on a triangular lattice, but the particle centers do not. What happens if these particles are active? As shown in Fig. 2(c), two isolated active particles repel and exert torques, causing them to turn away and separate due to combined passive torque and active self-propulsion. However, in a dense environment, shown in Fig. 2(d), they cannot separate and must cooperate to achieve a stable steady state where net interaction force and torque are nearly zero. This steady state occurs when the particles align in the same direction, with centers and off-center sites forming distinct triangular lattices.
In the regime of no noise, active particles with off-center repulsive interaction sites will form motile perfect crystals, shown in Fig. 2(d). As noise increases, two new dynamics emerge: translational diffusion of the particle centers and rotational diffusion of the particles’ directions of motion. These effects cause the particle centers to deviate from the perfect crystal sites into solid-like, liquid-like, and gas-like states depending on noise levels, repulsive interaction strength, and particle density. However, torques still align the particles, allowing the swarm to maintain directional motion, though the arrangement of particle centers may becomes disordered. In the regime of high noise intensity, the coupled passive-active interactions are no longer strong enough to align the particles, resulting in the loss of directional collective motion. We focus on the dynamics and phases of the polar state, well beyond the regime of dynamics near the isotropic-to-polar transition.49
In our study, each square simulation box of side length L under periodic boundary conditions contains N particles of radius a, each with a director ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) ≡ (cos
≡ (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), moving with an active self-propulsion velocity vs = vs
θ), moving with an active self-propulsion velocity vs = vs![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) in a fluid of viscosity μ, while experiencing translational and orientational diffusion with coefficients Dt = kBT/Ct and Do = kBT/Co, respectively. Here,
in a fluid of viscosity μ, while experiencing translational and orientational diffusion with coefficients Dt = kBT/Ct and Do = kBT/Co, respectively. Here,  is the Stokes drag coefficient.50 For each particle, the off-center repulsive interaction site is located at
is the Stokes drag coefficient.50 For each particle, the off-center repulsive interaction site is located at ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif)
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) from the center and in our simulations we set
from the center and in our simulations we set  . The interaction sites are modeled by a force between two magnetic moments perpendicular to the direction of motion.43,49 The site in the jth particle repels the site of the kth particle by a force
. The interaction sites are modeled by a force between two magnetic moments perpendicular to the direction of motion.43,49 The site in the jth particle repels the site of the kth particle by a force
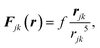 | (1) |
 , which leads to an additional translational velocity Ct−1Fk and angular velocity Co−1Lk, with the torque about the kth particle center given by Lk =
, which leads to an additional translational velocity Ct−1Fk and angular velocity Co−1Lk, with the torque about the kth particle center given by Lk = ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif)
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) k × Fk.
k × Fk.
In the absence of off-center repulsive interaction sites (f = 0), the Péclet number Pe = avs/Dt which is the dimensionless parameter that quantifies the rate of translational displacement relative to spatial diffusion suffices to characterize the system. On the other hand, when off-center repulsion sites are incorporated into the particle structure (f ≠ 0), two effects emerge. One is the repulsive force that tries to keep the particles apart, tending to place them on a hexagonal lattice (Fig. 2(d)), while the active propulsive force Ctvs may bring the particles closer. The competition between these two forces is quantified by the dimensionless parameter  . The other effect is the competition between the aligning torque about the particle center due to repulsive interactions and the dis-aligning torque CoDo due to random noise. Consistent with our earlier study,49 we define
. The other effect is the competition between the aligning torque about the particle center due to repulsive interactions and the dis-aligning torque CoDo due to random noise. Consistent with our earlier study,49 we define 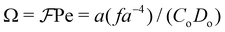 as the ratio of the timescales for orientational diffusion and magnetic rotation. This parameter serves as a measure of the propensity of the particles to align due to repulsive torque against thermal orientational fluctuations.
as the ratio of the timescales for orientational diffusion and magnetic rotation. This parameter serves as a measure of the propensity of the particles to align due to repulsive torque against thermal orientational fluctuations.
We use the particle radius a as the unit of length and τs = a/vs as the unit of time, where τs represents the time required for an active particle to translate a distance equal to its radius. Therefore, the governing equations for the position x of the particle center and orientation θ of the particle director ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) are
are
 | (2) |
 | (3) |
![[F with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0046_0303.gif) k = (fa−4)−1Fk is the net dimensionless force on the ith off-center site due to other off-center sites. The term
k = (fa−4)−1Fk is the net dimensionless force on the ith off-center site due to other off-center sites. The term| v(c.c.)jk = 10[(rjk − 1)−2 − 1][1 − H(rjk − 2)], | (4) |
The simulations cover a range of volume fractions, ϕ = πa2/d2, from 0.126 (d = 5a) to 0.785 (d = 2a), where 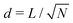 is the average inter-particle distance. Developing a continuum kinetic model and using linear stability analysis, Nourhani and Saintillan49 showed that the isotropic-to-polar transition occurs at the critical value
is the average inter-particle distance. Developing a continuum kinetic model and using linear stability analysis, Nourhani and Saintillan49 showed that the isotropic-to-polar transition occurs at the critical value
 | (5) |
We quantify the particle configuration in the collective dynamics using the swarm polarity |p|, along with the spatial arrangement and degree of crystallinity of the particles, through the local Ψ(6)local and global Ψ(6)global hexatic bond orders. The polarity,
 | (6) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) j represents the direction of the jth swimmer's self-propulsion velocity. The averaging is performed over all particles in the frame. We are also interested in the solid-like and fluid-like behavior as a result of the local and global arrangement of the particles.
j represents the direction of the jth swimmer's self-propulsion velocity. The averaging is performed over all particles in the frame. We are also interested in the solid-like and fluid-like behavior as a result of the local and global arrangement of the particles.
In a given frame, for particle j surrounded by Nnn nearest Voronoi neighbors, the complex hexatic bond-order parameter,
 | (7) |
| Ψ(6)local = 〈|ψ(6)j|〉, Ψ(6)global = |〈ψ(6)j〉|, | (8) |
 .
.
We simulate N = 242 = 576 particles over a duration of 2500τs, starting from a square lattice with lattice constant d∈[2a, 5a] and random initial orientations, as exemplified in Fig. 3(a)–(c). Sampling is performed every 0.1τs, resulting in 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001 frames for statistical analysis in each simulation. The majority of the simulations reached steady state within t < 500τs, and all of them by t = 1000τs. The results of the simulations are presented in Fig. 3 and 4. For each frame, |p|, Ψ(6)local, and Ψ(6)global are calculated by averaging over the particles in that frame. The data in Fig. 3(e)–(g) show the time evolution of these order parameters across several frames. The data presented in Fig. 4 represent the time average of the quantities over 10
001 frames for statistical analysis in each simulation. The majority of the simulations reached steady state within t < 500τs, and all of them by t = 1000τs. The results of the simulations are presented in Fig. 3 and 4. For each frame, |p|, Ψ(6)local, and Ψ(6)global are calculated by averaging over the particles in that frame. The data in Fig. 3(e)–(g) show the time evolution of these order parameters across several frames. The data presented in Fig. 4 represent the time average of the quantities over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001 frames in the time domain t∈[1500τs, 2500τs], where the system is in the steady-state regime, with error bars indicating the standard deviation of temporal variations.
001 frames in the time domain t∈[1500τs, 2500τs], where the system is in the steady-state regime, with error bars indicating the standard deviation of temporal variations.
 | ||
| Fig. 3 Example systems, identified by (Pe, Ω, ϕ, Ψ(6)local), exhibiting solid-like (50, 5000, 0.431, 0.951), liquid-like (500, 500, 0.785, 0.586), and gas-like (50, 500, 0.196, 0.379) behavior. (a)–(c) Corresponding frames at different times, starting from a square lattice with random initial orientations to the steady state, represented by the last frame in each row. (d) The color map for the direction θ of the swimmer director in degrees. The time evolution of (e) polarization, (f) local bond order, and (g) global bond order for these systems. The Supplementary video Fig 3-video.m4v (ESI†) demonstrates the time evolution of the swarms. | ||
We intuitively define solid-like behavior as a state where particles cannot change their neighbors during collective motion. In liquid-like behavior, particles may change their neighbors slowly, while in gas-like polar dynamics, particles can easily change their neighbors and make large scale displacements. Quantitatively speaking, the lower bound of the local bond order parameter often used to detect crystalline order is 0.7.51,52 Roughly approximating the gas-like state as a random configuration of particles with six nearest neighbors, Jensen's inequality sets the upper bound 6−1/2 = 0.408 for the local bond order parameter. Additionally, a numerical simulation of the average of 109 samples of six random unit vectors resulted in Ψ(6)local = 0.3656 ± 0.002 for the approximate gas-like phase. Therefore, we define the range 0.4 ≲ Ψ(6)local ≲ 0.7 as corresponding to the liquid-like phase. Values below this range correspond to the gas-like phase, while those above represent the solid-like phase. To illustrate representatives of these phases, Fig. 3 shows three examples with different values of Ψ(6)local demonstrating solid-like (0.951), liquid-like (0.586), and gas-like (0.379) behavior. Fig. 3(a)–(c) show the corresponding snapshots at different times, with the last frame representing an example of the steady state.
Fig. 3(e)–(g) show the time evolution of three order parameters: polarity |p|, local bond order Ψ(6)local, and global bond order Ψ(6)global. As shown in Fig. 3(e), all three systems eventually reach a polarized state. The liquid-like system approaches its steady state sooner than the others, as particles can quickly change neighbors and rearrange. In the gas-like system, particles can reorganize more easily, but it takes longer for particles to influence each other's orientation and for the swarm to polarize. In the solid-like behavior, the repulsive interactions are strong enough that the particles begin to reorient locally, creating polarized regions that gradually grow and merge, leading to a fully polarized state.
Fig. 3(f) and (g) show the behavior of the local Ψ(6)local and global Ψ(6)global bond order parameters, respectively. The solid-like system, after polarization, shows a transient state with hexagonal regions connected by a grain boundary, as seen in Fig. 3(a). The coexistence of these regions is marked by blue bands in Fig. 3(e)–(g). During this phase, the local bond order is higher than in the liquid-like and gas-like systems, but the boundary distorts the global order. Eventually, the grain boundaries dissolve, and the system attains global hexagonal order, though slightly distorted by noise. In dense systems or those with strong repulsion, kinetic trapping may prevent this dissolution, blocking the transition to global hexagonal symmetry, even if thermodynamically feasible.
The liquid-like system exhibits a transient state reminiscent of motility-induced phase separation, where particles aggregate and create free volume, as shown in Fig. 3(b). The local structures approach hexagonal symmetry, leading to an increase in local and global bond order parameters, marked by the red bands in Fig. 3(e)–(g). However, the particles reorient due to the torques induced by the off-center sites, aligning and repelling each other, which disrupts the local hexagonal symmetry. This results in a reduction of local and global bond order parameters at steady state. In the gas-like system, the local bond order is less than 0.4, and the global bond order is nearly zero, indicating an absence of global hexagonal symmetry.
Fig. 4(a)–(c) shows the polarization, local bond order, and global bond order, respectively, for a set of pairs (Pe, Ω) as a function of the volume fraction ϕ. As discussed earlier, the data represent temporal averages over the time domain t∈[1500τs, 2500τs], with error bars indicating the standard deviation of temporal variations. The trends between polarity and bond order do not appear to be similar. For example, in the cases of  (100, 5000) and ★ (500, 5000), over most of the explored region of ϕ, the polarization for ★ exceeds that of
(100, 5000) and ★ (500, 5000), over most of the explored region of ϕ, the polarization for ★ exceeds that of  , while for the bond orders, that trend does not hold. As another example, the polarization for ■ (50, 500) is always less than for ◆ (500, 500), while the bond order is higher. Therefore, to deduce a trend and understand the interplay between the parameters, we introduce the concepts of force-range ϕF and torque-range ϕL volume fractions.
, while for the bond orders, that trend does not hold. As another example, the polarization for ■ (50, 500) is always less than for ◆ (500, 500), while the bond order is higher. Therefore, to deduce a trend and understand the interplay between the parameters, we introduce the concepts of force-range ϕF and torque-range ϕL volume fractions.
We start by defining the force-range RF and torque-range RL effective radii, shown in Fig. 4(d) and (e), respectively. Consider two swimmers approaching each other until they reach an approximate distance of 2RF, where the self-propulsion force is balanced by the off-center repulsion, keeping them apart. This gives f(2RF)−4 ≈ Ctvs, leading to the force-range effective radius  . Similarly, as shown in Fig. 4(e), we define the torque-range effective radius RL as the distance at which the orientational noise is balanced by the repulsive torque, af (2RL)−4 ≈ CoDo, leading to RL ≈ (a/2)Ω1/4. Correspondingly, we can define a force-range volume fraction
. Similarly, as shown in Fig. 4(e), we define the torque-range effective radius RL as the distance at which the orientational noise is balanced by the repulsive torque, af (2RL)−4 ≈ CoDo, leading to RL ≈ (a/2)Ω1/4. Correspondingly, we can define a force-range volume fraction  and, similarly, a torque-range volume fraction
and, similarly, a torque-range volume fraction  . As an example, the force-range and torque-range volume fractions (ϕF, ϕL) for the systems shown in Fig. 3 are as follows: solid-like (1.078, 7.619), liquid-like (0.196, 4.388), and gas-like (0.155, 1.096). Although the volume fraction ϕ for the liquid-like (0.785) system is higher than that of the solid-like (0.431) system, the pair (ϕF, ϕL) is smaller.
. As an example, the force-range and torque-range volume fractions (ϕF, ϕL) for the systems shown in Fig. 3 are as follows: solid-like (1.078, 7.619), liquid-like (0.196, 4.388), and gas-like (0.155, 1.096). Although the volume fraction ϕ for the liquid-like (0.785) system is higher than that of the solid-like (0.431) system, the pair (ϕF, ϕL) is smaller.
The ratio of these effective radii and volume fractions
 | (9) |
With the definitions of effective volume fractions ϕF and ϕL, we can construct composite dimensionless quantities to explain the system's universal behavior and collapse the data in Fig. 4(a)–(c) into master curves. Starting with polarization, as shown in Fig. 4(g), a particle must fall within the overlap of the torque-range circles of at least two others to balance orientational noise, making the interactions a function of ϕL2. Swarm polarization also depends on the average orientation of the particles, which is influenced by the amplitude of the variation of particle orientation around the swarm's polarization direction. The extent of the angular fluctuation between the directors of the central particle and the aligning particle is proportional to  . Lower orientational diffusivity reduces this variation amplitude, introducing a factor of
. Lower orientational diffusivity reduces this variation amplitude, introducing a factor of  . Therefore, the composite dimensionless parameter
. Therefore, the composite dimensionless parameter  captures the essential polar interactions. For instance, for the systems shown in Fig. 3, the values of this parameter are solid-like (2.9 × 103), liquid-like (9.63 × 103), and gas-like (6 × 101). As shown in Fig. 4(i), plotting polarization against the composite dimensionless parameter ϕL2Pe reveals a master curve, with polarization increasing as this parameter grows. In the range ϕL2Pe ≳ 103, the polarization is nearly equal to one.
captures the essential polar interactions. For instance, for the systems shown in Fig. 3, the values of this parameter are solid-like (2.9 × 103), liquid-like (9.63 × 103), and gas-like (6 × 101). As shown in Fig. 4(i), plotting polarization against the composite dimensionless parameter ϕL2Pe reveals a master curve, with polarization increasing as this parameter grows. In the range ϕL2Pe ≳ 103, the polarization is nearly equal to one.
For bond orders, we have two objectives. As shown in Fig. 4(h), one goal is to keep the particle aligned with other particles, which requires them to fall within the overlap of the torque-range circles of two particles, introducing a factor of ϕL2. The other goal is to ensure the particles stay apart, which requires them to be within the overlap of the force-range circles, quantified by ϕF2. Therefore, we expect the composite dimensionless parameter ϕF2ϕL2 to define the particle arrangement and orientation in space, thereby determining the bond orders. For example, for the systems presented in Fig. 3, the values of this parameter are solid-like (67.4), liquid-like (0.74), and gas-like (0.03). As shown in Fig. 4(j) and (k), plotting local and global bond orders against ϕF2ϕL2 results in the data collapsing into master curves. The transition from gas-like to solid-like occurs over a broader range of ϕF2ϕL2 for the local bond order compared to the global bond order. This is because, in most of the liquid-like phase, the system lacks global hexagonal symmetry, whereas individual particles may exhibit local symmetry in their immediate Voronoi neighbors.
In conclusion, this study discusses a paradigm for engineering collective dynamics in active colloids, specifically through the design of off-center repulsive interaction sites. By mimicking the behavior of natural systems like schools of fish, these colloids demonstrate the ability to self-organize into polar swarms with long-range order and coherent directional motion, even without significant hydrodynamic interactions. The findings highlight the emergence of coupled passive-active interactions that enable unique control over particle alignment and motion. This work not only advances our understanding of active matter but also provides a versatile platform for developing biomimetic applications in transport, engineering, and microrobotics. The study paves the way for future exploration of collective behaviors in active systems, particularly in overcoming the challenges of aggregation and achieving controlled, coherent motion.
Data availability
This article is a theory paper, the data are the result of running the simulations of the equations written in the draft. No additional data from experimentation or other than what is already presented in the figures.Conflicts of interest
There are no conflicts to declare.Acknowledgements
I extend my sincere gratitude to Paul E. Lammert, Vincent H. Crespi, and David Saintillan for their insightful discussions and valuable comments. I also thank Seyed Amin Nabavizadeh for help with GPU programming and Rafe Md Abu Zayed for running some simulations. I wish to acknowledge the support from the National Science Foundation CAREER award, grant number CBET-2238915.References
- F. Soto, E. Karshalev, F. Zhang, B. E. F. de Avila, A. Nourhani and J. Wang, Chem. Rev., 2022, 122, 5365–5403 CrossRef CAS PubMed.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. Aditi Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- D. Saintillan and M. J. Shelley, C. R. Phys., 2013, 14, 497–517 CrossRef CAS.
- D. L. Koch and G. Subramanian, Annu. Rev. Fluid Mech., 2011, 43, 637–659 CrossRef.
- B. Liebchen and A. K. Mukhopadhyay, J. Phys.: Condens. Matter, 2021, 34, 083002 CrossRef PubMed.
- C. Dombrowski, L. Cisneros, S. Chatkaew, R. E. Goldstein and J. O. Kessler, Phys. Rev. Lett., 2004, 93, 098103 CrossRef PubMed.
- L. H. Cisneros, R. Cortez, C. Dombrowski, R. E. Goldstein and J. O. Kessler, Exp. Fluids, 2007, 43, 737–753 CrossRef.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef CAS PubMed.
- J. Dunkel, S. Heidenreich, K. Drescher, H. H. Wensink, M. Bar and R. E. Goldstein, Phys. Rev. Lett., 2013, 110, 228102 Search PubMed.
- J. Gachelin, A. Rousselet, A. Lindner and E. Clement, N. J. Phys., 2014, 16, 025003 CrossRef.
- F. J. Nedelec, T. Surrey, A. C. Maggs and S. Leibler, Nature, 1997, 389, 305 Search PubMed.
- T. Surrey, F. Nédélec, S. Leibler and E. Karsenti, Science, 2001, 292, 1167–1171 Search PubMed.
- T. Sanchez, D. Chen, S. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- Y. Sumino, K. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chate and K. Oiwa, Nature, 2012, 483, 228–452 CrossRef PubMed.
- M. J. Shelley, Annu. Rev. Fluid Mech., 2016, 48, 487–506 CrossRef.
- A. Nourhani, V. H. Crespi and P. E. Lammert, Phys. Rev. E, 2015, 91, 062303 CrossRef PubMed.
- A. Nourhani and P. E. Lammert, Phys. Rev. Lett., 2016, 116, 178302 CrossRef PubMed.
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. S. Angelo, Y. Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, J. Am. Chem. Soc., 2004, 126, 13424–13431 CrossRef CAS PubMed.
- S. J. Ebbens and J. R. Howse, Soft Matter, 2010, 6, 726–738 RSC.
- J. Wang, Nanomachines: Fundamentals and Applications, Wiley, 2013 Search PubMed.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matt. Phys., 2015, 6, 219–244 CrossRef CAS.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702 CrossRef PubMed.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS PubMed.
- J. Schwarz-Linek, C. Valeriani, A. Cacciuto, M. E. Cates, D. Marenduzzo, A. N. Morozov and W. C. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4052–4057 CrossRef CAS PubMed.
- J. Arlt, V. A. Martinez, A. Dawson, T. Pilizota and W. C. K. Poon, Nat. Commun., 2018, 9, 768 CrossRef PubMed.
- M. N. van der Linden, L. C. Alexander, D. G. A. L. Aarts and O. Dauchot, Phys. Rev. Lett., 2019, 123, 098001 CrossRef CAS PubMed.
- B. Liebchen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2017, 118, 268001 CrossRef PubMed.
- F. Fadda, D. A. Matoz-Fernandez, R. van Roij and S. Jabbari-Farouji, Soft Matter, 2023, 19, 2297–2310 RSC.
- J. N. Johnson, A. Nourhani, R. Peralta, B. Thiesing, C. J. Mann, P. E. Lammert and J. G. Gibbs, Phys. Rev. E, 2017, 95, 042609 CrossRef PubMed.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226–1229 CrossRef CAS PubMed.
- R. S. Negi, R. G. Winkler and G. Gompper, Phys. Rev. Res., 2024, 6, 013118 CrossRef CAS.
- J. Grauer, F. J. Schwarzendahl, H. Löwen and B. Liebchen, Mach. Learn.: Sci. Technol., 2024, 5, 015014 Search PubMed.
- G. Quincke, Annu. Phys. Chem., 1896, 59, 417 CrossRef.
- T. B. Jones, IEEE Trans. Ind. Appl., 1984, 4, 845–849 Search PubMed.
- D. Das and D. Saintillan, Phy. Rev. E, 2013, 87, 043014 CrossRef PubMed.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- A. Bricard, J.-B. Caussin, D. Das, C. Savoie, V. Chikkadi, K. Shitara, O. Chepizhko, F. Peruani, D. Saintillan and D. Bartolo, Nat. Commun., 2015, 6, 7470 CrossRef CAS PubMed.
- H. Karani, G. E. Pradillo and P. M. Vlahovska, Phys. Rev. Lett., 2019, 123, 208002 CrossRef CAS PubMed.
- S. Das, M. Ciarchi, Z. Zhou, J. Yan, J. Zhang and R. Alert, Phys. Rev. X, 2024, 14, 031008 CAS.
- J. Yan, M. Han, J. Zhang, C. Xu, E. Luijten and S. Granick, Nat. Mater., 2016, 15, 1095–1099 CrossRef CAS PubMed.
- A. Nourhani, D. Brown, N. Pletzer and J. G. Gibbs, Adv. Mater., 2017, 29, 1703910 CrossRef PubMed.
- M. Kaynak, A. Ozcelik, A. Nourhani, P. E. Lammert, V. H. Crespi and T. J. Huang, Lab Chip, 2017, 17, 395–400 RSC.
- D. Ahmed, M. Lu, A. Nourhani, P. Lammert, Z. Stratton, H. Muddana, V. H. Crespi and T. J. Huang, Sci. Rep., 2015, 5, 1–8 Search PubMed.
- T. He, Y. Yang and X.-B. Chen, Nanoscale, 2024, 16, 12696–12734 RSC.
- P. Dillmann, G. Maret and P. Keim, Eur. Phys. J.: Spec. Top., 2013, 222, 2941–2959 Search PubMed.
- F. Ebert, P. Dillmann, G. Maret and P. Keim, Rev. Sci. Instrum., 2009, 80, 083902 CrossRef CAS PubMed.
- A. Nourhani and D. Saintillan, Phys. Rev. E, 2021, 103, L040601 CrossRef CAS PubMed.
- A. Nourhani, Y. M. Byun, P. E. Lammert, A. Borhan and V. H. Crespi, Phys. Rev. E, 2013, 88, 062317 CrossRef PubMed.
- Y. L. Wu, D. Derks, A. van Blaaderen and A. Imhof, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10564–10569 CrossRef CAS PubMed.
- K. H. Nagamanasa, S. Gokhale, R. Ganapathy and A. Sood, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11323–11326 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01298d |
| This journal is © The Royal Society of Chemistry 2025 |




![[upper bond 2 start]](https://www.rsc.org/images/entities/char_e014.gif) (50, 1000),
(50, 1000), ![[pentagon filled]](https://www.rsc.org/images/entities/char_e13d.gif) (100, 1000),
(100, 1000), ![[hexagon filled, flat-side down]](https://www.rsc.org/images/entities/char_e039.gif) (500, 1000),
(500, 1000), 

![[scr F, script letter F]](https://www.rsc.org/images/entities/i_char_e141.gif)

