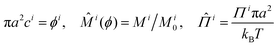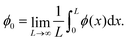Open Access Article
Open Access ArticleBinary mixtures of active Brownian particles with distinct nonzero activities†
Nicholas J.
Lauersdorf
,
Ehssan
Nazockdast
 * and
Daphne
Klotsa
* and
Daphne
Klotsa
 *
*
Department of Applied Physical Sciences, University of North Carolina at Chapel Hill, USA. E-mail: ehssan@email.unc.edu; dklotsa@email.unc.edu
First published on 17th July 2025
Abstract
We computationally study suspensions of slow and fast active Brownian particles that have undergone motility induced phase separation and are in the steady state. Such mixtures, of varying non-zero activity, remain largely unexplored even though they are relevant in a plethora of systems and applications ranging from cellular biophysics to drone swarms. Our mixtures are modulated by their activity ratios (PeR), which we find to encode information by giving rise to three regimes, each of which display their unique emergent behaviors. Specifically, we found non-monotonic behavior of macroscopic properties, e.g. density and pressure, as a function of activity ratio, microphase separation of fast and slow particle domains, increased fluctuations on the interface and severe avalanche events compared to monodisperse active systems. Our approach of simultaneously varying the two activities of the particle species allowed us to discover these behaviors and explain the microscopic physical mechanisms that drive them.
1 Introduction
Active matter describes nonequilibrium systems comprised of components that locally consume energy to move, such as swarms of bacteria and clusters of self-propelled colloids. Past studies on monodisperse systems and minimal models have led to the discovery of a range of remarkable emergent phenomena including swarming and flocking and pattern formation.1–3 One of these phenomena relevant to this study is motility-induced phase separation (MIPS), where a suspension of self-propelled particles undergoes a liquid–gas phase separation at sufficiently large self-propulsion speed and particle density, even in the complete absence of attractive interparticle forces.4,5 MIPS has been observed in experiments of self-phoretic and light-activated colloidal particles6 as well as 2D and 3D simulations of these systems.4,7–12 A simple physical explanation for MIPS is that under sufficiently large self-propulsion speed and particle density the timescale for particle collision becomes smaller than the time for the particle to rotate and escape the cluster through random diffusion and other mechanisms. This leads to a stable cluster and/or phase segregated domain.There are, however, several physical parameters in synthetic and natural systems that make the collective dynamics of active Brownian particles (ABPs) more complex.13 For example, in addition to near-contact repulsive steric interaction, chemically- or thermally-active particles can interact non-locally through the solute concentration14,15 or temperature fields16 that themselves are coupled to the configuration and velocities of the underlying particles. Furthermore, the particles can interact through their self-generated flows i.e., hydrodynamic interactions, which can lead to qualitative changes in the emergent states. The nature of hydrodynamic interactions is such that near-field lubrication forces, far-field interactions and particle shape all contribute to the collective behavior observed in the system.17–19
Adding complexity to the system, studies of polydisperse mixtures have included components of different sizes,20,21 shapes,22,23 interactions,24–32 and propulsion mechanisms.22,26,33–39 The relative activities of the particles have mostly been varied in the limiting case of active/passive mixtures through simulations and theory40–51 and experimentally,52–54 passive particles in active baths55–66 and active particles with static obstacles.25,67–74 However, mixtures of particles with distinct nonzero active driving forces remain largely unexplored, even though they are relevant in a variety of systems ranging from fundamental physics to applications, as we explain next. Some recent studies are an exception and show there is growing interest.75–80
Studying active/active mixtures is interesting from a fundamental physics standpoint, since it is a simple nonequilibrium model system that challenges our understanding of what collective behavior to expect, and what quantities equilibrate; still, it is sufficiently simple to allow theoretical progress from first principles. We often think of activity as a temperature analogue. While fast particles can effectively exchange activity with slower ones when in contact, as has been observed in active/passive61,72,81–87 and slow/fast79 systems, they do not reach a uniform activity and so the answer is unclear. In biology there are many active matter systems of importance that are relevant to biophysics and medicine, and they are typically polydisperse including in their motility,88–92 such as bacteria and sperm cells. Furthermore in synthetic systems, limitations in fabrication techniques give rise to a distribution of swim speeds in self-propelled colloids,93–96 but there is limited understanding of how that affects the emergent behavior. Finally, from a soft-matter and materials physics perspective, tuning the relative activities of particles opens a new design parameter space with potentially a wealth of physics providing opportunities for more control in designing dynamic complex assemblies. Active matter mixtures exhibit behaviors akin to those found in living systems e.g. nonequilibrium transitions, microphase separation, and bistable states that have not been observed before.
In this article we perform simulations of binary active mixtures of fast and slow active Brownian particles (ABPs) that have undergone motility induced phase separation (MIPS) and are in the steady state. In the absence of prior study of this specific regime, we chose to ignore the more complex non-local phoretic and hydrodynamic interactions and studied the simplest model-system of ABPs of the same size but with two distinct activities, where particles interact only through conserved interparticle forces. Specifically, we studied the properties of the phase separated system as a function of the ratio of the slow to fast particle activities, 0 ≤ PeR ≤ 1, and discovered three regimes corresponding to small, intermediate and large activity ratios. At large activity ratios the fast and slow particles are uniformly mixed and the behavior is analogous to monodisperse ABP suspensions, even when the slow activity is just a third of the fast. At intermediate and small activity ratios, when the particles are increasingly heterogeneous in their activities, is where we see the most interesting behavior: microscopically, the system exhibits microphase separation, increased avalanche events and fluctuations, and active herding (slow particles pushed by the fast ones). We also found nonmonotonic behavior in macroscopic quantities, including cluster pressure, density and compressibility. To obtain a deeper understanding, we developed a coarse-grained continuum model, which provided further insight and whose predictions were in good agreement with the simulation results. We thus propose a physical mechanism that links microscopic and macroscopic behavior and explains the observed emergent phenomena.
2 Model & methods
Using HOOMD-blue,97–99 we simulated N = 5 × 104 circular ABPs of diameter σ = 1.0, confined to a two-dimensional, periodic box of constant area fraction (ϕ = 0.6). Particles translate and rotate over time (measured in units of the rotational diffusion time, τr) in accordance with overdamped Langevin dynamics: | (1) |
 | (2) |
![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) is the rate of change over time of the angle between the orientation unit vector and x-axis such that
is the rate of change over time of the angle between the orientation unit vector and x-axis such that ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) = (cos
= (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), the term −ξv is the translational viscous drag force of the fluid, and
θ), the term −ξv is the translational viscous drag force of the fluid, and  and
and  are the stochastic thermal force and torque respectively, which have zero time-average and 2kBT and 2kBT variance respectively. Particles interact via the Weeks–Chandler–Anderson (WCA) potential with a soft repulsive well depth
are the stochastic thermal force and torque respectively, which have zero time-average and 2kBT and 2kBT variance respectively. Particles interact via the Weeks–Chandler–Anderson (WCA) potential with a soft repulsive well depth  :
: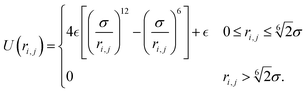 | (3) |
The interparticle force applied by particle j on particle i is the gradient of this potential, FWCA(r) = −∇rU, and is given by
 | (4) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) = ri,j/‖ri,j‖ is the relative separation unit vector. Each particle is subject to an active force, Fa = ξvp
= ri,j/‖ri,j‖ is the relative separation unit vector. Each particle is subject to an active force, Fa = ξvp![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) , where vp is the swim speed in the absence of collisions and ξ = 3πησ is the translational drag coefficient from an implicit solvent of dynamic viscosity η = 1/3πσ. The active force is applied along a body axis, defined by the unit vector
, where vp is the swim speed in the absence of collisions and ξ = 3πησ is the translational drag coefficient from an implicit solvent of dynamic viscosity η = 1/3πσ. The active force is applied along a body axis, defined by the unit vector ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) , that randomly reorients according to rotational diffusion via a characteristic timescale τr = Dr−1 = 1/3 where Dr is the rotational diffusion constant.
, that randomly reorients according to rotational diffusion via a characteristic timescale τr = Dr−1 = 1/3 where Dr is the rotational diffusion constant.
The activity is quantified by the Péclet number, Pe = 3vpτr/σ. Note that the activity is modulated in this work via the preferred swim speed (vp), which also determines the active force magnitude. We simulated mixtures of fast (PeF) and slow (PeS) ABPs whose activities (PeF, PeS) were varied independently between 0 and 500. The particle fractions χF and χS, where χF = 1.0 − χS, were varied between 0.2 and 0.8 while the total packing fraction remained fixed at ϕ = 0.6. We ran a range of relative fractions; in the main article, for simplicity, we show results for χF = χS = 0.5, but the findings remain the same, see Section S1 (ESI†) for a detailed discussion and additional results. The Péclet number for fast (PeF) and slow (PeS) particles is varied separately within the range 0–500 in steps of 50 with finer step sizes used near the non-monotonic inflection point in mechanical properties, and PeS ≤ PeF. We define the activity ratio  , ranging from a monodisperse active system (PeR = 1) to the most heterogeneous (PeR = 0) which is a mixture of passive and active particles. It is useful to also define the net activity, PeNet = χSPeS + χFPeF,75 ranging between 0 and 500. Since the fast and slow activities are varied independently, each activity ratio can correspond to multiple net activities. We ran 204 simulations of 50
, ranging from a monodisperse active system (PeR = 1) to the most heterogeneous (PeR = 0) which is a mixture of passive and active particles. It is useful to also define the net activity, PeNet = χSPeS + χFPeF,75 ranging between 0 and 500. Since the fast and slow activities are varied independently, each activity ratio can correspond to multiple net activities. We ran 204 simulations of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 (fast
50 (fast![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) slow) systems and 487 in total, including other particle fractions; see Fig. 1(a).
slow) systems and 487 in total, including other particle fractions; see Fig. 1(a).
The systems studied here have undergone MIPS and reached the steady state. We ran very long simulations (1800τr) using a variety of initial conditions, e.g. random gas and differently instantiated clusters. Unlike previous works40 we found that all initializations eventually led to the same steady-states for PeR ≥ 0.2. For PeR < 0.2, the large fluctuations in the cluster size prolong the onset of MIPS; hence, for low activity ratios we instantiated the clusters and then observed them melt or persist over long times, see Section S2 (ESI†) for a detailed discussion. We distinguish three phases shown in Fig. 1(b): (1) a dilute gas with random alignment of active forces; (2) a bulk with uniform high density and also random alignment of active forces; and (3) an interface, that sits between the bulk and the gas, and is characterized by a transition from high to low density, a net alignment of particles’ active forces and a net compressive force towards the center of the cluster100 (Section S3, ESI†).
3 Results
We first studied the macroscopic mechanical properties of the bulk phase. We began by computing the force moment acting on particle i in the dense phase from all the other particles, Si: | (5) |
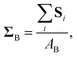 | (6) |
 .
.
In monodisperse systems, pressure exhibits a nearly linear dependence with activity.100,102 To remove this dependence and focus on the activity ratio, for each system we normalized the pressure by the computed pressure at activity ratio 1, denoted as Π0B. This non-dimensionalization collapses all the data from different net activities into a single curve (Fig. 2(a)(i)). As shown, the dimensionless pressure displays nonmonotonic variations with activity ratio with a minimum around PeR ≈ 0.35, followed by an increase and then a plateau at small activity ratios, PeR < 0.175. The number density of particles in the bulk phase (nB) and compressibility  also show non-monotonic behavior with PeR similar to the pressure, (Fig. 2(a)(ii) and (iii)). We can thus define three regimes in terms of the activity ratio: large 0.35 < PeR ≤ 1, intermediate 0.175 < PeR < 0.35 and small PeR < 0.175. These regimes emerge naturally and consistently from all our results obtained from many independently measured quantities, as will be shown.
also show non-monotonic behavior with PeR similar to the pressure, (Fig. 2(a)(ii) and (iii)). We can thus define three regimes in terms of the activity ratio: large 0.35 < PeR ≤ 1, intermediate 0.175 < PeR < 0.35 and small PeR < 0.175. These regimes emerge naturally and consistently from all our results obtained from many independently measured quantities, as will be shown.
 | ||
| Fig. 2 (a) Bulk (cluster) (i) interparticle pressure, (ii) number density, and (iii) compressibility measured in simulation normalized by their respective values in the monodisperse (same activity, PeR = 1) case, as a function of activity ratio (PeR) and colored by the net activity (PeNet). (b) The steady-state fast particle fraction in the bulk phase (χFB, green circle) and the interface (χFI, orange cross) measured in simulation as a function of activity ratio (PeR). The solid black line represents the 1D-continuum model predictions. In (a) and (b), three regimes, corresponding to three range of activity ratios (small, intermediate, and large), are visualized using the background color and separated by dashed black lines. (c) Number density of slow (blue) and fast (red) particles for our ABP simulation (dots) and 1D continuum model (solid line) as a function of distance from the cluster's center of mass (r) normalized by the cluster radius (rc) for PeR = 0.1, 0.3, and 1.0. As the number density monotonically decreases from the cluster's center in the continuum model, we defined the start of the interface as the center of the cluster and determined the end of the interface using our interface identification method, see the ESI.† | ||
To explore the microscopic basis of this nonmonotonic behavior, we computed the relative composition of fast and slow particles in the cluster (Fig. 2(b)). Note that similar to the dimensionless pressure, the fraction of fast (and slow) particles is only a function of activity ratio and independent of the net activity. We observe that as PeR decreases the fast particle fraction increases in the bulk and the interface, particularly for intermediate and low PeR (Fig. 2(b)). At the interface, because the active forces are aligned, an increase in the number of fast particles leads to a larger compression force pressing towards the bulk. Hence, the otherwise counterintuitive uptick in the bulk pressure at intermediate PeR (Fig. 2(a)(i)) may result from this increase in compression force. However, it remains unclear why there are more fast particles in the cluster in the intermediate and low PeR regimes. To search for answers, we next considered the spatial distribution of fast and slow particles.
As shown in Fig. 2(c), for large activity ratios, including the monodisperse case PeR = 1, the number density of fast and slow particles is nearly equal and increases across the interface from a low uniform value in the gas to a large uniform value in the bulk. For intermediate and low activity ratios, however, we see a split in how fast and slow particles are distributed. At the interface, the particle fraction radially transitions from majority slow particles nearest to the gas to majority fast nearest to the bulk, similar to active/passive MIPS45 and slow and fast ABPs assembling on a rigid wall.80 This observation can be understood by thinking of the dense cluster as a rigid boundary, on which fast and slow particles assemble. In the simplest case of a dilute suspension of fast and slow point particles, the density variations with distance from the rigid boundary (bulk surface), x, simplify to nS,F ≈ nS,F0 + E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2xPe(S,F)/σ), where n0 is the net (average) density of slow or fast particles in the gas phase, σ is the diameter of the particles and E is an integration constant determined by boundary conditions; see Appendix A for details. As a result, we expect the fast particles to concentrate on the interior part of the interface, next to the bulk phase and form a thinner boundary layer, compared to slow particles. This is in agreement with simulation results (Fig. 2(c)).
exp(−2xPe(S,F)/σ), where n0 is the net (average) density of slow or fast particles in the gas phase, σ is the diameter of the particles and E is an integration constant determined by boundary conditions; see Appendix A for details. As a result, we expect the fast particles to concentrate on the interior part of the interface, next to the bulk phase and form a thinner boundary layer, compared to slow particles. This is in agreement with simulation results (Fig. 2(c)).
A close inspection of simulation movies (Movies M1 and M8, ESI†) revealed that instead of two distinct radial layers, we actually observe microphase separated domains of fast and slow particles at the interface, which dynamically get integrated into the bulk (Fig. 3(a)). To quantify microphase separation as a function of activity ratio, we computed the pair probability density of observing slow–slow, slow–fast and fast–fast pairs as nearest neighbors in both the bulk and interface normalized by the average slow or fast particle fraction of the respective phase. In other words, the computed probability is not affected by the concentration difference between fast and slow particles. For a given activity pair ij where i and j can be either slow, S, or fast, F:
| Sij = χijn/χi | (7) |
Simulation results indicate that microphase separated domains start at the interface and move into the bulk (Fig. 3(a)). To test this, we developed a 1D coarse-grained model that solves for the time-dependent variations in the number density and average alignment of two different active species in ABP suspensions. The only ingredients of the model are thermal diffusion, activity, and interparticle forces; details are provided in Appendix A. Interestingly, the model predicted that during the early stages of MIPS, at intermediate activity ratios, the interface and bulk are primarily composed of fast particles. With time, the density of fast particles is reduced, while the density of slow particles is increased. This supports that microphase separation starts at the interface and gets incorporated into the bulk (Appendix A).
The model also correctly predicts the enrichment of fast particles in the dense phase at low and intermediate PeR; see the solid line in Fig. 2(b). However, the model cannot predict the observed non-monotonic variations of fast particle fraction with activity ratio. This discrepancy can be due to the multiple simplifying assumptions of the coarse-grained theory. For example, the model assumes 1D geometry, and uses models for particle pressure that are based on simulation data in large area fractions (Fig. 5). Thus, the predictions are expected to be less accurate at the interface and in the gas phase. See Appendix A for more details on the underlying assumptions of the model and the expressions for pressure. Interestingly, this minimal model can still predict the splitting of the number densities of slow and fast particles at the interface as observed in simulations. Fig. 2(c)(i) and (ii) compare the simulation data (circles) against the coarse-grained model (solid lines).
In monodisperse systems the active particles leave the interface when they orient away from the cluster. The net desorption rate is therefore proportional to the inverse of rotational diffusion timescale of the particles, the local number density of particles at the interface and the cluster perimeter: ktheoryoff = 2πrcσnI/τr, where rc is the cluster radius that includes the bulk phase and the interface. However, in simulations it has been shown that the desorption of a particle coincides with large groups of particles collectively escaping from the cluster via avalanche-like events.8,80,100,104–106 While the compression force from the aligned active forces at the interface balances the repulsive bulk interparticle forces on average during steady state, the compression force at the interface fluctuates both over space and time as interface particles reorient and desorb. We expect that in our active mixtures the presence of microphase-separated domains especially at the interface would lead to stronger fluctuations in the compression force (that holds the cluster together) and thus more severe avalanche events.
To test this hypothesis, we ran ABP simulations and computed the desorption rate of particles from the cluster at different activity ratios.
The avalanche parameter, κ, is defined as the ratio of the desorption rate from simulations, ksimd, to the desorption rate based on the theory:8κ = ksimoff/ktheoryoff, where larger values denote stronger avalanche events. We also computed the fluctuations of the average compression force at the interface, integrated over the thickness of the interface and over time, at different activity ratios defined by
 | (8) |
 | (9) |
Both the avalanche parameter and compression force heterogeneity were normalized by their corresponding values in the monodisperse system, in order to study the effect of activity ratio. We found that the avalanche parameter and the compression force fluctuations trace each other over the entire range of activity ratios, see Fig. 3(c). More importantly, both parameters closely follow the trend observed in the bulk (and interface) segregation parameter: they remain nearly unchanged at large activity ratios and show a sharp increase at intermediate and low activity ratios. Indeed, the avalanche events at intermediate and low Peclet ratios are so severe that up to half of the particles in the cluster escape each time (Fig. S4, Movies M1, M2, and M9, ESI†). In contrast, at high activity ratios fewer than 2% of the cluster particles escape during avalanche events (Fig. S4 and Movie M3, ESI†).
The steady state microstructure is determined by the balance of adsorption and desorption of each particle species. Thus, we expect the strong avalanche events at intermediate and low PeR (i.e. high desorption), to be balanced by enhanced adsorption. Indeed, simulations show that fast particles push and deposit slow particles from the gas onto the interface, a process we call active herding (Section S5 and Movie M8, ESI†). As they do so, the fast particles push through the slow-particle layer at the interface and assemble closer to the bulk boundary or move into the bulk phase.
To gain a deeper physical understanding of active herding, we simulated a dilute suspension of ABPs with two distinct activities that does not undergo MIPS. We modulated the total gas area fraction (ϕG = 0.05, 0.10, 0.15, 0.20, 0.25, and 0.3), the fast particle fraction (χFG = 0.2, 0.5, and 0.8), and activity ratio (0 ≤ PeR ≤ 1) and measured the velocity of each species. As shown in Fig. 3(d), the propulsion speed of fast particles is reduced (〈vF〉 < vFp) with increasing the total gas fraction, and remains unchanged with the activity ratio. We observe the same trend for slow particles in large activity ratio regime (PeR > 0.35). However, the behavior is reversed (〈vS〉 > vSp) in intermediate and low activity ratios (PeR ≤ 0.35) and this effect is amplified with increasing total gas area fraction. This is consistent with the observation that the fast and slow particles are more likely to collide and stay in contact for longer times at intermediate and low activity ratios (see Section S6, ESI†). This behavior is overall in line with the observed active herding process, where the fast particles in the gas phase help bring the slow particles to the cluster interface and incorporate them into the bulk phase. Note that the particle pressure expression used in the coarse-grained model is based on simulation data in dense area fractions (ϕ ≥ 0.6) and is not expected to accurately predict the interactions in the dilute and semi-dilute limit; thus, active herding that occurs at the interface and the gas phase cannot be accurately captured within this model. This may be the reason why the model cannot predict the observed non-monotonic variations of fast particle fraction between low and intermediate activity ratios (Fig. 2b). See Appendix A for a detailed discussion.
4 Conclusions
Based on these observations, we propose the following mechanism for the steady state of binary active mixtures at intermediate and low PeR, summarized in Fig. 4: MIPS begins with the nucleation of small clusters of fast particles. These clusters act as rigid boundaries on which slow and fast particles adsorb. Fast particles herd slow particles leading to enhanced adsorption of slow particles. As the activity ratio is decreased the cluster, including the interface and the bulk phase, becomes more enriched with fast particles, while the net density remains roughly unchanged with activity ratio. Having a larger fraction of fast particles at the interface leads to stronger compressive active forces at the interface and the nonmonotonic increase of pressure and other macroscopic quantities. The difference in activities leads to microphase separation of slow and fast particles at the interface, with fast particles assembling at the inner layer closer to the bulk, and the slow particles assembling at the outer layer of the interface closer to the gas phase. As more particles assemble around the existing interface, the cluster grows in size and the phase-separated slow and fast particles that were making up the interface at earlier times get integrated to the cluster. The microphase-separated domains at the interface lead to larger fluctuations in the compression force which in turn leads to more severe avalanche events. The process repeats with the re-adsorption of fast and slow particles from the gas onto the interface through active herding. | ||
| Fig. 4 Schematic of the proposed mechanism showing the process of active herding, microphase separation, and enhanced avalanche events. | ||
We have shown that our approach of continuously varying the activities of two particle species revealed the existence of three regimes of Péclet ratio, previously unknown. The regimes that emerge are robust and demonstrate several distinct structural and dynamical features on a microscopic and a macroscopic scale. Thus, the behavior of mixtures is not a simple interpolation between the active monodisperse case and active/passive; rather there is a richness of behavior in between the extremes. Based on our results, we proposed a mechanism that describes the dynamic steady-state of the system at low and intermediate PeR through a series of steps that include interesting nonequilibrium phenomena including active herding, microphase separation, active force fluctuations and strong avalanche events at the interface. Finally, we emphasize the role of the interface, which compartmentalizes the bulk, acting like a semi-permeable membrane that selectively filters out slow particles and allows fast particles in. In other words, the interior structure of the cluster is modulated by the structure and mechanics of the interface.
Finally, we note that the current study neglects the phoretic and hydrodynamic interactions between the particles. These interactions are present in many synthetic and biological systems, such as suspensions of Janus particles and bacterial suspensions and are expected to lead to qualitative changes in the phase diagram as well as the composition of each phase. Detailed simulations that can directly model these interactions are needed to study their effects on the structure and dynamics of binary ABPs with distinct activities.
Conflicts of interest
There are no conflicts to declare.Data availability
The simulation submission and data analysis scripts of this article are available in the GitHub repository at https://github.com/njlauersdorf/ABPs.Appendices
A: 1D coarse-grained model for active Brownian particles
We follow the derivations of Saintillan & Shelley,107 and Brady and co-workers108,109 and write down the zeroth, first and second moments of Smoluchowski equation for probability density of ABPs that correspond to the concentration field c, polar order parameter n and the nematic order parameter, Q, which are defined as | (10) |
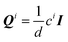 , where I is the identity tensor and d is the system's dimension. Using these expressions and after integrating Smoluchowski equation, we obtain the following conservation equations for the average concentration and polar order parameter.
, where I is the identity tensor and d is the system's dimension. Using these expressions and after integrating Smoluchowski equation, we obtain the following conservation equations for the average concentration and polar order parameter. | (11a) |
 | (11b) |
We use the following scales to non-dimensionalize the system of equations in 2D:
![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) i and
i and ![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) i are the area fraction, dimensionless mobility, and pressure of the ith phase.
i are the area fraction, dimensionless mobility, and pressure of the ith phase.
Slow and fast particles in our system have the same size and isolated particle mobility. We assume that the mobility of slow and fast particles is independent of activity and only a function of the local total area fraction: ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) F =
F = ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) S =
S = ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) (ϕ), where ϕ = ϕF + ϕS is the total area fraction at a given point, and S and F stand for slow and fast phase. Furthermore, we apply a mixture law for computing the pressure in each phase
(ϕ), where ϕ = ϕF + ϕS is the total area fraction at a given point, and S and F stand for slow and fast phase. Furthermore, we apply a mixture law for computing the pressure in each phase ![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) i = χi
i = χi![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) with χi = (ϕi/ϕ). Taking Dt = a2/τr, and substituting these expressions yields the following dimensionless equations:
with χi = (ϕi/ϕ). Taking Dt = a2/τr, and substituting these expressions yields the following dimensionless equations:
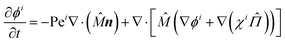 | (12a) |
 | (12b) |
The dimensionless mobility and pressure depend only on the local total area fraction, which determines the strength of the many-body inter-particle interactions. Modeling these many-body interactions within the Smoluchowski field theory requires solving for pair distribution functions and using those to compute the ensemble average mobility and stress.110 The purpose of our coarse-grained model is to give further intuition about phase-separation at the cluster interface and the enrichment of the fast particles in the cluster. Thus, instead of using the mentioned systematic approach,110 we use simplified scaling relationships that are confirmed by simulations and theory to approximate these interactions. Furthermore, for simplicity, we solve eqn (12) in 1D:
 | (13a) |
 | (13b) |
We use the computed values of interparticle pressure inside the cluster phase in our particle simulations (shown in Fig. 5) as approximations of inter-particle pressure at larger area fractions (ϕ ≥ 0.6). The data can be fitted very well with the polynomial
![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) ≈ 0.01πa2(1 + ϕ)12.144. ≈ 0.01πa2(1 + ϕ)12.144. |
Note, however, that this expression is only accurate at large area fractions in the bulk phase, where particles are almost trapped and do not undergo large displacements. In this regime, the computed pressure is only a function of the net area fraction and independent of the activity ratio and the relative composition of the slow and fast particles. This approximation becomes less accurate at lower area fractions, corresponding to the interface and the gas phase. In this regime the dynamics of slow and fast particles and hence the stress generated by their interactions are dependent on their relative activities and area fractions. This is clearly shown in the simulations of the dilute suspensions with two activities, shown in Fig. 3(d) in the main text. We see that at low activity ratios the fast particles increase the average speed of slow particles, which we refer to as active herding in the main text. The model in its current form cannot accurately account for active herding. Meanwhile, dilute theories based on Smoluchowski equation can be used to derive expressions for pressure in the dilute regime.111 These theories are for hard-sphere interparticle interactions and need to be modified to include soft interaction potentials, used here. One can, then, construct the pressure approximation with the correct asymptotic behavior in both dilute and dense limits. We have not pursued this here.
Next, we present our approximate model for particle mobility. In the dilute limit we have ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) (ϕ ≪ 1) ≈ 1 − 2ϕ for hard-sphere suspensions. This expression produces negative numbers for ϕ > 0.50. To circumvent this and expand the expression to larger area fractions, we approximate the resistance (
(ϕ ≪ 1) ≈ 1 − 2ϕ for hard-sphere suspensions. This expression produces negative numbers for ϕ > 0.50. To circumvent this and expand the expression to larger area fractions, we approximate the resistance (![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) −1) by including the first four terms that appear in the geometric series that correspond to (1 − 2ϕ)−1:
−1) by including the first four terms that appear in the geometric series that correspond to (1 − 2ϕ)−1:
![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) −1 ≈ 1 + 2ϕ + 4ϕ2 + 8ϕ3. −1 ≈ 1 + 2ϕ + 4ϕ2 + 8ϕ3. |
Note that this approximation for mobility assumes hard-sphere interparticle forces, and so the effective size of the particle remains unchanged with activity. However, in our simulations the particles interact through the soft Weeks–Chandler potential (see eqn (3) in the main text). Thus, the effective size of the particle is reduced with increasing activity, which is why the area fractions in the cluster can go as high as ϕB = 1.6 (Fig. 5). A more accurate expression for mobility would also include net activity as a parameter. Obtaining these approximations require extending the kinetic theories from hard-sphere to soft particles and also performing appropriate particle simulations; these fall outside of the scope of this work.
Finally, for numerical stability we added fourth-order derivatives  to eqn (13a) and (13b), respectively. We chose
to eqn (13a) and (13b), respectively. We chose  , where L the size of the 1D simulations: x ∈ [−L,L]. Reducing these values by another order of magnitude did not change the steady-state predictions, but also produced several smaller phase segregated domains. Resolving the dynamics of these domains requires smaller time-steps and finer discretizations; the total time needed to reach steady-state also increases, which is effectively similar to increasing the box size in discrete simulations. This completes the formulation of the coarse-grained model. We used a fifth-order implicit–explicit finite difference method to solve the governing nonlinear equations in a 1D periodic domain. We performed convergence studies to ensure the numerical accuracy of our solutions. The results presented here (Fig. 6) and in the main text were obtained using N = 200 equally spaced discretization points.
, where L the size of the 1D simulations: x ∈ [−L,L]. Reducing these values by another order of magnitude did not change the steady-state predictions, but also produced several smaller phase segregated domains. Resolving the dynamics of these domains requires smaller time-steps and finer discretizations; the total time needed to reach steady-state also increases, which is effectively similar to increasing the box size in discrete simulations. This completes the formulation of the coarse-grained model. We used a fifth-order implicit–explicit finite difference method to solve the governing nonlinear equations in a 1D periodic domain. We performed convergence studies to ensure the numerical accuracy of our solutions. The results presented here (Fig. 6) and in the main text were obtained using N = 200 equally spaced discretization points.
![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) ≈ 1 and
≈ 1 and ![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) → 0. At steady-state the equations simplify to
→ 0. At steady-state the equations simplify to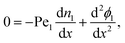 | (14a) |
 | (14b) |
 | (14c) |
 | (14d) |
So we get
 | (15) |
Substituting for n1 and n2 in eqn (14c) and (14d) gives
 | (16) |
ϕi = Ei![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λix) + Fi exp(−λix) + Fi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(λix) + Gi, exp(λix) + Gi, | (17) |
We can rewrite eqn (17) in terms of ϕ0:
ϕi = ϕ(0,i) − aPei−1 + Ei![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Peix). exp(−Peix). | (18) |
For Pei ≫ 1 we have aPei−1 → 0, which yields ϕi ≈ ϕ(0,i) + Ei![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Peix). Hence, theory dilute theory predicts the formation of a boundary layer with thickness Pei−1 at the interface, recalling that Pei = PeS for the slow particle phase and Pei = PeF for the fast particle phase. The value of Ei may also be determined by setting a boundary condition for n at the interface, but its exact value is not important for the physical analysis discussed in the main text.
exp(−Peix). Hence, theory dilute theory predicts the formation of a boundary layer with thickness Pei−1 at the interface, recalling that Pei = PeS for the slow particle phase and Pei = PeF for the fast particle phase. The value of Ei may also be determined by setting a boundary condition for n at the interface, but its exact value is not important for the physical analysis discussed in the main text.
Acknowledgements
N. J. L. acknowledges support via the Department of Defense (DoD) National Defense Science and Engineering Graduate (NDSEG) Research Fellowship. D. K. acknowledges a Department of Energy (DOE) grant DE-SC0023001.Notes and references
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- G. Gompper, R. G. Winkler, T. Speck, A. Solon, C. Nardini, F. Peruani, H. Löwen, R. Golestanian, U. B. Kaupp, L. Alvarez, T. K. Rboe, E. Lauga, W. C. Poon, A. Desimone, S. Muintildeos-Landin, A. Fischer, N. A. Söker, F. Cichos, R. Kapral, P. Gaspard, M. Ripoll, F. Sagues, A. Doostmohammadi, J. M. Yeomans, I. S. Aranson, C. Bechinger, H. Stark, C. K. Hemelrijk, F. J. Nedelec, T. Sarkar, T. Aryaksama, M. Lacroix, G. Duclos, V. Yashunsky, P. Silberzan, M. Arroyo and S. Kale, J. Phys.: Condens. Matter, 2020, 32, 1–67 CrossRef PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- J. O'Byrne, Y. Kafri, J. Tailleur and F. van Wijland, Nat. Rev. Phys., 2022, 4, 167–183 CrossRef.
- J. L. Moran and J. D. Posner, Annu. Rev. Fluid Mech., 2017, 49, 511–540 CrossRef.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 1–5 CrossRef PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 1–5 CrossRef PubMed.
- J. Palacci, S. Sacanna, S. Kim, G. Yi, D. J. Pine and P. M. Chaikin, Philos. Trans. R. Soc., A, 2014, 1–19 Search PubMed.
- T. Speck, J. Bialké, A. M. Menzel and H. Löwen, Phys. Rev. Lett., 2014, 112, 1–5 CrossRef.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 1–5 CrossRef PubMed.
- T. Bäuerle, A. Fischer, T. Speck and C. Bechinger, Nat. Commun., 2018, 9, 1–8 CrossRef PubMed.
- A. Zöttl and H. Stark, Annu. Rev. Condens. Matter Phys., 2023, 14, 109–127 CrossRef.
- N. Sharifi-Mood, A. Mozaffari and U. M. Córdova-Figueroa, J. Fluid Mech., 2016, 798, 910–954 CrossRef.
- O. Pohl and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 1–11 CrossRef CAS PubMed.
- M. Wagner, S. Roca-Bonet and M. Ripoll, Eur. Phys. J. E:Soft Matter Biol. Phys., 2021, 44, 1–11 CrossRef PubMed.
- T. Ishikawa, J. R.Soc., Interface, 2009, 6, 815–834 CrossRef PubMed.
- N. Yoshinaga and T. B. Liverpool, Phys. Rev. E, 2017, 96, 020603 CrossRef PubMed.
- M. Theers, E. Westphal, K. Qi, R. G. Winkler and G. Gompper, Soft Matter, 2018, 14, 8590–8603 RSC.
- X. Yang, M. L. Manning and M. C. Marchetti, Soft Matter, 2014, 10, 6477–6484 RSC.
- S. R. McCandlish, A. Baskaran and M. F. Hagan, Soft Matter, 2012, 8, 2527–2534 RSC.
- N. H. P. Nguyen, D. Klotsa, M. Engel and S. C. Glotzer, Phys. Rev. Lett., 2014, 112, 1–5 Search PubMed.
- S. E. Moran, P. W. Schönhöfer and S. C. Glotzer, New J. Phys., 2022, 24, 063007 CrossRef.
- J. Bartnick, M. Heinen, A. V. Ivlev and H. Löwen, J. Phys.: Condens. Matter, 2016, 28, 025102 CrossRef PubMed.
- O. Chepizhko and F. Peruani, Phys. Rev. Lett., 2013, 111, 1–5 CrossRef PubMed.
- J. Chen, X. Lei, Y. Xiang, M. Duan, X. Peng and H. P. Zhang, Phys. Rev. Lett., 2024, 132, 118301 CrossRef CAS PubMed.
- J. Agudo-Canalejo and R. Golestanian, Phys. Rev. Lett., 2019, 123, 18101 CrossRef CAS PubMed.
- Y. Duan, J. Agudo-Canalejo, R. Golestanian and B. Mahault, Phys. Rev. Lett., 2023, 131, 148301 CrossRef CAS PubMed.
- A. Dinelli, J. O’Byrne, A. Curatolo, Y. Zhao, P. Sollich and J. Tailleur, Nat. Commun., 2023, 14, 1–10 Search PubMed.
- H. Alston, L. Cocconi and T. Bertrand, Phys. Rev. Lett., 2023, 131, 258301 CrossRef CAS PubMed.
- A. V. Ivlev, J. Bartnick, M. Heinen, C. R. Du, V. Nosenko and H. Löwen, Phys. Rev. X, 2015, 5, 1–10 CAS.
- S. Saha, J. Agudo-Canalejo and R. Golestanian, Phys. Rev. X, 2020, 10, 41009 CAS.
- D. Levis and B. Liebchen, Phys. Rev. E, 2019, 100, 1–8 CrossRef PubMed.
- K. Yeo, E. Lushi and P. M. Vlahovska, Phys. Rev. Lett., 2015, 114, 1–5 Search PubMed.
- D. Bárdfalvy, S. Anjum, C. Nardini, A. Morozov and J. Stenhammar, Phys. Rev. Lett., 2020, 125, 18003 CrossRef PubMed.
- B. Q. Ai, Z. G. Shao and W. R. Zhong, Soft Matter, 2018, 14, 4388–4395 RSC.
- S. J. Kole, G. P. Alexander, S. Ramaswamy and A. Maitra, Phys. Rev. Lett., 2021, 126, 248001 CrossRef CAS PubMed.
- L. Caprini and H. Löwen, Phys. Rev. Lett., 2023, 130, 148202 CrossRef CAS PubMed.
- P. Arora, A. K. Sood and R. Ganapathy, Sci. Adv., 2021, 7, 1–7 Search PubMed.
- J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2015, 114, 1–5 CrossRef PubMed.
- S. C. Takatori and J. F. Brady, Soft Matter, 2015, 11, 7920–7931 RSC.
- R. Wittkowski, J. Stenhammar and M. E. Cates, New J. Phys., 2017, 19, 1–16 CrossRef.
- P. Dolai, A. Simha and S. Mishra, Soft Matter, 2018, 14, 6137–6145 RSC.
- B. V. D. Meer, V. Prymidis, M. Dijkstra and L. Filion, J. Chem. Phys., 2020, 152, 144901 CrossRef PubMed.
- A. Wysocki, R. G. Winkler and G. Gompper, New J. Phys., 2016, 18, 123030 CrossRef.
- D. R. Rodriguez, F. Alarcon, R. Martinez, J. Ramírez and C. Valeriani, Soft Matter, 2020, 16, 1162–1169 RSC.
- Y. Du, H. Jiang and Z. Hou, Soft Matter, 2019, 15, 2020–2031 RSC.
- G. H. Xu and B. Q. Ai, Soft Matter, 2021, 17, 7124–7132 RSC.
- B. Q. Ai, B. Y. Zhou and X. M. Zhang, Soft Matter, 2020, 16, 4710–4717 RSC.
- D. F. Hinz, A. Panchenko, T. Y. Kim and E. Fried, Soft Matter, 2014, 10, 9082–9089 RSC.
- R. C. Maloney, G. J. Liao, S. H. Klapp and C. K. Hall, Soft Matter, 2020, 16, 3779–3791 RSC.
- S. Gokhale, J. Li, A. Solon, J. Gore and N. Fakhri, Phys. Rev. E, 2022, 105, 054605 CrossRef CAS PubMed.
- D. Grober, I. Palaia, M. C. Uçar, E. Hannezo, A. Šarić and J. Palacci, Nat. Phys., 2023, 19, 1680–1688 Search PubMed.
- P. Kushwaha, V. Semwal, S. Maity, S. Mishra and V. Chikkadi, Phys. Rev. E, 2023, 108, 034603 CrossRef CAS PubMed.
- A. Morozov and D. Marenduzzo, Soft Matter, 2014, 10, 2748–2758 RSC.
- D. O. Pushkin and J. M. Yeomans, Phys. Rev. Lett., 2013, 111, 1–5 CrossRef PubMed.
- Z. Lin, J. L. Thiffeault and S. Childress, J. Fluid Mech., 2011, 669, 167–177 CrossRef.
- T. Ishikawa, J. T. Locsei and T. J. Pedley, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 82, 1–15 CrossRef PubMed.
- P. T. Underhill, J. P. Hernandez-Ortiz and M. D. Graham, Phys. Rev. Lett., 2008, 100, 1–4 CrossRef PubMed.
- Z. Preisler and M. Dijkstra, Soft Matter, 2016, 12, 6043–6048 RSC.
- Y. Wang, Z. Shen, Y. Xia, G. Feng and W. Tian, Chin. Phys. B, 2020, 29, 053103 CrossRef.
- K. Cheng, P. Liu, M. Yang and M. Hou, Soft Matter, 2022, 18, 2541–2548 RSC.
- J. Shea, G. Jung and F. Schmid, Soft Matter, 2024, 20, 1767–1785 RSC.
- R. S. Yadav, S. Sharma, R. Metzler and R. Chakrabarti, Soft Matter, 2024, 20, 3910–3922 RSC.
- C. Valeriani, M. Li, J. Novosel, J. Arlt and D. Marenduzzo, Soft Matter, 2011, 7, 5228–5238 RSC.
- K. Goswami and R. Metzler, Soft Matter, 2023, 19, 8802–8819 RSC.
- D. M. van Roon, G. Volpe, M. M. T. da Gama and N. A. Araújo, Soft Matter, 2022, 18, 6899–6906 RSC.
- S. Wu, J.-X. Li and Q.-L. Lei, Soft Matter, 2022, 18, 9263–9272 RSC.
- C. Tiwari and S. P. Singh, Soft Matter, 2024, 20, 4816–4826 RSC.
- J. Xing Pan, H. Wei, M. Jiao Qi, H. Fang Wang, J. Jun Zhang, W. de Tian and K. Chen, Soft Matter, 2020, 16, 5545–5551 RSC.
- S. Das and R. Chelakkot, Soft Matter, 2020, 16, 7250–7255 RSC.
- P. Forgács, A. Libál, C. Reichhardt and C. J. Reichhardt, Phys. Rev. E, 2021, 104, 1–11 CrossRef PubMed.
- N. Nikola, A. P. Solon, Y. Kafri, M. Kardar, J. Tailleur and R. Voituriez, Phys. Rev. Lett., 2016, 117, 098001 CrossRef PubMed.
- R. Martinez, F. Alarcon, J. L. Aragones and C. Valeriani, Soft Matter, 2020, 16, 4739–4745 RSC.
- T. Kolb, T. Kolb and D. Klotsa, Soft Matter, 2020, 16, 1967–1978 RSC.
- P. D. Castro, F. M. Rocha, S. Diles, R. Soto and P. Sollich, Soft Matter, 2021, 17, 9926–9936 RSC.
- P. de Castro, S. Diles, R. Soto and P. Sollich, Soft Matter, 2021, 17, 2050–2061 RSC.
- M. Rojas-Vega, P. de Castro and R. Soto, Eur. Phys. J. E:Soft Matter Biol. Phys., 2023, 46, 1–11 CrossRef PubMed.
- D. Debnath, P. K. Ghosh, V. R. Misko, Y. Li, F. Marchesoni and F. Nori, Nanoscale, 2020, 12, 9717–9726 RSC.
- M. Rojas-Vega, P. D. Castro and R. Soto, Phys. Rev. E, 2023, 107, 14608 CrossRef CAS PubMed.
- L. G. Wilson, V. A. Martinez, J. Schwarz-Linek, J. Tailleur, G. Bryant, P. N. Pusey and W. C. Poon, Phys. Rev. Lett., 2011, 106, 7–10 Search PubMed.
- D. T. Chen, A. W. Lau, L. A. Hough, M. F. Islam, M. Goulian, T. C. Lubensky and A. G. Yodh, Phys. Rev. Lett., 2007, 99, 1–4 Search PubMed.
- X. L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017–3020 CrossRef CAS PubMed.
- G. L. Miño, J. Dunstan, A. Rousselet, E. Clément and R. Soto, J. Fluid Mech., 2013, 729, 423–444 CrossRef.
- L. Restrepo-Pérez, L. Soler, C. S. Martínez-Cisneros, S. Sánchez and O. G. Schmidt, Lab Chip, 2014, 14, 1515–1518 RSC.
- O. Granek, Y. Kafri and J. Tailleur, Phys. Rev. Lett., 2022, 129, 38001 CrossRef CAS PubMed.
- Y. Baek, A. P. Solon, X. Xu, N. Nikola and Y. Kafri, Phys. Rev. Lett., 2018, 120, 58002 CrossRef CAS PubMed.
- A. Gough, A. Stern, J. Maier, T. Lezon, T.-Y. Shun, C. Chennubhotla, M. Haney, S. Schurdak and D. Taylor, 2015 IEEE Summer Topicals Meeting Series, SUM 2015, 2018, vol. 10, pp. 1–13.
- D. J. Knight and K. J. Girling, Lancet, 2003, 361, 1831 CrossRef CAS PubMed.
- K. L. Heck and T. A. Thoman, J. Exp. Mar. Biol. Ecol., 1981, 53, 125–134 CrossRef.
- P. P. Klamser, L. Gómez-Nava, T. Landgraf, J. W. Jolles, D. Bierbach and P. Romanczuk, Front. Phys., 2021, 9, 1–11 Search PubMed.
- M. Forget, S. Adiba, L. G. Brunnet and S. D. Monte, Front. Ecol. Evol., 2022, 10, 1–18 Search PubMed.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 105, 1–4 CrossRef PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–939 CrossRef CAS PubMed.
- S. Ebbens, R. A. Jones, A. J. Ryan, R. Golestanian and J. R. Howse, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 82, 6–9 CrossRef PubMed.
- T. C. Lee, M. Alarcón-Correa, C. Miksch, K. Hahn, J. G. Gibbs and P. Fischer, Nano Lett., 2014, 14, 2407–2412 CrossRef CAS PubMed.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363 CrossRef CAS.
- J. Glaser, T. D. Nguyen, J. A. Anderson, P. Lui, F. Spiga, J. A. Millan, D. C. Morse and S. C. Glotzer, Comput. Phys. Commun., 2015, 192, 97–107 CrossRef CAS.
- J. A. Anderson, C. D. Lorenz and A. Travesset, J. Comput. Phys., 2008, 227(10), 5342–5359 CrossRef.
- N. Lauersdorf, T. Kolb, M. Moradi, E. Nazockdast and D. Klotsa, Soft Matter, 2021, 17, 6337–6351 RSC.
- A. K. Omar, Z. G. Wang and J. F. Brady, Phys. Rev. E, 2020, 101, 12604 CrossRef CAS PubMed.
- A. K. Omar, Y. Wu, Z. G. Wang and J. F. Brady, ACS Nano, 2019, 13, 560–572 CrossRef CAS PubMed.
- N. K. Agrawal and P. S. Mahapatra, Phys. Rev. E, 2021, 104, 1–11 Search PubMed.
- R. Soto and R. Golestanian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 1–7 CrossRef PubMed.
- C. J. Reichhardt and C. Reichhardt, New J. Phys., 2018, 20, 1–9 CrossRef.
- C. Reichhardt and C. J. Reichhardt, Phys. Rev. E, 2018, 97, 1–13 CrossRef PubMed.
- D. Saintillan and M. J. Shelley, Theory of Active Suspensions, in Complex Fluids in Biological Systems: Experiment, Theory, and Computation, ed. S. E. Spagnolie, Springer, New York, NY, 2015, pp. 319–355 DOI:10.1007/978-1-4939-2065-5_9.
- W. Yan and J. F. Brady, J. Fluid Mech., 2015, 785, R1.1–R1.11 Search PubMed.
- A. K. Omar, H. Row, S. A. Mallory and J. F. Brady, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, 1–10 CrossRef PubMed.
- M. Te Vrugt, J. Bickmann and R. Wittkowski, J. Phys.: Condens. Matter, 2023, 35, 313001 CrossRef PubMed.
- W. Yan and J. F. Brady, Soft Matter, 2015, 11, 6235–6244 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details of simulations, analytical routines, and supporting figures (.png). See DOI: https://doi.org/10.1039/d4sm01290a |
| This journal is © The Royal Society of Chemistry 2025 |