Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Increased water presence in phospholipid fluid bilayers upon addition of lysolipids†
Fernanda
Alvarado Galindo
 *ab,
Joachim
Venzmer
c,
Najet
Mahmoudi
*ab,
Joachim
Venzmer
c,
Najet
Mahmoudi
 d,
Michael
Gradzielski
d,
Michael
Gradzielski
 b and
Ingo
Hoffmann
b and
Ingo
Hoffmann
 *a
*a
aInstitut Max von Laue-Paul Langevin (ILL), F-38042 Grenoble Cedex 9, France. E-mail: hoffmann@ill.fr
bStranski-Laboratorium für Physikalische und Theoretische Chemie, Institut für Chemie, Technische Universität Berlin, Straße des 17. Juni 124, Sekr. TC 7, D-10623 Berlin, Germany
cEvonik Operations GmbH, Essen, Germany
dRutherford Appleton Laboratory, ISIS facility, Science and Technology Facilities Council, Harwell Science & Innovation Campus, OX11 0QX, Didcot, UK
First published on 26th March 2025
Abstract
In spite of the numerous studies dealing with the interaction between lipid membranes and surfactants at subsolubilizing membrane concentrations, quantifying detailed bilayer structure, as for instance pore formation, on phospholipid bilayers upon addition of single chain lipids continues to be a challenge. Herein, we analyze the effects of lysophosphatidylcholine (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 LPC or lysolipid) on soybean phosphatidylcholine (SPC) extruded liposomes, where vesicles containing additional LPC exhibit approximately a 10% reduction in size as indicated by dynamic light scattering experiments. Most importantly, we benefit from the non-perturbing nature of small-angle neutron scattering (SANS) measurements to determine the degree of water incorporation presumably through the surfactant stabilized pores along the fluid bilayers. Model-free analysis of SANS curves reveals that the membrane part of the pure SPC vesicles contain 3.3% v of water. As the lysolipid is added to the dispersion, the volume fraction of water counted into the lipid membrane (
1 LPC or lysolipid) on soybean phosphatidylcholine (SPC) extruded liposomes, where vesicles containing additional LPC exhibit approximately a 10% reduction in size as indicated by dynamic light scattering experiments. Most importantly, we benefit from the non-perturbing nature of small-angle neutron scattering (SANS) measurements to determine the degree of water incorporation presumably through the surfactant stabilized pores along the fluid bilayers. Model-free analysis of SANS curves reveals that the membrane part of the pure SPC vesicles contain 3.3% v of water. As the lysolipid is added to the dispersion, the volume fraction of water counted into the lipid membrane ( ) increases to 15–20%. Finally, assuming
) increases to 15–20%. Finally, assuming 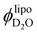 to be equivalent to the volume fraction of pores within the bilayers we estimate the pore size and density.
to be equivalent to the volume fraction of pores within the bilayers we estimate the pore size and density.
1 Introduction
Phospholipids (PLs) self-assemble when dispersed in an aqueous solution and form closed concentric bilayers commonly known as liposomes. Thanks to particle morphology and ability to encapsulate hydrophobic, hydrophilic, or amphiphilic molecules, PL liposomes have become an established delivery form in pharmacology and cosmetics.1–3 The enveloped active ingredients can be released under pre-stated conditions,4 for which membrane properties become an important aspect for industrial formulations where a balance between excellent barrier properties and extremely permeable liposomes has to be met.5Membrane permeation can be altered by external factors (temperature, pH, light, etc.) or by lipid composition. For the latter, it is known that adding surfactants to liposomal dispersions disrupts the membrane since they alter the bilayer organization by inducing curvature stress.
Thus, surfactant-membrane interactions have been an intensive topic of study over the years.6,7 Surfactants partition into the lipid bilayer from the bulk solution,8 starting from concentrations below their critical micellar concentration (CMC) (4–8.3 μM for lysolipids9). Subsequent alterations to the bilayer depend on the properties of the amphiphile and the speed of flip-flop motion between the inner and outer monolayers. This motion is classified into “slow” and “fast” based on the exchange rate and time needed for membrane solubilization.10 For example, lysophosphatidylcholines (LPCs) are considered “slow” surfactants as their bulky headgroup inhibits fast exchange between the monolayers.11 SDS (another “slow” agent) has a flip-flop rate of minutes to hours at room temperature, whereas “fast” amphiphiles have a flipping rate on the order of 0.5 s.12
When surfactant molecules are present in both the inner and outer monolayers, they may cause a discontinuity in the bilayer, forming transient holes (or pores) along the liposome surface.13 Such an event is possible if the amphiphiles cover the pore edges and prevent exposure of the hydrophobic bilayer core to the aqueous environment. Pore formation has been evidenced by results from optical microscopy,14,15 kinetic measurements16 and molecular dynamics (MD) simulations.12
Consequently, the barrier properties of the bilayer are reduced, resulting in increased membrane permeability upon addition of a surfactant, as observed through fluorescence,4,17 glucose,18 and ion exchange19,20 studies. The increased permeability observed through release assays has also been correlated to a decrease in the bending modulus of the membrane.21–24 Thus, it is clear that fluid PL bilayers will suffer gradual structural changes in the presence of a lysolipid before suffering disintegration under formation of mixed micelles (starting at 30% mol lysolipid, although an exact number depends on the precise molecular composition20,25).
Here, we are interested in the changes on soybean phosphatidylcholine (SPC) fluid bilayers when prepared with LPC at subsolubilizing concentrations. Our study involves systematically introducing LPC to a high-quality SPC mixture (≥94% PC) containing no more than 3% LPC. First, we employ light and small-angle neutron scattering (SANS) as non-perturbing techniques that capture the changes in particle size and bilayer morphology, respectively. In SANS experiments, we benefit from the difference in scattering length density between hydrogen and deuterium to examine our systems and estimate the volume fraction of water incorporated into the liposome membrane by model-free analysis of the curves, providing valuable information about the incorporation of water in the membrane at different LPC concentrations.
2 Materials and methods
2.1 Materials
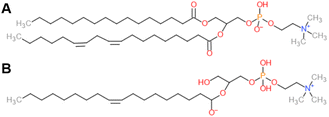
Soybean phosphatidylcholine (SPC), Lipoid S100, at >94% phosphatidylcholine (PC) was kindly supplied by Lipoid, France. We assume a scattering length density of 0.32 × 1010 cm−2 for SPC, based on an average composition C42H80NO8P (Fig. 1) and a density of 1.01 g cm−3.26 For 1-oleoyl-2-hydroxy-sn-glycero-3-phosphocholine (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 LysoPC, Avanti, c) at PC > 99%, we assume a SLD of 0.39 × 1010 cm−2 and a density of 1.08 g mL−1. LPC density was calculated assuming a lysolipid volume of ∼800 Å3, considering reported volumes of DOPC and PC headgroups of ∼1300 Å3 and ∼ 300 Å3, respectively.27 LPC and deuterium oxide (D2O, 99.9%) were purchased from Sigma Aldrich, France. Lipids were used as received.
1 LysoPC, Avanti, c) at PC > 99%, we assume a SLD of 0.39 × 1010 cm−2 and a density of 1.08 g mL−1. LPC density was calculated assuming a lysolipid volume of ∼800 Å3, considering reported volumes of DOPC and PC headgroups of ∼1300 Å3 and ∼ 300 Å3, respectively.27 LPC and deuterium oxide (D2O, 99.9%) were purchased from Sigma Aldrich, France. Lipids were used as received.
2.2 Preparation of phospholipid liposomes
Liposomes containing SPC and SPC-lysophosphatidylcholine (LPC) were obtained by mixing the lipids in aqueous solution with a magnetic stirrer and extruding the lipid dispersion at least 21 times through a polycarbonate membrane with a mini extruder (Avanti Polar Lipids, United States) at room temperature (RT). SPC content was fixed at 0.5% w and either 0.01% w, 0.02% w, or 0.05% w LPC was added to the mixture. Samples for small-angle neutron scattering (SANS) experiments were dispersed in heavy water (D2O) and extruded for 21 times with a 200 nm and a 100 nm membrane, each (total of 42 times), as to reduce particle size to the accessible q-range in SANS.2.3 Light scattering
Dynamic (DLS) and static light scattering (SLS) were realized using an ALV/CGS-3 Compact Goniometer system with a HeNe Laser (wavelength λ = 632.8 nm) at a temperature T = 25 °C. Intensity autocorrelation functions g(2) were recorded using an ALV7004/FAST real time multiple tau digital correlator. The scattering angle was set to 90°. All measurements were repeated 5 times and averaged with an acquisition time of 30 s for each individual measurement. SLS experiments were performed at different angles to access a q-range of 0.0009 1 Å−1 < q < 0.0024 1 Å−1, where q is the magnitude of the scattering vector q = (4πns/λ)sin(θ/2) and ns the refractive index of the solvent. Forward scattering (I0) can be calculated using the Guinier approximation (eqn (SI 1), ESI†), whereas the mass-average molecular weight is obtained by inputting I0 in eqn (SI 2), ESI.†2.4 Small-angle neutron scattering (SANS)
SANS experiments were carried out on the Sans2d diffractometer at the ISIS Pulsed Neutron Source (STFC Rutherford Appleton Laboratory, Didcot, U.K.). Samples were loaded in 2 mm cuvettes and placed in the sample holder under temperature control of 25 °C. A q-range of 0.0023–0.99 1 Å−1 was accessible utilizing an incident wavelength range of 1.75–14.4 Å and merging data recorded on two detectors positioned 8 m and 4 m away from the sample. Data reduction including correction for background, empty cell scattering, transmissions, detector efficiency, data radial averaging and transformation to absolute intensities was done using the software Mantid.28 To convert to absolute scale a solid blend of hydrogenated and perdeuterated polystyrene sample was used.For a system with two components and sharp interfaces the scattering invariant
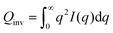 | (1) |
| Qinv = 2π2ϕ1ϕ2ΔSLD2, | (2) |
| ϕlipo = ϕSPC + ϕLPC + βϕwat | (3) |
| ϕsolvent = (1 − β)ϕwat, | (4) |
 | (5) |
If no solvent were to penetrate the liposome phase, β in eqn (3)–(5) would equal zero and the theoretical invariant (Qtheoinv) was calculated as such.29 However, if water was to penetrate the membrane and β > 0, then for small β, ϕlipo increases linearly, while ΔSLDlipo decreases linearly and as the latter enters eqn (2) quadratically, the overall value of Qinv decreases. See Fig. SI3 and eqn (SI 12) (ESI†) for the graphic and analytical relation between Qinv and β.
3 Results and discussion
3.1 Light scattering
DLS measurements were performed on SPC and SPC/LPC liposomes extruded with a 100 nm membrane. The hydrodynamic radius (Rh) was calculated from the Stokes–Einstein relation with the relaxation rate obtained from cumulant analysis of the correlation curves.Comparing the Rhvs. LPC content in Fig. 2, we observe that samples with added lysolipid have a smaller particle size as the Rh of SPC liposomes is ∼60 nm and reduces to ∼55 nm for the three studied SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC ratios (98
LPC ratios (98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 96
2, 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 91
4, 91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9). In addition, the polydispersity index (PDI) increases from 0.03 to 0.1, so the systems have a low, yet increasing, polydispersity (Table 1). The likely explanation for the reduction of the size is the reduction of the membrane rigidity, as addition of LPC has been reported to reduce the bending modulus by a factor 4.21 The softer membranes are then more easily deformed during extrusion, leading to formation of smaller vesicles. For a comparison, it might be noted that subsequent addition of lysolipids leads to almost no size change for liposomes formed by the rehydration or sonication processes.30
9). In addition, the polydispersity index (PDI) increases from 0.03 to 0.1, so the systems have a low, yet increasing, polydispersity (Table 1). The likely explanation for the reduction of the size is the reduction of the membrane rigidity, as addition of LPC has been reported to reduce the bending modulus by a factor 4.21 The softer membranes are then more easily deformed during extrusion, leading to formation of smaller vesicles. For a comparison, it might be noted that subsequent addition of lysolipids leads to almost no size change for liposomes formed by the rehydration or sonication processes.30
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC ratios. Apparent vesicular molecular weight (MWlipo) was estimated from the forward scattering obtained by SLS. The number of bilayers or lamellarity (Nbi) was assessed by comparing MWlipo with that of a unilamellar vesicle (ULV), calculated from the experimental Rh and bilayer thickness (δ) values reported in the literature.31 Lipid density was assumed to be 1.01 g cm−3
LPC ratios. Apparent vesicular molecular weight (MWlipo) was estimated from the forward scattering obtained by SLS. The number of bilayers or lamellarity (Nbi) was assessed by comparing MWlipo with that of a unilamellar vesicle (ULV), calculated from the experimental Rh and bilayer thickness (δ) values reported in the literature.31 Lipid density was assumed to be 1.01 g cm−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 whereas bilayer spacing was obtained from the SANS curves presented in Fig. SI 5a (ESI)
26 whereas bilayer spacing was obtained from the SANS curves presented in Fig. SI 5a (ESI)
SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC LPC |
R h (nm) | Shape factor (Rg/Rh) | MWlipo × 108 (g mol−1) | δ (nm) | δ solvent (nm) | N bi |
|---|---|---|---|---|---|---|
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
60.5 ± 1.1 | 1.09 ± 0.09 | 1.850 | 3.9 | 3.2 | 1.65 |
98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
56.1 ± 2.3 | 1.08 ± 0.14 | 1.424 | 3.8 | 3.4 | 1.53 |
96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
54.1 ± 2.6 | 1.06 ± 0.15 | 1.265 | 3.7 | 3.0 | 1.50 |
91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 9 |
55.6 ± 2.9 | 1.06 ± 0.16 | 1.322 | 3.6 | 3.0 | 1.50 |
Results from SLS experiments summarized in Table 1 support the reduction in particle size observed by DLS since we observe a decrease in radius of gyration (Rg) that is well correlated to a reduction in the vesicular molecular weight (MWlipo), estimated using eqn (SI 2) (ESI†). MWlipo is compared to the molecular weight of unilamellar vesicles (ULV) to estimate the lamellarity (Nbi) in our systems assuming a double bilayer with a spacing between the bilayers of 2 nm.32
The molecular weight of ULVs was calculated from Rh and using a lipid density of 1.01 g cm−3.26 Since the bilayer thickness is known to decrease in the presence of lysolipids,33 literature values were used to estimate Nbi.
As a result, we find a value of Nbi ∼ 1.6 for pure SPC liposomes that decreases down to Nbi ∼ 1.5 with added LPC. It is conceivable for bilamellar and unilamellar vesicles (ULV) to coexist in the extruded dispersion, as vesicles with more than one bilayer are known to persist in spite of the extrusion process.34 To increase the abundance of ULVs without modifying the chemical composition of the bilayer, or of the aqueous environment, shearing with a smaller membrane pore size is required.34
A reduction of Nbi at higher lysolipid ratios is in line with the idea that softer membranes are more easily deformed by extrusion, making it easier to disrupt the multillamelarity of the vesicles. Moreover, we calculated the shape factor defined as Rg/Rh which provides an indication of particle morphology. A value of 1, close to our values is characteristic of hollow spheres, i.e. confirming that the two bilayers are close together.35
3.2 Small-angle neutron scattering
To elucidate the changes in liposome structure and composition, we study LPC containing liposomes with SANS. The difference of scattering length density between deuterium and hydrogen atoms allows the study of structural changes. In particular, we exploit the information provided by the scattering invariant (Qinv) (eqn (1)) from our SPC–LPC assemblies.The SANS curves presented in Fig. 3 follow mostly a q−2.3 decay in the mid-q region (0.001 1 Å−1 < q < 0.005 1 Å−1) at the studied SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC ratios. A power-law of −2 is characteristic of flat surfaces and consequently, would be expected for large unilamellar vesicles where the surface properties dominate. For smaller sized vesicles and for increasing number of shells, the multilamellar vesicles exhibit compact volume properties (spheres) and the exponent of the power-law increases.36 The multilamellarity of the vesicles is further corroborated by the weak peak at about 0.1 1 Å−1. Therefore, we decided to fit the curves as a weighted sum of uni- and bilamellar vesicles according to the results for Nbi from light scattering (see Table 1). The relative standard deviation for modelling was set to 0.3 for the vesicle radius and bilayer thickness. The complete set of parameters employed is shown in Table SI 4 (ESI†).
LPC ratios. A power-law of −2 is characteristic of flat surfaces and consequently, would be expected for large unilamellar vesicles where the surface properties dominate. For smaller sized vesicles and for increasing number of shells, the multilamellar vesicles exhibit compact volume properties (spheres) and the exponent of the power-law increases.36 The multilamellarity of the vesicles is further corroborated by the weak peak at about 0.1 1 Å−1. Therefore, we decided to fit the curves as a weighted sum of uni- and bilamellar vesicles according to the results for Nbi from light scattering (see Table 1). The relative standard deviation for modelling was set to 0.3 for the vesicle radius and bilayer thickness. The complete set of parameters employed is shown in Table SI 4 (ESI†).
 | ||
Fig. 3 Kratky plots (I(q)q2vs. q) of SANS data of liposomes extruded with a 100 nm pore size membrane at different SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC ratios. At increasing LPC content, liposomes become more unilamellar and more polydisperse. Dashed lines correspond to data fits using a combination of unilamellar and multilamellar vesicle form factor (see Table SI 4, ESI† for a summary of the fitting parameters). Curves are shifted by a factor 1, 5, 20 and 100 for easier visualization. LPC ratios. At increasing LPC content, liposomes become more unilamellar and more polydisperse. Dashed lines correspond to data fits using a combination of unilamellar and multilamellar vesicle form factor (see Table SI 4, ESI† for a summary of the fitting parameters). Curves are shifted by a factor 1, 5, 20 and 100 for easier visualization. | ||
In qualitative agreement with the results from light scattering, it can be seen that the shallow peak at 0.1 1 Å−1 becomes weaker as more LPC is added, which means that the vesicles become more unilamellar and the form factor minimum at about 0.006 1 Å−1 becomes more smeared out, which means that the vesicles become more polydisperse and/or softer.37 From light scattering and SANS investigations, it is evident that LPC promotes the presence of ULVs rather than multilamellar vesicles (MLVs). If LPC softens the membrane, the bilayers may be easily deformed by the extrusion process and this would lead to reduced lamellarity. Additionally, LPC is known to alter the bilayer structure, allowing an increase in area per-lipid in the outer monolayer and a compression of the inner one. This structural modification promotes increased curvature, which could also disfavor the formation of MLVs.38
3.3 Presence of water in liposome bilayers using the scattering invariant analysis
The scattering invariant (Qinv, eqn (1)) is an integral parameter independent from the structure, interparticle interactions, or the distribution of domains, and is a constant directly proportional to the square of the contrast between two domains of different, constant SLD in the system (eqn (2)), where one typically makes the assumption that such a simplified description of a scattering system can be done, as in our case for the aqueous domain and the part constituting the bilayers. More importantly, Qinv depends on the volume fraction of the lipids (ϕlipo) and such a relation is important in that it will change if the bilayer swells.As a consequence, the contrast between the components (ΔSLD) will be modified since the scattering length density of the self-assemblies will have an additional contribution, that is, of the incorporated water (eqn (5)) and the experimental invariant decreases upon water incorporation as described in Section 2.4.
To analyze how the experimental Qinv deviates from the estimated theoretical value, Qtheoinv is calculated by mass balance, assuming water does not penetrate the membrane. This corresponds to β = 0 with eqn (3)–(5) and Qtheoinv was calculated as such. The experimental invariants were obtained from SANS curves as described by eqn (1) and are presented in Fig. 4. On the one hand, we observe that Qtheoinv grows with addition of lysolipid to the system due to the increase of the lipid volume fraction. On the other hand, it is apparent that Qinv drops with small amounts of added LPC and grows again at higher LPC contents but remains smaller than Qtheoinv by a relatively constant offset, while the experimental and theoretical values show good agreement for SPC without added LPC. This indicates the presence of small amounts of water in the SPC bilayers. See Table SI 3 (ESI†) for detailed results of the numerical and extrapolated values taken into account for derivation of Qinv.
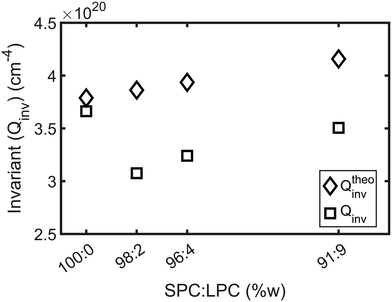 | ||
Fig. 4 Comparison of the theoretical (Qtheoinv) and experimental (Qinv) scattering invariants obtained from the model-free analysis of SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC liposomes SANS curves. Qinv systematically fall short from Qtheoinv, derived from mass balance from parameters detailed in Table SI 2 (ESI†) at all the studied SPC LPC liposomes SANS curves. Qinv systematically fall short from Qtheoinv, derived from mass balance from parameters detailed in Table SI 2 (ESI†) at all the studied SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC ratios. LPC ratios. | ||
One hypothetical possibility for the lower Qinv values would be a dissolution of lipids into the solvent, but given the molecular architecture of the lipids and low CMC of the lysolipid (between 4–8.3 μM9) this is a very unlikely scenario. Here, we work above the cmc from the lowest LPC ratio, where the LPC concentration is 191 μM. Therefore, the logical answer is that the lower Qinv values result from an increased water presence within the lipid membrane, potentially due to the presence of surfactant stabilized pores.14,16,39,40 Consequently, this would increase ϕlipo and decrease ΔSLD as previously explained.
To quantify the fraction of water incorporated into the lipid phase (β), we solved eqn (3)–(5) (see eqn (SI 13) (ESI†)) to estimate the volume fraction of solvent that needs to be incorporated in the membrane to explain the deviations in Qinv. Thereafter we calculated the fraction of water contained in the lipid part of the system ( ) and show our results in Fig. 5.
) and show our results in Fig. 5.
 | ||
Fig. 5 Graphic representation of the calculated volume fractions of D2O incorporated to the SPC liposomes from model-free analysis of SANS curves. The presence of water in the membrane increases upon addition of a lysophosphatidylcholine (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, LPC) of similar chain-length to that of the SPC. Assuming deviations of the scattering invariant (Qinv) to the values calculated by mass balance, the amount of water within the membrane core responsible for said deviations was estimated with eqn (SI 13) (ESI†). On the top, the hydration number ND2O (molecules of water per molecule of lipid) estimated from 1, LPC) of similar chain-length to that of the SPC. Assuming deviations of the scattering invariant (Qinv) to the values calculated by mass balance, the amount of water within the membrane core responsible for said deviations was estimated with eqn (SI 13) (ESI†). On the top, the hydration number ND2O (molecules of water per molecule of lipid) estimated from  . . | ||
Based on the calculated values, the SPC sample with no added lysolipid is only slightly hydrated as  is approximately 3%. However, the fraction of incorporated water increases strongly upon the addition of LPC as
is approximately 3%. However, the fraction of incorporated water increases strongly upon the addition of LPC as  rises to 20% at a 98
rises to 20% at a 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 SPC
2 SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC ratio and slightly decreases to 15% upon further addition of the lysolipid.
LPC ratio and slightly decreases to 15% upon further addition of the lysolipid.
The fact that  does not increase further when increasing the SPC
does not increase further when increasing the SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC ratio past 98
LPC ratio past 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 might indicate that extra LPC forms small micelles, which would be essentially invisible next to the vesicles in the SANS curves41 and they are not accounted for in the proposed pore model since they would have no water. Thus, if the additional LPC forms dry micelles, the water volume within the membrane pores should remain constant. Given the relation
2 might indicate that extra LPC forms small micelles, which would be essentially invisible next to the vesicles in the SANS curves41 and they are not accounted for in the proposed pore model since they would have no water. Thus, if the additional LPC forms dry micelles, the water volume within the membrane pores should remain constant. Given the relation  , an increase in lipid concentration and constant amount of incorporated water would decrease
, an increase in lipid concentration and constant amount of incorporated water would decrease  , which is the trend observed in Fig. 5. This would also explain the consistent differences between Qinv and Qtheoinv observed in Fig. 4.
, which is the trend observed in Fig. 5. This would also explain the consistent differences between Qinv and Qtheoinv observed in Fig. 4.
It is also possible that this increased water content is due to simple diffusion. According to Seu et al. the removal of an alkyl chain by addition of LPC should reduce van der Waals interactions and make the membrane more fluid.42 This could be correlated to the increased membrane permeability deduced also by coarse grained simulations. However, it remains unclear whether these changes are due to modifications in the area-per-lipid or due to the appearance of transient pores.43
What is certain is that the architecture of LPC plays an important role in the bilayer properties. For instance, a similar surfactant like monopalmitoyl-glycerol, single C16 alkyl chain with a glycerol backbone but without the bulky PC headgroup, was not observed to increase bilayer permeability unlike its C16 lysolipid counterpart.44 It is with the presence of lysolipid that readjustments of area-per-lipid take place to adapt to the local curvature.38,45
To corroborate if the values resulting from the invariant analysis are feasible, we estimated the hydration number ND2O (water molecules per lipid molecule) from  . Assuming that all the lipids partake in the self-assembly, we calculated the number of surfactant molecules in the dispersion from the lipid concentrations and molecular weights following eqn (SI 14) (ESI†), attributing the corresponding number of water molecules per lipid from
. Assuming that all the lipids partake in the self-assembly, we calculated the number of surfactant molecules in the dispersion from the lipid concentrations and molecular weights following eqn (SI 14) (ESI†), attributing the corresponding number of water molecules per lipid from 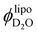 .
.
For liposomes with added LPCs, ND2O ranges from 7.6 to 11.7 (Fig. 5). This degree of hydration is comparable to the NH2O reported for PC dispersions with lipids of similar chain-length (NH2O = 8–13).46–48 However, it is likely that our ND2O falls short for a fully hydrated lipid bilayer since the hydrated lipid headgroups are mostly invisible for SANS, given that they are not really incorporated into what geometrically is to be considered as the bilayer and that concerns hydration water molecules on the surface of the bilayers pointing to the aqueous part of the system. This then leads one to wonder where exactly this large amount of extra water seen upon addition of LPC is located within the bilayer. For sure this shows that here a structural change of the bilayer must have occurred. One logical option one could think of would be the formation of pores/holes within the bilayer, which are stabilized by the LPC.
At low concentrations, the lysolipid should be incorporated into the lipid bilayer and the inverted cone structure of LPC would promote positive curvature of the membrane.33,38 Further addition of surfactant should create LPC enriched regions with a localized high curvature. This structural feature should foster the formation of pores or domains of high curvature to prevent exposure of the hydrophobic bilayer core to water. Past a critical SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC ratio, the membrane will no longer be able to accommodate more surfactant and beyond this critical point, further LPC will assemble in form of micelles.40 Unfortunately, we would not be able to corroborate the formation of micelles with the employed contrast, since the micelle scattering signal would be effectively shadowed by that of the vesicles (Fig. SI 6, ESI†).
LPC ratio, the membrane will no longer be able to accommodate more surfactant and beyond this critical point, further LPC will assemble in form of micelles.40 Unfortunately, we would not be able to corroborate the formation of micelles with the employed contrast, since the micelle scattering signal would be effectively shadowed by that of the vesicles (Fig. SI 6, ESI†).
Here we observe increased water presence in the liposomes and suggest which structural changes may explain this. Further experiments such as permeability studies, could shed some light on the matter, keeping in mind that we presume to be in the presence of small pores. Therefore, size of the hydrophilic solute and liposome preparation method would be relevant for comparison of the results.
3.4 Estimating pore size and density
While our results do not allow us to differentiate between transient pores or diffusion, we can nevertheless estimate the size and density of pores if the added water in the membrane was due to pores based on some simple geometrical considerations. Assuming that LPC promotes the formation of transient pores, we can estimate a pore radius (Rpores) and area density (ρpore) making the following assumptions: (1) the LPC stabilizes the pores and therefore the headgroup area of the LPC forms the pore walls. (2) We assume that all of the LPC is found in the pore walls. (3) The water in the membranes corresponds to the pore volume. With these assumptions, we obtain a volume to area ratio and, assuming a specific shape, we can calculate a pore size, which can be used to calculate a pore area density. For the sake of simplicity, we assume a simple cylindrical shape of the pores (see Fig. 6(A)) so that Vcylinder/Acylinder = Rcylinder/2, which is obviously an oversimplification but should still yield a reasonable ballpark number.
corresponds to the pore volume. With these assumptions, we obtain a volume to area ratio and, assuming a specific shape, we can calculate a pore size, which can be used to calculate a pore area density. For the sake of simplicity, we assume a simple cylindrical shape of the pores (see Fig. 6(A)) so that Vcylinder/Acylinder = Rcylinder/2, which is obviously an oversimplification but should still yield a reasonable ballpark number.
Looking at Fig. 5 it is clear that our assumptions only hold (at most) up to an SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC ratio of 98
LPC ratio of 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 as further addition of LPC does not lead to an increase of water in the membranes and we simply take the slope between the sample without LPC and the sample with SPC
2 as further addition of LPC does not lead to an increase of water in the membranes and we simply take the slope between the sample without LPC and the sample with SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC 98
LPC 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to obtain a volume ratio Vpores/VLPC = 10.8 (see Fig. SI 7, ESI†). With the known molecular weight (MWLPC= 521.67 g mol−1), specific volume (
2 to obtain a volume ratio Vpores/VLPC = 10.8 (see Fig. SI 7, ESI†). With the known molecular weight (MWLPC= 521.67 g mol−1), specific volume (![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) LPC = 0.9246 mL g−1 assuming a VLPC of 800 Å3 based on reported volumes for DOPC and PC headgroups27) and headgroup area of LPC (ALPC ≃ 70 Å2(ref. 23 and 49)), we can convert the volume VlipoLPC to an area and with that calculate a pore radius according to
LPC = 0.9246 mL g−1 assuming a VLPC of 800 Å3 based on reported volumes for DOPC and PC headgroups27) and headgroup area of LPC (ALPC ≃ 70 Å2(ref. 23 and 49)), we can convert the volume VlipoLPC to an area and with that calculate a pore radius according to
 | (6) |
The values obtained for Rpores seem rather large and if there were pores with a size on the order of 20 nm it should be possible to detect them using electron microscopy. However, to the best of our knowledge the existence of such pores has not been reported before. In addition, such large pores would have sharp boundaries and the water contained in them would scatter as part of the bulk solution and not the liposome. Then, the variation in the scattering invariant should be explained differently. So, we have to assume that there either are no pores or the pores are significantly smaller than suggested by our calculations, a few nm at most.
Looking at eqn (6) the pore radius would decrease if AporesLPC would increase and we could relax assumption 1, and instead of assuming that the pore walls are made of LPC exclusively as shown in Fig. 6, we could simply assume that LPC is enriched in the pore walls. Pores on the order of 2 nm would be very difficult to detect by electron microscopy. Such pores would result from eqn (6) if we assume that only 10% of the headgroup area in the pore walls comes from LPC, so that there is a molecular ratio of SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC of 9
LPC of 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, with similar headgroup area for both SPC and LPC, which would still mean that LPC is significantly enriched in the (hypothetical) pores compared to the bulk ratio of 14
1, with similar headgroup area for both SPC and LPC, which would still mean that LPC is significantly enriched in the (hypothetical) pores compared to the bulk ratio of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Nevertheless, we make use of Rpores to estimate a pore density and the percentage of the vesicle area covered by pores considering a dispersion of unilamellar vesicles (Table 2).
1. Nevertheless, we make use of Rpores to estimate a pore density and the percentage of the vesicle area covered by pores considering a dispersion of unilamellar vesicles (Table 2).
4 Conclusions
In this article, the effect of the presence of small amounts of lysophosphatidylcholine (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, LPC) on soybean phosphatidylcholine (SPC) liposomes has been studied using light scattering and small-angle neutron scattering (SANS). We find that extrusion of liposomes with added LPC results in smaller liposomes which is probably a result of extruding bilayers of lower rigidity.21,22 Most importantly, results of our model-free analysis of SANS curves suggest that the presence of water in the liposomes increases with added LPC as the fraction of incorporated water in the membrane rises to about 10–15% in dispersions with a higher LPC ratio. This could be assigned to the formation of LPC stabilized pores that allow for an increased water fraction to penetrate across the lipid bilayer, but, of course, could also arise from other structural changes of the bilayer. Accordingly, we estimate a pore size and density from said volume fraction for the different LPC ratios. However, if pores of the estimated sizes were present, they should be evidenced by other techniques such as electron microscopy, which to the best of our knowledge, is not the case. So, we assume that there either are no pores or if there should be pores in the membrane, the walls of these pores do not exclusively consist of LPC but can be enriched in LPC even though the addition of LPC promotes the incorporation of water in the membranes.
1, LPC) on soybean phosphatidylcholine (SPC) liposomes has been studied using light scattering and small-angle neutron scattering (SANS). We find that extrusion of liposomes with added LPC results in smaller liposomes which is probably a result of extruding bilayers of lower rigidity.21,22 Most importantly, results of our model-free analysis of SANS curves suggest that the presence of water in the liposomes increases with added LPC as the fraction of incorporated water in the membrane rises to about 10–15% in dispersions with a higher LPC ratio. This could be assigned to the formation of LPC stabilized pores that allow for an increased water fraction to penetrate across the lipid bilayer, but, of course, could also arise from other structural changes of the bilayer. Accordingly, we estimate a pore size and density from said volume fraction for the different LPC ratios. However, if pores of the estimated sizes were present, they should be evidenced by other techniques such as electron microscopy, which to the best of our knowledge, is not the case. So, we assume that there either are no pores or if there should be pores in the membrane, the walls of these pores do not exclusively consist of LPC but can be enriched in LPC even though the addition of LPC promotes the incorporation of water in the membranes.
Furthermore, the difference in values of hydrodynamic radius (Rh), and water presence within the bilayer are modest for the different samples with added LPC at the different ratios (SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC 98
LPC 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 96
2, 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 91
4, 91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9). That is: Rh values vary between 54–56 nm and the volume fraction of incorporated water with respect to the lipid fraction between 15–20% v. In other words, rather small amounts of LPC affect the properties of the liposomes, but addition of more LPC does not have a significant further impact. It is possible for lysolipids to start forming micelles at the employed concentrations, in which case additional LPC would only continue to contribute to the micellar assembly.11 Additional LPC molecules would apparently not stabilize further the transient pores. This could explain why
9). That is: Rh values vary between 54–56 nm and the volume fraction of incorporated water with respect to the lipid fraction between 15–20% v. In other words, rather small amounts of LPC affect the properties of the liposomes, but addition of more LPC does not have a significant further impact. It is possible for lysolipids to start forming micelles at the employed concentrations, in which case additional LPC would only continue to contribute to the micellar assembly.11 Additional LPC molecules would apparently not stabilize further the transient pores. This could explain why  slightly decreases at higher SPC
slightly decreases at higher SPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LPC ratios.
LPC ratios.
Author contributions
F. A. designed and performed the experiments, analyzed and interpreted the data, and wrote the manuscript; I. H. helped with data interpretation, contributed to the writing of the manuscript, and dealt with project administration; M. G. conceptualized the work, contributed to the writing of the manuscript, and dealt with project administration; J. V. helped with conceptualization of the work, editing of the manuscript and project administration; N. M. performed the SANS measurements and data integration; All authors have read and agreed to the published version of the manuscript.Data availability
The data supporting this article have been included as part of the ESI.† SANS data for this article is available at https://doi.org/10.5286/ISIS.E.RB2210042.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Unions Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 847439. The authors gratefully acknowledge the ISIS facility, Didcot, UK, for the SANS beamtime. We gratefully acknowledge the Partnership for Soft Condensed Matter (PSCM) for access to support laboratories.Notes and references
- D. Lasic and D. Papahadjopoulos, Medical applications of liposomes, Elsevier Science Bv, 1998 Search PubMed.
- G. Gregoriadis, Nature, 1977, 265, 407–411 CrossRef CAS PubMed.
- M. Malmsten, Soft Matter, 2006, 2, 760–769 RSC.
- J. Ruiz, F. M. Goñi and A. Alonso, Biochim. Biophys. Acta, 1988, 937, 127–134 CrossRef CAS PubMed.
- G. Nasr, H. Greige-Gerges, A. Elaissari and N. Khreich, Int. J. Pharm., 2020, 580, 119198 CrossRef CAS PubMed.
- F. Goñi and A. Alonso, An. R. Acad. Nac. Farm., 2021, 53–96 Search PubMed.
- H. Heerklotz, Q. Rev. Biophys., 2008, 41, 205–264 CrossRef CAS PubMed.
- D. Lichtenberg, E. Opatowski and M. M. Kozlov, Biochim. Biophys. Acta, 2000, 1508, 1–19 CrossRef CAS PubMed.
- R. E. Stafford, T. Fanni and E. A. Dennis, Biochemistry, 1989, 28, 5113–5120 CrossRef CAS PubMed.
- V. A. Bjørnestad and R. Lund, Langmuir, 2023, 39, 3914–3933 CrossRef PubMed.
- H. Y. Fan, D. Das and H. Heerklotz, Langmuir, 2016, 32, 11655–11663 CrossRef CAS PubMed.
- A. Pizzirusso, A. De Nicola, G. J. A. Sevink, A. Correa, M. Cascella, T. Kawakatsu, M. Rocco, Y. Zhao, M. Celino and G. Milano, Phys. Chem. Chem. Phys., 2017, 19, 29780–29794 RSC.
- J. Israelachvili, S. Marčelja and R. Horn, Q. Rev. Biophys., 1980, 13(2), 121–200 CrossRef CAS PubMed.
- T. P. Sudbrack, N. L. Archilha, R. Itri and K. A. Riske, J. Phys. Chem. B, 2011, 115, 269–277 CrossRef CAS PubMed.
- E. Karatekin, O. Sandre, H. Guitouni, N. Borghi, P.-H. Puech and F. Brochard-Wyart, Biophys. J., 2003, 84, 1734–1749 CrossRef CAS PubMed.
- D. Velluto, C. Gasbarri, G. Angelini and A. Fontana, J. Phys. Chem. B, 2011, 115, 8130–8137 CrossRef CAS PubMed.
- J. Davidsen, O. G. Mouritsen and K. Jørgensen, Biochim. Biophys. Acta, Biomembr., 2002, 1564, 256–262 CrossRef CAS PubMed.
- T. Kitagawa, K. Inoue and S. Nojima, J. Biochem., 1976, 79, 1123–1133 CrossRef CAS PubMed.
- R. T. Hamilton and E. W. Kaler, J. Phys. Chem., 1990, 94, 2560–2566 CrossRef CAS.
- C. Van Echteld, B. De Kruijff, J. Mandersloot and J. De Gier, Biochim. Biophys. Acta, Biomembr., 1981, 649, 211–220 CrossRef CAS PubMed.
- T. J. McIntosh, S. Advani, R. E. Burton, D. V. Zhelev, D. Needham and S. A. Simon, Biochemistry, 1995, 34, 8520–8532 CrossRef CAS PubMed.
- D. Otten, M. F. Brown and K. Beyer, J. Phys. Chem. B, 2000, 104, 12119–12129 CrossRef CAS.
- J. R. Henriksen, T. L. Andresen, L. N. Feldborg, L. Duelund and J. H. Ipsen, Biophys. J., 2010, 98, 2199–2205 CrossRef CAS PubMed.
- R. S. Gracià, N. Bezlyepkina, R. L. Knorr, R. Lipowsky and R. Dimova, Soft Matter, 2010, 6, 1472–1482 RSC.
- V. Kumar, B. Malewicz and W. Baumann, Biophys. J., 1989, 55, 789–792 CrossRef CAS PubMed.
- J. H. Van Zanten and H. G. Monbouquette, J. Colloid Interface Sci., 1991, 146, 330–336 CrossRef CAS.
- J. F. Nagle, R. M. Venable, E. Maroclo-Kemmerling, S. Tristram-Nagle, P. E. Harper and R. W. Pastor, J. Phys. Chem. B, 2019, 123, 2697–2709 CrossRef CAS PubMed.
- Mantid: Manipulation and Analysis Toolkit for Instrument Data, Mantid Project, 2013 DOI:10.5286/SOFTWARE/MANTID.
- F. Alvarado Galindo, J. Venzmer, S. Prévost, I. Hoffmann and M. Gradzielski, Colloids Surf., A, 2024, 702, 135014 CrossRef CAS.
- A. Alonso, R. Sáez, A. Villena and F. M. Goñi, J. Membr. Biol., 1982, 67, 55–62 CrossRef CAS PubMed.
- J. Mandersloot, F. Reman, L. Van Deenen and J. De Gier, Biochim. Biophys. Acta, Biomembr., 1975, 382, 22–26 CrossRef CAS PubMed.
- M. Müller, S. Mackeben and C. C. Müller-Goymann, Int. J. Pharm., 2004, 274, 139–148 CrossRef PubMed.
- S. Y. Woo and H. Lee, Phys. Chem. Chem. Phys., 2017, 19, 21340–21349 RSC.
- H. L. Scott, A. Skinkle, E. G. Kelley, M. N. Waxham, I. Levental and F. A. Heberle, Biophys. J., 2019, 117, 1381–1386 CrossRef CAS PubMed.
- W. Schärtl, Light Scattering from Polymer Solutions and Nanoparticle Dispersions, Springer Laboratory, 2007 Search PubMed.
- H. Frielinghaus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 051603 CrossRef PubMed.
- M. Gradzielski, D. Langevin and B. Farago, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 3900–3919 CrossRef CAS PubMed.
- J. Yoo and Q. Cui, Biophys. J., 2009, 97, 2267–2276 CrossRef CAS PubMed.
- P. Vinson, Y. Talmon and A. Walter, Biophys. J., 1989, 56, 669–681 CrossRef CAS PubMed.
- D. Lichtenberg, H. Ahyayauch and F. M. Goñi, Biophys. J., 2013, 105, 289–299 CrossRef CAS PubMed.
- O. A. Ogunsola, M. E. Kraeling, S. Zhong, D. J. Pochan, R. L. Bronaugh and S. R. Raghavan, Soft Matter, 2012, 8, 10226–10232 RSC.
- K. J. Seu, L. R. Cambrea, R. M. Everly and J. S. Hovis, Biophys. J., 2006, 91, 3727–3735 CrossRef CAS PubMed.
- N. D. Winter and G. C. Schatz, J. Phys. Chem. B, 2010, 114, 5053–5060 CrossRef CAS PubMed.
- J. K. Mills and D. Needham, Biochim. Biophys. Acta, Biomembr., 2005, 1716, 77–96 CrossRef CAS PubMed.
- V. V. Kumar, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 444–448 CrossRef CAS PubMed.
- C. Faure, L. Bonakdar and E. J. Dufourc, FEBS Lett., 1997, 405, 263–266 CrossRef CAS PubMed.
- O. Tirosh, Y. Barenholz, J. Katzhendler and A. Priev, Biophys. J., 1998, 74, 1371–1379 CrossRef CAS PubMed.
- P. Balgavý, M. Dubničková, N. Kučerka, M. A. Kiselev, S. P. Yaradaikin and D. Uhríková, Biochim. Biophys. Acta, Biomembr., 2001, 1512, 40–52 CrossRef PubMed.
- J. F. Nagle and S. Tristram-Nagle, Biochim. Biophys. Acta, Biomembr., 2000, 1469, 159–195 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01211a |
| This journal is © The Royal Society of Chemistry 2025 |