Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thin free-standing liquid films manipulation: device design to turn on/off gravity in flow regimes for thickness map control and for material structuring†
Paolo
Iaccarino‡
 abc,
Zhe
Wang‡
bd,
Andrea
Marfuggi
bc,
Simone
Russo
b,
Vincenzo
Ferraro
be,
Giuseppe
Vitiello
abc,
Zhe
Wang‡
bd,
Andrea
Marfuggi
bc,
Simone
Russo
b,
Vincenzo
Ferraro
be,
Giuseppe
Vitiello
 bf,
Sara
Coppola
d and
Ernesto
Di Maio
bf,
Sara
Coppola
d and
Ernesto
Di Maio
 *bc
*bc
aScuola Superiore Meridionale, Largo San Marcellino 10, 80138 Naples, Italy
bDipartimento di Ingegneria Chimica, dei Materiali e della Produzione Industriale, P.le Tecchio 80, 80125 Naples, Italy. E-mail: edimaio@unina.it
cFoamlab, P.le Tecchio 80, 80125 Naples, Italy
dInstitute of Applied Sciences and Intelligent Systems “E. Caianiello”, Italian National Research Council (ISASI-CNR), Via Campi Flegrei 34, 80078 Pozzuoli (Naples), Italy
eDipartimento di Ingegneria e Architettura, University of Parma, Via delle Scienze 181, 43124 Parma, Italy
fCSGI, Center for Colloid and Surface Science, Via della Lastruccia 3, 50019 Florence, Italy
First published on 31st October 2024
Abstract
The manipulation and control of free-standing liquid film drainage dynamics is of paramount importance in many technological fields and related products, ranging from liquid lenses to liquid foams and 2D structures. In this context, we theoretically design and introduce a device where we can reversibly drive flow regime switch between viscous-capillary and viscous-gravity in a thin free-standing liquid film by altering its shape, allowing us to manipulate and stabilize the film thickness over time. The device, which mainly consists of a syringe pump, a pressure transducer, and a 3D-printed cylinder, is coupled with a digital holography setup to measure, in real time, the evolution of the local film thickness map, revealing characteristic features of viscous-capillary and viscous-gravity driven drainage regimes. By using polyvinyl alcohol/water concentrated solutions, we are also able to produce viscoelastic membranes after manipulation and water evaporation, which presents manipulation history-dependent geometrical properties. Furthermore, using a system composed of carboxymethyl cellulose, water, and rod-like zinc oxide nanoparticles, we show a clear effect of film manipulation on particle rearrangement. We believe this device could represent a starting point for the development of a useful and practical tool to study thin liquid film dynamics and to produce novel (patterned) 2D structures for the numerous scientific and technical fields where they are of use.
1 Introduction
Free-standing liquid films, i.e., with both interfaces exposed to a different fluid phase (commonly, a gas),1 represent unique objects in soft matter and play a key role in many scientific and technological areas,2–8 including the countless bubble-based technologies.9 Their dynamics, enriched with instabilities and self-patterning ability,10–12 is governed by viscous, inertial, capillary, gravity, Marangoni, and disjoining forces. Different flow regimes have been observed, depending on the prevailing mechanisms, which often overlap, challenging the modeling and comprehension of the observed behavior.13–15In their use, it is desirable to manipulate the stability and thickness through flows,16e.g., for continuous particle separation or insect barrier applications.17 In the complicated bubble dynamics of liquid foams, the drainage dynamics of liquid films between bubbles strongly influences the foam coarsening and bubble coalescence, leading to a gravity-driven macroscopic phase separation18,19 and eventually to collapse.20 In fact, a quantitative agreement has recently been observed between experimental results on the drainage dynamics of a single free-standing liquid film and the corresponding macroscopic liquid foam.19,21
Manipulation of thickness and stability of free-standing liquid films through flows is also of relevance if the free-standing film is loaded with micro- or nano-particles, because the hydrodynamic long-range interactions in quasi-2D flows (as, indeed, in the case of free-standing liquid films22) are different compared to the ones in a bulky 3D fluid, and govern the particle dynamics.23 Particles can also interact via surface waves or ripples on the liquid–air interfaces.23 Their presence on a liquid–fluid interface affects the surface properties as a result of the numerous interparticle forces acting in the system: they have a strong contribution on the surface pressure,24 dilatational elasticity and response to shear deformation of the interface,25 to name a few. If the thickness of the free-standing film is less than or comparable to the particle dimension, the particles can adsorb simultaneously at both interfaces and move according to the slope of the interfaces;26,27 if the particle concentration is high, a 2D granular film with a peculiar mechanical behaviour can be obtained.28 Changes in driving forces at the fluid–fluid interfaces can be used to obtain tunable particle configurations: different colloidal particles configurations have been obtained by elastocapillary driven assembly,29 while 2D nano-particles arrangements have been obtained via Marangoni stresses assembly30 and capillary-driven assembly.31 To freeze the structure and create a free-standing particle arrangement, the liquid evaporation play a crucial role and should be carefully tuned.26,32 Thin free-standing film manipulation could be of paramount importance to produce 2D granular films and heterostructures of micro- and nano-particles.
The device commonly used to investigate the dynamics of free standing films under different conditions is the Sheludko cell.33–36 The system developed by Mysels and Jones37 was also widely used and improved to investigate disjoining pressure terms.38,39 Chatzigiannakis et al. first addressed the problem of studying the phenomenon of free-standing film thickening due to changes in hydrostatic pressure gradients by developing a pressure-controlled dynamic thin-film balance.40,41 Ferraro et al. developed a hybrid opto-mechanical tool to study capillary-driven drainage and leveling42 and, very recently, the same authors proposed a dynamic wire-pull rubber diaphragm combined with digital holography to obtain a full-field quantitative thickness analysis of multi-shape and multi-material thin films.43 However, none of the aforementioned works addressed the possibility of changing the driving forces (such that, for example, gravity force starts to prevail on the capillary force) but required changes in the device geometry and/or materials. Digital holography (DH) is considered the optimal liquid film thickness mapping strategy, allowing no contact mode real-time full-field measurement capabilities.44,45 Due to a numerical refocusing ability of DH, the complete thickness evolution of the films can be acquired even if the films are formed at different height levels46 such in the case of droplets47 or bubbles.48 Moreover, the full-field complex dynamic thickness evolution of the film can be reassembled in a spatio-temporal coordinate system, being converted into an intuitive data curve to allow better analysis.43,46
In this work, we design, develop and test an experimental apparatus able to manipulate a free-standing liquid film and induce (reversible, periodic) transitions between viscous-capillary and viscous-gravity flow regimes by changing the film shape. To this end, a thin free-standing liquid film is formed in a circular plate and, using a syringe pump (like a bubble pipe), by inflating or deflating the bubble, a positive dome or negative dome is produced. Gravity force is thereby allowed to enter the flow dynamics at will, with Bond (Bo) numbers imposed in the range [−6.25, 6.25] (here, + or − to underline the ability of the apparatus to reverse the flow regime with the sign of the dome curvature by pumping/withdrawing). DH is used to obtain a real-time full-field thickness measurement to characterize the flow regimes and film thickness. With the polyvinyl alcohol (PVA)/water model solutions and well-designed volume histories, we tested the different flow regimes in a static and dynamic manner. Furthermore, by using periodic bubble volume histories, we are able to avoid film rupture, stabilizing the film thickness in space and time. Water evaporation allowed us to obtain a viscoelastic membrane with geometrical and material properties that depend on the imposed volume history. Using aqueous solutions of carboxymethyl cellulose (CMC), we investigate the effect of different volume histories on the structuring/orientation at a micro-scale of the polymer after solvent evaporation. Moreover, by adding rod-like zinc oxide nanoparticles (ZnO-NPs) to such solutions, we tried to give insights into the effect of film manipulation on the particles rearrangement.
2 Device design
This section describes the design process to provide a device capable of working and transiting in two different regimes, namely the viscous-capillary regime (when the film is flat) and the viscous-gravity regime, the latter in two different geometrical configurations, positive or negative dome. Let us consider the sketch in Fig. 1(a), which represents the bubble inflated at any time t. The bubble is supposed to have a spherical dome shape, where α(t) is the height of the dome and ϕ is the basal radius of the dome (and of the Teflon holder, a ring with an inner radius of 7.5 × 10−3 m). | ||
Fig. 1 (a) 3D sketch of the bubble and its cross section (in the Teflon ring holder, see the Methods section) at a given time t. The inner radius of the Teflon holder is indicated by ϕ, the dome height is indicated by α, and the thickness (referred to an average thickness for our modeling purposes) in indicated by δ. (b) Bond number, Bo, as function of the dome height. For Bo ≪ 1 (i.e., 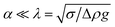 , where λ is the capillary length), the fluid dynamic regime is viscous-capillary driven; for Bo ≫ 1 (i.e., α ≫ λ), the fluid-dynamic regime is viscous-gravity driven. The transition between the regimes starts when Bo = 0.25.49 (c) Representation of the case- and piecewise-defined volume history for thickness stabilization. , where λ is the capillary length), the fluid dynamic regime is viscous-capillary driven; for Bo ≫ 1 (i.e., α ≫ λ), the fluid-dynamic regime is viscous-gravity driven. The transition between the regimes starts when Bo = 0.25.49 (c) Representation of the case- and piecewise-defined volume history for thickness stabilization. | ||
The Bond number is defined as the ratio of gravity to capillary forces, and it is essential to study the dynamics of dome-shaped (or bubble-shaped) thin liquid films.49,50 Since the bubble dome height is time dependent, we define a time-dependent Bond number, Bo(t), as follow:
 | (1) |
 , we can rewrite eqn (1) as
, we can rewrite eqn (1) as | (2) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−6 m), the in-plane flow dominates, and, under the following assumptions:
(10−6 m), the in-plane flow dominates, and, under the following assumptions:
• the interfaces are rigid and nearly parallel;
• the axial velocity is small compared to the radial velocity;
• angular dependencies and angular velocities are negligible;
• the variation of the radial velocity with the radial coordinate is much less than its variation in the thickness direction;
• there is no gravitational effect in the thickness direction; the lubrication approximation applies.16 A rough estimation of the thinning velocity can be done by the Reynolds equation for thin films:16,19,33,51
 | (3) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−5 m) from preliminary thickness measurements) and ΔPavg is the average pressure drop across the film (the time-dependent term), that in our model can be defined as16,33
(10−5 m) from preliminary thickness measurements) and ΔPavg is the average pressure drop across the film (the time-dependent term), that in our model can be defined as16,33| ΔPavg = Pg + Pσ − Π | (4) |
 | (5) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−2 m) for our geometry), and Π is the disjoining pressure. We stress that under these assumptions, we can focus only on the drainage dynamics within the film, while effects on the scale of the dome radius/height can be accounted for in terms of boundary conditions52 (that is, in our case, ΔPavg). It should be emphasized that strong similarities exists between dynamic characteristics of such free-standing liquid films and those of bubble dynamics: in fact, the above mentioned theory has also proven to be efficient in modeling thin liquid film drainage between colliding bubbles.52–54 The disjoining pressure can be expressed by three terms, in particular, Π = ΠvdW + ΠECT + ΠSR, where ΠvdW, ΠECT and ΠSR are the disjoining pressure contributions due to van der Waals interaction, electrostatic forces and short-range interactions, respectively.55,56 We neglect short-range and electrostatic forces because the film thickness is everywhere of the order of 10 μm (as a consequence, Π ∼ ΠvdW).19 By comparing the van der Waals interactions term and the capillary pressure, we obtain Pσ/ΠvdW = 6σπδ3/(Ak) ∼ 102, where A is the Hamaker constant for PVA, assumed to be 4.4 × 10−20 J57 and k = 1/RB is the meniscus curvature, estimated to be equal to 102 m−1 from preliminary thickness maps obtained using the holographic setup. Hence, the disjoining pressure can always be neglected, and ΔPavg = Pg + Pσ. It should be noted that by changing α(t), one changes the relative contribution of Pg and Pσ. Let us consider the flat-film scenario, in which Bo(t) ≪ 1 and α(t) ≪ 1. As a consequence, ΔPavg ∼ Pσ. From eqn (3) we obtain vReσ =
(10−2 m) for our geometry), and Π is the disjoining pressure. We stress that under these assumptions, we can focus only on the drainage dynamics within the film, while effects on the scale of the dome radius/height can be accounted for in terms of boundary conditions52 (that is, in our case, ΔPavg). It should be emphasized that strong similarities exists between dynamic characteristics of such free-standing liquid films and those of bubble dynamics: in fact, the above mentioned theory has also proven to be efficient in modeling thin liquid film drainage between colliding bubbles.52–54 The disjoining pressure can be expressed by three terms, in particular, Π = ΠvdW + ΠECT + ΠSR, where ΠvdW, ΠECT and ΠSR are the disjoining pressure contributions due to van der Waals interaction, electrostatic forces and short-range interactions, respectively.55,56 We neglect short-range and electrostatic forces because the film thickness is everywhere of the order of 10 μm (as a consequence, Π ∼ ΠvdW).19 By comparing the van der Waals interactions term and the capillary pressure, we obtain Pσ/ΠvdW = 6σπδ3/(Ak) ∼ 102, where A is the Hamaker constant for PVA, assumed to be 4.4 × 10−20 J57 and k = 1/RB is the meniscus curvature, estimated to be equal to 102 m−1 from preliminary thickness maps obtained using the holographic setup. Hence, the disjoining pressure can always be neglected, and ΔPavg = Pg + Pσ. It should be noted that by changing α(t), one changes the relative contribution of Pg and Pσ. Let us consider the flat-film scenario, in which Bo(t) ≪ 1 and α(t) ≪ 1. As a consequence, ΔPavg ∼ Pσ. From eqn (3) we obtain vReσ = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−9 m s−1), according to previous studies.15 In our case, the Reynolds number is Re = ρvReσδ/η = 10−11, and capillary and viscous forces control the drainage dynamics in the flat-film scenario. The thinning is controlled by the film Capillary number, Caf:58
(10−9 m s−1), according to previous studies.15 In our case, the Reynolds number is Re = ρvReσδ/η = 10−11, and capillary and viscous forces control the drainage dynamics in the flat-film scenario. The thinning is controlled by the film Capillary number, Caf:58 | (6) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−3), and we observed that the film is dimpled (i.e., interfaces are no more plane-parallel); this observation is in agreement with the study proposed by Chatzigiannakis et al.15 Therefore, in our case, eqn (3) can underestimate the true thinning velocity.16 Let us consider the inflated (or deflated) film scenario, in which |α(t)| ≫ 0.5λ (and therefore Bo(t) ≫ 1). From eqn (3) we obtain vRe =
(10−3), and we observed that the film is dimpled (i.e., interfaces are no more plane-parallel); this observation is in agreement with the study proposed by Chatzigiannakis et al.15 Therefore, in our case, eqn (3) can underestimate the true thinning velocity.16 Let us consider the inflated (or deflated) film scenario, in which |α(t)| ≫ 0.5λ (and therefore Bo(t) ≫ 1). From eqn (3) we obtain vRe = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−8 m s−1) with ΔPavg ∼ 50 Pa. The same order of magnitude for the thinning velocity has been obtained by Chatzigiannakis et al. with a pressure of 50 Pa imposed by their developed pressure-controlled dynamic thin-film balance.40 Here, Re = ρvRegδ/η = 10−10, and the gravity and viscous forces control the drainage dynamics in the positive dome and negative dome scenario. In this situation, a time-dependent Galilei (Ga(t)) number can be used to characterize the dynamics:
(10−8 m s−1) with ΔPavg ∼ 50 Pa. The same order of magnitude for the thinning velocity has been obtained by Chatzigiannakis et al. with a pressure of 50 Pa imposed by their developed pressure-controlled dynamic thin-film balance.40 Here, Re = ρvRegδ/η = 10−10, and the gravity and viscous forces control the drainage dynamics in the positive dome and negative dome scenario. In this situation, a time-dependent Galilei (Ga(t)) number can be used to characterize the dynamics: | (7) |
2.1 Stabilizing film thickness
With the aim of stabilizing the film thickness, we impose the volume history, V(t), composed of periodic inflating and deflating cycles. Such V(t) is herein defined by three parameters, that is, the maximum volume inflated (or pumped), Vmax,i, the maximum volume deflated (or withdrawed), Vmax,d, and the quarter-cycle time, tcyc. We choose the viscous-gravity regime to control the film thickness, and since we want to continuously and symmetrically reverse the viscous-gravity flow, we also have Vmax = Vmax,i = Vmax,d. In this way, the inflating (or pumping) velocity (vi) and the deflating (or withdrawing) velocity (vd) are equal, such that vi = vd = v = Vmax/tcyc. Having defined these parameters, the volume history to stabilize the film thickness is described as the case and piecewise-defined function: | (8) |
 | (9) |
 | (10) |
 ), and V*(t*) is the non-dimensional volume. The non-dimensional form of eqn (8) becomes:
), and V*(t*) is the non-dimensional volume. The non-dimensional form of eqn (8) becomes: | (11) |
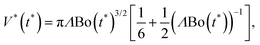 | (12) |
 . It is important to point out that for large bare bubbles, the bubble thickness is highly nonuniform due to viscous-gravity flows and the evaporation process,64 and we observe similar behavior for polymer/solvent bubbles in preliminary experiments (and as will be better observed and described for the positive and negative dome scenarios). This in principle can alter the dome shape, invalidating the hypothesis of the model and hence the stabilization procedure. However, since in our case the direction of the viscous-gravity flow is continuously reversed, the bubble maintains a dome shape with a relatively uniform thickness, allowing us to consider the effect of gravity on the dome shape (but not on the film average thickness) as negligible, since α(t) ≫ δ also holds in all experiments50 (excluding the flat-film scenario, in which, as discussed, gravity does not play a major role). Due to the continuous evaporation of the solvent over time, structuring occurs and the material becomes a viscoelastic solid (η → ∞). In this case, in the flat-film scenario, Caf → ∞, and in the inflated (or deflated) scenario, Ga(t) → 0. In particular, we expect the final and transient mechanical properties of the film, as well as material properties (e.g., crystallinity and molecular orientation) to depend on V(t). Therefore, to continuously monitor the film response and mechanical properties, we measure the pressure difference between the bubble and the outside, ΔP(t). To monitor the film thickness of the bubble and to check that the drainage is acting effectively as designed, we use digital holography (DH). To conclude, it should be pointed out that model parameters, such as viscosity and surface tension, as well as evaporation kinetics,65 are dependent on both temperature and humidity. All experiments conducted in this study are carried out under controlled conditions of temperature (22 ± 2 °C) and humidity (70 ± 10%). To predict the behavior of the free-standing film under fluctuating temperature and humidity, the dependencies of the model parameters and evaporation kinetics on these variables should be incorporated into the previous discussion, which we will address in future works.
. It is important to point out that for large bare bubbles, the bubble thickness is highly nonuniform due to viscous-gravity flows and the evaporation process,64 and we observe similar behavior for polymer/solvent bubbles in preliminary experiments (and as will be better observed and described for the positive and negative dome scenarios). This in principle can alter the dome shape, invalidating the hypothesis of the model and hence the stabilization procedure. However, since in our case the direction of the viscous-gravity flow is continuously reversed, the bubble maintains a dome shape with a relatively uniform thickness, allowing us to consider the effect of gravity on the dome shape (but not on the film average thickness) as negligible, since α(t) ≫ δ also holds in all experiments50 (excluding the flat-film scenario, in which, as discussed, gravity does not play a major role). Due to the continuous evaporation of the solvent over time, structuring occurs and the material becomes a viscoelastic solid (η → ∞). In this case, in the flat-film scenario, Caf → ∞, and in the inflated (or deflated) scenario, Ga(t) → 0. In particular, we expect the final and transient mechanical properties of the film, as well as material properties (e.g., crystallinity and molecular orientation) to depend on V(t). Therefore, to continuously monitor the film response and mechanical properties, we measure the pressure difference between the bubble and the outside, ΔP(t). To monitor the film thickness of the bubble and to check that the drainage is acting effectively as designed, we use digital holography (DH). To conclude, it should be pointed out that model parameters, such as viscosity and surface tension, as well as evaporation kinetics,65 are dependent on both temperature and humidity. All experiments conducted in this study are carried out under controlled conditions of temperature (22 ± 2 °C) and humidity (70 ± 10%). To predict the behavior of the free-standing film under fluctuating temperature and humidity, the dependencies of the model parameters and evaporation kinetics on these variables should be incorporated into the previous discussion, which we will address in future works.
3 Materials
3.1 PVA/water solution
Polyvinyl-alcohol (PVA, Mowiol® 8–88 Mw ∼ 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da, Sigma Aldrich) and demineralized water were used to prepare the test solution. PVA was added to demineralized water to obtain a 10 wt% (weight percentage) PVA/water solution, and it was stirred magnetically overnight at room temperature (monitored at 21 °C) to ensure the solubilization of PVA.
000 Da, Sigma Aldrich) and demineralized water were used to prepare the test solution. PVA was added to demineralized water to obtain a 10 wt% (weight percentage) PVA/water solution, and it was stirred magnetically overnight at room temperature (monitored at 21 °C) to ensure the solubilization of PVA.
3.2 CMC/water solution
The CMC/water solution 5% w/w was prepared by adding sodium salt of carboxymethylcellulose (Sigma Aldrich) to bi-distilled water at 40 °C. After 4 hours of magnetic stirring, the desired solution is produced. Then, air bubbles were removed from the solution by letting it cool to room temperature.663.3 Rod-like ZnO-NPs
Rod-like ZnO-NPs were synthesised by mixing 0.264 g of zinc acetate in 72 mL of ethanol and 1.68 mL of triethanolamine. The solution was vigorously stirred and 8 mL of distilled water was added. The system was then placed inside a stove in a Teflon mini-reactor for 2 hours at 120 °C. The ZnO-NPs suspension was centrifuged three times at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 rpm for 15 minutes each to wash ZnO-NPs from chemical residues of the synthesis. Finally, the system was dried at 80 °C overnight in an oven (in ESI,† Section S2 and Fig. S2, more details about the morphology of ZnO-NP are shown).
500 rpm for 15 minutes each to wash ZnO-NPs from chemical residues of the synthesis. Finally, the system was dried at 80 °C overnight in an oven (in ESI,† Section S2 and Fig. S2, more details about the morphology of ZnO-NP are shown).
3.4 CMC/water/ZnO-NPs solution
The rod-like ZnO-NPs were dispersed in the CMC/water solution using the Qsonica Q500 Sonicator® (4 cycles of 10 seconds sonication with 2 seconds pause), and a CMC/water/ZnO-NPs solution is produced. We also verified that the inclusion of ZnO-NPs in the CMC/water solution and sonication process have no effect on the morphology and optical properties of ZnO-NPs (see ESI,† Section S3 and Fig. S3, S4).4 Methods
4.1 Device setup
The experimental setup schematic is reported in Fig. 2(a)–(c). A fully programmable syringe pump (Model NE-1000, New Era Pump Systems) and a differential pressure transducer (Type 226A, 10 torr full scale, MKS Baratron) are connected to a 3D printed cylinder appropriately designed to allocate the sample holder and the connection tubes to the syringe pump and the pressure transducer. The syringe dimension of the syringe pump is selected according to required volume changes (see Section 2) and to pump specifications to minimize the error of the linear actuator (pump has a lag time switching from pumping and withdrawing and vice versa of the order of ∼0.2 s). Using the RS-232 protocol and the pump programming language, a MATLAB code that can synchronize the volume history imposed by the pump and the instant-by-instant pressure data acquisition is developed. In real time, the current signal of the pressure transducer is elaborated through a pressure reader (PR 4000, Mod. Single Channel, MKS Instruments) and directly red and plotted by the MATLAB code (Fig. 2(a)). As sample holder for the stabilization study we use a non-wettable Teflon ring 0.75 mm thick, with an inner diameter of 15 mm and an outer diameter of 16 mm (Fig. 2(b)). To ensure constant boundary conditions for the free-standing film, the inner surface of the Teflon ring is metallized with Au–Pd alloy (30 nm thick, with 208HR high resolution sputter coater, Cressington Scientific Instruments, Watford, England). Alternatively, for the structuring study and the study on the effect of ZnO-NPs, we use a Teflon cup of 15.45 mm external diameter and 9.5 mm internal diameter, shown in Fig. 2(c). Again, a 0.75 mm in height annular internal part is metallized with Au–Pd alloy (30 nm thick, with 208HR high resolution sputter coater, Cressington Scientific Instruments, Watford, England). The smaller inner diameter (9.5 mm) with respect to the Teflon ring is used to guarantee a fixed position of the free-standing film (that must be anchored to the gold metallization) even when moving to progressively higher Vmax, to obtain a different degree of stretching.4.2 Test procedure
The Teflon ring is pulled from a pool of the liquid solution under investigation, and a free-standing liquid film is produced. Then, the Teflon ring with the free-standing film is weighted by an analytical balance (MS Semi-Micro Model, Mettler Toledo, Milan, Italy) to determine the weight (and then the volume, knowing the density) of the solution. The mass of the liquid solution is 39 ± 12 mg.The Teflon ring with the free-standing film is then placed between two rubber gaskets to ensure sealing and then pressed into the cylinder, with a discharge valve opened to avoid pre-inflation of the bubble. The discharge valve is closed and the test begins by imposing the volume history described for the specific scenario reported below. The test ends when the film ruptures or, for the case of the periodic pumping, pressure attains a stationary condition (the film is solidified, resembling an elastic membrane). The free-standing solid films used as the reference for structuring are prepared by letting water evaporate from the free-standing liquid film, without any imposed volume history.
4.3 Inline characterization
To quantitatively evaluate the thickness evolution of bubbles during dynamic processes, off-axis holographic geometry is used to provide real-time recording. The system is based on an off-axis Mach–Zehnder interferometer and two sets of telescopic lens groups are used to adjust the imaging field of view (FoV).46 Herein, the conventional digital holographic film thickness mapping strategy is implemented, and a full life cycle thickness calibration is used to reveal the local thickness of bubbles.44 Considering that the local thickness of the bubbles varies on the micron scale, He–Ne laser (wavelength is 632.8 nm) is chosen to be the light source of recording system. The laser beam emitted by Thorlabs HNL100LB is first expanded by the beam expander (BE). Then a light beam lifter, which formed by two mirrors, is used to lift the expanded laser beam for achieving vertical irradiation for recording samples. After the beam is lifted, it is split into two beams via first beam splitter (BS). Here, the reflected beam is set as the holographic object beam, and transmitted beam is set as holographic reference beam. The object beam illuminates onto the bubble sample after being reflected by M2. Once object beam pass through the sample, it will carry the entire light field information of it. After this, the object beam is reflected by a mirror and enters the pair of telescopic lenses of the object arm. Lenses L1, L2 and L3 composed of two sets of telescopic systems with the same magnification, which is M = 1/3. Among them, L1 is set in object arm and L2 is set in reference arm. The focal length of L1 and L2 is 150 mm, L3 is 50 mm. BS2 is set in back focus plane of both L1 and L2, it used to combine object beam and reference beam. Here, the object beam is transmitted through BS2, while the reference beam is reflected by BS2. BS2 creates an off-axis angle α between them, allowing the generation of off-axis digital holograms. Finally, the object beam and reference beam pass through L3 and form interference fringes on the camera screen.Two different cameras were used depending on the volume history imposed, which are the high-speed CMOS camera with frame rate 100 FPS and pixel size 12 μm (model MC1310) and the CCD camera with frame rate 15 FPS and pixel size 4.54 μm (model XIMEA MD028MU-SY), depending on the experimental part. In flat film and periodic pumping, the thickness evolution of the film is expected to be relatively continuous, so the spatial sampling frequency requirement for the recording system is lower, but we need high time resolution, and high-speed CMOS with larger pixel size and higher sampling frequency is more suitable. However, for inflation or deflation experiments, it is expected that the formed films could have a big phase difference between the edge and the center, so it is necessary to use a CCD camera with the smaller pixel size to increase the spatial resolution. For extracting film thickness information using DH, the phase information of the local film thickness can be obtained. The phase information is based on the optical path difference between the object beam and the reference beam, which is related to the thickness of the film multiplied by its refractive index (RI). Thus, once we reconstruct the phase ψ from digital hologram, the local thickness h of the film can be calculated by formula:
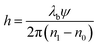 | (13) |
4.4 Offline characterization
Attenuated total reflectance/Fourier-transform infrared (ATR/FTIR) spectra of CMC and CMC/ZnO-NPs films were recorded in 4000–400 cm−1 with 32 repetitions scans averaged for each spectrum using a Nicolet instrument, Nexus model. Resolution was 4 cm−1 and interval scanning was 2 cm−1.5 Results
The section results is divided in two subsections. Film dynamics manipulation reports the effect of different volume histories on the thickness map evolution of the free-standing liquid film. This section presents results related to the geometrical effect of the volume histories on the manipulated free-standing liquid films. Material structuring reports the effect of different volume histories on the material properties (e.g., crystallinity, orientation) of the solid viscoelastic membrane obtained after different manipulation histories.5.1 Film dynamics manipulation
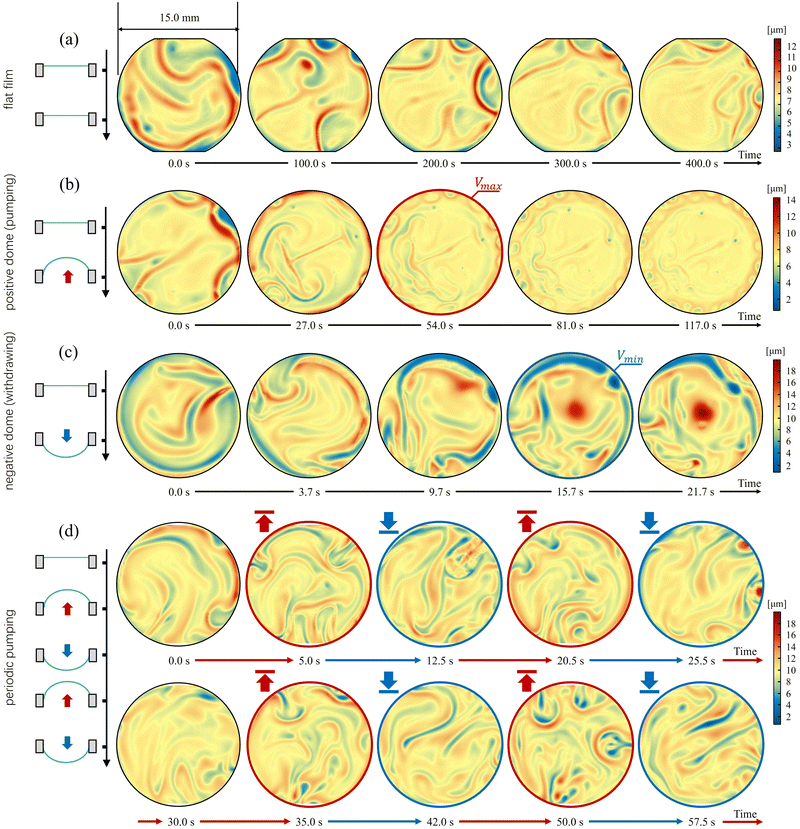
In this section, by manipulating flow regimes, we investigate the effect of the volume history on the thickness map evolution of the thin film. To do so, four different scenarios are considered: (i) flat film, in which the film is unperturbed in time (i.e., V(t) = VF(t), as detailed below); (ii) positive dome (V(t) = VP(t)); (iii) negative dome (V(t) = VN(t)) and (iv) periodic (V(t) = Vn(t), as in eqn (8)). A first qualitative analysis by means of selected thickness map images will be drawn for the different scenarios, followed by a detailed quantitative spatio-temporal analysis showing thickness evolution. Reported images are relative to a specific experiment, while three replicates are performed for each scenario.In Fig. 3(a), the results of the flat film (i) thickness map over time are shown (VF(t) = 0, with t ∈ [0,∞[). In this case, the film maintains over 400 s until rupture occurs. Images reveal the non-uniformity of the thickness, expected in view of the underlying literature about similar systems and driven by asymmetries and the occurrence of Marangoni flows. Due to leveling, thickness non-uniformities appear to rapidly change with time in the first 100 s of the experiment, while their fade and rearrangement kinetics slow down in time due to solvent evaporation.67
Fig. 3(b) shows the thickness map evolution of the liquid film in the positive dome scenario, with
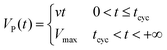 | (14) |
As can be seen from images corresponding to 54.0 s to 117.0 s, Marangoni flow appears around the edge of the film; meanwhile, edge thickening can be found due to the viscous-gravity driven drainage from the center of the bubble.
Fig. 3(c) shows the thickness map evolution of the liquid film in the negative dome scenario, with
 | (15) |
Fig. 3(d) shows the thickness map evolution of the liquid film in the periodic scenario illustrated in Fig. 1(c). As the film moves between positive and negative dome shapes, its thickness mapping exhibits periodic changes, as it is expected due to the reverse direction of the viscous-gravity drainage. In the periodic scenario, rupture was not observed until solidification of the film by water evaporation, after approximately 1 hour.
Although the full-field thickness distribution can effectively explain the film state in a qualitative way, it lacks quantitative information of the dynamic evolution process. For this reason, an analysis method based on a reassembly of spatio-temporal thickness information is used to reveal the changing process of film thickness under different scenarios. An obvious cylindrical coordinate system allows us to describe the thickness map evolution by using plots in which the angle-averaged thickness is reported as a function of the radial coordinate and time (for a more detailed description of the adopted spatio-temporal procedure, see ESI,† Section S4).
The results are shown in Fig. 4(a)–(l). Fig. 4(a) shows the spatio-temporal data analysis for the flat film scenario. The leveling process and the subsequent drainage process can be clearly observed. The entire process of the evolution of the film thickness lasts 449 s until rupture occurs. The corrugated structure in the reassembled space-time coordinate system indicates the occurrence and movement of leveling flows and drainage flows. The vertical symmetrization phenomenon is known to occur on a universal timescale τv = ηδ/γ.67 When the experiment starts, η = 0.1 Pa s and τv = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10−3 s). It means that in-plane drainage governs the film dynamics,67 at least in the first part of the experiment. Then, as a result of evaporation of the solvent, τv increases and becomes comparable to the experimental timescale.
(10−3 s). It means that in-plane drainage governs the film dynamics,67 at least in the first part of the experiment. Then, as a result of evaporation of the solvent, τv increases and becomes comparable to the experimental timescale.
Fig. 4(b) shows the spatio-temporal data analysis for the positive dome scenario. In the early stage of film pumping, it can be observed that the liquid flows rapidly from the center to the edge. Once the positive bubble film is formed (i.e., when Vmax is reached), liquid accumulation occurs at the edges of the film, and its thickness is significantly higher than that close to center. Interestingly, it can be found that under the action of Marangoni flows, in the high film thickness area at the edge an high thickness wave appears, which moves from the edge to the center of film (see the thickness changes from 81 s to 135 s). This proves that the space-time model coupled with the developed device can effectively reveal the dynamic process of the film.
Fig. 4(c) shows the spatio-temporal data analysis for the negative dome scenario. The negative pressure accelerates the rupture of the film, so the entire thickness evolution process only lasts 23.3 s. For the short period before the film rupture, there is a large liquid accumulation in the center of film, which could be the main reason for quick film rupture.
Fig. 4(d) shows the spatio-temporal data analysis for the periodic pumping scenario, and hence, it shows the results of the application of the periodic volume history described in Section 2. This type of the periodic pumped film has the longest lifetime compared with other three scenario; in particular, the film does not fracture, and it is a good candidate for the free-standing film structuring. Here, we show the thickness evolution for 97.5 s in the space-time coordinate system.
The overall thickness of film remains constant; only in the center area there are periodic thickness changes, and these thickness peaks present the times when the film is in the negative structure, according with the imposed pumping/withdrawing frequency. This time-dependent scenario is obviously different from the previous three. Although there are some small local thickness fluctuations, the overall thickness distribution remains stable in time.
To further demonstrate that the periodic pumping process allows for the formation of a stable liquid film (and, as we will see later, a structured membrane), the thickness information (before the film rupture in the case of positive, negative and flat film scenarios) is further analyzed.
Fig. 4(e)–(g) show the average thickness distribution curves for the selected period before film rupture. As shown in the box of Fig. 4(a)–(c), we take the time average of the data for one fifth total holding time. The thickness profile obtained by quadratic averaging over time will show the overall thickness trend. In the case of positive film and negative film, thicker areas appear at the edges and center respectively, as shown in Fig. 4(f) and (g), these are consistent with the observed results from models. Meanwhile, the flat film results in Fig. 4(f) show that the thickness of the film under gravity drainage slowly decreases outward in the radial direction; the slight rise near the edge is thought to be caused by Marangoni flow.
For the periodic pumping scenario, since film rupture is not observed during the pumping time, we chose to display the film thickness distribution in two periods: the up cycle and down cycle (Fig. 4(h)) with solid and dotted lines, respectively. Interestingly, in the result of the up cycle, a non-uniform distribution of film thickness is observed; in the down cycle, a liquid accumulation occurs. Except for changes near the center of the film, the overall thickness of the film remains within a stable range, which is 8.4 ± 0.6 μm. This set of results further proves that wave pumping can effectively create a stable liquid film.
Fig. 4(i)–(l) show the curves of the average thickness of the waist region of the film that change with time. In Fig. 4(a)–(d), the shadow areas inside the coordinate system mark the region where the calculation is performed; for all four models, the area within the radius from 1.8 mm to 7.2 mm is used for the calculation. In Fig. 4(j), once the film is formed in the positive dome configuration, the thickness will rise slowly at first, then quickly fall and then rise slowly again. The early slow thickness increase corresponds to the accumulation of liquid on the Teflon ring; the second increase due to Marangoni flow. In the flat film scenario, the average thickness of the waist of the film will gradually decrease with time, as shown in Fig. 4(i). The curve in Fig. 4(k) is related to the negative dome configuration. The average waist thickness increases rapidly as film is formed. Again, the most interesting curve is the thickness curve of the periodic pumping (Fig. 4(l)). During the complete recording time, the waist thickness does not change significantly and remained stable at 8.5 ± 0.2 μm. The results show that periodic pumping can effectively form a stable liquid film and greatly increase the retention time. Moreover, this is true even if the initial film volume is increased: by increasing the solution dosage to 60 ± 15 mg for film fabrication, we show that the periodic-pumped films exhibit excellent stability over the overall film thickness.
In Fig. 5(a)–(e), we show the experimental results and data analysis of two experiments, E1 and E2. They are performed under the same conditions as before, except for the larger volume of the solution. Fig. 5(a) and (b) show the thickness mapping of selected time points of experiments E1 and E2, respectively. Due to the increase in the solution used to form the films, the film thickness mappings exhibit more complex patterns, indicating the relationship between the film thickness and the capillary number.14 For two experimental datasets, the same spatio-temporal analysis is performed (the results are shown in Fig. 5(c) and (d)). It is worth to note that, when the film is in the negative bubble dome scenario, the thickness at the center exceeds the limit of holographic phase unwrapping,68,69 and the thickness increase cannot be accurately reconstructed in the radius 0 to 1.8 mm area (as expected, this problem exists in both experiments). However, for the other areas, DH successfully achieves thickness retrieval: it can be seen from the comparison of models that the thickness distribution in the waist area maintains a stable state during the periodic process. Fig. 5(e) shows the thickness distribution curves over time. It can be seen that the film thickness stabilized at the same level for both experiments. For experiment 1 (E1, blue curve), in which we used 39 ± 12 mg solution to form the film, the stable waist thickness is 10.1 ± 0.2 μm and its floating range is ∼1.5%; for experiment 2 (E2, red curve), in which we used 60 ± 15 mg solution to form the film, the stable waist thickness is 10.1 ± 0.1 μm and its floating range is ∼2.3%.
5.2 Material structuring
The observed thickness stabilization encouraged us to exploit the setup to form novel solid (viscoelastic) membranes. At the micro-scale scale, it is expected that periodic pumping can change crystallinity and other order parameters. In the present section, we investigate the effect of the periodic pumping on the constitutive material rather than on the geometry of the film, both at the macro-scale (continuum mechanical response) and at the micro-scale (crystallinity and order parameters). First (early cycles: model for the surface tension measurement), we derive a simple expression to link the time-dependent volume with the time-dependent pressure, that can be useful to predict the mechanical response of the liquid film at early cycles or to measure the surface tension, if not available. Then (late cycles: pressure build-up and structuring), we show the progressive increase of maximum pressure as a function of time for a periodic pumping experiment, that is the reflection of the evaporation process and, as shown later, of the structuring of the material. Indeed, we will show the differences at the micro-scale between the unstructured film (i.e., flat film scenario) and structured film. | (16) |
| α(t)3 + cα(t) + q(t) = 0, | (17) |
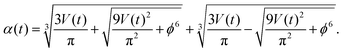 | (18) |
 | (19) |
 | (20) |
 , since λ is not the characteristic length scale in this problem. Hence, we can obtain the non-dimensional form of eqn (19) (see ESI† for calculations):
, since λ is not the characteristic length scale in this problem. Hence, we can obtain the non-dimensional form of eqn (19) (see ESI† for calculations):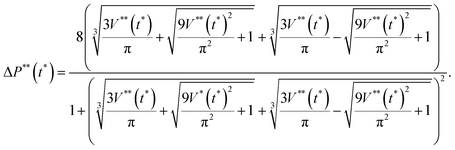 | (21) |
 | ||
| Fig. 6 Fitting of the experimental data with eqn (19). The top-left inset table reports the fitting result, along with the related statistical parameters. The bottom-right inset plot reports the first three cycles of the imposed volume history (with the parameters as obtained in Section 2.1), where the yellow filled region highlights the portion of volume history we have considered for the fitting procedure. | ||
One of the advantages of periodic pumping volume history is that it is possible to keep track of variations in mechanical properties, because it is a dynamic scenario that cycle-by-cycle probes the bending stiffness (due to the out-of-plane deformations) of the membrane.
In the literature, experiments on inflated membranes are considered a very useful tool for characterization of the behaviour of the material.72 It is also worth noting that an exact closed-form solution to the inflation problem of circular membranes (as in our case) does not exist even for the simplest case of a linearly elastic material,73 and solving the problem numerically for a material with time-dependent properties is beyond the scope of this work.
However, we can infer that the higher the measured maximum pressure (the force to inflate the membrane), the higher the bending stiffness of the membrane. Due to solvent evaporation, the elastic contribution starts to prevail on the viscous contribution.
Fig. 7(a) shows the pressure variation as a function of time in a periodic pumping experiment, where the pressure history designed in Section 2 is imposed.
All experiments show the same trend, where red dots are computed as local maximums of the measured pressure. As expected, the pressure increases monotonically, reflecting the solvent evaporation. After roughly 3000 s, local maximums also appear around a zero pressure: these are effects due to the wrinkles of the viscoelastic membrane. When wrinkles are produced, during pumping we have two stages. First, as air is pumped, the wrinkles have to be “stretched” in order to produce a viscoelastic membrane with an almost dome shape. This is a geometrical assessment and is very compliant, so the measured pressure is almost constant in time during this stage. Second, after a spherical dome is produced, the only way to increase the volume of the bubble is to biaxially stretch the membrane, a less compliant mechanism that creates large strain in the material and governs the pressure increase. The appearance of wrinkles does not mean that the evaporation is complete but means that the solvent evaporated at least in the central part of the film. However, after approximately 5000 s, an almost stable pressure is reached, and experiments were stopped. We think that the slight increase could be due to the progressive alignment of the polymer chains in the solid membrane and a very slow kinetics of solvent evaporation.
The pattern of the solid viscoelastic membrane obtained by letting the solvent evaporate (flat film scenario) and by periodic pumping are shown in Fig. 7(b). It can be seen that, with respect to the film obtained without pumping, the membrane obtained by periodic pumping shows a clear radial pattern in thickness. It is reasonable to suppose that the wavelength of the pattern will be a function of the imposed pressure history, and this will be the subject of further developments.
To check for effects of periodic pumping on the material structuring at the micro-scale, we use as sample material a 5% CMC/water solution and the Teflon cup as sample holder (Fig. 2(c)). ATR/FT-IR spectra of pure CMC films obtained by different volume histories are shown in Fig. 8(a). More precisely, (i) the sample CMC neat has been obtained by water evaporation in a flat film scenario, (ii) the sample CMC 0.25 has been obtained in the periodic pumping scenario (as schematically depicted in Fig. 1(c)) with v = 110 μL s−1 and Vmax = 250 μL and (iii) the sample CMC 0.5 has been obtained in the periodic pumping scenario with v = 110 μL s−1 and Vmax = 500 μL. The characteristic feature bands of CMC samples are shown in the spectra. The wide 3402 cm−1 band corresponds to O–H stretching vibration74 and the 2919 cm−1 band is assigned to C–H asymmetrical stretching vibration of CH2. The 1585 cm−1 peak matches the carboxyl group (COO) asymmetric stretching while the 1412 cm−1 peak corresponds to CH2 scissoring vibration. Furthermore, the OH bending motion is confirmed by the 1322 cm−1 peak, whereas C–O stretching motion is verified by the 1052 cm−1 peak. Finally, the 906 cm−1 is attributed to CH2 rocking motion.66
Cellulose-like materials structure and degree of intermolecular regularity can be investigated using the empirical hydrogen bond intensity (HBI) index and the total crystallinity index (TCI). The former is defined as the ratio of peak 3336 cm−1 to 1336 cm−1 intensity,75 respectively the OH group stretching vibration peak and the OH group bending motion peak. HBI index is related to the degree of intermolecular regularity and the amount of bound water.76 The total crystallinity index (TCI, first introduced by Nelson and O'Connor as the ratio of absorption bands at 1372 cm−1 and 2900 cm−1 (ref. 77)) is an empirical parameter used to assess crystallinity in cellulosic materials. TCI and HBI have opposite behaviours: when the former exhibits maxima, the latter shows minima.78Table 1 shows the HBI and TCI values of CMC films obtained by different volume histories. The comparison of data from Table 1 shows that samples subjected to higher stress from periodic pumping manipulation have a higher crystallinity compared to the non-manipulated CMC film.78 This may occur because the stresses induced by the inflation and deflation treatments can orient CMC chains, facilitating the formation of crystals. To check for effects on nanoparticle rearrangements, we added to the CMC/water solution rod-like ZnO-NPs (produced as described in Section 3.3). The rod-like morphology of ZnO-NPs is suitable for investigating the effect of different flow regimes, since anisotropic nanoparticles can align in flow due to shear forces.79,80 HBI and TCI were calculated for the CMC/ZnO-NPs films to check for the effect of the periodic pumping on the ZnO-NPs dispersion (Table 2). Here, (i) as before, the sample CMC neat has been obtained by solvent evaporation in a flat film scenario, (ii) the sample CMC/ZnO-NPs neat has been obtained by solvent evaporation in a flat film scenario, and (iii) the sample CMC/ZnO-NPs 0.25 has been obtained in the periodic pumping scenario with v = 110 μL s−1 and Vmax = 250 μL.
| Sample | HBI | TCI |
|---|---|---|
| CMC neat | 1.50 | 0.90 |
| CMC 0.25 | 1.29 | 1.37 |
| CMC 0.5 | 1.15 | 1.42 |
| Sample | HBI | TCI |
|---|---|---|
| CMC neat | 1.50 | 0.90 |
| CMC/ZnO-NPs neat | 1.31 | 0.98 |
| CMC/ZnO-NPs 0.25 | 1.09 | 1.53 |
It can be seen that HBI decreases after the dispersion of ZnO-NPs within the film, even without any kind of manipulation (CMC/ZnO-NPs neat in Table 2). A possible interpretation of the results is that ZnO-NPs interacted with the hydroxyl groups, leading to a lower HBI for CMC/ZnO-NPs films compared to those from pure CMC films.76 Interestingly, TCI is increased (and HBI is decreased) in the periodic pumping manipulated film CMC/ZnO-NPs film, and it is higher than the film manipulated in the same way (second row of Table 1) but without ZnO-NPs. Therefore, it seems that ZnO-NPs improve molecular order in the sample, and this can be due to the creation of ZnO-NPs arrangements (see also ESI,† Section S6). In particular, it can be seen from Fig. 8(b) that ZnO-NPs form clusters (white dots in the SEM image) in the CMC viscoelastic membrane. If the CMC viscoelastic membrane is produced from a periodic pumping scenario, ZnO-NPs form linearly shaped clusters according to the flow fronts. Such clusters are then frozen due to viscosity increase after solvent evaporation. In fact, it is known that the viscosity of the solution (that in our case is time-dependent due to solvent evaporation) is a key factor in particle rearrangement.79 In future studies, fluorescent particles will be used, which will allow us to track them and hence providing the opportunity to analyze the dynamics of their rearrangement.
6 Conclusions
Inspired by the possibility of studying free-standing liquid film dynamics and guided by the idea of using the results to produce new materials, structures and particles rearrangements, we have designed a device that manipulates a free-standing liquid film, capable of working and transiting in two different regimes (the viscous-capillary regime and the viscous-gravity) by manipulating its shape. We have then demonstrated that the device, by the periodic inflation/deflation of a the free-standing film, can effectively achieve a radial thickness map stabilization of a liquid thin free-standing film, both in space and time. Finally, we have proved that different macromolecular rearrangements and crystallinity degrees can be obtained when the film is subjected to inflation/deflation cycles with respect to the flat-film scenario, and that the film manipulation has an effect on nanoparticles eventually dispersed in the solution. In further developments, the volume history may be designed to achieve a controlled degree of crystallization and a desired non-uniform radial thickness profile. A further design variable can be the evaporation kinetics, that can be controlled by modifying the setup and controlling temperature and humidity.Author contributions
P. I. – conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing (original draft), visualization. Z. W. – methodology, software, formal analysis, investigation, data curation, writing (original draft), visualization. A. M. – methodology, validation, formal analysis, investigation, data curation, writing (original draft), visualization. S. R. – investigation, formal analysis. V. F. – methodology, investigation. G. V. – methodology, resources, writing (original draft & review and editing), visualization, supervision. S. C. – methodology, supervision. E. D. M. – conceptualization, methodology, resources, writing (original draft & review and editing), visualization, supervision, project administration, funding acquisition.Data availability
The data that support the findings of this study are openly available on figshare, DOI: https://doi.org/10.6084/m9.figshare.26509957.Conflicts of interest
There are no conflicts to declare.References
- C. Bohley and R. Stannarius, Soft Matter, 2008, 4, 683–702 RSC.
- J.-Z. Wang, S.-L. Chou, H. Liu, G. X. Wang, C. Zhong, S. Y. Chew and H. K. Liu, Mater. Lett., 2009, 63, 2352–2354 CrossRef CAS.
- Y. Jiang, M. Zhang, X. Duan, H. Zhang and W. Pang, Appl. Phys. Lett., 2017, 111, 023505 CrossRef.
- T. Pitchford, C. Huang, R. Pindak and J. Goodby, Phys. Rev. Lett., 1986, 57, 1239 CrossRef CAS PubMed.
- T.-Y. Teng, J. Appl. Crystallogr., 1990, 23, 387–391 CrossRef CAS.
- V. Krishnan, K. Sakakibara, T. Mori, J. P. Hill and K. Ariga, Curr. Opin. Colloid Interface Sci., 2011, 16, 459–469 CrossRef CAS.
- J. Nie, Z. Wang, Z. Ren, S. Li, X. Chen and Z. Lin Wang, Nat. Commun., 2019, 10, 1–10 CrossRef CAS.
- C.-P. Chiu, T.-J. Chiang, J.-K. Chen, F.-C. Chang, F.-H. Ko, C.-W. Chu, S.-W. Kuo and S.-K. Fan, J. Adhes. Sci. Technol., 2012, 26, 1773–1788 CrossRef CAS.
- C. Qiao, D. Yang, X. Mao, L. Xie, L. Gong, X. Peng, Q. Peng, T. Wang, H. Zhang and H. Zeng, Appl. Phys. Rev., 2021, 8(1), 011315 CAS.
- M. F. Schatz and G. P. Neitzel, Annu. Rev. Fluid Mech., 2001, 33, 93–127 CrossRef.
- A. Mohammadtabar, H. Nazaripoor, A. Riad, A. Hemmati and M. Sadrzadeh, Phys. Fluids, 2020, 32, 024106 CrossRef CAS.
- R. P. White and J. E. Lipson, Soft Matter, 2021, 17, 9755–9764 RSC.
- A. Oron, S. H. Davis and S. G. Bankoff, Rev. Mod. Phys., 1997, 69, 931–980 CrossRef CAS.
- E. Chatzigiannakis, N. Jaensson and J. Vermant, Curr. Opin. Colloid Interface Sci., 2021, 53, 101441 CrossRef CAS.
- E. Chatzigiannakis, Y. Chen, R. Bachnak, C. S. Dutcher and J. Vermant, Rheol. Acta, 2022, 61, 745–759 CrossRef CAS.
- J. Coons, P. Halley, S. McGlashan and T. Tran-Cong, Adv. Colloid Interface Sci., 2003, 105, 3–62 CrossRef CAS.
- B. B. Stogin, L. Gockowski, H. Feldstein, H. Claure, J. Wang and T.-S. Wong, Sci. Adv., 2018, 4, eaat3276 CrossRef CAS PubMed.
- W. Drenckhan and S. Hutzler, Adv. Colloid Interface Sci., 2015, 224, 1–16 CrossRef CAS PubMed.
- A. Mikhailovskaya, E. Chatzigiannakis, D. Renggli, J. Vermant and C. Monteux, Langmuir, 2022, 38, 10768–10780 CrossRef CAS PubMed.
- E. Rio and A.-L. Biance, ChemPhysChem, 2014, 15, 3692–3707 CrossRef CAS.
- E. Chatzigiannakis, J. Yang, L. Sagis and C. V. Nikiforidis, available at SSRN 4928284.
- P. Chakraborty, T. Tran and G. Gioia, J. Elasticity, 2011, 104, 105–114 CrossRef.
- C. Cheung, Y. Hwang, X. Wu and H. Choi, Phys. Rev. Lett., 1996, 76, 2531 CrossRef CAS PubMed.
- R. Mears, I. Muntz and J. H. Thijssen, Soft Matter, 2020, 16, 9347–9356 RSC.
- P. A. Kralchevsky, N. D. Denkov and K. D. Danov, Langmuir, 2001, 17, 7694–7705 CrossRef CAS.
- A. Yadav and M. S. Tirumkudulu, Soft Matter, 2017, 13, 4520–4525 RSC.
- A. Yadav, E. J. Hinch and M. S. Tirumkudulu, Phys. Rev. Lett., 2019, 122, 098001 CrossRef CAS PubMed.
- J. Lalieu, A. Seguin and G. Gauthier, Soft Matter, 2023, 19, 6838–6843 RSC.
- M. A. Gharbi, D. A. Beller, N. Sharifi-Mood, R. Gupta, R. D. Kamien, S. Yang and K. J. Stebe, Langmuir, 2018, 34, 2006–2013 CrossRef CAS PubMed.
- X. Lin, G. Fang, Y. Liu, Y. He, L. Wang and B. Dong, J. Phys. Chem. Lett., 2020, 11, 3573–3581 CrossRef CAS PubMed.
- D. Liu, C. Li, F. Zhou, T. Zhang, G. Liu, W. Cai and Y. Li, Adv. Mater. Interfaces, 2017, 4, 1600976 CrossRef.
- Z.-Z. Gu, D. Wang and H. Möhwald, Soft Matter, 2007, 3, 68–70 RSC.
- A. Sheludko, Adv. Colloid Interface Sci., 1967, 1, 391–464 CrossRef CAS.
- Y. Zhang and V. Sharma, Soft Matter, 2015, 11, 4408–4417 RSC.
- M. Chen, S. Feijen, G. Sala, M. Meinders, H. van Valenberg, A. van Hooijdonk and E. van der Linden, Food Hydrocolloids, 2018, 74, 342–348 CrossRef CAS.
- X. Zhu, D. Wang and V. S. Craig, Langmuir, 2019, 35, 7641–7649 CrossRef CAS PubMed.
- K. J. Mysels and M. N. Jones, Discuss. Faraday Soc., 1966, 42, 42–50 RSC.
- V. Bergeron and C. Radke, Langmuir, 1992, 8, 3020–3026 CrossRef CAS.
- D. Exerowa, D. Kashchiev and D. Platikanov, Adv. Colloid Interface Sci., 1992, 40, 201–256 CrossRef CAS PubMed.
- E. Chatzigiannakis, P. Veenstra, D. Ten Bosch and J. Vermant, Soft Matter, 2020, 16, 9410–9422 RSC.
- E. Chatzigiannakis and J. Vermant, Soft Matter, 2021, 17, 4790–4803 RSC.
- V. Ferraro, M. M. Villone, V. Tkachenko, L. Miccio, L. Lombardi, D. Tammaro, E. Di Maio, G. D'Avino and P. L. Maffettone, J. Colloid Interface Sci., 2021, 596, 493–499 CrossRef CAS PubMed.
- V. Ferraro, Z. Wang, S. Coppola, E. Di Maio and P. L. Maffettone, Colloids Surf., A, 2024, 694, 134067 CrossRef CAS.
- Z. Wang, L. Miccio, S. Coppola, V. Bianco, P. Memmolo, V. Tkachenko, V. Ferraro, E. Di Maio, P. L. Maffettone and P. Ferraro, Light: Adv. Manuf., 2022, 3, 151–176 Search PubMed.
- D. R. Guildenbecher, L. Engvall, J. Gao, T. W. Grasser, P. L. Reu and J. Chen, Exp. Fluids, 2014, 55, 1–9 CrossRef CAS.
- B. Mandracchia, Z. Wang, V. Ferraro, M. M. Villone, E. Di Maio, P. L. Maffettone and P. Ferraro, Light: Sci. Appl., 2019, 8, 20 CrossRef.
- S. Lakshman, W. Tewes, K. Harth, J. H. Snoeijer and D. Lohse, J. Fluid Mech., 2021, 920, A3 CrossRef CAS.
- W. S. Wong, A. Naga, L. Hauer, P. Baumli, H. Bauer, K. I. Hegner, M. DAcunzi, A. Kaltbeitzel, H.-J. Butt and D. Vollmer, Nat. Commun., 2021, 12, 5358 CrossRef CAS PubMed.
- C. Nguyen, H. Gonnermann, Y. Chen, C. Huber, A. Maiorano, A. Gouldstone and J. Dufek, Geochem., Geophys., Geosyst., 2013, 14, 3616–3631 CrossRef.
- H. Kočárková, F. Rouyer and F. Pigeonneau, Phys. Fluids, 2013, 25(2), 022105 CrossRef.
- I. B. Ivanov, Pure Appl. Chem., 1980, 52, 1241–1262 CAS.
- D. Y. Chan, E. Klaseboer and R. Manica, Soft Matter, 2011, 7, 2235–2264 RSC.
- B. Liu, R. Manica, Z. Xu and Q. Liu, Curr. Opin. Colloid Interface Sci., 2020, 50, 101374 CrossRef CAS.
- R. Song, L. Zhang, Z. Yi, Y. Zhou, H. Yuan and L. Han, AIChE J., 2023, 69, e18044 CrossRef CAS.
- S. I. Karakashev, D. S. Ivanova, Z. K. Angarska, E. D. Manev, R. Tsekov, B. Radoev, R. Slavchov and A. V. Nguyen, Colloids Surf., A, 2010, 365, 122–136 CrossRef CAS.
- S. I. Karakashev and E. D. Manev, Adv. Colloid Interface Sci., 2015, 222, 398–412 CrossRef CAS.
- J. Lyklema and T. Van Vliet, Faraday Discuss. Chem. Soc., 1978, 65, 25–32 RSC.
- D. Y. Chan, E. Klaseboer and R. Manica, Soft Matter, 2009, 5, 2858–2861 RSC.
- B. P. Radoev, A. D. Scheludko and E. D. Manev, J. Colloid Interface Sci., 1983, 95, 254–265 CrossRef CAS.
- G. O. Yahya, S. A. Ali and E. Z. Hamad, Polymer, 1996, 37, 1183–1188 CrossRef CAS.
- A. Bhattacharya and P. Ray, J. Appl. Polym. Sci., 2004, 93, 122–130 CrossRef CAS.
- L. Jia and X.-H. Qin, J. Therm. Anal. Calorim., 2013, 112, 595–605 CrossRef CAS.
- G. d Debrégeas, P.-G. De Gennes and F. Brochard-Wyart, Science, 1998, 279, 1704–1707 CrossRef PubMed.
- C. Bartlett, A. T. Oratis, M. Santin and J. C. Bird, Nat. Commun., 2023, 14, 877 CrossRef CAS.
- J.-B. Salmon, F. Doumenc and B. Guerrier, Phys. Rev. E, 2017, 96, 032612 CrossRef.
- R. Badry, M. M. El-Nahass, N. Nada, H. Elhaes and M. A. Ibrahim, Sci. Rep., 2023, 13, 1123 CrossRef CAS.
- V. Bertin, J. Niven, H. A. Stone, T. Salez, E. Raphael and K. Dalnoki-Veress, Phys. Rev. Lett., 2020, 124, 184502 CrossRef CAS PubMed.
- D. Parshall and M. K. Kim, Appl. Opt., 2006, 45, 451–459 CrossRef PubMed.
- G. Pedrini, I. Alexeenko, W. Osten and H. J. Tiziani, Appl. Opt., 2003, 42, 5846–5854 CrossRef PubMed.
- F. Behroozi and P. Behroozi, Am. J. Phys., 2011, 79, 1089–1093 CrossRef CAS.
- J. Zhou, X. Man, Y. Jiang and M. Doi, Adv. Mater., 2017, 29, 1703769 CrossRef PubMed.
- Y. Li, J. A. Nemes and A. Derdouri, Polym. Eng. Sci., 2001, 41, 1399–1412 CrossRef CAS.
- M. Pelliciari, S. Sirotti, A. Aloisio and A. M. Tarantino, Int. J. Mech. Sci., 2022, 226, 107383 CrossRef.
- M. Morsi, A. Oraby, A. Elshahawy and R. Abd El-Hady, J. Mater. Res. Technol., 2019, 8, 5996–6010 CrossRef CAS.
- A.-A. M. Nada, S. Kamel and M. El-Sakhawy, Polym. Degrad. Stab., 2000, 70, 347–355 CrossRef CAS.
- A. Kljun, T. A. Benians, F. Goubet, F. Meulewaeter, J. P. Knox and R. S. Blackburn, Biomacromolecules, 2011, 12, 4121–4126 CrossRef CAS PubMed.
- M. L. Nelson and R. T. O'Connor, J. Appl. Polym. Sci., 1964, 8, 1311–1324 CrossRef CAS.
- J. Široky, R. S. Blackburn, T. Bechtold, J. Taylor and P. White, Cellulose, 2010, 17, 103–115 CrossRef.
- M. Alizadehgiashi, A. Khabibullin, Y. Li, E. Prince, M. Abolhasani and E. Kumacheva, Langmuir, 2018, 34, 322–330 CrossRef CAS PubMed.
- A. A. Moud and A. A. Moud, Int. J. Biol. Macromol., 2023, 232, 123391 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00951g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |